sebagai, dan dua buah variabel dan dapat digunakan untuk memparameterisasi sebuah permukaan sebagai

4

2.1

Definisi Manifold [13]

Manifold adalah generalisasi dari ide-ide yang familiar tentang kurva dan permukaan pada ruang Euclidean. Sebuah kurva pada ruang Euclidean berdimensi tiga dapat diparameterisasi oleh suatu variabel tunggal, sebut saja sebagai , dan dua buah variabel dan dapat digunakan untuk

memparameterisasi sebuah permukaan sebagai . Sebuah

kurva dan permukaan dapat dianggap homeomorphic pada dan secara berurutan. Sebuah manifold, pada umumnya, homeomorphic pada secara lokal, tetapi bisa saja homeomorphic pada secara global. Apabila sebuah manifold homeomorphic secara lokal pada , kita dapat memberikan sebuah kumpulan bilangan pada setiap titik pada manifold sebagai koordinat lokal. Jadi bisa saja setiap titik pada manifold tersebut dapat memiliki dua koordinat atau lebih. Yang terpenting adalah transformasi antar koordinat harus smooth. Jadi sebenarnya hal yang paling esensial di dalam teori manifold adalah smoothness. Misalkan terdapat bola dengan jari-jari satuan pada ruang . Permukaan ini dapat diparametersisasi dengan beberapa kemungkinan koordinat, misalkan dengan sistem koordinat polar dan koordinat stereografik. Parameter pada koordinat polar dan didefinisikan oleh

dimana berjalan dari sampai dan berjalan dari sampai . Mereka dapat juga dicari dengan persamaan

(2.1.2)

Gambar 1. Koordinat polar dan koordinat stereografik dari titik pada lingkaran [13].

Koordinat stereografik adalah proyeksi dari Kutub Utara pada bidang ekuatorial seperti ditunjukkan pada gambar 1. Pertama-tama tarik garis dari Kutub Utara menuju titik pada lingkaran dan teruskan garis itu

menuju ke bidang ekuatorial . Garis itu akan berpotongan dengan bidang ekuatorial pada titik . dan inilah yang disebut sebagai koordinat titik dalam sistem koordinat stereografik. Melalui persamaan garis akan kita dapatkan koordinat stereografik sebagai berikut

(2.1.3) sedangkan hubungan antara koordinat polar dan koordinat stereografik adalah

(2.1.4) Tentu saja koordinat polar dengan sumbu polar yang berbeda ataupun proyeksi dari titik yang berbeda pada boleh digunakan. Pada teori tentang manifold satu hal yang paling mendasar adalah bahwa semua sistem koordinat sama. Hal ini tentu saja juga sesuai dengan prinsip dasar pada fisika yaitu sebuah sistem fisis memiliki kelakuan yang sama pada setiap koordinat yang digunakan untuk mengukurnya.

Hal lain yang bisa kita dapatkan dari contoh di atas adalah bahwa tidak ada sistem koordinat yang dapat digunakan di setiap titik secara bersamaan. Ambil contoh misalnya koordinat polar pada pada bidang ekuatorialnya. Jika kita biarkan berjalan dari sampai maka akan berubah secara kontinu sampai . Pada titik ini mempunyai diskontinuitas dari menuju dan titik-titik yang berdekatan dengan titik tersebut memiliki nilai yang cukup jauh berbeda. Jalan alternatif adalah kita dapat melanjutkan melampaui . Kalau kita mengambil jalan ini maka kita akan menemukan kesulitan lain yaitu: pada setiap titik kita harus memiliki nilai yang tak hingga banyaknya, berbeda antara

satu dengan yang lainnya dengan nilai sebesar kelipatan bilangan bulat dari . Kesulitan yang lain juga muncul pada kutub. Pada titik ini tidak terdefinisi sama sekali. Koordinat stereografik juga memiliki kesulitan pada Kutub Utara atau pada titik proyeksi yang tidak diproyeksikan pada bidang ekuatorial; dan titik yang berdekatan dengan Kutub Utara memiliki koordinat stereografik yang berbeda cukup jauh.

Jadi kita tidak dapat menciptakan sebuah sistem koordinat tunggal yang memenuhi kondisi berikut.

i. Setiap titik-titik yang berdekatan satu sama lain memiliki koordinat yang berdekatan;

ii. Setiap titik memiliki koordinat yang unik.

Akan tetapi kita dapat menciptakan sebuah sistem koordinat yang memenuhi kondisi berikut.

i. Setiap titik-titik yang berdekatan satu sama lain memiliki koordinat yang berdekatan paling tidak pada satu sistem koordinat;

ii. Setiap titik memiliki koordinat yang unik pada setiap sistem koordinat yang bersangkutan;

iii. Jika dua buah sistem koordinat saling overlap, maka mereka terhubungkan satu sama lain secara smooth.

Tanpa ketiga syarat di atas, maka sebuah fungsi yang differensiabel pada satu sistem koordinat belum tentu differensiabel pada sistem koordinat lain.

adalah sebuah manifold differensiabel berdimensi jika memenuhi syarat-syarat berikut ini.

i. adalah sebuah ruang topologi;

ii. disajikan dalam bentuk pasangan ;

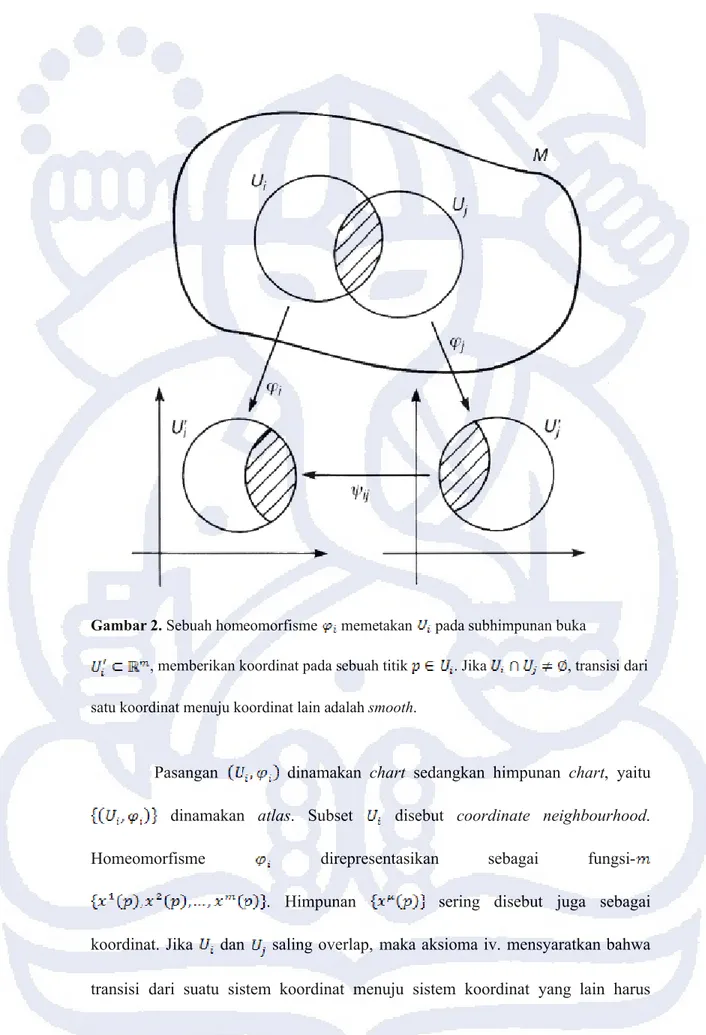
iii. adalah himpunan buka yang menutupi , yaitu . adalah homeomorfisme dari pada suatu himpunan buka ; dan

iv. Jika dan memenuhi hubungan , maka pemetaan

dari menuju adalah

Gambar 2. Sebuah homeomorfisme memetakan pada subhimpunan buka

, memberikan koordinat pada sebuah titik . Jika , transisi dari satu koordinat menuju koordinat lain adalah smooth.

Pasangan dinamakan chart sedangkan himpunan chart, yaitu dinamakan atlas. Subset disebut coordinate neighbourhood.

Homeomorfisme direpresentasikan sebagai

fungsi-. Himpunan sering disebut juga sebagai koordinat. Jika dan saling overlap, maka aksioma iv. mensyaratkan bahwa transisi dari suatu sistem koordinat menuju sistem koordinat yang lain harus

smooth . Pemetaan memetakan setiap koordinat pada

sebuah titik , dan pemetaan memetakan pada titik

yang sama dan transisi dari menuju , , diberikan oleh buah fungsi dengan buah variabel. Transformasi koordinat adalah bentuk eksplisit dari pemetaan . Sehingga differensiabilitas, seperti yang telah diketahui dalam dasar kalkulus, yaitu transformasi koordinat adalah differensiabel apabila setiap fungsi differensiabel. Kita dapat saja membatasi differensiabilitas sampai pada orde ke- . Bagaimanapun, tentu saja pembatasan ini tidak menghasilkan kesimpulan apa-apa. Kita hanya memerlukan persyaratan bahwa transformasi koordinat differensiabel secara infinit, yaitu .

Jika gabungan dari dua buah atlas, yaitu dan juga adalah sebuah atlas, kedua atlas ini disebut compatible. Kompatibilitas adalah relasi ekivalen, relasi ekivalen yang menunjukkan kompatibilitas disebut differentiable structure. Dan juga atlas yang kompatibel menunjukkan differentiable structure yang sama pada .

2.2

Manifold Differensiabel

Konsep manifold differensiabel diperlukan untuk menerapkan metode dari kalkulus differensial pada ruang yang lebih umum dari . Contoh dari sebuah manifold differensiabel adalah permukaan regular pada . Sebuah subset adalah sebuah permukaan regular jika, untuk setiap titik terdapat

sebuah lingkungan di sekitar dan sebuah pemetaan

dari sebuah himpunan buka pada , sedemikian sehingga: i. adalah homeomorfisme yang differensiabel;

ii. Differensial adalah injektif untuk semua .

Pemetaan disebut parameterisasi dari pada titik . Hasil yang paling penting dari definisi mengenai permukaan regular adalah fakta bahwa transisi dari satu parameterisasi ke parameterisasi lain adalah diffeomorfisme. Yaitu jika dan adalah dua parameterisasi sedemikian sehingga

, maka pemetaan dan

adalah differensiabel. Maka secara intuitif sebuah permukaan regular adalah gabungan dari himpunan buka di , sedemikian rupa sehingga ketika dua himpunan buka beririsan satu sama lain transisi dari himpunan buka yang satu ke himpunan buka yang lain adalah differensiabel, sebagai akibatnya maka dapat diterapkan kalkulus.

Definisi 2.4.1 Sebuah manifold differensiabel berdimensi adalah sebuah himpunan dan kumpulan pemetaan injektif dari himpunan buka ke sedemikian sehingga:

ii. Untuk suatu , dengan , himpunan dan adalah himpunan buka di dan pemetaan adalah differensiabel (gambar 4).

Gambar 3. Hubungan antara dan .

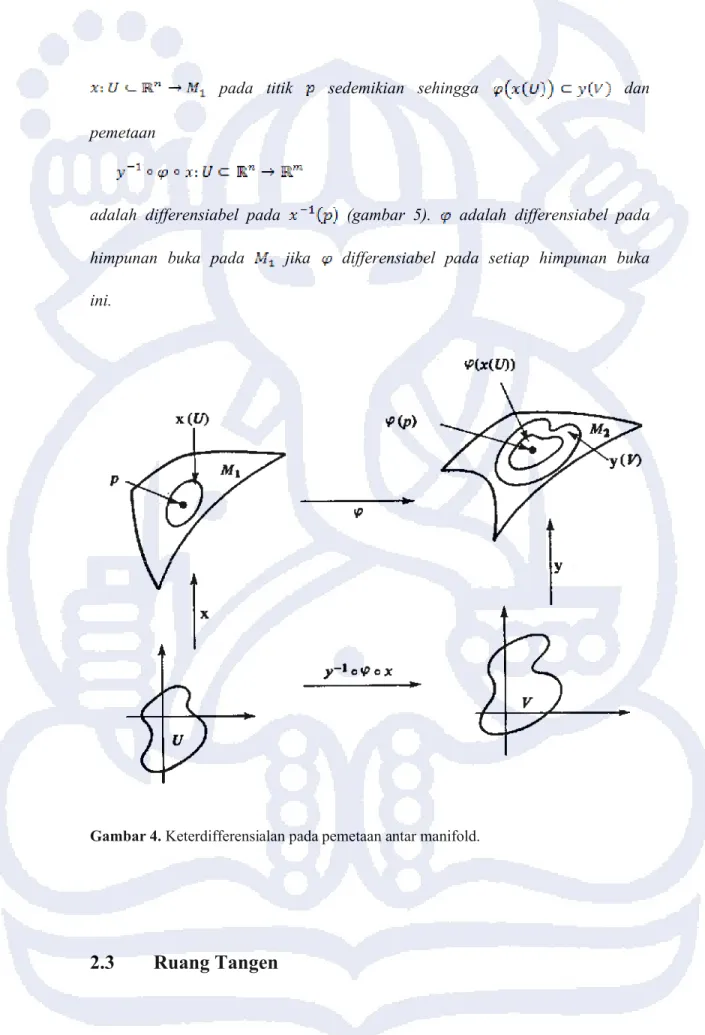
Definisi 2.4.2 Misalkan dan adalah manifold differensiabel. Sebuah

pemetaan adalah differensiabel pada titik jika diberikan parameterisasi pada titik terdapat sebuah parameterisasi

pada titik sedemikian sehingga dan pemetaan

adalah differensiabel pada (gambar 5). adalah differensiabel pada himpunan buka pada jika differensiabel pada setiap himpunan buka ini.

Gambar 4. Keterdifferensialan pada pemetaan antar manifold.

Selanjutnya, kita akan mengembangkan ide mengenai vektor tangen pada manifold differensiabel. Untuk permukaan pada , sebuah vektor tangen pada sebuah titik pada permukaan didefinisikan sebagai “kecepatan” pada dari sebuah kurva yang melewati titik . Kita harus menemukan karakteristik dari vektor tangen yang akan mensubstitusikan ide mengenai “kecepatan”. Misalkan

adalah differensiabel pada , dengan . Tulis

(2.3.1)

Jadi . Sekarang misalkan fungsi

differensiabel yang didefinisikan pada lingkungan di . Kita akan mengkomposisikan dengan dan mengekspresikan turunan berarahnya dalam bentuk vektor sebagai

(2.3.2) Jadi, turunan berarah yang diekspresikan dalam bentuk vektor bergantung secara unik pada . Ini adalah karakteristik yang akan digunakan untuk mendefinisikan vektor tangen pada sebuah manifold.

Definisi 2.5.1 Misalkan adalah manifold differensiabel. Sebuah fungsi

differensiabel disebut kurva pada . Misalkan ,

dan misalkan adalah himpunan funsi pada yang differensiabel pada titik . Vektor tangen pada kurva pada adalah fungsi diberikan oleh

(2.3.3) Sebuah vektor tangen pada adalah vektor tangen pada pada suatu kurva

dengan . Himpunan dari semua vektor tangen pada pada akan dinotasikan sebagai .

Jika kita memilih parameterisasi pada , kita dapat mengekspresikan fungsi dan kurva dalam parameterisasi ini sebagai

(2.3.4) (2.3.5) didapatkan

.

Dalam kata lain, vektor dapat diekspresikan dalam parameterisasi sebagai (2.3.6)

Gambar 5. Vektor tangen dari sebuah titik pada .

Ekspresi menunjukkan vektor tangen terhadap kurva pada hanya bergantung pada turunan dalam suatu sistem koordinat. , dengan operasi yang biasa dilakukan pada fungsi akan membentuk ruang vektor berdimensi , dan pilihan parameterisasi menunjukkan basis yang bersangkutan pada (gambar 6). Ruang vektor disebut ruang tangen dari pada titik .