BAB 2
TINJAUAN PUSTAKA
2.1 Kriptografi
Kriptografi pada awalnya dijabarkan sebagai ilmu yang mempelajari bagaimana menyembunyikan pesan. Namun pada pengertian modern kriptografi adalah ilmu yang bersandarkan pada teknik matematika untuk berurusan dengan keamanan informasi seperti kerahasiaan, keutuhan data dan otentikasi entitas. Jadi pengertian kriptografi modern adalah tidak saja berurusan hanya dengan penyembunyian pesan namun lebih pada sekumpulan teknik yang menyediakan keamanan informasi. Kriptografi klasik umumnya merupakan teknik penyandian dengan kunci simetrik dan menyembunyikan pesan yang memiliki arti ke sebuah pesan yang nampaknya tidak memiliki arti dengan metode pergantian huruf (substitusi) atau transpose (pertukaran
tempat).
2.1.1 Sistem Kriptografi
Sistem kriptografi terdiri dari 5 bagian, yaitu :
1. Plaintext: pesan atau data dalam bentuk aslinya yang dapat terbaca. Plaintext adalah masukan bagi algoritma enkripsi. Untuk selanjutnya digunakan istilah teks
asli sebagai padanan kata plaintext.
2. Secret Key: secret key yang juga merupakan masukan bagi algoritma enkripsi merupakan nilai yang bebas terhadap teks asli dan menentukan hasil keluaran algoritma enkipsi. Untuk selanjutnya digunakan istilah kunci rahasia sebagai padanan kata secret key.
4. Algoritma Enkripsi: algoritma enkripsi memiliki 2 masukan teks asli dan kunci rahasia. Algoritma enkripsi melakukan transformasi terhadap teks asli sehingga menghasilkan teks sandi.
5. Algoritma Dekripsi: algoritma dekripsi memiliki 2 masukan yaitu teks sandi dan kunci rahasia. Algoritma dekripsi memulihkan kembali teks sandi menjadi teks asli bila kunci rahasia yang dipakai algoritma dekripsi sama dengan kunci rahasia yang dipakai algoritma enkripsi (Sadikin, 2012).
Algoritma
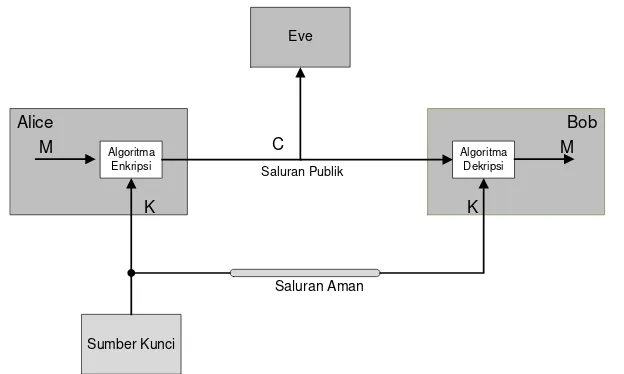
Gambar 2.1 Sistem Kriptografi Konvensional Sumber Gambar: (Sadikin, 2012)
Pada Gambar 2.1 kunci rahasia dibangkitkan oleh pembangkit kunci dan dikirim melalui saluran aman ke pihak penyandi (encryptor) maupun penerima sandi (decryptor). Teks sandi dikirim melalui saluran umum sehingga ada pihak ketiga yang dapat membaca teks sandi itu (Sadikin, 2012).
2.2 Sistem Kriptografi RSA
Pada tahun 1977, Rivest, Shamir, dan Adleman merumuskan algoritma praktis yang mengimplementasikan sistem kriptografi kunci publik yang disebut dengan sistem kriptografi RSA. Meskipun pada tahun 1977 badan sandi Inggris memublikasikan bahwa Clifford Cock telah merumuskan sistem kriptografi RSA 3 tahun lebih dahulu daripada Rivest, Shamir dan Adleman.
dengan n = p · q, p dan q adalah bilangan prima dan Φ (n) = (p – 1) (q – 1). Gambar 2.2 mengilustrasikan sistem kriptografi kunci publik RSA (Sadikin, 2012).
C = Pemod n
Teks asli Enkripsi Teks sandi Dekripsi
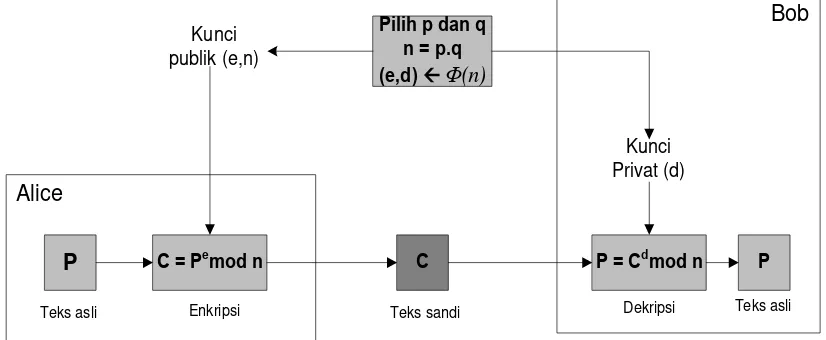
Gambar 2.2 Sistem kriptografi dengan kunci publik RSA.
Sumber Gambar: (Sadikin, 2012)
Pada Gambar 2.2 digambarkan skema sistem kriptografi RSA biasa tanpa tambahan modifikasi apapun dimana terdapat kunci public (n,e) dan kunci private d. Nilai n dapat diakses oleh publik, sehingga rentan terhadap serangan faktorisasi. Pada saat ini RSA yang dianggap aman adalah RSA dengan ukuran 1024 sampai dengan 2048 bit
(Sadikin, 2012).
Sistem kriptografi RSA dapat dimodifikasi, beberapa varian yang ada diantaranya: RSA-CRT, Multiprime-RSA, Takagi-RSA (Galbraith, 2012). Modifikasi ini muncul untuk meningkatkan waktu komputasi dan tingkat keamanan algoritma RSA dari berbagai serangan. Sistem Kriptografi RSA biasanya dimanfaatkan sebagai pengaman pesan pendek misalnya sebagai otentikasi atau digital signature (Sadikin, 2012).
2.2.1 Algoritma RSA
Proses atau cara kerja dari algoritma RSA dapat dilihat sebagai berikut:
1. Menentukan dua bilangan prima p ≠ q secara acak dan terpisah untuk tiap-tiap p dan q.
2. Melakukan perhitungan n = p · q (n merupakan hasil perkalian dari p dikalikan dengan q).
4. Menentukan nilai e dengan syarat bahwa bilangan tersebut merupakan bilangan
bulat (integer) 1 < e < Φ (n) dan nilai GCD (Φ (n), e) = 1 dimana e ialah kunci
publik.
5. Menghitung kunci dekripsi yang dilakukan dengan perhitungan kunci enkripsi
dengan rumus d ≡ e -1 (mod Φ (n)) dimana d ialah kunci privat.
6. Setelah mendapatkan kunci-kunci tersebut maka dapat dilakukan proses enkripsi
maupun proses dekripsi.
7. Rumus untuk melakukan proses enkripsi adalah C = P emod n.
8. Rumus untuk melakukan proses dekripsi adalah P = C d mod n (Simarmata, 2012).
Contoh:
Diketahui bilangan prima p = 17 dan q = 31.
Selanjutnya dihitung parameter kunci publik (e, n) sebagai berikut: n = p · q = 17 · 31 = 527
Φ (n)= (p – 1) · (q – 1) = 16 x 30 = 480
Misalnya e dipilih 77, nilai 77 memenuhi syarat karena GCD (480, 77) = 1. Jadi kunci publik (Kpublik) = (77, 527).
Sedangkan parameter d = 77-1 mod 480 = 293. Jadi kunci privat (Kprivat)=293.
2.3 Algoritma Miller-Rabin
Algoritma Miller-Rabin merupakan algoritma probabilistik yang menguji keprimaan sebuah bilangan yang diberikan berdasarkan pada Fermat’s LittleTheorem. Algoritma
Miller-Rabin menghitung deret berikut secara berulang : �� ≡ �2� ≡ �22� ≡ ⋯ ≡
�2�−1� ≡ �2��(����). Pada perhitungan �2�� dilakukan pengujian Fermat dan
pengujian kepemilikan akar kuadrat untuk i = 0, 1, 2, …, k . Jika pengujian akar kuadrat ialah positif, n dideklarasikan sebagai bilangan komposit. Jika pengujian Fermat ialah positif, maka n mungkin bilangan prima (Sadikin, 2012).
Berikut Algoritma Miller-Rabin:
1. Input sebuah bilangan yang akan diuji keprimaannya yaitu n. 2. Jika n < 2 atau n habis dibagi 2, maka n bukan prima (STOP).
4. Pilih sebuah bilangan acak a (1 < a < n-1).
5. x = am mod n. Jika x = 1 atau x = n-1, maka lanjutkan ke tahap 9.
6. x = x2 mod n. Jika x = 1, maka n bukan prima (STOP). Jika x = n-1, maka
lanjutkan ke tahap 9.
7. Lakukan perulangan pada tahap 6 sebanyak k-1. 8. Jika x != n-1, maka n bukan prima (STOP).
9. Lakukan perulangan pada tahap 4-8 sebanyak t (panjang digit n). 10. n mungkin prima (Sadikin, 2012).
2.4 Algoritma Euclid GCD
Algoritma Euclid merupakan salah satu metode untuk menemukan Greatest Common Divisor (GCD).
Berikut Algoritma Euclid GCD:
1. Input 2 buah bilangan yang akan dicari GCD-nya yaitu m dan n. 2. Usahakan agar m > n. Jika tidak, maka tukar nilai m dan n. 3. Hitung r = m mod n.
4. Selama r != 0, lakukan: m = n,
n = r,
r = m mod n.
5. Maka, nilai n saat ini adalah GCD dari m dan n.
2.5 Metode Pollard ρ
Metode Pollard ρ (baca Pollard Rho) dipublikasikan oleh John Pollard pada tahun 1975. Metode ini dipilih untuk menemukan faktor prima dari bilangan bulat yang besar dengan hanya menggunakan jumlah lokasi memori yang konstan (Sutomo, 2005). Metode ini dikenal sebagi metode faktorisasi Pollard Monte Carlo. Algoritma Pollard ρ berdasar pada hal berikut ini:
1. Terdapat x1 dan x2 sehingga s relatif prima terhadap (x1– x2) tetapi N tidak relatif
2. Dapat dibuktikan bahwa s = GCD (x1 – x2) sehingga GCD(x1 – x2, N) dapat
bernilai 1 atau sebuah faktor N (Sadikin, 2012).
Metode Pollard ρ ialah metode probabilistik untuk memfaktorkan sebuah angka N dengan mengiterasikan sebuah fungsi polynomial di dalam modulo N. Umumnya fungsi yang digunakan ialah f(x) = x2+1, karena telah terbukti bekerja dengan baik untuk masalah faktorisasi, namun fungsi polynomial lain dapat digunakan. John Pollard menyarankan untuk membandingkan x1.i dengan x2.i untuk i = 1, 2, 3, …. Untuk setiap i, diperiksa apakah GCD(x1.i – x2.i, N) merupakan faktor pembagi dari N. Jika GCD(x1.i – x2.i, N) bernilai 1 atau N, maka proses iterasi dilanjutkan hingga faktor pembagi ditemukan (Barnes, 2004).
Berikut Algoritma Pollard ρ:
1. Input sebuah bilangan yang akan difaktorkan yaitu N.
2. Terdapat x1 dan x2. Dipilih seed (x1 = 2, dan x2 = x1) dan fungsi polynomial
f(x) = x2+1.
3. Lakukan perhitungan pada x1 = f(x1) dan x2 = f(f(x2)).
4. Dilakukan perhitungan modulus pada x1= x1 mod N dan x2 = x2 mod N. 5. Dilakukan perhitungan GCD untuk mencari faktor yaitu s = GCD(|xi- x2.i|, N) 6. Lakukan perulangan pada tahap 3, 4 dan 5 hinnga s ≠ 1 dan s ≠ N
7. Jika s ≠ 1 dan s ≠ N, maka kedua faktor N ialah s dan N/s (Barnes, 2004).
Kompleksitas algoritma Pollard ρ membutuhkan perhitungan aritmatika sebanyak √s,
akan tetapi karena s diharapkan lebih kecil atau sama dengan √N maka tetap saja algoritma faktorisasi Pollard ρ tidak memungkinkan untuk bilangan integer besar.
Kompleksitas operasi-bit Pollard ρ adalah eksponensial yaitu, O(2nb/4) dengan nb adalah jumlah bit N (Sutomo, 2005).
x7≡ x9≡ 7 (mod 29)
x6≡ 8 (mod 29)
x5 = 226 ≡ 23 (mod 29)
x4 = 3146 ≡ 14 (mod 29)
x3 = 677 ≡ 10 (mod 29)
x2 = 26
x1 = 5
x0 = 2
x8≡ x10≡ 21 (mod 29)
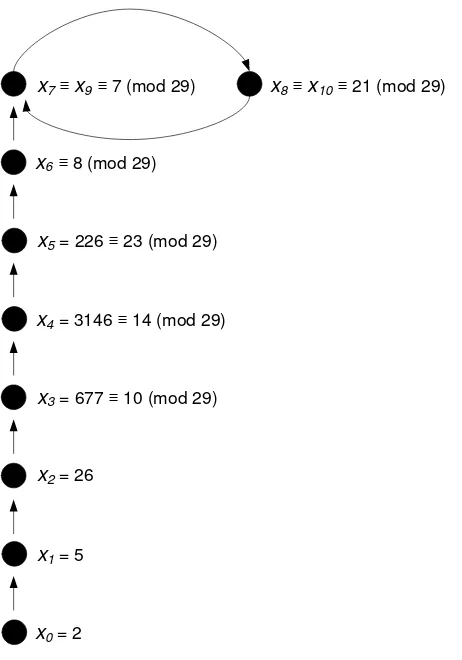
Gambar 2.3 Illustrasi Metode Pollard ρ
Gambar 2.3 menunjukkan bahwa ketika x9 dicapai, perhitungan berada dalam periode bolak-balik x7 dan x8. Ini membentuk sebuah sirkuit. Bentuk ini mengingatkan pada simbol yunani ρ (baca rho) (Mollin, 2005).
Pada RSA dengan n berukuran 1024 bit, maka faktorisasi dengan algoritma Pollard ρ membutuhkan paling tidak 2256 operasi aritmatika. Misalnya sebuah komputer mampu melakukan operasi sebanyak 230 per detiknya maka faktorisasi Pollard ρ membutuhkan 2226 detik (Sadikin, 2012).
2.5.1. Modifikasi Pollardρ
fungsi polynomial pembangkit bilangan prima dengan harapan bahwa akan didapat faktor dari sebuah bilangan N dengan lebih cepat.
2.5.2. Fungsi Polynomial
Legendre mengatakan bahwa tidak ada fungsi algebra rasional yang selalu menghasilkan bilangan prima. Fungsi polynomial terbaik yang dapat membangkitkan sangat banyak bilangan prima menurut Euler (1772), Nagel (1951), Gardner (1984), Ball dan Coxeter (1987) yaitu: n2 + n + 41 yang menghasilkan bilangan prima berbeda untuk 40 urutan bilangan bulat n = 0 - 39. Menurut Legendre pada tahun 1798, Fungsi n2 – n +41 menghasilkan 40 bilangan prima untuk n = 1 – 40 dan bilangan tersebut disebut sebagai “Euler Numbers”. Fungsi polynomial digunakan dalam membangkitkan deret bilangan pada metode Pollard ρ. Berikut merupakan tabel fungsi polynomial hasil modifikasi yang digunakan dalam penelitian ini.
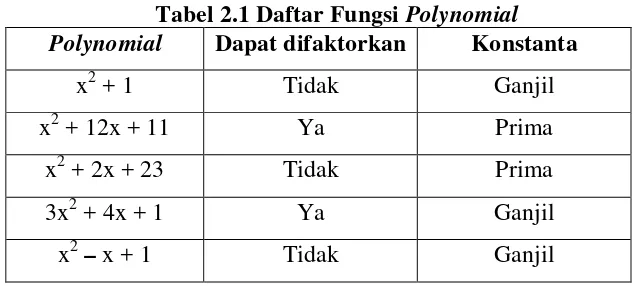
Tabel 2.1 Daftar Fungsi Polynomial Polynomial Dapat difaktorkan Konstanta
x2 + 1 Tidak Ganjil
x2 + 12x + 11 Ya Prima
x2 + 2x + 23 Tidak Prima
3x2 + 4x + 1 Ya Ganjil
x2 – x + 1 Tidak Ganjil
Pada Tabel 2.1 terdapat 5 fungsi polynomial yang berbeda. Fungsi x2 + 1 merupakan fungsi polynomial standard yang paling sering digunakan pada metode Pollard ρ, sedangkan sisanya merupakan fungsi polynomial modifikasi yang dibangun berdasarkan 2 kriteria, yaitu: apakah fungsi polynomial tersebut dapat difaktorkan dan nilai konstanta dari fungsi tersebut.
2.5.3. Faktorisasi Kunci RSA dengan Metode Pollardρ
Sistem Kriptografi RSA memiliki kunci publik (e, n) untuk enkripsi dan kunci privat (d) untuk dekripsi. Dengan memfaktorkan (n) akan didapat p dan q. Kemudian
Contoh:
Diketahui Kunci public (e, n) dimana e = 77, n = 527. Kemudian n akan difaktorkan untuk mendapatkan p dan q sehingga N = n = 527. Selanjutnya dicari faktor dari N dengan metode Pollard ρ.
1. Dipilih seed dan fungsi polynomial.
x1= 2, x2 = x1 dan f(x) = x2+1.
2. Lakukan perhitungan pada x1 = f(x1) dan x2 = f(f(x2)).
x1= x12 + 1 = 22 + 1 = 5, x2 = x22 + 1 = 22 + 1 = 5, x2 = x22 + 1 = 52 + 1 = 26.
3. Dilakukan perhitungan modulus pada x1= x1 mod N dan x2 = x2 mod N.
x1 = 5 mod 527 = 5 x2 = 26 mod 527 = 26
4. Dilakukan perhitungan GCD untuk mencari faktor yaitu s = GCD(|x1- x2|, N)
s = GCD(|5-26|, 527) = 1
5. Lakukan perulangan pada tahap 2, 3 dan 4 hinnga s ≠ 1 dan s ≠ N
x1= x12 + 1 = 52 + 1 = 26 x2 = x22 + 1 = 262 + 1 = 677 x2 = x22 + 1 = 6772 + 1 = 458330. x1 = 26 mod 527 = 26 x2 = 458330 mod 527 = 367 s = GCD(|26-367|, 527) = 31
6. Jika s ≠ 1 dan s ≠ N, maka kedua faktor N ialah p dan q dimana p = s = 31 dan
q = N / s = 527 / 31 = 17
Selanjutnya dengan memanfaatkan p dan q tersebut dapat dihitung kunci privat d dengan algoritma RSA.
Φ (n)= (p – 1) x (q – 1) = 16 x 30 = 480
2.6 Tinjauan Penelitian yang Relevan
1. B.R. Ambedkar dan S.S. Bedi dari MJP Rohilkhand University mengangkat judul
penelitian “A New Factorization Method to Factorize RSA Public Key Encryption”. Pada penelitian ini, metode faktorisasi baru diajukan untuk mendapatkan faktor dari sebuah bilangan bulat positif N. Penelitian ini berfokus pada faktorisasi pada seluruh bilangan bulat trivial dan nontrivial dan membutuhkan tahap yang lebih sedikit untuk proses faktorisasi RSA modulus N. Metode ini didasarkan pada metode Pollard ρ (Ambedkar & Bedi 2011).
2. Kuldeep Singh, Rajesh Verma dan Ritika Chehal mengangkat judul penelitian
“Modified Prime Number Factorization Algorithm (MPFA) for RSA Public Key Encryption”. Penelitian ini berfokus pada faktorisasi pada seluruh bilangan bulat trivial dan nontrivial seperti halnya metode Fermat dan membutuhkan tahap yang lebih sedikit untuk proses faktorisasi RSA modulus N. Hasil eksperimen
menunjukkan peningkatan kecepatan faktorisasi dibandingkan metode lain seperti Trial Division method, Fermat Factorization, Brent’s Factorization method dan Pollard ρ factorization method (Singh & Verma 2012).
3. Prasasti Imani dari Institut Pertanian Bogor mengangkat judul skripsi “Analisis
Keamanan Kriptosistem Kunci Publik RSA”. Tugas Akhir ini bertujuan untuk mempelajari dan menganalisis algoritma RSA serta beberapa kemungkinan serangan yang dapat dilakukan oleh musuh terhadap kriptosistem ini. Salah satu serangannya yaitu analisis algoritma faktorisasi bilangan komposit menggunakan Pollard ρ. Hasil dari penganalisisan menunjukkan bahwa inti keamanan RSA adalah pada masalah RSA dan faktorisasi bilangan komposit (Imani, 2002). 4. Toni Sutomo dari Universitas Indonesia mengangkat judul skripsinya “Metode