Studi Karakteristik Fisik Muara Sungai Batang Natal Kabupaten Mandailing Natal Chapter III V

(1)

Dimana C(x) adalah konsentrasi pada posisi x. Kemudian Gauss menurunkan persamaan diatas menjadi :

... (2.7)

Parameter yang digunakannya lebih menekankan pada distribusi yang bervariasi. Variasi dari suatu nilai dapat ditunjukkan dalam persamaan berikut :

... (2.8)

dimana :

Px = Deskripsi dari variasi yang dipengaruhi pada titik tinjau

σp = Variasi

BAB III

(2)

3.1. TEMPAT dan WAKTU

Muara Batang Natal terletak di Kecamatan Natal yang berjarak sekitar 100 km dari Panyabungan, Ibu Kota Kabupaten Madina. Lokasi pekerjaan dapat dicapai dari Medan melalui jalan raya dengan kendaraan bermotor ke arah Selatan melalui rute Medan-Tebing Tinggi – Pematang Siantar-Tarutung - Sipirok - Padang Sidimpuan – Penyabungan - Natal dengan jarak +750 km. Alternatif lain adalah dari Padang, Sumatera Barat melalui jalan raya lintas barat Sumatera rute Padang – Padang Panjang – Bukit Tinggi – Lubuk Sikaping – Penyabungan - Natal yang berjarak sekitar +350 km. Mengingat kondisi jalan raya Penyabungan – Natal yang berliku dengan kondisi di beberapa ruas jalan rusak berat dan dalam perbaikan, jarak 100 km ditempuh dalam waktu 4,5 jam perjalanan

3.1.1. Kondisi Lokasi Studi

1. Kondisi Fisik

 Kondisi Umum

Kabupaten Mandailing Natal secara geografis terletak antara 00.10’ – 10050’ Lintang Utara dan 950.50’ – 100010’ Bujur Timur. Wilayah administrasi Mandailing Natal dibagi atas 17 Kecamatan dan 375 desa/kelurahan yang ditetapkan oleh Pemerintah Republik Indonesia dengan Undang-Undang No. 12 tahun 1998 pada tanggal 23

November 1998.

(3)

 Sebelah Utara Kabupaten Tapanuli Selatan

 Sebelah Selatan dengan Propinsi Sumatera Barat

 Sebelah Timur dengan Propinsi Sumatera Barat

 Sebelah Barat dengan Samudera Indonesia

Gambar 3. 1 Lokasi Penelitian

Lokasi Penelit ian

(4)

Gambar 3. 2 Sketsa Lokasi Penelitian di Muara Batang Natal, Madina

3.1.2 Kondisi Muara Batang Natal

(5)

untuk transportasi, menurut informasi pemda setempat terdapat ± 100 buah

perahu motor yang setiap harinya keluar masuk di muara sungai.

Di sebelah kanan muara Batang Natal terdapat berbagai

infrastruktur pemerintah antara lain Tempat Pelelangan Ikan (TPI),

kantor Dinas Kelautan dan Perikanan, pasar, pertokon, mesjid, dan

pemukiman penduduk yang padat.

Kondisi muara pada saat survei dilakukan menunjukan dalam

kondisi air surut, kedalaman mulut muara ± 1 meter. Di sebelah kiri dan

kanan muara terdapat sandbar atau gosong pasir yang menjorok jauh ke

arah laut.

3.2. BAHAN dan ALAT

Mengingat data primer pada penelitian ini hanya satu yaitu salinitas maka hanya akan ada satu alat yang dipergunakan pada penilitian ini yaitu alat untuk mengukur salinitas atau tingkat keasinan pada air yang biasa disebut dengan alat

(6)

Gambar 3. 3 Contoh alat

salinometer

3.3. RANCANGAN PENELITIAN

Rancangan penelitian untuk Tugas Akhir ini dapat dilihat dari diagram alir pada Gambar 3.4.

3.4. PELAKSANAAN PENELITIAN

(7)

beserta kecepatan arus. Setelah seluruh data didapat, maka dimulai lah

pemodelan dengan menggunakan program Microsoft Excel berdasarkan

buku

Estuarine: Monitoring and Modeling the Physical System,

(Jack

Hardisty,2007).

M ulai

Pengum pulan Dat a

(8)

Gambar 3. 4 Diagram Alir Penelitian

Pada pemodelan bathimetri tahapan awal yang dilakukan adalah

mencari nilai koefisien lebar (

a

) dan nilai koefisien kedalaman (

b

) dengan

menggunakan metode

trial and error

, hal ini dilakukan untuk

mendapatkan kesesuaian antara lebar dan kedalaman yang asli terhadap

pemodelan agar tidak terlalu jauh perbedaannya. Setelah mendapatkan

nilai koefisien tersebut, yang dilakukan selanjutnya adalah memasukkan

kembali nilai

a

dan

b

ke persamaan Wright et al (1973) dengan

menggunakan Microsoft Excel untuk mendapatkan nilai lebar dan

kedalaman pemodelan seluruhnya. Contoh hasil dari pemodelan bathimetri

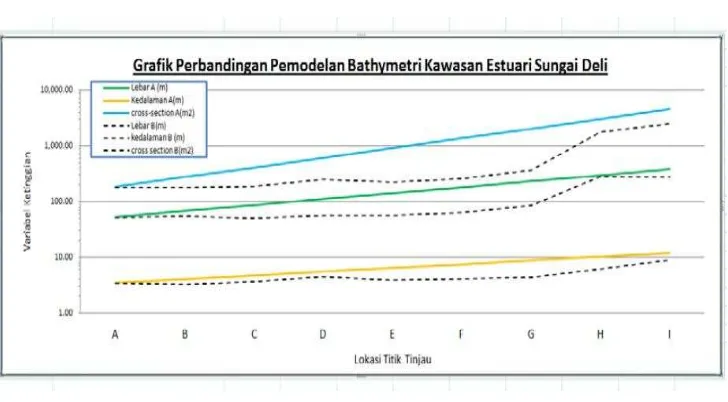
ini bisa dilihat dari Gambar 3.5 dibawah ini.

(9)

Grafik diatas menjelaskan perbandingan bathimetri Muara Sungai Batang Natal antara kondisi eksisting terhadap pemodelan. Dimana pada grafik tersebut garis putus-putus menunjukkan kondisi bathimetri pada kondisi eksisting sedangkan garis lurus menunjukkan pemodelannya.

Untuk pemodelan pasang surut tahapan awal yang dilakukan adalah

dengan mencari komponen-komponen pasang surut baik dari yang ada di

lapangan maupun pemodelan kemudian hitung fluktuasi muka air laut

keduanya dan diperbandingkan. Contoh hasil dari pemodelan pasang surut

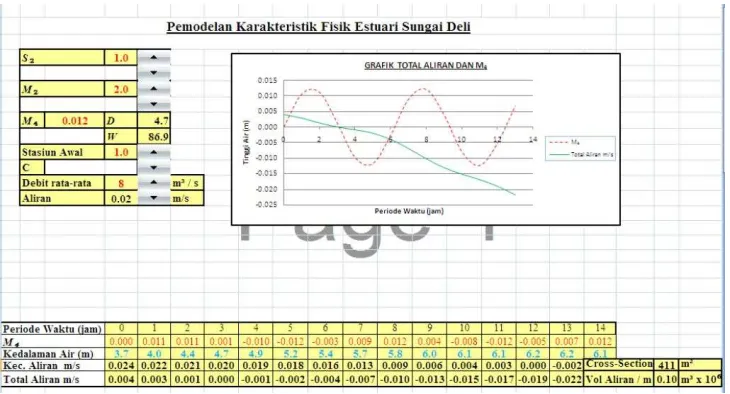
dapat dilihat dari Gambar 3.6 dan 3.7 dibawah ini

(10)

Gambar 3. 7 Contoh hasil akhir pemodelan Sungai Deli menggunakan

Microsoft Excel

Grafik diatas menjelaskan fluktuasi yang disebabkan oleh pasang

surut air laut dan pengaruh komponen M

4

di tiap titik tinjau pada jam

tertentu.

Pemodelan aliran menjelaskan berapa besar air yang mengalir, dan

pengaruh deretan perubahan dari volume air, penurunan air, dan

pertambahan dari kedalaman air tiap titik pengamatan. Contoh pemodelan

aliran air dapat dilihat dari Gambar 3.8 dibawah ini.

Gambar 3. 8 Contoh pemodelan aliran pada Sungai Deli

(11)

Kemudian hasil dari pemodelan bathimetri, pasang surut, arus, dan

salinitas akan dibandingkan dengan keadaan dilapangan berdasarkan data

yang ada yang pada akhirnya akan ditarik kesimpulan dan saran

berdasarkan perbandingan tersebut.

Pemodelan salinitas dilakukan dengan menggunakan metode Gauss

untuk mendapatkan grafik longitudinal salinitas menggunakan persamaan

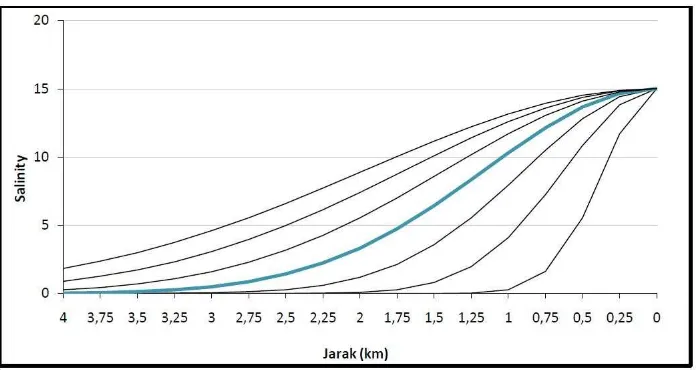
Gauss. Hasil dari pemodelan ini dapat dilihat pada Gambar 3.9 dibawah

ini.

Gambar 3. 9 Contoh grafik hasil pemodelan salinitas dengan menggunakan

persamaan Gauss pada Microsoft Excel

3.5. VARIABEL yang DIAMATI

Pada penelitian ini akan dilakukan empat pemodelan yang variabel-variabel yang akan diamati akan dijelaskan sebagai berikut :

3.5.1. Pemodelan Bathimetri

(12)

mulut muara (Do), kedalaman pada titik-titik pengamatan (Dx), serta panjang muara yang akan ditinjau.

3.5.2. Pemodelan Pasang Surut

Variabel yang akan diamati adalah komponen utama pasang surut seperti amplitudo semi diurnal matahari (AS2). Amplitudo semi diurnal bulan (AM2), serta fluktuasi muka air laut (ht).

3.5.3. Pemodelan Arus

Pada tahap ini variabel yang akan dicari adalah kecepatan arus pada muara.

3.5.4. Pemodelan Salinitas

Pada pemodelan ini variabel yang dicari adalah salinitias dari tiap- tiap titik tinjau pada muara.

BAB IV

(13)

4.1. PENYAJIAN DATA

4.1.1. Data Primer

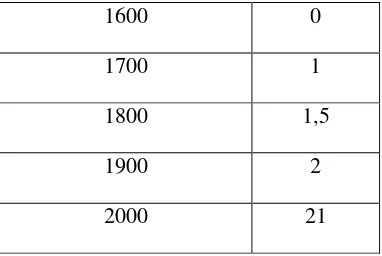
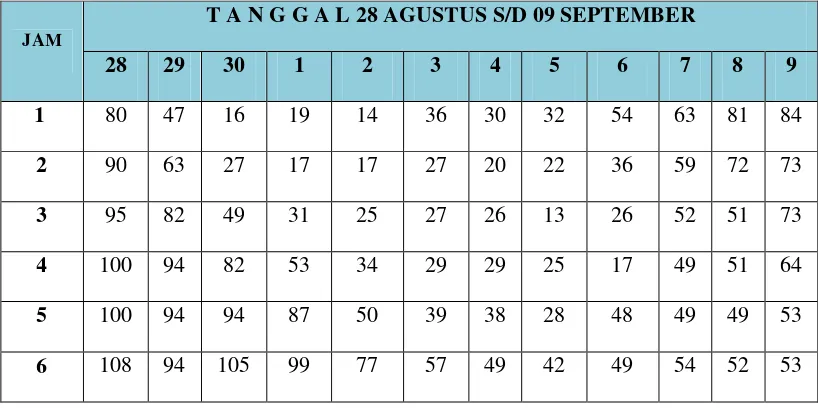
Data primer yang digunakan pada Tugas Akhir ini adalah data salinitas yang diambil langsung di Muara Sungai Batang Natal dengan menggunakan alat salinometer.Data salinitas tersebut dapat dilihat di Tabel 4.1 dibawah ini.

Tabel 4. 1 Data Salinitas Muara Sungai Batang Natal

(14)

1600 0

Data-data yang didapat dari Balai Wilayah Sungai adalah dalam bentuk data topografi (Tabel 4.2) dan data pasang surut (Tabel 4.3) di bawah ini :

a.

Data Topografi

Tabel 4. 2 Data Topografi Muara Batang Natal

(15)

Tabel diatas menjelaskan topografi dari titik-titik tinjau yang diukur dari hulu muara. Titik paling hulu adalah titik P19 yang kemudian bergerak ke hilir hingga mencapai muara sepanjang 2000 meter yaitu titik P59

b.

Data Pasang Surut

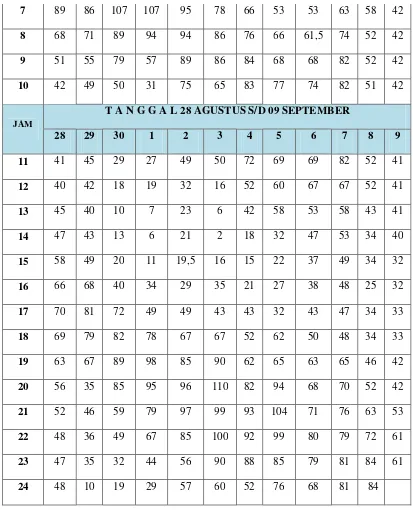
Tabel 4. 3 Data Pasang Surut Muara Sungai Batang Natal

(16)

Tabel diatas merupakan data sekunder berupa pengukuran pasang surut yang terjadi pada deaerah Pantai Natal, Kabupaten Mandailing Natal. Data diambil selama 12 hari dan 24 jam pada kawasan tersebut.

4.2. ANALISA MUARA SUNGAI BATANG NATAL

Analisa dan pemodelan akan dilakukan dengan menggunakan program Microsoft Excel dan diuji dalam bentuk-bentuk dasar suatu pemodelan numerik.

(17)

menghitungnya dengan rumus-rumus yang ada yang pada akhirnya akan ditampilkan berupa grafik perbandingan kondisi muara eksisting terhadap pemodelan dari parameter-parameter yang berpengaruh pada muara tersebut.

Sebelum melakukan pemodelan tahapan dasar yang harus dilakukan adalah penyesuaian keadaan muara berdasarkan data yang ada. Untuk itu digunakan metode trial and error pada rumus Wright et al. Metode trial and error ini digunakan untuk mencari koefisien lebar dan kedalaman muara (a & b).

Untuk mencari koefisien lebar muara (a) digunakan fungsi Wright et al (1973) berdasarkan lebar muara yaitu :

... ...(4.1)

dimana :

Wx = Lebar muara di titik x (m)

W0 = Lebar muara tepat di mulut muara (m)

x = jarak dari mulut muara ke titik tinjauan (m)

L = panjang muara (m)

a = koefisien lebar muara

(18)

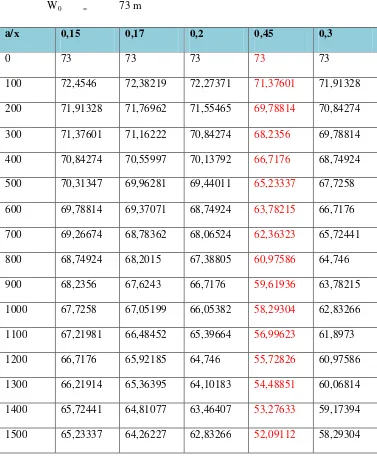
Tabel 4. 4. Hasil Perhitungan Lebar Muara dengan Metode Trial and Error

Untuk Mencari Nilai Koefisien Lebar (a)

L = 2000 m

W0 = 73 m

a/x 0,15 0,17 0,2 0,45 0,3

0 73 73 73 73 73

(19)

Hasil yang diperoleh dari perhitungan trial and error menunjukkan bahwa nilai koefisien a adalah sebesar 0,45. Nilai sebesar 0,45 diambil karena dianggap nilai yang paling mendekati dengan kondisi di lapangan.

(20)

(21)

0 10 20 30 40 50 60 70 80

0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100

a=0.2

a= 0.3

a=0.45

(22)

(23)

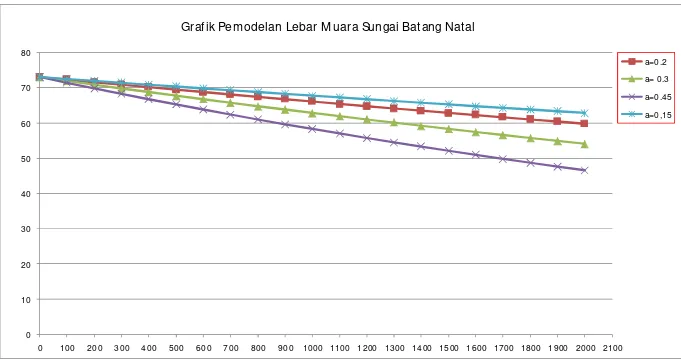
Grafik diatas adalah perbandingan hasil dari pencarian koefisien lebar muara menggunakan metode trial and error yang telah diplot kedalam grafik.

Setelah mencari nilai koefisien lebar muara (a), maka selanjutnya adalah mencari nilai koefisien kedalaman muara (b). Langkah-langkah untuk mencari nilai b sama dengan mencari nilai a yaitu dengan metode trial and error. Adapun persamaan eksponensial kedalaman muara adalah :

... ...(4.2) dimana :

Dx = kedalaman muara di titik x (m)

D0 = kedalaman muara tepat di mulut muara (m)

x = nilai ukur atau bentang jarak antar titik tinjauan (m) b = koefisien kedalaman muara

L = dimensi horizontal dari panjang kawasan muara (m)

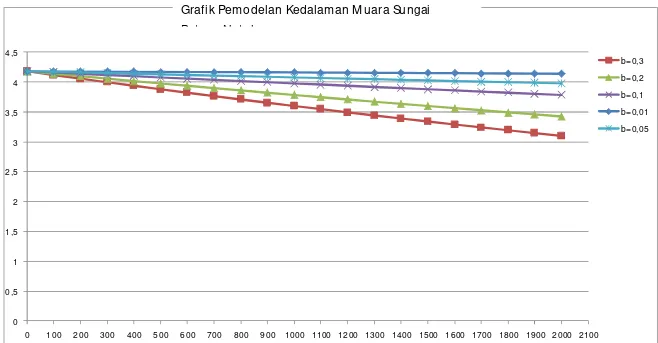
Hasil dari perhitungan nilai b menggunakan metode trial and error beserta grafik dapat dilihat pada Tabel 4.5 dan Grafik 4.2 :

Tabel 4. 5 Hasil Perhitungan Kedalaman Muara dengan Metode

Trial and Error

Untuk Mencari Nilai Koefisien

Kedalaman Muara (

b

)

b/h 0,01 0,05 0,1 0,2 0,3

0 4,18 4,18 4,18 4,18 4,18

(24)

Dari hasil perhitu

ngan trial and error maka diambil nilai b adalah sebesar 0,1. Seperti yang telah dijelaskan sebelumnya, nilai tersebut diambil karena dianggap nilai yang paling mendekati dengan keadaan muara yang sebenarnya.

400 4,171649 4,138413 4,097239 4,016117 3,9366 500 4,169564 4,128081 4,076806 3,97616 3,877998

b/h 0,01 0,05 0,1 0,2 0,3

(25)

(26)

0 0,5 1 1,5 2 2,5 3 3,5 4 4,5

0 100 200 300 400 500 600 700 800 900 1000 1100 1200 1300 1400 1500 1600 1700 1800 1900 2000 2100

b=0,3

b=0,2

b=0,1

b=0,01

b=0,05

Grafik Pemodelan Kedalaman M uara Sungai

(27)

(28)

Hasil dari perhitungan koefisien lebar dan kedalaman pada muara di atas kemudian dapat kita masukkan di tabel perbandingan. Untuk melihat perbandingan kedalaman dan lebar muara sebenarnya dengan pemodelan, berikut ini akan dibahas perhitungan dan tahapan-tahapan pemodelan yang akan diahas secara bertahap.

4.2.1. Pemodelan Bathymetri

A. Mendefinisikan Muara dengan Pemodelan

Tahapan awal dalam mengerjakan pemodelan muara ini adalah

dengan menentukan nilai dari data-data pada muara, yaitu lebar,

kedalaman, dan

cross-section

.

Kemudian buka file baru pada Microsoft Excel, dan ubah halaman

pertama (

sheet 1

) dengan “model”. Setelah itu pada halaman kedua (

sheet

2 ) diubah juga namanya menjadi “

bathymetri”

dengan format tulisan yang

sama dengan halaman “model”.

Kemudian menentukan titik-titiknya dan masukkan data lokasi

tinjauan seperti berikut ini :

D20 input dengan P.19 (lokasi awal tinjauan)

E20 input dengan P.21 (lokasi tinjauan berikutnya dengan jarak

100 m)

F20 input dengan P.23 (lokasi tinjauan berikutnya dengan jarak

100 m)

. . .

(29)

Kemudian ketik judul data yang akan diinput nantinya yang ingin

kita peroleh dari hasil pemodelan ini, masing-masing dengan “Jarak dari

Mulut Muara”, “Lebar Muara”, “Kedalaman Muara”, dan “

Cross Section

”

pada kolom C21, C22, C23, dan C24. Setelah itu input nilai jarak yang ada

pada titik tinjau, yakni 2000 pada D21, 1900 pada E21, 1800 pada F21,

dan seterusnya sampai di X21 ataupun titik 0 (mulut muara), (Gambar 4.1).

Gambar 4. 1 Tahapan Awal Pekerjaan Perhitungan Pemodelan

Selanjutnya kita tinggal menginput data-data yang tersedia. Dan kemudian di plot kedalam grafik yang nantinya akan menunjukkan perbandingan dengan kawasan yang akan kita modelkan.

(30)

Begitu juga dengan kedalaman kawasan yang akan ditinjau, kolom diisi dimulai dari D23 sampai kepada kolom X23. Setelah semua data lebar dan kedalaman sudah diinput, kita akan mendapatkan nilai dari cross section dari tiap titik yang akan ditinjau. Nilai cross section dimasukkan dari kolom D24 hingga X24.

Setelah selesai menginput data-data diatas, kemudian data-data tersebut kita plot dalam bentuk grafik sehingga tampak seperti Gambar 4.2 dibawah ini.

Gambar 4. 2 Hasil Keseluruhan Pemodelan Kondisi Eksisting

Muara Sungai Batang Natal

(31)

B. Pemodelan Lebar Kawasan Muara Sungai Batang Natal

Pemodelan lebar muara dilakukan sebagai data dasar dari

perencanaan muara yang nantinya dapat digunakan untuk mengetahui

keadaan yang lebih baik terhadap muara tersebut.

Lebar muara dihitung dengan rumus yang telah dijabarkan

sebelumnya yaitu dengan menggunkan persamaan Wright et al. Langkah

pengerjaan pemodelan ini sama seperti sebelumnya. Jika sebelumnya data

yang di input adalah kondisi eksisting dari muara maka pada pemodelan

ini data yang di input adalah data yang berdasarkan kondisi eksisting

muara yang telah di masukkan ke dalam persamaan Wright et al.

Pengerjaan pemodelan dilakukan pada halaman yang baru dimulai

dari kolom AC27:31 sampai dengan kolom AX27:31. Kemudian kita input

kolom seperti yang sebelumnya yaitu judul data dan nilai data tersebut.

Tahap pertama yang dilakukan adalah memilih kolom AD29

dimana kolom tersebut akan di isi dengan nilai pemodelan lebar muara

yang telah menggunakan persamaan Wright et al. Input data dilakukan

dengan cara mengetik :

=732,7^(-0,45AD28/2000)

(32)

merupakan tanda pembagi dan “2000” merupakan panjang muara yang

diamati dalam satuan meter.

Setelah formula di atas dimasukkan kemudian tekan “enter” maka

pada kolom tersebut kemudian akan menunjukkan hasil dari formula

pemodelan lebar yaitu sebesar 46.69 m pada jarak 2 km dari mulut muara.

Kemudian formula pada kolom AD29 dicopy pada kolom-kolom

selanjutnya sampai pada kolom AX39 (mulut muara).

Hasil pemodelan lebar kawasan muara sungai batang natal dapat dilihat

pada Gambar 4.3.

Gambar 4. 3 Pemodelan Lebar Muara Sungai Batang Natal

dengan Rumus Wright et.al.

C. Pemodelan Kedalaman Muara Sungai Batang Natal

(33)

= 4,22,7^(-0,1AD28/2000)

“4,2” merupakan nilai kedalaman pada mulut muara sungai batang natal.

“2,7” adalah konstanta eksponensial, sedangkan “0,1” merupakan

koefisien kedalaman (

b

) yang telah dicari sebelumnya dengan metode

trial

and error

.

Hasil dari formula tersebut adalah 3,80 meter. Nilai tersebut adalah

kedalaman pada jarak 2 km dari mulut muara. Setelah itu sama seperti

pemodelan lebar, copy formula yang sudah dibuat pada kolom-kolom

selanjutnya sampai kolom AX30 (mulut muara). Hasil dari pemodelan

kedalaman dapat dilihat pada Gambar 4.4

Gambar 4. 4 Pemodelan Kedalaman Muara dengan Rumus

Wright et.al

(34)

Ax = WxDx ... (4.3)

dimana :

Ax = Cross-section (m2)

Wx = lebar penampang muara (m) Dx = kedalaman muara (m)

Pilih cell AD31dan gunakan rumus diatas ke kolom AD31 yaitu perkalian antara lebar penampang di titik tinjau dengan kedalamannya dengan bentuk sebagai berikut :

= 46,69*3,80

(35)

Gambar 4. 5 Hasil Akhir Pemodelan Bathymetri Muara Sungai

Batang Natal

D. Grafik

(36)

Gambar 4. 6 Grafik Hasil Pemodelan Bathymetri Muara

Sungai Batang Natal

Setelah pemodelan diplot menjadi bentuk grafik, kemudian dibandingkan dengan keadaan yang sebenarnya. Grafik dibuat bertimpaan untuk nilai lebar, kedalaman, dan cross section. Sehingga tampak jelas perbedaan kondisi eksisting dengan pemodelan yang berdasarkan persamaan Wright et.al seperti Gambar 4.7 dibawah ini.

(37)

Gambar 4. 7 Grafik Perbandingan Bathymetri antara Pemodelan

dengan Keadaan Eksisting pada Kawasan Muara

Sungai Batang Natal

Setelah selesai data pemodelan dapat disusun kedalam bentuk Tabel 4.6 dan Tabel 4.7 agar lebih mudah dipahami.

Tabel 4. 6 Perhitungan Lebar Muara Sungai Batang Natal

Titik Tinjau Lebar Eksisting (m) Lebar Pemodelan (m)

(38)

Titik Tinjau Lebar Eksisting (m) Lebar Pemodelan (m)

P57 75 71,39

P59 73 73,00

Tabel 4. 7 Perhitungan Kedalaman Muara Sungai Batang Natal

Titik Tinjau Kedalaman Eksisting (m)

(39)

Dari tabel diatas dapat dilihat selisih yang paling jauh dengan kondisi di lapangan baik kedalaman dan lebar muara rterdapat pada titik P25 dan P31 untuk bagian lebar sejauh 21 m, sedangkan pada kedalaman perbedaan yang paling besar terdapat pada titik P39 dengan selisih 3 m.

4.2.2. Pemodelan Pasang Surut

A. Input Pasang Surut

Pemodelan pasang surut dapat diwakilkan oleh perhitungan dari

gelombang

S

2

(

solar semi-diurnal

),

M

2

(

lunar semi-diurnal

), dan

M

4

(

lunar

quarter-diurnal

).

Tahap pertama yang dilakukan dalam pemodelan pasang surut ini

adalah dengan membuka pemodelan

bathymetry

yang telah dibuat

sebelumnya kemudian di

save

dalam

file

baru dengan judul pasang surut.

Kemudian

sheet 3

diubah dengan judul “spring neaps”. Pada halaman

“model” masukkan variabel

S

2

pada

cell

B4,

M

2

pada B6,

M

4

pada B8,

P55 4,0 4,16

P57 4,2 4,18

(40)

“

Titik Tinjau

” pada B10, kedalaman atau “

D

” pada D8, dan Lebar atau

“

W

” pada D9. Letakkan

spinner

pada E4 sampai E7 kemudian E10 sampai

E11 untuk mengatur nilai

S

2

,

M

2

, dan

Titik Tinjau.

Format

spinner

pada

cell

E4 dan E5 dengan nilai

current value

sebesar 10, nilai minimum dengan 0, nilai maksimum dengan 100,

incremental change

dengan 1 dan

cell link

pada D4. Kemudian masukkan

rumus “=E4/10” pada D4. Copy

spinnner

pada E6 dan E7 dengan format

sama seperti

spinner

yang sebelumnya. Tetapi ubah

cell link

nya adalah E6

lalu masukkan rumus “=E6/10” pada D6. Kemudian copy lagi

spinner

untuk variabel “Titik Tinjau” pada

cell

E10 dengan nilai

current value

sebesar 100 nilai minimum 0, nilai maksimum 2000,

incremental change

dengan 100 dan

cell link

pada D10.

Kemudian buka

sheet bathymetry

dan input data-data jarak dan

kedalaman pada tiap-tiap titik pengamatan namun disusun secara terbalik

yaitu titik 0 pada

cell

C27 dan seterusnya hingga titik 2000 pada

cell

W27.

Kembali lagi ke halaman

model

dan masukkan formula berikut pada

cell

B11.

=LOOKUP(D10;bathymetry!C27:W27;bathymetry!C28:W28)

Hal ini bertujuan untuk menghubungkan data pada halaman bathymetry

(41)

Gambar 4. 8 Komponen Pasut Pada Kawasan Muara Sungai Batang

Natal

B. Model Amplitudo

Spring-Neap

Sebelum memulai pemodelan amplitudo

spring-neap

terlebih

dahulu kita harus mencari nilai dari komponen utama pasang surut

(

S

2

,M

2,

S

0

,

dll.). Namun nilai tersebut sudah diketahui karena merupakan

data sekunder yang berasal dari pihak Balai Wilayah Sungai Sumatera II

dimana pada data yang diberikan komponen-komponen tersebut telah

dihitung menggunakan metode kuadrat terkecil (

least square

).

(42)

Persamaan gerak harmonik dapat ditulis sebagai berikut :

K

= jumlah konstituen

Persamaan (4.4) dapat ditulis sebagai persamaan sudut untuk 1 konstituen



(t) S0 Acos



t Bsin



t ... (4.5)

(43)





Untuk mendapatkan error terkecil maka syarat yang harus dipenuhi

0

dan syarat yang harus dipenuhi :

1.



 



jika ketiga persamaan di atas dibuat dalam bentuk matriks maka

(44)

atau

Selanjutnya perhitungan peramalan elevasi muka air pasang surut dikerjakan dengan bahasa pemrograman komputer Fortran berdasarkan prinsip penjumlahan

trigonometrik dari masing harga amplitudo dan beda fase dari masing-masing komponen pasang surut.

Berdasarkan perhitungan tersebut didapat nilai-nilai pasang surut

yang dapat dilihat di Tabel 4.8 berikut :

Tabel 4. 8 Perhitungan Komponen Pasut Pada Muara Sungai

Batang Natal

Amplitudo

(cm)

S

0

M

2

S

2

N

2

K

1

O

1

55,98

19,93

39,31

5,71

23,43

7,26

Selanjutnya buka halaman spring-neap, input “waktu(jam)” pada cell B2, “S2 (m)” di C2, “M2 (m)” di D2, dan kolom E2 dengan “Total Kenaikan (m)”. Masukkan nilai 0 pada B3, kemudian “=B3+1” pada B4. Copy rumus tersebut sampai cell B339, yang menunjukkan pengamatan dilakukan pada 14 hari penuh. Setelah itu input persamaan untuk memasukkan nilai S2 :

(45)

dimana :

ht : Tinggi air

AS2 : Amplitudo dari S2

2πt : Waktu dalam radian 12 : Periode waktu dari S2

Untuk program excel persamaan diatas kita ubah menjadi seperti berikut ini :

=’Model’!$D$4*SIN(2*PI()*B3/12)

Dimana D4 adalah besar amplitudo dari S2, SIN mewakili fungsi sinus, 2*PI*()*B3 adalah waktu dalam radian, 12 merupakan periode waktu dari S2

(solar semi-diurnal) pasang surut dalam jam.

Untuk M2 kita juga memakai persamaan yang mirip dengan S2 yaitu:

...(4.5)

dimana :

ht : Tinggi air

AM2 : Amplitudo dari M2

2πt : Waktu dalam radian 12,42 : Periode waktu dari M2

(46)

=’Model’!$D$6*SIN(2*π*B3/12,42)

Dimana D6 adalah besar amplitudo dari M2, SIN merupakan fungsi sinus,

2*π*B3 adalah waktu dalam radian, 12,42 merupakan periode waktu dari M2 dalam jam. Untuk cell E3 input :

=C3+D3+0,45

0,45 merupakan datum elevasi kenaikan muka air yang dipengaruhi oleh S2 dan M2. Hasil dari pengerjaan spring neap dapat dilihat di Gambar 4.9 di bawah ini.

Gambar 4. 9 Komponen

spring neaps

di Muara Sungai Batang Natal

selama 14 hari

C. Pemodelan Amplitudo M

4

(47)

=LOOKUP(D10;bathymetry!C27:W27;bathymetry!C31:W31)

Formula diatas digunakan untuk memasukkan data-data kedalaman pada halaman bathimetri pada cell tersebut. Kemudian pada cell selanjutnya yaitu cell E9 pada halaman model input formula :

=LOOKUP(D10;bathymetry!C27:W27;bathymetry!C30:W30)

formula tersebut untuk memasukkan data-data lebar pada halaman bathimetri pada cell E9.

Untuk menghitung nilai M4 pada cell C8 digunakan persamaan sebagai berikut :

...(4.6)

dimana :

AM4 : Amplitudo dari M4

x : Jarak titik tinjau dari mulut muara

A2M2 : Kuadrat dari amplitudo lunar semi-diurnal g : percepatan gravitasi

Persamaan tersebut kita input kedalam Microsoft Excel dengan bentuk sebagai berikut :

(48)

“(2000-D10)” merupakan jarak muara pada titik tinjau. “D6*D6” merupakan kuadrat dari amplitudo lunar semi diurnal (M2), “6,21*3600” merupakan periode

lunar quarter-diurnal, “9,82” adalah nilai gravitasi bumi yaitu sebesar 9,82 m/s2. Dari hasil perhitungan menggunakan persamaan diatas maka didapat nilai dari M4 pada kawasan Muara Sungai Batang Natal adalah sebesar 0,00013.

Nilai M4 sebesar 0,00013 diatas merupakan nilai yang ada pada kondisi eksisting muara. Untuk nilai M4 pada pemodelannya dilakukan dengan cara yang sama, hanya saja yang membedakannya adalah nilai kedalaman dan lebar yang digunakan adalah nilai yang sudah dimodelkan berdasarkan persamaan Wright et al. Untuk nilai amplitudo M4 pada pemodelan didapat sebesar 0,00013.

D. Kurva

Spring-Neap

Kurva

spring-neap

menunjukkan fluktuasi muka air yang

berpengaruh pada pemodelan muara. Tahapan awal membuat kurva ini

adalah dengan menginput data-data yang diperlukan yaitu periode waktu

(jam), nilai M

4

, dan kedalaman air (m) berturut-turut pada

cell

A31, A32,

dan A33. Untuk periode waktu digunakan selama 14 jam berdasarkan

waktu pengamatan pasang surut, diisi pada

cell

D31 sampai R31 dimulai

dari 0 hingga 14.

(49)

...(4.7)

dimana :

ht : Tinggi air AM4 : Amplitudo M4

2πt : Waktu dalam radian 6,21 : Periode lunar quarter-diurnal

Kemudian input persamaan diatas menjadi :

=$C$8*SIN(2*PI()*D31/6,21)

Dimana “$C$8” adalah amplitudo dari M4, “(2*PI()*D31/6,21)” merupakan waktu yang digunakan dalam radian dalam jam. Untuk mendapatkan perubahan nilai kedalaman tiap jam akibat spring-neaps pada cell D33 sampai cell R33, maka formulanya didasarkan pada perhitungan spring-neaps yang telah dilakukan sebelumnya. Untuk itu formula yang kita input adalah :

=LOOKUP(D31;'spring-neaps'!$B$3:$B$339;'spring-neaps'!$E$3:$E$339)+D32-0,6+$E$8

(50)

Gambar 4. 10 Hasil perhitungan perubahan kedalaman air akibat

spring-neaps

yang telah di plot ke dalam grafik

Setelah didapat hasil perhitungan perubahan kedalaman akibat pengaruh spring-neaps pada kondisi eksisting, selanjutnya akan dibandingkan dengan hasil pemodelannya dengan cara yang sama berdasarkan spring-neaps pemodelan yang telah dibuat

sebelumnya. Untuk mendapatkan hasil perhitungan pemodelan perubahan kedalaman tersebut maka digunakan formula sebagai berikut :

=LOOKUP(X31;'spring-neaps'!$T$3:$T$339;'spring-neaps'!$W$3:$W$339)+X32-0,6+$Y$8

(51)

Gambar 4. 11 Hasil perhitungan perubahan kedalaman air pada pemodelan

muara yang telah diplot kedalam grafik

4.2.3. Pemodelan Arus (currents)

Telah dijelaskan sebelumnya bahwa pasang surut air laut memaksa untuk menghasilkan arus didalam sistem muara yang kompleks. Arus dasarnya yang tidak tenang dan bervariasi dari subkritis ke superkritis dalam setiap siklus pasang surut. Pada pemodelan ini, arus muara di modelkan dengan asusmsi bahwa perubahan kedalaman air mengarah kepada debit yang diketahui melalui potongan melintang, sehingga arus rata-rata (rasio volume air yang melewati potongan melintang) dapat ditentukan.

Debit air tawar dan pasang surut yang melalui penampang muara merupakan tingkat perubahan daripada volume air yang berasal dari hulu penampang. Tingkat perubahan volume air, pada gilirannya, merupakan

(52)

...(4.8)

dimana W0 dan D0 adalah lebar dan kedalaman pada mulut muara, L adalah panjang muara, adalah perubahan kedalaman pasang surut per detik, Q

adalah debit air tawar, dan a dan b adalah koefisien lebar dan kedalaman muara.

Dengan demikian, tujuan disini adalah hanya untuk menghitung volume air, yang melewati tiap penampang dan arus pasang surut rata-rata sepanjang siklus pasang surut.

Pada pemodelan arus ini akan dibagi dalam empat bagian, yaitu :

a.

Pemodelan perubahan volume air dari hulu muara

b.

Pemodelan aliran pasang surut

c.

Pemodelan aliran air tawar

d.

Pemodelan aliran total

A. Pemodelan Perubahan Volume Air dari Hulu Muara

Buka kembali file pemodelan pasang surut kemudian simpan

dengan nama “pemodelan arus”. Kemudian buka halaman

“bathimetri” dan input pada

cell

C33 :

=100*C30/1000000

(53)

tinjau, “C30/1000000” adalah lebar muara yang diubah ke satuan

10

6

m

3

.

Kemudian pilih

cell

selanjutnya yaitu D33 dan input :

=100*C30/1000000 + C33

(54)

Gambar 4. 12 Hasil dari pemodelan perubahan volume air dari

hulu muara

B. Pemodelan Aliran Pasang Surut

Untuk pemodelan aliran pasang surut, buka

sheet

“model”

kemudian pada

cell

S27 masukkan “Lokasi Titik Tinjau”,

kemudian R28 dengan “

cross-section

”, kemudian pada R29

“volume hulu/m pasut”.

Kemudian masukkan formula-formula yang diperlukan

untuk parameter-parameter diatas. Untuk mencari nilai

cross-section

maka input formula dibawah ini di

cell

sebelahnya yaitu

cell

R29 :

=LOOKUP(D10;bathymetry!C27:W27;bathymetry!C32:W32)

dengan satuan “m2” yang di input pada U28.

Untuk volume hulu/m pasut maka input formula berikut di cell

T29 :

(55)

dengan satuan “m3x106” yang diinput pada cell U29.

Dengan selesainya pemodelan diatas maka akan didapat nilai dari cross-section setiap titik tinjau dan nilai volume airnya. Sebagai contoh pada titik tinjau P19 yaitu titik tinjau paling hulu sejauh 2 km dari mulut muara didapat cross-section pada titik itu sebesar 238 m2, dengan volume airnya sebesar 0,007 m3x106.

Setelah itu, pada cell A28 input “arus pasut” kemudian masukkan nilai dari arus pasut di D28 dengan formula :

=$T$29*1000000*(E27-D27)/($T$28*3600)

dimana “T29” adalah nilai volume aliran pada titik tinjau P19 sebesar 0,007 m3x106, “E27-D27” merupakan hasil dari perubahan aktual pada kedalaman pasang surut air tiap jam, “T28” adalah nilai cross-section

pada titik tinjau yang dipilih, “3600” untuk mengkonversi aliran dari meter per jam ke meter per detik.

C. Pemodelan Aliran Air Tawar

(56)

Format

spinner

pada E12 dengan nilai minimum 1,

incremental change

1 dan nilai maksimum sebesar 100. Kemudian

pada D13 input formula :

=D12/T28

dimana D12 adalah besarnya debit rata-rata yaitu sebesar 30 m3/s dan T28 adalah besarnya cross-section pada titik P19. Kemudian didapat hasil sebesar 0,126 m/s, nilai tersebut merupakan kecepatan aliran.

D. Pemodelan Aliran Total

Input “Total Aliran m/s” pada

cell

A29 dan input formulanya

pada

cell

D29 sebagai berikut :

=D28-$D$13

kemudian copy hingga Q29, hasil dari diatas dapat berupa negatif ataupun positif, yang menunjukkan bahwa nilai positif merupakan keadaan banjir, sedangkan positif dalam keadaan surut.

(57)

Gambar 4. 13 Perhitungan Arus Pada Kondisi Eksisting

(58)

4.2.4. Pemodelan Salinitas

Untuk pemodelan salinitas, digunakan persamaan Gauss yaitu :

... (4.9)

dimana :

S(x) : Salinitas pada jarak x Exp : Bilangan eksponensial X : Jarak

σx : Koefisien Dispersi

Langkah selanjutnya yaitu mencari nilai koefisien dispersi (σx ), dengan

metode trial and error, sama seperti untuk mencari niali koefisien lebar dan panjang muara di awal bab ini. Nilai koefisien dispersi akan diambil berdasarkan keadaan yang paling mendekati di lapangan.

Hasil dari perhitungan pemodelan salinitas dengan menggunakan persamaan Gauss diatas dapat dilihat pada Tabel 4.9 sebagai berikut:

(59)

Dari hasil diatas dapat dilihat yang paling mendekati dengan salinitas muara pada kondisi eksisting ialah dengan menggunakan koefisien dispersi (σx) senilai 0,04678.

4.3. HASIL PEMODELAN MUARA SUNGAI BATANG NATAL

Dengan selesainya pemodelan salinitas diatas maka selesailah seluruh pemodelan matematis Muara Sungai Batang Natal dengan menggunakan program Microsoft Excel. Dibawah ini akan dilampirkan rangkuman gambar dari seluruh

0,3 _3,5771E-286 ₀ _2E-250 _3,687E-62 _0,064863 0,9 _1,8048E-119 _2,4E-291 _1,67E-104 _1,115E-25 _1,867354 1 _1,24251E-98 _1,12E-240 _2,906E-86 _4,05E-21 _2,8420409 1,1 _8,8635E-80 _7,76E-195 _9,258E-70 _5,411E-17 _4,1558727 1,2 _6,55166E-63 _8,06E-154 _5,402E-55 _2,659E-13 _5,8387833 1,3 _5,0181E-48 _1,25E-117 _5,772E-42 _4,808E-10 _7,8815331 1,4 3,98262E-35 2,906E-86 1,13E-30 3,198E-07 10,221797 1,5 _3,27521E-24 _1,008E-59 _4,05E-21 _7,826E-05 _12,737144 1,6 _2,79095E-15 _5,227E-38 _2,659E-13 _0,0070447 _15,24913 1,7 _2,46437E-08 _4,05E-21 _3,198E-07 _0,2332889 _17,540674 1,8 _0,002254772 _4,691E-09 _0,0070447 _2,8420409 _19,385443 1,9 _2,137667286 _0,0811843 _2,8420409 _12,737144 _20,584172

(60)

(61)

Titik Tinjau P19 P21 P23 P25 P27 P29 P31 P33 P35 P37 P39 P41 P43 P45 P47 P49 P51 P53 P55 P57 P59

Jarak dari Mulut Muara (m) 2000 1900 1800 1700 1600 1500 1400 1300 1200 1100 1000 900 800 700 600 500 400 300 200 100 0 Lebar Estuari (m) 66,00 60,00 58,00 70,00 50,00 66,00 74,00 52,00 60,00 70,00 62,00 62,00 76,00 58,00 50,00 68,00 52,00 50,00 66,00 75,00 73,00 Kedalaman Estuari (m) 3,6 4,2 3,4 4,1 3,2 3,7 3,8 6,7 2,3 3,1 7,2 3,1 4,8 3,2 3,9 3,6 4,8 4,3 4,0 4,2 4,2 cross section (m²) 237,60 252,00 197,20 287,00 160,00 244,20 281,20 348,40 138,00 217,70 446,40 190,96 364,80 185,60 195,00 244,80 249,60 215,00 264,00 315,00 306,60

(62)