PEMERINGKATAN TIM PADA INDONESIAN BASKETBALL LEAGUE
DENGAN PAGERANK GOOGLE
RAMAWAN GAFRIADI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2008
PEMERINGKATAN TIM PADA INDONESIAN BASKETBALL LEAGUE
DENGAN PAGERANK GOOGLE
RAMAWAN GAFRIADI
G54103033
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2008
ABSTRACT
RAMAWAN GAFRIADI. Ranking Indonesian Basketball League Teams Using Google PageRank. Supervised by AGAH DRAJAT GARNADI and FARIDA HANUM.
The Google search engine uses ranking as the main feature for webpage searching. Google’s webpage ranking is query-independent. This means computation of each webpage’s PageRank is done off-line and not during the search query initiated by the user. Google shows the query relevant web sites and displays them according to their predetermined rank. In order to calculate the PageRanks, Google uses a matrix derived from the graph representation of the internet.
The goal of this work is to use Google’s webpage ranking method to find ranking IBL (Indonesian Basketball League) teams. First, creating the IBL graph, after that constructing and modifying the matrix corresponding to the IBL graph. Secondly computing the vector containing the ranks of the teams based on their season’s performance. Finally based on this ranking, the following week’s winners can be predicted.
ABSTRAK
RAMAWAN GAFRIADI. Pemeringkatan Tim pada Indonesian Basketball League dengan
PageRank Google. Dibimbing oleh AGAH DRAJAT GARNADI dan FARIDA HANUM. Mesin pencari Google menggunakan pemeringkatan sebagai fitur utama untuk pencarian halaman web. Peringkat halaman (PageRank) pada web Google bersifat bebas antrian. Ini berarti komputasi setiap PageRank halaman-halaman web dilakukan secara off-line dan bukan dilakukan selama pencarian kata kunci (query) yang dimasukan pengguna (user). Google menampilkan situs-situs web yang relevan dengan query sesuai peringkat yang telah ditentukan sebelumnya. Untuk menghitung PageRank ini Google menggunakan suatu graf internet yang direpresentasikan dengan matriks.
Tujuan penelitian ini adalah menggunakan metode PageRank Google untuk menentukan peringkat tim pada IBL (Indonesian Basketball League). Pertama, dibuat graf IBL, kemudian dibangun dan dimodifikasi suatu matriks yang bersesuaian dengan graf IBL. Lalu dihitung vektor yang memuat peringkat-peringkat tim-tim tersebut berdasarkan penampilan setiap musimnya. Dari hasil pemeringkatan, pemenang-pemenang minggu berikutnya dapat diprediksi.
PEMERINGKATAN TIM PADA INDONESIAN BASKETBALL LEAGUE
DENGAN PAGERANK GOOGLE
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Oleh:
RAMAWAN GAFRIADI
G54103033
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
BOGOR
2008
Judul : Pemeringkatan Tim pada
Indonesian Basketball League
dengan
PageRank
Nama : Ramawan Gafriadi
NRP : G54103033
Menyetujui:
Pembimbing I,
Pembimbing II,
Drs. Agah Drajat Garnadi, Grad. Dipl.Sc.
NIP. 131 803 648
Dra. Farida Hanum, M.Si.
NIP. 131 956 709
Mengetahui:
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Dr. Drh. Hasim, DEA
NIP. 131 578 806
PRAKATA
Alhamdulillah, puji syukur penulis panjatkan kehadirat Allah SWT atas segala nikmat, rahmat dan karunia-Nya sehingga penulis akhirnya dapat menyelesaikan karya ilmiah yang berjudul Pemeringkatan Tim pada Indonesian Basketball League dengan PageRank Google. Shalawat dan salam semoga selalu senantiasa tercurah kepada Rasulullah Muhammad SAW beserta keluarga, sahabat, dan pengikutnya hingga akhir zaman.
Karya ilmiah ini penulis persembahkan untuk Ibunda tercinta Nina Iriani, S.Sos. dan almarhum Ayahanda tercinta Ir. Erwandi Gutawan yang telah mencurahkan segala kasih sayangnya dan doa yang tidak pernah putus untuk penulis. Adikku tersayang Gema Iqbal beserta seluruh keluarga besar yang berada di Serang dan Jambi yang penulis selalu doakan dan banggakan, serta saudari Prasetyaning Diah Rizky Lestari, S.Si. yang dengan kesabaran, ketulusan, dan kasih sayangnya memberikan dukungan yang luar biasa.
Terima kasih penulis ucapkan kepada berbagai pihak yang telah memberikan bantuan dalam penyusunan karya ilmiah ini. Kepada Bapak Drs. Agah Drajat Garnadi, Grad. Dipl.Sc. dan Ibu Dra. Farida Hanum M.Si. terima kasih atas bimbingan, motivasi, dan kesabarannya selama proses penyusunan karya ilmiah ini. Ibu Dr. Ir. Sri Nurdiati, M.Sc. terima kasih atas motivasi, kesabaran, dan kesediaannya menjadi dosen penguji dalam sidang karya ilmiah penulis. Manto, Dian, dan Sita terima kasih atas kesediaannya menjadi pembahas dalam seminar penulis.
Tak lupa penulis ingin mengucapkan terima kasih kepada sahabat-sahabat terbaik Matematika angkatan 40: Dillah, Rusli, Dimas, Aam, Beri, Azis, Ali, Ari, Komenk, Prima, Demi, Anton, Sawa, Mufti, Lili, Ucup, Abay, Kafi, Febrian, Jayu, Palkon, Vina, Jaja, Indah, Iwit, Ifni, Mika, Metha, Mita, Achie, Ami, Icha, Kawal, Elis, Ulfa, Marlin, Nchi, Yuda, Uli, Sriti, Agatha, Herni, Nisa, Dwi, Mayang, dan Arin atas persahabatan yang tiada akhir, serta seluruh civitas Matematika IPB yang tidak dapat penulis sebutkan satu persatu.
Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat khususnya bagi penulis dan pembaca pada umumnya.
Bogor, Maret 2008 Ramawan Gafriadi
RIWAYAT PENULIS
Penulis dilahirkan pada tanggal 13 April 1985 di Bogor sebagai anak pertama dari dua bersaudara. Ibunda penulis bernama Nina Iriani, S.Sos. dan Ayahanda penulis bernama Ir. Erwandi Gutawan (Alm).
Pada tahun 1997 penulis menyelesaikan pendidikan di SD Negeri Semplak 2 Bogor. Penulis melanjutkan pendidikan di SMP Negeri 1 Bogor pada tahun yang sama. Pada tahun 2000 penulis melanjutkan pendidikan di SMU Negeri 2 Bogor. Pada tahun 2003 penulis diterima di Institut Pertanian Bogor melalui jalur USMI dan melanjutkan pendidikan di Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA) Departemen Matematika.
Selama mengikuti kegiatan perkuliahan, penulis aktif di berbagai kegiatan kemahasiswaan yaitu sebagai staf ahli bidang seni dan olahraga Gugus Mahasiswa Matematika (GUMATIKA) periode 2003/2004 dan sebagai ketua departemen pengembangan sumber daya mahasiswa Badan Eksekutif Mahasiswa (BEM) FMIPA periode 2006/2007. Penulis juga aktif sebagai panitia dan penyelenggara pada beberapa acara, antara lain Masa Perkenalan Kampus Mahasiswa Baru (MPKMB) pada tahun 2006 dan 2007, PESTA SAINS NASIONAL pada tahun 2006 dan 2007, MIPA Sport Tournament (MISOTO) pada tahun 2006, Competition of Sport MIPA Faculty (COSMIC) pada tahun 2007, Pelatihan TOEFL dan Tes TOEFL Gratis pada tahun 2007. Selain itu penulis juga aktif sebagai asisten mata kuliah Komputasi Terapan untuk mahasiswa S2 Departemen Matematika pada tahun ajaran 2007/2008, dan mengikuti lomba kreatifitas mahasiswa serta seminar nasional matematika pada tahun 2007 di Bandung.
Selain aktif di berbagai kegiatan kemahasiswaan penulis juga aktif sebagai pecinta alam. Sebagai pecinta alam penulis telah mendaki beberapa gunung yang ada di pulau Jawa, yaitu Gunung Gede-Pangrango, Gunung Salak dan Gunung Semeru yang merupakan gunung tertinggi di pulau Jawa.
DAFTAR ISI
Halaman DAFTAR GAMBAR ... viii DAFTAR LAMPIRAN... viii I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan ... 1 II LANDASAN TEORI 2.1 Graf ... 1 2.2 Matriks ... 3 III GAMBARAN UMUM PAGERANK GOOGLE 3.1 Digraf little-web ... 4 3.2 Peringkat Halaman little-web ... 5 3.3 Pengubahan Matriks H Menjadi Matriks Stokastik dan Matriks Taktereduksi ... 6 IV PENERAPAN PAGERANK GOOGLE DALAM PEMERINGKATAN TIM PADA IBL 4.1 Digraf IBL Berbobot ... 8 4.2 Matris dan Peringkat Tim pada IBL... 9
V SIMPULAN... 11 DAFTAR PUSTAKA ... 11 LAMPIRAN... 12
DAFTAR GAMBAR
Halaman
1 Graf G=( , )V E ... 1
2 Digraf D=( , )V A ... 2
3 Graf connected... 2
4 Graf tidak connected... 2
5 Digraf strongly connected ... 2
6 Digraf tidak strongly connected... 2
7 Digraf F... 2
8 Graf berbobot F=( , )V A ... 3
9 Digraf little-web... 4
10 Digraf little-web dengan sisi berarah semu... 6
11 Digraf M... 6
12 Digraf N... 6
13 Digraf little-web dengan sisi berarah semu yang ditambahkan kembali... 7
14 Digraf IBL ... 9
DAFTAR LAMPIRAN
Halaman 1 Pembuktian Teorema 1... 13I PENDAHULUAN
1.1 Latar Belakang
Memprediksi hasil suatu pertandingan merupakan hal yang biasa dilakukan oleh banyak orang. Berbagai cara dilakukan untuk memprediksi hasil suatu pertandingan, misalnya dengan menggunakan penghitungan matematika biasa, menerka dengan intuisi, ataupun menggunakan bantuan paranormal. Hasil suatu pertandingan dipengaruhi oleh banyak variabel, misalnya banyaknya kemenangan, kekuatan penyerangan dan pertahanan, banyaknya pemain yang cedera, administrasi keuangan suatu tim dan lainnya. Dari berbagai variabel yang mempengaruhi hasil suatu pertandingan berikutnya, salah satunya adalah peringkat suatu tim dalam kompetisi.
Dalam memprediksi hasil suatu pertandingan banyak metode yang dapat digunakan. Setiap metode memberikan prediksi hasil pertandingan sesuai dengan hasil yang didapat, salah satu metode yang digunakan adalah metode pemeringkatan halaman (PageRank) Google.
Google merupakan salah satu situs (web) yang digunakan untuk mencari alamat web
lain. Berdasarkan situs www.google.com
kinerja Google sampai saat ini merupakan yang terbaik di bidangnya. Clive Moler, pembuat Matlab, mengartikan PageRank
sebagai komputasi matriks terbesar di dunia
[Moler, 2002]. Mesin pencari Google menggunakan PageRank pada halaman-halaman web untuk menentukan bagaimana halaman-halaman web tersebut ditampilkan sebagai hasil pencarian suatu web.
Salah satu cabang olahraga yang diunggulkan oleh Indonesia di wilayah Asia Tenggara adalah bola basket. Tim bola basket Indonesia merupakan salah satu tim terkuat di wilayah ini dan termasuk ke dalam sepuluh besar tim basket terkuat di wilayah Asia.
IBL (Indonesian Basketball League) merupakan suatu kompetisi bola basket di Indonesia yang berskala nasional dan diselenggarakan setiap tahun. Pemenang dari IBL akan mewakili Indonesia dalam kompetisi bola basket se-Asia Tenggara.
Ide Google mengenai pemeringkatan halaman web diterapkan untuk pemeringkatan tim pada IBL. Tim IBL dianggap sebagai halaman web dan hasil pertandingan digunakan untuk membuat hubungan antartim tersebut. Hasil pemeringkatan tersebut digunakan untuk memprediksi hasil suatu pertandingan.
1.2 Tujuan
Tujuan penelitian ini adalah menggunakan metode PageRank Google untuk menentukan peringkat tim yang bertanding pada IBL.
II LANDASAN TEORI
Untuk memahami metode PageRank
Google yang digunakan untuk menentukan peringkat tim yang bertanding pada IBL, diperlukan pemahaman teori graf, dan matriks.
2.1 Graf
Graf digunakan untuk merepresentasikan struktur internet dan struktur IBL.
Definisi 1 (Graf)
Suatu graf adalah pasangan terurut ( , , dengan V himpunan takkosong dan hingga dan E adalah himpunan pasangan takterurut yang menghubungkan elemen-elemen V dan dinotasikan dengan .
)
V E
( , )
G= V E
Elemen V dinamakan simpul (node), dan elemen E dinamakan sisi (edge), dinotasikan
sebagai {i,j}, yaitu sisi yang menghubungkan simpul i dengan simpul j, dengan i,j∈V.
[Foulds, 1992] Contoh 1
G:
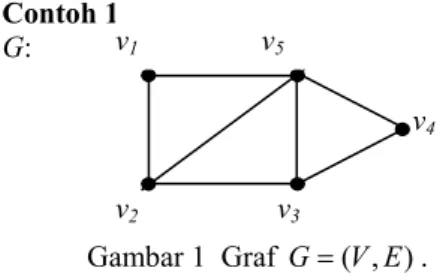
Gambar 1 Graf G=( , )V E .
Graf G pada Gambar 1 mempunyai himpunan simpul dan himpunan sisi
1 2 3 4 5 = { , , , , } V v v v v v v3 v2 v5 v1 v4
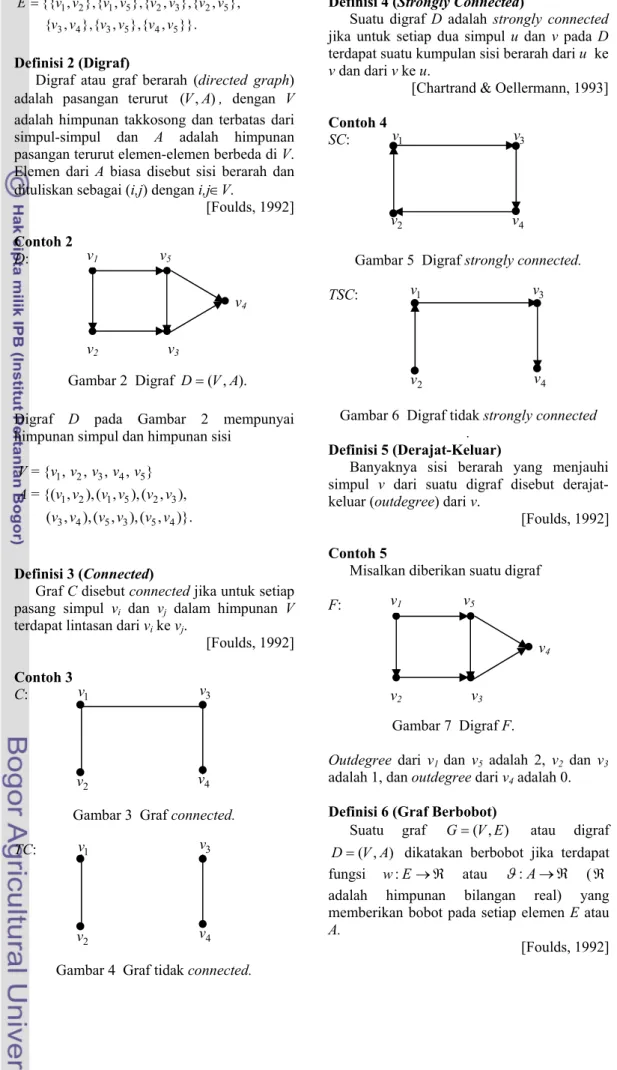
2 1 2 1 5 2 3 2 5 3 4 3 5 4 5 {{ , },{ , },{ , },{ , }, { , },{ , },{ , }}. E v v v v v v v v v v v v v v = Definisi 2 (Digraf)
Digraf atau graf berarah (directed graph) adalah pasangan terurut , dengan V
adalah himpunan takkosong dan terbatas dari simpul-simpul dan A adalah himpunan pasangan terurut elemen-elemen berbeda di V. Elemen dari A biasa disebut sisi berarah dan dituliskan sebagai (i,j) dengan i,j∈V.
( , )V A 4 v 2 v 2 v v4 2 v v4 [Foulds, 1992] Contoh 2 D: Gambar 2 Digraf D=( , ).V A
Digraf D pada Gambar 2 mempunyai himpunan simpul dan himpunan sisi
1 2 3 4 5 1 2 1 5 2 3 3 4 5 3 5 4 = { , , , , } = {( , ), ( , ), ( , ), ( , ), ( , ), ( , )}. V v v v v v A v v v v v v v v v v v v Definisi 3 (Connected)
GrafC disebut connected jika untuk setiap pasang simpul vi dan vj dalam himpunan V
terdapat lintasan dari vi ke vj.
[Foulds, 1992] Contoh 3
C:
Gambar 3 Graf connected. TC:
Gambar 4 Graf tidak connected.
Definisi 4 (Strongly Connected)
Suatu digraf D adalah strongly connected
jika untuk setiap dua simpul u dan v pada D
terdapat suatu kumpulan sisi berarah dari u ke
v dan dari v ke u.
[Chartrand & Oellermann, 1993] Contoh 4
SC:
Gambar 5 Digraf strongly connected. TSC:
Gambar 6 Digraf tidak strongly connected .
Definisi 5 (Derajat-Keluar)
Banyaknya sisi berarah yang menjauhi simpul v dari suatu digraf disebut derajat-keluar (outdegree) dari v.
[Foulds, 1992] Contoh 5
Misalkan diberikan suatu digraf
F: Gambar 7 Digraf F.
Outdegree dari v1 dan v5 adalah 2, v2 dan v3 adalah 1, dan outdegree dari v4adalah 0. Definisi 6 (Graf Berbobot)
Suatu graf G=( , )V E atau digraf
( , )
D= V A dikatakan berbobot jika terdapat fungsi w E: → ℜ atau ϑ:A→ ℜ (ℜ
adalah himpunan bilangan real) yang memberikan bobot pada setiap elemen E atau
A. [Foulds, 1992] v5 v4 v3 v2 v1 1 v v3 1 v v3 3 v 1 v 4 v 2 v 1 v v3 v5 v4 v3 v1 v2
3
Contoh 6
Misalkan diberikan fungsi bobot untuk digraf berbobot
:
w A→ ℜ
( , )
F = V A pada Gambar 8. Jika didefinisikan digraf F adalah:
F: 2 4 1 3 2 1
Gambar 8 Graf berbobot F=( , )V A . Nilai bobot adalah:
5 4 1 5 3 4 1 2 2 3 5 3 4 2 1 3. v v v v v v v v v v v v w w w w w w = = = = = = 2.2 Matriks
Suatu digraf direpresentasikan dan diproses menjadi matriks yang bersesuaian dengan digraf tersebut.
Definisi 7 (Matriks Taknegatif)
Suatu matriks A disebut matriks taknegatif jika dan disebut matriks positif jika
untuk setiap i dan j. 0 ij a ≥ 0 ij a > [Minc, 1988] Definisi 8 (Matriks Taknegatif yang Bersesuaian dengan Digraf)
(a) Matriks adjacency D dari suatu digraf
( , ) yang mempunyai n simpul adalah:
D= V A
( )dij n n×
=
D sehingga
jika terdapat sisi berarah 1 ; dari ke di 0 ; jika selainnya ij v v D d i j ⎧ ⎪ = ⎨ ⎪ ⎩ untuk ,v vi j∈V.
(b) Digraf D disebut bersesuaian dengan suatu matriks taknegatif D jika matriks taknegatif D mempunyai pola nol yang sama dengan pola nol pada matriks
adjacency dari digraf D.
[Minc, 1988]
Contoh 7
Misalkan diberikan digraf F pada Gambar 7. Matriks adjacency F dari digraf F pada Gambar 7 adalah: 0 1 0 0 1 0 0 1 0 0 . 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ F
Misalkan diberikan digraf F pada Gambar 7. Matriks taknegatif F yang bersesuaian dengan digraf F pada Gambar 7 antara lain:
0 1 0 0 2 0 0 1 0 0 . 0 0 0 2 0 0 0 0 0 0 0 0 3 4 0 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ F
Definisi 9 (Matriks Taktereduksi)
Matriks taknegatif A dikatakan sebagai matriks yang tereduksi jika terdapat suatu partisi dari himpunan indeks {1,2,...,n} ke dalam himpunan-himpunan takkosong yang saling lepas I1 dan I2 sehingga aij =0 apabila
1
i I∈ dan j I∈ 2. Jika tidak demikian, A disebut matriks yang taktereduksi.
[Leon, 2002] Contoh 8 (Matriks Tereduksi)
Misalkan 0 2 1 1 0 2 , 0 1 0 ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ T
misalkan I1={3} dan sehingga dan apabila
2 {1, 2}, I =
1 2 {1, 2,3}
I ∪I = aij =0 i I∈ 1
dan j I∈ 2. Oleh karena itu, T tereduksi.
Contoh 9 (Matriks Taktereduksi)
Misalkan 0 2 1 1 0 2 , 2 1 0 ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ T
matriks T taktereduksi jika tidak terdapat suatu partisi dari himpunan indeks {1,2,...,n} ke dalam himpunan-himpunan takkosong
v4
v3
v2
4
yang saling lepas I1 dan I2 sehingga aij =0 apabila i I∈ 1 dan j I∈ 2.
Misalkan I1={1,3} dan I2 ={2}, sehingga I1∪I2 ={1, 2,3} dan aij ≠0.
Misalkan dan sehingga
dan . Misalkan dan sehingga dan . Misalkan dan sehingga dan . Misalkan dan sehingga dan . Misalkan dan sehingga
dan . Oleh karena itu, T taktereduksi. 1 {1, 2} I = I2 ={3}, 1 2 {1, 2,3} I ∪I = aij ≠0 1 {2,3} I = I2 ={1}, 1 2 {1, 2,3} I ∪I = aij ≠0 1 {1} I = I2 ={2,3}, 1 2 {1, 2,3} I ∪I = aij ≠0 1 {2} I = I2 ={1,3}, 1 2 {1, 2,3} I ∪I = aij ≠0 1 {3} I = I2 ={1, 2}, 1 2 {1, 2,3} I ∪I = aij ≠0 Teorema 1
Matriks taknegatif adalah taktereduksi jika dan hanya jika digraf yang berpadanan adalah
strongly connected.
[Minc, 1988] Bukti lihat Lampiran 1.
Ilustrasi
Misalkan diberikan matriks taknegatif taktereduksi T pada Contoh 8, digraf yang bersesuaian adalah:
digraf tersebut strongly connected. Definisi 10 (Matriks Stokastik)
Suatu matriks A disebut stokastik jika memiliki entri-entri taknegatif dan jumlah entri-entri pada tiap baris adalah satu.
[Leon, 2002] Contoh 10 (Matriks Stokastik)
Misalkan . 0 1/ 3 1/ 3 1/ 3 1/ 4 1/ 4 1/ 4 1/ 4 1 0 0 0 0 1/ 2 0 1/ 2 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ A
Matriks A memiliki entri-entri taknegatif dan jumlah entri-entri pada tiap baris adalah satu.
III GAMBARAN UMUM PAGERANK GOOGLE
Dalam bab ini PageRank Google direpresentasikan dan dikembangkan melalui suatu contoh. Didefinisikan sebuah web kecil (little-web) dengan 5 halaman web.
3.1 Digraf little-web
Suatu graf berarah dibuat untuk merepresentasikan struktur little-web yang bersesuaian dengan little-web. Simpul-simpul pada digraf tersebut menyatakan halaman-halaman pada little-web dan sisi berarahnya menyatakan hubungan antarhalaman
little-web.
Gambar 9 Digraf little-web.
Dalam digraf little-web banyaknya hubungan dari suatu simpul disebut outdegree
simpul tersebut. Pada Gambar 9 halaman web
1 mempunyai hubungan dengan halaman web
3, halaman web 4, dan halaman web 5, sehingga outdegree halaman web 1 adalah tiga, tetapi outdegree halaman web 2 adalah 0, sehingga simpul ini disebut simpul berjuntai. Suatu matriks terhubungyang bersesuaian dengan digraf little-web dikonstruksi untuk menyatakan struktur pada jaringan little-web. Misalkan matriks tersebut diberi nama H. Matriks H mempunyai 5 baris dan 5 kolom. Entri dalam baris i dan kolom j menyatakan hubungan dari halaman webi ke halaman web j. Jika ada suatu hubungan dari halaman webi
ke web j, entri yang bersesuaian bernilai positif dan jika tidak ada hubungan entri bernilai 0. Nilai entri positif bergantung pada
outdegree halaman web i, dalam hal ini nilainya 1/outdegree halaman webi.
1 3 2 2 3 5 4 1
5
Matriks H yang bersesuaian dengan digraf
little-web adalah: . 0 0 1/ 3 1/ 3 1/ 3 0 0 0 0 0 0 1 0 0 0 1/ 2 0 1/ 2 0 0 1/ 2 0 0 1/ 2 0 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎝ H ⎟ ⎠
3.2 Peringkat Halaman little-web
Peringkat suatu halaman web P
didefinisikan sebagai: ( ) ( ) | | Q BP r Q r P Q ∈ =
∑
(1)dengan r(P) menyatakan peringkat suatu halaman web P, sedangkan BP menyatakan himpunan semua halaman web yang mengarah pada P, dan |Q| menyatakan outdegree suatu halaman web Q [Brin et al.,1999]. Jika halaman webP dan Q mempunyai hubungan satu sama lain maka peringkat P bergantung pada peringkat Q, dan sebaliknya. Nilai peringkat P bergantung pada nilai-nilai peringkat dan outdegree halaman web yang menunjuk pada P. Untuk peringkat suatu halaman webP setelah k+1 iterasi adalah:
1 ( ) ( ) | | k k Q BP r Q r P Q + ∈ =
∑
(2).Peringkat awal halaman-halaman little-web adalah 1/n yang ekuivalen dengan tingkat kepentingan yang sama untuk semua halaman
web. Karena ada 5 halaman web pada little-web pada Gambar 9 maka masing-masing menerima peringkat awal 1/5. Misalkan
halaman-halaman web pada little-web diberi nama P1, P2, P3, P4, dan P5. Vektor peringkat awal little-web adalah vektor baris yaitu:
(
)
(
)
0 0( ) 1 0( ) 2 0( ) 3 0( ) 4 0( )5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 . r P r P r P r P r P = = ZDengan menggunakan peringkat awal, ditunjukkan satu iterasi dari Persamaan (2), yaitu: 0 4 0 5 1 1 4 5 0 3 1 2 3 0 1 0 4 1 3 1 4 0 1 0 5 1 4 1 5 0 1 1 5 1 ( ) ( ) 1/ 5 1/ 5 1 ( ) | | | | 2 2 5 ( ) 1/ 5 1 ( ) | | 1 5 ( ) ( ) 1/ 5 1/ 5 1 ( ) | | | | 3 2 6 ( ) ( ) 1/ 5 1/ 5 1 ( ) | | | | 3 2 6 ( ) 1/ 5 1 ( ) . | | 3 15 r P r P r P P P r P r P P r P r P r P P P r P r P r P P P r P r P P = + = + = = = = = + = + = = + = + = = = =
Setelah satu iterasi, vektor peringkatnya adalah:
(
)
(
)
1 1( ) ( ) ( ) ( ) ( )1 1 2 1 3 1 4 1 5 1/ 5 1/ 5 1/ 6 1/ 6 1/15 . r P r P r P r P r P = = ZPerhatikan bahwa vektor peringkat Z1 pada
little-web bisa dinyatakan sebagai perkalian vektor peringkat awal dan matriks H, yaitu:
1= 0 . Z Z H
(
)
(
)
1 0 1/ 5 1/ 5 1/ 6 1/ 6 1/15 0 0 1/ 3 1/ 3 1/ 3 0 0 0 0 0 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 0 1 0 0 0 1/ 2 0 1/ 2 0 0 1/ 2 0 0 1/ 2 0 . = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = Z Z HVektor peringkat dapat dirumuskan sebagai perkalian vektor peringkat sebelumnya dan
6 Perhatikan bahwa 1 0 2 2 1 0 0 2 3 3 2 0 0 0 k. k = = = = = = = = Z Z H Z Z H Z HH Z H Z Z H Z H H Z H Z Z H #
Vektor peringkat little-web setelah k+1
adalah: (4). 1 1 0 k 1, 2,3,... k+ = + k= Z Z H
Matriks H harus bersesuaian dengan digraf little-web yang strongly connected, agar penghitungan berulang dari Persamaan (4) didapatkan [Brin etal.,1999].Agar matriks H bersesuaian dengan digraf little-web yang
strongly connected, matriks H dibuat menjadi stokastik dan matriks taktereduksi.
3.3 Pengubahan Matriks H Menjadi Matriks Stokastik dan Matriks Taktereduksi
Pengubahan dilakukan dengan mengganti baris yang semua entrinya bernilai 0 pada matriks H dengan 1/n, dengan adalah banyaknya halaman web pada little-web. Matriks stokastik yang baru disebut matriks S.
Little-web pada Gambar 9 mempunyai n
5
n= , sehingga matriks S adalah:
. 0 0 1 / 3 1 / 3 1 / 3 1 / 5 1/ 5 1 / 5 1 / 5 1 / 5 0 1 0 0 0 1 / 2 0 1 / 2 0 0 1 / 2 0 0 1/ 2 0 ⎛ ⎜ ⎜ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ S ⎞ ⎟ ⎟
Pengubahan ini mengakibatkan dibuatnya suatu sisi berarah semu dari simpul berjuntai ke setiap halaman web yang lain pada little-web, sehingga mengakibatkan outdegree
halaman web 2 adalah 5.
Gambar 10 Digraf little-web dengan sisi berarah semu.
Matriks stokastik S bersesuaian dengan suatu digraf baru yang mempunyai tambahan sisi berarah semu dari halaman web 2 ke halaman web yang lain, yaitu digraf little-web
yang strongly connected. Menurut Teorema 1 matriks S bersesuaian dengan digraf tersebut adalah taktereduksi. Akan tetapi, pengubahan matriks H menjadi matriks stokastik tidak selalu menghasilkan matriks taktereduksi [Brin etal.,1999].
Berikut diberikan ilustrasi dari pengubahan suatu matriks menjadi matriks stokastik tidak selalu menghasilkan matriks taktereduksi. Misalkan diberikan 0 0 0 0 0 1 , 0 1 0 ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ M
sehingga digraf M yang merepresentasikan matriks M adalah:
M:
Gambar 11 Digraf M.
Pengubahan dilakukan agar matriks M stokastik dengan mengganti baris yang semua entrinya bernilai 0 pada matriks M dengan 1/n, dengan adalah banyaknya simpul pada digraf M. Matriks stokastik yang baru disebut matriks N. Digraf M pada Gambar 11 mempunyai n 3 n= , sehingga 1/3 1/3 1/ 3 0 0 1 0 1 0 ⎛ ⎞ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ N ,
dan digraf N yang merepresentasikan matriks N adalah:
N:
Gambar 12 Digraf N.
Matriks N stokastik tetapi matriks N tereduksi karena digraf N yang merepresentasikan matriks N tidak strongly connected.
2 3 5 4 1 1 2 3 1 3 2
7
Kembali kepada matriks H, agar matriks H menjadi matriks stokastik dan matriks taktereduksi, sisi berarah semu ditambahkan kembali dari setiap halaman web ke setiap halaman web lainnya dengan menambahkan suatu matriks T dan disebut matriks S T+ .
Gambar 13 Digraf little-web dengan sisi berarah semu yang ditambahkan kembali.
Matriks Tdapat ditulis sebagai , dengan E adalah suatu vektor baris yang nilai entri-entrinya adalah 1, dan vektor V adalah suatu vektor baris yang merepresentasikan peluang halaman web dipilih pada little-web
dengan semua entrinya bernilai positif dan jumlahnya adalah 1. Misalkan peluang setiap halaman web adalah 1/5 sehingga
T = T E V
(
1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 ,)
= V dan misalkan(
1 1 1 1 1)
= E sehingga 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 ⎛ ⎜ ⎜ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ T ⎞ ⎟ ⎟ 1/ 5 1/ 5 8 /15 8 /15 8 /15 2 / 5 2 / 5 2 / 5 2 / 5 2 / 5 . 1/ 5 6 / 5 1/ 5 1/ 5 1/ 5 7 /10 1/ 5 7 /10 1/ 5 1/ 5 7 /10 1/ 5 1/ 5 7 /10 1/ 5 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ + = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ S TSemua entri matriks bernilai positif dan taktereduksi karena digraf little web strongly connected, tetapi matriks ini tidak stokastik. Matriks
+
S T
+
S T diubah menjadi matriks yang baru yang disebut matriks G. Misalkan dipilih suatu bilangan αantara 0 dan 1 sehingga G=αS+ −(1 α)T. Bilangan α
merepresentasikan akurasi proses pemeringkatan yang dipengaruhi oleh matriks S dan matriks T. Berdasarkan situs
www.google.com, Google menggunakan
0.85
α = , yang berarti dalam proses pemeringkatan, 85% dipengaruhi oleh matriks S, begitu pula nilai α pada little-web.
Vektor peringkat little-web setelah k+1
menjadi
1 1, 2,3,...
k+ = k k=
Z Z G (5).
Matriks G taktereduksi dan stokastik adalah: 3/100 3/100 47 /150 47 /150 47 /150 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 3/100 22/ 25 3/100 3/100 3/100 91/ 200 3/100 91/ 200 3/100 3/100 91/ 200 3/100 3/100 91/ 200 3/100 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ G
Vektor peringkat setelah satu iterasi menjadi 1 117 117 617 617 181 . 500 500 3000 3000 1500 ⎛ ⎞ = ⎜⎝ ⎟⎠ Z
Vektor peringkat setelah dua iterasi adalah: 2 1 3 /100 3/100 47 /150 47 /150 47 /150 1/ 5 1/ 5 1/ 5 1/ 5 1/ 5 117 117 617 617 181 3 /100 22 / 25 3/100 3 /100 3 /100 500 500 3000 3000 1500 91/ 200 3/100 91/ 200 3 /100 3 /100 91/ 200 3/100 3/100 91/ 200 3 /100 (0.2084 = ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎛ ⎞⎜ ⎟ = ⎜⎝ ⎟⎜⎠ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = Z Z G 72 0.244597 0.223488 0.187363 0.13608). 2 3 5 4 1
8
Jadi setelah 2 iterasi peringkat halaman
web 1 adalah 0.208472, peringkat halaman
web 2 adalah 0.244597, peringkat halaman
web 3 adalah 0.223488, peringkat halaman
web 4 adalah 0.187363, dan peringkat halaman web 5 adalah 0.13608. Kesimpulan dari contoh ini adalah peringkat halaman
little-web berdasarkan tingkat
kepentingannya, semakin tinggi nilai peringkat semakin tinggi tingkat kepentingannya, dengan peringkat pada
little-web adalah:
2 3 1 4 5 P P P P P .
IV PENERAPAN PAGERANK GOOGLE
DALAM PEMERINGKATAN TIM PADA IBL
Digraf IBL yang merepresentasikan digraf Google diproses untuk mendapatkan matriks IBL yang bersesuaian dan dihitung vektor peringkat dari matriks tersebut.
4.1 Digraf IBL Berbobot
Penerapan PageRank Google dalam pemeringkatan tim pada IBL dilakukan dengan
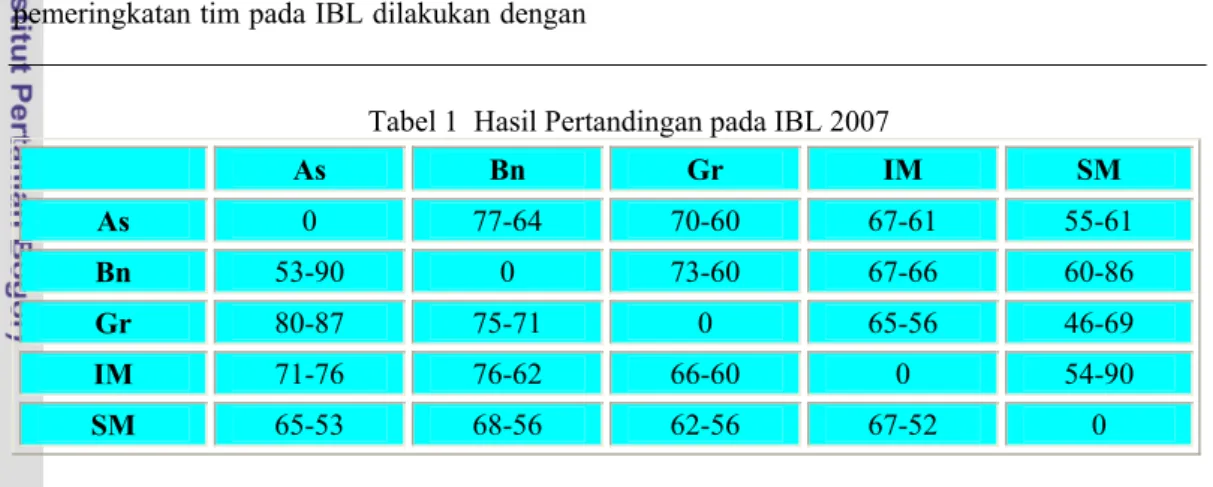
memilih lima tim teratas IBL yaitu Aspac (As), Bhineka Sritex (Bn), Garuda Panasia (Gr), Indonesia Muda (IM), dan Satria Muda Britama (SM). Data hasil pertandingan diperoleh dari www.amild.com/ibl2007/ dan dituliskan pada Tabel 1.
Tabel 1 Hasil Pertandingan pada IBL 2007
As Bn Gr IM SM As 0 77-64 70-60 67-61 55-61 Bn 53-90 0 73-60 67-66 60-86 Gr 80-87 75-71 0 65-56 46-69 IM 71-76 76-62 66-60 0 54-90 SM 65-53 68-56 62-56 67-52 0
Dari Tabel 1 akan dibuat digraf IBL. Setiap tim dalam IBL direpresentasikan oleh suatu simpul dalam digraf. Setiap dua kali tim bermain mereka membentuk suatu sisi berarah dan berbobot. Arah dari sisi berarah ini adalah dari tim yang kalah ke tim yang menang dan bobot dari sisi berarahnya sama dengan nilai positif selisih skor dalam pertandingan yang dimainkan.
Pada Tabel 1, SM menang melawan As dengan poin 61-55. Pertandingan ini menghasilkan sisi berarah dari As ke SM dengan bobot 6.
Begitu pula pada pertandingan selanjutnya antara As melawan SM dimana SM kembali menang dengan poin 65-53 yang menghasilkan sisi berarah dari As ke SM dengan bobot 12, sehingga dalam graf IBL menghasilkan sisi berarah dari As ke SM dengan bobot keseluruhan 18. Demikian pula dengan hasil pertandingan lainnya. Namun pada Tabel 1 SM selalu menang di setiap pertandingan ini menyebabkan outdegree SM adalah 0.
9
Digraf IBL adalah:
As Bn Gr SM 18 38 51 29 50 11 3 13 3 17 IM
Gambar 14 Digraf IBL. 4.2 Matriks dan Peringkat Tim pada IBL
Digraf IBL direpresentasikan oleh matriks I. Bobot pada sisi berarah (i,j) bersesuaian dengan jumlah nilai tim i untuk tim j.
Didefinisikan entri (i,j) dalam matriks I adalah: 1 ij ij n ij j w h w = =
∑
dengan ij adalah bobot pada sisi berarah dari tim i ke tim j. Matriks I adal
w ah: ⎟ ⎟ ⎟ ⎟ I As Bn Gr IM SM As 0 0 0 0 18/18 Bn 50/101 0 0 13/101 38/101 . Gr 17/49 3/49 0 0 29/49 IM 11/65 0 3/65 0 51/65 SM 0 0 0 0 0 ⎛ ⎞ ⎜ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎜ ⎜ ⎝ ⎠
Matriks I memiliki baris yang entri-entrinya semua bernilai nol. Matriks I diubah agar menjadi matriks stokastik dan matriks taktereduksi. Pengubahan dilakukan dengan mengganti nilai-nilai nol pada matriks I oleh 1/n dengan adalah banyaknya tim pada IBL. Matriks stokastik yang baru disebut matriks IB. Digraf IBL pada Gambar 11 mempunyai n 5 n= , sehingga matriks IB adalah: As Bn Gr IM SM As 0 0 0 0 18/18 Bn 50/101 0 0 13/101 38/101 . Gr 17/ 49 3/ 49 0 0 29/ 49 IM 11/ 65 0 3/ 65 0 51/ 65 SM 1/5 1/5 1/5 1/5 1/5 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ IB
Pengubahan matriks I dilakukan kembali dengan menambahkan matriks L dan dipilih suatu bilangan ,α matriks ini disebut matriks IBL, sehingga matriks IBL adalah:
(1 )
α α
= + −
IBL IB L.
Matriks Ldapat ditulis sebagai
Vektor personalisasi (V) merepresentasikan banyaknya kemenangan yang diraih dari keseluruhan pertandingan IBL dan E adalah vektor kolom yang semua entrinya bernilai 1. Dipilih
.
T
=
L E V
α =0.85, yang berarti dalam proses pemeringkatan, 85% dipengaruhi oleh matriks IB, dan merepresentasikan peringkat tim pada IBL setelah k iterasi, yaitu
k
P
1 .
k = k− ×
P P IBL
Matriks IB diperbaharui setiap minggu, dan pemenang pertandingan-pertandingan pada minggu selanjutnya diprediksi berdasarkan urutan peringkat tim. Jika semakin baik peringkat suatu tim terhadap lawannya maka peluang tim tersebut untuk menang akan lebih besar dibandingkan peluang lawannya untuk menang.
10
Berikut diberikan penghitungan setelah satu iterasi dan dua iterasi.
Nilai outdegree direpresentasikan dengan |nama tim|, dan r adalah peringkat tim IBL, dan adalah vektor peringkat awal, sehingga 0 P 0 0 0 0 0 ( ) 1/ 5 18 ( ) 1/ 5 101 ( ) 1/ 5 49 ( ) 1/ 5 65 ( ) 1/ 5 0 r As As r Bn Bn r Gr Gr r IM IM r SM SM = = = = = = = = = = 0 ( (0 ) 0( ) 0( ) 0( ) 0( )) ( 1/5 1/ 5 1/5 1/5 1/5 ). r As r Bn r Gr r IM r SM = = P
Penghitungan peringkat tim IBL setelah satu iterasi adalah:
0 0 0 1 0 1 0 1 0 1 ( ) ( ) ( ) ( ) | | | | | | 1/5 1/5 1/5 14699 101 49 65 1608425 ( ) 1/5 1 ( ) | | 49 245 ( ) 1/5 1 ( ) | | 65 325 ( ) 1/5 1 ( ) | | 101 505 r Bn r Gr r IM r As Bn Gr IM r Gr r Bn Gr r IM r Gr IM r Bn r IM Bn = + + = + + = = = = = = = = = = 0 0 0 0 1 ( ) ( ) ( ) ( ) ( ) | | | | | | | | 1/ 5 1/ 5 1/ 5 1/ 5 586267 . 18 101 49 65 28951650 r As r Bn r Gr r IM r SM As Bn Gr IM = + + + = + + + =
Vektor peringkat Z setelah satu iterasi adalah:
1 ( (1 ) 1( ) 1( ) 1( ) 1( )) 14699 1 1 1 586267 ( ) 1608425 245 325 505 28951650 r As r Bn r Gr r IM r SM = = P .
Penghitungan selanjutnya yaitu penghitungan peringkat tim IBL setelah dua iterasi. Misalkan diberikan
(
)
(
)
6 / 20 2/ 20 2 / 20 2 / 20 8/ 20 1 1 1 1 1 , = = V Emaka matriks L adalah:
3/10 1/10 1/10 1/10 2/5 3/10 1/10 1/10 1/10 2/5 . 3/10 1/10 1/10 1/10 2/5 3/10 1/10 1/10 1/10 2/5 3/10 1/10 1/10 1/10 2/5 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ L
Misalkan α =0.85, matriks IBL dan vektor peringkat IBL setelah dua iterasi adalah:
2 1 0.045 0.015 0.015 0.015 0.91 0.465792 0.015 0.015 0.124406 0.379802 0.339898 0.0670408 0.015 0.015 0.563061 0.188846 0.015 0.0542308 0.015 0.726923 0.215 0.185 0.185 0.185 0.23 (0.00808594 0.00418 ⎛ ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ = ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ ⎝ ⎠ = × = IBL P P IBL 051 0.00409807 0.00446694 0.0176959),
dan peringkat tim pada IBL secara berurutan dari peringkat satu sampai peringkat lima adalah:
11
V SIMPULAN DAN SARAN
5.1 Simpulan
Pemeringkatan tim pada IBL dapat dilakukan dengan menggunakan metode
PageRank Google. Pertama digraf IBL dibuat dan dijadikan digraf yang strongly connected.
Kemudian digraf IBL direpresentasikan dengan suatu matriks, sehingga matriks tersebut stokastik dan taktereduksi. Kemudian dihitung vektor peringkat yang memuat peringkat tim pada IBL tersebut berdasarkan hasil-hasil pertandingan pada setiap minggunya.
Vektor personalisasi dalam proses pemeringkatan dapat diubah untuk mencerminkan suatu statistik hipotesis, misalnya banyaknya kemenangan, kekuatan penyerangan dan pertahanan, banyaknya pemain yang cedera, administrasi keuangan suatu tim dan lainnya.
Matriks IBL diperbaharui setiap minggu, dan pemenang pertandingan-pertandingan pada minggu selanjutnya diprediksi berdasarkan urutan peringkat tim. Jika semakin baik peringkat suatu tim terhadap lawannya maka peluang tim tersebut untuk menang akan lebih besar dibandingkan peluang lawannya untuk menang.
5.2 Saran
Pada tulisan ini telah dibahas mengenai masalah pemeringkatan tim pada IBL yang menggunakan metode pemeringkatan pada halaman web Google. Akan lebih baik lagi jika metode pemeringkatan halaman web
Google ini digunakan untuk masalah pemeringkatan yang lebih kompleks, misalnya masalah pemeringkatan yang melibatkan lebih banyak lagi tim yang bertanding.
DAFTAR PUSTAKA
Brin, S. Page, L. Motwami, P & Winograd, T. 1999. The PageRank Citation Ranking: Bringing Order to the Web. Computer Science Department, Stanford University, Technical Report 1999-0120. Chartrand, G & Oellermann, O.R. 1993.
Applied and Algorithmic Graph Theory.
McGraw-Hill, New York.
Foulds, L. R. 1992. Graph Theory Applications. Springer-Verlag, New York.
Google.http://www.google.com/. [13 September 2007]
Govan, A. Y & Meyer, C. D. 2006. Ranking National Football League Teams Using
Google’s PageRank. Center for Research
in Scientific Computing, NorthCarolina State University, Raleigh, NC 27695-8205.
IBL 2007.http://www.amild.com/ibl2007/. [13 September 2007]
Leon, S. J. 2002. Linear Algebra with Applications, Sixth Edition. Prentice-Hall. New Jersey.
Minc, H. 1988. Nonnegative Matrices. John Wiley, New York.
Moler, C. 2002. The World’s Largest Matrix Computation. Matlab News and Notes.
12
13
Lampiran 1
Pembuktian Teorema 1 Teorema 1
Matriks taknegatif adalah taktereduksi jika dan hanya jika digraf yang berpadanan adalah
strongly connected.
[Minc, 1988] Bukti:
( )⇒ Misalkan matriks taknegatif dan taktereduksi dan digraf yang berpadanan dengan A adalah D. Akan dibuktikan bahwa D adalah strongly connected. Untuk setiap i, j terdapat bilangan bulat positif k sehingga dan D mempunyai sisi berarah yang menghubungkan setiap simpul i dengan simpul j. Akibatnya D strongly connected.
( )aij = A 0 k ij a >
( )⇐ Misalkan D adalah digraf yang strongly connected yang berpadanan dengan matriks taknegatif A. Akan dibuktikan bahwa A=( )aij adalah taktereduksi. Karena D yang strongly connected maka untuk setiap pasangan terurut dari simpul yang berbeda i dan j, terdapat sebuah sisi berarah di D yang menghubungkan simpul i dengan simpul j, sehingga matriks taktereduksi.
( )aij
=
A
14
Lampiran 2
Penghitungan dengan Mathematica 6
Vektor peringkat little web setelah satu iterasi adalah:
Matriks T pada little web adalah:
15
16
Vektor peringkat little web setelah dua iterasi adalah:
17