Model Log Linier untuk Empat Dimensi. Log Linier Model for Four Dimentions

(1)

Model Log Linier untuk Empat Dimensi

Log Linier Model for Four Dimentions

M. Aris Budiyono

1

, Sri Wahyuningsih

2

, Ika Purnamasari

3 1_{Mahasiswa Program Studi Statistika Fakultas MIPA Universitas Mulawarman}

2,3_{Dosen Program Studi Statistika Fakultas MIPA Universitas Mulawarman}

E-mail: [email protected], [email protected], [email protected]

Abstract

One of categorical data analysis is log linear models. Log linear models are used to look for patterns of relationships between a group of categorial variables includes the association of two variables, three variables, or more. Log linear models that include four associations of categorical variables called log linear model of the four-dimensional. Log linear models was the most appropriate to interpret the pattern of relationship. The purpose of this study is to elaborate the log linear model of four dimensions, determine the minimum sufficient statistics for each model four-dimensional linear log, specify the expected frequency estimate for the log linear model of four dimensions, and specify the most suitable four dimensions log linear model for duration of internet access by students MAN Unggul Tenggarong. Based on the research’s results, it is obtained that the log linear models for the four dimensions are 23 models. Each model has a different minimum sufficient statistics. SPSS is used to estimate the value of the expected frequency. The results of model’s application on Internet access MAN Unggul Tenggarong showed that, the most suitable log linear model four dimensions is

XYZ ijk WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk                            Log

Keywords: Categorical data analysis, log linear models, four dimention log linear models.

Pendahuluan

Dalam penelitian banyak ditemukan situasi dimana data yang dikumpulkan dapat dikategorikan menjadi satu atau lebih kategorik. Seperti jenis kelamin (laki-laki dan perempuan), tingkat pendidikan (SD,SMP, dan SMA) dan masih banyak lagi lainnya. Data yang terdiri dari beberapa kategori ini disebut data kategorik. Cara yang digunakan untuk menyajikan data kategorik agar sistematik perlu disusun dalam suatu tabel klasifikasi silang yang disebut tabel kontingensi. Untuk menganalisa data kategorik dapat digunakan model log linier. Dalam analisis ini akan dicari pola hubungan antar sekelompok variabel kategori yang mencakup asosiasi dua variabel, tiga variabel, atau lebih. Pola hubungan ini disajikan dalam bentuk model log linier. Model log linier yang paling tepat akan digunakan untuk menginterpretasikan pola hubungannya (Agresti, 2007).

Adapun aplikasi dari analisis log linier dapat dijumpai di berbagai studi kasus. Seperti saat ini yang peneliti lakukan yaitu mengenai akses internet pada pelajar MAN Unggul Tenggarong. Saat ini internet sudah menjadi kebutuhan pokok bagi setiap orang terutama pelajar dan mahasiswa. Hampir setiap hari pelajar mengakses internet di berbagai warung internet (warnet), smartphone ataupun melalui modem. Oleh karena itu frekuensi seberapa lama pelajar menggunakan fasilitas internet dipengaruhi beberapa faktor (variabel). Dalam skripsi ini

variabel yang dimaksud yaitu jurusan kelas, prestasi akademik, banyaknya uang saku perbulan dan waktu yang diperlukan untuk akses internet setiap harinya. Selanjutnya masing-masing variabel tersebut dibagi menjadi beberapa kategorik. Keempat variabel tersebut yang mempengaruhi banyak dan sedikitnya jumlah pelajar MAN Unggul Tenggarong di setiap sel dalam tabel kontingensi.

Oleh karena model log linier dua dan tiga dimensi telah banyak diturunkan dan diaplikasikan, maka dari itu penulis ingin menjabarkan model log linier dengan empat dimensi secara umum dengan judul “Model log linier untuk empat dimensi”.

Variabel Kategori

Variabel kategori adalah salah satu skala pengukuran yang memiliki seperangkat kategori. Seperti, philosophy politik yang sering diukur dengan “liberal”, “moderate”, atau “conservative (Agresti, 2002).

Tabel Kontingensi (Contingency)

Tabel yang memiliki I baris untuk variabel X dan J kolom untuk variabel Y dengan IJ sebagai hasil kombinasi probabilitasnya disebut tabel kontingensi (contingency table) atau tabel klasifikasi silang (cross-classification table). Tabel yang mengklasifikasikan silang antara dua variabel disebut tabel kontingensi dua arah (two way contingency table). Tabel yang

(2)

mengklasifikasikan silang tiga variabel disebut tabel kontingensi tiga arah (three way contingency table), dan begitu seterusnya. (Agresti, 2002)

Independence of Categorical Variables

Secara statistik, independensi adalah ekivalen dengan properti untuk semua probabilitas gabungan sama dengan produk probabilitas marjinalnya, j i ij   untuk i=1,2,…,I , j=1,2,…,J. (1) (Agresti, 2002). Resiko Relatif

Resiko relatif didefinisikan sebagai rasio

2 1  

(5) Hal tersebut dapat berupa bilangan real non-negatif. (Agresti, 2002).

Odds Rasio

Untuk probabilitas keberhasilan, odds rasio didefinisikan sebagai







    1 (6)

Menurut Agresti (2007), Odds rasio merupakan bilangan non-negatif, dengan

ketika sukses lebih memungkinkan daripada gagal. (Agresti, 2007).

Model Log Linier Dua Dimensi a) Model Independensi

Variabel baris ditunjukkan dengan X dan variabel kolom dengan Y. Syarat independensi memiliki rumus perkalian (multiplikatif) yaitu

j i ij n 

 . Jadi, model independensi memiliki rumus Y j X i ij        Log . (7)

Untuk efek pada baris dan kolom berturut-turut adalah iX dan

Y j

 . model ini disebut model independensi log linier (log linier model of independence) (Agresti, 2007). Parameter Xi

mempresentasikan efek dari pengklasifikasian pada baris i. Semakin besar nilai_iX, semakin besar juga setiap frekuensi harapan pada baris i, begitu juga untuk Y_j. (Agresti, 2007).

b) Model Lengkap (Saturated Model) Variabel yang secara statistika dependen biasanya memiliki model log linier yang lebih kompleks, yaitu XY ij Y j X i     _ij    Log (8)

Parameter

 

_ijXY adalah istilah asosiasi yang merefleksikan deviasi dari independensi.

Parameter ini mempresentasikan interaksi antara X dan Y, dimana efek dari satu variabel pada jumlah sel yang diharapkan bergantung pada tingkat variabel lain. (Agresti, 2007)

Model Log Linier Tiga Dimensi a) Model Independensi

Sebuah klasifikasi silang tiga arahIJKpada variabel respon X, Y, Z mempunyai beberapa potensi independensi. Dengan diasumsikan bahwa sebuah distribusi multinomial mempunyai probabilitas sel

 

_ijk ,

dan

  

_i _j _kijk 1. Model ini juga

mengaplikasikan sampling Poisson dengan mean

 

_ijk .

Untuk frekuensi harapan ,

independensi yang saling bebas (mutual independence) mempunyai rumus log linier sebagai berikut: Z k Y j X i ijk         

Log untuk semua

i,j, dan k. (9)

(Agresti, 2007). b) Model Lengkap

Model lengkap untuk log linier tiga dimensi adalah XYZ ijk YZ jk XZ ik XY ij Z k Y j X i ijk                  Log . (10) dimana IJK I i J j K k ijk

  

    1 1 1 log









 

 

  JK J j K k ijk X i 1 1 log    

 

   IK I i K k ijk Y j 1 1 log







 

 

  IJ I i J j ijk Z k 1 1 log , log log log 1 1 1 1 1







  

 



 



     IK JK K I i K k ijk J j K k ijk K k ijk XY ij , log log log 1 1 1 1 1







   

 



     IJ IK I I i J j ijk I i K k ijk I i ijk YZ jk

(3)

, log log log 1 1 1 1 1

_





   

 



     IJ JK J I i J j ijk J j K k ijk J j ijk XZ ik I J K I i ijk J j ijk K k ijk ijk XYZ ijk



   _ _   1 1 1 log log log log





IK JK I i K k ijk J j K k ijk

 

    _  1 1 1 1 log log  +







 

  IJ I i J j ijk 1 1 log , Dengan syarat :



       K k XYZ ijk J j XY ij I i J j K k I i XY ij Z k Y j X i 0 ...      

Analisis Model Log Linier

a) Model Log Linier Dua Dimensi

Uji Goodness of fit

Statistik Chi-square telah banyak dikenal dan dipergunakan untuk tabel kontingensi dua dimensi. Nilai statistik dihitung berdasarkan rumus sebagai berikut:







        _  j i ij ij ij E E O , 2 2  (11) dengan:

Oij = Observasi pada variabel ke-i dan j

Eij = Frekuensi harapan dalam sel-ij

Statistik dengan distribusi Chi-square mempunyai db = (i-1)(j-1) dimana i menyatakan banyaknya baris dan j menyatakan kolom dari suatu tabel. Tabel kontingensi 2 x 2 diperoleh

statistik Chi-square dengan derajat bebas (db) = (2-1)(2-1) = 1.

Tabel 1 Tabel Frekuensi Menurut W dan X Variabel X Variabel W Jumlah

W1 … Wj

X1 O11 … O1j B1

… … … … …

Xi Oi1 … Oij Bi

Jumlah K1 … Kj n

Berdasarkan Tabel 1, nilai Eij dapat dihitung

dengan memakai rumus: Eij =

n K Bi j

(12)

Selain menggunakan statistik uji Chi-square, perhitungan uji goodness of fit pada tabel kontingensi dua dimensi dapat menggunakan likelihood rasio yang dinyatakan sebagai likelihood ratio Chi-square (G2) sebagai berikut:



_                i j ij ij ij E O O G2 2 Log (13)

Statistik G2 juga mempunyai derajat bebas (db) = (i-1)(j-1).

Uji Independensi

Dalam tabel kontingensi dua arah dengan probabilitas gabungan untuk dua variabel respon, hipotesis nol untuk independensi statistik adalah

H0 : Kedua variabel independen

(_ij_i___juntuk semua i dan j). Untuk menguji H0, diidentifikasi

j i ij

ij n n 

 sebagai frekuensi harapan.

Untuk mengestimasi frekuensi harapan, subtitusi proporsi sampel untuk probabilitas marjinal yang tidak diketahui, maka

n n n n n n n n p np_i _j i j i j ij       _              ˆ (14)

Tanda ˆijdisebut estimasi frekuensi harapan

(estimated expectation frequencies). (Agresti, 2007).

Uji Homogenitas

Uji homogenitas digunakan untuk mengetahui apakah dua variabel bersifat homogen atau tidak.

Dengan hipotesis

H0 : Kedua variabel bersifat homogen.

Hipotesis nol (H0) akan ditolak apabila 2

hitung ≥ dan derajat bebas (db)

adalah (b-1)(k-1) dengan







  bk bk bk E E O 2 2 hitung  .

b) Model Log Linier Tiga Dimensi

Menentukan Statistik Cukup Minimal dan Fungsi Likelihood

Diasumsikan sebuah sampel

 

n_ijk untuk klasifikasi silang dari variabel-variabel X, Y dan Z. Diasumsikan variabel X, Y dan Z adalah variabel random Poisson dengan nilai frekuensi harapan

 

ijk . Fungsi kepadatan probabilitas

Poisson bersama dari nijk adalah



 i j k ijk n ijk n e ijk ijk ! ) (  (15) dengan ijk



: frekuensi harapan ijk

n

: frekuensi pengamatan pada beris ke-i, kolom ke-j dan layer ke-k.

(4)



i j k

: hasil kali seluruh frekuensi sel dalam tabel.

Model log linier untuk tabel tiga dimensi secara umum dapat disajikan dalam parsamaan berikut XYZ ijk YZ jk XZ ik XY ij Z k Y j X i ijk                  Log



XYZ



ijk YZ jk XZ ik XY ij Z k Y j X i ijk          exp        kemudian dibentuk log likelihood dari model di atas sehingga diperoleh

 

YZ jk j k jk XZ ik i k k i XY ij i j ij Z k i k Y j i j X i i i n n n n n n n L                              





           i j XYZ ijk YZ jk XZ ik XY ij Z k Y j X i k XYZ ijk i j k ijk n          exp (16) dengan adalah parameter dalam model (Bain dan Engelhardt, 1992).

Differensial terhadap masing-masing parameternya diperoleh              i j k YZ jk XZ ik Z k Y j X i n L ) exp( ) ( _ _ _ _ _ _   Karena YZ jk XY ik Z k Y j X i ijk              log ) exp( YZjk XY ik Z k Y j X i ijk              Sehingga



       i j k ijk n L _  ) ( Jika ( )0     L maka,



     i j k ijk n  0



    i j k ijk n        n



ˆ (17)       n



 berarti frekuensi harapan total sama dengan frekuensi pengamatan total sehingga hasilnya dapat dilihat pada Tabel 3 (Bain dan Engelhardt, 1991).

Estimasi Frekuensi Harapan

Misalkan diberikan sebuah simbol model (XY, YZ) dengan X dan Y adalah variabel bebas dan Z merupakan variabel terikat. Probabilitas sel ke-ij dengan diketahui probabilitas sel ke-k, dinotasikan dengan untuk X dan Y adalah:



 

_

     ijk k k i jk (18)

Karena pengambilan sampel yang berdistribusi Poisson, maka rumus yang

berkaitan dengan frekuensi harapan dengan



_ijk ijk F_ijk n



_ijk

n F yaitu:





k jk k i k k i jk k k i jk ijk n n n F             _ _ 



 

   ˆ ˆ ˆ

Menurut persamaan (20) dan ˆ___k n___k maka diperoleh: k jk k i ijk n n n      ˆ (19)

Jadi, nilai estimasi frekuensi harapannya menyesuaikan dengan masing-masing model.

Tabel 3 Tabel Statistik Cukup Minimal

Model Statistik Cukup Minimal

(X,Y,Z) (XY,Z) (XZ,Y) (YZ,X) (XY,YZ) (XZ,YZ) (XY,XZ) (XY,XZ,YZ) (XYZ)

Uji Goodness of fit

Untuk tabel kontingensi tiga dimensi, uji likelihood rasio adalah



_        i j k ijk ijk ijk n n G ˆ log 2 2 (20) dan uji Chi-Square adalah







  i j k ijk ijk ijk n    ˆ ˆ 2 ₍₂₁₎

Hipotesis yang diuji adalah :

H0 : Model log linier yang digunakan sesuai.

Apabila _hitung2 ≥ _2_(db₎ maka hipotesis nol (H0) ditolak, dan derajat bebas (db) untuk

masing-masing model log linier tiga dimensi dapat dilihat pada Tabel 4 (Agung, 2002). Partisi Chi-Square

Diberikan dua model parameter m1 dan m2

dengan m2 kasus khusus dari m1. Karena m2 lebih

sederhana dari m1 maka model m2 dikatakan

bersusun dengan m1, v1 dan v2 derajat bebas

sesaat dan v1 lebih kecil dari v2 maka

. (22)

Oleh sebab itu, diperoleh

mendekati distribusi Chi-square dengan derajat bebas v2 - v1 (Agresti, 2002).

(5)

Tabel 4 Derajat Bebas Model Log Linear Pada Tabel Kontingensi Berdimensi Tiga

No. Model Derajat Bebas

1 ( X,Y,Z) IJK – I – J – K + 2 2 (XY, Z) (IJ1)(K1) 3 (XZ, Y) (IK1)(J1) 4 (YZ, X) (JK1)(I1) 5 (XY, XZ) I(J1)(K1) 6 (XY, YZ) J(I1)(K1) 7 (XZ, YZ) K(I1)(J1) 8 (XY, XZ, YZ) (I1)(J1)(K1) 9 (XYZ) 0 Variabel Penelitian

Variabel yang digunakan pada penelitian terdapat 4 variabel, yaitu Jurusan Kelas (variable W) yang dibagi menjadi 2 kategori, yaitu IPA dan IPS, Prestasti Akademik (variabel X) yang dibagi menjadi 3 kategori yaitu tinggi (peringkat 1 – 10), sedang (peringkat 11 – 20) dan rendah (peringkat lebih dari 20), uang saku perhari (variabel Y) yang dibagi menjadi 3 kategori yaitu tinggi (lebih dari Rp. 20.000) , sedang (Rp. 11.000 – Rp. 20.000) dan rendah (kurang dari Rp. 10.000), dan akses internet perhari (variabel Z) yang dibagi menjadi 4 kategori yaitu sangat lama (lebih dari 2 jam), lama (1 – 2 jam), cukup lama(0,5 – 1 jam) dan sebentar (kurang dari 0,5 jam)..

Hasil dan Pembahasan

Model Log Linier Empat Dimensi a) Model Independensi

Jika W menyatakan variabel baris, X menyatakan variabel kolom, Y menyatakan variabel layer pertama dan Z merupakan variabel layer kedua. Dengann h merupakan jumlah baris, i merupakan jumlah kolom, j merupakan jumlah layer pertama dan k merupakan jumlah layer kedua.

Jika diketahui P (W,X,Y,Z) =



_hijk yang saling bebas sehingga : , k j i h hijk     (23) Peluang pengamatan dapat ditaksir dari frekuensi pengamatan maka diperoleh Persamaan :

, , ,                                  n n n n n n j j i i h h



dan ,            n n _k k  (24) dengan ,

sehingga frekuensi nilai harapannya diberikan dalam Persamaan : , k j i h hijk hijk n n                                  (25) Jika persamaan (25) dinyatakan dalam bentuk skala logaritma, maka didapatkan :

, log log log log log log k j i h ijk n                           ₍₂₆₎

jika semua variabel independen, maka log dari frekuensi harapan untuk sel (h, i, j, k) sehingga persamaan (27) ekuivalen dengan

, log



_hijk







W_h 



_iX 



Y_j 



Z_k (28) dimana : HIJK H h I i J j K k hijk

  

     1 1 1 1 log









 

  

   IJK I i J j K k hijk W h 1 1 1 log











  

  

HJK

H h J j K k hijk X i 1 1 1

log









 

  



HIK

H h I i K k hijk Y j 1 1 1

log







 

 

   HIJ H h I i J j hijk Z k 1 1 1 log dengan syarat :



        H h I i K k Z k J j Y j X j W h 1 1 1 1 0     b) Model Lengkap

Model yang memuat interaksi keempat variabelnya merupakan model lengkap, yaitu :

WXYZ hijk XYZ hjk WYZ hjk WXZ hik WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk                                  log (29) dengan



,



W_h,



_iX,



Y_j,



Z_k Sebagaimana dinyatakan pada persamaan (28) dan nilai parameter lainnya adalah:

(6)







   

  

 

        HJK IJK JK H h J j K k hijk I i J j K k hijk J j K k hijk WX hi 1 1 1 1 1 1 1 1 log log log







   

 

  

 

        HIK IJK IK H h I i K k hijk I i J j K k hijk I i K k hijk WY hj 1 1 1 1 1 1 1 1 log log log







   

 

  

 

        HIJ IJK IJ H h I i J j hijk I i J j K k hijk I i J j hijk WZ hk 1 1 1 1 1 1 1 1 log log log







   

 

  

 

        HIK HJK HK H h I i K k hijk H h J j K k hijk H h K k hijk XY ij 1 1 1 1 1 1 1 1 log log log HJK HJ H h J j K k hijk H h J j hijk XZ ik

  

 

     _  1 1 1 1 1 log log





   

 

   HIJ H h I i J j hijk 1 1 1 log HIJ HI H h I i J j hijk H h I i hijk YZ jk

 



     _  1 1 1 1 1 log log





   

 

   HIK H h I i K k hijk 1 1 1 log







       

 

  

 



                HIK HJK IJK IK HK JK K H h I i K k hijk H h J j K k hijk I i J j K k hijk I i K k hijk H h K k hijk J j K k hijk K k hijk WXY hij 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 log log log log log log log







       

 

  

 



                HIJ HJK IJK JK IJ HJ J H h I i J j hijk H h J j K k hijk I i J j K k hijk J j K k hijk I i J j hijk H h J j hijk J j hijk WXZ hik 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 log log log log log log log







       

 

  

 





                HIJ HIK IJK IK IJ HI I H h I i J j hijk H h I i K k hijk I i J j K k hijk I i K k hijk I i J j hijk H h I i hijk I i hijk WYZ hjk 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 log log log log log log log H I J K H h hijk I i hijk J j hijk K k hijk hijk WXYZ hijk



         1 1 1 1 log log log log log       HJ HI H h J j hijk H h I i hijk

 



    _  1 1 1 1 log log  IJ HK I i J j hijk H h K k hijk

 

    _  1 1 1 1 log log 











 

  

 

               

HIJ

HIK

HJK

IJK

JK

IK

H h I i J j hijk H h I i K k hijk H h J j K k hijk I i J j K k hijk J j K k hijk I i K k hijk 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

log

dengan syarat :



  



                 H h I i H h I i J j K k WXYZ hijk WX hi K k Z k J j Y j I i X i H h W h

λ

λ 1 1 1 1 1 1 1 1 1 1 0     

(7)

Analisis Model Log Linier Empat Dimensi a) Menentukan Statistik Cukup Minimal

Jika sebuah sampel untuk klasifikasi silang dari variabel-variabel W, X, Y dan Z, diasumsikan bahwa variabel W, X, Y dan Z adalah variabel random Poisson dengan nilai frekuensi harapan , maka fungsi kepadatan probabilitas Poisson bersama dari adalah

 



 h i j k hijk n hijk n e hijk hijk !



 (30) dengan : frekuensi harapan

: frekuensi pengamatan pada baris ke-h, kolom ke-i, layer pertama ke-j serta, layer kedua ke-k.

: hasil kali seluruh frekuensi sel dalam tabel.

Dalam bentuk logaritma, persamaan (40) dapat ditulis









 h i j h i j k hijk k hijk hijk n L(



) Log



Model log linier untuk tabel empat dimensi secara umum dapat disajikan dalam parsamaan berikut WXYZ hijk XYZ ijk WYZ hjk WXZ hik WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk                                  Log ) exp( WXYZ hijk XYZ ijk WYZ hjk WXZ hik WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk





               

kemudian dibentuk log likelihood dari model di atas sehingga diperoleh

 

X i i i W h h h n n n L  



___ 



___ WX hi h i hi Z k k k Y j j j n n n 











       WXYZ hijk h i j k hijk XYZ ijk i j k ijk WYZ hjk h j k jk h WXZ hik h i k k hi WXY hij h i j hij YZ jk j k jk XZ ik i k k i XY ij i j ij WZ hk h k k h WY hj h j j h n n n n n n n n n n









                        (31) XY ij WZ hk WY hj WX hi Z k Y j X i W h h i j k                  

_{   }

exp( ) XYZ ijk WYZ hjk WXZ hik WXY hij YZ jk XZ ik            

dengan adalah parameter dalam model.

Differensial terhadap masing-masing parameternya sehingga diperoleh

) exp( ) ( WXYZ hijk XYZ ijk WYZ hjk WXZ hik WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k h i j k Y j X i W h n L                                     

_

Karena WXYZ hijk XYZ ijk WYZ hjk WXZ hik WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk                                  log ) exp( WXYZ hijk XYZ ijk WYZ hjk WXZ hik WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk                                  Sehingga



    h i j k hijk n L _  ) ( Jika ( ) 0     L maka,



  h i j k hijk n  0 



h i j k hijk n  ____nn____

Dengan demikian akan diperoleh fungsi likelihood sebagai berikut:

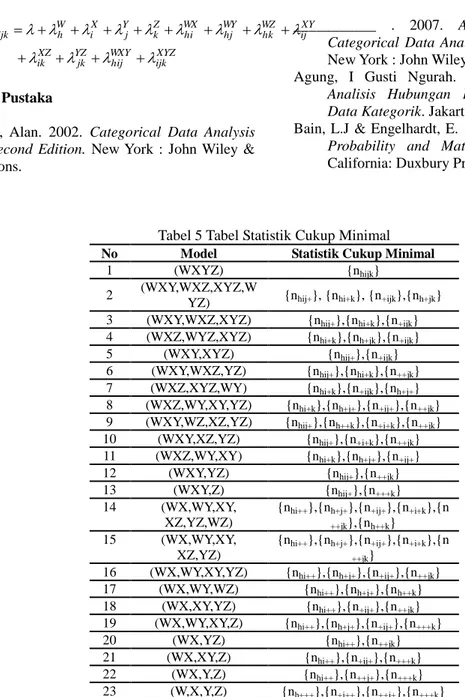
= n = = = = = = = = = = = = = = (32) Dalam persamaan (32) dan seterusnya merupakan koefisien dari masing – masing parameter maka dan seterusnya adalah statistik cukup minimal. Tabel 5 menunjukkan contoh model beserta statistik cukup minimalnya.

(8)

b) Estimasi Frekuensi Harapan

Misalkan sebuah model log linier empat dimensi (W, X, Y, Z) dengan W, X, Y dan Z adalah variabel bebas dan berdasarkan persamaan (32) sehingga estimasi frekuensi harapan untuk model (W, X, Y, Z) adalah:                  n n n n nh i j k hijk  (33)

c) Uji Goodness of fit

Berdasarkan pada uji goodness of fit pada tabel kontingensi tiga dimensi, maka dapat dirumuskan rumus goodness of fit untuk tabel empat dimensi sebagai berikut:



_        h i j hijk hijk k hijk n n G



 log 2 2 (34)

dan uji Chi-square adalah







  h i j k hijk hijk hijk n      2 ₍₃₅₎

Hipotesis yang diuji adalah :

H0 : Model log linier yang digunakan sesuai

H1 : Model log linier yang digunakan tidak

sesuai

Apabila



_hitung2 ≥



_tabel2 maka hipotesis nol (H0)

ditolak, dan derajat bebas (db) untuk masing-masing model log linier empat dimensi dapat dilihat pada Tabel 6 di bawah ini.

Tabel 6 Derajat Bebas Model Log Linear Empat Dimensi

d) Pemilihan Model

Pemilihan model terbaik dilakukan secara bertahap. Dimulai dengan pemilihan model yang dilakukan dengan memilih nilai G2 yang relatif kecil (lebih kecil dari ) diantara kombinasi model yang sesuai dengan dimensinya. Jika dengan kriteria tersebut diperoleh beberapa model maka dilakukan pemilihan model terbaik dengan partisi Chi-square. Sehingga diharapkan model terbaik yang diperoleh merupakan model yang sederhana.

Aplikasi

Data yang digunakan pada contoh ini merupakan data lamanya akses internet siswa-siswi kelas 2 dan 3 MAN Unggul Tenggarong menurut jurusan kelas, prestasi akademik, dan uang saku perhari. Data tersebut akan diaplikasikan dalam analisis model log linier empat dimensi.

a) Uji Validitas

Dilakukan uji validitas untuk masing – masing butir pertanyaan dengan hipotesis :

H0 : Butir pertanyaan tidak valid

H1 : Butir pertanyaan valid

Dengan taraf signifikansi = 5% dan daerah kritik menolak H0 apabila p-value < .

Menggunakan software SPSS versi 20, diperoleh p-value seperti pada Tabel 7. Keputusan yang dapat diambil berdasarkan hasil analisis adalah menolak H0 untuk kesemua butir pertanyaan

karena memiliki nilai p-value < . Dengan demikian dapat disimpulkan bahwa semua butir pertanyaan tersebut valid, kemudian butir pertanyaan yang valid berlanjut dengan pengujian reliabilitas.

Tabel 7 Hasil Uji Validitas Menggunakan Software SPSS V.20

Butir pertanyaan Pearson Correlation

Sig. (2-tailed)

N Jurusan kelas (butir

1) 0,275 0,006 100

Web yang dikunjungi

(butir 2) 0,529 0,000 100 Lamanya akses

internet perhari (butir 3)

0,511 0,004 100 Uang saku perhari

(butir 4) 0,473 0,005 100 Prestasi akademik

(butir 5) 0,433 0,000 100 b) Uji Reliabilitas

Tabel 8 Hasil Uji Reliabilitas Menggunakan Software SPSS V.20

Reliability Statistics

Cronbach's Alpha N of Items

0,210 5

Dilakukan uji reliabilitas untuk masing – masing butir pertanyaan dengan hipotesis :

H0 : Butir pertanyaan tidak reliabel

H1 : Butir pertanyaan reliabel

Dengan taraf signifikansi = 5% dan daerah kritik menolak H0 apabila Rhitung > Rtabel.

Rtabel. Menggunakan software SPSS versi 20,

diperoleh Rhitung seperti pada tabel 4.4 dengan

taraf signifikansi = 5% berdasarkan tabel R diperoleh nilai Rtabel = 0,195 untuk db = 98.

Keputusan yang dapat diambil berdasarkan hasil

analisis adalah menolak H0 karena memiliki nilai

Rhitung = 0,210 > Rtabel = 0,195. Dengan demikian

dapat disimpulkan bahwa semua butir pertanyaan reliabel.

c) Menentukan Statistik Cukup Minimal Statistik cukup minimal dari model-model loglinier merupakan koefisien dari masing-masing parameternya. Koefisien parameter ini diperoleh dari pengumpulan atau penjumlahan batas marjinal

(9)

d) Fungsi Likelihood

Setelah diperoleh statistik cukup minimal masing-masing model, selanjutnya dilakukan estimasi fungsi likelihood.

e) Estimasi Frekuensi Harapan

Setelah ditentukan statistik cukup minimal dan fungsi likelihood untuk semua modelnya, barulah dapat ditentukan estimasi frekuensi harapan.

f) Uji Goodness of fit

Dari model-model tersebut, kemudian dilakukan uji kecocokan model (goodness of fit) dengan data yang digunakan. Uji kecocokan model ini bertujuan mencari model mana saja yang cocok dengan data yang digunakan. Hipotesis yang digunakan adalah :

H0 : Model yang digunakan sesuai

H1 : Model yang digunakan tidak sesuai

dengan taraf signifikansi (α = 0,05) dan statistik

uji



_        h i j hijk hijk k hijk n n G



 log 2 2 serta daerah

kritis menolak H0 bila G2 ≥ tabel.

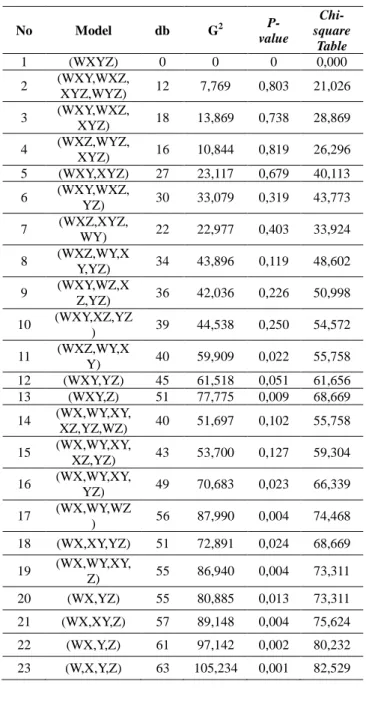
Dengan menggunakan software SPSS versi 20 didapatkan nilai G2 untuk masing-masing model seperti pada Tabel 9.

Chi-square Table didapat dari tabel Chi-square dengan derajat bebas (db) dan probabilitas (α = 0.05) tertentu. Berdasarkan Tabel 12 di atas, maka terlihat bahwa dari semua model yang ada terdapat tigabelas(13) model memiliki nilai likelihood ratio (G2) yang lebih kecil dari nilai Chi-square table. Sehingga ketigabelas model tersebut yang cocok adalah model no. 1, 2, 3, 4, 5, 6, 7,8, 9, 10, 12, 14, 15.

g) Partisi Chi-square

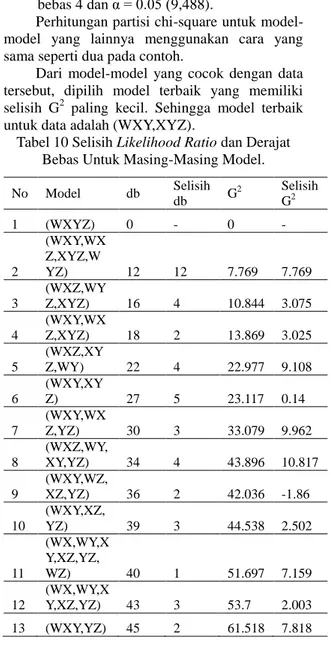
Dari ketigabelas model tersebut kemudian dilakukan pemilihan model terbaik untuk data. Pemilihan model ini menggunakan statistik uji partisi Chi-square. Berikut ditampilkan nilai-nilai likelihood ratio (G2), derajat bebas (db) dan selisihnya untuk masing-masing model.

1. Model (WXY,WXZ,WYZ,XYZ) cocok dengan data karena G2[(WXY,WXZ,WYZ,XYZ)|(WXYZ)] = 7,769 dan lebih kecil dari Chi-square table dengan derajat bebas 12 dan α = 0.05 (21,026).

2. Model (WXZ,WYZ,XYZ) cocok dengan data karena G2[(WXZ,WYZ,XYZ)|( WXY,WXZ,WYZ,XYZ) = 3,075 dan lebih

kecil dari Chi-square table dengan derajat bebas 4 dan α = 0.05 (9,488).

Perhitungan partisi chi-square untuk model-model yang lainnya menggunakan cara yang sama seperti dua pada contoh.

Dari model-model yang cocok dengan data tersebut, dipilih model terbaik yang memiliki selisih G2 paling kecil. Sehingga model terbaik untuk data adalah (WXY,XYZ).

Tabel 10 Selisih Likelihood Ratio dan Derajat Bebas Untuk Masing-Masing Model.

No Model db Selisih db G 2 Selisih G2 1 (WXYZ) 0 - 0 - 2 (WXY,WX Z,XYZ,W YZ) 12 12 7.769 7.769 3 (WXZ,WY Z,XYZ) 16 4 10.844 3.075 4 (WXY,WX Z,XYZ) 18 2 13.869 3.025 5 (WXZ,XY Z,WY) 22 4 22.977 9.108 6 (WXY,XY Z) 27 5 23.117 0.14 7 (WXY,WX Z,YZ) 30 3 33.079 9.962 8 (WXZ,WY, XY,YZ) 34 4 43.896 10.817 9 (WXY,WZ, XZ,YZ) 36 2 42.036 -1.86 10 (WXY,XZ, YZ) 39 3 44.538 2.502 11 (WX,WY,X Y,XZ,YZ, WZ) 40 1 51.697 7.159 12 (WX,WY,X Y,XZ,YZ) 43 3 53.7 2.003 13 (WXY,YZ) 45 2 61.518 7.818 Kesimpulan

Berdasarkan hasil penelitian yang telah dilakukan dapat disimpulkan bahwa terdapat 23 variasi model log linier yang memungkinkan untuk di uji pada empat dimensi. Masing-masing model memiliki statistik cukup minimal yang berbeda-beda. Estimasi frekuensi harapan untuk masing-masing modelnya juga berbeda-beda dengan derajat bebas yang berbeda pula. Namun dari ke-23 model tersebut dapat dilakukan uji kecocokan model dengan menggunakan uji chi-square dan likelihood. Uji partisi chi-chi-square dilakukan untuk mencari model terbaik. Dalam contoh kasus lamanya akses internet siswa MAN Unggul Tenggarong terlihat bahwa, model log linier empat dimensi yang cocok adalah

(10)

XYZ ijk WXY hij YZ jk XZ ik XY ij WZ hk WY hj WX hi Z k Y j X i W h hijk                            Log Daftar Pustaka

Agresti, Alan. 2002. Categorical Data Analysis Second Edition. New York : John Wiley & Sons.

___________ . 2007. An Introduction To Categorical Data Analysis Second Edition. New York : John Wiley & Sons.

Agung, I Gusti Ngurah. 2002. STATISTIKA: Analisis Hubungan Kausal Berdasarkan Data Kategorik. Jakarta: Rajawali Press. Bain, L.J & Engelhardt, E. 1992. Introduction to

Probability and Mathematical Statistics. California: Duxbury Press.

Tabel 5 Tabel Statistik Cukup Minimal

No Model Statistik Cukup Minimal

1 (WXYZ) {nhijk}

2 (WXY,WXZ,XYZ,W

YZ) {nhij+}, {nhi+k}, {n+ijk},{nh+jk}

3 (WXY,WXZ,XYZ) {nhij+},{nhi+k},{n+ijk}

4 (WXZ,WYZ,XYZ) {nhi+k},{nh+jk},{n+ijk}

5 (WXY,XYZ) {nhij+},{n+ijk}

6 (WXY,WXZ,YZ) {nhij+},{nhi+k},{n++jk}

7 (WXZ,XYZ,WY) {nhi+k},{n+ijk},{nh+j+}

8 (WXZ,WY,XY,YZ) {nhi+k},{nh+j+},{n+ij+},{n++jk}

9 (WXY,WZ,XZ,YZ) {nhij+},{nh++k},{n+i+k},{n++jk}

10 (WXY,XZ,YZ) {nhij+},{n+i+k},{n++jk}

11 (WXZ,WY,XY) {nhi+k},{nh+j+},{n+ij+}

12 (WXY,YZ) {nhij+},{n++jk}

13 (WXY,Z) {nhij+},{n+++k}

14 (WX,WY,XY, XZ,YZ,WZ)

{nhi++},{nh+j+},{n+ij+},{n+i+k},{n ++jk},{nh++k}

15 (WX,WY,XY, XZ,YZ)

{nhi++},{nh+j+},{n+ij+},{n+i+k},{n ++jk}

16 (WX,WY,XY,YZ) {nhi++},{nh+j+},{n+ij+},{n++jk}

17 (WX,WY,WZ) {nhi++},{nh+j+},{nh++k}

18 (WX,XY,YZ) {nhi++},{n+ij+},{n++jk}

19 (WX,WY,XY,Z) {nhi++},{nh+j+},{n+ij+},{n+++k}

20 (WX,YZ) {nhi++},{n++jk}

21 (WX,XY,Z) {nhi++},{n+ij+},{n+++k}

22 (WX,Y,Z) {nhi++},{n++j+},{n+++k}

(11)

Tabel 6 Derajat Bebas Model Log Linear Empat Dimensi

No Model Derajat Bebas (db)

1 (WXYZ) 0 2 (WXY,WXZ,XYZ,WYZ) 3 (WXY,WXZ,XYZ) 4 (WXZ,WYZ,XYZ) 5 (WXY,XYZ) 6 (WXY,WXZ,YZ) 7 (WXZ,XYZ,WY) 8 (WXZ,WY,XY,YZ) 9 (WXY,WZ,XZ,YZ) 10 (WXY,XZ,YZ) 11 (WXZ,WY,XY) 12 (WXY,YZ) 13 (WXY,Z) 14 (WX,WY,XY, XZ,YZ,WZ) 15 (WX,WY,XY, XZ,YZ) 16 (WX,WY,XY,YZ) 17 (WX,WY,WZ) 18 (WX,XY,YZ) 19 (WX,WY,XY,Z) 20 (WX,YZ) 21 (WX,XY,Z) 22 (WX,Y,Z) 23 (W,X,Y,Z)

(12)

Tabel 9. Nilai-Nilai G2 Beserta Chi-square Table untuk Uji Kecocokan Model No Model db G2 P-value Chi-square Table 1 (WXYZ) 0 0 0 0,000 2 (WXY,WXZ, XYZ,WYZ) 12 7,769 0,803 21,026 3 (WXY,WXZ, XYZ) 18 13,869 0,738 28,869 4 (WXZ,WYZ, XYZ) 16 10,844 0,819 26,296 5 (WXY,XYZ) 27 23,117 0,679 40,113 6 (WXY,WXZ, YZ) 30 33,079 0,319 43,773 7 (WXZ,XYZ, WY) 22 22,977 0,403 33,924 8 (WXZ,WY,X Y,YZ) 34 43,896 0,119 48,602 9 (WXY,WZ,X Z,YZ) 36 42,036 0,226 50,998 10 (WXY,XZ,YZ ) 39 44,538 0,250 54,572 11 (WXZ,WY,X Y) 40 59,909 0,022 55,758 12 (WXY,YZ) 45 61,518 0,051 61,656 13 (WXY,Z) 51 77,775 0,009 68,669 14 (WX,WY,XY, XZ,YZ,WZ) 40 51,697 0,102 55,758 15 (WX,WY,XY, XZ,YZ) 43 53,700 0,127 59,304 16 (WX,WY,XY, YZ) 49 70,683 0,023 66,339 17 (WX,WY,WZ ) 56 87,990 0,004 74,468 18 (WX,XY,YZ) 51 72,891 0,024 68,669 19 (WX,WY,XY, Z) 55 86,940 0,004 73,311 20 (WX,YZ) 55 80,885 0,013 73,311 21 (WX,XY,Z) 57 89,148 0,004 75,624 22 (WX,Y,Z) 61 97,142 0,002 80,232 23 (W,X,Y,Z) 63 105,234 0,001 82,529