PENERAPAN MASALAH LOGARITMA DISKRIT PADA KRIPTOGRAFI KUNCI PUBLIK

M-271

PENERAPAN MASALAH LOGARITMA DISKRIT

PADA KRIPTOGRAFI KUNCI PUBLIK

MUHAMAD ZAKI RIYANTO

Mahasiswa S2 Matematika, Universitas Gadjah Mada: Yogyakarta zaki@mail.ugm.ac.id

Abstrak

Diberikan G suatu grup siklik berhingga dengan gÎ G adalah elemen pembangun. Diberikan suatu xÎ G, masalah logaritma diskit pada G dengan basis g adalah mencari bilangan bulat nonnegatif terkecil n sedemikian hingga

g

n

=

x

. Pada makalah ini dibahas mengenai penerapan masalah logaritma diskrit pada kriptografi kunci publik.

Dapat ditunjukkan bahwa masalah logaritma diskrit dapat diterapkan untuk mengkonstruksi suatu sistem kripto yang digunakan untuk skema perjanjian kunci, enkripsi kunci publik, dan skema tanda tangan. Tingkat keamanan dari sistem kripto yang didasarkan pada masalah ini sebanding dengan tingkat kesulitan dalam menyelesaikan masalah logaritma diskrit.

Sistem kripto yang didasarkan pada masalah logaritma diskrit diantaranya adalah skema perjanjian kunci Diffie-Hellman, enkripsi dan skema tanda tangan ElGamal. Pada makalah ini, grup yang digunakan adalah grup multiplikatif bilangan bulat modulo prima ¢_p*, dan grup titik-titik kurva elliptik atas lapangan ¢_p.

Kata kunci: grup siklik, kriptografi, kunci publik, masalah logaritma diskrit

PENDAHULUAN

Kriptografi merupakan ilmu yang mempelajari teknik-teknik matematika yang berhubungan dengan aspek keamanan informasi, seperti aspek kerahasiaan, keabsahan, integritas, dan autentikasi. Secara umum, kriptografi terdiri dari proses enkripsi dan dekripsi. Enkripsi adalah proses penyandian dari suatu pesan yang dapat dimengerti, disebut dengan plainteks, dan menjadi suatu pesan yang tidak dapat dimengerti, disebut dengan cipherteks. Sedangkan proses sebaliknya disebut dengan dekripsi. Proses enkripsi dan dekripsi memerlukan suatu metode dan kunci tertentu. Prinsip dari kriptografi adalah untuk mengamankan pengiriman suatu pesan rahasia apabila dikirimkan melalui jalur yang tidak dapat dijamin keamanannya, sehingga rawan terjadi penyadapan dan manipulasi pesan. Penjelasan lebih rinci mengenai kriptografi dapat ditemui pada Schneier (1996).

Definisi 1. Suatu sistem kripto adalah suatu 5-tupel (, , , , ) dimana memenuhi kondisi berikut:

1.  adalah himpunan berhingga semua plainteks, 2.  adalah himpunan berhingga semua cipherteks,

3.  adalah himpunan berhingga semua kunci, disebut dengan ruang kunci,

4. Untuk setiap K∈, terdapat fungsi enkripsi

e

K

∈

 dan suatu fungsi dekripsi yang

bersesuaian yaitu

d

_K

∈

. Setiap

e

K

:



→

 dan

d

K

:



→

 merupakan suatu fungsi

sedemikian hingga

d

_K

(

e

_K

( )

x

)

=

x

, untuk setiap

x

∈

.

Berdasarkan sifat kuncinya, sistem kripto dibagi menjadi dua, yaitu sistem kripto kunci rahasia (simetris) dan sistem kripto kunci publik (asimetris). Pada sistem kripto kunci rahasia,

M-272

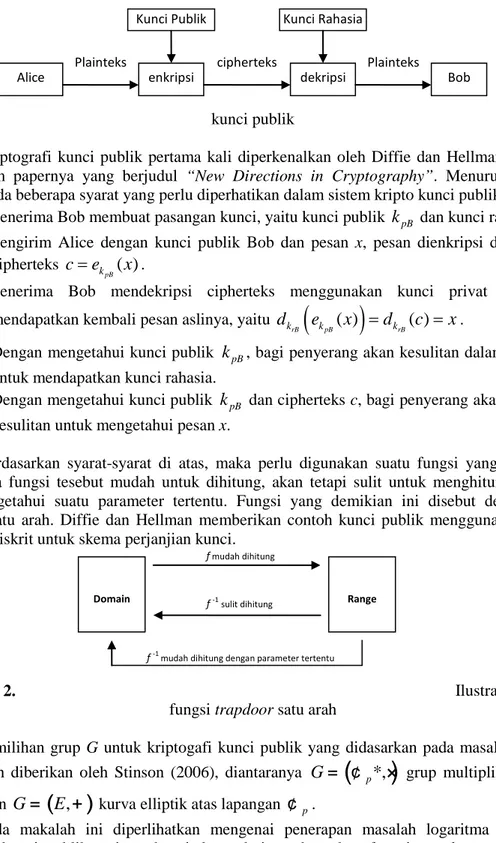
Alice Plainteks enkripsi cipherteks dekripsi Plainteks Bob Kunci Publik Kunci Rahasia

proses enkripsi dan dekripsi dilakukan menggunakan kunci rahasia yang sama. Sedangkan pada sistem kripto kunci publik, proses enkripsi dan dekripsinya menggunakan kunci yang berbeda, yaitu kunci publik untuk enkripsi, dan kunci rahasia yang digunakan untuk dekripsi.

Gambar 1.

Skema enkripsi

kunci publik

Kriptografi kunci publik pertama kali diperkenalkan oleh Diffie dan Hellman pada tahun 1976 dalam papernya yang berjudul “New Directions in Cryptography”. Menurut Diffie dan Hellman, ada beberapa syarat yang perlu diperhatikan dalam sistem kripto kunci publik, yaitu:

1. Penerima Bob membuat pasangan kunci, yaitu kunci publik k_pB dan kunci rahasia

k

_rB. 2. Pengirim Alice dengan kunci publik Bob dan pesan x, pesan dienkripsi dan diperoleh

cipherteks

( )

pB

k

c

=

e

x

.

3. Penerima Bob mendekripsi cipherteks menggunakan kunci privat Bob untuk mendapatkan kembali pesan aslinya, yaitu

(

( )

)

( )

rB pB rB

k k k

d

e

x

=

d

c

=

x

.

4. Dengan mengetahui kunci publik k_pB, bagi penyerang akan kesulitan dalam melakukan untuk mendapatkan kunci rahasia.

5. Dengan mengetahui kunci publik kpB dan cipherteks c, bagi penyerang akan mengalami

kesulitan untuk mengetahui pesan x.

Berdasarkan syarat-syarat di atas, maka perlu digunakan suatu fungsi yang mempunyai sifat bahwa fungsi tesebut mudah untuk dihitung, akan tetapi sulit untuk menghitung inversnya tanpa mengetahui suatu parameter tertentu. Fungsi yang demikian ini disebut dengan fungsi trapdoor satu arah. Diffie dan Hellman memberikan contoh kunci publik menggunakan masalah logaritma diskrit untuk skema perjanjian kunci.

Gambar 2. Ilustrasi dari suatu

fungsi trapdoor satu arah

Pemilihan grup G untuk kriptogafi kunci publik yang didasarkan pada masalah logaritma diskrit telah diberikan oleh Stinson (2006), diantaranya G =

(

¢ p*,×

)

grup multiplikatif modulo

prima p, dan

G

=

(

E

,

+

)

kurva elliptik atas lapangan ¢ _p.

Pada makalah ini diperlihatkan mengenai penerapan masalah logaritma diskrit pada kriptografi kunci publik, yaitu sebagai dasar dari pembentukan fungsi trapdoor satu-arah pada skema perjanjian kunci, enkripsi kunci publik, dan tanda tangan digital.

1. Masalah Logaritma Diskrit

Pada bagian ini dibahas mengenai pengantar dari masalah logaritma diskrit menggunakan grup

*

p

¢ dan kurva elliptik atas lapangan ¢_p.

Domain Range

f mudah dihitung

f -1_{sulit dihitung}

M-273 Teorema 2. Diberikan bilangan prima p, maka himpunan bilangan bulat modulo

¢

_p merupakan lapangan berhingga, dan

¢

_p

*

=

¢

_p

\ 0

{ }

merupakan grup siklik terhadap operasi mulitiplikasi.

Definisi 3. Diberikan bilangan prima p > 3. Kurva elliptik

E y

:

2

=

x

3

+

ax

+

b

atas ¢_p adalah himpunan semua titik-titik

(

x y Î

,

)

¢

_p

´

¢

_p yang memenuhi persamaan

(

)

2 3

mod

y

º

x

+

ax

+

b

p

,

dimana a b Î ¢, _p adalah suatu konstanta sedemikian hingga

4

a

3

+

27

b

2

º/

0 mod

(

p

)

, bersama dengan suatu titik

O

yang disebut dengan titik di tak berhingga. Kurva elliptik E dapat dinyatakan sebagai E:

{

(

x y,

)

Î ¢p´ ¢p:y2º x3+ax+b

(

modp

)

}

È O

{ }

.

Secara umum, kurva elliptik dapat didefinisikan atas sebarang lapangan. Berikut ini adalah gambar dari suatu kurva elliptik atas himpunan semua bilangan real ¡ .

Gambar 3. Kurva elliptik E₁:y2= x3- x dan ₂: 2 3 1 5

4 4

E y = x + x+ atas ¡ (Hankerson, 2004).

Pada kurva elliptik E berlaku operasi biner penjumlahan “+” sebagai berikut. Misalkan diketahui titik P Q, Î E, dengan

P

=

(

x y

₁

,

₁

)

dan

Q

=

(

x y

₂

,

₂

)

. Jika

x

₂

=

x

₁ dan

y

₂

= -

y

₁, maka

P+Q= O. Misalkan P+Q= O, maka didefinisikan

P

+

Q

=

(

x y

3

,

3

)

, dimana 2 3 1 2 x =

l

- x - x dan

y

3

=

l

(

x

1

-

x

3

)

-

y

1, dengan

(

)(

)

(

)

(

)

1 2 1 2 1 1 2 1 1 , jika 3 2 , jika . y y x x P Q x a y P Q

l

-ìï _{- - ¹} ïï = í ï _{+ =} ïïî

Selanjutnya didefinisikan bahwa P+O=O+ P= P.

Gambar 4. Ilustrasi geometris penjumlahan titik pada kurva elliptik atas ¡ . (Hankerson, 2004).

M-274

Teorema 4. Diberikan kurva elliptik E. Maka E membentuk grup komutatif terhadap operasi penjumlahan “+”.

Berikut ini diberikan definisi masalah logaritma diskrit.

Definisi 5. Diberikan G suatu grup siklik berhingga dengan gÎ G adalah elemen pembangun. Diberikan xÎ G elemen tak nol di G. Masalah logaritma diskrit pada G dengan basis g adalah masalah mencari bilangan bulat nonnegatif terkecil n sedemikian hingga

g

n

=

x

. Bilangan n disebut dengan logaritma diskit dari x.

Diketahui bahwa ¢ _p* merupakan grup siklik, maka ¢ _p* mempunyai elemen pembangun, misalkan

¢

_p

*

=

g

. Diberikan

x Î ¢

_p

*

, maka masalah logaritma diskrit pada

*

p

¢ dengan basis g adalah masalah mencari bilangan bulat nonnegatif terkecil n sedemikian hingga n

(

mod

)

g

º

x

p

. Semakin besar pemilihan bilangan prima p, maka masalah logaritma diskrit pada ¢_p* juga akan semakin sulit.

Diberikan kurva elliptik E atas ¢ _p. Diambil sebarang titik PÎ E, maka P membentuk subgrup siklik

P

. Misal diberikan titik

Q

Î

P

, maka masalah logaritma diskrit pada E dengan basis P adalah mencari bilangan bulat nonnegatif terkecil n sedemikian hingga Q= nP. Semakin besar order dari titik P, maka masalah logaritma diskritnya juga akan semakin sulit untuk diselesaikan.

Pada Hankerson (2004) dan Hooffstein (2008) telah dijelaskan mengenai tingkat kesulitan dari masalah logaritma diskit pada ¢_p* dan kurva elliptik E atas ¢_p. Pada Stinson (2006) telah dijelaskan beberapa metode untuk menyelesaikan masalah logaritma diskrit, seperti algoritma Shank’s, Pollard Rho, Pohling-Hellman, dan Index-Calculus. Untuk mempersulit masalah logaritma diskrit maka harus digunakan bilangan prima yang besar, Stinson (2006) menyarankan penggunaan bilangan prima

p »

2

160 untuk kurva elliptik, dan

p »

2

1880 untuk ¢ p*.

4. Skema Perjanjian Kunci

Skema perjanjian kunci digunakan untuk menyelesaikan masalah berikut ini. Misalkan Alice dan Bob akan saling mengirimkan pesan rahasia menggunakan sistem kripto simetris. Kendala yang dihadapi adalah bahwa keduanya harus menukarkan kunci rahasia melalui jalur komunikasi yang tidak aman. Masalah logaritma diskrit dapat digunakan untuk menyelesaikan masalah ini, seperti pada skema perjanjian kunci yang diusulkan oleh Diffie-Hellman berikut ini.

Tabel 1. Skema perjanjian kunci Diffie-Hellman pada ¢ _p*

Parameter Publik Alice dan Bob menyepakati: • Bilangan prima (besar) p.

• Suatu g elemen pembangun ¢_p*.

Perhitungan Privat • Alice memilih kunci rahasia berupa bilangan bulat a, dan menghitung

A

º

g

a

(

mod

p

)

.

• Bob memilih kunci rahasia berupa bilangan bulat b, dan menghitung

B

º

g

b

(

mod

p

)

.

Pertukaran Nilai Publik

• Alice mengirim nilai A kepada Bob. • Bob mengirim nilai B kepada Alice.

M-275

Perhitungan Privat _{• Alice menghitung}

_'

a

₍

_mod

₎

A

º

B

p

.

• Bob menghitung

B

'

º

A

a

(

mod

p

)

. Alice dan Bob telah menyepakati suatu nilai rahasia, yaitu

(

)

'

'

ab

mod

A

º

B

º

g

p

.

Tingkat keamanan dari skema perjanjian kunci Diffie-Hellman di atas, sebanding dengan tingkat kesulitan dari masalah logaritma diskrit. Misalkan pihak penyerang berhasil mengetahui nilai

g

a dan

g

b, dan dia juga telah mengetahui parameter publiknya yaitu grup ¢_p* dan elemen pembangun g. Jika pihak penyerang berhasil menyelesaikan masalah logaritma diskrit tersebut, maka penyerang dapat menemukan nilai a dan b, sehingga dapat menghitung

g

ab. Pada skema ini, perhitungan

A

=

g

a dan

B

=

g

b merupakan fungsi trapdoor satu-arah.

Berikut ini diberikan skema perjanjian kunci Diffie-Hellman mengunakan kurva elliptik atas lapangan ¢_p.

Tabel 2. Skema perjanjian kunci Diffie-Hellman Kurva Elliptik atas

¢

_p

Parameter Publik Alice dan Bob menyepakati: • Bilangan prima (besar) p. • Suatu kurva elliptik E atas

¢

_p. • Suatu titik P pada kurva elliptik E.

Perhitungan Privat _{• Alice memilih kunci rahasia berupa bilangan bulat}

A

n

, dan menghitung titik

Q

_A

=

n P

_A .

• Bob memilih kunci rahasia berupa bilangan bulat

n

_B, dan menghitung titik

Q

_B

=

n P

_B .

Pertukaran Nilai Publik

• Alice mengirim nilai

Q

_A kepada Bob. • Bob mengirim nilai

Q

_B kepada Alice. Perhitungan Privat • Alice menghitung titik

A B

n Q

. • Bob menghitung titik

n Q

_{B A}.

Alice dan Bob telah menyepakati suatu nilai rahasia, yaitu titik

(

)

(

)

A B A B B A B A

n Q

=

n

n P

=

n

n P

=

n Q

.

5. Enkripsi Kunci Publik

Skema perjanjian kunci hanya dapat digunakan untuk menyapakati suatu kunci tertentu, dan tidak dapat digunakan untuk menyampaikan suatu pesan rahasia. Masalah logaritma diskrit dapat diterapkan untuk membentuk suatu sistem kripto untuk enkripsi kunci publik. Pada tahun 1985 Taher ElGamal mengusulkan suatu sistem kripto yang didasarkan pada masalah logaritma diskrit atas  p*. Berikut ini diberikan sistem kripto ElGamal yang didasarkan pada masalah logaritma

M-276

Sistem Kripto: Sistem Kripto Kunci Publik ElGamal Kurva Elliptik atas  _p Diberikan bilangan prima (besar) p dan kurva elliptik E atas ¢ _p. Diberikan titik

PÎ E sedemikian hingga

P

merupakan subgrup siklik dengan order prima (besar).

Ditentukan = E,  = E E× . Didefinisikan

 =

{

( , , , ) :

E P Q n

Q

=

nP

}

. Nilai E, P, dan Q dipublikasikan, dan nilai n dirahasiakan.

Untuk K =( , , , )E P Q n , plainteks M∈E dan untuk suatu bilangan bulat acak rahasia

k

∈

{

0,1, 2,...,



( )

P

}

, didefinisikan 1 2

(

, )

(

,

)

K

e

M k

=

C C

dimana 1

C

=

kP

, dan 2

C

=

M

+

kQ

. Untuk

C C

₁

,

₂

∈

E

, didefinisikan 1 2 2 1

(

,

)

K

d

C C

=

C

−

nC

.

Sistem Kripto: Sistem Kripto Kunci Publik ElGamal pada  _p*

Diberikan bilangan prima (besar) p dan g adalah elemen pembangun



_p

*

. Ditentukan =  _p*,  =  _p*× _p*. Didefinisikan

 =

{

( , , , ) :p g a

β β

≡ga

(

modp

)

}

. Nilai p, g, dan

β

dipublikasikan, dan nilai a dirahasiakan.

Untuk K =( , , , )p g a

β

, plainteks m∈ _p* dan untuk suatu bilangan bulat acak rahasia

k

∈

{

0,1, 2,...,

p

−

2

}

, didefinisikan

( , )

( , )

K

e

m k

=

γ δ

dimana k

(

mod

)

g

p

γ ≡

, dan

(

mod

)

k

m

p

δ

≡

β

. Untuk

γ δ

, ∈_p*, didefinisikan

(

)

1

( , )

(

a

)

mod

K

d

γ δ

≡

δ γ

−

p

.

Gambar 5. Sistem kripto kunci publik ElGamal pada  p*

Gambar 6. Sistem kripto kunci publik ElGamal kurva elliptik atas  _p

Tingkat keamanan dari sistem kripto kunci publik ElGamal pada _p* sebanding dengan tingkat kesulitan dari masalah logaritma diskrit atas ¢_p* dengan basis g. Jika pihak penyerang mendapatkan kunci publik ( , , )p g

β

, dan berhasil menemukan bilangan a sedemikian hingga

(

mod

)

a

g

p

M-277 Sistem Kripto: Skema Tanda-tangan ElGamal pada  _p*

Diberikan bilangan prima (besar) p dan sebuah elemen pembangun g∈ _p*. Ditentukan =  _p*,  =  _p*× _p−1 dan

a

∈

{

0,1,...,

p

−

2

}

. Didefinisikan

 =

{

( , , , ) :p g a

β β

≡ga

(

modp

)

}

. Nilai p, g, dan

β

dipublikasikan, dan nilai a dirahasiakan.

Untuk K =( , , , )p g a

β

dan untuk suatu bilangan acak rahasia

k

∈

{

1, 2,...,

p

−

2

}

, didefinisikan

( )

,

( , )

K

sig

x k

=

γ δ

dimana

(

mod

)

k

g

p

γ

≡

. dan

(

) (

1

)

mod

1

x a

k

p

δ

_≡

₋

γ

−

₋

. Untuk x,

γ

∈_p* dan

d

Î ¢ _p-₁, didefinisikan

(

)

(

, ,

)

benar x

(

mod

)

K

ver x

g d

= Û

b g

g dº g p .

Demikian juga tingkat keamanan dari sistem kripto kunci publik ElGamal kurva elliptik atas



_p terletak pada tingkat kesulitan dari masalah logaritma diskrit pada kurva elliptik E dengan basis P.

6. Skema Tanda-tangan

Pada pengiriman pesan, tidak menutup kemungkinan bahwa pada saat pengiriman pesan, ada pihak ketiga yang dengan sengaja merubah dan memodifikasi isi pesan tersebut, sehingga perlu dilakukan proses otentikasi, yaitu untuk menunjukkan bahwa suatu pesan itu benar berasal dari seseorang. Salah satu cara untuk melakukan proses otentikasi adalah menggunakan skema tanda-tangan. Definisi 6. Suatu skema tanda-tangan adalah suatu 5-tupel (, , , , ), dimana memenuhi kondisi berikut:

1. adalah himpunan berhingga pesan, 2.  adalah himpunan berhingga tanda tangan,

3. adalah himpunan berhingga kunci, disebut ruang kunci,

4. Untuk setiap K Î K , terdapat fungsi tanda-tangan

sig Î S

_K dan fungsi verifikasi

K

ver Î

. Setiap

sig

_K

:

P

®

A

dan

ver

_K

:

P

´

A

®

{benar,salah} merupakan fungsi sedemikian hingga untuk setiap pesan x Î P dan untuk setiap tanda tangan y Î A , persamaan berikut ini dipenuhi:

(

)

( )

( )

benar, jika , salah, jika . K K K y sig x ver x y y sig x ì ₌ ïï = í ï ¹ ïî

Berikut ini diberikan suatu skema tanda-tangan yang menunjukkan bahwa masalah logaritma diskrit dapat diterapkan untuk membentuk suatu skema tanda tangan, seperti pada skema tanda tangan ElGamal. Skema ini merupakan modifikasi dari sistem kripto kunci publik ElGamal.

M-278

Sistem Kripto: Elliptic Curve Digital Signature Algorithm (ECDSA)

Diberikan bilangan prima (besar) p dan E adalah suatu kurva elliptik atas lapangan

p

 . Diberikan titik A pada E yang mempunyai order prima q (besar). Ditentukan

{

0,1 *

}

=

P

,  = _q*×_q*, dan didefinisikan

 =

{

( , , , , ) :

p q E A B

B

=

mA

}

, dimana 0£ m£ q- 1.

Nilai p, q, E, A, dan B dipublikasikan, dan nilai m dirahasiakan.

Untuk K =( , , , , , )p q E A m B dan untuk suatu bilangan acak rahasia

{

1, 2,...,

1

}

k

∈

q

−

, didefinisikan

( )

,

( , )

K

sig

x k

=

r s

dimana

(

,

)

kA

=

u v

mod

r

=

u

q

, dan

( )

(

)

1 SHA-1 mod s= k- x + mr q.

Jika diperoleh nilai r = 0 atau s = 0, maka dipilih nilai k yang lain.

Untuk

x Î

{

0,1 *

}

dan r s, ∈q*, proses verifikasi tanda-tangan dilakukan dengan

menghitung: 1

mod

w

=

s

-

q

( )

SHA-1

mod

i

=

w

x

q

mod j= wr q

(

u v

,

)

=

iA

+

jB

(

)

(

, ,

)

benar

mod

K

ver

x r s

=

Û

u

q

=

r

.

Sama seperti pada skema enkripsi kunci publik ElGamal, tingkat keamanan dari skema tanda-tangan digital ElGamal terletak pada kekuatan masalah logaritma diskrit pada



_p

*

dengan basis g.

Berikut ini diberikan sebuah skema tanda-tangan yang didasarkan pada masalah logaritma diskrit pada grup kurva elliptik yang disebut dengan Elliptic Curve Digital Signature Algorithm (ECDSA). Pada skema tanda-tangan ECDSA digunakan suatu fungsi yang disebut dengan fungsi hash, yaitu suatu fungsi dengan domain berupa data biner sebagai elemen dari

{

0,1 *

}

dengan panjang yang tidak ditentukan, dan menghasilkan nilai fungsi dengan panjang tetap. Fungsi hash dapat digunakan untuk membuktikan bahwa suatu pesan telah mengalami perubahan isi selama berlangsung proses pengiriman pesan. Saat ini terdapat beberapa fungsi hash yang digunakan, diantaranya adalah SHA-1 dan MD5, dan pada ECDSA digunakan fungsi hash SHA-1. Pembahasan selengkapnya mengenai fungsi hash SHA-1 dapat dilihat pada FIPS (2002).

Gambar 8. Elliptic Curve Digital Signature Algorithm

Kunci publik dari ECDSA adalah pasangan

(

p q E A B

, , , ,

)

dan kunci rahasianya adalah nilai m. Tingkat keamanannya terletak pada kekuatan masalah logaritma diskrit pada kurva elliptik E dengan basis A, yaitu sulitnya menemukan nilai m sedemikian hingga B= mA.

M-279 KESIMPULAN

Dari uraian di atas dapat disimpulkan bahwa masalah logaritma diskrit dapat diterapkan pada kriptografi kunci publik, yaitu digunakan untuk mengkonstruksi suatu fungsi trapdoor satu arah. Masalah logaritma diskrit dapat diterapkan pada konstruksi skema perjanjian kunci, enkripsi kunci publik, dan skema tanda-tangan. Tingkat keamanan dari suatu sistem kripto sebanding dengan tingkat kesulitan untuk menyelesaikan masalah logaritma diskrit.

Pembahasan selanjutnya yang dapat dilakukan adalah mengenai analisis kompleksitas dan metode penyelesaian masalah logaritma diskrit, seperti algoritma Shank’s, Pollard Rho, Pohling-Hellman, dan Index-Calculus. Selain itu juga perlu dikaji mengenai metode untuk mencari bilangan prima yang besar, perhitungan order dari suatu elemen grup, dan metode untuk menghitung operasi perpangkatan modulo dan penjumlahan titik-titik kurva elliptik dengan cepat dan efisien.

DAFTAR PUSTAKA

FIPS (Federal Information Processing Standard), 2002, Secure Hash Standard, Publication 180-2.

Hankerson, D., et.al., 2004, Guide to Elliptic Curve Cryptography, Springer-Verlag, New York.

Hooffstein, J. et.al., 2008, An Introduction to Mathematical Cryptography, Springer- Verlag, New York.

Menezes, Oorcshot, and Vanstone, 1996, Handbook of Applied Cryptography, CRC Press, Inc. USA.

Schneier, B, 1996, Applied Cryptography, Second Edition: Protocol, Algorithms and Source Code in C, John Wiley and Sons.

Stinson, D.R., 2006, Cryptography Theory and Practice, Chapman & Hall/CRC, Boca Raton, Florida.