BAB 2
LANDASAN TEORI
2.1 Kriptografi
Kriptografi adalah ilmu yang mempelajari bagaimana mengirim pesan secara rahasia sehingga hanya orang yang dituju saja yang dapat membaca pesan rahasia tersebut. Pesan asli disebut sebagai plaintext, dan pesan yang telah dirahasiakan disebut sebagai
ciphertext. Proses dalam mengubah plaintext menjadi ciphertext disebut sebagai
encryption (enkripsi). Proses sebaliknya, untuk mengembalikan ciphertext menjadi
plaintext di sisi penerima pesan disebut sebagai decryption (dekripsi).
2.2 Sistem Kriptografi
Sistem kriptografi terdiri dari 5 bagian, yaitu (Sadikin, 2012):
a. Plaintext: pesan atau data dalam bentuk aslinya yang dapat terbaca. Plaintext adalah masukan bagi algoritma enkripsi.
b. Secret Key: secret key atau kunci rahasia juga merupakan masukan bagi algoritma enkripsi merupakan nilai yang bebas terhadap teks asli dan menentukan hasil keluaran algoritma enkripsi.
c. Ciphertext: ciphertext adalah keluaran algoritma enkripsi. Ciphertext dapat dianggap sebagai pesan dalam bentuk tersembunyi. Algoritma enkripsi yang baik akan menghasilkan ciphertext yang terlihat acak.
d. Algoritma Enkripsi: algoritma enkripsi memiliki 2 masukan teks asli dan kunci rahasia. Algoritma enkripsi melakukan transformasi terhadap teks asli sehingga menghasilkan ciphertext.
e. Algoritma Dekripsi: algoritma dekripsi memiliki 2 masukan yaitu ciphertext dan kunci rahasia. Algoritma dekripsi memulihkan kembali teks sandi menjadi teks asli bila kunci rahasia yang dipakai algoritma dekripsi sama dengan kunci rahasia yang dipakai algoritma enkripsi.
2.3.1 Sistem Kriptografi Kunci Simetris
Sistem kriptografi kunci simetris menggunakan kunci yang sama untuk mengenkripsi
plaintext dan mendekripsi ciphertext, Diagram sistem kriptografi kunci simetris dapat dilihat pada Gambar 2.1.
Gambar 2.1 Diagram Sistem Kriptografi Kunci Simetris
Arti simbol: : Data : Proses : Aliran
Pada Gambar 2.1 dapat dilihat bahwa kunci yang digunakan untuk mengenkripsi dan mendekripsi sama yaitu K. Sistem kriptografi ini aman selama kunci rahasia dipastikan hanya diketahui oleh kedua pihak yang saling berkirim pesan. Namun cara untuk mengirim kunci menjadi masalah lain yang sulit untuk diamankan terutama dalam jalur publik seperti internet.
2.3.2 Sistem Kriptografi Kunci Asimetris
kunci yang dapat mendekripsi ciphertext yang telah dienkripsi dengan kunci publik. Diagram sistem kriptografi asimetris dapat dilihat pada Gambar 2.2.
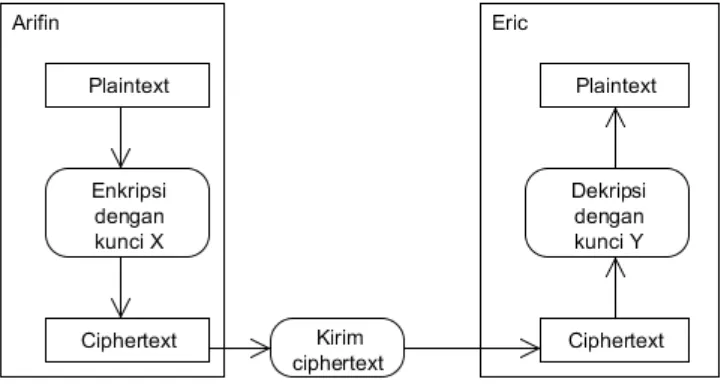
Gambar 2.2 Diagram Sistem Kriptografi Kunci Asimetris
Pada Gambar 2.2., kunci yang digunakan untuk mengenkripsi dan mendekripsi pesan berbeda, dimana Arifin menggunakan kunci X untuk mengenkripsi pesan menjadi ciphertext, lalu Eric sebagai penerima ciphertext akan mendekripsi pesan menggunakan kunci Y. Ciphertext tidak dapat dikembalikan menjadi plaintext jika Y
tidak diketahui. Disini X disebut sebagai public key dan Y disebut sebagai private key. Public key harus didistribusikan kepada siapapun yang ingin mengirim pesan secara rahasia kepada pemilik kunci sedangkan private key harus tetap disimpan secara rahasia.
Sistem kriptografi ini memiliki keunggulan dimana pengiriman kunci bukan lagi menjadi masalah karena kunci publik tidak akan menjadi masalah jika diketahui oleh siapapun.
2.4 Matematika untuk Sistem Kriptografi Asimetris
2.4.1 Greatest Common Divisor (GCD) dan Algoritma Euclid
Jika a dan b adalah bilangan bulat, maka Greatest Common Divisor (GCD) dari a dan
b adalah sebuah bilangan positif terbesar yang dapat membagi habis kedua bilangan tersebut.
Sebagai contoh, GCD dari 12 dan 18 adalah 6 karena 6 dapat membagi 12 dan 18 dan tidak ada bilangan yang lebih besar dari 6 yang dapat membagi 12 dan 18. Dapat ditulis:
GCD(12,18) = 6
Salah satu cara untuk mendapatkan GCD dari dua buah bilangan adalah dengan menggunakan Algoritma Euclid. Teorema Euclid menyatakan:
jika a = qb + r maka GCD(a,b) = GCD(b,r)
2.4.2. Relatif Prima
Dua buah bilangan a dan b dikatakan relatif prima jika GCD(a, b) = 1. Sebagai contoh 4 dan 7 adalah relatif prima karena GCD(4, 7) = 1.
2.4.3 Aritmatika Modular dan Kongruensi
Ketika masih kecil kita mempelajari „aritmatika jam‟ dimana angka berikutnya setelah 12 adalah 1 sehingga kita menuliskan (Hoffstein, 2008):
8 + 7 = 3 dan 2 − 5 = 9
ini masuk akal karena 7 jam setelah jam 8 adalah jam 3. Yang kita lakukan sebenarnya adalah menghitung 8 + 7 = 15 kemudian menguranginya 12 sehingga menghasilkan 3. Dan dengan cara yang sama 5 jam sebelum jam 2 adalah jam 9 dengan menghitung 2 – 5 = -3 kemudian menambahkannya dengan 12.
Konsep ini disebut sebagai dengan teori kongruensi. Kita katakan a dan b
kongruen m jika selisih a – b dapat dibagi dengan m. Ditulis sebagai berikut:
𝑎 ≡ 𝑏 (mod 𝑚)
untuk mengetahui a dan b kongruen, m disebut sebagai modulus.
6 + 9 ≡ 3 (mod 12) dan 2 − 3 ≡ 1 (mod 12)
2.4.4 Inversi Modulo
Jika dua buah bilangan a dan m relatif prima, maka dapat dipastikan terdapat sebuah bilangan b yang memenuhi:
𝑎 . 𝑏 ≡ 1 (mod 𝑚)
pada kongruensi diatas, b disebut sebagai invers modulo dari a modulo m.
2.4.5 Grup Perkalian
Sebuah grup perkalian (G, ×) dengan G merupakan himpunan simbol dan × adalah sebuah operator perkalian yang memenuhi kondisi (Sadikin, 2012):
1. ∀𝑎, 𝑏 ∈ 𝐺 ∶ 𝑎 × 𝑐 ∈ 𝐺 (Closure)
2. ∀𝑎, 𝑏, 𝑐 ∈ 𝐺 ∶ (𝑎 × 𝑏) × 𝑐 = 𝑎 × (𝑏 × 𝑐) (Asosiatif)
3. ∃ yang unik 𝑒 ∈ 𝐺 ∶ ∀𝑎 ∈ 𝐺 ∶ 𝑎 × 𝑒 = 𝑒 × 𝑎 = 𝑎 Elemen e disebut
sebagai elemen identitas.
4. ∀𝑎 ∈ 𝐺: ∃𝑎−1∈ 𝐺: 𝑎 × 𝑎−1= 𝑎−1× 𝑎 = 𝑒 (Invers)
2.4.6 Bilangan Prima
Bilangan prima adalah sebuah bilangan yang hanya dapat dibagi habis oleh 1 dan bilangan itu sendiri. Bilangan yang dapat dibagi habis oleh selain 1 dan bilangan itu sendiri disebut sebagai bilangan komposit. Semua bilangan positif integer n dapat dituliskan sebagai hasil product dari bilangan prima seperti berikut:
𝑛 = 𝑝1𝛼1𝑝2𝛼2… 𝑝𝑟𝛼𝑟 = ∏ 𝑝𝑗𝛼𝑗 𝑟
𝑗=1
2.4.7 Fermat’s Little Theorem
Teori fermat merupakan fondasi dari banyak pengetesan bilangan prima (Riesel, 2012). Jika p merupakan sebuah bilangan prima dan GCD(a, p) = 1, maka
dan sebaliknya jika n adalah sebuah bilangan komposit dan GCD(a, p) = 1, maka
𝑎𝑝−1 ≢ 1 𝑚𝑜𝑑 𝑝 2.4.8 Fungsi ϕ Euler
Fungsi ϕ Euler atau yang disebut juga fungsi totien euler, dilambangkan dengan ϕ(n) adalah banyaknya bilangan m yang relatif prima terhadap n dimana m < n (Mollin, 2007). Sebagai contoh jika p adalah bilangan prima, maka untuk semua 𝑗 ∈ 𝑁 dengan
𝑗 < 𝑝 pasti relatif prima terhadap p, maka ϕ(p) = p – 1.
Sebagai contoh beberapa hasil fungsi ϕ(n) adalah (Sadikin, 2012):
1. ϕ(1) = 0
2. ϕ(p) = p – 1 jika p adalah bilangan prima. Sebab semua elemen merupakan
prima relatif dengan p.
3. ϕ(m × n) = ϕ(m) × ϕ(n) jika m merupakan prima relatif dengan n. 4. ϕ(𝑝𝑒) = 𝑝𝑒− 𝑝𝑒−1 dengan p adalah bilangan prima.
2.4.9 Akar Primitif
Jika p adalah bilangan prima, maka terdapat sebuah elemen 𝑔 ∈ 𝐹𝑝∗ yang jika
dipangkatkan dengan setiap elemen di dalam 𝐹𝑝∗ (Hoffstein, 2008), misalkan:
𝐹𝑝∗= *1, 𝑔, 𝑔2, 𝑔3, … , 𝑔𝑝−2+.
elemen dengan properti ini disebut dengan akar primitif dari 𝐹𝑝 atau generator dari 𝐹𝑝∗. Elemen tersebut merupakan elemen dari 𝐹𝑝∗ memiliki order p – 1.
2.4.10. Algoritma Miller-Rabin
Algoritma Miller-Rabin merupakan algoritma probabilistik yang menguji keprimaan
sebuah bilangan yang diberikan berdasarkan pada Fermat’s LittleTheorem. Algoritma Miller-Rabin menghitung deret berikut secara berulang : 𝑎𝑚 ≡ 𝑎2𝑚 ≡ 𝑎22𝑚≡ ⋯ ≡ 𝑎2𝑘−1𝑚 ≡ 𝑎2𝑘𝑚(𝑚𝑜𝑑 𝑛). Pada perhitungan 𝑎2𝑖𝑚 dilakukan pengujian Fermat dan
pengujian kepemilikan akar kuadrat untuk i = 0, 1, 2, …, k . Jika pengujian akar kuadrat ialah positif, n dideklarasikan sebagai bilangan komposit. Jika pengujian
2.4.11 Discrete Log Problem
Jika g merupakan akar primitif dari 𝐹𝑝 dan h merupakan sebuah elemen yang tidak nol
pada 𝐹𝑝.Discrete Log Problem merupakan sebuah masalah dalam menemukan x yang
memenuhi persamaan berikut (Hoffstein, 2008):
𝑔𝑥 ≡ ℎ (mod 𝑝)
Pada persamaan diatas, x disebut sebagai logaritma diskrit dari h untuk basis g dan ditulis sebagai log𝑔(ℎ).
2.4.12 Chinese Remainder Theorem
Chinese Remainder Theorem (CRT) diformulasikan sebagai penyelesaian permasalahan kongruen dengan modulus yang berbeda. Secara formal CRT menyelesaikan sistem persamaan kongruen berikut ini:
≡ 𝑎1 mod 𝑚1 ≡ 𝑎2 mod 𝑚2
. . . ≡ 𝑎𝑘 mod 𝑚𝑘
dengan nilai 𝑎1, 𝑎2, … , 𝑎𝑘 dan 𝑚1, 𝑚2, … , 𝑚𝑘 diketahui, dan x adalah bilangan yang perlu ditemukan.
Berikut adalah algoritma untuk menemukan x: a. Hitung = 𝑚1 × 𝑚2 × … × 𝑚𝑘
b. Hitung 1 =
𝑚1, 2 = 𝑚2, … , 𝑘= 𝑚𝑘
c. Temukan invers modulo untuk setiap 1−1, 2−1, … , 𝑘−1 terhadap 𝑚1, 𝑚2, … , 𝑚𝑘 d. Temukan x dengan menghitung
= ((𝑎1 × 1 × 1−1) + ⋯ + (𝑎𝑘 × 𝑘 × 𝑘−1))
2.5 Sistem Kriptografi ElGamal
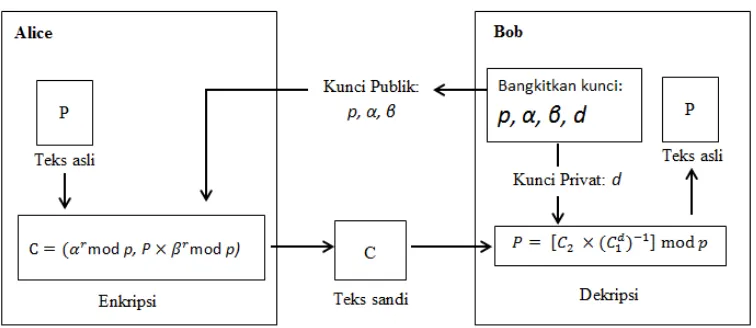
Gambar 2.3 Diagram Proses Sistem Kriptografi ElGamal
Sistem kriptografi ElGamal bekerja pada sebuah grup perkalian (𝑍𝑝∗,×) yang
pada grup itu persoalan logaritmik diskrit sulit untuk dipecahkan. Grup perkalian G dapat berupa grup perkalian siklik dengan α adalah akar primitif pada Zp dengan p
merupakan bilangan prima. (Sadikin, 2012)
2.5.1 Algoritma ElGamal
Algoritma kriptografi ElGamal adalah sebagai berikut:
a. Pembangkit kunci ElGamal
1. Pilih bilangan prima p yang cukup besar sebagai basis grup perkalian (𝑍𝑝∗,×) 2. Pilih α sebagai akar primitif pada grup (𝑍𝑝∗,×)
3. Pilih d yang memenuhi 1 ≤ d ≤ p – 2 4. Hitung β = 𝛼𝑑mod p
5. Kunci publik : (p, α, β) 6. Kunci privat : d
Setelah kunci publik dan kunci privat didapatkan, kunci publik akan didistribusikan kepada siapapun yang perlu untuk mengirimkan pesan secara rahasia (dienkripsi), sedangkan kunci privat dijaga kerahasiaannya untuk mendekripsi pesan yang telah dienkripsi dengan kunci publik.
b. Enkripsi Pesan
Orang yang menerima kunci publik dapat mengirimkan pesan secara rahasia kepada pemberi kunci, dengan langkah sebagai berikut:
2. Output : 𝐶1, 𝐶2 ∈ 𝑍𝑝∗
3. r ← 𝑍𝑝∗ {r dipilih secara acak} 4. 𝐶1 = 𝛼𝑟mod p
5. 𝐶2 = P×𝛽𝑟mod p c. Dekripsi Pesan
Setelah ciphertext diterima, maka pemegang kunci privat dapat mendekripsi pesan dengan cara sebagai berikut:
1. Input : 𝐾𝑝𝑟𝑖𝑣𝑎𝑡 = d, 𝐶1, 𝐶2 ∈𝑍𝑝∗ 2. Output : P ∈𝑍𝑝∗
3. 𝑃 = ,𝐶2 × (𝐶1𝑑)−1- mod 𝑝
2.5.2 Contoh Penerapan Algoritma Kriptografi ElGamal
Berikut ini adalah contoh penerapan dari algoritma kriptografi ElGamal, Misalkan Adit memiliki kunci ElGamal sebagai berikut:
Kunci publik : α = 345, β = 223, p = 379, Kunci privat : d = 43
Kemudian Adit mendistribusikan kunci publik kepada siapa saja yang mau mengirim pesan kepadanya. Arifin yang juga mendapatkan kunci publik key milik Adit akan mengenkripsi pesan menggunakan kunci publik yang diketahui sebagai berikut: Plaintext : mundur
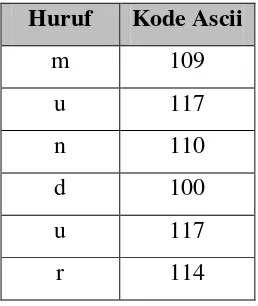
Kode ascii dari plaintext adalah:
Tabel 2.1 Kode ASCII dari Plaintext
Huruf Kode Ascii
2. Menghitung nilai C1 = 𝛼𝑟 mod 𝑝, sehingga didapati C1 = 10
3. Untuk setiap huruf dalam plaintext, dilakukan pengubahan nilai 𝐶2 = P × 𝛽𝑟mod 𝑝, sehingga didapati:
Tabel 2.2 Ciphertext 2, Hasil Enkripsi dari Plaintext‘mundur’
Huruf P = P× mod p
m 109 257
u 117 255
n 110 162
d 100 354
u 117 255
r 114 161
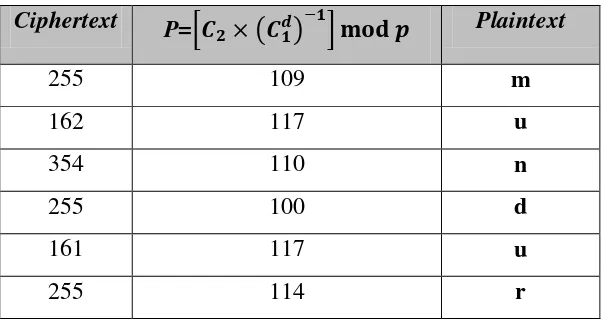
Setelah pesan terenkripsi, Arifin mengirim ciphertext 1 dan ciphertext 2 kepada Adit. Lalu Adit akan mendekripsi ciphertext tersebut kembali menjadi plaintext menggunakan kunci privat sebagai berikut:
Tabel 2.3 Hasil Dekripsi dari Ciphertext
Ciphertext P=[ × ( )− ] Plaintext
255 109 m
162 117 u
354 110 n
255 100 d
161 117 u
255 114 r
2.6 Kriptanalisis
Di dalam penelitian ini, penulis mengetahui algoritma kriptografi apa yang digunakan dan kunci publik yang telah didistribusikan. Dari itu diketahui bahwa ada algoritma yang dapat digunakan untuk memecahkan kunci privat. Sehingga teknik yang akan digunakan adalah membuat sebuah ciphertext dari kunci publik yang diketahui, lalu mencoba memecahkan kunci privatnya berdasarkan kunci publik dan ciphertext yang telah dibuat.
2.7 Algoritma Silver-Pohlig-Hellman
Algoritma Silver-Pohlig-Hellman (SPH) adalah sebuah algoritma untuk menghitung
logaritma diskrit dari sebuah grup perkalian. Cara kerja algoritma Silver-Pohlig
-Hellman dijabarkan sebagai berikut:
a. Diketahui α adalah generator𝑍𝑝∗, β ∈𝑍𝑝∗ , dan kita memiliki faktorisasi berikut:
𝑝 − 1 = ∏ 𝑝𝑗𝑎𝑗 𝑟
𝑗=1
𝑎𝑗 ∈ N
dimana 𝑝𝑗adalah distinct primes. Cara untuk menghitung 𝛼𝑒 ≡ 𝛽 (mod 𝑝) adalah
dengan menghitung e modulo 𝑝𝑗𝑎𝑗 untuk j = 1, 2, … , r, lalu gunakan Chinese Remainder Theorem.
b. Untuk menghitung setiap nilai e modulo 𝑝𝑗𝑎𝑗 kita harus menentukan e dengan basis 𝑝𝑗:
𝑒 = ∑ 𝑏𝑖(𝑗) 𝑝𝑗𝑖 𝑎𝑗−1
𝑖=0
untuk menghitung 𝑏𝑖(𝑗), kita lakukan hal berikut.
b.1 Set 𝛽 = 𝛽0
b.2Temukan 𝑏0(𝑗) dengan cara sebagai berikut:
Hitunglah 𝛼(𝑝−1)𝑘 𝑝𝑗 𝑚𝑜𝑑 𝑝 untuk setiap k = 0, 1, …, 𝑝𝑗− 1 sampai kita
Pada kondisi diatas, k = 𝑏0(𝑗)
c. Temukan e dengan menggunakan Chinese Remainder Theorem .
Di bawah ini contoh dari penggunaan algoritma Silver-Pohlig-Hellman dalam memecahkan kunci privat ElGamal, Berdasarkan contoh pada penerapan kriptografi ElGamal, diketahui bahwa p = 379, α = 345 dan 𝛽0 = 𝛽 = 223. Kita ingin mencari kunci privat 𝑑 = log345(223). Pada perhitungan dibawah, semua persamaan berikut diasumsikan sebagai modulo 379.
k 0 1
𝛼(𝑝−1)𝑘 𝑝1 1 3126 ≡ 51
i 0 1 2
𝛽𝑖 223 339 255
𝛽𝑖(𝑝−1) 𝑝2𝑖+1 223126 ≡ 51 33942≡ 327 25514 ≡ 51
𝑏𝑖2 1 2 1
Disini kita dapati 𝑏0 = 1, 𝑏1= 2, 𝑏2 = 1 . Maka kita dapati representasi basis 3 dari log345(223) 𝑚𝑜𝑑 27 adalah:
∑ 𝑏𝑖2𝑝2𝑖 𝑎2−1
𝑖=0
= 1 . 30 + 2 . 31+ 1 . 32 ≡ 16 (mod 27)
Untuk 𝑝3 = 7:
𝛽0(𝑝−1) 𝑝2 = 223378 7 ≡ 195
k 0 1
𝛼(𝑝−1)𝑘 𝑝1 1 354≡ 195
Disini kita dapati 𝑏0 = 1. Maka kita dapati representasi basis 7 dari log345(223) 𝑚𝑜𝑑 7 adalah:
∑ 𝑏𝑖3𝑝3𝑖 𝑎3−1
𝑖=0
= 1 . 70 ≡ 1 (mod 7)
Lalu kita akan mencari nilai e dengan menggunakan Chinese Remainder Theorem untuk setiap nilai 𝑒𝑗 pada basis 𝑝𝑗. Dan kita dapati bahwa e = 43, jika nilai e disubstitusikan pada persamaan awal, maka:
34543 ≡ 223 (mod 379)
2.8 Tinjauan Penelitian yang Relevan
Berikut adalah penelitian yang membahas seputar algoritma kriptografi ElGamal: a. Andrian. Y. (2013) membuat penelitian yang berfokus pada penggunaan elemen
primitif dan elemen non-primitif pada kunci publik ElGamal. Hasil penelitian menunjukkan bahwa Elemen primitif maupun elemen non-primitif tidak mempengaruhi proses enkripsi, proses dekripsi, dan besarnya file hasil enkripsi. b. Asmar. N. D. (2008) membentuk sebuah sistem yang mengamankan data dan
informasi dengan menggunakan Algoritma ElGamal. Hasil penelitian mengungkapkan bahwa Algoritma kriptografi asimetris seperti ElGamal sangat baik digunakan untuk mengatasi masalah distribusi kunci.