GEOMETRI KABUR Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh: Nancy Hartono NIM: 043114013

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

Presented as Partial Fulfillment of the Requirements To Obtain the SARJANA SAINS Degree

In Mathematics

By: Nancy Hartono

Student Number: 043114013

MATHEMATICS STUDY PROGRAM MATHEMATICS DEPARTMENT SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

v

Serahkanlah hidupmu kepada Tuhan dan percayalah kepada-Nya;

dan Ia akan bertindak.

(Mzm 37:5)

Segala sesuatu indah pada waktunya. (Pengkotbah 3:11)

Skripsi ini kupersembahkan untuk:

Tuhan Yesus Kristus, terima kasih Tuhan karena dengan berkatmu aku dapat menyelesaikan tugas terakhirku sebagai mahasiswa dan selalu setia mendengarkan semua isi hatiku…

Papa dan Mama tercinta… Terima kasih atas cinta dan kasih sayang

serta doa dan motivasi yang telah diberikan selama ini. Aku bersyukur dapat

membuat papa dan mama tersenyum dan kelak dapat membahagiakan papa dan

mama.

Ko Thomas, Ce Rina, Ko Joko, Dannys, Catherine, dan Daniel…

Aku sangat bersyukur memiliki kakak yang selalu mendukung dan menjagaku

dan aku senang memiliki adik dan keponakan-keponakan yang lucu…

Ko Rey…Kamu adalah anugerah terindah yang Tuhan berikan buat Nancy dan

semangat dalam hidupku…

vii

viii

geometry presented in this thesis includes fuzzy point, fuzzy distance between two

fuzzy points, fuzzy line, area and perimeter of a fuzzy subset, height and width of a

fuzzy subset, fuzzy rectangle, and fuzzy triangle. To discuss fuzzy geometry, we need

to understand fuzzy sets and important notions of fuzzy sets such as support, cut,

x

sehingga karena kasih dan karunia-Nya skripsi ini dapat terselesaikan tepat waktu.

Dalam penyusunan skripsi ini penulis membutuhkan bantuan dari berbagai

pihak. Oleh karena itu, dengan segala kerendahan hati penulis ingin menyampaikan

ucapan terima kasih kepada :

1. Romo Prof. Dr. Frans Susilo, S.J., selaku dosen pembimbing yang dengan rendah

hati bersedia meluangkan banyak waktu luang dan dengan penuh kesabaran telah

membimbing selama penyusunan skripsi ini.

2. Papa dan mama tercinta untuk cinta, kasih sayang, pengorbanan, doa, motivasi

dan kepercayaan yang diberikan kepada penulis.

3. Ibu Maria Vianney Any Herawati, S.Si., M.Si., selaku dosen penguji.

4. Bapak Herry Pribawanto Suryawan, S.Si., M.Si., selaku sdosen penguji dan telah

bersedia meminjamkan beberapa buku kepada penulis.

5. Ibu Lusia Krismiyati Budiasih, S.Si., M.Si., selaku Kaprodi Matematika

FST-USD dan Dosen Pembimbing Akademik angkatan 2004 yang telah memberikan

doa, saran, nasehat, dan dukungan kepada penulis.

6. Bapak Yosef Agung Cahyanta, S.T., M.T., selaku Dekan FST-USD.

7. Bapak dan Ibu dosen yang telah memberikan ilmu kepada penulis.

8. Bapak Tukija dan Ibu Linda atas dukungan yang pernah diberikan dan telah

xi

besar yang telah memberikan doa dan dukungan kepada penulis.

11. Pasanganku, Rey, yang selalu menemaniku di saat senang maupun sedih, dan

memberikan semangat serta dukungan.

12. Sahabat terbaikku di Matematika’04, Lili, Teodora, Siska, Retno, Ratna, Eny,

Dwi, Lina dan Yohanes, yang telah memberikan dukungan serta terima kasih

untuk kesediaan menjadi teman curhatku dan kebersamaan kita selama ini.

13. Sahabat-sahabatku, Fitri, Nur, Ardian, Aris, Resti, Budi, Veronica, Eunike,

Yoshita, dan Peter, terima kasih atas dukungan dan kebersamaan kita selama ini.

14. Semua pihak yang telah membantu yang tidak dapat disebutkan satu persatu.

Penulis menyadari kekurangan dalam skripsi ini, untuk itu saran dan kritik

sangat diharapkan dalam peningkatan kualitas skripsi ini, dan akhirnya penulis

berharap semoga skripsi ini dapat bermanfaat bagi semua pihak.

Yogyakarta, Februari 2009

Penulis,

xii

HALAMAN JUDUL DALAM BAHASA INGGRIS ……….. ii

HALAMAN PERSETUJUAN PEMBIMBING ... iii

HALAMAN PENGESAHAN ……….. iv

HALAMAN PERSEMBAHAN ………... v

HALAMAN PERNYATAAN KEASLIAN KARYA ……….. vi

HALAMAN ABSTRAK ………... vii

HALAMAN ABSTRACT ……… viii

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS ……… ix

KATA PENGANTAR ………. x

DAFTAR ISI ... xii

BAB I PENDAHULUAN ... 1

A. Latar Belakang Masalah ... 1

B. Perumusan Masalah ... 5

C. Batasan Masalah ... 5

D. Tujuan Penulisan ... 6

E. Manfaat Penulisan ... 6

F. Metode Penelitian ... 6

xiii

C. Segiempat ... 33

BAB III HIMPUNAN KABUR ... 49

A. Himpunan Kabur ... 49

B. Fungsi Keanggotaan ... 55

C. Operasi Baku pada Himpunan Kabur ... 56

D. Relasi Kabur ... 58

BAB IV GEOMETRI KABUR ... 70

A. Introduksi ... 70

B. Titik Kabur ... 73

C. Jarak Kabur antara Dua Titik Kabur ... 74

D. Garis Kabur ……… 83

E. Luas dan Keliling Himpunan Bagian Kabur ……...……… 86

F. Tinggi dan Lebar Himpunan Bagian Kabur ……… 90

G. Segiempat Kabur ……….. 93

H. Segitiga Kabur ……….………. 101

BAB V PENUTUP ... 105

A. Kesimpulan ... 105

B. Saran ... 107

BAB I

PENDAHULUAN

A. Latar Belakang

Pelopor geometri adalah orang Mesir kuno (sekitar 2500 tahun SM). Dengan

kemampuan persepsi dan abstraksinya, manusia memperoleh pemahaman mengenai

bangun (misalnya: lingkaran, segitiga, segiempat), sifat-sifat bangun, relasi antar

bangun dan ukuran bangun. Orang Mesir meneruskan pengetahuannya kepada orang

Yunani yang menciptakan istilah “Geometri” (ukuran bumi). Orang Yunani (sekitar

600 tahun SM) mengembangkan pengetahuan geometri menjadi pengetahuan yang

abstrak dan dilengkapi dengan metode pembuktian yang bersifat deduktif.

Perkembangan tersebut terjadi dalam dua perguruan yang terkenal, yaitu yang

didirikan oleh Thales (624-548 SM) dan oleh Pythagoras (580-500 SM), keduanya

memberi kontribusi yang sangat besar dalam perkembangan sains, musik dan filsafat.

Metode deduktif Thales dan Pythagoras mencapai puncaknya dalam karya

“Euclides” berjudul “Elementa” (sekitar 300 tahun SM) yang menyusun geometri

secara aksiomatis.

Definisi dalam geometri Euclides:

a. Titik adalah sesuatu yang tidak mempunyai bagian.

c. Bidang adalah sesuatu yang mempunyai panjang dan lebar.

d. Sudut adalah inklinasi atau sela antara dua garis yang berpotongan.

e. Lingkaran adalah suatu bangun datar yang termuat dalam suatu kurva

sedemikian sehingga semua garis lurus yang melalui suatu titik dalam

bangun itu memotong kurva itu sama panjang.

Himpunan kabur diciptakan oleh Lotfi Asker Zadeh, seorang guru besar pada

University of California, Berkeley, Amerika Serikat. Sejak tahun 1960 Profesor

Zadeh telah merasa bahwa sistem analisis matematik tradisional yang dikenal sampai

saat itu bersifat terlalu eksak sehingga tidak dapat berfungsi dalam banyak masalah

dunia nyata yang seringkali amat kompleks. Dan pada tahun 1965, Profesor Zadeh

mempublikasikan karangan ilmiahnya yang berjudul “Fuzzy Sets”, yang oleh para

pakar di kemudian hari dianggap sebagai karya monumental yang melahirkan bahasa

baru yang diimpikan itu. Terobosan baru yang diperkenalkan Zadeh dalam karangan

tersebut adalah memperluas konsep “himpunan klasik” menjadi “himpunan kabur”

(fuzzy set), dalam arti bahwa himpunan klasik (himpunan tegas, crisp set) merupakan

kejadian khusus dari himpunan yang kabur itu. Dalam teori himpunan klasik, yang

dikembangkan oleh Georg Cantor (1845-1918), himpunan didefinisikan sebagai suatu

koleksi obyek-obyek yang terdefinisi secara tegas, dalam arti dapat ditentukan secara

tegas apakah suatu obyek adalah anggota himpunan itu atau tidak. Dengan demikian,

suatu fungsi X_A :X {0,1}, yang disebut fungsi karakteristik dari himpunan A, di

mana untuk setiap xX

) (x X_A =

Dengan memperluas konsep fungsi karakteristik itu, Zadeh mendefinisikan

himpunan kabur dengan suatu fungsi yang disebut “fungsi keanggotaan”

(membership function) dan nilai fungsi itu disebut “derajat keanggotaan”, yang

selanjutnya disebut “himpunan kabur” (fuzzy set). Derajat keanggotaan dinyatakan

dengan suatu bilangan real dalam selang tertutp [0,1]. Dengan perkataan lain, fungsi

keanggotaan dari suatu himpunan kabur A~ dalam semesta X adalah pemetaan _A~

dari X ke selang [0,1], yaitu ~ :X [0,1]

A

 . Nilai fungsi ~(x)

A

 menyatakan derajat

keanggotaan unsur xX dalam himpunan kabur A~. Nilai fungsi sama dengan 1

menyatakan keanggotaan penuh, dan nilai fungsi sama dengan 0 menyatakan

samasekali bukan anggota himpunan kabur tersebut.

Secara matematis suatu himpunan kabur A~ dalam semesta X dapat dinyatakan

sebagai himpunan pasangan terurut

} |

)) ( , {( ~

~ x x X

x A

A 

 

1 untuk xA

di mana _A~ adalah fungsi keanggotaan dari himpunan kabur A

~

, yang merupakan

suatu pemetaan dari himpunan semestaXke selang tertutup [0,1]. Apabila semesta X

adalah himpunan yang kontinu, maka himpunan kabur A~ seringkali dinyatakan

dengan







X x

A x x

A~ ~( )/

di mana lambang



di sini bukan lambang integral seperti yang dikenal dalam

kalkulus, tetapi melambangkan keseluruhan unsur-unsur xX bersama dengan

derajat keanggotaannya dalam himpunan kabur A~ . Apabila semesta X adalah

himpunan yang diskret, maka himpunan kabur A~ seringkali dinyatakan dengan







X x

A x x

A~ ~( )/

di mana lambang



di sini tidak melambangkan operasi penjumlahan seperti yang

dikenal dalam aritmatika, tetapi melambangkan keseluruhan unsur-unsur xX

bersama dengan derajat keanggotaannya dalam himpunan kabur A~.

Atas dasar teori himpunan kabur itu, Zadeh kemudian membangun logika kabur

(fuzzy logic) yang mendasari penalaran yang melibatkan konsep-konsep kabur. Teori

himpunan dan logika kabur ternyata berkembang dengan amat pesat, yang

kabur adalah geometri dengan dasar himpunannya berupa himpunan kabur. Geometri

kabur dikembangkan oleh Rosenfeld, Buckley dan Eslami. Teori geometri kabur yang

dijelaskan oleh Rosenfeld, Buckley dan Eslami dapat diaplikasikan untuk mengenali

pola, komputer grafis, dan pemrosesan gambar. Dalam skripsi ini akan dibahas

teorinya saja mengenai geometri kabur.

B. Perumusan Masalah

Berdasarkan uraian yang dikemukakan dalam latar belakang di atas, pokok

permasalahan dalam skripsi ini adalah

a. Apa yang dimaksud dengan titik dan garis kabur?

b. Apa yang dimaksud dengan jarak kabur antara titik-titik kabur?

c. Apa yang dimaksud dengan segitiga dan segiempat kabur?

d. Apa yang dimaksud dengan luas dan keliling himpunan bagian kabur?

e. Apa yang dimaksud dengan tinggi dan lebar himpunan bagian kabur?

C. Batasan Masalah

Dalam penulisan skripsi ini akan dibahas geometri kabur dengan lingkup

geometri Euclides. Tetapi tidak semua bagian geometri Euclides akan dibahas dalam

skripsi ini. Geometri Euclides yang akan dibahas adalah titik, garis, bidang (segitiga

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah untuk mempelajari teori himpunan kabur dan

logika kabur yang diaplikasikan dalam bidang matematika, khususnya geometri

kabur.

E. Manfaat Penulisan

Manfaat penulisan skripsi ini adalah supaya untuk lebih memahami teori

himpunan kabur dan logika kabur yang diaplikasikan dalam bidang matematika,

khususnya geometri kabur.

F. Metode Penulisan

Metode penulisan skripsi ini adalah dengan menggunakan metode studi pustaka,

yaitu mempelajari buku-buku yang berhubungan dengan geometri kabur.

G. Sistematika Penulisan

BAB I PENDAHULUAN

A. Latar Belakang

C. Batasan Masalah

D. Tujuan Penulisan

E. Manfaat Penulisan

F. Metode Penulisan

G. Sistematika Penulisan

BAB II Geometri Euclides

A. Titik, Garis, dan Sudut

B. Segitiga

C. Segiempat

BAB III Himpunan Kabur

A. Himpunan Kabur

B. Fungsi Keanggotaan

C. Operasi Baku pada Himpunan Kabur

D. Relasi Kabur

BAB IV Geometri Kabur

A. Introduksi

B. Titik Kabur

C. Jarak Kabur antara Dua Titik Kabur

E. Luas dan Keliling Himpunan Bagian Kabur

F. Tinggi dan Lebar Himpunan Bagian Kabur

G. Segiempat Kabur

H. Segitiga Kabur

BAB V Penutup

A. Kesimpulan

BAB II

GEOMETRI EUCLIDES

A. Titik, Garis, dan Sudut

Bangun yang sederhana dalam geometri meliputi titik, garis, dan sudut. Titik

adalah sesuatu yang tidak mempunyai bagian. Garis adalah sekumpulan titik yang

saling berhubungan.

Definisi 2.1.1

Suatu ruas garis AB adalah himpunan yang terdiri dari titik Adan B dan semua

titik Cyang terletak pada garis melalui Adan Bdan terletak di antara Adan B.

Definisi 2.1.2

Panjangruas garis AB adalah bilangan real positif yang menyatakan jarak antara

titik Adan titik B, dan dinotasikan dengan AB.

Definisi 2.1.3

Dua ruas garis dikatakan kongruenjika dan hanya jika kedua ruas garis tersebut

memiliki panjang yang sama.

Definisi 2.1.4

Titik bagi ruas garis AB adalah suatu titik Cpada ruas garis tersebut sedemikian

sehingga AC kongruen dengan CB.

Definisi 2.1.5

Suatu sinar garis AB adalah himpunan yang terdiri dari ruas garis AB dan

semua titik C yang terletak pada garis melalui A dan B sedemikian sehingga B

terletak di antara Adan C.

A B

C

Definisi 2.1.6

Sudut dengan titik sudut Aterdiri dari titik Asendiri dan dua sinar garis AB dan

AC (yang disebut sisi-sisi sudut) dan dilambangkan dengan BAC atau A.

Definisi 2.1.7

Ukuran derajat suatu sudut adalah suatu bilangan real antara 0 dan 180. Ukuran

derajat A dinotasikan dengan mA. Dua buah sudut dikatakan kongruen jika

kedua sudut itu mempunyai ukuran sudut yang sama.

Definisi 2.1.8

Garis bagi BAC adalah suatu sinar garis AD sedemikian sehingga BAD

kongruen dengan DAC.

A B

C

A B

C

Definisi 2.1.9

Dua buah sudut dikatakan bertolak belakangbila titik sudutnya berimpit dan

sisi-sisinya membentuk dua buah garis.

Definisi 2.1.10

Dua buah sudut dikatakan pelurus bila satu sisinya berimpit dan sisi-sisi lainnya

terletak pada garis yang sama dengan arah yang berlawanan.

Definisi 2.1.11

Suatu sudut disebut siku-siku jika sudut itu kongruen dengan sudut pelurusnya.

Ukuran sudut siku-siku adalah 90 . Jika dua buah sudut adalah pelurus, maka jumlah 

ukuran kedua sudut itu adalah 180 .

D A B

Definisi 2.1.12

Dua garis berpotongan dikatakan tegak lurusbila salah satu sudut yang terbentuk

pada perpotongan kedua garis itu adalah sudut siku-siku.

Definisi 2.1.13

Dua garis dikatakan sejajarjika kedua garis itu tidak berpotongan.

Teorema 2.1.1

Jika dua garis lurus berpotongan, maka sudut-sudut bertolak belakang yang

terbentuk adalah kongruen.

Bukti

Menurut Definisi 2.1.9 dan 2.1.11, maka

   

a m b 180

m … (1)

dan

1

l

2

l a

a b

    

a m b 180

m … (2)

Dari persamaan (1) dan (2) diperoleh

b m a m b m a

m       . Jadi

.

a m a

m    Demikian pula mbmb_. ∎

B. Segitiga

Segitiga ABC (ABC) adalah suatu bangun yang terdiri dari tiga buah titik A, B,

dan Cyang tidak segaris (yang disebut titik sudut) dan tiga buah ruas garis AB, BC,

dan CA (disebut sisi). Jumlah ukuran sudut suatu segitiga adalah 180 .

Definisi 2.2.1

Garis tinggi dalam suatu segitiga adalah garis yang melalui sebuah titik sudut

segitiga itu dan tegak lurus sisi depannya atau perpanjangan sisi di depannya.

A

B C

Definisi 2.2.2

Garis bagi dalam suatu segitiga adalah garis yang membagi dua sama besar

sebuah sudut segitiga itu.

Definisi 2.2.3

Garis berat dalam suatu segitiga adalah garis yang melalui sebuah titik sudut

segitiga itu dan titik tengah sisi di depannya.

Definisi 2.2.4

Suatu segitiga disebut siku-sikujika salah satu sudutnya adalah siku-siku. Sisi-sisi

pada sudut siku-sikunya disebut kakidan sisi yang lainnya disebut sisi miring.

A

C B

D

A

C B

Teorema 2.2.1

Jika A dan B adalah sudut-sudut dalam segitiga siku-siku dan sudut yang

lainnya adalah sudut siku-sikunya, maka mAmB90.

Bukti

     

A m B m C 180

m

Menurut Definisi 2.1.11, mC 90, maka mAmB90180.

Jadi, mAmB90. ∎

Teorema 2.2.2

Misalkan l₁ dan l₂ dua buah garis dan misalkan ksuatu garis yang memotong l₁

pada P₁ dan l₂ pada P₂, dengan P₁ P₂. Misalkan P₁ dan P₂ adalah sudut-sudut

antara k, l₁ dan k, l₂, pada sisi yang sama l₁, l₂. Jika mP₁ mP₂ , maka l₁ dan l₂

adalah sejajar.

A

Bukti

Andaikan l₁ dan l₂ berpotongan pada titik M.

Misalkan Q titik pada k. Karena mP₁ mP₂ dan mP₁QM mP₂QM dan

  

  

P₁QM m P₁ m QMP₁ 180

m

  

  

P₂QM m P₂ m QMP₂ 180

m

1

l

2

l

1

P

2

P

k

M

k

Q

1

l

2

l

1

P

2

maka diperoleh QMP₁ = QMP₂.

Jadi mP₁MP₂ mQMP₂ mQMP₁ 0, yang berarti P₁ P₂. Kontradiksi

dengan asumsi P₁ P₂. Jadi l₁ dan l₂ tidak berpotongan, yaitu l₁ dan l₂ sejajar. ∎

Definisi 2.2.5

Misalkan tsuatu garis yang melewati garis-garisldan mdan mempertemukan l

pada A dan mpada A, dengan A A. Pilih titik Bdan Cpada garis ldan B dan

C pada garis m, dengan Cdan C pada sisi yang sama dari t.

Maka CAA dan BAA disebut sudut-sudut dalam berseberangan, demikian

pula CAA dan BAA. Sedangkan BAD dan BAA disebut sudut-sudut

sehadap, demikian pula CAD dan CAA.

 _



A

B

B

t

l

m

C



 _A

D

 

Teorema 2.2.3

Jika sebuah garis memotong dua buah garis yang sejajar, maka sudut-sudut dalam

berseberangannya kongruen.

Bukti

Misalkan garis l₄ memotong tegak lurus garis l₁ dan l₂ yang sejajar dan

memotong l₃ di titik P.

Menurut Teorema 2.2.1, mPQRmQPR 90

dan mPSTmSPT 90.

3

l

1

l

2

l

3

l

1

l

2

l

4

l P

U Q

R

Jadi mPQRmQPR mPST mSPT .

Karena mQPR mSPT, maka mPQR mPST.

Menurut Teorema 2.1.1, mPQR mSQU .

Jadi, mSQU mPST . ∎

Akibat 2.2.4

Jika sebuah garis memotong dua buah garis yang sejajar, maka sudut-sudut

sehadapnya kongruen.

Bukti

Menurut Teorema 2.1.1 dan Teorema 2.2.3, maka mamcmb. ∎

a

b

3

l

1

l

2

Definisi 2.2.6

Misalkan ABC adalah segitiga siku-siku di C, dengan panjang sisi-sisi kakinya

a dan b, dan panjang sisi miringnya c.

Didefinisikan

c b B 

 )

sin( dan

c a B 

 )

cos( .

Aturan Sinus

Misalkan ABC dengan panjang sisi-sisinya a, b, dan c, dengan a sebagai

panjang sisi di depan sudut A, bsebagai panjang sisi di depan sudut B, dan csebagai

panjang sisi di depan sudut C, maka

) sin( ) sin( )

sin( C

c B

b A

a

   

 .

A

B C

a

Bukti

Dengan AD adalah garis tinggi, maka

c

Dengan BE adalah garis tinggi, maka

Jadi,

Aturan Cosinus

Misalkan ABC dengan panjang sisi-sisinya a, b, dan c, dengan a sebagai

panjang sisi di depan sudut A, bsebagai panjang sisi di depan sudut B, dan csebagai

panjang sisi di depan sudut C, maka

CD

Kalikan kedua ruas dengan a, maka diperoleh

)

Kalikan kedua ruas dengan b, maka diperoleh

)

Kalikan kedua ruas dengan c, maka diperoleh

2 cos( )

2

C ab

c  



) cos( 2

2 2 2

C ab

b a

c     . ∎

Definisi 2.2.7

Dua segitiga dikatakan kongruen jika titik-titik sudut kedua segitiga itu dapat

dipasangkan sedemikian sehingga sisi-sisi dan sudut-sudut bersesuaian adalah

kongruen. Jika ABC kongruen dengan DEF, maka ditulis ABCDEF.

Teorema 2.2.5

Dua buah segitiga adalah kongruen jika dua sisi dan sudut yang diapit oleh kedua

sisi itu kongruen (SAS: Side-Angle-Side).

A

B

C

X

Y

Bukti

Misalkan diberikan ABC dan XYZ dengan AB XY , AC XZ dan

X A

 . Maka dengan Aturan Cosinus:

A AC

AB AC

AB

BC2  2  2 2( )( )cos

= XY2 XZ2 2(XY)(XZ)cosX

= YZ2.

Jadi BCYZ.

Dan dengan Aturan Sinus:

A BC B

AC

 

 sin

sin

BC A AC

B ( )(sin )

sin  

YZ X XZ)(sin )

( 



= sinY .

Dan dengan aturan Sinus:

A BC C

AB

 

 sin

BC A AB

C ( )(sin )

sin  

YZ X XY)(sin )

( 



= sinZ .

Maka BC = YZ, BY , dan CZ . Jadi, dengan Definisi 2.2.8

XYZ ABC

 . ∎

Teorema 2.2.6

Dua buah segitiga adalah kongruen jika dua sudut dan sisi yang diapit kedua

sudut itu kongruen (ASA: Angle-Side-Angle)

Bukti

Misalkan diberikan ABC dan XYZ dengan AB XY , AX , dan

Y B 

 .

A

B

C

X

Y

Maka dengan Aturan Sinus:

C AB A

BC

 

 sin

sin

C A AB

BC

  

sin

) )(sin (

=

Z X XY

 

sin

) )(sin (

= YZ.

Jadi, dengan Teorema 2.2.5 (SAS) ABCXYZ.∎

Teorema 2.2.7

Dua buah segitiga adalah kongruen jika dua sudut dan sisi di hadapan salah satu

sudut itu kongruen (AAS: Angle-Angle-Side).

A

B

C

X

Y

Bukti

Misalkan diberikan ABC dan XYZ dengan BC YZ , AX , dan

Y B 

 .

Maka dengan Aturan Sinus:

A BC C

AB

 

 sin

sin

A C BC

AB

  

sin

) )(sin (

=

X Z YZ

 

sin

) )(sin (

= XY.

Jadi, dengan Teorema 2.2.5 (SAS) ABCXYZ.∎

Teorema 2.2.8

Dua buah segitiga adalah kongruen jika ketiga sisinya yang bersesuaian adalah

kongruen (SSS: Side-Side-Side).

A

B

C

X

Y

Bukti

Misalkan diberikan ABC dan XYZ dengan AB XY , BC YZ , dan

XZ AC  .

Maka dengan Aturan Cosinus:

)

Definisi 2.2.8

Suatu segitiga disebut samakaki jika segitiga itu mempunyai dua buah sisi yang

kongruen. Kedua sisi yang kongruen itu disebut kaki dan sisi yang ketiga disebut

alas. Sudut yang diapit oleh kedua kaki segitiga samakaki disebut disebut sudut

Teorema 2.2.9

Kedua sudut alas segitiga samakaki adalah kongruen.

Bukti

Diketahui ABC samakaki dengan AC= CB.

Misalnya CDadalah garis berat.

Maka AC= CB, CD= CD, dan AD= DB.

Jadi, dengan Teorema 2.2.8 (SSS) ACDBCD.

Akibatnya: mAmB.

Jadi, terbukti bahwa kedua sudut alas segitiga samakaki adalah kongruen.∎

A B

C

C. Segiempat

Definisi 2.3.1

Segiempat ABCD adalah suatu bangun yang terdiri dari empat buah titik A, B, C,

dan Ddan empat buah ruas garis AB, BC, CD, dan DA sedemikian sehingga tidak

ada tiga titik darinya yang terletak pada sebuah garis dan tidak ada sepasang ruas

garis darinya yang berpotongan kecuali di titik-titik ujungnya. Ruas-ruas garis AB ,

BC, CD, dan DA disebut sisi dan AC, dan BD disebut diagonal dari segiempat

itu.

Definisi 2.3.2

Suatu segiempat disebut persegi jika semua sisinya adalah kongruen dan semua

sudutnya adalah siku-siku. Luas persegi didefinisikan sebagai kuadrat panjang

sisi-sisinya.

Definisi 2.3.3

Suatu segiempat disebut persegi panjang jika semua sudutnya adalah siku-siku.

panjang sisi yang lainnya disebut tinggi. Luas persegi panjang didefinisikan sebagai

hasil kali alas dan tingginya.

Definisi 2.3.4

Suatu segiempat disebut jajaran genjang jika sisi-sisi yang berhadapan adalah

sejajar.

Definisi 2.3.5

Jika salah satu sisi suatu jajaran genjang kita sebut sisi alas, maka tinggijajaran

genjang itu relatif terhadap alas tersebut adalah jarak tegak lurus antara sisi alas itu

dan sisi di hadapannya.

Definisi 2.3.6

Dua buah bangun geometri dikatakan ekivalen jika masing-masing bangun itu

terdiri dari berhingga banyak segi-banyak sedemikian sehingga semua segi-banyak

Contoh 2.3.1

Jajaran genjang ABCDdan EBCFadalah ekivalen, karena jajaran genjang ABCD

terdiri dari segiempat EBCDdan AEB, sedangkan jajaran genjang EBCFterdiri dari

segiempat EBCD dan DFC. Segiempat EBCD kongruen dengan dirinya sendiri,

sedangkan AEB dan DFC adalah kongruen, karena ABDC , EBFC, dan

C B 

 .

Definisi 2.3.7

Dua buah bangun geometri yang ekivalen dikatakan mempunyai luas yang sama.

Teorema 2.3.1

Luas suatu segitiga siku adalah setengah hasil kali panjang sisi-sisi

siku-sikunya.

A

B C

D

Bukti

Diberikan segitiga siku-siku ABC dengan b dan h adalah panjang sisi-sisi

siku-sikunya.

Dibuat persegi panjang ABCD dengan CD sejajar dengan AB dan AD sejajar

dengan BC.

Dengan Teorema 2.2.5 (SAS), ABCACD, dan dengan Definisi 2.3.6 dan

Definisi 2.3.7, ABC dan ACD mempunyai luas yang sama. Menurut Definisi

2.3.3, Luas ABCD= bh. Luas ABCD= luas ABC + luas ACD = 2  luas ABC.

Jadi, luas ABC =

2 1

luas ABCD= .

2 1

bh ∎

A B

C

b h

b h

D

A B

Teorema 2.3.2

Luas segitiga adalah setengah hasil kali panjang sisi alas dan tingginya.

Bukti

Kasus 1

Diberikan segitiga ABC dengan b sebagai panjang sisi alas dan h sebagai tinggi

(panjang garis tinggi CD).

Jika panjang AD adalah b₁ dan panjang DB adalah b₂, maka luas segitiga

siku-siku ADCadalah b1h

2 1

dan luas segitiga siku-siku CDBadalah .

2 1

2h

b

Luas segitiga ABC= luas ADC + luas CDB

= b₁h

2 1

+ b₂h

2 1

= (b b )h

2 1

2 1 

= .

2 1

bh ∎

h

b1 b2

A B

C

Kasus 2

Diberikan segitiga ABCdengan bsebagai panjang sisi alas dan hsebagai tinggi.

Untuk menghitung luas segitiga ABC tersebut, dibentuk persegi panjang DBEC

sebagai berikut:

Luas persegi panjang DBEC = luas DAC + luas ABC + luas BEC

h b b )

(  ₁ = b1h

2 1

+ luas ABC + (b b)h

2 1

1



h b

bh ₁ = b₁h

2 1

+ luas ABC + bh

2 1

+ b₁h

2 1

h b

bh ₁ = luas ABC + bh

2 1

+ b₁h

Luas ABC = .

2 1

bh ∎

A B

C

b

1

b h

D

Teorema 2.3.3

Sisi-sisi yang berhadapan pada suatu jajaran genjang mempunyai panjang yang

sama.

Bukti

Diberikan jajaran genjang ABCD dengan diagonal AC. Menurut Teorema 2.2.3,

karena AB sejajar dengan CD, maka m2m3, dan karena AD sejajar dengan

BC , maka m1m4. AC berimpit pada kedua segitiga ACD dan CAB.

Menurut Teorema 2.2.6 (ASA), maka ACD  CAB. Jadi AB = CD dan AD =

CB.∎

Teorema 2.3.4

Luas suatu jajaran genjang adalah hasil kali panjang sisi alas dan tingginya.

Bukti

Diberikan jajaran genjang dengan bsebagai panjang sisi alas dan hsebagai tinggi.

A _B

C D

1 2

Menurut Teorema 2.3.3, salah satu diagonalnya membagi jajaran genjang itu

menjadi dua segitiga yang kongruen. Menurut Teorema 2.3.2, luas segitiga adalah

setengah hasil kali panjang sisi alas dan tingginya, yaitu bh

2 1

.

Maka luas jajaran genjang adalah ) .

2 1 (

2 bh bh ∎

Teorema 2.3.5

Jika sebuah garis sejajar dengan salah satu sisi suatu segitiga dan memotong

sisi-sisi yang lain pada dua titik yang berbeda, maka garis ini membagi sisi-sisi-sisi-sisi yang

dipotong itu menjadi bagian-bagian yang sebanding.

Bukti

h

A

B C

D _E

G

l

Misalkan garis l sejajar dengan BC dalam ABC, dan memotong sisi-sisi AB

Kemudian, dibuat garis dari titik Dyang tegak lurus pada AC dan memotong AC di

BED

 dan CED mempunyai luas yang sama karena mempunyai alas dan tinggi

yang sama, sehingga



Akibat 2.3.6

Diberikan asumsi seperti pada Teorema 2.3.5, maka

Teorema 2.3.7

Jika sebuah garis memotong dua sisi pada suatu segitiga sehingga bagian-bagian

yang dipotong oleh garis tersebut adalah sebanding, maka garis tersebut sejajar

dengan sisi yang ketiga.

Bukti

Misalkan garis l memotong sisi-sisi AB dan AC dari ABC di titik-titik D dan

Esedemikian sehingga

AE AC AD AB

 .

Tarik garis m sejajar dengan BC melalui D. Garis m memotong AC di titik F.

Dengan Akibat 2.3.6 diperoleh

AF AC AD AB _

.

B C

A

D

F

E l

m >

Maka

AF AC AE AC



sehingga

AE= AF.

Hal ini mengakibatkan bahwa E = Fdan l= m.

Jadi, lsejajar dengan BC. ∎

Definisi 2.3.8

Dua buah segitiga dikatakan sebangun (dengan lambang ) jika titik-titik sudut

kedua segitiga itu dapat dipasangkan sedemikian sehingga sisi-sisi yang bersesuaian

sebanding dan sudut-sudut yang bersesuaian kongruen.

XYZ ABC

 jika dan hanya jika

YZ BC XZ AC XY

AB _{ }

dan

Z C Y B X

A    

Teorema 2.3.8

Dua buah segitiga adalah sebangun jika ketiga sudut segitiga yang satu kongruen

dengan ketiga sudut bersesuaian segitiga lainnya.

Bukti

Misalkan diberikan ABC dan DEF dengan AD , BE , dan

F C 

 . Jika AB kongruen dengan DE, maka kedua segitiga tersebut kongruen

dengan Teorema 2.2.7 (AAS) dan karenanya juga sebangun.

Misalkan AB dan DE tidak kongruen, dengan DE  AB. Maka ada titik G di

antara D dan E sedemikian sehingga DG AB. Dan misalkan AC dan DF tidak

kongruen, dengan DFAC , maka ada titik H pada DF sedemikian sehingga

A

B C

D

E F

G H

X

Y Z

A

AC

DH  . Karena, mAmD, ABCDGH(SAS), sehingga mGmB.

Karena B dan E kongruen, maka mGmE. Maka menurut Teorema 2.2.2,

GH sejajar dengan EF . Dengan Akibat 2.3.6 diperoleh:

.

DF DH DE

DG



Karena DG AB dan DH  AC, maka diperoleh:

.

DF AC DE AB _

Misalkan AB dan DE tidak kongruen, dengan DE  AB. Maka ada titik K di

antara D dan E sedemikian sehingga EK AB. Dan misalkan BC dan EF tidak

kongruen, dengan EFBC , maka ada titik L pada EF sedemikian sehingga

BC

EL . Karena, mE mB , ABCDGH (SAS), sehingga mCmL.

Karena C dan F kongruen, maka mF mL. Maka menurut Teorema 2.2.2,

KL sejajar dengan DF . Dengan Akibat 2.3.6 diperoleh:

.

EF EL DE EK



A

B C

D

E F

K

Karena EK AB dan EL BC, maka diperoleh:

.

EF BC DE

AB



Jadi diperoleh:

EF BC DF AC DE AB



 .

Jadi, menurut Definisi 2.3.8 ABCDEF. ∎

Teorema 2.3.9

Dua buah segitiga adalah sebangun jika dua sisi segitiga yang satu sebanding

dengan dua sisi yang bersesuaian segitiga lainnya dan sudut yang diapit oleh kedua

sisi itu adalah kongruen.

A

B _C

G H

D

Bukti

Misalkan ABC dan DEF diberikan dengan asumsi seperti dalam Teorema,

yaitu

DF AC DE

AB

 dan mAmD.

Jika AB dan AC kongruen dengan pasangannya dalam DEF , maka kedua segitiga

tersebut adalah kongruen dengan Teorema 2.2.5 (SAS) dan karenanya juga sebangun.

Misalkan ABDE, maka ada titik G pada AB sedemikian sehingga AG= DE. Dan

misalkan ACDF , maka ada titik H pada AC sedeimikian sehingga AH = DF.

Maka menurut Teorema 2.2.5 (SAS) AGHDEF.

Karena AG= DEdan AH= DF, maka

AH AC AG AB _

sehingga menurut Teorema 2.3.7 GH sejajar dengan BC. Dan menurut Akibat 2.2.4,

B m G

m   dan mH mC. Karena AGHDEF, maka mBmE dan

F m C

m   .

BAB III

HIMPUNAN KABUR

A. Himpunan Kabur

Himpunan kabur merupakan perluasan dari konsep himpunan tegas, yaitu

himpunan yang terdefinisi secara tegas dalam arti bahwa untuk setiap elemen dalam

semestanya selalu dapat ditentukan secara tegas apakah ia merupakan anggota dari

himpunan itu atau tidak. Dalam kenyataannya tidak semua himpunan yang kita

jumpai dalam kehidupan sehari-hari terdefinisi secara demikian itu, misalnya

himpunan orang yang tinggi, himpunan mahasiswa pandai, dan sebagainya. Pada

himpunan orang yang tinggi, misalnya, kita tidak dapat menentukan secara tegas

apakah seseorang adalah tinggi atau tidak. Jika misalnya kita definisikan bahwa

“orang tinggi” adalah orang yang tingginya lebih besar atau sama dengan 1.75 meter,

maka orang yang tingginya 1.74 meter menurut definisi tersebut termasuk orang yang

tidak tinggi. Sulit bagi kita untuk menerima bahwa orang yang tingginya 1.74 meter

itu tidak termasuk orang yang tinggi.

Untuk mengatasi permasalahan himpunan dengan batas yang tidak tegas itu,

Zadeh mengaitkan himpunan semacam itu dengan suatu fungsi yang menyatakan

derajat kesesuaian unsur-unsur dalam semestanya dengan konsep yang merupakan

nilai fungsi itu disebut derajat keanggotaan suatu unsur dalam himpunan itu, yang

selanjutnya disebut himpunan kabur. Derajat keanggotaan dinyatakan dengan suatu

bilangan real dalam selang tertutup [0, 1]. Dengan perkataan lain, fungsi keanggotaan

dari suatu himpunan kabur A~ dalam semesta Xadalah pemetaan

A~

 dari Xke selang

[0, 1], yaitu ~:X [0,1] A

 . Nilai fungsi

A

~

 (x) menyatakan derajat keanggotaan

unsur x Xdalam himpunan kabur A~.

Secara matematis suatu himpunan kabur A~ dalam semesta X dapat dinyatakan

sebagai himpunan pasangan terurut

} |

)) ( , {( ~

~ x x X

x

A _A 

di mana _A~ adalah fungsi keanggotaan dari himpunan kabur A~, yang merupakan

suatu pemetaan dari himpunan semestaX ke selang tertutup [0, 1]. Apabila semesta

Xadalah himpunan yang kontinu, maka himpunan kabur A~ seringkali dinyatakan

dengan







X x

A x x

A~ ~( )/

di mana lambang



di sini bukan lambang integral seperti yang dikenal dalam

derajat keanggotaannya dalam himpunan kabur A~ . Apabila semesta X adalah

himpunan yang diskret, maka himpunan kabur A~ seringkali dinyatakan dengan







X x

A x x

A~ ~( )/

di mana lambang



di sini tidak melambangkan operasi penjumlahan seperti yang

dikenal dalam aritmatika, tetapi melambangkan keseluruhan unsur-unsur xX

bersama dengan derajat keanggotaannya dalam himpunan kabur A~.

Contoh 3.1.1

Dalam semesta X = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5}, misalkan himpunan kabur

A~ adalah himpunan bilangan real yang dekat dengan nol. Maka







X x

A x x

A~ ~( )/

= 0.1 / -4 + 0.3 / -3 + 0.5 / -2 + 0.7 / -1 + 1 / 0 + 0.7 / 1 + 0.5 / 2 + 0.3 / 3 + 0.1

/ 4.

Dua buah himpunan kabur A~ dan B~ dalam semesta X dikatakan sama, dengan

) ( )

( ~

~ x x

B

A 

 

untuk setiap x X. Himpunan kabur A~ dikatakan merupakan himpunan bagiandari

himpunan kabur B~, dengan lambang A~  B~, bila dan hanya bila

) ( )

( ~

~ x x

B

A 

 

untuk setiap x X. Jadi A~ = B~ bila dan hanya bila A~  B~ dan B~  A~.

Pendukung (support) dari suatu himpunan kabur A~, yang dilambangkan

Pend( A~ ) adalah himpunan tegas yang memuat semua unsur dari semesta yang

mempunyai derajat keanggotaan taknol dalam A~, yaitu

Pend(A~) = {x  X| ~(x)

A

 > 0}.

Tinggi (height) dari suatu himpunan kabur A~ , yang dilambangkan dengan

Tinggi(A~), didefinisikan sebagai

Tinggi(A~) = sup{ ~(x)}.

A X x



Himpunan kabur yang tingginya sama dengan 1 disebut himpunan kabur normal,

sedangkan himpunan kabur yang tingginya kurang dari 1 disebut himpunan kabur

subnormal.

Untuk suatu bilangan [0,1], potongan- dari suatu himpunan kabur A~, yang

dilambangkan dengan A_, adalah himpunan tegas yang memuat semua elemen dari

semesta dengan derajat keanggotaan dalam A~ yang lebih besar atau sama dengan  ,

yaitu

}. ) ( |

{ ~ 

  xX x 

A

A

Sedangkan potongan- kuatdari himpunan kabur A~ adalah himpunan tegas

}. ) ( |

{ ~ 

  xX x 

A _A

Suatu himpunan kabur dalam semesta ℝndisebut konveksbila untuk setiap  (0,1]

potongan- dari himpunan kabur itu adalah himpunan (tegas) yang konveks.

Teorema 3.1.1

B. Fungsi Keanggotaan

Setiap himpunan kabur dapat dinyatakan dengan suatu fungsi keanggotaan. Ada

beberapa cara untuk menyatakan himpunan kabur dengan fungsi keanggotaannya.

Untuk semesta hingga diskret biasanya dipakai cara daftar, yaitu daftar

angota-anggota semesta bersama derajat keangota-anggotaannya, seperti misalnya diberikan dalam

Contoh 3.1.1.

Untuk semesta takhingga yang kontinu, cara yang paling sering digunakan adalah

cara analitik untuk menyatakan fungsi keanggotaan himpunan kabur yang

bersangkutan dalam bentuk suatu formula matematis yang dapat disajikan dalam

bentuk grafik.

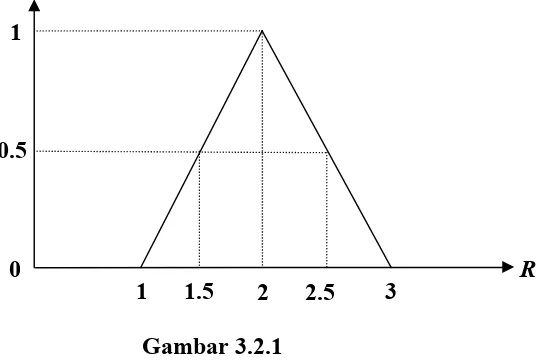
Contoh 3.2.1

Himpunan kabur A~ adalah bilangan real yang dekat dengan 2 dapat dinyatakan

dengan menggunakan fungsi keanggotaan sebagai berikut:

x– 1 untuk 1  x  2

3 –xuntuk 2  x  3

0 untuk lainnya 

) (

~ x

yang grafiknya adalah sebagai berikut

Gambar 3.2.1

C. Operasi Baku pada Himpunan Kabur

Operasi baku pada himpunan kabur yang akan didefinisikan adalah operasi uner

“komplemen” dan operasi-operasi biner “gabungan” dan “irisan”. Komplemen dari

suatu himpunan kabur A~ adalah himpunan kabur A~ dengan fungsi keanggotaan

) ( 1 )

( ~

~ x x

A

A 

 _  

untuk setiap x X. Gabungandua buah himpunan kabur A~ dan B~ adalah himpunan

kabur A~B~ dengan fungsi keanggotaan



~( ) ~ x

B A

 max { ~(x), ~(x)} B

A 

 0

0.5 1

untuk setiap x  X. Sedangkan irisan dua buah himpunan kabur A~ dan B~ adalah

himpunan kabur A~B~ dengan fungsi keanggotaan



~( ) ~ x

B A

 min { ~(x), ~(x)} B

A 



untuk setiap x X.

Suatu pemetaan t:[0,1][0,1][0,1] disebut irisan kabur (norma-t) jika

memenuhi aksioma-aksioma sebagai berikut:

a. t(x,1)t(1,x)x dan t(0, 0) = 0 (syarat batas)

b. t(x,y)t(y,x) (syarat komutatif)

c. Jika xx dan y y, maka t(x,y)t(x,y) (syarat takturun)

d. t(t(x,y),z)t(x,t(y,z)) (syarat asosiatif)

Operasi min{x, y} untuk x,y[0,1] merupakan suatu contoh dari norma-t:

a. min{x, 1} = min{1, x} = x dan min{0, 0} = 0 (syarat batas)

b. min{x, y} = min{y, x} (syarat komutatif)

c. Jika xx dan y y, maka min{x, y}  min{x,y} (syarat takturun)

d. min{min{x, y}, z} = min{x, min{y, z}} (syarat asosiatif)

Contoh 3.3.1

Misalkan dalam semesta X = {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6} diketahui

himpunan-himpunan kabur A~ = 0.3 / -3 + 0.5 / -2 + 0.7 / -1 + 1 / 0 + 0.7 / 1 + 0.5 / 2

+ 0.3 / 3 dan B~ = 0.1 / -1 + 0.3 / 0 + 0.8 / 1 + 1 / 2 + 0. 7 / 3 + 0.4 / 4 + 0.2 / 5, maka

A~ = 1 / -4 + 0.7 / -3 + 0.5 / -2 + 0.3 / -1 + 0.3 / 1 + 0.5 / 2 + 0.7 / 3 + 1 / 4 + 1

/ 5 + 1 / 6

B

A~ ~ = 0.3 / -3 + 0.5 / -2 + 0.7 / -1 + 1 / 0 + 0.8 / 1 + 1 / 2 + 0.7 / 3 + 0.4 / 4 +

0.2 / 5

B

A~ ~ = 0.1 / -1 + 0.3 / 0 + 0.7 / 1 + 0.5 / 2 + 0.3 / 3.

D. Relasi Kabur

Relasi kabur R~ antara elemen-elemen dalam himpunan X dengan elemen-elemen

dalam himpunanYdidefinisikan sebagai himpunan bagian kabur dari darab Cartesius

X  Y, yaitu himpunan kabur

}. )

, ( | )) , ( ), , {(( ~

~ x y x y X Y

y x

R  _R  

Relasi kabur R~ itu juga disebut relasi kabur pada himpunan (semesta) X  Y. jika

Contoh 3.4.1

Misalkan X = {31, 78, 205}, Y = {1, 27, 119}, dan R~ adalah relasi kabur “jauh

lebih besar” antara elemen-elemen dalam X dengan elemen-elemen dalam Y. Maka

relasi R~ tersebut dapat disajikan sebagai

R~ = 0.3 / (31, 1) + 0.1 / (31, 27) + 0.5 / (78, 1) + 0.3 / (78, 27) + 0.9 / (205, 1) +

dengan elemen-elemen dalam himpunan Y dapat dinyatakan dalam bentuk suatu

matriks berukuran mn sebagai berikut



Contoh 3.4.2

Relasi kabur “jauh lebih besar” antara elemen-elemen dalam X dengan

elemen-elemen dalam Y dalam Contoh 3.4.1 di atas dapat disajikan dalam bentuk matriks

bujur-sangkar sebagai berikut:



1. Komposisi Relasi Kabur

Jika R~₁ adalah relasi kabur pada XY dan R~₂ adalah relasi kabur pada

R  adalah relasi kabur pada XZ dengan fungsi keanggotaan

Setiap norma-t menghasilkan suatu komposisi tertentu. Misalnya, jika diambil

operator “min” sebagai norma-t, maka diperoleh relasi komposit R~₁R~₂ dengan

fungsi keanggotaan

)}.

Komposisi ini sering disebut komposisi sup-min. Kalau sebagai norma-t diambil

operator “darab aljabar”, maka diperoleh relasi komposit R~₁R~₂ dengan fungsi

Komposisi ini sering disebut komposisi sup-darab.

Contoh 3.4.3

Misalnya X = {31, 78, 205}, Y = {1, 27, 119} dan Z = {10, 225, 94}, dan relasi

kabur R~₁ adalah relasi “jauh lebih besar” antara elemen-elemen dalam X dengan

elemen-elemen dalam Yyang disajikan dalam bentuk matriks sebagai berikut:

Misalkan R~₂ adalah relasi kabur “jauh lebih kecil” antara elemen-elemen dalam

penjumlahan diganti operasi “max” sebagai berikut:



dikerjakan seperti komputasi perkalian matriks, di mana operasi perkalian seperti

komputasi perkalian matriks dan operasi penjumlahan diganti operasi “max sebagai

2. Relasi Kabur Khusus

untuk setiap xX. Relasi kabur R~ dikatakan bersifat simetrikbila dan hanya bila

)

untuk setiap x,yX. Relasi kabur R~ dikatakan bersifat antisimetrik bila dan hanya

simetrik dari R~ terlihat dari corak simetrik matriks tersebut terhadap diagonal

utamanya, yaitu a_ij = a_ji. Relasi kabur R~ bersifat antisimetrik apabila a_ij = 0 atau

ji

a = 0 untuk i j. Relasi kabur R~ adalah transitif bila R~R~R~.

Suatu relasi kabur R~ pada semesta X yang bersifat refleksif, simetrik, dan

transitif disebut relasi ekivalensi kabur, sedangkan relasi kabur R~ yang bersifat

refleksif dan simetrik disebut relasi kompatibilitas kabur. Relasi kabur R~ pada

semesta X yang bersifat refleksif, transitif, dan antisimetrik disebut relasi urutan

parsial kabur. Ketiga relasi kabur khusus tersebut bersifat layak-potongan, yaitu

setiap potongan- dari relasi ekivalensi kabur adalah relasi ekivalensi tegas, setiap

potongan- dari relasi kompatibilitas kabur adalah relasi kompatibilitas tegas, dan

setiap potongan- dari relasi urutan parsial kabur adalah relasi urutan parsial tegas.

Contoh 3.4.3

Jika R~ adalah relasi kabur pada semesta X= {a, b, c, d, e} yang disajikan dengan

matriks berikut:

Maka R~ adalah relasi kabur yang refleksif dan antisimetrik (sebab ~(x,y)0 R



atau ~(y,x)0 R

 untuk x y). Selanjutnya dengan komposisi sup-min diperoleh:



yang berarti R~ bersifat transitif. Jadi R~ adalah relasi urutan parsial kabur. Untuk 

= 0.5, potongan- dari R~ adalah

yang merupakan relasi urutan parsial tegas pada X.

Definisi 3.4.1

Himpunan semua himpunan bagian dari A disebut himpunan kuasa dari A, dan

Definisi 3.4.2

Suatu fungsi tegas f :X Y dikatakan dikaburkanbila fungsi tersebut diperluas

menjadi fungsi f :F(X) F(Y), di mana F(X) dan F(Y) berturut-turut adalah

himpunan kuasa kaburdari semesta Xdan Y, yaitu himpunan semua himpunan kabur

dalam Xdan dalam Y.

Prinsip Perluasan

Suatu fungsi tegas f :X Y dikaburkan dengan memperluas fungsi tersebut

Definisi 3.4.3

Bilangan kabur didefinisikan sebagai himpunan kabur dalam semesta himpunan

semua bilangan real ℝyang memenuhi empat sifat berikut ini:

b. Mempunyai pendukung yang terbatas

c. Semua potongan- -nya adalah selang tertutup dalam ℝ.

d. Konveks.

Bilangan kabur yang paling banyak dipakai dalam aplikasi adalah bilangan kabur

dengan fungsi keanggotaan segitiga, yang disebut bilangan kabur segitiga. Jelas

bahwa jenis bilangan kabur tersebut memenuhi keempat sifat bilangan kabur seperti

didefinisikan di atas.

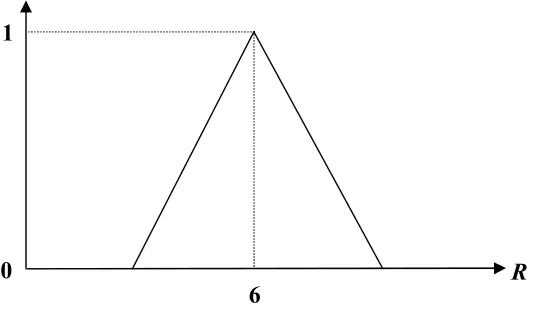
Contoh 3.4.1

Bilangan kabur “kurang lebih 6” dapat dinyatakan sebagai himpunan kabur 6~

dengan fungsi keanggotaan segitiga sebagai berikut:

Gambar 3.4.1. Bilangan kabur 6~

0 1

` Definisi 3.4.4

Misalkan A~ dan B~ adalah dua buah bilangan kabur dalam ℝ. Dengan Prinsip

Perluasan dapat didefinisikan penjumlahan A~ dan B~, yaitu A~B~, sebagai bilangan

kabur dalam ℝdengan fungsi keanggotaan

)

bilangan kabur dalam ℝdengan fungsi keanggotaan

)}

Teorema 3.4.1

Bukti

Ambil sebarang z(AB)_. Maka ~_~(z).

B

A Andaikan

BAB IV

GEOMETRI KABUR

A. Introduksi

Definisi 4.1.1

Suatu himpunan tegas A dalam semesta X dapat didefinisikan dengan

menggunakan suatu fungsi _A :X {0,1}, yang disebut fungsi karakteristik dari

himpunan A, di mana untuk setiap xX

  

  

. untuk 0

untuk 1 ) (

A x

A x x

A



Definisi 4.1.2

Misalkan X adalah himpunan takkosong dan misalkan T P(X) . Maka T

disebut topologipada Xjika

a. ,X T.

b. Gabungan anggota-anggota Tadalah anggota T.

Anggota dari Tdisebut himpunan terbuka. Pasangan (X, T) disebut ruang topologi.

Definisi 4.1.3

Suatu topologi kabur pada X adalah keluarga FT dari himpunan bagian kabur

dalam Xyang memenuhi kondisi berikut:

a. ,X FT .

b. Jika A~,B~FT, maka A~B~FT.

c. Jika A~_iFT untuk setiap iI, maka _iI A~_iFT, di mana I adalah suatu

himpunan indeks.

Jika FT adalah suatu topologi kabur pada X, maka pasangan (X, FT) disebut ruang

topologi kabur. Setiap anggota dari FTdisebut himpunan bagian kabur terbuka.

Definisi 4.1.4

Sebuah fungsi f dari ℝ ke ℝ dikatakan semikontinu atas pada yℝ jika untuk

setiap  0, ada  0 sedemikian sehingga f(y) f(x) untuk setiap x ℝ

Definisi 4.1.5

Misalkan (X, FT) adalah ruang topologi kabur. Barisan himpunan bagian kabur

} , 2 , 1 | ~

{A_n n  dikatakan akhirnya termuat dalam himpunan bagian kabur A~ jika

ada bilangan bulat positif m sedemikian sehingga A~_n  A untuk semua nm, dan

dikatakan sering termuat dalam A~ jika untuk setiap bilangan bulat positif m, ada

bilangan bulat nsedemikian sehingga A~_n  A untuk nm.

Definisi 4.1.8

Misalkan (X, FT) adalah ruang topologi kabur. Suatu selimut dari himpunan

bagian kabur B~ adalah keluarga A dari himpunan bagian kabur X sedemikian

sehingga B~{A~|A~A}. Selimut A dari B~ disebut selimut terbuka dari B~ jika

setiap anggotaAadalah himpunan bagian kabur terbuka dari X. Suatu subselimutdari

Aadalah subkeluargadari Ayang juga merupakan selimut.

Definisi 4.1.9

Suatu ruang topologi kabur (X, FT) dikatakan kompakjika setiap selimut terbuka

B. Titik Kabur

Definisi 4.2.1

Misalkan (a, b)  ℝ2. Himpunan bagian kabur P~ dalam ℝ2 disebut titik kabur

pada (a, b), ditulis P~_(a,b), jika

a. _P~ adalah semikontinu atas.

b. Untuk setiap (x,y) ℝ2, ~(x,y) P

 = 1 jika dan hanya jika (x, y) = (a, b).

c. Untuk setiap [0,1], P_ adalah himpunan bagian konveks dan kompak

dalam ℝ2.

Konsep titik kabur didasarkan pada konsep vektor kabur dalam ℝn. Jika (a, b)  ℝ2

dan P~ titik kabur pada (a, b), maka P~ dapat divisualisasikan sebagai permukaan

dalam ℝ3dengan persamaan z ~(x,y)

P 

 , untuk (x,y) ℝ2.

Contoh 4.2.1

Misalkan A~ dan B~ adalah dua buah bilangan kabur, dengan ~(x)

A

 = 1 jika dan

hanya jika x = a dan ~(y)

B

kabur P~ dalam ℝ2 yang didefinisikan dengan ~(x,y) min{ ~(x), ~(y)) B A

P  

  untuk

setiap (x,y)ℝ2adalah titik kabur pada (a, b).

C. Jarak Kabur antara Dua Titik Kabur

Definisi 4.3.1

Misalkan X adalah himpunan takkosong dan d sebuah fungsi dari XX ke ℝ.

Maka ddisebut metrik pada X jika untuk setiap x,y,zX,

a. d(x,y) 0 dan d(x,x)0;

b. d(x,y)d(y,x);

c. d(x,z)d(x,y)d(y,z);

d. Jika x y, maka d(x,y)0.

Bilangan real d(x, y) disebut jarak antara x dan y. Kondisi (b) pada definisi di atas

disebut sifat simetri, dan kondisi (c) disebut sifat ketaksamaan segitiga. Jika Xadalah

himpunan takkosong dan d adalah fungsi dari X X ke ℝ yang memenuhi kondisi