APLIKASI BOROBUDUR ETHNOMATHEMATICS, MEDIA
PEMBELAJARAN MATEMATIKA SEBAGAI PENDUKUNG
PEMBELAJARAN GEOMETRI BERBASIS
ETNOMATEMATIKA
Ditulis oleh:
Miftah Rizqi Hanafi 11520241036 / 2011
UNIVERSITAS NEGERI YOGYAKARTA YOGYAKARTA
KATA PENGANTAR
Alhamdulillah, puji syukur kehadirat Allah SWT atas segala nikmat dan
karunia-Nya, sehingga kami mampu menyelesaikan karya tulis ini dengan judul “APLIKASI BOROBUDUR ETHNOMATHEMATICS, MEDIA
PEMBELAJARAN MATEMATIKA SEBAGAI PENDUKUNG
PEMBELAJARAN GEOMETRI BERBASIS ETNOMATEMATIKA” , yang disusun dalam rangka mengikuti Mapres UNY 2014.
Kami mengucapkan banyak terima kasih kepada berbagai pihak yang telah
membantu, serta memberikan masukan dan saran selama proses penulisan dan
penyusunan ini berlangsung, Pimpinan Universitas Negeri Yogyakarta, seluruh
dosen pengajar Pendidikan Teknik Informatika Universitas Negeri Yogyakarta.
Ungkapan terima kasih juga kami sampaikan kepada orang tua serta rekan-rekan
mahasiswa Pendidikan Teknik Informatika Universitas Negeri Yogyakarta, dan
pihak lain yang tidak dapat disebutkan satu persatu.
Kami menyadari bahwa dalam penulisan karya tulis ini masih banyak
terdapat kekurangan. Oleh karena itu, kritik dan saran yang bersifat membangun
sangat diperlukan demi kesempurnaan karya tulis ini, dan akan kami terima
dengan senang hati. Semoga hasil karya tulis ini dapat bermanfaat bagi semua
pihak, terutama dalam mengatasi permasalahan sistem pendidikan Indonesia,
khususnya matematika.
Yogyakarta, 27 Maret 2014
DAFTAR ISI
B. Software yang Digunakan dalam Pembuatan
Aplikasi Borobudur Ethnomathematics
C. Belajar Geometri Melalui Pendekatan
Budaya (Ethnomatematika)
9
10
11
III ANALISIS DAN SINTESIS 14
A. Perancangan Borobudur Ethnomathematics
B. Unjuk Kerja Borobudur Ethnomathematics
C. Analisis Borobudur Ethnomathematics
14
17
19
IV SIMPULAN DAN REKOMENDASI 22
DAFTAR GAMBAR
Gambar 1. Halaman Introduction 17
Gambar 2. Halaman Materi Bangun Ruang 18
Gambar 3. Halaman Materi Bangun Datar 18
DAFTAR TABEL
Tabel 1. Contoh Etnomatematika di Candi Borobudur 13
Aplikasi Borobudur Ethnomathematics, Media Pembelajaran Matematika Sebagai Pendukung Pembelajaran Geometri Berbasis Etnomatematika
Miftah Rizqi Hanafi [email protected] Universitas Negeri Yogyakarta
Abstrak
Pendidikan matematika di Indonesia membawa hasil yang masih jauh dari harapan. Hal ini ditunjukkan dengan dipublikasikannya hasil studi Programme for International Student Assessment (PISA) 2012. Hasil yang kurang menyenangkan ini disebabkan karena kurangnya kemampuan matematika siswa dalam menyelesaikan soal penalaran dan pemecahan masalah, ditambah lagi dengan proses pembelajaran matematika yang dilakukan kurang inovatif.. Pembelajaranpun kurang bervariasi, sehingga mempengaruhi minat siswa untuk mempelajari matematika lebih lanjut. Maka dari itu perlu sebuah inovasi dalam pembelajaran matematika. Salah satu pembelajaran matematika yang inovatif dapat dilakukan melalui pendekatan budaya atau yang disebut etnomatematika. Salah satu bentuk etnomatematika yang menarik untuk dieksplorasi adalah situs Candi Borobudur. Hal ini dikarenakan Candi Borobudur memiliki potensi untuk dimanfaatkan sebagai bahan ajar matematika yang memiliki nilai historis, lekat dengan masyarakat, kontekstual, dan bisa dijadikan sebagai model konkrit untuk memahami matematika. Makalah ini ditulis secara deskriptif, mulai dari meninjau masalah tentang mengapa siswa sulit untuk belajar matematika, terutama geometri. Setelah itu kami membuat rumusan masalah diikuti dengan mengumpulkan teori, kemudian menganalisa dan mendiskusikan data. Langkah terakhir adalah membuat kesimpulan dan rekomendasi. Media pembelajaran ini terdiri dari fungsi desain, skenario, dan storyboard. Hasil dari pembuatan karya tulis ini adalah media pembelajaran matematika yang didasarkan pada etnomatematika. Media pembelajaran ini dapat digunakan sebagai media pembelajaran di sekolah formal maupun di masyarakat umum. Melalui media pembelajaran ini, siswa dapat belajar matematika terutama geometri dengan mudah dan kontekstual. Untuk menganalisis media pembelajaran ini kami menggunakan analisis SWOT, di mana kami mengidentifikasi kekuatan, kelemahan, peluang, dan ancaman.
Abstract
The results of mathematics education in Indonesia is still far from expectations. This is indicated by the publication of the results of the study Programme for International Student Assessment ( PISA ) 2012. This result is due to the lack of mathematical skills of students in resolving a matter of reasoning and problem solving, coupled with mathematical learning process is done in less innovative. Learning tends to be monotonous, thus affecting the interest of the students to learn mathematics. Thus, it is necessary to make an innovation in learning mathematics. One of the innovative learning in mathematics can be done through cultural approach or called ethnomatematics. One form of ethnomathematics which is interesting to be explored is Borobudur Temple as Borobudur has the potential to be used as a mathematics instructional materials that has historical value, close to the community, contextual, and can serve as a concrete models for understanding mathematics. The paper was written descriptively, ranging from reviewing issues related to learning mathematics. After that, making the problem formulation followed by collecting theory, analyzing and discussing the data. The final step is making conclusions and recommendations. It consists of instructional media design functions, scenarios, and storyboards. Results of this paper is the application of geometry learning media based on ethnomatematics. This application can be used as learning media in formal and informal school. Through this application, students can learn geometry easily and contextually. To analyze this application we use a SWOT analysis, where we identify the strengths, weaknesses, opportunities, and threats.
BAB I PENDAHULUAN
A. Latar Belakang
Pendidikan matematika di Indonesia membawa hasil yang masih jauh
dari harapan. Hal ini ditunjukkan dengan dipublikasikannya hasil penelitian
yang dilakukan oleh TIMSS (Thrends International Mathematics Science
Study) pada tahun 2011 yang lalu. Hasil studi ini menunjukkan bahwa
penguasaan matematika siswa Indonesia kelas 8 SMP berada di peringkat 42
dari 45 negara. Indonesia hanya mampu mengumpulkan 406 poin dari skor
rata-rata 500. Poin Indonesia berada di antara negara benua Afrika seperti
Lebanon dengan 406 poin, Marocco dengan 376 poin, atau Ghana dengan
306 poin. Negara Asia Tenggara yang paling dekat adalah Malaysia dengan
426 poin.Sementara itu 5 besar peringkat tertinggi adalah Singapura, dikuti
oleh Cina, Jepang, Finlandia, serta Slovenia.
Hal yang tidak jauh berbeda juga diungkap oleh hasil studi Programme
for International Student Assessment (PISA) 2012. Indonesia berada di urutan
dua terbawah dari 65 peserta negara di dunia karena hanya mampu
mendapatkan skor 375 untuk penguasaan kemampuan matematika. Hasil ini
juga jauh berada di bawah rata-rata ke 65 negara di dunia yaitu sebesar 494
dan juga rata-rata yang ditetapkan oleh OECD (Organisation for Economics
Co-operation and Development) yaitu sebesar 500 poin.
Hasil yang ditunjukkan oleh TIMSS maupun PISA tentu merupakan
sebuah tamparan bagi bangsa Indonesia untuk segera introspeksi dan
berbenah diri. Pasalnya menurut Pranoto ada penelitian yang menyimpulkan bahwa anak yang penguasaan matematikanya kurang akan sulit “berjalan” di abad 21 ini. Hal ini tentu akan sangat berbahaya bagi kemajuan bangsa
ditengah persaingan dunia yang sangat ketat.
Hasil yang kurang menyenangkan ini disebakan karena kurangnya
pemecahan masalah akibat kurangnya pemberian porsi menalar dan
memecahkan masalah pada materi ajar dan soal-soal latihan yang diberikan
kepada siswa. Di sisi lain proses pembelajaran matematika yang dilakukan
saat ini saat ini cenderung terlalu kering, teoritis, kurang kontekstual, dan
bersifat semu. Pembelajaranpun kurang bervariasi, sehingga mempengaruhi
minat siswa untuk mempelajari matematika lebih lanjut. Maka dari itu perlu
sebuah inovasi dalam pembelajaran matematika.
Pembelajaran yang inovatif adalah pembelajaran yang dapat memberikan
keteladanan, membangun kemauan, dan mengembangkan potensi peserta
didik, seperti halnya yang dituangkan dalam Peraturan Menteri Pendidikan
dan Kebudayaan Republik Indonesia Nomor 65 tahun 2013 dimana proses
pembelajaran pada satuan pendidikan diselenggarakan secara interaktif,
inspiratif, menyenangkan, menantang, memotivasi peserta didik untuk
berpartisipasi aktif, serta memberikan ruang yang cukup bagi prakarsa,
kreativitas, dan kemandirian sesuai dengan bakat, minat, dan perkembangan
fisik serta psikologis peserta didik. Kegiatan pembelajaran menggunakan
pendekatan ilmiah (scientific) meliputi proses mengamati, menanya,
mengumpulkan data, mengasosiai, dan mengomunikasikan apa yang
dipelajari. Di samping itu, proses pembelajaran harus mempertimbangkan
kebhinekaan budaya, keragaman latar belakang dan karakteristik peserta didik.
Salah satu pembelajaran matematika yang inovatif dapat dilakukan
melalui pendekatan budaya atau yang disebut etnomatematika.
Etnomatematika bisa didefinisikan sebagai cara-cara khusus yang dilakukan
oleh suatu kelompok tertentu dalam melakukan aktivitas matematika.
Sementara itu bentuk dari etnomatematika berupa hasil dari aktivitas
matematika yang dimiliki atau berkembang pada kelompok itu sendiri, seperti
konsep-konsep matematika pada peniggalan budaya berupa candi dan prasasti,
peralatan tradisional, permainan tradisional, dan berbagai macam hasil
aktivitas yang sudah membudaya.
Salah satu bentuk etnomatematika yang menarik untuk dieksplorasi
Tengah. Dari sisi etnomatematika, Candi Borobudur memiliki banyak
potensi untuk dikaji, salah satunya adalah bentuk bangunan yang banyak
mengandung obyek geometri. Candi Borobudur memiliki potensi untuk
dimanfaatkan sebagai bahan ajar pembelajaran matematika yang inovatif
karena Candi Borobudur lekat dengan masyarakat, kontekstual, dan bisa
dijadikan sebagai model konkrit unutk memahami matematika.
Berdasarkan permasalahan di atas dibutuhkan sebuah terobosan baru
untuk menarik minat siswa dalam mempelajari matematika, terutama
geometri, yaitu dengan dibuatnya aplikasi Borobudur Ethnomathematics,
media pembelajaran matematika sebagai pendukung pembelajaran geometri
yang menyenangkan dan fresh bagi generasi saat ini. Sehingga pembelajaran
matematika akan lebih inovatif dan kontekstual. Selain itu, dengan adanya
teknologi pendukung seperti komputer dapat memudahkan siapa saja untuk
menggunakan apliakasi Borobudur Ethnomathematics tanpa menghilangkan
esensi dari pembelajaran geometri itu sendiri.
B. Rumusan Masalah
Rumusan Masalah yang difokuskan dalam penyusunan karya tulis ini
adalah sebagai berikut :
1. Bagaimana rancangan dari aplikasi Borobudur Ethnomathematics,
media pembelajaran matematika sebagai pendukung pembelajaran
geometri berbasis etnomatematika?
2. Bagaimana unjuk kerja dari aplikasi Borobudur Ethnomathematics,
media pembelajaran matematika sebagai pendukung pembelajaran
geometri berbasis etnomatematika?
3. Bagaimana analisis dari aplikasi Borobudur Ethnomathematics, media
pembelajaran matematika sebagai pendukung pembelajaran geometri
C. Tujuan Penulisan
Dari rumusan masalah di atas, tujuan penulisan karya tulis ini adalah
sebagai berikut:
1. Mengetahui rancangan dari aplikasi Borobudur Ethnomathematics,
media pembelajaran matematika sebagai pendukung pembelajaran
geometri berbasis etnomatematika.
2. Mengetahui unjuk kerja dari aplikasi Borobudur Ethnomathematics,
media pembelajaran matematika sebagai pendukung pembelajaran
geometri berbasis etnomatematika.
3. Mengetahui analisis dari aplikasi Borobudur Ethnomathematics,
media pembelajaran matematika sebagai pendukung pembelajaran
geometri berbasis etnomatematika.
D. Metode Studi
1. Sumber dan Jenis Data
Sumber data yang digunakan dalam karya tulis ini berupa
pustaka-pustaka yang ada, baik berupa buku-buku yang bersangkutan, artikel
maupun jurnal-jurnal yang mempunyai korelasi terhadap pembahasan
masalah. Di samping itu juga beberapa informasi yang diperoleh dari
berbagai sumber media, baik surat kabar maupun media elektronik yang
kesemuanya diterapkan dengan interpretasi pendukung dalam menyusun
ketajaman analisis. Jenis data yang digunakan dalam karya tulis ini
menggunakan data sekunder yang bersifat kualitatif maupun kuantitatif
untuk mendapatkan kajian dari penelusuran pustaka. Selain data sekunder,
data primer juga digunakan dalam karya tulis ini. Data primer karya tulis
ini berupa tampilan media pembelajaran lewat emulator pengembang
media.
2. Pengumpulan Data
Penulis dalam karya ilmiah ini menggunakan library research (studi
menggunakan objek kajian penelitian yang berfokus pada pustaka-pustaka.
Pustaka tersebut dapat berupa media cetak maupun eletronik yang valid,
berhubungan satu sama lain, relevan dengan kajian tulisan serta
mendukung uraian atau analisis pembahasan, serta dapat
dipertanggungjawabkan secara ilmiah.
3. Analisis Data
Setelah data yang diperlukan terkumpul, dilakukan pengolahan data
dengan menyusun secara sistematis dan logis. Teknik analisis data yang
dipilih adalah analisis deskriptif dengan tulisan yang bersifat deskriptif,
menggambarkan tentang pemanfaatan teknologi yaitu media pembelajaran
matematika terutama geometri berbasis etnomatematika.
Karya ilmiah yang berjudul “Aplikasi Borobudur Ethnomathematics, Media Pembelajaran Matematika Sebagai Pendukung Pembelajaran
Geometri Berbasis Etnomatematika” ditulis secara deskriptif dengan pendekatan kualitatif. Dalam penulisan ini menggambarkan secara rinci
rancangan fungsi, skenario, storyboard, dan unjuk kerja Borobudur
Ethnomathematics serta analisisnya.
4. Penarikan Kesimpulan dan Rekomendasi
Penarikan kesimpulam dalam karya tulis ini dapat dilakukan setelah
melakukan tahap-tahap penulisan. Tahap-tahap penulisan tersebut antara
lain:
a. Mengkaji data tentang berbagai media pembelajaran matematika
khususnya geometri dan teknologi yang berkembang saat ini.
b. Mengidentifikasi permasalahan yang terkait dengan topik yang
sedang dikaji dalam karya tulis ini.
c. Membuat rumusan masalah sesuai dengan fokus-fokus
d. Mengumpulkan teori-teori yang terkait dengan fokus permasalahan
yang diangkat sebagai bahan acuan guna mendukung ketajaman
analisis permasalahan yang ada.
e. Menyusun metode penulisan yang akan digunakan dalam karya
tulis.
f. Menganalisis dan membahas karya tulis “Aplikasi Borobudur
Ethnomathematics, Media Pembelajaran Matematika Sebagai
Pendukung Pembelajaran Geometri Berbasis Etnomatematika”.
g. Menarik kesimpulan berdasarkan rumusan masalah yang ada.
BAB II
TELAAH PUSTAKA
A. Penggunaan Media Pembelajaran
Menurut Gagne (1970) di Indriana Dina (2011: 14) menyatakan bahwa
media pembelajaran adalah berbagai komponen dalam lingkungan yang dapat
merangsang siswa untuk belajar. Menurut Yusufhadi Miarso (2004: 458)
memberikan batasan media pembelajaran sebagai segala sesuatu yang dapat
digunakan untuk menyampaikan pesan dan untuk merangsang pikiran,
perasaan, perhatian, dan kemampuan siswa sehingga dapat mendorong proses
belajar yang disengaja, terarah, dan terkendali.
Berdasarkan pendapat ahli tentang definisi media pembelajaran di atas,
maka dapat disimpulkan bahwa semua bentuk media pembelajaran adalah
cara yang digunakan oleh pendidik untuk menyampaikan pesan dan dapat
digunakan untuk merangsang perhatian, pikiran, perasaan , dan kemampuan
peserta siswa untuk membentuk lingkungan belajar yang kondusif dan
memicu proses pembelajaran yang efektif dan efisien.
Menurut Bruner (1966: 10-11) yang dikutip Azhar Arsyad (2007:7) ada
tiga tingkatan utama modus belajar, yaitu enactive (pengalaman langsung),
iconic (pengalaman pictorial atau gambar), dan symbolic (pengalaman
abstrak). Ketiga tingkat pengalaman ini saling berinteraksi delam upaya
memperoleh pengalaman (pengetahuan, keterampilan, atau sikap) yang baru.
Azhar Arsyad (2007:10) menuturkan lebih lanjut, salah satu yang banyak
dijadikan acuan sebagai landasan teori penggunaan media dalam proses belajar mengajar adalah Dale’s Cone of Experience (Kerucut Pengalaman Dale). Hasil belajar seseorang diperoleh mulai dari pengalaman langsung
(konkret), kenyataan yang ada di lingkungan kehidupan seseorang kemudain
melalui benda tiruan, sampai kepada lambing (abstrak).Semakin ke atas di
puncak kerucut semakin abstrak media penyampaian pesan itu. Edgar Dale
mengklasifikasi pengalaman belajar anak mulai dari hal-hal yang paling
pengalamn tersebut diikuti secara luas oleh kalangan pendidikan dalam
menentukan alat bantu apa seharusnya yang sesuai untuk pengalaman belajar
tertentu.
Menurut Azhar Arsyad (2007:25-27) ada beberapa manfaat praktis dari
penggunaan media pembelajaran di dalam proses belajar mengajar sebagai
berikut:
1. Media pembelajaran dapat memperjelas penyajian pesan dan
informasi sehingga dapat memperlancar, meningkatkan proses, serta
hasil belajar.
2. Media pembelajaran dapat meningkatkan dan mengarahkan perhatian
anak sehingga dapat menimbulkan motivasi belajar, interaksi yang
lebih langsung antara siswa dan lingkungannya, dan kemungkinan
siswa untuk belajar
3. Media pembelajaran dapat mengatasi keterbatasan indera, ruang, dan
waktu.
4. Media pembelajaran dapat memberikan kesamaan pengalaman kepada
siswa tentang peristiwa di lingkungan mereka, serta memungkinkan
terjadinya interaksi langsung dengan guru, masyarakat, dan
lingkungannya misalnya melalui karya wisata, kunjungan-kunjungan
ke museum, atau kebun binatang.
Dari pemaparan di atas dapat disimpulkan bahwa penggunaan media
pembelajaran sebagai alat bantu mengajar yang baik harus dapat
menggabungkan beberapa jenis indera yang turut serta selama penerimaan isi
pengajaran. Hal ini dimaksudkan agar kemampuan media dan materi yang
diberikan untuk bisa dipahami oleh siswa akan lebih banyak.
B. Software yang Digunakan dalam Pembuatan Aplikasi Borobudur Ethnomathematics
Dalam pembuatan aplikasi ini, digunakan software Adobe Flash CS 6.
yang didapatkan dari perangkat lunak ini dapat diputar di penjelajah Web
yang mempunyai format “.swf” yang telah disediakan adobe Flash player.
Alasan penggunaan adobe flash sebagai software pengembangan aplikasi
ini karena adobe flash memiliki fitur yang sangat lengkap dan mudah
digunakan. Selain dapat menghasilkan animasi dan gambar yang menarik,
software ini juga mampu menghasilkan media yang dinamis dan interaktif.
Keunggulan lain adalah software ini dilengkapi dengan action script yang
memungkinkan programmer untuk membuat fungsionalitas aplikasi yang
variatif, Reimers (2007). Gambar dan animasi hasil dari adobe flash ini
menggunakan tipe vektor sehingga memiliki kualitas yang bagus. Selain itu
kompresinya juga optimal sehingga aplikasi mampu berjalan dengan baik dan
ringan di komputer ataupun di web. Hal ini berguna untuk memudahkan user
dalam menggunakan aplikasi ini.
C. Belajar Geometri Melalui Pendekatan Budaya (Etnomatematika)
Matematika telah digunakan oleh banyak orang dalam banyak hal. Salah
satu cabang materi dalam matematika yang sering dijumpai dalam kehidupan
sehari-hari adalah geometri. Ada banyak masalah yang memiliki korelasi
dengan geometri, seperti konstruksi bangunan, jembatan, dan lain sebagainya.
Salah satu geometri dasar adalah tentang bangun datar dan bangun ruang.
Dalam bangun datar siswa akan belajar tentang persegi, lingkaran, persegi
panjang, dan sebagainya. Sementara dalam bangun ruang kita akan tahu
tentang karakteristik kubus, bola, balok, dan lain sebagainya.
Etnomatematika terdiri dari dua kata, etno (etnis/budaya) dan matematika.
Itu berarti bahwa dalam ethnomathematics, matematika terkait dengan budaya.
Selanjutnya, menurut Ascher di Rex Matang (2002) budaya berarti bahasa
masyarakat, tempat, tradisi, dan cara-cara pengorganisasian, menafsirkan,
konseptualisasi, dan memberikan makna terhadap dunia fisik dan sosial.
Dalam hal ini, kegiatan etnomatematika yang menghubungkan matematika
dan budaya dinilai sangat bermanfaat bagi siswa. Pembelajaran matematika
mengenai pemaknaan dari matematika yang tidak jauh dari kehidupan
manusia, Zhang (2010). Hal ini juga didukung oleh gagasan Snipes (2010)
yang mengatakan bahwa dengan menggunakan pendekatan budaya siswa
dapat melihat penggunaan konsep matematika yang beragam berdasarkan
perkembangan zaman di suatu masa tertentu.
Berdasarkan penelitian sebelumnya, menurut Rachmawati (2008)
etnomatematika dapat dijadikan sebagai ide alternatif untuk menjadi salah
satu pembelajaran yang inovatif, sebagai pengenalan terhadap matematika
formal, dan sebagai rujukan untuk pemecahan masalah matematika serta
pengaplikasian pembelajaran yang bersifat kontekstual. Sementara itu,
pembelajaran yang kontekstual adalah pembelajaran yang berdasar kepada
falsafah konstruktivisme dimana siswa belajar ketika siswa dapat memaknai
proses pembelajaran dan dapat mengintegrasikan pengetahuan yang baru
dengan pengetahuan dan pengalaman yang dialami sebelumnya, Johnson
(2002). Pada dasarnya setiap individual, telah memiliki pengetahuan awal
yang diperoleh dari lingkungan sosial dan budayanya. Maka dari itu yang
perlu dilakukan siswa adalah menghubungkan pembelajaran matematika
dengan hal-hal yang ada disekitarnya, sehingga pembelajaran tersebut tidak
hanya berlaku secara teoritis.
Berbagai cara dapat dilakukan untuk memasukkan etnomatematika dalam
pembelajaran matematika. Menurut Rachmawati (2008), keterampilan ini
membutuhkan kreativitas dari guru dalam memanfaatkan lingkungan
setempat. Salah satunya adalah dengan mengembangkan pengetahuan dasar
etnomatematika siswa dan mengintegrasikannya dengan penggunaan
teknologi.
Sementara itu, salah satu bentuk etnomatematika yang dapat dieksplorasi
adalah situs Candi Borobudur yang terletak di Kabupaten Magelang, Jawa
Tengah, Indonesia. Dalam hal etnomatematika, Candi Borobudur memiliki
banyak potensi untuk dipelajari, seperti pemodelan bangun datar ataupun
bangun ruang yang terdapat di dalam bangunan maupun relief dari Candi
objek pembelajaran matematika yang inovatif, karena Candi Borobudur erat
dengan masyarakat, kontekstual, dan dapat berfungsi sebagai model konkret
untuk memahami matematika. Melalui belajar geometri berbasis
etnomatematika di Candi Borobudur akan menjadi peluang bagi guru untuk
mengintegrasikan matematika dengan budaya. Ini berarti bahwa selama
belajar matematika, siswa juga mendapatkan pengetahuan tentang Candi
Borobudur yang merupakan salah satu aspek dari pengetahuan budaya.
Berikut ini adalah contoh penggunaan etnomatematika sebagai salah satu
alternatif pengenalan objek geometri
Tabel 1. Contoh Etnomatematika di Candi Borobudur
Objek Candi Borobudur Interpretasi
Gambar di samping adalah relief berbentuk
segitiga yang berada pada pintu selatan candi
Borobudur. Relief ini dapat dikenalkan kepada
siswa sebagai bangun datar segitiga yang berada
di candi Borobudur
Siswa dapat mengamati bahwa dinding candi
Borobudur terdiri dari susunan batu yang
berbentuk balok jika dipandang sebagai bangun
ruang, sedangkan jika dipandang sebagai bangun
BAB III
ANALISIS DAN SINTESIS
A. Perancangan Borobudur Ethnomathematics
Perancangan didefinisikan sebagai penggambaran, perencanaan, dan
pembuatan sketsa atau pengaturan dari beberapa elemen yang terpisah ke
dalam kesatuan yang utuh. Tujuan dari proses perancangan sebuah system
adalah untuk memenuhi kebutuhan pengguna system dan memberi gambaran
yang jelas dan rinci dengan rancangan bagan yang lengkap, sehingga
pembuatan media pembelajaran menjadi mudah dan terarah dalam
mengimplementasikan rancangan sistem, ke dalam sebuah program aplikasi.
Perancangan yang dilakukan meliputi perancangan fungsi, skenario, dan
storyboard aplikasi Borobudur Ethnomathematics.
1. Fungsi-fungsi yang dihasilkan
Fungsi-fungsi yang terbentuk dari pembuatan media pembelajaran
geometri berbasis ethnomatematika ini adalah:
a. Fungsi Introduction. Fungsi ini digunakan sebagai halaman pembuka
yang berisi judul aplikasi media pembelajaran dan identitas pembuat
media pembelajaran.
b. Fungsi Main Menu. Fungsi ini digunakan untuk menampilkan
menu-menu yang ada di dalam aplikasi media pembelajaran.
c. Fungsi Materi. Fungsi ini disediakan untuk memuat materi yang ada
di dalam media pembelajaran. Materi pembelajaran meliputi bangun
datar dan bangun ruang.
d. Fungsi Evaluasi. Fungsi ini digunakan untuk menampilkan halaman
yang berisi soal-soal sebagai evaluasi dari materi yang telah
diberikan.
e. Fungsi Bantuan. Fungsi ini untuk menampilkan petunjuk
penggunaan media pembelajaran.
2. Skenario
Skenario dalam penggunaan media pembelajaran ini dapat diuraikan
sebagai berikut:
a. Proses penggunaan diawali dengan membuka file Borobudur
Ethnomathematics. User akan masuk pada fungsi Introduction untuk
pertama kali.
b. Setelah halaman intro maka akan muncul halaman Main Menu.
c. Setelah muncul halaman Main Menu, user dapat melakukan:
1) Memilih menu-menu yang tersedia di dalam media pembelajaran.
2) Memilih menu Exit untuk keluar dari aplikasi.
3) Pada halaman Main Menu, user dapat memilih menu-menu yang
disediakan.
4) User dapat melihat petunjuk penggunaan aplikasi pada halaman
bantuan.
Gambar di samping adalah halaman
intro, dengan rincian:
(1) Judul media pembelajaran
(2) Identitas pembuat media
pembelajaran
Gambar di samping adalah pengenalan
(3) Tombol Introduksi
Gambar di samping adalah halaman
topik materi utama, dengan rincian:
(1) Peta Candi Borobudur
(2) Bagian-bagian Candi
Borobudur
(3) Informasi tentang bangun datar
dan bangun ruang
Gambar di samping adalah halaman
topik materi utama, dengan rincian:
B. Unjuk Kerja Aplikasi Borobudur Ethnomathematics
Setelah rancangan media pembelajaran disusun, maka langkah
selanjutnya adalah melihat unjuk kerja dari media pembelajaran tersebut
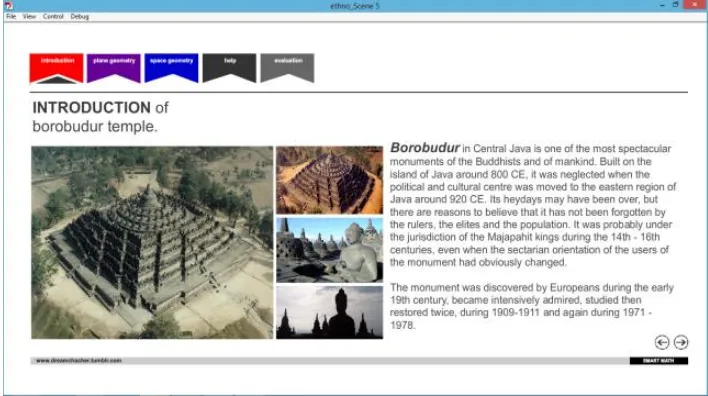
Gambar 1. Halaman Introduction
(4) Tombol menuju halaman
bangun datar
(5) Tombol menuju halaman
bangun ruang
(6) Tombol menuju halaman
evaluasi
(7) Tombol menuju halaman
bantuan
Gambar 2. Halaman Materi Bangun Ruang
\
Gambar 4. Halaman Evaluasi
Tampilan pada gambar 1 adalah halaman intro. Halaman intro ini berisi
pengenalan awal mengenai Candi Borobududr. Di dalam halaman ini akan
muncul informasi mengenai Candi Borobudur. Pada halaman ini user dapat
memilih menu selanjutnya, dimana tombol menu terletak di bagian kiri
atas.Tampilan pada gambar 2 adalah halaman bangun ruang, halaman ini
berisi materi tentang bangun ruang. Halaman ini tetap dilengkapi tombol
menu untuk kembai ke halaman Introduction maupun ke menu lainnya.
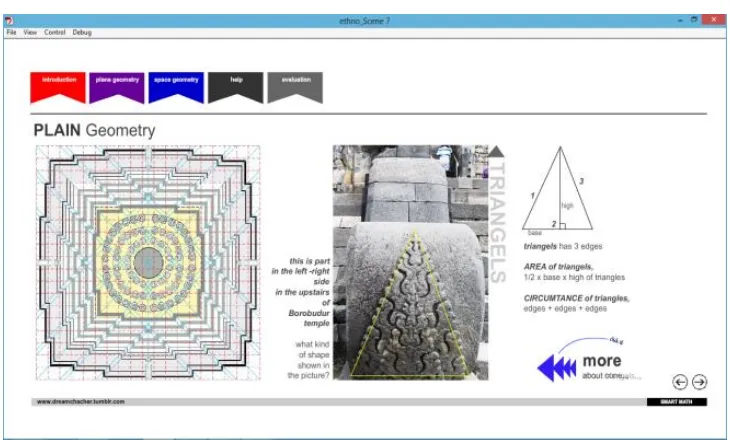
Tampilan pada gambar 3 adalah halaman bangun datar. Halaman ini berisi
materi tentang bangun ruang. Gambar berikutnya yaitu Gambar 4 adalah
halaman evaluasi, halaman ini menampilkan halaman untuk user mengasah
kemampuan mereka setelah mempelajari materi yang disediakan.
C. Analisis Aplikasi Borobudur Ethnomathematics
Setelah melihat tampilan Borobudur Ethnomathematics sebagai media
pembelajaran, kami juga menganalisis produk tersebut. Analisis yang kami
gunakan dalam karya tulis ini adalah analisis SWOT ( Strength, Weakness,
dan ancaman produk. Analisis ini juga dapat menjelaskan kelayakan produk
kami. Adapun analisis SWOT sebagai berikut:
1. Strength (Kekuatan)
Borobudur Ethnomathematics sebagai media pembelajaran
pengenalan geometri mempunyai beberapa kelebihan, antara lain:
a. Fun learning, media pembelajaran ini menyenangkan sehingga
dapat menarik minat siswa dalam belajar matematika terutama
geometri.
b. Borobudur Ethnomathematics dirancang sebagai media
pembelajaran matematika berbasis etnik, jadi selain belajar
matematika user juga mendapat pengetahuan tentang budaya,
utamanya Candi Borobudur.
c. Interaktif, media pembelajaran ini merupakan media
pembelajaran interaktif dimana user juga belajar secara aktif.
2. Weakness (Kelemahan)
Kelemahan dari media pembelajaran ini hanya dapat dijalankan pada
media yang kompatibel dengan flash. Namun saat ini sudah banyak
browser yang mendukung adanya flash player, seperti pada Google
Chrome dan Firefox yang sudah menyediakan ekstensi flash player di
dalamnya, sehingga media pembelajaran ini dapat dijalankan melalui
browser tersebut.
3. Opportunity (Peluang)
Peluang yang ada pada Borobudur Ethnomathematics antara lain :
a. Dari sisi ekonomi, dengan kemasan dan desain yang menarik
maka media ini berpeluang untuk diperjual belikan kepada
masyarakat yang membutuhkan alternatif media pembelajaran.
b. Dari sisi pariwisata, media ini dapat digunakan sebagai alternatif
pengenalan hasil budaya Indonesia yakni candi Borobudur dan
c. Dari sisi sosial, media pembelajaran ini dapat disebar luaskan
secara gratis dengan bekerja sama dengan pihak-pihak tertentu
yang memperhatikan dunia pendidikan atau melalui media internet.
d. Media pembelajaran matematika khususnya geometri ini dapat
dikembangkan untuk media pembelajaran lainnya.
4. Threat (Ancaman)
Ancaman yang muncul dengan adanya media pembelajaran
Borobudur Ethnomathematics ini adalah banyaknya media pembelajaran
geometri lain yang berkembang. Namun walaupun demikian, media ini
tetap memiliki ciri khas tersendiri yaitu dengan digunakannya candi
Borobudur sebagai obyek pembelajaran matematika sehingga mampu
BAB IV
SIMPULAN DAN REKOMENDASI
A. Kesimpulan
Dari uraian dan pembahasan yang telah dilakukan, maka dapat ditarik
beberapa kesimpulan sebagai berikut:
1. Rancangan dari Borobudur Ethnomathematics, media pembelajaran
matematika berbasis etnomatematika untuk mendukung siswa
belajar geometri terdiri dari rancangan fungsi, skenario, dan
storyboard.
2. Hasil unjuk kerja dari Borobudur Ethnomathematics, media
pembelajaran matematika berbasis etnomatematika untuk
mendukung siswa belajar geometri ini menampilkan halaman intro,
halaman bangun datar,halaman bangun ruang, dan halaman evaluasi.
3. Analisis Borobudur Ethnomathematics, media pembelajaran
matematika berbasis etnomatematika untuk mendukung siswa
belajar geometri terdiri dari analisis kekuatan, kelemahan, peluang,
dan ancaman media pembelajaran.
B. Saran
Saran dari hasil penulisan karya tulis ini adalah:
1. Mengembangkan media pembelajaran ini lebih lanjut dengan
melakukan penelitian pengembangan media.
2. Melakukan kerjasama instansi terkait untuk menyebarluaskan
Borobudur Ethnomathematics, media pembelajaran matematika
DAFTAR PUSTAKA
Adhi (editor). (2012). 70 Persen Anak Indonesia Sulit Hidup di Abad 21. Diambil
pada tanggal 10 November 2013, dari
http://edukasi.kompas.com/read/2012/04/04/15495046/70.Persen. Anak.Indonesia.Sulit.Hidup.di.Abad.21
Ascher, M. (1991). Ethnomathematics: A Multicultural View of Mathematical Ideas. New York: Chapman & Hall.
Azhar, Arsyad. (2004). Media Pembelajaran. Jakarta: PT. Raja Grafindo Persada.
Badan Standar Nasional Pendidikan. (2013). Peraturan Menteri Pendidikan dan Kebudayaan Republik Indonesia Nomor 65 tahun 2013 tentang Standar Proses Pendidikan Dasar dan Menengah.
Borobudur Temple Compounds. (2013). Diambil pada tanggal 10 Agustus 2013, dari UNESCO. http://whc.unesco.org/en/list/592.
Indriana, Dina. (2011). Mengenal Ragam Gaya Pembelajaran Efektif. Jogjakarta : Diva Press.
Johnson, Elaine B. (2002). Contextual Teaching and Learning: Why It Is and Why
It’s Here to Stay. United Kingdom: Corwin Press, Inc.
Matang, Rex. (2002). The Role of Ethnomathematics in Mathematics Education in Papua New Guinea: Implication for Mathematics Curriculum. Journal of Educational Studies Vol 24 (1) June 2002.
Miarso, Yusufhadi. (2004). Menyemai Benih Teknologi Pendidikan. Jakarta: Prenada Media.
Mulis, Martin, dkk. (2011). TIMSS 2012 International Results in Mathematics.2. .
Diambil pada tanggal 1 April 2014, dari
http://timssandpirls.bc.edu/timss2012/downloads/T11_IR_Mathematics_Ful lBook.pdf
OECD. (2012). Result from te 2012 data collection. Diambil pada tanggal 8 April 2014, dari http://www.oecd.org/pisa/aboutpisa/pisa-2012-participants.htm
Rachmawati, Inda. (2013). Eksplorasi Etnomatematika Masyarakat Sidoarjo. E-Journal Unesa
Snipes, Vincent and Pamela Moses. (2013). Linking Mathematics and Culture to Teach Geometry Concepts. Journal for Research in Mathematics Education.