PENGANTAR
Geometri transformasi adalah cabang ilmu matematika yang membahas berbagai bangun tampak dan perubahan posisinya sesuai aturan yang ditentukan.
Geometri transformasi bukan suatu hal yang baru bagi pembaca, ia sering sekali kita jumpai dalam kehidupan sehari-hari dalam aktivitas harian seperti bercermin, berpindah tempat, dan lain sebagainya.
Geometri transformasi sering dianggap sebagai suatu ilmu murni saja tanpa mengetahui kebermaknaan serta manfaatnya secara realita. Materi geometri transformasi secara bermakna sering kita jumpai dalam aktivitas bermain yang dilakukan anak-anak di taman bermain sewaktu menggunakan alat permainan edukatif. Pada tingkatan berikutnya Geometri transformasi menjadi materi pelajaran Sekolah Dasar dan Sekolah Menengah Pertama berupa materi Dilatasi Kesebangunan dan pada tingkat Sekolah Menengah Atas dengan materi geseran, rotasi dan pencerminan. Pada tingkat perguruan tinggi khusus untuk mahasiswa yang mendalami matematika sebagai calon guru, geometri transformasi adalah materi penting yang harus dikuasai.
Geometri transformasi akan bermakna pemahamannya jika materi yang dikuasai mahasiswa lebih realistik dan dekat dengan kesehariannya. Penggunaan kata “realistik” sebenarnya berasal dari bahasa Belanda “zich realiseren” yang berarti untuk dibayangkan. Menurut Van del Heuvel-Puhuizen, penggunaan kata
“realistik”, tidak sekedar menunjukan adanya suatu koneksi dengan dunia nyata tetapi lebih mengacu pada fokus Pendidikan Matematika Realistik dalam penempatan penekanan penggunaan sesuatu yang bisa dibayangkan oleh mahasiswa “. (Ariyadi , 2012, p. 21). Pendekatan realistis merupakan suatu upaya yang dapat dimanfaatkan dalam menyajikan pemahaman geometri transformasi bagi pembaca sehingga lebih bermakna.
Pendekatan realistik lebih menekankan pada penggunaan sesuatu yang bisa dibayangkan. Usaha pendekatan sehingga apa yang dibayangkan bisa menjadi nyata bagi pembaca bisa dilakukan dengan memunculkan visualisasi gambaran transformasi itu sendiri. Setiap pemahaman ataupun teori yang disertai lukisan geometri akan menjadi hal yang menyenangkan untuk bisa dipahami lebih dalam. Penyajian lukisan geometri selain secara manual, dalam sajian ini akan dibantu dengan memanfaatkan aplikasi Geogebra.
Geogebra adalah perangkat lunak (software) matematika yang bersifat dinamis dan dipergunakan untuk pembelajaran matematika di sekolah. GeoGebra merupakan sistem interaktif yang menggabungkan geometri, aljabar dan kalkulus.
Lebih dari itu, GeoGebra juga menyediakan fasiltas (tools) untuk peluang dan statistika. Pada versi 5, GeoGebra sudah memiliki fasilitas untuk geometri dimensi tiga (ruang).
Dengan GeoGebra, kita dapat mengonstruksi (menggambar) titik, vektor, ruas garis, garis, polygon atau segi banyak, dan irisan kerucut (lingkaran, ellips, parabola, hiperbola), serta fungsi. Setelah dimasukkan ke dalam Geogebra, objek- objek matematika ini dapat dimodifikasi secara dinamis. Di pihak lain, persamaan
dan koordinat dapat dimasukkan langsung pada GeoGebra sehingga GeoGebra juga dapat menangani variabel-variabel angka, vektor dan titik.
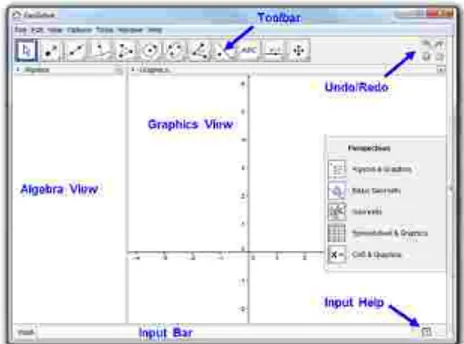
Berikut tampilan dasar (desktop) GeoGebra.
Gambar 1 : Jendela Awal
Berdasarkan gambar 1 diketahui bahwa secara dasar Geogebra memiliki tampilan dasar sebagai berikut :
• Tampilan Grafik (Graphics View): pada jendela ini kita dapat membuat konstruksi geometri, seperti titik, garis, ruas garis, lingkaran, dan sebagainya.
GeoGebra menyiapkan 2 jendela grafik.
• Tampilan Aljabar (Algebra View): Pada jendela ini muncul angka (konstanta), variabel, dan titik koordinat yang bersesuaian dengan tampilan grafiknya. Jadi GeoGebra menampilan bentuk geometri dan bentuk aljabar secara bersamaan.
• Bilah Masukan (Input Bar): pada jendela ini , kita dapat memasukkan bentuk aljabar seperti angka, variabel, fungsi dengan menggunakan papan ketik (keyboard).
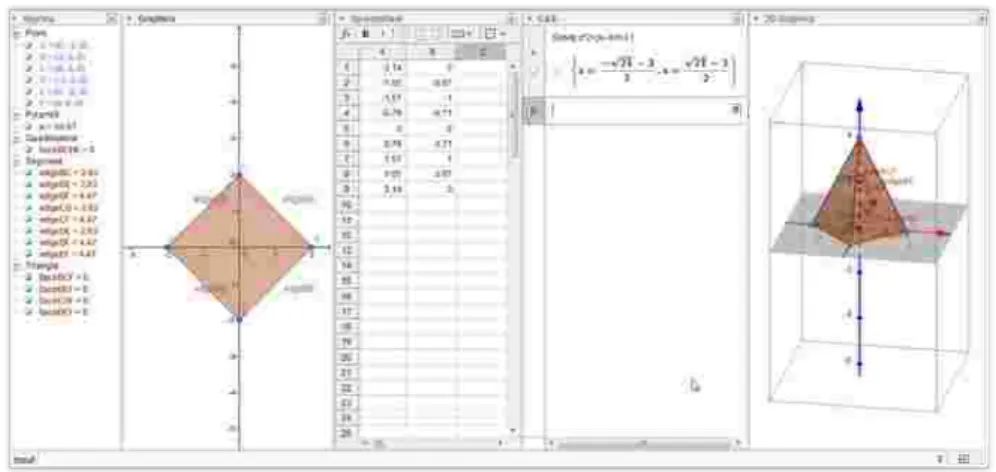
Untuk tingkat lanjut masih ada beberapa jendela tampilan GeoGebra, yaitu
• Tampilan Spreadsheet (Spreadsheet View): pada jendela ini kita dapat bekerja dengan daftar angka-angka menggunakan formula dan fungsi seperti pada MS Excel.
• Tampilan CAS (Computer Algebra System): jendela ini digunakan untuk bekerja dengan matematika simbolik, seperti menyelesaikan persamaan atau sistem persamaan.
• Tampilan Grafik 3D, khusus GeoGebra versi 5: Jendela ini untuk melihat bangun ruang, seperti kubus, limas, prisma, dan lain sebagainya serta untuk mempelajari sifat-sifat geometri tiga dimensi, seperti bidang melalui tiga titik, sudut antara garis dan bidang, sudut antara garis bersilangan, dan lain sebagainya.
Gambar 2 : Layar Kerja
Menu (menu bar) pada gambar 2 merupakan daftar pilihan untuk melakukan navigasi program Geogebra. Karena isi dari menu bar ini relatif umum seperti pada operasi window secara umum maka kita lewati karena dapat dipelajari sambil jalan oleh pembaca sekalian.
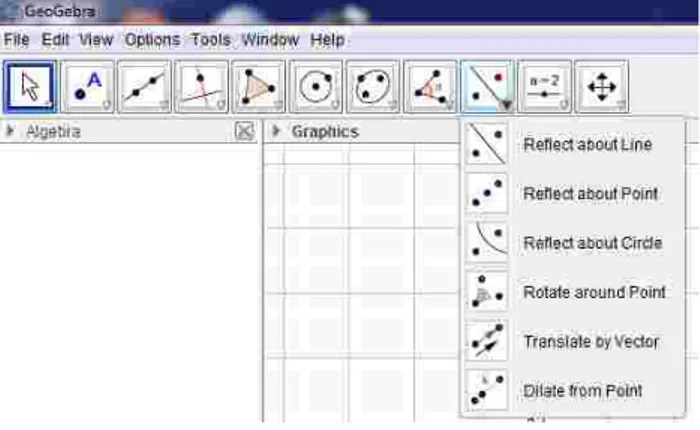
Gambar 3: Menu Bar
Pada gambar 3 di atas, bagian yang paling penting diketahui pembaca adalah menu geometri transformasi. Pada menu geometri transformasi ini tersedia diantaranya:
Titik
Garis
Hubunga n Garis
Segi Banyak
Lingkara n
Irisan Kerucut
Sudut Transfor
masi Geometri
INSERT TEKS &
GAMBAR Slinder
Gambar 4 : Menu khusus pada geometri Transformasi
Gambar 4 menjelaskan menu pada geometri transformasi yang terdiri atas refleksi, rotasi, translasi dan dilatasi. Untuk lebih rinci akan dijelaskan sebagai berikut:
a. Reflect about Line. Menu ini digunakan untuk merefleksikan atau mencermin benda dengan cermin yang dimaksud berupa sebuah garis.
b. Reflect abaut Point. Menu ini digunakan untuk Merefleksikan atau mencerminkan benda dengan cerminnya berupa sebuah titik.
c. Reflect about Circle. Menu ini digunakan untuk merefleksikan atau m d. encermin benda dengan cermin yang dimaksud berupa sebuah lingkaran.
e. Rotate around Point. Menu ini digunakan untuk merotasikan benda dengan pusat rotasi adalah sebuah titik.
f. Translate by Vector. Menu ini digunakan untuk menggeser benda dengan vektor tertentu.
g. Dilate from Point. Menu ini digunakan untuk mendilatasikan benda terhadap titik tertentu sebagai pusat dilatasi.
Penggunaan masing-masing menu ini akan dirinci pada penjelasan setiap bab yang bersesuaian dengan trasformasi yang dimaksud. Penggunaan menu pada aplikasi Geogebra bermanfaat bagi pembaca untuk lebih memposisikan geometri yang ada pada bayangan menjadi proses yang benar nyata dan realistis.
BAB 1 TRANSFORMASI
A. Pengertian Transformasi (T)
Transformasi T adalah fungsi satu-satu dari himpunan titik-titik dalam bidang euclides kepada himpunan yang sama dibidang euclid. Dengan mengambil semesta bidang euclides berarti seluruh teori geometri Euclides dianggap berlaku di dalamnya. Jadi T ini selalu mempunyai invers dan inversnya pun berupa transformasi. I disebut transformasi Identitas bila I(P) = P untuk setiap P dalam bidang. (Susanta, 1990: 22). Jenis-jenis transformasi yaitu: Translasi (pergerseran), Refleksi (pencerminan), Rotasi (perputaran), setengah putaran dan Dilatasi (penskalaan).
Transformasi memiliki sifat diantaranya kolineasi, isometri dan involusi. Suatu transformasi disebut kolineasi bila hasil transformasi sebuah garis (lurus), akan berupa garis lagi. Dapat dipahami bila g garis maka T adalah suatu kolineasi, bila T(g) berupa garis lagi. Isometri adalah transformasi yang mempertahankan jarak (panjang suatu garis). Isometri adalah suatu transformasi atas refleksi (pencerminan), translasi (pergeseran) dan rotasi (perputaran) maupun setengah putaran pada sebuah garis yang mempertahankan jarak ( panjang suatu ruas garis).
Isometri dilambangkan dengan U. Sedangkan involusi yaitu hasilkali transformasi akan menghasilkan dirinya sendiri. Berdasarkan sebuah Teorema : invers dari setiap refleksi garis adalah refleksi garis itu sendiri. Suatu transformasi yang inversnya adalah transformasi itu sendiri dinamakan involiusi, jadi refleksi garis adalah suatu involusi.
Suatu isometri pada sebuah transformasi memiliki sifat-sifat yang dapat dijabarkan sebagai berikut:
1. Memetakan garis menjadi garis.
2. Mempertahankan besar sudut.
3. Mempertahankan kesejajaran.
Berikut ini akan dibuktikan sifat-sifat di atas:
1. Memetakan garis menjadi garis
Andaikan g sebuah garis dan T suatu isometri. kita akan membuktikan bahwa T(g) = h adalah suatu garis juga.
g h
Ambil A ∈ g dan B ∈ g. Maka A' = T(A) ∈ h, B' = T (B) ∈ h ; melalui A' dan B' ada satu garis. Misalnya h'.
Untuk ini akan dibuktikan h' ⊂ h dan h ⊂ h'.
a. Bukti h' ⊂ h
Ambil X' ∈ h'. Oleh karena bidang kita adalah bidang Euclides. Kita andaikan (A' X B' ), artinya A' X + XB' =A'B'. Oleh karena T suatu isometri. Jadi suatu transformasi maka ada X sehingga T (X) = X’ dan oleh karena T suatu isometri maka AX = A'X; begitu pula XB = XB'.
Jadi AX + XB = AB.
Ini berarti bahwa A.X.B segaris pada g. Ini berarti bahwa X = T (X) ∈ h sehingga h' ⊂ h sebab bukti serupa berlaku untuk posisi X dengan (XA' B') atau (A'B'X).
b. Bukti h ⊂ h'
Ambil lagi y ∈ h. Maka ada y ∈ g sehingga T(y) = y dengan y misalnya (A Y B). Artinya Y ∈ g dan AY + YB = AB. Oleh karena T sebuah isometri maka A'Y = AY, Y B' = YB, A'B' = AB. Sehingga A'Y + Y B'
= A'B'. Ini berarti bahwa A'.Y.B' segaris, yaitu garis yang melalui A' dan B'. Oleh karena h' satu-satunya garis melalui A' dan B' maka Y ∈ h'.
Jadi haruslah h ⊂ h'. Bukti serupa berlaku untuk keadaan ( Y A B) atau ( A B Y). Sehingga h = h'.
Jadi kalau g sebuah garis maka h = T( g) adalah sebuah garis.
AB = A'B' 2. Mempertahankan besar sudut
Ambil sebuah ∠ ABC
Andaikan A' = T(A), B' = T(B), C' = T(C).
Menurut (1) maka A' B' dan B' C' adalah garis lurus. Oleh karena ∠ABC = BA ∪ BC maka ∠ A' B'C'= B'A' ∪ B'C' sedangkan A'B' = AB, B'C' = BC, C'A' = CA. Sehingga ∆ABC = ∆A'B'C'.
Jadi ∠A' B'C' = ∠ABC sehingga suatu isometri, mempertahankan besarnya sebuah sudut.
3. Mempertahankan kesejajaran
Kita harus memperhatikan bahwa a'// b'.
Andaikan a' memotong b' disebuah titik P jadi P ∈ a dan P ∈ b. Oleh karena T sebuah transformasi maka ada P sehingga T (B)= P dengan P ∈ a dan P ∈ b. Ini berarti bahwa a memotong b di p.
Jadi bertentangan dengan yang diketahui bahwa a// b, maka pengandaian bahwa a' memotong b' salah. Jadi haruslah a'//b'.
Berdasarkan ketiga pembuktian di atas terlihat bahwa Isometri mempertahankan ukuran dan bentuk. Isometri memiliki keunikan sifat sehingga isometri dapat dikomposisikan tapi tetap memperahankan ukuran dan bentuk.
Berikut dijelaskan tentang aturan komposisi 2 isometri.
Dalil T1: Komposisi Isometri
Komposisi dua buah isometri adalah sebuah isometri.
Bukti : Ambil dua isometri, T1 dan T2 terjadi komposisi dari , T1 dan T2 yaitu:
1. T1 ∘ T2
2. T2 ∘T1
Karena T1 ∘ T2 = T2 ∘T1 adalah isometri maka akan di buktikan adalah T1 ∘ T2 isometri.
Ambil dua titik sebarang A,B ∈ V, misalkan T2 (A)= A1, T2(B)= B1 dan T1(A1)=A’ ,T1(B1) = B’ maka
T1 ∘ T2 (A) = T1 [T2 (A)] = T1 (A1) = A’
T2 ∘T1 (B) = T2 [T2 (B)] = T1 (B1) = B’
Karena T2 isometri maka A’B’ = AB, dan karena T1 isometri maka B’A’ = A1B1 karena A’B’ = A1B1 dan A1B1 = AB, jadi T1 ∘ T2 suatu isometri.
Grup Isometri
Bila suatu grup hanya mempunyai n (terhingga) buah anggota maka himpunan ini disebut grup hingga berderajat n. Bila banyak anggotanya tak hingga, maka grupnya disebut grup tak hingga.
Jika untuk suatu transformasi T terdapat bilangan asli terkecil n sehingga Tn = I maka T disebut berderajat n dan {T, T2, T3, . . ., Tn} menyusun grup hingga berderajat n yang disebut grup siklik yang dibangkitkan oleh T dengan lambang <T> = {T, T2, T3, . . ., Tn}.
Transformasi T menjadi pembangkit <T> berarti setiap anggota <T>
merupakan kelipatan T. Jika tidak terdapat bilangan n seperti di atas maka T dikatakan berderajat tak hingga.
1. Himpunan ϰ = {S,H} menyusun suatu grup dengan R sebagai pembangkitnya.
Hasilkali RS atau SR adalah suatu R. Hasil kali RR akan memberikan suatu R atau S dan akhirnya hasil kali SS adalah suatu S, sehingga dapat disimpulkan bahwa himpunan {S,R}
adalah tertutup.
2. Himpunan ϑ = {S,R} menyusun grup.
Grup ini disebut grup gerakan tegar “rigid motion” atau
“motion”, karena seolah-olah benda sekadar dipindahkan tanpa mengubah bentuk atau membaliknya. Dari segi geometri, ϑ adalah himpunan isometri searah, sedangkan himpunan isometri yang berlawanan tidak mungkin menyusun grup karena J tidak ada di dalamnya.
3. Himpunan isometri 𝓊𝓊 = {U} = {S, R, M, G} menyusun grup.
Himpunan isometri 𝓊𝓊 adalah himpunan bagian ϰ (himpunan kolineasi) sedang ϰ terbukti menyusun grup. Untuk sebarang dua isometri maka hasilkalinya juga termasuk dalam 𝓊𝓊. Demikian juga inversnya isometri, jadi terbukti bahwa 𝓊𝓊 menyusun grup yang kemudian disebut grup isometri.
Bagian ini akan dijelaskan lebih lanjut pada pokok bahasan berikut.
B. Hasil Kali Dua Transformasi
Hasil kali 2 transformasi mengikuti aturan fungsi komposisi. Hasil kali dua transformasi dapat didefinisikan sebagai berikut:
Definisi : Andaikan F dan G dua transformasi, dengan F = V.V
G = V.V
Maka produk atau komposisi dari F dan G yang ditulis sebagai G o F didefinisikan sebagai :
( G o F ) (P) = G [ F (P) ] . V P →V
Defenisi di atas tidak perlu dijelaskan sesuai aturan sementara itu urutannya akan dijelaskan pada teorema-teorema berikut.
Teorema(T2) :
Jika F : V V dan G : V V masing – masing suatu transformasi, maka hasil kali H = G 0 F : V V adalah juga suatu transformasi Buktikan :
Untuk ini harus di buktikan dua hal yaitu:
1) H subjektif 2) H injektif
1) Oleh karena F transformasi maka daerah nilai F adalah seluruh bidang V , dan daerah asal G juga seluruh bidang V sebab G transformasi juga. Ambil 𝑦𝑦 ∈ 𝑉𝑉
apakah ada x sehingga H (x ) = y ? Karena G transformasi maka untuk setiap 𝑦𝑦 ∈ 𝑉𝑉 , ada z ∈ 𝑉𝑉 sehingga y = G (z) ,karena F suatu transformasi maka pada z ini ada x∈V
sehingga z = F (X) .
Maka y = [Z (x ) ] atau y = G [ F (X)] atau y = ( G o F ) (X) Jadi y = H (x ).
sedemikian sehingga f (a) = b → b = f (a) y∈ b, x sedemikian sehingga f (x)=y → y= f (x) Ada bilangan Z= H (x)
Ambil Z ∈ V , maka ada y ∈ V sedemikian sehingga Z = g(y), karena ada y ∈ V maka terdapat X ∈ V sedemikian sehingga Y=f(x)
2) Untuk membuktikan bahwa H injektif ,harus kita perlihatkan bahwa kalau P=Q maka H (P) = H(Q). Andaikan H(P) = H (Q) ,maka G[F(P)] = G[F(Q)]. Oleh karena G injektif maka F(P) = F(G). Karena F injektif maka pula P = Q ini bertentangan dengan pengandaian bahwa P=Q. Jadi pemisalan bahwa H(P) = H(Q) tidak benar .Sehingga haruslah H (P)= H(Q).
Karena g injektif maka f(p) = f(q)
P q
F(p) F(q)
g{f(p)}
g{f(q)}
C. SOAL DAN PEMBAHASAN Contoh soal 1 :
Andaikan G sebuah garis dan T sebuah transformasi
F : V.V yang didefinisikan sbagai berikut X(g) maka T (X) = X JIKA x (g) maka T ( X ) adalah titik tengah ruas garis dari x ke g yang tegak lurus
Jelas T suatu transformasi (buktikan). Apakah T suatu transformasi
? Ambil kemudian transformasikan kedua. Misalkan sebagai berikut : Ambil sebuah garis h, g dan x. M adalah reflexi dari garis h jadi hasilkali Mh[T(x)] = Y adalah suatu tranformasi pula sehingga Y = (Mh o T ) (X ). Apakah hasil kali ini merupakan isometri selidiki pada contoh di atas kebetulan Mh o T = T o Mh untuk membuktikanlah pada gambar garis g sebagai sumbu x suatu sistim koordinat ortogonal dan garis h sebagai sumbu Y .Titik potong h dan g kita ambil sebagai titik asal.
Andaikan x = ( x, y ) maka T (x) = ( x,½ y) dan Mh [T ( x) ]= (- x,½ y) Oleh karena Mh [T ( x) ]= T[Mh (X) maka Mh o T ( x )= T o Mh akan tetapi sifat komutatif tersebut tidak selalu berlaku .untuk memperlihatkan ini ambil lagi garis g dan garis h yang tidak tegak lurus pada g lihat gambar:
Tampak bahwa Mh[T ( x) ] T[Mh (X)].
Jadi MhoT(x)= ToMh . Dari contoh di atas dapat dikatakan bahwa apabila S dan T transformasi maka S o T = T o S Buktikanlah bahwa memang Mh [T ( x) ] T[Mh (X)] pada gambar di samping.
Hasil kali transformasi yang telah di bahas di atas tidak hanya terbatas pada dua transformasi andaikan T1, T2, transformasi – transformasi. Kita dapat menyusun terlebih dahulu hasil kali T1 o T2 kemudian dikalikan dengan T3 untuk hasil kali transformasi kita tulis 2 (T1 , T2
Jadi andaikan :
P’= T1 , (P).P’= T2 (P’ ).P’= T3 (P’).P (T3 (T2 . T1 ) (P) = T3 (T2 . T1 (P)))
= T3 (T2 (P’ ) )
= (T3 (P’) = P1..
Kita dapat mengalihkan sebagai berikut : (T3 (T2 .) (P)= (T 3 . T2 ) (T1 (P) )
= (T3 . T2 ) (P)
= T3 (T2 (P)
= T3 (P’ ) = P
Jadi hasil kali transformasi bersifat asosiatif kita dapat juga mengatakan bahwa
= T3 (T2 . T1 ) = (T3 . T2 ). T1
Contoh Soal 2
Tunjukkanlah apakah fungsi tersebut transformasi ! 1. F(x,y) = (𝑥𝑥 + 5, 𝑦𝑦 − 3)
Jawab:
𝑥𝑥′= 𝑥𝑥 + 5 𝑦𝑦′ = 𝑦𝑦 − 3 𝑥𝑥 = 𝑥𝑥′+ 5 𝑦𝑦 = 𝑦𝑦′− 3
𝑔𝑔: 𝑎𝑎𝑥𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐 = 0 𝑎𝑎(𝑥𝑥′+ 5) + 𝑏𝑏(𝑦𝑦′− 3) + 𝑐𝑐 = 0
𝑎𝑎𝑥𝑥′+ 5𝑎𝑎 + 𝑏𝑏𝑦𝑦′− 3𝑏𝑏 + 𝑐𝑐 = 0
𝑔𝑔′: 𝑎𝑎𝑥𝑥′+ 𝑏𝑏𝑦𝑦′+ 5𝑎𝑎 − 3𝑏𝑏 + 𝑐𝑐 = 0 →persamaan garis Karena 𝑔𝑔′= 0 adalah garis maka F(x,y) bersifat kolineasi.
*F(x,y) = (𝑥𝑥 + 5, 𝑦𝑦 − 3)
Jarak 𝐴𝐴(𝑥𝑥1, 𝑦𝑦1) ke 𝐵𝐵(𝑥𝑥1, 𝑦𝑦1) = jarak 𝐴𝐴(𝑥𝑥1′, 𝑦𝑦1′) ke 𝐵𝐵(𝑥𝑥2′, 𝑦𝑦2′) Adt: �(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2 𝐹𝐹(𝑥𝑥1, 𝑦𝑦1) = (𝑥𝑥1+ 5 𝑦𝑦1− 3)
𝐹𝐹(𝑥𝑥2, 𝑦𝑦2) = (𝑥𝑥2+ 5 𝑦𝑦2− 3)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
=�((𝑥𝑥2+ 5) − 𝑥𝑥1 + 5))2+ ((𝑦𝑦2− 3) − (𝑦𝑦2− 3))2
= �(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 →isometri Jadi, F(x,y) = (𝑥𝑥 + 5, 𝑦𝑦 − 3) adalah transformasi.
2. F(x,y) = (2𝑥𝑥 + 3𝑦𝑦, 𝑦𝑦 + 6) Jawab:
𝑥𝑥′= 2𝑥𝑥 + 3𝑦𝑦 𝑦𝑦′ = 𝑦𝑦 + 6
2𝑥𝑥 = 𝑥𝑥′+ 3𝑦𝑦 𝑦𝑦 = 𝑦𝑦′+ 6 𝑥𝑥 = 𝑥𝑥′+ 3𝑦𝑦
2 𝑥𝑥 = 𝑥𝑥′+ 3(𝑦𝑦′+ 6)
2 𝑥𝑥 =𝑥𝑥′+ 3𝑦𝑦′+ 18 g: 𝑎𝑎𝑥𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐 = 0 2
𝑎𝑎 �𝑥𝑥′+3𝑦𝑦2′+18� + 𝑏𝑏(𝑦𝑦′+ 6) + 𝑐𝑐 = 0
𝑎𝑎𝑥𝑥′+3𝑎𝑎𝑦𝑦′+18
2 + 𝑏𝑏𝑦𝑦′+ 6𝑏𝑏 + 𝑐𝑐 = 0 → 𝑥𝑥2 𝑎𝑎𝑥𝑥′+ 3𝑎𝑎𝑦𝑦′+ 18𝑎𝑎 + 2𝑏𝑏𝑦𝑦′+ 12𝑏𝑏 + 2𝑐𝑐 = 0 𝑎𝑎𝑥𝑥′+ 3𝑎𝑎𝑦𝑦′+ 2𝑏𝑏𝑦𝑦′+ 18𝑎𝑎 + 12𝑏𝑏 + 2𝑐𝑐 = 0
𝑎𝑎𝑥𝑥′+ 5(𝑎𝑎 + 𝑏𝑏)𝑦𝑦′+ 18𝑎𝑎 + 12𝑏𝑏 + 2𝑐𝑐 = 0 → pers. garis Karena 𝑔𝑔′= 𝑔𝑔 adalah garis maka 𝐹𝐹(𝑥𝑥, 𝑦𝑦) bersifat kolineasi
* 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (2𝑥𝑥 + 3𝑦𝑦, 𝑦𝑦 + 6)
Jarak 𝐴𝐴(𝑥𝑥1, 𝑦𝑦1) ke 𝐵𝐵(𝑥𝑥1, 𝑦𝑦1) = jarak 𝐴𝐴(𝑥𝑥1′, 𝑦𝑦1′) ke 𝐵𝐵(𝑥𝑥2′, 𝑦𝑦2′)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2 𝐹𝐹(𝑥𝑥1, 𝑦𝑦1) = (2𝑥𝑥1+ 3𝑦𝑦1, 𝑦𝑦1+ 6)
𝐹𝐹(𝑥𝑥2, 𝑦𝑦2) = (2𝑥𝑥2+ 3𝑦𝑦2, 𝑦𝑦2+ 6)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �{(2𝑥𝑥2+ 3𝑦𝑦2) − (2𝑥𝑥1+ 3𝑦𝑦1)}2+ {(𝑦𝑦2+ 6) − (𝑦𝑦1+ 6)}2
= �{2(𝑥𝑥2− 𝑥𝑥1) + 3(𝑦𝑦2− 𝑦𝑦1)}2+ (𝑦𝑦2− 𝑦𝑦1)2
= �4(𝑥𝑥2− 𝑥𝑥1)2+ 9(𝑦𝑦2− 𝑦𝑦1)2+ (𝑦𝑦2− 𝑦𝑦1)2
= �4(𝑥𝑥2− 𝑥𝑥1)2+ 10(𝑦𝑦2− 𝑦𝑦1)2 → bukan isometri Jadi, 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (2𝑥𝑥 + 3𝑦𝑦, 𝑦𝑦 + 6) adalah bukan transformasi.
3. 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (−𝑥𝑥, 𝑦𝑦2) Jawab:
𝑥𝑥′= −𝑥𝑥 𝑦𝑦′ = 𝑦𝑦2 𝑥𝑥 = −𝑥𝑥′ 𝑦𝑦 = �𝑦𝑦′
g: 𝑎𝑎𝑥𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐 = 0
𝑎𝑎(−𝑥𝑥) + 𝑏𝑏 ��𝑦𝑦′� + 𝑐𝑐 = 0
g: −𝑎𝑎𝑥𝑥 + 𝑏𝑏�𝑦𝑦′+ 𝑐𝑐 = 0 → persamaan garis
karena 𝑔𝑔 = 𝑔𝑔′ adalah garis maka 𝐹𝐹(𝑥𝑥, 𝑦𝑦) bersifat kolineasi
* 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (−𝑥𝑥, 𝑦𝑦2)
Jarak 𝐴𝐴(𝑥𝑥1, 𝑦𝑦1) ke 𝐵𝐵(𝑥𝑥1, 𝑦𝑦1) = jarak 𝐴𝐴(𝑥𝑥1′, 𝑦𝑦1′) ke 𝐵𝐵(𝑥𝑥2′, 𝑦𝑦2′)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2 𝐹𝐹(𝑥𝑥1, 𝑦𝑦1) = (−𝑥𝑥1, 𝑦𝑦12)
𝐹𝐹(𝑥𝑥2, 𝑦𝑦2) = (−𝑥𝑥2, 𝑦𝑦22)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �(−𝑥𝑥2+ 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2
= �−(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 → bukan isometri Jadi, 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (−𝑥𝑥, 𝑦𝑦2) adalah bukan transformasi
4. 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (3𝑥𝑥 − 2𝑦𝑦, 𝑦𝑦 − 7) 𝑥𝑥′= 3𝑥𝑥 − 2𝑦𝑦 𝑦𝑦′ = 𝑦𝑦 − 7
3𝑥𝑥 = 𝑥𝑥′−2𝑦𝑦3 𝑦𝑦 = 𝑦𝑦′− 7 𝑥𝑥 =𝑥𝑥′− 2(𝑦𝑦′− 7)
3 𝑥𝑥 =𝑥𝑥′− 2𝑦𝑦′+ 14 𝑔𝑔′: 𝑎𝑎𝑥𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐 = 0 3
𝑎𝑎 �𝑥𝑥′−2𝑦𝑦3′+14� + 𝑏𝑏(𝑦𝑦′− 7) + 𝑐𝑐 = 0
𝑎𝑎′−2𝑎𝑎𝑦𝑦′+14𝑎𝑎
3 + 𝑏𝑏𝑦𝑦′− 7𝑏𝑏 + 𝑐𝑐 = 0→ 𝑥𝑥3 𝑎𝑎𝑥𝑥′− 2𝑎𝑎𝑦𝑦′+ 14𝑎𝑎 + 3𝑏𝑏𝑦𝑦′− 21𝑏𝑏 + 3𝑐𝑐 = 0 𝑎𝑎𝑥𝑥′− 2𝑎𝑎𝑦𝑦′+ 3𝑏𝑏𝑦𝑦′+ 14𝑎𝑎 − 21𝑏𝑏 + 3𝑐𝑐 = 0
𝑎𝑎𝑥𝑥′+ (𝑎𝑎 + 𝑏𝑏)𝑦𝑦′+ 14𝑎𝑎 − 21𝑏𝑏 + 3𝑐𝑐 = 0 → pers. Garis Karena 𝑔𝑔 = 𝑔𝑔′ adalah garis maka 𝐹𝐹(𝑥𝑥, 𝑦𝑦) bersifat kolineasi
* 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (3𝑥𝑥 − 2𝑦𝑦, 𝑦𝑦 − 7)
Jarak 𝐴𝐴(𝑥𝑥1, 𝑦𝑦1) ke 𝐵𝐵(𝑥𝑥1, 𝑦𝑦1) = jarak 𝐴𝐴(𝑥𝑥1′, 𝑦𝑦1′) ke 𝐵𝐵(𝑥𝑥2′, 𝑦𝑦2′)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2 𝐹𝐹(𝑥𝑥1, 𝑦𝑦1) = (3𝑥𝑥1− 2𝑦𝑦1, 𝑦𝑦1− 7) 𝐹𝐹(𝑥𝑥2, 𝑦𝑦2) = (3𝑥𝑥2 − 2𝑦𝑦2, 𝑦𝑦2− 7)
�(𝑥𝑥2− 𝑥𝑥1)2+ (𝑦𝑦2− 𝑦𝑦1)2 = �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �(𝑥𝑥2′ − 𝑥𝑥1′)2+ (𝑦𝑦2′ − 𝑦𝑦1′)2
= �{(3𝑥𝑥2− 𝑦𝑦2) − (3𝑥𝑥1− 2𝑦𝑦1)}2+ {(𝑦𝑦2− 7) − (𝑦𝑦1− 7)}2
= �{3(𝑥𝑥2− 𝑥𝑥1) − 2(𝑦𝑦2− 𝑦𝑦1)}2+ (𝑦𝑦2− 𝑦𝑦1)2
= �9(𝑥𝑥2− 𝑥𝑥1)2− 4(𝑦𝑦2− 𝑦𝑦1)2+ (𝑦𝑦2− 𝑦𝑦1)2
= �9(𝑥𝑥2− 𝑥𝑥1)2− 3(𝑦𝑦2 − 𝑦𝑦1)2→ bukan isometri Jadi, 𝐹𝐹(𝑥𝑥, 𝑦𝑦) = (3𝑥𝑥 − 2𝑦𝑦, 𝑦𝑦 − 7) adalah bukan isometri
5. Buktikan lah 𝑇𝑇(𝑥𝑥, 𝑦𝑦) = (2𝑥𝑥 + 𝑦𝑦, 𝑥𝑥 − 2𝑦𝑦) merupakan suatu kolineasi.
Jawab:
𝑥𝑥′= 2𝑥𝑥 + 𝑦𝑦 𝑦𝑦′ = 𝑥𝑥 − 2𝑦𝑦 2𝑥𝑥 = 𝑥𝑥′+ 𝑦𝑦 2𝑦𝑦 = 𝑦𝑦′− 𝑥𝑥 𝑥𝑥 =𝑥𝑥′2+𝑦𝑦 𝑦𝑦 =𝑦𝑦′−𝑥𝑥2 𝑔𝑔: 𝑎𝑎𝑥𝑥 + 𝑏𝑏𝑦𝑦 + 𝑐𝑐 = 0
𝑎𝑎 �𝑥𝑥′+𝑦𝑦2 � + 𝑏𝑏 �𝑦𝑦′2−𝑥𝑥� + 𝑐𝑐 = 0
𝑎𝑎𝑥𝑥′+𝑎𝑎𝑦𝑦
2 +𝑏𝑏𝑦𝑦′2−𝑏𝑏𝑥𝑥 + 𝑐𝑐 = 0 → × 2
𝑎𝑎𝑥𝑥′+ 𝑎𝑎𝑦𝑦 + 𝑏𝑏𝑦𝑦′− 𝑏𝑏𝑥𝑥 + 2𝑐𝑐 = 0
𝑔𝑔′: 𝑎𝑎𝑥𝑥′+ 𝑏𝑏𝑦𝑦′+ 𝑎𝑎𝑦𝑦 − 𝑏𝑏𝑥𝑥 + 2𝑐𝑐 = 0 → persamaan garis Jadi, karena 𝑔𝑔 = 𝑔𝑔′ adalah garis maka 𝑇𝑇(𝑥𝑥, 𝑦𝑦) bersifat kolineasi.
BAB 2 TRANSLASI(GESERAN)/S
Penggunaan aplikasi geogebra untuk memvisualisasikan Translasi dapat dilakukan dengan langkah sebagai berikut :
a. Buka aplikasi geogebra dengan tampilan layar aljabar dan geometri 2 dimensi
b. Pilih menu Point untuk membuat bangun geometri berupa titik A.
c. Pilih menu untuk membuat vektor
d. Pilih menu geometri transformasi berupa Translate by Vector, kemudian sorot titik (bangun geometri)
e. Diperoleh bayangan hasil transformasi
Setelah mengetahui penggunaan geogebra untuk membantau me-relistik- kan pemahaman, berikut akan kita bahas materi tentang translasi/geseran tersebut.
A. Pengertian Translasi (S)
Secara umum Translasi/geseran ialah perpindahan atau pergeseran titik atau bangun geometri dalam jarak dan arah yang sama. Jarak dan arah yang sama itu ditentukan oleh suatu ruas garis yang berarah. Secara teori translasi/geseran Defenisikan: Suatu padanan S dinamakan suatu geseran apabila ada ruas garis berarah AB sehingga setiap titik P pada bidang menjadi P’ dengan SAB(P) = P’ dan PP’ = AB.
Suatu titik atau sistem mengalami pergeseran namun tidak merubah bentuk, karena setiap titik penyusun sistem mengalami pergeseran yang sama.
Contoh: Sebuah titik P(x,y) ditranslasikan sejauh a satuan sepanjang sumbu x dan y satuan sepanjang sumbu y, diperoleh peta titik P’(x’,y’).
Gambar S.1
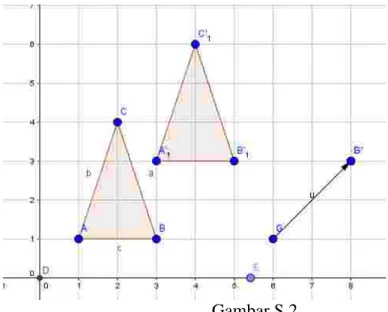
Berdasarkan defenisi tersebut translasi/geseran memiliki ciri-ciri yaitu terdapat vektor geser, benda yang akan digeser dan hasil geseran. Bayangan hasil geseran yang berupa bangun geometri akan mengalami perpindahan dari suatu sumber asal sesuai jarak dan arah vektor yang menggesernya. Didalam operasi translasi, bangun geometri bayangan kongruen terhadap bangun geometri semula, misalkan segitiga ABC yang digeser oleh vektor u akan menghasilkan segitiga A’B’C’ yang sama dan sebangun seperti berikut:
Gambar S.2 Translasi dinyatakan dalam bentuk pasangan bilangan
Translasi T dapat dinyatakan dalam bentuk pasangan terurut dua bilangan
�𝑎𝑎𝑏𝑏� dan ditulis sebagai: 𝑇𝑇 = �𝑎𝑎 Ket : 𝑏𝑏�
a. a dan b masing − masing disebut sebagai komponen translasi b. a menyatakan komponen translasi dalam arah sumbu x
1) jika a > 0,
maka arah pergeserannya adalah a satuan ke kanan 2) jika a < 0,
maka arah pergeserannya adalah |a| satuan ke kiri c. b menyatakan komponen translasi dalam arah sumbu y
1) jika b > 0,
maka arah pergeserannya adalah b satuan ke atas 2) jika b < 0,
maka arah pergeserannya adalah |b| satuan ke bawah.
Berdasarkan gambar S2 di atas tampak bahwa bangun geometri segitiga ABC ditranslasikan sehingga diperoleh bangun bayangan segitiga A’B’C’.
Dalam operasi translasi itu terjadi titik berikut:
1) A → A’, ditentukan oleh ruas garis berarah AA’
2) B → B’, ditentukan oleh ruas garis berarah BB’
3) C → C’, ditentukan oleh ruas garis berarah CC’
Dengan AA’ = BB’ = CC’
Perhatikan bahwa dalam operasi translasi ini, segitiga A’B’C’ kongruen dengan segitiga ABC. Setiap ruas garis berarah menentukan sebuah translasi.
Kalau AB suatu garis berarah maka dengan lambang SAB kita maksud sebuah geseran yang sesuai dengan AB.
B. Menentukan koordinat titik bayangan oleh translasi tertentu (Rumus translasi/geseran)
Jika titik 𝑃𝑃(𝑥𝑥, 𝑦𝑦) ini ditranslasikan oleh 𝑇𝑇 = �𝑎𝑎𝑏𝑏�, maka diperoleh bayangan titik 𝑃𝑃′(𝑥𝑥′, 𝑦𝑦′) dan berlaku hubungan:
𝑃𝑃(𝑥𝑥, 𝑦𝑦) 𝑜𝑜𝑜𝑜𝑜𝑜ℎ 𝑇𝑇 = �𝑎𝑎𝑏𝑏�,𝑃𝑃′ = (𝑥𝑥 + 𝑎𝑎, 𝑦𝑦 + 𝑏𝑏) Secara aljabar posisi bayangan hasil translasi dapat kita tentukan dengan terlebih dahulu menentukan posisinya pada koordinat kartesius sebagai berikut:
𝑥𝑥′ = 𝑥𝑥 + 𝑎𝑎 𝑦𝑦′ = 𝑦𝑦 + 𝑏𝑏
Dari ga mbar di atas Vektor 𝐴𝐴𝐵𝐵������⃗ =
−
− YA YB
XA XB
a = XB – XA
b = YB – YA 𝐴𝐴𝐵𝐵
������⃗ =
b
a , jadi PP′�������⃗ =
−
− y y
x x
' ' Misalkan titik P(x, y)
SAB(P) = P’(x’, y’), dari defenisi 𝑃𝑃𝑃𝑃′������⃗ = 𝐴𝐴𝐵𝐵�����⃗
−
− y y
x x
'
' =
b a
⇔
' ' y
x =
y
x +
b a
⇔
' ' y
x =
+ + b y
a
x
⇔ ∀ P(x, y) di SAB =
b
a maka P’(x’, y’),
' ' y
x =
+ + b y
a x
Sehingga
b
a disebut vektor geseran, dengan rumus di atas akan
mudah membuktikan bahwa geseran tertutup terhadap komposisi transformasi.
C. Dalil-dalil tentang translasi/Geseran Dalil S.1
SAB= SCD bila dan hanya bila AB = CD Bukti :
Misalkan titik P∈V SAB (P) =P’
SCD (P)=P”
(i) Adit : 𝑨𝑨𝑨𝑨������⃗ = 𝑪𝑪𝑪𝑪������⃗, (Bukti ruas kanan)
⇒
SAB (P) = P’ , 𝑃𝑃𝑃𝑃′������⃗ = 𝑨𝑨𝑨𝑨������⃗SCD (P) = P” , 𝑃𝑃𝑃𝑃"�������⃗ = 𝑪𝑪𝑪𝑪������⃗
SAB (P) = SCD (P) Artinya :
𝑃𝑃𝑃𝑃′
������⃗ = 𝑨𝑨𝑨𝑨������⃗ = 𝑃𝑃𝑃𝑃"�������⃗ = 𝑪𝑪𝑪𝑪������⃗
𝑨𝑨𝑨𝑨������⃗ = 𝑪𝑪𝑪𝑪������⃗
(ii) Adit: SAB=SCD , (Bukti ruas kiri)
⇐
𝑨𝑨𝑨𝑨������⃗ = 𝑪𝑪𝑪𝑪������⃗𝑨𝑨𝑨𝑨������⃗ = 𝑃𝑃𝑃𝑃′������⃗, SAB (P) =P’
𝑪𝑪𝑪𝑪������⃗=𝑃𝑃𝑃𝑃"�������⃗, SCD (P) = P”
Karena AB = CD Maka PP’ =PP”, berarti P’ =P”
SAB (P) = P’ = P” = SCD (P) Diperoleh SAB = SCD
Terbukti SAB = SCD
Berdasarkan (i) dan (ii) maka terbukti SAB= SCD bila dan hanya bila AB = CD Dalil S.2
Bila A, B, C tiga titik tak segaris maka SAB =SCD bila dan hanya bila CABD merupakan jejaran genjang
Bukti:
(i) Adit CABD adalah jejargenjang (Bukti ruas kanan)
⇒
A, B dan C tidak segaris maka:Ada titik D∈V ∃ 𝑨𝑨𝑨𝑨������⃗//𝑪𝑪𝑪𝑪������⃗
SAB = SCD dari dari dalil S.1, diperoleh 𝑨𝑨𝑨𝑨������⃗ = 𝑪𝑪𝑪𝑪������⃗
karena 𝑨𝑨𝑨𝑨������⃗ = 𝑪𝑪𝑪𝑪������⃗ di mana 𝑨𝑨𝑨𝑨������⃗//𝑪𝑪𝑪𝑪������⃗ berarti CABD jejargenjang
(ii) Adit:SAB=SCD (Bukti ruas kiri)
⇐
CABD jejargenjang maka diperoleh 𝑨𝑨𝑨𝑨�������⃗ = 𝑪𝑪𝑪𝑪������⃗ dan 𝑨𝑨𝑨𝑨������⃗//𝑪𝑪𝑪𝑪������⃗Berdasar dalil S.1 𝑨𝑨𝑨𝑨������⃗ = 𝑪𝑪𝑪𝑪������⃗ SAB=SCD
∴ Dari bukti ruas kiri dan ruas kanan maka terbukti
Dalil S.3
Geseran adalah suatu isometri A B
P P’ P P’ Q Q’
Q Q’
Bukti.
Bahwa S adalah transformasi adalah cukup jelas. Misalkan SAB
memetakan P ke P’ dan Q ke Q’, berarti PP’ = QQ’ = AB.
Akan dibuktikan P’Q’ = PQ Kejadian
a) Bila P,P’, Q tidak segaris maka (dalil S.2) QPP’Q’ jejaran genjang, sehingga 𝑷𝑷𝑷𝑷������⃗ =𝑷𝑷′𝑷𝑷′���������⃗ jadi P’Q’ =PQ
b) Bila P ‘P’ , Q segaris maka Q’ akan terletak pada garis yang sama, dengan aljabar vector,
𝑷𝑷𝑷𝑷�������⃗ = 𝑷𝑷𝑷𝑷′′ �������⃗ +𝑷𝑷 𝑷𝑷��������⃗ ′ 𝑷𝑷��������⃗ =𝑷𝑷 𝑷𝑷′𝑷𝑷′ ��������⃗ − 𝑷𝑷𝑷𝑷′′ �������⃗
=𝑷𝑷𝑷𝑷������⃗ + 𝑷𝑷𝑷𝑷′��������⃗ − 𝑷𝑷 𝑷𝑷′��������⃗ (𝑷𝑷𝑷𝑷′��������⃗=𝑷𝑷𝑷𝑷′�������⃗) =𝑷𝑷𝑷𝑷������⃗ +𝑷𝑷𝑷𝑷′�������⃗ − 𝑷𝑷𝑷𝑷′�������⃗
=𝑷𝑷𝑷𝑷������⃗
∴ Berarti SAB Suatu isometri
∴ Karena setiap isometri adalah kolineasi maka dengan bukti di atas dapat disimpulkan bahwa geseran suatu kolineasi.
Dalil S.4
Geseran mempertahankan arah garis Bukti:
Misalkan : P ,Q 𝜖𝜖 V
SAB (P) = P’ adalah AB = PP’= QQ’
Karena PP’= QQ’ 𝑷𝑷𝑷𝑷′�������⃗//𝑷𝑷𝑷𝑷�������⃗ ′ SAB(Q) = Q’ AB = QQ’
Andaikan P ,P’,Q Tidak segaris SAB (P) = P’ 𝑷𝑷𝑷𝑷′�������⃗ = 𝑨𝑨𝑨𝑨������⃗
SAB(Q) = Q’ 𝑷𝑷𝑷𝑷′��������⃗ = 𝑨𝑨𝑨𝑨������⃗
𝑷𝑷𝑷𝑷′�������⃗ = 𝑨𝑨𝑨𝑨������⃗ = 𝑷𝑷𝑷𝑷�������⃗ ′
• Karena P.P’ dan Q tidak segaris maka menurut dalil S.2 P P’ Q Q’
adalah jajargenjang berarti 𝑷𝑷𝑷𝑷′�������⃗ //𝑷𝑷𝑷𝑷′��������⃗
SAB Mempertahankan arah garis Hasil kali dua geseran
Dalil S.5
Hasilkali dua geseran SAB dan SCD adalah geseran SPQ dengan 𝑷𝑷𝑷𝑷������⃗ = 𝑨𝑨𝑨𝑨������⃗ + 𝑪𝑪𝑪𝑪������⃗
Bukti:
a) Geometri
Ambil vektor 𝑨𝑨𝑨𝑨������⃗, 𝑪𝑪𝑪𝑪������⃗ dan 𝑷𝑷𝑷𝑷������⃗ , V dengan 𝑷𝑷𝑷𝑷������⃗ = 𝑨𝑨𝑨𝑨������⃗ + 𝑪𝑪𝑪𝑪������⃗ pilih T ∈ V
Maka :
SAB (T) = T’ 𝑻𝑻𝑻𝑻′������⃗ = 𝑨𝑨𝑨𝑨������⃗
SCD (T’) = T” 𝑻𝑻′𝑻𝑻"��������⃗ = 𝑪𝑪𝑪𝑪������⃗
SCD SAB (T) = SCD (T’) = T”
SCD SAB (T)
= SPQ (T) = T”
Di mana:
𝑇𝑇𝑇𝑇"
�������⃗ = 𝑇𝑇𝑇𝑇′������⃗ + 𝑇𝑇′𝑇𝑇"��������⃗
=𝐴𝐴𝐵𝐵�����⃗ + 𝐶𝐶𝐶𝐶 ������⃗ = 𝑃𝑃𝑃𝑃�����⃗
b) Secara analitik
Misalkan 𝑨𝑨𝑨𝑨������⃗ =�𝑎𝑎𝑏𝑏�, 𝑪𝑪𝑪𝑪������⃗ = �𝑐𝑐𝑑𝑑�, P(x,y) SAB (P) = P’(x’,y’), �𝑥𝑥′𝑦𝑦′� =
+ + b y
a x
SCD (P”) = P”(x”,y”) , �𝑥𝑥"𝑦𝑦"�=�𝑥𝑥′ + 𝑐𝑐
𝑦𝑦′ + 𝑑𝑑�
Maka:
SCD SAB (P) = SCD SAB (P)
= SCD (P’)
=P”
Dimana P”(x”,y”) �𝑥𝑥"𝑦𝑦"�= �𝑥𝑥′ + 𝑐𝑐
𝑦𝑦′ + 𝑑𝑑�
= �𝑥𝑥 + 𝑎𝑎 + 𝑐𝑐 𝑦𝑦 + 𝑏𝑏 + 𝑑𝑑�
= �𝑥𝑥 + (𝑎𝑎 + 𝑐𝑐)𝑦𝑦 + (𝑏𝑏 + 𝑑𝑑)�
= �𝑥𝑥
𝑦𝑦� + �𝑎𝑎 + 𝑐𝑐 𝑏𝑏 + 𝑑𝑑�
∴ Adalah vektor geseran SCD SAB (P)= SPQ = �𝑝𝑝
𝑞𝑞� = �𝑎𝑎 + 𝑐𝑐
𝑏𝑏 + 𝑑𝑑� bersifat komutatif.
Dalil S.6
Terhadap SAB≠ I tidak terdapat titik tetap. Semua garis yang sejajar AB akan menjadi garis tetap.
Bukti: (Secara analitis) (i) Mencari titik tetap:
Ambil A ≠ B dan AB = �𝑝𝑝 𝑞𝑞� ≠ �0
0�
Maka rumus SAB dapat ditulis �𝑥𝑥′ 𝑦𝑦′� = �𝑥𝑥
𝑦𝑦� + �𝑝𝑝 𝑞𝑞�
Untuk mencari titik tetap haruslah : 𝑥𝑥 + 𝑝𝑝 = 𝑥𝑥, 𝑦𝑦 + 𝑞𝑞 = 𝑦𝑦 diperoleh 𝑝𝑝 = 𝑞𝑞 = 0
Hal ini bertentangan dengan ketentuan, jadi tidak ada titik tetap.
(ii) Mencari garis tetap
Misalkan h’ adalah pemetaan dari h, di mana persamaan ℎ: 𝑎𝑎𝑥𝑥′+ 𝑏𝑏𝑦𝑦′+ 𝑐𝑐 = 0
ℎ: 𝑎𝑎𝑥𝑥 + 𝑏𝑏𝑦𝑦 + 𝑎𝑎𝑝𝑝 + 𝑏𝑏𝑞𝑞 + 𝑐𝑐 = 0
kedua persamaan harus identik, yang berarti 𝑎𝑎
𝑎𝑎 =𝑏𝑏𝑏𝑏 = 𝑎𝑎𝑝𝑝 +𝑏𝑏𝑞𝑞 +𝑐𝑐 𝑐𝑐
di mana 1 = 𝑎𝑎𝑝𝑝 +𝑏𝑏𝑞𝑞+𝑐𝑐 𝑐𝑐
𝑐𝑐 = 𝑎𝑎𝑝𝑝 + 𝑏𝑏𝑞𝑞 + 𝑐𝑐 𝑐𝑐 − 𝑐𝑐 = 𝑎𝑎𝑝𝑝 + 𝑏𝑏𝑞𝑞
0 = 𝑎𝑎𝑝𝑝 + 𝑏𝑏𝑞𝑞 berarti 𝑎𝑎𝑝𝑝 = −𝑏𝑏𝑞𝑞 atau Arah vektor geser adalah 𝑞𝑞
𝑝𝑝 = −𝑎𝑎𝑏𝑏 = 𝑔𝑔𝑔𝑔𝑎𝑎𝑑𝑑𝑔𝑔𝑜𝑜𝑔𝑔 ℎ′(= 𝑔𝑔𝑔𝑔𝑎𝑎𝑑𝑑𝑔𝑔𝑜𝑜𝑔𝑔 ℎ) Terbukti garis sejajar AB akan menjadi garis tetap.
Dalil S.7
Himpunan geseran menyusun suatu grup abelian.
Bukti:
Misalkan himpunan £ adalah himpunan dari geseran-geseran dan T(x,y) adalah titik sebarang.
Akan dibuktikan bahwa £ adalah grup abelian.
Perhatikan:
Suatu himpunan dikatakan sebagai grup jika:
a) tertutup terhadap operasi biner ∘ b) bersifat asosiatif c) memuat identitas d) memiliki invers dan £ dikatakan grup abelian jika dan hanya jika £ grup dan bersifat komutatif, ∀ 𝑥𝑥, 𝑦𝑦 ∈ £ → x ∘ 𝑦𝑦 = 𝑦𝑦 ∘ 𝑥𝑥.
a. Akan ditunjukkan £ tertutup terhadap operasi ∘
Misalkan AB = (a,b), CD = (c,d), MN =(m,n) dan P = (x,y) Akan dicari SAB SCD (P) dan SAB SCD (P)
Perhatikan
SAB SCD (P) = 𝑆𝑆𝑨𝑨𝑨𝑨𝑆𝑆𝑪𝑪𝑪𝑪(𝑥𝑥, 𝑦𝑦)
= 𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥 + 𝑐𝑐, 𝑦𝑦 + 𝑑𝑑)
= [(𝑥𝑥 + 𝑐𝑐) + 𝑎𝑎, (𝑦𝑦 + 𝑑𝑑) + 𝑏𝑏]
= (𝑥𝑥 + 𝑎𝑎 + 𝑐𝑐, 𝑦𝑦 + 𝑏𝑏 + 𝑑𝑑) = 𝑃𝑃"
dan
SCD SAB (P) = 𝑆𝑆𝑪𝑪𝑪𝑪𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥, 𝑦𝑦)
= 𝑆𝑆𝑪𝑪𝑪𝑪(𝑥𝑥 + 𝑎𝑎, 𝑦𝑦 + 𝑏𝑏)
= [(𝑥𝑥 + 𝑎𝑎) + 𝑐𝑐, (𝑦𝑦 + 𝑏𝑏) + 𝑑𝑑]
= (𝑥𝑥 + 𝑎𝑎 + 𝑐𝑐, 𝑦𝑦 + 𝑏𝑏 + 𝑑𝑑) = 𝑃𝑃"
Misalkan 𝑥𝑥 + 𝑎𝑎 + 𝑐𝑐 = 𝑚𝑚 dan 𝑦𝑦 + 𝑏𝑏 + 𝑑𝑑 = 𝑔𝑔 sehingga P”(m,n) Dapat dilihat bahwa 𝑆𝑆𝑨𝑨𝑨𝑨𝑆𝑆𝑪𝑪𝑪𝑪(𝑥𝑥, 𝑦𝑦) = 𝑆𝑆𝑪𝑪𝑪𝑪𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥, 𝑦𝑦) = 𝑃𝑃"(𝑚𝑚, 𝑔𝑔) dan P” merupakan geseran lagi (dalil S.5) misalkan SMN.
∴ Hal ini menunjukkan bahwa geseran terbukti bersifat tertutup terhadap operasi biner dan bersifat komutatif.
b. Akan ditunjukkan £ bersifat assosiatif
∀ SCD, SAB, SPQ ∈£ maka (𝑆𝑆𝑨𝑨𝑨𝑨𝑆𝑆𝑪𝑪𝑪𝑪) 𝑆𝑆𝑷𝑷𝑷𝑷 = 𝑆𝑆𝑨𝑨𝑨𝑨(𝑆𝑆𝑪𝑪𝑪𝑪𝑆𝑆𝑷𝑷𝑷𝑷) ∴ £ bersifat asosiatif
c. Akan ditunjukkan £ memuat identitas
∀ 𝑆𝑆 ∈ £ ∃ I ∈ £ sehinga S I = S dan I S = S Misalkan SAB, I dan P(x,y)
𝑆𝑆𝑨𝑨𝑨𝑨𝐼𝐼(𝑥𝑥, 𝑦𝑦) = 𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥 + 0, 𝑦𝑦 + 0) = 𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥, 𝑦𝑦) = (𝑥𝑥 + 𝑎𝑎, 𝑦𝑦 + 𝑏𝑏) dan
𝐼𝐼𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥, 𝑦𝑦) = 𝐼𝐼(𝑥𝑥 + 𝑎𝑎, 𝑦𝑦 + 𝑏𝑏) = �(𝑥𝑥 + 𝑎𝑎) + 0, (𝑦𝑦 + 𝑏𝑏) + 0�
= (𝑥𝑥 + 𝑎𝑎, 𝑦𝑦 + 𝑏𝑏) = 𝑆𝑆𝑨𝑨𝑨𝑨
∴ £ memuat identitas
d. Akan ditunjukkan £ memiliki invers
∀ 𝑆𝑆 ∈ £ ∃ S−1 ∈ £ sehinga SS−1 = I dan S−1S = I Misalkan SAB, I dan P(x,y)
𝑆𝑆𝑨𝑨𝑨𝑨𝑆𝑆𝑨𝑨𝑨𝑨−1(𝑥𝑥, 𝑦𝑦) = 𝑆𝑆𝑨𝑨𝑨𝑨�𝑥𝑥 + (−𝑎𝑎), 𝑦𝑦 + (−𝑏𝑏)� = 𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥 − 𝑎𝑎, 𝑦𝑦 − 𝑏𝑏)
= �(𝑥𝑥 − 𝑎𝑎) + 𝑎𝑎, (𝑦𝑦 − 𝑏𝑏) + 𝑏𝑏� = (𝑥𝑥 − 𝑎𝑎 + 𝑎𝑎, 𝑦𝑦 − 𝑏𝑏 + 𝑏𝑏)
= (𝑥𝑥 + 0, 𝑦𝑦 + 0) = 𝐼𝐼 𝑆𝑆𝑨𝑨𝑨𝑨−1𝑆𝑆𝑨𝑨𝑨𝑨(𝑥𝑥, 𝑦𝑦) = 𝑆𝑆𝑨𝑨𝑨𝑨−1(𝑥𝑥 + 𝑎𝑎, 𝑦𝑦 + 𝑏𝑏)
= �(𝑥𝑥 + 𝑎𝑎) − 𝑎𝑎, (𝑦𝑦 + 𝑏𝑏) − 𝑏𝑏�
= (𝑥𝑥 + 0, 𝑦𝑦 + 0) = 𝐼𝐼
∴ Dari poin a, b, c dan d terbukti himpunan geseran menyusun suatu grup abelian.
D. SOAL-SOAL TENTANG TRANSLASI 1. Diketahui titik A,B,C yang taksegaris.
a. Lukislah𝑆𝑆𝑨𝑨𝑨𝑨(𝐴𝐴) dan 𝑆𝑆𝑨𝑨𝑨𝑨(𝐵𝐵) b. Lukislah𝑆𝑆𝑨𝑨𝑨𝑨(𝐶𝐶)
Jawaban :
Diketahui titik-titik A, B, dan C yang tak segaris
Penyelesaian:
a.
B = SAB(A) A’ = SAB(B) b.
C’ = SAB(C)
2. Diketahui titik A,B,C,D,P dan garis g seperti anda lihat pada gambar:
Lukislah:
a. 𝑆𝑆𝑪𝑪𝑪𝑪 𝑆𝑆𝑨𝑨𝑨𝑨 (𝑃𝑃)
b. Garis h sehingga 𝑆𝑆𝑨𝑨𝑨𝑨 𝑆𝑆𝑪𝑪𝑪𝑪 (𝑃𝑃) = g Penyelesaian:
a.
𝑺𝑺𝑨𝑨𝑨𝑨(𝑷𝑷) = 𝒑𝒑′ , Dimana 𝑃𝑃𝑃𝑃′����� = 𝐴𝐴𝐵𝐵����
𝑮𝑮𝑨𝑨𝑨𝑨(𝑷𝑷) = 𝒑𝒑′′ Dimana 𝑃𝑃′𝑃𝑃′′������ = 𝐶𝐶𝐶𝐶����
b. 𝑮𝑮𝑨𝑨𝑨𝑨(𝑷𝑷) = 𝒑𝒑′ Dimana 𝑃𝑃𝑃𝑃′����� = 𝐵𝐵𝐴𝐴����
𝑮𝑮𝑪𝑪𝑪𝑪(𝑷𝑷𝑷𝑷) = 𝒑𝒑′′ Dimana 𝑃𝑃′𝑃𝑃′′������ = 𝐶𝐶𝐶𝐶����
3. Tentukan bayangan dari titik P(-1, 1), titik R(2, -4), dan titik S(-3, -1) oleh translasi T= �23�
Penyelesaian:
Dengan menerapkan aturan translasi P(x, y) oleh T = �𝑎𝑎𝑏𝑏� P’(x + a, y + b), maka diperoleh:
Bayangan dari titik P(-1, 1)
P(-1, 1), T = �23� Q’(-1 + 2, 1 + 3) = Q’(1, 4) Bayangan dari titik R(2, -4)
R(2, -4), T = �23� R’(2 + 2, -4 + 3) = R’(4, -1) Bayangan dari titik S(-3, -1)
S(-3, -1), T = �23� S’(-3 + 2, -1 + 3) = S’(-1, 2) Jadi bayangan dari titik P(-1, 1), titik R(2, -4), dan titik S(-3, -1) oleh translasi T = �23� adalah titik P’(1, 4), titik R’(4, -1), dan titik S’(-1, 2).
4. Oleh suatu translasi, peta titik (1, -5) adalah (7, -8). Bayangan kurva y = x2 + 4x – 12 oleh translasi tersebut adalah…..
Diketahui P = (1,5) dan P’ = (7,-8) Parabola y = x2 + 4x – 12
Adt : y’ = ... ? Penyelesaian :
Sebelum menentukan persamaan y’ terlebih dahulu kita tentukan vektor geser, misalkan T = �𝑎𝑎𝑏𝑏�
(1, -5) oleh T �𝑎𝑎𝑏𝑏� (1 + ɑ, -5 + b) = (7, -8)
1 + ɑ = 7 ɑ = 6 -5 + b = -8 b = -3
Maka diperoleh vektor geser T = � 6−3�
Maka x’ = x + 6 y’ = y - 3
x’ – 6 = x y’ + 3 = y subsitusi ke persamaan
y = x2 + 4x – 12
y’ + 3 = (x’ – 6)2 + 4(x’ – 6) -12
y’ + 3 = (x’)2 – 12x’ + 36 + 4x’ – 24 – 12 y’ = (x’)2 – 8x’ – 3
jadi bayangan kurva yaitu y = x2 – 8x - 3
5. Diketahui ∆ CDE dengan koordinat C(0, 0), D(3, 0), E(3, 5). Tentukan koordinat bayangan ∆ C’D’E’ tersebut bila ditranslasi oleh T = �13�
Penyelesaian:
(0, 0) oleh T = �13� (0 + 1, 0 + 3) = O’(1, 3) (3, 0) oleh T = �13� (3 + 1, 0 + 3) = A’ (4, 3)
(3, 5) oleh T = �13� (3 + 1, 5 + 3) = B’ (4, 8)
6. Tentukan bayangan dari lingkaran (x – 2)2 + (y – 1)2 = 9 jika ditranslasikan oleh : T= �34�
Jawab :
Misalkan titik P(a,b) adalah titik pada lingkaran, sehingga persamaan dapat ditulis : (a – 2)2 + (b – 1)2 = 9.
Titik P ditranslasi dengan T= �34� diperoleh titik T’ sbb : T= �34� P(1,4) → P’(1 + 2,4 + 3)
Maka : a’ = a + 3 dan b’ = b + 3 a = a’ – 3 dan b = b’ – 3 Substitusi ke persamaan :
(a’ – 3– 2)2 + (b’ – 4– 1)2 = 9 (a’ – 5)2 + (b’ – 5)2 = 9
Jadi bayangan lingkaran : (x – 5)2 + (y – 5)2 = 9
SOAL LATIHAN
BAB 3 SETENGAH PUTARAN/H
Penggunaan aplikasi geogebra untuk memvisualisasikan setengah putaran dapat dilakukan dengan langkah sebagai berikut :
a. Buka aplikasi geogebra dengan tampilan layar aljabar dan geometri 2 dimensi
b. Pilih menu Point untuk membuat bangun geometri berupa titik A dan titik P sebagai pusat setengah putaran
c. Pilih menu geometri transformasi berupa Rotate around Point, kemudian sorot titik (bangun geometri) dan pusatnya
d. Diperoleh bayangan hasil transformasi dengan sudut setengah putaran sebesar 180 derajat berlawanan arah jarum jam.
Setelah mengetahui penggunaan geogebra untuk membantau me- relistik-kan pemahaman, berikut akan kita bahas materi tentang setengah putaran yang merupakan kasus khusus dari rotasi dimana sudut rotasinya 1800. Setengah putaran dibahas terlebih dahulu karena sifat khususnya terkait dengan materi terdahulu.
A. Definisi Setengah Putaran
Setengah putaran terhadap titik P (dengan pusat P) dilambangkan dengan HP, adalah pemetaan yang memenuhi untuk sebarang titik A di bidang (x,y) :
1. Jika P ≠ A maka titik P titik tengah PP’
HP(A) = A’
2. Jika P = A maka HP (A)=A=P
Berdasarkan gambar di atas terlihat bahwa jarak benda ke pusat setengah putaran sama dengan jarak pusat ke bayangannya. Semakin dekat benda ke pusat maka bayangan juga akan semakin dekat (perhatikan titik B,P dan B’). Pada saat benda berada pada pusat setengah putaran maka bayangan juga berada pada titik yang sama.
B. DALIL SETENGAH PUTARAN Dalil H.1
Setengah putaran merupakan suatu involusi. Ini berarti bahwa HP2 =I dan
P
P H
H −1 =
Bukti: Menurut definisi sebagai berikut :
∀A≠P, Hp(A) = A’, P titik tengah AA , dan H' p(A’) = A, P titik tengah A'A, maka :
Hp Hp(A) = Hp (Hp(A)) = Hp (A’)
= A
Hp2
(A) = A Hp2 (A) = I
Terbukti H bersifat involusi.
Secara Analitik perumusan setengah putaran dapat diturunkan sebagai berikut:
Misalkan P(a,b)sebagai pusat putar dan Hp memetakan A(x,y) ke A’(x’,y’) maka
𝑎𝑎 =𝑥𝑥 + 𝑥𝑥′
2 𝑏𝑏 =𝑦𝑦 + 𝑦𝑦′
Atau x’ = -x + 2a 2 y’ = -y + 2b
Jadi jika P(a,b) maka :
Hp = (x,y)→(x’,y’) dengan �𝑥𝑥𝑦𝑦′′� = − �𝑥𝑥
𝑦𝑦� + 2 �𝑎𝑎 𝑏𝑏�
bila pusat diambil di 0(0,0) rumus menjadi x’ = -x
y’ = -y
Dalil H.2
Setengah putaran merupakan suatu isometri.
Bukti: cara I
MisalkanA,B,P∈v,danA≠B≠P Hp(A) = A’, P titik tengahAA ' Hp(B) = B’, P titik tengahBB ' Akan dibuktikan: A'B'= AB
Perhatikan gambar berikut!
−
= −
y b
x a y
x 2 2 ' '
i. Perhatikan segitiga ABP dan segitiga A’B’P’
• AP = PA’
• BP = PB’
Sehingga AB= A' B' ii. m∠APB=m∠A' PB'
Dari (i) dan (ii) terbukti H isometri.
Cara II.
Pusat putaran kita impitkan dengan pangkal koordinat sehingga rumusnya menjadi
−
=
−
= y y
x x
' '
titik A
(
x1, y1)
dipetakan ke A'(
x1',y1')
dantitik B
(
x2, y2)
dipetakan ke B'(
x2',y2')
, setengah putaran dikatakansuatu isometri jika A’B’ = AB, maka
2 1 2 2
1 2 1
2 2 1
2' ') ( ' ') ( ) ( )
( '
'B x x y y x x y y
A = − + − = − + + − +
=
2 1 2 2 1
2 ) ( )
(x −x + y −y
= AB
Jadi terbukti bahwa H mempertahankan jarak, maka H adalah suatu isometri dan dengan sendirinya H adalah suatu kolineasi.
Bukti H bersifat kolineasi dari gambar dalil H.2
• secara geometri perhatikan:
' ' PB A m APB m∠ = ∠
terbukti bahwa H mempertahankan besar sudut
• secara analitik
H bersifat kolineasi untuk setiap garis g∈v maka Hp(g) = g’
adalah garis g'∈v g : ax + by + c = 0