Olteanu Emil 2. 88KB Jun 04 2011 12:09:19 AM

α P'

AN ORIGINAL METHOD OF PROVING THE FORMULA

OF A TRIGONOMETRIC FUNCTION OF A SUM OF

ANGLES

by Emil Olteanu

Abstract: The formulas for calculating the trigonometric functions whose angle sum or differences can be deduced from one another. However, we have to prove one of these formulas. Considering this problem with multiple implications in trigonometry, we searched for various methods of solving this formula and we searched for relations with different other mathematics chapters (linear algebra, analysis in complex etc.). We searched for several proofs for the initial formula, of which the method of the fictitious scalar product is an original one.

Proving the trigonometric functions of the angle sums and differences is a problem starting from an initial formula, then the rest of the formulas (including for double and triple angles and many other formulas) are deduced from these. I give below a series of such proofs (the fictitious scalar product method is original), considering that they make a connection between different chapters of mathematics.

1. Geometric proof. We start from the following drawing:

Figure 1.

β

α

a OA = r = 1 OP' = cos(β)

OP = OP' cos(α) = cos(β)cos(α) OM = cos(α+β)

NP' = sin(β)

MP = NP' sin(α) = sin(β)sin(α) but OM = OP - MP, results the formula

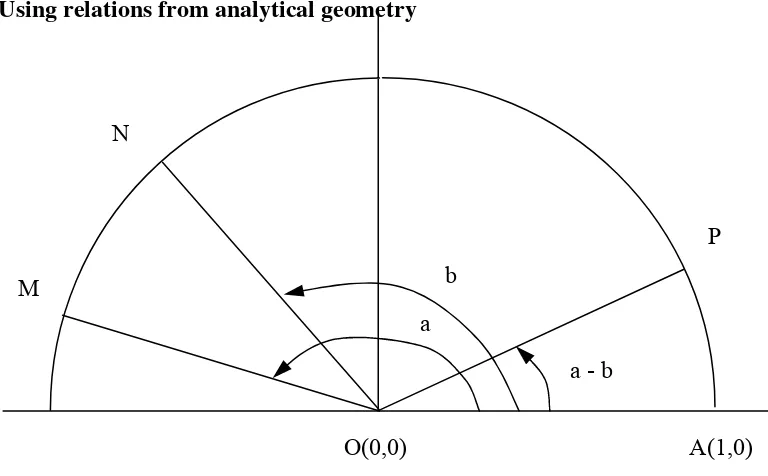
[image:2.595.129.513.253.491.2]

cos(α+β) = cos(α)cos(β) - sin(α)sin(β) 2. Using relations from analytical geometry

Figure 2.

The points O, A, M, N and P have the following coordinates: O (0,0);

A (1,0); M (cos(a), sin(a)); N (cos(b), sin(b));

O(0,0) A(1,0) M

N

b

a - b

P (cos(a-b), sin(a-b)).

|MN|2 = (cos(a) - cos(b))2 + (sin(a) - sin(b))2 =

cos2(a) - 2cos(a)cos(b) + cos2(b) + sin2(a) - 2sin(a)sin(b) + sin2(b) = 2 - 2(cos(a)cos(b) + sin(a)sin(b))

|AP|2 = (cos(a-b) - 1)2 + sin2(a-b) =

cos2(a-b) - 2cos(a-b) + 1 + sin2(a-b) = 2 - 2cos(a-b) but |MN| = |AP| , results

cos(a-b) = cos(a)cos(b) + sin(a)sin(b) 3. We use relations from vectorial analysis.

We start from the scalar product formula.

( )

a b ab

b

a• = cos ,

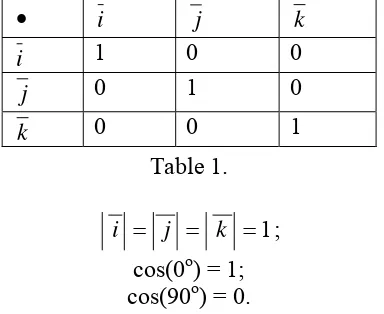
[image:3.595.210.402.392.549.2]

for the vectors i, j şi k, the module of which is one, the scalar product table is the following:

Table 1.

1

= =

= j k

i ;

cos(0o) = 1; cos(90o) = 0. In plane we have the vectorial relations:

( )

( )

(

i j

)

a

j a i a

a = x + y = cosα + sinα × ;

• i j k

i 1 0 0

j 0 1 0

( )

( )

(

i j

)

b

j b i b

[image:4.595.119.498.107.488.2]

b= _x + _y = cos β + sin β × .

Figure 3.

The angle between the vectors a and b is:

( )

a,b = α−β

( )

=

(

α−β

)

=

•b abcosa,b abcos a

( )

( )

(

+

)

•

(

( )

+

( )

)

= =

•b aicosα jsinα bicos β jsin β

a

( ) ( )

( ) ( )

( ) ( )

( ) ( )

(

• + • + • + •

)

=

=abi icosα cos β i jcosα sin β j isinα cos β j jsinα sin β

( ) ( )

( ) ( )

(

cosα cos β +sinα sin β

)

= ab

results

(

α β

)

cos

( ) ( )

α cos β sin

( ) ( )

α sin β

cos − = +

4. Using a product created for this proof (which in this material we shall call fictitious scalar product).

We introduce a new type of scalar product, for instance:

) , sin(a b ab

b a⊗ =

a

b

α

α - β

We have the following properties:

1

= = j

i ;

( )

0 0 sin 0 = =

⊗i

i ;

( )

0 0 sin 0 = =

⊗ j

j ;

( )

90 1 sin − 0 =− =

⊗ j

i ;

( )

90 1 sin 0 = =

⊗i j

For the vectors i and j, the module of which is one, the scalar product table is the following:

⊗ i j

i 0 -1

j 1 0

Table 2. According to the prior proof results:

(

α−β

)

= ⊗b absin a

From the relations:

( )

( )

(

)

( )

( )

(

)

    + = + = + = + = b j i j b i b b a j i j a i a a y x y x β β α α sin cos sin cos Results:

( )

( )

(

+

)

⊗

(

( )

+

( )

)

= =

⊗b a icosα jsinα b icos β jsin β

a

( ) ( )

( ) ( )

( ) ( )

( ) ( )

(

⊗ + ⊗ + ⊗ + ⊗

)

=

( ) ( )

( ) ( )

(

−cosα sin β +sinα cos β

)

=ab

From these relations results:

(

α β

)

cos

( ) ( )

α sin β sin

( ) ( )

α cos β sin

( ) ( )

α cos β cos

( ) ( )

α sin β

sin − =− + = −

There are also other methods to prove a trigonometric formula of a sum or difference/differences of angles. For instance, it can be solved with the help of Euler’s formulas:

( )

( )

( )

( )

   

− =

+ =

− _{x i x}

e

x i x e

ix ix

sin cos

sin cos

.

References:

[1] W. Kecs - Complemente de matematici cu aplicaţii în tehnică (Mathematics complements with technical applications) , Editura Tehnică, Bucureşti, 1981. [2] I. Gh. Şabac - Matematici speciale (Special Mathematics) , Editura Didacticăşi Pedagogică, Bucureşti, 1981.

[3] Crstici Borislav (coordonator), ş.a. - Matematici speciale (Special Mathematics), Editura Didacticăşi Pedagogică, Bucureşti, 1981.

Author: