Copyright 1996 Lawrence C. Marsh
1.0
PowerPoint Slides for
Undergraduate Econometrics
by
Lawrence C. Marsh
To accompany: Undergraduate Econometrics
by Carter Hill, William Griffiths and George Judge
1
Copyright 1996 Lawrence C. Marsh
The Role of
Econometrics
in Economic Analysis
Chapter 1
Copyright © 1997 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express written permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages, caused by the use of these programs or from the use of the information contained herein.
1.1 Copyright 1996 Lawrence C. Marsh
Using Information:
1. Information from
economic theory.
2. Information from
economic data.
The Role of Econometrics
1.2
Copyright 1996 Lawrence C. Marsh
Understanding Economic Relationships:
federal budget
Dow-Jones Stock Index
trade
deficit Federal Reserve
Discount Rate
capital gains tax
rent control laws short term treasury bills
power of labor unions
crime rate inflation
unemployment
money supply
1.3 Copyright 1996 Lawrence C. Marsh
economic theory
economic data
}
economic decisions
To use information effectively:
*Econometrics* helps us combine economic theory and economic data .
Economic Decisions
1.4Copyright 1996 Lawrence C. Marsh
Consumption, c, is some function of income, i :
c = f(i)
For applied econometric analysis this consumption function must be specified more precisely.
The Consumption Function
1.5Copyright 1996 Lawrence C. Marsh
demand, qd, for an individual commodity:
qd = f( p, pc, ps, i )
supply, qs, of an individual commodity:
qs = f( p, pc, pf )
p = own price; pc = price of complements;
ps = price of substitutes; i = income
p = own price; pc = price of competitive products;
ps = price of substitutes; pf = price of factor inputs
demand
2
Copyright 1996 Lawrence C. Marsh
Listing the variables in an economic relationship is not enough.
For effective policy we must know the amount of change
needed for a policy instrument to bring about the desired effect:
How much ?
• By how much should the Federal Reserve raise interest rates to prevent inflation?
• By how much can the price of football tickets be increased and still fill the stadium?
1.7 Copyright 1996 Lawrence C. Marsh
Answering the How Much? question
Need to estimate parameters that are both:
1. unknown and
2. unobservable
1.8
Copyright 1996 Lawrence C. Marsh
Average or systematic behavior over many individuals or many firms.
Not a single individual or single firm. Economists are concerned with the unemployment rate and not whether a particular individual gets a job.
The Statistical Model
1.9 Copyright 1996 Lawrence C. Marsh
The Statistical Model
Actual vs. Predicted Consumption:
Actual = systematic part + random error
Systematic part provides prediction, f(i), but actual will miss by random error, e. Consumption, c, is function, f, of income, i, with error, e:
c = f(i) + e
1.10
Copyright 1996 Lawrence C. Marsh
c = f(i) + e
Need to define f(i) in some way.
To make consumption, c, a linear function of income, i :
f(i) = β1 + β2 i
The statistical model then becomes: c = β1 + β2 i + e
The Consumption Function
1.11 Copyright 1996 Lawrence C. Marsh• Dependent variable , y, is focus of study
(predict or explain changes in dependent variable).
• Explanatory variables, X2 and X3, help us explain observed changes in the dependent variable.
y = β1 + β2 X2 + β3 X3 + e
The Econometric Model
3
Copyright 1996 Lawrence C. Marsh Statistical Models
Controlled (experimental) vs.
Uncontrolled (observational)
Uncontrolled experiment (econometrics) explaining consump-tion, y : price, X2, and income, X3, vary at the same time. Controlled experiment (“pure” science) explaining mass, y : pressure, X2, held constant when varying temperature, X3, and vice versa.
1.13 Copyright 1996 Lawrence C. Marsh
Econometric
model
• economic model
economic variables and parameters.
• statistical model
sampling process with its parameters.
• data
observed values of the variables.
1.14
Copyright 1996 Lawrence C. Marsh
• Uncertainty regarding an outcome.
• Relationships suggested by economic theory. • Assumptions and hypotheses to be specified. • Sampling process including functional form. • Obtaining data for the analysis.
• Estimation rule with good statistical properties. • Fit and test model using software package. • Analyze and evaluate implications of the results. • Problems suggest approaches for further research.
The Practice of Econometrics
1.15 Copyright 1996 Lawrence C. Marsh
Note: the textbook uses the following symbol to mark sections with advanced material
:
“Skippy”
1.16
Copyright 1996 Lawrence C. Marsh
Some Basic
Probability
Concepts
Chapter 2
Copyright © 1997 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express written permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages, caused by the use of these programs or from the use of the information contained herein.
2.1 Copyright 1996 Lawrence C. Marsh
random variable:
A variable whose value is unknown until it is observed. The value of a random variable results from an experiment.
The term random variable implies the existence of some known or unknown probability distribution defined over the set of all possible values of that variable.
In contrast, an arbitrary variable does not have a probability distribution associated with its values.
4
Copyright 1996 Lawrence C. Marsh
Controlled experiment values of explanatory variables are chosen with great care in accordance with an appropriate experimental design.
Uncontrolled experiment values of explanatory variables consist of nonexperimental observations over which the analyst has no control.
2.3 Copyright 1996 Lawrence C. Marsh
discrete random variable:
A discrete random variable can take only a finite number of values, that can be counted by using the positive integers.
Example: Prize money from the following lottery is a discrete random variable:
first prize: $1,000 second prize: $50 third prize: $5.75
since it has only four (a finite number) (count: 1,2,3,4) of possible outcomes:
$0.00; $5.75; $50.00; $1,000.00
Discrete Random Variable
2.4Copyright 1996 Lawrence C. Marsh
continuous random variable: A continuous random variable can take any real value (not just whole numbers) in at least one interval on the real line.
Examples:
Gross national product (GNP) money supply
interest rates price of eggs household income expenditure on clothing
Continuous Random Variable
2.5Copyright 1996 Lawrence C. Marsh
A discrete random variable that is restricted to two possible values (usually 0 and 1) is called a dummy variable (also, binary or indicator variable).
Dummy variables account for qualitative differences: gender (0=male, 1=female),
race (0=white, 1=nonwhite), citizenship (0=U.S., 1=not U.S.), income class (0=poor, 1=rich).
Dummy Variable
2.6Copyright 1996 Lawrence C. Marsh
A list of all of the possible values taken by a discrete random variable along with their chances of occurring is called a probability function or probability density function (pdf).
die x f(x)
one dot 1 1/6 two dots 2 1/6 three dots 3 1/6 four dots 4 1/6 five dots 5 1/6 six dots 6 1/6
2.7 Copyright 1996 Lawrence C. Marsh
A discrete random variable X has pdf, f(x), which is the probability
that X takes on the value x.
f(x) = P(X=x)
0 < f(x) < 1
If X takes on the n values: x1, x2, . . . , xn,
then f(x1) + f(x2)+. . .+f(xn) = 1.
Therefore,
5
Copyright 1996 Lawrence C. Marsh Probability, f(x), for a discrete random variable, X, can be represented by height:
0 1 2 3 X
number, X, on Dean’s List of three roommates f(x)
0.2 0.4
0.1 0.3
2.9 Copyright 1996 Lawrence C. Marsh
A continuous random variable uses
area under a curve rather than the height, f(x), to represent probability:
f(x)
X $34,000. $55,000. per capita income, X, in the United States
0.1324 0.8676
red area
green area
2.10
Copyright 1996 Lawrence C. Marsh
Since a continuous random variable has an
uncountably infinite number of values, the probability of one occurring is zero.
P [ X = a ] = P [ a < X < a ] = 0
Probability is represented by area. Height alone has no area. An interval for X is needed to get
an area under the curve.
2.11 Copyright 1996 Lawrence C. Marsh
P [ a < X < b ] =
∫
f(x) dxb
a
The area under a curve is the integral of the equation that generates the curve:
For continuous random variables it is the integral of f(x), and not f(x) itself, which defines the area and, therefore, the probability.
2.12
Copyright 1996 Lawrence C. Marsh
n
Rule 2: Σ axi = a Σxi i = 1 i = 1
n
Rule 1: Σxi = x1 + x2 + . . . + xn i = 1
n
Rule 3: Σ (xi +yi) = Σxi + Σyi
i = 1 i = 1 i = 1
n n n
Note that summation is a linear operator which means it operates term by term.
Rules of Summation
2.13Copyright 1996 Lawrence C. Marsh
Rule 4: Σ (axi +byi) = a Σxi + b Σyi
i = 1 i = 1 i = 1
n n n
Rules of Summation (continued)
Rule 5: x = Σxi = i = 1
n n
1 x1 + x2 + . . . + xn
n
The definition of x as given in Rule 5 implies the following important fact:
Σ (xi− x) = 0 i = 1
n
6
Copyright 1996 Lawrence C. Marsh
Rule 6: Σf(xi) = f(x1) + f(x2) + . . . + f(xn)
i = 1
n
Notation: Σf(xi) = Σf(xi) = Σf(xi)
n x i i = 1
n
Rule 7: Σ Σ f(xi,yj) = Σ [ f(xi,y1) + f(xi,y2)+. . .+ f(xi,ym)] i = 1 i = 1
n m
j = 1
The order of summation does not matter :
Σ Σ f(xi,yj) = Σ Σ f(xi,yj) i = 1
n m
j = 1 j = 1
m n
i = 1
Rules of Summation (continued)
2.15 Copyright 1996 Lawrence C. Marsh
The
mean
or arithmetic average of a
random variable is its mathematical
expectation or expected value, EX.
The Mean of a Random Variable
2.16
Copyright 1996 Lawrence C. Marsh
Expected Value
There are two entirely different, but mathematically equivalent, ways of determining the expected value:
1. Empirically:
The expected value of a random variable, X, is the average value of the random variable in an infinite number of repetitions of the experiment.
In other words, draw an infinite number of samples, and average the values of X that you get.
2.17 Copyright 1996 Lawrence C. Marsh
Expected Value
2. Analytically:
The expected value of a discrete random variable, X, is determined by weighting all the possible values of X by the corresponding probability density function values, f(x), and summing them up.
E[X] = x1f(x1) + x2f(x2) + . . . + xnf(xn)
In other words:
2.18
Copyright 1996 Lawrence C. Marsh
In the empirical case when the
sample goes to infinity the values
of X occur with a frequency
equal to the corresponding f(x)
in the analytical expression.
As sample size goes to infinity, the
empirical and analytical methods
will produce the same value.
Empirical vs. Analytical
2.19 Copyright 1996 Lawrence C. Marshx =
Σ
xin i = 1
where n is the number of sample observations.
Empirical (sample) mean:
E[X] =
Σ
xif(xi)i = 1 n
where n is the number of possible values of xi.
Analytical mean:
Notice how the meaning of n changes.
7
Copyright 1996 Lawrence C. Marsh
E X =
Σ
xi f(xi)i=1
n
The expected value of X-squared:
E X =
Σ
xi f(xi)i=1
n
2 2
It is important to notice thatf(xi) does not change!
The expected value of X-cubed:
E X =
Σ
xi f(xi)i=1
n
3 3
The expected value of X:
2.21 Copyright 1996 Lawrence C. Marsh
EX = 0 (.1) + 1 (.3) + 2 (.3) + 3 (.2) + 4 (.1)
2
EX = 0 (.1) + 1 (.3) + 2 (.3) + 3 (.2) + 4 (.1) 2 2 2 2 2
= 1.9
= 0 + .3 + 1.2 + 1.8 + 1.6
= 4.9
3
EX = 0 (.1) + 1 (.3) + 2 (.3) + 3 (.2) +4 (.1)3 3 3 3 3 = 0 + .3 + 2.4 + 5.4 + 6.4
= 14.5
2.22
Copyright 1996 Lawrence C. Marsh
E[g(X)]
=
Σ
g(
xi)
f(xi)n i = 1
g(X) = g1(X) + g2(X)
E[g(X)]
=
Σ [
g1(xi) + g2(xi)]f(xi)n i = 1
E[g(X)]
=
Σ
g1(xi)f(xi) +Σ
g2(xi)f(xi)n i = 1
n i = 1
E[g(X)]
=
E[g1(X)] + E[g2(X)]2.23 Copyright 1996 Lawrence C. Marsh
Adding
and
Subtracting
Random Variables
E(X-Y) = E(X) - E(Y)
E(X+Y) = E(X) + E(Y)
2.24
Copyright 1996 Lawrence C. Marsh
E(X+a) = E(X) + a
Adding
a
constant
to a variable will
add a constant to its expected value:
Multiplying by
constant
will multiply
its expected value by that constant:
E(bX) = b E(X)
2.25 Copyright 1996 Lawrence C. Marsh
var(X) = average squared deviations around the mean of X.
var(X) = expected value of the squared deviations around the expected value of X.
var(X) =E [(X - EX) ] 2
8
Copyright 1996 Lawrence C. Marsh
var(X) =E [(X - EX) ]
=E [X - 2XEX + (EX) ]
2 2
2
=E(X ) - 2 EX EX + E (EX)
2 2
=E(X ) - 2 (EX) + (EX) 2 2 2 =E(X ) - (EX) 2 2
var(X) =E [(X - EX) ] 2
var(X) = E(X ) - (EX) 2 2
2.27 Copyright 1996 Lawrence C. Marsh
variance
of a discrete
random variable, X:
standard deviation is square root of variance
var ( X ) =
(x
i- EX )
2f(x
i)
i = 1 n
∑
2.28
Copyright 1996 Lawrence C. Marsh
xi f(xi) (xi - EX) (xi - EX) f(xi)
2 .1 2 - 4.3 = -2.3 5.29 (.1) = .529
3 .3 3 - 4.3 = -1.3 1.69 (.3) = .507
4 .1 4 - 4.3 = - .3 .09 (.1) = .009
5 .2 5 - 4.3 = .7 .49 (.2) = .098
6 .3 6 - 4.3 = 1.7 2.89 (.3) = .867
Σ xi f(xi) = .2 + .9 + .4 + 1.0 + 1.8 = 4.3
Σ (xi - EX) f(xi) = .529 + .507 + .009 + .098 + .867 = 2.01
2
2
calculate the variance for a
discrete random variable, X:
i = 1 n
n i = 1
2.29 Copyright 1996 Lawrence C. Marsh
Z = a + cX
var(Z) = var(a + cX)
= E [(a+cX) - E(a+cX)]
= c var(X)
2
2
var(a + cX) = c var(X)
22.30
Copyright 1996 Lawrence C. Marsh
A
joint
probability density function,
f(x,y), provides the probabilities
associated with the joint occurrence
of all of the possible pairs of X and Y.
Joint pdf
2.31Copyright 1996 Lawrence C. Marsh
college grads in household
.15
.05
.45
.35
joint pdf
f(x,y)
Y = 1 Y = 2vacation homes owned
X = 0
X = 1
Survey of College City, NY
f
(0,1)f
(0,2)f
(1,1)f
(1,2)9
Copyright 1996 Lawrence C. Marsh
E[g(X,Y)] =
Σ
Σ
g(x
i,y
j) f(x
i,y
j)
i j
E(XY) = (0)(1)(.45)+(0)(2)(.15)+(1)(1)(.05)+(1)(2)(.35)=.75
E(XY) =
Σ
iΣ
x
iy
jf(x
i,y
j)
j
Calculating the expected value of
functions of two random variables.
2.33 Copyright 1996 Lawrence C. Marsh
The
marginal
probability density functions,
f(x) and f(y), for discrete random variables,
can be obtained by summing over the f(x,y)
with respect to the values of Y to obtain f(x)
with respect to the values of X to obtain f(y).
f(x
i) =
Σ
f(x
i,y
j)
f(y
j) =
Σ
f(x
i,y
j)
i j
Marginal pdf
2.34Copyright 1996 Lawrence C. Marsh
.15
.05
.45
.35
marginal
Y = 1 Y = 2
X = 0
X = 1
.60
.40
.50
.50
f
(X = 1)f
(X = 0)f
(Y = 1)f
(Y = 2)marginal pdf for Y:
marginal pdf for X:
2.35 Copyright 1996 Lawrence C. Marsh
The
conditional
probability density
functions of X given Y=y , f(x
|
y),
and of Y given X=x , f(y
|
x),
are obtained by dividing f(x,y) by f(y)
to get f(x
|
y) and by f(x) to get f(y
|
x).
f(x
|
y) =
f(x,y)
f(y
|
x) =
f(x,y)
f(y)
f(x)
Conditional pdf
2.36Copyright 1996 Lawrence C. Marsh
.15
.05
.45
.35
conditonal
Y = 1 Y = 2
X = 0
X = 1
.60
.40
.50
.50
.25 .75
.875 .125 .90
.10 .70
.30
f(Y=2|X= 0)=.25
f(Y=1|X = 0)=.75
f(Y=2|X = 1)=.875
f(X=0|Y=2)=.30
f(X=1|Y=2)=.70
f(X=0|Y=1)=.90
f(X=1|Y=1)=.10
f(Y=1|X = 1)=.125
2.37 Copyright 1996 Lawrence C. Marsh
X and Y are
independent
random
variables if their joint pdf, f(x,y),
is the product of their respective
marginal pdfs, f(x) and f(y) .
f(x
i,y
j) = f(x
i) f(y
j)
for independence this must hold for all pairs of i and j
10
Copyright 1996 Lawrence C. Marsh
.15
.05
.45
.35
not independent
Y = 1 Y = 2
X = 0
X = 1
.60
.40
.50
.50
f
(X = 1)f
(X = 0)f
(Y = 1)f
(Y = 2)marginal pdf for Y:
marginal pdf for X: .50x.60=.30 .50x.60=.30
.50x.40=.20 .50x.40=.20
The calculations in the boxes show the numbers required to have
independence.
2.39 Copyright 1996 Lawrence C. Marsh
The
covariance
between two random
variables, X and Y, measures the
linear association between them.
cov(X,Y) = E[(X - EX)(Y-EY)]
Note that variance is a special case of covariance.
cov(X,X) = var(X) = E[(X - EX) ]
2Covariance
2.40Copyright 1996 Lawrence C. Marsh
cov(X,Y) =E [(X - EX)(Y-EY)]
=E [XY - X EY - Y EX + EX EY]
=E(XY) - 2 EX EY + EX EY
=E(XY) - EX EY
cov(X,Y) =E [(X - EX)(Y-EY)]
cov(X,Y) = E(XY) - EX EY
=E(XY) - EX EY - EY EX + EX EY
2.41 Copyright 1996 Lawrence C. Marsh
.15
.05
.45
.35
Y = 1 Y = 2X = 0
X = 1
.60
.40
.50
.50
EX=0(.60)+1(.40)=.40 EY=1(.50)+2(.50)=1.50E(XY) = (0)(1)(.45)+(0)(2)(.15)+(1)(1)(.05)+(1)(2)(.35)=.75
EX EY = (.40)(1.50) = .60
cov(X,Y) = E(XY) - EX EY = .75 - (.40)(1.50) = .75 - .60 = .15
covariance
2.42Copyright 1996 Lawrence C. Marsh
The
correlation
between two random
variables X and Y is their covariance
divided by the square roots of their
respective variances.
Correlation is a pure number falling between -1 and 1.
cov(X,Y)
ρ
(X,Y) =
var(X) var(Y)
Correlation
2.43Copyright 1996 Lawrence C. Marsh
.15
.05
.45
.35
Y = 1 Y = 2X = 0
X = 1
.60
.40
.50
.50
EX=.40 EY=1.50cov(X,Y) = .15
correlation
EX=0(.60)+1(.40)=2 2 2 .40
var(X) = E(X ) - (EX) = .40 - (.40) = .24
2 2 2
EY=1(.50)+2(.50) = .50 + 2.0 = 2.50
2 2 2
var(Y) = E(Y ) - (EY) = 2.50 - (1.50) = .25
2 2 2
ρ(X,Y) = cov(X,Y)
var(X) var(Y)
11
Copyright 1996 Lawrence C. Marsh
Independent random variables
have zero covariance and,
therefore, zero correlation.
The converse is not true.
Zero Covariance & Correlation
2.45 Copyright 1996 Lawrence C. Marsh
The expected value of the weighted sum
of random variables is the sum of the
expectations of the individual terms.
Since expectation is a linear operator, it can be applied term by term.
E[c
1X + c
2Y] = c
1EX + c
2EY
E[c
1X
1+...+ c
nX
n] = c
1EX
1+...+ c
nEX
n In general, for random variables X1, . . . , Xn :2.46
Copyright 1996 Lawrence C. Marsh The variance of a weighted sum of random
variables is the sum of the variances, each times the square of the weight, plus twice the covariances of all the random variables times the products of their weights.
var(c1X + c2Y)=c1 var(X)+c2 var(Y) + 2c1c2cov(X,Y)
2 2
var(c1X − c2Y) = c21 var(X)+c2 2var(Y) − 2c1c2cov(X,Y) Weighted sum of random variables:
Weighted difference of random variables:
2.47 Copyright 1996 Lawrence C. Marsh
The Normal Distribution
Y ~ N(
β
,
σ
2
)
f(y) =
2
π
σ
21
exp
β
y
f(y)
2
σ
2(y -
β
)
2-2.48
Copyright 1996 Lawrence C. Marsh
The Standardized Normal
Z ~ N(
0
,
1
)
f(z) =
2
π
1exp
-
2
z
2Z = (y -
β
)/
σ
2.49 Copyright 1996 Lawrence C. Marsh
P [ Y > a ] = P > = P Z > Y - σβ a - σβ a - σβ
β
y
f(y)
a
12
Copyright 1996 Lawrence C. Marsh
P [ a < Y < b ] = P < <
= P < Z < a - β Y - β
σ
σ b - σβ
a - β
σ
b - β
σ
β
y
f(y)
a
Y ~ N(
β
,
σ
2)
b
2.51 Copyright 1996 Lawrence C. Marsh
Y1 ~ N(β1,σ12), Y2 ~ N(β2,σ22), . . . , Yn ~ N(βn,σn2)
W = c
1Y
1+ c
2Y
2+ . . . + c
nY
nLinear combinations of jointly
normally distributed random variables
are themselves normally distributed.
W ~ N
[
E(W), var(W)
]
2.52
Copyright 1996 Lawrence C. Marsh
mean: E[V] = E[
χ
(m) ] = mIf Z1, Z2, . . . , Zm denote m independent
N(0,1) random variables, and
V = Z21 + Z22 + . . . + Z2m, then V ~
χ
(m) 2 V is chi-square with m degrees of freedom.Chi-Square
variance: var[V] = var[
χ
(m) ] = 2mIf Z1, Z2, . . . , Zm denote m independent
N(0,1) random variables, and
V = Z21 + Z22 + . . . + Z2m, then V ~
χ
(m) 2 V is chi-square with m degrees of freedom.2
2
2.53 Copyright 1996 Lawrence C. Marsh
mean: E[
t
] = E[t
(m) ] = 0 symmetric about zerovariance: var[
t
] = var[t
(m) ] = m / (m−
2)If Z ~ N(0,1) and V ~
χ
(m) and if Z and Vare independent then,
~
t
(m)t
is student-t with m degrees of freedom. 2t =
ZV m
Student - t
2.54Copyright 1996 Lawrence C. Marsh
If V1 ~
χ
(m1) and V2 ~
χ
(m2) and if V1 and V2 are independent, then~ F
(m 1,m2)F
is an F statistic with m1 numeratordegrees of freedom and m2 denominator
degrees of freedom. 2
F =
V1 m1 V2
m 2
2
F Statistic
2.55Copyright 1996 Lawrence C. Marsh
The Simple Linear
Regression
Model
Chapter 3
Copyright © 1997 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express written permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages, caused by the use of these programs or from the use of the information contained herein.
13
Copyright 1996 Lawrence C. Marsh
1. Estimate a relationship among economic variables, such as y = f(x).
2. Forecast or predict the value of one variable, y, based on the value of another variable, x.
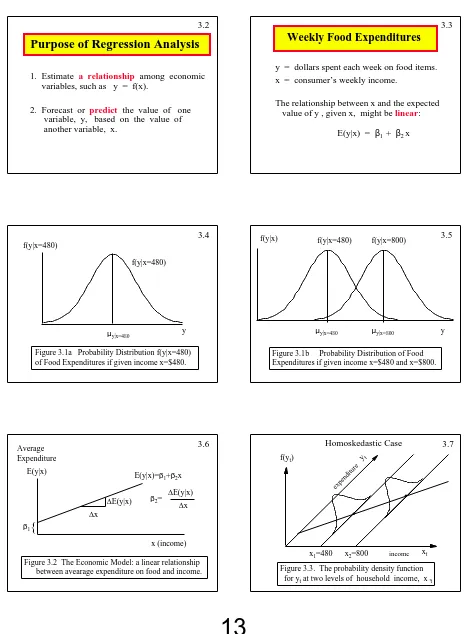
Purpose of Regression Analysis
3.2 Copyright 1996 Lawrence C. Marsh
Weekly Food Expenditures
y = dollars spent each week on food items. x = consumer’s weekly income.
The relationship between x and the expected value of y , given x, might be linear:
E(y|x) = β1 + β2 x
3.3
Copyright 1996 Lawrence C. Marsh f(y|x=480)
f(y|x=480)
y µy|x=480
Figure 3.1a Probability Distribution f(y|x=480) of Food Expenditures if given income x=$480.
3.4 f(y|x) Copyright 1996 Lawrence C. Marsh
f(y|x=480) f(y|x=800)
[image:14.612.72.537.92.726.2]y µy|x=480 µy|x=800
Figure 3.1b Probability Distribution of Food Expenditures if given income x=$480 and x=$800.
3.5
Copyright 1996 Lawrence C. Marsh
{
β1
∆x
∆E(y|x) E(y|x)
Average Expenditure
x (income) E(y|x)=β1+β2x
β2=
∆E(y|x) ∆x
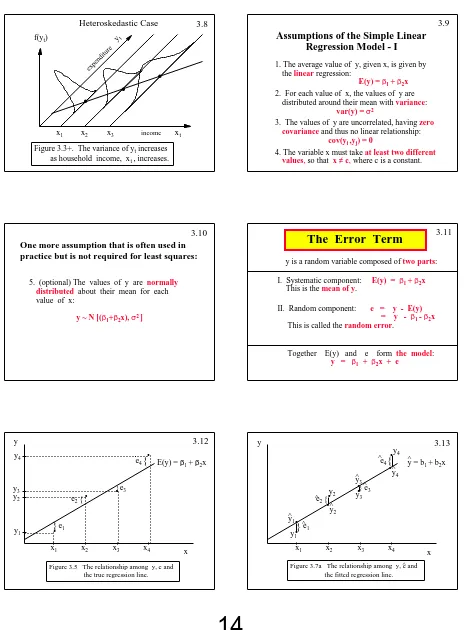
Figure 3.2 The Economic Model: a linear relationship between avearage expenditure on food and income.
3.6 Copyright 1996 Lawrence C. Marsh
.
.
xt
x1=480 x2=800
yt
f(yt)
Figure 3.3. The probability density function for yt at two levels of household income, xt
expenditure
Homoskedastic Case
income
14
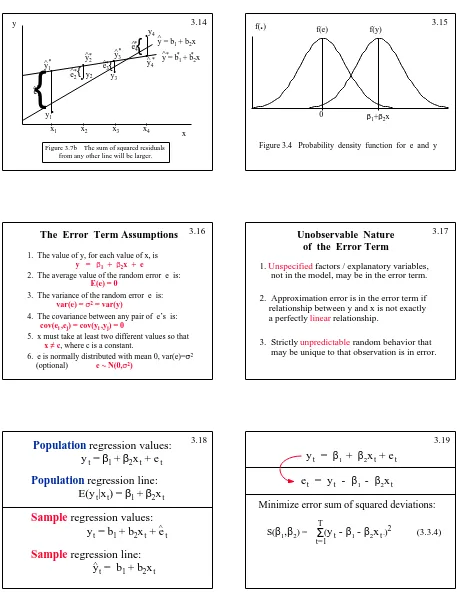
Copyright 1996 Lawrence C. Marsh
.
xt
x1 x2
[image:15.612.75.540.94.724.2]yt f(yt)
Figure 3.3+. The variance of yt increases
as household income, xt , increases. expenditure
Heteroskedastic Case
x3
.
.
income
3.8 Copyright 1996 Lawrence C. Marsh
Assumptions of the Simple Linear
Regression Model - I
1. The average value of y, given x, is given by the linear regression:
E(y) = β1 + β2x
2. For each value of x, the values of y are distributed around their mean with variance:
var(y) = σ2
3. The values of y are uncorrelated, having zero covariance and thus no linear relationship:
cov(yi ,yj) = 0
4. The variable x must take at least two different values, so that x ≠ c, where c is a constant.
3.9
Copyright 1996 Lawrence C. Marsh
5. (optional) The values of y are normally distributed about their mean for each value of x:
y ~ N [(β1+β2x), σ2 ]
One more assumption that is often used in practice but is not required for least squares:
3.10 Copyright 1996 Lawrence C. Marsh
The Error Term
y is a random variable composed of two parts:
I. Systematic component: E(y) = β1 + β2x
This is the mean of y.
II. Random component: e = y - E(y) = y - β1 - β2x
This is called the random error.
Together E(y) and e form the model:
y = β1 + β2x + e
3.11
Copyright 1996 Lawrence C. Marsh
Figure 3.5 The relationship among y, e and the true regression line.
.
.
.
.
y4 y1 y2 y3x1 x2 x3 x4
}
}
{{
e1 e2 e3e4 E(y) = β1 + β2x
x
y 3.12 Copyright 1996 Lawrence C. Marsh
}
.
}.
.
.
y4 y1y2 y
3
x1 x2 x3 x4
[image:15.612.77.291.108.262.2]{
{
e1 e2 e3 e4 x yFigure 3.7a The relationship among y, e and the fitted regression line.
^
y = b1 + b2x
15
Copyright 1996 Lawrence C. Marsh
{
{
.
.
.
.
.
y4
y1
y2 y3
x1 x2 x3 x4 x
[image:16.612.77.535.95.704.2]y
Figure 3.7b The sum of squared residuals from any other line will be larger.
y = b1 + b2x
^
.
.
.
y1
^
y3
^
y4
^ y = b^* *1 + b*2x *
e1
^*
e2
^*
y2
^*
e3
^* * e^*4
*
{
{
3.14 f(
.
) Copyright 1996 Lawrence C. Marshf(e) f(y)
Figure 3.4 Probability density function for e and y
0 β1+β2x
3.15
Copyright 1996 Lawrence C. Marsh
The Error Term Assumptions
1. The value of y, for each value of x, is y = β1 + β2x + e
2. The average value of the random error e is:
E(e) = 0
3. The variance of the random error e is:
var(e) = σ2 = var(y)
4. The covariance between any pair of e’s is:
cov(ei ,ej) = cov(yi ,yj) = 0
5. x must take at least two different values so that
x ≠ c, where c is a constant.
6. e is normally distributed with mean 0, var(e)=σ2
(optional) e ~ N(0,σ2)
3.16
Unobservable Nature
Copyright 1996 Lawrence C. Marshof the Error Term
1. Unspecified factors / explanatory variables, not in the model, may be in the error term.
2. Approximation error is in the error term if relationship between y and x is not exactly a perfectly linear relationship.
3. Strictly unpredictable random behavior that may be unique to that observation is in error.
3.17
Copyright 1996 Lawrence C. Marsh
Population
regression values:
y
t=
β
1+
β
2x
t+ e
tPopulation
regression line:
E(y
t|x
t) =
β
1+
β
2x
tSample
regression values:
y
t= b
1+ b
2x
t+ e
tSample
regression line:
y
t= b
1+ b
2x
t^
^
3.18 Copyright 1996 Lawrence C. Marsh
y
t=
β
1+
β
2x
t+ e
tMinimize error sum of squared deviations:
S(β
1,
β
2) =Σ
(y
t-
β
1-
β
2x
t)2 (3.3.4)t=1 T
e
t= y
t-
β
1-
β
2x
t [image:16.612.320.533.108.224.2]16
Copyright 1996 Lawrence C. Marsh
Minimize w.
r.
t.
β
1and
β
2:
S(
β
1,
β
2) =Σ
(y
t-
β
1-
β
2x
t)2 (3.3.4)t =1 T
= - 2
Σ
(y
t-
β
1-
β
2x
t)= - 2
Σ
x
t (y
t-
β
1-
β
2x
t)∂S(
.
)∂β
1 ∂S(.
)∂β
2Set each of these two derivatives equal to zero and solve these two equations for the two unknowns:
β
1β
23.20 Copyright 1996 Lawrence C. Marsh
S(.)
S(.)
βi bi
.
.
.
Minimize w.
r.
t.
β
1and
β
2:
S(
.
) =Σ
(y
t-
β
1-
β
2x
t)2t =1 T
∂S(.) ∂βi
< 0
∂S(.) ∂βi
>0 ∂S(.)
∂βi
=0
3.21
Copyright 1996 Lawrence C. Marsh
To minimize S(.), you set the two derivatives equal to zero to get:
= - 2
Σ
(y
t-
b
1-
b
2x
t) = 0= - 2
Σ
x
t (y
t-
b
1-
b
2x
t) = 0∂S(
.
)∂β
1 ∂S(.
)∂β
2When these two terms are set to zero,
β
1 andβ
2 becomeb
1 andb
2 because they no longer represent just any value ofβ
1 andβ
2 but the specialvalues that correspond to the minimum of S(
.
) .3.22 Copyright 1996 Lawrence C. Marsh
- 2
Σ
(y
t-
b
1-
b
2x
t) = 0- 2
Σ
x
t (y
t-
b
1-
b
2x
t) = 0Σ
y
t-T
b
1-b
2Σ
x
t = 0Σ
x
ty
t-b
1Σ
x
t -b
2Σ
x
t 2 = 0T
b
1 +b
2Σ
x
t =Σ
y
tb
1Σ
x
t +b
2Σ
x
t =Σ
x
ty
t2
3.23
Copyright 1996 Lawrence C. Marsh
Solve for
b
1 andb
2 using definitions ofx
andy
T
b
1 +b
2Σ
x
t =Σ
y
tb
1Σ
x
t +b
2Σ
x
t =Σ
x
ty
t2
T
Σ
x
ty
t -Σ
x
tΣ
y
tT
Σ
x
t2- (
Σ
x
t)2b
2 =b
1 = y -b
2x
3.24 Copyright 1996 Lawrence C. Marsh
elasticities
percentage change in y percentage change in x
η = =
∆x/x ∆y/y
= ∆∆y x
x y
Using calculus, we can get the elasticity at a point:
η = lim ∆∆y x =
x y
∂y x ∂x y
∆x→0
17
Copyright 1996 Lawrence C. Marsh
E(y) =
β
1+
β
2x
∂
E(y)
∂
x
=
β
2applying elasticities
∂
E(y)
∂
x
=
β
2η
=
E(y)
x
E(y)
x
3.26 Copyright 1996 Lawrence C. Marsh
estimating elasticities
∂
y
∂
x
=
b
2η
=
y
x
y
x
^
y
t=
b
1+ b
2x
t= 4 + 1.5 x
t^
x
= 8 = average number of years of experiencey
= $10 = average wage rate
= 1.5 = 1.2
8
10
=
b
2η
y
x
^
3.27
Copyright 1996 Lawrence C. Marsh
Prediction
y
^t= 4 + 1.5 x
tEstimated regression equation:
x
t = years of experiencey
^t = predicted wage rateIf
x
t = 2 years, theny
t =$7.00
per hour.
^
If
x
t = 3 years, then y^t=
$8.50
per hour.
3.28 Copyright 1996 Lawrence C. Marsh
log-log models
ln(y) =
β
1+
β
2ln(x)
∂
ln(y)
∂
x
∂
ln(x)
∂
x
=
β
2∂
y
∂
x
=
β
21
y
∂
x
∂
x
1
x
3.29
Copyright 1996 Lawrence C. Marsh
∂
y
∂
x
=
β
21
y
∂
x
∂
x
1
x
=
β
2∂
y
∂
x
x
y
elasticity of y with respect to x:
=
β
2∂
y
∂
x
x
y
η
=
3.30 Copyright 1996 Lawrence C. Marsh
Properties of
Least
Squares
Estimators
Chapter 4
Copyright © 1997 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express written permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages, caused by the use of these programs or from the use of the information contained herein.
18
Copyright 1996 Lawrence C. Marsh
y
t=
household weekly food expendituresSimple Linear Regression Model
y
t=
β
1+
β
2x
t+
ε
tx
t=
household weekly incomeFor a given level of
x
t, the expected level of food expenditures will be:E(
y
t|
x
t)=
β
1+
β
2x
t4.2 Copyright 1996 Lawrence C. Marsh
1.
y
t=
β
1+
β
2x
t+
ε
t2.
E(
ε
t)
=
0 <=> E(
y
t)
=
β
1+
β
2x
t3.
var(
ε
t)
=
σ
2=
var(
y
t
)
4.
cov(
ε
i,
ε
j)
=
cov(
y
i,
y
j)
=
0
5.
x
t≠
c
for every observation6.
ε
t~N(0,
σ
2) <=>
y
t
~
N(
β
1+
β
2x
t,
σ
2)
Assumptions of the Simple
Linear Regression Model
4.3
Copyright 1996 Lawrence C. Marsh
The population parameters
β
1andβ
2 are unknown population constants.
The formulas that produce the sample estimates b1 and b2 are called the estimators of
β
1andβ
2.
When b0 and b1 are used to represent the formulas rather than specific values, they are called estimators of
β
1andβ
2 which are random variables because they are different from sample to sample.4.4 Copyright 1996 Lawrence C. Marsh
• If the least squares estimators b0 and b1
are random variables, then what are their their means, variances, covariances and probability distributions?
• Compare the properties of alternative
estimators to the properties of the least squares estimators.
Estimators are Random Variables
( estimates are not )
4.5
Copyright 1996 Lawrence C. Marsh
The Expected Values of b1 and b2
The least squares formulas (estimators) in the simple regression case:
b
2=
T
Σ
x
ty
t-
Σ
x
tΣ
y
tT
Σ
x
t2-(
Σ
x
t)
2b
1= y - b
2x
where
y =
Σ
y
t/ T
andx =
Σ
x
t/ T
(3.3.8a)(3.3.8b)
4.6 Substitute in
y
tCopyright 1996 Lawrence C. Marsh=
β
1+
β
2x
t+
ε
t to get:b
2=
β
2+
T
Σ
x
tε
t-
Σ
x
tΣε
tT
Σ
x
t2-(
Σ
x
t)
2The mean of
b
2 is:Eb
2=
β
2+
T
Σ
x
tE
ε
t-
Σ
x
tΣ
E
ε
tT
Σ
x
t2-(
Σ
x
t)
219
Copyright 1996 Lawrence C. Marsh
The result
Eb
2=
β
2 means that the distribution ofb
2 is centered atβ
2.Since the distribution of
b
2 is centered atβ
2 ,we say thatb
2 is an unbiased estimator ofβ
2.An Unbiased Estimator
4.8Copyright 1996 Lawrence C. Marsh
The unbiasedness result on the
previous slide assumes that we
are using the
correct model
.
If the model is of the wrong form
or is missing important variables,
then
E
ε
t≠
0
, then
Eb
2≠
β
2.
Wrong Model Specification
4.9Copyright 1996 Lawrence C. Marsh
Unbiased Estimator of the Intercept
In a similar manner, the estimator b
1of the intercept or constant term can be
shown to be an
unbiased
estimator of
β
1when the model is correctly specified.
Eb
1=
β
14.10 Copyright 1996 Lawrence C. Marsh
b
2=
T
Σ
x
ty
t−
Σ
x
tΣ
y
tT
Σ
x
t2−
(
Σ
x
t)
2 (3.3.8a)(4.2.6)
Equivalent expressions for b
2:
Expand and multiply top and bottom by T:
b
2=
Σ
(x
t−
x )
(
y
t−
y )
Σ(
x
t−
x
)
24.11
Copyright 1996 Lawrence C. Marsh
Variance of b
2Given that both yt and
ε
t have varianceσ
2, the variance of the estimator b2 is:b2 is a function of the yt values but var(b2) does not involve yt directly.
Σ(
x
t−
x
)
σ
22
var(b
2) =
4.12 Copyright 1996 Lawrence C. Marsh
Variance of b
1Τ Σ(
x
t−
x
)
2var(b
1) =
σ
2Σ
x
t2 the variance of the estimator b1 is:b
1= y
−
b
2x
Given20
Copyright 1996 Lawrence C. Marsh
Covariance of b
1and b
2Σ(
x
t−
x
)
2cov(b
1,b
2) =
σ
2−
x
If x = 0, slope can change without affecting the variance.
4.14
What factors determine
Copyright 1996 Lawrence C. Marshvariance and covariance ?
1. σ 2: uncertainty about y
t values uncertainty about b1, b2 and their relationship. 2. The more spread out the xt values are then the more
confidence we have in b1, b2, etc. 3. The larger the sample size, T, the smaller the
variances and covariances. 4. The variance b1 is large when the (squared) xt values
are far from zero (in either direction). 5. Changing the slope, b2, has no effect on the intercept,
b1, when the sample mean is zero. But if sample mean is positive, the covariance between b1 and b2 will be negative, and vice versa.
4.15
Copyright 1996 Lawrence C. Marsh
Gauss-Markov Theorm
Under the first five assumptions of the simple, linear regression model, the ordinary least squares estimators b1 and b2 have the smallest variance of all linear and unbiased estimators of
β1 and β2. This means that b1and b2 are the Best Linear Unbiased Estimators
(BLUE) of β1 and β2.
4.16 Copyright 1996 Lawrence C. Marsh
implications of Gauss-Markov
1. b1 and b2 are “best” within the class of linear and unbiased estimators.
2. “Best” means smallest variance
within the class of linear/unbiased. 3. All of the first five assumptions must
hold to satisfy Gauss-Markov. 4. Gauss-Markov does not require
assumption six: normality.
5. G-Markov is not based on the least squares principle but on b1 and b2.
4.17
Copyright 1996 Lawrence C. Marsh
G-Markov implications (continued)
6. If we are not satisfied with restricting our estimation to the class of linear and unbiased estimators, we should ignore the Gauss-Markov Theorem and use some nonlinear and/or biased estimator instead. (Note: a biased or nonlinear estimator could have smaller variance
than those satisfying Gauss-Markov.) 7. Gauss-Markov applies to the b1 and b2
estimators and not to particular sample values (estimates) of b1 and b2.
4.18
Probability Distribution
Copyright 1996 Lawrence C. Marshof Least Squares Estimators
b
2~ N
β
2,
Σ(
x
t−
x
)
σ
22
b
1~ N
β
1,
Τ Σ(
x
t
−
x
)
2σ
2Σ
x
t 221
Copyright 1996 Lawrence C. Marsh
y
tand
ε
tnormally distributed
The least squares estimator of β2 can be expressed as a linear combination of yt’s:
b
2=
Σ
w
ty
tb
1= y
−
b
2x
Σ(
x
t−
x
)
2where w
t=
(
x
t−
x
)
This means that b1and b2 are normal since linear combinations of normals are normal.
4.20 Copyright 1996 Lawrence C. Marsh
normally distributed under
The Central Limit Theorem
If the first five Gauss-Markov assumptions hold, and sample size, T, is sufficiently large, then the least squares estimators, b1 and b2, have a distribution that approximates the normal distribution with greater accuracy the larger the value of sample size, T.
4.21
Copyright 1996 Lawrence C. Marsh
Consistency
We would like our estimators, b1 and b2, to collapse onto the true population values, β1 and β2, as
sample size, T, goes to infinity.
One way to achieve this consistency property is for the variances of b1 and b2 to go to zero as T goes to infinity.
Since the formulas for the variances of the least squares estimators b1 and b2 show that their
variances do, in fact, go to zero, then b1 and b2,
are consistent estimators of β1 and β2.
4.22
Estimating the variance
Copyright 1996 Lawrence C. Marshof the error term,
σ
2e
^
t= y
t−
b
1−
b
2x
tΣ
e
^
tt =1 T 2
T− 2
σ
2=
σ
2is an unbiased estimator ofσ
2^
^
4.23
Copyright 1996 Lawrence C. Marsh
The Least Squares
Predictor, y
^
oG iven a value of the explanatory variable, Xo, w e w ould like to predict a value of the dependent variable, yo.
The least squares predictor is:
y
o= b
1+ b
2x
o (4.7.2)^
4.24 Copyright 1996 Lawrence C. Marsh
Inference
in the Simple
Regression Model
Chapter 5
Copyright © 1997 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express written permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages, caused by the use of these programs or from the use of the information contained herein.
22
Copyright 1996 Lawrence C. Marsh
1.
y
t=
β
1+
β
2x
t+
ε
t2. E(
ε
t)
=
0 <=> E(
y
t)
=
β
1+
β
2x
t3. var(
ε
t)
=
σ
2=
var(
y
t
)
4. cov(
ε
i,
ε
j)
=
cov(
y
i,
y
j)
=
0
5.
x
t≠
c
for every observation6.
ε
t~N(0,
σ
2) <=>
y
t
~
N(
β
1+
β
2x
t,
σ
2)
Assumptions of the Simple
Linear Regression Model
5.2 Copyright 1996 Lawrence C. Marsh
Probability D istribution
of Least Squares Estim ators
b
1~ N
β
1,
Τ Σ(
x
t
−
x
)
2σ
2Σ
x
t 2b
2~ N
β
2,
Σ(
x
t−
x
)
σ
22
5.3
Copyright 1996 Lawrence C. Marsh
σ
^
2=
Τ − 2e
^t2Σ
Unbiased estimator of the error variance:
σ
2σ
2^
(Τ − 2)
∼
Τ − 2
χ
Transform to a chi-square distribution:
Error Variance Estimation
5.4Copyright 1996 Lawrence C. Marsh We make a correct decision if:
• The null hypothesis is false and we decide to reject it.
• The null hypothesis is true and we decide not to reject it.
Our decision is incorrect if:
• The null hypothesis is true and we decide to reject it. This is a type I error.
• The null hypothesis is false and we decide not to reject it. This is a type II error.
5.5
Copyright 1996 Lawrence C. Marsh
b
2~ N
β
2,
Σ(
x
t−
x
)
σ
22
Create a standardized normal random variable, Z, by subtracting the mean of b2 and dividing by its standard deviation:
b
2− β
2var(b
2)
Ζ
=
∼ Ν(0,1)
5.6 Copyright 1996 Lawrence C. Marsh
Simple Linear Regression
y
t=
β
1+
β
2x
t+
ε
twhere E
ε
t = 0y
t~
N(
β
1+
β
2x
t,
σ
2)
since Ey
t=
β
1+
β
2x
tε
t=
y
t−
β
1−
β
2x
tTherefore,
ε
t~ N(0,
σ
2) .
23
Copyright 1996 Lawrence C. Marsh
Create a Chi-Square
ε
t~ N(0,
σ
2) but want N(0,
1
) .
(
ε
t/
σ)
~ N(0,
1
) Standard Normal .
(
ε
t/
σ)
2~
χ
2(1)Chi-Square
.
5.8 Copyright 1996 Lawrence C. Marsh
Sum of Chi-Squares
Σ
t=1(
ε
t/
σ)
2=
(
ε
1/
σ)
2+ (
ε
2/
σ)
2+. . .+ (
ε
T/
σ)
2χ
2(1)+
χ
2(1)+. . .+
χ
2(1)=
χ
2(Τ)Therefore,
Σ
t=1(
ε
t/
σ)
2∼
χ
2(Τ)5.9
Copyright 1996 Lawrence C. Marsh
Since the errors
ε
t=
y
t−
β
1−
β
2x
t are not observable, we estimate them with the sample residualse
t=
y
t−
b
1−
b
2x
t. Unlike the errors, the sample residuals arenot independent since they use up two degrees
of freedom by usingb1 and b2 to estimate β1 and β2.
We get only T
−
2 degrees of freedom instead of T.Chi-Square degrees of freedom
5.10Copyright 1996 Lawrence C. Marsh
Student-t Distribution
t = ~ t
Z
(m)V / m
where Z ~ N(0,1)
and V ~
χ
2(m)5.11
Copyright 1996 Lawrence C. Marsh
t = ~ t
Z
(m)V /
(
T
−
2)
where Z =
(b
2− β
2)
var(b
2)
and var(b
2) =
σ
2Σ
( x
i−
x )
25.12 Copyright 1996 Lawrence C. Marsh
t =
Z
V / (T-2)
(b
2− β
2)
var(b
2)
t =
(T
−
2)
σ
2σ
2^
(
T
−
2)
V =
(T
−
2)
σ
2σ
2^
24
Copyright 1996 Lawrence C. Marsh
var(b
2) =
σ
2Σ
( x
i−
x )
2(b
2− β
2)
σ
2Σ
( x
i−
x )
2t = =
(T−2)
σ
2σ
2^
(T− 2)
(b
2− β
2)
σ
2Σ
( x
i−
x )
2^
notice the
cancellations
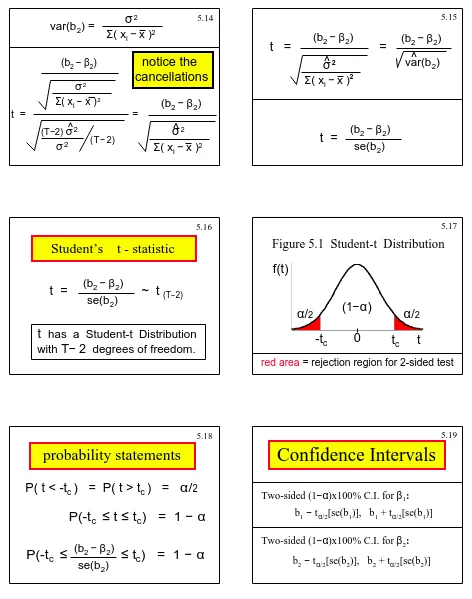
5.14 Copyright 1996 Lawrence C. Marsh
(b
2− β
2)
σ
2Σ
( x
i−
x )
2^
t = =
(b
2− β
2)
var(b
^
2)
t =
(b
2− β
2)
se(b
2)
5.15
Copyright 1996 Lawrence C. Marsh
Student’s t - statistic
t = ~ t
(b
2− β
2)
(T−2)se(b
2)
t
has a Student-t Distribution
with
T
−
2
degrees of freedom.
[image:25.612.70.542.100.699.2]5.16 Copyright 1996 Lawrence C. Marsh
Figure 5.1 Student-t Distribution
(
1−α
)
t
0
f(t)
-t
ct
cα
/
2α
/
2red area
= rejection region for 2-sided test
5.17
Copyright 1996 Lawrence C. Marsh
probability statements
P(-t
c≤
t
≤
t
c) = 1
−
α
P( t < -t
c) = P( t > t
c) =
α/
2
P(-t
c≤
(b
2− β
2)
≤
t
c) = 1
−
α
se(b
2)
5.18 Copyright 1996 Lawrence C. Marsh
Confidence Intervals
Two-sided (1
−α
)x100% C.I. for
β
1:
b
1−
t
α/2[se(b
1)], b
1+ t
α/2[se(b
1)]
b
2−
t
α/2[se(b
2)], b
2+ t
α/2[se(b
2)]
Two-sided (1
−α
)x100% C.I. for
β
2:
25
Copyright 1996 Lawrence C. Marsh
Student-t vs. Normal Distribution
1. Both are symmetric bell-shaped distributions.
2. Student-t distribution has fatter tails than the normal.
3. Student-t converges to the normal for infinite sample.
4. Student-t conditional on degrees of freedom (df).
5. Normal is a good approximation of Student-t for the first few decimal places when df > 30 or so.
5.20 Copyright 1996 Lawrence C. Marsh
Hypothesis Tests
1. A null hypothesis, H
0.
2. An alternative hypothesis, H
1.
3. A test statistic.
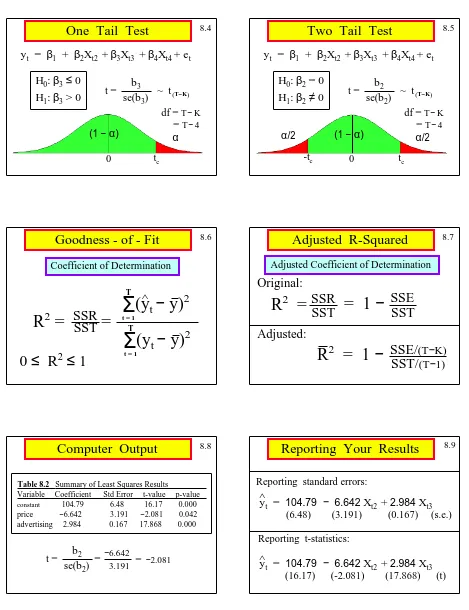
4. A rejection region.
5.21
Copyright 1996 Lawrence C. Marsh
Rejection Rules
1. Two-Sided Test:
If the value of the test statistic falls in the critical region in either tail of the t-distribution, then we reject the null hypothesis in favor of the alternative.
2. Left-Tail Test:
If the value of the test statistic falls in the critical region which lies in the left tail of the t-distribution, then we reject the null hypothesis in favor of the alternative.
2. Right-Tail Test:
If the value of the test statistic falls in the critical region which lies in the right tail of the t-distribution, then we reject the null hypothesis in favor of the alternative.
5.22 Copyright 1996 Lawrence C. Marsh
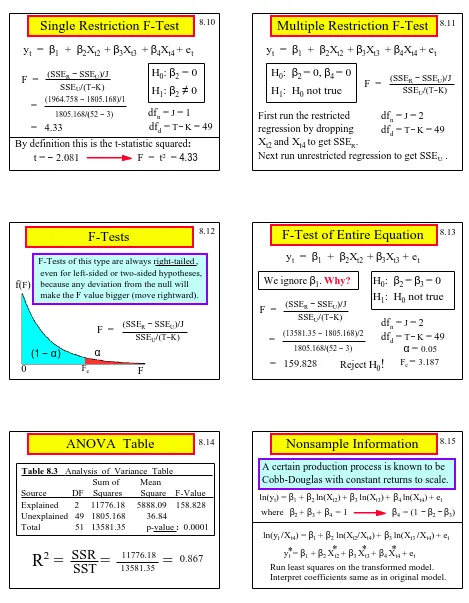
Format for Hypothesis Testing
1. Determine null and alternative hypotheses. 2. Specify the test statistic and its distribution
as if the null hypothesis were true.
3. Select
α
and determine the rejection region. 4. Calculate the sample value of test statistic. 5. State your conclusion.5.23
Copyright 1996 Lawrence C. Marsh
practical vs. statistical
significance in economics
Practically but not statistically significant:
When sample size is very small, a large average gap between the salaries of men and women might not be statistically significant.
Statistically but not practically significant:
When sample size is very large, a small correlation (say, ρ = 0.00000001) between the winning numbers in the PowerBall Lottery and the Dow-Jones Stock Market Index might be statistically significant.
5.24 Copyright 1996 Lawrence C. Marsh
Type I and Type II errors
Type I error:
We make the mistake of rejecting the null hypothesis when it is true.
α
= P(rejecting H0 when it is true).Type II error:
We make the mistake of failing to reject the null hypothesis when it is false.
26
Copyright 1996 Lawrence C. Marsh
Prediction Intervals
A (1
−α
)x100% prediction interval for y
ois:
y
o± t
cse( f )
^
se( f ) = var( f )
^
f = y
^
o−
y
oΣ(
x
t−
x
)
2var( f ) =
^
σ
21 + +
1
Τ
(
x
o−
x
)
2^
5.26 Copyright 1996 Lawrence C. Marsh
The Simple Linear
Regression Model
Chapter 6
Copyright © 1997 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express written permission of the copyright owner is unlawful. Request for further information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages, caused by the use of these programs or from the use of the information contained herein.
6.1
Copyright 1996 Lawrence C. Marsh
Explaining Variation in
y
t
Predicting y
twithout any explanatory variables:
y
t=
β
1+ e
tΣ
e
t=
Σ
(y
t−
β
1)
22
t = 1 t = 1
T T
=
−2
Σ
(y
t−
b
1) = 0
∂Σ
e
2tt = 1
t = 1 T
T
∂
β
1Σ
(y
t−
b
1) = 0
t = 1 T
Σ
y
t−
Tb
1= 0
t = 1 T
b
1= y
Why not y?
6.2 Copyright 1996 Lawrence C. Marsh
Explaining Variation in
y
t
y
t
= b
1
+ b
2
x
t
+ e
^
t
Unexplained variation:
y
t
= b
1
+ b
2
x
t
^
Explained variation:
e
t
= y
t
−
y
^
t
= y
t
−
b
1
−
b
2
x
t
^
6.3
Copyright 1996 Lawrence C. Marsh
Explaining Variation in
y
t
y
t
= y
t
+ e
^
t
Why not y?
^
y
t
−
y = y
^
t
−
y + e
^
t
using y as baseline
SST = SSR + SSE
Σ
(y
t
−
y)
2
=
Σ
(y
t
−
y)
2
+
Σ
e
t
t = 1 T
^
^
T T
t = 1 t = 1
2 cross product
term drops
out
6.4 Copyright 1996 Lawrence C. Marsh
Total Variation in
y
t
SST = total sum of squares
SST measures variation of
y
t aroundy
Σ
(y
t
−
y)
2
t = 1 T
SST
=
27
Copyright 1996 Lawrence C. Marsh
Explained Variation in
y
t
SSR = regression sum of squares
y
t
= b
1
+ b
2
x
t
^
Fitted y
^
tvalues:
SSR measures variation of
y
^t aroundy
Σ
(y
t
−
y)
2
t = 1 T
SSR
=
^
6.6 Copyright 1996 Lawrence C. Marsh
Unexplained Varia