Klaksifikasi Hadron dan Meson sebagai
Representasi Uniter pada Sistem Partikel
Elementer
Mulyadi
NPM : 0399020527
Departemen Fisika
Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Indonesia
Halaman Persetujuan
Skripsi : Klaksifikasi Hadron dan Meson sebagai Representasi Uniter pada Sistem Partikel Elementer
Nama : Mulyadi NPM : 0399020527
Skripsi ini telah diperiksa dan disetujui
Pembimbing
Dr.Terry Mart
Penguji I Penguji II
Kata Pengantar
Partikel-partikel Subnuklir merupakan kumpulan partikel yang unik. Salah sat-unya adalah karena beberapa sifat istimewa yang terkait satu sama lain melalui kesimetrian. Kesimetrian partikel-patrikel ini dapat dipelajari dalam suatu topik pembelajaran di Fisika yang kerap dikenal sebagai Teori Grup. Sesungguhnya Teori Grup bukan hanya membahas representasi dan klaksifikasi ”cantik” dari partikel-partikel subnuklir, namun pada sistem many-body lainnya seperti pada molekul-molekul dapat dipelajari melalui Teori Grup.
Tepat tanggal 1 juni 2002, Saya ingat pertama kali bertemu Pak Terry di Salemba untuk membicarakan masalah tugas akhir, karena saya tertarik di bidan-gnya beliau, Fisika Nuklir-Partikel teoritik. Saya tidak menyangka, karena banyak masalah dan lain-lain tugas akhir saya terbengkalai sampai bulan maret tahun ini. Tentu saja topik yang saya bawakan berbeda dengan yang seharusnya saya dapat kalau saya memulai Skripsi 2 tahun silam. Pemilihan topik ini sangat baik dilakukan oleh Pak Terry, karena Grup Fisika teoritik di Jurusan kita memang membutuhkan pengetahuan tersebut, karena ternyata banyak jurnal ilmiah di bidang nuklir-partikel teoritik ternyata tidak terlepas dengan pembahasan Grup seperti yang baru saja dilakukan ”Bapak” Nofirwan, S.si pada tugas akhir beliau semester lalu.
di Fisika ; Pak Rachmat W.Adi, yang sangat memberi dukungan moral terhadap studi saya di jurusan Fisika UI; Pak Herbert P.Simanjuntak, yang sangat mem-pengaruhi apresiasi saya terhadap Fisika; Pak M.Hikam, yang mempercayai saya menjadi asisten untuk mata kuliah Fisika statistik; Ibu Rosari Saleh, alias ibu ”Oca”, yang banyak memberikan masukan-masukan mengenai hal-hal lain di lu-ar Fisika selama saya kuliah dengan beliau; dan segenap dosen-dosen lain yang saking banyaknya tidak bisa saya sebutkan satu-persatu. Dari pihak mahasiswa, saya tak lupa ucapkan terima kasih kepada, ”Pak” Nofirwan, S.si; Julio, S.si; Freddy Simanjuntak, S.si; Anton wiranata; Yunita; Nowo Riveli; Ardi mustofa; dll
Daftar Isi
Halaman Persetujuan ii
Kata Pengantar iii
Daftar Isi v
Daftar Gambar vii
Daftar Tabel viii
1 Pendahuluan 1
1.1 Latar Belakang . . . 1
1.2 Perumusan Masalah . . . 2
1.3 Metode Penelitian . . . 6
1.4 Tujuan . . . 6
2 Tinjauan Pustaka 7 2.1 Elemen-elemen Teori Grup . . . 7
2.1.1 Definisi Grup . . . 7
2.1.2 Subgrup . . . 11
2.1.3 Isomorfisme dan Homomorfisme . . . 11
2.1.4 Kelas . . . 12
2.1.5 Perkalian Langsung Grup . . . 14
2.2 Representasi Linier Grup . . . 15
2.2.1 Definisi Representasi Grup . . . 15
2.2.2 Representasi Matriks . . . 16
2.2.3 Representasi Ekivalen . . . 16
2.2.4 Representasi Uniter . . . 17
2.2.5 Representasi Iredusibel . . . 18
2.2.7 Perkalian Luar Representasi . . . 21
2.2.8 Perkalian Dalam . . . 24
3 Grup Lie 29 3.1 Transformasi infinitesimal . . . 29
3.2 Konstanta Struktur . . . 32
3.3 Generator . . . 34
3.4 Grup Simpel dan Semi-Simpel . . . 38
3.5 Aljabar Simpel dan Semi-simpel . . . 42
3.6 Beberapa contoh Grup Lie . . . 42
3.7 Kekompakan . . . 47
3.8 Penjumlahan langsung dan Semi-langsung dari Aljabar Lie . . . . 48
3.9 Representasi Kontradingen . . . 49
4 Hasil dan Pembahasan 51 4.1 Sifat umum Grup-grup Uniter . . . 52
4.2 Grup SU(2) . . . 54
4.3 Homomorfisme SU(2) dengan R3 . . . 55
4.4 Multiplet . . . 58
4.5 Grup SU(3) . . . 59
4.5.1 Transformasi Infinitesimal . . . 59
4.5.2 Osilator harmonik 3 dimensi . . . 64
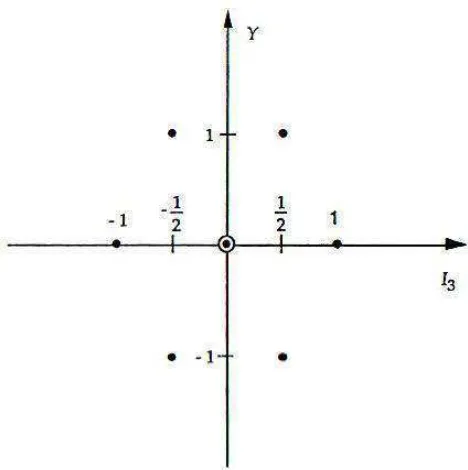
4.5.3 Diagram Bobot untuk representasi fundamental . . . 66
4.5.4 Pelabelan irreps SU(3) . . . 68
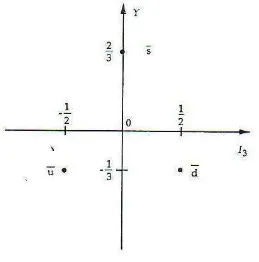
4.5.5 Representasi Kompleks Konjugat . . . 76
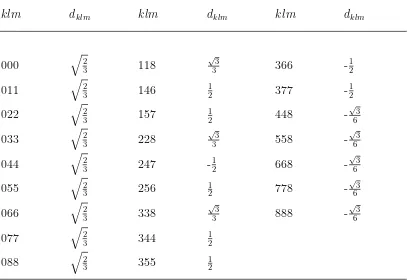
4.5.6 Klaksifikasi Hadron . . . 79
4.5.7 Klaksifikasi Meson . . . 83
4.5.8 Formula massa Gell-Mann – Okubo . . . 86
4.6 Grup di atas SU(3) . . . 90
4.6.1 Kuark dengan citarasa dan spin . . . 90
Daftar Gambar
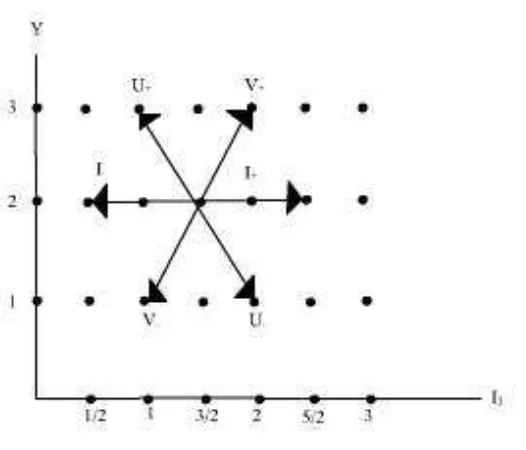
4.1 Diagram Bobot Representasi Fundamental SU(3) . . . 68 4.2 Aksi dari operator tangga pada bidang I3-Y . . . 68 4.3 Diagram Bobot Tipikal suatu representasi SU(3) dengan λ = 6
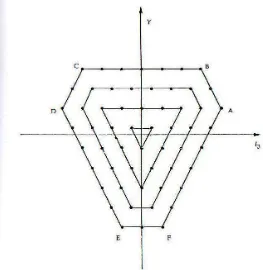
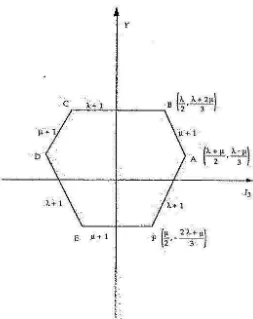
dan µ= 2 . . . 75 4.4 Kontur dari suatu diagram bobot . . . 76 4.5 Diagram Bobot Tipikal SU(3) untuk (λµ)=(11) λ = 6. Diagram
bobot memiliki multiplisitas 2 yang ditandai titik yang dilingkari 77 4.6 Diagram Bobot Tipikal suatu representasi kompleks konjugat ¯3
SU(3) . . . 79 4.7 (a)Oktet Baryon (Jπ = 1
2 +
). (b) Dekuplet Baryon (Jπ = 3 2 +
) . . . 83 4.8 (a)Meson pseudoskalar JP = 0−.(b) Meson vektorJP = 1− . . . . 85
Daftar Tabel
1.1 Beberapa kesimetrian dalam Fisika . . . 5
2.1 Tabel perkalian grup S3 . . . 10
3.1 Sifat matriks yang relevan terhadap definisi bermacam grup kontinu 43 3.2 Macam-macam Grup Lie . . . 44
4.1 Nilai-nilai Konstanta dklm yang didefinisikan menurut dan . . . . 63
Bab 1
Pendahuluan
Alam semesta kita ini sangat menarik dan unik. Salah satu ”keajaiban” alam yaitu terdapatnya kesimetrian. Kesimetrian merupakan atribut alamiah dalam dunia fisis dan oleh karena itu merupakan titik awal dari segala hukum fisis. Untuk mempelajari kesimetrian , Kita akan menggunakan Teori Grup, karena teori grup merupakan cabang matematika yang cocok untuk mempelajari kes-imetrian sistem-sistem fisis. Dasarnya adalah Hamiltonian ataupun Lagrangian dari sistem, karena kesimetrian suatu sistem fisis dinyatakan oleh Lagrangian dan Hamiltonian sistem tersebut. Teori Grup dapat menjelaskan berbagai keteratu-ran sifat dan besaketeratu-ran fisis yang teramati dan dapat membantu menyederhanakan dan menyatukan hukum fisika dari sistem-sistem yang jelas berbeda. Teori grup merupakan ”alat” yang bermanfaat untuk memahami perilaku sistem dimana ter-dapat kesimetrian di dalamnya. Berkaitan dengan kesimetrian, dalam skripsi ini juga akan dibahas mengenai kesimetrian yang dipelajari dalam mekanika kuan-tum. Mula-mula terdapat kesimetrian permutasi untuk partikel identik, yang tekait pada grup simetrik. Peran dari grup simetri ini adalah untuk menjamin bahwa fungsi gelombang partikel dapat mencakup sifat ketidakdapat-terbedakan secara tepat dan sesuai. Selain itu Kesimetrian juga merupakan sifat alamiah dari alam , karena beberapa hal cenderung memiliki preferensi yang sama.
1.1
Latar Belakang
mekanika kuantum.
Pada zaman sekarang, dalam perkembangan fisika modern, khususnya pada bidang fisika energi tinggi, kesimetrian memainkan peran yang sangat penting dan sangat diperlukan. Saat ini, para fisikawan percaya bahwa semua interaksi fundamental dapat dideskripsikan melalui teori gauge, yaitu teori yang menje-laskan kesimetrian gauge. Aspek lain yang tak kalah penting adalah perluasan teori dari grup Lie ke pembahasan kesupersimetrian. Konsep-konsep ini sedang diaplikasikan ke fisika partikel, teori medan kuantum (Quantum Field Theory), dan gravitasi dalam bentuk teori string dan superstring. Latar belakang pemil-ihan topik ini adalah untuk mempelajari topik Teori Grup secara literatur dan menggunakannya dalam representasi uniter untuk kasus partikel-partikel subnuk-lir.
1.2
Perumusan Masalah
Dalam mekanika kuantum, terdapat 5 macam kesimetrian . Beberapa diantaranya dan konsekuensinya diringkas pada tabel 1.1.
1. Kesimetrian permutasi diskret
Dalam mekanika kuantum, nilai ekspektasi besaran-besaran fisika tidak berubah terhadap permutasi partikel-partikel identik. Transformasi per-mutasi membentuk sebuah grup yang disebut grup simetrik Sn
2. Kesimetrian ruang-waktu kontinu
(a) Translasi dalam ruang
r′ =r+ρ (1.1)
(b) Translasi waktu
t′ =t+t
0 (1.2)
Kesimetrian terjadi berdasarkan asumsi kehomogenan waktu. Ini artinya waktu awal dapat dipilih secara sembarang, suatu fenomena fisis dapat dilakukan pada sembarang waktu, atau dengan kata lain: Tidak ter-dapat waktu absolut. Hal ini berlaku untuk sistem yang konservatif, dimana medan luar tidak bergantung waktu. Lagrangian dan Hamil-tonian sistem yang demikian tidak bergantung waktu dan konsekuensi dari kesimetrian ini adalah hukum kekekalan energi.
(c) Rotasi dalam ruang 3 dimensi
x′ =Rijxj (i, j = 1,2,3) (1.3)
dimanaxiadalah komponen-komponen dari suatu vektordanRijadalah
matriks rotasi. Kesimetrian rotasi berasal dari asumsi keisotropikan ruang atau ketiadaan preferensi arah. Kesimetrian ini juga menun-jukkan bahwa sifat dari suatu sistem tidak bergantung pada orien-tasi sistem tersebut di dalam ruang. Konsekuensi dari kesimetrian ini adalah hukum kekekalan momentum angular.
(d) Transformasi Lorentz
x′µ = Λµ
νxν (µ, ν = 0,1,2,3) (1.4)
dimana xν merupakan suatu titik di dalam ruang-waktu Minkowski.
Persamaan(1.4) merupakan transformasi Lorentz antara 2 sistem yang bergerak relatif secara beraturan. Dalam relativitas khusus, Hukum-hukum fisis diformulasikan sedemikian sehingga Hukum-hukum tersebut iden-tik untuk semua kerangka acuan inersial. Dalam batas non relativisiden-tik, hukum fisika invarian terhadap transformasi galileo, yaitu bahwa tidak terdapat kecepatan absolut. Konsekuensi dari kesimetrian ini adalah hukum kekekalan yang terkait dengan generator dari grup Lorentz.
3. Kesimetrian ruang-waktu diskret
(a) Pembalikan ruang (pencerminan),P, dimana
Dalam mekanika kuantum, operasi pembalikan ruang didefinisikan oleh operator uniter yang menghasilkan suatu bilangan kuantum yang dise-but paritas, yang selalu kekal pada setiap interaksi alam, kecuali pada interaksi lemah.
(b) Pembalikan waktu, T, dimana
t→ −t (1.6)
Ini adalah perubahan arah aliran waktu. Diperkenalkan dalam mekani-ka kuantum oleh Wigner tahun 1932. Hukum-hukum fisimekani-ka secara umum simetrik terhadap waktu, kecuali misalnya untuk peluruhan K0
(c) Transformasi-transformasi simetri dari point groups, yang merupakan jenis transformasi dimana paling sedikit satu buah titik dari suatu sistem benda dalam ruang yang tetap pada posisinya, dan titik pa-da benpa-da tersebut menempati posisi yang sama setelah transformasi. Contohnya: rotasi terhadap sumbu tetap dan pencerminan terhadap suatu bidang.. Untuk material yang tak berhingga (tak tercacah), sepeti kisi kristal, translasi terhadap segmen tertentu juga temasuk agar diperoleh kesimetrian dasar dalam fisika molekul dan zat padat.
4. kesimetrian besaran internal kontinu
Berkaitan dengan transformasi-transformasi yang bekerja dalam ruang de-rajat kebebasan intrinsik pada partikel-partikel subnuklir, sebagai contoh, spin, cita rasa(flavor), color. FlavorF merupakan suatu derajat kebebasan yang bergantung pada beberapa derajat kebebasan lainnya yaiu: isospin I,
hypercharge Y,Charm C,Beauty B, dan Topness T. Kesimetrian in-ternal lebih sulit untuk dipelajari karena tidak nyata bila dibandingkan dengan Grup simetri. Pengalaman menunjukkan bahwa beberapa trans-formasi yang relevan akan membentuk grup yang uniter. Secara khusus, Keinvarianan terhadap transformasi-transformasi yang dideskripsikan de-ngan grup uniter U(1) akan menghasilkan kekekalan bilangan muatan dan partikel (khusus untuk Lepton, dan Baryon). Kesimetrian isospin dari in-teraksi kuat, yang dideskripsikan olehSUI(2), merupakan pengejawantahan
dari (hampir) kedegenerasian massa proton dan neutron. Bentuk alternatif lainnya adalah kesimetrianSUF(2) yang menjelaskan kedegenerasian massa
Asumsi teoritik Transformasi simetrik Konsekuensi
Ketidakterbedakan partikel identik Permutasi Statistik Fermi-Dirac
Kehomogenan Ruang Translasi Ruang Kekekalan Momentum Linier Kehomogenan Waktu Translasi Waktu Kekekalan Energi
Keisotropikan Ruang rotasi 3 dimensi Kekekalan Momentum Angular Ketiadaan kecepatan absolut Transformasi Lorentz Kekekalan Generator Grup Lorentz
Tabel 1.1: Beberapa kesimetrian dalam Fisika
5. kesimetrian besaran internal diskret.
(a) Konjugasi muatan, C. Dengan transformasi ini, tanda suatu muatan listrik berubah dari positif ke negartif dan sebaliknya. Ini merupakan kesimetrian antara partikel dan antipartikel. Dalam kerangka kerja persamaan Dirac, konjugasi muatan merupakan operator antiuniter , tetapi dalam teori medan merupakan operator uniter. Eksperimen-eksperimen yang mengkonfirmasi ketidakkekalan paritas dalam inter-aksi lemah juga memberi bukti terhadapC-violationatau keasimetrian partikel dan antipartikel.
(b) Paritas-G. Transformasi yang terkait dengan kesimetrian ini merepre-sentasikan konjugasi muatan yang dikombinasikan dengan rotasi sebe-sar π di dalam ruang isospin suatu partikel. Dalam interaksi kuat, paritas-G terkekalkan.
1.3
Metode Penelitian
Penelitian yang dilakukan di sini sifatnya hanya teoritik. Karena itu diperlukan suatu kerangka kerja yang sistematis dalam menerangkan proses-proses fisika yang terjadi. Kerangka kerja teoritik yang digunakan adalah teori grup dengan bersum-ber pada bebersum-berapa literatur utama, dan karena skripsi ini sifatnya studi literatur, maka akan terdapat banyak landasan teori dan tinjauan pustaka yang menyertai sebagai pendahuluan yang komplit terhadap pembahasan utama yang singkat
1.4
Tujuan
Bab 2
Tinjauan Pustaka
2.1
Elemen-elemen Teori Grup
Terdapat beberapa definisi dan pemahaman dasar dalam Teori Grup, antara lain definisi grup itu sendiri, pengertian kelas, subgrup, dan perkalian langsung.
2.1.1
Definisi Grup
Suatu himpunan G yang terdiri dari elemen-elemen transformasi g membentuk suatu grup jika memenuhi syarat-syarat berikut:
1. Hasil dari penerapan sembarang transformasi secara berturut-turut
g1 ∈G, g2 ∈G
merupakan suatu transformasi baru yang juga terdapat di dalam himpunan tersebut:
g1g2 =g ∈G (2.1)
Relasi ini disebut produk atau hukum komposisi
2. Hukum komposisi memenuhi sifat asosiatif untuk semuag1, g2, g3 ∈G,
(g1g2)g3 =g1(g2g3) (2.2)
3. Salah satu elemen transformasi merupakan elemen identitas, yaitu bahwa e∈G sedemikian sehingga
4. Kalau suatu elemen transformasi terdapat dalam himpunan tersebut, ma-ka invers dari transformasi itu juga terdapat dalam himpunan tersebut sedemikian sehingga:
gg−1 =g−1g =e (2.4)
Walaupun sifat asosiatif berlaku untuk semua grup, maka tidak demikian halnya dengan sifat komutatif. Namun terdapat grup yang memnuhi sifat komutatif, yang disebut grup abelian. Secara umum, dilihat dari kuantitas elemen dalam suatu grup, maka grup dapat dibagi menjadi 2 jenis utama, yaitu: (1) Grup berhingga (finite groups), (2) Grup tak berhingga (infinite groups).
Grup berhingga
Grup berhingga merupakan suatu grup dengan jumlah elemen yang berhingga N, dengan N menyatakan orde dari grup tersebut. Ada beberapa contoh Grup berhingga, 2 diantaranya adalah : Grup titik (Point groups) dan Grup simetrik (Symmetric groups)
1. Grup titik (Point groups)
Grup ini terkait dengan kesimetrian benda dimana minimal satu titik tetap pada posisi semula setelah proses transformasi terjadi. Transformasi-transformasi dalam grup ini tidak merubah jark dan dapat dibangun dari 3 jenis trans-formasi dasar:
(a) Rotasi sudut tertentu terhadap sumbu tertentu
jika sudutnya 2π/n, transformasi tersebut ditandai dengan Cn.
(b) Refleksi terhadap bidang
(c) Translasi
kesimetrian ini terjadi hanya pada benda tak berhingga yang meru-pakan ekstrapolasi dari benda yang nyata
2. Grup simetrik (Symmetric groups)
pembentuk sistem. Semua permutasi yang mungkin dari sekumpulan par-tikel membentuk Grup simetrik. Sebuah sistem parpar-tikel identik dideskrip-sikan dengan fungsi gelombang yang bersifat simetrik untuk boson dan anti-simetrik untuk fermion. Pandang nobjek dalam urutan 1,2,..,n. Permutasi menyatakan transisi dari urutan demikian menjadi urutan lain,a1, a2, ..., an.
Notasi untuk transisi ini adalah:
Pa =
Pada persamaan di atas, elemen-elemen dalam suatu kolom dapat saling dipertukarkan, yang artinya kita dapat mulai dari urutan awal sembarang, namun kita selalu melakukan pertukaran dari urutan i keai . Contoh:
Pa =
Jika permutasi di atas ini bekerja pada fungsi gelombang 5-partikel, kita akan peroleh
Paψ(1,2,3,4,5) =ψ(5,3,2,1,4) (2.7)
Permutasidari n objek menghasilkan suatu grup berorde N = n! , dengan elemen identitas:
Sedangkan invers dari sembarang elemen Pa adalah
P−1
Jika dalam grup terdapat suatu elemen permutasi lain
Pb =
maka penerapan Pa dan Pb secara berturut-turut, kita akan dapatkan
per-mutasi lain (yang juga merupakan elemen dari grup)
e (12) (13) (23) (123) (132)
Tabel 2.1: Tabel perkalian grup S3
Sebagai contoh:
Grup S3 merupakan salah satu contoh grup permutasi yang cukup sederhana
dan baik untuk dipelajari. Ada 3!=6 elemen grup S3 yaitu:
e =
Dari grup ini dapat dirancang tabel perkalian grup yang mengatur aturan perkalian antar elemen grup seperti yang diperlihatkan pada tabel (2.1):
Grup tak berhingga
Terdapat pula grup dengan banyak elemen tak berhingga. Grup semacam ini terpecah ke dalam 2 kategori
1. Grup Diskrit
memiliki elemen yang dapat dicacah karena dari satu elemen ke elemen lain terdapat perbedaan yang jelas
2. Grup Kontinu
terdapat banyak sekali elemen sehingga perbedaannya tidak jelas (kontinu). Namun pada skripsi ini, penekanan akan dilakukan pada grup kontinu de-ngan jumlah parameter berhingga.
2.1.2
Subgrup
Dari elemen-elemen grup kontinu G maupun diskrit, kita dapat memilih suatu subset H dan menuliskan
H ⊂G atau G⊃H (2.14)
untuk mengsimbolisasikan bahwa subset H terkandung dalam G. Jika subset H sendiri membentuk grup, maka H disebut subgrup dari G
Koset
Jika g merupakan salah satu elemen dari G, maka kita dapat membentuk him-punan elemen-elemen gH dengan mengalikan g dengan semua elemen H, maka terdapat korespondensi satu - satu antara H dan gH. Jika g ∈ H maka gH sendiri merupakan subgrup. Namun jika g ∈G dan tidak dikandung olehh, ma-ka gH bukan merupakan suatu grup karena tidak mengandung elemen identitas. gH yang terbentuk ini disebut sebagai koset kiri (lef t coset) dari H. Dengan cara yang analog, dapat didefinisikan koset kanan (right coset) Hg. Sembarang elemenGmerupakan bagian dari baik H, atau salah satu dari kosetnya. Sebagai contoh perhatikan kembali tabel (2.1) yang terdiri dari 4 subgrup berikut:
H1, e,(12)
H2, e,(13) (2.15)
H3, e,(23)
H4, e,(123),(132)
2.1.3
Isomorfisme dan Homomorfisme
Dua buah grup G dan G′ dikatakan isomorfik jika terdapat korespondensi
satu-satu antara elemen-elemen mereka, yaitu bahwa untuk setiap g ∈ G, terdap-at sterdap-atu dan hanya sterdap-atu g′ ∈ G′, korespondensi g ↔ g′ kekal terhadap hukum
perkalian.
saling isomorfik:
rotasiπ terhadap sumbu-x ↔(12)(34)↔a rotasi π terhadap sumbu-y ↔(13)(24)↔b rotasi π terhadap sumbu-z ↔(14)(23) ↔c
perkalian 3 rotasi di atas ↔(1)(2)(3)(4)↔e (2.16) Sedangkan sebuah grup G dikatakan homomorfik dengan G′, jika untuk
sem-barang g ∈ G, terdapat korespondensi antara tiap g′ ∈ G′ dengan minimal satu
g sedemikian sehingga g′
1g′2 =g′ atau G→G′. Contoh homomorfisme ada pada
baba 4 pada pembahasan homomorfisme antara SU(2) dengan O(3)
2.1.4
Kelas
Dua elemen adan bdari grupG dikatakan konjugat satu sama lain jika terdapat elemen ketiga x0 ∈Gsedemikian sehingga:
b =x0ax−01 atau a =x−01bx0 (2.17)
Jika 2 elemen a dan b konjugat terhadap c, maka ketiganya saling konjugat satu sama lain.
Kelas konjugasi (ataus kelas) merupakan sehimpunan elemen yang konjugat ter-hadap suatu elemen tertentu melalui seluruh elemen grup. Dari pembahasan di atas, dapat disimpulkan bahwa semua elemen dalam sautu kelas saling konjugat satu sama lain. Elemen-elemen suatu grup dibagi-bagi menjadi kelas-kelas yang berbeda. Jika kita tandai kelas-kelas dari suatu grupGdenganCi(i= 1,2, ..., K),
maka grup tersebut dapat ditulis sebagai gabungan kelas-kelas nya
G=C1∪C2∪...∪CK (2.18)
dimana K ≤ N untuk suatu grup berhingga berorde N. Sebagai contoh, ki-ta pandang kembali grup S3, kita pilih elemen (123) dan dengan menggunakan
berikut:
e(123)e= (123)
(12)(123)(12)−1 = (12)(13) = (132)
(13)(123)(13)−1 = (13)(23) = (132) (2.19)
(23)(123)(23)−1 = (23)(12) = (132)
(123)(23)(123)−1 = (123)
(132)(123)(132)−1 = (123)
Dengan proses yang serupa dengan di atas, kita dapatkan ternyata untuk S3
terdapat 3 buah kelas C1, C2, C3 dengan anggota-anggota sebagai berikut: C1 =
{e}, C2 ={(12),(13),(23)}, C3 ={(123),(132)}
Partisi
Permutasi dapat ditulis sebagai produk dari siklus tertutup tanpa elemen yang sama. Anggap dalam suatu permutasi dari n objek, siklus yang panjangnya i muncul sebanyak ki kali, maka haruslah
k1+ 2k2+ 3k3+...+nkn=n (2.20)
dimana ki ≥ 0. Setiap struktur siklik merepresentasi kelas, sehingga tiap set
bilangan bulat ki yang memenuhi (2.20) berkorespon dengan suatu kelas dari
grup Sn. Kita dapat perkenalkan lagi bilangan bulat
λ1 =k1 +k2+...+kn
λ2 = +k2+...+kn
.
.
λn= kn (2.21)
sehingga persamaan (2.20) menjadi:
λ1+λ2+...+λn=n (2.22)
dimana, λ1 ≥λ2 ≥...≥λn≥0
suku λi
k1 =λ1 −λ2
k2 =λ2 −λ3
. (2.23)
.
kn=λn
Dengan kata lain, terdaapt korespondensi satu-satu antara himpunan [k1, k2, ..., kn]
dan [λ1, λ2, ...λn]. Artinya terdapat korespondensi satu-satu antara suatu partisi
λ dengan suatu struktur siklik atau kelas, dan banyaknya partisin sama dengan banyaknya kelas dari Sn
2.1.5
Perkalian Langsung Grup
Kita dapat definisikan suatu grup G sebagai perkalian langsung antara 2 grup lain H1 dan H2 jika
1. semua elemen H1 commute dengan semua elemen H2
2. H1 dan H2 hanya memiliki satu elemen yang sama yaitu elemen identitas
3. Suatu elemen G dapat secara unik ditulis sebagai perkalian h1 ∈ H1 dan
h2 ∈H2:
g =h1h2 =h2h1 (2.24)
Dalam definisi yang lebih luas,Gmerupakan perkalian langsung jika ia isomopfik terhadap H1×H2. Perkalian langsung dapat diperumum ke lebih dari 2 faktor
asalkan semua Hi(i = 1,2, ..., n) kommut antar mereka. Semua grup ini harus
berbeda dan satu-satunya elemen yang sama hanya elemen identitas. Suatu sifat penting adalah bahwa tiap Hi merupakan subgrup invarian dari G
Suatu grup G merupakan produk semi langsung jika grup ini memiliki subgrup H1 dan H2 sedemikian sehingga
1. H1 merupakan subgrup invarian dari G
2. H1 dan H2 hanya memiliki elemen identitas sebagai satu-satunya elemen
yang sama
2.2
Representasi Linier Grup
Dalam mekanika kuantum, kita tertarik pada sifat-sifat keadaan eigen terhadap bermacam transformasi. Teori Grup menawarkan suatu cara sistematik untuk menemukan sifat-sifat ini dari kesimetrian Hamiltonian. Keadaan eigen memben-tukruang vektor linier yang menyediakan representasi matriks dari grup transfor-masi G. Coba kita tandai represntasi yang demikian itu denganD(g) dimana g merupakan salah satu elemen dari G
Kasus yang sederhana secara trivial dari suatu representasi diperoleh untuk grup pembalikan (inversi) dimana matriks berukuran 1×1. Dua elemen dari grup adalah elemen identitas e(x → x) dan P(x → −x). Untuk sembarang keadaan dengan paritas genap, π = +1, representasinya adalah
D(e) = 1 D(P) = 1 (2.25)
Keadaan dengan paritas ganjil, π=−1, memberikan representasi
D(e) = 1 D(P) = −1 (2.26)
Suatu representasi dibentuk dari matriks-matriks sebanyak jumlah elemen dalam grup.
2.2.1
Definisi Representasi Grup
Suatu grup Γ dari operator-operator linier didefinisikan dalam ruang vektor berdi-mensi berhinggaLdikatakan suatu representasi linier dari suatu sembarang grup G jika G homomorfik terhadap Γ. Coba kita sebut operator yang berkaitan de-ngan g ∈G denganS(g). Maka kita peroleh
S(g1)S(g2) =S(g1g2) (2.27)
S(e) =e (2.28)
S(g−1) = S−1(g) (2.29)
Relasi ketiga berasal dari fakta bahwa operatorS(g) haruslah non-singular, yaitu bahwa ia memiliki invers S−1(g) agar dapat memenuhi aksioma suatu grup.
Se-hingga dapat kita tuliskan
S(g)S−1(g) =e (2.30)
Padahal gg−1 =e mengakibatkan
S(g)S(g1) = S(e) =e (2.31)
2.2.2
Representasi Matriks
Jika dimensi Ladalah n maka suatu representasi memilii derajat n atau dengan kata lain representasi tersebut berdimensi-n. Malahan,operator-operator S(g) menghasilkan matriks-matriks berukuran n×n yang bekerja pada vektor basis
|1>,|2>, ...,|n > dari L
S(g)|k >=XDikµ(g)|i > (2.32) Matriks-matriks Dµ(g) membentuk representasi matriks dari grup G. Biasanya
matriks ini diberikan indeks superskrip µ yang berkaitan dengan dimensi dari representasi. Notasi yang umum untuk suatu representasi matriks adalah Γ atau D.
Coba kita ambil suatu set fungsiψ1, ψ2, ...ψnyang berkorespon dengan nilai eigen
yang sama dari suatu hamiltonian H. MisalnyaH invarian terhadap grup trans-formasi Γ yaitu
[H, S(g)] = 0 (2.33)
maka sembarang fungsi baru S(g)ψi berkorespon dengan nilai eigen yang sama.
Matriks transformasi dari ψi ke S(g)ψi merupakan suatu representasi linier dari
G. Ini merupakan suatu kasus khusus dari apa yang sering disebut sebagai sub-space invarian dalam teori grup. Dalam suatu ruang linier L, sangatlah mungkin untuk menemukan suatu subspaceL′ dengan vektor basisψ
i memiliki sifat bahwa
suatu vektor yang telah ditransformasi S(g)ψi juga merupakan elemen dari L′.
Maka L′ dikatakan subspace invarian jika sifat ini dimiliki oleh semua
transfor-masi S(g) dari transformasi Γ
2.2.3
Representasi Ekivalen
Ambil 2 buah representasi S(g) danS′(g) berturut-turut dalamLdanL′. Jika L
dan L′ memiliki dimensi yang sama dan dapat dicari operator linier non-singular
M yang mengubah L dan L′ ke satu sama lain sedemikian sehingga
M S(g) =S′(g)M (2.34)
untuk tiap g maka 2 representasi tersebut dikatakan ekivalen. Dengan kata lain, jika kita mengubah basis di dalam ruangLdengan matriksM representasi terse-but akan menjadi
Sembarang transformasi dari suatu matriks yang memiliki bentuk (2.35) dikatakan transformasi keserupaan
2.2.4
Representasi Uniter
Dalam mekanika kuantum, fungsi gelombang merupakan vektor keadaan atau kombinasi linier dari vektor-vektor keadaan, yaitu keadaan eigenψi dari
hamilto-nian. ψi membentuk ruang Hilbert, yang mana dalam produk skalar didefinisikan
dengan
< ψi|ψj >=< ψj|ψi >∗ (2.36)
Vektor basis ψi dapa dipilih yang ortonormal yaitu memenuhi:
< ψi|ψj > δij (2.37)
Suatu operatr U dikatakan unitary jika
< U φ, U ψ >=< φ, ψ > (2.38)
Untuk basis ortonormal, hal ini mengimplikasikan
< U ψi|U ψj >=< ψi|ψj >=δij untuk semuai, j (2.39)
Matriks yang berasosiasi dengan U dalam basis ortonormal merupakan matriks unitary
U U† =U†U = 1 (2.40)
Jika operator-operator dari suatu representasi S(g) dari suatu grup G bersifat uniter, maka representasinya disebut representasi uniter. Kebanyakan grup yang menarik di Fisika memiliki representasi uniter atau representasi yang dapat di-ubah menjadi transformasi uniter.
Dalam subbab ini ada suatu teori penting: Setiap representasi ekivalen terhadap suatu representasi uniter untuk grup Lie kompak yang berhingga.
Bukti: Untuk grup berhingga ada suatu pembuktian yang baku seperti yang akan dijabarkan di bawah ini.
Kita perkenalkan suatu operator penjumlahan invarian berikut
H2 = 1 N
X
h∈G
S†(h)S(h) (2.41)
bahwa nilai eigennya real dan positif. Maka adalah sah jika kita definisikan suatu akar dari operator H berikut:
H= (H2)12 (2.42)
Operator H memberikan representasi ekivalen
S′(g) =HS(g)H−1 (2.43)
yang akan kita buktikan bersifat uniter. Mula-mula kita tunjukkan dahulu bahwa
S†(g)H2S(g) = 1 N
X
h∈G
S†(g)S†S(h)S(g)
= 1
N
X
h∈G
S†(hg)S(hg) (2.44)
= 1
N
X
h′∈G
S†(h′)S(h′)
= H2
dimana h′ = hg juga dijumlahkan terhadap seluruh elemen G, disusun ulang
dengan perkalian di sisi kanan, dengan elemen tetapg. Mengalikan (2.44) dengan H−1 di sebelah kiri danS−1H−1 di sebelah kanan, kita peroleh
H−1S†(g)H =HS−1H−1 (2.45)
atau secara alternatif, dengan menggunakan fakta bahwa H bersifat hermitian,
¡
HS(g)H−1¢†=¡HS(g)H−1¢−1 (2.46)
atau dengan menggunakan definisi (2.43)
S′†(g) =S′−1(g) (2.47)
yang membuktikan bahwa representasi ekivalenS′bersifat uniter. Bukti ini dapat
diperumum untuk grup Lie kompak melalui penggunaan integrasi invarian ter-hadap elemen-elemen grup alih-alih menggunakan penjumlahan invarian (2.41).
2.2.5
Representasi Iredusibel
basis untuk representasi iredusibel.
Jika dalam ruang vektor linier L, kita dapat menemukan suatu basis dimana matriks-matriksD(g) dari representasi berdimensi-ndapat secara simultan ditulis dalam bentuk:
untuk semua elemen g dari grup G, representasi D(g) dikatakan redusibel. Blok matriks di sini adalah 2 matriks persegi D1 dan D2 berdimensi n
1 dan n2 dan 2
matriks segiempat, dimana salah satunya memiliki semua elemen sama dengan nol yaitu pada matriks yang terletak pada sebelah kiri bawah. Bentuk yang demikian menunjukkan keberadaan subspace invarian L1 berdimensi n
1. Coba
vektor-vektor yang merupakan bagian dari L1 saja. Maka
kita tuliskan µ
yaitu bahwa vektor yang telah bertransformasi juga merupakan bagian dari L1.
Coba sekarang kita ambil vektor
µ
0 X2
¶
yang merupakan milik/bagian dariL2,
maka hasilnya
yaitu suatu vektor yang menjadi bagian dari keseluruhan ruang. Maka, agar L2 menjadi subspace invarian, kita harus mengambil C = 0. Jika matriks C
nol, representasi D dikatakan f ully redusibel. Maka, terdapat suatu subspace invarian kedua L2 berdimensi n
2 dan keseluruhan ruang L dapat ditulis sebagai
penjumlahan langsung
L=L1 +L2 (2.51)
dan representasi D merupakan penjumlahan
D=D1+D2 (2.52)
Jika untuk representasi tertentuD, tidak ada transformasi keserupaan yang mem-bawa matriks-matriks D(g) ke dalam bentuk diagonal secara simultan untuk se-muag ∈Gmaka representasi tersebut dikatakan iredusibel atau disingkat irreps. Dalam kasus representasi f ully redusibel, matriks D1 dan D2 dapat direduksi
lebih jauh lagi menjadi penjumlahan matriks-matriks berdimensi lebih kecil lagi yang iredusibel. Notasi untuk penjumlahan yang didefinisikan menurut () adalah
Untuk representasi uniter, redusibilitas secara langsung berarti f ully redusibel. Coba kita ambil suatu basis ortonormal e1
i ∈L1, e2i ∈L2:
(e1
i, e1j) = (e2i, e2j) = δij (e1i, e2j) = 0 (2.54)
Keinvarianan subspace L1 berarti bahwa
S(g)e1i =
n1
X
j=1
D1jie1j (2.55)
sedangkan, untuk suatu vektor dalam L2, kita punya
S(g)e2j =
Relasi ortogonalitas (2.54) memberikan
Cij = (e1i, S(g)e2j) (2.57)
Namun secara definisi S merupakan operator uniter yang menghasilkan
Cij =< S−1(g)e1i, e2j >=< S(g−1)e1i, e2j >= 0 (2.58)
jadi matriksC dalam persamaan (2.50) memiliki semua elemen sama dengan nol. MakaL2 juga merupakan subspace invarian. Representasi redusibel dapat
dipec-ah lagi dan lagi menjadi blok-blok matriks sepanjang diagonalnya sampai hanya mengandung representasi iredusibel. Dalam mekanika kuantum, mereduksi su-atu representasi berkaitan erat dengan eliminasi kedegenerasian atau melengkapi pelabelan fungsi gelombang. Hal ini terjadi karena jika suatu representasi ire-dusibel untuk keseluruhan grup, bisa jadi representasi tersebut reire-dusibel bagi subgrupnya.
2.2.6
Perkalian langsung Representasi
Dari 2 representasi matriks,Dµ1(g) danDµ2(g) berdimesnin
1, dann2, kita dapat
mengkonstruksi suatu representasi Dµ(g) sebagai suatu produk /perkalian
lang-sung atau kronecker dari 2 matriks . Ini merupakan matriks berukuran n1×n2
dengan elemen-elemen yang dilabeli 2 indeks
Dµik,jl(g) =Dµ1 ij (g)D
µ2
kl(g) (2.59)
Matriks Dµ mendeskripsikan sifat transformasi dari produk fungsi ψ1
jψ2l, jika
dan ψ2. Fungsi fungsi ini dapat mendeskripkan 2 partikel-partikel yang berbeda
atau bagian-bagian yang independen dari sistem yang sama. Secara terpisah kita peroleh
S(g)ψ1j =XDµ1ij ψi1; S(g)ψl2 =XDklµ2ψ2k
dan untuk sistem gabungan kita peroleh
S(g)ψ1
jψ2l =
X
Dµ1ij Dklµ2ψ1
iψk2
= XDµik,jlψi1ψ2k
Perkalian langsung menawarkan suatu cara untuk menghasilkan representasi-representasi baru dari representasi-representasi lama. Jika Dµ1
dan Dµ2
iredusibel, maka secara umum matriks Dµ bersifat redusibel. Orang tertarik untuk menemukan
irreps yang mana yang terjadi dalam Dµ. Masalah matematis ini memiliki
im-plikasi yang penting dalam fisika. Misalnya, dalam kopling 2 momentum sudut j1 dan j2 yang menghasilkan |j1 −j2| ≤ j ≤ j1+j2, terkait dengan irreps grup
rotasi yang diperoleh dari perkalian langsung 2 irreps yang berkorespon dengan µ1 =j1 dan µ2 =j2
2.2.7
Perkalian Luar Representasi
Untuk grup simetrik, orang biasanya memperkenalkan 2 jenis perkalian (pro-duk) representasi.Yang pertama adalah perkalian langsung /perkalian dalam yang terkait dengan produk fungsi dari partikel yang sama. Sedangkan perkalian luar terkait dengan produk fungsi-fungsi dari partikel-partikel berbeda.
Dalam Fisika, orang biasanya mempunyai 2 sistem partikel 1,2,...,m dan m+ 1, m+2, ...nyang dideskripsikan oleh fungsi gelombangψ[f1](1,2, ..., m) danψ[f2](m+
1, m+ 2, ..., n) dari kesimetrian tertentu [f1],[f2] berturut-turut terhadap
permu-tasi partikel. Dengan kata lain, ψ[f1] merupakan bagian dari subspace invarian
dari irreps [f1] dan ψ[f2] merupakan bagian dari subspace invarian dari irreps
[f2]. Sekarang kita hendak mengkonstruksi keadaan-keadaan produk dari sistem
terkombinasi ψ[f1]
(1,2, ..., m)ψ[f2]
(m+ 1, m+ 2, ..., n). Masalahnya adalah men-cari kesimetrian permutasi [f] yang mungkin dari total fungsiψ[f](1,2, ..., m, m+
1, m + 2, ..., n). Nilai dari [f] diberikan oleh perkalian luar. Jadi, melakukan perkalian luar dari 2 irreps [f1] dariSn1 dan [f2] dariSn2, berarti mendekomposisi
matriks yang merupakan representasi redusibel dari Sn1+n2 ke dalam suku-suku
dapat tuliskan
[f1]⊗[f2] = [f2]⊗[f1] =
X
[f]
m[f][f] (2.60)
Mula-mula pandang kasus paling sederhana dimana salah satu dari sistem diben-tuk oleh satu partikel saja, yaitu ambil [f2] = [1]. Untuk sistem lain ambil
mis-alnya irreps [f1] = [321] dari S6. Hasilnya harus merupakan suatu penjumlahan
dari irreps dari S7
⊗ a =
a
+
a
+ a + a (2.61)
Diagram pada sisi kanan diperoleh dari [321] dengan menempelkan kotak tamba-han a dengan semua cara yang mungkin sedemikian sehingga diperoleh diagram young yang benar. Jika pada akhirnya kita memilih Young tableau dideskripsikan dengan simbol YamanuchiY1=(312211) kita dapat menuliskan (2.61) dalam
ben-tuk eksplisit
n2 6= 1, cara yang diterapkan adalah meletakkan kotak label-label awal (sesuai
penjumlahan irreps [f] dari S8
Dalam suku-suku partisi, diagram young di atas dapat ditulis
[22]⊗[212] = [431] + [4212] + [2312] + [3212] + [322] + [3221] + [3213] (2.64) Dalam contoh in, tiap representasi [f] dari S8 muncul dengan multisiplitas lebih
dari satu. Sangatlah mungkin mengetes validitas dari hasil reduksi dengan meng-gunakan argumen dimensionalitas. Dimensi-dimensi dari partisi yang terhubung melalui perkalian luar memenuhi persamaan yang merupakan konsekuensi dari persamaan (2.60) berikut:
Dengan menggunakan argumen yang berdasar pada dimensi suatu irreps, suatu uji coba alternatif dapat dicapai dengan mempertimbangkan bahwa semua dia-gram young yang muncul pada sisi kiri dan kanan persamaan (2.60) berasosiasi dengan irreps yang sama dari SU(N). Untuk SU(N) maka persamaan dimensi yang harus dipenuhi adalah:
dSU[f1](N)×dSU[f2](N) =X
[f]
m[f]dSU[f](N) (2.66)
dimana dimesi dari SU(N) sendiri menurut representasi [f] adalah
dSU[f](N)=
5 merupakan bilangan yang menyatakan jumlah baris terbesar yang muncul pa-da diagram yang sama papa-da sisi kanan persamaan (2.63)pa-dan (2.64). Lalu dengan menggunakan (2.67) untuk SU(5) kita peroleh
d[22] = 50 d[212
]= 45 d[431] = 1050 d[332] = 315
d[3221] = 175 d[2312]= 10 d[4212]= 450 d[3212]= 210
d[3212
]= 40
yang memenuhi (2.66)
2.2.8
Perkalian Dalam
Perkalian dalam sering juga disebut perkalian kronecker atau perkalian langsung representasi karena mengacu kepada perkalian irreps dari Sn. Aplikasi fisis dari
perkalian dalam dapat dimengerti misalnya pada suatu partikel mikroskopik yang dideskripsikan dengan suatu fungsi gelombang ψ yang biasanya dinyatakan seba-gai suatu perkalian dari beberapa fungsi, masing-masing mepresentasikan suatu derajat kebebasan. Misalnya, untuk sebuah kuark , terdiri dari 3 derajat ke-bebasan koordinat ruang R, spin χ, citarasa φ, dan warna C. Untuk suatu sistem dengan n partikel, kita dapat memperlakukan kesimetrian permutasi se-cara individual pada setiap derajat kebebasan dan mengkonstruksi suatu fungsi gelombang total dari kesimetrian Sn tertentu. Peran dari perkalian dalam adalah
menyediakan fungsi gelombang n-partikel dari kesimetrian yang dikehendaki se-bagai suatu kombinasi linier dari perkalian fungsi, masing-masing faktor dalam fungsi ini merepresentasikan suatu derajat kebebasan dan memiliki kesimetrian permutasi yang cocok dengan kesimetrian fungsi gelombang secara total.
Secara umum, perkalian dalam dari 2 buah irreps [f′] dan [f′′] dari S
n
membangk-itkan penjumlahan irreps Sn
[f′]×[f′′] =Xm[f][f] (2.68)
Ini dikatakan sebagai deret Clebsch −Gordan dari Sn. Subspace invarian [f]
dibentuk oleh vektor-vektor |[f]Y > didefinisikan sebagai jumlah dari perkalian
|[f′]Y′ > dan |[f′′]Y′′> melalui
|[f]Y >= X
Y′,Y′′
S([f′]Y′[f′′]Y′′|[f′]Y′)|[f′]Y′ >|[f′′]Y′′ > (2.69)
Koefisien-koefisien S([f′]Y′[f′′]Y′′|[f]Y) merupakan koefisien Clebsch−Gordan
trans-formasi antara basis-basis |[f]Y > dan |[f′]Y′ > |[f′′]Y′′ >. Dengan
menggu-nakan sifat ortogonalitas dari matriks ini, kita dapat mengubah relasi (2.69) untuk menghasilkan
|[f′]Y′ >|[f′′]Y′′ >=X
[f]Y
S([f′]Y′[f′′]Y′′|[f]Y)|[f]Y > (2.70)
Sekarang, kita akan pelajari perkalian S3.
Ruang spin dan isospin suatu nukleon dapat menghasilkan ruang berdimensi-4 dengan perkalian langsung. Sembarang vektor x dalam ruang ini dapat ditulis sebagai
x=
u↑ u↓ d↑ d↓
(2.71)
dan kita dapat memperkenalkan aksi dari grup
SU(4)⊃SUS(2)×SUI(2)
dimana sisi kanan persamaan merupakan perkalian langsung dari SUS(2) yang
bekerja pada ruang spin dan SUI(2) bekerja pada ruang isospin. Dimensi dari [2]
dan [11] sebagai irreps SU(4) dapat dihitung menggunakan formula (2.67) dan menghasilkan
dSU[2](4) = 10 dSU[11](4) = 6 (2.72)
Representasi-representasi [2] dan [11] dari SU(4) dapat didekomposisikan dengan cara berikut:
SU(4) = SU(2)× SU(2) + SU(2)× SU(2)(2.73)
SU(4) = SU(2) × SU(2) + SU(2) × SU(2) (2.74)
Dari persamaan di atas dapat dicek bahwa ternyata dimensi dari masing-masing representasi juga memenuhi persamaan tersebut.
Untuk S3, perkalian dalam dapat diperoleh sebagai perluasan dari teknik yang
dijelaskan di atas. Coba kita anggap bahwa masing-masing dari 3 objek-objek ini adalah suatu partikel, yang mana merupakan vektor SU(4). Mula-mula kita kerjakan perkalian luar [2] dari S2 dan [1] dari S1:
Ini juga merupakan perkalian langsung dari 2 irreps SU(4) yang diindikasikan oleh diagram young dan dimensi mereka. Pada sisi lain, pada sisi kiri persamaan di atas, kita dapat gunakan relasi (2.73) dan
SU(4) = SU(2) × SU(2) (2.76)
untuk memperoleh
⊗ =
× + ×
⊗
³
× ´
=³ ⊗ ´×³ ⊗ ´+
⊗
×
⊗
=
+
×
+
+ ×
= × + × + ×
+2 × (2.77)
Sekarang, kita dapat identifikasi 2 suku pada sisi kanan persamaan (2.75) sebagai
SU(4) = SU(2)× SU(2) + SU(2)× SU(2)
(2.78) dan
SU(4) = SU(2)× SU(2) + SU(2)× SU(2)
+ SU(2)× SU(2) (2.79)
Ini adalah dekomposisi dari irreps SU(4) ke dalam irreps SU(2)×SU(2). Suku per-tama pada sisi kanan persamaan (2.78) harusnya kita antispiasi karena perkalian dari 2 keadaan simetrik menghasilkan keadaan simetrik.
Berikutnya pandang perkalian luar berikut
dan dengan menggunakan relasi (2.74) dan (??) pada sisi kiri persamaan, kita
Dengan memperhitungkan (2.79) kita dapaka identitas
SU(4) = SU(2) × SU(2) (2.82)
Dari sudut pandang S3, kita dapat menggunakan relasi (2.78),(2.79),(2.82)
un-tuk memperoleh deret Clebsch−Gordan. Misalnya, jika kita mencari perkalian dalam [21] × [21], ternyata itu muncul sekali masing-masing pada persamaan (2.78),(2.79),(2.82), sehingga dapat kita tuliskan
[21]×[21] = [3] + [21] + [13] (2.83)
dengan analogi, kitapun bisa dapatkan
[3]×[3] = [3] (2.84)
[3]×[21] = [21]×[3] = [21] (2.85)
Untuk kelengkapan kita dapat tambahkan deret-deret Clebsch−Gordan berikut
[3]×[13] = [13] (2.86)
[13]×[13] = [3] (2.87)
deret Clebsch−Gordan, kita harus menggunakan minimal SU(4). Sesungguh-nya relasi semacam (2.86) merupakan kasus khusus dari deretClebsch−Gordan yang lebih umum yang mana Suntuk sebarang [f] dari Sn tertentu memenuhi
persamaan
[f]×[1n] = [1n]×[f] = [ ˜f] (2.88) dimana [ ˜f] menyatakan representasi konjugat dari [f]. Deret persamaan (??) merupakan kasus khusus dari (2.88) karena partisi [21] bersifat self−conjugate. Sifat lain yang cukup berguna adalah
[f]×[˜g] = [˜g]×[g] (2.89)
[f]×[g] = [ ˜f]×[˜g] (2.90)
mereka alngsung diperoleh dari sifat komutatif dan distributif dari perkalian dalam
([f]×[g])×[h] = [f]×([g]×[h]) = ([f]×[h])×[g] (2.91) Dengan mengambil [h] = [1n] dan menggunakan (2.88) kita bisa turunkan (2.89),dan
Bab 3
Grup Lie
Grup Lie merupakan grup kontinu dengan jumlah elemen tak terhingga. Walau demikian, elemen-elemen di dalam grup ini dapat dilabeli dengan himpunan berhingga r parameter-parameter real yang kontinu. Oleh sebab itu, Grup Lie kadang disebut juga sebagai Grup kontinu berhingga (finite continous group). Grup Lie ini dikembangkan oleh ahli matematika kebangsaan Norwegia, Sophus Lie. Tidak seperti Grup diskret sebelumnya, Grup Lie ini tidak mungkin dibu-at tabel perkalian grup nya. Namun struktur grup ini ditentukan melalui se-himpunan hubungan komutasi antara generator-generator dari grup, yang mana banyaknya generator ini juga sama dengan r
3.1
Transformasi infinitesimal
Pandang sehimpunannvariabelxi
0(i= 1,2, ..., n) yang merepresentasikan
koordinat-koordinat suatu titik dalam basis tertentu di dalam ruang berdimensi-n. Trans-formasi basis mengubah xi
0 menjadi xi melalui persamaan
xi =fi(x1
0, x20, ..., xn0;a1, a2, ..., ar) (3.1)
dimana aρ(ρ = 1,2, ..., r) merupakan sehimpunan parameter bebas real dan fi
merupakan fungsi analitik dan bergantung secara esensial pada aρ. Dengan kata
lain, aρ menentukan fi secara unik dan komplit, yang artinya tidak ada 2 atau
lebih transformasi (dengan parameter berbeda) yang sama untuk semua nilai x0
dan r menyatakan jumlah terkecil parameter yang dibutuhkan. Dalam notasi yang lebih singkat, (3.1) dapat ditulis
dimana sehimpunan transformasi bergantung pada parameter a dan memetakan titik x0 ke x. Sehimpunan transformasi fi membentuk grup jika memenuhi
ak-sioma berikut:
1. Dua transformasi berturut-turut menghasilkan transformasi lain yang juga merupakan anggota himpunan yang sama. misalnya:
x=f(x0;a) dan x′ =f(x;b) (3.3)
dan lalu
x′ =f(x;b) =f(f(x
0;a);b) = f(x0;c) =f(x0;ϕ(a;b) (3.4)
yang menyatakan bahwa terdapatnya sehimpunan parametercρyang
didefin-isikan melalui
cρ =ϕρ(a;b) (3.5)
yang berarti bahwa ϕ merupakan fungsi analitik dari a dan b, yaitu ia mengandung semua turunan orde berapapun terhadap a dan b
2. Untuk tiap transformasi terdapat invers yang unik
x0 =f(x; ¯a) (3.6)
yang juga merupakan elemen dari himpunan yang sama. Keunikan nilai ¯a dijamin oleh kondisi
¯ ¯ ¯ ¯
∂f ∂x0
¯ ¯ ¯
¯6= 0 (3.7)
yaitu bahwa jacobian dari transformasi tidak boleh bernilai nol.
3. terdapat transformasi identitas dan didefinisikan sebagai berikut:
x0 =f(x; ¯a) = f(f(x0;a); ¯a) =f(x0;ϕ(a; ¯a)) =f(x0;a0) (3.8)
untuk kemudahan, dapat dipilih
aρ0 = 0 (ρ= 1,2, ..., n) (3.9)
”sekitar” elemen identitas ini menentukan struktur grup secara keseluruhan.
Dari sifat yang dibahas di atas, kita dapat tuliskan 2 ekspresi ekivalen berikut:
x=f(x0;a) (3.10)
x=f(x; 0) (3.11)
Suatu transformasi infinitesimalx+dxdapat diperoleh dengan 2 cara: mendifer-ensialkan (3.10)
x+dx=f(x0;a+da) (3.12)
atau dengan memperkenalkan parameter infinitesimal δa sedimikian sehingga
x+dx=f(x;δa) (3.13)
dan menulis ulang persamaan(3.15) sebagai
dxi =uiσ(x)δaσ (3.17)
Sama seperti persamaan (3.4), kita dapat tulis
x=dx=f(x;δa) =f(f(x0;a);δa) = f(x0;ϕ(a;δa))
Dari ekivalensi antara (3.13) dan (3.14) dapat ditulis
a+da=ϕ(a;δa) (3.18)
Jika dipilih δa= 0 maka
x=f(x; 0) =f(x0;ϕ(a; 0)
sehingga
a=ϕ(a; 0) (3.19)
3.2
Konstanta Struktur
Untuk perubahan infinitesimal δaτ dalam parameter-parameter aτ , persamaan
(3.18) dapat ditulis sebagai
a+da=ϕ(a;δa) = ϕ(a; 0) + ∂ϕ(a;b)
menggunakan (3.19) didapat bahwa
daρ =µρτδaτ (3.21)
dimana
µρτ(a) = ∂ϕ(a;b)
∂bτ b=0 (3.22)
yaitu bahwa daρ merupakan kombinasi linier dari δaτ, dan sebaliknya,δaτ dapat
ditulis sebagai kombinasi linier dari daρ jika matriks µρ
τ tak singular. Dengan
mendefinisikan λ sedemikian sehingga
λµ= 1 atau λσρµρτ =δτσ (3.23)
kita dapat tuliskan
δaσ =λσρ(a)daρ (3.24)
dengan notasi ini, persamaan (3.17) dapat ditulis sebagai
dxi =uiσ(x)λσρ(a)daρ (3.25)
Pada sisi lain persamaan (3.14) dapat ditulis sebagai
dxi = ∂xi
Syarat cukup dan syarat perlu dari sistem adalah
∂2xi
∂aσ∂aρ =
∂2xi
∂aρ∂aσ (3.28)
syarat ini menghasilkan persamaan
atau dengan menggunakan persamaan (3.23), kita dapatkan
σ tidak bergantung padaaτ menurut definisi(3.16), diferensiasi terhadap
persamaan (3.30) menghasilkan
τ saling bebas linier dan tidak bergantung terhadap indeks τ.
Ini berasal dari sifat bahwa parameter-parameter aτ esensial dalam transformasi
(3.1). Karena ui
τ saling bebas linier, maka
∂cτ κδ
∂aρ = 0 (3.34)
yaitu bahwa cτ
κδ tidak bergantung a. Besaran cτκδ disebut konstanta struk-tur dari grup Lie, dan memainkan peran yang penting dalam sifat grup. Dari persamaan (3.30) didapat bahwa
cτκδ =−cτδκ (3.35)
Secara definisi, parameter-parameter grup Lie bersifat real , dan semua relasi yang mendeskripsikan struktur grup harus menyangkut bilangan real. Inilah sebabnya konstanta struktur harus berupa bilangan real. Dari konstanta struktur, kita dapat mengkonstruksi suatu tensor rank 2 yang simetrik
gρτ =cµρλcλτ µ (3.36)
yang disebut sebagai tensor metriks atau Killing form. Sifatnya telah digunakan oleh Cartan untuk membedakan grup-grup semi simpel dari grup-grup lainnya. Tensorgρτ juga bermanfaat untuk menaikkan dan menurunkan indeks dari
struk-tur konstan. Misalnya
cµνσ =cλµνgλσ (3.37)
3.3
Generator
Pandang sebuah fungsi F dari koordinat xi. Suatu transformasi infinitesimal
xi →xi+dxi mengubah F dengan perubahan yang kecil sekali melalui
dF = ∂F ∂xidx
i =δσui σ
∂F ∂xi =δa
σX
σF (3.38)
dimana operator-operator
Xσ =uiσ
∂
∂xi (3.39)
disebut operator-operator infinitesimal atau generator dari grup transformasi yang telah didefinisikan menurut (3.2). dari (3.30) ternyata, dapat ditulis relasi komutasi berikut
[Xκ, Xδ] =cτκδXτ (3.40)
Sifat bebas linier dari ui
τ menghantarkan ke sifat bebas linier dari operator Xτ.
Mereka membentuk ruang vektor berdimensi-r. Produk Lie atau ’Lie product’ dari sembarang 2 vektor basis ruang ini didefinisikan melalui komutator mereka, yang memerikan vektor basis lain (di ruang yang sama). Ini artinya sehimpunan basis vektor ini bersifat tertutup terhadap hukum perkalian grup. Operator-operator infinitesimal r membentuk ruang vektor berdimensi-r yang dikarakter-isasi oleh besaran-besaran ΣaτX
τ. Melalui cara inilah, Generator atau
operator-operator ini membentukAljabar Lie real. Untuk setiap grup Lie terdapat aljabar Lie real yang unik. Meski demikian, beberapa grup Lie non-isomorfik dapat berkorespon teerhadap aljabar Lie real yang sama.
Suatu aljabar Lie L berdimensi n(≥1) memiliki sifat berikut:
[Xρ, Xσ]∈ L Xρ, Xσ ∈ L (3.41)
[αXρ+βXσ, Xτ =α[Xρ, Xτ] +β[Xσ, Xτ] (3.42)
untuk Xρ, Xσ, Xτ ∈ L dan semua bilangan real α dan β;
[Xρ, Xσ] =−[Xσ, Xρ] (3.43)
[[Xρ, Xσ], Xτ] + [[Xσ, Xτ], Xρ] + [[Xτ, Xρ], Xσ] = 0 (3.44)
Ini merupakan identitas jacobi atau kondisi assosiatif.
Penerapan persamaan (3.40) ke dalam persamaan (3.44) menghasilkan hubungan
yang merupakan relasi penting dan merupakan sifat penting konstanta struktur selain (3.35). Persamaan (3.35) dan (3.45) berasal dari asumsi bahwa trans-formasi fi membentuk grup. Sebaliknya, mulai dari persamaan-persamaan ini,
kita dapat mencari semua nilai u dan λ yang memenuhi persamaan (3.30) dan (3.32), dan menentukan xi yang memenuhi (3.27) dan membentuk sebuah grup.
Ada suatu perhitungan sederhana yang membuktikan bahwa konstanta struk-tur cρσλ bersifat antisimetrik terhadap transposisi 2 sembarang indeks, dan
in-varian terhadap sembarang permutasi sirkular. Persamaan (3.35) membuktikan keantisimetrian terhadap transposisi 2 indeks pertama, sehingga cukup bagi kita untuk membuktikan keantisimetrian terhadap transposisi indeks 2 dan 3. Dari persamaan (3.36) dan (3.37), ternyata:
cρσλ =cτρσgτ λ =cτρσcντ µc µ λν
menerapkan sifat (3.45) pada faktor pertama dan kedua, persamaan di atas dapat ditulis ulang sebagai
cρσλ =−cτσµcντ ρc µ
λν−cτµρcντ σc µ λν
dan dengan menggunakan (3.35) untuk faktor kedua dari suku pertama dan faktor ketiga untuk suku kedua, kita dapatkan
cρσλ =cτσµcνρτc µ
λν +cτµρcντ σc µ νλ
Sekarang kita permutasikan λ dengan σ pada sisi kiri dan sisi kanan persamaan di atas, sehingga menghasilkan
cρσλ =cτλµcνρτcσνµ +cτµρcντ λcµνσ
menerapkan (3.35) pada semua c dan menyusun ulang suku-suku dan faktor-faktor akan menghasilkan
cρσλ =−cµσνcτρµcνλτ −cντ ρcµνσcτµλ
Lalu melakukan permutasi melingkar dari indeks-indeks berulang µ → τ → ν pada suku pertama dan τ →µ→ν pada suku kedua, kita dapatkan
cρσλ=−cτσµcνρτcµλν −cτµρcντ σcµνλ =−cρσλ
yang membuktikan keantisimetrian terhadap permutasi λ dengan σ. Menurut sifat konstanta struktur pada persamaan kedua di atas dan sifat kesimetrian dari gρτ, kita dapat tuliskan
Dengan menggunakan persamaan (3.38), kita dapat tuliskan
F(x+dx) = F(x) + ∂F ∂xidx
i =S
δaF (3.46)
dimana operator
Sδa= 1 +δaσXσ (3.47)
mempengarui perubahan infinitesimalF →F+dF yang diimbas oleh parameter-parameter infinitesimal δaσ. Dua buah transformasi infinitesimal berturut-turut
SδaSδb bekerja padaF memerikan transformasi infinitesimal lainnya
SδaSδb= (1 +δaσXσ)(1 +δbρXρ) = 1 +δaσXσ+δbρXρ (3.48)
karena hanya orde pertama yang harus dipertahankan. Persamaan (3.48) me-nunjukkan bahwa perkalian 2 elemen grup berkorespon dengan penjumlahan parameter-parameter transformasi infinitesimal. Sekarang coba kita pandang satu buah parameter grup Lie berhingga (bukan infinitesimal) berorde-1 dan menuliskan perubahan infinitesimalnya dari parameter tersebut, a, δa sebagai
δa= a
N (3.49)
denganN menyatakan bilangan sembarang yang besar. Menerapkan transformasi (3.47) sebanyak N kali, kita akan peroleh
Sa= (1 +
a NX)
N
yang mana, untuk limit N → ∞, menjadi
Sa=eaX (3.50)
dan dapat diperumum ke grup berorde-r dengan menuliskan
Sa=ea
ρX
ρ (3.51)
dimana aρ berkoresponden dengan parameter-parameter grup ”kanonik” yang
istimewa. Invers dari transformasi (3.51) dapat ditulis
Sa−1 =e−aρXρ (3.52)
yang ternyata merupakan transformasi dengan tanda berlawanan dengan trans-formasi (3.51). Secara umum, operator infinitesimal Xρ tidak saling commute,
sebagai ekspansi taylor orde pertama dari (3.51) dengan aρ → δaρ. Terkadang
jika suku-suku orde pertama hasil ekspansi saling meniadakan, maka kita harus mempertahankan suku orde 2 dari ekspansi taylor (3.51) dan (3.52) tersebut.
Sa= 1 +δaσXσ+
1 2δa
σδaρX
σXρ (3.53)
Sa= 1−δaσXσ +
1 2δa
σδaρX
σXρ (3.54)
Salah satu teorema fundamental Lie menjamin bahwa kita tidak pernah membu-tuhkan orde yang lebih tinggi dari 2, karena mereka terkait dengan komutator-komutator dan hal ini mendefinisikan struktur grup. Contoh tipikal yang akan diperlihatkan di sini adalah produk SaSbSa−1Sb−1. Perhitungan secara langsung
dari persamaan (3.53) dan (3.54) memberikan
SaSbSa−1Sb−1 = 1 +δa
σδbρ[X
σ, Xρ] (3.55)
Dalam aplikasi fisis grup Lie, generator Xσ (atau kombinasi linier dari mereka)
berkorespon dengan observabel-observabel. Invarian suatu hamiltonian terhadap transformasi grup berarti
[H, Sa] = 0 (3.56)
yang mana dengan menggunakan Pers. (3.56) (3.47) atau (3.51) akan meng-hasilkan
[H, Xσ] = 0 (3.57)
karena aσ atauδaσ bebas linier stau sama lain. Maka sifat invarian dari
hamilto-nian terhadap transformasi-transformasi yang membentuk grup Lie berarti bahwa H commute dengan semua generator grup tersebut. Berikut ini terdapat suatu contoh penentuan generator-generator grup Lie.
Tentukan generator-generator dan Aljabar Lie dari transformasi linier berikut:
x′ =ax+b
Elemen identitas dari transformasi adalah x′ =x. Transformasi infinitesimal di
sekitar elemn identitas memberikan
x′ = (1 +δa)x+δb
maka
Terhadap transformasi ini F(x) berubah secara infinitesimal menjadi:
F(x+dx) =F(x) +dxdF
dx = [1 + (δax+δb)]F
sehingga terdapat 2 generator:
Xa=x
d
dx, Xb = d dx
sehingga Aljabar Lienya adalah:
[Xa, Xb] =x
3.4
Grup Simpel dan Semi-Simpel
Sekarang, kita akan menggunakan persamaan (3.55) untuk menemukan beberapa sifat konstanta struktur dari grup simpel dan semi-simpel. Terlepas dari itu, , kita dapat melihat bahwa persamaan (3.55) mempunyai konsekuensi langsung terhadap grup abelian dimana
SaSb =SbSa
atau
SaSbSa−1Sb−1 = 1
menggunakan (3.55), kita dapatkan
1 +δaρδbσ[Xρ, Xσ] = 1 (3.58)
maka
[Xρ, Xσ] = 0 (3.59)
konsekuensinya, semua konstanta struktur untuk grup abelian bernilai 0
cτρσ = 0 untuk semua ρ, σ, τ (3.60)
Aljabar dari suatu grup abelian dikatakan bersifat abelian atau komutatif. Pada bagian 2.2, kita lihat bahwa suatu subgrup merupakan himpunan bagian S′ dari
elemen-elemen sautu grup S yang membentuk juga grup dengan hukum komposisi yang sama. Ambil elemen-elemen S′
aSb′ ∈S′ dan juga
menggunakan (3.55) pada sisi kiri dan (3.47) pada sisi kanan persamaan (3.61), kita dapatkan
1 +δaρδbσ[Xρ, Xσ] = 1 +δcτXτ (3.62)
Dari (3.40), kita juga bisa dapati
r
dimana r berada pada orde S dan p berada pada orde S’. Karena r > p, kita dapat membagi penjumlahan pada sisi kiri menjadi 2 kontribusi penjumlahan yang berbeda dan menuliskan:
p
Xτ adalah besaran-besaran yang bebas linier, , yang mana
p Dengan definisi invariansubgrup yang telah dibahas sebelumnya, suatu invarian subgrup H adaalh suatu subgrup dari S jika ia mengandung semua konjugat-konjugat dari elemen-elemennya. Coba kita tandai orde dari H dan S berturut-turut p dan r dengan (p < r)dan anggap h1 ∈H dan s1 ∈S sehingga
sh1s−1 ∈H
dan juga
sh1s−1h−11 =h2 ∈H (3.66)
menggunakan (3.55) pada sisi kiri dan (3.47) pada sisi kanan, kita dapat tuliskan
1 +δsρδhσ1[Xρ, Xσ] = 1 +δhτ2Xτ
atau, berdasarkan persamaan (3.40), kita dapatkan
dimana penjumlahan terhadap indeks-indeks yang berulang telah ditulis secara eksplisit . Seperti pada kasus sebelumnya penjumlahan terhadap τ pada sisi kiri dapat dipecah menjadi 2 bagian:
p
Dari kebergantungan linier generator-generator , ternyata
r
1 variasi-variasi yang saling bebas, akhirnya dapat
disim-pulkan
cτρσ = 0 untuk τ > p, σ ≤pdan untuk sembarang ρ (3.70)
Misalnya terdapat suatu grup memiliki subgrup invarian yang abelian. Jika indeks-indeks dari generator dari subgrup invarian abelian ditandai dengan ¯ρ,σ¯λ, ...¯ maka menurut persamaan (3.36) kita dapat tuliskan
gρσ¯ =cµρλcλσµ¯ =−c
µ ρλcλµσ¯
sdan menggunakan persamaan (3.70) untuk faktor kedua pada ekspresi di atas kita dapatkan
gρσ¯ =−cµρλ¯c ¯
λ µ¯σ
dan menggunakan persamaan (3.70) lagi pada faktor pertama , elemen tensor gρσ¯
menjadi
Faktor kedua di atas adalah suatu konstanta struktur dari subgrup invarian abelian dan berdasarkan persamaan (3.60), kita peroleh
gρ¯σ = 0 (3.71)
ini berarti
det|gρσ|= 0 (3.72)
yang merupakan syarat perlu untuk suatu grup agar tidak bersifat semi-simpel. Kebalikannya
merupakan syarat cukup untuk suatu grup agar bersifat semi-simpel. Kondisi (3.73) berarti bahwa matriks gρσ memiliki invers gρσ
′
yang memenuhi
gρσgρσ
′
=δσσ′ (3.74)
Ada sebuah contoh bahwa grup euclidian dalam 2 dimensiE2 didefinisikan
menu-rut transformasi
x′ =xcosθ+ysinθ−ρ
1
y′ =−xsinθ+ycosθ−ρ
2
tidak bersifat semi-simpel . Transformasi pertama di atas secara geometris merep-resentasikan 2 operasi berturut-turut:
1. Suatu translasi titik asal sistem koordinat oleh ρ = (ρ1, ρ2), dalam sistem
baru, vektor r= (x, y) memiliki komponen-komponen x′ =x−ρ1, y′ =y−ρ2
2. suatu rotasi melalui sudut θ terhadap sumbu z dari sistem yang telah ter-translasi
Sekarang, pandang suatu rotasi infinitesimal
cosθ ≈1, sinθ ≈θ maka
x′−x=θy−ρ
1
y′ −y=−θx−ρ2
Suatu fungsi skalar dapat berubah menjadi
F(xi+dxi) =F(xi) +dx∂F
pada tiap parameter infinitesimal,θ, ρ1, ρ2, terdapat generator-generator yang
berkorespondensi dengan mereka menurut definisi (3.38), yaitu:
Aljabar-aljabar yang dapat dibentuk dari generator-generator ini adalah
[X1, X2] =X3, X[X1, X3] =−X2, [X2, X3] = 0
maka
c312 = 1, c213 =−1, c123 = 0 dan
gρσ =
−2 0 0
0 0 0
0 0 0
yang meninjukkan bahwa grup di atas tidak bersifat semi-simpel karena
det|gρσ|= 0
3.5
Aljabar Simpel dan Semi-simpel
Konsep-konsep dari grup Lie simpel dan semi-simpel dapat diperkenalkan melalui aljabar yang dideskripsikan oleh grup tersebut. Untuk keperluan ini, kita perlu mendefinisikan sub aljabar. Dalam analoginya dengan subgrup, suatu sub aljabar
L′ dari suatu aljabar Lie adalah suatu himpunan bagian dari L yang dengan
sendirinya membentuk suatu aljabar dengan komutator yang sama dengan yang dimiliki L.
L′ dikatakan sub aljabar yang sejati (propersubalgebra) dariLjika paling sedikit
satu elemen dari L tidak terkandung di dalam L′. karena demikian, dimensi L′
lebih kecil daripada dimensi L′.
Suatu sub aljabarL′ dariLdikatakan membentuk sub aljabar invarian atau ideal
dari L jika komutator
[Xρ, Xσ] =cτρσXτ ∈ L′ (3.75)
untuk semua Xρ ∈ L dan Xσ ∈ L. Definisi ini ekivalen dengan persamaan
(3.70). Jika alajabar L mengandung anggota-anggota yang tak terdapat dalam sub aljabar ideal, maka sub aljabar ideal ini dikatakan proper ideal.
3.6
Beberapa contoh Grup Lie
nama grup sifat
Simetrik a=aT
Skew-Simetrik a=−aT
Orthogonal a−1 =aT
Real a=a∗
imajiner a=−a∗
Hermitian a=a†
Skew Hermitian a=−a†
Uniter a−1 =a†
Tabel 3.1: Sifat matriks yang relevan terhadap definisi bermacam grup kontinu
Hukum komposisi grup adalah perkalian matriks yang memiliki sifat asosiatif. Elemen-elemen suatu matriks bisa bersifat real (R) atau kompleks (C). Dalam aplikasi fisis matriks-matriks ini, secara umum ditandai dengan a, berasal dari suatu transformasi dari suatu ruang vektor x = (x1, x2, x3, ...xn) menjadi ruang
vektor lain x′ = (x′
1, x′2, ..., x′n)
x′ =ax (3.76)
Suatu grup transformasi dapat didefinisikan melalui sifat-sifat a. Sebuah daf-tar sifat-sifat matriks yang relevan diberikan pada tabel 3.1. n2 buah elemn
matriks baik kompleks maupun real adalah parameter-parameter yang bervari-asi secara kontinu. Konstrain yang dinyatakan oleh sifat-sifat yang tertera pada tabel 3.1 biasanya membatasi banyaknya parameter-parameter independen. Pa-da tabel 3.2 dijabarkan beberapa grup yang paling penting. Grup Linier umum GL(n,C)terdiri dari matriks-matriks kompleks berderajat n merupakan grup ma-triks linier terbesar. Grup-grup lain yang didaftarkan di bawah merupakan sub-grup dari sub-grup ini. Orde dari sub-grup GL(n,C) diberikan oleh 2 kali banyaknya elemen matriksn2, karena tiap elemen matriks berupa bilangan kompleks.
Pada-hal , grup GL(n,R) yang elemen-elemennya matriks real, berorde n2. Ternyata
GL(n,C)⊃GL(n,R) (3.77)
Nama Grup Definisi Orde Keterangan Linier umum Kompleks
GL(n,C)
det a6= 0 2n2 GL(n,C)⊃
GL(n,R)
Linier umum Real
GL(n,R) atau GL(n)
a = a∗
det a 6= 0 n2
Spesial Linier Kompleks SL(n,C)
det a=1 2n2−2 SL(n,C)⊃SL(n,R)
Spesial Linier Real SL(n,R) atau SL(n)
a = a∗
det a= 1
n2−1
Uniter U(n) atau Un a−1 = a†
—det a—=1
n2 Isomorfik
de-ngan GL(n,R)
Tabel 3.2: Macam-macam Grup Lie
dan pada kasus kedua , 1 konstrain, yang memberikan orde SL(n, C) , 2n2−2, dan orde SL(n,R n2−1. Ternyata
GL(n,C)⊃SL(n,C)⊃SL(n,R) (3.78) Elemen-elemen dari sautu grup unitary adalah berupa matriks-matriks uniter. Sifat keunitarian menjamin bahwa transformasi linier (3.76) mempertahankan keinvarianan bentuk kuadratik hermitian
n
X
i=1
xix∗i (3.79)
kondisi keunitarian
aa† =a†a= 1 (3.80)
menghasilkan konsekuensi
det a=eiϕ (3.81)
dan mengakibatkan n konstrain dari elemen-elemen diagonal dan n(n−1) dari elemen matriks non diagonal, menyisakan
n2−n−n(n−1) =n2 (3.82)