PEMODELAN MATEMATIS PENYEBARAN VIRUS HEPATITIS A DAN PENYELESAIANNYA MENGGUNAKAN METODE RUNGE-KUTTA
ORDE TIGA
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Chatarina Wahyu Trirenfi Hartati NIM: 173114052
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
i
PEMODELAN MATEMATIS PENYEBARAN VIRUS HEPATITIS A DAN PENYELESAIANNYA MENGGUNAKAN METODE RUNGE-KUTTA
ORDE TIGA
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Chatarina Wahyu Trirenfi Hartati NIM: 173114052
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
MATHEMATICAL MODELING OF THE SPREAD OF HEPATITIS A VIRUS AND ITS SOLUTION USING THE THIRD ORDER
RUNGE-KUTTA METHOD
Final Project
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written By:
Chatarina Wahyu Trirenfi Hartati Student ID: 173114052
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
HALAMAN PERSEMBAHAN
“Sebab Aku ini mengetahui rancangan-rancangan apa yang ada pada-Ku mengenai kamu, demikianlah firman TUHAN, yaitu rancangan damai sejahtera dan bukan rancangan kecelakaan, untuk memberikan kepadamu hari depan yang
penuh harapan. Yeremia 29:11”
Karya ini saya persembahkan untuk: Tuhan Yesus Kristus yang senantiasa selalu menyertai dan memberkati dalam setiap langkah saya, dan kedua orang tua saya tercinta, Antonius Kirnadi dan
viii ABSTRAK
Tugas akhir ini membahas tentang penyelesaian suatu masalah pada penyebaran penyakit tertentu, yaitu pada penyakit hepatitis A. Penyebaran virus hepatitis A ini dimodelkan secara matematis dengan menggunakan model epidemi SIR (Suceptible-Infected-Recovered) berupa suatu sistem persamaan yang terdiri atas tiga persamaan diferensial biasa. Masalah tersebut diselesaikan dengan menggunakan metode Runge-Kutta orde tiga. Metode Runge-Kutta adalah suatu metode yang digunakan untuk menyelesaikan masalah nilai awal pada persamaan diferensial linear maupun non linear dengan syarat awal. Metode Runge-Kutta orde tiga banyak dipakai untuk menyelesaikan permasalahan nilai awal karena memiliki tingkat ketelitian yang lebih tinggi dibandingkan dengan metode Runge-Kutta orde satu dan dua. Dengan demikian, dari hasil yang diperoleh dalam tugas akhir ini dapat digunakan untuk mengetahui penyebaran penyakit hepatitis A. Dalam jangka waktu yang lama, penyelesaian model matematika menuju titik ekuilibriumnya.
ix ABSTRACT
This final project discusses about solving a problem of the spread of a certain disease, namely hepatitis A. The spread of the hepatitis A virus is modeled mathematically using the SIR (Suceptible-Infected-Recovered) epidemic model is a system equations of three ordinary differential equations. This problem was solved using the third order Runge-Kutta method. The Runge-Kutta method used to solve initial value problems in linear and non-linear differential equations with initial conditions. The third order Runge Kutta method is widely used to solve initial value problems because it has a higher level of accuracy than the first and second order Runge-Kutta methods. Thus, the results obtained in this final project can be used to determine the spread of hepatitis A. Over a long period of time, the solution of a mathematical model goes to the equilibrium point.
x
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Tuhan Yang Maha Esa karena atas berkat dan penyertaan-Nya, penulis dapat menyelesaikan tugas akhir ini dengan baik dan lancar. Tugas akhir yang berjudul “Pemodelan Matematis Penyebaran Virus Hepatitis A dan Penyelesaiannya Menggunakan Metode Runge-Kutta Orde Tiga” merupakan salah satu syarat yang harus dipenuhi oleh penulis untuk memperoleh gelar Sarjana Matematika (S.Mat.) pada Fakultas Sains dan Teknologi Universitas Sanata Dharma Yogyakarta.
Banyak tantangan dan kesulitan yang penulis hadapi dalam proses penulisan tugas akhir ini, namun berkat penyertaan Tuhan serta bantuan dan dukungan dari semua pihak, penulis dapat menyelesaikan tugas akhir ini. Dengan demikian, penulis ingin mengucapkan terima kasih kepada:
1. Bapak Sudi Mungkasi, S.Si., M.Math.Sc., Ph.D., selaku Dekan Fakultas Sains dan Teknologi sekaligus dosen pembimbing tugas akhir yang telah meluangkan waktu, tenaga, dan pikiran serta dengan penuh kesabaran membimbing dan memberikan masukan serta arahan kepada penulis.
2. Bapak Y.G. Hartono, S.Si., M.Sc., Ph.D., selaku Ketua Program Studi Matematika dan dosen pembimbing akademik.
3. Romo Prof. Dr. Frans Susilo, S.J., Bapak Ir. Ig. Aris Dwiatmoko, M.Sc., Bapak Dr. rer. nat. Herry Pribawanto Suryawan, S.Si., M.Si., Bapak Ricky Aditya, M.Sc., Ibu M.V. Any Herawati, S.Si., M.Si., dan Ibu Dr. Lusia Krismiyati Budiasih. S.Si., M.Si., selaku dosen Program Studi Matematika yang telah memberikan ilmu dan pengalaman selama masa perkuliahan.
4. Perpustakaan Universitas Sanata Dharma dan staf sekretariat Fakultas Sains dan Teknologi yang telah membantu dalam proses administrasi dan akademik. 5. Kedua orang tua, Bapak Antonius Kirnadi dan Ibu MM. Tukiyem atas segala kasih sayang, doa dan dukungan yang diberikan kepada penulis, dan kepada
xii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN ... v
PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI ... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
BAB I PENDAHULUAN ... 1 A. Latar Belakang ... 1 B. Rumusan Masalah ... 3 C. Batasan Masalah... 4 D. Tujuan Penulisan ... 4 E. Manfaat Penulisan ... 4 F. Metode Penelitian ... 4 G. Statistika Penulisan ... 4
BAB II MODEL MATEMATIS DAN TOPIK TERKAIT ... 6
xiii B. Persamaan Diferensial ... 7 C. Pemodelan Matematis ... 9 D. Model SIR ... 10 E. Turunan Numerik ... 11 F. Metode Runge-Kutta ... 14
BAB III MODEL PENYEBARAN VIRUS HEPATITIS A ... 20
A. Asumsi-Asumsi dalam Pemodelan... 20
B. Pembentukan Model ... 23
C. Titik Kesetimbangan (Titik Ekuilibrium) ... 25
D. Penyelesaian Model SIR pada Penyakit Hepatitis A Menggunakan Metode Runge-Kutta Orde Tiga ... 31
BAB IV PENYELESAIAN NUMERIS MODEL PENYEBARAN VIRUS HEPATITIS A ... 33 A. Simulasi Numeris ... 33 B. Diskusi Hasil ... 49 BAB V PENUTUP ... 50 A. Kesimpulan ... 50 B. Saran ... 51 DAFTAR PUSTAKA ... 52 LAMPIRAN ... 53
1 BAB I PENDAHULUAN
Dalam bab ini akan dijelaskan mengenai latar belakang, rumusan masalah, batasan masalah, tujuan penulisan, manfaat penulisan, metode penulisan, dan sistematika dari tugas akhir ini.
A. Latar Belakang
Matematika dapat diterapkan dalam kehidupan sehari-hari dan di berbagai bidang ilmu pengetahuan. Penerapan matematika dalam bidang ilmu pengetahuan, misalnya untuk membuat model matematis dari masalah-masalah atau fenomena-fenomena yang ada. Model tersebut dapat diselesaikan dengan menggunakan berbagai metode yang ada dalam matematika. Model matematis adalah representasi dari fenomena dunia nyata ke dalam bentuk matematika (Giordano, et al., 1997).
Pemodelan matematis dapat diterapkan dalam berbagai bidang, misalnya dalam bidang teknologi, industri, ekonomi, fisika, biologi, dan sebagainya. Permasalahan yang ada dapat diselesaikan dengan menggunakan model matematis tanpa harus melakukan eksperimen secara langsung. Contoh pemodelan matematis dalam bidang biologi adalah penyebaran virus pada penyakit yang dapat menular dari individu satu ke individu lain, misalnya virus hepatitis A.
Hepatitis A adalah peradangan organ hati yang disebabkan oleh infeksi virus hepatitis A (HAV) yang dapat menular ke orang lain. Penyebaran virus hepatitis A terjadi melalui jalur fecal-oral. Virus hepatitis A dapat menyebar dengan mudah masuk ke dalam tubuh ketika seseorang mengonsumsi makanan atau minuman yang terkontaminasi tinja yang mengandung HAV atau disebabkan oleh sanitasi yang buruk. Hepatitis A masih menjadi permasalahan kesehatan yang cukup mengkhawatirkan dan sering ditemukan, khususnya di negara-negara berkembang termasuk Indonesia (de Guimaraens & Codeco, 2005).
2
Persamaan diferensial merupakan persamaan yang menyatakan hubungan antara suatu fungsi dengan turunan-turunannya. Persamaan diferensial dapat digunakan untuk menyimulasikan dinamika populasi dan dapat diselesaikan secara numeris menggunakan perangkat lunak MATLAB. Berdasarkan banyaknya variabel bebas yang terlibat, persamaan diferensial dapat diklasifikasikan menjadi dua, yaitu persamaan diferensial biasa dan persamaan diferensial parsial. Persamaan diferensial biasa adalah persamaan diferensial yang hanya memuat satu variabel bebas saja, sedangkan persamaan diferensial parsial adalah persamaan diferensial yang memuat lebih dari satu variabel bebas. Persamaan diferensial dapat diselesaikan dengan menggunakan berbagai metode, misalnya metode Euler, metode Heun, metode beda hingga, dan metode Runge-Kutta orde tiga.
Metode Runge-Kutta adalah suatu metode yang digunakan untuk menyelesaikan masalah nilai awal pada persamaan diferensial linear maupun nonlinear. Metode ini diselesaikan secara numeris sehingga mendapatkan penyelesaian yang mendekati penyelesaian analitisnya. Masalah nilai awal dalam persamaan diferensial orde satu berbentuk (Boyce & DiPrima, 2013):
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦), 𝑦(𝑡0) = 𝑦0.
Rumus Runge-Kutta orde tiga melibatkan nilai-nilai 𝑓(𝑡, 𝑦) pada titik yang berbeda pada interval 𝑡𝑛 ≤ 𝑡 ≤ 𝑡𝑛+1, dengan ℎ = 𝑡𝑛+1− 𝑡𝑛 yaitu:
𝑦𝑛+1 = 𝑦𝑛+ ℎ (𝑘1+ 4𝑘2+ 𝑘3 6 ), dimana 𝑘1 = 𝑓(𝑡𝑛 , 𝑦𝑛), 𝑘2 = 𝑓 (𝑡𝑛+ 1 2ℎ , 𝑦𝑛+ 1 2ℎ𝑘1), 𝑘3 = 𝑓(𝑡𝑛 + ℎ , 𝑦𝑛− ℎ𝑘1+ 2ℎ𝑘2).
Dalam tugas akhir ini, metode Runge-Kutta orde tiga akan digunakan untuk menyelesaikan model matematis penyebaran virus Hepatitis A dalam bentuk sistem persamaan diferensial sebagai berikut (de Guimaraens & Codeco, 2005):
{ 𝑑𝑆(𝑡) 𝑑𝑡 = µ𝑁 − 𝑚𝑆(𝑡) − 𝑐𝛽𝐼(𝑡)𝑆(𝑡) 𝑑𝐼(𝑡) 𝑑𝑡 = 𝑐𝛽𝑆(𝑡)𝐼(𝑡) − (𝑚 + 𝛾)𝐼(𝑡) 𝑑𝑅(𝑡) 𝑑𝑡 = 𝛾𝐼(𝑡) − 𝑚𝑅(𝑡)
dengan 𝑆 (Susceptible) adalah individu yang beresiko terinfeksi, 𝐼 (Infected) adalah individu yang terinfeksi dan dapat menularkan infeksi ke orang lain, dan 𝑅 (Recovered) adalah individu yang pernah terinfeksi namun sekarang telah benar-benar pulih, 𝑡 adalah variabel waktu,dan parameter-parameter yang terlibat, yaitu:
1) 𝜇 adalah laju kelahiran per kapita.
2) 𝑁 adalah jumlah individu dalam suatu populasi. 3) 𝑚 menotasikan laju kematian individu yang terinfeksi.
4) 𝑐 melambangkan jumlah kontak yang berpotensi infektif yang dimiliki orang yang rentan terinfeksi per hari.
5) 𝛽 adalah parameter kemungkinan bahwa seseorang benar-benar akan terinfeksi setelah melakukan kontak dengan infektif.
6) 𝛾 adalah parameter individu yang pulih dari infeksi (𝛾 = 1
30 per hari).
B. Rumusan Masalah
Rumusan masalah dalam tugas akhir adalah:
1. Bagaimana memodelkan penyebaran virus hepatitis A dalam populasi manusia? 2. Bagaimana menyelesaikan model penyebaran virus hepatitis A dengan metode
4
C. Batasan Masalah
Pembahasan dalam tugas akhir ini terbatas pada bagaimana memodelkan penyebaran virus hepatitis A dan penyelesaiannya menggunakan metode Runge-Kutta orde tiga.
D. Tujuan Penulisan
Tujuan penulisan tugas akhir adalah:
1. Memodelkan penyebaran virus hepatitis A dalam populasi manusia.
2. Mencari penyelesaian model matematis pada penyebaran virus hepatitis A dan simulasinya dengan metode Runge-Kutta orde tiga.
E. Manfaat Penulisan
Manfaat yang diperoleh dari tugas akhir ini adalah mengetahui cara memodelkan penyebaran virus hepatitis A dan penyelesaiannya menggunakan metode Runge-Kutta orde tiga.
F. Metode Penelitian
Metode penelitian yang digunakan untuk menyusun tugas akhir ini adalah metode studi pustaka dengan membaca dan mempelajari jurnal-jurnal dan buku-buku matematika, serta melakukan simulasi dengan perangkat lunak komputer menggunakan MATLAB.
G. Sistematika Penulisan
Tugas akhir ini disusun dengan sistematika penulisan sebagai berikut: BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penelitian
G. Sistematika Penulisan
BAB II MODEL MATEMATISDAN TOPIK TERKAIT A. Hepatitis A B. Persamaan Diferensial C. Pemodelan Matematis D. Model SIR E. Turunan Numerik F. Metode Runge-Kutta
BAB III MODEL PENYEBARAN VIRUS HEPATITIS A A. Asumsi-Asumsi dalam Pemodelan
B. Pembentukan Model
C. Titik Kesetimbangan (Titik Ekuilibrium)
D. Penyelesaian Model SIR pada Penyakit Hepatitis A Menggunakan Metode Runge-Kutta Orde Tiga
BAB IV PENYELESAIAN NUMERIS MODEL PENYEBARAN VIRUS HEPATITIS A A. Simulasi Numeris B. Diskusi Hasil BAB V PENUTUP A. Kesimpulan B. Saran DAFTAR PUSTAKA
6 BAB II
MODEL MATEMATIS DAN TOPIK TERKAIT
Dalam bab ini akan dibahas mengenai model matematis dan penjelasan topik terkait dari tugas akhir ini. Landasan teori yang digunakan adalah hepatitis A, persamaan diferensial, pemodelan matematis, model SIR, turunan numerik, dan metode Runge-Kutta.
A. Hepatitis A
Hepatitis merupakan penyakit peradangan hati yang disebabkan oleh virus hepatitis, perlemakan, obatan-obatan, alkohol, parasit maupun oleh virus lainnya. Ada lima macam hepatitis, yaitu hepatitis A, B, C, D, dan E serta yang masih menjadi endemis di Indonesia ada tiga, yaitu hepatitis A, B, dan C. Tahapan yang dialami oleh penderita hepatitis berawal dari hati sehat, hepatitis akut, hepatitis kronis, kemudian sirosis hati bahkan 1/3 dari penderita hepatitis akan mengalami sirosis. Setelah penderita mengalami sirosis 10-15% akan menjadi kanker sebesar 23% kemudian setelah mengidap sirosis selama 5 tahun penderita akan mengalami gagal hati yang dapat berujung pada kematian (Kemenkes, 2020).
Hepatitis A adalah peradangan organ hati yang disebabkan oleh infeksi virus hepatitis A (HAV) yang dapat menular ke orang lain. Penyebaran virus hepatitis A terjadi melalui jalur fecal-oral. Virus hepatitis A dapat menyebar dengan mudah masuk ke dalam tubuh ketika seseorang mengonsumsi makanan atau minuman yang terkontaminasi tinja yang mengandung HAV atau disebabkan oleh sanitasi yang buruk (de Guimaraens, 2005). Hepatitis A dapat sembuh dengan sendirinya namun juga dapat menyebabkan kejadian yang luar biasa apabila seseorang tidak membiasakan diri untuk hidup bersih dan sehat.
Tanda atau gejala seseorang terkena virus hepatitis A adalah: 1. Mudah lelah
3. Nyeri pada sisi kanan atas di bawah tulang rusuk 4. Nafsu makan berkurang
5. Demam 6. Nyeri sendi.
Hepatitis A dapat dicegah dengan cara menjaga kebersihan misalnya mengonsumsi makanan dan minuman yang higienis, mencuci tangan sebelum makan, dan memperhatikan kebersihkan lingkungan sekitar tempat tinggal dan tidak melakukan kontak dengan penderita hepatitis A. Virus ini juga dapat dicegah dengan memberikan vaksin untuk mencegah penularan virus hepatitis A (HAV) tersebut.
B. Persamaan Diferensial
Persamaan direfensial merupakan persamaan yang menyatakan hubungan antara suatu fungsi dengan turunan-turunannya. Berdasarkan banyaknya variabel bebas yang terlibat, persamaan diferensial dapat diklasifikasikan menjadi dua, yaitu persamaan direfensial biasa dan persamaan diferensial parsial. Klasifikasi penting dari persamaan diferensial apakah persamaan tersebut linear atau nonlinear. Klasifikasi persamaan diferensial lainnya bergantung pada jumlah fungsi yang tidak diketahui yang terlibat dalam persamaan tersebut, jika terdapat dua atau lebih fungsi yang tidak diketahui maka diperlukan sistem persamaan. Sistem persamaan diferensial, misalnya pada Lotka-Volterra, predator-prey, dan persamaan penting lainnya dalam model ekologi (Boyce & DiPrima, 2013).
Definisi 2.1
Persamaan diferensial biasa adalah suatu persamaan diferensial yang hanya memuat fungsi satu variabel bebas saja dan hanya melibatkan turunan biasa.
Definisi 2.2
Persamaan diferensial parsial adalah suatu persamaan diferensial yang memuat fungsi dua atau lebih variabel bebas dan melibatkan turunan parsial.
8
Contoh 2.1
Berikut adalah contoh persamaan diferensial biasa: 𝐿𝑑 2𝑄(𝑡) 𝑑𝑡2 + 𝑅 𝑑𝑄(𝑡) 𝑑𝑡 + 1 𝐶𝑄(𝑡) = 𝐸(𝑡) (2.1) dimana variabel 𝑡 merupakan variabel bebas dan variabel 𝑄 merupakan variabel terikat.
Contoh 2.2
Berikut adalah contoh persamaan diferensial parsial: 𝛼2𝜕
2𝑢(𝑥, 𝑡)
𝜕𝑥2 =
𝜕𝑢(𝑥, 𝑡)
𝜕𝑡 (2.2) dimana variabel 𝑥 dan 𝑡 merupakan variabel bebas dan variabel 𝑢 merupakan variabel terikat.
Contoh 2.3
Berikut adalah contoh sistem persamaan diferensial: 𝑑𝑥(𝑡)
𝑑𝑡 = 𝑎𝑥 − 𝛼𝑥𝑦 𝑑𝑦(𝑡)
𝑑𝑡 = −𝑐𝑦 + 𝛾𝑥𝑦 (2.3) dimana 𝑥(𝑡) dan 𝑦(𝑡) merupakan populasi dari suatu spesies dan 𝑎, 𝛼, 𝑐, 𝛾 merupakan konstanta.
Orde dari persamaan diferensial adalah tingkat turunan tertinggi dalam persamaan diferensial tersebut. Persamaan (2.1) merupakan persamaan diferensial biasa orde dua dan persamaan (2.2) merupakan persamaan diferensial parsial orde dua. Secara umum, persamaan diferensial orde 𝑛 berbentuk:
𝐹[𝑡, 𝑢(𝑡), 𝑢′(𝑡), … , 𝑢(𝑛)(𝑡)] = 0 (2.4)
atau dengan mensubstitusi 𝑢(𝑡), 𝑢′(𝑡), … , 𝑢(𝑛)(𝑡) = 𝑦, 𝑦′, … , 𝑦(𝑛) sehingga
diperoleh persamaan diferensial seperti berikut:
Contoh 2.4
𝑦′′′+ 2𝑒𝑡𝑦′′+ 𝑦𝑦′ = 𝑡4 (2.6)
Persamaan (2.6) merupakan persamaan diferensial orde tiga untuk 𝑦 = 𝑢(𝑡).
Definisi 2.3
Persamaan diferensial biasa
𝐹[𝑡, 𝑦, 𝑦′, … , 𝑦(𝑛)] = 0
dikatakan linear jika 𝐹 merupakan fungsi linear dari 𝑦, 𝑦′, … , 𝑦(𝑛), definisi tersebut
berlaku juga pada persamaan diferensial parsial. Secara umum, persamaan diferensial biasa linear orde 𝑛 berbentuk:
𝑎0(𝑡)𝑦(𝑛)+ 𝑎1(𝑡)𝑦(𝑛−1)+ ⋯ + 𝑎𝑛(𝑡)𝑦 = 𝑔(𝑡) (2.7)
Contoh 2.5
Persamaan (2.1) merupakan contoh persamaan diferensial biasa linear orde dua, dan persamaan (2.2) merupakan contoh persamaan diferensial parsial linear orde dua.
Suatu persamaan yang tidak berbentuk seperti (2.7) disebut sebagai persamaan non linear. Persamaan (2.6) merupakan persamaan diferensial non linear orde tiga karena terdapat 𝑦𝑦′.
C. Pemodelan Matematis
Pemodelan matematis adalah representasi dari fenomena dunia nyata ke dalam bentuk matematika (Giordano, et al., 1997). Model tersebut dapat diselesaikan dengan menggunakan berbagai metode yang ada dalam matematika. Pemodelan matematis dapat digunakan untuk memprediksi nilai variabel pada periode waktu tertentu dari suatu permasalahan yang ada di dunia nyata. Nilai variabel tersebut dapat berupa populasi, nilai hampiran (pendekatan), atau jumlah individu dengan suatu penyakit tertentu. Dalam pemodelan matematis terdapat langkah-langkah untuk memecahkan suatu masalah.
10
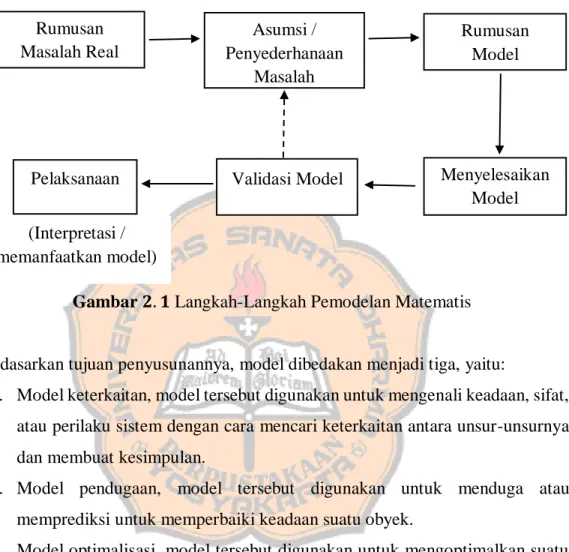
Adapun langkah-langkah dalam pembentukan pemodelan matematis seperti tampak dalam Gambar 2.1.
Gambar 𝟐. 𝟏 Langkah-Langkah Pemodelan Matematis
Berdasarkan tujuan penyusunannya, model dibedakan menjadi tiga, yaitu:
1. Model keterkaitan, model tersebut digunakan untuk mengenali keadaan, sifat, atau perilaku sistem dengan cara mencari keterkaitan antara unsur-unsurnya dan membuat kesimpulan.
2. Model pendugaan, model tersebut digunakan untuk menduga atau memprediksi untuk memperbaiki keadaan suatu obyek.
3. Model optimalisasi, model tersebut digunakan untuk mengoptimalkan suatu obyek tertentu.
D. Model SIR
Model SIR merupakan salah satu model epidemi yang digunakan untuk menggambarkan perilaku penyebaran penyakit menular pada manusia. Pada model SIR populasi manusia dibagi menjadi tiga kelompok, yaitu:
1. Suscebtible (S) merupakan individu yang rentan terinfeksi.
2. Infected (I) merupakan individu yang terinfeksi dan mampu menularkan infeksi ke orang lain.
Rumusan Masalah Real
Pelaksanaan Validasi Model Menyelesaikan Model Rumusan Model Matematika Asumsi / Penyederhanaan Masalah (Interpretasi / memanfaatkan model)
3. Recovered (R) merupakan individu yang pernah terinfeksi namun telah benar-benar pulih.
Variabel 𝑆, 𝐼 dan 𝑅 menunjukkan jumlah individu di masing-masing kelompok pada periode waktu tertentu (𝑡), dan jumlah atau total populasi (𝑁) adalah jumlahan dari ketiga kelompok populasi 𝑆, 𝐼 dan 𝑅 tersebut, yaitu 𝑁 = 𝑆 + 𝐼 + 𝑅.
Gambar 2.2 Diagram Model SIR
Pada Gambar 2.2, 𝛽 merupakan parameter kemungkinan bahwa seseorang akan terinfeksi setelah melakukan kontak dengan infektif dan 𝛾 merupakan parameter individu yang pulih dari infeksi. Dengan demikian model SIR dapat ditulis dalam bentuk persamaan, sebagai berikut (Kiss, et al., 2017):
𝑑𝑆(𝑡) 𝑑𝑡 = −𝛽𝐼(𝑡) 𝑆(𝑡) 𝑁 , 𝑑𝐼(𝑡) 𝑑𝑡 = 𝛽𝐼(𝑡) 𝑆(𝑡) 𝑁 − 𝛾𝐼(𝑡) , (2.8) 𝑑𝑅(𝑡) 𝑑𝑡 = 𝛾𝐼(𝑡). E. Turunan Numerik
Turunan dari fungsi 𝑓 pada 𝑥0 adalah (Burden and Faires, 1993)
𝑓′(𝑥 0) = limℎ→0 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ S I R 𝛽𝐼𝑆 𝑁 𝛾𝐼
12
untuk nilai ℎ yang cukup kecil maka pendekatan untuk mencari nilai 𝑓′(𝑥
0) dapat dihitung dengan 𝑓′(𝑥 0) = 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ Untuk mendekati 𝑓′(𝑥
0), yang pertama misalkan 𝑥0∈ (𝑎, 𝑏) dimana 𝑓 ∈ 𝐶2[𝑎, 𝑏]
dan 𝑥1= 𝑥0+ ℎ untuk setiap ℎ ≠ 0 yang cukup kecil untuk memastikan bahwa 𝑥1 ∈ [𝑎, 𝑏]. Selanjutnya untuk mendapatkan polinomial Lagrange yang pertama yaitu 𝑃0,1(𝑥) untuk 𝑓 ditentukan menggunakan 𝑥0 dan 𝑥1, dengan kesalahan dari sukunya: 𝑓(𝑥) = 𝑃0,1(𝑥) +(𝑥 − 𝑥0)(𝑥 − 𝑥1) 2! 𝑓 ′′(𝜉(𝑥)) = 𝑓(𝑥0)(𝑥 − 𝑥0− ℎ) −ℎ + 𝑓(𝑥0+ ℎ)(𝑥 − 𝑥0) ℎ + (𝑥 − 𝑥0)(𝑥 − 𝑥0− ℎ) 2 𝑓 ′′(𝜉(𝑥))
untuk setiap 𝜉(𝑥) antara 𝑥0 dan 𝑥1. Fungsi 𝑓(𝑥) jika diturunkan maka diperoleh
𝑓′(𝑥) = 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ + 𝐷𝑥[ (𝑥 − 𝑥0)(𝑥 − 𝑥0− ℎ) 2 𝑓 ′′(𝜉(𝑥))] =𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ + 2(𝑥 − 𝑥0) − ℎ 2 𝑓 ′′(𝜉(𝑥)) +(𝑥 − 𝑥0)(𝑥 − 𝑥0− ℎ) 2 𝐷𝑥(𝑓 ′′(𝜉(𝑥)))
Dengan mengeliminasi suku-suku yang memuat 𝜉(𝑥), sehingga diperoleh 𝑓′(𝑥) ≈𝑓(𝑥0+ ℎ) − 𝑓(𝑥0)
ℎ
Dengan demikian, terdapat tiga pendekatan dalam menghitung nilai 𝑓′(𝑥0) secara numerik, yaitu:
1. Beda maju (forward difference) 𝑓′(𝑥
0) ≈
𝑓(𝑥0+ ℎ) − 𝑓(𝑥0)
ℎ
untuk ℎ > 0.
2. Beda mundur (backward difference) 𝑓′(𝑥
0) ≈
𝑓(𝑥0) − 𝑓(𝑥0− ℎ) ℎ
untuk ℎ < 0.
3. Beda pusat (central difference) 𝑓′(𝑥
0) ≈
𝑓(𝑥0+ ℎ) − 𝑓(𝑥0− ℎ) 2ℎ
Dimana jarak antara 𝑥0− ℎ dan 𝑥0+ ℎ adalah 2ℎ.
Contoh 2.7
Contoh diambil dari buku Burden & Faires (1993)
Gunakan rumus beda maju untuk mendekati turunan dari 𝑓(𝑥) = ln 𝑥 pada 𝑥0 = 1,8 dengan ℎ = 0,1. Penyelesaian: 𝑥0 = 1,8 ℎ = 0,1 𝑥0− ℎ 𝑥0 𝑥0 𝑥0+ ℎ 𝑥0− ℎ
14
Rumus beda maju:
𝑓′(𝑥0) ≈ 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ sehingga, 𝑓′(1,8) ≈𝑓(1,8 + 0,1) − 𝑓(1,8) ℎ ≈ln 1,9 − ln 1,8 0,1 = 0,64185389 − 0,58778667 0,1 = 0,5406722 F. Metode Runge-Kutta
Metode Runge-Kutta adalah suatu metode yang digunakan untuk menyelesaikan masalah nilai awal pada persamaan diferensial linear maupun non linear dengan syarat awal. Metode Runge-Kutta orde tiga banyak dipakai untuk menyelesaikan permasalahan nilai awal karena memiliki tingkat ketelitian yang lebih tinggi dibandingkan dengan metode Runge-Kutta orde satu dan dua. Masalah nilai awal dalam persamaan diferensial orde satu berbentuk sebagai berikut (Boyce and DiPrima, 2013):
𝑑𝑦
𝑑𝑡 = 𝑓(𝑡, 𝑦) , 𝑦(𝑡0) = 𝑦0 (2.9) Metode Runge-Kutta orde tiga dibentuk dari deret Taylor terpotong:
𝑦𝑛+1 = 𝑦𝑖 + 𝑓(𝑡𝑛, 𝑦𝑛)ℎ + 1 2!𝑓 ′(𝑡 𝑛, 𝑦𝑛)ℎ2+ 1 3!𝑓 ′′(𝑡 𝑛, 𝑦𝑛)ℎ3 (2.10)
Metode Runge-Kutta orde tiga berbentuk sebagai berikut:
𝑦𝑛+1 = 𝑦𝑛+ (𝑤1𝑘1+ 𝑤2𝑘2+ 𝑤3𝑘3)ℎ (2.11) dimana,
𝑘1 = 𝑓(𝑡𝑛 , 𝑦𝑛), (2.12) 𝑘2 = 𝑓(𝑡𝑛+ 𝛼2ℎ , 𝑦𝑛+ 𝛽21ℎ𝑘1), (2.13)
𝑘3 = 𝑓(𝑡𝑛 + 𝛼3ℎ , 𝑦𝑛+ 𝛽31ℎ𝑘1+ 𝛽32ℎ𝑘2). (2.14) Dengan menggunakan deret Taylor diperoleh persamaannya adalah (Ralston and Rabinowits, 1978): 𝑤1+ 𝑤2+ 𝑤3 = 1 𝛼2𝑤2+ 𝛼3𝑤3 =1 2 𝛼22𝑤2+ 𝛼32𝑤3 = 1 3 (2.15) 𝛼2𝛽32𝑤3 =1 6 𝛼2 = 𝛽21 𝛼3 = 𝛽31+ 𝛽32 persamaan (2.15) dapat ditulis sebagai berikut:
𝑤1 = 1 +2 − 3(𝛼2+ 𝛼3) 6𝛼2𝛼3 𝑤2 = 3𝛼3 − 2 6𝛼2(𝛼3 − 𝛼2) 𝑤3 = 2 − 3𝛼2 6𝛼2(𝛼3− 𝛼2) 𝛼2 ≠ 𝛼3 ; 𝛼2, 𝛼3 ≠ 0 (2.16) 𝛽21 = 𝛼2 𝛽31 =3𝛼2𝛼3(1 − 𝛼2) − 𝛼3 2 𝛼2(2 − 3𝛼2) 𝛽32 = 𝛼3(𝛼3− 𝛼2) 𝛼2(2 − 3𝛼2) Sehingga diperoleh solusi dari persamaan (2.15) adalah:
16 𝛼2 =1 2 , 𝛼3 = 1 , 𝛼32 =3 2 , 𝛼2 2 = −7 4 (2.17) 𝛽31 = −1 , 𝛽32 = 2 , 𝑤1 =1 6, 𝑤2 = 2 3, 𝑤3 = 1 6 .
Hasil yang didapatkan pada persamaan (2.17) disubtitusi pada persamaan (2.11), sehingga diperoleh rumus metode Runge-Kutta orde tiga sebagai berikut:
𝑦𝑛+1 = 𝑦𝑛+ ℎ (𝑘1+ 4𝑘2+ 𝑘3 6 ) (2.18) dimana, 𝑘1 = 𝑓(𝑡𝑛 , 𝑦𝑛), (2.19) 𝑘2 = 𝑓 (𝑡𝑛+ 1 2ℎ , 𝑦𝑛 + 1 2ℎ𝑘1), (2.20) 𝑘3 = 𝑓(𝑡𝑛+ ℎ , 𝑦𝑛− ℎ𝑘1+ 2ℎ𝑘2), (2.21) dengan ℎ = 𝑡𝑛+1− 𝑡𝑛.
Karena metode Runge-Kutta diturunkan dari metode Taylor sehingga Final global
error/FGE-nya adalah berorde 𝑂(ℎ𝑁). Di sini, 𝑁 adalah orde dari metode
Runge-Kutta.
Contoh 2.6
Contoh diambil dari buku Karan S.Surana (2019). Diberikan persamaan diferensial orde satu sebagai berikut
𝑑𝑢
𝑑𝑡 = 𝑡 + 4
dengan 𝑢(0) = 1 ∀𝑡 ∈ (𝑡1, 𝑡2) = (0, 𝜏) = Ω𝑡 , 𝜏 > 0.
Tentukan 𝑢 pada 𝑡 = 0,2 dan 𝑡 = 0,4 menggunakan ∆𝑡 = 0,2. Penyelesaian: Untuk 𝑖 = 1: 𝑡 = 𝑡1 = 0, 𝑢1 = 1, 𝑓(𝑢, 𝑡) = 𝑢 + 𝑡, ℎ = 0, Untuk 𝑖 = 2: 𝑡 = 𝑡2 = ∆𝑡 = 0,2 dimana ∆𝑡 = ℎ = 0,2 𝑘1 = 𝑓(𝑢1, 𝑡1) = 1 + 0 = 1 𝑘2 = 𝑓 (𝑢1+ ℎ 2𝑘1 , 𝑡1+ ℎ 2) = (1 +1(0,2) 2 ) + (0 + 0,2 2 ) = 1,2 𝑘3 = 𝑓(𝑢1+ 2ℎ𝑘2− ℎ𝑘1 , 𝑡1+ ℎ ) = (1 + 2(0,2)(1,2) − 0,2(1)) + (0 + 0,2) = 1,48 𝑢2 = 𝑢1+ ℎ (𝑘1+ 4𝑘2+ 𝑘3 6 ) = 1 + 0,2 (1 + 4(1,2) + 1,48 6 )
18 = 1,24267 Untuk 𝑖 = 3: 𝑡 = 𝑡3 = 2. ∆𝑡 = 0,4 dimana ∆𝑡 = ℎ = 0,2 𝑘1 = 𝑓(𝑢2, 𝑡2) = 𝑢2 + 𝑡2 = 1,24267 + 0,2 = 1,44267 𝑘2 = 𝑓 (𝑢2+ℎ 2𝑘1 , 𝑡2+ ℎ 2) = (1,24267 + 1,44267 (0,2 2 )) + (0,2 + 0,2 2 ) = 1,686937 𝑘3 = 𝑓(𝑢1+ 2ℎ𝑘2− ℎ𝑘1 , 𝑡1+ ℎ ) = (1,2426 + 2(0.2)(1,686937) − (0,2)(1,44267)) + (0,2 + 0,2) = 2,0289 𝑢3 = 𝑢2+ ℎ (𝑘1+ 4𝑘2+ 𝑘3 6 ) = 1,24267 + 0,2 (1,44267 + 4(686937) + 2,0289 6 ) = 1,583315
Tabel 2.1 Hasil Penyelesaian 𝑡 𝑢 𝑑𝑢 𝑑𝑡 = 𝑓(𝑢, 𝑡) 0 1 1 0,2 1,24267 1,44267 0,4 1,583315 1,983315
20 BAB III
MODEL PENYEBARAN VIRUS HEPATITIS A
Dalam bab ini akan dibahas mengenai asumsi-asumsi dalam pemodelan dan pembentukan model pada penyebaran virus hepatitis A.
A. Asumsi-Asumsi dalam Pemodelan
Asumsi yang digunakan dalam pemodelan pada penyebaran virus hepatitis A adalah:
1) Jumlah total populasi tidak konstan.
2) Mempertimbangkan laju pertumbuhan penduduk dan laju kematian. 3) Periode waktu yang digunakan adalah per hari.
4) Tidak adanya vaksinasi (seronegative).
5) Penularan virus terjadi dari individu ke individu.
Model SIR pada penyebaran virus hepatitis A dikelompokkan menjadi beberapa populasi, yaitu:
1) Susceptible adalah individu yang rentan terhadap penyakit.
2) Infected adalah individu yang terinfeksi dan dapat menularkan infeksi ke orang lain.
3) Recovered adalah individu yang telah pulih atau sembuh dari penyakit.
Adapun variabel dan parameter yang digunakan dalam pemodelan penyebaran virus hepatitis A adalah:
1) 𝑆(𝑡) adalah jumlah individu yang rentan pada periode waktu (𝑡) dalam suatu populasi (𝑁).
2) 𝐼(𝑡) adalah jumlah individu yang terinfeksi pada periode waktu (𝑡) dalam suatu populasi (𝑁).
3) 𝑅(𝑡) adalah jumlah individu yang pulih atau sembuh pada periode waktu (𝑡) dalam suatu populasi (𝑁).
4) 𝑡 merupakan variabel waktu dalam satuan hari. 5) 𝑁 adalah jumlah individu dalam suatu populasi. 6) 𝜇 adalah laju kelahiran per kapita.
7) 𝑚 menotasikan laju kematian individu yang terinfeksi.
8) 𝑐 melambangkan jumlah kontak yang berpotensi infektif yang dimiliki orang yang rentan terinfeksi per hari.
9) 𝛽 adalah parameter kemungkinan bahwa seseorang benar-benar akan terinfeksi setelah melakukan kontak dengan infektif.
10) 𝛾 adalah parameter individu yang pulih dari infeksi (𝛾 = 1
30 per hari).
Parameter dan nilai awal yang akan digunakan untuk mensimulasikan model pada tugas akhir ini, dengan menggunakan program MATLAB disajikan dalam Tabel 3.1 dan Tabel 3.2.
Tabel 3.1 Parameter dan Nilai Awal yang Digunakan dalam Tugas Akhir ini.
Nilai-nilai ini diambil oleh penulis sebagai studi mandiri. Parameter atau Nilai Awal Nilai Simulasi 1 Simulasi 2 𝑡 (hari) 500 500 𝜇 0,0002 0,0002 𝑚 0,005 0,005 𝑐𝛽 0,01 0,01 𝛾 1/30 1/30 𝑁(0) 100 1000
22
𝑆(0) 90 990
𝐼(0) 10 10
𝑅(0) 0 0
Parameter dan nilai awal pada Tabel 3.1 diperoleh dengan melihat hasil dari plot grafiknya menggunakan program MATLAB, dimana nilai parameter yang digunakan adalah lebih dari nol dan kurang dari satu.
Tabel 𝟑. 𝟐 Parameter dan Nilai Awal untuk Simulasi penyebaran virus Hepatitis A (de Guimaraens & Codeco, 2005).
Parameter atau Nilai Awal Nilai
𝑡 (hari) 90 𝜇 0,00005 𝑚 0,0002 𝑐𝛽 0,0001 𝛾 0,3 𝑁(0) 12700 𝑆(0) 11200 𝐼(0) 1000 𝑅(0) 500
Tabel 3.2 merupakan parameter dan nilai awal yang digunakan untuk mensimulasikan model penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga menggunakan program MATLAB.
B. Pembentukan Model
Penyebaran penyakit hepatitis A dalam suatu populasi dapat digambarkan dalam skema berikut:
Gambar 3.1 Skema Penyebaran Penyakit Hepatitis A
Skema model SIR pada Gambar 3.1 menyatakan hubungan antar individu-individu pada kelas rentan (Susceptible), terinfeksi (infected) dan pulih (recovered) dengan parameter dan variabel terkait. Pada keadaan awal semua individu yang baru lahir, dimana laju kelahiran dilambangkan dengan 𝜇 akan masuk ke dalam kelas rentan
(Susceptible), kemudian jika individu pada kelas rentan melakukan interaksi
dengan individu yang terinfeksi dan mampu menularkan penyakit (Infected) maka akan mengakibatkan individu yang berada pada kelas terinfeksi (Infected) jumlahnya akan bertambah namun individu yang berada pada kelas rentan
(Susceptible) jumlahnya akan berkurang, dan individu yang terinfeksi yang sudah
pulih atau sembuh akan masuk pada kelas pulih (Recovered) sehingga secara otomatis individu yang berada pada kelas terinfeksi (Infected) jumlahnya akan berkurang dan individu pada kelas pulih (Recovered) jumlahnya akan bertambah. Dengan demikian setiap populasi pada model SIR jumlahnya akan bertambah dan berkurang jika terjadi transmisi antara Susceptible, Infected, dan Recovered.
Pada Gambar 3.1 dapat dilihat bahwa setiap populasi pada model SIR tersebut terdapat kematian, dimana laju kematian dilambangkan dengan 𝑚. Kematian pada masing-masing populasi tersebut baik disebabkan oleh penyakit itu sendiri maupun oleh faktor lainnya, sehingga faktor kematian juga dapat menyebabkan berkurangnya populasi Susceptible, Infected, dan Recovered.
S I R
𝜇𝑁 𝑐𝛽𝐼𝑆 𝛾𝐼
24
Berdasarkan skema dan penjelasan di atas maka diperoleh formulasi model SIR pada penyakit hepatitis A sebagai berikut:
1. Populasi susceptible (S) [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] = [ 𝑙𝑎𝑗𝑢 𝑘𝑒𝑙𝑎ℎ𝑖𝑟𝑎𝑛] × [ 𝑡𝑜𝑡𝑎𝑙 𝑝𝑜𝑝𝑢𝑙𝑎𝑠𝑖] − [ 𝑙𝑎𝑗𝑢 𝑘𝑒𝑚𝑎𝑡𝑖𝑎𝑛] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] − [ 𝑗𝑢𝑚𝑙𝑎ℎ 𝑘𝑜𝑛𝑡𝑎𝑘 𝑦𝑎𝑛𝑔 𝑏𝑒𝑟𝑝𝑜𝑡𝑒𝑛𝑠𝑖 𝑖𝑛𝑓𝑒𝑘𝑡𝑖𝑓 𝑦𝑎𝑛𝑔 𝑑𝑖𝑚𝑖𝑙𝑖𝑘𝑖 𝑜𝑙𝑒ℎ 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 ] × [ 𝑙𝑎𝑗𝑢 𝑖𝑛𝑓𝑒𝑘𝑠𝑖] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ]
2. Populasi infected (I)
[ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] = [ 𝑗𝑢𝑚𝑙𝑎ℎ 𝑘𝑜𝑛𝑡𝑎𝑘 𝑦𝑎𝑛𝑔 𝑏𝑒𝑟𝑝𝑜𝑡𝑒𝑛𝑠𝑖 𝑖𝑛𝑓𝑒𝑘𝑡𝑖𝑓 𝑦𝑎𝑛𝑔 𝑑𝑖𝑚𝑖𝑙𝑖𝑘𝑖 𝑜𝑙𝑒ℎ 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 ] × [ 𝑙𝑎𝑗𝑢 𝑖𝑛𝑓𝑒𝑘𝑠𝑖] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] − ([ 𝑙𝑎𝑗𝑢 𝑘𝑒𝑚𝑎𝑡𝑖𝑎𝑛] + [ 𝑙𝑎𝑗𝑢 𝑝𝑒𝑚𝑢𝑙𝑖ℎ𝑎𝑛]) × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] 3. Populasi recovered (R) [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑝𝑢𝑙𝑖ℎ 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ] = [ 𝑙𝑎𝑗𝑢 𝑝𝑒𝑚𝑢𝑙𝑖ℎ𝑎𝑛] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑖𝑛𝑓𝑒𝑘𝑠𝑖 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ]
− [ 𝑙𝑎𝑗𝑢 𝑘𝑒𝑚𝑎𝑡𝑖𝑎𝑛] × [ 𝑏𝑎𝑛𝑦𝑎𝑘𝑛𝑦𝑎 𝑖𝑛𝑑𝑖𝑣𝑖𝑑𝑢 𝑦𝑎𝑛𝑔 𝑟𝑒𝑛𝑡𝑎𝑛 𝑠𝑒𝑡𝑒𝑙𝑎ℎ 𝑝𝑒𝑟𝑖𝑜𝑑𝑒 𝑤𝑎𝑘𝑡𝑢 𝑡 ]
Sehingga diperoleh model matematis pada penyebaran virus hepatitis A dalam bentuk sistem persamaan diferensial sebagai berikut:
𝑑𝑆(𝑡) 𝑑𝑡 = µ𝑁 − 𝑚𝑆(𝑡) − 𝑐𝛽𝐼(𝑡)𝑆(𝑡), 𝑑𝐼(𝑡) 𝑑𝑡 = 𝑐𝛽𝑆(𝑡)𝐼(𝑡) − (𝑚 + 𝛾)𝐼(𝑡), (3.1) 𝑑𝑅(𝑡) 𝑑𝑡 = 𝛾𝐼(𝑡) − 𝑚𝑅(𝑡).
C. Titik Kesetimbangan (Titik Ekuilibrium)
Titik kesetimbangan dapat diperoleh dengan beberapa cara, salah satunya adalah dengan membuat ruas kiri pada sistem persamaan (3.1) sama dengan nol. Sehingga diperoleh sistem persamaan sebagai berikut:
µ𝑁 − 𝑚𝑆 − 𝑐𝛽𝐼𝑆 = 0
𝑐𝛽𝑆𝐼 − (𝑚 + 𝛾)𝐼 = 0 (3.2) 𝛾𝐼 − 𝑚𝑅 = 0
Dari persamaan yang pertama pada sistem persamaan (3.2) diperoleh
µ𝑁 − 𝑚𝑆 − 𝑐𝛽𝐼𝑆 = 0 ⇔ µ𝑁 − 𝑚𝑆 = 𝑐𝛽𝐼𝑆 ⇔ µ𝑁 − 𝑚𝑆
𝑐𝛽𝑆 = 𝐼 (3.3)
Kemudian substitusi persamaan (3.3) ke persamaan dua pada sistem persamaan (3.2), sehingga diperoleh
26 𝑐𝛽𝑆𝐼 − (𝑚 + 𝛾)𝐼 = 0 ⇔ 𝑐𝛽𝑆 (µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ) − (𝑚 + 𝛾) ( µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ) = 0 ⇔ (µ𝑁 − 𝑚𝑆) − (𝑚 + 𝛾) (µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ) = 0 ⇔ (µ𝑁 − 𝑚𝑆) [1 −𝑚 + 𝛾 𝑐𝛽𝑆 ] = 0 ⇔ 𝑆 =µ𝑁 𝑚 ˅ 𝑆 = 𝑚 + 𝛾 𝑐𝛽 Jadi diperoleh 𝑆1 = µ𝑁 𝑚 (3.4) atau 𝑆2 =𝑚 + 𝛾 𝑐𝛽 (3.5)
Kemudian substitusi persamaan (3.3) ke persamaan tiga pada sistem persamaan (3.2), sehingga diperoleh
𝛾𝐼 − 𝑚𝑅 = 0 ⇔ 𝛾 (µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ) − 𝑚𝑅 = 0 ⇔ 𝛾 (µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ) = 𝑚𝑅 ⇔ 𝛾 (µ𝑁 − 𝑚𝑆𝑐𝛽𝑆 ) 𝑚 = 𝑅 (3.6)
Langkah selanjutnya adalah mencari titik kesetimbangan pada 𝑆1 dan 𝑆2.
1. Titik kesetimbangan pada 𝑆1 dicari dengan mensubstitusikan persamaan (3.4) ke persamaan (3.3) dan persamaan (3.6).
𝐼 =µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ⇔ 𝐼 =µ𝑁 − 𝑚 ( µ𝑁 𝑚 ) 𝑐𝛽 (µ𝑁𝑚 ) ⇔ 𝐼 =µ𝑁 − µ𝑁 𝑐𝛽 (µ𝑁𝑚 ) ⇔ 𝐼 = 0 𝑐𝛽 (µ𝑁𝑚 ) = 0
Selanjutnya, substitusikan persamaan (3.4) ke persamaan (3.6) diperoleh
𝑅 = 𝛾 (µ𝑁 − 𝑚𝑆𝑐𝛽𝑆 ) 𝑚 ⇔ 𝑅 = 𝛾 (µ𝑁 − 𝑚 ( µ𝑁 𝑚 ) 𝑐𝛽 (µ𝑁𝑚) ) 𝑚 ⇔ 𝑅 = 𝛾 (µ𝑁 − µ𝑁 𝑐𝛽 (µ𝑁𝑚 ) ) 𝑚 ⇔ 𝑅 = 0 𝑚= 0
Sehingga diperoleh titik kesetimbangan pada 𝑆1 dari sistem persamaan (3.2), yaitu
𝑆 =µ𝑁 𝑚
28
𝐼 = 0 𝑅 = 0
2. Titik kesetimbangan pada 𝑆2 dicari dengan mensubstitusikan persamaan (3.5) ke persamaan (3.3) dan persamaan (3.6).
Substitusikan persamaan (3.5) ke persamaan (3.3) diperoleh
𝐼∗= µ𝑁 − 𝑚𝑆 𝑐𝛽𝑆 ⇔ 𝐼∗ = µ𝑁 − 𝑚 (𝑚 + 𝛾𝑐𝛽 ) 𝑐𝛽 (𝑚 + 𝛾𝑐𝛽 ) ⇔ 𝐼∗ = µ𝑁 − 𝑚 (𝑚 + 𝛾𝑐𝛽 ) 𝑚 + 𝛾 ⇔ 𝐼∗ = µ𝑁 𝑚 + 𝛾− 𝑚 𝑐𝛽
Selanjutnya, substitusikan persamaan (3.5) ke persamaan (3.6) diperoleh
𝑅∗ = 𝛾 (µ𝑁 − 𝑚𝑆𝑐𝛽𝑆 ) 𝑚 ⇔ 𝑅∗ = 𝛾 ( µ𝑁 − 𝑚 (𝑚 + 𝛾𝑐𝛽 ) 𝑐𝛽 (𝑚 + 𝛾𝑐𝛽 ) ) 𝑚
⇔ 𝑅∗ = 𝛾 ( µ𝑁 − 𝑚 (𝑚 + 𝛾𝑐𝛽 ) 𝑚 + 𝛾 ) 𝑚 ⇔ 𝑅∗ = 𝛾 (𝑚 + 𝛾 −µ𝑁 𝑐𝛽)𝑚 𝑚 ⇔ 𝑅∗ = 𝛾µ𝑁 𝑚(𝑚 + 𝛾)− 𝛾 𝑐𝛽 ⇔ 𝑅∗ = 𝛾µ𝑁 𝑚2+ 𝑚𝛾− 𝛾 𝑐𝛽 atau 𝑅∗ = 𝑁(𝑡) − 𝐼∗− 𝑆∗.
Sehingga diperoleh titik kesetimbangan pada 𝑆2 dari sistem persamaan (3.2), yaitu 𝑆∗ = 𝑚 + 𝛾 𝑐𝛽 𝐼∗= µ𝑁(𝑡) 𝑚 + 𝛾− 𝑚 𝑐𝛽 𝑅∗ = 𝑁(𝑡) − 𝐼∗− 𝑆∗
Dengan demikian, model matematika pada virus hepatitis A pada sistem persamaan (3.2) mempunyai dua titik kesetimbangan, yaitu
1. Titik kesetimbangan bebas penyakit 𝐸0 = (𝑆, 𝐼, 𝑅) = (µ𝑁(𝑡)
𝑚 , 0,0)
2. Titik kesetimbangan yang terdapat penyakit 𝐸∗ = (𝑆∗, 𝐼∗, 𝑅∗) = (𝑚 + 𝛾 𝑐𝛽 , µ𝑁(𝑡) 𝑚 + 𝛾− 𝑚 𝑐𝛽 , 𝑁(𝑡) − 𝐼 ∗− 𝑆∗)
30
Tanpa intervensi
Dimulai dengan mendeskripsikan dinamika temporal pada penyakit hepatitis A menurut persamaan (3.1). Jika diberikan cukup waktu, maka sistem akan mencapai titik equilibrium positif, yaitu:
𝑆∗ = 𝑚 + 𝛾 𝑐𝛽 𝐼∗= µ𝑁 𝑚 + 𝛾− 𝑚 𝑐𝛽 𝑅∗ = 𝑁(𝑡) − 𝐼∗− 𝑆∗
Dalam titik kesetimbangan tersebut, hubungan antara laju kontak dan seroprevalensi hepatitis A tidak linier. Seroprevalensi adalah jumlah individu dalam suatu populasi yang menunjukkan hasil positif untuk suatu penyakit tertentu berdasarkan specimen serologi (serum darah). Misalnya dalam suatu komunitas dengan jumlah total populasi 1000 individu, maka diharapkan terjadi seroprevalensi sebesar 50% ketika tingkat kontak atau 𝑐𝛽 = 0,0002 (yaitu 2 kontak per orang per 10 hari).
Ketika sistem persamaan (3.1) diselesaikan secara numerik untuk nilai yang berbeda dari tingkat infeksi, maka akan diperoleh dua jenis hasil, yaitu baik infeksi bertahan pada tingkat yang rendah dalam suatu populasi dan tidak ada wabah yang diamati (setelah transien awal), atau rantai wabah diharapkan sebelum populasi yang terinfeksi mengendap pada titik kesetimbangannya.
Dengan intervensi
Tujuan akhir dari strategi kesehatan masyarakat adalah untuk mengubah dinamika penularan suatu penyakit sedemikian rupa sehingga jika seorang individu yang terinfeksi datang ke suatu komunitas tertentu, maka individu tersebut tidak akan memicu suatu epidemi. Secara matematis berarti
𝑑𝐼 𝑑𝑡< 0.
Pada hepatitis A, intervensi dapat bertindak dalam dua cara, yaitu mengurangi jumlah individu yang rentan (𝑆) dengan vaksinasi, atau mengurangi tingkat kontak (𝑐) dengan sanitasi. Dari sistem persamaan (3.1) diperoleh bahwa 𝑑𝐼
𝑑𝑡 < 0 yang
berarti
𝑐 < 𝑚 + 𝛾
𝛽𝑆 . (3.7)
D. Penyelesaian Model SIR pada Penyakit Hepatitis A Menggunakan Metode Runge-Kutta Orde Tiga
Model matematis pada penyebaran virus hepatitis A dalam bentuk sistem persamaan diferensial yang telah diperoleh adalah sistem persamaan (3.1). Persamaan tersebut diselesaikan dengan menggunakan metode Runge-Kutta orde tiga dengan mengkonstruksi model sesuai dengan persamaan (2.18) − (2.21), sehingga diperoleh: 𝑆𝑛+1 = 𝑆𝑛+ ℎ ( 𝑘1+ 4𝑘2+ 𝑘3 6 ) 𝐼𝑛+1 = 𝐼𝑛+ ℎ ( 𝑘1+ 4𝑘2+ 𝑘3 6 ) (3.8) 𝑅𝑛+1 = 𝑅𝑛+ ℎ ( 𝑘1+ 4𝑘2+ 𝑘3 6 ) dimana, 𝑘1𝑆 = (𝜇𝑁 − 𝑚𝑆𝑛 − 𝑐𝛽𝐼𝑛𝑆𝑛) (3.9) 𝑘1𝐼 = (𝑐𝛽𝑆𝑛𝐼𝑛− (𝑚 + 𝛾)𝐼𝑛) (3.10) 𝑘1𝑅 = (𝛾𝐼𝑛 − 𝑚𝑅𝑛) (3.11)
32 𝑘2𝑆 = (𝜇𝑁 − 𝑚 (𝑆𝑛+1 2ℎ𝑘1𝑆) − 𝑐𝛽 (𝐼𝑛+ 1 2ℎ𝑘1𝐼) (𝑆𝑛 + 1 2ℎ𝑘1𝑆)) (3.12) 𝑘2𝐼 = (𝑐𝛽 (𝑆𝑛+1 2ℎ𝑘1𝑆) (𝐼𝑛+ 1 2ℎ𝑘1𝐼) − (𝑚 + 𝛾) (𝐼𝑛+ 1 2ℎ𝑘1𝐼)) (3.13) 𝑘2𝑅 = (𝛾 (𝐼𝑛+ 1 2ℎ𝑘1𝐼) − 𝑚 (𝑅𝑛+ 1 2ℎ𝑘1𝑅)) (3.14) 𝑘3𝑆 = (𝜇𝑁 − 𝑚(𝑆𝑛− ℎ𝑘1𝑆+ 2ℎ𝑘2𝑆) − 𝑐𝛽(𝐼𝑛− ℎ𝑘1𝐼+ 2ℎ𝑘2𝐼)(𝑆𝑛 − ℎ𝑘1𝑆+ 2ℎ𝑘2𝑆)) (3.15) 𝑘3𝐼 = (𝑐𝛽(𝑆𝑛 − ℎ𝑘1𝑆 + 2ℎ𝑘2𝑆)(𝐼𝑛− ℎ𝑘1𝐼+ 2ℎ𝑘2𝐼) − (𝑚 + 𝛾)(𝐼𝑛− ℎ𝑘1𝐼+ 2ℎ𝑘2𝐼)) (3.16) 𝑘3𝑅 = (𝛾(𝐼𝑛− ℎ𝑘1𝐼 + 2ℎ𝑘2𝐼) − 𝑚(𝑅𝑛 − ℎ𝑘1𝑅+ 2ℎ𝑘2𝑅)) (3.17)
33 BAB IV
PENYELESAIAN NUMERIS MODEL PENYEBARAN VIRUS HEPATITIS A
Dalam bab ini akan dibahas mengenai penyelesaian numeris model penyebaran virus hepatitis A menggunakan program MATLAB.
A. Simulasi Numeris
Model SIR (Susceptible-Infected-Recovered) pada penyebaran virus hepatitis A akan diselesaikan dengan menggunakan metode Runge-Kutta orde tiga, dimana simulasi dan pengamatannya menggunakan nilai ℎ = 0,01. Dengan menggunakan bantuan program MATLAB diperoleh simulasi sebagai berikut:
1. Simulasi I (Studi Hasil)
Dengan menggunakan parameter dan nilai awal yang telah diketahui pada Tabel 3.1 untuk simulasi I yang mana digunakan sebagai studi hasil, dimana total populasi (𝑁) sebanyak 100 individu dan pengamatannya dibatasi dengan periode waktu selama 500 hari, maka diperoleh grafik penyelesaian dari sistem persamaan model SIR sebagai berikut:
34
a. Populasi Susceptible
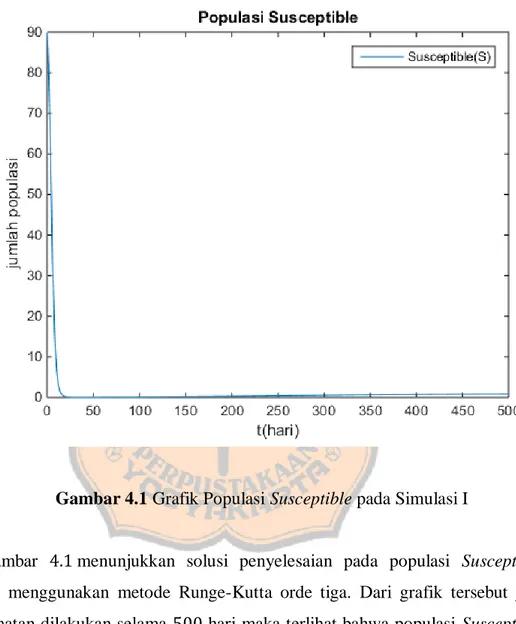
Gambar 4.1 Grafik Populasi Susceptible pada Simulasi I
Gambar 4.1 menunjukkan solusi penyelesaian pada populasi Susceptible dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut jika pengamatan dilakukan selama 500 hari maka terlihat bahwa populasi Susceptible mengalami penurunan dan jumlah populasi pada kelompok Susceptible akan terus berkurang. Pada kondisi ini semua individu yang tidak masuk dalam kelompok
b. Populasi Infected
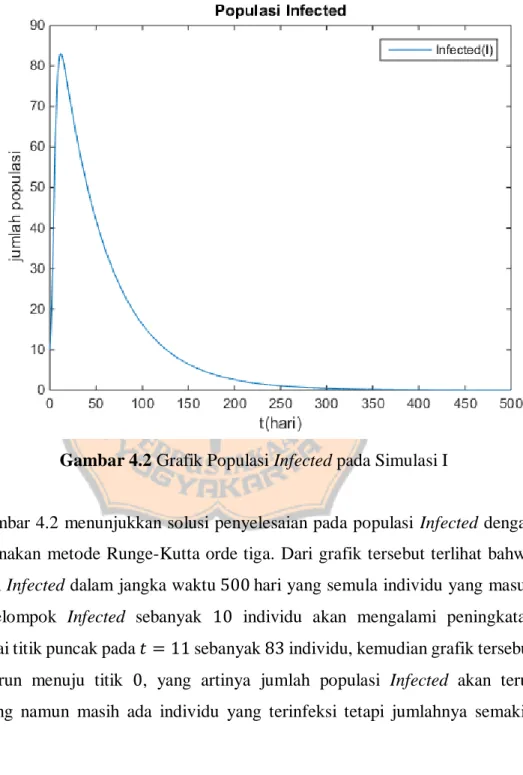
Gambar 4.2 Grafik Populasi Infected pada Simulasi I
Gambar 4.2 menunjukkan solusi penyelesaian pada populasi Infected dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut terlihat bahwa populasi Infected dalam jangka waktu 500 hari yang semula individu yang masuk pada kelompok Infected sebanyak 10 individu akan mengalami peningkatan mencapai titik puncak pada 𝑡 = 11 sebanyak 83 individu, kemudian grafik tersebut akan turun menuju titik 0, yang artinya jumlah populasi Infected akan terus berkurang namun masih ada individu yang terinfeksi tetapi jumlahnya semakin sedikit.
36
c. Populasi Recovered
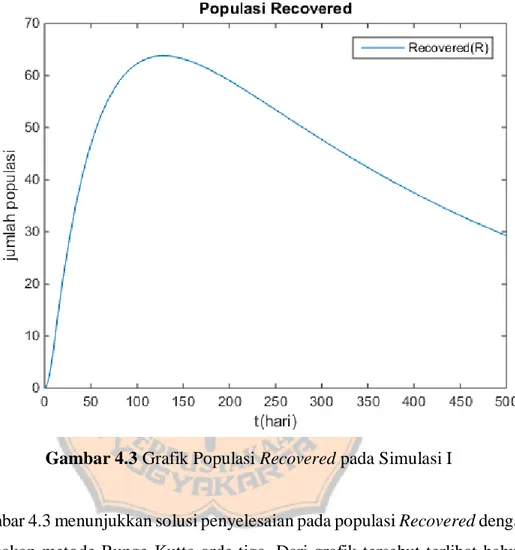
Gambar 4.3 Grafik Populasi Recovered pada Simulasi I
Gambar 4.3 menunjukkan solusi penyelesaian pada populasi Recovered dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut terlihat bahwa populasi Recovered dalam jangka waktu 500 hari akan mengalami peningkatan, namun seiring berjalannya waktu populasi tersebut akan menurun dan menuju pada titik ekuilibriumnya.
d. Populasi Total
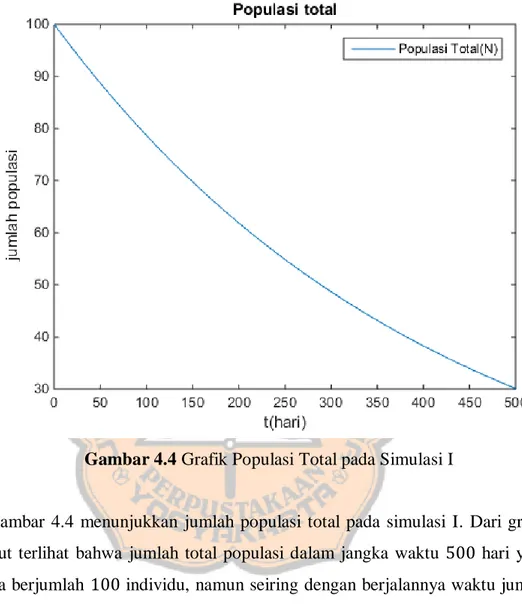
Gambar 4.4 Grafik Populasi Total pada Simulasi I
Gambar 4.4 menunjukkan jumlah populasi total pada simulasi I. Dari grafik tersebut terlihat bahwa jumlah total populasi dalam jangka waktu 500 hari yang semula berjumlah 100 individu, namun seiring dengan berjalannya waktu jumlah populasi tersebut akan terus berkurang.
38
e. Populasi SIR (Susceptible-Infected-Recovered)
Gambar 4.5 Grafik Populasi Model SIR pada Simulasi I
Gambar 4.5 menunjukkan solusi penyelesaian model SIR dengan menggunakan metode Runge-Kutta orde tiga. Pada simulasi ini jika waktu pengamatan dilakukan selama 500 hari maka akan terjadi proses epidemi pada setiap populasi, dimana populasi Susceptible akan mengalami penurunan, dan populasi Infected akan mengalami kenaikan namun pada waktu tertentu populasi tersebut akan semakin berkurang. Pada grafik tersebut terlihat bahwa populasi
Recovered atau yang sembuh jumlahnya akan bertambah namun seiring berjalannya
waktu jumlah populasi Recovered akan mengalami penurunan. Seiring berjalannya waktu ketiga populasi tersebut akan menuju pada titik ekuilibrium terdapat penyakit, yaitu 𝐸∗= (4, 0, 26).
2. Simulasi II (Studi Hasil)
Dengan menggunakan parameter dan nilai awal yang telah diketahui pada Tabel 3.1 untuk simulasi II, dimana total populasi (𝑁) sebanyak 1000 individu dan pengamatannya dibatasi dengan periode waktu selama 500 hari, maka diperoleh grafik penyelesaian dari sistem persamaan model SIR sebagai berikut:
a. Populasi Susceptible
Gambar 4.6 Grafik Populasi Susceptible pada Simulasi II
Gambar 4.6 menunjukkan solusi penyelesaian pada populasi Susceptible dengan menggunakan metode Runge-Kutta orde tiga dan dengan menggunakan data awal yang telah diketahui pada Tabel 3.1. Dari grafik tersebut jika pengamatan dilakukan selama 500 hari maka terlihat bahwa populasi Susceptible mengalami penurunan dan jumlah populasi pada kelompok Susceptible akan terus berkurang, yang semula dari 990 individu akan berkurang menuju 0, artinya pada waktu
40
tertentu individu yang masuk dalam kelompok Susceptible akan hampir habis (tidak ada).
b. Populasi Infected
Gambar 4.7 Grafik Populasi Infected pada Simulasi II
Gambar 4.7 menunjukkan solusi penyelesaian pada populasi Infected (simulasi II) dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut terlihat bahwa populasi Infected dalam jangka waktu 500 hari yang semula individu yang masuk pada kelompok Infected sebanyak 10 individu dari total populasi sebanyak 1000 individu akan mengalami peningkatan mencapai titik puncak pada 𝑡 = 2 sebanyak 972 individu, kemudian grafik tersebut akan turun namun tidak menuju titik 0, yang artinya jumlah populasi Infected akan terus berkurang namun pada waktu tertentu masih ada individu yang terinfeksi tetapi jumlahnya semakin sedikit.
c. Populasi Recovered
Gambar 4.8 Grafik Populasi Recovered pada Simulasi II
Gambar 4.8 menunjukkan solusi penyelesaian pada populasi Recovered (simulasi II) dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik simulasi II tersebut terlihat bahwa jumlah populasi Recovered dalam jangka waktu 500 hari akan mengalami peningkatan seperti pada grafik Recovered simulasi I, namun seiring dengan berjalannya waktu populasi tersebut akan mengalami penurunan menuju pada titik ekuilibriumnya.
42
d. Populasi Total
Gambar 4.9 Grafik Populasi Total pada Simulasi I
Gambar 4.9 menunjukkan jumlah populasi total pada simulasi II. Dari grafik tersebut terlihat bahwa jumlah total populasi dalam jangka waktu 500 hari yang semula berjumlah 1000 individu, namun seiring dengan berjalannya waktu jumlah populasi tersebut akan terus berkurang.
e. Populasi SIR (Susceptible-Infected-Recovered)
Gambar 4.10 Grafik Populasi Model SIR pada Simulasi II
Gambar 4.10 menunjukkan solusi penyelesaian model SIR (simulasi II) dengan menggunakan metode Runge-Kutta orde tiga. Pada simulasi II ini jika waktu pengamatan dilakukan selama 500 hari dengan total populasi sebanyak 1000 individu maka akan terjadi proses epidemi pada setiap populasi, dimana populasi
Susceptible akan mengalami penurunan, populasi Infected akan mengalami
kenaikan namun pada waktu tertentu populasi tersebut akan semakin berkurang, dan populasi Recovered atau yang sembuh jumlahnya akan bertambah, namun seiring dengan berjalannya waktu jumlah populasi Recovered juga akan mengalami penurunan. Seiring berjalannya waktu ke tiga populasi tersebut akan menuju pada titik ekuilibrium terdapat penyakit, yaitu 𝐸∗ = (4, 0, 296).
44
3. Simulasi Penyebaran Virus Hepatitis A (HAV)
Dengan menggunakan parameter dan nilai awal yang telah diketahui pada Tabel 3.2 untuk simulasi penyebaran virus hepatitis A, dimana total populasi (𝑁) sebanyak 12700 individu dan pengamatannya dibatasi dengan periode waktu selama 90 hari, maka diperoleh grafik penyelesaian dari sistem persamaan model SIR pada penyebaran virus hepatitis A sebagai berikut:
a. Populasi Susceptible
Gambar 4.11 Grafik Populasi Susceptible pada Penyebaran Virus
Hepatitis A
Gambar 4.11 menunjukkan solusi penyelesaian pada populasi Susceptible pada penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut jika pengamatan dilakukan selama 90 hari maka terlihat bahwa populasi Susceptible mengalami penurunan dimana jumlah populasi Susceptible awal adalah sebanyak 11200 individu dan seiring berjalannya waktu jumlah
populasi pada kelompok Susceptible akan terus berkurang dan menuju pada titik ekuilibriumnys. Pada kondisi ini semua individu yang tidak masuk dalam kelompok
Infected akan dianggap rentan dan masuk ke dalam kelompok Susceptible. b. Populasi Infected
Gambar 4.12 Grafik Populasi Infected pada Penyebaran Virus Hepatitis A
Gambar 4.12 menunjukkan solusi penyelesaian pada populasi Infected pada penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut terlihat bahwa populasi Infected dalam jangka waktu 90 hari yang semula individu yang masuk pada kelompok Infected sebanyak 1000 individu akan mengalami peningkatan mencapai titik puncak pada 𝑡 = 8 sebanyak 5240 individu, kemudian seiring dengan berjalannya waktu grafik tersebut akan turun menuju titik ekuilibriumnya, yang artinya jumlah populasi Infected akan terus berkurang.
46
c. Populasi Recovered
Gambar 4.13 Grafik Populasi Recovered pada Penyebaran Virus
Hepatitis A
Gambar 4.13 menunjukkan solusi penyelesaian pada populasi Recovered pada penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga. Dari grafik tersebut terlihat bahwa populasi Recovered dalam jangka waktu 90 hari akan terus mengalami peningkatan, jumlah populasi Recovered yang semula sebanyak 500 individu tersebut nantinya akan terus mengalami peningkatan, artinya jumlah populasi yang sembuh atau pulih akan semakin bertambah, dan seiring dengan berjalannya waktu grafik tersebut akan menuju pada titik ekuilibriumnya.
d. Populasi Total
Gambar 4.14 Grafik Populasi Total pada Penyebaran Virus Hepatitis A
Gambar 4.14 menunjukkan jumlah populasi total pada penyebaran virus hepatitis A. Dari grafik tersebut terlihat bahwa jumlah total populasi dalam jangka waktu 90 hari yang semula berjumlah 12700 individu, namun seiring dengan berjalannya waktu jumlah populasi tersebut akan terus berkurang. Hal tersebut dikarenakan ada individu yang terinfeksi kemudian mati.
48
e. Populasi SIR
Gambar 4.15 Grafik Populasi Model SIR pada Penyebaran Virus
Hepatitis A
Gambar 4.15 menunjukkan solusi penyelesaian model SIR pada penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga. Pada simulasi tersebut jika waktu pengamatan dilakukan selama 90 hari maka akan terjadi proses epidemi pada setiap populasi, dimana populasi Susceptible akan mengalami penurunan, dan populasi Infected akan mengalami kenaikan namun pada waktu tertentu populasi tersebut akan semakin berkurang. Pada grafik tersebut terlihat bahwa populasi Recovered atau yang sembuh jumlahnya akan terus bertambah. Seiring dengan berjalannya waktu ketiga populasi tersebut akan menuju ke titik ekuilibrium terdapat penyakit, yaitu 𝐸∗= (227, 0, 12383).
B. Diskusi Hasil
Pada bagian sebelumnya telah diperoleh hasil penyelesaian numerik dari model SIR pada penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga. Dari hasil tersebut dapat digunakan untuk melihat bagaimana perilaku penyebaran virus hepatitis A (HAV) pada setiap masing-masing populasi. Metode numerik yang digunakan dalam penelitian ini adalah metode Runge-Kutta orde tiga. Metode Runge-Kutta merupakan suatu metode yang digunakan untuk menyelesaikan masalah nilai awal pada persamaan diferensial linear maupun non linear dengan syarat awal. Metode Runge-Kutta orde tiga ini digunakan untuk menyelesaikan sistem persamaan pada model SIR pada penyebaran virus hepatitis A. Pada model SIR terdapat tiga populasi, yaitu populasi Susceptible dimana semua populasi dianggap rentan, populasi Infected, yaitu populasi yang terinfeksi dan yang ketiga adalah populasi Recovered yang mana individu yang telah pulih (sembuh) nantinya akan masuk pada kelas ini. Untuk mendapatkan hasil penyelesaian, dibutuhkan syarat awal (nilai awal), dimana nilai awal yang digunakan dalam tugas akhir ini adalah 𝑆(0) = 11200, 𝐼(0) = 1000, dan 𝑅(0) = 500, sehingga dengan menggunakan nilai awal tersebut dapat diperoleh hasil penyelesaian numerik dari sistem persamaan pada model SIR dan grafik simulasi numerik seperti yang ada pada bagian sebelumnya.
50 BAB V PENUTUP
Dalam bab ini akan dibahas mengenai kesimpulan dari pembahasan dalam tugas akhir ini dan saran yang ditujukan untuk pembaca.
A. Kesimpulan
Metode Runge-Kutta merupakan suatu metode yang digunakan untuk menyelesaikan masalah nilai awal pada persamaan diferensial linear maupun non linear dengan syarat awal. Metode Runge-Kutta orde tiga banyak dipakai untuk menyelesaikan permasalahan nilai awal karena memiliki tingkat ketelitian yang lebih tinggi dibandingkan dengan metode Runge-Kutta orde satu dan dua.
Penyebaran virus pada penyakit hepatitis A dimodelkan dalam model epidemi SIR. Model epidemi SIR terdapat tiga kelas, yaitu kelompok individu yang rentan
(Susceptible), kelompok individu yang terinfeksi (Infected), dan kelompok individu
yang telah sembuh atau pulih (Recovered). Sistem persamaan pada model SIR penyebaran virus hepatitis A ini diselesaikan menggunakan metode Runge-Kutta orde tiga. Hasil penyelesaian dari sistem persamaan pada model SIR pada penyebaran virus hepatitis A ini berupa grafik penyelesaian numerik yang dihasilkan menggunakan program MATLAB. Dari hasil analisis pada grafik penyelesaian numerik metode Runge-Kutta orde tiga berhasil menyelesaikan sistem persamaan model SIR pada penyebaran virus hepatitis A, dan parameter-parameter yang terlibat mempengaruhi penularan atau penyebaran virus hepatitis A dari individu satu ke individu lain.
B. Saran
Dalam tugas akhir ini penulis membahas mengenai penyebaran virus hepatitis A dengan menggunakan metode Runge-Kutta orde tiga. Dalam penulisan tugas akhir ini penulis menyadari bahwa masih ada banyak kekurangannya. Jika ke depannya ada peneliti yang ingin melakukan penelitian mengenai penyakit ini, penulis menyarankan mungkin dapat menggunakan metode lainnya yang dapat menghasilkan akurasi yang lebih optimal (erornya kecil), atau jika dalam penelitian ini, penyebaran virusnya terjadi dari orang ke orang, maka peneliti selanjutnya dapat melakukan penelitian dimana penyebaran virusnya terjadi di dalam tubuh manusia.
52
DAFTAR PUSTAKA
Boyce, W. E. and DiPrima, R. C. (2013). Elementary Differential Equations and
Boundary Value Problems. (10th Edition). New York: John Wiley & Sons. Burden, R. L., and Faires J. D. (1993). Numerical Analysis. (9𝑡ℎ Edition). Boston:
Brooks/Cole.
de Guimaraens, M. A. and Codeco, C. T. (2005). Experiments with Mathematical Models to Simulate Hepatitis A Population Dynamics under Different Levels of Endemicity. Cadernos de Saúde Pública. 21(5):1531–1539.
https://doi.org/10.1590/S0102-311X2005000500026 Diakses pada tanggal 10 Februari 2020.
Giordano, F. R., Fox, W. P., Horton, S. B., and Weir, M. D.(1997). A First Course
in Mathematical Modeling. (5th Edition). Pacific Grove: Brooks/Cole Publishing Company.
Kemenkes. (2020). Termasuk Silent Killer, Hepatitis Bisa Dicegah dan Diobati. Jakarta: Menkes RI.
https://www.kemkes.go.id/article/view/20072900002/termasuk-silent-killer-hepatitis-bisa-dicegah-dan-diobati.html Diakses pada tanggal 11 September 2020.
Kiss, I. Z., Miller, C. J., Simon, P. L. (2017). Mathematics of Epidemic on Networks
from Exact to Approximate Models. New York: Springer.
Ralston, A., and Rabinowitz, P. (1978). A First Course in Numerical Analysis. (2𝑡ℎ Edition). New York: Dover Publications, Inc.
Surana, K. S. (2019). Numerical Methods and Methods of Approximation in Science
53 LAMPIRAN
Berikut adalah kode program MATLAB yang digunakan untuk melakukan simulasi pada sistem persamaan model SIR pada penyebaran virus hepatitis A:
A. Program MATLAB untuk Simulasi I
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Penyelesaian Numeris dengan Metode RK 3 % % pada Sistem Persamaan SIR untuk Simulasi I % %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc clear
close all
h=0.01; %input nilai delta t
t=0:h:500; %input interval t
n=length(t);
%input nilai awal dan parameter
N(1)=100; S(1)=90; I(1)=10; R(1)=0; mu=0.0002; m=0.005; cbetta=0.01; gamma=1/30;
%penyelesaian numerik dengan metode Runge-Kutta orde 3 SIR
for i=1:n-1 k1S=(mu*N(i))-(m*S(i))-(cbetta*I(i)*S(i)); k1I=(cbetta*S(i)*I(i))-((m+gamma)*I(i)); k1R=(gamma*I(i))-(m*R(i)); k2S=(mu*N(i))-(m*(S(i)+0.5*h*k1S))-((cbetta*(I(i)+0.5*h*k1I)*(S(i)+0.5*h*k1S))); k2I=(cbetta*(S(i)+0.5*h*k1S)*(I(i)+0.5*h*k1I))-((m+gamma)*(I(i)+0.5*h*k1I)); k2R=(gamma*(I(i)+0.5*h*k1I))-(m*(R(i)+0.5*h*k1R)); k3S=(mu*N(i))-(m*(S(i)-h*k1S+2*h*k2S))-((cbetta*(I(i)-h*k1I+2*h*k2I)*(S(i)-h*k1S+2*h*k2S))); k3I=(cbetta*(S(i)-h*k1S+2*h*k2S)*(I(i)-h*k1I+2*h*k2I))-((m+gamma)*(I(i)-h*k1I+2*h*k2I)); k3R=(gamma*(I(i)-h*k1I+2*h*k2I))-(m*(R(i)-h*k1R+2*h*k2R));
54 S(i+1)=S(i)+(h*((k1S+k2S+k3S)/6)); I(i+1)=I(i)+(h*((k1I+k2I+k3I)/6)); R(i+1)=R(i)+(h*((k1R+k2R+k3R)/6)); N(i+1)=S(i+1)+I(i+1)+R(i+1); end
%plot populasi Susceptible
plot(t,S)
%grid on %hold on
legend('Susceptible(S)')
title('Populasi Susceptible')
xlabel('t(hari)')
ylabel('jumlah populasi')
%plot populasi Infected
figure plot(t,I)
%grid on %hold on
legend('Infected(I)')
title('Populasi Infected')
xlabel('t(hari)')
ylabel('jumlah populasi')
%plot populasi Recovered
figure plot(t,R)
%grid on %hold on
legend('Recovered(R)')
title('Populasi Recovered')
xlabel('t(hari)')
ylabel('jumlah populasi')
%plot populasi total
figure plot(t,N)
%grid on %hold on
legend('Populasi Total(N)')
title('Populasi total')
xlabel('t(hari)')
ylabel('jumlah populasi')
%plot model SIR
figure
plot(t,S,'g',t,I,'r',t,R,'b')
legend('Susceptible(S)','Infected(I)','Recovered(R)')
title('Model SIR (Simulasi 1)')
xlabel('t(hari)')