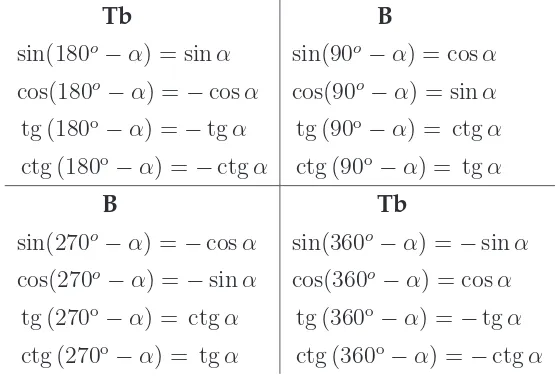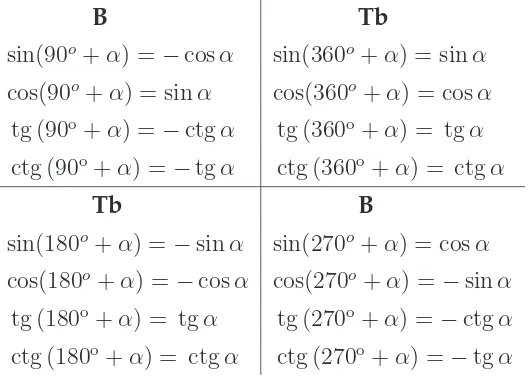Contents iv
List of Tables v
List of Figures vi
1 Mathematics Proof Method
Metode Pembuktian Matematis 1
1.1 Direct Proof
Bukti Langsung . . . 3 1.2 Indirect Proof
Bukti Tak Langsung . . . 6
2 Number Theory
Teori Bilangan 11
2.1 Divisibility
Keterbagian . . . 11 2.2 Special Number
Bilangan Khusus . . . 14 2.2.1 A Prime and Composite Number
Bilangan Prima dan Komposit . . . 14 2.2.2 Perfect Square
Bilangan Kuadrat Sempurna . . . 15
2.3 GCD dan Algoritma Euclid . . . 17 2.4 Modular Arithmetic
Modulo Aritmatik . . . 19 2.5 Linear Diophantine Equations
Persamaan Linier Diophantin . . . 23
3 Algebra Functions
Fungsi Aljabar 28
3.1 Polynomials Inequality
Pertidaksamaan Polinomial . . . 28 3.1.1 Inverse Function
Fungsi Invers . . . 32 3.1.2 Arithmetic and Geometric Sequence
Barisan Aritmatik dan Geometrik . . . 34 3.2 Arithmetic, Geometric, Harmonic, and Quadratic Means
Rataan Aritmatik, Geometrik, Harmonik dan
Kuadratik . . . 43 3.3 The Polynomials and Remainder Theorem
Suku Banyak dan Teorema Sisa . . . 47 3.3.1 Polynomials Division
Pembagian Suku Banyak . . . 47 3.3.2 Remainder Theorem
Teorema Sisa . . . 49 3.3.3 Factor Theorem
3.3.4 Properties of Polynomial Roots
Sifat-Sifat Akar-Akar Suku Banyak . . . 50
4 Trigonometry
Trigonometri 57
4.1 Trigonometric Function
Fungsi Trigonometri . . . 58 4.1.1 Sine and Cosine Rule
Aturan Sinus dan Cosinus . . . 63 4.1.2 Formulas of Sum and Difference of Angles
Rumus-rumus Jumlah dan Selisih Sudut . . . 65 4.1.3 Trigonometric Equation
Persamaan Trigonometri . . . 69 4.2 Limit Fungsi . . . 71
4.2.1 Solution Techniques
Metode Penyelesaian . . . 75 4.2.2 Limit of Algebraic Function
Limit Fungsi Aljabar . . . 76 4.2.3 Limit of Trigonometric Function
Limit Fungsi Trigonometri . . . 79
5 Geometri 86
6 Kombinatorika 125
6.1 Permutasi dan Kombinasi . . . 125
6.2 Prinsip Inklusi-Ekslusi dan Peluang . . . 126
6.3 Koefisien Binomial . . . 127
6.4 Prinsip Sarang Merpati . . . 131
6.5 Paritas . . . 132
6.6 Relasi Rekurensi . . . 133
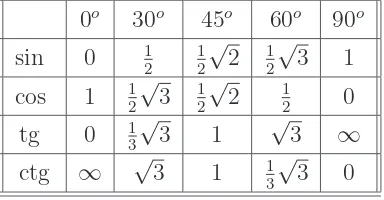
4.1 Trigonometric quadrant system . . . 59 4.2 The value of trigonometric functions for special angles . . . 60 4.3 The value of trigonometric functions for any angle(Xo−α) . . . 61 4.4 The value of trigonometric functions for negative angles . . . 62 4.5 The value of trigonometric functions for any angle(Xo+α) . . . 62
3.1 Squares in the circles. . . 37
4.1 The right triangle trigonometric system . . . 58
4.2 Triangle and circle of radiusR . . . 64
4.3 Sum and Difference of Angles . . . 66
5.1 . . . 86
Mathematics Proof Method
Metode Pembuktian Matematis
In mathematics, a proof is a convincing demonstration (within the accepted stan-dards of a field study) to show that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single exception.
Dalam matematika, bukti adalah suatu demonstarasi meyakinkan (mengikuti beberapa standar yang diterima dari suatu bidang kajian tertentu) untuk me-nunjukkan bahwa pernyataan matematika itu betul-betul benar. Pembuktian lebih diperoleh dari penarikan kesimpulan secara deduktif dibandingkan den-gan penarikan kesimpulan yang secara induktif atau empiris. Denden-gan demikian, bukti harus menunjukkan bahwa sebuah pernyataan itu adalah benar disegala hal tanpa suatu perkecualian sedikitpun.
The statement that is proved is often called atheorem. Once a theorem is proved, it can be used as the basis to prove further statements. A theorem may also be referred to as alemma, that is a sub theorem, especially if it is intended for use as a stepping stone in the proof of another theorem. An implication of theorems or lemmas is known as acorollary. An unproved proposition that is believed to be true is known as aconjecture.
Sebuah pernyataan yang sudah terbuktikan disebut denganteorema. Sekali teo-rema itu terbuktikan maka hal ini dapat digunakan sebagai dasar untuk mem-buktikan pernyataan-pernyataan selanjutnya. Kadangkala teorema disebut juga
dengan lemma, bagian kecil dari teorema, khusunya jika hal ini digunakan seba-gai batu loncatan untuk membuktikan teorema-teorema lainnya. Sebuah akibat dari beberapa teorema atau lemma disebut dengan korolary. Sebuah pernyataan yang tidak terbuktikan namun diyakini kebenarannya dikenal dengan istilah konjektur.
Proofs employ logic but usually include some amount of natural language which usually admits some ambiguity. In fact, the vast majority of proofs in writ-ten mathematics can be considered as applications of rigorous informal logic. Purely formal proofs, written in symbolic language instead of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical prac-tice, quasi-empiricism in mathematics, and so-called folk mathematics (in both senses of that term). Therefore, the philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.
Mathematics statement can be either true or false. A statement which is always true is called atautology, a statement which is always false is called a contradic-tion. To prove a truth of mathematics statement, we need a proof technique. Ba-sically, there are two types of proof technique, namely direct proof and indirect proof. In the following, we describe how the two techniques are implemented in proving the truth of a statement.
Pernyataan matematika dapat bernilai benar atau salah. Suatu pernyataan yang selalu bernilai benar disebuttautologi, sedangkan pernyataan yang selalu berni-lai salah disebutkontradiksi. Untuk membuktikan kebenaran suatu pernyataan matematika dibutuhkan suatu metode pembuktian. Pada prinsipnya terdapat dua metode pembuktian, yaitu bukti langsung dan bukti tak langsung. Berikut ini akan dijelaskan bagaimana kedua metode itu diterapkan untuk membuk-tikan kebenaran suatu pernyataan.
1.1
Direct Proof
Bukti Langsung
In this case, to prove a truth of mathematics statement is utilized a direct way with a particular technique in direction of having a conclusion. In general, there are three direct proofs, namely one way proof (implication), two ways proof (biimplication/equivalence) and mathematics induction. Some examples of the use of those methods are presented in the following.
Lemma 1.1.1 Ifnis a natural number then1 + 2 + 3 +· · ·+n= n2(n+ 1)for anyn.
Lema 1.1.1 Jikan suatu bilangan asli maka1 + 2 + 3 +· · ·+n = n
2(n+ 1) untuk
setiapn.
Proof. Implication Proof: SupposeUn = n2 =⇒ Un+1 = (n+ 1)2 = n2+ 2n+ 1 =⇒Un+1−Un= 2n+ 1. Then we have
Bukti. Pembuktian Implikasi: MisalUn =n2 =⇒Un+1 = (n+ 1)2 =n2+ 2n+
1 =⇒Un+1−Un= 2n+ 1. Maka didapat
Un+1−Un = 2n+ 1
Un−Un−1 = 2(n−1) + 1
...
U3−U2 = 2·2 + 1
U2−U1 = 2·1 + 1.
Sum up thenequations above, we get
Jumlahkan seluruhnpersamaan di atas maka akan didapat
Un+1−U1 = 2(1 + 2 +· · ·+n) + (1 + 1 +· · ·+ 1)
1 + 2 +· · ·+n = n
2+n
2
Therefore
Dengan demikian1 + 2 +· · ·+n= n
2(n+ 1). ✷
Lemma 1.1.2 Leta, bbe two integer numbers andnbe a positif integer. For any integer
n,n|aandn|bwill give the same remainder if and only ifn|(a−b).
Proof. Equivalence Proof:
Bukti. Pembuktian Ekuivalensi:
(=⇒)
Letsbe a remainder ofaandbdivided byn, we havea=kn+sandb =jn+s
for0≤s≤ndank, j ∈I.
Misal sisa pembagian bilangan a dan b oleh n adalah s maka a = kn+s dan
b=jn+s, dengan0≤s≤ndank, j ∈I.
a−b = (kn+s)−(jn+s) = (kn−jn)
= (k−j)n.
Sincek, j ∈ I, k −j = pwhere pis also integer, and a−b = pn, it shows that
n|(a−b).
Karenak, j ∈Imakak−j =p dimanapjuga bilangan bulat, sehinggaa−b =pn, yang artinyan|(a−b).
(⇐=)
Suppose thatn|(a−b). We will prove thataandbwill give the same remainder when they are divided byn. Leta=kn+s1andb =jn+s2 for0≤ s1 ≤ nand 0≤s2 ≤n, we will show thats1 =s2.
Misal n|(a −b). Akan dibuktikan bahwa a dan b akan mempunyai sisa yang sama bila dibagi n. Misala = kn+s1 dan b = jn+s2 untuk 0 ≤ s1 ≤ n dan
0≤s2 ≤n, maka akan ditunjukkans1 =s2.
a−b = pn a = b+pn
= (jn+s2) +pn
= (j+p)n+s2
Since the remainder ofn|ais single, we haves2 =s1
Karena sisa darin|aadalah tunggal makas2 =s1. ✷
Lemma 1.1.3 Prove that3|(22n−1)forn≥1.
Lema 1.1.3 Buktikan bahwa3|(22n−1)untukn ≥1.
Proof. Mathematics Induction. Forn = 1−→3|(22−1)−→3|3(true). Suppose it is true forn=k, we have3|(22k−1). Thus, is that true forn=k+ 1?
Bukti. Induksi Matematika. Untukn = 1−→3|(22 −1)−→3|3(benar). Misal
benar untukn =kmaka3|(22k−1). Selanjutnya apakah benar untukn=k+ 1? 3|(22(k+1)−1) ?
3|(22k+2−1)
3|(22k·22 −1)
3|(22k·22−22+ 3)
3|(22(22k−1) + 3).
Since3|22(22k−1)and3|3. It follows that3|(22(22k−1) + 3), hence it is also true forn =k+ 1.
Karena3|22(22k−1)dan3|3maka3|(22(22k−1) + 3). Sehingga hal ini juga benar
untukn =k+ 1. ✷
1.2
Indirect Proof
Bukti Tak Langsung
general, there are two indirect proofs, namely contradictive proof and contra-positive proof. Contradictive proof is also called reductio ad absurdum proof. For instance, we will proof thatAis true, we start the proof by assuming thatA
is not true. Contrapositive proof is obtained by finding a contraposition of an implication statement in logic math. For instance, we will proof thatp −→ qis true, we start the proof by determining the contraposition ofp −→ (q∨r), i.e. ∼(q∨r)−→∼p. As we know, in logic mathp−→(q∨r) =∼(q∨r)−→∼p. In the following, we present how to use these methods.
Dalam teknik pembuktian ini, fakta-fakta yang ada tidak digunakan secara lang-sung untuk menuju pada kesimpulan. Pembuktia dimulai justru dari hal se-baliknya. Secara umum terdapat dua pembuktian tak langsung, yakni pembuk-tian kontradiksidanpembuktian kontraposisi. Pembuktian kontradiksi disebut juga pembuktian kemustahilan. Misal yang akan dibuktikan adalah benarnya perny-ataan A, maka pembuktian dimulai dengan mengandaikan bahwa A adalah salah. Pembuktian kontraposisi diperoleh dari menentukan kontraposisi dari sebuah pernyataan implikasi dalam logika matematika. Misal akan dibuktikan bahwa pernyataanp=⇒(q∨r)benar, maka pembuktian diawali dengan menen-tukan kontraposisi darip =⇒ (q∨r), yaitu ∼ (q∨r) =⇒∼ p. Seperti yang kita ketahui, dalam logika matematikap=⇒ (q∨r) =∼ (q∨r) =⇒∼ p. Berikut ini kita jelaskan bagaimana menggunakan metode pembuktian ini.
Lemma 1.2.1 Prove that√2is an irrational number.
Lema 1.2.1 Buktikan bahwa√2adalah suatu bilangan irasional.
Proof. Contradictive Proof. Suppose that √2 is a rational number. We will have √2 = a
b, where a
b is a simplified form. By squaring the two sides, we obtaina2 = 2b2. It follows thata2 is even which implies thatais even. Suppose
Since both a and b are even, ab is not a simplified form any more, which is a contradiction.
Bukti. Pembuktian kontradiksi. Misal√2adalah bilangan rasional maka√2 = a
b (dimana a
b adalah bentuk yang paling sederhana). Kuadratkan kedua ruasnya
diperoleha2 = 2b2, sehinggaa2 adalah bilangan genap danapasti genap. Misal
a = 2k −→ (2k)2 = 2b2 −→ b2 = 2k2 yang berakibatb juga genap. Bilaadan b
adalah sama-sama genap maka ab bukan bentuk yang paling sederhana lagi, ini
jelas kontradiktif. ✷
Lemma 1.2.2 Prove that ifm+n ≥73thenm ≥37orn≥37, form, n∈I.
Lema 1.2.2 Buktikan bahwa jika m +n ≥ 73 maka m ≥ 37 atau n ≥ 37, untuk
m, n∈I.
Proof. Contrapositive Proof. Consider the statement as a logic expressionp=⇒ (q∨r), wherep ≡ m+n ≥ 73,q ≡ m ≥37andr ≡ n ≥ 37. The contraposition of the statement is∼ (q∨r) =⇒∼ por(∼ q∧ ∼ r) =⇒∼ p. Therefore, to prove the truth of the statement above, we can start proving that ifm <37andn < 37 thenm+n <73. Suppose the two any numbers arem ≤36dann≤36, we have
m+n ≤36 + 36 −→m+n ≤72−→m+n <73. It completes the prove that if
m+n≥73thenm≥37orn≥37, form, n∈I.
Bukti. Pembuktian kontraposisi. Misal pernyataan tersebut disajikan dalam
p=⇒(q∨r), dimanap≡m+n ≥73,q ≡m≥ 37danr≡n ≥37. Kontraposisi pernyataan tersebut adalah∼(q∨r) =⇒∼ patau(∼q∧∼r) =⇒∼ p. Sehingga untuk membuktikan kebenaran pernyataan di atas dapat dimulai dengan mem-buktikan bahwa jikam <37dann <37makam+n <73. Misal sebarang dua bilangan itu adalahm ≤ 36dan n ≤ 36, maka m+n ≤ 36 + 36 −→ m+n ≤
72 −→ m+n < 73, terbukti. Sehingga terbukti pulalah kebenaran pernyataan
PROBLEMS ANDSOLUTIONS
SOAL-SOAL DANPEMBAHASAN
1. Prove that(an+b)m =bm mod n. Buktikan bahwa(an+b)m=bm mod n.
Solution. Direct Proof.To prove(an+b)m =bm mod n, we need to show that there exists an integerksuch that(an+b)m−bm =kn.
Solusi. Bukti Langsung. Untuk membuktikan (an+b)m = bm mod n
perlu ditunjukkan bahwa terdapat bilangan bulat k sedemikian hingga
(an+b)m−bm =kn.
(an+b)m−bm =
µ
(an)m+m(an)m−1b+...+m(an)bm−1+bm
¶
−bn
= (an)m+m(an)m−1b+...+m(an)bm−1+bm−bm = (an)m+m(an)m−1b+...+m(an)bm−1
=
µ
(a)mnm−1+m(a)m−1nm−1b+...+m(a)bm−1bm−1
¶
n
Letk =
µ
(a)mnm−1+m(a)m−1nm−1b+...+m(a)bm−1bm−1
¶
, hence we get
(an+b)m−bm =kn. Therefore(an+b)m =bm mod n. Bilak =
µ
(a)mnm−1+m(a)m−1nm−1b+...+m(a)bm−1bm−1
¶
, maka didapat
(an+b)m−bm =kn. Sehingga(an+b)m =bm mod n.
2. Ifpis a prime number andp|a1a2...anthenp|ai for any1≤i≤n.
Jikapadalah bilangan prima danp|a1a2...anmakap|aiuntuk sebarang1≤
i≤n.
Assume it is true forP(k), that is ifp|a1a2...akthen p|ai for any1 ≤ i ≤ k. We will show thatP(k+1)is also true. Sincep|a1a2...akak+1andpis a prime number, it holdsp|a1a2...ak orp|a(k+1). From the two possibilities, we have
p|aifor1≤i≤k+ 1asP(k)is true. It concludes thatP(k+ 1)is also true. Solusi. Induksi Matematika. MisalP(k)adalah representasi dari perny-ataan tersebut. Langkah I : Jika p|a1, jelas bahwa P|ai untuk suatu 1 ≤
i ≤ 1. Langkah II : Misalkan p(k) benar, artinya jika p|a1a2...ak maka p|ai
untuk suatu 1 ≤ i ≤ k. Akan dibuktikan bahwa P(k + 1) benar. Dike-tahuip|a1a2...akak+1, maka karenapbilangan prima berlakup|a1a2...akatau
P|a(k+1). Dari kedua kemungkinan ini dikombinasikan, karenaP(k)
berni-lai benar, maka didapatkan untuk suatu1≤i≤k+ 1. Jadi terbukti bahwa
P(k+ 1)bernilai benar.
3. Prove that ifxm is divisible by a primep, thenxis also divisible byp. Bukatikan bahwa jika xm habis dibagi bilangan prima p, maka x habis
dibagip.
Solution. Sincepdividesxm, we havep|xmorp|x.xm−1. Sincepis a prime, we have p|x or p|xm−1. Suppose pdoes not divide x, it follows p|xm−1 or
p|x.xm−2. Repeat the process, we will be able to show thatp|x.
Solusi. Karenapmembagi habis xm, didapatp|xm ataup|x.xm−1. Karena
p adalah bilangan prima maka p|x atau p|xm−1. Andaikan p tidak habis
membagix, makap|xm−1ataup|x.xm−2. Jika proses diteruskan maka akan
Number Theory
Teori Bilangan
2.1
Divisibility
Keterbagian
When 13 is divided by 5, it will give quotient 2 and remainder 3, denoted by 13
5 = 2 + 3
5 or13 = 2×5 + 3. In general, for any positive integers aandb there exists a unique pair(q, r)of nonnegative integers such that b = q ×a+r and 0< r < a. We say thatqis the quotient andris the remainder whenbis divided bya. Ifr = 0then we say thatbis divisible byaoradividesb, denoted bya|b. Ifbis not divisible byathen we denote asa∤b.
Jika 13 dibagi 5 maka hasil baginya 2 dan sisanya 3 dan ditulis: 135 = 2 + 3 5 atau
13 = 2×5+3. Secara umum, apabilaabilangan bulat danbbilangan bulat positif, maka ada tepat satu bilangan bulatqdanrsedemikian hinggab =q×a+rdan
0< r < a. Dalam hal ini,qdisebut hasil bagi danradalah sisa pembagian bilab
dibagia. Jikar = 0maka dikatakanbhabis dibagiadan ditulisa|b. Bilabtidak habis dibagiamaka ditulisa ∤b.
Lemma 2.1.1 (1) Ifa|b thena|bcfor anyc∈I; (2) Ifa|bandb|cthena|c; (3) Ifab|c
thena|candb|c; (4) Ifa|bandb|athena=±b; (5) Ifa|banda|cthena|(bx+cy)for any integersxandy.
Lema 2.1.1 (1) Jikaa|bmakaa|bcuntuk sebarangc∈I; (2) jikaa|bdanb|cmakaa|c; (3) jikaab|cmakaa|cdanb|c; (4) jika a|bdanb|amakaa = ±b; (5) jikaa|bdana|c
makaa|(bx+cy)untuk sebarang bilangan bulatxdany.
Proof. Property (1): If a|b then b = ka, and if b|cthen c = lb = l(ka) = (kl)a. It implies that a|c. Property (3): If a|b then b = ka −→ bx = kxa, if a|c then
c=la−→cy=kya. We havebx+cy = (kx+ly)a, thereforea|(bx+cy).
Bukti. Sifat (1): a|b makab = ka, dan b|c makac = lb = l(ka) = (kl)a maka
a|c. Sifat (3): a|bmakab =ka−→bx =kxa, dana|cmakac= la−→cy =kya. Kemudianbx+cy = (kx+ly)amakaa|(bx+cy). ✷
Lemma 2.1.2 A numberais divisible by2nif the lastndigit of the number is divisible by2n.
Lema 2.1.2 Suatu bilanganahabis dibagi2njikanangka terkhir dari bilangan tersebut
habis dibagi2n.
Proof. Suppose n = 1, thus 2 divides a if the last digit of the number is di-visible by 2. Let a = . . . a3a2a1a0, we have a = 10(. . . a3a2a1) + a0. Since 2|10(. . . a3a2a1),a0 must be divisible by 2 to have2|a.
Bukti. Misal n = 1, berarti a habis dibagi 2 jika angka terakhir dari bilangan tersebut habis dibadi 2. Misala =. . . a3, a2a1a0 makaa = 10(. . . a3, a2a1) +a0.
Karena2|10(. . . a3, a2a1)a0 harus habis dibagi 2 untuk memperoleh2|a. ✷
Example. Is 173332 divisible by 8? Since23|332, we have8|173332.
Example. Is13+ 23+· · ·+ 1003divisible by 7? False, as we have13+ 23+· · ·+ 1003 = (1 + 2 + 3 +· · ·+ 100)2 = (5050)2 = 25502500and7∤25502500.
Contoh. Apakah13+ 23+· · ·+ 1003habis dibagi 7? Tidak, karena13+ 23+· · ·+
1003 = (1 + 2 + 3 +· · ·+ 100)2 = (5050)2 = 25502500dan7∤25502500.
Lemma 2.1.3 A numbera = anan−1. . . a1a0 is respectively divisible by 3,9 and 11 if the sum of its digits satisfies respectively the following:(an+an−1+an−2+· · ·+a1+a0) is divisible by 3;(an+an−1+an−2+· · ·+a1+a0)is divisible by 9; and(an−an−1+
an−2−an−3+. . .)is divisible by 11.
Lema 2.1.3 Suatu bilangan a = anan−1. . . a1a0 berturut-turut habis dibagi 3,9 dan
11 jika jumlah angka-angkanya memenuhi masing-masing sifat berikut: (an+an−1+
an−2+· · ·+a1+a0)habis dibagi 3;(an+an−1+an−2+· · ·+a1+a0)habis dibagi 9;
dan(an−an−1+an−2−an−3+. . .)habis dibagi 11.
Proof. Bukti.
a = anan−1. . . a1a0
= an×10n+an−1×10n−1 +. . . a1×101+a0×100
= an×(9 + 1)n+an−1×(9 + 1)n−1+. . . a1×(9 + 1)1 +a0×(9 + 1)0
= an[9n+n·9n−1 +· · ·+ 9n] +an+an−1[9n−1+ (n−1)·9n−2+ · · ·+ 9(n−1)] +an−1+· · ·+ 9a1+a1+a0
= an[9n+n·9n−1 +· · ·+ 9n] +an−1[9n−1+ (n−1)·9n−2+· · ·+
9(n−1)] +· · ·+ 9a1+an+an−1+· · ·+a1+a0
= K(a) +Q(a)
Since(3∧9)|K(a), it must be(3∧9)|Q(a)to have(3∧9)|a.
2.2
Special Number
Bilangan Khusus
2.2.1
A Prime and Composite Number
Bilangan Prima dan Komposit
The integer p > 1is called a prime number if there is no integer d with d > 1 andd6=psuch thatd|p. Any integern >1has at least one prime divisor. Ifnis a prime, then that prime divisor isn itself. An integern > 1that is not a prime is calledcomposite.
Bilangan bulat p > 1 disebut sebuah bilangan prima jika tidak ada bilangan bulatd dimana d > 1dan d 6= psedemikian hingga d|p. Setiap bilangan bulat
n > 1 mempunyai paling sedikit satu pembagi prima. Jikan adalah bilangan prima, maka pembagi primanya adalah bilngann itu sendiri. Sebuah bilangan bulatn >1yang bukan bilngan prima disebut bilangankomposit.
Theorem 2.2.1 Eratosthenes. For any composite n, there exists a primep such that
p|n and p ≤ √n. In other words ”If there does not exist a prime pwhich divides n, wherep≤√n, thennis a prime”.
Teorema 2.2.1 Eratosthenes. Untuk setiap bilangan komposit nada bilangan prima
psehinggap|n danp ≤ √n. Dengan kata lain ”Jika tidak ada bilangan primapyang dapat membagindenganp≤√nmakanadalah bilangan prima”.
Example. Are 157 and 221 prime numbers?. The primes which are less than √
Contoh. Apakah bilangan 157 dan 221 bilangan prima?. Bilangan-bilangan prima yang lebih kecil dari√157adalah 2, 3, 5, 7, 11. Karena tidak ada satupun dari bilangan- bilangan prima itu yang dapat membagi 157, maka 157 meru-pakan bilangan prima. Kemudian bilangan - bilangan prima yang lebih kecil dari√221adalah 2, 3, 5, 7, 11, 13. Karena13|221maka 221 merupakan bilangan komposit.
2.2.2
Perfect Square
Bilangan Kuadrat Sempurna
Any perfect square satisfies the following three properties:
• The possible ones of perfect square number is either 0, 1, 4, 5, 6, dan 9.
• If 4 divides a perfect square then the remainder is either 0 or 1.
• Ifpis a prime andp|x2thenp|z, wherez =x2/p.
Sebarang bilangan kuadrat sempurna memenuhi tiga sifat berikut ini:
• Angka satuan yang mungkin untuk bilangan kuadrat sempurna adalah 0, 1, 4, 5, 6, atau 9.
• Jika 4 membagi bilangan kuadrat sempurna maka sisanya 0 atau 1.
• Jikapbilangan prima danp|x2 makap|z, dimanaz=x2/p.
Example. Obtain a perfect square whose digits arek, k+ 1, k+ 2,3k, k+ 3.
Solution. The ones of the number isk+3, it follows thatkcan be either1,2,3or 6. Whilst the tens is3k, it follows thatkcan be either0,1,2or3. They imply that the possiblek is either1,2or3which give perfect square numbers12334,23465 or 34596. Since the remainder of 12334 divided by4 is 2, it gives that12334 is not a perfect square. The remainder of23465divided by 4 is 1 and5|23465, but 5 ∤ 4693, so that 23465is not a perfect square. Now, 4|34596, and we have the following
Solusi. Angka satuan bilangan kuadrat ini adalahk+ 3sehinggakyang mung-kin adalah1,2,3,6. Sedangkan angka puluhannya adalah3kmakakyang mung-kin adalah 0,1,2,3. Dari kedua kemungkinan ini diperoleh k yang mungkin adalah1,2,3, dengan demikian bilangan kuadrat yang mungkin adalah12334,
23465,34596. Karena12334dibagi4bersisa 2 maka12334bukan bilangan kuadrat. Bilangan23465 dibagi 4 bersisa 1 dan 5|23465, akan tetapi 5 ∤ 4693 maka23465
bukan bilangan kuadrat. Sekarang, bilangan4|34596, dan berikut ini berlaku
2 | 34596
2 | 17298
3 | 8649
3 | 2883
31 | 961
31 | 31
Therefore,34596 = 22·32·312 = 1862 which is a perfect square.
2.3
GCD dan Algoritma Euclid
Leta, bbe any integers. An integerdsatisfyingd|a andd|b is called a common divisor ofaandb. The biggest (respectively, smallest) value ofdis calledGreater Common Divisor/GCD, denoted byGCD(a, b))(respectively,Least Common Mul-tiple/LCM, denoted byLCM(a, b))). Several techniques have been developed to obtain GCD or LCM, one of them is Euclidean algorithm.
Misaladanb sembarang bilangan bulat. Bilangan bulatdyang memenuhi sifat
d|adand|bdisebut faktor persekutuan dariadanb. Nilai terbesar dariddisebut faktor persekutuan terbesar atau FPB dan ditulis denganF P B(a, b)sedangkan nilai terkecil dariddisebut kelipatan persekutuan terkecil atau KPK dan ditulis
KP K(a, b). Beberapa tekni telah dikembangkan untuk menentukan FPB dan KPK, salah satunya adalah algoritma Euclid.
Algorithm 2.3.1 Euclidean Algorithm. Given two integer numbersaandbwitha > b >0,GCD(a, b)can be obtained by repeating the following algorithm:
a = q1b+r1; 0< r1 < b
b = q2r1+r2; 0< r2 < r1
r1 = q3r2+r3; 0< r3 < r2 ...
rn−2 = qnrn−1 +rn; 0< rn< rn−1
rn−1 = qn+1rn+ 0
If rn is the last divisor of the division process which gives a remainder 0 then rn is
GCD(a, b).
a > b >0, makaGCD(a, b)bisa dicari dengan mengulang algoritma berikut:
a = q1b+r1; 0< r1 < b
b = q2r1+r2; 0< r2 < r1
r1 = q3r2+r3; 0< r3 < r2
...
rn−2 = qnrn−1 +rn; 0< rn< rn−1
rn−1 = qn+1rn+ 0
Jika rn merupakan pembagi terakhir dari pembagian di atas yang memberikan sisa 0
makarnmerupakanGCD(a, b).
Example. Determine GCD(4840,1512). Using Euclidean Algorithm, the solu-tion is the following:
Contoh. TentukanGCD(4840,1512). Dengan menggunakan Algoritma Euclid maka solusinya adalah sebagai berikut:
4840 = 3×1512 + 304
1512 = 4×304 + 296
304 = 1×296 + 8
296 = 37×8 + 0
Therefore
JadiGCD(4840,1512) = 8.
Lemma 2.3.1 Anya|candb|cimplyab|cif and only ifGCD(a, b) = 1.
Example. 3|30and5|30imply3×5|30asGCD(3,5) = 1, however2|30and6|30 imply2×6∤30asGCD(2,6)6= 1.
Contoh. 3|30dan5|30maka3×5|30karenaGCD(3,5) = 1, akan tetapi2|30dan
6|30maka2×6∤30karenaGCD(2,6)6= 1.
2.4
Modular Arithmetic
Modulo Aritmatik
Let a, b, and m be integers, with m > 1. We say that a and b are congruent modulom, denoted by a≡ b(modm), if the remainder ofadivided by m andb
divided bymare the same.
Diberikan bilangan bulata, bdan mdimana m > 1. Bilangan adikatakan kon-gruen denganb modulo m, dituliskan dengan a ≡ b(modm), jika sisa pemba-gianaolehmdanbolehmmemberikan sisa yang sama.
Lemma 2.4.1 Ifaandbare congruent modulomthenm|(a−b).
Lema 2.4.1 Jikaadanbkongruen modulommakam|(a−b).
Proof. a≡b(modm) =⇒a=q1m+randb =q2m+r. Hencea−b= (q1−q2)m, it followsm|(a−b).
Bukti. a ≡ b(modm) =⇒ a = q1m +r dan b = q2m +r. Kemudian a−b =
Lemma 2.4.2 (1)a≡b(modm), b ≡a(modm)are equivalent witha−b≡0 (modm); (2) ifa ≡ b(modm)and b ≡ c(modm)then a ≡ c(modm); (3) ifa ≡ b(modm) andd|mthena≡ b(modd); (4) ifa≡ b(modm)andc≡d(modm)thenax+cy ≡ bx+dy(modm)andac≡bd(modm), for anyx, y ∈I.
Lema 2.4.2 (1)a≡b(modm), b ≡a(modm)adalah setara dengana−b≡0 (modm)
; (2) jika a ≡ b(modm) dan b ≡ c(modm) maka a ≡ c(modm); (3) jika a ≡ b(modm)dan d|mmaka a ≡ b(modd); (4) jikaa ≡ b(modm)danc ≡ d(modm)
makaax+cy ≡bx+dy(modm)danac≡bd(modm), untuk sebarangx, y ∈I.
Proof. a ≡ b(modm) −→ m|(a −b) and c ≡ d(modm) −→ m|(c−d). From Lemma 2.1.1, we havem|((a−b)x+(c−d)y)orm|((ax+cy)−(bx+dy)), therefore
ax+cy≡bx+dy(modm).
Bukti. a ≡ b(modm) −→ m|(a−b) dan c ≡ d(modm) −→ m|(c−d). Sesuai Lema 2.1.1 didapatm|((a−b)x+ (c−d)y)ataum|((ax+cy)−(bx+dy)), sehingga
ax+cy≡bx+dy(modm). ✷
It follows from Lemma 2.4.2, iff(x)is a polynomial of integer coefficients and
a≡b(modm)thenf(a)≡f(b) (modm).
Akibat dari Lemma 2.4.2, jikaf(x)adalah suatu fungsi polinom dengan koefisien-koefisien bilangan bulat dana≡b(modm)makaf(a)≡f(b) (modm).
Example. Prove that for any naturaln,S = 2903n−803n+261n−464nis divisible by 7 and 271. Furthermore, prove that1897|S.
Contoh. Buktikan bahwa untuk setiap bilangan aslinmakaS = 2903n−803n+ 261n−464nhabis dibagi 7 dan 271. Buktikan juga bahwa1897|S.
and 271|S. Furthermore, since1897 = 7×271 and GCD(7,271) = 1, it follows from Lemma 2.3.1 that1897|S.
Solusi. Karena2903≡803 (mod 7)dan464≡261 (mod 7), demikian juga2903≡ 464 (mod 271) dan 803 ≡ 261 (mod 271) maka sesuai dengan Lema 2.4.2(4) di-pastikan bahwa7|Sdan271|S. Selanjutnya karena1897 = 7×271danGCD(7,271) = 1, maka sesuai Lema 2.3.1 terbukti1897|S.
Lemma 2.4.3 (am+b)n≡bn(modm)
Lema 2.4.3 (am+b)n≡bn(modm)
Proof. The proof is the same with showing that there exists an integer k such that(am+b)n−bn=km.
Bukti. Pembuktian ini sama artinya dengan membuktikan ada bilangan bulat
ksehingga(am+b)n−bn=km.
(am+b)n−bn = (am)n+n(am)n−1·b+· · ·+n(am)bn−1+bn−bn
= {a(am)n−1+an(am)n−2+· · ·+an(b)n−1}m
= km.
✷
Example. Determine the ones of19971991.
Contoh. Tentukan angka satuan bilangan19971991.
Solusi. Dengan menggunakan Lema 2.4.3 maka solusinya adalah sebagai berikut: The ones(Angka satuan) 19971991 = The remainder(Sisa bagi)19971991 oleh 10
= (199×10 + 7)1991 (mod 10)
= 71991 (mod 10)
= 74×497+3 (mod 10)
= (74)497×73 (mod 10)
= (2401)497×343 (mod 10)
= (240×10 + 1)497×(34×10 + 3) (mod 10)
= 1×3 (mod 10)
= 3 (mod 10)
Thereforre, the ones of19971991 is 3.
Sehingga, angka satuan bilangan19971991 adalah 3.
It is easy to see that powering numbers0,1,2, . . . ,9give the following ones/units: 0 =>0→ 1type,1 => 1→1type,2 =>2,4,8,6 →4types,3 =>3,9,7,1→4 types,4 =>4,6→2types,5 =>5→1type,6 =>6→1type,7 =>7,9,3,1→ 4types,8 =>8,4,2,6→4types,9 =>9,1→2types.
Mudah dicermati bahwa perpangkatan bilangan0,1,2, . . . ,9akan menghasilkan angka satuan berikut: 0 => 0 → 1 jenis,1 => 1 → 1 jenis,2 => 2,4,8,6 → 4
jenis,3 = 3,9,7,1 → 4jenis,4 => 4,6 → 2jenis,5 => 5→ 1jenis,6 => 6 →1
Dengan demikian pencarian angka satuan dari perpangkatan bilangan dapat dilakukan dengan cara berikut: Misal pada contoh soal di atas. Berapa angka satuan bilangan 19971991. Karena angka satuan bilangan dasar adalah angka 7
maka angka satuan perpangkatan bilangan ini akan meliputi 4 jenis yaitu 7,9,3,1. Selanjutnya1991/4 = 4×497 + 3sehingga19971991 = 19974×497+3yang berakibat
angka satuan dari 73 → 3. Dengan demikian angka satuan bilangan 19971991
adalah 3.
Example. Determine the ones of345678292784383951.
Contoh. Tentukan angka satuan bilangan345678292784383951.
Solution. Since the ones of the base is4, the ones of the exponential number contains 2 types, namely 4,6. Thus 383951/2 = 2×191975 + 1, it implies that 345678292784383951 = 3456782927842×191975+1 which follows the ones of 41 → 4. Therefore the ones of345678292784383951is 4.
Solusi. Karena angka satuan bilangan dasarnya adalah 4maka angka satuan perpangkatan bilangan ini akan meliputi 2 jenis yaitu 4,6. Selanjutnya tentukan
2|383951 = 2×191975 + 1sehingga345678292784383951 = 3456782927842×191975+1
yang berakibat angka satuan dari41 → 4. Dengan demikian angka satuan
bi-langan345678292784383951adalah 4.
2.5
Linear Diophantine Equations
Persamaan Linier Diophantin
An equation of the formax+by = cwherea, b, c are fixed integers anda, bare all different from zero is called a linear Diophantine equation if the solutionsx, y
Persamaan ax + by = c dengan a, b, c bilangan-bilangan bulat dan a, b dua-duanya bukan nol disebut persamaan linier Diophantine jika penyelesaiannya dicari untuk bilangan-bilangan bulat.
Theorem 2.5.1 Diophantine equationax+by =cis solvable if and only ifGCD(a, b)|c.
Teorema 2.5.1 Persamaan Diophantineax+by=cmempunyai penyelesaian jika dan hanya jikaGCD(a, b)|c.
Proof. Letd = GCD(a, b)andd|c. We haved|c⇐⇒ c =kdfor any integersk. Whilstd|GCD(a, b)⇐⇒am+bn=dfor anymandnsuch that:
k(am+bn) =kd
a(km) +b(kn) = c,
it implies thatx=mk dany=nk
Bukti. Misal d = GCD(a, b) dan d|c, maka d|c ⇐⇒ c = kd untuk sebarang bilangan bulat k. Sedangkan d|GCD(a, b) ⇐⇒ am+bn = d untuk sebarang bilangan bulatmdannsehingga:
k(am+bn) =kd a(km) +b(kn) = c,
berartix=mkdany=nk
Theorem 2.5.2 Ifd=GCD(a, b)andx0, y0are the solutions of Diophantine equation
ax+by=c, then the general solutions are
x=x0+
b
dk and y =y0− a
Teorema 2.5.2 Jika d = GCD(a, b) dan x0, y0 merupakan penyelesaian persamaan
Diophantineax+by=c, maka penyelelesaian umum persamaan tersebut adalah :
x=x0+
b
dk dan y=y0 − a
dk; dengankparameter bilangan bulat.
Example. Find the general solutions of Diophantine equation738x+ 621y= 45. Contoh. Tentukan solusi umum dari persamaan Diophantine738x+ 621y= 45. Solution. FindingGCD(738,621)with Euclidean Algorithm
Solusi. MencariGCD(738,621)dengan Alogaritma Euclide
738 = 1×621 + 117
621 = 5×117 + 36
117 = 3×36 + 9
36 = 4×9 + 0.
we getGCD(738,621) = 9. Since9|45, the equation is solvable. Consider the 9 as a linear combination of 738 and 621.
diperolehGCD(738,621) = 9. Karena9|45maka persamaan di atas mempunyai penyelesaian. Jadikan 9 sebagai kombinasi linear dari 738 dan 621.
9 = 117−3·36
= 117−3(621−5×117) =−3×621 + 16×117
= −3×621 + 16(738−621)
9 = 16×738−19×621
multiplying the two sides by 5, we get45 = 80×738−45×621. It implies that
Kalikan kedua ruas dengan 5, diperoleh 45 = 80× 738 −45× 621, sehingga didapatx0 = 80, y0 =−95. Dengan demikian penyelesaian umumnya adalah:
x = 80 +621
9 k= 80 + 69k
y = −95− 738
9 k =−95−82k
PROBLEMS ANDSOLUTIONS
SOAL-SOAL DANPEMBAHASAN
1. A numberAis the smallest natural number which is a product of the small-est three of prime number. Determine two numbers between200and 300 which gives the same prime factor withA.
BilanganAadalah bilangan asli terkecil yang merupakan hasil kali dari3
bilangan prima terkecil. Sebutkan dua buah bilangan di antara 200 dan
300yang mempunyai faktor prima yang serupa dengan bilanganA. Solution. A = 2.3.5 = 30, the desired numbers are 24.3.5 = 240 and 2.32.5 = 270
Solusi. A= 2.3.5 = 30, jadi bilangan yang dicari adalah24.3.5 = 240dan
2.32.5 = 270
2. P(n)is a multiplication of the digits of numbern, andS(n)is summation of its digits. Determine the ones ofn satisfying P(n) +S(n) = n if n is a number consisting two digits.
P(n)didefinisikan sebagai perkalian antara angka-angka bilangan n dan
Solution. Assume the numbernisab, we havea, bas a tens and ones. Solution. Asumsikan bilangan tersebut adalahab, maka kita mengartikan
asebagai puluhan danbsebagai satuan.
P(n) +S(n) = n a.b+ (a+b) = ab a.b+ (a+b) = 10a+b
ab = 9a=a9
Therefore, the ones of the number is 9
Dari sini didapatkan bahwa satuan bilangannadalah9
3. What is the remainder of13+ 23 + 33+...+ 1003 divided by 7? Berapakah sisa pembagian13+ 23+ 33+...+ 1003 oleh 7?
Proof. Bukti.
13+ 23+ 33+...+ 1003 = (1 + 2 + 3 +...+ 100)3 = (5050)2
= (101x50)2(mod 7)
= (101)2x(50)2(mod 7)
= (2x72+ 3)2x(72 + 1)2(mod 7)
= 32x1 (mod 7)
= 9 (mod 7)
Algebra Functions
Fungsi Aljabar
3.1
Polynomials Inequality
Pertidaksamaan Polinomial
In this section, we will show how so solve inequalities. Solving an inequality means finding all of its solutions. A solution of an inequality is a number which when substituted for the variable makes the inequality a true statement.
Dalam bagian ini, akan dipelajari bagaimana menyelesaikan pertidaksamaan. Menyelesaikan pertidaksamaan berarti mencari semua himpunnan penyelesa-ian. Penyelesaian dari pertidakasamaan adalah sebuah bilangan dimana pada saat bilangan itu disubstitusikan maka pertidaksamaan menjadi pernyataan yang benar.
Some properties related to inequality are as follows:
• Ifa > bthena=b+k, for anyk.
• Ifa > bthena+c > b+canda.c > b.cwherec >0.
• Ifa > bandb > cthena > c.
• Ifa > bandc > dthena+c > b+d.
• Ifa > b >0then1/a >1/b, and ifa/b >0thena.b >0.
Beberapa sifat-sifat terkait dengan pertidaksamaan adalah sebagai berikut:
• Jikaa > bmakaa=b+k, untuk sebarangk.
• Jikaa > bmakaa+c > b+cdana.c > b.cdimanac >0.
• Jikaa > bdanb > cmakaa > c.
• Jikaa > bdanc > dmakaa+c > b+d.
• Jikaa > b >0maka1/a >1/b, dan jikaa/b >0makaa.b > 0.
In general, we present inequality polynomials as:
Secara umum pertidaksamaan fungsi dinyatakan sebagai
a0xn+a1xn−1+· · ·+an−1x+an ≥ · ∨ · ≤0
The following steps shows how to solve inequality:.
• factorizing the polynomials, if it is not factorizible then consider whether the function is definite or not.
• Draw a number line and show the roots of polynomial equality on it.
• Put sign+or− on each interval of the number line respecting to the fol-lowing rules:
– Consider the coefficient of the highest order of the inequality.
– If the coefficient of the the highest order is positive (respectively, or negative) then the right side of line number interval is+(respectively, or−). Hence, place an alternate sign on the remaining interval.
Lagkah-langkah berikut menunjukkan bagaimana cara menyelesaikan persamaan ini.
• Lakukan memfaktorkan terhadap fungsi polinomial, bila tidak dapat di-faktorkan pertimbangkan apakah fungsi tersebut definit.
• Gambar sebuah garis bilangan dan letakkan semua akar-akar persamaan polinomial dalam garis bilangan.
• Berikan tanda+atau−pada setiap interval dengan prinsip berikut: – Lihat koefisien pangkat tinggi pertidaksamaan tersebut.
– Jika koefisien pangkat tertingginya positif maka interval paling kanan adalah+, bila negatif maka tulis−dan kemudian interval selanjutnya secara bergantian berlawanan tanda.
– Lihat tanda pertidaksamaannya dan cocokkan dengan tanda tanda dalam interval untuk menentukan himpunan penyelesaiannya.
Example. Determinexsatisfying inequalityx2−2x−80≤0and
Contoh. Tentukan nilai-nilaixyang memenuhi kedua pertidaksamaanx2−2x−
80≤0dan
(2x−5)501(x2−3x−4)(−x2+ 7x−80)(x3+ 4x2−x+ 1)2000
(x+ 1)(x+ 14)51 ≥0
Solution. To solve this inequality we should consider discriminantD=b2−4ac of quadratic functionax2+bx+c = 0. If D < 0and a > 0then the quadratic function is positive definite, IfD <0anda <0the quadratic function is negative definite. Furthermore, all number of even power must be positive.
Solusi. Untuk menyelesaikan pertidaksamaan ini maka kita harus ingat kon-sep Deskriminan D = b2 −4acuntuk fungsi kuadratik ax2 +bx +c = 0. Bila
D < 0dan a > 0maka fungsi kuadratik adalah definit positif, BilaD < 0dan
a < 0maka fungsi kuadratik adalah definit negatif. Kemudian setiap bilangan yang berpangkat genap pasti bernilai positif.
x2−2x−80 ≤ 0
(x−10)(x+ 8) ≤ 0⇐⇒Hp1 ={x| −8≤x≤10}
Whilst(Sedangkan)
(2x−5)501(x2−3x−4)(−x2+ 7x−80)(x3+ 4x2−x+ 1)2000
(x+ 1)(x+ 14)51 ≥ 0
(2x−5)501(x−4)⊖ ⊕
(x+ 14)51 ≥ 0
For (Untuk) x6=−14, (2x−5)501(x−4)(x+ 14)51⊖ ⊕ ≥ 0
For (Untuk) x6=−14, (2x−5)501(x−4)(x+ 14)51
| {z }
⊖
⊖ ≥ 0
It follows (Berarti) (2x−5)501(x−4)(x+ 14)51 ≤ 0
Therefore (Sehingga) Hp2 ={x| −14< x≤
5
2 · ∨ ·x≥4}
Since the problem shows a conjunction relation then both solution setsHp1 and
Hp2must be joined. It implies thatHp={x| −8≤x≤ 52 · ∨ ·4≤x≤10}. Karena masalah di atas menunjukkan relasi konjungsi, maka kedua himpunan penyelesaianHp1 danHp2 harus digabung. Sehingga diperolehHp={x| −8≤
x≤ 52 · ∨ ·4≤x≤10}.
Example. The value ofxsatisfying inequality(x−2)4(−x2 −x−10)|x2−x− 1|(−x+ 1)2 ≤1is. . .
Contoh. Hargaxyang memenuhi pertidaksamaan(x−2)4(−x2−x−10)|x2−
(A) x≤ −1 ∨ 0≤x≤1 ∨ x≥2
(B) −12 ≤x≤0 ∨ 32 ≤x≤2
(C) −1≤x≤0 ∨ 1≤x≤2
(D) −12 < x≤ 32
(E) Allx(Semua hargax)
3.1.1
Inverse Function
Fungsi Invers
Iff is a function fromAtoB then aninverse functionforf is a function in the opposite direction, fromB toA, with the property that a round trip (a composi-tion) fromAtoB toA (or fromB toAtoB) returns each element of the initial set to itself. Thus, if an input x into the function produces an output y, then inputtingyinto the inverse functionf−1 (readf inverse, not to be confused with exponentiation) produces the outputx. Not every function has an inverse; those that are calledinvertible.
Jikaf adalah fungsi dariAkeBmakafungsi inversuntukfadalah suatu fungsi balikan yang berlawanana arah, yaitu dari B ke A, dengan sifat rute balikan itu (komposisi fungsi) adalah dari A ke B ke A (atau dari B keA keB) akan mengembalikan masing-masing element dari himpunan asal ke elemen-element itu sendiri. Dengan kata lain, jika dimasukkanxke dalam fungsi memberikan hasily, maka dengan memasukkan nilaiyke dalam fungsi inversf−1(bacaf
Theorem 3.1.1 Iff(x) is function withx ∈ ℜthen inverse functionf−1(x) satisfies the following:
Teorema 3.1.1 Jikaf(x)suatu fungsi dalamx∈ ℜmaka fungsi inversf−1(x)memenuhi
hal berikut:
1. f◦f−1(x) =x· ∧ ·(f◦g)−1(x) =g−1◦f−1(x)
2. f(x) =ax+b =⇒f−1(x) = x−b a
3. f(x) = ax+b
cx+d =⇒f−
1(x) = −dx+b cx−a 4. f(x) =ax2+bx+c=⇒f−1
12 (x) =−2ba ±
q
1
a
¡
x+ D
4a
¢
5. f(x) =√ax+b =⇒f−1(x) = x2−b
a
6. f(x) =ax+b· ∧ ·f◦g =px+q =⇒g(x) = px+aq−b
7. f(x) =abx=⇒f−1(x) = alogx b
Bukti. For no. 4. From (1), we know that f ◦f−1(x) = x, so that for f(x) =
ax2+bx+cwe get
Proof. Untuk nomor 4. Dari (1) dipahami bahwaf◦f−1(x) =xsehingga untuk
f(x) = ax2+bx+cdiperoleh
f(f−1) = x a(f−1)2+b(f−1) +c = x
a(f−1)2+b(f−1) +c−x = 0
f−1
12 = −
b
2a ±
s
1
a
µ
x+ b
2−4ac
4a
¶
3.1.2
Arithmetic and Geometric Sequence
Barisan Aritmatik dan Geometrik
In mathematics, anarithmetic sequenceor arithmetic progression is a sequence of numbers such that the difference of any two successive members of the se-quence is a constant. For instance, the sese-quence 3,5,7,9,11,13, . . . is an metic progression with common difference 2. The sum of the terms of a arith-metic progression is known as aarithmetic series. Thus, the general form of a arithmetic sequence is a, a+b, a+ 2b, . . . , a+ (n−1)b; and that of a geometric series is(a) + (a+b) + (a+ 2b) +· · ·+ (a+ (n−1)b).
Dalam matematika, suatu barisan aritmatika atau urutan aritmatika didefin-isikan sebagai barisan bilangan sedemikian hingga beda dari dua bilangan yang berurutan dari barisan itu adalah konstan. Sebagai contoh, barisan bilangan
3,5,7,9,11,13, . . . adalah barisan aritmatika dengan beda 2. Jumlah suku-suku dari barisan arimatika disebut dengan deret aritimatika. Bentuk umum dari barisan aritmatika adalah a, a +b, a+ 2b, . . . , a + (n − 1)b; sedangkan bentuk umum dari deret aritmatika adalah(a) + (a+b) + (a+ 2b) +· · ·+ (a+ (n−1)b). Meanwhile, Ageometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero num-ber called the common ratio. For example, the sequence 2, 6, 18, 54,. . . is a geometric progression with common ratio 3. Similarly 10, 5, 2.5, 1.25, . . . is a geometric sequence with common ratio 1/2. The sum of the terms of a geo-metric progression is known as a geometric series. Thus, the general form of a geometric sequence is a, ar, ar2, ar3, ar4, . . .; and that of a geometric series is
a+ar+ar2 +ar3+ar4+. . .
se-belumnya dengan bilangan konstan yang tidak nol, yang disebut dengan ra-sio dan rara-sio ini selalu sama. Sebagai contoh, barisan bilangan 2, 6, 18, 54,. . .
adalah barisan geometrik dengan rasio 3. Sama hanya dengan barisan 10, 5, 2.5, 1.25, . . . adalah barisan geometrik dengan rasio 1/2. Jumlah suku-suku dari barisan geometrik ini disebut denganderet geometrik. Bentuk umum dari barisan geometri adalah a, ar, ar2, ar3, ar4, . . .; sedangkan bentuk umum dari
deret geometri adalaha+ar+ar2+ar3 +ar4+. . .
Lemma 3.1.1 Given an arithmetic sequencea+(a+b)+(a+2b)+· · ·+(a+(n−1)b), whereais an initial term anbis a deference of any two successive terms. Then, we have the followings:
Lema 3.1.1 Diberikan suatu deret aritmatikaa+(a+b)+(a+2b)+· · ·+(a+(n−1)b), dimanaa adalah nilai suku awal dan b adalah beda suku-suku yang berurutan, maka beberapa hal berikut berlaku:
Un = a+ (n−1)b (3.1)
Sn =
n
2[U1+Un] (3.2)
Sn =
n
2[2a+ (n−1)b] (3.3)
Ut = a+ 1
2(n−1)b (3.4)
Lema 3.1.2 Jika diantara dua buah bilangan yang berurutan dari suatu deret arit-matika disisipik buah bilangan dan membentuk deret aritmatika baru maka
b′ = b
k+ 1 (3.5)
n′ = n+ (n−1)k (3.6)
Lemma 3.1.3 Leta+ar+ar2 +· · ·+arn−1 be a geometric sequence, wherea, rare respectively an initial value and ratio. The followings hold for this squence
Lema 3.1.3 Diberikan suatu deret geometrik a+ar +ar2 +· · · +arn−1, dimana a
adalah nilai suku awal dan r adalah rasio suku-suku yang berurutan. Beberapa hal berikut berlaku untuk deret ini.
Un = arn−1 (3.7)
Sn =
a(rn−1)
r−1 , r >1 (3.8)
Sn =
a(1−rn)
1−r , r <1 (3.9) Ut = a
√
rn−1 (3.10)
Lemma 3.1.4 If we insert someknumbers on between any two successive numbers of geometric sequence and they form a new geometric sequence, then
Lema 3.1.4 Jika diantara dua buah bilangan yang berurutan dari suatu deret geometrik disisipikbuah bilangan dan membentuk deret geometrik baru maka
r′ = k+1√
r (3.11)
Lemma 3.1.5 For arithmetic and geometric series satisfyUn =Sn−S(n−1).
Lema 3.1.5 Untuk deret aritmatik maupun geometrik berlakuUn =Sn−S(n−1).
Lemma 3.1.6 An infinite convergence geometric series, where|r| < 1, satisfiesS∞ = a
1−r.
Lema 3.1.6 Untuk deret geometrik tak hingga konvergen, dimana |r| < 1, berlaku
S∞= 1−ar.
Example. Determine the sum of all radius of circles whose numbers are infinity. Example. Tentukan jumlah seluruh jari-jari lingkaran berikut ini sampai pada banyaknya lingkaran tak higga.
∞
Furthermore, how to find the n-term of sequence1,4,11,22,37, . . .. Both formu-lasUn can not be used to answer this problems as the sequence does not have a common difference at first layer, namely 3,7,11,15. Thus then, this sequence admits an arithmetic sequence of common difference 4. The solution can be ob-tained by considering polynomialf(x) =akxk+ak−1xk−1+ak−2xk−2+· · ·+a0x0. Selanjutnya, bagaimana menentukan suku ke−ndari barisan bilangan:1,4,11,
22,37, . . .. Kedua rumus Un di atas tidak dapat dipakai untuk menjawab
per-tanyaan ini, sebab beda pada layer pertama tidak sama, yaitu 3,7,11,15, baru kemudian barisan beda ini merupakan barisan aritmatika dengan beda 4. So-lusinya diperoleh dari mempertimbangkan fungsi polinomial f(x) = akxk +
ak−1xk−1+ak−2xk−2+· · ·+a0x0.
Lemma 3.1.7 Letf(x) = a1x+a0;x = 1,2, . . . , n be a linear function series of the polynomial, it has common differenceb =a1 at firs layer.
Lema 3.1.7 Misal deret fungsi linear dari polinomial di atas adalah f(x) = a1x+
a0;x= 1,2, . . . , n, maka deret ini mempunyai bedab =a1pada layer pertama.
Proof. An expansion of the linear function for then-terms is as follows: Bukti. Ekspansi fungsi linear sampai suku ke−nadalah sebagai berikut:
a1+a0,2a1 +a0, . . . , a1(n−3) +a0, a1(n−2) +a0, a1(n−1) +a0, a1n+a0
hence the common difference of the successive terms isb = f(n)−f(n−1) =
f(n−1)−f(n−2) =· · ·=f(2)−f(1) =a1, namely
sehingga beda dari suku-suku yang berurutan adalah b = f(n)−f(n − 1) =
f(n−1)−f(n−2) =· · ·=f(2)−f(1) =a1, yaitu
a1+a0,2a1 +a0
| {z }
a1
, . . . , a1(n−3) +a0, a1(n−2) +a0
| {z }
a1
, a1(n−1) +a0, a1n+a0
| {z }
Lema 3.1.8 Letf(x) = a2x2+a1x+a0;x= 1,2, . . . , nbe a quadratic function series of the polynomial, it has common differenceb= 2a2 at second layer.
Lema 3.1.9 Misal deret fungsi kuadrat dari polinomial di atas adalahf(x) = a2x2+
a1x+a0;x= 1,2, . . . , n, maka deret ini mempunyai bedab = 2a2 pada layer kedua.
Proof. An expansion of the quadratic function for then-terms is as follows: Bukti. Ekspansi fungsi quadratic untuk suku ke−nadalah sebagai berikut:
a2+a1 +a0,4a2+ 2a1+a0, . . . , a2(n−1)2+a1(n−1) +a0, a2n2+a1n+a0
hence the differences of the successive terms are as follows:
sehingga beda layer pertama dari suku-suku yang berurutan adalah sebagai berikut:
bn = f(n)−f(n−1) = 2a2n−a2 +a1 = (2n−1)a2+a1
bn−1 = f(n−1)−f(n−2) = 2a2n−3a2+a1 = (2n−3)a2+a1
bn−2 = f(n−2)−f(n−3) = 2a2n−5a2+a1 = (2n−5)a2+a1
...
b3 = f(3)−f(2) = 5a2+a1
b2 = f(2)−f(1) = 3a2+a1.
Therefore, the common difference of the successive terms of the difference se-quence of the first layer is
Dengan demikian, beda dari suku-suku yang berurutan pada barisan beda un-tuk layer pertama adalah
or atau
a2 +a1+a0, 4a2+
| {z }
3a2+a1
2a1+a0, 9a2+
| {z }
5a2+a1
3a1+a0, 16a2+
| {z }
7a2+a1
4a1+a0, 25a2+
| {z }
9a2+a1→Layer I
5a1 +a0
| {z }
2a2
| {z }
2a2
| {z }
2a2→Layer II
✷
Lema 3.1.10 Letf(x) =a3x3+a2x2 +a1x+a0;x = 1,2, . . . , n, be a cubic function series of the polynomial, it has common differenceb = 6a3 at third layer.
Lema 3.1.11 Misal deret fungsi kubik dari polinomial di atas adalah f(x) = a3x3 +
a2x2 +a1x+a0;x = 1,2, . . . , n, maka deret ini mempunyai bedab = 6a3 pada layer
ketiga.
Proof. As exercise.
Bukti. Sebagai latihan. ✷
We conclude inductively in the following theorem:
Secara induktif dapat disimpulkan dalam teorema berikut:
Theorem 3.1.2 The series of polynomial functionf(x) =akxk+ak−1xk−1+ak−2xk−2+ · · ·+a0x0;x= 1,2, . . . , nhas a common differenceb=k!ak at layerk.
Teorema 3.1.2 Deret fungsi polinomialf(x) =akxk+ak−1xk−1+ak−2xk−2+· · ·+
Proof. As exercise.
Bukti. Sebagai latihan. ✷
Example. Given a series15 + 32 + 63 + 108 + 167 +. . .. Obtain then−term and then−sum.
Example. Diberikan suatu deret15 + 32 + 63 + 108 + 167 +. . .. Tentukan suku ke−ndan jumlah ke−n.
Solution. The series above forms the following Solusi. Deret di atas akan mengikuti pola berikut
15 + 32
| {z }
17
+ 63
| {z }
31
+ 108
| {z }
45
+ 167
| {z }
59
+. . .
| {z }
14 | {z }14 | {z }14
Since the series has a common difference at second layer, we have k = 2 and the functionf(x) = a2x2 +a1x+a0. We need to find the coefficientsa2, a1, a0. Theorem 3.1.2 impliesb = k!ak = 2!a2 = 14 → a2 = 7, it follows f(x) = 7x2+
a1x+a0. LetUn=f(n)andUn= 7n2+a1n+a0. We have the following:
Karena deret fungsi mempunyai beda yang sama pada layer kedua makak = 2
dan rumusf(x) = a2x2+a1x+a0. Selanjutnya perlu dicari koefisiena2, a1, a0.
Dari Theorema 3.1.2 diperoleh b = k!ak = 2!a2 = 14 → a2 = 7. Sehingga
f(x) = 7x2 +a
1x+a0. Misal Un = f(n) dan Un = 7n2 +a1n+a0, maka akan
didapat:
n= 1 → 7 +a1+a0 = 15→a1+a0 = 8
n= 2 → 28 + 2a1+a0 = 32→2a1+a0 = 4
From both equations, we have a1 = −4 dan a0 = 12 which implies that the
Dari kedua persamaan diperoleh nilai a1 = −4 dan a0 = 12. Sehingga suku
ke−nadalahUn = 7n2−4n+ 12.
To find then−sum of the above series, we consider the following series
Untuk menentukan jumlah ke−ndari deret di atas, maka kita lihat deret berikut
Un → 15,32,63,108,167, . . .
Sn → 15,47,110,218,385, . . . 15, 47
| {z }
32
,110
| {z }
63
, 218
| {z }
108
, 385
| {z }
167
+. . .
| {z }
31 | {z }45 | {z }59
| {z }
14 | {z }14
Since the sequence of function has a common difference on the third layer, we have k = 3 and function f(x) = a3x3 +a2x2 +a1x+a0. We need to find the coefficientsa3, a2, a1, a0. Theorem 3.1.2 implies b = k!ak = 3!a3 = 14 → a3 = 73. Hencef(x) = 7
3x 3+a
2x2+a1x+a0. LetSn=f(n)andSn = 73n3+a2n2+a1n+a0. We have the following:
Karena deret fungsi mempunyai beda yang sama pada layer ketiga makak = 3
dan rumus f(x) = a3x3 +a2x2 +a1x+a0. Selanjutnya perlu dicari koefisien
a3, a2, a1, a0. Dari Theorema 3.1.2 diperoleh b = k!ak = 3!a3 = 14 → a3 = 73.
Sehinggaf(x) = 73x3+a
2x2+a1x+a0. MisalSn =f(n)makaSn = 73n3+a2n2+
a1n+a0, maka akan didapat:
n= 1 → 7
3 +a2+a1+a0 = 15→a2+a1+a0 = 38
3
n= 2 → 56
3 + 4a2+ 2a1+a0 = 47→4a2+ 2a1+a0 = 85
3
n= 3 → 189
3 + 9a2+ 3a1+a0 = 110→9a2+ 3a1+a0 = 141
3
Dengan menyelesaikan ketiga persamaan di atas diperoleh nilaia2 = 32, a1 = 676
dana0 = 0. Sehingga jumlah suku ke−nadalahSn= 73n3+ 32n2+ 676n. ✷
3.2
Arithmetic, Geometric, Harmonic, and Quadratic
Means
Rataan Aritmatik, Geometrik, Harmonik dan
Kuadratik
In mathematics or statistics, anarithmetic meanof a list of numbers is the sum of all of the list divided by the number of items in the list. The arithmetic mean is the most commonly-used type of average and is often referred to simply as the average. A geometric mean is a type of mean or average, which indicates a central tendency of numbers. It is similar to arithmetic mean, which is what most people think of with the word ”average,” except that instead of adding the set of numbers and then dividing the sum by the count of numbers in the set
n, the numbers are multiplied and then the nth root of the resulting product is taken. A harmonic mean(formerly sometimes called the subcontrary mean) is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired. A quadratic meanis a type of average which is calculated as the square root of the mean of the squares.
hanyalah rata-rata, namun dalam rata-rata seluruh bilangan dalam daftar di-jumlahkan kemudian dibagi dengan banyaknya bilangan dalam daftar, untuk rataan geometrik semua bilangan dalam daftar dikalikan kemudian ditarik akar pangkat n. Rataan harmonik (dulu disebut sebagai kebalikan rataan) adalah jenis lain dari rata-rata. Biasanya ini sesuai untuk menentukan rata-rata yang mempertimbangkan tingkatan.Rataan kuadratikadalah tipe dari rata-rata yang diperoleh dari menarik akar kuadrat dari rata-rata kuadratnya.
Let AM=