INTEGRAL. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 45

INTEGRAL

Departemen Matematika FMIPA IPB Bogor, 2012

Topik Bahasan

1 Pendahuluan 2 Anti-turunan

3 Luas di Bawah Kurva 4 Integral Tentu

5 Teorema Dasar Kalkulus 6 Integral Taktentu 7 Aturan Substitusi 8 Telaah Konsep

Pendahuluan

Beberapa Terapan Integral

Peramalan jumlah populasi (penduduk, bakteri, dsb.) di masa yang akan datang.

Penentuan ketinggian pesawat ulang-alik pada waktu tertentu. Penentuan konsumsi energi di Jakarta pada suatu hari.

Anti-turunan

Anti-turunan

De…nisi

Fungsi F disebut anti-turunan dari fungsi f pada interval I jika F0(x) =f(x)untuk setiap x₂I. Contoh (Anti-turunan) 1 f(x) =x3)F(x) = 1₄x4 2 f(x) =x3)F(x) = 1 4x4+5 3 f(x) =cos x)F(x) =sin x

Anti-turunan

Teorema (Anti-turunan Umum)

Jika F anti-turunan dari f pada interval I, maka anti-turunan dari f yang paling umum adalah

F(x) +C (1)

Anti-turunan

Formula Anti-turunan

No. Fungsi Anti-turunan

1. kf(x) kF(x) +C 2. f(x) g(x) F(x) G(x) +C 3. xn, n₆₌ 1 xn+1/(n+1) +C 4. sin x cos x+C 5. cos x sin x+C 6. sec2_{x tan x+C} 7. csc2x cot x+C

8. sec x tan x sec x+C

9. csc x cot x csc x+C

Luas di Bawah Kurva

Luas di Bawah Kurva

Konsep integral dapat didekati dengan gagasan penentuan luas daerah bidang rata

Bagaimana menentukan luas daerah bidang rata S yang dibatasi oleh:

Luas di Bawah Kurva

Ilustrasi Pendekatan Persegi Panjang untuk Menghitung

Luas

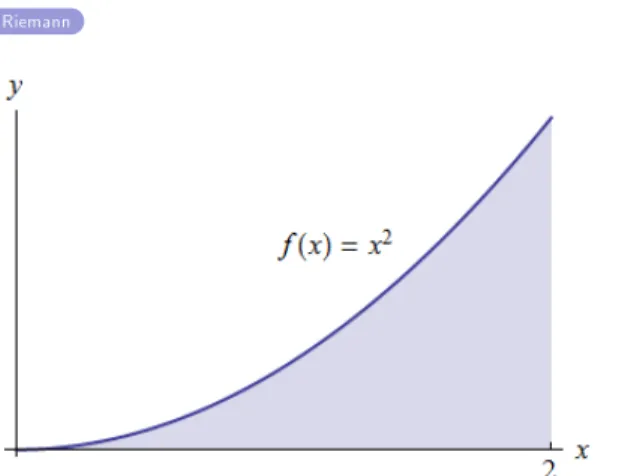
Ingin ditentukan luas daerah yang dibatasi kurva f(x) =x2_{, sumbu-x,}

x=0, x=2 dengan pendekatan persegi panjang.

Luas di Bawah Kurva

Pendekatan Persegi Panjang untuk Menghitung Luas

Buat n persegi panjang dengan luas A1, A2, . . . , An,

luas A dari daerah S didekati dengan penjumlahan luas n persegi

panjang_!A A1+A2+ +An=Rn,

Luas di Bawah Kurva

Penghitungan Luas dengan Pendekatan Persegi Panjang

Untuk menentukan luas daerah S yang dibatasi oleh: kurva kontinu

y=f(x) 0, sumbu x, garis x=a, x=b, lakukan:

Bagi interval[a, b]menjadi n interval bagian[a=x0, x1],

[x1, x2], . . . , [xn 1, xn=b] dengan panjang yang sama, yakni ∆x= b a_n , sehingga berlakuxi =a+i∆x, i=1, 2, . . . , n.

Pada setiap interval bagian

[xi 1, xi] buat persegi panjang

dengan lebar∆x dan panjang

f(x_i), sehingga luasA_i =

Luas di Bawah Kurva

De…nisi

Luas A dari daerah S yang dibatasi oleh kurva kontinu y=f(x) 0,

sumbu x, garis x=a, x=b adalah

A= lim n!∞Rn = nlim!∞ n ∑ i=1 f(xi)∆x = lim n!∞[f(x1)∆x+f(x2)∆x+ +f(xn)∆x] (2) dengan ∆x= (b a)/n, xi=a+i∆x, i=1, 2, . . . , n.

Luas di Bawah Kurva

Formula Notasi Sigma

1. _∑n i=1 c = c n 2. ∑n i=1 c xi = c n ∑ i=1 xi 3. ∑n i=1 x_i y_i = _∑n i=1 x_{i ∑}n i=1 y_i 4. ∑n i=1 i = n(n+1) 2 5. ∑n i=1 i2 = n(n+1) (2n+1) 6 6. ∑n i=1 i3 ₌ n(n+1) 2 2 (3) c= konstanta.

Luas di Bawah Kurva Contoh

Gunakan pendekatan persegi panjang untuk menentukan luas daerah yang dibatasi kurvaf(x) =x2_{, sumbu-x, x=0, x=2, dengan}

Integral Tentu

Integral Tentu

Konsep Jumlah RiemannRn= ∑ni=1f(xi)∆x pada(2)dapat diperluas untuk daerah yang ada di bawah sumbu-x (S2). Jumlah Riemann pada S2 negatif karena f(xi) <0.

Pada interval [a, b], lambang limit Jumlah Riemann dapat diganti dengan lambang integral tentu,

limn_!∞∑n_i=1f(xi)∆x=

Rb

Integral Tentu

Integral Tentu De…nisi (Integral Tentu)

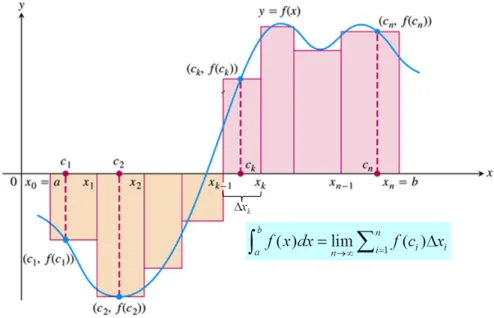
Integral tentu fungsi f dari a ke b adalah

Z b a f(x)dx = lim n!∞ n ∑ i=1 f(ci)∆x (4)

denganci 2 [xi 1, xi],∆x = (b a)/n,[xi 1, xi]adalah interval bagian ke-i dari [a, b] = [x0, xn], i =1, 2, . . . , n.

Titik sampelci pada interval bagian [xi 1, xi]dapat berupa: titik ujung kanan,ci=xi

titik ujung kiri,ci =xi 1 titik tengah,ci = (xi 1+xi)/2

Syarat cukup agarf terintegralkan pada [a, b] adalah f kontinu pada

Integral Tentu

Dari Notasi Sigma ke Integral

LambangR_abf(x)dx₎

R

: integral ( bentuk "S" = sum) a, b : batas bawah,atas integral

f(x): integran (fungsi yang diintegralkan) dx : diintegralkan terhadap variabel x

Integral Tentu

Integral Tentu

Hasil Evaluasi Integral Tentu

Rb

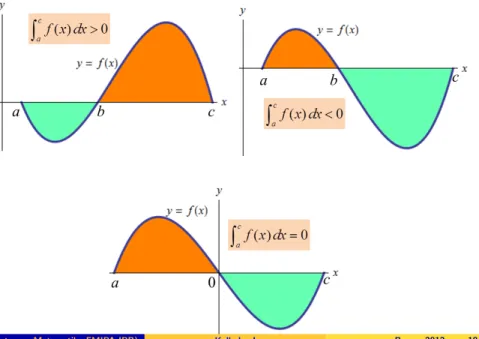
a f(x)dx, b a menghasilkan sebuah bilangan dengan salah satu dari tiga kemungkinan berikut:

>0

seluruh daerah berada di atas sumbu-x

luas daerah di atas sumbu-x>luas daerah di bawah sumbu-x

<0

seluruh daerah berada di bawah sumbu-x

luas daerah di bawah sumbu-x> luas daerah di atas sumbu-x

=0

f(x) =0 atau a=b

Integral Tentu Soal (Konsep Integral Tentu)

1 Gunakan de…nisi integral tentu (dengan titik ujung kanan) untuk

menghitung R₀2 x2 _{x dx, jawab: lim}

n!∞ 2 3+ 4 3n2+ 2 n = 2 3

2 Gunakan de…nisi integral tentu untuk menunjukkan bahwa

Rb a x dx=

b2 _a2

2 .

3 Hitung integral berikut dengan menafsirkannya sebagai bentuk luas.

a) R₀2 1+p4 x2 _{dx, jawab: 2+π}

b) R2₂(1 _jx_j)dx, jawab: 0

4 Ungkapkan limit berikut dalam bentuk integral tentu.

a) lim n!∞ 12 n3 + 22 n3 + + n2 n3 b) lim n!∞ 1 n 1 1+ (1/n)2 + 1 1+ (2/n)2 + + 1 1+ (n/n)2

Integral Tentu

Sifat-sifat Integral Tentu

Integral Tentu

Sifat-sifat Integral Tentu

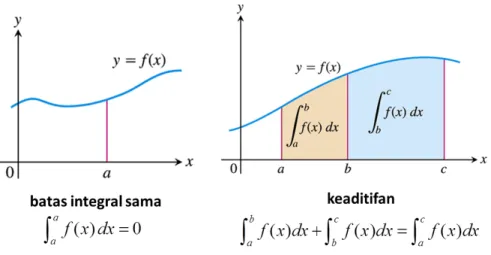
Sifat Umum 1 Ra b f(x)dx= Rb a f(x)dx 2 Ra a f(x)dx=0 3 Rb a c dx=c(b a) 4 R_abc f(x)dx=cR_abf(x)dx 5 Rb a [f(x) g(x)]dx= Rb a f(x)dx Rb a g(x)dx 6 Rb a f(x)dx+ Rc b f(x)dx= Rc a f(x)dx

Integral Tentu

Soal (Sifat Integral I)

1 Diketahui R₀2f(x)dx=4 dan R₂0(g(x) f(x))dx=5. Gunakan

sifat-sifat integral untuk menghitung:

a) R₂0(2f(x) 3)dx b) R₀2g(x)dx, jawab: a. 2 b. 1 2 R1 0 f(t)dt=2, R4 0 f(t)dt= 6, dan R4 3 f(t)dt=1. Hitung R3 1 f(t)dt. jawab: 9

Integral Tentu

Integral Tentu

Sifat-sifat Integral Tentu

Sifat Pembandingan 1 Jika f(x) 0, x2 [a, b], maka Rb a f(x)dx 0 2 Jika f(x) g(x), x2 [a, b], maka Rb a f(x)dx Rb a g(x)dx 3 Jika m f(x) M, x2 [a, b], maka m(b a) R_abf(x)dx M(b a)

Integral Tentu

Soal

Gunakan sifat pembandingan integral untuk memeriksa kebenaran pertidaksamaan berikut tanpa menghitung integral.

1 2 R1 1 p 1+x2_{dx 2}p₂ 2 1/2 R2 1 1 xdx 1 3 R3 1 p x4_{+1 dx>26/3 (diketahui:} Rb a x2dx= 1 3 b 3 _a3 ₎

Teorema Dasar Kalkulus

Teorema Dasar Kalkulus

Pengantar

Kalkulus diferensial muncul dari permasalahan garis singgung.

Kalkulus integral muncul dari permasalahan luas daerah: perhitungan rumit seperti limit Jumlah Riemann.

Sepintas, keduanya tampak tidak berkaitan.

Newton dan Leibniz menemukan bahwa keduanya saling terkait. Konsep yang mengaitkan kalkulus integral dengan kalkulus diferensial: Teorema Dasar Kalkulus (TDK).

Teorema Dasar Kalkulus

Teorema Dasar Kalkulus

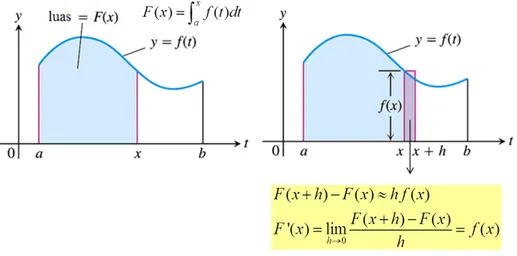
Teorema (Teorema Dasar Kalkulus 1)

Jika f kontinu pada [a, b], maka F(x) =R_axf(t)dt kontinu pada [a, b], terturunkan pada (a, b), dan turunannya adalahf(x);

Teorema Dasar Kalkulus Soal (TDK-1) Tentukan: 1 d dx Z x 0 1 1+t2dt, 2 d dx Z _x2 0 sin t dt,

petunjuk: u=x2_{, jawab: 2x sin x}2

3 d

dx Z g2(x)

g1(x)

f(t)dt, jawab: f(g2(x))g0₂(x) f(g1(x))g0₁(x)

4 fungsi f dan konstanta a yang memenuhi 6+

Z _x a f(t) t2 dt=2 p x, x>0, jawab: f(x) =x3/2, a=9.

Teorema Dasar Kalkulus

Teorema Dasar Kalkulus 2

Konsep

Dari TDK-1: G(x) =R_axf(t)dt₎G0(x) =f(x) (G anti-turunan f ). Catat bahwaG(a) =R_aaf(t)dt=0.

Misalkan F anti-turunan lain dari f , maka F(x) =G(x) +C F(b) F(a) = [G(b) +C] [G(a) +C] = G(b) G(a) =G(b) = R_abf(t)dt=R_abf(x)dx Jadi Rb a f(x)dx=F(b) F(a)

Teorema Dasar Kalkulus

Teorema (Teorema Dasar Kalkulus 2)

Jika f kontinu pada [a, b] danF sebarang anti-turunan f pada[a, b], maka

Rb

a f(x)dx =F(x)jba =F(b) F(a) (6)

TDK-2 memberi cara yang mudah dalam mengevaluasi integral tentu, jauh lebih mudah dibandingkan menggunakan limit Jumlah Riemann. Berdasarkan TDK-2, untuk mengevaluasi integral tentu f pada[a, b]:

tentukan anti-turunanF dari f , evaluasiF(b) F(a).

Teorema Dasar Kalkulus Soal Tentukan: 1 Rπ/2 0 cos x dx, jawab: 1 2 R4 1 3 2 p x+_x42 dx, jawab: 10 3 R2 1xjxj dx, jawab: 7/3 4 d dx Z _x 0

Integral Taktentu

Integral Taktentu

De…nisi (Integral Taktentu)

Misalkan F adalah anti-turunan f . Integral taktentu f(x)terhadapx adalah

R

f(x)dx=F(x) +C (7)

Hasilintegral tentu(persamaan 4) berupa suatu bilangan, hasil integral taktentu berupa fungsi.

Integral Taktentu

Formula Integral Taktentu

1 R kf(x)dx=kR f(x)dx 2 R (f(x) g(x))dx= R f(x)dx R g(x)dx 3 R xndx=xn+1/(n+1) +C, n6= 1 4 R sin x dx= cos x+C 5 R cos x dx=sin x+C 6 R sec2x dx=tan x+C 7 R csc2x dx = cot x+C

8 R sec x tan x dx=sec x+C

Aturan Substitusi

Aturan Substitusi

Aturan substitusi digunakan pada kasus:

sulit menentukan anti-turunan integran secara langsung, tetapi bagian tertentu integran dapat dimisalkan dengan variabel baru sehingga lebih mudah dicari anti-turunannya.

Contoh Ingin ditentukan R 2p2x+3 dx Solusi O Misalkan u=2x+3)du/dx=2)du=2dx) R 2p2x+3dx =R pudu = 2₃u3/2+C = 2₃(2x+3)3/2+C

Aturan Substitusi R 2p2x+3dx= ? Jika u=g(x) =2x+3, g0(x) =2=du/dx, f(u) =pu, maka berlaku R 2p2x+3dx =R f(g(x))g0(x)dx =R f(u)du

Aturan Substitusi

Teorema (Aturan Substitusi)

Jika u=g(x)adalah fungsi terturunkan dan f kontinu pada Wg, maka

R f(g(x))g0(x)dx=R f(u)du Rb a f(g(x))g0(x)dx= Rg(b) g(a) f(u)du

Aturan Substitusi

Integral Fungsi Simetri

Aturan Substitusi

Integral Fungsi Simetri

Dengan menggunakan aturan substitusi, dapat ditunjukkan

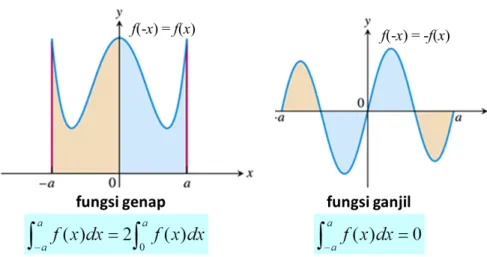
1 Jika f fungsi genap, maka

Ra af(x)dx=2 R0 af(x)dx =2 Ra 0 f(x)dx (8)

2 Jika f fungsi ganjil, maka Ra

Aturan Substitusi Soal (Aturan Substitusi)

Evaluasi integral (1 5)berikut:

1

Z

x sin x2dx, jawab: 1₂cos x2+C

2 Z 2 1 x p 2 x dx, jawab: 14/15 3 Z 1 0 x 3p_x2_{+1 dx, jawab: 2/15} p₂₊₁ 4 Z _π/2 π/2 x2_{sin x} 1+x6 dx, jawab: 0 5 Z 1 0 x p 1 x4_{dx, jawab: π/8}

6 Gunakan aturan substitusi untuk menunjukkan

a Jikaf genap, maka

Z a

f(x)dx=2

Z a

Aturan Substitusi

Ekspresi Integral Taktentu Tidak Khas

Soal

Tunjukkan bahwa R sin x cos x dx menghasilkan ekspresi berbeda dengan

substitusi

i) u=sin x, ii) u=cos x, iii) u=2x berdasarkan kesamaan

sin 2x=2 sin x cos x

) Hal tersebut menunjukkan bahwa fungsi yang dihasilkan dari integral

Telaah Konsep

Telaah Konsep I

Kuis Benar-Salah

1 Jika f dan g kontinu pada[a, b], maka Rb a f(x)g(x)dx= Rb a f(x)dx Rb a g(x)dx .

2 Jika f kontinu pada[a, b], maka Rb

a xf(x)dx=x Rb a f(x)dx. 3 Jika Rb a f(x) dx=0, maka f(x) =0, x2 [a, b]. 4 Jika Rb a [f(x)] 2 dx=0, maka f(x) =0, x_{2 [}a, b].

5 Jika f kontinu pada[a, b] danf(x) 0, maka Rb a p f(x)dx= q_R b a f(x)dx

6 Jika f(x) g(x) pada[a, b], maka Rb

a jf(x)j dx

Rb

a jg(x)jdx.

7 Jika f(x) g(x) pada[a, b], maka Rb

a f(x)dx

Rb

a g(x)dx .

Telaah Konsep

Telaah Konsep II

Kuis Benar-Salah

9 Jika F0(x) =G0(x), x2 [a, b], maka F(b) F(a) =G(b) G(a). 10 Jika F(x)adalah anti-turunan dari f(x), makaF(2x)adalah

anti-turunan darif(2x). 11 Z 1 1 x 3 _2x7₊ sin x 1+x2 dx=0. 12 Z 11 11 ax 2_{+bx+c dx=2}Z 11 0 ax 2_{+c dx.} 13 Z 3 1 cos 2_{x dx=} Z 1 5 cos 2_{x dx+}Z 3 5 cos 2_{x dx.} 14 d dx Z _x2 1 1 1+t2dt= 1 1+x4. 15 lim n!∞ n ∑ i=1 cos 2i n = Z 2 0 cos x dx.

Telaah Konsep

Tentang Slide

Penyusun: N. K. Kutha Ardana (Dosen Dep. Matematika FMIPA IPB)

Versi: 2012 (sejak 2009)