FUNGSI BANYAK VARIABEL DAN PENERAPANNYA
Teks penuh
Gambar

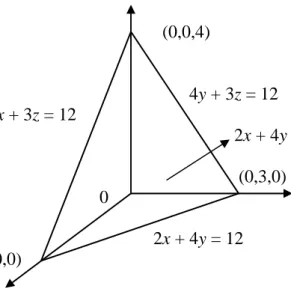


Dokumen terkait
Harapan penelitian adalah individu mampu memahami bahwa komunikasi non verbal yang dibingkai dalam sebuah karya seni memiliki makna sehingga karya seni tidak hanya dilihat
Pembuatan pelaporan penggunaan dana Bantuan Operasional Sekolah secara konvensional dapat menimbulkan beberapa masalah, antara lain kesalahan dalam perhitungan data
Berdasarkan kandungan dalam unsur epoksi dan mengambilkira data toksikologi penyediaan yang sama, didapati penyediaan ini boleh menyebabkan rengsaan dan alahan kepada kulit dan
• Memahami interaksi (baik positif maupun negatif) antara tanaman tahunan (pohon) dengan tanaman setahun (semusim) yang ditanam pada tempat dan waktu yang sama ditinjau
Pada hamparan ini komponen teknologi yang telah dihasilkan lewat penelitian dapat dikaji secara holistik dengan integrasi berbagai komoditas yang memungkinkan secara
(1) Seksi Sarana dan Prasarana Perikanan dipimpin oleh Kepala Seksi yang mempunyai tugas pokok membantu Kepala Bidang Pengelolaan Perikanan dalam melaksanakan koordinasi,
Sebelum masuk lebih jauh pada pembahasan negara Islam dalam perspektif Fazlur Rahman, perlu diketahui terdapat tiga golongan yang memiliki pendapat masing-masing mengenai
Simpulan: belimbing wuluh merupakan salah satu alternatif dalam penyembuhan penyakit acne vulgaris dikarenakan ekstrak belimbing wuluh memiliki kemampuan