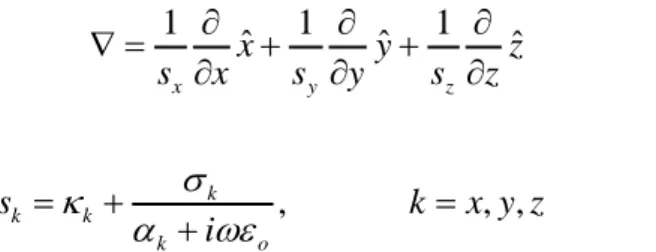Pemodelan Georadar 2D dengan
Metode Beda Hingga Domain Waktu
A. Sulaiman 1 dan M. Taufik 2
1 Pusat Teknologi Inventarisasi Sumberdaya Alam (PTISDA) - BPPT, Jakarta, Indonesia, 2 Pusat Teknologi Informasi dan Komunikasi (PTIK) - BPPT, Jakarta, Indonesia
Email: [email protected]
Abstrak
Salah satu teknologi elektromagnetik dalam ilmu kebumian adalah metode Ground Penetrating Radar (GPR) . Metode ini mencoba memetakan kondisi bawah permukaan tanah dengan menggunakan medan elektromagnetik frekuensi tinggi. Makalah ini menyajikan suatu pemodelan untuk GPR dengan metode beda hingga domain waktu. Setelah meninjau sepintas metode GPR maka pembahasan dilanjutkan dengan persamaan pembangun model. Pemodelan ditulis dengan Matlab dan akan dipaparkan dalam bab selanjutnya. Pembahasan diakhiri dengan contoh penerapannya.
Kata kunci: Elektromagnetik, Ground Penetrating Radar, metode beda hingga domain waktu,
pemodelan
Abstract
One of the electromagnetic technology in earth science is a method of Ground Penetrating Radar (GPR). This method tries to map the subsurface soil conditions by using high-frequency electromagnetic fields. This paper presents a modeling for GPR with the finite difference time domain method. After a cursory review of the GPR method then the discussion continued with the equation of the model builder. Modeling is written with Matlab and will be presented in subsequent chapters. The discussion concludes with examples of its application.
Keywords: Electromagnetic, Ground Penetrating Radar, finite difference time domain, model builder
1. Pendahuluan
Georadar atau Ground Penetrating Radar (GPR) adalah salah satu metode geofisika yang bertujuan untuk mencitra kondisi bawah permukaan Bumi. Metode ini bersifat tidak merusak dan mempunyai resolusi yang tinggi, tetapi terbatas sampai kedalaman beberapa puluh meter saja. Meskipun demikian ternyata GPR dapat digunakan untuk banyak pengkajian seperti eksplorasi mineral, analisis sumber air tanah, studi arkeologi, studi keretakan jalan atau bendungan dan lain sebagainya. Penerapan yang tak kalah menarik adalah lingkungan seperti prediksi dan penentuan lokasi daerah bawah permukaan yang terkontaminasi zat pencemar (Knight, 2001).
GPR sebenarnya bekerja atas dasar teknologi yang sudah lama yaitu Radar yang merupakan warisan perang Dunia ke dua. Prinsipnya adalah alat ini memencarkan (transmisi) dan menerima (refleksi) gelombang elektromagnetik (EM) frekuensi tinggi yaitu antara 1MHz – 1GHz (Daniel, 2004). Dalam pengambilan data ada beberapa cara misalnya pemancar berada dilokasi tetap sedangkan penerima bergerak disepanjang daerah yang ingin dipetakan. Cara lain adalah pemancar dan penerima bergerak bersama-sama disepanjang daerah survei. Pencitraan yang diperoleh dengan cara ini muncul dalam bentuk dua dimensi (2D). Jika kita memetakan dalam bentuk grid maka dengan interpolasi kita akan mendapatkan gambaran tiga dimensi (3D).
Secara teori sinyal yang dipancarkan GPR haruslah pulsa tunggal (wavelet), tetapi hal ini sulit secara praktik, jadi biasanya orang menyebut frekuensi pusatnya seperti 50, 200 atau 400 MHz. Sebuah citra GPR merupakan kumpulan dari sinyal yang diperoleh dari wavelet yang telah mengalami peristiwa hamburan dengan material di dalam Bumi. Hamburan ini terjadi karena material Bumi mempunyai sifat
listrik-magnet yang dinyatakan dalam variabel permitivitas listrik (), konduktivitas listrik () dan permeabilitas magnetik (). Medan elektromagnetik yang ditangkap GPR akan bergantung dari variabel di atas. Jadi sebuah sinyal yang dipancarkan GPR pada prinsipnya harus mempunyai frekuensi tunggal dan terpolarisasi linier sebagai berikut (Balasnis, 1999),
(1) di mana E0 dan B0 adalah amplitude (kompleks), frekuensi sudut, konstanta
atenuasi dan parameter fase yang diberikan oleh ,
(2). Data GPR adalah amplitude dan waktu (travel time). Jika kita mengetahui kecepatan gelombang EM maka kita dapat menentukan amplitude sebagai fungsi dari kedalaman. Kecepatan gelombang EM dinyatakan oleh v=/ jadi kecepatan merupakan fungsi dari sifat listrik-magnet dari medium yang dilaluinya. Karena GPR bekerja pada frekuensi tinggi maka biasanya orang mengadakan aproksimasi yaitu konduktitas kecil (<<), aproksimasi ini dikenal dengan nama “low-loss conditions”. Asumsi lain adalah sifat magnetik tanah dianggap konstan yaitu ~0 sehingga
kecepatan dan konstanta atenuasi akan dinyatakan berturut-turut sebagai v=1/(o), =0.5(o/).
Relasi ini menunjukkan bahwa kecepatan atau penentuan kedalaman dikontrol oleh permitivitas listrik sedangkan atenuasi dikontrol oleh konduktivitas. Jika konduktivitas besar misalnya tanah lempung maka atenuasi sangat besar dan pencintraan hanya bisa sampai kedalaman 1 meter saja (Knight, 2001). Jika konduktivitasnya kecil seperti pasir atau gravel maka kedalaman pencitraan lebih besar sampai beberapa meter (puluh meter, jika kelembaban kecil). Dari uraian di atas jelas bahwa pencitraan bawah permukaan dengan GPR tergantung pada sifat dielektrik material geologi bawah permukaan.
z i t z o z t i z oe e B z t Be e E t z E , ; , 2 1 2 1 1 1 2 ; 1 1 2 2 2 Gambar 1. Survei dengan GPR sangat tergantung kepada kondisi elektrisitas bawah permukaan (B-scan dan akusisi data). GPR dengan teknologi bowtie antenna buatan
RCS - PT Solusi 247.
Interpretasi adalah bagian tersulit dari metode GPR karena obyek yang tampak tidaklah mencerminkan gambaran asli benda yang bersangkutan. Misalkan benda dengan obyek silinder akan tampak pada citra berupa profil hiperbola. Akan menjadi lebih rumit dan memusingkan jika kita ingin mencitrakan struktur geologi misalnya. Salah satu cara untuk memandu geofisikawan untuk mendapatkan interpretasi adalah dengan membuat model bagaimana citra medan EM jika kita memberikan struktur dengan sifat-sifat dielektrik yang kita tentukan. Karena umumnya GPR mempunyai teknik akusisi B-scan maka akan dipaparkan pemodelan dua dimensi (2D).
Pada dasarnya pemodelan dalam GPR adalah menyelesaikan persamaan Maxwell dengan syarat batas yang kita tentukan. Karena geometri obyek yang tidak sederhana (seperti silinder, bola dll) maka solusi analitik tidak dapat diperoleh, sebagai gantinya digunakan hampiran atau metode numerik. Pada bagian dua akan dipaparkan persamaan model dan syarat batasnya. Pada bagian ketiga akan dipaparkan bentuk diskrit model numerik dengan metode beda hingga domain waktu. Bagian ke empat berisikan implementasi model dengan Matlab dan paper ini diakhiri dengan suatu rangkuman.
2. Model GPR 2D
Dalam makalah ini hanya dibahas system GPR dengan teknik survei refleksi di permukaan (surface-based reflection). Hasil citra dan teknik survei metode ini dapat dilihat pada Gambar 1. Pada dasarnya penjalaran medan EM akan memenuhi persamaan Maxwell. Dengan model survei permukaan maka kita telah menetapkan suatu syarat batas sehingga persamaan Maxwell akan terkendala dengan syarat batas. Jadi dikatakan medan EM akan mempunyai suatu mode yang dinamakan mode transvers-magnetik (TM) (Balanis, 1989 dan Irving, 2006). Persamaan Maxwell dalam mode ini dinyatakan sebagai berikut,
(3) (4) Persamaan Maxwell yang lain yaitu non monopol magnetik dan divergensi E selalu dipenuhi. Karena bentuk struktur bawah permukaan yang kompleks maka vektor gradien akan memenuhi sistem koordinat variabel sebagai berikut (Irving, 2006),
(5) di mana
(6) yang merupakan sistem koordinat variabel dengan variasi hanya dalam arah k atau arah jalar gelombang. Persamaan (3) dan (4) menyatakan bagaimana medan EM menjalar di suatu medium. Pada dasarnya jika kita berikan suatu sinyal katakanlah
t H E t E E H z z s y y s x x sx y z ˆ 1 ˆ 1 ˆ 1 z y x k i s o k k k k , , ,
Ey(i)=E0 exp(-ikx) maka dengan menyelesaikan persamaan tersebut beserta syarat
batasnya kita akan mendapatkan medan terhambur dari sistem yang bersangkutan. Untuk obyek yang sederhana seperti silinder maka dia akan mempunyai syarat batas yang sederhana pula sehingga menyelesaikan persamaan (3) dan (4) dapat dilakukan secara analitik. Sebagai contoh hamburan medan E akibat benda berbentuk silinder yang mempunyai konduktivitas sempurna adalah (Balanis, 1989):
(7) di mana J dan H adalah fungsi Bassel dan Hankel berturut-turut. Meskipun mempunyai bentuk yang sederhana tetapi hamburan medan EM mengalami depolarisasi tergantung dari orientasi silinder terhadap antena, sifat elektisitas silinder dan radius silinder dibandingkan panjang gelombang datang (Radzevicius and Daniels, 2000). Pengetahuan ini menentukan kita dalam pelaksanaan akusisi data. Sebagai contoh, jika kita menggunakan antena dipole dengan polarisasi linier untuk mendeteksi pipa besi maka citra yang paling jelas terjadi pada saat sumbu utama dipole sejajar dengan sumbu pipa.
Pada kenyataanya di lapangan, kita tidak bisa berharap suatu obyek mempunyai bentuk yang sederhana seperti silinder, kotak atau bola. Terlebih jika obyek yang kita petakan berbentuk struktur geologi. Di samping itu kebanyakan obyek lain seperti batu-batu dan permukaan yang tidak rata akan menimbulkan efek clutter pada citra GPR. Untuk membantu melakukan interpretasi maka diperlukan suatu model bagaimana citra hamburan medan EM disuatu daerah dengan bentuk geometri yang kita desain sendiri. Karena obyek tidaklah sederhana maka mau tidak mau kita harus menggunakan metode numerik. Metode numerik untuk elektromagnetik yang sangat populer adalah metode beda hingga domain waktu yang akan dipaparkan berikut ini. 3. Metode Beda Hingga Domain Waktu dengan Matlab
Metode beda hingga domain waktu atau finite difference time domain (FDTD) menjadi sangat populer dalam elektromagnetik karena ddapat dijalankan secara efisien cukup hanya dalam komputer personal saja. Kentungan menggunakan FDTD adalah (Daniels, 2004):
tidak memerlukan fungsi Green,
langsung menyelesaikan persamaan Maxwell tanpa perlu melalui potensial skalar,
penyelesaiannya eksplisit,
robust, akurat dan langsung dalam implementasinya,
sifat elektrisitas dan konduktivitas diperhitungkan,
dapat digunakan dengan bentuk geometri batas yang kompleks dan
dapat ditulis dalam banyak bahasa pemrograman
Sekarang, tinjau medan EM tanpa kehadiran konduktivitas medium. Dalam keadaan satu dimensi di mana medan EM menjalar katakanlah dalam arah x dan tak ada variasi dalam arah y,z (∂z = ∂y = 0) ditulis sbagai berikut,
(8)
n r H R H R J i E E n n n n n s z cos ) 2 ( ) 2 ( 0 ) (
t E x Hz y t H x Ey z (9) Metode numerik pada umumnya tidak bisa menyelesaikan persamaan ini secara langsung karena persaman (7) dan (8) saling terkopling. Biasanya persamaan tersebut dibuat menjadi tak terkopling dengan cara menurunkan salah satu persamaan terhadap t dan mensubtitusikan persamaan yang lainnya sehingga diperoleh,
(10) Ini dinamakan persamaan gelombang dan mudah diselesaikan dengan metode numerik pada umumnya seperti elemen hingga atau beda hingga. Penyelesaian persamaan gelombang tersebut ternyata tidak robust. Dengan metode FDTD menjadi robust karena diselesaikan secara langsung dari persamaan (7) dan (8) di mana medan listrik E dan medan magnetik H saling tersambung melalui waktu dan grid ruang. Dengan algoritme ini maka variasi medan listrik akan memproduksi variasi medan magnet dan begitu pula sebaliknya. Diskritisasi persamaan (7) dan (8) dinyatakan sebagai berikut (Sullivan, 2000),
(11)
(12) Implementasi dengan Matlab sangat sederhana karena Matlab telah mempunyai pseudocode (yang dipakai adalah diff) sehingga program menjadi:
Hz(1:M)=0; Ey(1:M+1)=0; for n=1:N, Ey(1)=sumber(n); Hz=Hy-dt./mu.*diff(Ey)/dx; Ey(2:M)=Ey(2:M)-dt./ep.*diff(Hz)/dx ; end
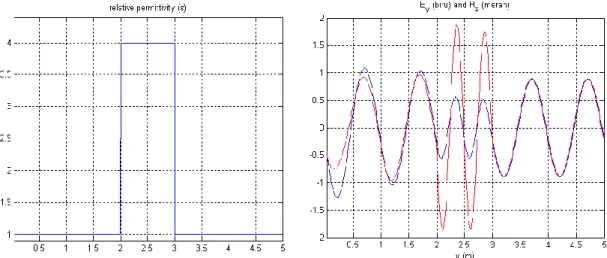
Jadi jelas bahwa dengan memberikan suatu sumber medan E maka medan elektromagnetik dapat ditentukan dengan memasukkan nilai dan . Sebagai contoh akan diberikan perhitungan FDTD untuk propagasi medan Ey dan Hz dalam arah x. Simulasi di jalankan dengan permitivitas vakum 0=8.854x10-12 dan permeabilitas
vakum 0=x4x10-7, permeabilitas relative 1 dan konduktivitas nol.
Program ditulis dengan Matlab yang diadopsi dari Scott Hudson, Washington State University. Terlihat medan Ey dan Hz akan mempunyai profil yang sama setelah melewati medium, tetapi medan Hz mempunyai amplitude yang lebih tinggi
dibanding medan Ey dalam medium dengan permitivitas konstan. Intensitas medan
elektromagnetik (I≈ Ey2 + Hz2) akan tinggi di medium dengan permitivitas lebih tingi
jika dibandingkan disekelilingnya.
0 2 2 2 2 z y H E t x x E E t H H n k y n k y n k z n k z 2 1 1 1 2 1 2 1 2 1 x H H t E E z nk n k z n k y n k y 21 2 1 2 1 2 1 1 1
Gambar 2. Propagasi medan Ey dan Hz dalam medium dengan permitivitas
berbentuk kotak.
Seperti telah diuraikan di atas, bahwa untuk model survei permukaan maka kita sudah berurusan dengan medan elektromagnetik mode TM. Asumsikan medan menjalar dalam arah x dan bervariasi dalam arah z (kedalaman) maka persamaan (3), (4) dan (5) dapat dituliskan dalam komponennya sebagai berikut (Sullivan, 2000),
(13) (14) (15) Dalam bahasa Matlab maka suatu persamaan supaya lebih efisien dalam perhitungan, harus dinyatakan dalam bentuk matriks. Dalam hal 2 dimensi diperlukan kondisi batas sehingga gelombang akan terabsorbsi pada batas, jika tidak maka akan menghasilkan pola yang tak teratur sehingga akan menimbulkan ambiguitas. Syarat batas yang sering dipakai dalam pemodelan GPR adalah perfectly matched layer (PML). Dalam daerah batas dengan PML sx dan sz merupakan bilangan kompleks.
Salah satu mengimplementasikan metode ini adalah dengan menerapkan konvolusi medan E dan H dengan suatu fungsi dari parameter medan (,) yang menyatakan sifat listrik magnet dari medium yang bersangkutan. Karena persamaan (13), (14) dan (15) dalam domain waktu maka konvolusi dilakuakn dengan menerapkan invers transform Fourier dari persamaan (6) yaitu (Irving, 2006):
(16) z E s H i y z x 1 x E s H i y x z 1 z H s x H s E i E x z z x y y 1 1
t t u
t
t
t t s k k k k k k k k k 2 0 2 0 exp 1di mana adalah fungsi delta Dirac dan u adalah fungsi tangga Heaviside. Dengan dikonvolusikan fungsi ini maka persamaan (13), (14) dan (15) akan menjadi,
(17) (18)
(19) Langkah selanjutnya adalah menuliskan persamaan ini dalam bentuk matrik (diskrit). Bentuk beda hingga domain waktu dari persamaan (17), (18) dan (19) dengan syarat batas (16) adalah (Irving, 2006):
(20)
(21)
(22) di mana koefisien dinyatakan oleh:
(23)
z E t z E t H y z y z x 1
x E t x E t H y x y x z 1
z H t x H t z H x H t E E x z z x x z z x y y 1 1
n j i H j i c n j i y n j i y n j i y n j i y j i bz n j i x n j i x xz D E E E E D H H 2 1 2 1 2 1 2 1 2 1 2 1 2 1 , , 1 , , , 1 2 , , , , 27 27
n j i H j i c n j i y n j i y n j i y n j i y j i bx n j i z n j i z zx D E E E E D H H , , , 1 , , 1 , 2 , , , 2 1 2 1 2 1 2 1 2 1 2 1 2 1 27 27
2 1 2 1 2 1 2 3 2 1 2 1 2 1 2 3 2 1 2 3 2 1 2 3 2 1 2 1 2 1 2 1 2 1 2 3 2 1 , , , , , , , , , , , , , , , 1 , 27 27 27 27 n j i E n j i E j i c n j i x n j i x n j i x n j i x j i bz n j i z n j i z n j i z n j i z j i bx n j i y j i a n j i y yz yx C H H H H C H H H H C E C E
t D k t D t t C k t t C t t C c k bk c k bk a ; 24 ; 2 1 24 2 1 ; 2 1 2 1 1 1 1 1 1dan fungsi konvolusi dinyatakan oleh:
(24)
(25)
(26)
(27) dengan koefisien A dan B diberikan oleh:
(28) Seperti biasa, indeks bawah menyatakan koordinat ruang (x,z) dan indeks atas menyatakan koordinat waktu. Program Matlab untuk model di atas telah dibuat oleh Irving dan Knight (2006). Disini tidak akan diberikan list programnya karena terlalu panjang, tetapi bagi pembaca yang berminat dapat mengunduhnya di http://www.iamg.org/CGEditor/index.htm.
4. Implementasi Matlab untuk model 2D
Step penting dalam pemodelan FDTD adalah pemilihan diskritasi waktu dan ruang yang memadai. Jika kita memilih x, z dan t sebesar mungkin maka komputasi akan semakin singkat, tetapi jika semakin kecil maka komputasi semakin lama. Pada pemilihan grid yang besar skema FDTD malah menjadi tidak stabil dan itu akan mempengaruhi perhitungan medan listrik dan medan magnetiknya. Disini akan digunakan kriteria grid sebagai berikut ,
(29) di mana min dan min adalah permeabilitas magnetik dan permitivitas listrik terkecil yang diset diseluruh grid. Program Matlab untuk penentuan grid ini dinyatakan dalam finddt.m dan finddx.m. Variasi spatial mempengaruhi pada variasi permitivitas dan
n
j i y n j i y n j i y n j i x j i z n j i H j i z n j i Hxz B xz A , E , 2 E , 1 E , E , 1 1 , , , 2 27 27 1 2 1 2 1 2 1
n
j i y n j i y n j i y n j i y j i x n j i H j i x n j i Hzx B zx A , E 2, E 1, E , E 1, 1 , , , 2 27 27 1 2 1 2 1 2 1
2
1 2 3 2 1 2 1 2 1 2 1 2 1 2 3 2 1 2 1 , , , , , , , , 27 27 n j i z n j i z n j i z n j i z j i x n j i E j i x n j i Eyx B yx A H H H H 2 1 2 3 2 1 2 1 2 1 2 1 2 1 2 3 2 1 2 1 , , , , , , , , 27 27 n j i x n j i x n j i x n j i x j i z n j i E j i z n j i Eyz B yz A H H H H
k k k k k k k k k k k t B B A 0 2 1 ; exp 2 2 min min max 1 1 7 6 z x t konduktivitas di mana akan dinyatakan dalam skema penentuan sebagai berikut:
x,z= 1 di dalam grid, dan x,z = 1+( d/ )m(xmax,zmax 1) di dalam daerah PML. Di mana d adalah jarak PML dengan batasnya dan adalah kedalaman daerah PML. Sedangkan x,z memenuhi x,z = 0 di dalam grid dan x,z = (d/ )mxmax,zmax. Di mana harga maksimum untuk adalah xmax,zmax = (m+1) /(150√rk) di mana r adalah permitivtas dielektrik relatif di dalam grid terdekat dengan PML. Program Matlab untuk mode TM dinyatakan dalam nama file TM model2d. Sebagai input adalah matriks yang berisi sifat listrik pada semua sumber dan lokasi reciever. Sumber pulsa yang digunakan adalah fungsi jendela Blackman-Harris turunan pertama yang ternormalisasi. Pembangkit fungsi ini dinyatakan dalam subprogram blackharrispulse.m. Frekuensi dominan yang dihasilkan adalah 50, 100 dan 200 MHz. Untuk mendapatkan hasil yang mulus digunakan interpolasi grid yang dinyatakan oleh gridinterp.m, sedangkan untuk mencocokkan grid dengan PML digunakan padgrid.m.
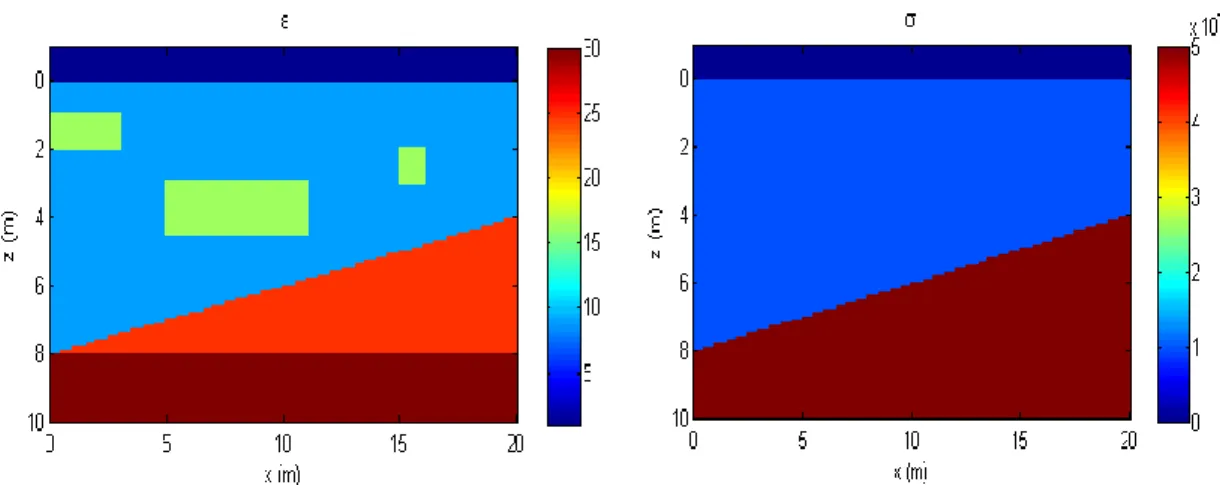
Disini akan diberikan contoh pemodelan untuk survei GPR tipe reflektif permukaan sehingga kita akan berurusan dengan mode TM. Untuk tipe reflektif, suatu daerah survei dimodelkan dengan sifat dielektrik (Gambar 3).
Lapisan pertama adalah daerah sedimen dengan permitivitas rekatif r=9 dan
= 1mS/m. Sedangkan lapisan kedua adal h sebuah benda anomali berupa sebuah material jenuh dengan sifat listrik r=16 dan = 1mS/m. Lapisan terakhir berupa bed rock dengan sifat dielektrik r=25 dan r=30 dan = 5mS/m. Dalam model ini kita mempunyai grid x = z = 0.04m dan _t = 0.08 nanosecond (ns). Hasil simulasi model dengan program TMmodel2d.m dinyatakan dalam Gambar 4.
Pada t = 52ns medan listrik menabrak benda anomali yaitu berupa material jenuh dan front gelombang menampakkan pola yang tak simetris. Pada t = 116ns, gelombang telah menabrak benda anomali kedua dan menabrak bedrock lapisan pertama. Pada t = 192ns gelombang menabrak benda anomali ketiga dan bedrock yang kedua. Pada t = 244 ns energi telah sampai di permukaan yang berasal dari semua refleksi gelombang yang dihasilkan baik dari benda anomali maupun bedrock. Inilah citra yang akan dibandingkan dengan pengukuran di lapangan.
Gambar 4. Hasil simulasi medan E dengan metode FDTD 5. Kesimpulan
Model numerik 2D yang dikembangkan oleh Irving dan Knight (2006) dapat digunakan untuk pemodelan survei GPR untuk tipe reflektif permukaan. Penulisan program dengan Matlab akan memudahkan perhitungan karena dapat dilakukan hanya dengan Personal Computer (PC) dan memberikan hasil yang cukup baik. Bentuk benda anomali dapat kita desain sendiri sesuai dengan keperluan. Model ini dapat pula digunakan untuk survei GPR dengan lintasan yang sangat panjang dan model ini diharapkan diterapkan untuk keperluan tertentu seperti mendeteksi daerah yang terkontaminasi limbah (cairan).
Ucapan Terima Kasih
Hasil kajian ini terjadi karena interaksi penulis dengan Devisi Radar and Communication System PT Solusi 247, terutama dengan Dr. Ir. Adrian A. Lestari, Ir Andi Januar, Prof. Ir. Liarto MSc, Ir. Deni Yuliansyah dan Ir. Dedi „Jorge‟ Sutomo.
Daftar Pustaka
Balasnis, C.A. 1989. Advanced Engineering Electromagnetics. John Wiley and Son, New York.
Daniel, D.J. 2004. Ground Penetrating Radar. IEEE Radar Series, London.
Irving, J.D. 2006. Improving Tomographic Estimates of Subsurface Electromagnetic Wave Velocity Obtaned From Ground Penetrating Radar Data. PhD Disertation, Stanford University.
Irving, J and Knight, R. 2006. Numerical modeling of ground-penetrating radar in 2-D using MATLAB, Computers and Geosciences, Vol. 32, pp. 1247-1258. Knight, R. 2001. Ground Penetrating Radar for Environment Application.
Annu.Rev.Earth Planet. Sci, Vol. 29, pp. 229-55.
Radzevicius, S.J. and Daniels, J.J. 2000. Ground Penetrating Radar Polarization and Scattering from Cylinders. J. Applied Geophysics, Vol. 45, pp. 111-125.
Sullivan, D.M. 2000. Electromagnetic Simulation Using the FDTD Methods. IEEE Press series on RF and Microwaves Technology.