PENERAPAN ALGORITME GENETIKA UNTUK
PENDUGAAN PARAMETER PADA METODE PEMULUSAN
EKSPONENSIAL HOLT-WINTERS
ADAM MUHAMMAD RIDWAN
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2016
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Penerapan Algoritme Genetika untuk Pendugaan Parameter pada Metode Pemulusan Eksponensial Holt-Winters adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Mei 2016 Adam Muhammad Ridwan NIM G14120008
ABSTRAK
ADAM MUHAMMAD RIDWAN. Penerapan Algoritme Genetika untuk Pendugaan Parameter pada Metode Pemulusan Eksponensial Holt-Winters. Dibimbing oleh AJI HAMIM WIGENA dan ANIK DJURAIDAH.
Metode pemulusan eksponensial Holt-Winters dengan tiga parameter dapat digunakan untuk prediksi data deret waktu yang memiliki pola musiman. Penelitian ini menggunakan algoritme genetika (AG) untuk menduga parameter optimum yang meminimumkan nilai RMSE dan kemudian dibandingkan dengan golden section (GS). Data yang digunakan adalah data observasi suhu per 3 jam pada periode 21-30 Juli 2012 yang memiliki pola musiman. Hasil penelitian menunjukkan bahwa penduga parameter dengan AG lebih baik daripada penduga parameter dengan GS pada data pemodelan. Kemampuan prediksi satu waktu ke depan dengan metode Holt-Winters AG lebih baik dibandingkan dengan metode Holt-Wintes GS pada model aditif dan multiplikatif. Kemampuan prediksi delapan waktu ke depan dengan metode Holt-Winters AG lebih baik dibandingkan dengan metode Holt-Winters GS pada model multiplikatif, namun sama dengan metode Holt-Winters GS pada model aditif.
Kata kunci: algoritme genetika, golden section, pemulusan eksponensial Holt-Winters
ABSTRACT
ADAM MUHAMMAD RIDWAN. The Application of Genetic Algorithm to Estimate Parameter of Holt-Winters Exponential Smoothing Methods. Supervised by AJI HAMIM WIGENA and ANIK DJURAIDAH.
Holt-Winters exponential smoothing with three parameters can be used to forecast time series data with seasonal pattern. This study uses a genetic algorithm (AG) to estimate the optimum parameters that minimize RMSE values and then compared to the golden section (GS). The data used is the temperature observation data per 3 hours in the period 21 to 30 July 2012, with a seasonal pattern. The results showed that the estimated parameters with AG gave better results compared to the estimated parameters with GS for the modeling data. The one-step-ahead forecast ability of Holt-Winters AG method was better then that of Holt-Winters GS method on additive and multiplicative model. The eight-step-ahead forecast ability of Holt-Winters AG method was also better then that of Holt-Holt-Winters GS method on multiplicative model, but was the same as that of Holt-Winters GS method on the additive model.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Statistika
pada
Departemen Statistika
PENERAPAN ALGORITME GENETIKA UNTUK
PENDUGAAN PARAMETER PADA METODE PEMULUSAN
EKSPONENSIAL HOLT-WINTERS
ADAM MUHAMMAD RIDWAN
DEPARTEMEN STATISTIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2016
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Maret 2016 ini ialah pemulusan data deret waktu, dengan judul Penerapan Algoritme Genetika untuk Pendugaan Parameter pada Metode Pemulusan Eksponensial Holt-Winters.
Terima kasih penulis ucapkan kepada Bapak Dr Anang Kurnia, MSi selaku ketua departemen statistika. Bapak Dr Ir Aji Hamim Wigena, MSc dan Ibu Dr Ir Anik Djuraidah, MS selaku pembimbing. Ibu Akbar Rizki, MSi selaku penguji luar. Di samping itu, penghargaan penulis sampaikan kepada rekan-rekan mahasiswa statistika, yang telah membantu memberikan kritik dan saran. Ungkapan terima kasih juga disampaikan kepada ayah, ibu, serta seluruh keluarga, atas segala doa dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Mei 2016
DAFTAR ISI
DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 1 METODE 2 Data 2 Metode 2HASIL DAN PEMBAHASAN 5
Analisis Deskriptif 5
Pendugaan Parameter Holt-Winters 5
Hasil Prediksi Suhu untuk 8 Waktu (1 hari) ke Depan 9 Hasil Prediksi Suhu untuk 1 Waktu (3 jam) ke Depan 10
SIMPULAN DAN SARAN 12
Simpulan 12
DAFTAR PUSTAKA 12
LAMPIRAN 14
DAFTAR TABEL
1 Pembagian data pemodelan dan data prediksi 2 2 Hasil pendugaan parameter menggunakan AG dan GS 6 3 Simpangan baku nilai RMSE metode Holt-Winters 9 4 Nilai RMSEP untuk prediksi 8 waktu (1 hari) 9 5 Nilai RMSEP untuk prediksi 1 waktu (3 jam) 12
DAFTAR GAMBAR
1 Plot data suhu per 3 jam pada periode 21-30 Juli 2012 5 2 Hasil pemulusan Holt-Winters dengan (a) parameter solusi AG dan (b)
parameter solusi GS. 7
3 Nilai RMSE metode Holt-Winters (a) model aditif dan (b) model
multiplikatif 8
4 Hasil prediksi metode Holt-Winters 8 waktu (1 hari) ke depan (a) model
aditif dan (b) model multiplikatif. 10
5 Hasil prediksi metode Holt-Winters 1 waktu (3 jam) ke depan (a) model
aditif dan (b) model multiplikatif. 11
DAFTAR LAMPIRAN
1 Lampiran 1 Hasil pemulusan menggunakan penduga parameter dengan
AG dan GS untuk model aditif 14
2 Lampiran 2 Hasil pemulusan menggunakan penduga parameter dengan
AG dan GS untuk model multiplikatif 15
3 Lampiran 3 Hasil prediksi 8 waktu (1 hari) ke depan menggunakan penduga parameter dengan AG dan GS untuk (a) model aditif dan (b)
model multiplikatif 16
4 Lampiran 4 Lebar selang kepercayaan 95% bagi prediksi 8 waktu (1
hari) 18
5 Lampiran 5 Selang kepercayaan 95% bagi hasil prediksi 8 waktu (1 hari) ke depan menggunakan penduga parameter dengan AG dan GS untuk (a)
model aditif dan (b) model multiplikatif 19
6 Lampiran 6 Hasil prediksi 1 waktu (3 jam) ke depan mengunakan penduga parameter dengan AG dan GS untuk (a) model aditif dan (b) model
multiplikatif 21
7 Lampiran 7 Lebar selang kepercayaan 95% bagi prediksi 1 waktu (3
jam) 23
8 Lampiran 8 Selang kepercayaan 95% bagi hasil prediksi 1 waktu (3 jam) ke depan mengunakan penduga parameter dengan AG dan GS untuk (a)
PENDAHULUAN
Latar Belakang
Prediksi pada data deret waktu mengasumsikan bahwa data deret waktu merupakan gabungan antara pola dan galat acak. Menurut Montgomery et al. (2008), teknik pemulusan efektif untuk memperlihatkan pola tersembunyi dalam data deret waktu. Salah satu metode pemulusan yang digunakan pada data deret waktu yang memiliki pola tren dan musiman adalah metode pemulusan eksponensial Holt-Winters yang selanjutnya akan disebut metode Holt-Winters. Metode pemulusan ini menggunakan dua tipe model, yaitu model aditif dan model multiplikatif (Kalekar 2004). Kedua model tersebut memerlukan tiga parameter yang dapat ditentukan secara subjektif maupun secara objektif. Pendugaan secara subjektif dilakukan berdasarkan pengalaman atau penelitian yang telah dilakukan sebelumnya. Pendugaan secara objektif dilakukan dengan mencari nilai parameter yang baik, yaitu nilai parameter yang menghasilkan nilai ukuran kesalahan prediksi atau galat yang kecil. Salah satu ukuran kesalahan prediksi yang dapat digunakan adalah root mean square error (RMSE).
Pendugaan nilai parameter pada metode pemulusan eksponensial secara objektif dapat dilakukan dengan menggunakan algoritme non-linear programming. Penelitian yang dilakukan Nurhidayati (2011) menggunakan metode pencarian dikotomi untuk menduga nilai parameter pada metode eksponensial tunggal. Penelitian Yuwida et al. (2012) menggunakan metode golden section (GS) untuk menentukan nilai parameter pada metode pemulusan eksponensial ganda, namun belum menghasilkan nilai kesalahan prediksi yang minimum. Penelitian Mahkya (2014) menduga parameter pada metode Holt-Winters.
Metode golden section digunakan untuk mencari minimum lokal yang berada dalam interval yang dipilih (Cheney dan Kincaid 2008). Metode ini tidak memberikan jaminan untuk mendapatkan nilai minimum global. Oleh karena itu peneliti tertarik menggunakan algoritme genetika (AG) sebagai metode alternatif untuk menyelesaikan masalah tersebut. Menurut Sivanandam dan Deepa (2008), algoritme genetika mencari solusi dari kumpulan solusi sehingga menambah kesempatan mendapatkan minimum global. Pendugaan parameter akan dilakukan berdasarkn RMSE minimum.
Tujuan Penelitian
Penelitian ini bertujuan mengkaji penerapan algoritme genetika untuk pendugaan parameter pada metode pemulusan eksponensial Holt-Winters model aditif dan model multiplikatif dan membandingkan dengan metode golden section.
2
METODE
Data
Data yang digunakan dalam penelitian ini adalah data observasi suhu di stasiun meteorologi Medan pada periode 21-30 Juli 2012 yang diambil setiap tiga jam. Data suhu dibagi menjadi 8 set data pemodelan dan dan 8 set data prediksi, selengkapnya pada Tabel 1.
Tabel 1 Pembagian data pemodelan dan data prediksi
Data Hari ke- Data Hari ke-
Pemodelan 1 1-2 Prediksi 1 3 Pemodelan 2 1-3 Prediksi 2 4 Pemodelan 3 1-4 Prediksi 3 5 Pemodelan 4 1-5 Prediksi 4 6 Pemodelan 5 1-6 Prediksi 5 7 Pemodelan 6 1-7 Prediksi 6 8 Pemodelan 7 1-8 Prediksi 7 9 Pemodelan 8 1-9 Prediksi 8 10 Metode
Metode Holt-Winters digunakan untuk data yang memiliki faktor trend dan musiman. Metode Holt-Winters merupakan metode pemulusan eksponensial dengan tiga unsur yaitu level, trend, dan musiman (Mongomery et al. 2008). Ada dua tipe model yang digunakan pada metode Holt-Winters, yaitu model aditif dan model multiplikatif.
1. Model aditif
Metode Holt-Winters model aditif dituliskan dalam persamaan berikut: Lt=α(yt-St-s)+(1-α)(Lt-1+Bt-1)
Bt=β(Lt-Lt-1)+(1-β)Bt-1
St=γ(yt-Lt)+(1-γ)St-s
Ft=Lt-1+Bt-1+St-s 2. Model multiplikatif
Metode Holt-Winters model multiplikatif dituliskan dalam persamaan berikut: Lt=α(yt/St-s)+(1-α)(Lt-1+Bt-1) Bt=β(Lt-Lt-1)+(1-β)Bt-1 St=γ(yt/Lt)+(1-γ)St-s Ft=(Lt-1+Bt-1)St-s dengan: s : periode musiman.
yt: nilai observasi pada waktu ke-t.
Lt: nilai pemulusan level pada waktu ke-t dengan 𝛼 adalah bobot pada level. Bt: nilai pemulusan trend pada waktu ke-t dengan 𝛽 adalah bobot pada
3 St : nilai pemulusan musim pada waktu ke-t dengan 𝛾 adalah bobot pada
musim.
Ft : nilai prediksi pada waktu ke-t.
Langkah-langkah yang dilakukan pada penelitian ini adalah sebagai berikut: 1. Melakukan pendugaan parameter menggunakan algoritme genetika.
Algoritme genetika merupakan metode yang dapat menyelesaikan masalah pengoptimuman dan bekerja berdasarkan prinsip evolusi dan genetika (Haupt dan Haupt 2004; Sivanandam dan Deepa 2008). Tahapan-tahapan dalam algoritme genetika adalah sebagai berikut: a. Menentukan fungsi pengepasan (fitness), yaitu:
RMSE=√1
𝑛∑(𝑦𝑡− 𝑦̂𝑡)2 𝑛
𝑡=1 dengan:
yt:nilai observasi pada waktu ke-t. 𝑦̂𝑡:nilai prediksi pada waktu ke-t. b. Membangkitkan populasi awal
Sebanyak N individu berupa vektor (𝛼 𝛽 𝛾) dibangkitkan dari sebaran seragam(0,1) yang merepresentasikan setiap kemungkinan solusi (Sivanandan dan Deepa 2008).
c. Mengevaluasi nilai RMSE semua individu dalam populasi. d. Melakukan seleksi
Individu diseleksi dengan mengambil secara acak individu dengan peluang yang ditentukan menggunakan metode linear ranking, yaitu metode untuk menentukan peluang terpilih berdasarkan peringkat individu (Yu dan Gen 2010). Individu yang memiliki nilai RMSE terkecil memiliki peringkat 1 dan yang terburuk N. Peluang terpilih 𝑝𝑖 untuk individu ke-i dituliskan dengan persamaan
pi=q-(peringkati-1)r dengan r= 2 N(N-1) dan q= 2 N
e. Melakukan pindah silang (crossover)
Pindah silang menggunakan metode blend crossover. Metode tersebut bekerja pada tingkat gen untuk xi1 dan xi2 dengan ketentuan xi1<x
i
2, sehingga gen individu anak adalah sebagai berikut (Yu dan Gen 2010)
xia=seragam((xi1-0.5d),(xi2+0.5d)) dengan
d=xi2-xi1
xi1:gen ke-i individu ke-1. xi2:gen ke-i individu ke-2. xia:gen ke-i individu anak. f. Melakukan mutasi
4
Mutasi menggunakan metode uniform random mutation (mutasi acak seragam). Untuk xij sebagai gen ke-j dari individu ke-i yang terpilih dengan peluang sebesar pm akan diganti dengan nilai acak yang mengikuti sebaran seragam(0,1) (Yu dan Gen 2010).
g. Tempatkan individu baru ke populasi baru.
h. Ulangi langkah b sampai g sehingga banyaknya iterasi maksimum yaitu 1000 iterasi atau berturut-turut sebanyak 50 generasi menghasilkan nilai pengepasan yang sama.
2. Melakukan pendugaan parameter menggunakan metode golden section. Metode golden section menggunakan prinsip mengurangi batas nilai peubah sehingga meminimumkan fungsi objektif (Kiusalaas 2005). Tahapan-tahapan yang dilakukan dalam metode golden section adalah sebagai berikut (Mahkya 2014):
a. Menentukan batas bawah a1, a2, dan a3; batas atas b1, b2, dan b3 serta nilai toleransi berhentinya iterasi 𝜖 = 1 × 10−5, dengan batas bawah bernilai 0 dan batas atas bernilai 1.
b. Menentukan nilai awal 𝛼1 = ra1 + (1-r)b1 𝛽1 = ra2 + (1-r)b2 𝛾1 = ra3 + (1-r)b3 𝛼2 = a1 + b1-𝛼1 𝛽2 = a2 + b2-𝛽1 𝛾2 = a3 + b3-𝛾1 dengan r = 0.618
c. Mencari RMSE maksimum diantara kombinasi (𝛼𝑖 𝛽𝑗 𝛾𝑘) dengan i=1,2; j=1,2; dan k=1,2.
d. Mengurangi batas berdasarkan kriteria Golden Section.
e. Mengulangi langkah b dan c sampai |𝛼2 - 𝛼1| ≤ ϵ, |𝛽2 - 𝛽1| ≤ ϵ dan |𝛾2- 𝛾1| ≤ ϵ.
Penelitian ini dilakukan dengan menggunakan software R 3.2.3 dan menggunakan package GA yang dikembangkan oleh Scrucca pada tahun 2013 untuk algoritme genetika dan package stats untuk metode Holt-Winters.
Prosedur Analisis pada Data
Prosedur analisis yang dilakukan dengan menggunakan data pemodelan sebagai berikut :
1. Melakukan pendugaan parameter sebanyak 100 kali ulangan menggunakan AG.
2. Hitung nilai rata-rata parameter dari 100 kali ulangan yang memiliki nilai RMSE minimum.
3. Melakukan pendugaan parameter menggunakan metode GS dan hitung nilai RMSE.
4. Melakukan prediksi untuk 8 waktu ke depan dan prediksi 1 waktu ke depan dengan data yang diperbaharui sebanyak 8 waktu menggunakan parameter AG.
5 6. Melakukan prediksi untuk 8 waktu ke depan dan prediksi 1 waktu ke depan dengan data yang diperbaharui sebanyak 8 waktu menggunakan parameter GS.
7. Menghitung nilai RMSEP pada data prediksi.
8. Lakukan prosedur tersebut untuk model aditif dan model multiplikatif. 9. Ulangi untuk 8 set data pemodelan dan data prediksi.
10. Membandingkan GA dan GS berdasarkan nilai RMSE dan RMSEP.
HASIL DAN PEMBAHASAN
Analisis Deskriptif
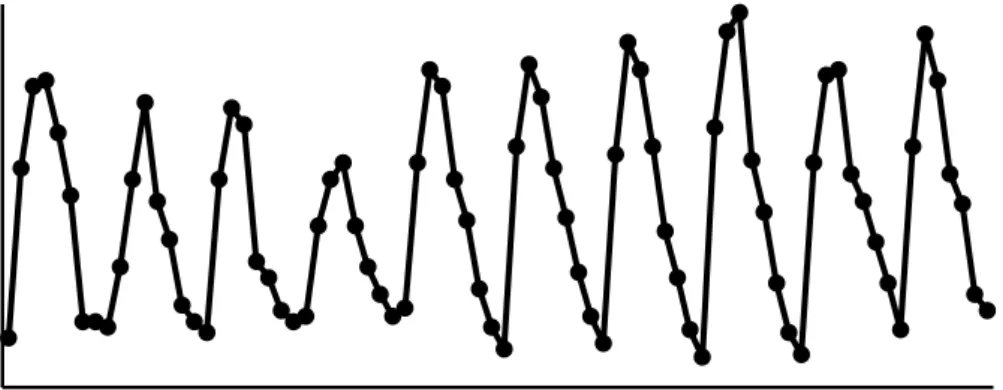
Data hasil observasi suhu per 3 jam yang digunakan memiliki nilai rata-rata sebesar 28.3 oC. Suhu minimum sebesar 23.1 oC dan suhu maksimum sebesar 35.7 oC. Data tersebut memiliki pola musiman yang berulang setiap 1 hari. Suhu mencapai minimum pada pukul 00.00 WIB kemudian meningkat sampai mencapai maksimum pada pukul 09.00 WIB kemudian menurun kembali. Rentang suhu terkecil ada pada hari ke 4 sedangkan rentang suhu terbesar ada pada hari ke 8. Pada Gambar 1 terlihat adanya perubahan pola pada hari ke 1 sampai hari ke 4 dan hari ke 5 sampai ke 10. Pada 4 hari pertama terjadi penurunan suhu maksimum setiap harinya. Sedangkan hari ke 5 sampai hari ke 10 terjadi peningkatan suhu maksimum setiap harinya.
Gambar 1 Plot data suhu per 3 jam pada periode 21-30 Juli 2012 Pendugaan Parameter Holt-Winters
Nilai parameter level (𝛼) yang semakin besar menunjukkan bahwa kontribusi komponen level pada waktu sekarang lebih besar dibandingkan komponen level pada waktu sebelumnya. Nilai parameter trend ( 𝛽 ) yang semakin besar menunjukkan bahwa kontribusi komponen trend pada waktu sekarang lebih besar dibandingkan komponen trend pada waktu sebelumnya. Nilai parameter musiman (𝛾) yang semakin besar menunjukkan bahwa kontribusi komponen musiman pada waktu sekarang lebih besar dibandingkan komponen musiman pada waktu
22 24 26 28 30 32 34 36 1 9 17 25 33 41 49 57 65 73 S uhu ( oC) Waktu (3 jam)
6
sebelumnya. Nilai parameter yang tepat akan menghasilkan nilai RMSE yang minimum.
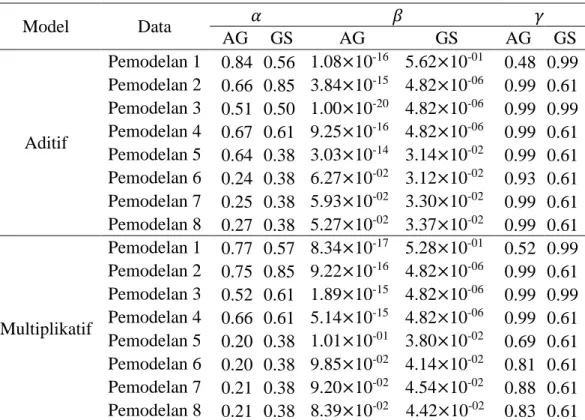
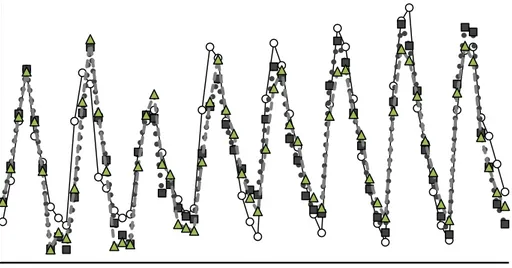
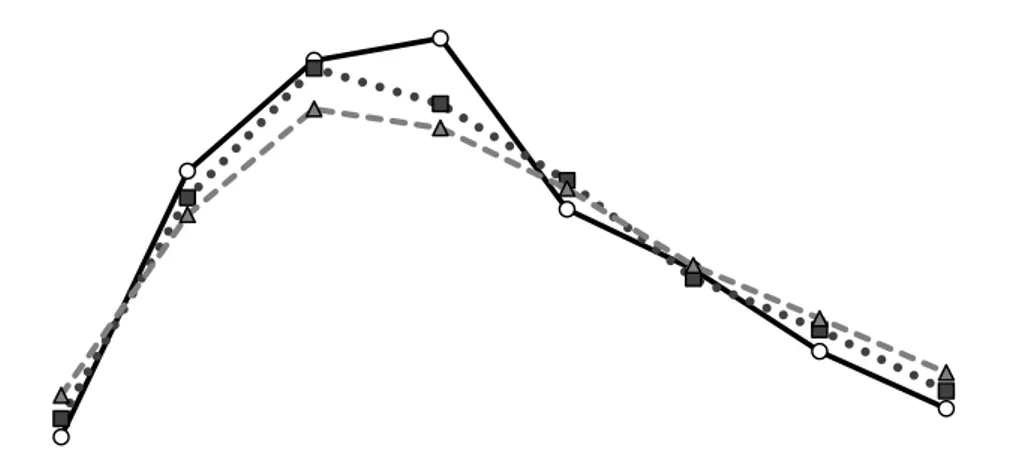
Metode Holt-Winters yang menggunakan penduga parameter dengan AG selanjutnya akan disebut metode Holt-Winters AG dan metode Holt-Winters yang menggunakan penduga parameter dengan GS selanjutnya akan disebut metode Holt-Winters GS. Metode Holt-Winters AG model multiplikatif menghasilkan nilai RMSE yang lebih kecil dibandingkan model aditif pada semua data pemodelan. Nilai dugaan ketiga parameter model multiplikatif yang dihasilkan pada data pemodelan 4 dan pada data pemodelan 5 berubah cukup besar. Nilai dugaan parameter 𝛼 dan 𝛽 model aditif juga berubah cukup besar pada data pemodelan 5 dan 6. Hal ini bisa disebabkan oleh adanya perubahan pola pada hari ke 5. Metode Holt-Winters GS model multiplikatif menghasilkan nilai RMSE yang lebih kecil dibandingkan model aditif pada semua data pemodelan. Nilai dugaan parameter model multiplikatif dan model aditif yang dihasilkan sama pada semua data pemodelan kecuali pada data pemodelan 3 yang menghasilkan nilai dugaan parameter 𝛼 yang berbeda untuk kedua model, dapat dilihat pada Tabel 2. Hasil metode Holt-Winters model aditif menggunakan penduga parameter dengan AG dan GS pada data pemodelan 8 dapat dilihat pada Gambar 2 (a), untuk data pemodelan lain dapat dilihat pada Lampiran 1 dan hasil metode Holt-Winters model multiplikatif menggunakan penduga parameter dengan AG dan GS pada data pemodelan 8 dapat dilihat pada Gambar 2 (b), untuk data pemodelan lain dapat dilihat pada Lampiran 2.
Tabel 2 Hasil pendugaan parameter menggunakan AG dan GS
Model Data 𝛼 𝛽 𝛾 AG GS AG GS AG GS Aditif Pemodelan 1 0.84 0.56 1.08×10-16 5.62×10-01 0.48 0.99 Pemodelan 2 0.66 0.85 3.84×10-15 4.82×10-06 0.99 0.61 Pemodelan 3 0.51 0.50 1.00×10-20 4.82×10-06 0.99 0.99 Pemodelan 4 0.67 0.61 9.25×10-16 4.82×10-06 0.99 0.61 Pemodelan 5 0.64 0.38 3.03×10-14 3.14×10-02 0.99 0.61 Pemodelan 6 0.24 0.38 6.27×10-02 3.12×10-02 0.93 0.61 Pemodelan 7 0.25 0.38 5.93×10-02 3.30×10-02 0.99 0.61 Pemodelan 8 0.27 0.38 5.27×10-02 3.37×10-02 0.99 0.61 Multiplikatif Pemodelan 1 0.77 0.57 8.34×10-17 5.28×10-01 0.52 0.99 Pemodelan 2 0.75 0.85 9.22×10-16 4.82×10-06 0.99 0.61 Pemodelan 3 0.52 0.61 1.89×10-15 4.82×10-06 0.99 0.99 Pemodelan 4 0.66 0.61 5.14×10-15 4.82×10-06 0.99 0.61 Pemodelan 5 0.20 0.38 1.01×10-01 3.80×10-02 0.69 0.61 Pemodelan 6 0.20 0.38 9.85×10-02 4.14×10-02 0.81 0.61 Pemodelan 7 0.21 0.38 9.20×10-02 4.54×10-02 0.88 0.61 Pemodelan 8 0.21 0.38 8.39×10-02 4.42×10-02 0.83 0.61
7
Gambar 2 Hasil pemulusan Holt-Winters dengan (a) parameter solusi AG dan (b) parameter solusi GS. —o— Aktual, •••■••• AG, ---▲--- GS.
Populasi awal pada AG dibangkitkan secara acak dari sebaran seragam(0,1) dalam algoritme genetika menyebabkan dugaan parameter yang dihasilkan dari setiap proses pendugaan menggunakan algoritme ini berbeda. Oleh karena itu, pada penelitian ini proses pendugaan menggunakan algoritme genetika diulang sebanyak 100 kali. Sehingga pada proses ini akan menghasilkan 100 nilai RMSE untuk masing-masing model. Simpangan baku RMSE yang dihasilkan metode Holt-Winters AG sangat kecil menunjukkan bahwa algoritme genetika cukup konsiten walaupun menggunakan pembangkitan populasi awal secara acak. Ukuran data yang semakin besar cenderung meningkatkan keragaman nilai RMSE seperti yang dapat dilihat pada Tabel 3. Hasil pendugaan parameter menggunakan algoritme genetika menghasilkan nilai RMSE yang lebih kecil dibandingkan dengan
22 24 26 28 30 32 34 36 1 9 17 25 33 41 49 57 S uhu ( oC) Waktu (3 jam)
(b)
Aktual AG GS 22 24 26 28 30 32 34 36 1 9 17 25 33 41 49 57 S uhu ( oC) Waktu (3 jam)(a)
8
menggunakan metode golden section pada semua data pemodelan, baik untuk model aditif maupun model, dapat dilihat pada Gambar 3. Penduga parameter dengan AG pada model multiplikatif menghasilkan nilai RMSE yang paling kecil pada semua data pemodelan. Hal tersebut sesuai dengan pola data pada Gambar 1 yang membentuk pola multiplikatif menurun pada hari ke 1 sampai hari ke 4 dan pola multiplikatif meningkat pada hari ke 5 dan hari selanjutnya.
Gambar 3 Nilai RMSE metode Holt-Winters (a) model aditif dan (b) model multiplikatif 0 0.5 1 1.5 2 1 2 3 4 5 6 7 8 S uhu ( o C) Data pemodelan
(a)
0 0.5 1 1.5 2 1 2 3 4 5 6 7 8 S uhu ( oC) Data pemodelan (b)9
Tabel 3 Simpangan baku nilai RMSE metode Holt-Winters
Data Model Aditif Multiplikatif Pemodelan 1 1.48×10-16 3.35×10-16 Pemodelan 2 2.34×10-13 3.58×10-13 Pemodelan 3 2.99×10-12 2.92×10-12 Pemodelan 4 3.77×10-09 4.08×10-12 Pemodelan 5 5.53×10-03 2.32×10-08 Pemodelan 6 2.10×10-08 9.00×10-08 Pemodelan 7 7.01×10-07 3.89×10-08 Pemodelan 8 7.10×10-07 9.80 ×10-07
Hasil Prediksi Suhu untuk 8 Waktu (1 hari) ke Depan
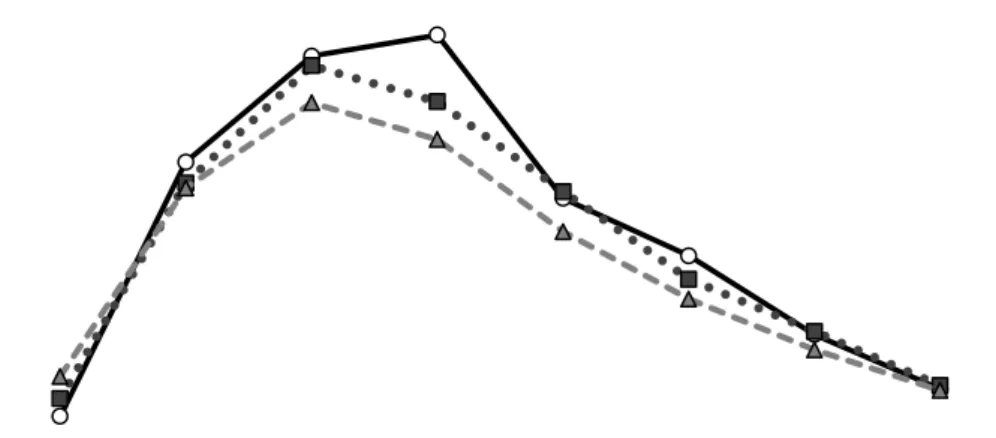
Suatu metode prediksi dikatakan baik apabila menghasilkan ukuran kesalahan prediksi yang kecil. Prediksi dilakukan menggunakan parameter dengan AG dan golden section pada model aditif dan multplikatif. Kemampuan prediksi metode Holt-Winters AG lebih baik pada data prediksi data prediksi 1, 2, 3, dan 6 untuk model aditif dan pada data prediksi 1, 2, 5, 6 dan 8 untuk model multiplikatif. Sedangkan kemampuan prediksi metode Holt-Winters GS lebih baik pada data prediksi 4, 5, 7, dan 8 untuk model aditif dan pada data prediksi 3, 4, dan 7 untuk model multiplikatif, dapat dilihat pada Tabel 4. Hasil prediksi pada data prediksi 6 dapat dilihat pada Gambar 4, data prediksi lain dapat dilihat pada Lampiran 3.
Selang kepercayaan 95% bagi nilai prediksi menggunakan penduga parameter dengan AG memiliki lebar selang yang lebih kecil dibandingkan dengan GS. Hal tersebut terdapat pada data prediksi 1, 2, 6, 7, dan 8 untuk model aditif dan pada data prediksi 1, 2, 3, 5, 6, 7, dan 8 untuk model multiplikatif, selengkapnya dapat dilihat pada Lampiran 4. Selang kepercayaan yang dihasilkan juga mencakup seluruh nilai aktual pada semua data prediksi kecuali pada data prediksi 1, 3, dan 4, selengkapnya pada Lampiran 5.
Tabel 4 Nilai RMSEP untuk prediksi 8 waktu (1 hari)
Data Aditif Multiplikatif
AG GS AG GS Prediksi 1 2.02 3.66 1.93 3.47 Prediksi 2 1.06 1.37 1.03 1.27 Prediksi 3 2.95 2.96 2.98 2.73 Prediksi 4 2.89 2.72 2.98 2.77 Prediksi 5 2.53 1.31 0.74 1.22 Prediksi 6 0.90 1.59 0.90 1.51 Prediksi 7 1.35 1.27 1.34 1.21 Prediksi 8 1.52 1.37 1.50 1.75
10
Gambar 4 Hasil prediksi metode Holt-Winters 8 waktu (1 hari) ke depan (a) model aditif dan (b) model multiplikatif. —o— Aktual, •••■••• AG, ---▲--- GS.
Hasil Prediksi Suhu untuk 1 Waktu (3 jam) ke Depan
Kemampuan prediksi metode Holt-Winters AG memiliki hasil yang lebih baik pada 5 data prediksi, yaitu pada data prediksi 1, 2, 3, 4, dan 6 untuk model aditif; dan pada data prediksi 1, 2, 4, 5, dan 6 untuk model multiplikatif. Pada data prediksi 6 kemampuan prediksi metode Holt-Winters AG memiliki nilai RMSEP dua kali lebih kecil dibandingkan dengan menggunakan metode Holt-Winters GS, selengkapnya dapat dilihat pada Tabel 5. Hasil prediksi pada data prediksi 6 dapat dilihat pada Gambar 5, untuk data prediksi lain dapat dilihat pada Lampiran 6.
Selang kepercayaan 95% bagi nilai prediksi yang dihasilkan metode Holt-Winters menggunakan parameter AG memiliki lebar selang yang lebih kecil. Hal
22 27 32 37 1 2 3 4 5 6 7 8 S uhu ( o C) Waktu (3 jam) (a) 22 27 32 37 1 2 3 4 5 6 7 8 S uhu ( o C) Waktu (3 jam)
(b)
11 tersebut dapat dilihat pada seluruh data prediksi untuk model aditif dan pada data prediksi 1, 3, dan 5 untuk model multiplikatif, selengkapnya dapat dilihat pada Lampiran 7. Selang kepercayaan yang dihasilkan juga mencakup seluruh nilai aktual pada semua data prediksi kecuali pada data prediksi 1, 3, dan 4, selengkapnya pada Lampiran 8.
Gambar 5 Hasil prediksi metode Holt-Winters 1 waktu (3 jam) ke depan (a) model aditif dan (b) model multiplikatif. —o— Aktual, •••■••• AG, ---▲--- GS. 22 27 32 37 1 2 3 4 5 6 7 8 S uhu ( oC) Waktu (3 jam)
(a)
22 27 32 37 1 2 3 4 5 6 7 8 S uhu ( oC ) Waktu (3 jam)(b)
12
Tabel 5 Nilai RMSEP untuk prediksi 1 waktu (3 jam)
Data Aditif Multiplikatif
AG GS AG GS Prediksi 1 2.24 2.79 2.18 2.76 Prediksi 2 0.96 1.37 1.01 1.28 Prediksi 3 1.62 1.63 1.54 1.43 Prediksi 4 1.59 1.68 1.66 1.73 Prediksi 5 1.52 1.26 0.77 1.24 Prediksi 6 0.94 1.45 0.95 1.43 Prediksi 7 1.40 1.08 1.33 1.04 Prediksi 8 1.02 0.82 1.09 0.92
SIMPULAN DAN SARAN
Simpulan
Penduga parameter dengan AG lebih baik daripada penduga parameter dengan GS pada data pemodelan. Kemampuan prediksi satu waktu ke depan dengan metode Holt-Winters AG lebih baik dibandingkan dengan metode Holt-Wintes GS pada model aditif dan multiplikatif. Kemampuan prediksi delapan waktu ke depan dengan metode Winters AG lebih baik dibandingkan dengan metode Holt-Winters GS pada model multiplikatif, namun sama dengan metode Holt-Holt-Winters GS pada model aditif.
DAFTAR PUSTAKA
Cheney W, Kincaid D. 2008. Numerical Mathematics and Computing Sixth edition. United State of America (US): Thomson Brooks/Cole.
Haupt RL, Haupt SE. 2004. Practical Genetic Algorithms Second Edition. New Jersey (US): J Wiley.
Kalekar PS. 2004. Time Series Forecasting using Holt-Winters. Kanwal Rekhi School of Information Technology.
Kiusalaas J. 2005. Numerical Methods in Engineering with MATLAB. United State of America (US): Cambridge University.
Mahkya DA. 2014. Aplikasi Metode Golden Section untuk Optimasi Parameter pada Metode Exponential Smoothing. Jurnal Gaussian. 3(4): 605-614.
Montgomery DC, Jennings CL, Kulahci M. 2008. Introduction to Time Series Analysis and Forecasting. New Jersey (US): J Wiley.
Nurhidayati EN. 2011. Aplikasi Algoritma Nonlinear Programming Untuk Mengoptimalkan Parameter Alfa Dalam metode Pemulusan Eksponensial Satu Parameter. Institut Teknologi Sepuluh Nopember.
Scrucca L. 2013. GA: A Package for Genetic Algorithms in R. Journal of Statistics Software. 53(4): 1-37.
13 Sivanandam SN, Deepa SN. 2008. Introductions to Genetic Algorithms. New York
(US): Springer.
Yu X, Gen M. 2010. Introduction to Evolutionary Algorithms. Berlin (DE): Springer.
Yuwida N, Hananfi L, Wahyuningsih N. 2012. Estimasi Parameter alpha dan gamma dalam Pemulusan Eksponensial Ganda Dua Parameter dengan Metode Modifikasi Golden Section. Jurnal Sains dan Seni ITS. 1(1):18-22.
14
Lampiran 1 Hasil pemulusan menggunakan penduga parameter dengan AG dan GS untuk model aditif
15 Lampiran 2 Hasil pemulusan menggunakan penduga parameter dengan AG dan GS
untuk model multiplikatif
16
Lampiran 3 Hasil prediksi 8 waktu (1 hari) ke depan menggunakan penduga parameter dengan AG dan GS untuk (a) model aditif dan (b) model multiplikatif
17 Lanjutan
...
18
Lampiran 4 Lebar selang kepercayaan 95% bagi prediksi 8 waktu (1 hari)
Aditif Multiplikatif
Data AG GS Data AG GS Data AG GS Data AG GS
Prediksi 1 3.93 4.14 Prediksi 5 5.81 5.93 Prediksi 1 3.08 3.65 Prediksi 5 4.28 4.44 5.14 5.54 6.91 6.38 4.27 5.09 4.58 5.26 6.11 7.46 7.86 6.82 5.45 7.47 4.90 5.97 6.95 9.77 8.70 7.25 6.50 10.48 5.12 6.41 7.70 12.40 9.47 7.69 6.55 11.94 5.22 6.57 8.38 15.30 10.18 8.12 6.73 13.83 5.38 6.87 9.01 18.44 10.85 8.56 6.42 14.51 5.50 7.06 9.60 21.79 11.47 8.99 13.98 18.08 80.12 93.84 Prediksi 2 6.74 6.88 Prediksi 6 5.45 5.78 Prediksi 2 6.57 6.29 Prediksi 6 4.51 4.32 8.09 9.05 5.63 6.21 8.66 8.93 4.77 5.18 9.24 10.79 5.83 6.64 10.53 11.37 5.06 5.93 10.27 12.29 6.05 7.06 12.17 13.53 5.24 6.33 11.20 13.62 6.28 7.49 12.29 13.70 5.33 6.47 12.06 14.83 6.52 7.91 12.97 14.20 5.40 6.67 12.86 15.96 6.78 8.33 12.66 13.60 5.52 6.90 13.62 17.00 7.05 8.76 29.22 28.74 285.27 125.67 Prediksi 3 5.74 5.74 Prediksi 7 5.24 5.77 Prediksi 3 5.61 5.65 Prediksi 7 4.61 4.31 6.46 6.44 5.43 6.20 6.54 6.90 4.88 5.23 7.11 7.06 5.64 6.63 7.38 8.03 5.17 6.00 7.70 7.64 5.86 7.06 8.10 8.98 5.39 6.45 8.25 8.17 6.10 7.49 8.21 9.15 5.38 6.45 8.77 8.67 6.35 7.91 8.56 9.60 5.49 6.68 9.26 9.15 6.61 8.34 8.79 9.76 5.56 6.87 9.72 9.60 6.88 8.77 24.84 25.10 202.51 385.21 Prediksi 4 5.76 5.97 Prediksi 8 5.24 5.57 Prediksi 4 5.60 4.94 Prediksi 8 4.41 4.16 6.95 7.02 5.45 5.99 7.07 6.42 4.68 5.04 7.95 7.93 5.67 6.41 8.30 7.69 4.99 5.81 8.85 8.74 5.91 6.82 9.20 8.67 5.23 6.28 9.66 9.49 6.16 7.24 9.43 8.86 5.25 6.27 10.41 10.18 6.42 7.65 9.95 9.33 5.40 6.52 11.11 10.83 6.69 8.07 10.09 9.34 5.50 6.69 11.76 11.44 6.97 8.49 24.86 22.02 61.79 71.88
19 Lampiran 5 Selang kepercayaan 95% bagi hasil prediksi 8 waktu (1 hari) ke depan menggunakan penduga parameter dengan AG dan GS untuk (a) model aditif dan (b) model multiplikatif
20
21 Lampiran 6 Hasil prediksi 1 waktu (3 jam) ke depan mengunakan penduga
parameter dengan AG dan GSuntuk (a) model aditif dan (b) model multiplikatif
22
23 Lampiran 7 Lebar selang kepercayaan 95% bagi prediksi 1 waktu (3 jam)
Aditif Multiplikatif
Data AG GS Data AG GS Data AG GS Data AG GS
Prediksi 1 3.93 4.14 Prediksi 5 5.81 5.93 Prediksi 1 3.08 3.65 Prediksi 5 4.28 4.44 3.69 4.03 5.76 5.94 2.90 3.56 4.28 4.44 5.27 4.60 5.75 5.87 4.46 4.32 4.25 4.39 5.02 4.62 5.94 5.93 4.26 4.55 4.21 4.44 6.22 6.98 5.89 5.89 5.55 7.38 4.16 4.41 6.68 7.44 5.82 5.83 5.98 7.79 4.12 4.37 6.56 7.36 5.90 5.83 5.81 7.64 4.10 4.36 7.15 8.45 5.85 5.78 6.17 8.36 4.06 4.33 Prediksi 2 6.74 6.88 Prediksi 6 5.45 5.78 Prediksi 2 6.57 6.29 Prediksi 6 4.51 4.32 6.59 6.67 5.42 5.79 6.39 6.10 4.49 4.33 6.39 6.49 5.37 5.76 6.21 5.94 4.45 4.31 6.25 6.40 5.32 5.75 6.08 5.87 4.41 4.30 6.17 6.47 5.35 5.85 6.04 5.92 4.45 4.40 6.02 6.30 5.34 5.82 5.89 5.77 4.44 4.37 5.91 6.16 5.29 5.77 5.77 5.64 4.39 4.33 5.94 6.51 5.27 5.76 5.89 5.91 4.37 4.32 Prediksi 3 5.74 5.74 Prediksi 7 5.24 5.77 Prediksi 3 5.61 5.65 Prediksi 7 4.61 4.31 5.68 5.68 5.20 5.76 5.55 5.58 4.57 4.30 5.88 5.88 5.22 5.74 5.76 5.77 4.60 4.29 6.06 6.07 5.23 5.69 5.95 5.86 4.62 4.25 5.96 5.97 5.22 5.65 5.86 5.83 4.60 4.22 5.91 5.91 5.18 5.62 5.79 5.79 4.57 4.20 5.86 5.86 5.19 5.62 5.73 5.74 4.57 4.19 5.89 5.89 5.24 5.61 5.73 5.69 4.60 4.19 Prediksi 4 5.76 5.97 Prediksi 8 5.24 5.57 Prediksi 4 5.60 4.94 Prediksi 8 4.41 4.16 5.69 5.90 5.20 5.56 5.53 4.88 4.37 4.14 6.07 6.29 5.17 5.56 5.99 5.29 4.36 4.16 6.11 6.34 5.13 5.52 6.06 5.34 4.33 4.14 6.06 6.32 5.22 5.53 6.01 5.33 4.41 4.15 5.99 6.25 5.21 5.49 5.93 5.26 4.41 4.12 5.96 6.20 5.18 5.45 5.89 5.22 4.38 4.10 5.89 6.12 5.20 5.43 5.82 5.15 4.41 4.08 18
24
Lampiran 8 Selang kepercayaan 95% bagi hasil prediksi 1 waktu (3 jam) ke depan mengunakan penduga parameter dengan AG dan GS untuk (a) model aditif dan (b) model multiplikatif
25 Lanjutan...
26
RIWAYAT HIDUP
Penulis dilahirkan di Cianjur tanggal 12 Mei 1994 yang merupakan anak pertama dari pasangan Bpak Iwan Sugilar dan Ibu Ida Daryati. Penulis menyelesaikan jenjang SMA di SMAN 1 Cianjur pada tahun 2012 dan diterima sebagai mahasiswa Intitut Pertanian Bogor pada tahun yang sama.
Selama menjadi mahasiswa di Institut Pertanian Bogor penulis pernah menjadi asisten praktikum mata kuliah Penerapan Komputer pada semeter genap 2013/2014, semester ganjil 2014/2015, dan semester genap 2014/2015; asisten praktikum mata kuliah Komputasi Statistika pada semester ganjil 2014/2015; asisten praktikum mata kuliah Teknik Optimasi dan Komputasi pada semester ganjil 2015/2016; asisten praktikum mata kuliah Komputasi Numerik pada semester genap 2015/2016; dan asisten responsi mata kuliah Rancangan Percobaan pada semester genap 2015/2016.
Penulis pernah menjadi ketua asrama C2 Tingkat Persiapan Bersama IPB periode 2012/2013, ketua Departemen Database Center di Himpunan Keprofesian Gamma Sigma Beta (GSB) Statistika FMIPA IPB periode 2014/2015. Penulis aktif dalam bidang kepanitian sebagai ketua divisi dana usaha Masa Perkenalan Kampus Mahasiswa Baru IPB tahun 2013, ketua divisi dana usaha Pekan Olah Raga Statistika Departemen Statistika FMIPA IPB tahun 2013, ketua divisi pendamping kelompok Masa Perkenalan Fakultas FMIPA IPB tahun 2014, dan ketua divisi kompetisi Kompetisi Statistika Junior dalam rangkaian Pesta Sains Nasional 2015. Pada Bulan Juli-Agustus 2015 penulis melaksanakan praktik lapang di libang BMKG, Jakarta Pusat.