METODOLOGI PENELITIAN
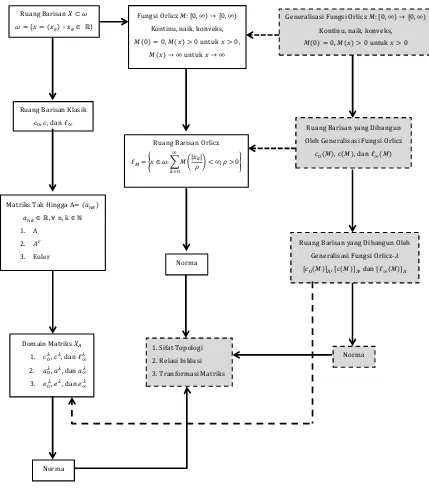
Pada bab ini disampaikan metodologi yang digunakan penulis dalam melakukan penelitian ini. Selain itu, diberikan langkah-langkah sistematis dan diagram alir penelitian sebagai penjelasan tentang proses yang akan dilakukan penulis dalam melakukan penelitian.
Metodologi yang digunakan dalam penelitian ini adalah menggunakan metode kepustakaan, yaitu dengan mengumpulkan, membaca, dan mempela-jari referensi-referensi jurnal, buku-buku yang berkaitan, maupun informasi-informasi yang didapat dari internet. Berikut ini adalah langkah-langkah yang dilakukan penulis dalam melakukan penelitian ini, yaitu:
1. Mendefinisikan ruang barisan konvergen dan terbatas yang dibangun oleh generalisasi fungsi Orlicz. Dalam hal ini, ruang barisan ini disebut ruang barisan konvergen dan terbatas yang dibangun oleh generalisasi fungsi Orlicz, yaituc0(M),c(M), danℓ∞(M).
2. Memformulasikan beberapa ruang barisan baru dengan memanfaatkan ruang barisan pada poin 1 dan matriks tak hingga Λ. Dalam hal ini, ruang barisan ini disebut ruang barisan konvergen dan terbatas yang dibangun oleh generalisasi fungsi Orlicz-λ, yaitu [c0(M)]Λ, [c(M)]Λ, dan
[ℓ∞(M)]Λ.
3. Meneliti sifat-sifat topologi dari ruang barisan pada poin 2 terhadap norma yang didefinisikan.
4. Meneliti relasi inklusi yang bersesuaian dari ruang barisan pada poin 1 dan ruang barisan pada poin 2.
5. Meneliti karakteristik transformasi matriks dari ruang barisan pada poin 1 ke ruang barisan yang sama.
� = {� = �� ∶ ��∈ ℝ}
Ruang Barisan � ⊂ �
Ruang Barisan Klasik
�0, �, dan ℓ∞
���∈ ℝ, ∀ n, k ∈ ℕ
Matriks Tak Hingga A= ���
1. Λ
2. �� 3. Euler
Domain Matriks ��
1. �0�, ��, dan ℓ∞� 2. �0�, ��, dan �∞�
3. �0�, ��, dan �∞�
Norma
Fungsi Orlicz �: [0, ∞ → [0, ∞
Kontinu, naik, konveks,
� 0 = 0, � � > 0 untuk � > 0,
� � → ∞ untuk � → ∞
ℓ�= {� ∈ �: ∑ � |���| < ∞, � > 0 ∞
�=0
} Ruang Barisan Orlicz
Norma
Generalisasi Fungsi Orlicz �: [0, ∞ → [0, ∞
Kontinu, naik, konveks,
� 0 = 0, � � > 0 untuk � > 0
Ruang Barisan yang Dibangun
Oleh Generalisasi Fungsi Orlicz
�0 �, � �, dan ℓ∞�
Ruang Barisan yang Dibangun Oleh
Generalisasi Fungsi Orlicz-�
[�0 � ]Λ, [� � ]Λ, dan [ℓ∞� ]Λ
Norma 1. Sifat Topologi
2. Relasi Inklusi
HASIL DAN PEMBAHASAN
.1. Barisan Konvergen dan Terbatas-λ
Definisi 4.1.1. Diberikan barisan bilangan real positif naik kuatλ= (λk)∞k=0
yang menuju tak hingga; yaitu
0< λ0 < λ1 <· · · dan λk→ ∞ untuk k→ ∞. (4.1.1)
Barisan x = (xk) ∈ ω dikatakan konvergen-λ jika terdapat l ∈ R sehingga
Λn(x) → l untuk n → ∞. Dengan kata lain, untuk setiap ǫ > 0 terdapat
n0 ∈N, sehingga untuk setiapn ≥n0 berlaku|Λn(x)−l|< ǫ, dengan
Λn(x) =
1 λn
n X
k=0
(λk−λk−1)xk (4.1.2)
untuk setiap n ∈ N. Dalam hal ini, bilangan l disebut limit-λ dari barisan (xk) dan barisan (xk) disebut barisan konvergen-λ ke l. Adapun untuk setiap
unsur dengan indeks negatif, didefinisikan sama dengan nol, yaituλ−1 = 0 dan
x−1 = 0.
Diberikan barisan (xn) dan a ∈ R dengan limn→∞xn = a. Berarti,
limn→∞xn−a= 0. Akibatnya, limn→∞|xn−a|= 0. Oleh karena itu, diperoleh
lim
n→∞
1 λn
n X
k=0
(λk−λk−1)|xk−a| !
(4.1.3)
= lim
n→∞
1 λn
λ0|x0−a|+ (λ1−λ0)|x1−a|+ (λ2−λ1)|x2−a|+· · ·+
(λn−1−λn−2)|xn−1−a|+ (λn−λn−1)|xn−a|
Selanjutnya, karena 1
Dengan menggunakan persamaan (4.1.3), diperoleh
lim
konvergen-λ kea.
Hasil tersebut di atas dapat dinyatakan pada pernyataan dasar berikut.
Lemma 4.1.2. Setiap barisan konvergen, berakibat konvergen-λdengan nilai kekonvergenannya sama.
Lemma 4.1.3. Diberikan barisan (xk) konvergen-λ. Jika barisan (xk)
kon-vergen, maka nilai kekonvergenannya sama dengan limit-λ dari barisan (xk).
Bukti. Diketahui barisan (xk) konvergen-λ, berarti terdapat l ∈ R sehingga
Λk(x) → l untuk k → ∞. Dalam hal ini, l merupakan limit-λ dari barisan
(xk). Selanjutnya, diasumsikan barisan (xk) konvergen, berarti terdapatl′ ∈R
sehingga xk → l′ untuk k → ∞, atau untuk sebarang ǫ > 0 terdapat k0 ∈ N
l′ =l. Untuk itu, karena x
k →l′, maka menurut Lemma 3.1.2 berlaku
lim
k→∞Λk(x)−l
′ = lim
k→∞
1 λk
k X
j=0
(λj −λj−1)(xj−l′) !
= 0.
Hal ini menunjukkan bahwa Λk(x)→l′ untukk → ∞. Karena limit dari suatu
barisan bernilai tunggal, maka l′ = l. Dengan kata lain, nilai kekonvergenan
barisan (xk) sama dengan limit-λ dari barisan (xk).
Selanjutnya, diberikan barisan x= (xk) ∈ω dan n ≥1. Dengan
meng-gunakan persamaan (4.1.2) diperoleh
xn−Λn(x) =
1 λn
n X
i=0
(λi−λi−1)(xn−xi) (4.1.4)
= 1 λn
n−1 X
i=0
(λi−λi−1)(xn−xi)
= 1 λn
n−1 X
i=0
(λi−λi−1) n X
k=i+1
(xk−xk−1)
= 1 λn
n−1 X
i=0
(λi−λi−1) n X
k=1
(xk−xk−1)
= 1 λn
n X
k=1
(xk−xk−1) n−1 X
i=0
(λi−λi−1)
= 1 λn
n X
k=1
(xk−xk−1) k−1 X
i=0
(λi−λi−1)
= 1 λn
n X
k=1
λk−1(xk−xk−1).
Oleh karena itu, untuk sebarang barisanx= (xk)∈ω dapat dibentuk barisan
S(x) = (Sn(x))∞n=0 = (xn−Λn(x))∞n=0, dengan
S0(x) = 0, dan (4.1.5)
Sn(x) =
1 λn
n X
k=1
Dari pernyataan di atas, diperoleh lemma berikut.
Lemma 4.1.4. Diberikan barisan (xk) konvergen-λ. Barisan (xk) konvergen
jika dan hanya jika S(x)∈c0.
Bukti. Diberikan barisan (xk) konvergen-λ dan diasumsikan barisan (xk)
kon-vergen. Karena (xk) konvergen di R, maka (xk) merupakan barisan Cauchy.
Artinya, untuk sebarang bilangan ǫ > 0 terdapat k0 ∈ N sehingga untuk
seti-ap j ≥ k ≥ k0 berlaku |xj −xk| < ǫ. Oleh karena itu, |xk−xk−1| < ǫ untuk
sebarang bilangan ǫ >0 dan untuk setiap k > k−1≥k0. Akibatnya,
lim
n→∞Sn(x) = limn→∞
1 λn
n X
k=1
λk−1(xk−xk−1) !
= 0.
Hal ini berarti S(x) = (Sn(x))∞n=0∈c0.
Sebaliknya, jika S(x) ∈ c0, maka limn→∞Sn(x) = 0. Oleh karena itu,
diperoleh
lim
n→∞Sn(x) = limn→∞xn−Λn(x)
= lim
n→∞xn−nlim→∞Λn(x)
= lim
n→∞xn−l = 0.
Hal ini menunjukkan bahwa limn→∞xn = l. Dengan kata lain, barisan (xk)
konvergen ke l ∈R.
Definisi 4.1.5. Barisan (xk) dikatakanterbatas-λ, apabila sup n∈N
|Λn(x)|<∞.
Contoh 4.1.6. Barisan e= (ek) terbatas-λ.
Dari definisi barisan terbatas-λ, diperoleh lemma berikut.
Lemma 4.1.7. Jika barisan (xk) terbatas, maka (xk) terbatas-λ.
Bukti. Diketahui barisan (xk) terbatas, berarti terdapat bilangan M > 0
yaitu ada bilangan real positif M1 sehingga supn∈N|Λn(x)| ≤M1. Karena
|Λn(x)|=
1 λn
n X
k=0
(λk−λk−1)xk
≤ 1
λn n X
k=0
(λk−λk−1)|xk|
≤ 1
λn n X
k=0
(λk−λk−1)M =M
untuk setiap n∈N, maka dapat diambil M1 =M sehingga
|Λn(x)| ≤M1 untuk setiapn ∈N.
Oleh karena itu, menurut sifat kelengkapan di R, terdapat supn∈N|Λn(x)|
de-ngan supn∈N|Λn(x)| ≤ M1 < ∞. Dengan demikian, terbukti bahwa barisan
(xk) terbatas-λ.
Sifat keterbatasan suatu barisan konvergen, juga berlaku pada barisan konvergen-λ. Hal ini ditunjukkan oleh teorema berikut.
Teorema 4.1.8. Jika barisan (xk) konvergen-λ, maka (xk) terbatas-λ.
Bukti. Diketahui barisan (xk) konvergen-λ, berarti ada bilangan reallsehingga
Λn(x) → l untuk n → ∞. Akan dibuktikan bahwa barisan (xk) terbatas-λ.
Untuk itu, karena Λn(x) → l, berarti untuk setiap ǫ > 0 terdapat n0 ∈ N
sehingga untuk setiapn ≥n0 berlaku|Λn(x)−l|< ǫ. Akibatnya, untuk setiap
n ≥n0 diperoleh
|Λn(x)|=|Λn(x)−l+l|
≤ |Λn(x)−l|+|l|
< ǫ+|l|.
Selanjutnya, dianggap M = sup{|Λ0(x)|,|Λ1(x)|,· · · , ǫ+|l|}, maka
|Λn(x)| ≤M untuk setiap n∈N.
Kebalikan dari teorema di atas belum tentu berlaku.
Contoh 4.1.9. Barisan ((−1)k) terbatas-λ dan tidak konvergen-λ.
Lemma 4.1.10. Diberikan barisan (xk) terbatas-λ. Barisan (xk) terbatas jika
dan hanya jika S(x)∈ℓ∞.
Bukti. Diketahui barisan (xk) terbatas-λ. Berarti, supn∈N|Λn(x)| < ∞.
Se-lanjutnya, diasumsikan barisan (xk) terbatas, yaitu terdapat suatu bilangan
N > 0 sehingga |xk| ≤ N untuk setiap k ∈ N. Karena Sn(x) = xn−Λn(x)
untuk setiap n∈N, maka diperoleh
|Sn(x)|=|xn−Λn(x)|
≤ |xn|+|Λn(x)|
≤N +N0
untuk setiap n ∈ N dan untuk suatu bilangan N0 > 0, dengan N0 ≥ |Λn(x)|
untuk setiapn∈N. Selanjutnya, dipilihN1 =N+N0. Oleh karena itu, untuk
setiap n∈N diperoleh
|Sn(x)| ≤N1.
Hal ini menunjukkan bahwa barisan (Sn(x))∞n=0 terbatas. Dengan kata lain,
S(x) = (Sn(x))∈ℓ∞.
Sebaliknya, diasumsikan barisan (Sn(x))∞n=0 ∈ ℓ∞. Berarti, terdapat
suatu bilangan N0 > 0 sehingga |Sn(x)| =
1 λn
n X
k=1
λk−1(xk−xk−1)
≤ N0
untuk setiap n ∈ N. Karena xn−Λn(x) = Sn(x) untuk setiap n ∈ N, maka
diperoleh
|xn|=|Sn(x) + Λn(x)|
≤ |Sn(x)|+|Λn(x)|
≤N0+N1
untuk N1 > 0 dengan N1 ≥ |Λn(x)| untuk setiap n ∈ N. Dengan kata lain,
untuk setiap k ∈ N diperoleh |xk| ≤ N2, dengan N2 = N0 +N1. Hal ini
menunjukkan bahwa barisan x= (xk) terbatas.
aturan
λnk =
λk−λk−1
λn
; untuk 0≤k ≤n
0 ; untuk k > n
untuk setiapn, k ∈N. Transformasi-Λ adalah suatu fungsi Λ :X →Y dengan aturan x 7→ Λx = (Λn(x)), dengan barisan Λ(x) = (Λn(x))∞n=0 didefinisikan
oleh persamaan (4.1.2), untuk sebarang ruang barisan X dan Y. Selanjutnya, jika barisan x = (xk) ∈ ω konvergen-λ ke suatu bilangan l, maka Λn(x) → l
untuk n → ∞. Dalam hal ini, barisan x = (xk) dikatakan terjumlah-Λ (Λ
-summable).
4.2. Topologi Norma Pada Ruang Barisan Konvergen dan Terbatas
yang Dibangun Oleh Generalisasi Fungsi Orlicz-λ
Diberikan ruang barisan konvergen, konvergen ke nol, dan terbatas yang masing-masing ditulis dengan notasi c, c0, dan ℓ∞; yaitu
c=
x= (xk)∈ω: (∃ l∈R) xk→l, k → ∞
,
c0 =
x= (xk)∈ω:xk →0, k → ∞
, dan
ℓ∞ =
x= (xk)∈ω: sup k∈N
|xk|<∞
.
Ruang barisan c, c0, dan ℓ∞, masing-masing merupakan ruang Banach
ter-hadap norma k · k∞; yaitukxk∞ = supk∈N|xk|.
Fungsi M : [0,∞) → [0,∞) yang bersifat kontinu, naik, konveks, de-ngan M(0) = 0, M(x) > 0 untuk x > 0, dan M(x) → ∞ untuk x → ∞
disebut fungsi Orlicz. Apabila sifat konveks dari fungsi Orlicz M diganti de-ngan M(x + y) ≤ M(x) + M(y) untuk setiap x, y ∈ [0,∞), maka fungsi Orlicz M disebut fungsi modulus (Ruckle 1973; Maddox 1986). Fungsi Orlicz M dikatakan memenuhi kondisi-∆2 jika terdapat konstanta K > 0 sehingga
M(2x)≤KM(x) untuk setiap x∈[0,∞).
konvergen yang dibangun oleh generalisasi fungsi Orlicz, ruang barisan kon-vergen ke nol yang dibangun oleh generalisasi fungsi Orlicz, dan ruang barisan
terbatas yang dibangun oleh generalisasi fungsi Orlicz; yaitu
c(M) =
x= (xk)∈ω: (∃ ρ >0, l ∈R)M
|xk|
ρ
→l, k → ∞
,
c0(M) =
x= (xk)∈ω: (∃ ρ >0)M
|xk|
ρ
→0, k → ∞
, dan
ℓ∞(M) =
x= (xk)∈ω: (∃ ρ >0) sup k∈N
M
|xk|
ρ
<∞
.
Diberikan matriks tak hingga Λ = (λnk)∞n,k=0 dengan
λnk =
λk−λk−1
λn
; untuk 0≤k ≤n
0 ; untuk k > n
untuk setiapn, k ∈N. Transformasi-Λ adalah suatu fungsi Λ :X →Y dengan aturan x 7→ Λx = (Λn(x)), untuk sebarang ruang barisan X dan Y. Dalam
hal ini, barisan Λ(x) = (Λn(x))∞n=0 didefinisikan oleh
Λn(x) =
1 λn
n X
k=0
(λk−λk−1)xk
untuk setiap n∈N.
Apabila diberikan sebarang ruang barisan X dan matriks tak hingga A, maka ruang barisan yang ditulis dengan notasi XA; yaitu
XA =
x= (xk)∈ω:Ax∈X
domain matriks yang didefinisikan sebagai berikut:
[c(M)]Λ =
x= (xk)∈ω: (∃ ρ >0, l ∈R) M
|Λn(x)|
ρ
→l, n→ ∞
,
[c0(M)]Λ =
x= (xk)∈ω: (∃ ρ >0) M
|Λn(x)|
ρ
→0, n→ ∞
, dan
[ℓ∞(M)]Λ =
x= (xk)∈ω: (∃ ρ >0) sup n∈N
M
|Λn(x)|
ρ
<∞
.
Ruang barisan ini masing-masing disebut ruang barisan konvergen yang
diba-ngun oleh generalisasi fungsi Orlicz-λ, ruang barisan konvergen ke nol yang
dibangun oleh generalisasi fungsi Orlicz-λ, dan ruang barisan terbatas yang
dibangun oleh generalisasi fungsi Orlicz-λ. Selanjutnya, agar lebih sederhana,
ketiga ruang barisan ini disebut ruang barisan konvergen dan terbatas yang
dibangun oleh generalisasi fungsi Orlicz-λ. Pada bagian ini, akan dibahas
beberapa sifat topologi dari ruang barisan konvergen dan terbatas yang diba-ngun oleh generalisasi fungsi Orlicz-λ terhadap norma yang akan diberikan.
Teorema 4.2.1. Ruang barisan [c(M)]Λ, [c0(M)]Λ, dan [ℓ∞(M)]Λ
masing-masing merupakan ruang linier.
Bukti. (1) Akan dibuktikan ruang barisan [c(M)]Λ merupakan ruang linier
bagian.
Diambil sebarangx, y ∈[c(M)]Λ, berarti adaρ1, ρ2 >0 danl1, l2 ∈Rsehingga
M
|Λn(x)|
ρ1
→l1 dan M
|Λn(y)|
ρ2
→l2
untuk n→ ∞. Dipilihρ = max{ρ1, ρ2}, berarti
1
ρ ≤
1 ρ1
atau 1
ρ ≤
1 ρ2
maka diperoleh
Selanjutnya, diambil sebarang bilangan realα. Menurut sifat Archimedean, terdapat n0 ∈N sehingga α ≤ |α| ≤2n0. Karena generalisasi fungsi OrliczM
memenuhi kondisi-∆2, maka terdapat bilanganK >0 sehingga diperoleh
M
konvergen untuk n → ∞. Jadi, ada bilangan l′ sehingga
ruang barisan [c0(M)]Λ merupakan ruang linier.
(2) Akan dibuktikan ruang barisan [ℓ∞(M)]Λ merupakan ruang linier.
Diambil sebarang x, y ∈[ℓ∞(M)]Λ, berarti terdapat ρ1, ρ2 >0 sehingga
jutnya, diambil sebarang skalarα dan β. Karena generalisasi fungsi OrliczM bersifat naik, konveks, dan memenuhi kondisi-∆2, maka diperoleh
sup
Bukti. (1) Karena ρ > 0, berarti cukup jelas bahwa kxk ≥ 0. Selanjutnya,
dianggap kxk= 0, maka untuk sebarang bilangan ǫ >0 berlaku
kxk= inf
suatu bilangan ρǫ dengan 0< ρǫ < ǫsehingga
sup
n∈N
M
|Λn(x)|
ρǫ
≤1.
Oleh karena itu, diperoleh
sup
n∈N
M
|Λn(x)|
ǫ
≤sup
n∈N
M
|Λn(x)|
ρǫ
≤1.
Oleh karena itu, untuk setiapn∈NdiperolehM
|Λn(x)|
ǫ
≤1. Selanjutnya,
karena generalisasi fungsi Orlicz M bersifat konveks, maka diperoleh
M(|Λn(x)|) =M
ǫ |Λn(x)| ǫ
≤ǫ·M
|Λn(x)|
ǫ
≤ǫ
untuk setiap n ∈ N. Karena berlaku untuk sebarang ǫ > 0, maka diperoleh M(|Λn(x)|) = 0 untuk setiapn∈N. KarenaM merupakan generalisasi fungsi
Orlicz, maka diperoleh
|Λn(x)|=
1 λn
n X
k=0
(λk−λk−1)xk
= 0
untuk setiap n∈N. Akibatnya,
n X
k=0
λk−λk−1
λn
xk= 0
untuk setiap n ∈ N. Akan diperlihatkan bahwa xk = 0 untuk setiap k ∈ N.
Untuk itu, dengan menggunakan induksi matematika, diambiln = 0, diperoleh
λ0−λ−1
λ0
x0 =x0 = 0.
Selanjutnya, dianggap benar untuk n=m, yaitu
m X
k=0
λk−λk−1
λm
Oleh karena itu, untuk n=m+ 1, diperoleh
Sebaliknya, dianggap x = 0. Karena M merupakan generalisasi fungsi Orlicz, maka diperoleh
sup
Hal ini menunjukkan bahwa
kxk= inf
untuk sebarang bilangan realα. Apabila diambilα = 0, maka peroalan cukup jelas. Untuk itu, diasumsikan α6= 0, maka diperoleh
x, y ∈[X(M)]Λ, berarti terdapat ρ1, ρ2 >0 sehingga
Oleh karena itu, diperoleh
M
fungsi Orlicz M memenuhi sifat naik dan konveks, maka diperoleh
M
untuk setiap n∈N. Hal ini menunjukkan bahwa
sup
untuk setiap n∈N, maka diperoleh
Oleh karena itu, diperoleh
kx+yk= inf
ρ >0 : sup
n∈N
M
|Λn(x+y)|
ρ
≤1
≤inf
ρ1 >0 : sup n∈N
M
|Λn(x)|
ρ1
≤1
+ inf
ρ2 >0 : sup n∈N
M
|Λn(y)|
ρ2
≤1
=kxk+kyk.
Dari hasil (1), (2), dan (3), terbukti bahwa fungsi dengan aturan
kxk[X(M)]Λ = inf
ρ >0 : sup
n∈N
M
|Λn(x)|
ρ
≤1
merupakan norma. Oleh karena itu, [X(M)]Λ merupakan ruang bernorma
untuk X ={c, c0, ℓ∞}.
Pada pembahasan di subbab selanjutnya, akan diperlihatkan bahwa ruang barisan [X(M)]Λ untuk X = {c0, c, ℓ∞} masing-masing saling memuat atau
termuat antara satu dengan yang lainnya. Dengan kata lain, akan diperli-hatkan bahwa [c0(M)]Λmerupakan himpunan bagian dari [c(M)]Λdan [c(M)]Λ
merupakan himpunan bagian dari [ℓ∞(M)]Λ. Oleh karena itu, hal ini yang
menjamin bahwa terdapat nilai supremum dari M
|Λn(x)|
ρ
untuk setiap
n ∈ N dan untuk suatu bilangan ρ > 0. Untuk selanjutnya, yang dimaksud dengan norma k · k adalah k · k[X(M)]Λ, dan yang dimaksud dengan X adalah himpunan {c, c0, ℓ∞}.
Teorema 4.2.3. [X(M)]Λ merupakan ruang Banach terhadap normak · k.
Bukti. (1) Akan dibuktikan untukX =ℓ∞, yaitu pada ruang barisan [ℓ∞(M)]Λ.
Untuk itu, diambil sebarang barisan Cauchy (xi) ⊂ [ℓ
∞(M)]Λ, dengan xi =
(xi
0, xi1, xi2,· · ·) untuk setiap i ∈ N. Karena (xi) merupakan barisan Cauchy,
berarti untuk sebarang bilangan ǫ >0 terdapat i0 ∈N, sehingga untuk setiap
j ≥i≥i0 berlaku
kxj−xik= inf
ρ >0 : sup
n∈N
M
|Λn(xj−xi)|
ρ
≤1
< ǫ.
Karena terpenuhi untuk sebarang bilangan ǫ >0, maka terdapat suatu bilan-gan ρǫ dengan 0< ρǫ < ǫsehingga
sup
n∈N
M
|Λn(xj −xi)|
ρǫ
Oleh karena itu, diperoleh
sup
n∈N
M
|Λn(xj −xi)|
ǫ
≤sup
n∈N
M
|Λn(xj −xi)|
ρǫ
≤1
untuk setiap j ≥ i ≥i0. Oleh karena itu, untuk setiapj ≥i ≥ i0 dan setiap
n ∈N diperoleh
M
|Λn(xj −xi)|
ǫ
≤1.
Selanjutnya, karena M bersifat konveks, maka diperoleh
M |Λn(xj −xi)|
=M
ǫ|Λn(xj−xi)|
ǫ
≤ǫ·M
|Λn(xj −xi)|
ǫ
≤ǫ.
Karena berlaku untuk sebarang ǫ >0, maka diperoleh
M |Λn(xj −xi)|
= 0
untuk setiap j ≥i ≥i0 dan setiap n ∈ N. Karena M merupakan generalisasi
fungsi Orlicz, berarti |Λn(xj −xi)| = 0 untuk setiap j ≥ i ≥ i0 dan setiap
n ∈N. Jadi,
1 λn
n X
k=0
(λk−λk−1)(xjk−x i k) = 0
untuk setiap j ≥ i ≥ i0 dan setiap n ∈ N. Karena (λk) merupakan barisan
bilangan real positif naik kuat, maka dengan menggunakan induksi matematika dapat diperoleh xjk −xi
k = 0 untuk setiap k ∈ N dan setiap j ≥ i ≥ i0.
Akibatnya, |xjk−xi
k| = 0 untuk setiap k ∈ N dan setiap j ≥ i ≥ i0. Dengan
kata lain,|xjk−xi
k|< ǫ untuk sebarang bilangan ǫ >0,j ≥i≥i0, dan k ∈N.
Hal ini berarti barisan (xjk) dengan (x j
k) = (x0k, x1k, x2k,· · ·) merupakan barisan
Cauchy di R untuk setiap k ∈ N. Karena R bersifat lengkap, maka barisan (xjk) konvergen ke suatu xk ∈R. Dengan kata lain, lim
j→∞x
j
k =xk untuk setiap
k ∈ N. Selanjutnya, apabila dibentuk barisan x = (xk) = (x0, x1, x2,· · ·),
maka diperoleh
untuk setiap i≥i0 dan setiap n∈N. Dengan kata lain, untuk suatu bilangan
ρ >0, berlaku
untuk setiap i ≥ i0. Oleh karena itu, dengan menggunakan definisi norma
diperoleh
untuk setiap i≥i0. Hal ini menunjukkan bahwa
xi →x untuk i→ ∞ atau lim i→∞x
i =x. (i)
Selanjutnya, akan dibuktikan bahwa x ∈ [ℓ∞(M)]Λ. Karena xi ∈ [ℓ∞(M)]Λ
untuk sebarang i ∈ N yang fix, berarti terdapat bilangan ρ > 0 sehingga
sup
< ∞. Selanjutnya, karena generalisasi fungsi Orlicz M
bersifat naik, konveks, dan memenuhi kondisi-∆2, maka diperoleh
untuk suatu bilangan K1, K2 >0. Hal ini menunjukkan bahwa
x∈[ℓ∞(M)]Λ. (ii)
Dari hasil (i) dan (ii) diperoleh kesimpulan bahwa [ℓ∞(M)]Λmerupakan ruang
Banach.
(2) Akan dibuktikan bahwa [c(M)]Λ merupakan ruang Banach. Dalam
hal ini, cukup dibuktikan bahwa [c(M)]Λ merupakan ruang bagian tertutup
dari [ℓ∞(M)]Λ. Untuk itu, diambil sebarang x ∈ [c(M)]Λ, berarti ada ρ > 0
Dengan kata lain, untuk sebarang bilangan ǫ > 0 terdapat n0 ∈ N, sehingga
untuk setiap n≥n0 berlaku
Oleh karena itu, diperoleh
Kemudian dipilihK = sup
naM merupakan generalisasi fungsi Orlicz, maka diperoleh
M
untuk setiap n∈N. Akibatnya,
karena M bersifat naik, konveks, dan memenuhi kondisi-∆2, maka diperoleh
terpenuhi untuk sebarang bilangan ǫ >0, maka diperoleh
sup
untuk setiap n∈N. Jadi, diperoleh
M
fix, berarti terdapat ρ > 0 sehinggaM
|Λn(xi)|
ρ
konvergen untuk n → ∞.
Jadi, terdapat bilangan real l sehingga
K0
Oleh karena itu, diperoleh
M
pakan ruang bagian tertutup dari [ℓ∞(M)]Λ. Jadi, [c(M)]Λ merupakan ruang
Banach terhadap norma k · k.
hal ini, cukup dibuktikan bahwa [c0(M)]Λ merupakan ruang bagian tertutup
dari [c(M)]Λ. Untuk itu, diambil sebarang x ∈ [c0(M)]Λ, berarti ada ρ > 0
sehingga M
|Λn(x)|
ρ
→0 untuk n → ∞. Selanjutnya diambil l = 0, maka
diperoleh
M
|Λn(x)|
ρ
→l untuk n → ∞.
Hal ini menunjukkan bahwa [c0(M)]Λ ⊂ [c(M)]Λ. Selanjutnya, akan
dibuk-tikan bahwa [c0(M)]Λ bersifat tertutup terhadap [c(M)]Λ. Untuk itu, diambil
sebarang barisan (xi) ⊂ [c
0(M)]Λ yang konvergen ke x ∈ [c(M)]Λ. Karena
xi →x untuk i→ ∞, berarti untuk sebarang bilangan ǫ >0 terdapat i 0 ∈N
sehingga untuk setiap i≥i0 berlakukx−xik< ǫ. Dengan kata lain,
kx−xik= inf
ρ >0 : sup
n∈N
M
|Λn(x−xi)|
ρ
≤1
< ǫ.
Karena berlaku untuk sebarang ǫ > 0, maka terdapat ρǫ dengan 0 < ρǫ < ǫ
sehingga
sup
n∈N
M
|Λn(x−xi)|
ρǫ
≤1.
Akibatnya,
sup
n∈N
M
|Λn(x−xi)|
ǫ
≤sup
n∈N
M
|Λn(x−xi)|
ρǫ
≤1.
Oleh karena itu, untuk setiap n∈N diperoleh
M
|Λn(x−xi)|
ǫ
≤1.
Selanjutnya, karena M bersifat konveks, maka diperoleh
M |Λn(x−xi)|
≤ǫ·M
|Λn(x−xi)|
ǫ
≤ǫ.
Dengan kata lain, M(|Λn(x−xi)|) → 0 untuk n → ∞. Karena generalisasi
fungsi OrliczM kontinu, maka diperoleh|Λn(x−xi)| →0 untuk n→ ∞. Oleh
karena itu, untuk suatu bilanganρ >0 diperoleh |Λn(x−xi)|
ρ →0 untukn → ∞.
Karena M bersifat kontinu, maka diperoleh
M
|Λn(x−xi)|
ρ
Selanjutnya diambil xi ∈ [c
0(M)]Λ untuk sebarang i ∈ N yang fix. Berarti
terdapat ρ > 0 sehingga M
pakan ruang bagian tertutup dari [c(M)]Λ. Jadi, [c0(M)]Λ merupakan ruang
Banach.
Teorema 4.2.4. [X(M)]Λ merupakan ruang-BK terhadap norma k · k.
Bukti. Diambil sebarang barisan x ∈ [X(M)]Λ dan sebarang bilangan ǫ >
0. Karena bilangan ǫ > 0 sebarang, berarti terdapat bilangan δ = ǫ 2 > 0.
Karena berlaku untuk sebarang bilangan ǫ > 0, maka terdapat ρǫ dengan
0< ρǫ< ǫ sehingga
Oleh karena itu, diperoleh
Akibatnya, untuk setiapn ∈N, diperolehM
|Λn(x−y)|
ǫ
≤1. Selanjutnya,
karena M bersifat konveks, maka diperoleh
M(|Λn(x−y)|)≤ǫ M
|Λn(x−y)|
ǫ
≤ǫ.
Karena berlaku untuk sebarang bilangan ǫ > 0, berarti M(|Λn(x−y)|) = 0
untuk setiap n ∈ N. Selanjutnya, karena M merupakan generalisasi fungsi Orlicz, berarti |Λn(x−y)|= 0 untuk setiap n∈N. Hal ini berakibat bahwa
1 λn
n X
k=0
(λk−λk−1)(xk−yk) = 0
untuk setiapn ∈N. Karena (λk) merupakan barisan bilangan real positif naik
kuat, maka dengan menggunakan induksi matematika diperoleh |xk−yk|< ǫ
untuk setiap k ∈ N dan untuk sebarang bilangan ǫ > 0. Oleh karena itu, diperoleh
|pk(x)−pk(y)|=|xk−yk|< ǫ
untuk setiap k ∈ N. Karena x ∈ [X(M)]Λ sebarang, maka fungsi pk kontinu
pada ruang Banach [X(M)]Λ. Jadi, [X(M)]Λ merupakan ruang-BK terhadap
norma k · k.
Teorema 4.2.5. [c0(M)]Λ merupakan ruang-AK terhadap norma k · k.
Bukti. Diambil sebarang x∈[c0(M)]Λ, berarti terdapat ρ >0 sehingga
M
|Λn(x)|
ρ
→0 untukn→ ∞.
Karena [c0(M)]Λ ruang bernorma, maka berlaku
kxk= inf
ρ >0 : sup
n∈N
M
|Λn(x)|
ρ
≤1
.
Oleh karena itu, untuk sebarang bilangan ǫ > 0, terdapat m0 ∈ N sehingga
diperoleh
sup
n≥m0
M |
1 λn
Pn
k=0(λk−λk−1)xk|
ǫ
!
Selanjutnya, didefinisikan barisan x[m] dengan aturan
x[m]=
m X
k=0
xke[k] untuk setiap m∈N.
Oleh karena itu, untuk setiap m≥m0, diperoleh
kx−x[m]k= inf
(
ρ >0 : sup
n≥m0+1
M |
1 λn
Pn
k=0(λk−λk−1)xk|
ρ
!
≤1
)
≤inf
(
ρ >0 : sup
n≥m+1
M |
1 λn
Pn
k=0(λk−λk−1)xk|
ρ
!
≤1
)
< ǫ.
Dengan kata lain, kx−x[m]k →0 untuk m → ∞. Jadi, [c
0(M)]Λ merupakan
ruang-AK.
Teorema 4.2.6. [X(M)]Λ merupakan isomorfik norma (norm isomorphic)
terhadap X(M); yaitu
[X(M)]Λ ∼=X(M).
Bukti. Pertama sekali didefinisikan operator TΛ : [X(M)]Λ → X(M) dengan
aturan x7→TΛ(x) = Λ(x) = (Λn(x))∞n=0. Akan dibuktikan bahwa operator TΛ
linier, bijektif, dan mempertahankan sifat norma. Untuk itu, diambil sebarang x, y ∈[X(M)]Λ dan sebarang skalarα, β. Maka diperoleh
TΛ(αx+βy) = (Λn(αx) + Λn(βy)) (i)
=α(Λn(x)) +β(Λn(y)) = αTΛ(x) +βTΛ(y).
Hal ini menunjukkan bahwa operatorTΛbersifat linier. Selanjutnya, diperoleh
Ker(TΛ) =
x∈[X(M)]Λ:TΛ(x) = 0
=
x∈[X(M)]Λ: Λ(x) =
1 λn
n X
k=0
(λk−λk−1)xk= 0,∀ n ∈N
=
x∈[X(M)]Λ:xk = 0,∀ k ∈N
=
x∈[X(M)]Λ:x= 0
=
0
.
y∈X(M). Didefinisikan operator TΛ−1 :X(M)→[X(M)]Λ dengan aturan
y7→TΛ−1(y) = x=
k X
j=k−1
(−1)k−j λj λk−λk−1
yj !∞
k=0
.
Oleh karena itu diperoleh
TΛ(x) = n X
k=0
λk−λk−1
λn
xk !
(iii)
=
n X
k=0
λk−λk−1
λn
k X
j=k−1
(−1)k−j λj λk−λk−1
yj !
=
n X
k=0
λkyk−λk−1yk−1
λn
!
= (yn) =y.
Hal ini menunjukkan bahwa operator linier TΛ bersifat surjektif. Dengan kata
lain, operator linier TΛ bersifat bijektif. Selanjutnya, untuk melengkapi
pem-buktian teorema, diambil sebarang TΛ(x)∈X(M) untukx∈[X(M)]Λ. Maka
diperoleh
kTΛ(x)kX(M) =kΛ(x)kX(M) (iv)
= inf
ρ >0 : sup
n∈N
M
|Λn(x)|
ρ
≤1
=kxk[X(M)]Λ.
Dari hasil (i), (ii), (iii), dan (iv), diperoleh bahwa operator linier bijektif TΛ
merupakan isomorfisma norma. Jadi, [X(M)]Λ∼=X(M).
4.3. Relasi Inklusi Pada Ruang Barisan Konvergen dan Terbatas yang Dibangun Oleh Generalisasi Fungsi Orlicz-λ
Pada bagian ini akan diperlihatkan beberapa relasi inklusi yang bersesuaian pada ruang barisan konvergen dan terbatas yang dibangun oleh generalisasi fungsi Orlicz-λ, dan ruang barisan konvergen dan terbatas yang dibangun oleh generalisasi fungsi Orlicz.
inklusi berikut berlaku kuat, yaitu
[c0(M)]Λ ⊂[c(M)]Λ ⊂[ℓ∞(M)]Λ.
Bukti. Telah diperlihatkan pada pembuktian Teorema 4.2.3 bahwa [c0(M)]Λ
merupakan ruang bagian dari [c(M)]Λ, dan [c(M)]Λ merupakan ruang bagian
dari [ℓ∞(M)]Λ. Oleh karena itu, di dalam pembuktian ini akan diperlihatkan
bahwa relasi inklusi [c0(M)]Λ ⊂ [c(M)]Λ ⊂ [ℓ∞(M)]Λ bersifat kuat. Untuk
itu, diambil sebarang x ∈ [c(M)]Λ dan suatu bilangan real l 6= 0 sehingga
M
|Λn(x)|
ρ
→ l untuk n → ∞ dan untuk suatu bilangan ρ > 0. Jadi,
x∈[c(M)]Λ\[c0(M)]Λ. Oleh karena itu, diperoleh
[c0(M)]Λ ⊂[c(M)]Λ. (i)
Selanjutnya, diambil barisan x= (xk) yang didefinisikan oleh
xk =
λk+λk−1
λk−λk−1
(−1)k+ 2
untuk setiap k∈N. Diperoleh
|Λn(x)|=
n X
k=0
λk−λk−1
λn
λk+λk−1
λk−λk−1
(−1)k+ 2
=
n X
k=0
λk+λk−1
λn
(−1)k+ 2 n X
k=0
λk−λk−1
λn
=|(−1)n+ 2|
untuk setiap n∈N. Jadi,
M
|Λn(x)|
ρ
=M
|(−1)n+ 2|
ρ
untuk setiap n ∈ N dan suatu bilangan ρ > 0. Hal ini menunjukkan bahwa
barisan
M
|Λn(x)|
ρ
∈ ℓ∞\c. Dengan kata lain, x ∈ [ℓ∞(M)]Λ\[c(M)]Λ.
Oleh karena itu, diperoleh
[c(M)]Λ ⊂[ℓ∞(M)]Λ. (ii)
Teorema 4.3.2. Diberikan c0(M) ⊂ [c0(M)]Λ dan c(M) ⊂ [c(M)]Λ. Relasi
inklusi c0(M) = [c0(M)]Λ dan c(M) = [c(M)]Λ masing-masing terpenuhi jika
dan hanya jika S(x)∈c0(M) untuk setiap xdi [c0(M)]Λ dan [c(M)]Λ.
Bukti. (1) Akan dibuktikan bahwa c0(M) = [c0(M)]Λ jika dan hanya jika
barisan S(x) ∈ c0(M) untuk setiap x ∈ [c0(M)]Λ. Untuk itu, diasumsikan
c0(M) = [c0(M)]Λ. Apabila diambil sebarang x ∈ [c0(M)]Λ, berarti terdapat
suatu bilanganρ >0 sehinggaM
|Λn(x)|
ρ
→0 untukn→ ∞. Dengan kata
lain, untuk sebarang bilangan ǫ > 0 terdapat n0 ∈ N, sehingga untuk setiap
n ≥ n0 berlaku
M
|Λn(x)|
ρ
< ǫ. Karena berlaku untuk sebarang ǫ > 0,
maka diperoleh
M
|Λn(x)|
ρ
= 0 untuk setiapn∈N.
Karena M merupakan generalisasi fungsi Orlicz, maka |Λn(x)|
ρ = 0 untuk setiap n∈N. Oleh karena itu, untuk setiap n∈N diperoleh
|Λn(x)|=|
1 λn
n X
k=0
(λk−λk−1)xk|= 0.
Akibatnya,
Λn(x) =
1 λn
n X
k=0
(λk−λk−1)xk = 0 untuk setiap n∈N.
Karena (λk) merupakan barisan bilangan real positif naik kuat, maka dengan
menggunakan induksi matematika dapat diperoleh xk= 0 untuk setiap k ∈N.
Dengan kata lain, untuk suatu bilangan ǫ >0 diperoleh |xk| < ǫ untuk setiap
k ∈ N. Hal ini menunjukkan bahwa barisan (xk) konvergen ke nol di R.
KarenaRbersifat lengkap, maka (xk) merupakan barisan Cauchy, yaitu untuk
sebarang bilangan ǫ > 0 terdapat k0 ∈ N, sehingga untuk setiap k ≥ j ≥ k0
berlaku |xk−xj| < ǫ. Jadi, |xk−xk−1|< ǫ untuk setiap k > k−1≥ k0 dan
sebarang bilangan ǫ >0. Akibatnya,
lim
n→∞Sn(x) = limn→∞
1 λn
n X
k=0
Karena M kontinu, maka untuk suatu bilangan ρ >0 diperoleh
lim
n→∞M
|Sn(x)|
ρ
= 0.
Jadi, S(x) = (Sn(x))∞n=0 ∈c0(M).
Sebaliknya, diasumsikan S(x) ∈ c0(M) untuk setiap x ∈ [c0(M)]Λ.
Karena M bersifat naik, konveks, dan memenuhi kondisi-∆2, serta Sn(x) =
xn−Λn(x) untuk setiap n ∈N, maka diperoleh
M
|xn|
ρ
≤M
|xn−Sn(x)|
ρ +
|Sn(x)|
ρ
≤ 1
2M
2|xn−Sn(x)|
ρ
+ 1 2M
2|Sn(x)|
ρ
≤ K0
2 M
|Λn(x)|
ρ
+K1 2 M
|Sn(x)|
ρ
untuk setiapn∈Ndan untuk suatu bilanganK0, K1 >0. KarenaM
|Λn(x)|
ρ
→
0 dan M
|Sn(x)|
ρ
→0 untuk n→ ∞, maka diperoleh
K0
2 M
|Λn(x)|
ρ
+ K1 2 M
|Sn(x)|
ρ
→0 untuk n→ ∞.
Jadi,
M
|xn|
ρ
→0 untuk n→ ∞.
Dengan kata lain, x∈c0(M). Hal ini menunjukkan bahwa [c0(M)]Λ⊂c0(M).
Karena c0(M) ⊂ [c0(M)]Λ dan [c0(M)]Λ ⊂ c0(M), maka dapat disimpulkan
bahwa c0(M) = [c0(M)]Λ.
(2) Akan dibuktikan c(M) = [c(M)]Λ jika dan hanya jika S(x) ∈ c0(M)
untuk setiap x∈ [c(M)]Λ. Untuk itu, diasumsikan c(M) = [c(M)]Λ. Apabila
diambil sebarangx∈[c(M)]Λ, makax∈c(M). Hal ini berarti terdapat suatu
bilanganρ >0 danl ∈RsehinggaM
|xk|
ρ
→l untukn → ∞. Selanjutnya,
karena generalisasi fungsi Orlicz M bersifat kontinu, maka |xk|
ρ → l
′ untuk
k → ∞ dengan l′ =M−1(l). Dengan kata lain, |x
k| → l1 =ρl′ untuk k→ ∞.
Selanjutnya, apabila xk ≥ 0 untuk setiap k ∈ N, maka xk = |xk| → l1 untuk
k → ∞. Kemudian, apabila xk < 0 untuk setiap k ∈ N, maka diperoleh
Hal ini menunjukkan bahwa barisan (xk) konvergen di R. Karena R bersifat
lengkap, maka (xk) merupakan barisan Cauchy, yaitu untuk sebarang bilangan
ǫ >0 terdapatk0 ∈N, sehingga untuk setiapk ≥j ≥k0 berlaku|xk−xj|< ǫ.
Jadi, |xk−xk−1|< ǫuntuk setiapk > k−1≥k0 dan sebarang bilanganǫ >0.
Akibatnya,
lim
n→∞Sn(x) = limn→∞
1 λn
n X
k=0
λk−1(xk−xk−1) = 0.
Karena M kontinu, maka untuk suatu bilangan ρ >0 diperoleh
lim
n→∞M
|Sn(x)|
ρ
= 0.
Jadi, S(x) = (Sn(x))∞n=0 ∈c0(M).
Sebaliknya, diasumsikanS(x)∈c0(M) untuk setiapx∈[c(M)]Λ. Karena
M bersifat naik, konveks, dan memenuhi kondisi-∆2, sertaSn(x) = xn−Λn(x)
untuk setiap n∈N, maka diperoleh
M
|xn|
ρ
≤M
|xn−Λn(x)|
ρ +
|Λn(x)|
ρ
≤ 1
2M
2|xn−Λn(x)|
ρ
+ 1 2M
2|Λn(x)|
ρ
≤ K0
2 M
|Sn(x)|
ρ
+K1 2 M
|Λn(x)|
ρ
untuk setiapn∈Ndan untuk suatu bilanganK0, K1 >0. KarenaM
|Sn(x)|
ρ
→
0 dan M
|Λn(x)|
ρ
→luntuk n→ ∞dan untuk suatu bilangan reall, maka
diperoleh
K0
2 M
|Sn(x)|
ρ
+ K1 2 M
|Λn(x)|
ρ
→l′ = K1
2 l untukn → ∞.
Jadi,
M
|xn|
ρ
→l′ untukn → ∞.
Dengan kata lain, x ∈ c(M). Hal ini menunjukkan bahwa [c(M)]Λ ⊂ c(M).
Karenac(M)⊂[c(M)]Λ dan [c(M)]Λ⊂c(M), maka dapat disimpulkan bahwa
hanya jikaS(x)∈ℓ∞(M) untuk setiap x∈[ℓ∞(M)]Λ.
untuk suatu bilanganρ >0. KarenaM bersifat naik, konveks, dan memenuhi kondisi-∆2, serta Sn(x) = xn−Λn(x) untuk setiap n∈N, maka diperoleh
Karena M bersifat naik, konveks, dan memenuhi kondisi-∆2, serta Sn(x) =
ga M
|Λn(x)|
ρ
→ 0 dan M
|xk|
ρ
→ l untuk n → ∞ dan untuk suatu
bilangan real l. Karena M
|Λn(x)|
ρ
→ 0 untuk n → ∞, berarti untuk
se-barang bilanganǫ >0 terdapatn0 ∈N, sehingga untuk setiapn ≥n0 berlaku
M
|Λn(x)|
ρ
< ǫ. Karena berlaku untuk sebarangǫ >0, maka diperoleh
M
|Λn(x)|
ρ
= 0 untuk setiapn∈N.
Karena M merupakan generalisasi fungsi Orlicz, maka |Λn(x)|
ρ = 0 untuk setiap n∈N. Oleh karena itu, untuk setiap n∈N diperoleh
|Λn(x)|=|
1 λn
n X
k=0
(λk−λk−1)xk|= 0.
Akibatnya,
Λn(x) =
1 λn
n X
k=0
(λk−λk−1)xk = 0 untuk setiap n∈N.
Karena (λk) merupakan barisan bilangan real positif naik kuat, maka dengan
menggunakan induksi matematika dapat diperoleh xk= 0 untuk setiap k ∈N.
Karena M bersifat kontinu, maka untuk suatu bilangan ρ >0 diperoleh
lim
k→∞M
|xk|
ρ
= 0.
Hal ini menunjukkan bahwa x ∈ c0(M). Jadi, [c0(M)]Λ ∩ c(M) ⊂ c0(M).
Karenac0(M)⊂[c0(M)]Λ∩c(M) dan [c0(M)]Λ∩c(M)⊂c0(M), maka dapat
disimpulkan bahwa [c0(M)]Λ∩c(M) = c0(M).
Selanjutnya, apabila diberikanc(M),ℓ∞(M), dan [c(M)]Λ, maka relasi inklusi
[c(M)]Λ ∩ ℓ∞(M) = c(M) belum tentu berlaku. Untuk itu, diasumsikan
λk =k+ 1 dan xk= (−1)k+ 1 untuk setiap k ∈N. Diperoleh
Λn(x) =
1 λn
n X
(−1)k+ 1
= 1 λn
n X
(−1)k+
n X
1
!
= 1 λn
n X
(−1)k+n
untuk setiap n∈N. Dalam hal ini diperoleh
KarenaM kontinu, maka terdapat bilangan real l sehingga M
untuk setiap k∈N. Hal ini menunjukkan bahwa
Selanjutnya, diberikan x = (xk)∈ ω dan n ≥1. Dengan menggunakan
persamaan (4.1.4) dan (4.1.5) diperoleh
Sn(x) =
untuk setiap n∈N. Akibatnya,
Di sisi lain, dengan menggunakan definisi barisan λ= (λk)∞k=0 pada
per-samaan (4.1.1), dapat diperoleh bahwa λk+1 λk
>1 untuk setiap k ∈N. Karena
generalisasi fungsi Orlicz M bersifat naik, maka diperolehM
λk+1
λk
> M(1)
untuk setiap k∈N. Oleh karena itu, untuk setiap k∈N dapat diperoleh
M(1)≤inf
Jadi, hanya terdapat dua kondisi yang berlaku pada barisan λ= (λk); yaitu
lim inf
Untuk kondisi yang pertama, yaitu lim inf
k→∞ M
λk+1
λk
> M(1), diperoleh
M(1) <inf
untuk setiap j ∈N. Oleh karena itu, diperoleh
M(1) < M
< M(0) untuk setiap j ∈ N. Selanjutnya, karena
setiap j ∈N. Oleh karena itu, diperoleh
1 2
1− λj+1
λj
<0 ⇐⇒ 1−λj+1
λj
<0
⇐⇒ 1< λj+1 λj
⇐⇒ λj
λj+1
<1
⇐⇒ 0< λj+1−λj λj+1
untuk setiap j ∈ N. Karena generalisasi fungsi Orlicz M bersifat naik, maka
untuk setiap k ∈ N diperoleh M(0) < M
λk+1−λk
λk+1
. Oleh karena itu,
diperoleh
lim inf
k→∞ M
λk+1−λk
λk+1
>0.
Sebaliknya, diasumsikan lim inf
k→∞ M
λk+1−λk
λk+1
> 0, maka diperoleh
inf
M
λj+1−λj
λj+1
;j ≥k
>0 untuk setiapk ∈N. Oleh karena itu, untuk
setiap j ∈ N diperoleh M
λj+1−λj
λj+1
>0. Selanjutnya, karena generalisasi
fungsi OrliczM bersifat naik, berarti λj+1−λj λj+1
>0 untuk setiap j ∈N. Oleh
karena itu, diperoleh
0< λj+1−λj λj+1
⇐⇒ 0<1− λj
λj+1
⇐⇒ λj
λj+1
<1
⇐⇒ 1< λj+1 λj
untuk setiap j ∈ N. Karena generalisasi fungsi Orlicz M bersifat naik, maka
diperoleh M(1)< M
λk+1
λk
untuk setiap k ∈N. Oleh karena itu, diperoleh
lim inf
k→∞ M
λk+1
λk
> M(1).
Jadi, dapat disimpulkan bahwa lim inf
k→∞ M
λk+1
λk
> M(1) jika dan hanya
ji-ka lim inf
k→∞ M
λk+1−λk
λk+1
lim inf
k→∞ M
λk+1
λk
=M(1) jika dan hanya jika lim inf
k→∞ M
λk+1−λk
λk+1
= 0.
Dari hasil tersebut di atas, dapat digunakan dalam membuktikan teorema berikut:
Teorema 4.3.5. Diberikan sebarang barisanλ= (λk) yang memenuhi (3.1.1).
Diperoleh
(a)
λk
λk−λk−1
/
∈ℓ∞(M) jika dan hanya jika lim inf
k→∞ M
λk+1
λk
=M(1).
(b)
λk
λk−λk−1
∈ℓ∞(M) jika dan hanya jika lim inf
k→∞ M
λk+1
λk
> M(1).
Bukti. (a) Pertama-tama diasumsikan barisan
λk
λk−λk−1
/
∈ ℓ∞(M).
Be-rarti, untuk setiap bilangan N0 >0 terdapat j ∈Nsehingga
M
λj/(λj −λj−1)
ρ
> N0 untuk suatu bilangan ρ >0.
Karena generalisasi fungsi Orlicz M bersifat naik, maka
λj/(λj −λj−1)
ρ > N1 untuk suatu bilangan N1 >0.
Dengan kata lain, λj λj −λj−1
> N untuk setiap j ∈N dengan N =ρN1. Oleh
karena itu, λj −λj−1 λj
< 1
N untuk setiap j ∈ N. Selanjutnya, untuk setiap j ∈N diperoleh
λj+1
λj
= λj+1 λj−λj−1
· λj −λj−1
λj
< λj+1 λj −λj−1
· 1
N.
Karena λj+1 λj−λj−1
> λj λj−λj−1
> N untuk setiap j ∈N, maka diperoleh
λj+1
λj−λj−1
· 1
N >1 untuk setiap j ∈N.
Kemudian, karena λj+1 λj −λj−1
· 1
N >1 dan
λj+1
λj−λj−1
· 1
N > λj+1
λj
untuk setiap
j ∈N, maka diperoleh
Jadi, karena λj+1 λj
≮1 untuk setiapj ∈N, maka λj+1 λj
≥1 untuk setiapj ∈N.
Karena generalisasi fungsi Orlicz M bersifat naik, maka diperoleh
M
Oleh karena itu, diperoleh
inf
Selanjutnya, untuk setiap k ∈N diperoleh
inf
Oleh karena itu, diperoleh
lim
Sebaliknya, diasumsikan lim inf
k→∞ M
barang bilangan ǫ >0 terdapat k0 ∈N, sehingga untuk setiap k ≥k0 berlaku
M(1)−ǫ < M
untuk setiap k ≥ k0. Karena berlaku untuk sebarang ǫ > 0, maka diperoleh
M(1)−M
setiap k ∈Ndiperoleh
λk
Karena generalisasi fungsi Orlicz M bersifat naik, maka untuk setiap k ∈ N
dan untuk setiap bilangan ρ >0 diperoleh
M
Hal ini menunjukkan bahwa barisan
(b) Pertama-tama diasumsikan barisan
dengan menggunakan Teorema 4.3.5 (a) diperoleh lim inf
k→∞ M
Dengan kata lain, lim inf
k→∞ M
Sebaliknya, diasumsikan lim inf
k→∞ M
λk+1
λk
> M(1). Berarti, dengan
menggunakan Teorema 4.3.5 (a) diperoleh barisan
λk
λk−λk−1
∈ℓ∞(M).
Teorema 4.3.6. Inklusi X(M) ⊂[X(M)]Λ berlaku kuat jika dan hanya jika
lim inf
nakan Teorema 4.3.3, berarti terdapat barisan x∈[ℓ∞(M)]Λ sehingga barisan
S(x) = (Sn(x))∞n=0 ∈/ ℓ∞(M). Karena x ∈ [ℓ∞(M)]Λ, berarti Λ(x) ∈ ℓ∞(M).
Karena generalisasi fungsi Orlicz M bersifat naik, konveks, dan memenuhi kondisi-∆2, maka diperoleh
sup
sehingga diperoleh M
|Sn0(x)| ρ
> N0 untuk suatu bilangan ρ > 0. Karena
generalisasi fungsi Orlicz M bersifat naik, maka diperoleh |Sn(x)|
ρ > N1 untuk suatu bilangan N1 > 0 dan untuk setiap n ∈ N. Dengan kata lain, |Sn(x)| >
N2 = ρN1 untuk setiap n ∈ N. Selanjutnya, karena (Λn(x)−Λn−1(x))∞n=0 ∈
ℓ∞(M), berarti terdapat suatu bilangan N3 >0 sehingga untuk setiap n ∈N
ρN4 untuk setiap n ∈ N. Oleh karena itu, dengan menggunakan persamaan
untuk setiap n ∈N. Karena generalisasi fungsi Orlicz M bersifat naik, maka untuk suatu bilangan ρ >0 diperoleh
M
untuk setiap n ∈ N. Hal ini menunjukkan bahwa
Oleh karena itu, barisan
ℓ∞(M). Akibatnya, Teorema 4.3.5 menjamin bahwa lim inf
n→∞ M
Sebaliknya, diasumsikan lim inf
n→∞ M
nakan Teorema 4.3.5, diperoleh barisan
Karena lim inf
n→∞ M
λn+1
λn
= M(1), berarti untuk sebarang bilangan ǫ > 0
Oleh karena itu, diperoleh
untuk setiap n ∈ N. Karena M merupakan generalisasi fungsi Orlicz, maka untuk setiap n∈N diperoleh
M
< ǫ untuk setiap n ∈ N. Karena berlaku untuk
sebarang ǫ >0 dan M merupakan generalisasi fungsi Orlicz, maka diperoleh
1
Oleh karena itu, diperoleh
M
untuk setiap k∈N, maka diperoleh
untuk setiapk ∈N. Karena λk λk−λk−1
> λk λk+1
untuk setiapk ∈N, dan karena
generalisasi fungsi OrliczM bersifat naik, maka untuk setiapk∈Ndan untuk suatu bilangan ρ >0 diperoleh
M
Hal ini menunjukkan bahwa barisan
Dengan menggunakan Teorema 4.3.2, berarti terdapat barisan x ∈ [c(M)]Λ
dan y ∈ [c0(M)]Λ, sehingga S(x) ∈/ c0(M) dan S(y) ∈/ c0(M). Selanjutnya,
karena x ∈ [c(M)]Λ, berarti Λ(x) ∈ c(M). Karena generalisasi fungsi Orlicz
M bersifat naik, konveks, dan memenuhi kondisi-∆2, maka diperoleh
berarti untuk sebarang bilangan ǫ >0 terdapat n0 ∈N sehingga
Hal ini menunjukkan bahwa S(x) ∈/ ℓ∞(M). Selanjutnya, karena barisan
S(x)∈/ ℓ∞(M), berarti untuk setiap N0 >0 terdapat n0 ∈ N, sehingga
diper-> N0 untuk suatu bilangan ρ > 0. Karena generalisasi
fungsi Orlicz M bersifat naik, maka diperoleh |Sn(x)|
ρ > N1 untuk suatu
bi-untuk suatu bilanganρ >0. Karena generalisasi fungsi OrliczM bersifat naik,
maka diperoleh |Λn(x)−Λn−1(x)|
ρ ≤N4untuk suatu bilanganN4. Dengan ka-ta lain, |Λn(x)−Λn−1(x)| ≤N5 =ρN4 untuk setiap n ∈N. Oleh karena itu,
dengan menggunakan persamaan (3.3.1) diperoleh
untuk setiap n ∈N. Karena generalisasi fungsi Orlicz M bersifat naik, maka untuk suatu bilangan ρ >0 diperoleh
M
untuk setiap n ∈ N. Hal ini menunjukkan bahwa
Oleh karena itu, barisan
∈ ℓ∞(M). Akibatnya, dengan menggunakan Teorema 4.3.5
diperoleh bahwa lim inf
n→∞ M
diperoleh
disimpulkan bahwa barisan
Akibatnya, Teorema 4.3.5 menjamin bahwa lim inf
n→∞ M
Sebaliknya, diasumsikan bahwa lim inf
k→∞ M
lanjutnya, karena lim inf
k→∞ M
λk−λk−1
λk
= 0, maka terdapat barisan bagian
(λkr)
∞
r=0 dari barisan λ= (λk) sehingga diperoleh
lim
Kemudian, dipilihkr+1−kr ≥2 untuk setiapr ∈N, dan didefinisikan barisan
yk=
1 ; untukk =kr
−
λk−1−λk−2
λk−λk−1
; untukk =kr+ 1
0 ; untuk yang lainnya.
(4.3.3)
Hal ini menunjukkan bahwa barisan y= (yk) tidak konvergen. Karena
gener-alisasi fungsi Orlicz M bersifat kontinu, maka diperoleh y = (yk)∈/ c(M) dan
y= (yk)∈/ c0(M). Selanjutnya, untuk setiap n∈N diperoleh
Λn(y) =
λn−λn−1
λn
; untuk n=kr
0 ; untuk yang lainnya.
Kemudian, karena generalisasi fungsi Orlicz M bersifat kontinu, maka dari persamaan (4.3.2) diperoleh λkr −λkr−1
λkr
→ 0 untuk r → ∞. Oleh karena
itu, untuk n = kr diperoleh
λn−λn−1
λn
→ 0 untuk n → ∞. Selanjutnya,
untuk suatu bilangan ρ > 0 dapat diperoleh M
λn−λn−1
ρλn
→ 0. Artinya,
barisan Λ(y) = (Λn(y))∞n=0 ∈ c0(M). Hal ini menunjukkan bahwa barisan
y = (yk) ∈ [c0(M)]Λ. Akibatnya, barisan y = (yk) ∈ [c(M)]Λ. Jadi, karena
y = (yk) berada di [c0(M)]Λ dan [c(M)]Λ tetapi tidak berada di c0(M) dan
c(M), maka inklusi c0(M)⊂[c0(M)]Λ dan c(M)⊂[c(M)]Λ berlaku kuat.
Teorema 4.3.7. Inklusi X(M) = [X(M)]Λ berlaku jika dan hanya jika
lim inf
n→∞ M
λn+1
λn
> M(1).
Bukti. DiasumsikanX(M) = [X(M)]Λ. Dengan menggunakan Teorema 4.3.6,
diperoleh lim inf
n→∞ M
λn+1
λn
6
=M(1). Jadi, lim inf
n→∞ M
λn+1
λn
> M(1).
Sebaliknya, diasumsikan lim inf
n→∞ M
λn+1
λn
> M(1). Teorema 4.3.5 (a)
menjamin bahwa barisan
λn
λn−λn−1
∈ℓ∞(M). Dengan kata lain, terdapat
suatu bilangan K >0 sehingga untuk setiap n∈N berlaku
M
λn
ρ(λn−λn−1)
dapat diperoleh bahwa λn λn−λn−1
≤ ρK0 untuk suatu bilangan ρ, K0 > 0
dengan M(K0) = K. Selanjutnya, diperoleh
λn−λn−1+λn−1
λn−λn−1
≤ρK0 ⇐⇒ 1 +
λn−1
λn−λn−1
≤ρK0
⇐⇒ λn−1
λn−λn−1
≤ρK0−1
⇐⇒ λn−1
ρ(λn−λn−1)
≤K0−
1 ρ
untuk setiap n ∈ N. Dengan mengambil suatu bilangan K1 = K0 −
1 ρ > 0, maka diperoleh λn−1
ρ(λn−λn−1)
≤ K1 untuk setiap n ∈ N. Karena generalisasi
fungsi Orlicz M bersifat naik, maka diperoleh
M
λn−1
ρ(λn−λn−1)
≤M(K1)
untuk setiap n ∈ N. Hal ini menunjukkan bahwa
λn−1
λn−λn−1
∈ ℓ∞(M).
Selanjutnya, diambil sebarang x ∈ [c(M)]Λ, berarti Λ(x) ∈ c(M). Artinya,
terdapat l ∈ R dan suatu bilangan ρ > 0 sehingga M
|Λn(x)|
ρ
→ l untuk
n → ∞. Oleh karena itu, diperoleh M
|Λn−1(x)|
ρ
→ l untuk n → ∞.
Karena generalisasi fungsi Orlicz M kontinu, maka terdapat l0 = M−1(l)
se-hingga |Λn(x)|
ρ → l0 dan
|Λn−1(x)|
ρ → l0 untuk n → ∞. Dengan kata lain,
|Λn(x)| → l1 dan |Λn−1(x)| → l1 untuk n → ∞ dengan l1 = ρl0.
Selanjut-nya, apabila Λn(x)≥ 0 dan Λn−1(x)≥ 0 untuk setiap n ∈N, maka diperoleh
Λn(x) =|Λn(x)| → l1 dan Λn−1(x) =|Λn−1(x)| → l1 untuk n → ∞.
Kemudi-an, apabila Λn(x) < 0 dan Λn−1(x) < 0 untuk setiap n ∈ N, maka diperoleh
−Λn(x) = |Λn(x)| → l1 dan −Λn−1(x) =|Λn−1(x)| → l1 untuk n → ∞.
Den-gan kata lain, Λn(x) → −l1 dan Λn−1(x) → −l1 untuk n → ∞. Oleh karena
itu, untuk setiap n∈N diperoleh
lim
n→∞(Λn(x)−Λn−1(x)) = limn→∞Λn(x)−nlim→∞Λn−1(x) = 0.
Selanjutnya, dari persamaan (4.3.1) diperoleh
Sn(x) =
λn−1
λn−λn−1
Λn(x)−Λn−1(x)
Karena generalisasi fungsi OrliczM kontinu, maka untuk suatu bilanganρ >0,
diperoleh M
|Sn(x)|
ρ
→ 0 untuk n → ∞. Dengan kata lain, barisan
(Sn(x))∞n=0 ∈ c0(M). Karena untuk sebarang barisan x ∈ [c(M)]Λ berlaku
S(x)∈c0(M), maka menurut Teorema 4.3.2 diperoleh [c(M)]Λ =c(M).
Selanjutnya, untuk sebarang x∈[c0(M)]Λ yang diambil, diperoleh
bah-wa Λ(x) ∈ c0(M). Oleh karena itu, barisan (Λn(x)−Λn−1(x))∞n=0 ∈ c0(M).
Akibatnya, dari persamaan (4.3.1) diperoleh S(x) = (Sn(x))∞n=0 ∈ c0(M).
Karena untuk sebarang x ∈ [c0(M)]Λ berlaku S(x) = (Sn(x))∞n=0 ∈ c0(M),
maka menurut Teorema 4.3.2 diperoleh [c0(M)]Λ =c0(M).
Selanjutnya, diambil sebarang x ∈ [ℓ∞(M)]Λ, berarti Λ(x) ∈ ℓ∞(M).
Oleh karena itu, barisan (Λn(x)−Λn−1(x))∞n=0 ∈ ℓ∞(M). Artinya, terdapat
N0 >0 sehingga untuk setiapn ∈N berlaku
M
Λn(x)−Λn−1(x)
ρ
≤N0
untuk suatu bilangan ρ > 0. Selanjutnya, karena ( λn−1 λn−λn−1
) ∈ ℓ∞(M),
berarti terdapat N1 >0 sehingga untuk setiap n∈N berlaku
M
λn−1
ρ(λn−λn−1)
≤N1
untuk suatu bilanganρ >0. Karena generalisasi fungsi OrliczM bersifat naik, maka untuk suatu bilangan N2, N3 >0 diperoleh
Λn(x)−Λn−1(x)
ρ ≤N2 dan
λn−1
ρ(λn−λn−1)
≤N3
untuk setiap n ∈ N. Oleh karena itu terdapat N4, N5 >0 dengan N4 = ρN2
dan N5 =ρN3, sehingga diperoleh
Λn(x)−Λn−1(x)≤N4 dan
λn−1
λn−λn−1
≤N5
untuk setiap n∈N. Jadi, dengan menggunakan persamaan (4.3.1) diperoleh
|Sn(x)|=
λn−1
λn−λn−1
naik, maka untuk setiap n ∈N dan untuk suatu bilangan ρ >0 diperoleh
M
|Sn(x)|
ρ
≤M
N5 ·N4
ρ
.
Hal ini menunjukkan bahwa barisan
M
|Sn(x)|
ρ
terbatas. Dengan kata
lain, barisan S(x) = (Sn(x))∞n=0 ∈ ℓ∞(M). Karena untuk setiap barisan x ∈
[ℓ∞(M)]Λ berlaku S(x) ∈ ℓ∞(M), maka menurut Teorema 4.3.3 diperoleh
bahwa [ℓ∞(M)]Λ=ℓ∞(M).
Teorema 4.3.8. Diberikan ruang [c0(M)]Λ dan c(M) yang saling overlap,
dan ruang [c(M)]Λ dan ℓ∞(M) yang saling overlap. Diperoleh:
(a) Inklusi c(M)⊂[c0(M)]Λ tidak berlaku.
(b) Inklusi ℓ∞(M)⊂[c(M)]Λ tidak berlaku.
Bukti. (a) Dengan menggunakan Teorema 3.3.4 diperoleh bahwa ruang barisan
[c0(M)]Λ dan c(M) saling overlap. Selanjutnya, didefinisikan barisanx= (xk)
dengan aturan xk = 1 untuk setiap k ∈ N. Oleh karena itu, untuk suatu
bilangan ρ >0 diperoleh
lim
k→∞M
|xk|
ρ
= lim
k→∞M
1 ρ
=M
1 ρ
.
Hal ini menunjukkan bahwa barisan x= (xk)∈c(M). Di sisi lain, diperoleh
lim
n→∞M
|Λn(x)|
ρ
= lim
n→∞M
1 ρ
=M
1 ρ
6
= 0.
Jadi,x∈c(M) tetapix /∈[c0(M)]Λ. Akibatnya, relasi inklusic(M)⊂[c0(M)]Λ
tidak berlaku.
(b) Dengan menggunakan Teorema 4.3.2 dipeoroleh bahwac(M)⊂[c(M)]Λ.
Selanjutnya, apabila diambil sebarang x ∈ c(M), berarti terdapat bilangan
ρ > 0 dan l ∈ R sehingga M
|xk|
ρ
→ l untuk k → ∞. Karena barisan
M
|xk|
ρ
konvergen, maka
M
|xk|
ρ
terbatas. Jadi, x ∈ ℓ∞(M).
Oleh karena itu, c(M) ⊂ [c(M)]Λ ∩ ℓ∞(M). Hal ini menunjukkan bahwa
y= (yk) dengan aturan
yk = (−1)k
λk+λk−1
λk−λk−1
+ 1 untuk setiap k∈N.
Oleh karena itu, untuk setiap n∈N diperoleh
Λn(y) =
1 λn
n X
k=0
(λk−λk−1)
(−1)kλk+λk−1 λk−λk−1
+ 1
= 1 λn
n X
k=0
(−1)k(λ
k+λk−1) + (λk−λk−1)
= 1 λn
n X
k=0
(−1)k(λ
k+λk−1) +
1 λn
n X
k=0
(λk−λk−1)
= (−1)n+ 1.
Jadi, untuk suatu bilangan ρ >0 diperoleh
M
|Λn(y)|
ρ
=M
|(−1)n+ 1|
ρ
untuk setiap n∈N.
Hal ini menunjukkan bahwa barisan
M
|Λn(y)|
ρ
tidak konvergen untuk
setiap n ∈N. Dengan kata lain, barisany = (yk)∈[c(M)]Λ. Oleh karena itu,
inklusi ℓ∞(M)⊂[c(M)]Λ tidak berlaku.
Teorema 4.3.9. Diberikan lim inf
n→∞ M
λn+1
λn
=M(1). Diperoleh:
(a) Inklusi c(M)⊂[c0(M)]Λ dan [c0(M)]Λ ⊂c(M) tidak berlaku.
(b) Inklusi ℓ∞(M)⊂[c0(M)]Λ dan [c0(M)]Λ⊂ℓ∞(M) tidak berlaku.
(c) Inklusi ℓ∞(M)⊂[c(M)]Λ dan [c(M)]Λ ⊂ℓ∞(M) tidak berlaku.
Bukti. (a) Dengan menggunakan Teorema 4.3.8 (a) diperoleh bahwa inklusi
c(M)⊂[c0(M)]Λtidak berlaku. Selanjutnya, pada pembuktian Teorema 4.3.6,
diperoleh bahwa apabila diberikan barisan y = (yk) dengan yk didefinisikan
oleh persamaan (4.3.3), dan dipilih kr+1−kr ≥ 2 untuk setiap r ∈ N, maka
barisan y ∈ [c0(M)]Λ namun y /∈ c(M). Jadi, inklusi [c0(M)]Λ ⊂ c(M) tidak
berlaku.
(b) Dengan menggunakan Teorema 4.3.8 (b) diperoleh bahwa terdapat
barisan x = (xk) yang berada di ℓ∞(M), tetapi barisan
M
|Λn(x)|
ρ
nol. Jadi, dapat diperoleh bahwa inklusiℓ∞(M)⊂[c0(M)]Λtidak berlaku.
Se-lanjutnya, karena karena lim inf
k→∞ M
λk+1
λk
=M(1), maka telah diperlihatkan
pada pembuktian Teorema 4.3.6 bahwa terdapat barisan bagian (λkr)
∞
r=0 dari
barisan λ= (λk) sehingga diperoleh
lim
Hal ini menunjukkan bahwa barisan
konvergen ke nol.
Akibatnya, barisan
terbatas. Artinya, terdapat suatu
bilangan N >0 sehingga untuk setiapr ∈Ndiperoleh
M
Selanjutnya, karena generalisasi fungsi OrliczM bersifat naik, maka diperoleh λkr −λkr−1
λkr
≤ N0 untuk setiap r ∈ N dan untuk suatu bilangan N0 > 0.
Oleh karena itu, diperoleh N1 =
1
0 ; untuk yang lainnya.
untuk setiap k ∈ N. Karena 0 < N1 ≤
λkr λkr −λkr−1
untuk setiap r ∈ N dan
untuk suatu bilangan N1 >0, maka diperoleh
0<(N1)α≤
λkr λkr −λkr−1
α
untuk 0 < α < 1. Karena generalisasi fungsi Orlicz M bersifat naik, maka untuk suatu bilangan ρ >0 diperoleh
untuk setiap n∈N diperoleh
n X
k=0
(λk−λk−1)xk =
(λn−λn−1)
λn
λn−λn−1 α
; untukn =kr,
0 ; untuk yang lainnya.
Oleh karena itu, untuk setiap n∈N diperoleh
Λn(x) =
λn−λn−1
λn
1−α
; untuk n=kr,
0 ; untuk yang lainnya.
Kemudian, karena generalisasi fungsi Orlicz M bersifat kontinu, maka dari persamaan (4.3.2) diperoleh lim
r→∞
λkr −λkr−1 λkr
= 0. Jadi, untuk n = kr dan
0< α <1, diperoleh
lim
n→∞
λn−λn−1
λn
1−α
= lim
n→∞
λn−λn−1
λn
λn−λn−1
λn
−α
= lim
n→∞
λn−λn−1
λn
lim
n→∞
λn−λn−1
λn
−α
= 0.
Karena generalisasi fungsi Orlicz M kontinu, maka untuk suatu ρ >0,
diper-oleh M
|Λn(x)|
ρ
→ 0. Hal ini menunjukkan bahwa barisan x ∈ [c0(M)]Λ.
Karena x ∈ [c0(M)]Λ\ℓ∞(M), maka dapat disimpulkan bahwa relasi inklusi
[c0(M)]Λ ⊂ ℓ∞(M) tidak berlaku. Oleh karena itu, ℓ∞(M) ⊂ [c0(M)]Λ dan
[c0(M)]Λ ⊂ℓ∞(M) masing-masing tidak berlaku.
(c) Dengan menggunakan Teorema 4.3.8 (b), diperolehℓ∞(M)⊂[c(M)]Λ
tidak berlaku. Selanjutnya, telah diperlihatkan pada pembuktian Teorema 4.3.9 (b) bahwa terdapat barisan x = (xk) yang berada di [c0(M)]Λ tetapi
tidak berada di ℓ∞(M). Karena x∈[c0(M)]Λ, maka Teorema 4.3.1 menjamin
bahwa x ∈ [c(M)]Λ. Jadi, x ∈ [c(M)]Λ\ℓ∞(M). Dengan kata lain, inklusi
[c(M)]Λ ⊂ ℓ∞(M) tidak berlaku. Oleh karena itu, inklusi ℓ∞(M) ⊂ [c(M)]Λ
dan [c(M)]Λ ⊂ℓ∞(M) tidak berlaku.
4.4. Transformasi Matriks Pada Ruang Barisan Konvergen dan Ter-batas yang Dibangun Oleh Generalisasi Fungsi Orlicz
Trans-x7→Ax= (An(x))∞n=0; yaitu
Koleksi semua transformasi matriks tak hingga dariX keY ditulis dengan no-tasi (X, Y). Oleh karena itu, teori transformasi matriks erat kaitannya dengan karakteristik di (X, Y). Dengan kata lain, A∈(X, Y) jika dan hanya jika
Pada subbab ini, akan diperlihatkan beberapa karakteristik kelas transfor-masi matriks pada ruang barisan konvergen dan terbatas yang dibangun oleh generalisasi fungsi Orlicz.
4.4.1. Transformasi Matriks Pada Ruang Barisan Konvergen yang Dibangun Oleh Generalisasi Fungsi Orlicz
Pada bagian ini, akan diperlihatkan beberapa karakteristik (X, Y), untuk X dan Y merupakan ruang barisan konvergen yang dibangun oleh generalisasi fungsi Orlicz.
Bukti. Pertama-tama diasumsikan A ∈(c(M), c(M)). Berarti, An(x)
konver-Selanjutnya, didefinisikan barisan x= (xk) dengan aturan
xk =sgn(ank) =
untuk setiap k ∈ N dan untuk setiap n ∈ N. Oleh karena itu, untuk suatu bilangan ρ >0 diperoleh
sup
Jadi, syarat perlu (i) terpenuhi.
Selanjutnya, dipilih barisan x= (xj) dengan aturan
xj =e
sebarang x ∈ c(M), berarti terdapat ρ > 0 sehingga lim
n→∞M
ada. Oleh karena itu, diperoleh
untuk setiap k ∈ N. Jadi, lim
n→∞M
|ank|
ρ
ada untuk setiap k ∈ N. Hal ini
menunjukkan bahwa syarat perlu (ii) terpenuhi.
Selanjutnya, dipilih barisan x = (xk) dengan aturan xk = 1 untuk setiap
k ∈ N. Oleh karena itu, untuk suatu bilangan ρ > 0 dan untuk setiap k ∈ N, terdapat
lim
n→∞M
|P∞
k=0ankxk|
ρ
= lim
n→∞M
|P∞ k=0ank|
ρ
untuk setiap k∈N. Hal ini menunjukkan bahwa syarat perlu (iii) terpenuhi. Sebaliknya, diasumsikan syarat (i), (ii), dan (iii) berlaku. Akan ditun-jukkan A ∈(c(M), c(M)). Untuk itu, diambil sebarang x ∈c(M) dan n ∈ N. Karena x∈c(M), berarti terdapat suatu bilangan ρ >0 dan r0 ∈R sehingga
M
|xk|
ρ
→ r0 untuk k → ∞. Selanjutnya, karena generalisasi fungsi
Or-licz M naik pada interval [0,∞), bersifat konveks, dan memenuhi kondisi-∆2,
maka diperoleh
M
|P∞
k=0ankxk|
ρ
=M
|P∞
k=0ank(xk−r) + P∞
k=0ankr|
ρ
≤M
|P∞
k=0ank(xk−r)|+|r P∞
k=0ank|
ρ
≤ 1
2M
2|P∞
k=0ank(xk−r)|
ρ
+1 2M
2r|P∞ k=0ank|
ρ
≤ K0
2 M
|P∞
k=0ank(xk−r)|
ρ
+ 1 2M
2m0+1|P∞
k=0ank|
ρ
≤ K0
2 M
|P∞
k=0ank(xk−r)|
ρ
+ K
m0+1
1
2 M
|P∞ k=0ank|
ρ
dalam bentuk lain, yaitu
untuk setiap n ∈ N dan untuk suatu bilangan real positif r. Karena syarat (iii) terpenuhi, maka diperoleh
lim
Selanjutnya, karena generalisasi fungsi Orlicz M kontinu, maka |xk|
ρ → r1
untuk k → ∞ dengan r1 = M−1(r0). Dengan kata lain, |xk| → r untuk
r = ρr1. Kemudian, apabila xk ≥ 0 untuk setiap k ∈ N, maka |xk| = xk.
Oleh karena itu, xk →r untuk k → ∞. Apabila xk <0 untuk setiap k ∈ N,
maka |xk| = −xk. Oleh karena itu, −xk → r untuk k → ∞. Dengan kata
lain, xk+r →0 untukk → ∞. Selanjutnya, karena generalisasi fungsi Orlicz
M bersifat kontinu, maka diperoleh lim
A∈(c(M), c(M)).
Teorema 4.4.2. A ∈(c0(M), c0(M)) jika dan hanya jika
(i) sup
n∈N
M
P∞ k=0|ank|
ρ
<∞,
(ii) lim
n→∞M
|ank|
ρ
= 0 untuk setiap k∈N.
Bukti. Diasumsikan A ∈ (c0(M), c0(M)). Berarti, An(x) konvergen untuk
setiap n ∈ N dan setiap x ∈ c0(M), dan barisan Ax = (An(x))∞n=0 ∈ c0(M).
Selanjutnya, didefinisikan barisan x= (xk) dengan aturan
xk=e [n] k =
(
1 ; untuk k=n 0 ; untuk k6=n
untuk setiap k∈N. Oleh karena itu, untuk suatu bilangan ρ >0 diperoleh
M
|P∞
k=0ankxk|
ρ
=M
P∞
k=0anke[n]k
ρ
=M
|ank|
ρ
untuk setiap n ∈ N. Karena barisan Ax = (An(x))∞n=0 ∈ c0(M), maka untuk
setiap k ∈Ndiperoleh
lim
n→∞M
|ank|
ρ
= lim
n→∞M
|P∞
k=0ankxk|
ρ
= 0.
Hal ini menunjukkan bahwa syarat perlu (ii) dipenuhi. Selanjutnya, didefi-nisikan barisan x= (xk) dengan aturan
xk =sgn(ank) =
1 ; untuk ank >0
0 ; untuk ank = 0
−1 ; untuk ank <0
untuk setiap k∈N. Oleh karena itu, untuk suatu bilangan ρ >0 diperoleh
sup
n∈N
M
P∞ k=0|ank|
ρ
= sup
n∈N
M
|P∞
k=0|ank||
ρ
= sup
n∈N
M
|P∞
k=0ankxk|
ρ