THE MINIMUM SPECTRAL RADIUS OF GRAPHS WITH A GIVEN
CLIQUE NUMBER∗
DRAGAN STEVANOVI ´C† AND PIERRE HANSEN‡
Abstract. In this paper, it is shown that among connected graphs with maximum clique sizeω,
the minimum value of the spectral radius of adjacency matrix is attained for a kite graphP Kn−ω,ω,
which consists of a complete graph Kω to a vertex of which a pathPn−ω is attached. For any fixedω, a small interval to which the spectral radii of kitesP Km,ω,m≥1, belong is exhibited.
Key words. Adjacency matrix, Largest eigenvalue, Spectral radius, Clique number, Kite graph.
AMS subject classifications. 05C35, 05C50, 05C69.
1. Introduction. All graphs in this note are simple and undirected. For a graphG, letA(G) denote its adjacency matrix,ρ(G) the spectral radius ofA(G), and PG≡PG(λ) the characteristic polynomial ofA(G). For other undefined notions, the
reader is referred to [2].
Brualdi and Solheid [3] proposed the following general problem, which became one of the classic problems of spectral graph theory:
Given a set G of graphs, find an upper bound for the spectral radius in this set and characterize the graphs in which the maximal spectral radius is attained.
Such extremal graphs, for example, asymptotically have more closed walks of any given length than the other graphs in the set. However, let us point out that it may be of (practical) interest to characterize the graphs having the minimum spectral radius as well: Wang et al. [15] recently proposed a new analytic model that accurately models the propagation of computer viruses on arbitrary network graph G, which, under reasonable approximations, has an epidemic threshold of 1/ρ(G), below which the number of infected nodes in the network decays exponentially. Thus, the computer networks with smaller spectral radii are more resistant to virus propagation.
∗Received by the editors July 9, 2007. Accepted for publication February 1, 2008.Handling Editor: Richard A. Brualdi.
†FAMNIT, University of Primorska, Koper, Slovenia, and PMF, University of Niˇs, Niˇs, Ser-bia ([email protected]). Supported partially by the research grant 144015G of the SerSer-bian Ministry of Science and Environmental Protection, the research program P1-0285 of the Slovenian Agency for Research and the HEC Data Mining Chair.
As expected, there are far less results on the minimum spectral radius than on the maximum spectral radius of graphs: some recent results are given in [1, 8], while the older results are presented in Section 3 of [6].
We study here the setGn,ω, n ≥ω ≥ 2, of connected graphs of ordern with a
maximum clique sizeω. Recently, Nikiforov [12] showed that the Tur´an graphs attain the maximum spectral radius in Gn,ω. Experimenting with the computer system
AutoGraphiX[4], which is well suited to find extremal graphs and support conjecture making, we observed that kite graphs attain the minimum spectral radius in Gn,ω.
Recall that the kite graph P Km,w is a graph on m+w vertices obtained from the
pathPmand the complete graphKwby adding an edge between an end vertex ofPm
and a vertex ofKw. This observation turned out to be correct. Specifically,
Theorem 1.1. If G∈ Gn,ω,n≥ω≥2, then
ρ(G)≥ρ(P Kn−ω,ω).
The equality holds if and only if Gis isomorphic toP Kn−ω,ω.
We are also interested to find a good estimate ofρ(P Km,ω). It is obvious that
ρ(P K0,ω) =ρ(Kω) =ω−1.
However, the other values ofρ(P Km,ω) are not that straightforward to obtain. For any
m≥0,P Km,ωis a proper subgraph ofP Km+1,ω, so the sequence ¡
ρ(P Km,ω) ¢
m≥0is
strictly increasing. Further, withρ(P Km,ω) being bounded from above by ω (recall
that the spectral radius is at most the maximum vertex degree, see, e.g., [5, p. 85]), we see that limm→∞ρ(P Km,ω) exists with a value betweenω−1 andω. Thus, the
valuesρ(P K1,ω) and limm→∞ρ(P Km,ω) represent the sharp lower and upper bound
onρ(P Km,∞),m≥1. These values turn out to be very close to each other.
Theorem 1.2. For any integersω≥3 andm≥1,
ω−1 + 1 ω2 +
1
ω3 < ρ(P Km,ω)< ω−1 +
1 4ω +
1 ω2−2ω.
The proofs of these theorems are given in the next two sections.
2. Proof of Theorem 1.1. We will use the following auxiliary results in the proof. The first lemma is by Li and Feng from [9], and is also found as Theorem 6.2.2 in [6].
Lemma 2.1. Let uandv be two adjacent vertices of the connected graphG and
pendent paths of length k at u and length l at v. If k ≥ l ≥ 1, then ρ(G(k, l)) > ρ(G(k+ 1, l−1)).
The next lemma is by Zhang, Zhang and Zhang [16], and is also found as Theo-rem 6.2.3 of [6]. LetSvwT denote the graph obtained from disjoint graphsS, T by adding an edge joining the vertexv ofSto the vertexwofT. Further, letSv denote
the graph obtained fromS by adding a pendent edge at vertexv.
Lemma 2.2. If PSu(λ)< PSv(λ) for all λ > ρ(Su), then ρ(SvwT)< ρ(SuwT)
for any vertex wof T.
Remark 2.3. Note that the formulation of previous lemma in [6] contains a typo:
instead ofx > µ1(Hv)it should contain the conditionx > µ1(Hu).
We may prove the following lemma on the basis of the previous two.
Lemma 2.4. Let vw be a bridge of a connected graph G and suppose that there
is a path of length k, k≥1, attached at v, withu being the other end vertex of this path. Then
ρ(G−vw+uw)≤ρ(G),
with equality if and only if the vertexv has degree two.
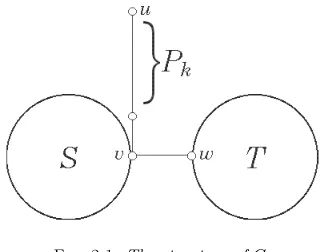
[image:3.612.175.337.465.591.2]Proof of Lemma 2.4. LetSandT be the subgraphs ofGas indicated in Figure 2.1. Ifv has degree two, thenG−vw+uw∼=Gand the statement follows.
Fig. 2.1.The structure ofG.
Suppose now that the degree of v is at least three, i.e., that S is a non-trivial graph. Let S′ denote the subgraph formed by S and the path fromv to u. In the
terms of Lemmas 2.1 and 2.2, we have that
S′
u=S(k+ 1,0), S ′
v =S(k,1).
Thus, from Lemma 2.2 it follows that
ρ(G−vw+uw) =ρ(S′uwT)< ρ(S′vwT) =ρ(G).
Proof of Theorem 1.1. Suppose thatnandω, n≥ω≥2, are given.
If n= ω, then Gn,ω consists of a single graphKn, which is also a (degenerate)
kite graphP K0,n.
Ifω= 2, then the pathPn has the minimum spectral radius among all connected
graphs of order n[5, p. 78], and thus also in Gn,2. Note that the pathPn is also a
(degenerate) kite graphP Kn,0=P Kn−1,1=P Kn−2,2.
Thus, suppose thatn > ω ≥3. We will transform an arbitrary graphG∈ Gn,ω,
containing a cliqueK of sizeω, into a kite graph P Kn−ω,ω, in such a way that the
spectral radius of transformed graph decreases at each step.
i) It is known that deletion of an edge from a connected graph strictly decreases its spectral radius [5]. In order to keep a graph withinGn,ω, we may delete from G
any edge not inK which belongs to a cycle. LetG1be a subgraph of Gobtained by
deleting such edges in an arbitrary order as long as they exist. G1 will then consist
of a cliqueK with a number of rooted trees attached to clique vertices.
ii) At this step, we will “flatten out” the trees attached to clique vertices. Let T be a rooted tree ofG1, attached to a clique vertex. Letube the leaf ofT farthest
from the cliqueK, and letvbe the vertex ofT of degree at least three, that is closest tou. IfT is not a path, then there is a neighborwofvinT, which is not on the path fromv to u. Then in the tree T−vw+uw the distance from the farthest leaf to K increases, while from Lemma 2.4 its spectral radius decreases. Processing further with edge deletions and additions by always choosing farthest leaves in rooted trees, we decrease the spectral radius at each iteration until we reach a graphG2in which
every rooted tree, attached to a vertex ofK, becomes a path.
iii) We may suppose that the graph G2 consists of clique K and the paths
Pk1, Pk2, . . . , Pkm attached to m distinct vertices of K. With the repeated use of
Lemma 2.1 to paths Pk1 and Pki, 2 ≤i ≤m, we may decrease the spectral radius
ofG2 until the attached paths Pk2, . . . ,Pkm disappear, and we finally arrive to the
kite graphP Kn−ω,ω.
Since we have (strictly) decreased the spectral radius at each step, we may con-clude that the kite graphP Kn−ω,ω has smaller spectral radius than any other graph
3. Proof of Theorem 1.2. To prove this theorem, we estimate the values of ρ(P K1,ω) and limm→∞ρ(P Km,ω) in the next two subsections.
3.1. Estimatingρ(P K1,ω). Letxbe a principal eigenvector ofP K1,ω, letube
a leaf ofP K1,ωand letvbe the neighbor ofu. All other vertices ofP K1,ωare similar,
and sinceρ(P K1,ω) is a simple eigenvalue, we have thatxhas the same value, name
ity, at these vertices. Now the eigenvalue equation atu,vand arbitrary other vertex ofP K1,ω reads (where we write justρforρ(P K1,m)):
ρxu=xv,
ρxv=xu+ (ω−1)y,
ρy= (ω−2)y+xv.
These equations, taken together, imply that
ρ3−(ω−2)ρ2−ωρ+ (ω−2) = 0.
Introducing the variable changeρ=ω−1 +σ, the above cubic equation transforms into
σ3+ (2ω−1)σ2+ (ω2−ω−1)σ−1 = 0.
While solving this cubic equation explicitly is possible, the obtained solution is cum-bersome and sports at least the square root of a sixth degree polynomial inω (which itself is not a square). However, if we denote
f(σ) =σ3+ (2ω
−1)σ2+ (ω2
−ω−1)σ−1,
we can see that, forω≥3,
f
µ 1
ω2 µ
1 + 1 ω
¶¶
= 1 ω6
µ
1 + 1 ω
¶3
+ (2ω−1) 1 ω4
µ
1 + 1 ω
¶2
+ (ω2
−ω−1) 1 ω2
µ
1 + 1 ω
¶ −1
=− 2 ω2 +
1 ω3 + Θ
µ 1 ω4 ¶ <0, while f µ 1 ω2 µ
1 + 2 ω
¶¶
= 1 ω6
µ
1 + 2 ω
¶3
+ (2ω−1) 1 ω4
µ
1 + 2 ω
¶2
+ (ω2−ω−1) 1 ω2
µ
1 + 2 ω ¶ −1 = 1 ω − 3 ω2 + Θ
µ 1
ω4 ¶
Thus, a root off(σ) belongs to the interval ω2(1 + ω),ω2(1 + ω) of length ω3, and
we conclude that, form≥1,
ρ(P Km,ω)≥ρ(P K1,ω)> ω−1 +
1 ω2
µ
1 + 1 ω
¶
is a simple, yet rather good lower bound.
3.2. Estimatinglimm→∞ρ(P Km,ω). LetP K∞,ωdenote theinfinitekite graph
which consists of a cliqueKω, to one vertex of which an infinite path is attached. A
textbook introduction to infinite graphs may be found in Chapter 8 of [7], while the more specific results on the spectra of infinite graphs appear in [10, 11].
In particular, for an infinite graph G with bounded vertex degrees, let ρ(G) denote the spectral radius of the adjacency matrix ofG. We say that a sequence of subgraphsGn converges toG, if each edge ofGis contained in all but finitely many
of theGn. From Theorem 4.13 of [11] we have that the sequenceρ(Gn) converges to
ρ(G) from below. In particular,
ρ(P K∞,ω) = lim
m→∞ρ(P Km,ω).
We are set to determine the value ofρ(P K∞,ω) by finding a valueµand a positive
vectorxsuch that
A(P K∞,ω)x=µx
(3.1)
holds. In general, we may not say thatµis an eigenvalue ofP K∞,ωas it may happen
that the vectorxdoes not belong to the space on whichA(P K∞,ω) acts as a linear
operator. Nevertheless, the equality µ = ρ(P K∞,ω) is ensured from Theorem 6.2
of [11] (see [13, 14] for further details), which states that, for realµ and an infinite, connected and locally finite graphG, the inequalityA(G)x≤µxhas a nonnegative solution x6= 0 if and only ifµ≥ρ(G), and if the equalityA(G)x=µxholds, then µ=ρ(G). Moreover, the vectorxis unique in such case (up to constant multiples). The rest of this subsection is devoted to finding a pair (µ, x) which satisfies (3.1).
Let us denote the common component ofxat the clique vertices byx−1, the
com-ponent at a clique vertex to which the path is attached byx0, and the components at
path vertices byx1,x2,x3, . . . , respectively. The equation (3.1) yields the following:
µx−1= (ω−2)x−1+x0
(3.2)
µx0= (ω−1)x−1+x1
(3.3)
µxi=xi−1+xi+1, i≥1.
The equation (3.4) represents a familiar linear recurrence equation. Forµ = 2, the positivity ofxi implies thatω= 2 and, in such case, the solution is given by
xi=i+ 2, i≥ −1.
Forµ >2, (3.4) has the solution in the form
xi=ati1+bt i
2, i≥0,
whereaandbare constants, and
t1=
µ−pµ2−4
2 , t2=
µ+pµ2−4
2
are the distinct solutions of the characteristic equationµt= 1 +t2.
Whenω≥3, the components of the positive unit eigenvector of any finiteP Km,ω
decrease along the path from the clique towards its leaf. Besides the fact that ρ(P K∞,ω) = limm→∞ρ(P Km,ω) and as we would also like xto be a limit of these
eigenvectors, we may impose additional condition that limi→∞xi= 0. This translates
intob= 0 and, with appropriate scaling, we may suppose that
x0= 1, x1=t1.
The equations (3.2, 3.3) then lead to
1 µ−ω+ 2 =
µ−t1
ω−1.
After replacing the value oft1and simplifying yields the quadratic equation
µ2−(ω−3)µ− µ
2ω−2 + 1 ω−2
¶
= 0,
whose positive solution is
µ= ω−3 +
q
(ω+ 1)2+ 4 ω−2
2 .
It is straightforward to see thatµandxsatisfy (3.1), and therefore, for every finitem, it follows that
ρ(P Km,ω)< ρ(P K∞,ω) =
ω−3 +q(ω+ 1)2+ 4 ω−2
2 .
Finally, from the simple inequality√1 +x≤1 + x
2, we get
ρ(P K∞,ω) =
ω 2
Ã
1− 3 ω +
s
1 + 2 ω +
1 ω2+
4 ω2(ω−2)
!
≤ω−1 + 1 4ω +
1 ω2
REFERENCES
[1] F. Belardo, E.M. Li Marzi and S. Simi´c. Some results on the index of unicyclic graphs.Linear Algebra Appl., 416:1048–1059, 2006.
[2] J.A. Bondy and U.S.R. Murty.Graph Theory with Applications. Macmillan Press, New York, 1976.
[3] R.A. Brualdi and E.S. Solheid. On the spectral radius of complementary acyclic matrices of zeros and ones.SIAM J. Algebra. Discrete Method7:265–272, 1986.
[4] G. Caporossi and P. Hansen. Variable Neighborhood Search for Extremal Graphs, I. The AutoGraphiX System.Discrete Math., 212:29–44, 2000.
[5] D. Cvetkovi´c, M. Doob and H. Sachs.Spectra of Graphs—Theory and Application. 3rd edition, Johann Ambrosius Barth Verlag, 1995.
[6] D. Cvetkovi´c, P. Rowlinson and S. Simi´c.Eigenspaces of Graphs. Encyclopedia of Mathematics and Its Applications, Vol.66, Cambridge University Press, Cambridge, 1997.
[7] R. Diestel. Graph Theory. Third edition, Graduate Texts in Mathematics, Vol. 173, Springer-Verlag, Heidelberg-New York, 2005.
[8] E. van Dam and R. Kooij. The minimal spectral radius of graphs with a given diameter.Linear Algebra Appl., 423:408–419, 2007.
[9] Q. Li and K. Feng. On the largest eigenvalue of a graph.Acta Math. Appl. Sinica, 2:167–175, 1979 (in Chinese).
[10] B. Mohar. The Spectrum of an Infinite Graph. Linear Algebra Appl., 48:245–256, 1982. [11] B. Mohar and W. Woess. A Survey on Spectra of Infinite Graphs. Bull. London Math. Soc,
21:209–234, 1989.
[12] V. Nikiforov. Bounds on Graph Eigenvalues, II. Preprint. Available at http://arxiv.org/pdf/math/0612461.
[13] W.E. Pruitt. Eigenvalues of Non-negative Matrices. Ann. Math. Statist., 35:1797–1800, 1964. [14] D. Vere-Jones. Ergodic Properties of Non-negative Matrices I. Pacific J. Math., 22:361–386,
1967.
[15] Y. Wang, D. Chakrabarti, C. Wang, and C. Faloutsos. Epidemic spreading in real networks: an eigenvalue viewpoint. in 22nd Symposium in Reliable Distributed Computing, Florence, Italy, October 6–8, 2003.