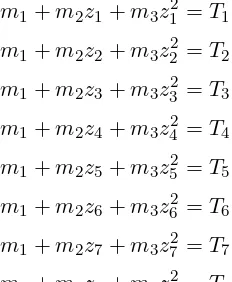Komputasi untuk Sains dan Teknik
-Dalam
Matlab-Supriyanto Suparno
( Website: http://supriyanto.fisika.ui.edu )
( Email: supri@fisika.ui.ac.id atau supri92@gmail.com )
Edisi III
Revisi terakhir tgl: 25 Agustus 2008
Kata Pengantar
Alhamdulillah, buku ini memasuki edisi ke-3. Penomoran edisi ini sebenarnya hanya untuk menandakan perubahan isi buku yang semakin kaya metode numerik dibandingkan dengan edisi-edisi sebelumnya. Pengayaan isi buku ini, sejujurnya, berasal dari sejumlah pertanyaan yang sampai ke mailbox saya, entah itu dalam bentuk konsultasi Tugas Akhir mahasiswa S1 sebagaimana yang penulis terima dari mahasiswa UNPAD, UDAYANA, UNESA dan UNSRI serta UI sendiri, ataupun sekedar pertanyaan seputar pekerjaan rumah seperti yang biasa di-tanyakan oleh para mahasiswa dari Univ. Pakuan, Bogor.
Pertanyaan-pertanyaan itu menjadikan saya sadar bahwa buku edisi ke-II yang berjumlah 187 halaman, ternyata belum bisa memenuhi kebutuhan banyak mahasiswa yang memerlukan teknik pengolahan data secara numerik. Karenanya,insya Allah, pada edisi ke-III ini, saya akan menyajikan sebagian besar yang masih kurang lengkap itu secara bertahap.
Ibarat pohon yang akan terus tumbuh semakin besar, buku ini pun memiliki tabiat per-tumbuhan sebagaimana pohon itu. Mulai ditulis pada tahun 2005 dengan isi yang seadanya, pokoknya asal tercatat. Kemudian di tahun 2006akhir menjadi catatan perkuliahan Komputasi Fisika. Pengayaan isi terus berlangsung hingga akhir 2007. Lalu di awal tahun 2008 diisi den-gan tambahan materi perkuliahan Analisis Numerik. Itulah yang saya maksud denden-gan tabiat pertumbuhan dari buku ini. Jika saya ditugaskan untuk mengajar mata kuliah Komputasi Fisika lagi pada awal September 2008, saya bertekad akan menurunkan seluruh isi buku ini kepada mahasiswa yang akan mengambil kuliah tersebut. Jadi materi Komputasi Fisika tahun 2007 dan materi Analisis Numerik 2008, digabung jadi satu kedalam satu semester dengan na-ma na-mata kuliah Komputasi Fisika. Kepada rekan-rekan na-mahasiswa yang akan ngambilmata kuliah tersebut, saya sampaikan permohonan maaf jika rencana ini akan membuat anda ku-rang tidur karenabakal semakin lama berada di depan komputer, menyelesaikan tugas dan
report.
Secara garis besar, ilmu fisika dapat dipelajari lewat 3 jalan, yaitu pertama, dengan meng-gunakan konsep atau teori fisika yang akhirnya melahirkan fisika teori. Kedua, dengan cara eksperimen yang menghasilkan aliran fisika eksperimental, dan ketiga, fisika bisa dipelajari lewat simulasi fenomena alam yang sangat mengandalkan komputer serta algoritma numerik. Tujuan penyusunan buku ini adalah untuk meletakkan pondasi dasar dari bangunan pema-haman akan metode-metode komputasi yang banyak digunakan untuk mensimulasikan fenom-ena fisika.
Rujukan utama buku ini bersumber pada buku teks standar yang sangat populer di dunia komputasi, yaitu buku yang ditulis oleh Richard L. Burden dan J. Douglas Faires dengan judul
Numerical Analysisedisi ke-7, diterbitkan oleh Penerbit Brooks/Cole, Thomson Learning Aca-demic Resource Center. Disamping itu, buku ini dilengkapi oleh sejumlah contoh aplikasi komputasi pada upaya penyelesaian problem-problem fisika.
Pada edisi ke-3 ini saya mulai mencoba membiasakan diri menulisscriptdalam lingkungan
PythondanOctave. Padahal, dalam edisi ke-2 yang lalu, scriptnumerik disalin ke dalam 2 bahasa pemrograman, yaituFortran77danMatlab. Namun mayoritas ditulis dalam Matlab. Saya ingin ganti kePython, lantaran dengan Python ataupunOctave, saya dan juga maha-siswa saya tidak perlu menginstalMatlabbajakan ke dalam komputer kami masing-masing.
Buku yang sedang anda baca ini masih jauh dari sempurna. Keterkaitan antar Bab berikut isi-nya masih perlu perbaikan. Kondisi ini berpotensi membuat anda bingung, atau setidaknya menjadi kurang fokus. Oleh karena itu saya menghimbau kepada pembaca untuk menfokuskan diri melalui penjelasan singkat berikut ini:
• Bab 1 berisi pengenalan matrik, operasi matrik, inisialisasi matrik pada Matlab dan For-tran. Saran saya, setiap pembaca yang masih pemula di dunia pemrograman, harus menguasai Bab I terlebih dahulu. Disamping itu penjelasan lebih terperinci tentang bagaimana menentukan indeksi,jdankdalam prosesloopingdisajikan pada Bab I, un-tuk memberi pondasi yang kokoh bagi berdirinya bangunan pemahaman akan teknik-teknik numerik selanjutnya.
• Untuk mempelajari metode Finite-Difference, dianjurkan mulai dari Bab 1, Bab 2, Bab 4, Bab 7, dan Bab 8.
• Untuk mempelajari dasar-dasar inversi, dianjurkan mulai dari Bab 1, Bab 2, dan Bab 3.
Akhirnya saya ingin mengucapkan rasa terima kasih yang tak terhingga kepada Dede Djuhana yang telah berkenan memberikan format LATEX-nya sehingga tampilan tulisan pada
buku ini benar-benar layaknya sebuah buku yang siap dicetak. Tak lupa, saya pun sepatutnya berterima kasih kepada seluruh rekan diskusi yaitu para mahasiswa yang telah mengambil mata kuliah Komputasi Fisika PTA 2006/2007 di Departemen Fisika, FMIPA, Universitas In-donesia. Kepada seluruh mahasiswa dari berbagai universitas di Timur dan di Barat Indonesia juga perlu saya tulis disini sebagai ungkapan terima kasih atas pertanyaan-pertanyaan mereka yang turut memperkaya isi buku ini.
Walaupun buku ini masih jauh dari sempurna, namun semoga ia dapat menyumbangkan kontribusi yang berarti bagi terciptanya gelombang kebangkitan ilmu pengetahuan pada diri anak bangsa Indonesia yang saat ini sedang terpuruk. Saya wariskan ilmu ini untuk siswa dan mahasiswa Indonesia dimanapun mereka berada. Kalian berhak memanfaatkan buku ini. Saya izinkan kalian untuk meng-copydan menggunakan buku ini selama itu ditujukan untuk belajar dan bukan untuk tujuan komersial, kecuali kalau saya dapat bagian komisi-nya :) . Bagi yang ingin berdiskusi, memberikan masukan, kritikan dan saran, silakan dikirimkan ke email:
supri92@gmail.com
Daftar Isi
Lembar Persembahan i
Kata Pengantar iii
Daftar Isi iv
Daftar Gambar vii
Daftar Tabel x
1 Matrik dan Komputasi 1
1.1 Pengenalan matrik . . . 1
1.2 Inisialisasi matrik dalam memori komputer . . . 2
1.3 Macam-macam matrik . . . 3
1.3.1 Matrik transpose . . . 3
1.3.2 Matrik bujursangkar . . . 3
1.3.3 Matrik simetrik . . . 3
1.3.4 Matrik diagonal . . . 4
1.3.5 Matrik identitas . . . 4
1.3.6 Matrik upper-triangular . . . 4
1.3.7 Matrik lower-triangular . . . 4
1.3.8 Matrik tridiagonal . . . 5
1.3.9 Matrik diagonal dominan . . . 5
1.3.10 Matrikpositive-definite . . . 5
1.3.11 Vektor-baris dan vektor-kolom . . . 6
1.4 Operasi matematika . . . 7
1.4.1 Penjumlahan matrik . . . 7
1.4.2 Komputasi penjumlahan matrik . . . 8
1.4.3 Perkalian matrik . . . 10
1.4.4 Komputasi perkalian matrik . . . 12
1.4.5 Perkalian matrik dan vektor-kolom . . . 14
1.4.6 Komputasi perkalian matrik dan vektor-kolom . . . 15
1.5 Penutup . . . 16
1.6 Latihan . . . 16
2 Metode Eliminasi Gauss 17 2.1 Sistem persamaan linear . . . 17
2.2 Triangularisasi dan Substitusi Mundur . . . 18
2.3 Matrik dan Eliminasi Gauss . . . 21
2.4 Algoritma eliminasi Gauss . . . 23
2.4.1 Algoritma . . . 25
2.5 Contoh aplikasi . . . 29
2.5.1 Menghitung arus listrik . . . 29
2.6 Menghitung invers matrik . . . 31
2.7 Penutup . . . 37
3 Aplikasi Eliminasi Gauss pada Masalah Inversi 39 3.1 Inversi Model Garis . . . 39
3.1.1 Script matlab inversi model garis . . . 42
3.2 Inversi Model Parabola . . . 45
3.2.1 Script matlab inversi model parabola . . . 48
3.3 Inversi Model Bidang . . . 51
3.4 Contoh aplikasi . . . 53
3.4.1 Menghitung gravitasi di planet X . . . 53
4 MetodeLU Decomposition 61 4.1 Faktorisasi matrik . . . 61
4.2 Algoritma . . . 65
5 Metode Iterasi 71 5.1 Kelebihan Vektor-kolom . . . 71
5.2 Pengertian Norm . . . 72
5.2.1 Scriptperhitungan norm dalam Matlab . . . 72
5.2.2 Perhitungan norm-selisih . . . 73
5.3 Iterasi Jacobi . . . 73
5.3.1 ScriptMatlab metode iterasi Jacobi . . . 76
5.3.2 OptimasiscriptMatlab untuk menghitung iterasi . . . 79
5.3.3 Algoritma . . . 81
5.3.4 Program dalam Fortran . . . 82
5.4 Iterasi Gauss-Seidel . . . 83
5.4.1 Scriptiterasi Gauss-Seidel . . . 84
5.4.2 Algoritma . . . 85
5.4.3 Scriptiterasi Gauss-Seidel dalam Fortran . . . 86
5.5 Iterasi dengan Relaksasi . . . 87
5.5.1 Algoritma Iterasi Relaksasi . . . 89
6 Interpolasi 91 6.1 Interpolasi Lagrange . . . 91
vii
7 Diferensial Numerik 101
7.1 Metode Euler . . . 101
7.2 Metode Runge Kutta . . . 107
7.2.1 Aplikasi: Pengisian muatan pada kapasitor . . . 110
7.3 MetodeFinite Difference. . . 115
7.3.1 ScriptFinite-Difference . . . 118
7.3.2 Aplikasi . . . 123
7.4 Persamaan Diferensial Parsial . . . 124
7.5 PDP eliptik . . . 125
7.5.1 Contoh pertama . . . 127
7.5.2 ScriptMatlab untuk PDP Elliptik . . . 130
7.5.3 Contoh kedua . . . 132
7.6 PDP parabolik . . . 133
7.6.1 MetodeForward-difference . . . 133
7.6.2 Contoh ketiga: One dimensional heat equation . . . 134
7.6.3 MetodeBackward-difference . . . 139
7.6.4 Metode Crank-Nicolson . . . 143
7.7 PDP Hiperbolik . . . 146
7.7.1 Contoh . . . 148
7.8 Latihan . . . 149
8 Integral Numerik 151 8.1 Metode Trapezoida . . . 151
8.2 Metode Simpson . . . 152
8.3 Metode Composite-Simpson . . . 153
8.4 Adaptive Quardrature . . . 155
8.5 Gaussian Quadrature . . . 156
8.5.1 Contoh . . . 156
8.5.2 Latihan . . . 157
9 Mencari Akar 159 9.1 Metode Newton . . . 159
10 Metode Monte Carlo 161 10.1 Penyederhanaan . . . 161
11 Inversi 165 11.1 Inversi Linear . . . 165
11.2 Inversi Non-Linear . . . 168
Daftar Pustaka 171
Daftar Gambar
3.1 Sebaran data observasi antara temperatur dan kedalaman . . . 40
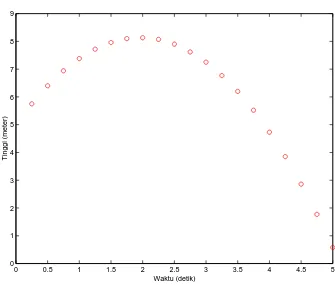
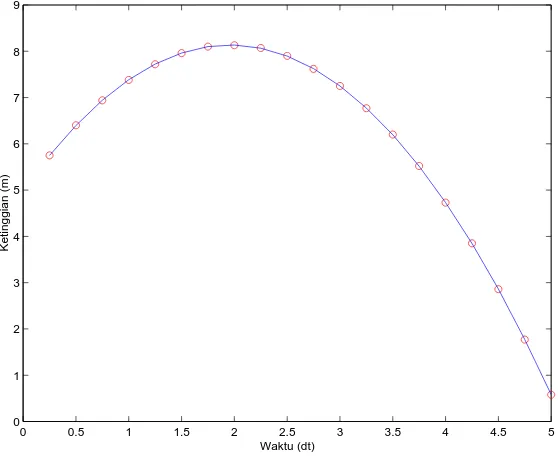
3.2 Grafik data pengukuran gerak batu . . . 54
3.3 Grafik hasil inversi parabola . . . 57
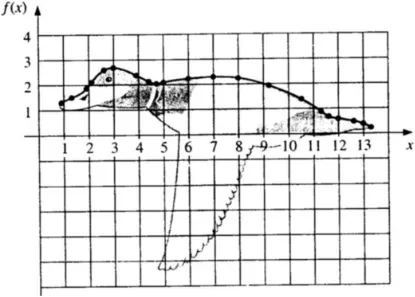
6.1 Fungsif(x)dengan sejumlah titik data . . . 93
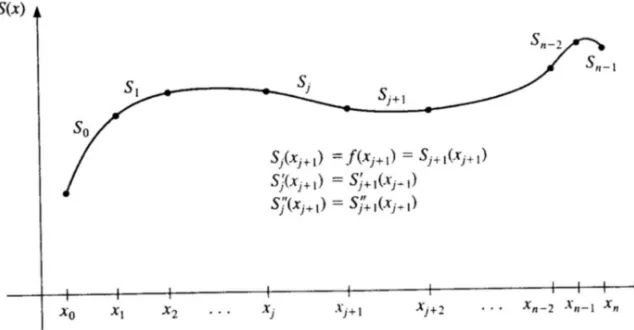
6.2 Pendekatan dengan polinomial cubic spline . . . 93
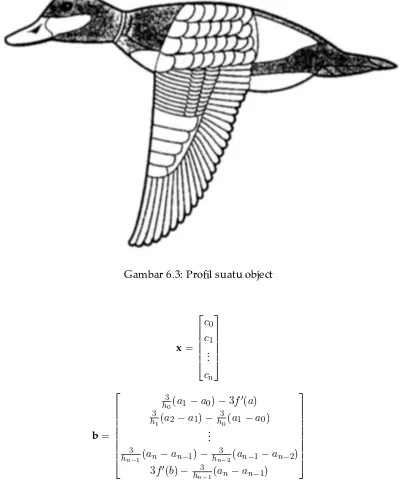
6.3 Profil suatu object . . . 98
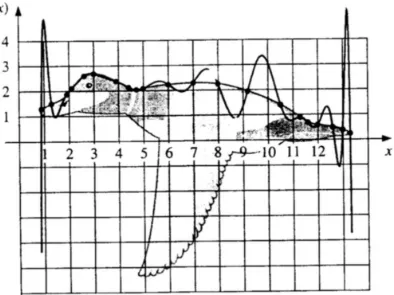
6.4 Sampling titik data . . . 99
6.5 Hasil interpolasi cubic spline . . . 99
6.6 Hasil interpolasi lagrange . . . 100
7.1 Kiri: Kurvay(t)dengan pasangan titik absis dan ordinat dimana jarak titik absis sebe-sarh. Pasangant1 adalahy(t1), pasangant2 adalahy(t2), begitu seterusnya. Kanan: Garis singgung yang menyinggung kurvay(t)pada t=a, kemudian berdasarkan garis singgung tersebut, ditentukan pasangan t1 sebagaiw1. Perhatikan gambar itu sekali lagi!w1dany(t1)beda tipis alias tidak sama persis. . . 102
7.2 Kurva biru adalah solusi exact, dimana lingkaran-lingkaran kecil warna biru pada kurva menunjukkan posisi pasangan absistdan ordinaty(t)yang dihitung oleh Persamaan (7.9). Sedangkan titik-titik merah mengacu pada hasil perhitungan metode euler, yaitu nilaiwi. . . 106
7.3 Kurva biru adalah solusi exact, dimana lingkaran-lingkaran kecil warna biru pada kurva menunjukkan posisi pasangan absistdan ordinaty(t)yang dihitung oleh Persamaan (7.9). Sedangkan titik-titik merah mengacu pada hasil perhitungan metode Runge Kutta orde 4, yaitu nilaiwi. . . 110
7.4 Rangkaian RC . . . 111
7.5 Kurva pengisian muatanq(charging) terhadap waktut . . . 115
7.6 Kurva suatu fungsif(x)yang dibagi sama besar berjarakh. Evaluasi kurva yang dilakukan Finite-Differencedimulai dari batas bawahX0 = ahingga batas atas x6 =b . . . 116
7.7 Skemagrid linesdanmesh pointspada aplikasi metodeFinite-Difference . . . 126
7.8 Susunangrid linesdanmesh pointsuntuk mensimulasikan distribusi temperatur pada lempeng logam sesuai contoh satu . . . 128
7.9 Sebatang logam dengan posisi titik-titik simulasi (mesh-points) distribusi temperatur. Jarak antar titik ditentukan sebesarh= 0,1. . . 135
7.10 Intervalmesh-pointsdengan jarakh= 0,1dalam interval waktuk= 0,0005 . . . 135
7.11 Posisimesh-points. Arahxmenunjukkan posisi titik-titik yang dihitung dengan
forward-difference, sedangkan arahtmenunjukkan perubahan waktu yg makin meningkat . . . . 135
8.1 Metode Trapezoida. Gambar sebelah kiri menunjukkan kurva fungsif(x)dengan batas bawah integral adalah a dan batas atas b. Gambar sebelah kanan menunjukan cara metode Trapesoida menghitung luas area integrasi, dimana luas area adalah sama den-gan luas trapesium di bawah kurvaf(x)dalam batas-batasadanb . . . 152
8.2 Metode Simpson. Gambar sebelah kiri menunjukkan kurva fungsif(x)dengan batas bawah integral adalah a dan batas atas b. Gambar sebelah kanan menunjukan cara metode Simpson menghitung luas area integrasi, dimana area integrasi di bawah kurva f(x)dibagi 2 dalam batas-batasadanb . . . 152
8.3 Metode Composite Simpson. Kurva fungsif(x)dengan batas bawah integral adalaha dan batas atasb. Luas area integrasi dipecah menjadi 8 area kecil dengan lebar masing-masing adalahh. . . 154
9.1 Metode Newton . . . 160
10.1 Lingkaran dan bujursangkar . . . 161
10.2 Dart yang menancap pada bidang lingkaran dan bujursangkar . . . 162
Daftar Tabel
3.1 Data temperatur bawah permukaan tanah terhadap kedalaman . . . 39
3.2 Data temperatur bawah permukaan tanah terhadap kedalaman . . . 45
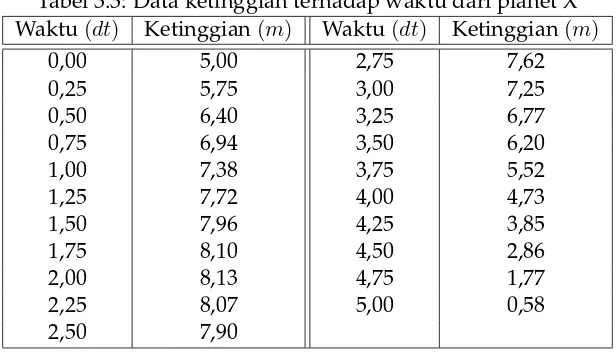
3.3 Data ketinggian terhadap waktu dari planet X . . . 53
5.1 Hasil akhir elemen-elemen vektorxhingga iterasi ke-10 . . . 79
5.2 Hasil perhitungan norm-selisih (denganℓ2) hingga iterasi ke-10 . . . 80
5.3 Hasil Iterasi Gauss-Seidel . . . 84
5.4 Hasil perhitungan iterasi Gauss-Seidel . . . 88
5.5 Hasil perhitungan iterasi Relaksasi denganω= 1,25. . . 88
7.1 Solusi yang ditawarkan oleh metode eulerwidan solusi exacty(ti)serta selisih antara keduanya . . . 105
7.2 Solusi yang ditawarkan oleh metode Runge Kutta orde 4 (wi) dan solusi exact y(ti)serta selisih antara keduanya . . . 110
7.3 Perbandingan antara hasil perhitungan numerik lewat metode Runge Kutta dan hasil perhitungan dari solusi exact, yaitu persamaan (7.16) . . . 114
7.4 Hasil simulasi distribusi panas bergantung waktu dalam 1-dimensi. Kolom ke-2 adalah solusi analitik/exact, kolom ke-3 dan ke-5 adalah solusi numerikforward-difference. Kolom ke-4 dan ke-6 adalah selisih antara solusi analitik dan numerik . . . 139
7.5 Hasil simulasi distribusi panas bergantung waktu dalam 1-dimensi dengan metode backward-differencedimanak= 0,01 . . . 143
7.6 Hasil simulasi distribusi panas bergantung waktu (t) dalam 1-dimensi dengan metodebackward-differencedan Crank-Nicolson . . . 146
8.1 Polinomial Legendre untukn=2,3,4 dan 5 . . . 156
Bab 1
Matrik dan Komputasi
✍Objektif :
⊲ Mengenalkan matrik dan jenis-jenis matrik.
⊲ Mengenalkan operasi penjumlahan dan perkalian matrik.
⊲ Mendeklarasikan elemen-elemen matrik ke dalam memori komputer.
⊲ Membuat script operasi matrik.
1.1 Pengenalan matrik
Notasi suatu matrik berukurannxm ditulis dengan huruf besar dan dicetak tebal, misalnya
An×m. Hurufnmenyatakan jumlah baris, dan hurufmjumlah kolom. Suatu matrik tersusun
dari elemen-elemen yang dinyatakan dengan huruf kecil diikuti angka-angka indeks, misalnya
aij, dimana indeksi menunjukan posisi baris ke-idan indeksj menentukan posisi kolom ke-j.
A= (aij) =
a11 a12 . . . a1m
a21 a22 . . . a2m
..
. ... ...
an1 an2 . . . anm
(1.1)
Contoh 1: MatrikA2×3
A= "
3 8 5 6 4 7 #
dimana masing-masing elemennya adalaha11 = 3, a12 = 8, a13 = 5, a21 = 6, a22 = 4, dan
a23= 7.
Contoh 2: MatrikB3×2
B=
1 3 5 9 2 4
dimana masing-masing elemennya adalahb11 = 1, b12 = 3, b21 = 5, b22 = 9, b31 = 2, dan
b32= 4.
1.2 Inisialisasi matrik dalam memori komputer
Dalam bahasa pemrograman Fortran77, cara mengisi memori komputer dengan elemen-elemen matrikA2×3, sesuai dengan Contoh 1 adalah
1 A(1,1) = 3
2 A(1,2) = 8
3 A(1,3) = 5
4 A(2,1) = 6
5 A(2,2) = 4
6 A(2,3) = 7
Sedangkan untuk matrikB3×2, sesuai Contoh 2 adalah
1 B(1,1) = 1
2 B(1,2) = 3
3 B(2,1) = 5
4 B(2,2) = 9
5 B(3,1) = 2
6 B(3,2) = 4
Sementara dalam Matlab, cara mengisi memori komputer dengan elemen-elemen matrik
A2×3, sesuai dengan Contoh 1 adalah
1 clear all
2 clc
3
4 A(1,1) = 3;
5 A(1,2) = 8;
6 A(1,3) = 5;
7 A(2,1) = 6;
8 A(2,2) = 4;
9 A(2,3) = 7;
10 A
Sedangkan untuk matrikB3×2, sesuai Contoh 2 adalah
1 clear all
2 clc
3
4 B(1,1) = 1;
5 B(1,2) = 3;
6 B(2,1) = 5;
7 B(2,2) = 9;
8 B(3,1) = 2;
9 B(3,2) = 4;
10 B
1.3. MACAM-MACAM MATRIK 3
1 clear all
2 clc
3
4 A=[ 3 8 5
5 6 4 7 ];
6
7 B=[ 1 3
8 5 9
9 2 4 ];
atau
1 clear all
2 clc
3
4 A=[ 3 8 5 ; 6 4 7 ];
5 B=[ 1 3 ; 5 9 ; 2 4];
1.3 Macam-macam matrik
1.3.1 Matrik transpose
Operasi transpose terhadap suatu matrik akan menukar elemen-elemen dalam satu kolom menjadi elemen-elemen dalam satu baris; demikian pula sebaliknya. Notasi matrik tranpose adalahAT atauAt.
Contoh 3: Operasi transpose terhadap matrikA
A= "
3 8 5 6 4 7 #
At=
3 6 8 4 5 7
1.3.2 Matrik bujursangkar
Matrik bujursangkar adalah matrik yang jumlah baris dan jumlah kolomnya sama.
Contoh 4: Matrik bujursangkar berukuran 3x3 atau sering juga disebut matrik bujursangkar orde 3
A=
1 3 8 5 9 7 2 4 6
1.3.3 Matrik simetrik
Contoh 5: Matrik simetrik
1.3.4 Matrik diagonal
Matrik diagonal adalah matrik bujursangkar yang seluruh elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonalnya.
Contoh 6: Matrik diagonal orde 3
A=
1.3.5 Matrik identitas
Matrik identitas adalah matrik bujursangkar yang semua elemen-nya bernilai 0 (nol), kecuali elemen-elemen diagonal yang seluruhnya bernilai 1.
Contoh 7: Matrik identitas orde 3
I=
1.3.6 Matrik upper-triangular
Matrik upper-tringular adalah matrik bujursangkar yang seluruh elemen dibawah elemen di-agonal bernilai 0 (nol).
Contoh 8: Matrik upper-triangular
A=
1.3.7 Matrik lower-triangular
1.3. MACAM-MACAM MATRIK 5
Contoh 9: Matrik lower-triangular
A=
1.3.8 Matrik tridiagonal
Matrik tridiagonal adalah matrik bujursangkar yang seluruh elemen bukan 0 (nol) berada dis-ekitar elemen diagonal, sementara elemen lainnya bernilai 0 (nol).
Contoh 10: Matrik tridiagonal
A=
1.3.9 Matrik diagonal dominan
Matrik diagonal dominan adalah matrik bujursangkar yang memenuhi
|aii|> n
X
j=1,j6=i
|aij| (1.2)
dimanai=1,2,3,..n. Coba perhatikan matrik-matrik berikut ini
A=
matrikAdisebut matrik diagonal dominan. Sekarang perhatikan elemen diagonal matrikB, |6|<|4|+| −3|,| −2|<|4|+|0|, dan|1|<| −3|+|0|. Dengan demikian, matrikBbukan matrik diagonal dominan.
1.3.10 Matrikpositive-definite
Suatu matrik dikatakanpositive-definitebila matrik tersebut simetrik dan memenuhi
Contoh 11: Diketahui matrik simetrik berikut
untuk menguji apakah matrikAbersifatpositive-definite, maka
xtAx = hx1 x2 x3
Dari sini dapat disimpulkan bahwa matrikAbersifatpositive-definite, karena memenuhi
x21+ (x1−x2)2+ (x2−x3)2+x23 >0
kecuali jikax1=x2=x3=0.
1.3.11 Vektor-baris dan vektor-kolom
Notasi vektor biasanya dinyatakan dengan huruf kecil dan dicetak tebal. Suatu matrik dina-makan vektor-baris berukuran m, bila hanya memiliki satu baris danm kolom, yang diny-atakan sebagai berikut
a=ha11 a12 . . . a1m
i
=ha1 a2 . . . am
i
(1.4)
Sedangkan suatu matrik dinamakan vektor-kolom berukurann, bila hanya memiliki satu kolom dannbaris, yang dinyatakan sebagai berikut
1.4. OPERASI MATEMATIKA 7
1.4 Operasi matematika
1.4.1 Penjumlahan matrik
Operasi penjumlahan pada dua buah matrik hanya bisa dilakukan bila kedua matrik tersebut berukuran sama. Misalnya matrikC2×3
C= "
9 5 3 7 2 1 #
dijumlahkan dengan matrikA2×3, lalu hasilnya (misalnya) dinamakan matrikD2×3
D=A+C
D =
"
3 8 5 6 4 7 #
+ "
9 5 3 7 2 1 #
= "
3 + 9 8 + 5 5 + 3 6 + 7 4 + 2 7 + 1 #
= "
12 13 8 13 6 8 #
Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi penjumlahan antara matrikA2×3 danC2×3, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik tersebut, yaitu
"
d11 d12 d13
d21 d22 d23 #
= "
a11+c11 a12+c12 a13+c13
a21+c21 a22+c22 a23+c23 #
Dijabarkan satu persatu sebagai berikut
d11=a11+c11
d12=a12+c12
d13=a13+c13 (1.6)
d21=a21+c21
d22=a22+c22
d23=a23+c23
Dari sini dapat diturunkan sebuah rumus umum penjumlahan dua buah matrik
dij =aij+cij (1.7)
1.4.2 Komputasi penjumlahan matrik
Berdasarkan contoh operasi penjumlahan di atas, indeksj pada persamaan (1.7) lebih cepat berubah dibanding indeksisebagaimana ditulis pada persamaan (1.6),
d11=a11+c11
d12=a12+c12
d13=a13+c13
Jelas terlihat, ketika indeks i masih bernilai 1, indeks j sudah berubah dari nilai 1 sampai 3. Hal ini membawa konsekuensi pada scriptpemrograman, dimana looping untuk indeks j
harus diletakkan di dalamloopingindeksi. Pokoknya yanglooping-nya paling cepat harus diletakkan paling dalam; sebaliknya, looping paling luar adalah looping yang indeksnya paling jarang berubah.
Dalam matlab, algoritma penjumlahan dua matrik ditulis sebagai berikut:
1 for i=1:2
2 for j=1:3
3 D(i,j)=A(i,j)+C(i,j);
4 end
5 end
Sedangkan dalam Fortran77, operasi penjumlahan antara matrik ditulis sebagai berikut:A2×3 danC2×3adalah
1 do i=1,2
2 do j=1,3
3 D(i,j)=A(i,j)+C(i,j)
4 end do
5 end do
Perhatikan kedua script di atas! Penulisan indeksiharus didahulukan daripada indeksj. Perlu dicatat bahwa ukuran matrik tidak terbatas hanya 2x3. Tentu saja anda bisa men-gubah ukurannya sesuai dengan keperluan atau kebutuhan anda. Jika ukuran matrik diny-atakan secara umum sebagainxm, dimananadalah jumlah baris danmadalah jumlah kolom, maka bentuk pernyataan komputasinya dalam matlab menjadi
1 for i=1:n
2 for j=1:m
3 D(i,j)=A(i,j)+C(i,j);
4 end
5 end
sedangkan dalam Fortran77
1 do i=1,n
2 do j=1,m
1.4. OPERASI MATEMATIKA 9
4 end do
5 end do
Sekarang, mari kita lengkapi dengan contoh sebagai berikut: diketahui matrikA2×3
A= "
3 8 5 6 4 7 #
dan matrikC2×3
C= "
9 5 3 7 2 1 #
Program untuk menjumlahkan kedua matrik tersebut dalam matlab adalah:
1 clear all
2 clc
3
4 A(1,1) = 3;
5 A(1,2) = 8;
6 A(1,3) = 5;
7 A(2,1) = 6;
8 A(2,2) = 4;
9 A(2,3) = 7;
10 C(1,1) = 9;
11 C(1,2) = 5;
12 C(1,3) = 3;
13 C(2,1) = 7;
14 C(2,2) = 2;
15 C(2,3) = 1;
16 n=2
17 m=3
18 for i=1:n
19 for j=1:m
20 D(i,j)=A(i,j)+C(i,j);
21 end
22 end
sedangkan dalam Fortran77
1 A(1,1) = 3
2 A(1,2) = 8
3 A(1,3) = 5
4 A(2,1) = 6
5 A(2,2) = 4
6 A(2,3) = 7
7 C(1,1) = 9
8 C(1,2) = 5
9 C(1,3) = 3
10 C(2,1) = 7
11 C(2,2) = 2
12 C(2,3) = 1
13 n=2
14 m=3
15 do i=1,n
17 D(i,j)=A(i,j)+C(i,j)
18 end do
19 end do
1.4.3 Perkalian matrik
Operasi perkalian dua buah matrik hanya bisa dilakukan bila jumlah kolom matrik pertama sama dengan jumlah baris matrik kedua. Jadi kedua matrik tersebut tidak harus berukuran sama seperti pada penjumlahan dua matrik. Misalnya matrikA2×3 dikalikan dengan matrik B3×2, lalu hasilnya (misalnya) dinamakan matrikE2×2
E2×2 =A2×3.B3×2
E =
"
3 8 5 6 4 7 #
1 3 5 9 2 4
= "
3.1 + 8.5 + 5.2 3.3 + 8.9 + 5.4 6.1 + 4.5 + 7.2 6.3 + 4.9 + 7.4 #
= "
53 101 40 82
#
Tanpa mempedulikan nilai elemen-elemen masing-masing matrik, operasi perkalian antara matrikA2×3 danB3×2, bisa juga dinyatakan dalam indeks masing-masing dari kedua matrik tersebut, yaitu
"
e11 e12
e21 e22 #
= "
a11.b11+a12.b21+a13.b31 a11.b12+a12.b22+a13.b32
a21.b11+a22.b21+a23.b31 a21.b12+a22.b22+a23.b32 #
Bila dijabarkan, maka elemen-elemen matrikE2×2adalah
e11=a11.b11+a12.b21+a13.b31 (1.8)
e12=a11.b12+a12.b22+a13.b32 (1.9)
e21=a21.b11+a22.b21+a23.b31 (1.10)
e22=a21.b12+a22.b22+a23.b32 (1.11)
Sejenak, mari kita amati perubahan pasangan angka-angka indeks yang mengiringi elemene,
1.4. OPERASI MATEMATIKA 11
pertama pada elemeneseperti berikut ini
e1..=..
e1..=..
e2..=..
e2..=..
Pola perubahan yang sama akan kita dapati pada angka indeks pertama dari elemena
e1..=a1...b...+a1...b...+a1...b...
e1..=a1...b...+a1...b...+a1...b...
e2..=a2...b...+a2...b...+a2...b...
e2..=a2...b...+a2...b...+a2...b...
Dengan demikian kita bisa mencantumkan huruf i sebagai pengganti angka-angka indeks yang polanya sama
ei.. =ai...b...+ai...b...+ai...b...
ei.. =ai...b...+ai...b...+ai...b...
ei.. =ai...b...+ai...b...+ai...b...
ei.. =ai...b...+ai...b...+ai...b...
dimanaibergerak mulai dari angka 1 hingga angka 2, atau kita nyatakani=1,2. Selanjutnya, masih dari persamaan (1.8) sampai persamaan (1.11), marilah kita perhatikan perubahan angka indeks masih pada elemenedan elemenb,
ei1 =ai...b..1+ai...b..1+ai...b..1
ei2 =ai...b..2+ai...b..2+ai...b..2
ei1 =ai...b..1+ai...b..1+ai...b..1
ei2 =ai...b..2+ai...b..2+ai...b..2
Dengan demikian kita bisa mencantumkan huruf j sebagai pengganti angka-angka indeks yang polanya sama
eij =ai...b..j+ai...b..j+ai...b..j
eij =ai...b..j+ai...b..j+ai...b..j
eij =ai...b..j+ai...b..j+ai...b..j
dimanajbergerak mulai dari angka 1 hingga angka 2, atau kita nyatakanj=1,2. Selanjutnya, masih dari persamaan (1.8) sampai persamaan (1.11), mari kita perhatikan perubahan angka indeks masih pada elemenadan elemenb, dimana kita akan dapati pola sebagai berikut
eij =ai1.b1j +ai2.b2j+ai3.b3j
eij =ai1.b1j +ai2.b2j+ai3.b3j
eij =ai1.b1j +ai2.b2j+ai3.b3j
eij =ai1.b1j +ai2.b2j+ai3.b3j
Dan kita bisa mencantumkan huruf k sebagai pengganti angka-angka indeks yang polanya sama, dimanakbergerak mulai dari angka 1 hingga angka 3, atau kita nyatakank=1,2,3.
eij =aik.bkj+aik.bkj+aik.bkj
eij =aik.bkj+aik.bkj+aik.bkj
eij =aik.bkj+aik.bkj+aik.bkj
eij =aik.bkj+aik.bkj+aik.bkj
Kemudian secara sederhana dapat ditulis sebagai berikut
eij =aik.bkj+aik.bkj+aik.bkj (1.12)
Selanjutnya dapat ditulis pula formula berikut
eij =
3 X
k=1
aikbkj (1.13)
dimanai=1,2;j=1,2; dank=1,2,3.
Berdasarkan contoh ini, maka secara umum bila ada matrikAn×myang dikalikan dengan
ma-trikBm×p, akan didapatkan matrikEn×pdimana elemen-elemen matrikEmemenuhi
eij = m
X
k=1
aikbkj (1.14)
dengani=1,2,. . . ,n;j=1,2. . . ,p; dank=1,2. . . ,m.
1.4.4 Komputasi perkalian matrik
Komputasi operasi perkalian antara matrikA2×3danB3×2dilakukan melalui 2 tahap;pertama adalah memberikan nilai 0 (nol) pada elemen-elemen matrikE2×2dengan cara (dalam matlab)
1 for i=1:2
2 for j=1:2
3 E(i,j)=0.0;
4 end
1.4. OPERASI MATEMATIKA 13
dalam Fortran77
1 do i=1,2
2 do j=1,2
3 E(i,j)=0.0
4 end do
5 end do
keduaadalah menghitung perkalian matrik dengan cara (dalam matlab)
1 for i=1:2
2 for j=1:2
3 for k=1:3
4 E(i,j)=E(i,j)+A(i,k)*B(k,j);
5 end
6 end
7 end
dalam Fortran77
1 do i=1,2
2 do j=1,2
3 do k=1,3
4 E(i,j)=E(i,j)+A(i,k)*B(k,j)
5 end do
6 end do
7 end do
Sebentar.., sebelum dilanjut tolong perhatikan penempatan indeksi,jdankpadascriptdi atas. Mengapa indeksididahulukan daripada indeksj dank? Ini bukan sesuatu yang kebetulan. Dan ini juga bukan sekedar mengikuti urutan huruf abjad i,j,k. Sekali lagi ingin saya tegaskan bahwa penempatan yang demikian semata-mata mengikuti aturan umum yaituloopingyang indeksnya berubah paling cepat harus diletakkan paling dalam; sebaliknya,loopingpaling luar adalahlooping yang indeksnya paling jarang berubah. Kalau anda perhatikan dengan teliti, pasti anda akan menemukan fakta bahwa indeks k paling cepat berubah. Kemudian disusul oleh indeks j. Lalu yang paling jarang berubah adalah indeks i. Itulah sebabnya, penempatan urutan indeks pada script di atas harus dimulai dari iterlebih dahulu sebagai
loopingterluar, kemudian indeksj, dan yang terakhir indeksksebagailoopingterdalam. Tentu saja anda bisa mengubah ukurannya sesuai dengan keperluan atau kebutuhan anda. Jika ukuran matrikAdinyatakan secara umum sebagainxmdan matrikBberukuranmxp, maka bentuk pernyataan komputasinya dalam Matlab menjadi
1 for i=1:n
2 for j=1:p
3 E(i,j)=0.0;
4 end
5 end
7 for j=1:p
8 for k=1:m
9 E(i,j)=E(i,j)+A(i,k)*B(k,j);
10 end
11 end
12 end
dalam Fortran77
1 do i=1,n
2 do j=1,p
3 E(i,j)=0.0
4 end do
5 end do
6 do i=1,n
7 do j=1,p
8 do k=1,m
9 E(i,j)=E(i,j)+A(i,k)*B(k,j)
10 end do
11 end do
12 end do
dimana akan diperoleh hasil berupa matrikEyang berukurannxp.
1.4.5 Perkalian matrik dan vektor-kolom
Operasi perkalian antara matrik dan vektor-kolom sebenarnya sama saja dengan perkalian an-tara dua matrik. Hanya saja ukuran vektor-kolom boleh dibilang spesial yaitumx1, dimana
mmerupakan jumlah baris sementara jumlah kolomnya hanya satu. Misalnya matrik A, pa-da contoh 1, dikalikan dengan vektor-kolom x yang berukuran3 x 1 atau disingkat dengan mengatakan vektor-kolomxberukuran3, lalu hasilnya (misalnya) dinamakan vektor-kolomy
y=Ax
y =
"
3 8 5 6 4 7 #
2 3 4
= "
3.2 + 8.3 + 5.4 6.2 + 4.3 + 7.4 #
= "
50 52 #
Sekali lagi, tanpa mempedulikan nilai elemen-elemen masing-masing, operasi perkalian antara matrikAdan vektor-kolomx, bisa juga dinyatakan dalam indeksnya masing-masing, yaitu
"
y1
y2 #
= "
a11.x1+a12.x2+a13.x3
1.4. OPERASI MATEMATIKA 15
Bila dijabarkan, maka elemen-elemen vektor-kolomyadalah
y1 =a11.x1+a12.x2+a13.x3
y2 =a21.x1+a22.x2+a23.x3
kemudian secara sederhana dapat diwakili oleh rumus berikut
yi=
3 X
j=1
aijxj
dimanai=1,2.
Berdasarkan contoh tersebut, secara umum bila ada matrikAberukurannxmyang dikalikan dengan vektor-kolomxberukuranm, maka akan didapatkan vektor-kolomyberukurannx1
dimana elemen-elemen vektor-kolomymemenuhi
yi= m
X
j=1
aijxj (1.15)
dengani=1,2,. . . ,n.
1.4.6 Komputasi perkalian matrik dan vektor-kolom
Sama seperti perkalian dua matrik, komputasi untuk operasi perkalian antara matrikA beruku-rannxmdan vektor-kolomxberukuranmdilakukan melalui 2 tahap; pertama adalah mem-berikan nilai 0 (nol) pada elemen-elemen vektor-kolomyyang berukurann. Lalu tahap kedua adalah melakukan proses perkalian. Kedua tahapan ini digabung jadi satu dalam program berikut ini
1 for i=1:n
2 b(i,1)=0.0;
3 end
4 for i=1:n
5 for j=1:m
6 b(i,1)=b(i,1)+A(i,j)*x(j,1);
7 end
8 end
dan dalam Fortran
1 do i=1,n
2 b(i,1)=0.0
3 end do
4 do i=1,n
5 do j=1,m
6 b(i,1)=b(i,1)+A(i,j)*x(j,1)
7 end do
1.5 Penutup
Demikianlah catatan singkat dan sederhana mengenai jenis-jenis matrik dasar yang seringkali dijumpai dalam pengolahan data fisika secara numerik. Semuanya akan dijadikan acuan atau referensi pada pembahasan topik-topik numerik yang akan datang.
1.6 Latihan
Diketahui matrikA, matrikB, dan vektorxsebagai berikut
A=
1 3 −6 −2 5 9 7 5.6 2 4 8 −1 2.3 1.4 0.8 −2.3
B=
8 1 4 21 3 10 5 0.1 7 −2 9 −5 2.7 −12 −8.9 5.7
x=
0.4178
−2.9587 56.3069
8.1
1. Buatlah script untuk menyelesaikan penjumlahan matrikAdan matrikB.
2. Buatlah script untuk menyelesaikan perkalian matrikAdan matrikB.
3. Buatlah script untuk menyelesaikan perkalian matrikAdan vektorx.
Bab 2
Metode Eliminasi Gauss
✍Objektif :
⊲ Mengenalkan sistem persamaan linear.
⊲ Mengenalkan teknik triangularisasi dan substitusi mundur.
⊲ Aplikasi metode Eliminasi Gauss menggunakan matrik.
⊲ Membuat algoritma metode Eliminasi Gauss.
⊲ Menghitung invers matrik menggunakan metode Eliminasi Gauss.
2.1 Sistem persamaan linear
Secara umum, sistem persamaan linear dinyatakan sebagai berikut
Pn: an1x1+an2x2+...+annxn=bn (2.1)
dimanaadanbmerupakan konstanta,xadalah variable,n= 1,2,3, ....
Contoh pertama
Misalnya ada sistem persamaan linear yang terdiri dari empat buah persamaan yaitu P1,
P2,P3, danP4seperti berikut ini:
P1: x1 + x2 + 3x4 = 4
P2: 2x1 + x2 − x3 + x4 = 1
P3: 3x1 − x2 − x3 + 2x4 = -3
P4: −x1 + 2x2 + 3x3 − x4 = 4
Problem dari sistem persamaan linear adalah bagaimana mencari nilai pengganti bagi vari-abelx1,x2,x3, danx4sehingga semua persamaan diatas menjadi benar. Langkah awal penye-lesaian problem tersebut adalah dengan melakukan penyederhanaan sistem persamaan linear.
2.2 Triangularisasi dan Substitusi Mundur
Ada banyak jalan untuk mendapatkan bentuk yang lebih sederhana, namun masalahnya, ki-ta ingin mendapatkan sebuah algoritma program yang nantinya bisa berjalan di komputer, sedemikian rupa sehingga apapun persamaannya, bisa disederhanakan oleh komputer. Kita akan berpatokan pada tiga buah aturan operasi untuk menyederhanakan sistem persamaan linear di atas, yaitu
• PersamaanPidapat dikalikan dengan sembarang konstantaλ, lalu hasilnya ditempatkan
di posisi persamaanPi. Simbol operasi ini adalah(λPi)→(Pi).
• PersamaanPj dapat dikalikan dengan sembarang konstanta λ kemudian dijumlahkan
dengan persamaanPi, lalu hasilnya ditempatkan di posisi persamaanPi. Simbol operasi
ini adalah(Pi+λPj)→(Pi).
• PersamaanPidanPj dapat bertukar posisi. Simbol operasi ini adalah(Pi)↔(Pj).
Maka dengan berpegang pada aturan-aturan tersebut, problem sistem persamaan linear di atas akan diselesaikan dengan langkah-langkah berikut ini:
1. Gunakan persamaanP1untuk menghilangkan variabelx1 dari persamaanP2, P3 danP4 dengan cara(P2−2P1)→(P2),(P3−3P1)→(P3)dan(P4+P1)→(P4). Hasilnya akan seperti ini
P1 : x1+x2+ 3x4 = 4,
P2 : −x2−x3−5x4 = −7,
P3 : −4x2−x3−7x4 = −15,
P4 : 3x2+ 3x3+ 2x4 = 8
2. Gunakan persamaan P2 untuk menghilangkan variabel x2 dari persamaan P3 dan P4 dengan cara(P3−4P2)→(P3)dan(P4+ 3P2)→(P4). Hasilnya akan seperti ini
P1 : x1+x2+ 3x4 = 4,
P2: −x2−x3−5x4 = −7,
P3 : 3x3+ 13x4 = 13,
P4 : −13x4 = −13
Kalaux3masih ada di persamaanP4, dibutuhkan satu operasi lagi untuk menghilangkan-nya. Namun hasil operasi pada langkah ke-2 ternyata sudah otomatis menghilangkanx3. Bentuk akhir dari keempat persamaan di atas, dikenal sebagai bentuktriangular.
2.2. TRIANGULARISASI DAN SUBSTITUSI MUNDUR 19
memakan waktu lama dibandingkan sebelum disederhanakan. Sekali kita mendapatkan nilai pengganti bagi variabelx4, makax3,x2 danx1akan diperoleh dengan mudah dan cepat, sebagaimana yang dijelaskan pada langkah berikutnya.
3. Selanjutnya kita jalankan prosesbackward-substitution. Melalui proses ini, yang perta-ma kali didapat adalah nilai pengganti bagi variabelx4, kemudianx3, lalu diikutix2, dan akhirnyax1.
P4 : x4 = −
13
−13 = 1,
P3: x3 =
1
3(13−13x4) = 1
3(13−13) = 0,
P2 : x2 =−(−7 + 5x4+x3) = −(−7 + 5 + 0) = 2,
P1 : x1= 4−3x4−x2 = 4−3−2 =−1
Jadi solusinya adalah x1 = −1, x2 = 2, x3 = 0 danx4 = 1. Coba sekarang anda cek, apakah semua solusi ini cocok dan tepat bila dimasukan ke sistem persamaan linear yang pertama, yaitu yang belum disederhanakan?
Contoh kedua
Misalnya ada sistem persamaan linear, terdiri dari empat buah persamaan yaituP1,P2,P3, danP4seperti berikut ini:
P1 : x1 − x2 + 2x3 − x4 = -8
P2 : 2x1 − 2x2 + 3x3 − 3x4 = -20
P3 : x1 + x2 + x3 = -2
P4 : x1 − x2 + 4x3 + 3x4 = 4
Seperti contoh pertama, solusi sistem persamaan linear di atas akan dicari dengan langkah-langkah berikut ini:
1. Gunakan persamaanP1 untuk menghilangkanx1 dari persamaanP2, P3 danP4 dengan cara(P2−2P1)→(P2),(P3−P1)→(P3)dan(P4−P1)→(P4). Hasilnya akan seperti ini
P1 : x1−x2+ 2x3−x4 = −8,
P2 : −x3−x4 = −4,
P3: 2x2−x3+x4 = 6,
P4 : 2x3+ 4x4 = 12
Perhatikan persamaanP2! Akibat dari langkah yang pertama tadi, x2 hilang dari per-samaanP2. Kondisi ini bisa menggagalkan proses triangularisasi. Untuk itu, posisi P2 mesti ditukar dengan persamaan yang berada dibawahnya, yaitu P3 atau P4. Supaya proses triangularisasi dilanjutkan kembali, maka yang paling cocok adalah ditukar den-ganP3.
2. Tukar posisi persamaanP2 dengan persamaanP3,(P2 ↔P3). Hasilnya akan seperti ini
P1 : x1−x2+ 2x3−x4 = −8,
P2: 2x2−x3+x4 = 6,
P3: −x3−x4 = −4,
P4 : 2x3+ 4x4 = 12
3. Gunakan persamaanP3untuk menghilangkanx3 dari persamaanP4 dengan cara(P4 −
2P3)→(P4). Hasilnya akan seperti ini
P1: x1−x2+ 2x3−x4 = −8,
P2 : 2x2−x3+x4 = 6,
P3: −x3−x4 = −4,
P4 : 2x4 = 4
2.3. MATRIK DAN ELIMINASI GAUSS 21
4. Selanjutnya adalah proses backward-substitution. Melalui proses ini, yang pertama kali didapat solusinya adalahx4, kemudianx3, lalu diikutix2, dan akhirnyax1.
P4: x4 =
Berdasarkan kedua contoh di atas, untuk mendapatkan solusi sistem persamaan linear, diper-lukan operasitriangularisasidan prosesbackward-substitution. Katabackward-substitution
kalau diterjemahkan kedalam bahasa indonesia, menjadisubstitusi-mundur. Gabungan pros-es triangularisasi dan substitusi-mundur untuk menyelpros-esaikan sistem persamaan linear dike-nal sebagai metodeeliminasi gauss.
2.3 Matrik dan Eliminasi Gauss
Sejumlah matrik bisa digunakan untuk menyatakan suatu sistem persamaan linear. Sejenak, mari kita kembali lagi melihat sistem persamaan linear secara umum seperti berikut ini:
a11x1+a12x2+. . .+a1nxn = b1
a21x1+a22x2+. . .+a2nxn = b2
. . . = . . .
. . . = . . . an1x1+an2x2+. . .+annxn = bn
Sementara, kalau dinyatakan dalam bentuk operasi matrik, maka akan seperti ini:
beruku-rannx(n+ 1)seperti berikut ini:
Berdasarkan contoh pertama yang ada dihalaman depan catatan ini, saya akan tunjukkan pros-es triangularisasi dan substitusi-mundur dalam operasi matrik terhadap sistem persamaan lin-ear yang terdiri dari empat persamaan matematika, yaitu (silakan lihat kembali contoh pertama):
Lalu kita dapat membuat matrik augment sebagai berikut:
Kemudian kita lakukan operasi triangularisai terhadap matrik augment, dimulai dari kolom pertama, yaitu
lalu dilanjutkan ke kolom berikutnya
masing-2.4. ALGORITMA ELIMINASI GAUSS 23
masing elemen berikut ini:
Dengan memperhatikan angka-angka indeks pada matrik augment di atas, kita akan menco-ba membuat rumusan proses substitusi-mundur untuk mendapatkan seluruh nilai pengganti variabelx. Dimulai darix4,
ini dapat dinyatakan dalam rumus umum, yaitu
xn= an,n+1
ini juga dapat dinyatakan dalam rumus umum yaitu:
xi=
ai,n+1−Pnj=i+1aijxj
aii
Proses triangularisasi dan substitusi-mundur dibakukan menjadi algoritma metode eliminasi gauss yang dapat diterapkan dalam berbagai bahasa pemrograman komputer, misalnya for-tran, C, java, pascal, matlab, dan lain-lain.
2.4 Algoritma eliminasi Gauss
Secara umum, sistem persamaan linear adalah sebagai berikut:
a11x1+a12x2+. . .+a1nxn = b1
a21x1+a22x2+. . .+a2nxn = b2 ..
. ... = ...
an1x1+an2x2+. . .+annxn = bn
Algoritma dasar metode eliminasi gauss, adalah sebagai berikut:
yang berukurannx(n+ 1)seperti berikut ini:
Jelas terlihat bahwa elemen-elemen yang menempati kolom terakhir matrik augment adalah nilai daribi; yaituai,n+1=bidimanai= 1,2, ..., n.
2. Periksalah elemen-elemen pivot. Apakah ada yang bernilai nol? Elemen-elemen pivot adalah elemen-elemen yang menempati diagonal suatu matrik, yaitu a11, a22, ..., ann
atau disingkataii. Jikaaii6= 0, bisa dilanjutkan ke langkah no.3. Namun, jika ada elemen
diagonal yang bernilai nol,aii = 0, maka baris dimana elemen itu berada harus ditukar
posisinya dengan baris yang ada dibawahnya,(Pi) ↔ (Pj)dimanaj =i+ 1, i+ 2, ..., n,
sampai elemen diagonal matrik menjadi tidak nol,aii6= 0. (Kalau kurang jelas, silakan lihat
lagi contoh kedua yang ada dihalaman 3. Sebaiknya, walaupun elemen diagonalnya tidak nol, namun mendekati nol (misalnya 0,03), maka proses pertukaran ini dilakukan juga).
3. Proses triangularisasi. Lakukanlah operasi berikut:
Pj−
4. Hitunglah nilaixndengan cara:
xn=
2.4. ALGORITMA ELIMINASI GAUSS 25
2.4.1 Algoritma
Algoritma metode eliminasi gauss untuk menyelesaikannxnsistem persamaan linear.
P1: a11x1+a12x2+. . .+a1nxn = b1
P2: a21x1+a22x2+. . .+a2nxn = b2 ..
. ... ... = ...
Pn: an1x1+an2x2+. . .+annxn = bn
INPUT: sejumlah persamaan linear dimana konstanta-konstanta-nya menjadi elemen-elemen matrik augmentA= (aij), dengan1≤i≤ndan1≤j≤n+ 1.
OUTPUT: solusix1, x2, x3, ..., xnatau pesan kesalahan yang mengatakan bahwasistem
per-samaan linear tidak memiliki solusi yang unik.
• Langkah 1:Inputkan konstanta-konstanta dari sistem persamaan linear kedalam elemen-elemenmatrik augment, yaitu suatu matrik yang berukurannx(n+ 1)seperti berikut ini:
a11 a12 . . . a1n | b1
a21 a22 . . . a2n | b2 ..
. ... ... | ...
an1 an2 . . . ann | bn
=
a11 a12 . . . a1n | a1,n+1
a21 a22 . . . a2n | a2,n+1 ..
. ... ... | ...
an1 an2 . . . ann | an,n+1
(2.9)
• Langkah 2:Untuki= 1, ..., n−1, lakukan Langkah 3 sampai Langkah 5.
• Langkah 3: Definisikanpsebagai integer dimanai ≤p ≤ n. Lalu pastikan bahwa
api 6= 0. Jika ada elemen diagonal yang bernilai nol (aii = 0), maka program harus
mencari dan memeriksa elemen-elemen yang tidak bernilai nol dalam kolom yang sama dengan kolom tempat elemen diagonal tersebut berada. Jadi saat proses ini berlangsung, integeri(indeks dari kolom) dibuat konstan, sementara integerp (in-deks dari baris) bergerak darip = isampaip = n. Bila ternyata setelah mencapai elemen paling bawah dalam kolom tersebut, yaitu saat p = n tetap didapat nilai
api = 0, maka sebuah pesan dimunculkan: sistem persamaan linear tidak memiliki
solusi yang unik. Lalu program berakhir: STOP.
• Langkah 4: Namun jika sebelum integerp mencapai nilaip = n sudah diperoleh elemen yang tidak nol (api 6= 0), maka bisa dipastikan p 6= i. Jika p 6= i maka
lakukan proses pertukaran (Pp)↔(Pi).
• Langkah 5:Untukj=i+ 1, .., n, lakukan Langkah 6 dan Langkah 7.
• Langkah 6:Tentukanmji,
mji=
aji
• Langkah 7:Lakukan proses triangularisasi,
(Pj −mjiPi)→(Pj)
• Langkah 8: Setelah proses triangularisasi dilalui, periksalahann. Jikaann = 0, kirimkan
pesan:sistem persamaan linear tidak memiliki solusi yang unik. Lalu program berakhir: STOP.
• Langkah 9:Jikaann 6= 0, lakukan proses substitusi mundur, dimulai dengan menentukan
xn,
xn= an,n+1
ann
• Langkah 10:Untuki=n−1, ...,1tentukanxi,
xi =
ai,n+1−Pnj=i+1aijxj
aii
• Langkah 11:Diperoleh solusi yaitux1, x2, ..., xn. Algoritma telah dijalankan dengan
suk-ses. STOP.
Saya telah membuat program sederhana dalam fortran untuk mewujudkan algoritma elim-inasi gauss. Saya berasumsi bahwa anda sudah menguasai dasar-dasar pemrograman dalam fortran. Program ini sudah dicoba di-compile dengan fortran77 under Linux Debian dan visual-fortranunder windows-XP.
Langkah-langkah yang tercantum pada program ini disesuaikan dengan langkah-langkah yang tertulis di atas. Dalam program ini, ukuran maksimum matrik augment adalah 10 x 11, untuk mencari 10 variabel yang tidak diketahui. Jika anda bermaksud memperbesar atau memperkecil ukuran matrik augment, silakan sesuaikan angka ukuran matrik yang anda in-ginkan pada statemen pertama dari program ini, yaitu statemen DIMENSION. Inilah program-nya,
1 DIMENSION A(10,11), X(10)
2 REAL MJI
3 WRITE (*,*) ’=PROGRAM ELIMINASI GAUSS=’
4 WRITE (*,*)
5 C LANGKAH 1: MEMASUKAN NILAI ELEMEN-ELEMEN MATRIK AUGMENT
6 WRITE (*,’(1X,A)’) ’JUMLAH PERSAMAAN ? ’
7 READ (*,*) N
8 WRITE (*,*)
9 WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK AUGMENT’
10 M = N + 1
11 DO 50 I = 1,N
12 DO 60 J = 1,M
13 WRITE (*,’(1X,A,I2,A,I2,A)’) ’A(’,I,’,’,J,’) = ’
14 READ (*,*) A(I,J)
15 60 CONTINUE
16 50 CONTINUE
17 WRITE (*,*)
2.4. ALGORITMA ELIMINASI GAUSS 27
19 WRITE (*,’(1X,A)’) ’MATRIK AUGMENT:’
20 DO 110 I = 1,N
21 WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,M)
22 110 CONTINUE
23 WRITE (*,*)
24 C LANGKAH 2: MEMERIKSA ELEMEN-ELEMEN PIVOT DAN PROSES TUKAR POSISI
25 NN = N-1
26 DO 10 I=1,NN
27 C LANGKAH 3: MENDEFINISIKAN P
28 P = I
29 100 IF (ABS(A(P,I)).GE.1.0E-20 .OR. P.GT.N) GOTO 200
30 P = P+1
31 GOTO 100
32 200 IF(P.EQ.N+1)THEN
33 C MENAMPILKAN PESAN TIDAK UNIK
34 WRITE(*,5)
35 GOTO 400
36 END IF
37 C LANGKAH 4: PROSES TUKAR POSISI
38 IF(P.NE.I) THEN
39 DO 20 JJ=1,M
40 C = A(I,JJ)
41 A(I,JJ) = A(P,JJ)
42 A(P,JJ) = C
43 20 CONTINUE
44 END IF
45 C LANGKAH 5: PERSIAPAN PROSES TRIANGULARISASI
46 JJ = I+1
47 DO 30 J=JJ,N
48 C LANGKAH 6: TENTUKAN MJI
49 MJI = A(J,I)/A(I,I)
50 C LANGKAH 7: MELAKUKAN PROSES TRIANGULARISASI
51 DO 40 K=JJ,M
52 A(J,K) = A(J,K)-MJI*A(I,K)
53 40 CONTINUE
54 A(J,I) = 0
55 30 CONTINUE
56 10 CONTINUE
57 C MENAMPILKAN HASIL TRIANGULARISASI
58 WRITE (*,’(1X,A)’) ’HASIL TRIANGULARISASI:’
59 DO 120 I = 1,N
60 WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,M)
61 120 CONTINUE
62 C LANGKAH 8: MEMERIKSA ELEMEN A(N,N)
63 IF(ABS(A(N,N)).LT.1.0E-20) THEN
64 C MENAMPILKAN PESAN TIDAK UNIK
65 WRITE(*,5)
66 GOTO 400
67 END IF
68 C LANGKAH 9: MENGHITUNG X(N)
69 X(N) = A(N,N+1)/A(N,N)
70 C LANGKAH 10: PROSES SUBSTITUSI MUNDUR
71 L = N-1
72 DO 15 K=1,L
73 I = L-K+1
74 JJ = I+1
75 SUM = 0.0
76 DO 16 KK=JJ,N
78 16 CONTINUE
79 X(I) = (A(I,N+1)-SUM)/A(I,I)
80 15 CONTINUE
81 C LANGKAH 11: MENAMPILKAN HASIL PERHITUNGAN
82 WRITE (*,*)
83 WRITE (*,7)
84 DO 18 I = 1,N
85 WRITE (*,’(1X,A,I2,A,F14.8)’) ’X(’,I,’) = ’,X(I)
86 18 CONTINUE
87 400 STOP
88
89 5 FORMAT(1X,’SISTEM LINEAR TIDAK MEMILIKI SOLUSI YANG UNIK’)
90 7 FORMAT(1X,’SOLUSI UNIK’)
91 END
Scripteliminasi gauss dalam matlab juga telah dibuat. Namun dalam anda perlu memodifikasi elemen-elemen matrik A agar sesuai dengan data yang hendak anda olah.
1 clear all
2 clc
3 A(1,1)=1;
4 A(1,2)=1;
5 A(1,3)=-1;
6 A(1,4)=0;
7 A(2,1)=6;
8 A(2,2)=-4;
9 A(2,3)=0;
10 A(2,4)=24;
11 A(3,1)=6;
12 A(3,2)=0;
13 A(3,3)=2;
14 A(3,4)=10;
15 A
16 n=3 %jumlah persamaan
17 pause
18
19 %========== Proses Triangularisasi =========
20 for j=1:(n-1)
21
22 %----mulai proses
pivot---23 if (A(j,j)==0)
24 for p=1:n+1
25 u=A(j,p);
26 v=A(j+1,p);
27 A(j+1,p)=u;
28 A(j,p)=v;
29 end
30 end
31 %----akhir proses
pivot---32 jj=j+1;
33 for i=jj:n
34 m=A(i,j)/A(j,j);
35 for k=1:(n+1)
36 A(i,k)=A(i,k)-(m*A(j,k));
37 end
38 end
39 end
2.5. CONTOH APLIKASI 29
41 pause
42 %========= Akhir Proses Triangularisasi ===
43
44 %---Proses Substitusi
mundur---45 x(n,1)=A(n,n+1)/A(n,n);
46
47 for i=n-1:-1:1
48 S=0;
49 for j=n:-1:i+1
50 S=S+A(i,j)*x(j,1);
51 end
52 x(i,1)=(A(i,n+1)-S)/A(i,i);
53 end
54 x
2.5 Contoh aplikasi
2.5.1 Menghitung arus listrik
Gunakan metode Eliminasi Gauss untuk menentukan arusi1, i2 dan i3 yang mengalir pada rangkaian berikut ini
jawab:
Berdasarkan Hukum Kirchhoff:
I1+I2 = I3
10−6I1−2I3 = 0 −14 + 6I1−10−4I2 = 0
Lalu kita susun ulang ketiga persamaan di atas menjadi seperti ini:
I1+I2−I3 = 0
6I1+ 2I3 = 10
Kemudian dinyatakan dalam bentuk matriks:
1 1 −1 6 −4 0 6 0 2
I1
I2
I3
=
0 24 10
Selanjutkan kita susun matriks augmentasi sebagai berikut:
1 1 −1 0 6 −4 0 24 6 0 2 10
Langkah berikutnya adalah menghitung matriks triangularisasi dengan langkah-langkah se-bagai berikut:
m= a21
a11
= 6
1 = 6
a21=a21−m.a11= 6−(6).(1) = 0
a22=a22−m.a12=−4−(6).(1) = −10
a23=a23−m.a13= 0−(6).(−1) = 6
a24=a24−m.a14= 24−(6).(0) = 24
m= a31
a11
= 6
1 = 6
a31=a31−m.a11= 6−(6).(1) = 0
a32=a32−m.a12= 0−(6).(1) = −6
a33=a33−m.a13= 2−(6).(−1) = 8
a34=a34−m.a14= 10−(6).(0) = 10
Sampai disini matriks augment mengalami perubahan menjadi
1 1 −1 0 0 −10 6 24 0 −6 8 10
2.6. MENGHITUNG INVERS MATRIK 31
Kelanjutan langkah menuju triangularisasi adalah
m= a32
a22
= −6
−10
a31=a31−m.a21= 0−( −
6
−10).(0) = 0
a32=a32−m.a22=−6−( −6
−10).(−10) = 0
a33=a33−m.a23= 8−( −
6
−10).(6) = 4,4
a34=a34−m.a24= 10−( −
6
−10).(24) = −4,4
maka matriks triangularisasi berhasil didapat yaitu
1 1 −1 0 0 −10 6 24 0 0 4,4 −4,4
Sekarang tinggal melakukan proses substitusi mundur
I3 =
a34
a33
= −4,4 4,4 =−1
I2 =
a24−a23.I3
a22
= 24−(6).(−1)
−10 =−3
I1=
a14−(a13.I3+a12.I2)
a11
= (0−[(−1).(−1) + (1).(−3)]
1 = 2
Dengan demikian, besar masing-masing arus pada rangkaian di atas adalahI1 = 2A,I2 =−3A danI3 =−1A. Tanda minus (-) memiliki arti bahwa arah arus yang sesungguhnya berlawanan arah dengan asumsi awal yang kita gunakan.
2.6 Menghitung invers matrik
Sekali lagi saya ulangi apa yang pernah kita bahas di awal bab ini yaitu bahwa sistem per-samaan linear dapat dinyatakan sebagai berikut:
a11x1+a12x2+. . .+a1nxn = b1
a21x1+a22x2+. . .+a2nxn = b2
. . . = . . . . . . = . . . an1x1+an2x2+. . .+annxn = bn
Sistem persamaan linear tersebut dapat dinyatakan dalam bentuk operasi matrik,
sehingga bentuknya menjadi seperti ini:
Dalam kaitannya dengan invers matrik, matrikAdisebut matriknon-singularjika matrik
Amemiliki matrik invers dirinya yaituA−1. Atau dengan kata lain, matrikA−1adalah invers dari matrik A. Jika matrik A tidak memiliki invers, maka matrik A disebut singular. Bila matrikAdikalikan dengan matrikA−1maka akan menghasilkan matrik identitasI, yaitu suatu matrik yang elemen-elemen diagonalnya bernilai 1.
AA−1 =I=
Bila keduanya dikalikan, maka akan menghasilkan matrik identitas,
AA−1=
2.6. MENGHITUNG INVERS MATRIK 33
dalam hal ini matrikA−1adalah
A−1 =
Elemen-elemen matrik invers, A−1 dapat diperoleh dengan menerapkan metode eliminasi gauss. Diawali dengan membentuk matrik augment:
Langkah berikutnya, matrik augment yang telah mengalami triangularisasi tersebut dipecah menjadi tiga buah matrik augment seperti berikut ini:
Langkah pamungkasnya adalah melakukan proses substitusi mundur pada ketiga matrik aug-ment di atas, sehingga diperoleh:
i11=−29
Hasil tersebut digabung menjadi sebuah matrik, yaitu matrikA−1,
A−1=
(mencari nilai x), dengan cara sebagai berikut
Ax = b
A−1Ax = A−1b Ix = A−1b
x = A−1b (2.12)
Contoh berikut ini akan menjelaskan prosesnya secara lebih rinci. Misalnya diketahui sistem persamaan linear
x1+ 2x2−x3 = 2
2x1+x2 = 3
−x1+x2+ 2x3 = 4
Bila dikonversikan kedalam operasi matrik menjadi
Berdasarkan persamaan (2.12), maka elemen-elemen vektorxdapat dicari dengan cara
x=A−1b linear menjadi lebih mudah bila matrik A−1 sudah diketahui. Sayangnya, untuk mendap-atkan matrikA−1, diperlukan langkah-langkah, seperti yang sudah dibahas pada contoh per-tama di atas, yang berakibat in-efisiensi proses penyelesaian (secara komputasi) bila diband-ingkan dengan metode eliminasi gauss untuk memecahkan sistem persamaan linear. Namun bagaimanapun, secara konseptual kita dianjurkan mengetahui cara bagaimana mendapatkan matrikA−1.
Saya telah memodifikasi program eliminasi gauss yang terdahulu, untuk keperluan perhi-tungan matrik invers. Program ini ditulis dengan bahasa fortran, sudah berhasil dikompilasi dalam Linux Debian (g77) dan Windows XP (Visual Fortran). Inilah programnya,
1 DIMENSION A(10,20), D(10,10), X(10)
2 REAL MJI
3 INTEGER TKR, BK, TK, Q
4 WRITE (*,*) ’=PROGRAM INVERS MATRIK DENGAN ELIMINASI GAUSS=’
2.6. MENGHITUNG INVERS MATRIK 35
6 C LANGKAH 1: MEMASUKAN NILAI ELEMEN-ELEMEN MATRIK A
7 WRITE (*,’(1X,A)’) ’JUMLAH PERSAMAAN ? ’
8 READ (*,*) N
9 WRITE (*,*)
10 WRITE (*,*) ’MASUKAN ELEMEN-ELEMEN MATRIK A’
11 M = N + 1
12 DO 50 I = 1,N
13 DO 60 J = 1,N
14 WRITE (*,’(1X,A,I2,A,I2,A)’) ’A(’,I,’,’,J,’) = ’
15 READ (*,*) A(I,J)
16 60 CONTINUE
17 50 CONTINUE
18 C LANGKAH 2: MENDEFINISIKAN MATRIK IDENTITAS
19 WRITE (*,*) ’MENDEFINISIKAN MATRIK IDENTITAS’
20 DO 70 I = 1,N
21 DO 80 J = M,N+N
22 A(I,J) = 0
23 IF (I+N .EQ. J) THEN
24 A(I,J) = 1
25 END IF
26 80 CONTINUE
27 70 CONTINUE
28 WRITE (*,*)
29 C MENAMPILKAN MATRIK AUGMENT
30 WRITE (*,’(1X,A)’) ’MATRIK AUGMENT:’
31 DO 110 I = 1,N
32 WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,N+N)
33 110 CONTINUE
34 WRITE (*,*)
35 C MENGHITUNG JUMLAH TUKAR (TKR) POSISI. MULA2 TKR = 0
36 TKR = 0
37 C MENGHITUNG JUMLAH OPERASI BAGI/KALI (BK).
38 BK = 0
39 C MENGHITUNG JUMLAH OPERASI TAMBAH/KURANG (TK).
40 TK = 0
41 C LANGKAH 3: MEMERIKSA ELEMEN2 PIVOT DAN PROSES TUKAR POSISI
42 NN = N-1
43 DO 10 I=1,NN
44 C LANGKAH 4: MENDEFINISIKAN P
45 P = I
46 100 IF (ABS(A(P,I)).GE.1.0E-20 .OR. P.GT.N) GOTO 200
47 P = P+1
48 GOTO 100
49 200 IF(P.EQ.N+1)THEN
50 C MENAMPILKAN PESAN SINGULAR
51 WRITE(*,5)
52 GOTO 400
53 END IF
54 C LANGKAH 5: PROSES TUKAR POSISI
55 IF(P.NE.I) THEN
56 DO 20 JJ=1,N+N
57 C = A(I,JJ)
58 A(I,JJ) = A(P,JJ)
59 A(P,JJ) = C
60 TKR = TKR + 1
61 20 CONTINUE
62 END IF
63 C LANGKAH 6: PERSIAPAN PROSES TRIANGULARISASI
65 DO 30 J=JJ,N
66 C LANGKAH 7: TENTUKAN MJI
67 MJI = A(J,I)/A(I,I)
68 BK = BK + 1
69 C LANGKAH 8: MELAKUKAN PROSES TRIANGULARISASI
70 DO 40 K=JJ,N+N
71 A(J,K) = A(J,K)-MJI*A(I,K)
72 BK = BK + 1
73 TK = TK + 1
74 40 CONTINUE
75 A(J,I) = 0
76 30 CONTINUE
77 10 CONTINUE
78 C MENAMPILKAN HASIL TRIANGULARISASI
79 WRITE (*,’(1X,A)’) ’HASIL TRIANGULARISASI:’
80 DO 120 I = 1,N
81 WRITE (*,’(1X,5(F14.8))’) (A(I,J),J=1,N+N)
82 120 CONTINUE
83 C LANGKAH 9: MEMERIKSA ELEMEN A(N,N)
84 IF(ABS(A(N,N)).LT.1.0E-20) THEN
85 C MENAMPILKAN PESAN SINGULAR
86 WRITE(*,5)
87 GOTO 400
88 END IF
89 DO 500 J = 1,N
90 Q=N+J
91 C LANGKAH 10: MENGHITUNG A(N,N)
92 D(J,N) = A(N,Q)/A(N,N)
93 BK = BK + 1
94 C LANGKAH 11: PROSES SUBSTITUSI MUNDUR
95 L = N-1
96 DO 15 K=1,L
97 I = L-K+1
98 JJ = I+1
99 SUM = 0.0
100 DO 16 KK=JJ,N
101 SUM = SUM+A(I,KK)*D(J,KK)
102 BK = BK + 1
103 TK = TK + 1
104 16 CONTINUE
105 D(J,I) = (A(I,Q)-SUM)/A(I,I)
106 BK = BK + 1
107 TK = TK + 1
108 15 CONTINUE
109 500 CONTINUE
110 C LANGKAH 12: MENAMPILKAN HASIL PERHITUNGAN
111 WRITE (*,*)
112 WRITE (*,’(1X,A)’) ’MATRIK INVERS:’
113 DO 220 I = 1,N
114 WRITE (*,’(1X,5(F14.8))’) (D(J,I),J=1,N)
115 220 CONTINUE
116 WRITE(*,8) TKR
117 WRITE(*,9) BK
118 WRITE(*,11) TK
119 400 STOP
120 5 FORMAT(1X,’MATRIK A BERSIFAT SINGULAR’)
121 8 FORMAT(1X,’JUMLAH TUKAR POSISI = ’,3X,I5)
122 9 FORMAT(1X,’JUMLAH OPERASI BAGI/KALI = ’,3X,I6)
2.7. PENUTUP 37
124 END
2.7 Penutup
Bab 3
Aplikasi Eliminasi Gauss pada Masalah
Inversi
✍Objektif :
⊲ Mengenalkan model garis.
⊲ Mengenalkan model parabola.
⊲ Mengenalkan model bidang.
Pada bab ini, saya mencoba menuliskan aplikasi Metode Eliminasi Gauss sebagai dasar-dasar teknik inversi yaitu meliputi model garis, model parabola dan model bidang. Uraian ap-likasi tersebut diawali dari ketersediaan data observasi, lalu sejumlah parameter model mesti dicari dengan teknik inversi. Mari kita mulai dari model garis.
3.1 Inversi Model Garis
Pengukuran temperatur terhadap kedalaman di bawah permukaan bumi menunjukkan bahwa semakin dalam, temperatur semakin tinggi. Misalnya telah dilakukan sebanyak empat kali (N
= 4) pengukuran temperatur (Ti) pada kedalaman yang berbeda beda (zi). Tabel pengukuran
secara sederhana disajikan seperti ini:
Tabel 3.1: Data temperatur bawah permukaan tanah terhadap kedalaman Pengukuran ke-i Kedalaman(m) Temperatur(OC)
1 z1 = 5 T1= 35
2 z2 = 16 T2= 57
3 z3 = 25 T3= 75
4 z4 = 100 T4= 225
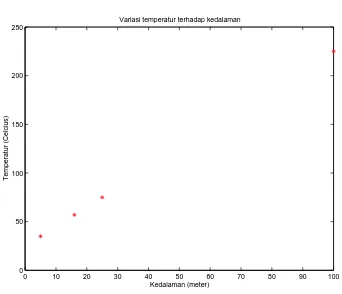
Grafik sebaran data observasi ditampilkan pada Gambar (3.1). Lalu kita berasumsi bahwa variasi temperatur terhadap kedalaman ditentukan oleh rumus berikut ini:
m1+m2zi=Ti (3.1)
0 10 20 30 40 50 60 70 80 90 100 0
50 100 150 200 250
Kedalaman (meter)
Temperatur (Celcius)
Variasi temperatur terhadap kedalaman
Gambar 3.1: Sebaran data observasi antara temperatur dan kedalaman
dimanam1danm2adalah konstanta-konstanta yang akan dicari. Rumus di atas disebutmodel matematika. Sedangkanm1danm2disebutparameter model. Pada model matematika di atas terdapat dua buah parameter model, (M = 2). Sementara jumlah data observasi ada empat,
(N = 4), yaitu nilai-nilai kedalaman,zi, dan temperatur,Ti. Berdasarkan model tersebut, kita
bisa menyatakan temperatur dan kedalaman masing-masing sebagai berikut:
m1+m2z1=T1
m1+m2z2=T2
m1+m2z3=T3
m1+m2z4=T4
Semua persamaan tersebut dapat dinyatakan dalam operasi matrik berikut ini:
1 z1
1 z2
1 z3
1 z4
"
m1
m2 #
=
T1
T2
T3
T4
(3.2)
Lalu ditulis secara singkat
Gm=d (3.3)
menda-3.1. INVERSI MODEL GARIS 41
patkan nilaim1danm2pada vektor kolomm? Manipulasi berikut ini bisa menjawabnya
GtGm=Gtd (3.4)
dimanatdisini maksudnya adalah tanda transpos matrik. Selanjutnya, untuk mendapatkan elemen-elemenm, diperlukan langkah-langkah perhitungan berikut ini:
1. Tentukan transpos dari matrik kernel, yaituGt
G=
3. Kemudian tentukan pulaGtd
Gtd=
4. Sekarang persamaan (3.4) dapat dinyatakan sebagai
"
5. Aplikasikan metodeEliminasi Gauss dengan Substitusi Mundur. Untuk itu, tentukan matrik augment-nya
tabel pengukuran dihalaman depan.
"
4 146 | 392 146 10906 | 25462
#
7. Lakukan proses triangularisasi dengan operasi (P2 −(36,5)P1) → P2. Saya sertakan pula indeks masing-masing elemen pada matrik augment sebagaimana yang telah saya lakukan pada catatan kuliah yang berjudulMetode Eliminasi Gauss. Hasilnya adalah
"
4 146 | 392 0 5577 | 11154
# =
"
a11 a12 | a13
a21 a22 | a23
#
8. Terakhir, tentukan konstantam1 danm2 yang merupakan elemen-elemen vektor kolom m, dengan proses substitusi mundur. Pertama tentukanm2
m2 =
a23
a22
= 11154 5577 = 2
lalu tentukanm1
m1 =
a13−a12m2
a11
= 392−(146)(2) 4 = 25
3.1.1 Script matlab inversi model garis
Script inversi model garis ini dibangun dari beberapa script yang sudah kita pelajari sebelum-nya, yaitu script transpose matriks, perkalian matrik dan script eliminasi gauss. Silakan pela-jari maksud tiap-tiap baris pada script ini.
1 clc
2 clear all
3
4 disp(’Data observasi’)
5 z1=5;
6 z2=16;
7 z3=25;
8 z4=100;
9
10 T(1,1)=35;
11 T(2,1)=57;
12 T(3,1)=75;
13 T(4,1)=225;
14
15 disp(’Elemen-elemen matriks kernel G’)
16 G(1,1)=1;
17 G(1,2)=z1;
18 G(2,1)=1;
19 G(2,2)=z2;
20 G(3,1)=1;
21 G(3,2)=z3;
22 G(4,1)=1;
23 G(4,2)=z4;
3.1. INVERSI MODEL GARIS 43
25 d=T;
26 d
27
28 N=4; %jumlah data
29 M=2; %model parameter
30
31 disp(’Mencari G transpos’)
32 for i=1:N
33 for j=1:M
34 GT(j,i)=G(i,j);
35 end
36 end
37 GT
38
39 disp(’Perkalian GT dan G’)
40 for i=1:M
41 for j=1:M
42 GTG(i,j)=0;
43 end
44 end
45 for i=1:M
46 for j=1:M
47 for k=1:N
48 GTG(i,j)=GTG(i,j)+GT(i,k)*G(k,j);
49 end
50 end
51 end
52 GTG
53
54 disp(’Perkalian GT dan d’)
55 for i=1:M
56 for j=1:1
57 GTd(i,j)=0;
58 end
59 end
60 for i=1:M
61 for j=1:1
62 for k=1:N
63 GTd(i,j)=GTd(i,j)+GT(i,k)*d(k,j);
64 end
65 end
66 end
67 GTd
68
69 A=GTG;
70 %====== Menggabungkan Vektor GTd kedalam matrik A ========
71 n=M;
72 for i=1:n
73 A(i,n+1)=GTd(i,1);
74 end
75 A
76
77 %&&&&&& Proses Eliminasi Gauss &&&&&&&&&&&&&&&&&&&&&&&&&
78 %---Proses
Triangularisasi---79 for j=1:(n-1)
80
81 %----mulai proses
pivot---82 if (A(j,j)==0)
84 u=A(j,p);
85 v=A(j+1,p);
86 A(j+1,p)=u;
87 A(j,p)=v;
88 end
89 end
90 %----akhir proses
pivot---91 jj=j+1;
92 for i=jj:n
93 m=A(i,j)/A(j,j);
94 for k=1:(n+1)
95 A(i,k)=A(i,k)-(m*A(j,k));
96 end
97 end
98 end
99
%---100
101 %---Proses Substitusi
mundur---102 x(n,1)=A(n,n+1)/A(n,n);
103
104 for i=n-1:-1:1
105 S=0;
106 for j=n:-1:i+1
107 S=S+A(i,j)*x(j,1);
108 end
109 x(i,1)=(A(i,n+1)-S)/A(i,i);
110 end
111 %&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
112 disp(’Model parameter yang dicari’)
113 m=x
Sebetulnya, matlab telah menyediakan fungsi-fungsi intrinsik yang bisa digunakan sehing-ga dapat memperkecil jumlah baris pada script di atas. Dari line 28 sampai line 113 dapat dipangkas menjadi
1 m=inv(G’*G)*G’*d %Proses inversi linear
Lalu mengapa kita harus bersusah payah membangun script yang begitu panjang bila mat-lab bisa melakukannya dengan mudah? Karena kita sedang mempelajari teknik-teknik kom-putasi untuk menyelesaikan problem sains dan teknik. Kita tidak sedang belajar matlab. Ja-di teknik-teknik yang Ja-dipelajari Ja-disini harus bisa Ja-diterapkan Ja-di selain matlab. Script singkat
m =inv(G′∗G)∗G′ ∗dhanya berlaku di matlab, sementara script yang panjangnya 113line