PERBANDINGAN PROGRAM DINAMIS DAN ALGORITMA GREEDY DALAM MENYELESAIKAN MASALAH CHINESE POSTMAN PROBLEM

PERBANDINGAN PROGRAM DINAMIS DAN ALGORITMA

GREEDY

DALAM MENYELESAIKAN MASALAH

CHINESE POSTMAN PROBLEM

Yudhi P M, Wamiliana dan Fitriani.

Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Lampung

Yudhi_pm@yahoo.com

Abstrak.PermasalahanChinese Postman Problemadalah bagaimana seorang tukang pos akan mengantarkan surat ke alamat-alamat sepanjang jalan di suatu daerah dan bagaimana ia merencanakan rute perjalanannya supaya ia melewati setiap jalan tepat sekali dan kembali lagi ke tempat awal keberangkatannya dengan jarak / waktu / ongkos seminimal mungkin. Lintasan dan sirkuit yang digunakan dalam penelitian ini adalah lintasan dan sirkuitEuler. Pada penelitian ini algoritmaGreedydibandingkan dengan Program Dinamis untuk menyelesaikan permasalahanChinese Postmandengan menggunakan peta wilayah kelurahan Kedaton Bandar Lampung sebagai contoh. Hasil penelitian menunjukan bahwa metode Program Dinamis menghasilkan nilai yang lebih baik.

Kata Kunci.Chinese Postman Problem, SirkuitEuler, algortima Greedy, program dinamis.

PENDAHULUAN

MasalahChinese Postman Problem(CPP) pertama kali diformulasikan dalam bentuk masalah untuk menentukan jalan terpendek bagi seorang tukang pos untuk melewati semua jalan yang ada dan kembali ke tempat semula. Masalah ini dikemukakan oleh Kwan Mei-Ko di awal 1960-an dalam jurnal Chinese Mathematics. Dalam istilah graf definisi CPP adalah mencari lintasan pada suatu graf berbobot yang terhubung yang melewati semua sisi (minimal sekali) dengan jumlah bobot minimum dari suatu simpul kembali ke simpul awal . Pada permasalahan

Chinese Postman Problem terdapat beberapa metode untuk menentukan jarak terpendek untuk memberikan solusi optimum pada permasalah tersebut seperti metode Program Dinamis dan AlgoritmaGreedy.

Graf G = (V,E) terdiri dariV= {ݒ_ଵ,ݒ_ଶ, … } yang disebutvertex / node(titik) yang tidak kosong, dan

E= {݁_௜௝; i, j∈V} yang unsur-unsurnya disebut

edge(garis) yang boleh kosong .Eulerianerupakan graf yang mempunyai derajat genap untuk semua

vertexnya dan setiapedgenya dilewati tepat satu kali. [1]

LintasanEulerialah lintasan yang melalui masing-masing edge di dalam graf tepat satu kali. Bila lintasan itu kembali ke simpul asal maka

membentuk lintasan tertutup (sirkuit), sehingga lintasan tertutup itu dinamakan sirkuitEuler. [6]

Postman Tourdalam suatu grafGadalahclosed walkyang melewati setiapedgenya dari G paling sedikit satu kali. [2]

Algoritma Greedymerupakan metode untuk menemukan solusi optimum dalam persoalan optimasi dengan solusi langkah per langkah.[4]

Program Dinamis (dynamic programming) adalah metode penyelesaian masalah dengan cara menguraikan solusi menjadi sekumpulan langkah (step) atau tahapan (stage) sedemikian sehingga solusi dari persoalan dapat dipandang dari serangkaian keputusan yang saling berkaitan.

Pada penyelesaian persoalan dengan metode ini terdapat sejumlah berhingga pilihan yang mungkin. Solusi pada setiap tahap dibangun dari hasil solusi tahap sebelumnya. Persyaratan optimasi dan kendala digunakan untuk membatasi sejumlah pilihan yang harus dipertimbangkan pada suatu tahap.

Prosiding Seminar dan Rapat

FMIPA Universitas Lampung, 10

METODE P

Adapun langkah-langkah yan penelitian adalah sebagai berik

1. Tentukan semua ver

dalam graf.

2. Tentukan semua k padavertexberderajat 3. Tentukan matching

minimum denga algoritmaGreedyda 4. Tambahkan edge y

langkah 3 terhadap g 5. Hitung panjang linta permasalahan Chin

jumlah dari semu ditambah dengan pe Langkah 4.

6. Tentukan / konstru menyatakan Euler

permasalahan Un Postman Problem.

1. Himpunan Kandidat Himpunan ini berisi elemen-e peluang untuk pembentuk sol 2. Himpunan Solusi

Himpunan ini berisi solusi da diselesaikan dan elemennya dalam himpunan kandidat, na atau dengan kata lain himpu bagian dari himpunan kandida 3. Fungsi Seleksi

Fungsi seleksi adalah fun kandidat yang paling m himpunan kandidat untuk d himpunan solusi agar solus Kandidat yang sudah terpilih tidak akan dipertimbangkan selanjutnya

4. Fungsi Kelayakan Fung fungsi yang memeriksa apak terpilih akan menimbulkan so kandidat tersebut bersama den yang terpilih tidak akan mel berlaku pada masalah. 5. Fungsi Obyektif

Fungsi oby yang memaksimalka nilai solusi. Tujuan satu saja solusi ter masing anggota himp

Pada program dinamis, rangk optimal dibuat dengan m optimalitas. Prinsip optimali

t Tahunan BKS PTN Barat 2013

10 – 12 Mei 2013

PENELITIAN

ang digunakan dalam erikut :

vertex berderajat ganjil

kemungkinan pairing

rajat ganjil.

g yang memiliki bobot ngan menggunakan

dan program dinamis. yang minimum pada p graf

ntasan yang optimal dari

hinese Postman adalah mua edge graf awal penambahan edge pada

truksikan sirkuit yang

ulerian tour dalam

Undirected Chinese

elemen yang memiliki solusi

dari permasalahan yang ya terdiri dari elemen namun tidak semuanya punan solusi ini adalah idat

fungsi yang memilih memungkinkan dari dimasukkan ke dalam lusi optimal terbentuk. ilih pada suatu langkah an lagi pada langkah

ngsi kelayakan adalah pakah suatu calon yang solusi yang layak, yaitu dengan himpunan solusi elanggar kendala yang

obyektif adalah fungsi lkan atau meminimalkan annya adalah memilih terbaik dari masing-impunan solusi.[7]

ngkaian keputusan yang menggunakan prinsip alitas ini adalah : jika

solusi total optimal, maka tahap ke-k juga optimal. Prin bahwa jika bekerja dari tah maka dapat menggunakan h

ktanpa harus kembali ke tah tahap k+1 = (ongkos yang ) + (ongkos dari tahapkke ta

Pada tahap n proses aka keadaan sn. Pembuatan ke

selanjutnya menggerakan pr tahap (n + 1). Kontribusi fungsi tujuan di bawah ke dihitung sebelumnya se Keputusan kebijakan xn ju

kontribusi kepada funngs kedua nilai ini dengan ben

fn(sn, xn), yaitu kontribusin

fungsi tujuan .

Pengoptimalan terhadap xn

Setelah ditemukanxn*danf

sn, prosedur penyelesaian s

mundur satu tahap. Sala mengkategorikan masalah p deterministik adalah dengan Sebagai contoh, tujuanny meminimumkan jumlah k tahap individual, atau un jumlah tersebut, atau untuk produk, dan seterusnya.[3]

HASIL DAN PEMBA

Berikut ini diberikan conto masalah Chinese Postman P

berarah peta wilayah konfig Lampung

2

ka bagian solusi sampai rinsip optimalitas berarti tahap k ke tahap k + 1, hasil optimal dari tahap tahap awal. Ongkos pada dihasilkan pada tahapk

e tahapk+ 1).[5]

kan berada pada suatu keputusan kebijakan xn

proses keadaansn+1pada

usi sesudahnya terhadap kebijakan optimal telah sebagai fn+1*(sn+1).

juga memberi beberapa gsi tujuan. Kombinasi benar akan memberikan

n tahap kedepan kepada

n fn*(sn) = fn(sn, xn*).

fn*(sn) untuk setiap nilai

sekarang siap bergerak alah satu cara untuk lah pemrograman dinamis an bentuk fungsi tujuan. nnya mungkin adalah kontribusi dari tahap-untuk memaksimumkan uk meminimumkan suatu

BAHASAN

ntoh kasus penyelesaian

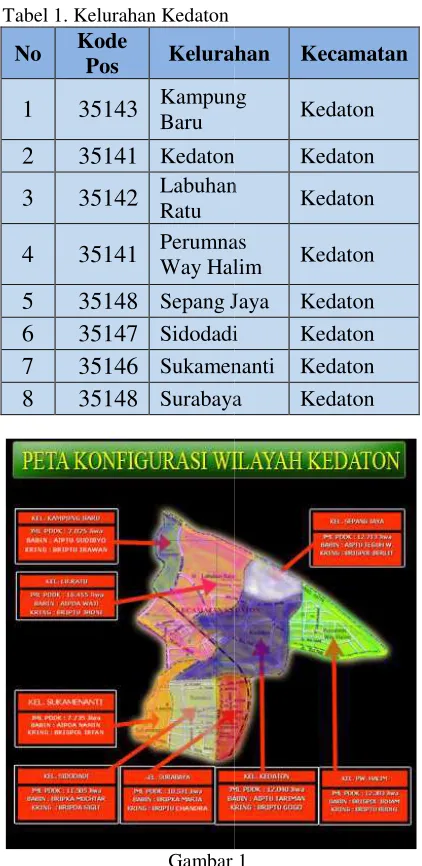
Tabel 1. Kelurahan Kedaton

No

Kode

Pos

Kelurah

1

35143

Kampung

Baru

2

35141

Kedaton

3

35142

Labuhan

Ratu

4

35141

Perumnas

Way Hal

5

35148

Sepang J

6

35147

Sidodadi

7

35146

Sukamena

8

35148

Surabaya

Gambar 1

Gambar di atas dapat direpres graf yang merepresentasikan wilayah Kedaton sebagai berik

Gambar 2

rahan

Kecamatan

pung

Kedaton

on

Kedaton

buhan

Kedaton

nas

alim

Kedaton

ng Jaya

Kedaton

di

Kedaton

enanti

Kedaton

ya

Kedaton

ar 1

resentasikan kedalam an peta konfigurasi erikut

ar 2

Dengan menggunakan bantu

Map, dapat diketahui jarak a terhubung berikut ini.

Gambar

Kelurahan Kampung Baru – Ratu = 3.2 km

Kelurahan Sukamenanti – Ke Ratu = 3.5 km

Kelurahan Sepang Jaya – Ke = 3.2 km

Kelurahan Kedaton – Kelura 2.6 km

Kelurahan Sepang Jaya – Ke Way halim = 1.6 km

Kelurahan Sepang jaya – Ke km

Kelurahan Perumnas Way ha Kedaton = 1.4 km

Kelurahan Sidodadi – Kelura km

Kelurahan Surabaya – Kelur km

Kelurahan Sukamenanti – Ke km

Kelurahan Sidodadi – Kelura km

ntuan pencitraanGoogle

k antara kelurahan yang

bar 3

– Kelurahan Labuhan

Kelurahan Labuhan

Kelurahan Labuhan ratu

urahan Labuhan ratu =

Kelurahan Permunas

Kelurahan Kedaton = 1.4

halim – Kelurahan

lurahan Kedaton = 2.5

lurahan Kedaton = 3.3

Kelurahan kedaton = 3.4

Prosiding Seminar dan Rapat

FMIPA Universitas Lampung, 10 Gambar 4

Tahap-tahap Penyelesaian

AlgoritmaGreedy

1. Pada setiap langka berbobot minimum yang me

vertex yang sudah terpilih d lain yang belum terpilih. 2. Lintasan dari vertex

baru haruslah merupak terpendek diantara semua l

vertexyang belum terpilih. Berikut ini adalah tahap-tah dengan menggunakan Algor

Tahap 1 : Penelusuran dim pada Gambar 1 terdapat 1 vertex

Sehingga, perjalan

vertex v3 yang m

bernilai 3,2

Tahap 2 : Dari vertex v3 ter

terhubung padav v7. Dari ketiga v

yang memiliki b

vertex v2bernilai

Tahap 3 : Dari vertex v2 ter

terhubung padav v5, v6, v7, v8

tersebut yang d dilalui adalah 5v

satu vertex yang

vertex v8. Dari

memiliki bobot ter

v4danv5bernilai

yang dipilih ada

vertex v5adalahv

Total jarak yang dapat ditemp

vertex v5dengan menggunaka

adalah 7,2 denganpath v1-v3

-t Tahunan BKS PTN Bara-t 2013

10 – 12 Mei 2013 ar 4

Masalah dengan

kah, ambil sisi yang menghubungkan sebuah ih dengan sebuahvertex

tex asal ke vertex yang akan lintasan yang a lintasannya ke

vertex-ih.

tahap penelusuran jalur goritmaGreedy:

imulai dari vertex v1

16. Pada vertex v1 ertex tunggal yaitu v3.

rjalanan harus melalui g memiliki bobot yang

terdapat 3 edge yang

vertex v3yaituv2, v5,

vertextersebut vertex

i bobot terkecil adalah ilai 2,6.

terdapat 6 edge yang

vertex v3yaituv3, v4,

. Dari keenamvertex

dapat diseleksi utnuk

vertex,karena terdapat ang telah dilalui yaitu ri kelima vertex yang t terkecil adalahvertex

ilai 1,4, sehinggavertex

dalah vertex v5, karena

vertextujuan.

mpuh darivertex v1ke

kan algoritma Greedy

-v2– v5.

Gambar

Penyelesaian Masalah deng Dinamis

Misalkanv1,v2, …,v4adalah

dikunjungi pada tahapk(k= Pada persoalan ini,Tahap(k

memilih simpul tujuan berik

Status(s) yang berhubungan masing tahap adalah simpul Relasi rekurensi berikut men terpendek :

xk : peubah keputusan pada

k sx

c

: bobot (cost) sisi dari

fk(s,xk) : total bobot lintasan

fk(s) : nilai minimum darifk

Tujuan program dinamis mendapatkanf2(v5) dengan c

terlebih dahulu

.

4

bar 6

engan Metode Program

lah simpul-simpul yang = 1, 2, 3, 4).

k) adalah proses rikutnya

an dengan masing-ul-simpul di dalam graf.

enyatakan lintasan

Gambar 7

Tahap 2 :fx(s) = minx2{cx2s+ f1(x2)},

Gambar 8

Tabel diatas diperoleh dari hasil perhitu berikut ini

f2(x2, s) =cx2s +f1(x2)

x2 =v3: f2(v3,v2) = 2,6 + 3,2 = 5,8

x2 =v3: f2(v3,v5) = 3,2 + 3,2 = 6,4

x2 =v3: f2(v3,v7) = 3,2 + 3,2 = 6,7

x1 s

Solusi optimum

f1(s) x

v3 3,2

x2

s

f2(x2, s) =cx2s +f1(x2)

Solu optim

v3 f2(s)

v2 5,8 5,8

v5 6,4 6,4

v7 6,7 6,7

itungan

v3-v5.

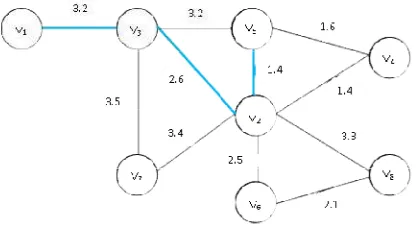
Gambar 9

Dari perbandingan kedua metode

pathdengan bobot minimum adalah menggunakan program dinamis de 34,6 km, yang dapat dilihat pada

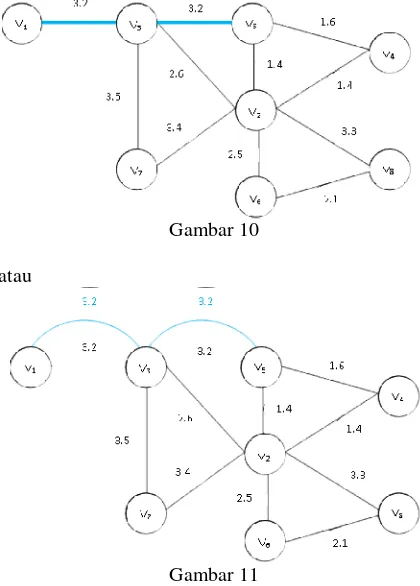
Gambar 10

atau

Gambar 11

Berikut adalah konstruksi yang me perjalananChinese Postman Prob

Kedaton Bandar Lampung

m x1*

v1

olusi timum

x2*

v3

v2

v2

de tersebut didapat alah dengan

dengan total jarak gambar berikut :

menyatakan jalan/rute

Prosiding Seminar dan Rapat Tahunan BKS PTN Barat 2013

FMIPA Universitas Lampung, 10 – 12 Mei 2013

6

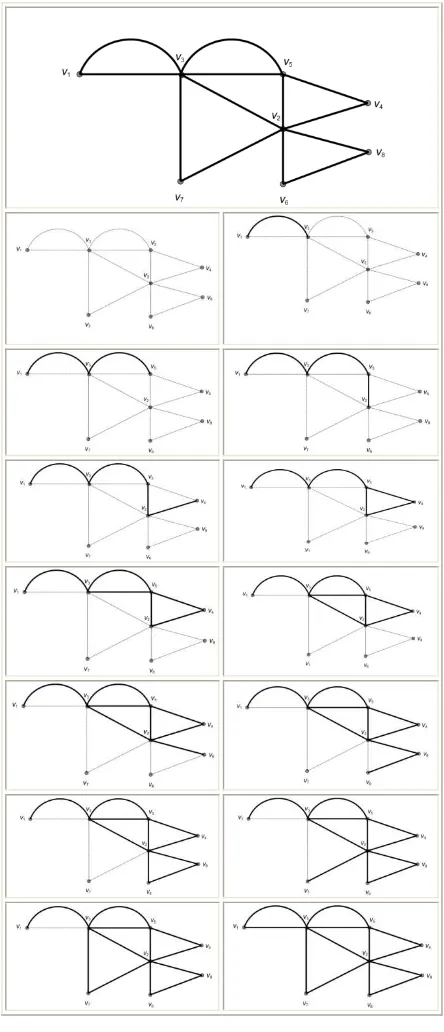
Gambar 12. Konstruksi garisEulerpada graf peta wilayah Kedaton.

Solusi sirkuit dariChinese Postman Problemtelah diperoleh dengan menyelesaikan konstruksi garis

Eulerpada graf tidak berarah dengan bobot 34,6 km dengan sirkuit

v1v3 v5v2 v4 v4 v5v3v2v8 v6 v2 v7 v3 v1

KESIMPULAN

Untuk kasus penentuan CPP pada kelurahan Kedaton didapat hasil bahwa Program Dinamis lebih baik dalam mengambil keputusan dan menghasilkan nilai optimal karena metode ini menguraikan solusi menjadi sekumpulan langkah atau tahapan sedemikian sehingga solusi dari persoalan dapat dipandang dari serangkaian keputusan yang saling berkaitan.

DAFTAR PUSTAKA

[1] Deo, N. (1989).Graph Theory with Applications to Engineering and Computer Science, Prentice-Hall of India Private Limited, New Delhi.

[2] Gross and Yellen. 2004. Graph Theory, CRC Press, LLC, New York.

[3] Hillier, F.S and Lieberman, G.J. (1994).

Pengantar Riset Operasi Jilid 1. Diterjemahkan Oleh Tim Editor Penerbit Erlangga, Jakarta.

[4] Kurniasari, Yeni. 2006.Penerapan Algoritma Greedy. PT Gramedia Pustaka Utama, Jakarta. [5] Munir, R. (2004). Diktat Kuliah IF2251 :

Program Dinamis, Bandung.

[6] Munir, R. (2008). Diktat Kuliah IF2091 :

Struktur Diskrit 4th, Bandung.