SIRKUIT EULER DAN PENENTUAN RUTE OPTIMAL AGUNG SURYA PERMADI

(1)

AGUNG SURYA PERMADI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ABSTRAK

AGUNG SURYA PERMADI. Sirkuit Euler dan Penentuan Rute Optimal. Dibimbing oleh FARIDA HANUM dan TONI BAKHTIAR.

Masalah Chinese Postman Problem (CPP) merupakan masalah penentuan rute optimal yang sangat terkenal. Dalam karya tulis ini, masalah CPP dikaji dengan menggunakan dua algoritme yaitu algoritme Fleury dan algoritme van Aardenne-Ehrenfest - de Bruijn. Solusi masalah CPP adalah rute optimal dengan kondisi setiap sisi dilewati tepat satu kali yang dikenal dengan sirkuit Euler. Proses graph balancing dalam pencarian sirkuit Euler dilakukan dengan menggunakan metode transportasi Orloff dan proses penentuan path ekstra terpendek diselesaikan dengan menggunakan algoritme Dijkstra. Dalam karya tulis ini, dibahas aplikasi metode pencarian sirkuit Euler pada kasus pengambilan sampah dengan tujuan menentukan rute pengambilan sampah yang terpendek.

(3)

by FARIDA HANUM and TONI BAKHTIAR.

Chinese Postman Problem (CPP) is well-known as a problem of determining the optimal route. In this work, the problem of CPP is studied by using two algorithms, namely Fleury algorithm and van Aardenne-Ehrenfest - de Bruijn algorithm. The solution of CPP can then be stated as an optimal route, which satisfies a condition, where every single edge must be traversed exactly once, i.e., Eulerian circuit. Graph balancing process in determining Eulerian circuit is done by using Orloff transportation method. The determination of extra shortest path is solved using Dijkstra algorithm. We discuss the application of determining Eulerian circuit for the case of determining the shortest route of garbage collection.

(4)

SIRKUIT EULER DAN PENENTUAN RUTE OPTIMAL

AGUNG SURYA PERMADI

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

Menyetujui

Tanggal Lulus:

Pembimbing I,

Dra. Farida Hanum, M.Si.

NIP: 19651019 199103 2 002

Pembimbing II,

Dr. Toni Bakhtiar, M.Sc.

NIP: 19720627 199702 1 002

Mengetahui:

Ketua Departemen,

Dr. Berlian Setiawaty, MS.

NIP: 19650505 198903 2 004

(6)

KATA PENGANTAR

Puji syukur penulis panjatkan kepada Allah swt atas berkat, rahmat dan kasih sayang-Nya sehingga penulis mampu menyelesaikan karya ilmiah ini. Berbagai kendala dialami oleh penulis sehingga banyak sekali orang yang membantu dan berkontribusi dalam pembuatan karya ilmiah ini. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih kepada:

1. Sang pencipta, Tuhan semesta alam Allah swt, atas maha karya-Nya yaitu bumi yang sempurna ini;

2. keluarga tercinta: papah (alm) dan mamah, ibu sebagai pemberi motivasi dan ayah sebagai sumber inspirasi, untuk Maya dan Dina yang selalu memberikan semangat dan doa.

3. Dra. Farida Hanum, M.Si. selaku dosen pembimbing I yang telah meluangkan waktu dan pikiran dalam membimbing, memberi motivasi, semangat dan doa;

4. Dr. Toni Bakhtiar, M.Sc. selaku dosen pembimbing II yang telah memberikan ilmu, kritik dan saran, motivasi serta doanya;

5. Drs. Prapto Tri Supriyo, M.Kom. selaku dosen penguji yang telah memberikan ilmu, saran dan doanya;

6. semua dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan;

7. staf Departemen Matematika: Bapak Yono, Hery, Bapak Deni, Ibu Ade, Epul, Bapak Bono dan Ibu Susi atas semangat dan doanya;

8. Ratna Ratu Alit atas semangat, saran, motivasi dan doanya;

9. sahabat yang selalu memberi semangat: Slamet Riyadi, Sabar, Andrew, Ali; 10. semua teman Matematika 42 yang selalu menjadi contoh yang baik; 11. semua teman Matematika 43 yang selalu menjadi bagian dari keluarga; 12. semua teman Matematika 44 yang selalu mendukung agar terus berkembang; 13. teman seperjuangan: Igoey, Apri, Sr, Irsyad, Deni;

14. Gumatika yang telah mengasah pribadi ini menjadi pribadi yang tangguh;

15. Bapak Ruslan, Bapak Andi, Bapak Thariq, Bapak Rully, Bapak Sri, Bapak Edi dan Bapak Ade yang telah memberi semangat dan masukan yang membangun serta kesempatan dalam berkarir;

16. semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.

Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.

Bogor, Juni 2010 Agung Surya Permadi

(7)

bersaudara, anak dari pasangan Agus Sukarna dan Yanti Susanti.

Pada tahun 2000 penulis lulus dari SD Bantarjati 6 Bogor kemudian tahun 2003 lulus dari SLTP Negeri 2 Bogor. Tahun 2006 penulis lulus dari SMA Negeri 3 Bogor dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur SPMB (Seleksi Penerimaan Mahasiswa Baru). Pada tahun 2007, penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Pengantar Metode Komputasi tahun ajaran 2008/2009, asisten mata kuliah Analisis Numerik tahun ajaran 2009/2010 dan asisten Metode Numerik untuk Pascasarjana Matematika tahun ajaran 2010/2011. Penulis juga aktif dalam mengajar Matematika bimbingan belajar privat maupun kelompok mahasiswa. Penulis pernah mengikuti seleksi olimpiade nasional Matematika dan IPA (ON-MIPA) sebagai wakil IPB pada tahun 2009. Penulis aktif dalam organisasi kemahasiswaan di kampus, seperti organisasi himpunan profesi Departemen Matematika yang dikenal dengan GUMATIKA (Gugus Mahasiswa Matematika) sebagai anggota Departemen Pengembangan Sumber Daya Mahasiswa (PSDM) tahun 2008/2009 dan sebagai ketua Departemen yang sama pada tahun 2009/2010. Selain itu, penulis juga terlibat dalam beberapa kegiatan, antara lain ketua panitia Try-Out Pengantar Matematika mahasiswa IPB 2007, koordinator Humas Matematika Ria dalam acara Pesta Sains se-Indonesia 2008, koordinator hubungan alumni mahasiswa Matematika 2008, ketua panitia Penerimaan Mahasiswa Matematika tahun ajaran baru 2009, ketua panitia acara Ramah Tamah Civitas Matematika 2009 (RATACI 2009).

(8)

DAFTAR ISI

Halaman DAFTAR GAMBAR ... ix DAFTAR LAMPIRAN ... x I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Tujuan Penulisan ... 1 1.3 Metode Penulisan ... 1 II LANDASANTEORI 2.1 Graf dan Digraf ... 1

2.2 Graf Euler ... 6

2.3 Undirected Chinese Postman Problem ... 6

2.4 Algoritme Fleury ... 7

2.5 Algoritme Dijkstra ... 8

III DIRECTEDCHINESEPOSTMANPROBLEM 3.1 DCPP sebagai Masalah Transportasi ... 9

3.2 Pencarian Sirkuit Euler dengan Algoritme Fleury ... 10

3.2.1 Aplikasi Pemrograman ... 11

3.3 Pencarian Sirkuit Euler dengan Algoritme van Aardenne-Ehrenfest - de Bruijn ... 12

IV APLIKASIPERMASALAHAN 4.1 Permasalahan Pengambilan Sampah ... 13

V SIMPULANDANSARAN 5.1 Simpulan ... 15

5.2 Saran ... 15

DAFTAR PUSTAKA ... 16

LAMPIRAN ... 17

(9)

DAFTAR GAMBAR

Halaman

1 Graf G = (V,E) ... 2

2 Graf berarah D = (V,E) ... 2

3 Graf berbobot ... 2

4 Multigraf ... 2

5 Multidigraf ... 2

6 Adjacent dan incident ... 3

7 Ilustrasi derajat pada graf ... 3

8 Ilustrasi graf unicursal ... 3

9 Ilustrasi digraf balance ... 3

10 Graf berarah ... 4

11 Spanning tree ... 5

12 Arborescence ... 5

13 Spanning arborescence ... 5

14 Graf Euler ... 6

15 Graf Euler balance untuk contoh algoritme Fleury ... 7

16 Iterasi pertama: inisialisasi v0 ... 7

17 Iterasi kedua: sisi {1,2} dihapus . ... 7

18 Iterasi ketiga: sisi {2,4} dihapus ... 7

19 Solusi sirkuit Euler dengan algoritme Fleury ... 8

20 Digraf contoh algoritme Dijkstra ... 8

21 Solusi path terpendek algoritme Dijkstra dengan verteks awal 1 ... 8

22 Skema masalah CPP ... 9

23 Digraf yang tidak balance ... 10

24 Digraf yang sudah balance ... 10

25 Penentuan sirkuit Euler pada digraf ... 11

26 Spanning arborescence untuk digraf pada Gambar 24 ... 12

27 Pelabelan pada arc ... 12

28 Peta lokasi TPS di Kampung Wayang ... 13

29 Digraf kasus Kayang dengan bobot pada sisi berarah (i,j) menyatakan jarak dari verteks i ke verteks j ... 14

30 Digraf kasus Kayang yang sudah balance ... 14

31 Spanning arborescence digraf kasus Kayang ... 15

32 Digraf kasus Kayang yang sudah dilabeli ... 15

(10)

DAFTAR LAMPIRAN

Halaman

1 Pembuktian Teorema 1 ... 18

2 Langkah solusi sirkuit Euler dengan menggunakan algoritme Fleury ... 18

3 Penentuan path terpendek dengan algoritme Dijkstra ... 20

4 Program LINGO 8.0 untuk menyelesaikan contoh masalah transportasi ... 20

5 Syntax program Mathematica 7.0 untuk menyelesaikan permasalahan perutean dengan dasar algoritme Fleury ... 20

6 Syntax program Mathematica 7.0 untuk menyelesaikan contoh kasus dengan menggunakan program pada Lampiran 5 ... 24

7 Penentuan cij dengan algoritme Dijkstra pada kasus Kayang ... 24

8 Syntax program LINGO 8.0 untuk menyelesaikan masalah transportasi pada kasus pengambilan sampah beserta hasil yang diperoleh ... 26

9 Syntax program Mathematica 7.0 untuk menyelesaikan rute pengambilan sampah pada kasus Kayang ... 26

10 Penentuan solusi sirkuit Euler pada kasus Kayang dengan algoritme Fleury ... 27

(11)

I PENDAHULUAN

1.1 Latar Belakang

Permasalahan seperti jaringan komunikasi, transportasi, penjadwalan, dan pencarian rute kini semakin banyak ditemui di tengah-tengah masyarakat. Masalah tersebut dimulai dari menemukan jarak yang paling optimal, hingga mencari biaya minimum perjalanan. Dengan menggunakan metode dan teori yang berkembang saat ini, berbagai masalah tersebut bisa dicari solusinya. Salah satu teori yang terkenal adalah teori graf. Aplikasi dalam teori graf sangat luas karena dalam teori graf banyak sekali metode yang bisa digunakan dengan kondisi yang bermacam-macam. Salah satu permasalahan graf yang terkenal adalah Chinese Postman Problem (CPP).

Masalah CPP pertama kali dikemukakan oleh Meigu Guan, seorang pakar matematika dari Universitas Shangtun, Cina, yang sehari-harinya menggunakan sebagian dari waktu luangnya untuk bekerja di kantor pos pada waktu revolusi kebudayaan Cina. “Tukang pos harus melewati semua sektor yang ditugaskan kepadanya sebelum kembali ke kantor pos. Permasalahannya adalah bagaimana menentukan jarak terpendek untuk tukang pos tersebut” Guan (1962) di dalam Eiselt et al. (1995). Dalam kasus ini, permasalahan yang muncul adalah bagaimana menentukan jarak minimum dengan kondisi setiap ruas jalan harus dilewati paling tidak satu kali. Pada dasarnya CPP memiliki banyak jenis yaitu undirected CPP (CPP yang tidak berarah), directed CPP (CPP yang berarah), dan mixed CPP (CPP gabungan antara tidak

berarah dan berarah). Dalam

perkembangannya ternyata masalah CPP ini bisa diaplikasikan tidak hanya dalam pengiriman pos saja, tetapi dalam hal lainnya seperti pengumpulan sampah berdasarkan rute

terpendeknya, pemindahan salju dengan biaya yang minimum, penentuan rute tercepat untuk bis sekolah, dll. CPP dapat dipandang sebagai masalah penentuan sirkuit Euler pada digraf yang balance. Sirkuit Euler dijamin ada jika digrafnya adalah digraf balance.

Dalam karya ilmiah ini akan dibahas prosedur untuk mencari sirkuit Euler pada digraf yang tidak balance, dengan terlebih dahulu menjadikan digraf tersebut menjadi

digraf balance dan kemudian

menyelesaikannya dengan menggunakan dua macam algoritme.

1.2 Tujuan Penulisan

Tujuan dari penulisan karya ilmiah ini meliputi:

1. mempelajari penyelesaian masalah

penentuan sirkuit Euler pada graf berarah dengan menggunakan algoritme Fleury dan algoritme van Aardenne-Ehrenfest - de Bruijn.

2. mengaplikasikan masalah pencarian sirkuit Euler ke dalam masalah penentuan rute pengambilan sampah.

1.3 Metode Penulisan

Metode yang digunakan dalam penulisan karya ilmiah ini adalah studi literatur. Materi dari karya ilmiah ini diambil dari jurnal yang berjudul Arc Routing Problem, part I: The Chinese Postman Problem yang disusun oleh H. A. Eiselt, G. Michel dan L. Gilbert pada tahun 1995. Di samping itu dalam pembuatan karya ilmiah ini, penulis menggunakan beberapa bahan penunjang dari buku dan situs internet yang terkait dengan topik karya ilmiah ini.

II LANDASAN TEORI

Dalam bab ini akan dibahas tentang teori-teori yang berkaitan dengan bahasan karya ilmiah ini.

2.1 Graf dan Digraf

Teori graf pertama kali dikenal sejak Euler (1736) meneliti tentang masalah jembatan Königsberg. Dua abad kemudian 1900-an, baru untuk pertama kalinya dibuat buku

tentang teori graf. Dalam periode yang sangat singkat, teori graf kini mengalami perkembangan yang sangat pesat.

Definisi 1 (Graf)

Suatu graf G adalah pasangan terurut (V,E) dengan V atau biasa disebut V(G) adalah himpunan berhingga dan takkosong dari elemen graf yang disebut verteks (node, point), sedangkan E atau biasa disebut E(G)

(12)

2

adalah himpunan pasangan yang menghubungkan dua elemen subset dari V yang disebut sisi (edge, line). Setiap sisi {u,v} pada V biasanya dinotasikan dengan uv atau vu. Banyaknya verteks dari suatu graf disebut order dan banyaknya sisi pada suatu graf disebut size.

(Chartrand & Zhang 2009)

Pada Gambar 1 diperlihatkan bahwa V = {u, v, w, x, y} dan E = {{u,v},{v,w},{v,x},{x,y}}.

Definisi 2 (Graf berarah/digraf)

Graf berarah (digraph) D adalah pasangan terurut (V,A) dengan V himpunan takkosong yang hingga, dan A himpunan pasangan terurut yang menghubungkan elemen-elemen

di V. Elemen-elemen dari A disebut sisi

berarah (arc). Sisi berarah (u,v) dinyatakan dengan garis berarah dari u ke v.

Pada Gambar 2 diperlihatkan bahwa V = {u, v, w, x} dan

A = {(u,w),(v,w),(w,x)}.

Definisi 3 (Graf/digraf berbobot)

Suatu graf G = (V,E) atau digraf D = (V,A) dikatakan berbobot jika terdapat sebuah fungsi

:

w E→R atau :A A→R (dengan R adalah himpunan bilangan real) yang memberikan sebuah bilangan real pada setiap sisi diEatau sisi berarah di A, disebut bobot. Setiap bobot

( )

w uv dengan uv E∈ atau uv A∈ dinotasikan dengan wuv.

(Foulds 1992)

Bobot tiap sisi untuk graf pada Gambar 3 adalah: wuv=12, wvz=29, wzx=7, wvx=89.

Definisi 4 (Multigraf/multidigraf)

Suatu graf (digraf) dikatakan multigraf (multidigraf) bila graf (digraf) tersebut memiliki lebih dari satu sisi (sisi berarah) yang incident dengan satu pasang verteks.

(Foulds 1992) Ilustrasi multigraf dapat dilihat pada Gambar 4 berikut.

Gambar 4 merupakan contoh multigraf karena verteks u dan w dihubungkan oleh lebih dari satu sisi. Ilustrasi multidigraf bisa dilihat pada Gambar 5 berikut.

Definisi 5 (Adjacent dan incident)

Misalkan u dan v verteks pada graf G. Verteks v dikatakan tetangga (adjacent) dari u jika ada sisi e yang menghubungkan verteks u dan v, yaitu e = uv. Himpunan semua tetangga dari verteks v dinotasikan dengan N(v). Jika e = uv adalah sisi pada graf G maka e dikatakan incident dengan verteks u dan v.

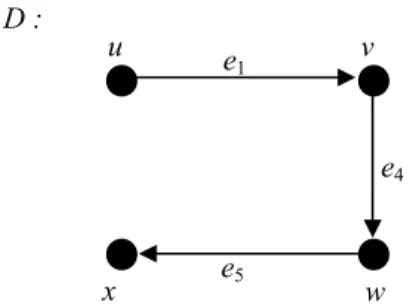
(Chartrand & Zhang 2009) D :

Gambar 2 Graf berarah D = (V, A).

v u w x u v w x y G :

Gambar 1 Graf G = (V, E).

G: G : Gambar 4 Multigraf. v u w _x z y t v x u w D : Gambar 5 Multidigraf. 29 12 89 7 u v z x

(13)

Ilustrasi adjacent dan incident diperlihatkan pada Gambar 6. Verteks u adjacent dengan verteks v dan x tetapi verteks u tidak adjacent dengan verteks w. Verteks u incident dengan sisi e1, tetapi verteks w tidak

incident dengan sisi e1. Definisi 6 (Derajat /degree)

Derajat suatu verteks v adalah banyaknya sisi yang incident dengan verteks v, dan dinotasikan dengan degG(v) atau deg v atau

d(v).

(Vasudev 2006)

Pada Gambar 7 terlihat bahwa

d(u) = 1 = d(z), d(w) = 2 =d(x), d(v) = 3=d(y).

Definisi 7 (Derajat masuk/in-degree)

Pada graf berarah, in-degree suatu verteks vi , yang dinotasikan dengan d–(vi), adalah banyaknya sisi berarah yang berakhir di verteks vi.

(Vasudev 2006) Pada Gambar 2 diperlihatkan derajat masuk tiap verteksnya

d–_{(u) = 0, d}–_{(v) = 0, d}–_{(x) = 1, d}–_{(w) = 2}

Definisi 8 (Derajat keluar/out-degree)

Pada graf berarah, out-degree suatu verteks vi, yang dinotasikan dengan d+(vi), adalah banyaknya sisi berarah yang dimulai dari verteks vi.

(Vasudev 2006) Pada Gambar 2 diperlihatkan derajat keluar tiap verteksnya

d+_{(x) = 0, d}+_{(u) = 1 = d}+_{(v) = d}+_(w).

Definisi 9 (Unicursal)

Suatu graf tidak berarah dikatakan unicursal jika setiap verteks pada graf tersebut memiliki derajat yang genap.

(Diestel 1997)

Pada Gambar 8 diperlihatkan grafnya unicursal karena tiap verteks memiliki derajat yang genap.

Definisi 10 (Balance)

Suatu digraf D dikatakan balance jika digraf tersebut pada setiap verteksnya memiliki δ(vi) = 0, dengan δ(vi) adalah selisih dari derajat masuk dengan derajat keluar dari verteks i.

(Diestel 1997)

Pada Gambar 9 diperlihatkan grafnya balance karena setiap verteks vi memiliki δ(vi) = 0.

Definisi 11 (Underlying graph)

Jika suatu graf G didapat dengan cara menghapus semua arah dari sisi berarah pada digraf D, maka graf G tersebut adalah underlying graph dari digraf D.

(Vasudev 2006) Ilustrasi underlying graph bisa dilihat dari Gambar 8 dan Gambar 9. Graf pada Gambar 8 merupakan underlying graph dari digraf pada Gambar 9.

Definisi 12 (Jalan /walk)

Walk W pada suatu graf G adalah barisan berhingga, W = viejvi+1ej+1...ekvm atau W = vi - vi+1 - ... - vm yang dimulai dari suatu verteks dan berakhir pada suatu verteks juga, sehingga setiap sisi di dalam barisan harus incident dengan verteks sebelum dan sesudahnya.

(Chartrand & Zhang 2009) Gambar 6 Adjacent dan incident.

G : e3 e1 e4 e5 e2 x w v u G :

Gambar 8 Ilustrasi graf unicursal.

D :

Gambar 9 Ilustrasi digraf balance. u x w v y G :

Gambar 7 Ilustrasi derajat pada graf. z

(14)

4

Ilustrasi walk pada suatu graf bisa dilihat pada Gambar 6, W = u e2x e5w e4v e3x adalah walk

pada graf G.

Definisi 13 (Walk berarah)

Walk berarah pada suatu digraf D adalah walk yang sesuai dengan arah sisinya atau tidak berlawanan arah.

(Vasudev 2006)

Ilustrasi walk berarah pada suatu digraf D bisa dilihat pada Gambar 10. W = u e1v e4w adalah

walk berarah.

Definisi 14 (Lintasan)

Lintasan (trail) pada suatu graf adalah walk dengan semua sisi dalam barisannya tidak berulang.

(Chartrand & Zhang 2009) Ilustrasi trail bisa dilihat pada Gambar 6, T = u e2x e5w e4v adalah trail.

Definisi 15 (Trail berarah)

Trail berarah pada suatu digraf adalah

walk berarah dengan semua sisi dalam

barisannya tidak berulang.

(Vasudev 2006) Ilustrasi trail berarah bisa dilihat pada Gambar 10, T = u e1v e4w e5x adalah trail

berarah.

Definisi 16 (Jalur)

Jalur (path) pada suatu graf adalah walk yang setiap verteks pada barisannya, hanya muncul satu kali.

(Vasudev 2006) Ilustrasi path bisa dilihat pada Gambar 6, P = u e1v e4w e5x adalah path pada graf G.

Definisi 17 (Path berarah)

Path berarah pada suatu digraf adalah walk berarah dengan semua verteks dalam barisannya tidak berulang.

(Vasudev 2006)

Ilustrasi path berarah bisa dilihat pada Gambar 10, P = u e1v e4w e5x adalah path

berarah.

Definisi 18 (Tertutup)

Walk pada suatu graf G dikatakan tertutup (closed) jika walk tersebut dimulai dan diakhiri pada verteks yang sama.

Definisi 19 (Sirkuit)

Pada graf tidak berarah, sirkuit (circuit) adalah trail tertutup yang takkosong.

(Chartrand & Oellermann 1993) Ilustrasi sirkuit bisa dilihat pada Gambar 6. C = u e1v e3x e2u merupakan sirkuit pada graf

G.

Definisi 20 (Sirkuit berarah)

Pada suatu digraf, sirkuit berarah adalah walk berarah yang tertutup di mana barisannya dimulai dan diakhiri pada verteks yang sama dengan tidak ada sisi yang diulang.

(Vasudev 2006) Ilustrasi sirkuit berarah bisa dilihat pada Gambar 10. C = v e3x e2u e1v merupakan

sirkuit berarah pada digraf D.

Definisi 21 (Semi-sirkuit)

Pada suatu digraf, semi-sirkuit adalah sirkuit pada underlying graph D, tetapi bukan merupakan sirkuit berarah pada digraf D tersebut.

(Vasudev 2006) Ilustrasi semi-sirkuit bisa dilihat pada Gambar 10. C = u e2x e3v e1u merupakan semi-sirkuit

pada digraf D.

Definisi 22 (Cycle)

Pada graf tidak berarah, cycle adalah path tertutup yang takkosong.

(Chartrand & Oellermann 1993) Ilustrasi cycle bisa dilihat pada Gambar 7. Graf pada Gambar 7 memiliki cycle C = v-w-y-x-v.

Definisi 23 (Cycle berarah)

Pada graf berarah, cycle adalah path berarah yang tertutup dan takkosong.

(Chartrand & Oellermann 1993) Gambar 10 Graf berarah.

D : e3 e1 e4 e5 e2 x w v u

(15)

Ilustrasi cycle berarah bisa dilihat pada Gambar 10. Digraf pada Gambar 10 memiliki cycle C = u e1v e3x e2u.

Definisi 24 (Terhubung/connected)

Suatu graf G disebut terhubung (connected) jika untuk setiap verteks dari G terhubung. Verteks u dengan v dikatakan terhubung jika ada setidaknya satu path dari verteks u ke v.

(Vasudev 2006)

Definisi 25 (Bridge)

Suatu sisi e di graf G yang terhubung

disebut bridge jika sisi e tersebut

menyebabkan graf menjadi tidak terhubung pada saat sisi e dihilangkan.

(Vasudev 2006) Pada Gambar 1 sisi e={u,v} merupakan bridge, karena jika sisi tersebut dihilangkan maka graf G menjadi tidak terhubung.

Definisi 26 (Subgraf)

Suatu graf H dikatakan subgraf dari graf

G jika V(H) V(G) dan E(H) E(G).

(Chartrand & Oellermann 1993) Graf pada Gambar 1 merupakan subgraf dari graf pada Gambar 7.

Definisi 27 (Spanning subgraph)

Suatu subgraf G dikatakan spanning

subgraph jika subgraf tersebut mengandung

semua verteks pada graf G.

(Vasudev 2006) Graf pada Gambar 7 merupakan spanning subgraph dari graf pada Gambar 8.

Definisi 28 (Tree pada graf)

Suatu graf terhubung yang tidak memiliki cycle disebut tree.

(Chartrand & Zhang 2009) Graf pada Gambar 1 merupakan tree karena tidak memiliki cycle.

Definisi 29 (Tree pada digraf)

Suatu digraf terhubung yang tidak memiliki cycle disebut tree pada digraf.

(Chartrand & Zhang 2009) Ilustrasi tree untuk digraf dapat dilihat pada Gambar 2.

Definisi 30 (Spanning tree)

Suatu spanning tree adalah spanning subgraph yang merupakan tree.

(Vasudev 2006)

Digraf pada Gambar 11 adalah spanning tree dari digraf pada Gambar 10.

Definisi 31 (Arborescence)

Graf berarah D disebut arborescence jika

i. D tidak memiliki sirkuit maupun

semi-sirkuit,

ii. pada D terdapat tepat satu verteks vr yang memiliki d–_(v

r) = 0.

Verteks vr disebut akar arborescence.

(Vasudev 2006)

Digraf pada Gambar 12 adalah suatu arborescence dengan verteks x sebagai akar arborescence.

Definisi 32 (Spanningarborescence)

Spanning arborescence pada digraf D

adalah spanning tree yang bersifat

arborescence.

(Vasudev 2006)

Ilustrasi spanning arborescence bisa dilihat pada Gambar 13. Digraf pada Gambar 13 merupakan spanning arborescence dari digraf pada Gambar 5, dengan akar arborescence-nya di x.

D :

Gambar 12 Arborescence. x

Gambar 11 Spanning tree. D : e1 e4 e5 x w v u x D :

Gambar 13 Spanning arborescence. y u z v t w _u y z

(16)

6

2.2 Graf Euler

Leonhard Euler (1707-1783) adalah seorang peneliti yang lahir di Swiss. Ia dipandang sebagai salah satu matematikawan terbesar sepanjang masa. Euler menyumbangkan berbagai penemuan penting di bidang yang beragam seperti kalkulus dan teori graf.

Dalam penelitiannya di bidang teori graf, Euler mengenalkan penemuan yang paling terkenal yaitu graf Euler. Berikut ini akan dijelaskan beberapa definisi yang berkaitan dengan graf Euler yang digunakan dalam karya ilmiah ini.

Definisi 33 (Lintasan Euler)

Lintasan (trail) Euler adalah lintasan yang melewati semua sisi pada graf G tepat satu kali.

(Vasudev 2006) Pada Gambar 6 T = x e5 w e4v e3 x e2 u e1 v

merupakan lintasan Euler.

Definisi 34 (Sirkuit Euler)

Sirkuit Euler adalah lintasan Euler yang tertutup.

(Vasudev 2006) Ilustrasi sirkuit Euler bisa dilihat pada Gambar 14. Sirkuit Euler dari graf G salah satunya adalah C = v e1 u e2 w e3 v e4 x e5 z e6

v.

Definisi 35 (Graf/digraf Euler)

Graf atau digraf yang memiliki sirkuit Euler disebut graf atau digraf Euler.

(Vasudev 2006) Ilustrasi graf Euler bisa dilihat pada Gambar 14. Graf G pada Gambar 14 merupakan graf Euler, karena graf tersebut memiliki sirkuit Euler.

Selanjutnya akan diberikan teorema-teorema yang digunakan sebagai dasar pengerjaan karya ilmiah ini.

Teorema 1

Suatu graf G merupakan graf Euler jika dan hanya jika setiap verteks pada graf G berderajat genap.

(Chartrand & Zhang 2009) Pembuktian Teorema 1 bisa dilihat pada Lampiran 1.

Teorema 2

Misalkan D suatu digraf terhubung yang takkosong, maka D adalah digraf Euler jika dan hanya jika d+_(v

i) = d–(vi) untuk setiap verteks pada digraf D (digraf balance).

2.3 Undirected Chinese Postman Problem

(UCPP)

Masalah CPP pertama kali dikemukakan oleh Meigu Guan atau Kwan Meiko, seorang pakar matematika dari Universitas Shangtun, Cina, maka tidak heran bahwa permasalahan ini dinamakan Chinese Postman Problem karena memang berasal dari Cina. Permasalahan CPP adalah masalah mencari lintasan pada suatu graf berbobot yang terhubung dan melewati semua sisi minimal satu kali dengan jumlah bobot minimum di mana verteks awal dan akhirnya harus sama (tertutup). Pada graf yang memiliki sirkuit Euler, maka lintasan manapun yang diambil hasilnya akan sama, karena tiap sisi pasti dilewati satu kali sehingga bobot minimum adalah jumlah bobot dari semua sisi yang ada, sedangkan untuk graf yang tidak memiliki sirkuit Euler, perlu dilewati suatu sisi sebanyak dua kali bahkan lebih (Thimbleby 2003).

Berdasarkan jenis grafnya masalah CPP dibagi menjadi dua jenis yaitu berarah (directed) yang dikenal sebagai DCPP dan tidak berarah (undirected) yang dikenal sebagai UCPP. UCPP adalah sebuah masalah yang tujuannya adalah mencari rute terpendek pada sebuah graf yang tidak berarah. Masalah UCPP dapat diselesaikan antara lain dengan menggunakan algoritme Fleury.

G:

Gambar 14 Graf Euler. v x e6 e1 u w z e2 e3 e4 e5

(17)

2.4 Algoritme Fleury

Misalkan G = (V, E) adalah graf terhubung yang semua verteksnya berderajat genap.

LANGKAH 1. Inisialisasikan i = 0. Dimulai dari verteks v0 dan didefinisikan trail

T0 : v0.

LANGKAH 2. Kemudian dimisalkan Ti= v0 e1 v1 e2 v2 e3 ... ei vi sebagai trail di antara v0

dan vi pada iterasi ke-i, lalu dipilih sebuah sisi

ei+1 yang menghubungkan vi dengan vi+1 yang

bukan merupakan bridge dari himpunan sisi Ei = E – {e1,e2,..,ei}. Jika ei+1 adalah bridge pada

subgraf yang didapat dari G setelah menghapus sisi yang dimiliki Ei dari E, dan tidak ada pilihan lain yang bisa diambil, maka sisi tersebut dimasukkan ke dalam trail Ti = v0

e1 v1 e2 v2 e3 ... ei vi ei+1. Jika tidak ada sisi lagi

yang bisa dipilih maka proses berhenti.

LANGKAH 3. Kemudian i diganti

menjadi i+1, lalu kembali ke Langkah 2. Trail yang terbentuk dari urutan sisi yang diambil merupakan sirkuit Euler pada graf G.

(Balakrishnan 1997)

Aplikasi Algoritme Fleury

Misalkan diberikan graf seperti pada Gambar 15.

Untuk mencari sirkuit Euler pada graf tersebut dengan algoritme Fleury, dilakukan prosedur sebagai berikut:

1. dipilih sembarang verteks, misalkan verteks (1) yang dilabeli sebagai v0,

2. dipilih sisi yang incident dengan v0 dan

bukan merupakan bridge pada graf. Misalkan sisi {1,2} dipilih, lalu sisi tersebut dihapus dan didefinisikan verteks 2 sebagai verteks v1, sehingga graf

menjadi seperti pada Gambar 17.

3. dipilih sisi {2,4} yang bukan bridge pada subgraf G, sehingga graf menjadi seperti pada Gambar 18.

Iterasi selanjutnya diberikan secara lengkap pada Lampiran 2. Setelah semua sisi dihapus, sehingga dihasilkan graf seperti pada Gambar 19, maka sirkuit Euler sudah bisa ditemukan. Gambar 15 Graf Euler balance untuk contoh

algoritme Fleury. 1 2 6 3 5 4 G: v0

Gambar 16 Iterasi pertama : inisialisasi v0. 1 2 6 3 5 4 G: v1 v0

Gambar 17 Iterasi kedua : sisi {1,2} dihapus.

1 2 6 3 5 4 G: v2 v1 v0

Gambar 18 Iterasi ketiga : sisi {2,4} dihapus.

1 2 6 3 5 4 G:

(18)

8

Dari urutan verteks yang dipilih dan sisi yang dihapus akan diperoleh solusi sirkuit Eulernya, yaitu C = v0 v1 v2 ... v10 v11 atau

bisa dituliskan dengan C = 1-2-4-6-5-4-3-5-3-2-6-1. Meskipun dimulai dari verteks yang sama, sirkuit Euler yang dihasilkan tidak selalu sama, bergantung pada urutan pengambilan atau penghapusan sisi. Contohnya C = 1-6-4-5-3-5-6-2-3-4-2-1.

Selain digunakan untuk mencari sirkuit Euler pada graf yang tidak berarah, algoritme ini juga bisa digunakan untuk mencari sirkuit Euler pada graf berarah.

2.5 Algoritme Dijkstra

Algoritme ini bisa digunakan untuk mencari path terpendek atau jarak terpendek pada graf atau digraf yang tidak berbobot maupun yang berbobot. Misalkan diberikan D = (V,E) dengan V = {1,2,...,n} adalah digraf berbobot dengan bobot pada tiap verteksnya taknegatif. Misalkan a(i,j) adalah bobot pada arc dari i ke j. Jika tidak ada arc dari i ke j maka a(i,j) bernilai +∞. Setiap verteks i dilabeli dengan L(i) yang menyatakan jarak terpendek dari verteks awal ke verteks i yang sifatnya permanen artinya pasti dipilih, sedangkan label L’(i) memiliki makna sama dengan L(i) namun sifatnya masih sementara artinya mungkin dipilih atupun tidak. Di setiap iterasi dibuat P yang menyatakan himpunan verteks dengan label L(i) dan T yang menyatakan himpunan verteks dengan label L’(i). Misalkan verteks awalnya di 1, maka diinisialisasikan, P = {1} dengan L(1) = 0 dan L’(j) = a(1, j) untuk semua j. Prosedur selesai ketika P = V. Setiap iterasi mempunyai dua langkah yaitu:

LANGKAH 1. Dicari verteks k pada T

dengan L’(k) berhingga dan minimum.

Kemudian k dijadikan anggota P, Jika tidak

ada k yang dimaksud maka proses berhenti,

karena tidak ada path dari 1 ke verteks lain

yang belum dilabeli. Iterasi juga berhenti jika P = V. Arc (i,k) dilabeli dengan i, yaitu verteks yang memiliki L’(k) yang minimum.

LANGKAH 2. L’(j) diganti oleh nilai terkecil antara L’(j) dan L(k) + a(k,j) untuk setiap j pada T, kembali ke Langkah 1.

(Balakrishnan 1997)

Contoh Algoritme Dijkstra

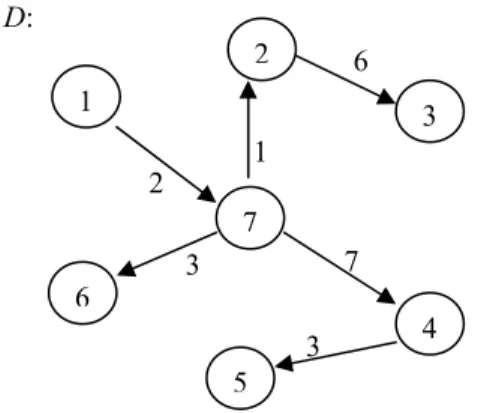
Diberikan digraf berbobot berikut:

Akan ditentukan jarak terpendek dari verteks 1 ke verteks lainnya. Maka dengan mengaplikasikan algoritme Dijkstra akan diperoleh path terpendek dari verteks 1 menuju verteks lain seperti pada Gambar 21 (detail penghitungannya dapat dilihat pada Lampiran 3).

Misalkan dicari jarak terdekat dari verteks 1 ke verteks 4 pada digraf Gambar 21, maka pathnya adalah P = 1-7-4 dengan jarak 9. Contoh lainnya misalkan dicari jarak terdekat dari verteks 1 ke verteks 6, maka path-nya

adalah P = 1-7-6 dengan jarak 5.

v0 v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 v11

Gambar 19 Solusi sirkuit Euler dengan algoritme Fleury. 1 2 6 3 5 4 G: D:

Gambar 20 Digraf contoh algoritme Dijkstra. 1 2 6 5 3 4 2 3 2 1 6 4 7 4 7 3 3 3 3 D:

Gambar 21 Solusi path terpendek algoritme Dijkstra dengan verteks awal 1. 1 2 6 5 3 3 2 1 6 7 4 7 3

(19)

III DIRECTED CHINESE POSTMAN PROBLEM

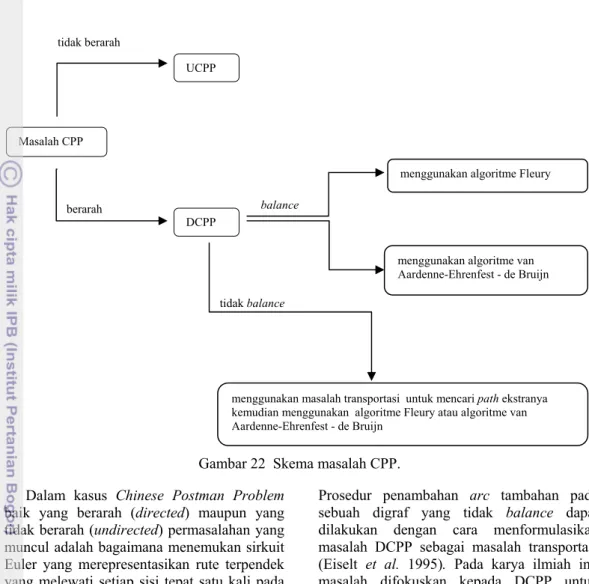
Dalam kasus Chinese Postman Problem baik yang berarah (directed) maupun yang tidak berarah (undirected) permasalahan yang muncul adalah bagaimana menemukan sirkuit Euler yang merepresentasikan rute terpendek yang melewati setiap sisi tepat satu kali pada suatu graf terhubung. Skema pada Gambar 22 menunjukkan bahwa masalah DCPP memiliki karakteristik metode pencarian solusi yang bermacam-macam.

Pencarian sirkuit Euler pada sebuah digraf dalam karya ilmiah ini dilakukan dengan dua metode, yaitu dengan menggunakan algoritme Fleury yang diadopsi dari kasus UCPP dan menggunakan algoritme van Aardenne-Ehrenfest dan de Bruijn yang dibahas di dalam Eiselt et al. (1995). Pada dasarnya dalam mencari sirkuit Euler pada suatu digraf D bisa langsung dicari dengan algoritme Fleury atau algoritme van Aardenne-Ehrenfest dan de Bruijn, asalkan digrafnya merupakan digraf yang balance. Tentunya jika suatu digraf merupakan digraf Euler, maka digraf tersebut pasti memiliki sirkuit Euler yang merupakan solusi optimalnya. Pada kasus digraf yang tidak balance, agar sirkuit Euler bisa didapatkan maka perlu ada penambahan sisi terhadap verteks yang tidak balance.

Prosedur penambahan arc tambahan pada sebuah digraf yang tidak balance dapat dilakukan dengan cara menformulasikan masalah DCPP sebagai masalah transportasi (Eiselt et al. 1995). Pada karya ilmiah ini, masalah difokuskan kepada DCPP untuk digraf yang tidak balance.

3.1 DCPP sebagai Masalah Transportasi

Berikut ini akan dijelaskan perumusan masalah transportasi untuk mencari path tambahan yang perlu dilewati agar ditemukan sirkuit Euler pada suatu digraf yang tidak balance.

Misalkan:

I = {vi} = himpunan verteks dengan derajat masuk lebih banyak dari derajat keluarnya.

J = {vj} = himpunan verteks dengan derajat keluar lebih banyak dari derajat masuknya.

cij = panjang path terpendek dari vi menuju vj. si = selisih antara derajat masuk dan derajat

keluar pada vi.

dj = selisih antara derajat keluar dan derajat masuk pada vj.

Gambar 22 Skema masalah CPP.

menggunakan algoritme van Aardenne-Ehrenfest - de Bruijn

menggunakan masalah transportasi untuk mencari path ekstranya kemudian menggunakan algoritme Fleury atau algoritme van Aardenne-Ehrenfest - de Bruijn Masalah CPP UCPP DCPP tidak berarah berarah balance tidak balance

(20)

10

xij = menyatakan banyaknya path berarah terpendek dari i ke j yang harus ditambahkan (Thimbleby 2003).

Formulasi masalah transportasinya adalah sebagai berikut: Minimumkan: ∈ ∈

∑ ∑

ij ij j v I v_i J c x (1) Kendala : ∈ =

∑

ij i j v J x s (v_i∈I) (2) ∈ =

∑

ij j i v Ix d (vj∈J) (3) xij ≥0 (vi∈I v, j∈J)(4)

Fungsi objektif pada masalah transportasi pada persamaan (1) menyatakan bahwa nilai objektif dari permasalahan ini adalah jumlah dari panjang path terpendek dikalikan dengan

banyaknya path yang harus dilewati.

Persamaan (2) menyatakan banyaknya path berarah dari suatu verteks ke verteks vi yang harus ditambahkan adalah sama dengan kelebihan derajat keluarnya. Persamaan (3) menyatakan banyaknya path berarah dari verteks vi ke verteks lain yang harus ditambahkan adalah sama dengan kelebihan derajat masuknya. Persamaan (4) menyatakan bahwa setiap variabel harus bernilai positif atau sama dengan nol, dengan kata lain tidak boleh bernilai negatif.

Berikut ini akan diberikan contoh kasus mengubah digraf berbobot yang tidak balance menjadi digraf berbobot yang balance.

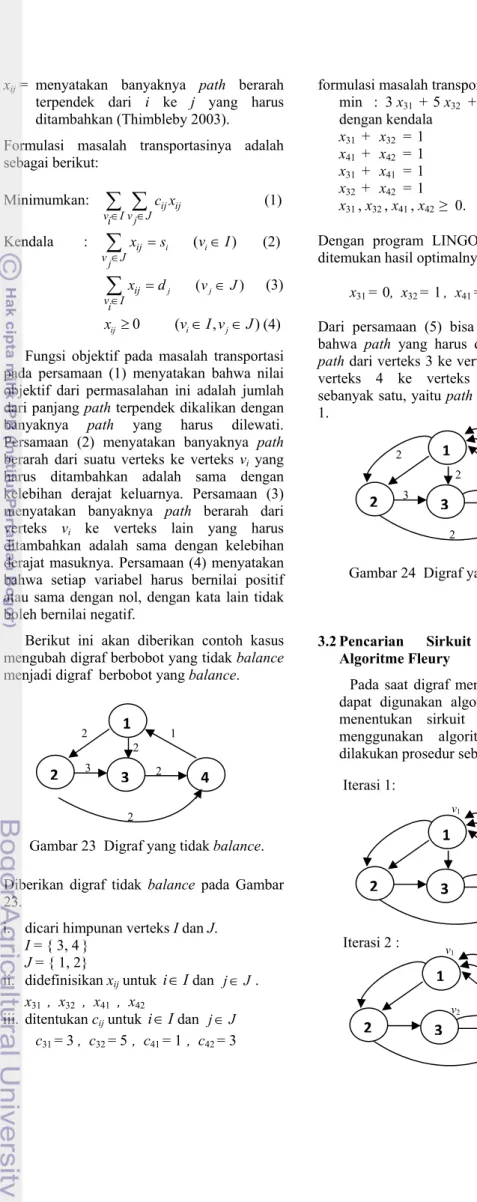
Diberikan digraf tidak balance pada Gambar 23.

i. dicari himpunan verteks I dan J. I = { 3, 4}

J = { 1, 2}

ii. didefinisikan xij untuk i I∈ dan j∈J. x31 , x32 , x41 , x42

iii. ditentukan cij untuk i I∈ dan j∈J c31= 3 , c32= 5 , c41= 1 , c42 = 3

formulasi masalah transportasinya adalah: min : 3 x31 + 5 x32 + 1 x41 + 3 x42 dengan kendala x31 + x32 = 1 x41 + x42 = 1 x31 + x41 = 1 x32 + x42 = 1 x31, x32, x41, x42 ≥ 0. Dengan program LINGO 8.0 (Lampiran 4) ditemukan hasil optimalnya adalah

x31= 0, x32= 1, x41= 1, x42= 0. (5)

Dari persamaan (5) bisa ditarik kesimpulan bahwa path yang harus ditambahkan adalah path dari verteks 3 ke verteks 2 dan path dari verteks 4 ke verteks 1 masing-masing sebanyak satu, yaitu path 3-1-2 dan path 4-1.

3.2Pencarian Sirkuit Euler dengan Algoritme Fleury

Pada saat digraf menjadi balance, maka dapat digunakan algoritme Fleury untuk menentukan sirkuit Eulernya. Dengan menggunakan algoritme Fleury maka dilakukan prosedur sebagai berikut.

2

Gambar 23 Digraf yang tidak balance.

1 2 3 4 2 3 1 2 2

Gambar 24 Digraf yang sudah balance.

1 2 ₃ ₄ 2 1 3 2 2 2 v1 Iterasi 1: 1 2 ₃ ₄ v2 v1 Iterasi 2 : 1 2 3 4

(21)

Pada Gambar 25, terlihat bahwa semua sisi telah terhapus sehingga bisa didapat sirkuit Eulernya yaitu: C = 1-3-4-1-2-3-4-1-2-4-1. dengan total bobot 18. Dapat dilihat bahwa jika banyaknya sisi pada digraf cukup banyak, maka diperlukan iterasi yang banyak pula. Untuk itu dibuat sebuah program komputer untuk mencari sirkuit Euler pada digraf berbobot dengan dasar algoritme Fleury.

3.2.1Aplikasi Pemrograman

Program komputer yang dibuat berdasarkan algoritme Fleury untuk menetukan sirkuit Euler ke dalam syntax Mathematica 7.0 bisa dilihat pada Lampiran 5. Pemrograman ini kemudian dicoba untuk menyelesaikan contoh kasus pada Gambar 23, sehingga didapatkan hasil sirkuit Eulernya C = 1-3-4-1-2-3-4-1-2-4 (lihat Lampiran 6).

Sirkuit Euler yang didapatkan dari penggunaan program komputer bisa saja berbeda dengan yang didapatkan secara manual. Namun, keadaan tersebut bukan merupakan suatu masalah karena tujuan dari algoritme ini adalah mencari sirkuit Euler yang melewati semua arc pada digraf, sehingga panjang sirkuit Eulernya pasti sama.

v3 v2 v1 Iterasi 3: 1 2 3 4 v4 v3 v2 v1 Iterasi 4: 1 2 3 4 v5 v4 v3 v2 v1 Iterasi 5: 1 2 ₃ ₄ v6 v6 v6 v6 v6 v7 v5 v4 v3 v2 v1 Iterasi 6: 1 2 3 4 v8 v7 v5 v4 v3 v2 v1 Iterasi 7: 1 2 3 4 v6 v5 v8 v7 v9 v4 v3 v2 v1 Iterasi 8: 1 2 ₃ ₄ v10 v5 v8 v7 v9 v4 v3 v2 v1 Iterasi 9: 1 2 ₃ ₄ v11 v10 v5 v8 v7 v9 v4 v3 v2 v1

Gambar 25 Penentuan sirkuit Euler pada digraf.

1

2 ₃ ₄

(22)

12

3.3 Pencarian Sirkuit Euler dengan Algoritme van Aardenne-Ehrenfest - de Bruijn

Berikut ini akan dibahas algoritme lain yang bisa menyelesaikan masalah DCPP yang disarankan oleh van Aardenne-Ehrenfest dan de Bruijn (1951) yang dijelaskan dalam Eiselt et al. (1995).

Algoritme van Aardenne-Ehrenfest - de Bruijn

LANGKAH 1. Dibangun sebuah spanning arborescence yang berakar di vr.

LANGKAH 2. Arc yang keluar dari vr dan verteks-verteks lain diurutkan dan dilabeli sedemikian hingga arc terakhir yang dilabeli adalah arc pada arborescence.

LANGKAH 3. Dimulai dari sembarang

verteks; arc dengan label terendah yang belum dilewati dipilih untuk sampai ke verteks berikutnya. Prosedur ini dilanjutkan hingga semua arc telah dilewati.

Berikut ini akan diberikan kasus sederhana yang sama dengan contoh sebelumnya pada algoritme Fleury untuk mengimplementasikan algoritme van Aardenne-Ehrenfest - de Bruijn dalam mencari sirkuit Euler pada sebuah digraf.

i. Diberikan digraf balance seperti pada Gambar 24. Digraf yang diberikan harus balance karena merupakan implikasi dari Teorema 2. Langkah pertama adalah ditentukan spanning arborescence pada digraf, misalkan diambil digraf berikut:

ii. Semua arc diurutkan dan dilabeli secara sembarang dengan label terakhir (terbesar) adalah label untuk arc yang dipakai di arborescence, sehingga digraf menjadi seperti berikut ini:

iii. Sirkuit Euler yang diperoleh, misalkan dimulai dari verteks 3, adalah C = 3-4-1-2-4-1-3-4-1-2-3, dengan total bobot 18. Jika dicari sirkuit Euler yang dimulai dari verteks 1 maka didapat C = 1-2-4-1-3-4-1-2-3-4-1.

Secara garis besar, solusi sirkuit Euler yang didapatkan baik menggunakan algoritme Fleury maupun algoritme van Aardenne-Ehrenfest - de Bruijn memang terlihat sama, tetapi terkadang ada perbedaan susunan path yang didapatkan, akan tetapi hal tersebut tidak menjadi masalah karena jika dilihat dari panjang sirkuit atau total bobotnya, pasti memiliki nilai yang sama.

Gambar 27 Pelabelan pada arc.

L2 L1 L2 L3 L1 L2 L1 L2 L3 L1 1 2 3 4

Gambar 26 Spanning arborescence untuk digraf pada gambar 24.

1

(23)

Sampah merupakan sesuatu yang sangat tidak menyehatkan jika tidak dikelola dengan baik. Di rumah, di kampus, di kantor, di tempat umum, bahkan di jalanan, sampah masih banyak berserakan. Sampah mempunyai tempat pembuangan sementara (TPS) dan tempat pembuangan akhir (TPA). Dinas Kebersihan selaku pihak yang terkait memiliki sistem pengambilan sampah tiap untuk periodenya. Pihak tersebut harus merumuskan bagaimana cara menentukan rute terbaik agar pengambilan sampah dapat berjalan dengan lancar dan optimal. Pada karya ilmiah ini akan dibahas rute pengambilan sampah di daerah Kampung Wayang (Kayang).

4.1 Permasalahan Pengambilan Sampah

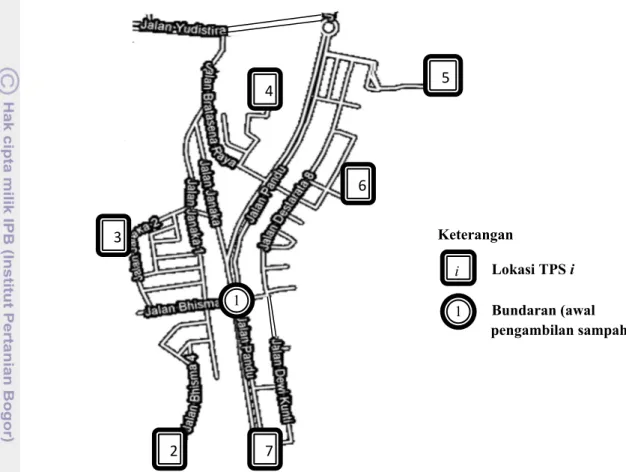
Sketsa pada Gambar 28 merupakan peta dari kondisi lingkungan daerah tersebut. Pada Gambar 28 yang disebut jalan utama adalah

jalan yang diberi nama tokoh wayang, sedangkan jalan yang lainnya yang tidak bernama disebut jalan atau blok pendek. Lokasi TPS pada tiap bloknya diperlihatkan dengan gambar “kotak”. Asumsi yang digunakan dalam masalah pengambilan sampah di lingkungan ini adalah sebagai berikut:

i. blok atau jalan yang pendek akan

digabung menjadi satu jalan dengan jalan utamanya,

ii. setiap jalan harus dilewati tanpa kecuali, agar keberadaan sampah yang ada di setiap gentong sampah rumah warga dapat diketahui,

iii.setiap jalan utama seperti jalan Bhisma, jalan Janaka, jalan Bratasena, jalan Dewi Kunti, jalan Destarata, dan jalan Pandu Raya memiliki TPS masing-masing sehingga petugas harus memeriksa juga setiap TPS tersebut,

Gambar 28 Peta lokasi TPS di Kampung Wayang.

IV APLIKASI PERMASALAHAN

Keterangan Lokasi TPS i Bundaran (awal pengambilan sampah) 2 3 7 4 6 5 i 1 1

(24)

14

iv. semua pekerjaan diawali di jalan arteri bundaran Pandu Raya dan berakhir di tempat yang sama,

v. diasumsikan bahwa total volume sampah tidak melebihi kapasitas dari truk sampah. Model graf yang bisa dibuat dari kasus ini adalah sebagai berikut:

Tabel 1 Keterangan digraf kasus Kayang Verteks Keterangan

1 Tempat awal dan akhir dari

pengambilan sampah yaitu bundaran Pandu Raya.

2 Lokasi TPS di jalan Bhisma. 3 Lokasi TPS di jalan Janaka. 4 Lokasi TPS di jalan Bratasena. 5 Lokasi TPS di jalan Destarata

Ujung.

6 Lokasi TPS di jalan Destarata Raya.

7 Lokasi TPS di jalan Dewi

Kunti.

Dengan menggunakan masalah tranportasi Orloff (1974) untuk mencari path ekstranya, maka:

i. dicari himpunan verteks I dan J. I = { 4, 5}

J = { 1, 6, 7}

ii. didefinisikan xij untuk i∈Idan j∈J. x41 , x46 , x47 , x51 , x56 , x57

iii.ditentukan cij untuk i∈Idan j∈J

c41= 112, c46= 95, c47= 122, c51 = 55, c56

= 38, c57= 65 (dicari dengan algoritme

Dijkstra pada Lampiran 7).

formulasi masalah transportasinya adalah: Min : 112 x41 + 95x46 + 122x47 + 55x51 + 38 x56 +65 x57 dengan kendala x41 + x46 + x47 = 1 x51 + x56 + x57 = 2 x41 + x51 = 1 x46 + x56 = 1 x47 + x57 = 1 x41, x46 , x47 , x51 , x56 , x57 ≥ 0 Dengan program LINGO 8.0 (Lampiran 8)

ditemukan hasil optimalnya adalah:

x41=1, x46=0, x47=0, x51=0, x56=1, x57=1 (6)

Dari persamaan (6) bisa ditarik kesimpulan bahwa path tambahan yang diperlukan adalah 4-5-6-1, 5-6 dan 5-6-7.

Digraf pada Gambar 30 merupakan digraf kasus Kayang yang sudah balance, sehingga bisa dicari solusi sirkuit Eulernya. Solusi sirkuit Euler yang dihasilkan dengan Mathematica 7.0 adalah C = 1-3-4-5-6-7-4-5-6-1-2-3-5-6-7-1-5-6-1 dengan total bobot 782 (Lampiran 9). Sirkuit Euler yang diperoleh secara manual dengan algoritme Fleury, adalah C = 1-2-3-4-5-6-1-3-5-6-1-5-6-7-4-5-6-7-1 dengan total bobot 782 (Lampiran 10). Kemudian sebagai perbandingan, masalah digraf kasus pengambilan sampah di Kayang pada Gambar 30, diselesaikan dengan algoritme van Aardenne-Ehrenfest - de Bruijn sebagai perbandingan bahwa urutan path-nya tidak tunggal namun solusinya tetap optimal.

77

Gambar 30 Digraf kasus Kayang yang sudah balance. 43 82 ₆₇ 17 48 33 57 38 27 18 60 1 4 ₅ 6 3 2 7 77

Gambar 29 Digraf kasus Kayang dengan bobot pada sisi berarah (i,j) menyatakan jarak dari verteks i ke verteks j. . 43 82 ₆₇ 17 48 33 57 38 27 18 60 1 4 ₅ 6 3 2 7

(25)

Misalkan spanning arborescence yang diperoleh dari langkah 1 pada digraf adalah sebagai berikut:

selanjutnya pelabelan dengan algoritme van Aardenne-Ehrenfest - de Bruijn untuk kasus Kayang diberikan pada Gambar 32.

Dari Gambar 32 dapat ditarik kesimpulan bahwa sirkuit Euler yang bisa dibentuk dari digraf dengan verteks awal di verteks 1 adalah C = 1-2-3-5-6-1-3-4-5-6-1-5-6-7-4-5-6-7-1 dengan total bobot 782.

V SIMPULAN DAN SARAN

5.1 Simpulan

CPP bisa diterapkan pada permasalahan graf yang berarah, yang kemudian dikenal sebagai DCPP. Di dalam karya ilmiah ini, penyelesaian masalah DCPP diselesaikan dengan algoritme Fleury dan algoritme van Aardenne-Ehrenfest - de Bruijn. Solusi yang diperoleh dengan kedua algoritme ini tidak tunggal, namun total jarak yang ditempuh masing-masing adalah sama. Dikarenakan algoritme Fleury tidak efektif untuk digraf dengan banyak arc, maka digunakan bantuan program Mathematica 7.0 untuk menentukan solusinya.

Dalam karya ilmiah ini permasalah DCPP diterapkan pada kasus pengambilan sampah di Kampung Wayang, dan dapat ditemukan solusi yaitu berupa rute pengambilan sampah yang optimal.

5.2 Saran

Jika ada yang ingin mendalami karya ilmiah ini, maka disarankan menggunakan barisan de Bruijn untuk menyelesaikan permasalahan DCPP. Metode tersebut terbilang unik dan menarik karena pengerjaannya berbasis pada bilangan biner. Dalam aplikasi pemrogramannya, Mathematica 7.0 mampu membuat program dengan dasar algoritme Fleury dengan baik, tetapi alangkah lebih baiknya jika menggunakan perangkat lunak yang berbasis bahasa Java, karena piranti lunak tersebut mampu memodifikasi program sedemikian rupa sehingga menghasilkan output yang lebih menarik.

Gambar 31 Spanning arborescence digraf kasus Kayang. 43 67 48 33 38 27 1 4 ₅ 6 3 2 7

vr _{Gambar 32 Digraf kasus Kayang yang}

sudah dilabeli. 1 4 ₅ 6 3 2 7 L1 L1 L3 L1 L1 L1 L1 L3 L2 L2 L2 L2 L2 L3 L2 L1 L4 L4

(26)

16

DAFTAR PUSTAKA

Balakrishnan VK. 1997. Schaum’s Outline of Theory and Problems of Graph Theory. New York: McGraw-Hill.

Bondy JA, Murty USR. 1976. Graph Theory with Applications. New York: Elsevier Science.

Chartrand G, Oellermann OR. 1993. Applied and Algorithmic Graph Theory. New York: McGraw-Hill.

Chartrand G, Zhang P. 2009. Chromatic Graph Theory. London: CRC Pr.

Diestel R. 1997. Graph Theory. New York: Springer-Verlag.

Eiselt HA, Gendreau M, Laporte G. 1995. Arc routing problem, Part 1: The Chinese postman problem. Operat Res 43(2): 231-242.

Foulds LR. 1992. Graph Theory Applications. New York: Springer Publishing.

Orloff CS. 1974. A fundamental problem in vehicle routing. Networks 4: 35-64.

Thimbleby H. 2003. The Directed Chinese Postman Problem. London: University College London Interaction Center.

Vasudev C. 2006. Graph Theory with Application. New Delhi: New Age International.

(27)

(28)

18

Lampiran 1 Pembuktian Teorema 1

Suatu graf G merupakan graf Euler jika dan hanya jika setiap verteks pada graf berderajat genap.

Bukti Teorema1

(=>) Misalkan G adalah graf Euler, maka G pasti mempunyai sirkuit Euler. Misalkan v adalah suatu verteks pada G yang bukan merupakan verteks awal ataupun verteks akhir pada sirkuit Euler di G. Karena diindikasikan bahwa di v C selalu ada sisi yang masuk ke v dan sisi yang keluar dari v, maka perjalanan melewati v satu kali berkontribusi pada derajat v sebanyak dua, akibatnya v pasti memiliki derajat yang genap. Kemudian andaikan v adalah verteks awal dan verteks akhir pada sirkuit Euler. Sebagai verteks awal, v berkontribusi derajat sebanyak satu, dan sebagai verteks akhir v juga berkontribusi derajat sebanyak satu sehingga derajat v dipastikan sebanyak dua, akibatnya v pasti memiliki derajat yang genap juga. Maka terbukti bahwa setiap verteks pada graf G memiliki derajat yang genap.

(<=) Misalkan G adalah graf terhubung yang memiliki derajat yang genap pada setiap verteksnya. Misalkan u adalah verteks pada G. Pertama akan ditunjukkan bahwa G mempunyai sirkuit u-u. Dibangun trail yang dimulai dari u yang memiliki sebanyak mungkin sisi pada G. Diklaim bahwa T adalah sirkuit dengan trail u-v dengan u ≠ v, maka pasti ada sejumlah ganjil sisi yang incident dengan v yang dimiliki oleh T. Dikarenakan derajat v pada G adalah genap, maka pasti setidaknya ada satu sisi yang incident dengan v yang bukan dimiliki oleh T. Dimisalkan vw adalah sisi yang dimaksud. Jika w ditambahkan pada T maka akan menjadi trail baru, sebut saja T’, dengan verteks awal di u yang memiliki sisi yang incident melebihi T, ini tidak mungkin. Maka T adalah sirkuit dengan verteks awal dan verteks akhirnya di u, sehingga disimpulkan bahwa T adalah sirkuit. Disimbolkan T menjadi C.

Jika C sirkuit Euler dari G, maka proses pembuktian teorema sudah lengkap. Andaikan C bukan sirkuit Euler, sehingga C tidak memuat semua sisi di G. karena G terhubungkan, maka terdapat verteks x di C yang incident dengan sisi yang bukan di C. Misalkan H = G – E(C). Karena setiap verteks incident dengan sisi yang genap pada C, maka H pasti genap. Dimisalkan H’ adalah komponen H yang memiliki x, maka H’ memiliki derajat yang genap. Dengan argumen yang sama sebelumnya, H’ pasti memiliki sirkuit C’ dengan verteks awal dan verteks akhir pada x. Dengan memasukan C’ pada C, terbentuk sirkuit u-u misalkan dinotasikan dengan C” pada G, akan terbentuk dengan jumlah sisi yang lebih banyak dari pada C, sehingga ini merupakan suatu kontradiksi karena jumlah sisi tersebut tidak boleh melebihi banyaknya sisi pada C.

Catatan

Definisi (komponen)

Misalkan G=(V,E) adalah graf. Subgraf terhubung yang maksimal di G disebut komponen G. (Diestel 1997)

Lampiran 2

Langkah solusi sirkuit Euler dengan menggunakan algoritme Fleury

Iterasi 3:

Diambil sisi yang incident dengan v1,

misalkan sisi {2,4}, dihapus dan didefinisikan sebagai v2.

Iterasi 4:

Sisi yang incident dengan v2 dihapus, misalkan

sisi {4,6}, dan didefinisikan sebagai v3.

v2 v0 v1 1 2 6 3 5 4 G: v2 v3 v0 v1 1 2 6 3 5 4 G:

(29)

Iterasi 5:

Sisi yang incident dengan v3 dihapus. Sisi

{6,1} adalah bridge, karena masih ada sisi lain yang bisa diambil selain sisi tersebut, maka sisi {6,1} tidak boleh diambil. Misalkan diambil sisi {6,5} dan didefinisikan v4.

.

Iterasi 6:

Sisi yang incident dengan v4 dihapus,

misalkan sisi {5,4}dan didefinisikan v5.

Iterasi 7:

Sisi yang incident dengan v5 dihapus,

misalkan sisi {4,3}. walaupun sisi ini adalah bridge, akan tetapi sisi ini tetap dipilih karena tidak ada sisi lain yang bukan bridge, dan didefinisikan v6.

Iterasi 8:

Sisi yang incident dengan v6 dihapus. Sisi

{3,2} tidak bisa diambil karena merupakan bridge, maka diambil sisi {3,5} dan didefinisikan v7.

Iterasi 9:

Sisi yang incident dengan v7 dihapus, diambil

sisi {5,3}, dan didefinisikan v8.

Iterasi 10:

Iterasi 11:

Iterasi 12:

Sisi yang incident dengan v10 dihapus.

Misalkan diambil sisi {6,1}, sisi satu-satunya yang belum dipilih, dan didefinisikan v11.

v7 v6 v5 v4 v2 v3 v0 v1 1 2 6 3 5 4 G: v8 v7 v6 v6 v4 v5 v3 v0 v1 1 2 6 3 5 4 G: v9 _v8 v7 v6 v5 v4 v2 v3 v0 v1 1 2 6 3 5 4 G: v10 v9 _v8 v7 v6 v5 v4 v2 v3 v0 v1 1 2 6 3 5 4 G: v11 v10 v9 _v8 v7 v6 v5 v4 v2 v3 v0 v1 1 2 6 3 5 4 G: v6 v5 v4 v2 v3 v0 v1 1 2 6 3 5 4 G: v4 v2 v3 v0 v1 1 2 6 3 5 4 G: v5 v4 v2 v3 v0 v1 1 2 6 3 5 4 G:

(30)

20

Lampiran 3

Penentuan path terpendek dengan algoritme Dijkstra

Iterasi 1:

Langkah 1. P = {1} dan L(1) = 0, L’(2) = 4 dan L’(7) = 2. Verteks 7 memiliki nilai yang minimum maka pilih dan labeli arc (1,7). Langkah 2. P = {1,7} dan L(7) = 2, L’(2) = min{4 , L(7) + a(7,2)}, L’(3) = min{+∞ , L(7) + a(7,3)}, L’(4) = min{+∞ , L(7) + a(7,4)}, L’(5) = min{+∞ , L(7) + a(7,5)}, L’(6) = min{+∞ , L(7) + a(7,6)}. Iterasi 2: Langkah 1. P = {1,7}, L(1) = 0 dan L(7) = 2, L’(2) = 3, L’(4) = 9, L’(6) = 5. Verteks 2 memiliki nilai yang minimum maka pilih dan labeli arc (7,2). Langkah 2. P = {1,7,2} dan L(7) = 2, L(2) = 3, L’(3) = min{+∞ , L(2) + a(2,3)}, L’(4) = min{9 , L(2) + a(2,4)}, L’(5) = min{+∞ , L(2) + a(2,5)}, L’(6) = min{5 , L(2) + a(2,6)}. Iterasi 3: Langkah 1. P = {1,7,2}, L(1) = 0, L(7) = 2 dan L(2) = 3, L’(3) = 9, L’(4) = 9, L’(6) = 5. Verteks 6 memiliki nilai yang minimum maka pilih dan labeli arc (7,6).

Langkah 2. P = {1,7,2,6} dan L(7) = 2, L(2) = 3, L(6) = 5, L’(3) = min{9 , L(6) + a(6,3)}, L’(4) = min{9 , L(6) + a(6,4)}, L’(5) = min{+∞ , L(6) + a(6,5)}. Iterasi 4: Langkah 1. P = {1,7,2,6}, L(1) = 0, L(7) = 2, L(2) = 3 dan L(6) = 5, L’(3) = 9, L’(4) = 9. Verteks 3 merupakan salah satu yang minimum, maka pilih dan labeli arc (2,3). Langkah 2. P = {1,7,2,6,3} dan L(7) = 2, L(2) = 3, L(6) = 5, L(3) = 9, L’(4) = min{9 , L(3) + a(3,4)}, L’(5) = min{+∞ , L(3) + a(3,5)}. Iterasi 5: Langkah 1. P = {1,7,2,6,3}, L(1) = 0, L(7) = 2, L(2) = 3, L(6) = 5 dan L(3) = 9, L’(4) = 9. Verteks 4 memiliki nilai yang minimum maka pilih dan labeli arc (7,4).

Langkah 2. P = {1,7,2,6,3,4} dan L(7) = 2, L(2) = 3, L(6) = 5, L(3) = 9, L(4) = 9, L’(5) = min{+∞ , L(4) + a(4,5)}. Iterasi 6: Langkah 1. P = {1,7,2,6,3,4}, L(1) = 0, L(7) = 2, L(2) = 3, L(6) = 5, L(3) = 9 dan L(4) = 9, L’(5) = 12. Verteks 5 dipilih dan labeli arc (4,5).

Langkah 2. L(5) = 12 dan P = V. Iterasi 7:

Langkah 1. Karena P = V maka iterasi berhenti.

Lampiran 4

Program LINGO 8.0 untuk menyelesaikan contoh masalah transportasi model:

! Set Vars:

! Define objective function;

min= 3*x31 + 5*x32 + 1*x41 + 3*x42; ! Define constraint; x31 + x41 = 1; x32 + x42 = 1; x31 + x32 = 1; x41 + x42 = 1; end Hasil eksekusi

Global optimal solution found at iteration: 0

Objectivevalue: 6.000000 Variable Value Reduced Cost X31 0.000000 0.000000 X32 1.000000 0.000000 X41 1.000000 0.000000 X42 0.000000 0.000000 Row Slack or Surplus Dual Price 1 6.000000 -1.000000 2 0.000000 -1.000000 3 0.000000 -3.000000 4 0.000000 -2.000000 5 0.000000 0.000000 Lampiran 5

Syntax program Mathematica 7.0 untuk menyelesaikan permasalahan perutean dengan dasar Algoritme Fleury

Input : DCPP[{verteks-i , verteks-j, bobot sisi (i,j) , label (i,j)},

{verteks-i+1 , verteks-j+1, bobot sisi (i+1,j+1) , label (i+1,j+1)},...,{dst}] dengan i dan j =1,2,3...N

(31)

Hf@from_, _D→_L⋅from =from;

Hf@_,to_D→_L⋅to=to;

Hf@from_, to_D→_L⋅edge =8from, to<; H_→count_ L⋅count =count;

DCPP@edges_ D:= Module@

8c, defined , δ, extraPaths , i, j, k, n, path, cheapest <, If@edges 8<, Throw@"graf kosong "DD;

H∗ inisialisasi ∗L

n=Max@Map@H ⋅edgeL&, edgesDD; c=Table@0, 8n<, 8n<D;

δ=Table@0, 8n<D;

defined =Table@False , 8n<, 8n<D; cheapest =Table@8<, 8n<,8n<D; path =Table@8<, 8n<, 8n<D; For@i=1, i≤Length @edgesD,i++,

Module @

8u=edgesPiT⋅from, v=edgesPiT⋅to, w=edgesPiT⋅weight <,

δPuT++; δPvT−−;

If@!defined Pu, vT »»w<cPu, vT, defined Pu, vT=True ;

cheapest Pu, vT=edgesPiT⋅name; cPu, vT=w;

pathPu, vT=edgesPiT; D

D D;

H∗ format penulisan fungsi ∗L 8from_, _, _, _<⋅from =from; 8_, to_, _, _<⋅to =to;

8_, _,weight_ , _<⋅weight =weight;

8_, _, _, name_<⋅name =name;

(32)

22 For@k=1, k≤n, k++, For@i=1, i≤n,i++, If@defined Pi,kT, For@j=1, j≤n,j++, If@defined Pk,jT, If@!defined Pi,jT »»cPi, jT>cPi, kT+cPk, jT, cPi, jT=cPi,kT+cPk, jT; defined Pi, jT=True ; pathPi,jT=pathPi,kT; D D D D D D; For@i=1, i≤n, i++,

If@cPi,iT<0, Throw@"merupakan sirkuit negatif "D, For@j=1, j≤n,j++,

If@!defined Pi, jT,

Throw@"tidak connected , pilih graf yang lain"D D

D D D; Module@

8neg, pos, variables , φ, constraints <, neg =Flatten @Position @δ, _ ? Negative D; pos =Flatten @Position @δ, _ ? Positive D; variables =Flatten @Outer@f, neg, posD;