BAB 2
LANDASAN TEORI
2.1. Graf
2.1.1. Definisi Graf
Teori Graf merupakan suatu diagram yang memuat informasi tertentu jika diinterpretasikan secara tepat. Dalam kehidupan sehari-hari graf digunakan untuk mengambarkan berbagai macam struktur yang ada. Tujuannya adalah sebagai visualisasi objek-objek agar lebih mudah dimengerti. Beberapa contoh graf yang sering dijumpai, antara lain struktur organisasi, bagan alir, pengambilan mata kuliah, peta, rangkaian listrik, dan lain-lain (Hendardi, A. 2012).
Banyak sekali struktur yang bisa dipresentasikan dengan graf, dan banyak masalah yang bisa diselesaikan dengan graf. Sering kali graf digunakan untuk mempresentasikan suatu jaringan. Misalkan jaringan jalan raya dengan kota sebagai simpul (vertex) dan jalan yang menghubungkan setiap kota sebagai sisi (edge) dan bobotnya (weight) adalah panjang dari jalan tersebut.
Secara matematis graf mendefinisikan sebagai pasangan himpunan (V, E), ditulis dengan notasi G= (V, E), yang dalam hal ini V adalah himpunan tidak kosong dari simpul-simpul (vertex atau node) dan E adalah himpunan sisi (edge) yang menghubungkan sepasang simpul (Munir, R. 2009)
Simpul (vertex) pada graf dapat dinyatakan dengan huruf, bilangan atau gabungan keduanya. Sedangkan sisi-sisi yang menghubungkan simpul u dengan simpul v dinyatakan dengan pasangan (u, v) atau dinyatakan dengan lambang 𝑒𝑒1,𝑒𝑒2, 𝑒𝑒3 dan seterusnya.
2.2. Teori Dasar Graf
Graf G didefinisikan sebagai pasangan himpunan (V,E), ditulis dengan notasi G=(V,E), yang dalam hal ini V adalah himpunan tidak kosong dari simpul-simpul dan E adalah himpunan sisi yang menghubungkan sepasang simpul (Munir, R. 2005).
V2
V1
V4 V5
V6
V3 e1
e3 e2 e6
e8
e9
e7
e4
e5
garis yang berhubungan dengannya disebut titik terasing (isolating point). Graf yang tidak memiliki titik (sehingga tidak mewakili garis) disebut garis kosong.
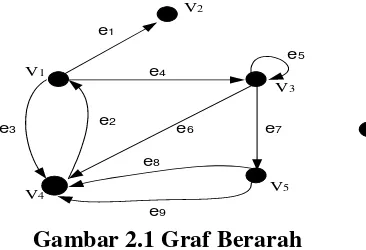
Jika semua garisnya berarah, maka grafnya disebut graf berarah (directed graph), atau sering disingkat digraph. Jika semua garisnya tidak berarah, maka grafnya disebut graf tak berarah (undirected graph). Sehinga dapat ditinjau dari arahnya, graf dapat dibagi menjadi dua yaitu graf berarah dan graf tidak berarah.
2.2.1. Graf Berarah (Directed Graf = Digraph)
Pada graf berarah, arah sisi/urutan ikut diperhatikan. Dalam suatu graf, lintasan (path) adalah urutan simpul, atau sisi yang dibentuk untuk bergerak dari satu simpul ke simpul yang lain. Dalam graf berarah, titik akhir dari sebuah busur akan menjadi titik awal dari busur berikutnya. Sirkuit adalah lintasan yang memiliki simpul awal dan akhir yang sama. Panjang lintasan adalah banyaknya sisi yang dilalui lintasan tersebut.
Suatu Graf berarah G terdiri dari himpunan titik-titik V(G) {𝑣𝑣1, 𝑣𝑣2, …}, himpunan
garis-garis E(G) {𝑒𝑒1, 𝑒𝑒2, … }, dan suatu fungsi yang mengawankan setiap garis dalam
E(G) ke suatu pasangan berurutan titik (𝑣𝑣𝑖𝑖, 𝑣𝑣𝑗𝑗). Jika 𝑒𝑒𝑘𝑘 = (𝑣𝑣𝑖𝑖, 𝑣𝑣𝑗𝑗) adalah suatu garis dalam
G, maka 𝑣𝑣𝑖𝑖 disebut titik awal 𝑒𝑒𝑘𝑘 dan 𝑣𝑣𝑗𝑗 disebut titik akhir 𝑒𝑒𝑘𝑘. Arah garis adalah dari 𝑣𝑣𝑖𝑖 ke
𝑣𝑣𝑗𝑗.
Jumlah garis yang keluar dari titik 𝑣𝑣𝑖𝑖 disebut derajat keluar (out degree) titik 𝑣𝑣𝑖𝑖 yang disimbolkan dengan 𝑑𝑑+(𝑣𝑣𝑖𝑖), sedangkan jumlah garis yang menuju ke titik 𝑣𝑣𝑖𝑖 disebut derajat masuk (in degree) titik 𝑣𝑣𝑖𝑖, yang disimbolkan dengan 𝑑𝑑−(𝑣𝑣𝑖𝑖).
Titik terasing adalah titik dalam G dimana derajat keluar dan derajat masuknya adalah 0. Titik pendant (tergantung) adalah titik dalam G dimana derajat masuk dan derajat keluarnya adalah 1. Dua garis berarah dikatakan paralel jika keduanya memiliki titik awal dan titik akhir yang sama.
Contoh:
Tentukan:
a. Himpunan titik-titik, himpunan garis-garis, dan fungsi perkawanan. b. Derajat masuk dan derajat keluar tiap titik.
c. Titik terasing dan titik pendant. d. Garis paralel.
Penyelesaian:
a. V(G) = {𝑣𝑣1, 𝑣𝑣2, 𝑣𝑣3, 𝑣𝑣4, 𝑣𝑣5, 𝑣𝑣6 }
E(G) = { 𝑒𝑒1,𝑒𝑒2, 𝑒𝑒3, 𝑒𝑒4, 𝑒𝑒5, 𝑒𝑒6, 𝑒𝑒7,𝑒𝑒8,𝑒𝑒9 }
Fungsi mengawankan garis-garis dengan pasangan titik-titik berikut
𝑒𝑒1 dengan (𝑣𝑣1,𝑣𝑣2)
𝑒𝑒2 dengan (𝑣𝑣4, 𝑣𝑣1)
𝑒𝑒3 dengan (𝑣𝑣1,𝑣𝑣4)
𝑒𝑒4 dengan (𝑣𝑣1,𝑣𝑣3)
𝑒𝑒5 dengan (𝑣𝑣3, 𝑣𝑣3)
𝑒𝑒6 dengan (𝑣𝑣3,𝑣𝑣4)
𝑒𝑒7 dengan (𝑣𝑣3, 𝑣𝑣5)
𝑒𝑒8 dengan (𝑣𝑣5, 𝑣𝑣4)
𝑒𝑒9 dengan (𝑣𝑣5, 𝑣𝑣4)
b. 𝑑𝑑+ (𝑣𝑣1) = 3 𝑑𝑑− (𝑣𝑣1) = 1
𝑑𝑑+ (𝑣𝑣2) = 0 𝑑𝑑− (𝑣𝑣2) = 1 𝑑𝑑+ (𝑣𝑣3) = 3 𝑑𝑑− (𝑣𝑣3) = 2 𝑑𝑑+ (𝑣𝑣4) = 1 𝑑𝑑− (𝑣𝑣4) = 4 𝑑𝑑+ (𝑣𝑣5) = 2 𝑑𝑑− (𝑣𝑣5) = 1 𝑑𝑑+ (𝑣𝑣6) = 0 𝑑𝑑− (𝑣𝑣6) = 0
Dapat dilihat bahwa dalam setiap graf berarah, ∑ 𝑑𝑑𝑖𝑖 +(𝑣𝑣𝑖𝑖) = ∑ 𝑑𝑑𝑖𝑖 −(𝑣𝑣𝑖𝑖) c. Titik terasing adalah 𝑣𝑣6.
Titik pendant 𝑣𝑣2.
d. Garis paralel adalah 𝑒𝑒8 dan 𝑒𝑒9, dapat dilihat bahwa 𝑒𝑒2 dan 𝑒𝑒3 bukanlah garis paralel karena arahnya berbeda.
2.2.1.1. Path Berarah dan Sirkuit Berarah
mengikuti arah garis. Untuk membedakan dengan graf tak berarah, maka walk, path berarah, dan sirkuit dalam graf berarah disebut walk berarah, path berarah, dan sirkuit berarah. Suatu graf berarah yang tidak memuat sirkuit berarah disebut Asiklik (Siang, J.J. 2009).
Contoh:
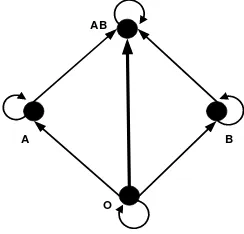
Ada 4 macam golongan darah, masing-masing A, B, AB, dan O. Darah golongan O dapat diberikan kepada semua golongan. Darah golongan A dan B dapat diberikan ke golongannya sendiri atau ke golongan O. Darah golongan AB hanya dapat diberikan pada pasien dengan golongan darah AB . Gambarkan graf berarah untuk menyatakan keadaan tersebut. Anggaplah garis dari 𝑣𝑣𝑖𝑖 ke 𝑣𝑣𝑗𝑗 menyatakan bahwa darah dari 𝑣𝑣𝑖𝑖 dapat diberikan
pada 𝑣𝑣𝑗𝑗. Apakah graf Asiklik?
Penyelesaian:
Graf berarah menyatakan keadaan transfusi darah yang mungkin dilakukan. Dapat dilihat bahwa dalam graf berarah tersebut tidak ada sirkuit berarah sehingga grafnya Asiklik.
Gambar 2.2 Path berarah
2.2.1.2. Graf Berarah Terhubung
Suatu graf tak berarah disebut terhubung jika ada walk yang menghubungkan setiap dua titiknya. Pengertian itu berlaku juga bagi graf berarah. Berdasarkan arah garisnya, dalam graf berarah dikenal dua jenis keterhubungan, yaitu terhubung kuat dan terhubung lemah.
Misalkan G adalah suatu graf berarah dan v, w adalah sembarang 2 titik dalam G. G disebut terhubung kuat jika ada path berarah dari v ke w. G disebut terhubung lemah, jika G tidak terhubung kuat, tetapi graf tak berarah yang bersesuaian dengan G terhubung.
AB
B
Contoh:
Manakah di antara graf-graf pada Gambar 2.3.yang terhubung kuat dan yang terhubung lemah?
𝐺𝐺1 𝐺𝐺2
Gambar 2.3 Graf berarah terhubung
Penyelesaian:
Dalam 𝐺𝐺1, setiap dua titik dapat dihubungkan dengan path berarah sehingga graf berarah
𝐺𝐺1 adalah graf terhubung kuat. Sebaliknya dalam 𝐺𝐺2, tidak ada path berarah yang menghubungkan 𝑣𝑣4 ke 𝑣𝑣3. Akan tetapi, jika semua arah garis dihilangkan (sehingga 𝐺𝐺2 menjadi graf tidak berarah), maka 𝐺𝐺2 merupakan graf yang terhubung. Jadi, 𝐺𝐺2 merupakan graf terhubung lemah.
2.2.1.3. Isomorfisma dalam Graf Berarah
Pengertian isomorfisma dalam graf berarah sama dengan isomorfisma pada graf tak berarah. Hanya saja pada isomorfisma graf berarah, korespondensi dibuat dengan memperhatikan arah garis.
Contoh
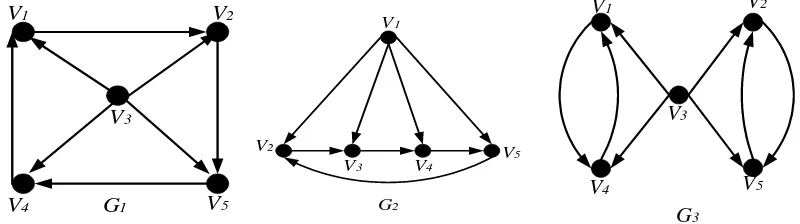
Tunjukkan bahwa graf 𝐺𝐺1 pada Gambar 2.4 isomorfis dengan 𝐺𝐺2, sedangkan 𝐺𝐺3 tidak isomorfis dengan 𝐺𝐺1
Penyelesaian:
Untuk membuktikan bahwa 𝐺𝐺1 isomorfis dengan 𝐺𝐺2, maka harus dibuat fungsi g : V(𝐺𝐺1) → V(𝐺𝐺2) dan h : E(𝐺𝐺1) → E(𝐺𝐺2)
yang mempertahankan titik-titik ujung serta arah garis.
Dalam 𝐺𝐺1, ada 4 garis yang keluar dari 𝑉𝑉3. Titik yang memiliki sifat seperti itu dalam 𝐺𝐺2 adalah titik 𝑣𝑣1, sehingga dibuat fungsi g sedemikian hingga
g(𝑣𝑣3) = 𝑣𝑣1, g(𝑣𝑣1) = 𝑣𝑣2, g(𝑣𝑣2) = 𝑣𝑣3, g(𝑣𝑣5) = 𝑣𝑣4, dan g(𝑣𝑣4) = 𝑣𝑣5 fungsi h adalah sebagai berikut:
h ((𝑣𝑣1, 𝑣𝑣2)) = (𝑣𝑣2,𝑣𝑣3) ; h ((𝑣𝑣2, 𝑣𝑣5)) = (𝑣𝑣3, 𝑣𝑣4) h ((𝑣𝑣5, 𝑣𝑣4)) = (𝑣𝑣4, 𝑣𝑣5) ; h ((𝑣𝑣4, 𝑣𝑣1)) = (𝑣𝑣5, 𝑣𝑣2) h ((𝑣𝑣3, 𝑣𝑣1)) = (𝑣𝑣1, 𝑣𝑣2) ; h ((𝑣𝑣3, 𝑣𝑣2)) = (𝑣𝑣1, 𝑣𝑣3) h ((𝑣𝑣3, 𝑣𝑣5)) = (𝑣𝑣1, 𝑣𝑣4) ; h ((𝑣𝑣3, 𝑣𝑣4)) = (𝑣𝑣1, 𝑣𝑣5)
pada fungsi g dan h dapat dilihat bahwa 𝐺𝐺1 isomorfis dengan 𝐺𝐺2. Selanjutnya, akan dibuktikan bahwa 𝐺𝐺3 tidak isomorfis dengan 𝐺𝐺1. Dalam 𝐺𝐺3, ada garis (𝑣𝑣1, 𝑣𝑣4) dan (𝑣𝑣4, 𝑣𝑣1). Jika 𝐺𝐺1 isomorfis dengan 𝐺𝐺3, maka harus ada fungsi h 𝐺𝐺3 → 𝐺𝐺1 demikian, sehingga h(𝑣𝑣1,
𝑣𝑣4) dan h(𝑣𝑣4, 𝑣𝑣1) merupakan garis-garis dalam 𝐺𝐺1 (dengan kata lain, ada titik 𝑣𝑣𝑖𝑖 dan 𝑣𝑣𝑗𝑗
dalam 𝐺𝐺1 demikian, sehingga ada garis dari 𝑣𝑣𝑖𝑖 ke 𝑣𝑣𝑗𝑗 dan dari 𝑣𝑣𝑗𝑗 ke 𝑣𝑣𝑖𝑖). Dalam 𝐺𝐺1 tidak ada
garis seperti itu sehingga 𝐺𝐺3 tidak isomorfis dengan 𝐺𝐺1.
2.2.2. Graf Tak Berarah (Undirected Graph)
Suatu graf G terdiri dari dua himpunan yang berhingga, yaitu himpunan simpul-simpul tak kosong (V(G)) dan himpunan jalur-jalur (E(G)). Jika semua jalurnya tidak berarah, maka grafnya disebut graf tak berarah (Siang, J.J. 2009).
2.2.2.1. Graf Bipartite (Bipartite Graph)
Suatu graf G disebut Graf Bipartite apabila V(G) merupakan gabungan dari dua himpunan tak kosong 𝑣𝑣1 dan 𝑣𝑣2 dan setiap garis dalam G menghubungkan suatu titik dalam 𝑣𝑣1 dengan titik dalam 𝑣𝑣3. Apabila dalam Graf Bipartite setiap titik dalam 𝑣𝑣1berhubungan dengan setiap titik dalam 𝑣𝑣2, maka grafnya disebut Graf Bipartite lengkap. Jika 𝑣𝑣1 terdiri dari m titik dan 𝑣𝑣2 terdiri dari n titik, maka Graf Bipartite lengkapnya sering diberi simbol
Contoh :
Tentukan mana di antara graf-graf pada Gambar 2.5 yang merupakan Graf Bipartite dan Bipartite Lengkap.
Gambar 2.5 Graf Bipartite
Penyelesaian:
a. Jelas bahwa titik-titik grafnya terbagi menjadi dua bagian, yaitu 𝑣𝑣1 = {𝑣𝑣1, 𝑣𝑣2, 𝑣𝑣3} dan
𝑣𝑣2 = {𝑣𝑣4, 𝑣𝑣5}. Setiap titik dalam 𝑣𝑣1 dihubungkan dengan setiap titik dalam 𝑣𝑣2 sehingga grafnya merupakan 𝐾𝐾3,2.
b. Hanya merupakan Graf Bipartite saja karena titik-titik dalam graf terbagi menjadi dua bagian, yaitu 𝑣𝑣1 = {𝑣𝑣1, 𝑣𝑣3} dan 𝑣𝑣2 = {𝑣𝑣2, 𝑣𝑣4}. Akan tetapi tidak semua titik dalam 𝑣𝑣1 dihubungkan dengan semua titik dalam 𝑣𝑣2 (𝑣𝑣1 tidak dihubungkan dengan 𝑣𝑣4).
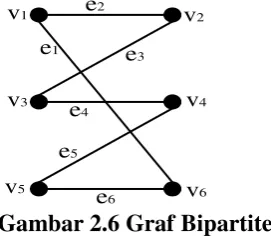
c. Dengan pengaturan letak titik-titiknya, maka graf gambar (c) dapat digambarkan sebagai graf.
Gambar 2.6 Graf Bipartite
Tampak bahwa titik-titiknya terbagi menjadi dua bagian, yaitu 𝑣𝑣1 = {𝑣𝑣1, 𝑣𝑣3, 𝑣𝑣5} dan 𝑣𝑣2 = {𝑣𝑣2, 𝑣𝑣4, 𝑣𝑣6}. Setiap menghubungkan sebuah titik dalam 𝑣𝑣1 dengan sebuah titik dalam 𝑣𝑣2 sehingga grafnya merupakan Graf Bipartite.
Posisi titik-titik dalam penggambaran graf kadang-kadang mempengaruhi pandangan, seperti halnya pada Gambar 2.5 bagian (c) dan (d). Dalam kedua graf tersebut, semua titik tampaknya terhubung dan tidak dapat dipisahkan walaupun kenyataannya tidaklah demikian. Oleh karena itu harus jeli dalam menentukan apakah suatu graf merupakan Graf Bipartite.
2.2.2.2. SubGraf
Konsep subgraf sama dengan konsep himpunan bagian. Dalam teori himpunan, himpunan A dikatakan merupakan himpunan bagian B bila hanya setiap anggota A merupakan B. Oleh karena graf merupakan himpunan yang terdiri dari titik dan garis, maka H dikatakan subgraf G, jika semua titik dan garis H juga merupakan titik dan garis dalam G. Secara formal, subgraf dapat didefinisikan sebagai berikut.
Misalkan G adalah suatu graf. Graf H dikatakn subgraf G bila dan hanya bila a. V(H) ⊆ V(G)
b. E(H) ⊆ E(G)
c. Setiap garis dalam H memiliki titik ujung yang sama dengan garis tersebut dalam G.
Dari definisi tersebut ada beberapa hal yang dapat diturunkan 1. Sebuah titik dalam G merupakan subgraf G.
2. Sebuah garis dalam G bersama-sama dengan titik-titik ujungnya merupakan subgraf G.
3. Dalam subgraf berlaku sifat transitif, jika H adalah subgraf G dan G adalah subgraf K, maka K adalah subgraf K.
Contoh:
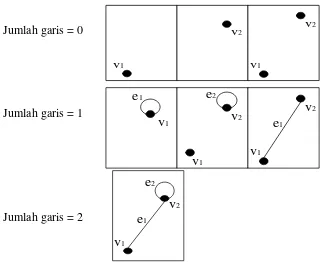
Gambarlah semua Subgraf yang mungkin dibentuk dari graf G pada Gambar 2.7.
Gambar 2.7 Sub Graf Penyelesaian:
G terdiri dari dua titik dan dua garis. Subgraf G yang mungkin dibentuk terdiri dari satu atau dua titik dan 0, satu atau dua garis. Semua Subgraf G yang mungkin dibuat dapat digambarkan sebagai berikut:
v1
v2
e2
Jumlah garis = 0
Jumlah garis = 1
Jumlah garis = 2
Gambar 2.8 Sub-Graf dari Gambar 2.7 2.2.2.3. Derajat (Degree)
Misalkan v adalah titik dalam suatu graf G. derajat titik v (simbol d(v)) adalah jumlah garis yang berhubungan dengan titik v dan garis suatu loop dihitung dua kali. Derajat total G
adalah jumlah derajat semua titik dalam G.
Contoh:
Tentukan derajat tiap-tiap titik dalam graf pada Gambar 2.9. Berapa derajat totalnya
Gambar 2.9 Derajat (Degree)
Penyelesaian:
d (𝑣𝑣1) = 4 garis yang berhubungan dengan 𝑣𝑣1 adalah 𝑒𝑒2, 𝑒𝑒3 dan loop 𝑒𝑒1 yang dihitung dua kali.
v1
v2
v1
v2
v1 v
2
v1
e1 e2
v1
v2
e1
v1
v2
e1
e2
e1
e2 e3
v1
v2
v3
v4
v5
v6
e4
d (𝑣𝑣2) = 2 garis yang berhubungan dengan 𝑣𝑣2 adalah 𝑒𝑒2 dan𝑒𝑒3.
d (𝑣𝑣3) dan d (𝑣𝑣5) = 1 karena garis yang berhubungan dengan 𝑣𝑣3 dan 𝑣𝑣5 adalah 𝑒𝑒4. d (𝑣𝑣4) = 2 garis yang berhubungan dengan 𝑣𝑣4 adalah loop 𝑒𝑒5 yang dihitung dua kali. d (𝑣𝑣6) = 0 karena tidak ada garis yang berhubungan dengan 𝑣𝑣6.
Derajat total = ∑6𝑖𝑖=1𝑑𝑑 (𝑣𝑣𝑖𝑖) = 4 + 2 + 1 + 2 + 1 + 0 = 10.
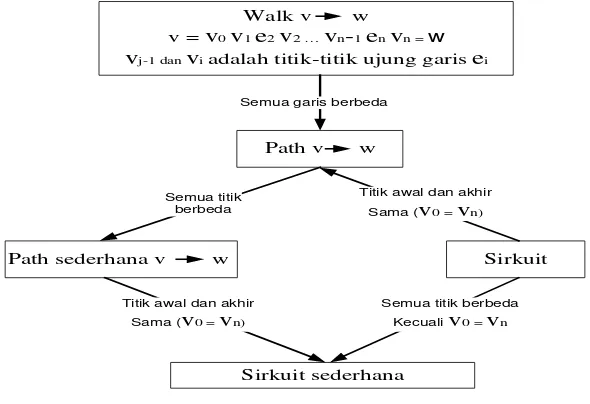
2.2.2.4. Path dan Sirkuit
Misalkan G adalah suatu graf. Misalkan pula v dan w adalah dua titik dalam G. Suatu Walk dari v dan w adalah barisan titik-titik berhubungan dan garis secara berselang-selang, diawali dari titik v dan diakhiri pada titik w.
Walk dengan panjang n dan v ke w dituliskan sebagai berikut 𝑣𝑣0 𝑒𝑒1 𝑣𝑣1 𝑒𝑒2 𝑣𝑣2… 𝑣𝑣𝑛𝑛−1 𝑒𝑒𝑛𝑛 𝑣𝑣𝑛𝑛 dengan 𝑣𝑣0 = v, 𝑣𝑣𝑛𝑛 = w, 𝑣𝑣𝑗𝑗 −1, dan 𝑣𝑣𝑖𝑖 adalah titik-titik ujung garis 𝑒𝑒𝑗𝑗. Path dengan panjang n
dari v ke w adalah walk dari v ke w yang semua garisnya berbeda. Path dari v ke w
dituliskan sebagai v = 𝑣𝑣0 𝑒𝑒1 𝑣𝑣1 𝑒𝑒2 𝑣𝑣2… 𝑣𝑣𝑛𝑛−1𝑒𝑒𝑛𝑛 𝑣𝑣𝑛𝑛 = w dengan 𝑒𝑒𝑖𝑖 ≠ w untuk i ≠ j.
Gambar 2.10 Bagan Alur Path dan Sirkuit
Path sederhana dengan panjang n dan v ke w adalah path dari v ke w berbentuk v =
𝑣𝑣0 𝑒𝑒1 𝑣𝑣1 𝑒𝑒2 𝑣𝑣2… 𝑣𝑣𝑛𝑛−1 𝑒𝑒𝑛𝑛 𝑣𝑣𝑛𝑛 = w dengan 𝑒𝑒𝑖𝑖 ≠ w untuk i ≠ j dan 𝑣𝑣𝑘𝑘 ≠ 𝑣𝑣𝑚𝑚 untuk k ≠ m. Sirkuit dengan panjang n adalah path yang dimulai dan diakhiri pada titik yang sama. Sirkuit adalah path yang berbentuk v = 𝑣𝑣0 𝑒𝑒1 𝑣𝑣1 𝑒𝑒2 𝑣𝑣2… 𝑣𝑣𝑛𝑛−1 𝑒𝑒𝑛𝑛 𝑣𝑣𝑛𝑛 = w dengan 𝑣𝑣0 = 𝑣𝑣𝑛𝑛. Sirkuit sederhana dengan panjang n adalah Sirkuit yang semua titiknya berbeda. Sirkuit sederhana berbentuk v = 𝑣𝑣0 𝑒𝑒1 𝑣𝑣1 𝑒𝑒2 𝑣𝑣2… 𝑣𝑣𝑛𝑛−1 𝑒𝑒𝑛𝑛 𝑣𝑣𝑛𝑛 = w dengan 𝑒𝑒𝑖𝑖 ≠ 𝑒𝑒𝑗𝑗 untuk i ≠ j dan
𝑣𝑣𝑘𝑘 ≠𝑣𝑣𝑚𝑚 untuk k ≠ m, kecuali 𝑣𝑣0 = 𝑣𝑣𝑛𝑛.
Walk v w
v = v0 v1 e2 v2 … vn-1 en vn = w
vj-1 dan vi adalah titik-titik ujung garis ei
Path v w
Path sederhana v w Sirkuit
Semua garis berbeda
Semua titik berbeda
Titik awal dan akhir Sama (v0 = vn)
Sirkuit sederhana
Titik awal dan akhir Sama (v0 = vn)
2.2.2.5. Sirkuit Euler
Sirkuit Euler adalah Sirkuit yang melalui tiap sisi dalam graf tepat satu kali (Siang, J.J. 2009) Untuk mengenang ahli matematika Leonhard Euler yang berhasil memperkenalkan graf untuk memecahkan masalah tujuh jembatan Koningsberg pada tahun 1736.
Kota Koningberg dibangun pada pertemuan dua cabang sungai Pregel. Kota tersebut terdiri dari sebuah pulau di tengah-tengah dan tujuh jembatan yang mengelilinginya.
Gambar 2.11 Jembatan Konigsberg
2.2.2.6. Graf Terhubung dan Tidak Terhubung
Misalkan G adalah suatu Graf. Dua titik v dan w dalam G dikatakan terhubung hanya ada walk dari v ke w. Graf G dikatakan terhubung bila hanya setiap dua titik dalam G
terhubung. Graf G dikatakan tidak terhubung bila ada dua titik dalam G yang tidak terhubung.
Contoh
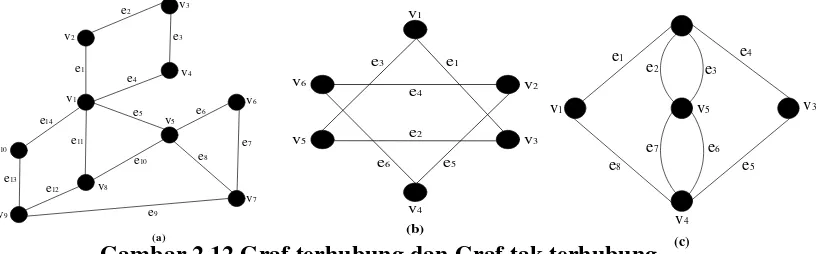
Tentukan mana di antara graf pada Gambar 2.12 yang merupakan Sirkuit Euler. carilah rute perjalanan kelilingnya
Gambar 2.12 Graf terhubung dan Graf tak terhubung
Penyelesaian:
a. d(𝑣𝑣2) = d(𝑣𝑣3) = d(𝑣𝑣4) = d(𝑣𝑣6) = d(𝑣𝑣10) = 2 d(𝑣𝑣5) = 4
d(𝑣𝑣7) = d(𝑣𝑣8) = d(𝑣𝑣9) = 3 d(𝑣𝑣1) = 5
karena ada titik yang berderajat ganjil, maka (a) bukanlah Sirkuit Euler.
b. Meskipun semua titiknya berderajat dua (genap), tetapi grafnya tidak terhubung. Jadi, (b) bukanlah Sirkuit Euler.
c. d(𝑣𝑣1) = d(𝑣𝑣3) = 2
d(𝑣𝑣2) = d(𝑣𝑣4) = d(𝑣𝑣5) = 4
karna graf (c) terhubung dan semua titiknya berderajat genap, maka (c) merupakan Sirkuit Euler.
2.2.2.7. Sirkuit Hamilton
Suatu graf terhubung G disebut Sirkuit Hamilton bila ada sirkuit yang mengunjungi setiap titiknya tepat satu kali kecuali titik awal yang sama dengan titik akhirnya.
Perhatikan perbedaaan Sirkuit Euler dan Sirkuit Hamilton. Dalam Sirkuit Euler, semua garis harus dilalui tepat satu kali, sedangkan semua titiknya boleh dikunjungi lebih dari satu kali. Sebaliknya, dalam Sirkuit Hamilton semua titik harus dikunjungi tepat satu kali dan tidak harus melalui semua garis. Dalam Sirkuit Euler, yang dipentingkan adalah garisnya. Sebaliknya dalam Sirkuit Hamilton, yang dipentingkan adalah kunjungan pada titiknya(Munir, R. 2009).
2.3. Representasi Graf dalam Matriks
Matriks dapat digunakan untuk menyatakan suatu graf. Hal itu sangat membantu untuk membuat program komputer yang berhubungan dengan graf. Dengan menyatakan graf sebagai suatu matriks, maka perhitungan-perhitungan yang diperlukan dapat dilakukan dengan mudah.
tersebut memiliki keuntungan yang berbeda-beda saat menyaring informasi yang dibutuhkan pada graf.
2.3.1. Representasi Graf Tak Berarah dalam Matriks
2.3.1.1. Matriks Hubung
Matriks Hubung (Adjacency Matrix) digunakan untuk menyatakan graf dengan cara menyatakannya dalam jumlah garis yang menghubungkan titik-titiknya. Jumlah baris (kolom) matriks hubung sama dengan jumlah titik dalam graf.
Misalkan G adalah graf tak berarah dengan titik-titik 𝑣𝑣1, 𝑣𝑣2, … 𝑣𝑣𝑛𝑛 ( n berhingga). Matriks hubung yang sesuai dengan graf G adalah matriks A = (𝑎𝑎𝑖𝑖𝑗𝑗) dengan 𝑎𝑎𝑖𝑖𝑗𝑗 = jumlah
garis yang menghubungkan titik 𝑣𝑣𝑖𝑖 dengan titik 𝑣𝑣𝑗𝑗, i, j = 1, 2,…, 𝑛𝑛.
2.3.1.2. Matriks Biner
Misalkan G adalah graf tanpa loop dengan n titik 𝑣𝑣1,𝑣𝑣2, … ,𝑣𝑣𝑛𝑛 dan k garis 𝑒𝑒1,𝑒𝑒2, … 𝑒𝑒𝑘𝑘. Matriks Biner yang sesuai dengan graf G adalah matriks A berukuran n x k yang elemennya adalah
Nama Matriks Biner diambil dari sifat matriks yang hanya berisi bilangan 0 atau 1 saja. Matriks Biner kadang-kadang disebut matriks (0-1) atau matriks insidensi (incidence matrix).
2.3.1.3 Matriks Sirkuit
Misalkan G adalah graf yang memuat q buah sirkuit sederhana dan e buah garis. Matriks sirkuit A = (𝑎𝑎𝑖𝑖𝑗𝑗) yang bersesuaian dengan G adalah matriks yang terdiri dari q baris dan e
kolom dengan elemen.
𝑎𝑎𝑖𝑖𝑗𝑗
1 jika titik vi berhubungan dengan garis ej
0 jika titik vi tidak berhubungan dengan garis ej
𝑎𝑎𝑖𝑖𝑗𝑗
2.3.2. Representasi Graf Berarah dalam Matriks
Cara menyatakan graf berarah dalam matriks sebenarnya tidak jauh berbeda dengan cara menyatakan graf tak berarah dalam suatu matriks. Perbedaannya hanya terletak pada keikutsertaan informasi tentang arah garis yang terdapat dalam graf berarah.
2.3.2.1. Matriks Hubung
Matriks Hubung untuk menyatakan suatu graf berarah banyak dipakai dalam berbagai disiplin ilmu berbeda-beda sehingga nama yang dimiliki berbeda-beda pula. Dalam Teori Otomata, matriks hubung dikenal dengan nama matriks transisi, yang dalam konsep relasi disebut matriks relasi dalam jaringan disebut matrik koneksi, dan lain-lain.
Misalkan G adalah graf berarah yang terdiri dari n titik tanpa garis paralel. Matriks Hubung yang sesuai dengan graf G adalah matriks bujur sangkar n x n, A = (𝑎𝑎𝑖𝑖𝑗𝑗) dengan
2.3.2.2. Matriks Sirkuit
Untuk menyatakan graf berarah ke dalam Matriks Sirkuit, perlu diperhatikan arah garis pembentuk sirkuitnya.
Misalkan G adalah graf berarah dengan e buah garis dan q buah sirkuit atau Sirkuit Berarah. Sembarang arah orientasi (searah/berlawanan dengan arah jarum jam) diberikan ke tiap-tiap sirkuit. Matriks Sirkuit yang bersesuaian dengan graf G adalah matriks A = (𝑎𝑎𝑖𝑖𝑗𝑗)dengan
Perbedaan Matriks Sirkuit untuk menyatakan graf berarah dan tidak berarah terletak pada tanda negatif pada elemen matriks, yang menyatakan bahwa garis yang
𝑎𝑎𝑖𝑖𝑗𝑗
1 jika ada garis vi ke titik vj
0 jika tidak ada garis vi ke titik vj
𝑎𝑎𝑖𝑖𝑗𝑗
1 jika sirkuit ke-i memuat garis ke-j
dan arah garis ke-j sama dengan arah orientasi -1 jika sirkuit ke-i memuat garis ke-j
bersesuaian memiliki arah yang berlawanan dengan arah orientasi yang didefinisikan. Orientasi yang diberlakukan pada setiap sirkuit dapat dibuat sembarang sehingga suatu graf berarah dapat dinyatakan dengan beberapa Matriks Sirkuit yang berbeda
2.4. Algoritma Floyd-Warshall
Algoritma Floyd-Warshall adalah sebuah algoritma analisis graf untuk mencari bobot minimum dari graf berarah. Algoritma Floyd-Warshall adalah matriks hubung graf berarah berlabel, dan keluarannya adalah path terpendek dari semua titik ke titik yang lain (Kamayudi, A. 2009).
Dalam usaha untuk mencari path terpendek, Algoritma Warshall memulai iterasi dari titik awalnya kemudian memperpanjang path dengan mengevaluasi titik demi titik hingga mencapai titik tujuan dengan jumlah bobot yang seminimum mungkin. Misalkan
𝑊𝑊0 adalah matriks hubung graf berarah berlebel mula-mula. 𝑊𝑊∗ adalah matriks hubung
minimal dengan 𝑊𝑊𝑖𝑖𝑗𝑗∗ = path terpendek dari titik 𝑣𝑣𝑖𝑖 ke𝑣𝑣𝑗𝑗.[4]
Algoritma Warshall untuk mencari path terpendek adalah sebagai berikut 1. W = 𝑊𝑊0
2. Untuk k = 1 hingga n, lakukan: Untuk i = 1 hingga n, lakukan
Untuk j = 1 hingga n lakukan
Jika W[i, j] > W[i, k] + W[k, j], maka Tukar W[i, j] dengan W[i, k] + W[k, j]
3 𝑊𝑊∗ = W
Dalam iterasinya untuk mencari path terpendek, Algoritma Warshall membentuk n matriks sesuai dengan iterasi-k. Hal ini menyebabkan waktu prosesnya lambat, terutama untuk n yang besar. Meskipun waktu prosesnya bukanlah yang tercepat, Algoritma Warshall sering dipergunakan untuk menghitung path terpendek karena kesederhanaannya. Program implementasinya Algoritma Warshall sangat mudahdibuat.
2.5. Algoritma Johnson
Algoritma Johnson adalah mengonstruksi graf yang baru dengan menambahkan graf baru pada graf dan memberi bobot sisi yang keluar dari titik baru tersebut dengan 0. Langkah selanjutnya adalah mencari lintasan terpendek dari titik baru ke semua titik lain.
Lintasan Terpendek tersebut digunakan untuk mengubah bobot semua sisi pada graf baru agar bobot semula bernilai positif. Setelah itu dicari lintasan terpendek dari tiap titik ke semua titik lain dengan mengubah hasilnya dengan menggunakan hasil dari perhitungan berupa matriks. Dari matriks ini dapat diketahui panjang lintasan terpendek dari titik ke semua titik lain.
Langkah Algoritma Johnson adalah sebagai berikut
1. Mengostruksi graf baru G, dengan cara menambahkan titik baru sehingga V’ = V + {s} dan E + {(s,v)v di V}
2. Setiap titik v di V 0 → w (s, v)
∞ → w (v, s)
3. Menjalankan Algoritma Bellman-Ford pada graf baru a. jika terdapat bobot negatif maka selesai
b. jika tidak terdapat bobot negatif maka hitung d(s, v) , v ∈ V 4. Setiap (u, v) di E
W(u, v) = w(u, v) + d (s, v) – d(s, v)
5. Setiap v di V, dijalankan Algoritma Djikstra untuk menghitung d(u, v) 6. D’ = d(u, v)
7. Setiap (u, v) di V ; d(u, v) = d(u, v) + d(sv) – d(s, u) 8. D = d(u, v)
Keterangan
w(s,v) = bobot sisi dari s ke v.
d(s,v) = panjang lintasan terpendek dari s ke v. w(u,v) = bobot sisi baru dari u ke v.
d(u,v) = panjang lintasan terpendek dari u ke v dan yang dihutung adalah bobot sisi baru (w).
d(u,v) = panjang lintasan terpendek dari u ke v.
D’ = matriks hasil perhitungan lintasan terpendek dari tiap-tiap pasangan titik dan bobot sisi yang digunakan adalah w.
Dalam Algoritma Johnson terdapat dua Algoritma untuk penyelesainnya, yaitu Algoritma Bellman-Ford dan Algoritma Djikstra.
2.5.1. Algoritma Bellman-Ford
Algoritma Bellman-Ford menghitung jarak terpendek (dari satu sumber) pada sebuah graf berbobot. Maksudnya dari satu sumber ialah bahwa ia menghitung semua jarak terpendek yang berawal dari satu vertex. Algoritma Dijkstra dapat lebih cepat mencari hal yang sama dengan syarat tidak ada (edge) yang berbobot negatif, maka Algoritma Bellman-Ford hanya digunakan jika ada sisi berbobot negatif.
2.5.2. Algoritma Dijkstra
Algoritma Dijkstra ditemukan oleh Edsger W. Dijkstra yang merupakan salah satu varian bentuk algoritma populer dalam pemecahan persoalan yang terkait dengan masalah optimasi dan bersifat sederhana. Algoritma ini menyelesaikan masalah untuk mencari lintasan terpendek ( sebuah lintasan yang mempunyai panjang minimum) dari vertex a ke vertex z dalam graf berbobot, bobot tersebut adalah bilangan positif jadi tidak dapat dilalui
oleh vertex negatif.
Dalam mencari solusi, Algoritma Dijkstra menggunakan prinsip greedy, yaitu mencari solusi optimum pada setiap langkah yang dilalui dengan tujuan untuk mendapatkan solusi optimum pada langkah selanjutnya yang akan mengarah pada solusi terbaik.
Algoritma ini mencari panjang lintasan terpendek dari vertex a ke z dalam sebuah graf berbobot. Langkah-langkah dalam menentukan lintasan terpendek pada Algoritma Dijkstra yaitu:
1. Pada awalnya pilih vertex dengan bobot yang terendah dari vertex yang belum dipilih, diinisialisasikan dengan ‘0’ dan yang sudah terpilih diinisialisasikan dengan ‘1’.
2. Bentuk tabel yang terdiri dari vertex, status, bobot. Lengkapi kolom bobot yang diperoleh dari jarak vertex sumber ke semua vertex yang langsung terhubung dengan vertex sumber tersebut.
3. Jika vertex sumber ditemukan maka tetapkan sebagai vertex terpilih.
5. Tentukan vertex sementara yang terhubung pada vertex yang sudah terpilih sebelumnya dan merupakan bobot terkecil dilihat dari tabel dan tentukan sebagai vertex terpilih berikutnya.
6. Apakah vertex yang terpilih merupakan vertex tujuan? Jika ya, maka kumpulan vertex terpilih merupakan rangkaian yang menunjukkan lintasan terpendek.
7. Begitu seterusnya hingga semua vertex terpilih.
2.6. JAVA
Java adalah bahasa pemrograman yang bersifat open source yang dikembangkan oleh Sun Microsistems sejak tahun 1991 (Hakim,R. & Ir.Sutarno, M.Si. 2009). Bahasa ini dikembangkan dengan model yang mirip dengan bahasa C++ dan Smalltalk, namun dirancang agar lebih mudah dipakai dan platform independent, yaitu dapat dijalankan di berbagai jenis sistem operasi dan arsitektur komputer.
Java sendiri merupakan bahasa pemrograman yang berbasis objek, maksudnya adalah semua aspek yang terdapat pada Java adalah objek, sehingga memudahkan untuk mendesain, membuat dan mengembangkan program Java dengan cepat. Kelebihan ini membuat program Java menjadi mudah untuk digunakan oleh banyak orang.
Pada Tahun 1996, Sun Microsistems secara resmi merilis versi awal Java yang kemudian terus berkembang hingga muncul JDK 1.1 (Java Development Kit versi 1.1). Perkembangan terus dilakukan hingga muncul versi baru yang disebut Java 2. Perubahan utama antara versi sebelumnya adalah adanya Swing yang merupakan teknologi Graphical User Interface (GUI) yang mampu menghasilkan aplikasi desktop yang benar-benar baik.
Dalam penelitian ini penulis menggunakan Java versi The Java 2 Platform, Standart Edition (J2SE) yang merupakan Teknologi Java edisi standar, yang digunakan
untuk penerapan Teknologi Java pada komputer desktop. Versi ini menyediakan lingkungan pengembangan yang kaya fitur, stabil, aman dan mendukung konektivitas basis data, rancangan antarmuka pemakai, masukan/keluaran, dan pemrograman jaringan.
2.7. UML (Unified Modeling Language)
Unified Modeling Language (UML) tidak mendefinisiskan proses standar tetapi
S & R.S. Wahyono. 2003). Hal ini dimaksudkan untuk mendukung proses perkembangan dengan Object Oriented. UML menyimpan informasi tentang struktur statis dan perilaku dinamis suatu sistem. Perilaku Dinamis mendefinisikan sejarah objek dari waktu ke waktu dan komunikasi antara objek-objek untuk mencapai tujuan.
UML terdiri atas pengelompokan diagram-diagram sistem menurut aspek atau sudut pandang tertentu. Diagram adalah yang menggambarkan permasalahan maupun solusi dari permasalahan suatu model. UML mempunyai 13 diagram, diantaranya Use Case Diagram, Class Diagram, Package Diagram, Object Diagram, Sequence Diagram,
Collaboration Diagram, StatiChart Diagram, Activity Diagram, Deployment Diagram,
Component Diagram, Composite Structure Diagram, Interaction Overview Diagram,
Timing Diagram. Tetapi yang sering digunakan adalah Use Case Diagram, Activity
Diagram, Sequence Diagram, dan Class Diagram.
2.7.1. Use Case Diagram (Diagram Pengguna Keadaan)
Use Case Diagram menggambarkan fungsionalitas yang diharapkan dari sebuah sistem.
Dalam pembuatan Use Case Diagram, yang ditekankan adalah “apa” yang diperbuat sistem, dan bukan “bagaimana”. Sebuah Use Case mempresentasikan sebuah interaksi antara aktor dengan sistem.
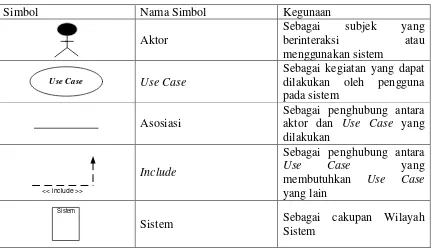
Berikut beberapa simbol yang digunakan pada Use Case Diagram di antaranya terdapat pada Tabel 2.1.
Tabel 2.1 Simbol Pada Use Case Diagram
Simbol Nama Simbol Kegunaan
Aktor
Sebagai subjek yang
berinteraksi atau menggunakan sistem
Use Case Use Case
Sebagai kegiatan yang dapat dilakukan oleh pengguna pada sistem
membutuhkan Use Case yang lain
Sistem
Sistem Sebagai cakupan Wilayah
2.7.2. Activity Diagram (Diagram Aktivitas)
Activity Diagram menggambarkan berbagai alur aktivitas dalam sistem yang sedang
dirancang, bagaimana masing-masing alur berawal, decision yang mungkin terjadi, dan bagaimana mereka berakhir. Sebuah aktivitas dapat direalisasikan oleh satu Use Case atau lebih. Aktivitas menggambarkan proses yang berjalan, sementara Use Case menggambarkan bagaimana aktor menggunakan sistem untuk melakukan aktivitas.
Berikut ini beberapa simbol yang digunakan pada Activity diagram dapat dilihat pada Tabel 2.2.
Tabel 2.2 Simbol pada Activity Diagram
Simbol Nama Simbol Kegunaan
Inisial node Awal aktivitas
Final Node Akhir Aktivitas
Action
Action Sebagai aktivitas yang
dilakukan oleh sistem
Control Flow Sebagai penghubung urutan
aktivitas
Decision Merupakan aktivitas
pengecekan kondisi
Exception handler Menunjukkan kondisi pengecualian apabila suatu action tidak dapat dilakukan
2.7.3. Class Diagram (Diagram Kelas)
Class adalah sebuah spesifikasi yang jika diinstansiasi akan menghasilkan sebuah objek
dan merupakan inti dari pengembangan dan desain berorientasi objek. Class menggambarkan keadaan (atribut/property) suatu sistem, sekaligus menawarkan layanan untuk memanipulasi keadaan tersebut (metode/fungsi).
Class Digram menggambarkan struktur dan deskripsi class, package, dan objek
Tabel 2.3 Simbol Pada Class Diagram
Simbol Nama Simbol Kegunaan
Class
Class
Sebagai kelas yang digunakan pada sistem
Generalization Menunjukkan hubungan
inheritance antar kelas
<<use>> Usage
Menunjukkan hubungan penggunaan suatu kelas dengan kelas yang lain
2.7.4. Sequence Diagram (Diagram Rangkaian)
Sequence Diagram menggambarkan interaksi antar-objek di dalam dan sekitar sistem
(termasuk pengguna, display, dan sebagainya) berupa message yang digambarkan terhadap waktu. Sequence Diagram terdiri atas dimensi vertikal (waktu) dan dimensi horizontal (objek-objek yang terkait). Sequence Diagram biasa digunakan untuk mengambarkan skenario atau rangkaian langkah-langkah yang dilakukan sebagai tanggapan dari sebuah event untuk menghasilkan output tertentu.
Berikut ini beberapa simbol yang digunakan pada Sequence Diagram dapat dilihat pada Tabel 2.4.
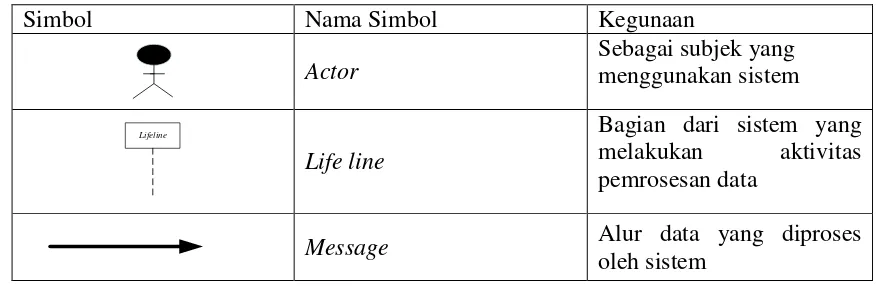
Tabel 2.4 Tabel simbol pada Sequence Diagram
Simbol Nama Simbol Kegunaan
Actor
Sebagai subjek yang menggunakan sistem
Lifeline
Life line
Bagian dari sistem yang melakukan aktivitas pemrosesan data
Message Alur data yang diproses
oleh sistem
2.8. Flowchart
simbol-simbol yang masing-masing simbol-simbol tersebut telah ditetapkan lebih dahulu fungsi dan atrinya.
Dua di antara beberapa Flowchart yang menggambarkan proses dengan komputer, yaitu :
1. Sistem Flowchart
Diagram Alur Sistem (Sistem Flowchart) merupakan bagan yang menunjukkan arus pekerjaan secara keseluruhan dari sistem. Bagan ini menjelaskan urutan dari prosedur-prosedur yang ada di dalam sistem.
2. Program Flowchart
Diagram Alur Program (Program Flowchart) merupakan bagan yang menjelaskan secara rinci langkah-langkah dari proses program.
Pada Tebel 2.5 menunjukkan seperangkat simbol diagram alur beserta fungsi dan manfaat yang digunakan dalam pembuatan langkah algoritma pemrograman.
Tabel 2.5. Simbol-Simbol Flowchart No Simbol Flowchart Keterangan Simbol
1 Start Komponen yang berfungsi untuk mengawali dan mengakhiri suatu proses
2 Data/Hasil Komponen yang mewakili input dan output
3 Sub Proses Komponen yang menyatakan
subproses/subprogram
4 Proses Komponen yang menyatakan setiap hasil dari
pengolahan proses.
5 Looping Komponen yang berfunsi untuk menyatakan
perulangan /melakukan berulang-ulang.
6 Decision Komponen yang berfunsi untuk menyatakan dua kemungkinan yang bernilai True dan False.
7 Connector Komponen yang berfungsi untuk menghubungkan halaman yang sama/one page connector, ataupun halaman yang berbeda/two page connector.
8 Alur Komponen yang berfungsi untuk menghubungkan