PEMODELAN NILAI OPSI TIPE EROPA EDY SUYONO

EDY SUYONO

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2008

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Pemodelan Nilai Opsi Tipe Eropa adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis.

Bogor, Juni 2008

EDY SUYONO. Modelling of European Options Price. Under direction of ENDAR HASAFAH NUGRAHANI and EFFENDI SYAHRIL.

Option is the right to sell or buy a specified quantity of some underlying asset by paying a specified exercise price, on or before an expiration date. There are two basic types of options, calls and puts. A call option is the right to buy and a put option is the right to sell the underlying asset. There are two types of options according to its execution time, i.e. American and European options. American options can be exercised at any time the holder wishes until the expiration date, while European options can only be exercised on the expiration date.

Modelling of option price usually is done analytically by determining solution of differential equation that is satisfied by the price of derivative asset, known as Black-Scholes equation. Because option price is a reflection of present value of expectation of difference between the exercise price and the stock price at expiration date, so it is necessary to study the option price through the concept of present value, as an alternative way to model the option price.

The result of this study shows that modelling of option price using differential equation method and present value approach give the same option price. Furthermore the results of ilustration give informations about the relation of the option price with its parameters as follow: First, increase in the current stock price causes the call option price also to increase, while the put option price, on the contrary, will decrease. Second, increase in the exercise price causes the call option price to decrease, while the put option price will increase. Third, the longer the expiration time the call option price will be higher, while the put option price doesn’t have the same tendency, but it depends on other parameters. Fourth, increase in the interest rate causes the call option price to increase, while the put option price will decrease. Finally, increase in the volatility causes the price of both call option and put option will increase.

RINGKASAN

EDY SUYONO. Pemodelan Nilai Opsi Tipe Eropa. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan EFFENDI SYAHRIL.

Opsi adalah suatu hak untuk menjual atau membeli suatu aset dengan harga tertentu, yang disebut harga eksekusi (exercise price atau strike price), pada atau sebelum waktu tertentu yang ditentukan, yang dikatakan waktu jatuh tempo (expiration date). Jika ditinjau dari hak melakukan eksekusi, opsi dapat dibagi menjadi dua jenis: opsi call memberikan hak untuk membeli, opsi put

memberikan hak untuk menjual. Berdasarkan periode melakukan eksekusi, opsi dibagi menjadi dua tipe: opsi Eropa memberikan hak kepada pemegang opsi untuk melakukan eksekusi pada akhir waktu jatuh tempo, sedangkan opsi Amerika eksekusi kapan saja sebelum kedaluwarsa. Penelitian ini khusus membahas opsi Eropa.

Secara rasional pemegang opsi call akan melakukan eksekusi jika harga aset yang mendasari di pasar lebih tinggi dari harga eksekusi, sedangkan pemegang opsi put akan melakukan eksekusi jika harga aset yang mendasari di pasar lebih rendah dari harga eksekusi. Hal ini dilakukan agar pemegang opsi memperoleh keuntungan (profit). Keputusan pemegang opsi untuk melakukan eksekusi terhadap opsi sangat tergantung oleh harga pasar suatu aset yang mendasari (underlying asset). Dalam hal ini kontrak opsi disebut aset turunan (derivative asset). Aset yang mendasari opsi pada penelitian ini adalah saham.

Pemodelan nilai opsi, secara analitik biasanya dilakukan dengan menentukan solusi dari persamaan diferensial untuk penentuan harga suatu aset turunan, yang dikenal sebagai persamaan Black-Scholes. Karena nilai opsi merupakan refleksi dari present value nilai harapan selisih harga eksekusi dengan harga saham pada waktu jatuh tempo, maka perlu dilakukan studi pemodelan nilai opsi melalui present value nilai harapan selisih harga eksekusi dengan harga saham pada waktu jatuh tempo, sebagai cara alternatif dalam pemodelan nilai opsi.

Untuk memberi gambaran secara matematis tentang penuruan nilai opsi serta kaitannya dengan harga saham pada saat tertentu, maka dalam penelitian ini akan dilakukan studi penurunan nilai opsi dengan dua pendekatan. Pertama, secara analitik menggunakan persamaan diferensial untuk penentuan harga suatu aset turunan. Pendekatan alternatif adalah menggunakan present value nilai harapan dari selisih harga eksekusi dengan harga saham pada waktu jatuh tempo.

Pemodelan nilai opsi berdasarkan persamaan diferensial penentuan harga suatu aset turunan dilakukan dengan menentukan solusi persamaan diferensial penentuan harga suatu aset turunan. Untuk menyelesaikan persamaan diferensial penentuan harga suatu aset turunan dilakukan dengan transformasi ke persamaan panas, kemudian ditentukan solusinya.

Dengan memperhatikan syarat batas untuk opsi call dan opsi put, serta memperhatikan syarat eksekusi untuk opsi call dan opsi put, diperoleh nilai opsi

call dan nilai opsi put pada saat t dengan harga saham S(t), waktu jatuh tempo T

dan harga eksekusi K adalah

(

)

(

)

( ) , ( ) ( ) r T t ( ) c t S t =S t N − +n σ T t− −Ke− − N −n

(

)

( )

(

)

, ( )

r T t

( )

( )

p t S t

=

Ke

− −

N n S t N n

−

−

σ

T t

−

n

T t

σ⎝ ⎠

=

−

Sedangkan nilai opsi call pada saat t = 0 adalah

(

0, (0)

)

(0)

(

)

rT ( )

c S =S N − +z

σ

T −Ke− N −z

(

0, (0)

)

rT ( ) (0)

(

)

p S =Ke− N z −S N z −σ T

dengan N adalah fungsi distribusi Normal (0,1), dan

2 (0) 1 ln 2 S r T K z T σ σ ⎛ ⎞ − −_⎜ − _⎟ ⎝ ⎠ =

Pemodelan nilai opsi dengan pendekatan present value nilai harapan selisih harga eksekusi dengan harga saham pada waktu jatuh tempo, dilakukan dengan menyatakan nilai opsi f t( ) sebagai

(

)

( )

( ) r T t ( )

f t =e− − E f T

Untuk opsi call nilai f T( )=

(

S T( )−K

)

+, sedangkan untuk opsi put nilai

(

( ) ( )

)

f T = K −S T +. Sehingga diperoleh model nilai opsi call dan model nilai opsi put yang sama dengan model nilai opsi yang diperoleh dengan menggunakan persamaan diferensial penentuan harga suatu aset turunan.

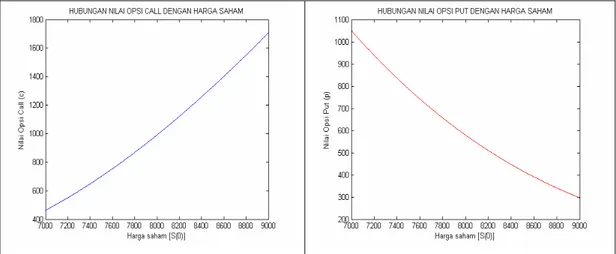
Berdasarkan hasil ilustrasi diperoleh informasi tentang pengaruh perubahan harga awal saham, harga eksekusi, waktu jatuh tempo, volatilitas, dan suku bunga terhadap nilai opsi sebagai berikut:

1. Semakin tinggi harga saham pada waktu kontrak opsi maka nilai opsi call

akan semakin tinggi, sedangkan nilai opsi put akan semakin rendah.

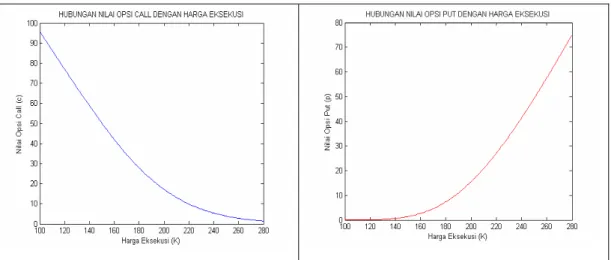
2. Semakin tinggi harga eksekusi, maka nilai opsi call akan semakin rendah, sedangkan nilai opsi put akan semakin tinggi.

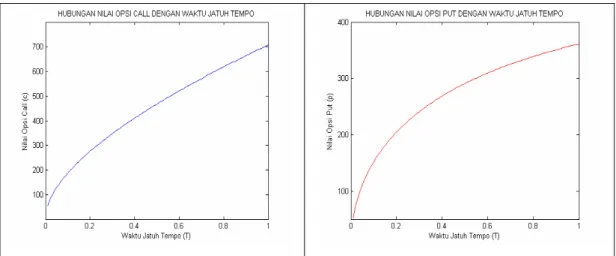
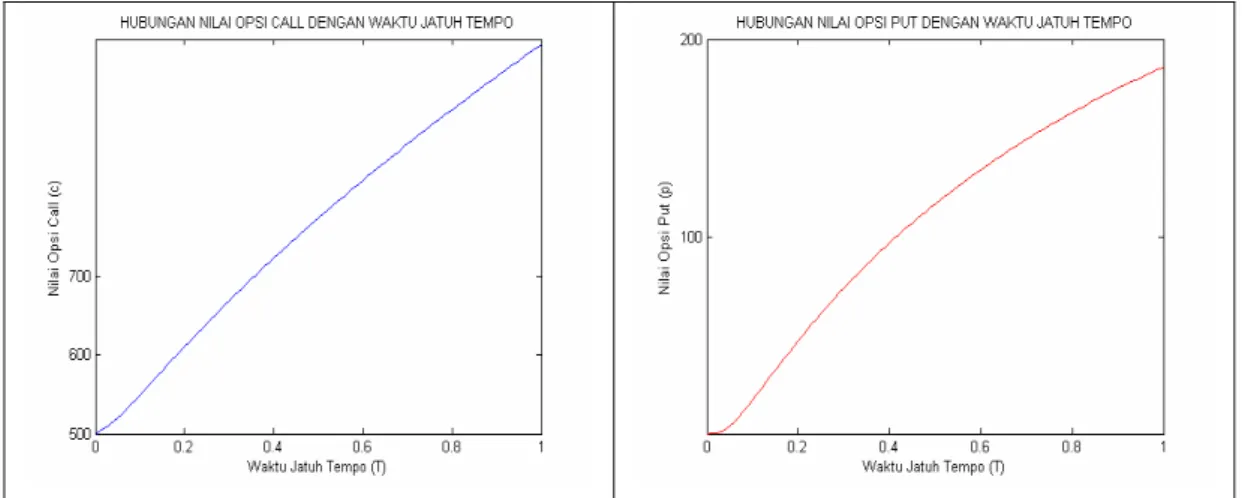
3. Semakin lama waktu jatuh tempo, maka nilai opsi call akan semakin tinggi, sedangkan nilai opsi put tidak memiliki kecenderungan tertentu yang sama, melainkan tergantung pada parameter lain.

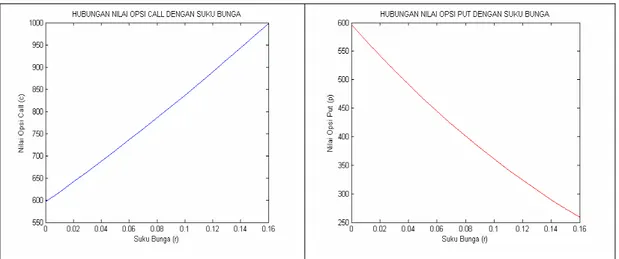
4. Semakin tinggi suku bunga, maka nilai opsi call akan semakin tinggi, sedangkan nilai opsi put akan semakin rendah.

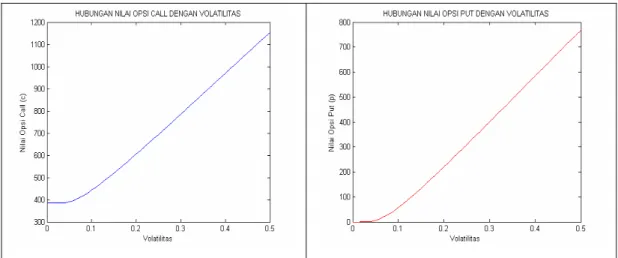
5. Semakin tinggi nilai volatilitas, maka nilai opsi call dan opsi put akan semakin tinggi.

©Hak cipta milik IPB, tahun 2008 Hak cipta dilindungi Undang-undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebut sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau tinjauan suatu masalah.

b. Pengutipan tidak merugikan kepentingan yang wajar IPB.

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis dalam bentuk apapun tanpa izin IPB.

PEMODELAN NILAI OPSI TIPE EROPA

EDY SUYONO

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada Departemen Matematika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2008

Nama : Edy Suyono NIM : G551060091

Disetujui Komisi Pembimbing

Dr. Ir. Endar H. Nugrahani, MS. Drs. Effendi Syahril, Grad. Dipl.Sc.

Ketua Anggota

Diketahui

Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan

Dr. Ir. Endar H. Nugrahani, MS. Prof. Dr. Ir. Khairil A. Notodiputro, MS.

Alhamdulillaahirabbil ‘alamiin.

Puji dan syukur penulis panjatkan kepada Allah SWT atas rahmat dan kuasa-Nya sehingga karya ilmiah ini berhasil diselesaikan. Shalawat serta salam semoga dilimpahkan kepada rasullullah Muhammad SAW, yang menjadi suri tauladan bagi umatNya dan senantiasa kita nantikan syafa’atNya di dunia sampai akherat.

Ucapan terima kasih atas pengorbanan dan permohonan maaf atas kurangnya perhatian serta kasih sayang penulis sampaikan kepada istri tercinta Nurul Aini beserta kedua buah hati penulis Fawwaz Ijlal Muqsith (Osith) dan Shofi Fairuz Zahidah (Shofi). Selanjutnya ucapan terima kasih dengan iringan doa Jazakumullah Ahsanal Jaza penulis sampaikan kepada:

1. Dr. Ir. Endar H. Nugrahani, MS dan Drs. Effendi Syahril, Grad. Dipl. Sc selaku pembimbing yang dengan penuh kesabaran memberikan bimbingan dan motivasi kepada penulis.

2. Donny Citra Lesmana, M.Sc selaku penguji yang telah memberikan saran dan kritiknya.

3. Departemen Agama Republik Indonesia, yang telah memberikan biaya kepada penulis selama menempuh pendidikan program magister di Institut Pertanian Bogor.

4. Teman-teman mahasiswa S-2 Matematika Terapan IPB angkatan 2006. 5. Semua pihak yang telah membantu penulis, yang tidak bisa penulis

sebutkan satu persatu.

Akhirnya penulis menyadari bahwa tulisan ini masih jauh dari sempurna. Oleh karena itu sumbangsih kritik dan saran demi kemajuan tulisan selanjutnya sangat penulis dambakan.

Semoga karya ilmiah ini bermanfaat.

Bogor, Juni 2008

Penulis,

RIWAYAT HIDUP

Penulis dilahirkan di Rembang pada tanggal 27 Juli 1970 sebagai anak kedua dari pasangan Lasmin dan Satini. Pendidikan sarjana ditempuh di jurusan Pendidikan Matematika, Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam IKIP Semarang, lulus tahun 1993. Kesempatan untuk melanjutkan ke program Magister pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor diperoleh pada tahun 2006. Beasiswa pendidikan pascasarjana diperoleh dari Departemen Agama Republik Indonesia.

Penulis bekerja sebagai staf pengajar di Madrasah Tsanawiyah Negeri Lasem Kabupaten Rembang sejak tahun 1995.

DAFTAR TABEL ... xi

DAFTAR GAMBAR ... xii

DAFTAR LAMPIRAN ... xiii

I PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Tujuan Penelitian ... 2 1.3 Sistematika Penulisan ... 3 II LANDASAN TEORI ... 4 2.1 Proses Stokastik ... 4

2.2 Proses Wiener (Gerak Brown) dan Gerak Brown Geometris ... 7

2.3 Lemma ... Itoˆ 8 III PERSAMAAN DIFERENSIAL UNTUK MENENTUKAN HARGA SUATU ASET TURUNAN ... 17

3.1 Harga Saham ... 17

3.2 Harga Obligasi ... 19

3.3 Nilai Aset Turunan ... 20

3.4 Persamaan Diferensial untuk Penentuan Harga Suatu Aset Turunan 20 3.5 Present Value Nilai Harapan Selisih Harga Eksekusi dengan Harga Saham ... 24

IV NILAI OPSI ... 25

4.1 Model Nilai Opsi Berdasarkan Persamaan Diferensial untuk Penentuan Harga Suatu Aset Turunan ... 25

4.1.1 Opsi Call ... 25

4.1.2 Opsi Put ... 28

4.2 Model Nilai Opsi Menggunakan Present Value Nilai Harapan Selisih Harga Eksekusi dengan Harga Saham pada Waktu Jatuh Tempo ... 29

4.2.1 Opsi Call ... 29

4.2.2 Opsi Put ... 34

4.3 Ilustrasi Model Nilai Opsi ... 37

V Kesimpulan ... 47

DAFTAR PUSTAKA ... 49

DAFTAR TABEL

Halaman 1. Nilai opsi call dan opsi put dengan parameter T = 0,5, K = 7.900,

t = 0, r = 0,08, dan σ =0, 35 ... 39 2. Nilai opsi call dan opsi put dengan parameter T = 0,75, S = 190,

t = 0, r = 0,08, dan σ =0, 25 ... 40 3. Nilai opsi call dan opsi put dengan parameter K = 4.500, K = 4.500,

t = 0, r = 0,08, dan σ =0, 3 ... 41 4. Nilai opsi call dan opsi put dengan parameter T = 1, S = 5.000, K = 5.000,

t = 0, dan σ =0, 3 ... 45 5. Nilai opsi call dan opsi put dengan parameter T = 1, S = 5.000, K = 5.000,

1. Hubungan antara nilai opsi dengan harga saham, dengan parameter

T = 0,5, K = 7.900, t = 0, r = 0,08, dan σ =0, 35... 39 2. Hubungan antara nilai opsi dengan harga eksekusi, dengan parameter

T = 0,75, S = 190, t = 0, r = 0,08, dan σ =0, 25... 40 3. Hubungan antara nilai opsi dengan waktu jatuh tempo, dengan parameter

K = 4.500, K = 4.500, t = 0, r = 0,08, dan σ =0, 3... 41 4. Hubungan antara nilai opsi dengan waktu jatuh tempo, dengan parameter

K = 4.500, K = 5.000, t = 0, r = 0,08, dan σ =0, 3... 42 5. Hubungan antara nilai opsi dengan waktu jatuh tempo, dengan parameter

K = 4.500, K = 5.400, t = 0, r = 0,08, dan σ =0, 3... 43 6. Hubungan antara nilai opsi dengan waktu jatuh tempo, dengan parameter

K = 4.500, K = 4.000, t = 0, r = 0,08, dan σ =0, 3... 43 7. Hubungan antara nilai opsi dengan suku bunga, dengan parameter

T = 1, S = 5.000, K = 5.000, t = 0, dan σ =0, 3 ... 45 8. Hubungan antara nilai opsi dengan volatilitas, dengan parameter

DAFTAR LAMPIRAN

Halaman A. Bukti E W t_⎣⎡

(

_{n k( +1)}

)

−W t

( )

_nk ⎤_⎦4 =3

(

t_{n k( +1)}−t_nk

)

2 ... 50 B. Fungsi Pembangkit Momen dari X t( ) ~N(0, )t ... 52 C. Bukti ... 53 1 2 ( 1) ( 1) 2 1 0 ( ) ( )( n n k nk n k nk k k t t maks t t t − + + = − ≤ − −

∑

t )

D. Solusi Persamaan Panas ... 54 E. Program Penentuan Nilai Opsi ... 58

1.1. Latar Belakang

Opsi menjadi suatu instrumen keuangan yang memegang peranan penting dalam suatu investasi. Seorang investor yang ingin melindungi investasinya dapat melakukan transaksi jual beli opsi, disamping jual beli saham. Opsi diartikan sebagai suatu hak untuk menjual atau membeli suatu aset dengan harga tertentu, yang disebut harga eksekusi (exercise price atau strike price), pada atau sebelum waktu tertentu yang ditentukan, yang dikatakan waktu jatuh tempo (expiration date). Jika ditinjau dari hak melakukan eksekusi, maka opsi dapat dibagi menjadi dua jenis, yaitu opsi call dan opsi put. Opsi call memberikan hak kepada pemegangnya untuk membeli suatu aset dengan harga tertentu, pada atau sebelum waktu jatuh tempo. Sedangkan opsi put memberikan hak kepada pemegangnya untuk menjual suatu aset dengan harga tertentu, pada atau sebelum waktu jatuh tempo. Berdasarkan waktu pelaksanaan eksekusi, opsi dibagi menjadi dua tipe, yaitu opsi Eropa dan opsi Amerika. Opsi Eropa memberikan hak kepada pemegang opsi untuk melakukan eksekusi pada akhir waktu jatuh tempo, sedangkan opsi Amerika memberikan hak kepada pemegang opsi untuk melakukan eksekusi kapan saja pada waktu sebelum kedaluwarsa (Figlewski et al.1990). Penelitian ini khusus membahas opsi Eropa. Sehingga jika tidak ada penyebutan secara khusus untuk opsi Amerika, artinya opsi yang dimaksud adalah opsi Eropa.

Secara rasional pemegang opsi call akan melakukan eksekusi jika harga aset yang mendasari di pasar lebih tinggi dari harga eksekusi, sedangkan pemegang opsi put akan melakukan eksekusi jika harga aset yang mendasari di pasar lebih rendah dari harga eksekusi. Hal ini dilakukan agar pemegang opsi memperoleh keuntungan (profit). Keputusan pemegang opsi untuk melakukan eksekusi terhadap opsi sangat tergantung pada harga pasar suatu aset yang mendasari (underlying asset). Dalam hal ini kontrak opsi disebut aset turunan (derivative asset). Aset yang mendasari opsi pada penelitian ini adalah saham.

Nilai opsi adalah biaya yang dikeluarkan oleh investor untuk mendapatkan kontrak opsi, yang pembayarannya dilakukan pada saat kontrak dibuat (Wilmott

opsi yang akurat sangat diperlukan investor dalam membuat dan memutuskan strategi perdagangannya.

Nilai opsi tergantung pada harga saham. Harga saham berubah seiring dengan perubahan waktu, sesuai dengan banyaknya permintaan dan penawaran yang tidak dapat ditentukan secara pasti. Sehingga perubahan harga saham dipengaruhi oleh perubahan waktu dan dipengaruhi pula oleh peubah-peubah pengganggu yang berupa peubah acak.

Nilai opsi merupakan refleksi dari present value nilai harapan selisih harga eksekusi dengan harga saham pada waktu jatuh tempo. Pemodelan nilai opsi, secara analitik biasanya dilakukan dengan menentukan solusi dari persamaan diferensial untuk penentuan harga suatu aset turunan, seperti yang dilakukan oleh Black dan Scholes. Karena nilai opsi merupakan refleksi dari present value nilai harapan selisih harga eksekusi dengan harga saham pada waktu jatuh tempo, maka perlu dilakukan studi pemodelan nilai opsi melalui present value nilai harapan selisih harga eksekusi dengan harga saham pada waktu jatuh tempo, sebagai cara alternatif dalam pemodelan nilai opsi.

Untuk memberi gambaran secara matematis tentang penuruan nilai opsi serta kaitannya dengan harga saham pada saat tertentu, maka dalam penelitian ini akan dilakukan studi penurunan nilai opsi secara analitik menggunakan persamaan diferensial untuk penentuan harga suatu aset turunan, dan menggunakan pendekatan present value nilai harapan dari selisih harga eksekusi dengan harga saham pada waktu jatuh tempo.

1.2. Tujuan Penelitian :

Tujuan dari penelitian ini adalah :

1. Menentukan model nilai opsi dengan menggunakan persamaan diferensial untuk penentuan harga suatu aset turunan (persamaan diferensial Black- Scholes-Merton).

2. Menentukan model nilai opsi dengan menggunakan pendekatan present value nilai harapan dari selisih harga eksekusi opsi dengan harga saham pada waktu jatuh tempo.

3. Menyajikan ilustrasi hubungan nilai opsi call dan opsi put dengan perubahan parameter-parameternya.

1.3. Sistematika Penulisan

Tulisan ini disusun dengan sistematika berikut. Bab 1 adalah pendahuluan, yang menyajikan latar belakang permasalahan dan tujuan penelitian. Bab 2 adalah landasan teori yang akan menjelaskan tentang proses stokastik, proses gerak Brown atau proses Wiener, dan lemma . Bab 3 akan membahas penurunan persamaan diferensial untuk penentuan harga suatu aset turunan, serta penentuan rumus bahwa nilai opsi merupakan present value nilai harapan selisih harga eksekusi dengan harga saham pada saat jatuh tempo. Selanjutnya pada bab 4 akan dibahas pemodelan nilai opsi berdasarkan persamaan diferensial untuk penentuan harga suatu aset turunan dan pemodelan nilai opsi menggunakan present value

nilai harapan selisih harga eksekusi dengan harga saham pada saat jatuh tempo. Dalam bab ini akan ditunjukkan juga ilustrasi perhitunganl nilai opsi yang akan memberikan beberapa contoh kasus kontrak opsi, yang selanjutnya diamati hubungan nilai opsi dengan parameter-parameter yang menentukan nilai opsi. Pada bab 5 akan diberikan kesimpulan yang diperoleh dalam penelitian ini.

ˆ Ito

LANDASAN TEORI

Pada bab ini diberikan beberapa konsep tentang proses ptokastik, proses gerak Brown atau proses Wiener, dan lemma Itoˆ.

2.1. Proses Stokastik

Pembahasan tentang harga opsi tidak dapat dilepaskan dari pembahasan harga saham. Karena harga saham berubah seiring dengan perubahan waktu dan bersifat tidak pasti, maka perubahan saham merupakan suatu proses stokastik. Sehingga perlu dijelaskan tentang proses stokastik.

Definisi 1 (Percobaan Acak)

Percobaan acak adalah suatu percobaan yang dapat diulang dalam kondisi yang sama, dengan hasil yang tidak dapat diprediksi dengan tepat, tetapi dapat diketahui semua kemungkinan hasilnya (Hogg et al, 2005).

Definisi 2 (Ruang Contoh)

Ruang contoh (sample space) adalah himpunan semua hasil yang mungkin dari suatu percobaan acak, dinotasikan dengan Ω (Grimmett & Stirzaker 1992).

Definisi 3 (Peubah Acak)

Misalnya Ω adalah ruang contoh dari percobaan acak. Fungsi X yang terdefinisi pada Ω yang memetakan setiap unsur ω∈Ω ke satu dan hanya satu bilangan real

disebut peubah acak (Hogg et al, 2005).

( )

X ω =x

Peubah acak dinotasikan dengan huruf kapital, misalnya X , Y , Z.

Sedangkan nilai peubah acak dinotasikan dengan huruf kecil seperti x, , .y z

Setiap peubah acak memiliki fungsi distribusi (sebaran) kumulatif, yang biasa disebut dengan fungsi distribusi.

Definisi 4 (Medan-σ )

Suatu himpunan disebut medan-σ dari ruang contoh Ω, jika anggota adalah himpunan bagian dari Ω, yang memenuhi syarat berikut (Hogg et al, 2005):

1) φ∈ .

3) Jika barisan himpunan A₁, , A₂ ...∈ , maka 1 i i A ∞ = ∈

∪

. Definisi 5 (Peluang)

Misalkan Ω adalah ruang contoh, dan adalah medan-σ dari . P suatu fungsi bernilai real yang didefinisikan pada , disebut suatu peluang, dan dikatakan peluang dari A, jika memenuhi syarat berikut (Hogg et al, 2005):

Ω

( )

P A

1) P A( )≥0, untuk semua A∈ . 2) P( )Ω =1.

3) Jika barisan himpunan A₁, , A₂ ...∈ , dan A_m ∩A_n =φ untuk semua

maka . , m ≠n 1 1 ( ) n n n n P A P A ∞ ∞ = = ⎛ _{⎞ =} ⎜ ⎟ ⎝

∪

⎠

∑

Definisi 6 (Fungsi Distribusi Kumulatif)

Misalkan X peubah acak. Fungsi distribusi kumulatif dari X didefinisikan oleh (Hogg et al, 2005)

(

)

( ) ( , ] ( )

F x =P −∞ x =P X ≤x .

Definisi 7 (Peubah Acak Kontinu)

Suatu peubah acak X adalah peubah acak kontinu jika fungsi distribusi kumulatif dari X, yang dinotasikan F x( ), adalah fungsi kontinu untuk semua x ∈ (Hogg

et al, 2005).

Definisi 8 (Fungsi Distribusi dan Fungsi Kepekatan Peluang Peubah Acak Kontinu)

Misalkan X peubah acak kontinu. Fungsi distribusi dari peubah acak X

didefinisikan:

( )

x

( )

F x f t dt −∞ =

_∫

( )

f t disebut fungsi kepekatan peluang dari peubah acak X .

Misalkan A = −∞( , ),x maka fungsi distribusi dari peubah acak X dapat ditulis sebagai (Ghahramani 2000)

( )

( ) ( )

( )

( )

x A F x P X A P X x f t dt f t dt −∞ = ∈ = ≤ =

∫

=

∫

.

Definisi 9 (Peubah Acak Saling Bebas)

Dua peubah acak dikatakan saling bebas jika untuk sembarang himpunan , kejadian {

dan

X Y

B

dan

A X ∈A} dan {Y ∈B} saling bebas, yaitu jika

(

,

)

(

) (

)

P X ∈A Y ∈B =P X ∈A P Y ∈B

(Ghahramani 2000).

Definisi 10 (Proses Stokastik)

Proses stokastik X ={X t( ), t∈H}adalah suatu koleksi (himpunan) dari peubah acak(Ross 1996).

Untuk setiap t pada himpunan indeks H, X(t) adalah suatu peubah acak. t

sering diinterpretasikan sebagai waktu (meskipun dalam berbagai penerapannya t

tidak selalu menyatakan waktu), dan X(t) diinterpretasikan sebagai keadaan (state) dari proses pada waktu t.

Definisi 11 (Proses Stokastik Waktu Diskret dan Proses Stokastik Waktu Kontinu)

Suatu proses stokastik X disebut proses stokastik dengan waktu diskret jika himpunan indeks H adalah himpunan tercacah (countable set), sedangkan X disebut proses stokastik dengan waktu kontinu jika H adalah kontinu(Ross 1996). Beberapa contoh dari proses stokastik dalam masalah finansial adalah sebagai berikut :

- Banyak klaim yang diajukan pemegang polis pada waktu tertentu. - Tingkat suku bunga deposito pada selang waktu tertentu.

- Harga saham pada selang waktu tertentu.

Dalam pembahasan selanjutnya dibatasi t adalah waktu, sedangkan X(t)

adalah peubah acak pada waktu t, dengan himpunan indeks H adalah kontinu, sehingga X disebut proses stokastik dengan waktu kontinu.

Definisi 12 (Inkremen Bebas)

Suatu proses stokastik dengan waktu kontinu {X t( ), t∈H}disebut memiliki inkremen bebas (independent increments) jika untuk semua t₀ < < < <t₁ t₂ ... t_n,

peubah acak X t( )₁ −X t( ), ( )₀ X t₂ −X t( ), ₁ ..., ( )X t_n −X t(_n−1) adalah saling bebas(independent) (Ross 1996).

Dengan kata lain, suatu proses stokastik dengan waktu kontinu X disebut memiliki inkremen bebas jika proses berubahnya nilai pada interval waktu yang tidak tumpang tindih (tidak overlap) adalah bebas.

Definisi 13 (Inkremen Stasioner)

Suatu proses stokastik dengan waktu kontinu {X t( ), t∈H}disebut memiliki inkremen stasioner (stationary increments) jika X t( + −s) X t( ) memiliki sebaran yang sama untuk semua nilai t (Ross 1996).

Dengan kata lain, suatu proses stokastik dengan waktu kontinu X disebut memiliki inkremen stasioner jika sebaran (distribusi) dari perubahan nilai antara sembarang dua titik hanya tergantung pada jarak antara kedua titik tersebut, dan tidak tergantung dari lokasi titik-titik tersebut.

2.2. Proses Wiener (Gerak Brown) dan Gerak Brown Geometris

Trend yang terjadi pada perubahan harga saham membentuk grafik eksponensial. Oleh karena itu dapat dikatakan bahwa perubahan harga saham akan mengikuti proses gerak Brown geometris (Baxter & Rennie 1997). Karena itu pembahasan gerak brown geometris tidak dapat terlepas dari pembahasan gerak Brown.

Definisi 14 (Nilai Harapan)

Jika X adalah peubah acak kontinu dengan fungsi kepekatan peluang f x( ), maka nilai harapan dari X adalah

( )

( ) .

E X xf x dx

∞ −∞

=

_∫

Nilai harapan dari X juga disebut rataan (mean), yang dinotasikan denganμ (Ghahramani 2000).

Definisi 15 (Varians)

Jika X peubah acak kontinu dengan E X

( )

=μ, maka varians dari X

didefinisikan oleh (Ghahramani 2000)

( )

(

)

2

Definisi 16 (Distribusi Normal)

Suatu peubah acak X dikatakan mempunyai distribusi normal jika fungsi kepekatan peluangnya adalah

2 1 1 ( ) exp , untuk . 2 2 x f x μ x σ σ π ⎧ ₋ ⎫ ⎪ ⎛ ⎞ ⎪ = _⎨− _{⎜ ⎟ ⎬} − ⎝ ⎠ ⎪ ⎪ ⎩ ⎭ ∞ < < ∞

Parameter μ dan σ2 masing-masing adalah rataan dan varians dari Hal ini sering ditulis

.

X

X berdistribusi

(

2

)

,

N μ σ . Jika X berdistribusi maka dikatakan

(0,1)

N X peubah acak normal baku (Hogg et al, 2005).

Definisi 17 (Proses Gerak Brown)

Proses stokastik {X t( ), t ≥0} disebut proses gerak Brown jika : 1. X (0)=0

2. mempunyai inkremen bebas stasioner (stationary independent increments)

{X t( ), t ≥0}

3. Untuk setiap t >0, ( )X t berdistribusi normal dengan rataan 0 dan varian

2

t

σ .

Proses gerak Brown sering juga disebut proses Wiener, dan jika σ=1 disebut gerak Brown baku (Ross 1996).

Jika gerak Brown baku, maka X(t) berdistribusi normal dengan rataan 0 dan varian t. Sehingga fungsi kepekatan peluangnya adalah:

{X t( ), t ≥0} 2_{/ 2} 1 ( ) . 2 x t f x e t π − =

Definisi 18 (Gerak Brown Geometris)

Jika { ( adalah gerak Brown baku, maka proses stokastik { (

yang didefinisikan disebut gerak Brown Geometris (Ross 1996).

), 0} X t t ≥ Z t), 0}t ≥ ( ) ( ) X t Z t =e 2.3. Lemma Itoˆ

Lemma pertama kali dimunculkan oleh Kiyoshi pada Nagoya Mathematics Journal pada tahun 1951. Lema digunakan sebagai sebuah metode menganalisis masalah ekonomi dan keuangan melalui dasar-dasar probabilitas (Malliaris & Brock 1982). Kemudian Black dan Scholes (1973) menggunakan lemma tersebut untuk menyelesaikan masalah-masalah ekonomi

ˆ

Ito Itoˆ

ˆ Ito

dan keuangan. Selanjutnya Baxter (1997), mengembangkan lebih lanjut pada masalah keuangan. Hal ini dikarenakan pada masalah keuangan terdapat fungsi peubah acak yang tidak dapat diselesaikan dengan kalkulus biasa.

Untuk menyelesaikan fungsi tersebut dilakukan melalui : 1. Formula Itoˆ

2. Persamaan diferensial stokastik

Keuntungan dari penggunaan lemma seperti yang disampaikan Malliaris adalah sebagai berikut :

ˆ Ito

1. Penurunan persamaan diferensial stokastik dapat menggunakan aturan-aturan pada kalkulus biasa.

2. Mempertahankan keberadaan proses gerak Brown. Artinya dengan menggunakan lemma , diferensial dari proses stokastik yang bergantung pada proses gerak Brown akan menjadi fungsi yang memuat proses stokastik gerak Brown (Malliaris & Brock 1982).

ˆ Ito

Selanjutnya lemma Itoˆ dituliskan sebagai berikut : Lemma 1 (Itoˆ)

Misalkan proses X(t) memenuhi persamaan diferensial stokastik

(2.1)

( ) ( ) ( ) ( )

dX t =a t dt +b t dW t

dengan W(t) proses Wiener, dan fungsi f t X t

(

,

( )

)

adalah kontinu dan mempunyai turunan f t X t_t( , ( )), f_X ( ,t X t( )), f_{X X}( ,t X t( )) kontinu. Maka proses f t X t

(

,

( )

)

juga memenuhi persamaan diferensial stokastik

(

)

(

)

(

)

(

)

2 1 ( , ( )) , ( ) , ( ) ( ) , ( ) ( ) 2 , ( ) ( ) ( ). t X X X X df t X t f t X t f t X t b t f t X t a t dt f t X t b t dW t ⎡ ⎤ =_⎢ + + _⎥ ⎣ ⎦ + (2.2)

Formula diatas disebut formula Itoˆ (Gihman & Skorohod 1972).

Untuk membuktikan formula tersebut dibutuhkan lemma dan teorema berikut :

ˆ Ito

Teorema 1 (Pertidaksamaan Markov)

Misalkan X peubah acak tak negatif. Untuk sembarang t >0,

( ) ( ) E X P X t t ≥ ≤ (Ghahramani 2000).

Bukti:

Misalkan f

( )

x fungsi kepekatan peluang dari peubah acak A himpunan nilai yang mungkin dari

. X , X dan B ={x ∈A x: ≥t}. Maka

( )

( )

( )

( )

(

)

. A B B E X =

∫

xf x dx ≥

∫

xf x dx ≥t f

∫

x dx =tP X ≥t Jadi ( ) ( ) E X . P X t t ≥ ≤ g

Teorema 2 (Pertidaksamaan Chebyshev)

Jika X suatu peubah acak dengan nilai harapan μ dan varians σ2

, maka untuk sembarang t >0

(

)

2 2 P X t t σ μ − ≥ ≤ (Ghahramani 2000). Bukti:

Karena (X −μ)2 ≥0 maka dengan pertidaksamaan Markov diperoleh

(

)

(

)

(

)

2 ₂ 2 2 2 2 E X P X t t t μ σ μ − − ≥ ≤ =

Pertidaksamaan Chebyshev dipenuhi karena

(

X −μ

)

2 ≥t2 setara dengan

X −μ ≥t g

Definisi 19 (Konvergen dalam Peluang)

Misalkan adalah barisan peubah acak yang didefinisikan pada suatu ruang contoh .

1, , , 2 3 ...

X X X

Ω Xn disebut konvergen dalam peluang ke peubah acak

,

X jika untuk setiap ε >0

(

)

lim _n 0

n→∞P X −X >ε =

(Ghahramani 2000).

Definisi 20 (Fungsi Pembangkit Momen)

Fungsi pembangkit momen (moment generating function) dari X didefinisikan sebagai

( )

( )

sX X

M s =E e

untuk s∈ asalkan nilai harapan E e

( )

sX ada (Hogg et al, 2005). Teorema 3 (Momen ke-n)

Misalkan X peubah acak dengan fungsi pembangkit momen M_X ( ).s Maka momen ke-n dari peubah acak X adalah

( )

( )

(0),

n n

X

E X =M

dimana M_X( )n ( )s adalah turunan ke-n dari M_X ( )s (Ghahramani 2000). Bukti:

( )

( )

( )

( )

(

)

(

)

( )

(

)

' " 2 ( ) ( ) ( ) sX X sX X sx sx sx sX sX X M s E e d M s E e ds d e f x dx ds d e f x dx ds xe f x dx E X e M s E X e ∞ −∞ ∞ −∞ ∞ −∞ = = = = = = =

∫

∫

∫

( )

(

)

( )

(

)

( )

( )

(3) 3 ( ) ( ) . . . 0 . sX X n n sX n X X M s E X e M s E X e M E X = = ⇒ = n 2 2 g Lemma 2

Misalkan t₁<t , dan W t( ) proses Wiener baku, t₁ =t_n0 <t_n1< <... t_nn =t , dan , maka ( 1) lim ( _{n k nk}) 0 n→∞maks tk + −t = 1 ₂ ( 1) 0 ( ) ( ) n n k nk k W t W t − + = ⎡ − ⎤ ⎣ ⎦

∑

konvergen dalam

Bukti: Misalkan 1 ₂ ( 1) 0 ( ) ( ) n n n k n k W t W t θ − ₊ = ⎡ ⎤ =

∑

_⎣ − _{k ⎦} ) maka

(

)

{

}

1 ₂ ( 1) 0 1 ₂ ( 1) 0 1 ₂ ( 1) ( 1) 0 ( ) ( ) ( ) ( ) ( ) var ( ) ( ) ( ) ( ) n n n k nk k n n k nk k n n k nk n k nk k E E W t W t E W t W t W t W t E W t W t θ − ₊ = − + = − + + = ⎛ _{⎡ ⎤} ⎞ = _{⎜ ⎣} − _{⎦ ⎟} ⎝ ⎠ ⎡ ⎤ = _⎣ − _⎦ ⎡ ⎤ ⎡ ⎤ = _⎣ − _⎦+ _⎣ − _⎦

∑

∑

∑

1 ( 1) 0 1 0 2 1 ( 1 0 2 1 var ( ) ( ) ... ( ) . n n k nk k n n n n nn n n nn n n W t W t t t t t t t t t E θ t t − + = − ⎡ ⎤ = _⎣ − _⎦ = − + − + + − = − = −

∑

Dengan kata lain rataan jumlah selisih kuadrat dari suatu proses gerak Brown hanya bergantung parameter waktu awal dan waktu akhir saja.

Selanjutnya dari kebebasan peubah ⎡_⎣W t( _{n k( +1)})−W t( _nk)⎤_⎦2 diperoleh

1 ₂ ( 1) 0 var( ) var ( ) ( ) . n n n k k W t W t θ − ₊ = ⎡ ⎤ =

∑

_⎣ − _{nk ⎦} Padahal

{

} {

2

}

2 2 2 ( 1) ( 1) ( 1) 4 ( 1) 2 ( 1) var ( ) ( ) ( ) ( ) ( ) ( ) E ( ) ( ) 3( ) . n k nk n k nk n k nk n k nk n k nk W t W t E W t W t E W t W t W t W t t t + + + + + ⎡ − ⎤ = ⎡ − ⎤ − ⎡ − ⎤ ⎣ ⎦ ⎣ ⎦ ⎣ ⎦ ⎡ ⎤ ≤ _⎣ − _⎦ = − (lihat lampiran A) 2 Sehingga 1 2 ( 1) 0 ( 1) 2 1 var( ) 3 ( ) 3 ( )( ) 0 (lihat lampiran C) n n n k nk k n k nk k t t maks t t t t θ − ₊ = + ≤ − ≤ − − →

∑

Dari ketaksamaan Chebyshev diperoleh

[

]

2 var( ) | ( ) | n n n P θ E θ ε θ ε − > ≤ .

Akibat 1 Jika t₁<t₂, maka

[

]

[

]

2 1 2 2 2 1 2 1 1 1 ( ) ( ) ( ) ( ) ( ) 2 2 2 t t W t dW t = W t − W t − t t

∫

− 1 2 (2.3) (Gihman & Skorohod 1972).

Bukti: Misalkan t₁=t_n0 <t_n1< <... t_nn =t ,

( )

( )

( )

(

_{( )}

)

( )

( )

(

_{( )}

)

( )

{

}

(

)

(

( )

)

(

)

( )

{

}

2 1 1 1 0 1 2 1 0 1 _{2 2} 2 ( 1) ( 1) 0 lim lim 1 lim ( ) 2 1 ( 2 t _n nk n k nk n k t n nk n k nk n k n n k nk n k nk n k W t dW t W t W t W t W t W t W t W t W t W t W t W − + →∞ ₌ − + →∞ ₌ − + + →∞ ₌ ⎡ ⎤ = _⎣ − _⎦ = − ⎡_⎣ ⎤_⎦ ⎡ ⎤ = − −_⎣ − _⎦ =

∑

∫

∑

∑

[

]

[

]

(

)

( )

[

]

[

]

1 ₂ 2 2 2 1 ( 1) 0 2 2 2 1 2 1 1 1 ) ( ) lim 2 2 1 1 1 ( ) ( ) ( ). 2 2 2 n n k nk n k t W t W t W t W t W t t t − + →∞ ₌ ⎡ ⎤ − − _⎣ − _⎦ = − − −

∑

g Teorema 4

Misalkan X₁ dan X₂ peubah acak.

1 1 1 2 2 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) dX t a t dt b t dW t dX t a t dt b t dW t = + = + maka 1 2 1 2 2 1 1 2 ( ( ) ( )) ( ) ( ) ( ) ( ) ( ) ( ) d X t X t =X t dX t +X t dX t +b t b t dt (2.4)

(Gihman & Skorohod 1972). Bukti: Dari (2.3) didapat

[

]

[

]

2 1 2 2 2 1 2 1 1 1 ( ) ( ) ( ) ( ) ( ). 2 2 2 t t W t dW t = W t − W t − t t

∫

− 1

Dengan penerapan teorema dasar kalkulus pada ruas kanan diperoleh

[

]

2 1 1 ( ) ( ) ( ) 2 2 W t dW t = d W t − dt atau

[

]

2 ( ) 2 ( ) ( ) . d W t = W t dW t +dt (2.5)

Untuk t₁<t₂ dengan partisi t₁=t_n0 <t_n1< <... t_nn =t₂, dan , maka ( 1) lim ( _{n k nk}) 0 n→∞maks tk + −t = 2 1 1 ( 1) ( 1) 0 ( ) ( ) lim ( )[ ] t _n n k n k nk n k t W t d t W t t t − + + →∞ ₌ =

∑

−

∫

2 1 1 ( 1) 0 ( ) lim ( ( ) t _n nk n k nk n k t tdW t t W t W t − + →∞ ₌ ⎡ ⎤ =

∑

_⎣ − _⎦

∫

. Sehingga 2 2 1 1 1 ( 1) ( 1) 0 2 2 1 1 ( ) ( ) ( ) lim ( ) ( ) ( ) ( ). t t _n n k n k nk nk n k t t W t d t tdW t t W t t W t t W t t W t − + + →∞ ₌ ⎡ ⎤ + = _⎣ − _⎦ = −

∑

∫

∫

Akibatnya ( ( )) ( ) ( ). d tW t =W t dt +tdW t (2.6)

Dengan asumsi bahwa fungsi-fungsi a t₁( )=a₁, ( )b t₁ =b₁, ( )a t₂ =a₂, ( )b t₂ =b₂

adalah konstan, maka

1 1 1 2 2 2 ( ) ( ) ( ) ( ) X t a t bW t X t a t b W t = + = + Sehingga 1 2 1 1 2 2 2 2 1 2 1 2 2 1 1 2 1 2 1 2 1 2 2 1 2 1 ( ( ) ( )) ([ ( )][ ( )]) ( ( ) ( ) [ ( )] ) 2 ( ) ( ) ( ) ( ) d X t X t d a t bW t a t b W t d a a t a b tW t a b tW t b b W t a a tdt a b tdW t a b W t dt a b tdW t a bW t dt = + + = + + + = + + + + 1 2 1 2 1 1 2 2 2 2 1 1 1 2 1 2 2 1 1 2 2 ( ) ( ) [ ( )][ ( )] [ ( )][ ( )] ( ) ( ) ( ) ( ) b b W t dW t b b dt a t bW t a dt b dW t a t b W t a dt b dW t b b dt X t dX t X t dX t b b + + = + + + + + + = + + dt. g

Lemma 3 Untuk semua m ≥2

1 ( 1) 2

( ( )) ( ( )) ( ) ( ( ))

2

m m m m

d W t =m W t −dW t + − W t m− dt

(Gihman & Skorohod 1972). Bukti:

Untuk m = 2 dapat dilihat pada (2.5). Selanjutnya misalkan berlaku untuk , maka untuk , dengan menggunakan Teorema 4 didapat

m =k

1

1 1 1 2 1 ( ( )) ( ( )) ( ) ( ) ( ( )) ( ( )) ( 1) ( ( )) ( ) ( )[ ( ( )) ( ) ( ( )) ] 2 ( ( )) ( 1) ( 1)( ( )) ( ) 2 k k k k k k k k d W t W t dW t W t d W t k W t dt k k W t dW t W t k W t dW t W t dt k W t dt k k k W t dW t + − − − − = + + − = + + + + = + + 1 (W t( ))k−dt. k

Sehingga menurut prinsip induksi matematika kesamaan berlaku untuk semua

. g

2

m ≥

Selanjutnya dengan mengambil f W t

(

( )

)

=

(

W t

( )

)

k+1 diperoleh akibat sebagai berikut:

Akibat 2

Jika f x( ) kontinu dan memiliki turunan kedua, maka

1

( ( )) '( ( )) ( ) "( ( )) 2

df W t =f W t dW t + f W t dt (2.7)

dengan f '( )x turunan pertama terhadap x, dan f "( )x turunan kedua terhadap x

(Gihman & Skorohod 1972). Lemma 4

Misalkan fungsi φ( , )t x didefinisikan untuk t∈[0, ],T x ∈ −∞ ∞( , )adalah fungsi kontinu dan terdiferensialkan terhadap t dan mempunyai turunan kedua yang kontinu terhadap x, maka

1

( , ( )) [ ( , ( )) ( , ( ))] ( , ( )) ( ) 2

t W W W

dφ t W t = φ t W t + φ t W t dt +φ t W t dW t (2.8)

Dengan ( , ),φ_t t x φ_X ( , ),t x φ_{X X} ( , )t x masing-masing adalah turunan pertama terhadap t, turunan pertama terhadap x, dan turunan kedua terhadap x (Gihman & Skorohod 1972).

Bukti:

Misalkan φ( , )t x =g t( ) ( ),ϕ x dengan g t( ) kontinu terdiferensialkan dan

( )x

ϕ kontinu terdiferensialkan kedua. Dari (2.6) dan (2.7) diperoleh ( , ( )) ( ( )) '( ) ( ) ( ( )) 1 [ ( ( )) '( ) ( ) "( ( ))] ( ) '( ( )) ( ) 2 1 [ ( , ( )) ( , ( ))] ( , ( )) ( ). 2 t W W W d t W t W t g t dt g t d W t W t g t g t W t dt g t W t dW t t W t t W t dt t W t dW t φ ϕ ϕ ϕ ϕ ϕ φ φ φ = + = + + = + + g

Berdasarkan teorema dan lemma di atas selanjutnya dapat dibuktikan formula Itoˆ(2.2) sebagai berikut:

Misalkan φ( ,t W t( ))=f t X t( , ( )) (2.9) dengan X t

( )

memenuhi persamaan (2.1), maka persamaan (2.9) akan memenuhi 2 ( , ( )) ( , ( )) ( ) ( , ( )) ( , ( )) ( ) ( , ( )) ( , ( ( )) ( ) ( , ( )). t t X W X W W X X t W t f t X t a t f t X t t W t b t f t X t t W t b t f t X t φ φ φ = + = =

Selanjutnya dengan menggunakan persamaan (2.8) diperoleh

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

2 2 1 ( , ( )) , ( ) ( ) , ( ) ( ) , ( ) 2 ( ) , ( ) ( ) 1 , ( ) , ( ) ( ) , ( ) ( ) 2 , ( ) ( ) ( t X X X X t X X X X df t X t f t X t a t f t X t b t f t X t dt b t f t X t dW t f t X t f t X t b t f t X t a t dt f t X t b t dW ⎡ ⎤ =_⎢ + + _⎥ ⎣ ⎦ + ⎡ ⎤ =_⎢ + + _⎥ ⎣ ⎦ + t). g

UNTUK MENENTUKAN HARGA SUATU ASET TURUNAN

Pembahasan harga opsi tidak dapat dilepaskan dari pembahasan tentang sekuritas lain yang berhubungan dengan haga opsi. Sehingga perlu dibahas masalah sekuritas yang berhubungan dengan harga opsi.

3.1. Harga Saham

Saham merupakan suatu bentuk aset finansial yang nilainya berubah-ubah mengikuti harga pasar pada suatu saat sesuai dengan banyaknya penawaran dan permintaan pada saat tersebut. Sehingga pada jangka waktu tertentu harga saham dapat mengalami kenaikan maupun penurunan atau bahkan dapat pula tidak mengalami perubahan harga. Jadi perubahan harga saham dipengaruhi oleh perubahan waktu dan dipengaruhi pula oleh peubah-peubah pengganggu yang berupa peubah acak dan mengikuti gerak Brown. Perubahan harga saham tersebut dapat dimodelkan sebagai berikut:

( ) ( )( ( ))

dS t =S t μdt +σdW t

atau dapat ditulis

( ) ( ) ( ) ( )

dS t =μS t dt +σS t dW t (3.1)

dimana :

( )

S t : harga saham

μ : harapan tingkat pendapatan investor (expected return), yang nilainya tergantung pada resiko pendapatan dari saham

σ : volatilitas dari harga saham

dt : periode waktu

( )

dW t : peubah acak dengan drift rate 0 dan variance rate 1, dimana proses stokastik yang mengikuti gerak Brown (Hull 2003).

( )

W t

Dengan demikian, perubahan harga saham tidak secara langsung dipengaruhi oleh

W(t), tetapi oleh dW(t).

Selanjutnya dari (3.1) dapat dicari harga saham dengan cara sebagai berikut:

( )

Misalkan y t S( , )=ln ( )S t atau S t( )=ey t( ) 2 2 2 1 1 0, , y y y t S S S ∂ ₌ ∂ ₌ ∂ _{= −} ∂ ∂ ∂ S

Menurut lemma Itoˆ

2 2 2 2 2 2 2 2 2 2 2 2 1 ( , ) ( ) 2 1 ( ( )) 2 1 1 1 ( ( )) 2 1 ( ) 2 y y y y dy t S S S dt SdW t t S S S y y y dt Sdt SdW t S dt t S S Sdt SdW t S dt S S dt dW t dt μ σ σ μ σ σ μ σ σ μ σ σ ⎛∂ ∂ ∂ ⎞ ∂ =_⎜ + + _⎟ + ∂ ∂ ∂ ∂ ⎝ ⎠ ∂ ∂ ∂ = + + + ∂ ∂ ∂ = + − = + − 2 1 ( ) ( ) 2 dt dW t μ σ σ = − +

atau dapat dinyatakan

2

1

( ) ( ) ( ).

2

dy t = μ− σ dt +σdW t (3.2)

Persamaan diferensial (3.2) mempunyai solusi

( )

( )

( )

( )

2 0 0 2 1 ( ) (0) 2 1 0 2 t t y t y ds dW s y t y t W t μ σ σ μ σ σ ⎛ ⎞ − = _⎜ − _⎟ + ⎝ ⎠ ⎛ ⎞ = +_⎜ − _⎟ + ⎝ ⎠

∫

∫

dimana y(0)merupakan nilai awal dari y t( ). Atau dapat dinyatakan

2 1 ( ) (0) exp ( ) ( ) 2 S t =S ⎡_⎢⎣ μ− σ t +σW t ⎦ ⎤ ⎥ (3.3)

dimana S(0) merupakan harga awal dari suatu saham.

Persamaan (3.3) menunjukkan bahwa harga saham mengikuti proses gerak Brown Geometris. Dengan mengingat sifat eksponensial, dapat disimpulkan bahwa harga saham tidak akan bernilai negatif, dan berdistribusi lognormal. Sehingga untuk T ≥t 2 1 ln ( ) ln (0) ( ) ( ) 2 S t = S + μ− σ t +σW t dan 2 1 ln ( ) ln (0) ( ) ( ) 2 S T = S + μ− σ T +σW T Selanjutnya diperoleh

2 1 ln ( ) ln ( ) ( )( ) ( ( ) ( )) 2 S T − S t = μ− σ T − +t σW T −W t atau 2 ( ) 1 ln ( )( ) ( ( ) ( )). ( ) 2 S T T t W T W t S t = μ− σ − +σ − (3.4)

Dengan menggunakan prosedur risk-neutral valuation yang menggunakan asumsi bahwa expected return dari underlying asset sama dengan risk-free interest rate (μ=r ), maka persamaan (3.4) menjadi

2 ( ) 1 ln ( )( ) ( ( ) ( )) ( ) 2 S T r T t W T W S t = − σ − +σ − t (3.5) dan 2 1 ( ) ( ) exp ( )( ) ( ( ) ( )) . 2 S T =S t ⎛_⎜ r− σ T − +t σW T −W t ⎝ ⎠ ⎞ ⎟ (3.6)

Selanjutnya diperoleh ekspektasi dan varians dari ln ( ) ( ) S T S t sebagai berikut:

(

)

(

( )

( )

)

(

)

2 2 ( ) 1 ln ( ) 2 1 2 S T E E r T t W T W S t r T t σ σ σ ⎡ ⎤₌ ⎡⎛ ₋ ⎞ _{− + −} ⎤ ⎜ ⎟ ⎢ ⎥ ⎢_{⎝ ⎠} ⎥ ⎣ ⎦ ⎣ ⎦ ⎛ ⎞ =_⎜ − _⎟ − ⎝ ⎠ t (3.7)

( )

( )

(

)

(

( )

( )

)

(

)

2 2 1 var ln var 2 . S T r T t W T W t S t T t σ σ σ ⎡ ⎤ _{⎡⎛ ⎞ ⎤} = − − + − ⎢ ⎥ ⎢_⎣⎜_⎝ ⎟_⎠ ⎥_⎦ ⎣ ⎦ = − (3.8) 3.2. Harga Obligasi

Obligasi merupakan suatu aset tanpa resiko yang bersifat deterministik, dengan tingkat suku bunga bernilai konstan. Sehingga perubahan harga obligasi dirumuskan sebagai berikut:

Misalnya B t( ) adalah harga obligasi pada waktu t, maka perubahannya adalah

( ) ( )

dB t =rB t dt (3.9)

dimana solusi dari persamaan diferensial tersebut adalah ( )B t =B(0)ert

3.3. Nilai Aset Turunan

Aset finansial dari suatu perseroan merupakan aset dalam bentuk saham atau obligasi. Sehingga nilai aset finansial dipengaruhi oleh saham

(

S t( )

)

dan obligasi

. Jika dimisalkan nilai aset finansial adalah

(

B t( )

)

f t S t B t

(

, ( ), ( )

)

, maka dapat ditulis

(

, ( ), ( )

)

( ) ( ) ( ) ( ) f t S t B t =φ t S t +ψ t B t (3.10) dimana

(

, ( ), ( )

)

f t S t B t adalah nilai aset finansial

( )t

φ adalah banyak unit saham

( )t

ψ adalah banyak unit obligasi.

Karena nilai aset finansial dipengaruhi oleh harga saham dan obligasi, maka

(

, ( ), ( )

)

f t S t B t merupakan nilai dari suatu aset turunan (derivative asset) pada waktu t. Dimana perubahan nilainya bergantung pada perubahan harga aset finansial lain, yaitu harga saham dan obligasi. Sehingga perubahan nilai aset finansial akan memenuhi

(

, ( ), ( )

)

( ) ( ) ( ) ( )

df t S t B t =φ t dS t +ψ t dB t (3.11)

Dengan mensubstitusi (3.1) dan (3.9) ke persamaan (3.11) diperoleh

(

)

[

]

(

)

, ( ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ). df t S t B t t S t dt S t dW t t rB t dt t S t t rB t dt t S t dW t φ μ σ ψ μφ ψ σφ = + + = + + (3.12)

Persamaan (3.12) merupakan refleksi proses perubahan nilai aset turunan yang disebabkan perubahan harga saham dan harga obligasi.

3.4. Persamaan Diferensial untuk Penentuan Harga Suatu Aset Turunan Untuk mendapatkan persamaan diferensial untuk penentuan harga aset turunan, dapat dilakukan dengan memisalkan f t S t

(

, ( ) ,

)

t ≤T merupakan harga aset turunan pada waktu t . Dari persamaan (3.1) berlaku lemma , sehingga diperoleh ˆ Ito

(

)

(

)

(

)

(

)

(

)

2 2 2 2 , ( ) 1 , ( ) , ( ) , ( ) ( ) ( ) 2 ( ) ( ) , ( ) ( ) ( ). ( ) f t S t f t S t f t S t df t S t S t S t dt t S t S t f t S t S t dW t S t σ μ σ ⎛∂ ∂ ∂ ⎞ =_⎜ + + _⎟ ∂ ∂ ∂ ⎝ ⎠ ∂ + ∂ (3.13)

Padahal dari persamaan (3.12)

(

, ( ), ( )

) (

( ) ( ) ( ) ( )

)

( ) ( ) ( ).

df t S t B t = μφ t S t +ψ t rB t dt +φ σt S t dW t (3.14)

Dengan menyamakan persamaan (3.13) dan (3.14) dapat dipilih

(

, ( )

)

( ) ( ) f t S t t S t φ =∂ ∂ (3.15) dan diperoleh

(

)

2

(

)

(

)

2 2 2 , ( ) 1 , ( ) , ( ) ( ) ( ) ( ) ( ) ( ) ( ). 2 ( ) ( ) f t S t f t S t f t S t t S t t rB t S t S t t S t S t μφ +ψ =∂ + ∂ σ +∂ μ ∂ ∂ ∂ (3.16)

Selanjutya substitusi persaman (3.15) ke persamaan (3.16) diperoleh

(

)

2

(

)

2 2 2 , ( ) 1 , ( ) ( ) ( ) ( ). 2 ( ) f t S t f t S t t rB t S t t S t ψ = ∂ + ∂ σ ∂ ∂ (3.17)

Selanjutnya dengan memisalkan f t S t

(

, ( )

)

=f t S t B t

(

, ( ), ( )

)

=f , dan substitusi persamaan (3.15) ke persamaan (3.10) diperoleh

( ) ( ) ( ) . ( ) f t B t f S t S t ψ = − ∂ ∂ (3.18)

Dengan mensubstitusi persamaan (3.18) ke persamaan (3.17) diperoleh

2 2 2 2 2 2 2 2 1 ( ) ( ) ( ) 2 ( ) 1 ( ) ( ) ( ) 2 ( ) f f f r f S t S t S t t S t f f f rf rS t S t S t t S t σ σ ⎛ ∂ ⎞ ∂ ∂ − = + ⎜ _∂ ⎟ _{∂ ∂} ⎝ ⎠ ∂ ∂ ∂ ⇔ − = + ∂ ∂ ∂ atau 2 2 2 2 1 ( ) ( ) 0. 2 ( ) ( ) f f f S t rS t rf t S t σ S t ∂ ₊ ∂ ₊ ∂ ∂ ∂ ∂ − = (3.19)

Persamaan (3.19) merupakan Persamaan diferensial untuk penentuan harga suatu aset turunan, yang dikenal dengan Persamaan Diferensial Black-Scholes-Merton (BSM) (Stampfli & Goodman 2001). Persamaan diferensial BSM mempunyai solusi yang berlaku untuk semua aset turunan, bergantung pada syarat batas yang digunakan oleh masing-masing jenis aset turunan (Hull 2003).

Selanjutnya untuk menyelesaikan persamaan diferensial (3.19) dilakukan dengan melakukan transformasi ke persamaan panas (Shiryaev 1997).

Definisikan 2 2 ( , ) ( ) ( , ) ln ( ) ( )( ) 2 t S T t Z Z t S S t r T t θ θ σ σ = = − = = + − − (3.20) dan ( ) ( , ) r T t ( , ( )). V =V θ Z =e − f t S t (3.21) Sehingga diperoleh 2 , 0 ( ) t S t θ _σ θ ∂ _{= −} ∂ ₌ ∂ ∂ dan 2 , 2 Z r t σ ⎛ ⎞ ∂ = −_⎜ − _⎟ ∂ _{⎝ ⎠} 1 . ( ) ( ) Z S t S t ∂ ₌ ∂ Dari persamaan (3.21) diperoleh

(

)

( ) ( ) ( ) ( ) ( ) 2 ( ) 2 , ( ) 2 r T t r T t r T t r T t r T t r T t f t S t e V f V e rV e t t dV e rV dt V Z V e rV Z t t V V e rV r Z θ θ σ _σ θ − − − − − − − − − − − − = ∂ _{= +} ∂ ∂ ∂ ⎛ ⎞ = _⎜ + _⎟ ⎝ ⎠ ∂ ∂ ∂ ∂ ⎛ ⎞ = _⎜ + + _⎟ ∂ ∂ ∂ ∂ ⎝ ⎠ ⎛ ⎛ ⎞ ∂ ∂ ⎞ = _⎜ −_⎜ − _{⎟ ∂} − ∂ ⎝ ⎠ ⎝ ⎠⎟ (3.22) dan ( ) ( ) ( ) 1 r T t r T t r T t f V e S S V Z V e Z S S V e S Z θ θ − − − − − − ∂ ₌ ∂ ∂ ∂ ∂ ∂ ∂ ∂ ⎛ ⎞ = _⎜ + _⎟ ∂ ∂ ∂ ∂ ⎝ ⎠ ∂ = ∂ (3.23) serta

2 2 ( ) ( ) ( ) 1 1 1 1 1 r T t r T t r T t f f S S S V e S S Z V V e S S Z Z S S V V e S Z S Z S S − − − − − − ∂ ₌ ∂ ∂⎛ ⎞ ⎜ ⎟ ∂ ∂ ⎝∂ ⎠ ∂ ⎛ ∂ ⎞ = _{⎜ ⎟} ∂ ⎝ ∂ ⎠ ⎡ ∂ ∂⎛ ⎞ ∂ ⎛ ∂ ⎞ = _{⎢ ⎜ ⎟}+ _{⎜ ⎟⎥} ∂ ⎝∂ ⎠ ∂ ⎝∂ ⎠ ⎣ ⎦ ⎡ ∂ ∂⎛ ⎞ ∂ ⎛ ∂ ⎞ = _{⎢ ⎜ ⎟}+ _{⎜ ⎟⎥} ∂ ⎝ ∂ ⎠ ∂ ⎝∂ ⎠ ⎣ ⎦ ⎤ ⎤ ( ) ( ) 2 2 ( ) 2 2 1 1 1 1 1 1 . r T t r T t r T t V Z V e S Z Z S Z S S V V e S Z Z S S Z V V e S Z Z − − − − − − ⎡ ∂ ∂⎛ ∂ ⎞ ∂ ⎛ ∂ = _{⎢ ⎜ ⎟}+ _{⎜ ⎥} ∂ ⎝∂ ∂ ⎠ ∂ ⎝∂ ⎣ ⎦ ⎡ ∂ ∂⎛ ⎞ ∂ ⎤ = _{⎢ ⎜ ⎟}− _⎥ ∂ ⎝∂ ⎠ ∂ ⎣ ⎦ ⎡∂ ∂ ⎤ = _⎢ − _⎥ ∂ ∂ ⎣ ⎦ ⎤ ⎞ ⎟ ⎠ (3.24) Selanjutnya dengan mensubstitusikan persamaan (3.22), (3.23), dan (3.24)

ke dalam persamaan (3.19) diperoleh

2 2 ( ) 2 ( ) 2 2 2 2 ( ) 1 1 2 2 1 0 r T t r T t r T t V V V V e rV r e S Z S Z V e rS rf S Z σ _{σ σ} θ − − − − − − ⎡ ₋⎛ ₋ ⎞∂ ₋ ∂ ⎤₊ ⎡ ⎛∂ ₋∂ ⎞ ⎢ ⎜ ⎟_{∂ ∂} ⎥ ⎢ ⎜_{∂ ∂} ⎟ ⎝ ⎠ ⎝ ⎠ ⎣ ⎦ ⎣ ∂ ⎡ ⎤ + _{⎢ ⎥}− = ∂ ⎣ ⎦ Z ⎤ ⎥ ⎦ 2 2 ( ) 2 2 2 2 1 1 0 2 2 2 r T t V V V V V V e rV r r rf Z Z Z Z Z σ _{σ σ σ} θ − − ⎡ ∂ ∂ ∂ ∂ ∂ ∂ ⎤ ⇔ _⎢ − + − + − + _⎥− ∂ ∂ ∂ ∂ ∂ ∂ ⎣ ⎦ = 2 ( ) 2 2 2 1 0 2 r T t V V e rV rf Z σ σ θ − − ⎡ ∂ ∂ ⎤ ⇔ _⎢ − + _⎥− ∂ ∂ ⎣ ⎦ = 2 ( ) 2 2 2 1 2 r T t V V e rV Z σ σ θ − − ⎡ ∂ ∂ ⎤ ⇔ _⎢ − + _⎥ ∂ ∂ ⎣ ⎦=rf 2 ( ) ( ) 2 2 2 1 . 2 r T t r T t V V rV e e rf Z σ σ θ − − − − ⎡ ∂ ∂ ⎤ ⇔ + _⎢− + ∂ ∂ ⎣ ⎦⎥= (3.25)

Dari persamaan (3.21) diperoleh

( )

.

r T t

rV e− − =rf

Sehingga (3.25) memberi hasil

2 ( ) 2 2 2 1 0. 2 r T t V V e Z σ σ θ − − ⎡₋ ∂ ₊ ∂ ⎤₌ ⎢ _{∂ ∂} ⎥ ⎣ ⎦

Dengan demikian 2 2 2 2 2 2 2 2 1 0 2 1 0 2 1 0. 2 V V Z V V Z V V Z σ σ θ θ θ ∂ ∂ − + ∂ ∂ ∂ ∂ ⇔ − + = ∂ ∂ ∂ ∂ ⇔ − = ∂ ∂ = (3.26) Persamaan (3.26) merupakan persamaan panas untuk V ( ,θ Z).

Dari lampiran D diperoleh penyelesaian dari persamaan panas (3.26) yaitu

2 ( ) 2 1 ( , ) ( ) 2 y Z V θ Z e θ h y dy πθ ∞ − − −∞ =

∫

(3.27)

dimana h y( )=V (0, )y merupakan syarat batas persamaan.

3.5. Present Value Nilai Harapan Selisih Harga Eksekusi dengan Harga Saham

Untuk menghitung present value nilai harapan selisih harga eksekusi (strike price) dengan harga saham dapat dilakukan dengan menghitung nilai aset turunan f t( ). Selanjutnya jika tingkat suku bunga aset tanpa resiko (obligasi) tidak bernilai nol ( , maka menurut Baxter (Baxter & Rennie, 1996) untuk menghitung nilai aset turunan

0

r ≠ )

( )

f t dilakukan dengan memperhitungkan proses diskonto terhadap harga obligasi. Sehingga diperoleh

(

)

(

)

(

)

1 ( ) ( ) ( ) ( ) ( ) ( ) ( ) rt rT r T t f t B t E B T f T e E e f T e E f T − − − − = = = (3.28)

Persamaan (3.28) menyatakan bahwa nilai aset turunan f t( ), merupakan

present value nilai harapan harga aset turunan pada saat yang akan datang, sebut . Pada opsi, harga aset turunan pada waktu T, yaitu

(

T T >t) f T( )merupakan

selisih harga eksekusi dengan harga saham pada saat T. Dengan demikian harga opsi f t( ), merupakan present value nilai harapan selisih harga eksekusi dengan harga saham pada saat jatuh tempo T.

4.1. Model Nilai Opsi Berdasarkan Persamaan Diferensial untuk Penentuan Harga Suatu Aset Turunan

4.1.1. Opsi Call

Sebagaimana dijelaskan pada BAB 3 bahwa persamaan diferensial untuk penentuan harga aset turunan mempunyai solusi yang berlaku untuk semua aset turunan, bergantung pada syarat batas yang digunakan oleh masing-masing jenis aset turunan. Untuk opsi call syarat batasnya menurut Shiryaev adalah

= (0, ) { y , 0} { ( ) , 0}

V y =maks e −K =maks S T −K ( ( )S T −K)+, dengan K adalah

harga eksekusi dan harga saham pada saat jatuh tempo (T). Untuk syarat batas

( )

S T

(0, ) ( )

V y =h y , maka ( )h y =( ( )S T −K)+, dengan y =ln ( )S T . Selanjutnya dari persamaan (3.21) dan (3.27) diperoleh

(

)

( ) , ( ) r T t f t S t =e− −V

(

)

2 ( ) ( ) 2 2 2 ( ) 2 2 ( ) 2 1 ( , ( )) ( ) 2 ln ( ) ln ( ) 2 1 ( ( ) ) exp ln ( ) 2 ( ) 2 ln ( ) ln ( ) 2 1 1 ( ( ) ) exp 2 2 ( ) y Z r T t r T t r T t f t S t e e h y dy S T S t r T t e S T K d S T T t S T S t r e S T K T t θ πθ σ σ πθ σ πσ ∞ ₋ − − − −∞ ∞ − − + −∞ − − + = ⎡ _{⎛ ⎛ ⎛ ⎞ ⎞⎞} ⎤ ⎢ ⎜_⎜ −⎜ + −⎜ ⎟ − ⎟⎟_⎟ ⎥ ⎢ _{⎝ ⎝ ⎝ ⎠ ⎠⎠} ⎥ = − _⎢− _⎥ − ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − + − = − − −

∫

∫

(

)

2 ln ( ). T t d S T T t σ ∞ −∞ ⎡ _{⎛ ⎛ ⎛ ⎞ ⎞⎞}⎤ ⎢ ⎜ ⎜ ⎜ ⎟ − ⎟⎟⎥ ⎢ _{⎜ ⎝ ⎝ ⎠ ⎠⎟}⎥ ⎢ _{⎜ − ⎟}⎥ ⎢ _{⎜ ⎟}⎥ ⎜ ⎟ ⎢ _{⎝ ⎠}⎥ ⎣ ⎦

∫

Dengan memperhatikan bahwa eksekusi opsi call dilakukan apabila harga saham di pasar lebih dari harga eksekusi, atau dengan kata lain eksekusi opsi call

dilakukan apabila dan tidak dieksekusi apabila . Sehingga batas bawah dari eksekusi opsi call adalah jika

( ) ,

S T >K S T( )≤K

( )

S T =K atau ln . Sedangkan batas atas harga saham untuk eksekusi opsi call tidak terbatas atau

, yang berakibat . Sehingga diperoleh

( ) ln

S T = K

( )