MODEL MATEMATIKA DAN ANALISIS KANDUNGAN OKSIGEN TERLARUT DALAM BADAN AIR YANG MENGALAMI EUTROFIKASI SRI LESTARI MAHMUD

MODEL MATEMATIKA DAN ANALISIS KANDUNGAN

OKSIGEN TERLARUT DALAM BADAN AIR

YANG MENGALAMI EUTROFIKASI

SRI LESTARI MAHMUD

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2014

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa tesis berjudul Model Matematika dan Analisis Kandungan Oksigen Terlarut dalam Badan Air yang Mengalami Eutrofikasi adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, September 2014

Sri Lestari Mahmud

RINGKASAN

SRI LESTARI MAHMUD. Model Matematika dan Analisis Kandungan Oksigen Terlarut dalam Badan Air yang Mengalami Eutrofikasi. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan PAIAN SIANTURI.

Eutrofikasi adalah proses pengayaan nutrien melalui proses dekomposisi yang dapat memicu terjadinya perubahan seperti peningkatan produksi alga yang mengakibatkan berkurangnya oksigen terlarut dalam badan air. Pengurangan kandungan oksigen terlarut dapat mengakibatkan kematian terhadap ikan dan komponen akuatik lainnya. Pada penelitian ini dibahas model matematika kandungan oksigen terlarut dalam badan air yang mengalami eutrofikasi.

Pada model ini terdapat enam variabel yang dipertimbangkan, yaitu konsentrasi nutrien, populasi alga, populasi makrofita, populasi zooplankton, kepadatan detritus dan konsentrasi oksigen terlarut. Ketika proses eutrofikasi terjadi, alga, makrofita dan zooplankton mati dan tenggelam ke bagian bawah badan air, sehingga terjadi pembusukan oleh dekomposer, yang akhirnya terbentuk detritus yang berlebihan. Detritus tersebut selanjutnya diubah menjadi nutrien melalui proses biokimia. Proses pengubahan detritus menjadi nutrien menggunakan banyak oksigen terlarut, sehingga mengurangi kandungan oksigen terlarut di badan air.

Dalam penelitian ini diperoleh enam titik tetap. Selanjutnya dilakukan analisis kestabilan pada titik tetap dengan mula-mula melinearisasi sistem kemudian mencari nilai eigen dari matriks Jacobiannya. Hasil analisis menunjukkan bahwa dari enam titik tetap, satu diantaranya stabil dan lima lainnya tidak stabil. Simulasi menunjukkan bahwa jika laju masuknya nutrisi ke dalam badan air mengalami kenaikan, maka populasi alga, makrofita, zooplankton dan detritus juga meningkat, sedangkan konsentrasi oksigen terlarut menurun. Selain itu, laju pengubahan detritus menjadi nutrien juga mempunyai pengaruh terhadap konsentrasi oksigen terlarut di mana jika laju pengubahan detritus menjadi nutrien meningkat, maka konsentrasi oksigen terlarut di badan air menurun. Simulasi numerik juga menunjukkan bahwa jika laju masuknya nutrisi di badan air adalah nol, maka populasi alga, makrofita, zooplankton dan kepadatan detritus juga cenderung menuju nol setelah periode waktu yang singkat sedangkan konsentrasi oksigen terlarut cenderung menuju nilai maksimum.

SUMMARY

SRI LESTARI MAHMUD. Mathematical Modeling and Analysis of Dissolved Oxygen Level in the Water Body with Eutrophication. Supervised by ENDAR HASAFAH NUGRAHANI and PAIAN SIANTURI.

Eutrophication is the enrichment of nutrients through decomposition processes that can lead to changes, such as increased production of algae, which reduces dissolved oxygen in the water body. Reduction of dissolved oxygen can lead to the death of fish and other aquatic components. This study presents and analyzes a mathematical model of dissolved oxygen in water bodies experiencing eutrophication.

In the mathematical model, there are six variables to be considered, namely the concentration of nutrients, algae population, macrophyte population, zooplankton population, density of detritus and dissolved oxygen concentration. When the process of eutrophication occurs, then algae, macrophytes and zooplankton die and sink to the bottom of water bodies resulting in decomposition by decomposers, which eventually formed excessive detritus. Detritus is then converted into nutrients through biochemical processes. The process of conversion of detritus into nutrients uses dissolved oxygen, thus reduces the dissolved oxygen content in the water body.

In this study, six fixed points are obtained. Analysis on the stability of the fixed points is carried out as follows. First step is to linearize the system, then compute the eigenvalues of the Jacobian matrix. It is found that among the six fixed points, one of them is stable and the other five are unstable. Simulations show that, if the rate of entry of nutriens into the body of water increase, then the population of algae, macrophytes, zooplankton and detritus also increase, however the concentration of dissolved oxygen decreases. In addition, the rate of conversion of detritus into nutrients also has an influence on the concentration of dissolved oxygen. If the rate of conversion of detritus into nutriens increases, then the concentration of dissolved oxygen in water bodies decreases. Numerical simulations show that if the rate of entry of nutrients in a body of water is zero, then the population of algae, macrophytes, zooplankton and detritus density also tends to zero after a short period of time, while the dissolved oxygen concentration tends towards a maximum value.

© Hak Cipta Milik IPB, Tahun 2014

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

Dilarang mengumumkan dan memperbanyak sebagian atau seluruh karya tulis ini dalam bentuk apa pun tanpa izin IPB

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains

pada

Program Studi Matematika Terapan

MODEL MATEMATIKA DAN ANALISIS KANDUNGAN

OKSIGEN TERLARUT DALAM BADAN AIR

YANG MENGALAMI EUTROFIKASI

SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR

BOGOR 2014

Judul Tesis : Model Matematika dan Analisis Kandungan Oksigen Terlarut dalam Badan Air yang Mengalami Eutrofikasi

Nama : Sri Lestari Mahmud NIM : G551120021 Disetujui oleh Komisi Pembimbing Dr Ir Endar H Nugrahani, MS Ketua Dr Paian Sianturi Anggota Diketahui oleh

Ketua Program Studi Matematika Terapan

Dr Jaharuddin, MS

Dekan Sekolah Pascasarjana

Dr Ir Dahrul Syah, MScAgr

PRAKATA

Puji dan syukur Penulis panjatkan kepada Allah Subhanahu wa ta’ala atas segala nikmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Februari 2014 ini ialah pemodelan matematika, dengan judul Model Matematika dan Analisis Kandungan Oksigen Terlarut dalam Badan Air yang Mengalami Eutrofikasi

Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada program studi Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis menyadari bahwa bantuan-bantuan dan arahan-arahan dari kedua pembimbing sangat membantu dalam menyelesaikan karya tulis ini. Terima kasih penulis ucapkan kepada Ibu Dr Ir Endar Hasafah Nugrahani, MS selaku pembimbing I dan Bapak Dr Paian Sianturi dan selaku pembimbing II.

Penulis juga menyampaikan terima kasih kepada:

1. Dr Jaharuddin, MS selaku Ketua Program Studi Matematika Terapan dan sekaligus penguji luar komisi pembimbing. .

2. Seluruh dosen dan staf pegawai tata usaha Departemen Matematika.

3. Direktorat Jenderal Pendidikan Tinggi (DIKTI) sebagai sponsor Beasiswa Unggulan.

4. Bapak Drs Eko Harsono, MT selaku peneliti LIPI yang menjadi narasumber tentang masalah eutrofikasi.

5. Orang tua, saudara dan seluruh keluarga yang selalu memberikan dorongan dan mendoakan untuk keberhasilan studi bagi penulis.

6. Seluruh mahasiswa Departemen Matematika khususnya teman-teman angkatan tahun 2012 di Program Studi S2 Matematika Terapan.

7. Teman-teman MSP dan BIOLOGI khususnya ka Apri, Anes, Hasan dan Efariana yang selalu memberikan masukan untuk masalah eutrofikasi.

8. Sahabat-sahabat yang tak dapat disebutkan satu persatu yang telah banyak membantu penulis dalam penyelesaian tesis ini.

Semoga segala bantuan, bimbingan, dan motivasi yang telah diberikan kepada penulis senantiasa mendapat balasan dari Allah Subhanahu wa ta’ala.

Akhirnya, semoga penulisan tesis ini dapat memperkaya pengalaman belajar serta wawasan kita semua.

Bogor, September 2014

DAFTAR ISI

DAFTAR TABEL vi DAFTAR GAMBAR vi DAFTAR LAMPIRAN vi 1 PENDAHULUAN 1 Latar Belakang 1 Tujuan Penelitian 2 2 TINJAUAN PUSTAKA 3 Oksigen Terlarut 3 Eutrofikasi 3

Sistem Persamaan Diferensial Biasa 4

Model Misra (2007) 5

Model Misra (2010) 7

3 HASIL DAN PEMBAHASAN 8

Modifikasi Model Matematika Kandungan Oksigen Terlarut 8

Penentuan Titik Tetap 11

Analisis Kestabilan Titik Tetap 15

Simulasi Numerik 21

4 SIMPULAN 24

DAFTAR PUSTAKA 25

LAMPIRAN 26

DAFTAR TABEL

1 Nilai Parameter Model 19

DAFTAR GAMBAR

1 Skema model Misra (2007) 6

2 Skema model Misra (2010) 8

3 Skema model matematika kandungan oksigen terlarut pada badan air

yang mengalami eutrofikasi 9

4 Grafik solusi perilaku kestabilan pada titik tetap E6. 20

5 Populasi alga terhadap t dengan nilai 𝑞 berbeda 21 6 Populasi zooplankton terhadap t dengan nilai 𝑞 berbeda 22 7 Populasi makrofita terhadap t dengan nilai 𝑞 berbeda 22 8 Kepadatan detritus terhadap t dengan nilai 𝑞 berbeda 22 9 Konsentrasi oksigen terlarut terhadap t dengan nilai 𝑞 berbeda 23 10 Konsentrasi oksigen terlarut terhadap t dengan nilai 𝜋₀ berbeda 23

DAFTAR LAMPIRAN

1 Sintaks mathematica untuk penentuan titik tetap 26 2 Unsur-unsur matriks jacobi untuk masing-masing titik tetap 33 3 Sintaks mathematica untuk penentuan nilai eigen 35

4 Simulasi kestabilan titik tetap E6 45

1

PENDAHULUAN

Latar Belakang

Air merupakan sumber daya alam yang sangat penting bagi kehidupan makhluk hidup sehingga harus dijaga kelestariannya agar di kemudian hari ketersediaan air tetap tercukupi. Air yang digunakan tersebut tentunya merupakan air yang bersih, sehat dan memenuhi standar kesehatan yaitu dalam kondisi yang tidak tercemar.

Definisi pencemaran air menurut surat Keputusan Mentri Negara Kependudukan dan Lingkungan Hidup No. 20 tahun 1990 adalah masuk atau dimasukkannya makhluk hidup, zat, energi dan atau komponen lain ke dalam air dan atau berubahnya tatanan air oleh kegiatan manusia atau oleh proses alam, sehingga kualitas air turun sampai ke tingkat tertentu yang menyebabkan air menjadi kurang atau tidak dapat berfungsi lagi sesuai dengan peruntukannya (Effendi 2003).

Misra (2010) menyatakan bahwa kegiatan manusia merupakan salah satu faktor utama yang mengakibatkan terjadinya pencemaran air di alam ini. Salah satu contohnya adalah untuk memaksimalkan hasil panen dan meningkatkan hasil produksi, petani menggunakan nitrogen, fosfor berbasis pupuk dan juga menggunakan herbisida dan insektisida, yang masing-masing digunakan untuk membunuh gulma dan serangga di lahan pertanian mereka. Sebagian dari jumlah pupuk, pestisida, herbisida dan insektisida ini telah digunakan oleh tanaman. Sisa dari bahan kimia yang tidak terpakai mengalir bersama ke badan air melalui air limpasan. Bahan kimia yang masuk melalui air limpasan tersebut mengandung fosfatdan nitrogen (senyawa nutrisi) sehingga badan air (danau) menjadi tercemar.

Selain itu, Misra (2010) juga mengatakan bahwa nutrisi yang masuk ke badan air tidak hanya berasal dari limbah pertanian, tetapi ada juga yang berasal dari limbah rumah tangga. Nutrisi yang terdapat dalam badan air, menyebabkan alga dan tumbuhan air lainnya tumbuh sangat cepat sehingga menyebabkan eutrofikasi. Eutrofikasi adalah proses pengayaan nutrien melalui proses dekomposisi yang dapat memicu terjadinya perubahan seperti peningkatan produksi alga atau tumbuhan makrofit lainnya yang menyebabkan berkurangnya oksigen terlarut dalam badan air.

Oksigen terlarut (Dissolved Oxygen = DO) adalah oksigen yang digunakan oleh mahluk hidup yang tinggal di dalam air baik hewan maupun tumbuhan untuk mempertahankan hidupnya. Oksigen terlarut ini dibutuhkan untuk pernapasan dan proses metabolisme atau pertukaran zat yang kemudian menghasilkan energi untuk pertumbuhan dan pembiakan (Kristanto 2004).

Kandungan oksigen terlarut dapat bersumber dari proses difusi oksigen yang berasal dari udara maupun proses fotosintesis oleh alga dan tumbuhan. Kadar oksigen dari kedua proses ini mengakibatkan peningkatan kandungan oksigen terlarut yang tidak terlalu tinggi. Semakin banyak nutrisi yang masuk ke badan air, maka populasi alga dan tumbuhan akan semakin banyak. Hal ini mengakibatkan alga dan tumbuhan menutupi permukaan air sehingga perpindahan oksigen dari udara ke air melalui difusi dan cahaya yang digunakan untuk proses fotosintesis juga menjadi berkurang (Misra 2010).

2

Selain itu, ketika alga dan tumbuhan mati dan tenggelam ke bagian bawah badan air, terjadi pembusukan oleh dekomposer yang akhirnya terbentuk detritus yang berlebihan. Detritus tersebut selanjutnya diubah menjadi nutrien melalui proses biokimia. Proses pengubahan detritus menjadi nutrisi menggunakan banyak oksigen terlarut, sehingga mengurangi kandungan oksigen terlarut di badan air. Penggunaan oksigen terlarut yang sangat besar pada proses biokimia mengakibatkan suplai oksigen terlarut bagi ikan dan komponen akuatik lainnya menjadi berkurang sehingga hal ini akan berpengaruh buruk terhadap kehidupan ikan dan kehidupan akuatik lainnya (Soeprobowati et al. 2012).

Berdasarkan permasalahan tentang oksigen terlarut pada badan air yang mengalami eutrofikasi, maka dibutuhkan suatu model matematika yang dapat menggambarkan fenomena-fenomena yang menyebabkan berubahnya kandungan oksigen teralarut serta menganalisis model untuk melihat dinamika populasi di badan air tersebut.

Model matematika dan analisis tentang oksigen terlarut ini telah banyak dikaji oleh beberapa peneliti. Voinov dan Tonkikh (1987) telah menyajikan sebuah model matematika taklinear untuk eutrofikasi di danau yang menyebabkan berkurangnya DO. Model tersebut mengasumsikan bahwa penyebab berkurangnya oksigen terlarut hanya dipengaruhi oleh nutrien, alga dan detritus. Model Voinov dan Tonkikh dikaji lebih lanjut oleh Misra (2007) dengan menambahkan parameter zooplankton pada model dan direkonstruksi kembali oleh Misra (2010) dengan menambahkan parameter makrofitadan mengabaikan parameter zooplankton pada model.

Penelitian ini akan mengkaji sebuah model modifikasi yang mengacu pada kajian Misra (2007) dan Misra (2010) dengan menambahkan sekaligus parameter zooplankton dan makrofita pada model matematika kandungan oksigen terlarut dalam badan air yang mengalami eutrofikasi.

Tujuan Penelitian Penelitian ini bertujuan untuk:

1 Melakukan modifikasi model matematika kandungan oksigen terlarut. 2 Menentukan titik tetap dan analisis kestabilan pada model.

3 Melakukan simulasi numerik terhadap model untuk menggambarkan keterkaitan antara konsentrasi nutrisi, populasi alga, makrofita, zooplankton, detritus dan kandungan oksigen terlarut dalam badan air yang mengalami eutrofikasi.

3

2

TINJAUAN PUSTAKA

Oksigen Terlarut

Oksigen terlarut adalah konsentrasi oksigen yang terlarut dalam air dan dapat diukur dalam satuan miligram per liter. Oksigen terlarut ini dibutuhkan oleh semua jasad hidup untuk proses pernapasan, metabolisme atau pertukaran zat yang kemudian menghasilkan energi untuk pertumbuhan dan pembiakan. Oksigen terlarut juga dapat dijadikan ukuran untuk menentukan kualitas air. Hal itu dikarenakan oksigen terlarut berperan dalam proses oksidasi dan reduksi bahan organik dan anorganik.

Oksigen terlarut dapat berasal dari fotosintesis tanaman air dan dari atmosfir (udara) yang masuk ke dalam air dengan kecepatan tertentu. Kadar oksigen akan lebih tinggi karena adanya proses difusi antara air dengan udara bebas serta adanya proses fotosintesis. Bertambahnya kedalaman menyebabkan terjadinya penurunan kadar oksigen terlarut, karena proses fotosintesis semakin berkurang dan kadar oksigen yang ada banyak digunakan untuk pernapasan dan oksidasi dan bahan-bahan organik dan anorganik (Kristanto 2004).

Eutrofikasi

Eutrofikasi didefinisikan sebagai pengayaan (enrichment) air dengan nutrien/unsur hara berupa bahan anorganik yang dibutuhkan oleh tumbuhan dan meningkatkan terjadinya peningkatan produktivitas primer perairan. Nutrien yang dimaksud adalah nitrogen dan fosfor. Eutrofikasi diklasifikasikan menjadi dua yaitu

artificial (cultural) eutrophication dan natural eutrophication. Eutrofikasi diklasifikasikan sebagai artificial (cultural) eutrophication apabila peningkatan unsur hara di perairan disebabkan oleh aktivitas manusia; dan diklasifikasikan sebagai natural eutrophication jika peningkatan unsur hara di perairan bukan disebabkan oleh aktivitas manusia, melainkan aktivitas alam (Effendi 2003).

Gejala eutrofikasi di perairan badan air biasanya ditunjukkan dengan melimpahnya konsentrasi unsur hara dan perubahan parameter kimia seperti oksigen terlarut, kandungan klorofil-a dan turbiditas serta produktivitas primer. Hal ini menyebabkan terjadinya peningkatan konsentrasi biomassa di bagian epilimnion badan air dan tingginya laju pengendapan alga ke bagian dalam kolom air, sehingga menjadikan kondisi anaerobik pada daerah hipolimnion (Gather dan Imboden 1985). Agustiyani (2004) mengemukakan hal yang senada bahwa meningkatnya unsur hara di badan air akan meningkatkan biomassa jenis organisme primer tetapi akan menurunkan jenis konsumer. Hal ini mengakibatkan melimpahnya salah satu jenis saja dan mengurangi varietas dan kualitas. Salah satu contohnya adalah melimpahnya alga yang biasa didominasi oleh blue green algae (alga biru-hijau) dan berkembangnya gulma air.

4

Sistem Persamaan Diferensial Biasa Sistem Persamaan Diferensial Biasa Linear

Misalkan suatu sistem persamaan diferensial biasa (SPDB) dinyatakan sebagai

𝒙̇ = 𝑨𝒙 + 𝒃; 𝒙(𝟎) = 𝒙_𝟎, 𝒙 ∈ ℝ𝒏 _(2.1)

dengan 𝑨 adalah matriks koefisien konstan berukuran 𝑛 x 𝑛 dan 𝒃 adalah vektor konstan. Sistem persamaan (2.1) dinamakan sistem persamaan diferensial linear orde satu dengan kondisi awal 𝒙(𝟎) = 𝒙𝟎. Jika 𝒃 = 𝟎, maka sistem dikatakan

homogen dan jika 𝒃 ≠ 𝟎, maka sistem dikatakan takhomogen (Tu 1994). Sistem Persamaan Diferensial Biasa Taklinear

Misalkan suatu sistem persamaan diferensial biasa (SPDB) dinyatakan sebagai 𝒙̇ = 𝑓(𝑡, 𝒙), (2.2) dengan 𝒙 = [ 𝑥1(𝑡) 𝑥₂(𝑡) ⋮ 𝑥𝑛(𝑡) ] dan 𝑓(𝑡, 𝒙) = [ 𝑓1(𝑡, 𝑥1, 𝑥2, … , 𝑥𝑛) 𝑓₂(𝑡, 𝑥₁, 𝑥₂, … , 𝑥_𝑛) ⋮ 𝑓_𝑛(𝑡, 𝑥1, 𝑥2, … , 𝑥𝑛) ]

adalah fungsi taklinear dalam 𝑥₁, 𝑥₂, … , 𝑥_𝑛. Sistem persamaan (2.2) disebut sistem persamaan diferensial biasa taklinear (Braun 1983).

Sistem Persamaan Diferensial Biasa Mandiri

Misalkan suatu sistem persamaan diferensial biasa (SPDB) dinyatakan sebagai

𝒙̇ = 𝑓(𝒙), 𝒙 ∈ ℝ𝒏_{, (2.3)}

dengan 𝑓 merupakan fungsi kontinu bernilai real dari 𝒙. Sistem persamaan (2.3) disebut sistem persamaan diferensial biasa mandiri (autonomous) karena tidak memuat 𝑡 secara eksplisit di dalamnya (Tu 1994).

Titik Tetap

Diberikan SPD Mandiri

𝒙̇ = 𝑓(𝒙), 𝒙 ∈ ℝ𝒏_.

Titik 𝒙̅ disebut titik tetap, jika 𝑓(𝒙̅) = 𝟎. Titik tetap disebut juga titik kritis atau titik kesetimbangan atau titik ekuilibrium (Tu 1994). Untuk selanjutnya digunakan istilah titik tetap.

Nilai Eigen dan Vektor Eigen

Diberikan matriks koefisien konstan 𝑨 berukuran 𝑛 × 𝑛 dan sistem persamaan diferensial biasa homogen 𝒙̇ = 𝑨𝒙, 𝒙(𝟎) = 𝒙_𝟎, 𝒙 ∈ ℝ𝒏. Suatu vektor taknol 𝒙 di dalam ℝ𝒏 disebut vektor eigen dari 𝑨 jika untuk suatu skalar 𝜆 berlaku

𝑨𝒙 = 𝜆𝒙. (2.4)

Nilai skalar 𝜆 dinamakan nilai eigen dari 𝑨. Untuk mencari nilai 𝝀 dari 𝑨, maka sistem persamaan (2.4) dapat ditulis

(𝑨 − 𝜆𝑰)𝒙 = 𝟎, (2.5) dengan 𝑰 adalah matriks identitas. Sistem persamaan (2.5) mempunyai solusi taknol

5

det (𝑨 − 𝜆𝑰) = 0. (2.6) Persamaan (2.6) merupakan persamaan karakteristik matriks 𝑨 (Anton dan Rorres

1995). Pelinearan

Analisis kestabilan dari suatu SPD taklinear dilakukan melalui model hasil pelinearan. Misalkan diberikan SPD taklinear sebagai berikut

𝒙̇ = 𝑓(𝒙). (2.7)

Dengan menggunakan ekspansi Taylor untuk suatu titik tetap 𝒙̅, maka sistem persamaan (2.7) dapat ditulis sebagai

𝒙̇ = 𝑨𝒙 + 𝝋(𝒙). (2.8)

Persamaan tersebut merupakan SPD taklinear dengan 𝑨 adalah matriks Jacobi,

𝑨 = 𝐷𝑓(𝒙̅) = 𝐷𝑓(𝒙)_𝒙=𝒙̅ = [ 𝜕𝑓₁ 𝜕𝑥₁ ⋯ 𝜕𝑓₁ 𝜕𝑥_𝑛 ⋮ ⋱ ⋮ 𝜕𝑓_𝑛 𝜕𝑥₁ ⋯ 𝜕𝑓_𝑛 𝜕𝑥_𝑛] = [ 𝑎11 ⋯ 𝑎1𝑛 ⋮ ⋱ ⋮ 𝑎_𝑛1 ⋯ 𝑎_𝑛𝑛]

dan 𝝋(𝒙) suku berorde tinggi yang bersifat lim

𝑛→0𝝋(𝒙) = 0.Akibatnya persamaan

diferensial (2.8) diberikan sebagai berikut

𝒙̇ = 𝑨𝒙. (2.9)

Persamaan (2.9) disebut pelinearan dari persamaan diferensial (2.7) (Tu 1994). Analisis Kestabilan Titik Tetap

Misalkan diberikan SPD mandiri sebagaimana pada sistem (2.3). Pelinearan selanjutnya dilakukan di sekitar titik tetap sesuai dengan persamaan (2.8), sehingga diperoleh persamaan (2.9). Analisis kestabilan SPD (2.3) dilakukan melalui analisis kestabilan SPD (2.9). Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigen matriks 𝑨, yaitu: 𝜆𝑖, 𝑖 = 1,2, … , 𝑛 yang diperoleh dari 𝑑𝑒𝑡 (𝑨 − 𝜆𝑰) =

0.

Secara umum kestabilan titik tetap mempunyai perilaku sebagai berikut : 1 Stabil, jika

a) Setiap nilai eigen real negatif (𝜆_𝑖 < 0 untuk setiap 𝑖), atau

b) Setiap nilai eigen kompleks yang memiliki bagian real negatif atau sama dengan nol, (𝑅𝑒(𝜆_𝑖) ≤ 0 untuk setiap 𝑖).

2 Takstabil, jika

a) Terdapat nilai eigen real positif atau sama dengan nol (𝜆_𝑖 ≥ 0 untuk suatu

𝑖), atau

b) Terdapat nilai eigen kompleks yang memiliki bagian real positif, (𝑅𝑒(𝜆_𝑖) >

0 untuk suatu 𝑖) (Tu 1994).

Model Misra (2007)

Model matematika taklinear dalam penelitian ini diusulkan dan dianalisa untuk mempelajari berkurangnya oksigen terlarut pada badan air yang mengalami

6

eutrofikasi karena pertumbuhan alga, zooplankton dan spesies biologi lainnya yang berlebihan, yang disebabkan oleh masukan nutrisi yang berlebihan di badan air.

Asumsi yang diberikan pada model ini yakni sebagai berikut:

 Populasi alga sepenuhnya bergantung pada nutrien dan zooplankton. Zooplankton berperan sebagai predator dari alga.

 Kadar oksigen terlarut dalam badan air meningkat karena difusi dan proses fotosintesis alga yang diasumsikan konstan.

 Detritus yang terbentuk diperoleh dari alga dan zooplankton yang mati yang kemudian didekomposisi menjadi nutrien.

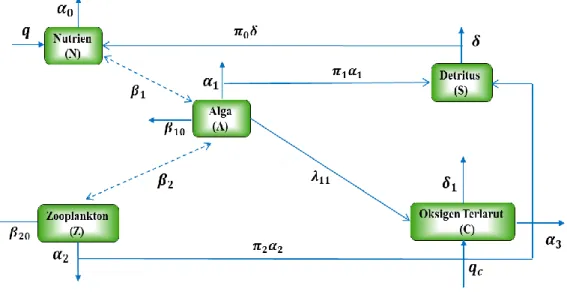
Variabel yang dipertimbangkan dalam model ini adalah konsentrasi nutrien (𝑁), kepadatan populasi alga (𝐴), kepadatan populasi zooplankton (𝑍), kepadatan detritus (𝑆) dan konsentrasi oksigen terlarut (𝐶 ). Secara skematis, pola berkurangnya oksigen terlarut dalam model ini digambarkan dalam diagram kompartemen yang disajikan pada Gambar 1. Model yang menggambarkan fenomena tersebut diformulasikan sebagai berikut

𝑑𝑁 𝑑𝑡 = 𝑞 + 𝜋0𝛿𝑆 − 𝛼0𝑁 − 𝛽1𝐴𝑁 𝑑𝐴 𝑑𝑡 = 𝜃1𝛽1𝑁𝐴 − 𝛼1𝐴 − 𝛽10𝐴2− 𝛽2𝐴 𝑑𝑍 𝑑𝑡 = 𝜃2𝛽2𝐴𝑍 − 𝛼2𝑍 − 𝛽20𝑍2 𝑑𝑆 𝑑𝑡 = 𝜋1𝛼1𝐴 + 𝜋2𝛼2𝑍 − 𝛿𝑆 𝑑𝐶 𝑑𝑡 = 𝑞𝑐 − 𝛼3𝐶 + 𝜆11𝐴 − 𝛿1𝑆 (2.10) dimana: 𝑁(0) ≥ 0, 𝐴(0) ≥ 0, 𝑍(0) ≥ 0, 𝑆(0) ≥ 0, 𝐶(0) ≥ 0.

Koefisien 𝛼0 dan 𝛼3 dalam model (2.10) masing-masing merupakan

koefisien positif yang menunjukkan laju berkurangnya nutrien dan oksigen terlarut secara alami dan positif. Koefisien 𝛼1 dan 𝛼2 masing-masing menunjukkan angka

kematian alami alga dan zooplankton sedangkan 𝛿 menunjukkan laju berkurangnya detritus karena proses biokimia yang terjadi di badan air. Koefisien 𝛽_1, 𝛽_{2 ,} 𝜃₁, 𝜃₂

7 adalah konstanta pembanding yang juga positif. Konstanta 𝛽₁₀ dan 𝛽₂₀ adalah koefisien laju berkurangnya alga dan zooplankton karena adanya interaksi diantara sesama alga dan zooplankton tersebut. Koefisien 𝜋₀, 𝜋₁ dan 𝜋₂ adalah konstanta pembanding dengan 0 < 𝜋₀, 𝜋₁, 𝜋₂ <1. Koefisien 𝜆₁₁ merupakan konstanta pembanding dari laju bertambahnya oksigen terlarut yang disebabkan alga sedangkan 𝛿1merupakan konstanta kesebandingan dari laju berkurangnya oksigen

terlarut akibat pengubahan detritus menjadi nutrien melalui proses biokimia. Model Misra (2010)

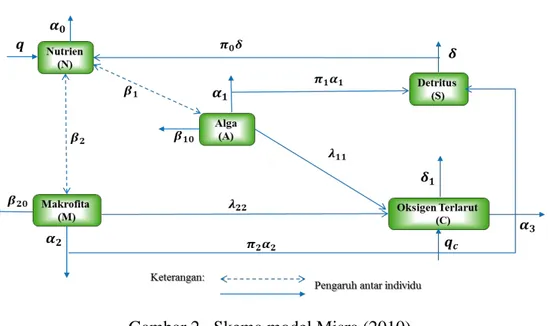
Model ini merupakan rekonstruksi dari model yang telah dirumuskan sebelumnya oleh Misra (2007) dengan menambahkan parameter makrofita dan mengabaikan parameter zooplankton pada model. Penelitian ini mengusulkan sebuah model matematika taklinear untuk menganalisis berkurangnya konsentrasi oksigen terlarut dalam badan air karena adanya pertumbuhan yang berlebihan dari alga dan makrofita yang disebabkan oleh masuknya nutrisi di badan air.

Asumsi yang diberikan pada model ini yakni sebagai berikut:

 Nutrisi terus menerus masuk ke badan air melalui air limpasan dengan laju konstan

 Laju pertumbuhan alga dan makrofita sepenuhnya bergantung pada nutrien

 Laju pertumbuhan detritus sebanding dengan populasi alga dan populasi makrofita

 Kadar oksigen terlarut dalam badan air meningkat karena difusi dan proses fotosintesis alga, yang diasumsikan konstan

Variabel yang dipertimbangkan dalam model ini adalah konsentrasi nutrisi (𝑁), populasi alga (𝐴), populasi makrofita (𝑀), kepadatan detritus (𝑆) dan konsentrasi oksigen terlarut (𝐶). Secara skematis, pola berkurangnya oksigen terlarut dalam model ini digambarkan dalam diagram kompartemen yang disajikan pada Gambar 2. Model yang menggambarkan fenomena tersebut diformulasikan sebagai berikut 𝑑𝑁 𝑑𝑡 = 𝑞 + 𝜋0𝛿𝑆 − 𝛼0𝐴 − 𝛽1𝑎𝑛 − 𝛽2𝑁𝑀 𝑑𝐴 𝑑𝑡 = 𝜃1𝛽1𝑁𝐴 − 𝛼1𝐴 − 𝛽10𝐴2 𝑑𝑀 𝑑𝑡 = 𝜃2𝛽2𝑁𝑀 − 𝛼2𝑀 − 𝛽20𝑀2 𝑑𝑆 𝑑𝑡 = 𝜋1𝛼1𝐴 + 𝜋2𝛼2𝑀 − 𝛿𝑆 𝑑𝐶 𝑑𝑡 = 𝑞𝑐− 𝛼3𝐶 + 𝜆11𝐴 + 𝜆22𝑀 − 𝛿1𝑆, (2.11) dimana 𝑁(0) ≥ 0, 𝐴(0) ≥ 0, 𝑀(0) ≥ 0, 𝑆(0) ≥ 0, 𝐶(0) ≥ 0.

Koefisien 𝛼₀ dan 𝛼₃ dalam model (2.11) merupakan koefisien positif yang masing-masing menunjukkan laju berkurangnya nutrien dan oksigen terlarut secara alami dan positif. Koefisien 𝛼1 dan 𝛼2 masing-masing menunjukkan angka

kematian alami alga dan makrofita sedangkan 𝛿 menunjukkan laju berkurangnya detritus karena proses biokimia yang terjadi di badan air. Koefisien 𝛽_1, 𝛽_{2 ,} 𝜃₁, 𝜃₂ adalah konstanta pembanding yang juga positif. Konstanta 𝛽₁₀ dan 𝛽₂₀ adalah

8

koefisien laju berkurangnya alga dan makrofita karena adanya interaksi diantara sesama alga dan makrofita tersebut. Koofisien 𝜋₀, 𝜋₁ dan 𝜋₂ adalah konstanta pembanding dengan 0 < 𝜋₀, 𝜋₁, 𝜋₂ <1. Koefisien 𝜆₁₁ dan 𝜆₂₂ merupakan konstanta pembanding dari laju bertambahnya oksigen terlarut yang disebabkan alga dan makrofita sedangkan 𝛿₁ merupakan konstanta kesebandingan dari laju berkurangnya oksigen terlarut akibat pengubahan detritus menjadi nutrien melalui proses biokimia.

3

HASIL DAN PEMBAHASAN

Modifikasi Model Matematika Kandungan Oksigen Terlarut

Pada bagian ini dilakukan modifikasi model matematika kandungan oksigen terlarut yang mengacu pada model yang telah dikembangkan oleh Misra (2007) dan Misra (2010). Namun, pada model ini ditambahkan sekaligus parameter zooplanktondanmakrofita yang pembahasannya juga disajikan dalam Mahmud et al. (2014). Variabel yang dipertimbangkan dalam model ini adalah konsentrasi nutrien (𝑁), populasi alga (𝐴), populasi makrofita (𝑀), populasi zooplankton(𝑍), kepadatan detritus (𝑆) dan konsentrasi oksigen terlarut (𝐶).

Model ini mengasumsikan bahwa jumlah laju aliran nutrisi yang berasal dari luar (limbah rumah tangga dan limbah pertanian) ke dalam badan air adalah 𝑞, yang berkurang dengan laju 𝛼₀𝑁. Selain itu, diasumsikan juga bahwa laju bertambahnya nutrien oleh detritus adalah 𝜋₀𝛿𝑆 dan laju berkurangnya nutrien oleh alga sebanding dengan populasi alga dan jumlah konsentrasi nutrien yaitu 𝑁𝐴 serta laju berkurangnya nutrien karena makrofita sebanding dengan populasi makrofita dan jumlah konsentrasi nutrien yaitu 𝑁𝑀. Hal ini mengakibatkan laju populasi alga sebanding dengan 𝑁𝐴 dan laju populasi makrofita adalah sebanding dengan 𝑁𝑀. Laju berkurangnya alga secara alami diasumsikan sebanding dengan kepadatannya dan laju berkurangnya alga akibat interaksi antara alga dan alga atau akibat

9 kesesakan sebanding dengan 𝐴2. Sama halnya dengan laju berkurangnya makrofita secara alami diasumsikan sebanding dengan kepadatannya 𝑀 dan laju berkurangnyamakrofita akibat interaksi antara makrofita dan makrofita itu sendiri atau akibat kesesakan sebanding dengan 𝑀2.

Laju berkurangnya alga oleh zooplankton sebagai predatornya dianggap sebanding dengan 𝐴𝑍 dan karenanya laju pertumbuhan zooplankton juga sebanding ke 𝐴𝑍. Laju berkurangnya zooplankton secara alami diasumsikan sebanding dengan kepadatannya 𝑍 dan laju berkurangnya karena interaksi antara zooplankton atau karena kesesakan sebanding dengan 𝑍2. Laju pertumbuhan detritus yang berasal dari alga, makrofita, dan zooplankton yang berkurang secara alami diasumsikan sebanding dengan 𝐴, 𝑀 dan 𝑍 serta laju berkurangnya detritus secara alami diasumsikan sebanding dengan 𝑆.

Berdasarkan uraian di atas, dapat dituliskan bahwa asumsi yang digunakan dalam model ini yakni sebagai berikut:

 Nutrisi masuk ke badan air melalui air limpasan bidang pertanian dan limbah rumah tangga, diasumsikan konstan.

 Laju pertumbuhan alga danmakrofita sepenuhnya bergantung pada nutrien

 Populasi zooplankton sepenuhnya bergantung pada alga

 Detritus yang diperoleh dari alga, makrofita dan zooplankton yang mati, kemudian didekomposisi melalui proses biokimiawi menjadi nutrien.

 Konsentrasi oksigen terlarut dalam badan air meningkat karena proses difusi dan proses fotosintesis alga dan makrofita yang diasumsikan konstan serta menurun akibat digunakan dalam proses pembentukan detritus menjadi nutrien.

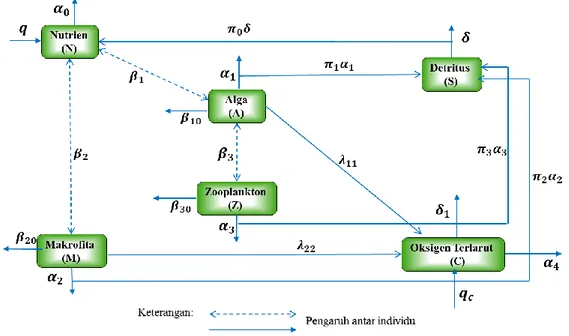
Secara skematis, pola berkurangnya oksigen terlarut dalam model ini digambarkan dalam diagram kompartemen yang disajikan pada Gambar 3.

Gambar 3 Skema model matematika kandungan oksigen terlarut pada badan air yang mengalami eutrofikasi

10

Model yang menggambarkan fenomena tersebut diformulasikan sebagai berikut

𝑑𝑁 𝑑𝑡 = 𝑞 + 𝜋0𝛿𝑆 − 𝛼0𝑁 − 𝛽1𝐴𝑁 − 𝛽2𝑁𝑀 𝑑𝐴 𝑑𝑡 = 𝜃1𝛽1𝑁𝐴 − 𝛼1𝐴 − 𝛽10𝐴2− 𝛽3𝐴𝑍 𝑑𝑀 𝑑𝑡 = 𝜃2𝛽2𝑁𝑀 − 𝛼2𝑀 − 𝛽20𝑀2 𝑑𝑍 𝑑𝑡 = 𝜃3𝛽3𝐴𝑍 − 𝛼3𝑍 − 𝛽30𝑍2 𝑑𝑆 𝑑𝑡 = 𝜋1𝛼1𝐴 + 𝜋2𝛼2𝑀 + 𝜋3𝛼3𝑍 − 𝛿𝑆 𝑑𝐶 𝑑𝑡 = 𝑞𝑐 − 𝛼4𝐶 + 𝜆11𝐴 + 𝜆22𝑀 − 𝛿1𝑆, (3.1) di mana 𝑁(0) ≥ 0, 𝐴(0) ≥ 0, 𝑀(0) ≥ 0, 𝑍(0) ≥ 0, 𝑆(0) ≥ 0, 𝐶(0) ≥ 0. Keterangan parameter dalam model (3.1) yakni sebagai berikut:

𝑞 : laju aliran nutrisi yang berasal dari luar (limbah rumah tangga dan limbah pertanian) ke badan air

q_c : laju bertambahnya oksigen terlarut oleh berbagai sumber

α0 : koefisien laju berkurangnya nutrien karena faktor alam

α1 : koefisien laju berkurangnya alga karena faktor alam

α2 : koefisien laju berkurangnya makrofita karena faktor alam

α3 : koefisien laju berkurangnya zooplankton karena faktor alam

α4 : koefisien laju berkurangnya konsentrasi oksigen terlarut karena

faktor alam

β₁ : koefisien laju berkurangnya nutrien karena alga

β₂ : koefisien laju berkurangnya nutrien karena makrofita

β₃ : koefisien laju berkurangnya alga karena zooplankton

β₁₀ : koefisien laju berkurangnya alga karena adanya interaksi antara alga (kepadatan alga)

β₂₀ : koefisien laju berkurangnya makrofita karena adanya interaksi antara makrofita (kepadatan makrofita)

β₃₀ : koefisien laju berkurangnya zooplankton karena adanya interaksi antara zooplankton (kepadatan zooplankton)

λ11 : koefisien laju bertambahnya oksigen terlarut karena alga λ22 : koefisien laju bertambahnya oksigen terlarut karena makrofita

δ : koefisien laju berkurangnya detritus karena faktor alam

𝛿1 : koefisien berkurangnya oksigen terlarut akibat pengubahan

detritus menjadi nutrien melalui proses biokimia

θ1,θ2,θ3 : konstanta pembanding yang positif

π0, π1, π2,π3 : konstanta pembanding dengan 0 < π0, 𝜋1, 𝜋2, 𝜋3 < 1

Sistem (3.1) inilah yang selanjutnya akan dianalisis. Analisis tersebut meliputi penentuan titik tetap dan kestabilan, serta simulasi numerik untuk menggambarkan kandungan oksigen terlarut di badan air yang mengalami eutrofikasi.

11 Penentuan Titik Tetap

Pada sub-bab ini akan dicari titik tetap dari sistem (3.1) yang dapat diperoleh dengan menyelesaikan sistem tersebut. Solusinya merupakan suatu kondisi yang diperoleh pada saat 𝑑𝑁_𝑑𝑡 =𝑑𝐴_𝑑𝑡 = 𝑑𝑀_𝑑𝑡 = 𝑑𝑍_𝑑𝑡 =𝑑𝑆_𝑑𝑡=𝑑𝐶_𝑑𝑡 = 0. Sistem tersebut memiliki enam jenis titik tetap yaitu 𝐸_𝑖(𝑁_𝑖∗, 𝐴_𝑖∗, 𝑀_𝑖∗, 𝑍_𝑖∗, 𝑆_𝑖∗, 𝐶_𝑖∗) dimana 𝑖 = 1, 2, 3, 4, 5, 6. Titik tetap 𝑬_𝟏(𝑵_𝟏∗, 𝟎, 𝟎, 𝟎, 𝟎, 𝑪_𝟏∗)

Pada titik tetap ini, alga, makrofita dan zooplankton belum ada pada badan air. Sejalan dengan hal tersebut, maka detritus pun belum terbentuk di badan air. Oleh karena itu, badan air belum tercemar, artinya nutrien tidak berpengaruh terhadap alga, makrofita, zooplankton dan detritus sehingga nilai 𝐴 = 0, 𝑀 = 0,

𝑍 = 0 dan 𝑆 = 0. Nilai-nilai dari titik tetap E1 diperoleh dengan menyelesaikan

persamaan di bawah ini

𝑞 + 𝜋₀𝛿𝑆 − 𝛼₀𝑁 − 𝛽₁𝐴𝑁 − 𝛽₂𝑁𝑀 =

0

𝑞𝑐 − 𝛼4𝐶 + 𝜆11𝐴 + 𝜆22𝑀 − 𝛿1𝑆 = 0,

(3.2) dengan mensubstitusi nilai 𝐴 = 0, 𝑀 = 0, 𝑍 = 0 dan 𝑆 = 0 ke dalam persamaan (3.2) diperoleh nilai 𝑁 dan 𝐶 yaitu

𝑁 =_𝛼𝑞

0 dan 𝐶 = 𝑞𝑐 𝛼4.

Sehingga titik tetap untuk 𝐸₁(𝑁₁∗, 0, 0, 0, 0, 𝐶₁∗) dimana alga, makrofita, zooplankton dan detritus belum ada pada badan air yaitu (𝑞 𝛼⁄ , 0, 0, 0, 0, 𝑞₀ 𝑐⁄ )_𝛼4 . Titik tetap 𝑬𝟐(𝑵𝟐∗, 𝟎, 𝑴𝟐∗, 𝟎, 𝑺𝟐∗, 𝑪𝟐∗)

Pada titik tetap ini, alga dan zooplankton belum ada pada badan air, maka badan air yang tercemar hanya berpengaruh pada populasi makrofita artinya nutrien hanya digunakan oleh makrofita sehingga nilai 𝐴 = 0 dan𝑍 = 0. Nilai-nilai dari titik tetap 𝐸₂ diperoleh dengan menyelesaikan persamaan di bawah ini:

𝑞 + 𝜋0𝛿𝑆 − 𝛼0𝑁 − 𝛽2𝑁𝑀 = 0

𝜃2𝛽2𝑁 − 𝛼2− 𝛽20𝑀 = 0

𝜋₂𝛼₂𝑀 − 𝛿𝑆 = 0

𝑞_𝑐 − 𝛼₄𝐶 + 𝜆₂₂𝑀 − 𝛿₁𝑆 = 0.

Sehingga diperoleh titik tetap 𝐸2 yaitu

(𝑁₂∗_{, 0, 𝑀} 2∗, 0, 𝑆2∗, 𝐶2∗), dengan 𝑀₂∗₌ 1 2𝛽₂𝛽₂₀(−𝛼2𝛽2− 𝛼0𝛽20+ 𝜋0𝜋2𝛼2𝛽2𝜃2 + √(4𝛽2𝛽20(−𝛼0𝛼2+ 𝑞𝛽2𝜃2) + (−𝛼2𝛽2− 𝛼0𝛽20+ 𝜋0𝜋2𝛼2𝛽2𝜃2)2)) 𝑁₂∗ ₌𝛼2+ 𝑀2∗𝛽20 𝛽₂𝜃₂ 𝑆₂∗ ₌𝑀2∗ 𝜋2𝛼2 𝛿 𝐶2∗ = 𝑞𝑐 − 𝑆2∗𝛿1+ 𝑀2∗𝜆22 𝛼4 .

12

Syarat agar titik tetap 𝐸₂ ada yaitu

−𝛼0𝛼2+ 𝑞 𝛽₂𝜃2> 0 dan

𝑞_𝑐 − 𝑆₂∗𝛿₁+ 𝑀₂∗𝜆₂₂> 0.

Titik tetap 𝑬_𝟑(𝑵_𝟑∗, 𝑨_𝟑∗, 𝟎, 𝟎, 𝑺_𝟑∗, 𝑪_𝟑∗)

Pada titik tetap ini, makrofita dan zooplankton belum ada pada badan air menyebabkan badan air yang tercemar hanya berpengaruh pada populasi alga artinya nutrien hanya digunakan oleh alga sehingga nilai 𝐴 = 0 dan𝑍 = 0. Nilai-nilai dari titik tetap E3 diperoleh dengan menyelesaikan persamaan di bawah ini:

𝑞 + 𝜋0𝛿𝑆 − 𝛼0𝑁 − 𝛽1𝑁𝐴 = 0

𝜃₁𝛽₁𝑁 − 𝛼₁ − 𝛽₁₀𝐴 = 0

𝜋₁𝛼₁𝐴 − 𝛿𝑆 = 0

𝑞_𝑐 − 𝛼₄𝐶 + 𝜆₁₁𝐴 − 𝛿₁𝑆 = 0,

Sehingga diperoleh titik tetap 𝐸3 yaitu

(𝑁3∗, 𝐴3∗, 0, 0, 𝑆3∗, 𝐶3∗), dengan 𝐴₃∗ = 1 2𝛽₁𝛽₁₀(−𝛼1𝛽1− 𝛼0𝛽10+ 𝜋0𝜋1𝛼1𝛽1𝜃1 + √4𝛽1𝛽10(−𝛼0𝛼1+ 𝑞𝛽1𝜃1) + (−𝛼1𝛽1− 𝛼0𝛽10+ 𝜋0𝜋1𝛼1𝛽1𝜃1)2) 𝑁₃∗ ₌𝛼1+ 𝐴3∗𝛽10 𝛽1𝜃1 𝑆₃∗ ₌ 𝐴3∗𝜋1𝛼1 𝛿 𝐶3∗= 𝑞_𝑐 − 𝑆₃∗𝛿₁+ 𝐴₃∗_𝜆 11 𝛼4 .

Syarat agar titik tetap 𝐸₃ ada yaitu

−𝛼₀𝛼₁+ 𝑞𝛽₁𝜃₁> 0 dan

𝑞_𝑐 − 𝑆₃∗𝛿₁+ 𝑎₃∗_𝜆

11 > 0.

Titik tetap 𝑬𝟒(𝑵𝟒∗, 𝑨𝟒∗, 𝟎, 𝒁𝟒∗, 𝑺𝟒∗, 𝑪𝟒∗)

Pada titik tetap ini, makrofita belum ada pada badan air, maka badan air yang tercemar berpengaruh pada populasi alga dan zooplankton sehingga nilai 𝑚 = 0. Nilai-nilai dari titik tetap E4 diperoleh dengan menyelesaikan persamaan di bawah ini 𝑞 + 𝜋₀𝛿𝑆 − 𝛼₀𝑁 − 𝛽₁𝑁𝐴 = 0 𝜃₁𝛽₁𝑁 − 𝛼₁− 𝛽₁₀𝐴 − 𝛽₃𝑍 = 0 𝜃₃𝛽₃𝐴 − 𝛼₃− 𝛽₃₀𝑍 = 0 𝜋₁𝛼₁𝐴 + 𝜋₃𝛼₃𝑍 − 𝛿𝑆 = 0 𝑞𝑐 − 𝛼4𝐶 + 𝜆11𝐴 − 𝛿1𝑆 = 0.

Sehingga diperoleh titik tetap E4 yaitu

13 dengan 𝐴4∗ = 1 2(−𝛽1𝛽10𝛽30− 𝛽1𝛽32𝜃3) (−𝛼3𝛽1𝛽3+ 𝛼1𝛽1𝛽30+ 𝛼0𝛽10𝛽30 − 𝜋0𝜋1𝛼1𝛽1𝛽30𝜃1+ 𝛼0𝛽32𝜃3− 𝜋0𝜋3𝛼3𝛽1𝛽3𝜃1𝜃3 − √(−4(𝛼0𝛼3𝛽3− 𝛼0𝛼1𝛽30− 𝜋0𝜋3𝛼32𝛽1𝜃1 + 𝑞𝛽₁𝛽₃₀𝜃₁)(−𝛽₁𝛽₁₀𝛽₃₀− 𝛽₁𝛽₃2𝜃₃) + (𝛼₃𝛽₁𝛽₃− 𝛼₁𝛽₁𝛽₃₀− 𝛼₀𝛽₁₀𝛽₃₀+ 𝜋₀𝜋₁𝛼₁𝛽₁𝛽₃₀𝜃₁ − 𝛼₀𝛽₃2𝜃₃ + 𝜋₀𝜋₃𝛼₃𝛽₁𝛽₃𝜃₁𝜃₃)2₎₎ 𝑁₄∗ ₌ −𝛼3𝛽3+ 𝛼1𝛽30+ 𝐴4∗𝛽10𝛽30+ 𝐴4∗𝛽32𝜃3 𝛽₁𝛽₃₀𝜃₁ 𝑍₄∗₌ −𝛼3+ 𝐴4∗𝛽3𝜃3 𝛽₃₀ 𝑆₄∗ ₌𝐴4∗𝜋1𝛼1𝛽30+ 𝜋3𝛼3(−𝛼3+ 𝐴∗4𝛽3𝜃3) 𝛽₃₀𝛿 𝐶₄∗ =𝑞𝑐− 𝑆4 ∗_𝛿 1+ 𝐴4∗𝜆11 𝛼₄ .

Syarat agar titik tetap 𝐸4 ada yaitu

𝛼0𝛼3𝛽3 − 𝛼0𝛼1𝛽30− 𝜋0𝜋3𝛼32𝛽1𝜃1+ 𝑞𝛽1𝛽30𝜃1 > 0 dan

−𝛼3+ 𝑎4∗𝛽3𝜃3 > 0 dan

𝑞𝑐 − 𝑆4∗𝛿1+ 𝑎4∗𝜆11 > 0.

Titik tetap 𝑬_𝟓(𝑵_𝟓∗, 𝑨_𝟓∗, 𝑴_𝟓∗, 𝟎, 𝑺_𝟓∗, 𝑪_𝟓∗)

Pada titik tetap ini, zooplankton belum ada pada badan air, maka badan air yang tercemar berpengaruh pada populasi alga dan makrofita sehingga nilai Z=0. Nilai-nilai dari titik tetap E5 diperoleh dengan menyelesaikan persamaan di bawah ini 𝑞 + 𝜋₀𝛿𝑆 − 𝛼₀𝑁 − 𝛽₁𝑁𝐴 − 𝛽₂𝑁𝑀 = 0 𝜃₁𝛽₁𝑁 − 𝛼₁− 𝛽₁₀𝐴 = 0 𝜃₂𝛽₂𝑁 − 𝛼₂− 𝛽₂₀𝑀 = 0 𝜋1𝛼1𝐴 + 𝜋2𝛼2𝑀 − 𝛿𝑆 = 0 𝑞𝑐 − 𝛼4𝐶 + 𝜆11𝐴 − 𝛿1𝑆 + 𝜆22𝑀 = 0.

Sehingga diperoleh titik tetap E5 yaitu

(𝑁5∗, 𝐴5∗, 𝑀5∗, 0 , 𝑆5∗, 𝐶5∗), dengan 𝑁₅∗ ₌ 1 2(−𝛽₁2𝛽₂₀𝜃₁− 𝛽₁₀𝛽₂2𝜃₂)(−𝛼2𝛽10𝛽2− 𝛼1𝛽1𝛽20+ 𝛼0𝛽10𝛽20 − 𝜋₀𝜋₁𝛼₁𝛽₁𝛽₂₀𝜃₁− 𝜋₀𝜋₂𝛼₂𝛽₁₀𝛽₂𝜃₂ −√(𝛼2𝛽10𝛽2+ −𝛼1𝛽1𝛽20− 𝛼0𝛽10𝛽20+ 𝜋0𝜋1𝛼1𝛽1𝛽20𝜃1+ 𝜋0𝜋2𝛼2𝛽10𝛽2𝜃2)2− 4(−𝜋0𝜋2𝛼22𝛽10− 𝜋0𝜋1𝛼12𝛽20+ 𝑞𝛽10𝛽20)(−𝛽12𝛽20𝜃1− 𝛽10𝛽22𝜃2) ) 𝐴₅∗ ₌−𝛼1+ 𝑁5∗𝛽1𝜃1 𝛽10 𝑀₅∗ ₌−𝛼2+ 𝑁5∗𝛽2𝜃2 𝛽₂₀

14 𝑆5∗ = 𝜋1𝛼1𝐴5∗ + 𝜋2𝛼2𝑀5∗ 𝛿 𝐶₅∗ = 𝑞𝑐 − 𝑆5 ∗_𝛿 1+ 𝐴5∗𝜆11+ 𝜆22𝑀5∗ 𝛼₄ .

Syarat agar titik tetap 𝐸5 ada yaitu

−𝜋₀𝜋₂𝛼₂2_𝛽 10− 𝜋0𝜋1𝛼12𝛽20+ 𝑞𝛽10𝛽20 > 0 dan −𝛼₁+ 𝑁₅∗_𝛽 1𝜃1 > 0 dan −𝛼₂+ 𝑁₅∗_𝛽 2𝜃2 > 0 dan 𝑞_𝑐− 𝑆₅∗𝛿₁+ 𝐴₅∗𝜆₁₁+ 𝜆₂₂𝑀₅∗_{> 0.} Titik tetap 𝑬_𝟔(𝑵_𝟔∗, 𝑨_𝟔∗, 𝑴∗_𝟔, 𝒁_𝟔∗, 𝑺_𝟔∗, 𝑪_𝟔∗)

Pada titik tetap ini, alga, makrofita dan zooplankton ketiganya menggunakan oksigen terlarut dalam badan air untuk bertahan hidup, sehingga badan air telah tercemar yang mengakibatkan kandungan oksigen terlarut akan rendah. Nilai-nilai dari titik tetap pada kondisi ini diperoleh dengan cara menyelesaikan persamaan dibawah ini: 𝑞 + 𝜋₀𝛿𝑆 − 𝛼₀𝑛 − 𝛽₁𝐴𝑁 − 𝛽₂𝑁𝑀 = 0 𝜃1𝛽1𝑁 − 𝛼1− 𝛽10𝐴 − 𝛽3𝑍 = 0 𝜃2𝛽2𝑁 − 𝛼2− 𝛽20𝑀 = 0 𝜃3𝛽3𝐴 − 𝛼3− 𝛽30𝑍 = 0 𝜋1𝛼1𝐴 + 𝜋2𝛼2𝑀 + 𝜋3𝛼3𝑍 − 𝛿𝑆 = 0 𝑞_𝑐 − 𝛼₄𝐶 + 𝜆₁₁𝐴 + 𝜆₂₂𝑀 − 𝛿₁𝑆 = 0.

Sehingga diperoleh titik tetap E6 yaitu

(𝑁₆∗_{, 𝐴} 6 ∗_{, 𝑀} 6∗, 𝑍6∗ , 𝑆6∗, 𝐶6∗), dengan 𝐴6∗ 𝑍6∗ = −𝛼3 + 𝐴6∗𝜃3𝛽3 𝛽30 𝑁6∗ = 𝛼₁+ 𝐴₆∗_𝛽 10+ 𝑍6∗𝛽3 𝜃₁𝛽₁ 𝑀6∗ = −𝛼₂+ 𝑁₆∗𝜃₂𝛽₂ 𝛽20 𝑆₆∗ = 𝑎6 ∗_𝜋 1𝛼1+ 𝑀6∗𝜋2𝛼2+ 𝜋3𝑍6∗𝛼3 𝛿 𝐶₆∗ = 𝑞𝑐 − 𝑆6 ∗_𝛿 1+ 𝐴∗6𝜆11+ 𝜆22𝑀62∗ 𝛼₄ ,

dimana 𝐴₆∗ dapat dilihat pada Lampiran 1. Syarat agar titik tetap 𝐸₆ ada yaitu:

−𝛼2𝛼3𝛽1𝛽2𝛽3𝛽30𝜃1+ 𝛼0𝛼3𝛽1𝛽20𝛽3𝛽30𝜃1+ 𝛼1𝛼2𝛽1𝛽2𝛽302𝜃1 − 𝛼0𝛼1𝛽1𝛽20𝛽302𝜃1− 𝜋0𝜋3𝛼32𝛽12𝛽20𝛽30𝜃12 +𝑞𝛽₁2𝛽₂₀𝛽₃₀2𝜃₁2− 𝛼32_𝛽 22𝛽32𝜃2+ 2𝛼1𝛼3𝛽22𝛽3𝛽30𝜃2− 𝛼12𝛽22𝛽302𝜃2 −𝜋0𝜋2𝛼2𝛼3𝛽1𝛽2𝛽3𝛽30𝜃1𝜃2+ 𝜋0𝜋2𝛼1𝛼2𝛽1𝛽2𝛽302𝜃1𝜃2 > 0 dan −𝛼3+ 𝐴6∗𝜃3𝛽3>0 dan −𝛼2+ 𝑁6∗𝜃2𝛽2 > 0 dan 𝑞_𝑐 − 𝑆₆∗𝛿₁+ 𝐴₆∗_𝜆 11+ 𝜆22𝑀6∗ > 0.

15 Analisis Kestabilan Titik Tetap

Pada bagian ini, akan dilakukan analisis untuk melihat sifat kestabilan pada masing-masing titik tetap. Untuk melihat sifat kestabilan di sekitar titik tetap, maka akan dilakukan pelinearan pada sistem (3.1) yang merupakan sistem persamaan diferensial taklinear. Jenis kestabilan tersebut ditentukan berdasarkan nilai eigen dari matriks Jacobian dari sistem yang sudah berbentuk linear.

Misalkan sistem persamaan (3.1) dituliskan sebagai berikut

𝛾(𝑁, 𝐴, 𝑀, 𝑍, 𝑆, 𝐶) = 𝑞 + 𝜋₀𝛿𝑆 − 𝛼₀𝑁 − 𝛽₁𝐴𝑁 − 𝛽₂𝑁𝑀 𝜁(𝑁, 𝐴, 𝑀, 𝑍, 𝑆, 𝐶) = 𝜃1𝛽1𝑁𝐴 − 𝛼1𝐴 − 𝛽10𝐴2− 𝛽3𝐴𝑍 𝜂(𝑁, 𝐴, 𝑀, 𝑍, 𝑆, 𝐶) = 𝜃2𝛽2𝑁𝑀 − 𝛼2𝑀 − 𝛽20𝑀2 𝜉(𝑁, 𝐴, 𝑀, 𝑍, 𝑆, 𝐶) = 𝜃₃𝛽₃𝐴𝑍 − 𝛼₃𝑍 − 𝛽₃₀𝑍2 𝜙(𝑁, 𝐴, 𝑀, 𝑍, 𝑆, 𝐶) = 𝜋1𝛼1𝐴 + 𝜋2𝛼2𝑀 + 𝜋3𝛼3𝑍 − 𝛿𝑆 𝜔(𝑁, 𝐴, 𝑀, 𝑍, 𝑆, 𝐶) = 𝑞𝑐− 𝛼4𝐶 + 𝜆11𝐴 + 𝜆22𝑀 − 𝛿1𝑆. (3.3)

Pelineran pada sistem (3.3) memperoleh matriks Jacobi sebagai berikut

𝑱 = ( 𝜕𝛾 𝜕𝑁 𝜕𝛾 𝜕𝐴 𝜕𝛾 𝜕𝑀 𝜕𝜁 𝜕𝑁 𝜕𝜁 𝜕𝐴 𝜕𝜁 𝜕𝑀 𝜕𝜂 𝜕𝑁 𝜕𝜂 𝜕𝐴 𝜕𝜂 𝜕𝑀 𝜕𝜉 𝜕𝑁 𝜕𝜉 𝜕𝐴 𝜕𝜉 𝜕𝑀 𝜕𝜙 𝜕𝑁 𝜕𝜙 𝜕𝐴 𝜕𝜙 𝜕𝑀 𝜕𝜔 𝜕𝑁 𝜕𝜔 𝜕𝐴 𝜕𝜔 𝜕𝑀 𝜕𝛾 𝜕𝑍 𝜕𝛾 𝜕𝑆 𝜕𝛾 𝜕𝐶 𝜕𝜁 𝜕𝑍 𝜕𝜁 𝜕𝑆 𝜕𝜁 𝜕𝐶 𝜕𝜂 𝜕𝑍 𝜕𝜂 𝜕𝑆 𝜕𝜂 𝜕𝐶 𝜕𝜉 𝜕𝑍 𝜕𝜉 𝜕𝑆 𝜕𝜉 𝜕𝐶 𝜕𝜙 𝜕𝑍 𝜕𝜙 𝜕𝑆 𝜕𝜙 𝜕𝐶 𝜕𝜔 𝜕𝑍 𝜕𝜔 𝜕𝑆 𝜕𝜔 𝜕𝐶) 𝑱 = ( 𝑙₁₁ −𝛽₁𝑁 −𝛽₂𝑁 𝜃₁𝛽₁𝐴 𝑙₂₂ 0 𝜃₂𝛽₂𝑀 0 𝑙₃₃ 0 𝜃₃𝛽₃𝑍 0 0 𝛼₁𝜋₁ 𝛼₂𝜋₂ 0 𝜆₁₁ 𝜆₂₂ 0 𝜋0𝛿 0 −𝛽3𝐴 0 0 0 0 0 𝑙44 0 0 𝛼3𝜋3 −𝛿 0 0 −𝛿1 −𝛼4) , (3.4) di mana 𝑙11= −𝛼0− 𝛽1𝐴−𝛽2𝑀, 𝑙22 = −𝛼1− 2𝛽10𝐴−𝛽3𝑍 + 𝜃1𝛽1𝑁, 𝑙₃₃= −𝛼₂− 2𝛽₂₀𝑀+𝜃₂𝛽₂𝑁, 𝑙₄₄= −𝛼₃− 2𝛽₃₀𝑍 + 𝜃₃𝛽₃𝐴.

Perilaku kestabilan dari sistem (3.1) akan dianalisis dengan mensubstitusikan nilai dari titik tetap 𝐸1, 𝐸2, 𝐸3, 𝐸4, 𝐸5 dan 𝐸6 ke dalam matriks Jacobi (3.4).

Menurut Tu (1994), sistem akan stabil jika nilai eigen dari matriks Jacobi ( 𝑱(𝐸𝑖))

semuanya bernilai riil negatif dan bersifat tidak stabil jika minimal ada satu nilai eigen dari matriks 𝑱_(𝐸𝑖) yang positif.

16

Kestabilan Titik Tetap 𝑬_𝟏

Pelinearan sistem (3.1) pada titik tetap 𝐸₁(𝑞 𝛼⁄ , 0, 0, 0, 0, 𝑞₀ 𝑐⁄ )_𝛼4 dapat dilakukan dengan mensubstitusikan nilai-nilai 𝐸₁ ke dalam matriks (3.4) sehingga diperoleh matriks Jacobi sebagai berikut

𝑱_(𝐸1) = ( 𝑙₁₁ 𝑙₁₂ 𝑙₁₃ 0 𝑙₂₂ 0 0 0 𝑙₃₃ 0 0 0 0 𝑙52 𝑙53 0 𝑙62 𝑙63 0 𝑙₁₅ 0 0 0 0 0 0 0 𝑙₄₄ 0 0 𝑙54 𝑙55 0 0 𝑙65 𝑙66) ,

di mana 𝑙11, 𝑙12, 𝑙13, … , 𝑙66 dapat dilihat pada Lampiran 2.

Kestabilan dari 𝐸₁ selanjutnya akan dianalisis berdasarkan nilai eigen dari matriks Jacobian tersebut. Berdasarkan matriks |𝑱_(𝐸1)− 𝝍𝑰| diperoleh enam nilai

eigen berikut 𝜓₁ = −𝛼₀ 𝜓2 = −𝛼₀𝛼₁+ 𝑞𝛽₁𝜃₁ 𝛼₀ 𝜓3 = −𝛼0𝛼2+ 𝑞𝛽2𝜃2 𝛼0 𝜓4 = −𝛼3 𝜓5 = −𝛿 𝜓₆ = −𝛼₄.

Hasil tersebut menunjukkan bahwa 𝜓1, 𝜓2, 𝜓3, dan 𝜓4 bernilai negatif

sedangkan 𝜓2bernilai negatif jika 𝑞𝛽1𝜃1 < 𝛼0𝛼1 dan 𝜓3bernilai negatif jika

𝑞𝛽2𝜃2 < 𝛼0𝛼2. Dengan demikian dapat disimpulkan bahwa titik tetap 𝐸1 stabil jika

syarat untuk nilai eigen 𝜓2 dan 𝜓3 dipenuhi. Sebaliknya, jika syarat tersebut tidak

terpenuhi, maka tetap 𝐸₁ tidak stabil. Kestabilan Titik Tetap 𝑬_𝟐

Pelinearan sistem (3.1) pada titik tetap 𝐸₂(𝑁₂∗, 0, 𝑀₂∗, 0, 𝑆₂∗, 𝐶₂∗) dapat dilakukan dengan mensubstitusikan nilai-nilai 𝐸₂ ke dalam matriks (3.4) sehingga diperoleh matriks Jacobi sebagai berikut

𝑱_(𝐸2) = ( 𝑙₁₁ 𝑙₁₂ 𝑙₁₃ 0 𝑙22 0 𝑙31 0 𝑙33 0 0 0 0 𝑙₅₂ 𝑙₅₃ 0 𝑙₆₂ 𝑙₆₃ 0 𝑙₁₅ 0 0 0 0 0 0 0 𝑙₄₄ 0 0 𝑙₅₄ 𝑙₅₅ 0 0 𝑙₆₅ 𝑙₆₆) ,

di mana 𝑙₁₁, 𝑙₁₂, 𝑙₁₃, … , 𝑙₆₆ dapat dilihat pada Lampiran 2.

Kestabilan dari 𝐸₂ selanjutnya akan dianalisis berdasarkan nilai eigen dari matriks

Jacobian tersebut. Berdasarkan matriks |𝑱_(𝐸2)− 𝝍𝑰| diperoleh enam nilai eigen

berikut 𝜓₁ = −𝛼₃ 𝜓₂ = −𝛼₄ 𝜓₃ = −𝛼₁+ 𝑁₂∗_𝛽 1𝜃1 𝜓₄ = 𝑝₂

17

𝜓5 = 𝑞2

𝜓6 = 𝑟2,

nilai 𝑝₂, 𝑞₂, 𝑟₂ dapat dilihat pada Lampiran 3.

Hasil tersebut menunjukkan bahwa 𝜓₁ dan 𝜓₂ bernilai negatif. Dengan demikian dapat disimpulkan bahwa titik tetap 𝐸2akan stabil jika 𝜓3,𝜓4,𝜓5,𝜓6

bernilai negatif sedangkan jika terdapat salah satu yang positif di antara empat nilai eigen tersebut, maka titik tetap 𝐸2 menjadi tidak stabil.

Kestabilan Titik Tetap 𝑬_𝟑

Pelinearan sistem (3.1) pada titik tetap 𝐸3(𝑁3∗, 𝐴∗3, 0, 0, 𝑆3∗, 𝐶3∗) dapat

dilakukan dengan mensubstitusikan nilai-nilai 𝐸3 ke dalam matriks (3.4) sehingga

diperoleh matriks Jacobi sebagai berikut

𝑱_(𝐸3) = ( 𝑙₁₁ 𝑙₁₂ 𝑙₁₃ 𝑙₂₁ 𝑙₂₂ 0 0 0 𝑙₃₃ 0 0 0 0 𝑙₅₂ 𝑙₅₃ 0 𝑙62 𝑙63 0 𝑙15 0 𝑙₂₄ 0 0 0 0 0 𝑙44 0 0 𝑙54 𝑙55 0 0 𝑙65 𝑙66) ,

di mana 𝑙₁₁, 𝑙₁₂, 𝑙₁₃, … , 𝑙₆₆ dapat dilihat pada Lampiran 2. Kestabilan dari 𝐸₃ selanjutnya akan dianalisis berdasarkan nilai eigen dari matriks Jacobian tersebut. Berdasarkan matriks |𝑱_(𝐸3)− 𝝍𝑰| diperoleh enam nilai eigen berikut

𝜓1 = −𝛼4 𝜓2 = −𝛼2+ 𝑁3∗𝛽1𝜃1 𝜓3 = −𝛼3+ 𝐴3∗𝛽3𝜃3 𝜓₄ = 𝑝₃ 𝜓₅ = 𝑞₃ 𝜓₆ = 𝑟₃,

nilai 𝑝₃, 𝑞₃, 𝑟₃ dapat dilihat pada Lampiran 3.

Hasil tersebut menunjukkan bahwa 𝜓₁ bernilai negatif. Dengan demikian dapat disimpulkan bahwa titik tetap 𝐸₃ akan stabil jika 𝜓₂, 𝜓₃, 𝜓₄, 𝜓₅, 𝜓₆ bernilai negatif sedangkan jika terdapat salah satu yang positif di antara lima nilai eigen tersebut, maka titik tetap 𝐸₃ menjadi tidak stabil.

Kestabilan Titik Tetap 𝑬_𝟒

Pelinearan sistem (3.1) pada titik tetap 𝐸₄(𝑁₄∗, 𝐴₄∗, 0, 𝑍₄∗, 𝑆₄∗, 𝐶₄∗) dapat dilakukan dengan mensubstitusikan nilai-nilai 𝐸₄ ke dalam matriks (3.4) sehingga diperoleh matriks Jacobi sebagai berikut

𝑱_(𝐸4) = ( 𝑙₁₁ 𝑙₁₂ 𝑙₁₃ 𝑙₂₁ 𝑙₂₂ 0 0 0 𝑙₃₃ 0 𝑙₄₂ 0 0 𝑙₅₂ 𝑙₅₃ 0 𝑙₆₂ 𝑙₆₃ 0 𝑙15 0 𝑙24 0 0 0 0 0 𝑙44 0 0 𝑙54 𝑙55 0 0 𝑙65 𝑙66) ,

di mana 𝑙₁₁, 𝑙₁₂, 𝑙₁₃, … , 𝑙₆₆ dapat dilihat pada Lampiran 2. Kestabilan dari 𝐸₄ selanjutnya akan dianalisis berdasarkan nilai eigen dari matriks Jacobian tersebut. Berdasarkan matriks |𝑱_(𝐸4)− 𝝍𝑰| diperoleh enam nilai eigen berikut

18 𝜓2 = −𝛼2+ 𝑁4∗𝛽2𝜃2 𝜓3 = 𝑝4 𝜓4 = 𝑞4 𝜓5 = 𝑟4 𝜓₆ = 𝑠₄,

nilai 𝑝4, 𝑞4, 𝑟4, 𝑠4 dapat dilihat pada Lampiran 3.

Hasil tersebut menunjukkan bahwa 𝜓1 bernilai negatif. Dengan demikian

dapat disimpulkan bahwa titik tetap 𝐸4 akan stabil jika 𝜓2, 𝜓3, 𝜓4, 𝜓5, 𝜓6 bernilai

negatif sedangkan jika terdapat salah satu yang positif di antara lima nilai eigen tersebut, maka titik tetap 𝐸4 menjadi tidak stabil.

Kestabilan Titik Tetap 𝑬_𝟓

Pelinearan sistem (3.1) pada titik tetap 𝐸5(𝑁5∗, 𝐴5∗, 𝑀5∗, 0 , 𝑆5∗, 𝐶5∗) dapat

dilakukan dengan mensubstitusikan nilai-nilai 𝐸5 ke dalam matriks (3.4) sehingga

diperoleh matriks Jacobi sebagai berikut

𝑱_(𝐸5) = ( 𝑙11 𝑙12 𝑙13 𝑙₂₁ 𝑙₂₂ 0 𝑙₃₁ 0 𝑙₃₃ 0 0 0 0 𝑙52 𝑙53 0 𝑙62 𝑙63 0 𝑙₁₅ 0 𝑙₂₄ 0 0 0 0 0 𝑙44 0 0 𝑙54 𝑙55 0 0 𝑙₆₅ 𝑙₆₆) ,

di mana 𝑙₁₁, 𝑙₁₂, 𝑙₁₃, … , 𝑙₆₆ dapat dilihat pada Lampiran 2. Kestabilan dari 𝐸₅ selanjutnya akan dianalisis berdasarkan nilai eigen dari matriks Jacobian tersebut. Berdasarkan matriks |𝑱_(𝐸4) − 𝝍𝑰| diperoleh enam nilai eigen berikut :

𝜓1 = −𝛼4 𝜓2 = −𝛼3+ 𝐴∗5𝛽3𝜃3 𝜓₃ = 𝑝₅ 𝜓₄ = 𝑞₅ 𝜓₅ = 𝑟₅ 𝜓6 = 𝑠5,

nilai 𝑝₅, 𝑞₅, 𝑟₅, 𝑠₅ dapat dilihat pada Lampiran 3.

Hasil tersebut menunjukkan bahwa 𝜓₁bernilai negatif. Dengan demikian dapat disimpulkan bahwa titik tetap 𝐸₅ akan stabil jika 𝜓₂, 𝜓₃, 𝜓₄, 𝜓₅, 𝜓₆ bernilai negatif sedangkan jika terdapat salah satu yang positif di antara lima nilai eigen tersebut, maka titik tetap 𝐸₅ menjadi tidak stabil.

Kestabilan Titik Tetap 𝑬_𝟔

Pelinearan sistem (3.1) pada titik tetap 𝐸₆(𝑁₆∗, 𝐴₆∗, 𝑀₆∗, 𝑍₆∗, 𝑆₆∗, 𝐶₆∗) dapat dilakukan dengan mensubstitusikan nilai-nilai 𝐸₆ ke dalam matriks (3.4) sehingga diperoleh matriks Jacobi sebagai berikut

𝑱(𝐸6) = ( 𝑙11 𝑙12 𝑙13 𝑙11 𝑙22 0 𝑙11 0 𝑙33 0 𝑙11 0 0 𝑙52 𝑙53 0 𝑙62 𝑙63 0 𝑙₁₅ 0 𝑙₁₁ 0 0 0 0 0 𝑙₄₄ 0 0 𝑙₅₄ 𝑙₅₅ 0 0 𝑙₆₅ 𝑙₆₆) ,

19 di mana 𝑙₁₁, 𝑙₁₂, 𝑙₁₃, … , 𝑙₆₆ dapat dilihat pada Lampiran 2. Kestabilan dari 𝐸₆ selanjutnya akan dianalisis berdasarkan nilai eigen dari matriks Jacobian tersebut. Berdasarkan matriks |𝑱_(𝐸4)− 𝝍𝑰| diperoleh enam nilai eigen berikut :

𝜓₁ = −𝛼₄ 𝜓₂ = 𝑝₆ 𝜓3 = 𝑞6 𝜓4 = 𝑟6 𝜓5 = 𝑠6 𝜓6 = 𝑡6,

nilai 𝑝₆, 𝑞₆, 𝑟₆, 𝑠₆, 𝑡₆ dapat dilihat pada Lampiran 3.

Hasil tersebut menunjukkan bahwa 𝜓₁bernilai negatif. Dengan demikian dapat disimpulkan bahwa titik tetap 𝐸6 akan stabil jika 𝜓2, 𝜓3, 𝜓4, 𝜓5, 𝜓6 bernilai

negatif sedangkan jika terdapat salah satu yang positif di antara lima nilai eigen tersebut, maka titik tetap 𝐸₆ menjadi tidak stabil.

Berdasarkan hasil analisis tersebut, sifat kestabilan dari masing-masing titik tetap belum dapat dikatakan stabil atau tidak. Sifat kestabilan titik tetap dari model akan diperiksa dengan pemberian nilai parameter pada bagian selanjutnya.

Nilai Parameter

Nilai-nilai parameter yang akan digunakan, diambil dari Amemiyaa et al.

(2007) dan Misra (2007, 2010). Nilai-nilai parameter tersebut disajikan pada Tabel 1.

Tabel 1 Nilai Parameter Model

Parameter Nilai Satuan

𝑞 0.5 mg l-1 _hari-1 𝑞𝑐 0.3 mg l-1 hari-1 𝛼0 0.005 hari-1 𝛼1 0.025 hari-1 𝛼2 0.02 hari-1 𝛼₃ 0.5 hari-1 𝛼₄ 0.01 hari-1 𝛽₁ 0.4 lmg-1 _hari-1 𝛽₂ 0.6 lmg-1 _hari-1 𝛽₃ 1 lmg-1 _hari-1 𝛽₁₀ 0.002 lmg-1 _hari-1 𝛽20 0.004 lmg-1 hari-1 𝛽30 2 lmg-1 hari-1 𝜆11 0.02 hari-1 𝜆22 0.02 hari-1 𝛿 0.04 hari-1 𝛿₁ 0.06 hari-1 𝜋₀ 0.02 non dimensi 𝜋₁ 0.9 non dimensi 𝜋₂ 0.9 non dimensi 𝜋₃ 0.9 non dimensi 𝜃1 0.9 non dimensi 𝜃2 0.9 non dimensi 𝜃3 1 non dimensi

20

Kestabilan Model

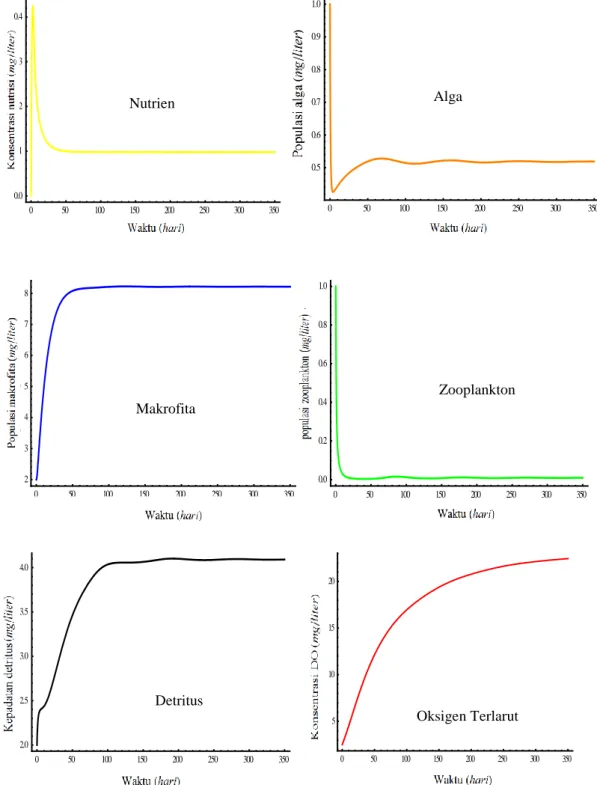
Model dalam sistem (3.1) memiliki enam titik tetap yang dapat ditunjukkan dengan solusi numerik menggunakan software Mathematica. Nilai dari masing-masing titik tetap dap at diperoleh dengan menggunakan nilai parameter pada Tabel 1 sehingga diperoleh 0 50 100 150 200 250 300 350 0.0 0.1 0.2 0.3 0.4 Waktu K o n s e n tr a s i n u tr is i 0 50 100 150 200 250 300 350 0.5 0.6 0.7 0.8 0.9 1.0 Waktu K ep ad at an P o p u la si al g a 0 50 100 150 200 250 300 350 2 3 4 5 6 7 8 Waktu K e p a d a ta n P o p u la si m a k ro fi ta 0 50 100 150 200 250 300 350 0.0 0.2 0.4 0.6 0.8 1.0 Waktu K e p a d a ta n p o p u la s i z o o p la n k to n 0 50 100 150 200 250 300 350 2.0 2.5 3.0 3.5 4.0 Waktu K ep ad at an d et ri tu s 0 50 100 150 200 250 300 350 5 10 15 20 Waktu K o n s e n tr a s i DO Nutrien Alga Makrofita Zooplankton Detritus Oksigen Terlarut

21 𝐸₁ = (100, 0, 0, 0, 0, 30) 𝐸2=(0.0994, 0, 8.4234 , 0, 3.7905, 24.1036) 𝐸₃=(0.1253, 10.0539, 0, 0, 5.6553, 16.1759) 𝐸4=(1.0422, 1.1956, 0, 0.3478, 4.5855, 4.8784) 𝐸5=(0.0892, 3.5553, 7.0415, 0, 5.1685, 20.1825) 𝐸₆=(0.0979, 0.5184, 8.2149, 0.0092, 4.0918, 22.9156).

Linearisasi dan perhitungan terhadap sistem (3.1) memperoleh matriks jacobian dan nilai eigen untuk masing-masing titik kesetimbangan. Selanjutnya dapat disimpulkan bahwa satu dari enam titik tetap tersebut yaitu 𝐸6memiliki sifat

stabil karena semua nilai eigennya bernilai negatif sedangkan lima titik tetap lainnya tidak stabil karena terdapat satu atau dua nilai eigennya yang positif.

Jika digunakan beberapa nilai awal dalam mensimulasikan sistem (3.1) untuk jangka waktu yang cukup, maka akan ditemui bahwa s olusi mendekti titik tetap

𝐸6. Hal ini ditunjukkan pada Gambar 4. Berdasarkan Gambar 4 terlihat bahwa

konsentrasi nutrien konvergen ke nilai stabil yaitu 0.09789. Populasi alga konvergen ke nilai stabil 0.51841. Populasi makrofita konvergen ke nilai stabil

8.21491. Populasi zooplankton konvergen ke nilai stabil 0.00920. Kepadatan

detritus konvergen ke nilai stabil 4.0918. Konsentrasi oksigen terlarut konvergen ke nilai stabil 22.9156. Dengan demikian terlihat bahwa sistem (3.1) stabil pada titik tetap 𝐸₆ = (0.0979, 0.5184, 8.2149, 0.0092, 4.0918, 22.9156).

Simulasi Numerik Simulasi laju masuknya nutrisi ke badan air (𝒒)

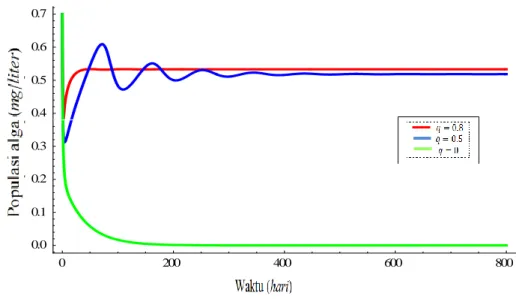
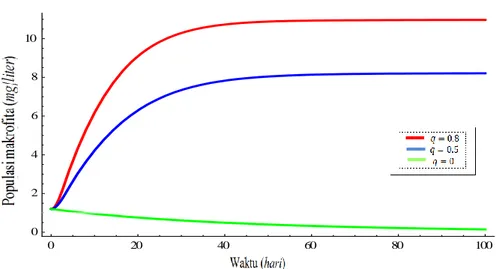
Simulasi ini dilakukan untuk menunjukkan pengaruh parameter 𝑞 terhadap populasi alga (𝐴), populasi makrofita (𝑀), populasi zooplankton (𝑍), kepadatan detritus (𝑆), dan konsentrasi oksigen terlarut (𝐶) dalam badan air yang mengalami eutrofikasi. Simulasi ini menggunakan nilai parameter yang ada pada Tabel 1 kecuali nilai 𝑞 yang dibuat bervariasi. Pengaruh parameter 𝑞 terhadap variabel-variabel tersebut dapat dilihat dalam Gambar 5, 6, 7, 8 dan 9.

0 200 400 600 800 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 Waktu K ep ad at an P op ul as i A lg a

22

Gambar 7 Populasi zooplankton terhadap t dengan nilai 𝑞 berbeda Gambar 6 Populasi makrofita terhadap t dengan nilai 𝑞 berbeda

0 20 40 60 80 100 0 2 4 6 8 10 Waktu K ep ad at an Po pu la si m ak ro fit a 0 200 400 600 800 0.00 0.05 0.10 0.15 0.20 Waktu ke pa da ta n pop ul as i zoo pl an kt on 0 50 100 150 200 250 300 350 0 1 2 3 4 5 Waktu K ep ad at an de tri tu s

23

Berdasarkan Gambar 5, 6, 7, 8 dan 9 terlihat bahwa jika laju masuknya nutrisi meningkat, maka populasi alga, makrofita, zooplankton dan kepadatan detritus juga meningkat, sedangkan konsentrasi oksigen terlarut menurun. Selain itu, dapat kita lihat juga bahwa jika laju masuknya nutrisi di badan air adalah nol, yaitu 𝑞 = 0, maka populasi alga, makrofita, zooplankton dan kepadatan detritus menuju nol setelah periode waktu yang singkat sedangkan konsentrasi oksigen terlarut naik menuju nilai maksimum. Hasil ini jelas karena sesuai dengan fakta bahwa nutrien yang terbentuk dari detritus tidak akan cukup untuk pertumbuhan populasi alga, makrofita dan zooplankton.

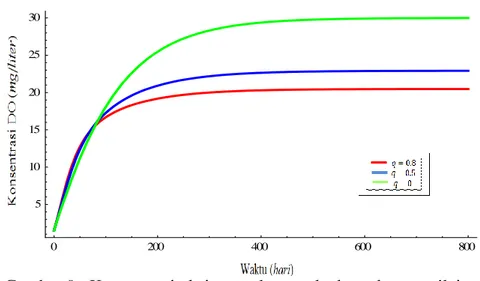
Simulasi laju pengubahan detritus menjadi nutrien (𝝅_𝟎)

Simulasi ini dilakukan untuk menunjukkan pengaruh parameter 𝜋₀ terhadap konsentrasi oksigen terlarut (𝐶) dalam badan air yang mengalami eutrofikasi. Simulasi ini masih men ggunakan nilai parameter yang ada pada Tabel 1 kecuali nilai 𝜋₀ yang dibuat bervariasi. Pengaruh parameter 𝜋₀terhadap konsentrasi oksigen terlarut (𝐶) tersebut ditunjukkan pada Gambar 10.

Gambar 9 Konsentrasi oksigen terlarut terhadap t dengan nilai 𝑞 berbeda 0 200 400 600 800 5 10 15 20 25 30 Waktu ko ns nt ra si DO 0 50 100 150 200 250 300 350 20 21 22 23 24 Waktu K on se nt ra si DO

Gambar 10 Konsentrasi oksigen terlarut terhadap t dengan nilai

24

Berdasarkan Gambar 10 terlihat bahwa jika laju pengubahan detritus menjadi nutrien meningkat, maka konsentrasi oksigen terlarut menurun. Pada awalnya konsentrasi oksigen terlarut tidak terlalu berbeda untuk setiap nilai 𝜋₀. Ketika 𝑡 >

300 penurunan konsentrasi oksigen terlarut sudah terlihat jelas di mana untuk 𝜋0 =

0.02, 0.5 dan 0.8 konsentrasi oksigen terlarut masing-masing mendekati nilai

23.151, 22.329 dan 21.872.Hal ini sesuai fakta bahwa dengan banyaknya detritus

yang tebentuk di dalam badan air, maka akan semakin banyak pula oksigen terlarut yang terpakai dalam proses biokimia untuk mengubah detritus menjadi nutrien, sehingga hal ini menyebabkan turunnya konsentrasi oksigen terlarut ketika laju pengubahan detritus meningkat. Oleh karena itu, kita dapat menyatakan bahwa suatu mekanisme kontrol yang tepat harus diterapkan untuk mengurangi laju pengubahan detritus menjadi nutrien agar oksigen terlarut dalam badan air tersedia dalam jumlah yang cukup sehingga terjadi keseimbangan dalam badan air.

4

SIMPULAN

Secara umum model yang dihasilkan dapat menunjukkan perilaku perubahan kandungan oksigen terlarut dalam badan air yang mengalami eutrofikasi. Perubahan nilai oksigen terlarut ini disebabkan oleh banyak faktor diantaranya nutrien, alga, makrofita, zooplankton dan detritus. Rincian hasil-hasil utama dalam tesis ini disimpulkan pada uraian berikut:

1 Hasil analisis model matematika dalam tesis ini memperoleh enam titik tetap, di mana satu diantaranya stabil dan lima tidak stabil.

2 Simulasi numerik menunjukkan bahwa jika laju masuknya nutrisi ke dalam badan air mengalami kenaikan, maka populasi alga, makrofita, zooplankton dan detritus juga meningkat, sedangkan konsentrasi oksigen terlarut menurun. 3 Laju pengubahan detritus menjadi nutrien juga mempunyai pengaruh terhadap

konsentrasi oksigen terlarut dimana jika laju pengubahan detritus menjadi nutrisi meningkat, maka konsentrasi oksigen terlarut di badan air menurun. 4 Simulasi juga menunjukkan bahwa, jika laju masuknya nutrisi di badan air

adalah nol, maka populasi alga, makrofita, zooplankton dan kepadatan detritus juga menuju nol setelah periode waktu yang singkat sedangkan konsentrasi oksigen terlarut naik menuju nilai maksimum.

Dengan adanya hasil tersebut, kita dapat mengatakan bahwa agar oksigen terlarut tersedia dalam jumlah yang cukup dalam badan air, maka beberapa mekanisme kontrol harus diterapkan. Misalnya dengan mengurangi beban masukan nutrisi ke dalam badan air dan melakukan proses aerasi.