TEOREMA TITIK TETAP BANACH
Skripsi
Diajukan untuk Memenuhi Salah satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Widaryatna Citra Nursanta NIM : 013114018
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SANATA DHARMA YOGYAKARTA
PERNYATAAN KEASLIAN KARYA
Saya menyatakan dengan sesungguhnya skripsi yang saya tulis ini tidak memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam daftar pustaka, sebagaimana layaknya karya ilmiah.
Yogyakarta, 1 Mei 2006 Penulis
INTISARI
Dalam skripsi ini dibahas mengenai titik tetap (fixed point). Banyak permasalahan matematika yang dapat diformulasikan dalam bentuk titik tetap. Teorema Titik Tetap Banach memberikan syarat cukup suatu fungsi dari ruang metrik lengkap ke dirinya sendiri mempunyai titik tetap yang tunggal.
ABSTRACT
This thesis discusses what is so called fixed point. Many mathematical problems can be formulated as fixed point problem. Banach Fixed Point Theorem gives a sufficient condition for a function from a complete metric space to it self to have a unique fixed point.
KATA PENGANTAR
Segala puji dan hormat kepada Tuhan Yesus atas segala berkat, pimpinan, kasih dan penyertaan-Nya sehingga penulis dapat menyelesaikan skripsi yang bejudul “TEOREMA TITIK TETAP BANACH”. Skripsi ini disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Matematika (S.Si) pada program studi Matematika di Fakutas MIPA Universitas Sanata Dharma, Yogyakarta.
Penyusunan skripsi ini tidak lepas dari bantuan berbagai pihak, baik berupa materi, moral, maupun spiritual. Penulis menyampaikan terima kasih yang sebesar-besarnya kepada :
1. Bapak Ir. Ign. Aris Dwiatmoko, M.Sc. selaku Dekan Fakultas MIPA Universitas Sanata Dharma.
2. Bapak Y.G. Hartono, S.Si, M.Sc. selaku Kaprodi Matematika Fakultas MIPA Universitas Sanata Dharma. Terima kasih karena mau merevisi skripsi saya hingga selesai.
3. Bapak Herry Pribawanto, S.Si. selaku dosen pembimbing. Terima kasih atas saran, ide, waktu serta kesabarannya dalam membimbing penulis.
4. Bapak Prof. Drs. Sumantri karena telah banyak membantu menyelesaikan masalah dalam penulisan.
6. Papa dan Mama kekasih, terima kasih buat kasih segala keperluan ku dalam menyelesaikan studi.
7. Dea’ku, makasih atas dukungan dan doanya buat Aya. Sorry kata pengantarnya aku copy. Tapi tenang aja, udah Aya ganti kok kata- katanya. Ayo.... Ujian...!!!!!
8. Papa dan Mama di Pendolo, terima kasih buat semua perhatiannya. Terima kasih udah mau jadi orang tua ku.
9. Teman-teman seperjuangan di math’01 (Dani.WA, Tabitha, Agnes, Andre, Ariel, Alam, Very, Ajenk, Erika, Indah, Maria, Deta, Fanya, Vrisca, Rita, Wiwit, Yuli, Upiek, Teddy, Dani). Juga buat teman-teman di PMK Ouikumene, thanks ya buat dukungan do’anya.
10. Papi Narno dan Mami Vera serta teman-teman di GKN Sonopakis, makasih buat do’a dan kebersamaannya ya.
11. Sahabat-sahabat’ku : Bimo, Ryo, en Sony. Ayo tanding maen PS lg. Hehehe.
Terima kasih juga penulis sampaikan kepada semua pihak yang tidak dapat penulis sebutkan satu-persatu.
DAFTAR ISI
Halaman
HALAMAN JUDUL... i
HALAMAN PENGESAHAN PEMBIMBING... ii
HALAMAN PENGESAHAN... iii
PERNYATAAN KEASLIAN KARYA... iv
ABSTRAK... v
ABSTRACT... vi
KATA PENGANTAR... vii
DAFTAR ISI... viii
ARTI LAMBANG... ix
BAB I PENDAHULUAN... 1
BAB II RUANG METRIK... 5
1. Ruang Metrik... 5
2. Himpunan Terbuka dan Fungsi Kontinu... 18
3. Kekonvergenan, Barisan Cauchy dan Kelengkapan... 28
4. Ruang Topologi... 42
BAB III TEOREMA TITIK TETAP BANACH... 45
1. Titik Tetap... 47
2. Teorema Titik Tetap Banach... 55
BAB IV PENERAPAN TEOREMA TITIK TETAP BANACH... 72
BAB V KESIMPULAN... 86
ARTI LAMBANG
q
p⇒ jika p maka q.
q
p⇔ p jika dan hanya jika q.
A
x∈ x anggota A.
B
A⊂ A himpunan bagian B.
0/ himpunan kosong.
[ ]
a,b interval tertutup.( )
a,b interval terbuka.f
go komposisi fungsi.
( )
x yd , jarak/metrik antara titik x dan y.
(
X,d)
ruang metrik.{ }
xn barisan dengan suku-suku xn.x
xn → barisan
{ }
xn konvergen ke x.Y X
f : → fungsi/pemetaan dari X ke Y.
( )
XC ruang fungsi kontinu terbatas bernilai
BAB I PENDAHULUAN 1.1 Latar Belakang
Salah satu bentuk penerapan matematika adalah untuk menyelesaikan suatu persamaan. Namun sebelum memecahkan masalah persamaan, perlu diketahui terlebih dahulu apakah persamaan tersebut mempunyai penyelesaian atau tidak.
Berikut ini akan diberikan fungsi f dengan variabel x, f kontinu pada interval tertutup
[ ]
a,b dan jika f(a) dan f(b) memiliki tanda yang berbeda, maka persamaan0 ) (x = f
mempunyai sedikitnya satu penyelesaian di dalam interval
[ ]
a,b .Untuk menyelesaikan persamaan di atas diperlukan Teorema Eksistensi atau teorema yang menjamin adanya suatu penyelesaian, sering dinyatakan dalam bentuk prinsip titik tetap (fixed point principles). Sebagai contoh, diperhatikan persamaan f(x)=0. Persamaan ini dapat ditulis dalam bentuk α f(x)+x=x dengan parameter positif α . Jika α f(x)+x dinyatakan sebagai F(x) diperoleh persamaan
x x
F( )= ...(*)
Titik x dalam persamaan (*) dikenal sebagai titik tetap. Oleh karena itu persamaan tersebut mempunyai sedikitnya satu penyelesaian di dalam interval
[ ]
a,b .(P) x2 =a ∈N
Sebagai contoh, jika a=4 maka x=2.
Setelah munculnya masalah, kemudian dirumuskan masalah titik tetap (fixed point problem/FPP) sebagai berikut :
0
2 − =
a x
(FPP) x2 +x−a=x
Masalah titik tetap di atas diselesaikan dengan successive substitution/SS yang menghasilkan approximate solution/AS.
(SS) Anggap x0 =1 (AS) xn+ =xn +xn −a
2
1 , untuk n=0,1,2,...
Kemudian dirumuskan FPP yang lebih abstrak, yaitu: x
x f( )=
Titik x dalam persamaan di atas dikenal sebagai titik tetap.
1.2. Perumusan Masalah
Dalam skripsi ini pokok permasalahan yang akan dibahas adalah: 1. Bagaimana motivasi munculnya konsep titik tetap?
2. Apa pengertian titik tetap?
3. Teorema Titik Tetap Banach dan pembuktiannya?
4. Bagaimana sifat lebih lanjut dan pengembangan Titik Tetap Banach?
1.3. Pembatasan Masalah
Skripsi ini dibatasi pada masalah pencarian syarat cukup fungsi dari ruang metrik lengkap ke dirinya sendiri mempunyai titik tetap. Penerapannya pun hanya dibatasi pada masalah penjaminan eksistensi dan ketunggalan persamaan diferensial linear orde satu.
1.4. Tujuan Penulisan
Penulisan skripsi ini bertujuan untuk memberi wawasan kepada pembaca tentang suatu sifat fungsi kontinu pada ruang metrik lengkap khususnya mengenai Teorema Titik Tetap Banach beserta penerapannya pada eksistensi dan ketunggalan penyelesaian persamaan diferensial linear orde satu.
1.5. Manfaat Penulisan
Manfaat dari penulisan skripsi ini yang sangat diharapkan adalah penulis dapat mengetahui dan memahami bagaimana sebenarnya sifat-sifat dan penerapan Teorema Titik Tetap Banach pada penyelesaian persamaan diferensial linear orde satu.
1.6. Metode Penulisan dan Sistematika Penulisan
BAB II RUANG METRIK
Pada bab ini akan dibahas mengenai ruang metrik, kekonvergenan, himpunan terbuka yang akan melandasi pembahasan bab-bab selanjutnya.
A. Ruang Metrik
Pada sub bab ini akan dibahas definisi dan contoh ruang metrik.
Definisi 2.1.1.
Diketahui himpunan X tidak kosong. Suatu metrik (metric) pada X adalah fungsi d dari X ×X ke R yang memenuhi aksioma-aksioma berikut:
a. d(p,q)≥0; untuk setiap p,q∈X. b. d(p,q)=0 jika dan hanya jika p = q. c. d(p,q)= d(q,p); untuk setiap p,q∈X
d. d(p,q)≤ d(p,r)+ d(r,q); untuk setiap p,q,r∈X (Pertidaksamaan segitiga)
Contoh 2.1.1
Diberikan X sebarang himpunan yang tidak kosong.
Didefinisikan fungsi d(x,y) =
⎩ ⎨ ⎧
= ≠
y x
y x , 0
, 1
, untuk setiap x,y∈X
Akan ditunjukkan (X,d) adalah ruang metrik. (i) d(x,y)≥0
(ii) d(x,y)=0 jika dan hanya jika x = y (iii) d(x,y) = d(y,x)
Untuk (i), (ii), dan (iii) jelas dari definisi fungsi d
( )
x,y di atas. (iv) Jika d(x,y)=0, jelas d(x,y) ≤ d(x,z) + d(z,y)Jika d(x,y)=1, kemungkinannya : a. x=z dan z≠y
d(x,y) ≤ d(x,z) + d(z,y) b. x≠z dan z=y
d(x,y) ≤ d(x,z) + d(z,y) c. x≠z dan z≠y
d(x,y) ≤ d(x,z) + d(z,y)
Untuk selanjutnya ruang metrik ini disebut ruang metrik diskrit.
Contoh 2.1.2
Diberikan X = R dan didefinisikan fungsi d : R×R→Rdengan definisi d(x,y)= x−y; untuk setiap x,y∈R.
(i) d(x,y) = x−y ≥0, jelas dari definisi. (ii) d(x,y) = x−y =0 jika dan hanya jika x=y. (iii) d(x,y) = x−y = −y+x
=−(y−x)
=−1 y−x
=1 y−x
= y−x
= d(y,x)
(iv) d(x,y) = x−y
=(x−z+z− y)
=(x−z)+(z−y)
≤ x−z + z−y
= d(x,z) + d(z,y)
Selanjutnya ruang metrik ini disebut ruang metrik biasa (usual metric space).
Contoh 2.1.3
Diberikan X = Rn dan didefinisikan fungsi d: Rn×Rn →R
dengan definisi
) , (x y
d = 2
1
1
2
)
( ⎟
⎠ ⎞ ⎜
⎝
⎛
∑
−= n
i
i i y
x , untuk setiap x =(x1,x2,...,xn),y =(y1,y2,...,yn)∈Rn.
(ii) d(x,y)= 0 jika dan hanya jika x = y 1. apabila )d(x,y = 0 maka
2 1
1
2
)
( ⎟
⎠ ⎞ ⎜
⎝
⎛ −
∑
= n
i
i i y
x = 0
2 2
2 2 2 1
1 ) ( ) ... ( )
(x −y + x −y + + xn −yn = 0
2 2
2 2 2 1
1 ) ( ) ... ( )
(x −y + x −y + + xn −yn = 0
2
)
(xi −yi = 0, untuk setiap i=1,..,n )
(xi −yi = 0, untuk setiap i=1,..,n
i
i y
x = , untuk setiap i=1,..,n.
Jadi terbukti jika d(x,y)= 0 maka x = y. 2. apabila x= y maka
berlaku xi = yi, untuk i = 1,2,3,...,n, sehingga diperoleh
) , (x y
d = 2
1
1
2
)
( ⎟
⎠ ⎞ ⎜
⎝
⎛
∑
−= n
i
i i y
x
= (x1 −y1)2 +(x2 −y2)2 +...+(xn −yn)2
= (x1 −x1)2 +(x2 −x2)2 +...+(xn −xn)2 = 0+0+...+0
=0
Jadi terbukti jika x= y maka d(x,y) = 0
) , (x y
d = 2
1 1 2 ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −
∑
= n i i i y x= (x1 −y1)2 +(x2 −y2)2 +...+(xn −yn)2
= 2 2
2 2 2 1
1 ) ( ) ... ( )
(y −x + y −x + + yn −xn
= 2 1 1 2 ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
− = n i i i x y=d(y,x).
(iv) d(x,y)≤ d(x,z)+ d(z,y)
Untuk membuktikan Pertidaksamaan segitiga untuk metrik ini dipergunakan pertidaksamaan Cauchy – Schwarz.
Pertidaksamaan Cauchy – Schwarz :
2 1 1 2 2 1 1 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ≤
∑
∑
∑
= = = n i i n i i n i iiy x y
x , untuk setiap x =(x1,x2,...,xn),
) ,..., ,
(y1 y2 yn
y= ∈Rn. Bukti:
Jika yi=0, untuk setiap 1 ≤ i ≤ n, maka secara trivial terbukti.
Anggap yi≠ 0, untuk suatu i, 1 ≤ i ≤ n, maka
∑
= > n 1 2 . 0 i i y
Jika t sebarang bilangan real, maka didapat
∑
= ≥ − n 1 2 0 ) ( i i i tyx atau 2 0
1 2 2 1
1
2 −
∑
+∑
≥∑
= = = n i i n i i i n ii t x y t y
x untuk semua t∈R
dan
∑
Oleh karena itu diskriminan persamaan kuadrat dalam t di atas adalah nonpositif, maka
D ≤ 0
0 4
2 − ≤
ac b 2 1 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛−
∑
= n i i iyx - 4
∑
= n 1 2 i i
y .
∑
= n 1 2 i i
x ≤ 0
4 2 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
= n i i iyx ≤ 4
∑
= n 1 2 i i
y .
∑
= n 1 2 i i x 2 n 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
= i i i yx ≤
∑
= n 1 2 i i
y .
∑
= n 1 2 i i
x atau
2 1 2 n 1 ) ( ⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
= i i i yx ≤ 2
1 n 1 2 n 1 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
∑
= = i i i i y x∑
= n 1 i i i yx ≤ 2
1 n 1 2 2 1 n 1 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
∑
= = i i i i y xJadi terbukti,
2 1
1 1 2 2
1 ⎥⎦
⎤ ⎢ ⎣ ⎡ ≤
∑ ∑
∑
= = = n i n i i i n i iiy x y
x = 2
1 n 1 2 2 1 n 1 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
∑
= = i i i i y x ,untuk setiap x =(x1,x2,...,xn),y =(y1,y2,...,yn)∈Rn. Sekarang akan dibuktikan pertidaksamaan segitiga,
) , (x y
d = 2
1 1 2 ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −
∑
= n i i i y x=
[
]
21 1 2 ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + −
∑
= n i i i ii z z y
=
[
]
2 1 1 2 ) ( ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + −∑
= n i i i ii z z y
x
=
[
]
21 1 2 2 ) ( ) )( ( 2 ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + − − + −
∑
= n i i i i i i i ii z x z z y z y
x
= 2
1
1 1 1
2 2 ) )( ( 2 ) ( ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − − + − + −
∑
∑
∑
= = = n i n i n i i i i i i i ii z z y x z z y
x
(Menggunakan Pertidaksamaan Cauchy – Schwarz)
≤ 2 1 1 1 2 1 2 1 2 1 2 1 2 2 ) ( ) ( 2 ) ( ) ( ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎝ ⎛ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − + − + −
∑
∑
∑
∑
= = = = n i n i n i i i n i i i i i ii z z y x z z y
x = 2 1 2 2 1 1 2 2 1 1 2 ) ( ) ( ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −
∑
∑
= = n i i i n i ii z z y
x
= 2
1 1 2 2 1 1 2 ) ( ) ( ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛
∑
−∑
= = n i i i n i ii z z y
x
= )d(x,z + d(z,y)
Terbukti )d(x,y ≤ d(x,z)+ d(z,y)
Untuk selanjutnya ruang metrik ini disebut ruang metrik Euclid.
Contoh 2.1.4
Diberikan X=R2 dan didefinisikan fungsi d: R2×R2 →Rdengan definisi )
, (x y
(i) d(x,y)≥0, jelas dari definisi. (ii) d(x,y)=0 jika dan hanya jika x = y
1. jika d(x,y)= 0 maka x = y
1 1 y
x − + x2 − y2 =0
i
i y
x − =0, untuk setiap i=1,2
i i y
x − = 0, untuk setiap i=1,2
i
i y
x = , untuk setiap i=1,2.
Jadi terbukti jika d(x,y)= 0 maka x = y 2. jika x = ymaka d(x,y)= 0
) , (x y
d = x1− y1 + x2 −y2 = x1−x1 + x2 −x2
=0 + 0
=0
Jadi terbukti jika x= y maka d(x,y) = 0
Dengan demikian d(x,y)= 0 jika dan hanya jika x = y. (iii) d(x,y) = d(y,x)
) , (x y
d = x1 −y1 + x2 −y2 = y1−x1 + y2 −x2
=d(y,x).
=(x1−z1)+(z1 −y1) + (x2 −z2)+(z2 − y2)
≤ x1−z1 + z1−y1 + x2 −z2 + z2 −y2
=( x1−z1 + x2 −z2 ) + ( z1− y1 + z2 −y2 )
=d(x,z)+ d(z,y)
Untuk selanjutnya ruang metrik ini disebut metrik segi empat pada R2.
Contoh 2.1.5
Diberikan X=R2 dan didefinisikan fungsi d: R2×R2 →R dengan definisi )
, (x y
d = maks { x1− y1 , x2 −y2 };untuk semuax=(x1,x2),y=(y1,y2)∈R 2
. Akan ditunjukkan (X,d) adalah ruang metrik.
(i) d(x,y)≥0, jelas dari definisi. (ii) d(x,y)=0 jika dan hanya jika x = y
1. jika d(x,y)= 0 maka x = y )
, (x y
d = maks { x1− y1 , x2 −y2 }= 0, berarti
1 1 y
x − =0 dan x2 −y2 =0
Jadi x1=y1 dan x2=y2, yang artinya x = y
2. jika x = ymaka d(x,y)= 0 )
, (x y
d = maks { x1 −y1 , x2 − y2 }
= maks { x1−x1 , x2 −x2 } = maks {0 , 0}
Jadi terbukti jika x= y maka d(x,y) = 0
Dengan demikian )d(x,y = 0 jika dan hanya jika x = y. (iii) d(x,y)= d(y,x)
) , (x y
d = maks { x1 −y1 , x2 − y2 }
= maks { y1−x1 , y2 −x2 }= d(y,x)
(iv) d(x,y)= maks { x1− y1 , x2 −y2 }
Misal d(x,y)= maks { x1− y1 , x2 −y2 } = x1 −y1
) , (x y
d = x1 −y1
= x1 −z1 +z1 −y1 ≤ x1−z1 + z1 −y1
≤ maks
{
x1 −z1, x2 −z2}
+ maks{
z1 −y1, z2 − y2}
=d(x,z)+ d(z,y)
Untuk kemungkinan d(x,y),d(x,z), dan d(z,y) yang lain dikerjakan dengan cara serupa.
Untuk selanjutnya ruang metrik ini disebut ruang metrik maksimum pada R2.
Contoh 2.1.6
Diketahui X= C
[ ]
a,b = {f :[ ]
a,b → R f kontinu}dan diketahui fungsi d :C[ ]
a,b ×C[ ]
a,b → R dengan definisi d(f1,f2) =[ ]ab x ,
sup
∈ { f1(x)− f2(x)},
karena d(f1,f2) =
[ ]ab x ,
sup
∈ { f1(x)− f2(x)} dan f1(x)− f2(x) ≥ 0, maka
[ ]ab x ,
sup
∈
{ f1(x)− f2(x)} ≥ 0
(ii) d(f1,f2) = 0 jika dan hanya jika f1 = f2 1. jika d(f1,f2) = 0 maka f1 = f2
d(f1,f2) = 0
[ ]ab x ,
sup
∈
{ f1(x)− f2(x)} = 0
) ( )
( 2
1 x f x
f − = 0
f1(x) = f2(x); untuk setiap x∈[a,b]. f1 = f2
2. jika f1 = f2 maka d(f1,f2) = 0,
karena f1 = f2 maka f1(x) = f2(x); untuk setiap x∈[a,b]. d(f1,f2) =
[ ]ab x ,
sup
∈
{ f1(x)− f2(x)}
=
[ ]ab x ,
sup
∈ { f1(x)− f1(x) }
=
[ ]ab x ,
sup
∈
{0 }
= 0 (iii) d(f1,f2) = d(f2,f1)
d(f1,f2) =
[ ]ab x ,
sup
∈ { f1(x)− f2(x)}
=
[ ]ab x ,
sup
∈ { f2(x)− f1(x)}
(iv) d(f1,f2) =
[ ]ab x ,
sup
∈ { f1(x)− f2(x)}
) ( )
( 2
1 x f x
f − = f1(x)− f3(x)+ f3(x)− f2(x) ≤ f1(x)− f3(x) + f3(x)− f2(x) ≤
[ ]ab x ,
sup
∈ { f1(x)− f3(x) } + x [ ]a,b
sup
∈ { f3(x)− f2(x) }
Jadi f1(x)− f2(x) ≤
[ ]ab x ,
sup
∈
{ f1(x)− f3(x) } +
[ ]ab x ,
sup
∈
{ f3(x)− f2(x)}
Hal ini berarti
{
f1(x)− f2(x)}
terbatas dengan[ ]ab x ,
sup
∈ { f1(x)− f3(x) }+x [ ]a,b
sup
∈ { f3(x)− f2(x)}sebagai batas atas.
Hal ini berakibat
[ ]ab x ,
sup
∈ { f1(x)− f2(x)}≤ x[ ]a,b
sup
∈ { f1(x)− f3(x) }+x[ ]a,b
sup
∈ { f3(x)− f2(x) }
atau d(f1,f2) ≤d(f1,f3) + d(f3,f2).
Contoh 2.1.7
Diketahui X= C
[ ]
0,1 = {f :[ ]
0,1 → R f kontinu} dan diketahui fungsi d:C[ ]
0,1 ×C[ ]
0,1 → R dengan definisid(f1,f2) =
∫
f x − f x dx1
0
2
1( ) ( ) ; untuk setiap f1, f2∈ C
[ ]
0,1 .Akan ditunjukkan (C
[ ]
0,1 ,d) ruang metrik.(i) d(f1,f2) =
∫
f x − f x dx1
0
2
1( ) ( ) ≥ 0, karena f1(x)− f2(x)≥ 0
1. jika d(f1,f2) = 0 maka f1 = f2
d(f1,f2) =
∫
f x − f x dx1
0
2
1( ) ( ) = 0
) ( )
( 2
1 x f x
f − = 0
f1(x) = f2(x); untuk setiap x∈[0,1]. f1 = f2
2 jika f1 = f2 maka d(f1,f2) = 0,
karena f1 = f2 maka f1(x) = f2(x); untuk setiap x∈[0,1].
d(f1,f2) =
∫
f x − f x dx1
0
2 1( ) ( )
=
∫
f x − f x dx1
0
1
1( ) ( ) =
∫
dx 10
0 = 0
(iii) d(f1,f2) = d(f2,f1)
d(f1,f2) =
∫
f x − f x dx1
0
2 1( ) ( )
=
∫
f x − f x dx1
0
1 2( ) ( )
= d(f2,f1)
(iv) d(f1,f2) =
∫
f x − f x dx1
0
2 1( ) ( )
=
∫
f x − f x + f x − f x dx1
0
2 3
3
1( ) ( ) ( ) ( )
=
∫
f x − f x + f x − f x dx1
0
2 3
3
1( ) ( )) ( ( ) ( ))
≤
∫
(
f x − f x + f x − f x)
dx1
0
2 3
3
1( ) ( ) ( ) ( )
≤
∫
f x − f x dx1
0
3
1( ) ( ) +
∫
f x − f x dx 10
2 3( ) ( )
≤ d(f1,f3) + d(f3,f2).
B. Himpunan Terbuka dan Fungsi Kontinu
Pada subbab ini akan dijelaskan hubungan antara himpunan terbuka dengan fungsi kontinu di dalam ruang metrik.
Definisi 2.2.1
Diberikan sebarang ruang metrik (X,d), x0∈X dan bilangan real r>0.
Bola terbuka, bola tertutup dan luasan bola dengan pusat x0 dan jari-jari r berturut-turut didefinisikan sebagai :
Bola terbuka (Open Ball) B(x0;r)=
{
x∈X d(x,x0)<r}
Bola tertutup (Closed Ball) B(x0;r)={
x∈X d(x,x0)≤r}
Luasan bola (Sphere) S(x0;r)=
{
x∈X d(x,x0)=r}
Dapat dilihat bahwa bola terbuka dengan radius r adalah himpunan semua titik di dalam X sehingga jaraknya terhadap pusat bola kurang dari r. Lebih jauh diperoleh hubungan :
) ; (x0 r
Contoh 2.2.1
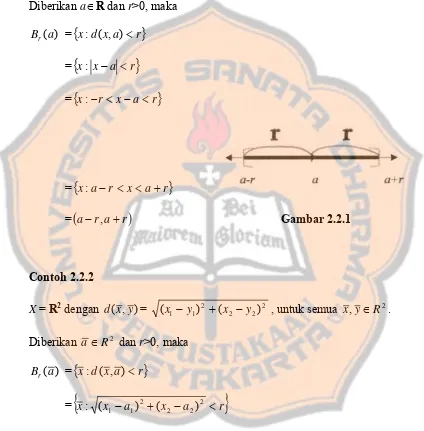
X=R dengan d(x,y) = x− y, untuk semua x,y∈R. Diberikan a∈R dan r>0, maka
) (a
Br =
{
x:d(x,a)<r}
={
x: x−a <r}
={
x:−r <x−a<r}
=
{
x:a−r <x<a+r}
=
(
a−r,a+r)
Gambar 2.2.1Contoh 2.2.2
X = R2 dengan d(x,y)= 2 2 2 2 1
1 ) ( )
(x − y + x −y , untuk semua , 2
R y x ∈ . Diberikan a∈R2 dan r>0, maka
) (a
Br =
{
x:d(x,a)<r}
=
{
x:(x1−a1)2 +(x2 −a2)2 <r2}
Gambar 2.2.2
Contoh 2.2.3
X = R2 dengan d(x,y)= x1−y1 + x2 −y2 Diberikan a∈R2 dan r>0, maka
) (a
Br =
{
x:d(x,a)<r}
=
{
x: x1−a1 + x2 −a2 <r}
Anggap (a1,a2) adalah pusat, maka, Br(a)=
{
x: x + y <r}
Untuk x = x1 −a1 dan y = x2 −a2Gambar 2.2.3
Contoh 2.2.4
X = R2 dengan d(x,y)=maks
{
x1−y1, x2 −y2}
. Diberikan a∈R2 dan r>0, maka) (a
Br =
{
x:d(x,a)<r}
=
{
x:maks{
x1 −a1, x2 −a2}
<r}
Dari kondisi di atas terdapat dua kemungkinan : (i) Jika maks
{
x1 −a1, x2 −a2}
= x1−a1 <r.Maka titik batasnya adalah :
1 1 a
x − =r r a
x1 − 1 = atau x1−a1 =−r r
a
x1 = 1+ atau x1 =a1 −r (ii) Jika maks
{
x1 −a1, x2 −a2}
= x2−a2 <r2 2 a
x − =r r a
x2 − 2 = atau x2 −a2 =−r r
a
x2 = 2 + atau x2 =a2 −r
Gambar 2.2.4
Contoh 2.2.5
[ ]
a b CX = , dengan
(
)
[ ]
{
( ) ( )}
sup ,
,
x g x f g
f d
b a x
− =
∈
Diketahui h∈C
[ ]
a,b dan r>0. Maka,) (h
Br =
( )
[ ]
{
}
⎭⎬⎫ ⎩
⎨
⎧ = − <
∈ f x h x r
h f d f
b a x
) ( ) ( sup ,
:
,
Gambar 2.2.5
Definisi 2.2.2
Diketahui X ruang metrik.
Himpunan K⊆X dikatakan terbuka jika untuk setiap x∈K terdapat bola terbuka B sehingga x∈B⊆K.
Himpunan K⊆X dikatakan tertutup jika komplemennya yaitu K
X
Kc = − terbuka.
Dari sini diperoleh bahwa setiap bola terbuka adalah himpunan terbuka dan setiap bola tertutup merupakan himpunan tertutup.
Bola terbuka B(x0,ε) dengan pusat x0 dan jari-jari ε >0 juga biasa disebut persekitaran-ε (ε-neighbourhood) dengan pusat x0 dan jari-jari ε. Himpunan A
disebut persekitaran dari x0 jika ada bola terbuka B(x0,ε)sehingga )
, ( 0
0 B x ε
setiap persekitaran dari x0 memuat x0; dan jika N adalah suatu persekitaran dari
0
x dan N⊂M maka M juga suatu persekitaran dari x0.
Titik x0 disebut titik dalam (interior point) himpunan M⊂X jika terdapat persekitaran N dari x0 sehingga x0∈ N⊂M. Jadi menurut definisi himpunan terbuka, himpunan M terbuka jika setiap anggotanya adalah titik dalam. Himpunan semua titik dalam M ditulis dengan M0 atau int(M). Lebih lanjut int(M) adalah himpunan terbuka terbesar yang termuat dalam M.
Himpunan terbuka memegang peran penting dalam kaitannya dengan karakterisasi fungsi kontinu pada ruang metrik.
Contoh 2.2.6
Himpunan kosong 0/ terbuka sekaligus tertutup. Bukti :
Menurut pelajaran logika, kondisional A⇒B selalu benar apabila diketahui A pernyataan yang salah. Maka pernyataan-pernyataan
(i) x∈0/ ⇒x titik interior 0/ (ii) 0/C =R terbuka⇒0/ tertutup.
Jadi himpunan kosong 0/ adalah terbuka sekaligus tertutup.
Definisi 2.2.3
Fungsi T : X →Y dikatakan kontinu di x0∈X jika untuk setiap ε >0 terdapat 0
>
δ sehingga berlaku d2
(
T(x),T(x0))
<ε untuk setiap x yang memenuhiδ
< ) , ( 0
1 x x
d . Fungsi T dikatakan kontinu jika T kontinu di setiap titik x∈X.
Teorema berikut menghubungkan konsep himpunan terbuka dalam ruang metrik dengan fungsi kontinu.
Teorema 2.2.1
Diketahui (X,d1), (Y,d2) ruang metrik
Fungsi T : X→Y kontinu jika dan hanya jika prapeta (preimage) setiap himpunan terbuka dalam Y juga terbuka dalam X.
Bukti :
⇒ Diketahui T kontinu.
Akan dibuktikan untuk semua himpunan terbuka S ⊆Y, )T−1(S terbuka dalam X.
Ambil sebarang himpunan S ⊆Y terbuka dan sebut T−1(S)= S0. Jika S0 adalah himpunan kosong maka S0 terbuka atau tertutup.
Untuk selanjutnya anggap S0 bukan himpunan kosong.
Karena S terbuka maka y0 adalah titik dalam S. Jadi ada persekitaran-ε dari y0 yaitu N. Karena T kontinu, ada persekitaran-δ dari x0 yaitu N0 sehinggaT(N0)=N.KarenaN ⊂S makaT−1(N)⊂T−1(S)atauN0 ⊂S0. Jadi terdapat persekitaran N0 dari x0 sehingga x0 ∈N0 ⊂S0
Terbukti x0 titik dalam S0. Jadi setiap anggota S0 adalah titik dalam. Dengan kata lain S0 =T−1(S)terbuka.
⇐ Diketahui prapeta setiap himpunan terbuka dalam Y juga terbuka dalam X Diambil sebarang x0∈X dan sebarang persekitaran-ε dari T(x0) yaitu N. Prapeta dari N yaitu N0 terbuka, karena N terbuka dan N0 memuat x0. Dari sini N0 juga memuat persekitaran-δ dari x0, yang dipetakan ke N karena N0 dipetakan ke N. Akibatnya menurut definisi T kontinu di x0. Lebih lanjut karena x0 sebarang anggota X terbukti T kontinu
Contoh 2.2.7 (Contoh Fungsi Kontinu)
Diambil X = Y =R terhadap metrik biasa. Dibentuk fungsi f :X →Y dengan definisi f(x)=x2; untuk semua x∈X .
Akan ditunjukkan fungsi f kontinu.
Dengan kata lain akan ditunjukkan f kontinu di setiap c∈X . Ambil sebarang c∈X .
Diberikan ε >0 harus dicari δ >0 sehingga untuk setiap x yang memenuhi
δ
< −c
Ditinjau nilai-nilai x dalam bola terbuka B1
( ) (
c = c−1,c+1)
yaitu nilai-nilai x dengan x−c <1.Akan ditunjukkan adanya bilangan δ >0 sehingga untuk x−c <δ berlaku
ε
< − 2 2
c
x .
Untuk x−c <1 maka x2 −c2 = x+c x−c =
(
x−c+2c)
x−c ≤(
1+ 2c)
x−c .Jadi untuk x−c <1 maka x2 −c2 <ε apabila
c c
x
2 1+
<
− ε
Dengan demikian jika diambil
⎪⎭ ⎪ ⎬ ⎫ ⎪⎩
⎪ ⎨ ⎧
+ =
c 2 1 , 1
min ε
δ maka apabila x−c <δ
berlaku x2 −c2 <ε . Terbukti f kontinu di c.
Karena pengambilan c sebarang maka terbukti f kontinu.
Pada bagian terakhir subbab ini akan dibahas mengenai titik limit dan penutup himpunan.
Definisi 2.2.4
Diketahui (X,d) ruang metrik dan M⊆X.
Titik x0∈X disebut titik limit atau titik akumulasi (accumulation point) M jika setiap persekitaran-ε dari x0 memuat titik lain anggota M selain x0.
Himpunan semua titik limit M ditulis dengan M' atau Md
Himpunan semua titik anggota M digabung dengan himpunan semua titik limit M disebut penutup (closure) himpunan M dan ditulis M .
Teorema 2.2.2
M M
M = ⇔ tertutup. Bukti:
Untuk sebarang M pasti tertutup Karena M =M ∪M'
Maka M tertutup
Contoh 2.2.8
X = R terhadap metrik biasa
(
1,2]
=A maka A0 =
( )
1,2 , A′=[ ]
1,2 , dan A= A∪A′=[ ]
1,2Contoh 2.2.9
X = R2 terhadap metrik maksimum
{
( , )∈ 2 −2≤ ≤4, −1< <5}
= x y R x y
M
Maka 0 =
{
( , )∈ 2 −2< <4, −1< <5}
y xR y x M
{
( , )∈ 2 −2≤ ≤4, −1≤ ≤5}
=′ x y R x y
M
{
( , )∈ 2 −2≤ ≤4, −1≤ ≤5}
=′ ∪
=M M x y R x y
M
C. Kekonvergenan, Barisan Cauchy dan Kelengkapan
kekonvergenan barisan. Sekarang akan dibahas secara singkat kekonvergenan barisan )(xn dalam sebarang ruang metrik (X,d).
Definisi 2.3.1 (Barisan Konvergen dan Limitnya)
Suatu barisan(xn)dalam ruang metrik (X,d) dikatakan konvergen jika ada x∈X sehingga
0 ) , (
lim =
∞
→ d xn x n
Titik x disebut limit barisan(xn)dan dapat ditulis x xn n→∞ =
lim atau singkatnya,
x xn → .
Barisan yang tidak konvergen disebut divergen.
Terlihat bahwa d menghasilkan barisan bilangan real an =d(xn,x) yang mendefinisikan konvergensi (xn). Oleh karena itu jika xn →x maka untuk setiap
0
>
ε , terdapat bilangan asli N =N(ε) sehingga apabila n> N berlaku )
; (x ε B xn∈ .
Contoh 2.3.2
Ambil X adalah selang terbuka
( )
0,1 ⊂R dengan metrik biasa d(x,y)= x−y .Kemudian barisan ⎟ ⎠ ⎞ ⎜
⎝ ⎛
K , 4 1 , 3 1 , 2 1
tidak konvergen sebab barisan ini konvergen ke
0 tetapi 0∉(0,1).
Sekarang dijelaskan dua sifat umum dari barisan konvergen, yaitu ketunggalan limit dan keterbatasan.
Definisi 2.3.2
Himpunan M ⊂ X dikatakan terbatas jika diameternya :
{
( , )}
sup ) (
,
y x d M
M y x ∈ =
δ
adalah terbatas. Jika M terbatas, maka terdapat bilangan real r > sup
{
( , )}
,
y x d
M y x ∈
sehingga )M ⊂ B(x0;r , dimana x0∈X adalah sebarang titik.
Oleh karena itu (xn)⊂ X dapat disebut barisan terbatas jika himpunan titik (xn) merupakan himpunan terbatas dalam X.
Oleh karena itu akan dijelaskan pada teorema berikut :
Teorema 2.3.1
Diketahui (X,d) adalah ruang metrik, maka :
Bukti :
(i). Anggap xn →x, jadi untuk setiap ε >0, ada bilangan asli N = N(ε) sehingga untuk setiap n> N berlaku d(xn,x)<ε .
Khususnya diambil ε =1 maka akan didapat N = N(1) dimana 1
) , (x x <
d n , untuk semua n> N.
Ambil α =max
{
d(x1,x),d(x2,x),K,d(xN,x)}
maka d(xi,x)<α , untuksemua i = 1,2,...,N.
Jadi untuk semua i = 1,2,... akan berlaku d(xi,x)<1+α Ini menunjukkan bahwa (xn)terbatas.
Misalkan xn →x dan xn →z, menggunakan pertidaksamaan segitiga didapatkan 00≤d(x,z)≤d(x,xn)+d(xn,z)→0+ .
Karena 0d(x,z)≥ dan d(x,z)≤0 maka d(x,z)=0 sehingga x = z. Dengan kata lain limit barisan (xn) adalah tunggal.
(ii) Dengan menggunakan pertidaksamaan segitiga )
, ( ) , ( ) , ( ) ,
(xn yn d xn x d x y d y yn
d ≤ + +
Maka didapat
) , ( ) , ( ) , ( ) ,
(xn yn d x y d xn x d y yn
d − ≤ +
) , ( ) , ( ) , ( ) ,
(x y d x y d x x d y y
d n n − ≤ n + n (i)
Dan dengan menukar peranan xn dengan x dan yn dengan y serta mengalikan dengan -1 diperoleh
) , ( ) , ( ) , ( ) ,
(x y d xn yn d xn x d y yn
(
d(xn,x)+d(y,yn))
≤d(xn,yn)−d(x,y)− (ii)
Dengan menggabung pertidaksamaan (i) dan (ii) maka didapat 0
0 0 ) , ( ) , ( ) , ( ) ,
(xn yn −d x y ≤d xn x +d y yn → + = d
sehingga d(xn,yn)−d(x,y) →0 yang berarti d(xn,yn)→d(x,y).
Kini akan didefinisikan mengenai konsep kelengkapan dari ruang metrik, yang mempunyai peranan penting dalam pembahasan selanjutnya.
Definisi 2.3.3 (Definisi Barisan Cauchy Bilangan Real)
Barisan )(xn adalah barisan Cauchy bilangan real jika dan hanya jika memenuhi kriteria kekonvergenan Cauchy yaitu apabila untuk setiap ε >0 maka terdapat
) (ε N
N = dimana xm −xn <ε, untuk setiap m,n> N.
Selanjutnya akan didefinisikan barisan Cauchy dalam ruang metrik dan hubungan kelengkapan dengan ruang metrik.
Definisi 2.3.4
Kemudian akan dibahas mengenai contoh-contoh dari kelengkapan dan kekonvergenan Cauchy.
Contoh 2.3.3
Garis real dan bidang kompleks adalah ruang metrik lengkap.
Contoh 2.3.4
Ruang R – {a} tidak lengkap karena tidak terdapat satu titik limit dari barisan real tertentu. Lebih jelas lagi, jika pada ruang R dihapus semua bilangan irasional maka ruang tersebut tidak lengkap. Pada selang terbuka (a,b) dengan metrik di R merupakan ruang metrik tidak lengkap.
Contoh 2.3.5
Diambil X=(0,1] menggunakan metrik biasa dan barisan (xn) dimana n xn = 1 dan
n=1,2,.... adalah suatu barisan Cauchy tetapi tidak konvergen karena titik 0 tidak terdapat pada X. Ini menggambarkan konsep dari kekonvergenan bukan merupakan sifat utama dari barisannya tetapi tergantung pada ruang di mana barisan tersebut berada.
Teorema 2.3.2
Bukti :
Diketahui xn →x, maka untuk semua ε >0 terdapat N =N(ε) dimana
2 ) , (x x <ε
d n untuk semua n> N
Akibatnya dengan menggunakan pertidaksamaan segitiga didapat untuk semua N
n
m, > berlaku
ε ε ε
= + < +
≤
2 2 ) , ( ) , ( ) ,
(xm xn d xm x d x xn d
Jadi terbukti bahwa (xn) adalah barisan Cauchy.
Selanjutnya akan dibahas mengenai penutup (closure) dari himpunan dan kaitannya dengan barisan konvergen.
Teorema 2.3.4
Diketahui M himpunan bagian tak kosong dari ruang metrik (X,d) dan M adalah penutup M maka :
(i) x∈M jika dan hanya jika terdapat barisan (xn) dalam M sehingga x
xn → .
(ii) M adalah tertutup jika dan hanya jika xn∈M dan xn →x berakibat
M x∈ . Bukti :
Jika x∈/M, maka x adalah titik limit dari M. Akibatnya untuk setiap K
, 2 , 1 =
n ( ;1)
n x
B memuat xn ∈M , dan xn →x karena 1 →0
n untuk
∞ →
n .
Sebaliknya, jika (xn) barisan dalam M dan xn →x, maka x∈M atau untuk setiap persekitaran dari x ada titik xn ≠ x, jadi x adalah titik limit dari M. Akibatnya x∈M , menggunakan definisi dari penutup.
(ii) M adalah tertutup jika dan hanya jika M =M .
Definisi 2.3.5
Diketahui (X,d) ruang metrik.
Himpunan Y ⊆ X disebut ruang bagian X jika (Y,d) merupakan ruang metrik.
Teorema 2.3.5
Ruang bagian M dari ruang metrik lengkap X adalah lengkap jika dan hanya jika M adalah tertutup dalam X.
Bukti :
Diketahui M adalah lengkap. Menggunakan teorema 2.3.4 (i), untuk setiap x∈M ada barisan (xn) dalam M dan xn →x. Karena (xn) adalah barisan Cauchy
Sebaliknya diketahui M tertutup dan (xn) barisan Cauchy dalam M. Kemudian X
x
xn → ∈ , yang mengakibatkan x∈M ( menggunakan teorema 2.3.4.(i)), dan M
x∈ sebab M =M (karena M tertutup). Akibatnya untuk sebarang barisan Cauchy )(xn konvergen dalam M. Jadi terbukti M lengkap.
Teorema berikut akan menunjukkan arti penting barisan konvergen dalam kaitannya dengan fungsi kontinu.
Teorema 2.3.6
Diketahui ruang-ruang metrik (X,d1) dan (Y,d2)
Fungsi T:X →Y kontinu di titik x0 ∈X jika dan hanya jika xn →x berakibat )
( )
(x T x0
T n → .
Bukti :
⇒Diasumsikan T kontinu di x0. Kemudian diberi sebarang ε >0, ada δ >0 sehingga apabila
δ
< ) , ( 0
1 x x
d maka d2
(
T(x),T(x0))
<εDiketahui xn →x0. Kemudian ada N dimana untuk semua n> N berlaku
δ
< ) ,
( 0
1 x x
d n Oleh karena itu, untuk semua n> N,
ε
< )) ( ), (
( 0
2 T x T x
d n
⇐Sebaliknya, diasumsikan jika xn →x0 maka T(xn)→T(x0)
Akan dibuktikan T kontinu di x0.
Andaikan T tidak kontinu, maka ada ε >0 dimana untuk setiap δ >0 untuk
0
x
x≠ yang memenuhi
δ
< ) , ( 0
1 x x
d tetapi d2
(
T(xn),T(x0))
≥εKhususnya, untuk n 1 =
δ terdapat xn maka berlaku
n x x d n
1 ) ,
( 0
1 < tetapi d2
(
T(xn),T(x0))
≥εDidapat dengan jelas xn →x0 tetapi
(
T(xn))
tidak konvergen ke T(x0). Timbul kontradiksi dengan T(xn)→T(x0).Jadi terbukti T kontinu di x0.
Berikut ini akan dijelaskan contoh-contoh ruang metrik lengkap dan ruang metrik tidak lengkap.
Untuk membuktikan kelengkapan ruang metrik (X,d) dilakukan dengan mengambil sebarang barisan Cauchy (xn) dalam X dan ditunjukkan bahwa (xn)
konvergen ke suatu x∈X. Perumusan umumnya sebagai berikut: (i) Dibentuk elemen x (untuk digunakan sebagai limit) (ii) Dibuktikan x dalam X.
Contoh 2.3.5
Ruang Euclid Rn adalah lengkap. Bukti :
Diketahui Rn merupakan ruang Euclid maka dapat didefinisikan
(
)
21 1 2 ) , ( ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − =
∑
= n j j j y xd ξ η
(
n)
x= ξ1,ξ2,L,ξ dan y=
(
η1,η2,L,ηn)
nR ∈
dimana x=
( )
ξj dan y=( )
ηj . Diambil sebarang barisan Cauchy (xm) dalam Rn ditulis xm =(
ξ1(m),L,ξn(m))
. Karena (xm) Cauchy maka untuk setiap ε >0 ada N sehingga berlaku(
ξ
ξ
)
⎟
⎟
<
ε
⎠
⎞
⎜
⎜
⎝
⎛
−
=
∑
= 2 1 2 1 ) ( ) ()
,
(
n j r j m j r mx
x
d
, (i)untuk semua m,r >N. Dengan mengkuadratkan, maka didapat untuk m,r >N dan j =1,L,n
(
ξ ( ) −ξ (r))
2 <ε2j m
j dan ξ −ξ <ε
) ( ) ( r j m j
Ini menunjukkan untuk setiap 1≤ j≤n,
(
ξj(1),ξj(2),L)
merupakan barisan Cauchy bilangan real. Menurut Teorema 2.3.3, maka ξj(m) →ξj untuk m→∞. Menggunakan n buah limit ini, dapat didefinisikan x=(
ξ1,L,ξn)
. Dengan jelasn
R
x∈ . Dari (i) untuk r →∞ berlaku
ε
≤ ) , (x x
untuk semua m>N. Ini menunjukkan bahwa x adalah limit dari (xm) dan terbukti kelengkapan dari Rn karena (xm) diambil sebarang barisan Cauchy.
Contoh 2.3.6
Ruang fungsi C
[ ]
a,b adalah lengkap. Bukti :Ambil sebarang (xm) barisan Cauchy dalam C
[ ]
a,b . Maka untuk ε >0, ada N dimana untuk semua m,n> N berlakuε
< −
=
∈ ( ) ( )
sup ) ,
(x x x t x t
d m n
J t n
m (*)
Dimana J =
[ ]
a,b . Akibatnya untuk sebarang t =t0∈J, ε<
− ( )
)
(t0 x t0
xm n
untuk semua m,n>N . Ini menunjukkan bahwa
(
x1(t0),x2(t0),L)
barisan Cauchy dalam R. Karena R lengkap maka xm(t0)→x(t0) untuk m→∞. Dengan cara ini dapat dikaitkan setiap t∈J dengan tepat satu bilangan real x(t).Hal ini mendefinisikan suatu fungsi x pada J. Selanjutnya akan ditunjukkan
[ ]
a b Cx∈ , dan xm →x. Dari (*) dan n→∞ didapat
ε
≤ −
∈ ( ) ( )
supxm t x t
J t
untuk m>N. Akibatnya untuk setiap t∈J berlaku, ε
≤
− ( )
untuk m≥ N. Ketaksamaan terakhir diatas menunjukkan bahwa (xm) konvergen menuju x pada
[ ]
a,b . Karena (xm) kontinu berarti jika diberikan ε >0 dapat ditemukan δ >0 sehingga2 ) ( )
(t −x p ≤ε
xm m bila
2
δ
< −p
t untuk semua
[ ]
a b pt, ∈ , dan diketahui (xm) konvergen berarti jika diberi ε >0 ada N∈Ν, untuk semua m≥N berlaku
2 ) ( )
(t −x t ≤ε
xm , untuk semua t∈
[ ]
a,b . Jadiuntuk semua t,t1∈
[ ]
a,b , x(t)−x(t1) = x(t)−xm(t)+xm(t)−x(t1) ε< −
+ −
≤ x(t) xm(t) xm(t) x(t1) .
Jadi x(t)−x(t1) <ε bila t−t1 = t−p+ p−t1 ≤ t− p + p−t <δ .
Ini menunjukkan bahwa x kontinu pada
[ ]
a,b . Akibatnya, karena xm kontinu padaJ dan barisan (xm) konvergen, maka limit x kontinu pada J. Jadi x∈C
[ ]
a,b dan xxm → . Maka terbukti ruang fungsi C
[ ]
a,b adalah lengkap.Berikut ini akan diberikan ruang metrik tidak lengkap
Contoh 2.3.7
Diketahui Q = himpunan semua bilangan rasional.
Barisan hampiran untuk 2; yaitu
(
1,4L1,41L1,414L1,4142L1,41421;L)
konvergen ke 2, tetapi 2∉Q. Jadi Q tidak lengkap. Contoh 2.3.8
dt t y t x y
x
d =
∫
1 −0 ( ) ( )
) ,
( , untuk setiap x,y∈C
[ ]
0,1 Maka ruang metrik X adalah tidak lengkap.Bukti :
Diandaikan X lengkap. Akan dibuktikan dengan contoh penyangkal.
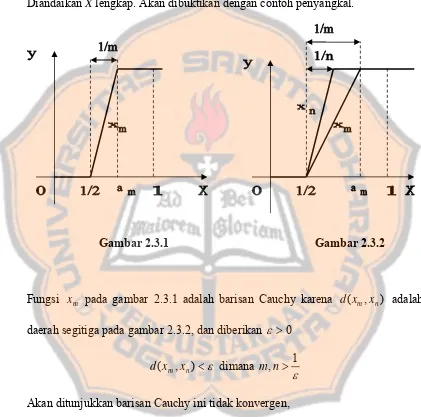
Gambar 2.3.1 Gambar 2.3.2
Fungsi xm pada gambar 2.3.1 adalah barisan Cauchy karena d(xm,xn) adalah
daerah segitiga pada gambar 2.3.2, dan diberikan ε >0
ε
< ) , (xm xn
d dimana
ε
1 ,n> m
Akan ditunjukkan barisan Cauchy ini tidak konvergen,
Diketahui 0xm(t)= , untuk
⎥⎦ ⎤ ⎢⎣ ⎡ ∈
2 1 , 0
t ,
2 1 2 1 )
(
− − =
m m
a t t
x untuk t∈⎢⎣⎡ ,am⎥⎦⎤ 2 1
1 ) (t =
dengan m am 1 2 1 +
= . Untuk setiap x∈Xberlaku
) , (x x
d m =
∫
1 −0 xm(t) x(t) dt
=
∫
∫
− +∫
− − − + − 1 2 1 0 21 ( ) 1 ( )
2 1 2 1 ) ( m m a a m dt t x dt t x a t dt t x
Karena fungsi yang diintegralkan tidak negatif, jadi d(xm,x)→0 dan berakibat masing-masing dari integral di ruas kanan mendekati nol, maka didapat
0 ) (t =
xm , untuk ⎟
⎠ ⎞ ⎢⎣ ⎡ ∈ 2 1 , 0
t , 1xm(t)= , untuk ⎜ ⎥⎦⎤ ⎝ ⎛ ∈ ,1
2 1
t .
Tetapi ini tidak mungkin untuk fungsi kontinu. Akibatnya (xm) tidak konvergen karena xm∉C
[ ]
0,1 .Jadi terbukti X tidak lengkap.
D. Ruang Topologi
Definisi 2.4.1
Diberikan himpunan X ≠0/. Koleksi X
2 ⊂
τ disebut topologi pada X jika memenuhi : (i) 0/∈τ dan X∈τ
(ii) jika U∈τ dan V∈τ maka U∩V∈τ
Anggota τ disebut himpunan terbuka.
Definisi 2.4.2
Ruang topologi adalah pasangan
(
X,τ)
, dengan X adalah suatu himpunan dan τ adalah topologi pada X.Contoh 2.4.1
{
a b c d e}
X = , , , , dan τ1 =
{
0/,X,{ } { } {
a , c,d , a,c,d} {
, b,c,d,e}
}
ruang topologi pada X karena :(i) 0/∈τ1 dan X∈τ1
(ii) jika U∈τ1 dan V∈τ1 maka U∩V∈τ1
(iii) jika Uα∈τ1 untuk setiap α∈I, maka
U
{
Uα :α∈I}
∈τ1Sementara itu τ2 =
{
0/,X,{ } { } {
a , c,d , a,c,d} {
, b,c,d}
}
bukan ruang topologi pada X karena ada salah satu aksioma yang tidak terpenuhi yaitu :jika U∈τ2 dan V ∈τ2 maka U ∩V ∈/τ2 yaitu untuk U =
{ }
c,d ∈τ2 dan{
, ,}
∈τ2= b c d
V maka U ∩V =
{ }
b ∈/τ2Definisi 2.4.3
Diketahui
(
X,τ1)
dan(
Y,τ2)
ruang topologi. Fungsi f :X →Y kontinu di Xsehingga f(U)⊆V. Fungsi f :X →Y dikatakan kontinu jika f kontinu di setiap titik anggota X.
Definisi 2.4.4
Diketahui
(
X,τ1)
dan(
Y,τ2)
ruang topologi. Fungsi f :X →Y dikatakan homeomorfisma apabila f bijektif, f kontinu, dan f −1 kontinu.Ruang topologi
(
X,τ1)
dan(
Y,τ2)
dikatakan homeomorfik jika terdapat homeomorfisma f :X →Y.Sifat dari suatu himpunan yang diawetkan oleh sebarang homeomorfisma disebut sifat topologi (topological property).
Contoh 2.4.3
Diambil X=Y dengan τ sebarang topologi pada X. Dibentuk fungsi f :X →Y adalah fungsi identitas. Karena f fungsi identitas maka f bijektif, f kontinu, dan
1
−
BAB III
TEOREMA TITIK TETAP BANACH
Salah satu bentuk penerapan matematika adalah untuk menyelesaikan suatu persamaan. Namun sebelum memecahkan masalah persamaan, perlu diketahui terlebih dahulu apakah persamaan tersebut mempunyai penyelesaian atau tidak.
Berikut ini akan diberikan fungsi f dengan variabel x, f kontinu pada interval tertutup
[ ]
a,b dan jika f(a) dan f(b) memiliki tanda yang berbeda, maka persamaan0 ) (x = f
mempunyai sedikitnya satu penyelesaian di dalam interval
[ ]
a,b .Untuk menyelesaiakan persamaan di atas diperlukan Teorema Eksistensi atau teorema yang menjamin adanya suatu penyelesaian, sering dinyatakan dalam bentuk prinsip titik tetap (fixed point principles). Sebagai contoh, diperhatikan persamaan f(x)=0. Persamaan ini ditulis dalam bentuk α f(x)+x=x dengan parameter positif α. Jika α f(x)+x dinyatakan sebagai F(x) diperoleh persamaan
x x
F( )= ...(*)
Titik x dalam persamaan (*) dikenal sebagai titik tetap. Oleh karena itu persamaan tersebut mempunyai sedikitnya satu penyelesaian di dalam interval
[ ]
a,b .(P) x2 =a ∈N
Sebagai contoh, jika a=4 maka x=2.
Setelah munculnya masalah, kemudian dirumuskan masalah titik tetap (fixed point problem/FPP) sebagai berikut :
0
2 − =
a x
(FPP) x2 +x−a=x
Masalah titik tetap di atas diselesaikan dengan successive substitution/SS yang menghasilkan approximate solution/AS.
(SS) Anggap x0 =1 (AS) xn+ =xn +xn −a
2
1 , untuk n=0,1,2,...
Kemudian dirumuskan FPP yang lebih abstrak, yaitu: x
x f( )=
Titik x dalam persamaan di atas dikenal sebagai titik tetap.
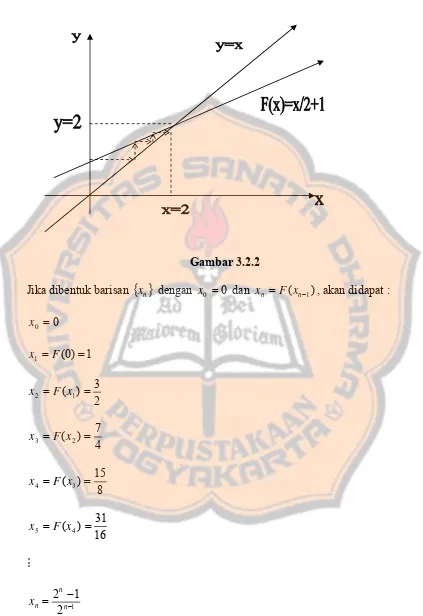
Pada bab ini akan dijelaskan mengenai teorema titik tetap Banach (Banach Fixed Point Theorem). Sebelumnya akan dibahas pengertian fungsi kontraksi (contraction mapping), kondisi Lipschitz (Lipschitz condition), dan titik tetap (fixed point) dalam suatu ruang metrik.
1. Titik Tetap (Fixed Point)
Pada subbab ini akan dibahas mengenai definisi titik tetap (fixed point) dalam suatu ruang metrik. Sebelumnya akan dibahas pengertian fungsi kontraksi (contraction mapping) dan kondisi Lipschitz (Lipschitz condition).
Definisi 3.1.1
Diketahui
(
X,d)
ruang metrik.Fungsi F :X →X disebut fungsi kontraksi (contraction mapping) pada X jika terdapat bilangan real α dengan 0≤α <1 sehingga
(
F(x1),F(x2))
d ≤α.d
(
x1,x2)
, untuk setiap x1,x2∈X .Contoh 3.1.1
Diberikan fungsi f :R→R dengan definisi 3 2 1 )
(x = x+
f merupakan fungsi
kontraksi pada R karena terdapat bilangan real α dengan 0≤α <1 sehingga
y x y x y x y
x y
f x
f ⎟ = − = − ≤ −
⎠ ⎞ ⎜
⎝
⎛ +
− + = −
3 2 2 <