1
Deskripsi Pemahaman Konsep Limit Fungsi
Pada Mahasiswa Jurusan Matematika
Yusuf Ramadana
1, a), Arsyad
1), dan Minggi
1)1)Jurusan Matematika FMIPA Universitas Negeri Makassar a) yusuf.ramadana20021996@gmail.com
Abstrak. Penelitian ini bertujuan untuk mendeskripsikan pemahaman konsep limit fungsi pada mahasiswa Jurusan Matematika. Penelitian ini merupakan penelitian kualitatif deskriptif dengan subjek sebanyak 8 orang. Instrumen yang digunakan adalah tes pemahaman konsep dan pedoman wawancara. Dari hasil penelitian diperoleh beberapa kategori-kategori pemahaman: (1) pemahaman faktual,, mendeskripsikan makna 𝜀 dan 𝛿 dengan cenderung mengaitkan pada kalimat berkuantor pada definisi limit fungsi serta mengaitkannya dengan makna intuitif limit fungsi, sebagai jarak pada masing-masing sumbu koordinat; mendeskripsikan makna nilai mutlak 0 < |𝑥 − 𝑐| < 𝛿 dan |𝑓(𝑥) − 𝐿| < 𝜀 dengan cenderung mengaitkannya dengan jarak, selisih serta mengaitkannya dengan makna intuitif limit fungsi; mendeskripsikan pernyataan 0 < |𝑥 − 𝑐| < 𝛿 → |𝑓(𝑥) − 𝐿| < 𝜀 dengan menekankan pada titik yang berada di sekitar titik yang dituju pada definisi limit fungsi dengan syarat-syarat tertentu yang berakibat nilai fungsinya juga memiliki syarat-syarat tertentu pula, serta ada pula subjek yang mengaitkannya dengan hubungan 𝜀 dan 𝛿. (2) Pemahaman interpretasi, pada dasarnya diperoleh dua kategori, yaitu dapat mengiterpretasi definisi limit fungsi dengan tepat, serta mengiterpretasi definisi limit fungsi dengan memaknai pernyataan implikasi di dalamnya secara terbalik. (3) Pemahaman sintaktik, pemahaman subjek pada negasi dari pernyataan implikasi dan kemampuan mengimplentasikan pemahamannya untuk menentukan negasi dari definisi limit fungsi masih kurang. (4) Pemahaman pembuktian, pemahaman yang kurang tentang logika matematika (pernyataan implikasi dan kalimat berkuantor), kemampuan yang kurang manipulasi aljabar dan kurangnya pemahaman tentang bukti matematis.
Kata Kunci: Pemahaman Konsep, Limit Fungsi.
Abstract. This research aims to describe the understanding of the concept of the limit of a function on Students of Mathematics Department. This research is a descriptive qualitative research with the subject of 8 students. The instruments used are a concept understanding test and a semi-structured interview protocol. The research results reveal several categories: (1) factual understanding, describing the meaning of 𝜀 and 𝛿 with tend to link this in quantified sentence in the definition of the limit of a function, the intuitive meaning of the limit of a function, and the distance to each of the coordinate axis; describing the meaning of absolute values 0 < |𝑥 − 𝑐| < 𝛿 and |𝑓(𝑥) − 𝐿| < 𝜀 with tend to assiciate them with the distance, difference and associatting them with the intuitive meaning of the limit of a function; describing the statement 0 < |𝑥 − 𝑐| < 𝛿 → |𝑓(𝑥) − 𝐿| < 𝜀 by emphasizing the points that being around the intended point with certain conditions which result in the values of the function also have a term also certain, it also gained subject who associate them with the relation between 𝜀 and 𝛿. (2) Interpreting understanding, basically retrieved two understandings, that can interprete the definition of the limit of a function appropriately, and interpreting the definition of the limit of a function by interpreting the implication statement in it reversely. (3) Syntactic understanding, the subject's understanding of the negation of the implication statement and the ability to implement his understanding to determine the negation of the definition of the limit function is still lacking. (4) Proving understanding, lack understanding about mathematical logic (implication statement and quantified sentences), lack ability in algebraic manipulation and lack of understanding of mathematical evidence.
2
PENDAHULUAN
Pembelajaran matematika tidak hanya berkaitan dengan keterampilan dalam menghitung dan menghafalkan rumus matematika sebanyak-banyaknya, namun juga harus memahami konsepnya. Kemampuan pemahaman konsep matematika sangat penting karena disamping menjadi salah satu tujuan pembelajaran matematika, kemampuan pemahaman konsep juga dapat membantu peserta didik untuk tidak hanya sekedar menghafal rumus, tetapi dapat mengerti dengan benar tentang makna dalam pembelajaran matematika (Pitaloka, Susilo & Mulyono, 2013). Belajar matematika dengan pemahaman konsep memerlukan daya nalar yang tinggi dikarenakan objek matematika yang bersifat abstrak, sehingga belajar matematika harus diarahkan pada pemahaman konsep-konsep yang akan mengantarkan individu untuk berpikir secara matematis dengan jelas dan pasti berdasarkan aturan-aturan yang logis dan sistematis.
Pembelajaran matematika harus dihayati dan ditekankan untuk menanamkan konsep matematika berdasarkan pemahaman. Ini dikarenakan pemahaman merupakan kemampuan untuk menangkap makna dan arti dari bahan yang dipelajari, sehingga pemahaman memudahkan terjadinya transfer (Hiebert & Carpenter, 1992). Pencapaian pemahaman suatu konsep matematika bukan suatu hal yang mudah disebabkan karena kemampuan dalam memahami suatu konsep matematika setiap individu berbeda-beda.
Salah satu konsep yang penting dalam matematika khususnya di perguruan tinggi adalah kalkulus. Berbagai persoalan matematika dapat diselesaikan dengan kalkulus seperti masalah optimumisasi, pemodelan hingga pada masalah-masalah yang berkaitan dengan fisika. Juter (2005) mengemukakan bahwa konsep limit fungsi merupakan bagian paling penting dalam kalkulus. Ia juga menyatakan bahwa bagaimana mungkin mahasiswa dapat memahami konsep turunan dan integral jika mahasiswa tersebut tidak memahami konsep limit. Konsep limit fungsi menjadi konsep krusial dan sebagai konsep prasyarat dalam mempelajari berbagai konsep matematika lainnya (Karatas, Guven & Cekmez 2011; Cetin, 2015). Salas dan Hille (1990) juga menyatakan bahwa tanpa limit, maka kalkulus tidak mugkin ada. Selain itu, Denbel (2014) menyatakan bahwa tanpa konsep limit fungsi maka cabang matematika paling penting yang disebut analisis juga tidak akan ada. Ini sejalan dengan pendapat Kim, Kang dan Lee (2015) bahwa konsep limit menjadi konsep dasar bagi kalkulus dan analasis matematika. Hal ini menggambarkan begitu pentingnya konsep limit fungsi. Oleh karena itu, dibutuhkan pemahaman konsep limit fungsi yang baik.
Akan tetapi masih terdapat beberapa mahasiswa yang belum terlalu memahami konsep limit fungsi tersebut (Cottrill, Dubinsky, Nichols, Schwingendorf, Thomas & Vidakovic, 1996), utamanya definisi formal limit fungsi. Roh (2005) mengemukakan bahwa masih terdapat mahasiswa yang kesulitan dalam memahami konsep limit fungsi terutama pada definisi formal limit fungsi sehingga pemahamannya tentang konsep tersebut masih kurang. Selain itu, masih terdapat juga mahasiswa yang belum dapat mengaplikasikan definsi formal limit fungsi untuk membuktikan kebenaran nilai limit fungsi (Bahar, Rahman & Minggi, 2012).
Adapun penelitian ini akan mengkaji pemahaman mahasiswa tenang konsep limit fungsi. Penelitian ini bertujuan untuk mendeskripsikan pemahaman mahasiswa tentang konsep limit fungsi di satu titik. Konsep limit fungsi dalam penelitian ini berkenaan dengan materi definisi formal limit fungsi (definisi 𝜀 − 𝛿) di satu titik pada bidang koordinat kartesius (koordinat siku-siku 2 dimensi). Materi definisi formal limit fungsi (definisi 𝜀 − 𝛿) tersebut diajarkan pada mata kuliah Kalkulus I.
KAJIAN TEORI
Pemahaman KonsepSecara bahasa, pemahaman konsep terdiri dari dua kata yaitu pemahaman dan konsep. Dalam taksonomi Bloom 1956, pemahaman adalah kemampuan untuk membentuk makna dari suatu
3 konsep. Contoh-contoh verbs yang berhubungan dengan pemahaman adalah menyatakan ulang, menjelaskan, mengekspresikan, mengidentifikassi, mendeskripsikan, mengilustrasikan, mengiterpretasikan, merepresentasikan (Wilson, 2016). Sedangkan yang dimaksud dengan pemahaman (Understanding) dalam revisi taksonomi Bloom oleh Anderson dan Krathwohl (Krathwohl, 2002) adalah pemahaman berarti membentuk makna dari tipe-tipe fungsi yang berbeda yang ditulis atau aktifitas pesan grafis seperti mengiterpretasikan, memberikan contoh, mengklasifikasikan, meringkas, menyimpulkan, memmbandingkan dan menjelaskan. Dalam mendeskripsikan pemahaman mahasiswa dalam penelitian ini, sebagian besar akan digunakan verbs tersebut, baik dari taksonomi Bloom 1956 maupun revisi taksonomi Bloom oleh Anderson dan Krathwohl 2001.
Konsep merupakan salah satu objek kajian matematika yang mendasar dan sangat penting. Menurut Soedjadi (2000), konsep adalah ide abstrak yang dapat digunakan untuk melakukan penggolongan atau klasifikasi. Pembentukan suatu konsep dapat melalui abstraksi, idealisasi, abstraksi dan idealisasi, serta penambahan syarat pada konsep terdahulu. Sedangkan konsep matematika merupakan jaringan ide kompleks yang dikembangkan dari definisi matematika dan konstruk mental (Sfard, 1991). Konsep-konsep tersebut memiliki keterkaitan antara satu dengan yang lainnya, maka mahasiswa harus lebih banyak diberikan kesempatan untuk melihat kaitan-kaitan dengan materi yang lain. Hal tersebut dimaksudkan agar mahasiswa dapat memahami materi matematika secara mendalam.
Hudojo (1990) menyatakan bahwa dalam mempelajari konsep B yang mendasarkan kepada konsep A, seseorang perlu memahami lebih dulu konsep A. Tanpa memahami konsep A, tidak mungkin orang tersebut memahami konsep B. Ini berarti, mempelajari matematika haruslah bertahap dan berurutan serta mendasar kepada pengalaman belajar yang lalu. Dengan demikian, pemahaman konsep sangat penting, karena dengan pemahaman konsep akan memudahkan siswa dalam mempelajari matematika.
Menurut Skemp (1976), terdapat dua jenis pemahaman konsep, yaitu pemahaman instrumental dan pemahaman relasional. Pemahaman instrumental dapat diartikan sebagai pemahaman atas konsep yang saling terpisah dan hanya menghafalkan rumus dalam melakukan perhitungan sederhana, sedangkan pemahaman relasional adalah pemahaman yang melibatkan pengetahuan mengenai apa yang dilakukan dan mengapa melakukan hal tersebut. Polya (Meel, 2003) mengidentifikasi empat jenis pemahaman, yaitu (1) Pemahaman mekanikal, mengingat dan menerapkan rumus secara rutin dan menghitung sederhana; (2) Pemahaman induktif, mencoba sesuatu dalam kasus sederhana dan tahu bahwa sesuatu itu berlaku dalam kasus serupa; (3) Pemahaman rasional, dapat membuktikan kebenaran sesuatu; (4) Pemahaman intuitif, dapat memperkirakan kebenaran sesuatu tanpa ragu-ragu sebelum menganalisis secara analitik. Sedangkan Pollatsek, Lima dan Well (1981)membagi pemahaman menjadi 3 kategori sebagai berikut: (1) pemahaman komputasional, yaitu dapat menerapkan sesuatu pada perhitungan rutin/sederhana, atau mengerjakan sesuatu secara algoritmik saja; (2) pemahaman fungsional, yaitu dapat mengaitkan sesuatu dengan hal lainnya secara benar dan menyadari proses yang dilakukannya; (3) pemahaman analog, yaitu dapat melibatkan gambaran visual atau kinestatik dari suatu konsep.
Pemahaman Konsep Limit Fungsi
Objek penelitian ini adalah konsep limit fungsi, terkhusus pada definisi formal limit fungsi di satu titik. Konsep tersebut menjadi konsep paling fundamental dalam kalkulus dasar (Syzdlik, 2000). Definisi formal limit fungsi (Purcell, Varberg & Ringdon, 2004) mengatakan bahwa lim
𝑥→𝑐𝑓(𝑥) = 𝐿 berarti untuk setiap 𝜀 > 0 yang diberikan, terdapat 𝛿 > 0 yang berpadanan sedemikian sehingga |𝑓(𝑥) − 𝑙| < 𝜀 asalkan bahwa 0 < |𝑥 − 𝑐| < 𝛿, yakni,
0 < |𝑥 − 𝑐| < 𝛿 ⟹ |𝑓(𝑥) − 𝐿| < 𝜀 (1) Dicatat bahwa 𝑓(𝑥) tidak harus terdefinisi di 𝑥 = 𝑐, tetapi 𝑓(𝑥) harus terdefinisi di semua 𝑥 lainnya di suatu interval yang memuat 𝑐. Kuantitas |𝑥 − 𝑐| adalah jarak antara titik 𝑥 dan titik 𝑐
4 pada garis bilangan, dan dapat mengukur seberapa dekat 𝑥 ke 𝑐 dengan menghitung |𝑥 − 𝑐|. Ketaksamaan |𝑥 − 𝑐| < 𝛿 menyatakan bahwa jarak antara 𝑥 dan 𝑦 kurang dari 𝛿, dengan kata lain, jarak 𝑥 dan 𝑐 lebih dekat dari nilai 𝛿. Sedangkan ketaksamaan 0 < |𝑥 − 𝑐| menyatakan bahwa 𝑥 tidak sama dengan 𝑐. Hal ini dapat dihubungkan dengan makna intuitif limit fungsi bahwa titik yang dikaji adalah titik yang berada di sekitar 𝑐 dan bukan titik 𝑐 itu.
Kuantitas 𝜀 adalah kuantitas yang menyatakan seberapa dekat 𝑓(𝑥) ke 𝐿. Sedangkan kuantitas 𝛿 menyatakan seberapa dekat harus dipilih 𝑥 di sekitar 𝑐, agar nilai fungsi dari 𝑥 memiliki selisih dengan 𝐿 kurang dari kuantitas 𝜀. Untuk membuktikan bahwa lim
𝑥→𝑐𝑓(𝑥) = 𝐿, terlebih dahulu diasumsikan bahwa seseorang memberikan sebarang nilai 𝜀 > 0, kemudian menentukan suatu nilai 𝛿 > 0 sehingga (1) terpenuhi.
Definisi formal limit fungsi memuat konsep-konsep matematika penting lainnya, seperti nilai mutlak dan logika matematika termasuk pernyataan implikasi dan kalimat berkuantor. Selain itu, dibutuhkan pemahaman dan kemampuan dalam melakukan manipulasi aljabar dan pembuktian matematis untuk melakukan validasi tentang kebenaran nilai limit fungsi. Oleh karena itu, berdasarkan pada apa yang dikemukakan oleh Hudojo (1990) sebelumnya maka untuk memahami definisi limit fungsi diperlukan pemahaman mendalam tentang konsep nilai mutlak dan logika matematika (pernyataan dan kalimat berkuantor) sebagai materi prasyaratnya. Selain itu, mampu melakukan manipulasi aljabar dan pembuktian matematis sebagai syarat untuk melakukan validasi kebenaran nilai limit fungsi. Dari sini, dapat disimpulkan bahwa untuk memahami konsep limit fungsi, diperlukan pemahaman mendalam tentang konsep nilai mutlak dan logika matematika serta mampu melakukan manipulasi aljabar dan pembuktian matematis. Sehingga dalam penelitian ini, pemahaman mengenai definisi formal limit fungsi dibagi menjadi beberapa bagian sebagaimana dipaparkan sebagai berikut.
1. Pemahaman Faktual
Pemahaman faktual merujuk pada pengetahuan faktualpada revisi taksonomi Bloom, yaitu unsur-unsur dasar yang harus dikenal mahasiswa untuk memahami suatu konsep (Krathwohl, 2002) atau dengan kata lain, merupakan materi-materi prasyarat suatu konsep.Sehingga dalam penelitian ini, pemahaman faktual adalah pemahaman yang menyangkut materi prasyarat konsep limit fungsi, terutama definisi limit fungsi. Adapun materi prasyarat dalam definisi formal limit fungsi adalah nilai mutlak dan logika matematika. Pemahaman tentang materi-materi prasyarat tersebut dibagi menjadi beberapa bagian, yaitu: (1) pemahaman tentang makna 𝜀 dan 𝛿; (2) pemahaman tentang makna nilai mutlak 0 < |𝑥 − 𝑐| < 𝛿 dan |𝑓(𝑥) − 𝐿| < 𝜀 ;(3) pemahaman tentang makna pernyataan implikasi 0 < |𝑥 − 𝑐| < 𝛿 ⟹ |𝑓(𝑥) − 𝐿| < 𝜀.
2. Pemahaman Interpretasi
Interpretasi/representasi adalah abstraksi dari ide-ide matematika atau skema kognitif yang dikembangkan mahasiswa melalui pengalamannya (Pape & Tchoshanov, 2011). Dengan kata lain, representasi seperti numeral, persamaan aljabar, grafik, tabel, diagram dan cart adalah penjelmaan eksternal dari suatu konsep matematikadan dapat membantunya dalam memahami konsep tersebut. “Menginterpretasi” merupakan salah satu verb yang menyangkut mengenai pemahaman, sebagaimana dijelaskan baik pada taksonomi Bloom 1956 maupun pada revisi taksonomi Bloom oleh Anderson dan Knathwohl (Wilson, 2001). Verb tersebut berkaitan dengan kemampuan dalam menginterpretasikan sebuah konsep dengan objek-objek tertentu. Sejalan dengan itu, Pemahaman interpretasi yang dimaksud dalam penelitian ini adalah pemahaman dalam menginterpretasi definisi formal limit fungsi dengan menggunakan grafik. Selain itu, Pemahaman Interpretasipada dasarnya relevan dengan pemahaman Analog oleh Pollatsek, Lima dan Well (1981).
3. Pemahaman Sintaktik
Pemahaman sintaktik merujuk pada syntactic proof production yang dikemukakan oleh Weber (2004), bahwaseseorang akan mengonstruk suatu bukti dengan melakukan manipulasi terhadap suatu definisi dengan benar dan fakta-fakta lainnya dengan cara yang diperbolehkan secara logika.
5 Sama halnya dengan syntactic proof production, pemahaman sintaktik yang dimaksud adalah pemahaman dalam melakukan manipulasi terhadap definisi limit fungsi dengan benar dan fakta-fakta lainnya dengan cara yang diperbolehkan secara logika, yaitu menegasikan definisi formal limit fungsi dengan menggunakan beberapa konsep prasyarat.
4. Pemahaman Pembuktian
Pembuktian berasal dari kata bukti, sehingga pemahaman pembuktian adalah pemahaman mahasiswa dalam melakukan pembuktian. Dalam penelitian ini, pembuktian yang dimaksud adalah pembuktian mengenai kebenaran nilai limit fungsi di suatu titik maupun pembuktian nilai limit fungsi di suatu titik bernilai salah. Pada dasarnya, pemahaman pembuktianrelevan dengan pemahaman rasional yang dikemukakan oleh Polya (Meel, 2003). Bukti dianggap sebagai pusat dari disiplin ilmu matematika dan menjadi kebiasaan oleh para matematikawan (Knuth, 2002). Seseorang tidak dapat mempelajari matematika tanpa belajar bukti matematis dan bagaimana membuatnya (Wu, 1996; Balacheff, 2010).Bukti hendaknya ditulis dalam format yang terstruktur dan jelas langkah demi langkah serta disertai dengan alasan yang jelas (Lamport, 1993). Dalam pembuktian matematis, diperlukan pemahaman dan penguasaan konsep dasar matematika yang baik (Santosa, 2013). Sehingga dalam membuktikan kebenaran nilai limit fungsi, hendaklah memiliki pemahaman konsep yang mendalam tentang materi prasyaratnya yaitu nilai mutlak dan logika matematika. Adapun kemampuan pembuktian matematis menurut Selden & Selden (2003) meliputi: (1) Kemampuan menyusun pembuktian; (2) Kemampuan memvalidasi bentuk pembuktian.
Berbagai penelitian sebelumnya telah dilakukan terkait pemahaman mahasiwa tentang konsep limit fungsi. Tall (1992) menemukan bahwa kemampuan mahasiswa melakukan manipulasi aljabar dalam pembuktian limit fungsi masih rendah serta pemahaman tentang kalimat berkuantor ganda dalam definisi formal limit fungsi juga masih kurang kurang. Terkait dengan validasi kebenaran nilai limit fungsi, Oktaviyanthi, Tatang dan Jarnawi (2018) menyimpulkan bahwa mahasiswa menggunakan strategi-strategi yang bervariasi untuk menyelesaikannya dengan menggunakan definisi formal. Secara umum, sistematika pemecahan masalah terdiri dari dua tahap, yaitu langkah (1) persiapan pembuktian (preparation of proof) dan (2) pembuktian (proving).
METODE PENELITIAN
Penelitian ini merupakan penelitian kualitatif dengan pendekatan deskriptif. Subjek pada penelitian ini berjumlah 8 orang yang merupakan mahasiswa jurusan Matematika semester 5. Subjek dipilih berdasarkan kesediaan subjek dalam mengikuti pengumpulan dan kemampuan subjek dalam mengomunikasikan pikirannya. Instrumen penelitian berupa tes pemahaman konsep wawancara semi terstruktur untuk mengidentifikasi pemahaman subjek terkait dengan konsep limit fungsi intrumen penelitian tersebut sebelumnya telah divalidasi oleh 2 orang ahli. Data yang terkumpul berupa jawaban tes pemahaman konsep dan transkrip wawancara yang dianalisis menggunakan teknik analisis dengan langkah-langkah reduksi data, penyajian data dan penarikan kesimpulan.
HASIL DAN PEMBAHASAN
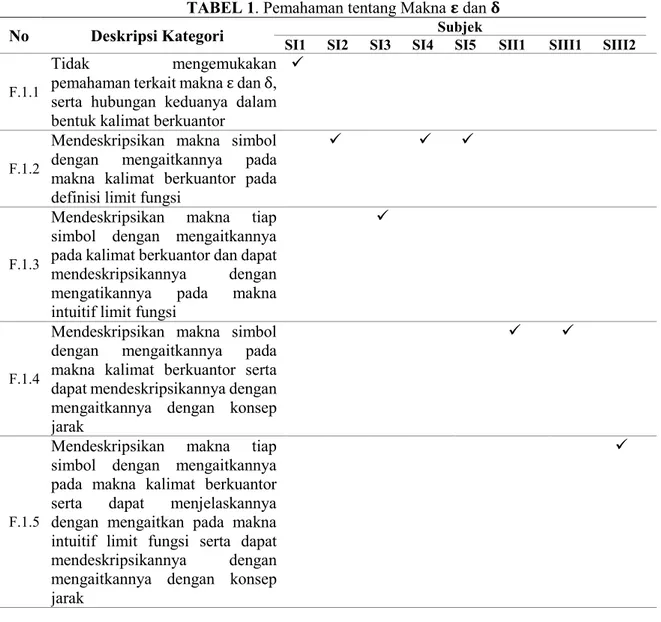
1. Pemahaman FaktualPendeskripsian pemahaman faktual terbagi menjadi tiga, yaitu: (a) pemahaman tentang makna 𝜀 dan 𝛿; (b) pemahaman tentang makna nilai mutlak; dan (c) pemahaman tentang makna pernyataan implikasi. Dari ketiga pemahaman faktual tersebut, masing-masing diperoleh beberapa kategori. Terdapat 5 kategori pemahaman terkait dengan makna ε dan δ terlihat pada Tabel 1. Pada kategori pertama (F.1.1), subjek tidak mengemukakan pemahamannya baik terkait makna 𝜀 maupun 𝛿. Pada kategori kedua (F.1.2), subjek mendeskripsikan makna 𝜀 dan 𝛿 dengan mengaitkan pada makna kalimat berkuantor. Subjek memahami bahwa 𝜀 merupakan bilangan real positif sebarang.
6 Ini dikarenakan pada definisi limit fungsi, didahului oleh kata “untuk setiap 𝜀 > 0”. Sementara itu, 𝛿 merupakan bilangan real positif yang berpadanan dengan 𝜀 yang diberikan.
Pada kategori ketiga (F.1.3), subjek tidak hanya mendeskripsikan simbol-simbol tersebut berdasarkan pada makna kalimat berkuantor, tetapi juga dengan mengaitkan pada makna intuitif limit fungsi. Dalam mengaitkan dengan makna intuitif limit fungsi, subjek mendeskripsikan bahwa nilai 𝜀 yang dipilih biasanya merupakan nilai yang kecil. Pada indikator keempat (F.1.4), subjek juga mendeskripsikan makna tiap simbol dengan mengaitkannya pada makna kalimat berkuantor. Selain itu, subjek juga dapat mendeskripsikan tiap simbol tersebut dengan mengaitkannya pada konsep jarak. Dalam mendeskripsikan makna tiap simbol sebagai jarak, subjek mengemukakannya sebagai jarak pada sumbu-sumbu koordinat. Subjek mengemukakan bahwa 𝜀 mengacu pada jarak 𝑓(𝑥) dan 𝐿 pada sumbu−𝑦 dan 𝛿 mengacu pada jarak 𝑥 dan 𝑐 pada sumbu−𝑥. Dapat dikatakan bahwa kategori pemahaman subjek pada kategori kelima (F.1.5) merupakan kategori pemahaman yang paling lengkap dibandingkan dengan kategori-kategori sebelumnya. Pada kategori ini, subjek Mendeskripsikan makna tiap simbol dengan mengaitkannya pada makna kalimat berkuantor. Selain itu, subjek juga dapat menjelaskannya dengan mengaitkan pada makna intuitif limit fungsi serta dapat menyatakannya sebagai suatu jarak masing-masing pada tiap sumbu koordinat.
TABEL 1. Pemahaman tentang Makna 𝛆 dan 𝛅
No Deskripsi Kategori SI1 SI2 SI3 SI4 Subjek SI5 SII1 SIII1 SIII2 F.1.1
Tidak mengemukakan
pemahaman terkait makna ε dan δ, serta hubungan keduanya dalam bentuk kalimat berkuantor
F.1.2
Mendeskripsikan makna simbol dengan mengaitkannya pada makna kalimat berkuantor pada definisi limit fungsi
F.1.3
Mendeskripsikan makna tiap simbol dengan mengaitkannya pada kalimat berkuantor dan dapat mendeskripsikannya dengan mengatikannya pada makna intuitif limit fungsi
F.1.4
Mendeskripsikan makna simbol dengan mengaitkannya pada makna kalimat berkuantor serta dapat mendeskripsikannya dengan mengaitkannya dengan konsep jarak
F.1.5
Mendeskripsikan makna tiap simbol dengan mengaitkannya pada makna kalimat berkuantor serta dapat menjelaskannya dengan mengaitkan pada makna intuitif limit fungsi serta dapat mendeskripsikannya dengan mengaitkannya dengan konsep jarak
7 Dari kelima kategori tersebut, diperoleh pemahaman subjek tentang makna ε dan δ yaitu mendeskripsikannya berdasaran pada kalimat berkuantor pada definisi limit fungsi, makna intuitif limit fungsi, dan sebagai jarak pada masing-masing sumbu koordinat. Terkait pendeskripsian makna 𝜀 dan 𝛿 sebagai jarak, ini pada dasarnya sama dengan yang dikemukakan oleh Hughes-Hallet, dkk (2013).
Pemahaman subjek mengenai makna nilai mutlak terdiri dari 5 kategori seperti terlihat pada Tabel 2. Pada kategori pertama (F.2.1), subjek tidak mengemukakan pemahamannya terkait dengan makna nilai mutlak, baik 0 < |𝑥 − 𝑐| < 𝛿 maupun|𝑓(𝑥) − 𝐿| < 𝜀. Pada kategori kedua (F.2.2), subjek mendeskripsikan makna tiap nilai mutlak dengan hanya berdasarkan pada apa yang dilihat. Subjek mendeskripsikan bahwa nilai mutlak dari 𝑥 kurang 𝑐 selalu kurang dari 𝛿 serta harga nilai mutlak dari 𝑓(𝑥) kurang dari 𝐿 selalu kurang dari 𝜀. Subjek mendeskripsikannya tanpa mengaitkan dengan objek matematika lainnya. Pada kategori ketiga (F.2.3), subjek mendeskripsikan makna nilai mutlak tersebut dengan berdasarkan pada makna intuitif limit fungsi. Subjek memahami bahwa 𝑥 tidak pernah sama dengan 𝑐. Ini dikarenakan pada makna intuitif limit fungsi, titik-titik yang ditinjau adalah titik-titik yang dekat dengan 𝑐 dan bukan titik 𝑐 sehingga 𝑥 tidak pernah sama dengan 𝑐. Subjek juga memahami bahwa 𝑓(𝑥) kurang 𝐿 bisa saja sama dengan nol atau dengan kata lain 𝑓(𝑥) = 𝐿.
Pada kategori keempat (F.2.4), subjek mendeskripsikan makna nilai mutlak berdasarkan pada makna jarak. Subjek mendeskripsikan bahwa jarak antara 𝑥 dan 𝑐 lebih dari nol dan kurang dari delta sehingga 𝑥 tidak boleh sama dengan 𝑐 serta jarak antara 𝑓(𝑥) dan 𝐿 kurang dari 𝜀. Pada kategori kelima (F.2.5), pemahaman subjek mancakup dua kategori sebelumnya. Selain itu, subjek juga dapat mendeskripsikannya berdasarkan pada makna selisih. Subjek mendeskripsikan makna nilai mutlak dengan berdasarkan pada makna selisih dengan menyatakan bahwa selisih dari 𝑥 dan 𝑐 lebih dari nol dan kurang dari 𝛿 serta selisih dati 𝑓(𝑥) dan 𝐿 kurang dari 𝜀.
TABEL 2. Pemahaman tentang Makna 𝟎 < |𝒙 − 𝒄| < 𝜹 dan |𝒇(𝒙) − 𝑳| < 𝜺
No Deskripsi Kategori Subjek
SI1 SI2 SI3 SI4 SI5 SI6 SI7 SI8
F.2.1
Tidak mengemukakan
pemahaman mengenai makna 0 < |𝑥 − 𝑐| < 𝛿 dan |𝑓(𝑥) − 𝐿| < 𝜀
F.2.2
Mendeskripsikan makna tiap nilai mutlak hanya berdasarkan pada apa yang dilihat.
F.2.3
Mendeskripsikan makna nilai mutlak berdasarkan pada makna intuitif limit fungsi.
F.2.4
Mendeskripsikan makna nilai mutlak berdasarkan pada makna jarak.
F.2.5
Mendeskripsikan makna nilai mutlak berdasarkan pada makna jarak maupun selisih serta dapat dapat mendeskripsikannya nilai mutlak tersebut berdasarkan pada makna intuitif limit fungsi.
Dari keempat kategori tersebut, pemahaman subjek pada dasarnya adalah mendeskripsikan makna nilai mutlak dengan cenderung mengaitkannya dengan jarak, selisih serta mengaitkannya dengan makna intuitif limit fungsi. selain itu, juga terdapat subjek yang mendeskripsikannya
8 berdasarkan pada apa yang dilihat. Pendeskripsian makna nilai mutlak berdasarkan pada makna jarak pada dasarnya sama seperti yang dikemukakan oleh Purcell, dkk (2004). Dijelaskan bajwa |𝑥 − 𝑐| < 𝛿 bermakna jarak antara 𝑥 dan 𝑐. sedangkan pendeskripsian berdasarkan pada makna selisih sama seperti yang dikemukakan oleh Sierpinska, Bobos dan Pruncut (2011). Sedangkan jika dilihat dari jenis-jenis pemahaman yang dikemukakan oleh Pollatsek, dkk (1981), pemahaman subjek pada ketiga kategori terakhir termasuk pemahaman fungsional.
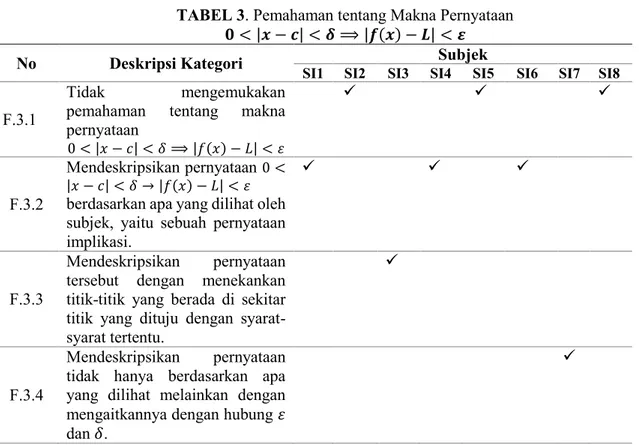
Pemahaman tentang pernyataan implikasi terdiri dari 4 kategori seperti terlihat pada Tabel 3. Pada kategori pertama (F.3.1), subjek tidak mengemukakan pemahamannya terkait dengan makna pernyataan implikasi tersebut. Pada kategori kedua (F.3.2), subjek memahami pernyataan tersebut sebagai implikasi (sebab akibat). Subjek mendeskripsikan bahwa jika 0 < |𝑥 − 𝑐| < 𝛿 maka |𝑓(𝑥) − 𝐿| < 𝜀. Subjek tidak mengemukakan lebih lanjut mengenai pernyataan implikasi tersebut. Pada kategori ketiga (F.3.3),subjek mendeskripsikan pernyataan tersebut tidak hanya berdasarkan pada apa yang dilihat. Subjek menekankan titik-titik yang berada di sekitar titik yang dituju dengan syarat-syarat tertentu. Syarat tersebut adalah selisihnya dengan 𝑐 kurang dari 𝛿 dan lebih dari nol. Syarat ini mengakibatkan nilai fungsi dari titik tersebut memiliki nilai selisih dengan 𝐿 kurang dari 𝜀 sebagaimana pada konsekuen di pernyataan implikasi tersebut. Sedangkan pada kategori keempat (F.3.4), subjek mendeskripsikan pernyataan tersebut berdasarkan pada hubungan 𝜀 dan 𝛿. Dalam mengaitkan antara 𝜀 dan 𝛿, subjek memahami bahwa 𝛿 mempengaruhi 𝜀.
TABEL 3. Pemahaman tentang Makna Pernyataan 𝟎 < |𝒙 − 𝒄| < 𝜹 ⟹ |𝒇(𝒙) − 𝑳| < 𝜺
No Deskripsi Kategori Subjek
SI1 SI2 SI3 SI4 SI5 SI6 SI7 SI8
F.3.1
Tidak mengemukakan
pemahaman tentang makna pernyataan 0 < |𝑥 − 𝑐| < 𝛿 ⟹ |𝑓(𝑥) − 𝐿| < 𝜀 F.3.2 Mendeskripsikan pernyataan 0 < |𝑥 − 𝑐| < 𝛿 → |𝑓(𝑥) − 𝐿| < 𝜀 berdasarkan apa yang dilihat oleh subjek, yaitu sebuah pernyataan implikasi.
F.3.3
Mendeskripsikan pernyataan tersebut dengan menekankan titik-titik yang berada di sekitar titik yang dituju dengan syarat-syarat tertentu.
F.3.4
Mendeskripsikan pernyataan tidak hanya berdasarkan apa yang dilihat melainkan dengan mengaitkannya dengan hubung 𝜀 dan 𝛿.
Dari keempat kategori tersebut, diperoleh bahwa subjek mendeskripsikan pernyataan tersebut dengan menekankan pada titik yang berada di sekitar titik yang dituju pada definisi limit fungsi dengan syarat-syarat tertentu. Ini berakibat nilai fungsinya juga memiliki syarat-syarat tertentu pula. Serta dengan mengaitkannya dengan hubungan 𝜀 dan 𝛿. Proses berpikir tersebut (menekankan pada titik dengan syarat tertentu) termasuk dalam domain process sebagaimana dikemukakan oleh Cottrill dkk (1992). Sementara itu, jika dilihat berdasarkan pemahaman oleh Pollatsek, dkk (1981), kategori ini termasuk dalam pemahaman fungsional. Selain itu, subjek
9 mendeskripsikan pernyataan implikasi dengan mengaitkan pada hubungan 𝜀 dan 𝛿 secara tidak tepat. 𝛿 pada umumnya dipengaruhi oleh 𝜀 (Bartle & Sherbert, 2000), bukan 𝛿 yang mempengaruhi 𝜀.
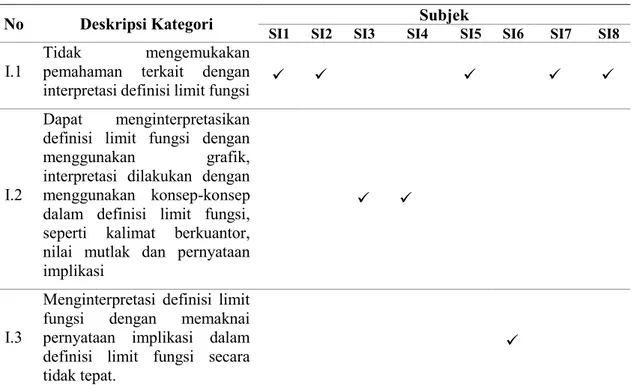
2. Pemahaman Interpretasi
Berdasarkan data yang telah diperoleh, terdapat dua kategori terkait pemahaman interpretasi seperti terlihat pada Tabel 4. Pada kategori pertama (I.1), subjek tidak mengemukakan pemahamannya terkait dengan interpretasi definisi limit fungsi dengan menggunakan grafik. Pada kategori kedua (I.2), subjek dapat menginterpretasikan definisi limit fungsi dengan menggunakan grafik. Subjek mampu menuliskan dan menjelaskannya. Pada kategori ketiga (I.3), subjek menginterpretasikan definisi limit fungsi dengan memaknai pernyataan implikasi dalam definisi limit fungsi secara tidak tepat. Dalam menginterpretasikannya, subjek memaknai pernyataan implikasi dalam definisi limit fungsi secara terbalik, subjek memperlihatkan dengan grafik bahwa jika nilai fungsinya berada pada di sekitar 𝐿 yang memiliki jarak kurang dari epsilon, maka titik-titik 𝑥-nya dari nilai fungsi tersebut akan berada di sekitar 𝑐 dengan jarak kurang dari 𝛿.
TABEL 4. Pemahaman Interpretasi
No Deskripsi Kategori SI1 SI2 SI3 SI4 Subjek SI5 SI6 SI7 SI8 I.1
Tidak mengemukakan
pemahaman terkait dengan
interpretasi definisi limit fungsi
I.2
Dapat menginterpretasikan definisi limit fungsi dengan menggunakan grafik, interpretasi dilakukan dengan menggunakan konsep-konsep dalam definisi limit fungsi, seperti kalimat berkuantor, nilai mutlak dan pernyataan implikasi
I.3
Menginterpretasi definisi limit fungsi dengan memaknai pernyataan implikasi dalam definisi limit fungsi secara tidak tepat.
Jika ditinjau dari teori pemahaman yang dikemukakan oleh Skemp (1976), maka pemahaman pada kategori kedua termasuk pemahaman relasional dikarenakan dalam menginterpretasikan definisi limit fungsi dengan menggunakan grafik, subjek mampu menuliskan dan
menjelaskannya. Pada dasarnya diperoleh dua pemahaman, yaitu dapat mengiterpretasi definisi limit fungsi dengan tepat, serta mengiterpretasi definisi limit fungsi dengan memaknai
pernyataan implikasi di dalamnya secara terbalik. 3. Pemahaman Sintaktik
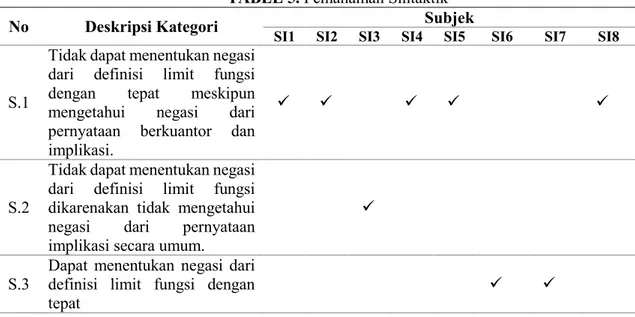
Terdapat 3 kategori pemahaman yang diperoleh terkait dengan pemahaman sintaktik seperti terlihat pada Tabel 5. Pada kategori pertama (S.1), subjek tidak dapat menentukan negasi definisi limit fungsi dengan tepat. Meskipun begitu, subjek telah mengetahui negasi dari kuantor universal dan kuantor eksistensial. Subjek juga telah mengetahui negasi dari pernyataan implikasi secara umum. Terkait dengan kategori kedua (S.2), dapat disimpulkan bahwa pada dasarnya subjek
10 masih kurang dalam mengimplementasikan pemahamannya. Pemahaman tersebut berupa negasi dari pernyataan berkuantor maupun implikasi untuk menentukan negasi dari definisi limit fungsi. Pada kategori ketiga (S.3), subjek juga tidak dapat menentukan negasi dari definisi limit fungsi. Ini disebabkan karena subjek tidak mengetahui negasi dari pernyataan implikasi secara implikasi. Sedangkan pada pada kategori keempat (S.4), subjek telah dapat menentukan negasi definisi limit fungsi dengan tepat. Subjek telah mengetahui negasi dari pernyataan berkuantor dan pernyataan implikasi dan dapat mengimplementasikannya dengan tepat.
TABEL 5. Pemahaman Sintaktik
No Deskripsi Kategori Subjek
SI1 SI2 SI3 SI4 SI5 SI6 SI7 SI8
S.1
Tidak dapat menentukan negasi dari definisi limit fungsi dengan tepat meskipun mengetahui negasi dari pernyataan berkuantor dan implikasi.
S.2
Tidak dapat menentukan negasi dari definisi limit fungsi dikarenakan tidak mengetahui negasi dari pernyataan implikasi secara umum.
S.3
Dapat menentukan negasi dari definisi limit fungsi dengan tepat
Berdasarkan kategori-kategori yang telah diperoleh terkait pemahaman sintaktik, dapat disimpulkan bahwa pada pemahaman sintaktik, pemahaman yang kurang terletak pada negasi dari pernyataan implikasi. Selain itu, kemampuan subjek dalam mengimplementasikan pemahamannya juga masih kurang.
4. Pemahaman Pembuktian
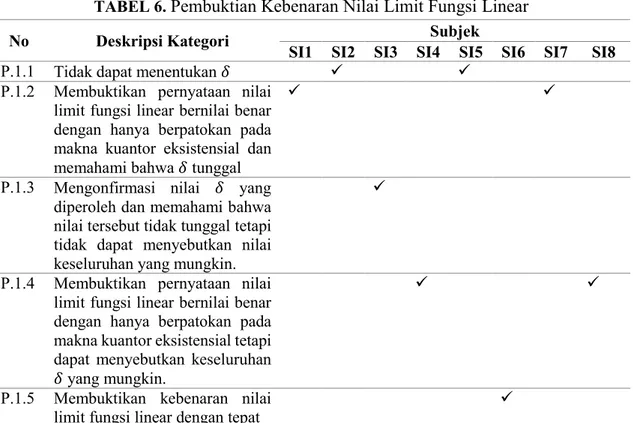
Pemahaman tentang pembuktian kebenaran nilai limit fungsi linear terdiri dari 6 kategori terlihat pada Tabel 6. Pada kategori pertama (P.1.1), subjek tidak dapat menentukan nilai 𝛿 > 0 yang berpadanan dengan 𝜀 > 0 yang diberikan. Subjek terkendala pada manipulasi aljabar yang masih kurang terutama pada ketaksamaan yang memuat nilai mutlak. Pada kategori kedua (P.1.2), subjek dapat menentukan nilai 𝛿 > 0 yang berpadanan dengan 𝜀 > 0 yang diberikan. Akan tetapi subjek memahami bahwa nilai tersebut tunggal. Subjek membuktikan pernyataan nilai limit fungsi linear bernilai benar dengan hanya berpatokan pada makna kuantor eksistensial. Subjek beranggapan bahwa jika 𝛿 telah ditentukan, maka pembuktian telah selesai. Artinya pernyataan telah terbukti benar. Padahal masih terdapat beberapa langkah berikutnya. Pada kategori ketiga (P.1.3), subjek dapat menentukan nilai 𝛿 serta subjek telah mengonfirmasi nilai tersebut. Subjek mengetahui bahwa nilai tersebut tidaklah tunggal dan berupa suatu interval, akan tetapi subjek tidak dapat menyebutkannya. Pada kategori keempat (P.1.4), subjek dapat menentukan nilai 𝛿 dan dapat menyebutkan keseluruhan nilai yang mungkin. Akan tetapi subjek membuktikan pernyataan nilai limit fungsi linear bernilai benar dengan hanya berpatokan pada makna kuantor eksistensial. Subjek beranggapan bahwa jika 𝛿 telah ditentukan, maka pembuktian telah selesai. Pada kategori kelima (P.1.5), subjek dapat membuktikan kebenaran nilai limit fungsi linear dengan tepat. Subjek melakukan konfirmasi terhadap 𝛿 yang telah diperoleh. Subjek membuat kesimpulan mengenai pembuktian yang telah dilakukan. Selain itu, subjek memahami bahwa 𝛿 yang diperoleh tidaklah tunggal serta subjek juga dapat menentukan keseluruhan nilai yang mungkin.
11 TABEL 6.
Pembuktian Kebenaran Nilai Limit Fungsi Linear
No Deskripsi Kategori Subjek
SI1 SI2 SI3 SI4 SI5 SI6 SI7 SI8
P.1.1 Tidak dapat menentukan 𝛿
P.1.2 Membuktikan pernyataan nilai limit fungsi linear bernilai benar dengan hanya berpatokan pada makna kuantor eksistensial dan memahami bahwa 𝛿 tunggal
P.1.3 Mengonfirmasi nilai 𝛿 yang diperoleh dan memahami bahwa nilai tersebut tidak tunggal tetapi tidak dapat menyebutkan nilai keseluruhan yang mungkin.
P.1.4 Membuktikan pernyataan nilai limit fungsi linear bernilai benar dengan hanya berpatokan pada makna kuantor eksistensial tetapi dapat menyebutkan keseluruhan 𝛿 yang mungkin.
P.1.5 Membuktikan kebenaran nilai limit fungsi linear dengan tepat
Sebagian besar subjek dapat menentukan kuantitas pada kuantor eksistensial (𝛿) dengan tepat, tetapi ada beberapa subjek yang menganggap bahwa kuantitas tersebut tunggal. Selain itu, terdapat juga subjek yang tidak dapat menentukan kuantitas tersebut. Subjek terkendala pada manipulasi aljabar. Hal ini berarti bahwa pemahaman dalam melakukan manipulasi aljabar masih kurang, ini sejalan dengan Tall (1992). Dalam hal pembuktian matematis, subjek hanya berpatokan pada penentuan nilai kuantitas pada kuantor eksistensial. Padahal menurut Selden & Selden (2003), perlu dilakukan validasi dari bentuk pembuktian tersebut, dalam hal ini konfirmasi kuantitas pada kuantor eksistensial. Selain itu, sebaiknya pembuktian ditutup dengan kesimpulan terkait dengan kebenaran nilai limit fungsi sebagaimana oleh Oktaviyanthi, Tatang dan Jarnawi (2018). Dari sini, dapat disimpulkan bahwa subjek kurang dalam penentuan nilai 𝛿 dan subjek terkendala pada manipulasi aljabar. Selain itu, subjek juga kurang dalam penyusunan bukti matematis. Ini didasarkan pada masih terdapatnya subjek yang tidak mengonfirmasi 𝛿 yang telah diperoleh serta tidak membuat kesimpulan mengenai pembuktian yang telah dilakukan.
TABEL 7. Pembuktian Kebenaran Nilai Limit Fungsi Kuadrat
No Deskripsi Kategori SI1 SI2 SI3 SI4 Subjek SI5 SI6 SI7 SI8
P.2.1 Tidak dapat menentukan 𝛿
P.2.2 Meninjau titik-titik di sekitaran titik yang didekati dengan syarat awal tertentu, akan tetapi tidak mempertimbangkan syarat tersebut dalam penentuan akhir 𝛿, serta tidak mengonfirmasi nilai tersebut dan tidak membuat kesimpulan mengenai pembuktian yang telah dilakukan.
12 P.2.3 Dapat menentukan 𝛿 dengan tepat
tetapi tidak dapat menjelaskan alasan logis mengenai pemilihan nilai tersebut, tidak mengonfirmasi 𝛿 yang telah diperoleh serta tidak membuat kesimpulan mengenai pembuktian yang telah dilakukan.
P.2.4 Dapat melakukan manipulasi aljabar dengan tepat untuk menentukan nilai 𝛿, meninjau titik-titik di sekitaran titik yang didekati tetapi tidak menegaskan mengenai nilai akhir 𝛿, dan tidak mengonfirmasinya, akan tetapi membuat kesimpulan mengenai pembuktian yang telah dilakukan.
P.2.5 Penentuan 𝛿 tidak dilakukan dengan meninjau titik di sekitaran titik yang dituju melainkan mengambil langsung titik yang dituju, tidak mengonfirmasi mengenai 𝛿 tetapi membuat kesimpulan mengenai kebenaran nilai limit fungsi.
Pembuktian kebenaran nilai limit fungsi kuadrat bernilai benar terdiri dari 5 kategori seperti pada Tabel 7. Pada kategori pertama (P.2.1), subjek terhenti pada penentuan nilai 𝛿. Ini menandakan bahwa kemampuan manipulasi aljabar subjek masih rendah.. Pada kategori kedua (P.2.2), subjek dapat melakukan manipulasi aljabar untuk menentukan 𝛿. Subjek meninjau titik-titik di sekitar titik yang dituju dengan memberikan syarat tertentu sebagai syarat awal untuk menentukan 𝛿. Akan tetapi subjek tidak mempertimbangkan syarat awal tersebut dalam penentuan nilai akhir 𝛿. Setelah penentuan nilai 𝛿, subjek tidak melakukan konfirmasi mengenai nilai tersebut dan tidak melakukan membuat kesimpulan mengenai pembuktian yang telah dilakukan. Pada kategori ketiga (P.2.3), subjek dapat menentukan nilai 𝛿 dengan tepat. Subjek meninjau titik-titik yang berada di sekitar titik yang dituju dengan memberikan syarat tertentu sebagai syarat awal untuk menentukan 𝛿. Setelah itu pada penentuan nilai akhir 𝛿, subjek juga melibatkan syarat awal tersebut. Akan tetapi subjek tidak dapat memberikan alasan logis terkait dengan penentuan 𝛿. Subjek tidak mengonfirmasi 𝛿 yang telah diperoleh dan tidak membuat kesimpulan mengenai pembuktian yang telah dilakukan.
Pada kategori keempat (P.2.4), subjek dapat melakukan manipulasi aljabar yang tepat menentukan nilai 𝛿. Subjek meninjau titik-titik yang berada di sekitar titik yang dituju dengan memberikan syarat tertentu sebagai syarat awal untuk menentukan 𝛿. Setelah itu pada penentuan nilai akhir 𝛿, subjek tidak menegaskan nilai dari 𝛿. subjek tidak menegaskan apakah 𝛿 adalah nilai pada syarat awal sebelumnya atau nilai dari hasil penguraian konsekuen pada pernyataan implikasi. Subjek juga tidak mengonfirmasi 𝛿 yang telah diperoleh. Akan tetapi, subjek membuat kesimpulan mengenai pembuktian yang telah dilakukan. Pada kategori kelima (P.2.5), subjek dapat melakukan manipulasi aljabar untuk penentuan nilai 𝛿. Akan tetapi subjek pada dasarnya tidak meninjau titik-titik yang berada di sekitar titik yang dituju. Subjek langsung mengambil langsung titik yang dituju. Setelah itu, subjek tidak mengonfirmasi nilai 𝛿 yang telah diperoleh. Subjek membuat kesimpulan mengenai pembuktian yang telah dilakukan.
13 Sebagian besar subjek terhenti pada penentuan kuantitas pada kuantor eksistensial yang menandakan bahwa pemahaman dalam melakukan manipulasi aljabar masih kurang seperti yang dikemukakan oleh Tall (1992). Selain itu, Selain itu, pemahaman logika matematika (pernyataan implikasi) pada dasarnya masih rendah karena subjek tidak mampu mengaitkan pemilihan 𝛿 dengan makna pernyataan implikasi dalam definisi limit fungsi tersebut. Dalam hal penentuan kuantitas pada kuantor eksistensial (nilai 𝛿), subjek meninjau titik-titik yang berada di sekitar titik yang dituju. Hanya satu subjek yang dapat menentukan kuantitas tersebut dengan tepat meskipun subjek tersebut tidak dapat menjelaskan alasannya. Jika ditinjau dari pemahaman oleh Skemp(1976), pemahaman tersebut termasuk dalam pemahaman instrumental. Tidak satupun subjek yang mengonfirmasi kuantitas pada kuantor eksistensial yang telah diperoleh, sebagian besar subjek tidak membuat kesimpulan mengenai pembuktian yang telah dilakukan.
Terdapat 3 kategori terkait dengan pembuktian nilai limit fungsi bernilai salah seperti terlihat pada Tabel 8. Pada kategori pertama (P.3.1), subjek tidak menuliskan jawaban terkait dengan pembuktian tersebut. Pada kategori kedua (P.3.2), subjek tidak menghubungkan pembuktian dengan negasi dari defnisi limit fungsi. Subjek hanya menguraikan anteseden dan konsekuen pada pernyataan implikasi dalam definisi limit fungsi. Karena mendapatkan nilai mutlak yang berbeda, maka subjek menyimpulkan bahwa nilai limit fungsi bernilai salah. Pada kategori ketiga (P.3.3), subjek mengaitkan pembuktian dengan negasi dari definisi limit fungsi. Subjek memilih suatu nilai 𝜀, kemudian menyatakan bahwa tidak ada 𝛿 yang memenuhi sehingga pernyataan implikasi pada definisi limit fungsi bernilai benar. akan tetapi, hal tersebut masih keliru karena masih terdapat 𝛿 sehingga pernyataan tersebut bernilai benar. kekeliruan ini terjadi karena subjek tidak mengonfirmasinya kembali. Pada kategori keempat (P.3.4), subjek juga memilih suatu nilai 𝜀. Subjek kemudian menyatakan bahwa tidak ada 𝛿 yang memenuhi sehingga pernyataan implikasi pada definisi limit fungsi bernilai benar. meskipun pemilihan 𝜀 benar, tetapi subjek tidak melakukan konfirmasi ulang terhadap nilai tersebut. Pada ketiga kategori tersebut, subjek telah membuat kesimpulan mengenai pembuktian yang telah dilakukan.
TABEL 8.
Pembuktian Nilai Limit Fungsi Bernilai Salah
No Deskripsi Kategori Subjek
SI1 SI2 SI3 SI4 SI5 SI6 SI7 SI8
P.3.1 Tidak menuliskan jawaban
P.3.2
Tidak menghubungkan pembuktian dengan negasi dari definisi limit fungsi.
P.3.3
Mengaitkan pembuktian dengan negasi dari definisi limit fungsi, akan tetapi implementasinya masih kurang.
P.3.4
Mengaitkan pembuktian dengan negasi dari definisi limit dengan tepat meskipun tidak melakukan konfirmasi mengenai kuantitas yang telah dipilih.
Dari dua kategori terakhir, subjek menghubungkan pembuktiannya dengan negasi dari definisi formal limit fungsi meskipun implementasinya masih kurang. Bentuk pembuktian tersebut pada dasarnya merupakan syntactic proof production oleh Weber (2004). Pada bagian ini subjek juga tidak mengonfirmasi kuantitas yang telah diperoleh. Akan tetapi subjek telah membuat kesimpulan mengenai pembuktian yang telah dil1akukan.
14 Dapat dilihat bahwa dalam pembuktian pemahaman, sebagian besar mahasiswa terhadang pada kemampuan manipulasi aljabar. Pemahaman subjek pada logika matematika terutama pada pernyataan implikasi dan pernyataan berkuantor masih kurang. Pemahaman subjek mengenai kuantitas 𝛿 juga masih rendah pada umumnya. Ini dapat dilihat bahwa subjek masih belum memahami himpunan nilai 𝛿 yang berpadanan dengan 𝜀 yang diberikan. Masih ada subjek yang memahami bahwa nilai tersebut adalah tunggal. Selain itu, masih banyak subjek yang tidak melakukan pembuktian matematis sebagaimana mestinya, seperti tidak mengonfirmasi kuantitas yang telah diperoleh dan tidak membuat kesimpulan mengenai pembuktian yang telah dilakukan. Ini menandakan kurangnya pemahaman tentang bukti matematis seperti yang ditemukan oleh Minggi, Paduppai dan Assagaf (2016).
KESIMPULAN
1. Pemahaman FaktualDari hasil penelitian, diperoleh pemahaman subjek tentang makna ε dan δ yaitu mendeskripsikannya berdasaran pada kalimat berkuantor pada definisi limit fungsi, makna intuitif limit fungsi, dan sebagai jarak pada masing-masing sumbu koordinat. Pemahaman tentang makna nilai mutlak dalam definisi formal limit fungsi yaitu mendeskripsikan makna nilai mutlak tersebut dengan cenderung mengaitkannya dengan jarak, selisih serta mengaitkannya dengan makna intuitif limit fungsi. Sedangkan pada pemahaman tentang makna pernyataan implikasi dalam definisi formal limit fungsi, diperoleh subjek mendeskripsikan pernyataan tersebut dengan menekankan pada titik yang berada di sekitar titik yang dituju pada definisi limit fungsi dengan syarat-syarat tertentu yang berakibat nilai fungsinya juga memiliki syarat-syarat tertentu pula, serta ada pula subjek yang mengaitkannya dengan hubungan 𝜀 dan 𝛿.
2. Pemahaman Interpretasi
Pada dasarnya diperoleh dua pemahaman, yaitu dapat mengiterpretasi definisi limit fungsi dengan tepat, serta mengiterpretasi definisi limit fungsi dengan memaknai pernyataan implikasi di dalamnya secara terbalik.
3. Pemahaman Sintaktik
Pemahaman subjek pada negasi dari pernyataan implikasi dan kemampuan mengimplentasikan pemahamannya untuk menentukan negasi dari definisi limit fungsi masih kurang.
4. Pemahaman Pembuktian
Pada dasarnya tidak dapat melakukan pembuktian dengan tepat dikarenakan kurangnya pemahaman tentang logika matematika (pernyataan implikasi dan kalimat berkuantor), kurangnya kekampuan dalam manipulasi aljabar dan kurangnya pemahaman tentang bukti matematis. Dari hasil penelitian ini, diharapkan untuk dilakukan penelitian lebih lanjut mengenai keempat bagian pemahaman dalam definisi limit fungsi tersebut baik secara terpisah maupun tidak. Mengingat pentingnya pemahaman tentang konsep limit fungsi, pada bagian pemahaman yang masih kurang terutama pada interpretasi, sintaktik dan pembuktian perlu dilakukan tindak lanjut. Tindak lanjut tersebut seperti mencari metode pembelajaran yang tepat agar pemahaman mahasiswa meningkat. Sebelum mempelajari definisi limit fungsi, hendaklah dipastikan bahwa mahasiswa memiliki pemahaman yang baik terhadap materi prasyarat definisi limit fungsi. Materi prasyarat tersebut adalah logika matematika, nilai mutlak dan bukti matematis.
DAFTAR PUSTAKA
Bahar E. E., Rahman, A. & Minggi, I. (2012). Analisis Pemahaman Mahasiswa terhadap Konsep Limit Fungsi di satu Titik (Studi Kasus pada Mahasiswa Jurusan Matematika FMIPA UNM. Jurnal Sainsmat, 1(2), 181-190.
15 Balacheff, N. (2010). Bridging Knowing and Proving in Mathematics: An Essay from A Didactical Perspective. Explanation and Proof in Mathematics, 115-135. Heidelberg:Springer.
Cetin, I. (2009). Students’ Understanding of Limit Concept: An APOS Perspective. Unpublished Master’s Thesis. Middle East Technical University, Ankara, Turkey.
Cottrill, J., Dubinsky, E., Nichols, D., Schwingendorf, K., Thomas, K., & Vidakovic, D. (1996). Understanding the limit concept: Beginning with a coordinated process schema. Journal of Mathematical Behavior, 15(2), 167-192.
Denbel, D. G. (2014). Students’ Misconceptions of the Limit Concept in a First Calculus Course. Journal of Education and Practice, 5(34). 24-40.
Doong-Joong Kim, Hyangim Kang, & Hyun-Joo Lee. (2015). Two Different Epistemologies about Limit Concepts. International Education Studies, 8(2), 138-145.
Hiebert, J. & Carpenter, P. (1992). Learning and Teaching with Understanding. Dalam Douglas A Growns (Ed.). Handbook of Research on Mathematics Teaching and Learning. New York: Macmillan Publishing Company.
Hudojo, H. (1990). Strategi Mengajar Belajar Matematika. Malang: Penerbit IKIP Malang. Hughes-Hallet, D., Gleason, A.M., McCallum, W.G. dkk. (2012). Calculus Sigle and
Multivariable 6th Edition. New York: JohnWiley & Sons. Inc.
Hung-Hsi Wu. (1996). The Role of Euclidean Geometry in High School. Journal of Mathematical Behavior, 15, 221-237.
Juter, K. (2005). Limits of Functions – how do students handle them. Phytagoras.11-20.
Karatas, I., Guven, B., & Cekmez, E. (2011). A Cross-Age Study of Students’ Understanding of Limit and Continuity Concepts. Bolema, Rion Claro (SP), 24(38), 245-264.
Knuth, E. J. (2002). Proof as a Tool for Learning Mathematics. The National Council of Teachers of Mathematics, 95(7), 486-490.
Krathwohl, D. R. (2002). A revision of Bloom's taxonomy: An overview. Theory into
practice, 41(4), 212-218.
Lamport, L. (1993). How to Write a Proof. Paolo Alto: Digital Equpiment Corporation.
Meel, D.E.. (2003). Models And Theories Of Mathematical Understanding: Comparingpirie And Kieren’s Models Of The Growth Of Mathematical Understanding And Apos Theory. Journal of CBMS Issues in Mathematics Education, vol. 12. Washington: AMS.
Minggi, I., Paduppai, D., & Assagaf, S. F. (2016). Penyebab Kesulitan Mahasiswa dalam
Pembuktian Matematika. Indonesian Journal of Educational Studies, 19(1).
Oktaviyanthi, R., Tatang, H., & Jarnawi, A. D. (2018). How does Pre-service Mathemataics Teacher Prove the Limit of A Function by Formal Definition?. Journal on Mathematics Education, 9(2), 195-212.
Pape, S.J. & Tchoshanov, M.A. (2011). The Role of Representation(s) in Developing Mathematical Understanding. Theory into Practice. 40(2), 118-127.
Pitaloka, Y., Susilo, B., & Mulyono, M. (2013). Keefektifan Model Pembelajaran Matematika Realistik Indonesia terhadap Kemampuan Pemahaman Konsep Matematika. Unnes Journal of Mathematics Education, 1(2)
Pollatsek, A., Lima, S., & Well, A.D. (1981). Concept or Computation: Students’ Understanding of the Mean. Educational Studies in Mathematics, 12(2), 191-204.
Purcell, E.J., Varberg, D., & Ringdon, S.E. (2004). Kalkulus Edisi 8 Varberg, Purcell, Ringdon. Diterjemahkan oleh: I Nyoman Susila. Jakarta: Erlangga.
Roh, K. H. (2005). College Students’ Intuitive Understanding of The Concept of Limit and Their Level of Reverse Thinking. Unpublished doctoral dissertation, The Ohio State University.
Salas, G.L. & Hille, E. (1990). Calculus: One and several variables, 6th Ed. New York:
John Wileyand Sons.
Santosa, C. A. H. F. (2013). Mengatasi Kesulitan Mahasiswa Ketika Melakukan Pembuktian Matematis Formal. Jurnal Pengajaran MIPA Universitas Sultan Ageng Tirtayasa Banten, 18(2), 152-160.
16 Selden, A. & Selden, J. (2012). Validations of Proofs Considered as Texts: Can Undergraduates Tell Whether an Argument Proves a Theorem?. Journal for Research in Mathematics Education, 34(1), 4-36.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and
objects as different sides of the same coin. Educational studies in mathematics, 22(1),
1-36.
Sierpineska, A., Bobos, G., & Pruncut, A. (2011). Teaching absolute value inequalities to mature students. Educational Studies in Mathematics. 78(3), 275-305.
Skemp, R. R. (1976). Relational Understanding and Instrumental Understanding. Mathematics Teaching, 77, 20-26.
Soedjadi. (2000). Kiat Pendidikan Matematika di Indonesia Konstansi Keadaan Masa Kini Menuju Harapan Masa Depan. Jakarta: Direktorat Jenderal Pendidikan Tinggi, Departemen Pendidikan Nasional.
Szydlik, J. E. (2000). Mathematical beliefs and conceptual understanding of the limit of
a function.
Journal for Research in Mathematics Education
, 258-276.
Tall, D. (1992). Proceeding of Working Group 3 on Students’ Difficulties in Calculus, ICME. 13-28.
Weber, K. (2004). A Framework For Describing The Porcesses That Undergraduates Use to Construct Proofs. Proceedings of the 28th Conference of the International Group for the Psychologyof Mathematics Education, Vol 4, pp 425-432.
Wilson, L. O. (2016). Anderson and Krathwohl–Bloom’s taxonomy revised. The second