Pengenalan Desain dan Analisis Algoritma

Pengenalan Desain dan Analisis Algoritma

Sebagai salah satu dasar dari ilmu komputer, algoritma merupakan hal yang sangat penting untuk dikuasai oleh orang-orang yang berkecimpung di dunia ilmu komputer, dari peneliti sampai ke praktisi. Tentunya penguasaan akan algoritma tidak cukup hanya sampai pada tahap mengetahui dan menggunakan algoritma yang tepat untuk menyelesaikan masalah. Seorang yang mengerti ilmu komputer harus juga mampu merancang dan mengembangkan sebuah algoritma

berdasarkan masalah-masalah yang ditemui. Tulisan ini bertujuan untuk memberikan pengertian mendasar mengenai perancangan (desain) dan pengembangan algoritma, agar pembaca dapat tidak hanya menggunakan algoritma yang sudah ada, tetapi juga merancang dan

mengembangkan algoritma sesuai dengan masalah yang akan diselesaikan.

Selain memberikan dasar perancangan, tulisan ini juga membahas jenis-jenis algoritma yang ada, untuk kemudian melakukan analisa terhadap beberapa algoritma untuk setiap jenisnya. Analisis algoritma dilakukan dengan tujuan utama agar pembaca dapat mengambil keputusan yang tepat dalam memilih algoritma untuk solusi.

Apa itu Algoritma?

Sebelum membahas mengenai perancangan ataupun analisis algoritma, tentunya kita terlebih dahulu harus mendefinisikan arti dari “Algoritma”. Apa itu algoritma?

Algoritma merupakan langkah-langkah (prosedur) yang harus dilakukan untuk menyelesaikan sebuah masalah.

Program komputer umumnya dibangun dengan menggunakan beberapa algoritma untuk

menyelesaikan sebuah permasalahan. Misalnya sebuah program pencarian teks seperti grep akan memerlukan algoritma khusus untuk membaca dan menelusuri file, algoritma lain untuk mencari teks yang tepat di dalam file, dan satu algoritma lagi untuk menampilkan hasil pencarian ke pengguna.

Dalam mendefinisikan algoritma, kita harus dapat mendefinisikan tiga hal utama dengan jelas, yaitu:

1. Masalah, yaitu sebuah persoalan yang ingin diselesaikan oleh sebuah algoritma. 2. Masukan, yaitu contoh data atau keadaan yang menjadi permasalahan.

3. Keluaran, yaitu bentuk akhir dari data atau keadaan setelah algoritma diimplementasikan ke masukan. Keluaran merupakan hasil ideal yang diinginkan dan dianggap telah

menyelesaikan masalah.

Contoh (dan Solusi) Algoritma

Masalah

Pengurutan sekumpulan nilai yang bernilai acak.

Masukan

Serangkaian data berukuran $n$.

Keluaran

Serangkaian data berukuran $n$, dengan urutan \(a_1 \leq a_2 \leq a_3 \leq ... \leq a_{n-1} \leq a_{n}\), di mana \(a_x\) adalah data pada posisi \(x\) dalam rangkaian.

Data masukan yang diinginkan merupakan rangkaian data, tanpa memperdulikan jenis data (angka, huruf, teks, dan lainnya). Contoh dari nilai masukan adalah [2, 5, 1, 3, 4] ataupun ["Doni", "Andi", "Budi", "Clara"]. Data keluaran yang diinginkan, tentunya adalah data masukan yang telah terurut: [1, 2, 3, 4, 5] dan ["Andi", "Budi", "Clara", "Doni"]. Untuk menyelesaikan masalah yang diberikan di atas, kita dapat menggunakan algoritma insertion sort. Kode di bawah menunjukkan implementasi insertion sort pada bahasa pemrograman python:

Implementasi insertion sort yang diberikan di atas menunjukkan bahwa pada dasarnya sebuah prosedur yang harus dijalankan untuk mengubah data masukan menjadi data keluaran, sehingga masalah dapat terselesaikan.

Algoritma yang Baik

Kita telah mengetahui dengan jelas makna dari algoritma, sehingga pertanyaan selanjutnya adalah algoritma seperti apa yang dapat dikatakan sebagai algoritma yang baik? Pada umumnya kita tidak ingin menggunakan algoritma yang salah untuk menyelesaikan masalah karena hal ini dapat menyebabkan masalah tidak diselesaikan dengan optimal, atau lebih buruknya, tidak diselesaikan sama sekali.

Sebuah algoritma yang baik memiliki sifat-sifat berikut:

1. Benar, di mana algoritma menyelesaikan masalah dengan tepat, sesuai dengan definisi masukan / keluaran algoritma yang diberikan.

3. Mudah diimplementasikan, artinya sebuah algoritma yang baik harus dapat dimengerti dengan mudah sehingga implementasi algoritma dapat dilakukan siapapun dengan pendidikan yang tepat, dalam waktu yang masuk akal.

Pada prakteknya, tentunya ketiga hal tersebut tidak dapat selalu tercapai. Kebenaran dari sebuah algoritma umumnya selalu dapat dicapai, setidaknya untuk nilai-nilai masukan umum, tetapi efisiensi dan kemudahan implementasi tidak selalu didapatkan. Begitupun, tentunya kita harus tetap berusaha mencapai ketiga hal tersebut dalam merancang sebuah algoritma.

Pembuktian Kebenaran Algoritma

Kita telah mengetahui bahwa sebuah algoritma yang baik adalah algoritma yang benar, efisien, dan mudah diimplementasikan. Pertanyaan berikutnya tentunya adalah, bagaimana kita

mengetahui bahwa sebuah algoritma telah benar? Algoritma yang efisien itu seperti apa? Bagaimana kita mengukur kemudahan implementasi sebuah algoritma?

Bagian ini akan membahas mengenai pertanyaan pertama, yaitu bagaimana kita dapat mengetahui kebenaran sebuah algoritma. Tentunya efisiensi dan kemudahan implementasi sebuah algoritma menjadi tidak penting jika algoritma tersebut tidak dapat memberikan hasil yang benar.

Definisi dari kebenaran algoritma yang digunakan pada tulisan ini adalah sebagai berikut: Sebuah algoritma dikatakan telah benar jika algoritma tersebut dapat memberikan keluaran yang benar jika menerima masukan sesuai dengan definisi algoritma tersebut, dan algoritma tersebut terbukti akan selalu dapat diterminasi (berakhir).

Pembuktian kebenaran sebuah algoritma sendiri dapat dilakukan dengan beberapa cara, misalnya:

1. Induksi Matematika, 2. Pembuktian kontradiktif, 3. Pembuktian kontrapositif, dan 4. Metode Formal.

Masing-masing alat pembuktian yang disebutkan memiliki kelebihan dan kekurangan masing-masing, serta kasus pengunaan yang berbeda-beda. Perlu diingat juga bahwa masih terdapat

sangat banyak alat-alat pembuktikan lainnya yang dapat digunakan, tetapi kita hanya membahas satu cara pembuktian (induksi matematika) saja sebagai pengenalan cara membuktikan

algoritma. Jika dibutuhkan, metode dan alat pembuktian lain akan dijelaskan lagi pada bagian yang relevan.

Induksi matematika merupakan alat pembuktian matematis yang digunakan untuk membuktikan pernyataan atau proses yang melibatkan perhitungan bilangan asli yang berulang. Contoh dari rumus matematis yang dapat dibuktikan dengan menggunakan induksi matematika yaitu perhitungan deret aritmatika, deret geometris, ataupun sigma bilangan.

Pembuktian menggunakan induksi matematika dilakukan dengan dua langkah, yaitu: 1. Melakukan pembuktian kasus dasar (base case), yaitu membuktikan bahwa sebuah

pernyataan (fungsi) matematika atau algoritma bernilai benar jika diaplikasikan pada bilangan pertama yang sah sesuai dengan spesifikasi fungsi atau algoritma tersebut. 2. Melakukan induksi, yaitu membuktikan bahwa kebenaran dari fungsi \(P(k+1)\) jika

kebenaran fungsi \(P(k)\) diketahui.

Dengan membuktikan kedua hal tersebut, kita dapat mengambil kesimpulan bahwa sebuah fungsi matematika atau algoritma bernilai benar untuk semua bilangan asli. Jika

diimplementasikan dengan tepat, induksi matematika dapat juga digunakan untuk membuktikan kebenaran algoritma rekursif seperti penelusuran pohon (tree).

Untuk lebih jelasnya, mari kita lihat beberapa contoh cara pembuktian yang dilakukan dengan menggunakan induksi matematika.

Contoh 1: Deret Aritmatika

Misalkan kita diminta untuk membuktikan bahwa pernyataan matematika untuk perhitungan deret aritmatika berikut:

\[1 + 2 + 3 + ... + n = \frac{n(n + 1)}{2}\]

adalah benar untuk semua bilangan bulat \(n \geq 1\).

Untuk membuktikan pernyataan matematika di atas, terlebih dahulu kita harus mengubah pernyataan matematika tersebut menjadi sebuah fungsi matematika:

\[P(k) = 1 + 2 + 3 + ... + n = \frac{k(k + 1)}{2}\]

dan kemudian membuktikan kebenarannya menggunakan induksi matematika. Seperti yang telah dijelaskan sebelumnya, kita harus menjalankan dua langkah untuk melakukan pembuktian dengan induksi:

1. Pembuktian Kasus Dasar

\[\begin{split}P(1)= 1 & = \frac{1(1+1)}{2} \\ 1 & = \frac{1(2)}{2} \\ 1 & = \frac{2}{2} \\ 1 & = 1\end{split}\]

karena hasil akhir dari ruas kanan dan ruas kiri adalah sama (\(1\)), maka dapat dikatakan bahwa kasus dasar telah terbukti.

2. Induksi

Untuk pembuktian induksi, kita harus membuktikan bahwa \(P(k) \rightarrow P(k + 1)\) bernilai benar.

Langkah pertama yang dapat kita lakukan yaitu menuliskan fungsi matematis dari \(P(k + 1)\) terlebih dahulu:

\[P(k + 1) = 1 + 2 + ... + k + (k + 1) = \frac{(k + 1)((k + 1) + 1)}{2}\]

dan kemudian kita harus membuktikan bahwa ruas kiri dan ruas kanan dari \(P(k + 1)\) adalah sama. Pembuktian akan kita lakukan dengan melakukan penurunan pada ruas kiri agar menjadi sama dengan ruas kanan:

\[\begin{split}1 + 2 + ... + k + (k + 1) & = (1 + 2 + ... + k) + (k + 1) \\ & = \frac{k(k + 1)} {2} + (k + 1) \\ & = \frac{k(k + 1) + 2(k + 1)}{2} \\ & = \frac{k^2 + 3k + 2}{2} \\ & = \ frac{(k + 1)(k + 2)}{2} \\ & = \frac{(k + 1)((k + 1) + 2)}{2}\end{split}\]

dan seperti yang dapat dilihat, ruas kiri dari \(P(k + 1)\) telah menjadi sama dengan ruas kanannya, sehingga dapat dikatakan bahwa tahap induksi telah berhasil dibuktikan benar. Dengan pembuktian kasus dasar dan induksi yang bernilai benar, kita dapat menyimpulkan bahwa \(P(n)\) bernilai benar untuk \(n \geq 1\).

Contoh 2: Pembuktian Hipotesa

Anda diminta untuk membuktikan hipotesa bahwa fungsi matematika \(n^3-n\) habis dibagi 6 untuk semua bilangan bulat \(n \geq 2\).

Langkah untuk membuktikan pernyataan tersebut sama dengan sebelumnya. Mulai dari definisi ulang fungsi matematikanya:

\[P(k) = k^3 - k\]

Dan kemudian lakukan induksi matematika, langkah demi langkah: 1. Pembuktian Kasus Dasar

\[\begin{split}P(1) & = 2^3 - 2 \\ & = 8 - 2 \\ & = 6\end{split}\]

karena \(6 \bmod 6 = 0\) maka telah dapat dibuktikan bahwa kasus dasar bernilai benar. 2. Induksi

Jika \(P(k)\) benar habis dibagi 6, maka \(P(k + 1)\), atau \((k + 1)^3 - (k + 1)\) harus juga habis dibagi 6. Mari kita lakukan pembuktiannya:

\[\begin{split}P(k + 1) & = (k + 1)^3 - (k + 1) \\ & = (k^3 + 3k^2 + 3k + 1) - k - 1 \\ & = k^3 - 3k^2 + 2k \\ & = k^3 - 3k^2 + 2k + k - k \\ & = k^3 - 3k^2 + 3k - k \\ & = k^3 - k + 3k^2 + 3k \\ & = (k^3 - k) + 3k(k + 1)\end{split}\]

dan dapat dilihat bagaimana \(P(k + 1)\) telah terbukti habis dibagi 6 karena: 1. \(k^3 - k\) habis dibagi 6, sesuai dengan hipotesa \(P(k)\), dan

2. \(3k(k + 1)\) habis dibagi 6 karena salah satu nikai dari \(k\) atau \(k + 1\) pasti merupakan bilangan genap, yang jika dikalikan dengan 3 akan habis dibagi 6. Setelah berhasil menyelesaikan dua langkah induksi, kita dapat menyimpulkan bahwa \ (P(k) = k^3 - k\) habis dibagi 6 untuk \(k \geq 2\).

Induksi Matematika untuk Pembuktian Algoritma

Seperti yang dapat dilihat dari apa yang telah kita pelajari pada bagian sebelumnya, induksi matematika jelas sangat berguna untuk membuktikan kebenaran sebuah teorema atau fungsi yang melibatkan perhitungan bilangan bulat yang berulang. Tetapi apa guna induksi matematika untuk membuktikan kebenaran sebuah algoritma?

Sebuah algoritma kerap kali akan memiliki bagian yang melakukan perhitungan bilangan atau data secara berulang. Kita dapat menggunakan konsep perulangan pada pemrograman untuk menerapkan perhitungan bilangan ataupun data secara berulang. Misalnya, algoritma berikut menghitung hasil kali dari dua buah bilangan bulat:

def kali(m, n):

\[f(m, n) = \sum_{i=1}^{n} m; n \geq 0\] atau lebih sederhananya:

\[m \times n = \underbrace{m + m + m + ... + m}_{\text{n kali}}\]

dan secara otomatis tentunya pernyataan matematis tersebut dapat kita buktikan dengan menggunakan induksi matematika. Pembuktian perulangan yang lebih kompleks sendiri dapat dilakukan dengan teknik yang dikenal dengan nama loop invariant, yang tidak akan dijelaskan pada tulisan ini.

Pemodelan Masalah

Pada bagian sebelumnya kita telah melihat bagaimana sebuah algoritma dituliskan menjadi fungsi matematika. Baik algoritma maupun fungsi matematika adalah sebuah model, yang digunakan untuk menggambarkan masalah yang ditemui pada dunia nyata, dan ingin diselesaikan, baik dengan menggunakan matematika ataupun program komputer. Dengan memiliki model masalah kita dapat lebih mudah mengerti masalah yang akan diselesaikan, yang akan menyebabkan solusi yang ditawarkan menjadi lebih baik.

Tetapi pertanyaannya tentunya adalah, bagaimana kita membuat model yang benar dari masalah-masalah yang ada? Bagian ini akan menjelaskan mengenai cara pembangunan model, baik secara matematis maupun algoritmik, yang benar.

Jenis-Jenis Model

Sebelum mulai membangun model permasalahan, tentunya kita terlebih dahulu harus

mengetahui jenis-jenis model yang ada. Terdapat enam jenis model yang umum digunakan untuk menggambarkan masalah dalam dunia algoritma / pemrograman, yaitu:

1. Model Numerik

Model Numerik Sapi

memberikan informasi sejumlah sapi yang ada di dalam kotak. Model numerik paling sederhana dan informatif yang dapat kita ambil dari gambar tersebut adalah ‘Lima ekor Sapi’ atau ‘Lima Sapi’.

2. Model Simbolik

Jika kita mengembangkan model numerik lebih jauh, kita kemudian dapat menambahkan simbol-simbol baru untuk melakukan pemrosesan terhadap angka-angka yang ada pada model numerik. Terdapat empat buah simbol dasar untuk pemrosesan angka, yaitu \(+, -, \times, \text{dan} \div\). Simbol \(=\) juga digunakan untuk menandakan kesamaan nilai antara ruas kiri dan ruas kanan dari \(=\).

Note

Simbol \(\times \text{dan} \div\) akan dituliskan sebagai \(*\) dan \(/\) pada tulisan ini, karena kedua simbol tersebut lebih umum digunakan pada lingkungan ilmu komputer. Jadi, sebuah ekspresi matematika seperti ini:

\[10 = 5 * 2\]

dapat dikatakan adalah sebuah model simbolik. Tentunya operator-operator numerik yang disebutkan sebelumnya memiliki aturan tertentu untuk beropearsi. Aturan-aturan umum yang kita temui untuk operator numerik yaitu:

1. Hukum Kumulatif, di mana \(a + b = b + a\) dan \(a * b = b * a\).

2. Hukum Asosiatif, di mana \(a + (b + c) = (a + b) + c\) dan \(a * (b * c) = (a * b) * c\).

4. Hukum Invers, yaitu \(a + (-a) = 0\) dan a * frac{1}{a} = 1. 5. Hukum Identitas, yaitu \(a + 0 = a$ dan $a * 1 = a\).

6. Perkalian dengan 0, yaitu \(a * 0 = 0\).

Penjelasan mengenai kegunaan dan cara kerja dari hukum-hukum tersebut tidak akan dibahas lagi, karena dianggap telah diketahui oleh pembaca. Yang perlu diperhatikan adalah bagaimana kita menuliskan simbol-simbol seperti $a$ dan $b$, untuk

melambangkan semua bilangan-bilangan yang mengikuti hukum-hukum di atas. Simbol-simbol yang dapat melambangkan bilangan atau nilai lain secara generik seperti ini dikenal dengan nama variabel.

Sebuah variabel merupakan simbol yang digunakan untuk merepresentasikan nilai yang dapat berubah kapanpun, tergantung dari nilai yang kita berikan kepada variabel tersebut. Variabel digunakan dalam model simbolik untuk mewakili nilai-nilai yang dapat berubah sewaktu-waktu, misalnya nilai yang harus dibaca dari masukan pengguna atau nilai yang diambil secara acak. Sebuah model bahkan dapat terdiri dari hanya variabel saja,

misalnya model matematika untuk menghitung luas sebuah persegi panjang dapat dituliskan seperti berikut:

\[L = p * l\]

di mana \(p\) dan \(l\) mewakili panjang dan lebar persegi panjang, yang nilainya selalu berbeda-beda, tergantung dengan persegi panjang yang akan dihitung luasnya. Nilai \(L\), yang merepersentasikan luas persegi panjang, sendiri bergantung kepada nilai \(p\) dan \ (l\), sehingga kita tidak akan mendapatkan nilai \(L\) yang konstan.

Deklarasi variabel sendiri dilakukan dengan menggunakan perintah $let$, seperti berikut: \[\text{let }L = \text{Luas Persegi}\]

Selain model-model dengan variabel, tentunya kita juga memiliki model-model yang memiliki bilangan konstan yang tidak berubah, misalnya untuk menghitung luas segitiga: \[L = \frac{1}{2} * a * t\]

atau model untuk menghitung keliling lingkaran: \[K = 2 * \pi * r\]

Dari berbagai komponen dan contoh model simbolik yang telah kita lihat, dapat disimpulkan bahwa model simbolik merupakan model yang menggambarkan interaksi dan operasi antar komponen numerik secara abstrak. Abstraksi dari komponen numerik (angka) pada model simbolik dilakukan dengan menggunakan variabel dan konstanta. 3. Model Spasial

Tidak semua permasalahan yang diselesaikan oleh matematika atau komputer selalu berhubungan langsung dengan angka. Terkadang kita menjumpai juga masalah-masalah yang berhubungan dengan representasi dunia nyata seperti perhitungan jarak dua objek atau pencarian jalur terdekat untuk kendaraan. Secara tradisional, model untuk

penyelesaian masalah seperti ini digambarkan dengan peta, graph, dan gambar-gambar teknis lainnya.

Untuk dunia komputer, model-model dunia nyata biasanya digambarkan dengan

menggunakan koordinat. Sistem koordinat yang paling populer digunakan dalam hal ini adalah koordinat kartesius. Koordinat kartesius merupakan sistem koordinat yang

menggambarkan sebuah nilai riil di dalam kumpulan nilai yang direpresentasikan dengan sebuah garis. Sistem kartesius dapat digambarkan dalam banyak dimensi, sesuai dengan jumlah kumpulan nilai yang digambarkan. Untuk memudahkan pengertian, gambar di bawah memperlihatkan contoh sistem koordinat kartesius dua dimensi:

Sistem Koordinat Kartesius

Data pada sistem kartesius dua dimensi dapat direpresentasikan dalam bentuk sebuah titik, yaitu kombinasi antara sumbu x dan sumbu y:

Titik pada Kartesius

atau sebuah garis, yang direpresentasikan dengan sebuah fungsi matematika:

Garis pada Kartesius

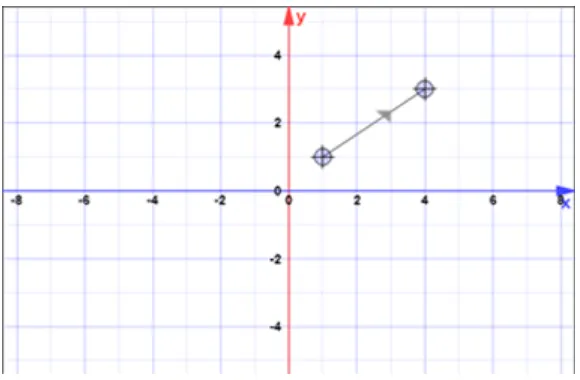
Garis Berarah pada Kartesius

dan yang terakhir, kita dapat juga merepresentasikan sebuah bentuk atau bidang, menggunakan kombinasi beberapa garis:

Bidang pada Kartesius

Untuk melakukan pemrosesan data-data yang ada di dalam sistem kartesius, kita dapat melakukan operasi terhadap titik-titik yang merepresentasikan data tersebut. Titik-titik direpresentasikan dalam bentuk matriks atau array. Misalnya, segitiga yang ada pada gambar di atas dapat direperesentasikan sebagai matriks berikut:

\[\begin{split}\begin{bmatrix} -3 & 4 & 1 \\ 1 & 3 & -2 \end{bmatrix}\end{split}\] Dan kemudian tentunya kita dapat melakukan operasi-operasi matriks untuk melakukan berbagai hal terhadap segitiga tersebut.

Model logis merupakan cara memodelkan masalah berdasarkan logika matematika. Terdapat empat cabang utama dari logika matematika, yaitu teori himpunan, teori model, teori rekursif, dan teori pembuktian. Masing-masing teori memiliki cara pemodelan yang berbeda-beda, untuk merepresentasikan masalah yang berbeda. Tulisan ini hanya akan membahas pemodelan logis pada bidang himpunan, dan relevansinya dengan salah satu sistem yang paling populer di dunia komputer: basis data.

Himpunan, seperti namanya, memodelkan sekumpulan entitas yang memiliki atribut (ciri khas) tertentu. Dalam menentukan atribut tujuan dari pengunaan himpunan lebih penting daripada kesamaan ciri khas dari entitas, sehingga terkadang atribut dari elemen-elemen dalam himpunan tidak selalu dapat dilihat dengan mudah. Misalnya, kita dapat

mendeklarasikan sebuah himpunan dengan nama “Himpunan Barang dalam Handbag” dengan isi berupa “handphone, gunting kuku, alat make-up, tissue, dompet, alat tulis, dan karet gelang”. Secara sekilas semua entitas yang ada di dalam himpunan tidak terlihat memiliki atribut yang jelas, meskipun himpunan ini adalah himpunan yang valid. Terdapat dua aturan khusus yang harus dipenuhi oleh sebuah himpunan, yaitu:

1. Himpunan harus didefinisikan dengan tepat. Sebuah entitas yang ada di dunia hanya dapat memiliki dua status berkaitan dengan himpunan yang didefinisikan:

TERMASUK dalam himpunan atau TIDAK TERMASUK. Tidak boleh ada elemen yang bersifat ambigu, dalam arti tidak jelas masuk ke dalam himpunan atau tidak. Misalnya, kita tidak dapat mendefinisikan sebuah himpunan yang berisi “Orang Tinggi” karena tidak terdapat definisi dari “tinggi” yang jelas. Apakah 170 cm termasuk tinggi? 180?

Yang dapat kita definisikan ialah himpunan yang berisi “Orang dengan tinggi badan di atas 175 cm”, sehingga tidak terdapat perdebatan mengenai apakah 170 cm termasuk tinggi atau tidak.

2. Setiap elemen dalam himpunan harus unik. Sebuah himpunan tidak boleh memiliki nilai ganda. Aturan ini menyebabkan banyak himpunan yang ada di dunia nyata tidak dapat direpresentasikan dengan himpunan matematika. Misalnya, kita dapat saja memiliki himpunan sendok yang terdiri dari banyak sendok identik. Dalam himpunan matematis, hal ini tidak diperbolehkan. Aturan ini juga menyebabkan penggabungan himpunan menjadi sedikit berbeda.

Himpunan berisi angka 1, 2, 3, 4 jika digabungkan dengan himpunan 3, 4, 5, 6 akan menghasilkan himpunan 1, 2, 3, 4, 5, 6. Ide “nilai unik” untuk setiap elemen dalam himpunan ini lah yang menjadi dasar dari pengindeksan dan primary key

dari basis data relasional.

Contoh Diagram Venn

Dari gambar diagram Venn di atas, kita dapat melihat bagaimana seluruh persegi adalah juga persegi panjang, dan baik persegi maupun persegi panjang adalah merupakan segi empat. Jika kita menambahkan jenis segi empat lainnya, misalnya trapesium, dapatkah anda menggambarkan diagram Venn-nya?

5. Model Statistik

Terdapat banyak permasalahan di dunia nyata yang tidak dapat dimodelkan dengan mudah menggunakan keempat model matematis yang telah kita bahas sebelumnya. Terkadang kita dihadapkan dengan permasalahan yang sangat kompleks, sampai-sampai memodelkan dan menganalisa setiap situasi yang mempengaruhi masalah tersebut akan menjadi sangat mahal, memerlukan banyak orang, dan banyak waktu.

Sebagai contoh, bayangkan jika kita diminta untuk melakukan prakiraan cuaca. Dengan menggunakan model matematis yang ada, kita akan memerlukan sangat banyak

kalkulasi, yang saling mempengaruhi satu sama lainnya. Praktisnya, kita harus mampu

melakukan simulasi terhadap seluruh elemen yang ada di bumi untuk melakukan

prakiraan cuaca dengan tepat. Hal ini tentunya sangat tidak efektif untuk dilakukan. Lalu bagaimana para ahli sekarang melakukan prakiraan cuaca?

Jawabannya adalah model statistik. Dengan mengumpulkan sampel data cuaca pada masa lalu, kita dapat melihat kecenderungan atau tren cuaca yang akan terjadi sesuai dengan keadaan cuaca kita sekarang. Pada dasarnya, sebuah model statistik melakukan analisa tren terhadap sampel data yang relevan untuk meniadakan ketidak pastian atau keadaan khusus. Dengan mengambil keadaan rata-rata dari sekumpulan data, kita akan

Gambar di atas menunjukkan contoh dari model statistik. Ingat, bahwa kesimpulan yang dapat diambil dari sebuah model statistik hanyalah berupa kecenderungan atau tren. Kita tidak bisa membuktikan sesuatu atau memberikan hasil yang pasti menggunakan statistik. Dapat dikatakan bahwa kalimat seperti “statistik membuktikan ...” pada tulisan ilmiah populer kurang tepat.

6. Pseudocode

Semua model matematis yang telah dijelaskan sebelumnya merupakan model matematika yang digunakan dan dimengerti oleh manusia. Jika ingin menggunakan model matematis tersebut di komputer, terlebih dahulu kita harus melakukan konversi menjadi kode program yang dapat dibaca dan dimengerti oleh komputer. Kode program sendiri dimodelkan dengan banyak cara, dan yang paling relevan dengan algoritma ialah pseudocode.

Pseudocode memberikan langkah-langkah penyelesaian masalah dengan menggunakan bahasa manusia, dengan sedikit batasan sesuai dengan konstruk logika komputer. Pseudocode tidak memiliki konstruk untuk bahasa pemrograman tertentu, sehingga pseudocode harus bisa diimplementasikan dengan bahasa pemrograman apapun. Berikut adalah contoh pseudocode sederhana:

for i = 1 to 5 do print i

end for

Untuk penjelasan lebih mendetail tentang pseudocode, silahkan baca kembali bahan kuliah untuk Pemrograman Dasar.

Kita telah melihat model matematis yang umum digunakan untuk menyelesaikan masalah. Pertanyaan selanjutnya tentunya adalah: kapan kita menggunakan model A dan kapan menggunakan model B? Bagaimana membuat model A menjadi kode program yang dapat dijalankan oleh komputer?

Pengembangan Model

Proses pengembangan model dapat dilakukan dengan beberapa langkah yang telah dibangun oleh para ahli matematika. Jika proses pengembangan model dilakukan mengikuti langkah-langkah yang ada, idealnya kita akan mendapatkan model yang tepat untuk permasalahan yang akan diselesaikan. Adapun langkah-langkah yang harus diambil untuk membangun sebuah model yaitu:

1. Apakah masalah yang dihadapi merupakan masalah yang memerlukan solusi matematis? Jika masalahnya merupakan masalah numerik (perhitungan angka) atau logis, maka jawabannya sudah pasti “ya”. Jika solusi dari masalah berupa pendapat, maka kemungkinan jawabannya adalah “tidak”.

kita dari akar masalah. Pisahkan antara fakta (informasi) yang relevan dari keseluruhan informasi yang didapatkan.

3. Fakta atau informasi tambahan apa yang kita perlukan untuk menyelesaikan masalah? Di mana atau bagaimana cara agar kita mendapatkan fakta-fakta tersebut?

4. Adakah langkah atau metode alami untuk menyelesaikan masalahnya? Metode alami artinya metode yang umumnya digunakan oleh manusia. Misalnya, untuk menghitung total dari sekumpulan nilai kita dapat menambahkan seluruh bilangan yang ada di dalam kumpulan nilai tersebut.

5. Apakah fakta-fakta yang ada dapat direpresentasikan oleh simbol matematis dan dikategorikan menjadi fakta yang “diketahui” dan “tidak diketahui”?

6. Apakah terdapat model lama yang dapat digunakan atau disesuaikan untuk menyelesaikan masalah kita?

7. Jika terdapat model yang telah dikembangkan sebelumnya untuk masalah kita, apakah model tersebut dapat diaplikasikan pada komputer?

8. Bagaimana kita dapat mengaplikasikan model dari solusi kita sehingga model tersebut dapat dibuat menjadi program komputer dengan mudah?

Dengan menjalankan langkah-langkah di atas, idealnya kita akan mendapatkan sebuah model solusi yang tepat untuk permasalahan kita. Untuk lebih jelasnya, mari kita aplikasikan model masalah yang ada ke contoh sebuah kasus!

Contoh: Perhitungan Bunga Pinjaman

Kita diminta untuk mengembangkan sebuah program komputer untuk sebuah perusahaan kredit ACME. Program yang akan kita kembangkan merupakan sistem untuk menghitung total jumlah yang harus dibayar oleh peminjam uang per tahunnya. Bunga pinjaman yang diberikan ACME adalah sebesar 15% per tahunnya.

Untuk membangun sistem perhitungan yang diminta, tentunya terlebih dahulu kita harus membangun modal solusi untuk perhitungan bunganya. Mari kita ikuti langkah-langkah untuk membangun model yang telah dijelaskan sebelumnya:

1. Apakah masalah yang dihadapi merupakan masalah yang memerlukan solusi matematis?

Ya. Perhitungan total bunga bunga jelas akan melibatkan matematika. 2. Fakta-fakta relevan apa saja yang diketahui?

Bunga pinjaman sebesar 15% per tahun.

3. Fakta atau informasi tambahan apa yang kita perlukan untuk menyelesaikan masalah?

1. Jumlah pinjaman awal. Untuk menghitung total pinjaman dengan bunganya jelas kita harus mengetahui jumlah pinjaman awal terlebih dahulu.

2. Lama pinjaman. Tanpa adanya lama pinjaman, kita tidak dapat mengetahui dengan pasti total bunga yang harus ditambahkan.

4. Adakah langkah atau metode alami untuk menyelesaikan masalahnya?

Ya, lakukan perhitungan bunga tiap tahunnya, dan tambahkan hasil kalkulasi tersebut sampai tahun pinjaman terakhir.

5. Apakah fakta-fakta yang ada dapat direpresentasikan oleh simbol matematis?

Dari fakta-fakta yang kita dapatkan pada langkah kedua dan ketiga, kita dapat mendefinisikan simbol matematis seperti berikut:

\[\begin{split}\text{let }b & = \text{bunga} \\ \text{let }p & = \text{jumlah

pinjaman} \\ \text{let }t & = \text{waktu pinjaman (per tahun)} \\ \text{let }T & = \ text{total pinjaman}\end{split}\]

6. Apakah terdapat model lama yang dapat digunakan untuk menyelesaikan masalah kita?

Ya, perhitungan bunga majemuk yang dimodelkan dengan rumus: \(T = p(1 + b)^t\). 7. Apakah model yang ada sebelumnya pada langkah 6 dapat diaplikasikan pada

komputer?

Kemungkinan tidak, karena perhitungan bunga majemuk merupakan perhitungan yang tidak banyak diketahui orang (terutama pada bidang pemrograman), dan juga memiliki banyak aturan kompleks yang harus dimengerti terlebih dahulu.

Karena kasus yang sederhana, kita akan lebih mudah mengimplementasikan algoritma kita sendiri, yang cukup melakukan iterasi dan menambahkan total pinjaman setiap tahunnya. Mari kita coba kembangkan model iterasi yang dapat digunakan.

Untuk tahun pertama, peminjam akan berhutang sebanyak: \[T = p + (15\% * p)\]

selanjutnya, untuk tahun kedua hutangnya akan bertambah menjadi: \[T' = T + (15\% * T)\]

\[T = T + (\frac{15}{100} * T)\]

yang akan dijalankan sebanyak $t$ kali, dengan nilai $T$ yang bertambah setiap iterasinya. Dengan informasi ini, kita dapat mengimplementasikan pseudocode seperti berikut:

yang kemudian akan kita implementasikan sebagai fungsi penghitung total pinjaman. 8. Bagaimana kita dapat mengaplikasikan model dari solusi kita sehingga model

tersebut dapat dibuat menjadi program komputer dengan mudah?

Pseudocode yang ada sudah sangat jelas, dan baris per barisnya dapat diimplementasikan secara langsung menggunakan bahasa pemrograman apapun.

Setelah mendapatkan model penyelesaian masalah sampai pada pseudocode-nya, kita kemudian dapat mengimplementasikan solusi yang dikembangkan menggunakan bahasa pemrograman yang diinginkan. Berikut adalah contoh implementasi algoritma tersebut pada python:

b = 15 T = 0

p = input("Masukkan jumlah pinjaman: ") t = input("Masukkan lama pinjaman: ")

T = int(p)

for i in range(1, int(t)): T = T + (15 / 100 * T)

print("Total pinjaman yang harus dibayarkan adalah: " + str(T))

Kesimpulan

Pada bagian ini kita telah mempelajari tentang ciri khas algoritma yang baik, yaitu benar, efisien, dan mudah diimplementasikan. Kita juga mempelajari bagaimana membuktikan sebuah

Terdapat enam jenis model matematis yang kita bahas, beserta dengan cara menggunakan model matematis tersebut ke kasus pada dunia nyata. Selanjutnya kita akan mempelajari bagaimana mengembangkan algoritma yang efisien, beserta definisi dari efisiensi algoritma tentunya.

Kompleksitas Algoritma

Pada bagian sebelumnya kita telah mempelajari mengenai algoritma yang baik, serta bagaimana membuktikan sebuah algoritma akan memberikan hasil yang benar. Selain memberikan hasil yang benar, efisiensi dari waktu eksekusi ataupun penggunaan memori dari algoritma adalah hal yang penting bagi sebuah algoritma. Bagian ini akan membahas bagaimana mengukur efisiensi sebuah algoritma, sehingga kita dapat memilih algoritma yang baik atau memperbaiki algoritma yang ada.

Langsung saja, kita mulai dengan sebuah contoh algoritma untuk menghitung perpangkatan dua bilangan. Hasil akhir dari kode yang akan dikembangkan direpresentasikan oleh fungsi

matematis berikut: \[f(x, y) = x^y\]

Salah satu implementasi sederhana untuk fungsi matematis di atas adalah: def pangkat(x, y):

hasil = 1

for i in range(0, y): hasil = x * hasil return hasil

Pada dasarnya yang kita lakukan pada kode di atas ialah mengkalikan x dengan dirinya sendiri sebanyak y kali, dan menyimpan hasil kali tersebut di dalam variabel hasil. Baris hasil = x * hasil melakukan perkalian x dengan dirinya sendiri, dan perulangan dilakukan untuk

memastikan baris ini dijalankan sebanyak y kali.

Dengan asumsi bahwa algoritma perpangkatan yang kita tuliskan di atas sudah benar, pertanyaan selanjutnya tentunya adalah: seberapa efisien kah algoritma tersebut?

Terdapat banyak cara untuk mengukur efisiensi sebuah algoritma, tentunya dengan kelebihan dan kekurangan dari masing-masing cara tersebut. Mari kita lihat cara mengukur efisiensi yang paling sederhana terlebih dahulu: melihat berapa langkah yang perlu dijalankan untuk

menyelesaikan algoritma tersebut. Jika kita memanggil fungsi pangkat seperti berikut: pangkat(2, 1)

Maka kode akan dieksekusi seperti berikut: hasil = 1

return hasil

yang kita perulangan for yang ada kita kembangkan akan menjadi: hasil = 1

hasil = 2 * hasil return hasil

Total terdapat tiga langkah yang perlu dijalankan untuk mendapatkan hasil pangkat yang

diinginkan. Sangat sederhana dan mudah. Bagaimana jika kita naikkan nilai dari y sehingga kita memanggil pangkat(2, 2)?

Kode yang dieksekusi akan menjadi: hasil = 1

dengan total 4 langkah eksekusi. Perhatikan bagaimana akibat dari meningkatkan nilai y, jumlah eksekusi dari kode di dalam loop meningkat. Berdasarkan apa yang kita dapatkan sejauh ini, kita dapat menyimpulkan bahwa jika dilakukan pemanggilan pangkat(2, 5) maka kita akan

mendapatkan hasil eksekusi:

dan seterusnya. Kesimpulan lain apa lagi yang bisa kita tarik dari hal ini? Ya, baris hasil = x * hasil dijalankan sebanyak y kali! Secara sederhana, tabel di bawah menampilkan berapa kali

setiap baris yang ada dalam fungsi pangkat dieksekusi:

Baris Kode | Jumlah Eksekusi

hasil = 1 | 1

sehingga kita dapat mengatakan bahwa fungsi pangkat akan selalu diselesaikan dalam 2 + y langkah. Melihat bagiamana y akan mempengaruhi jumlah langkah eksekusi, mari kita lihat seberapa banyak pengaruh y terhadap jumlah langkah eksekusi kode:

Y Proses Perhitungan Jumlah Langkah

1 2 + 1 3

10 2 + 10 12

100 2 + 100 102

1000 2 + 1000 1002

10000 2 + 10000 10002

Dari tabel di atas kita dapat melihat bagiamana semakin meningkatnya jumlah dari y, semakin nilai 2 yang ditambahkan menjadi tidak relevan. Perbedaan jumlah langkah 1000000 dengan 1000002 tentunya tidak banyak! Dengan begitu, kita dapat menyederhanakan fungsi perhitungan jumlah langkah pangkat dengan mengatakan bahwa fungsi pangkat akan selalu diselesaikan dalam y langkah. Dengan kata lain, kecepatan atau efisiensi dari fungsi pangkat bergantung kepada y.

Semakin besar nilai y, maka jumlah langkah eksekusi akan semakin meningkat. Hal ini tentunya sangat berpengaruh terhadap efisiensi total dari sebuah algoritma. Bayangkan jika jumlah langkah yang diperlukan bukanlah y, melainkan \(y^2\):

Y Jumlah Langkah (\(y\)) Jumlah Langkah (\(y^2\))

1 1 1

10 10 100

100 100 10000

1000 1000 1000000

10000 10000 100000000

Tingkat Pertumbuhan Fungsi Pangkat

Peningkatan jumlah langkah eksekusi seperti inilah yang menyebabkan kita mengukur efisiensi algoritma dengan ukuran pertumbuhan jumlah langkah eksekusi relatif terhadap jumlah data. Melihat grafik pertumbuhan yang diberikan, fungsi pangkat yang dikembangkan dapat dikatakan memiliki tingkat pertumbuhan yang linear.

Notasi Asimtotik

Perhitungan pertumbuhan fungsi seperti yang kita lakukan sebelumnya sangat krusial dalam menghitung efisiensi sebuah algoritma. Seperti layaknya hal-hal krusial lainnya pada ilmu komputer, tentunya fungsi pertumbuhan ini juga memiliki notasi matematika khusus. Penulisan fungsi pertumbuhan dilakukan dengan menggunakan notasi asmtotik.

Terdapat beberapa jenis notasi asimtotik, tetapi kita hanya akan menggunakan dan membahas satu notasi saja, yaitu notasi Big-O. Big-O dipilih karena merupakan notasi yang paling populer dan paling banyak digunakan pada kalangan peneliti ilmu komputer. Notasi Big-O digunakan untuk mengkategorikan algoritma ke dalam fungsi yang menggambarkan batas atas (upper limit) dari pertumbuhan sebuah fungsi ketika masukan dari fungsi tersebut bertambah banyak.

Singkatnya, perhitungan jumlah langkah dan pertumbuhannya yang kita lakukan pada bagian sebelumnya merupakan langkah-langkah untuk mendapatkan fungsi Big-O dari sebuah algoritma.

pertumbuhan linear yang kita kembangkan pada bagian sebelumnya memiliki kelas Big-O \ (O(n)\).

Karena berguna untuk mengkategorikan algoritma, terdapat beberapa jenis kelas efisiensi umum yang dijumpai dalam Big-O, yaitu:

Fungsi Big-O Nama

Apa guna dan penjelasan dari masing-masing kelas kompleksitas yang ada? Mari kita lihat satu per satu.

Kriteria Efisiensi Umum

Bagian ini akan menjelaskan beberapa contoh kriteria kompleksitas algoritma yang umum dijumpai, beserta dengan contoh kode algoritma yang memiliki kompleksitas tersebut.

O(1): Kompleksitas Konstan

Sebuah algoritma yang memiliki kompleksitas konstan tidak bertumbuh berdasarkan ukuran dari data atau masukan yang diterima algoritma tersebut. Bahkan, algoritma dengan kompleksitas ini tidak akan bertumbuh sama sekali. Berapapun ukuran data atau masukan yang diterima,

algoritma dengan kompleksitas konstan akan memiliki jumlah langkah yang sama untuk dieksekusi.

Karena sifatnya yang selalu memiliki jumlah langkah tetap, algoritma dengan kompleksitas merupakan algoritma paling efisien dari seluruh kriteria yang ada. Contoh dari algoritma yang memiliki kompleksitas konstan ialah algoritma yang digunakan untuk menambahkan elemen baru ke dalam linked list. Contoh implementasi algoritma ini pada bahasa C adalah sebagai berikut:

void add_list(node *anchor, node *new_list) {

new_list->next = anchor->next; anchor->next = new_list;

}

ukuran awal dari linked list yang ada. Dengan kata lain, berapapun ukuran linked list awal, langkah untuk untuk menambahkan elemen baru adalah konstan, yaitu dua langkah. Hal ini lah yang menyebabkan algoritma ini dikatakan memiliki kompleksitas konstan.

Tingkat pertumbuhan dari algoritma dengan kompleksitas konstan dapat dilihat pada gambar berikut:

Tingkat Pertumbunan Algoritma Kompleksitas Konstan

O(log n): Kompleksitas Logaritmik

Algoritma dengan kompleksitas logaritmik merupakan algoritma yang menyelesaikan masalah dengan membagi-bagi masalah tersebut menjadi beberapa bagian, sehingga masalah dapat diselesaikan tanpa harus melakukan komputasi atau pengecekan terhadap seluruh masukan. Contoh algoritma yang ada dalam kelas ini adalah algoritma binary search. Mari kita hitung nilai kompleksitas dari binary search!

Berikut adalah implementasi dari binary search dengan bahasa python: def binary_search(lst, search):

lower_bound = 0

upper_bound = len(lst) - 1

while True:

if upper_bound < lower_bound: print("Not found.")

return -1

i = (lower_bound + upper_bound) // 2

elif lst[i] > search: upper_bound = i - 1 else:

print("Element " + str(search) + " in " + str(i)) return 0

Mari kita hitung jumlah langkah yang diperlukan untuk mendapatkan kelas kompleksitas dari binary search. Berikut adalah tahapan perhitungan untuk mendapatkan jumlah langkah yang diperlukan:

1. Langkah yang akan selalu dieksekusi pada awal fungsi, yaitu inisialisasi lower_bound dan upper_bound: 2 langkah.

2. Pengecekan kondisi while (pengecekan tetap dilakukan, walaupun tidak ada perbandingan yang dijalankan): 1 langkah.

3. Pengecekan awal (if upper_bound < lower_bound): 1 langkah. 4. Inialisasi i: 1 langkah.

5. Pengecekan kondisi kedua (if lst[i] < search: ...), kasus terburuk (masuk pada else dan menjalankan kode di dalamnya): 4 langkah.

Dan setelah melalui langkah kelima, jika elemen belum ditemukan maka kita akan kembali ke langkah kedua. Perhatikan bahwa sejauh ini, meskipun elemen belum ditemukan atau dianggap tidak ditemukan, kita minimal harus menjalankan 2 langkah dan pada setiap perulangan while

kita menjalankan 7 langkah. Sampai di titik ini, model matematika untuk fungsi Big-O yang kita dapatkan ialah seperti berikut:

\[f(n) = 2 + 7(\text{jumlah perulangan})\]

Pertanyaan berikutnya, tentunya adalah berapa kali kita harus melakukan perulangan?

Berhentinya kondisi perulangan ditentukan oleh dua hal, yaitu: 1. Kondisi upper_bound < lower_bound, dan

2. Pengujian apakah lst[i] == search, yang diimplikasikan oleh perintah else.

Perhatikan juga bagaimana baik nilai upper_bound maupun lower_bound dipengaruhi secara langsung oleh i, sehingga dapat dikatakan bahwa kunci dari berhentinya perulangan ada pada i. Melalui baris kode ini:

i = (lower_bound + upper_bound) // 2

Kita melihat bahwa pada setiap iterasinya nilai i dibagi 2, sehingga untuk setiap iterasinya kita memotong jumlah data yang akan diproses (\(n\)) sebanyak setengahnya. Sejauh ini kita

memiliki model matematika seperti berikut (konstanta \(2\) dihilangkan karena tidak berpengaruh):

\[f(n) = 7f(\frac{n}{2})\]

\[\begin{split}f(n) & = 7f(\frac{n}{2}) \\ & = 7 * (7f(\frac{n}{4})) \\ & = 49f(\frac{n}{4}) \\ & = 49 * (7f(\frac{n}{8})) \\ & ... \\ & = 7^k f(\frac{n}{2^k})\end{split}\]

di mana kita ketahui kondisi dari pemberhentian perulangan adalah ketika sisa elemen list adalah 1, dengan kata lain:

\[\begin{split}\frac{n}{2^k} & = 1 \\ n & = 2^k \\ \log_2 n & = k\end{split}\]

Sehingga dapat dikatakan bahwa binary search memiliki kompleksitas \(O(\log_2n)\), atau sederhananya, \(O(\log n)\).

Tingkat pertumbuhan algoritma dengan kompleksitas logaritmik dapat dilihat pada gambar berikut:

Tingkat Pertumbunan Algoritma Kompleksitas Logaritmik

O(n): Kompleksitas Linear

Algoritma dengan kompleksitas linear bertumbuh selaras dengan pertumbuhan ukuran data. Jika algoritma ini memerlukan 10 langkah untuk menyelesaikan kalkulasi data berukuran 10, maka ia akan memerlukan 100 langkah untuk data berukuran 100. Contoh dari algoritma dengan

kompleksitas linear telah diberikan pada bagian sebelumnya, yaitu perhitungan pangkat bilangan. Contoh lain dari algoritma dengan kompleksitas linear adalah linear search.

Linear search melakukan pencarian dengan menelusuri elemen-elemen dalam list satu demi satu, mulai dari indeks paling rendah sampai indeks terakhir. Berikut adalah implementasi dari linear search pada python:

if lst[i] == search:

print("Nilai ditemukan pada posisi " + str(i)) return 0

print("Nilai tidak ditemukan.") return -1

Dengan menggunakan cara perhitungan yang sama pada perhitungan pangkat, kita bisa mendapatkan jumlah eksekusi kode seperti berikut (dengan asumsi n = len(lst)):

Kode Jumlah Eksekusi

for i in range(0, len(lst)) \(1\) if lst[i] == search \(n\) print("Nilai ditemukan... \(1\)

return 0 \(1\)

print("Nilai tidak ... \(1\)

return -1 \(1\)

Sehingga nilai kompleksitas dari linear search adalah \(5 + n\), atau dapat dituliskan sebagai \ (O(n)\). Adapun grafik pertumbuhan untuk kompleksitas \(O(n)\) adalah seperti berikut:

Tingkat Pertumbunan Algoritma Kompleksitas Linear

O(n log n)

Salah satu solusi yang paling sederhana ialah dengan menelusuri seluruh list, satu demi satu (kompleksitas: \(n\)) lalu mencari elemen yang bernilai invers dari elemen sekarang

menggunakan binary search (kompleksitas: \(\log n\)). Mari kita lihat contoh implementasi dari fungsi ini terlebih dahulu:

def zero_sum(lst): n = len(lst)

for i in range(0, n):

j = binary_search(lst, -1 * lst[i]) if j > i:

n1 = str(lst[i]) n2 = str(lst[j])

print("Zero sum: " + n1 + " and " + n2 + "\n")

Perhatikan bagaimana kita melakukan binary search sebanyak \(n\) kali, sehingga secara sederhana kompleksitas yang akan kita dapatkan adalah \(n * \log n = n \log n\). Adapun grafik pertumbuhan untuk kompleksitas \(O(n \log n)\) adalah seperti berikut:

Tingkat Pertumbunan Algoritma Kompleksitas n log n

O(\(n^m\)): Kompleksitas Polinomial

Algoritma dengan kompleksitas polinomial merupakan salah satu kelas algoritma yang tidak efisien, karena memerlukan jumlah langkah penyelesaian yang jauh lebih besar daripada jumlah data. Untuk lebih jelasnya, mari kita lihat salah satu contoh algoritma yang memiliki

kompleksitas polinomial: def kali(a, b): res = 0

for i in range(a): for j in range(b): res += 1

Algoritma di atas melakukan perkalian antara \(a\) dan \(b\), dengan melakukan penambahan \ (1\) sebanyak \(b\) kali, yang hasilnya ditambahkan sebanyak \(a\) kali. Mengabaikan dua langkah, yaitu awal (res = 0) dan akhir (return res) kode, kita dapat melihat total langkah yang diperlukan oleh perulangan bersarang yang ada seperti berikut:

Kode Jumlah Langkah

for i in range(b): \(a\)

res += 1 \(b\)

dan karena pada setiap iterasi kita harus menjalankan kode for i in range(b), maka dapat dikatakan kompleksitas dari kode di atas adalah:

\[a * b\]

yang ketika nilai \(a\) dan \(b\) sama akan menjadi: \[a^2\]

atau dapat ditulis sebagai \(n^2\) yang diabstrakkan sebagai \(n^m, m = 2\). Grafik pertumbuhan untuk kompleksitas polinomial adalah sebagai berikut:

Tingkat Pertumbunan Algoritma Kompleksitas Eksponensial

Perbandingan Pertumbuhan Seluruh Kompleksitas

Perbandingan Tingkat Pertumbuhan Tiap Kompleksitas

Pengembangan algoritma idealnya diusahakan mendapatkan kompleksitas \(O(1)\) atau \(O(\log n)\). Sayangnya pada kenyataannya kita tidak akan selalu mendapatkan kompleksitas terbaik dalam merancang algoritma. Jika tidak dapat mencapai kompleksitas maksimal, hal terbaik yang dapat kita lakukan ketika mengembangkan solusi dari masalah adalah melihat apakah masalah yang ada dapat diselesaikan dengan algoritma yang ada terlebih dahulu, sebelum

mengembangkan algoritma baru. Hal ini memastikan kita mendapatkan kompleksitas yang paling efisien sampai saat pengembangan solusi.

Kesimpulan

Pada bagian ini kita telah mempelajari bagaimana melakukan analisa efisiensi algoritma dengan menggunakan notasi Big-O. Kita juga melihat bagaimana algoritma yang paling efisien memiliki kompleksitas \(O(1)\), dengan kompleksitas \(O(n!)\) sebagai kelas kompleksitas yang paling tidak efisien. Dengan mengerti efisiensi algoritma, diharapkan pembaca dapat memilih dan merancang algoritma yang sesuai dengan kebutuhan untuk menyelesaikan masalah.

Rekursif

Salah satu konsep paling dasar dalam ilmu komputer dan pemrograman adalah pengunaan fungsi sebagai abstraksi untuk kode-kode yang digunakan berulang kali. Kedekatan ilmu komputer dengan matematika juga menyebabkan konsep-konsep fungsi pada matematika seringkali dijumpai. Salah satu konsep fungsi pada matematika yang ditemui pada ilmu komputer adalah fungsi rekursif: sebuah fungsi yang memanggil dirinya sendiri.

Kode berikut memperlihatkan contoh fungsi rekursif, untuk menghitung hasil kali dari dua bilangan:

def kali(a, b):

return a if b == 1 else a + kali(a, b - 1)

Bagaimana cara kerja fungsi rekursif ini? Sederhananya, selama nilai b bukan 1, fungsi akan terus memanggil perintah a + kali(a, b - 1), yang tiap tahapnya memanggil dirinya sendiri sambil mengurangi nilai b. Mari kita coba panggil fungsi kali dan uraikan langkah

pemanggilannya:

Perhatikan bahwa sebelum melakukan penambahan program melakukan pemanggilan fungsi rekursif terlebih dahulu sampai fungsi rekursif mengembalikan nilai pasti (\(2\)). Setelah menghilangkan semua pemanggilan fungsi, penambahan baru dilakukan, mulai dari nilai kembalian dari fungsi yang paling terakhir. Mari kita lihat contoh fungsi rekursif lainnya, yang digunakan untuk melakukan perhitungan faktorial:

def faktorial(n):

return n if n == 1 else n * faktorial(n - 1)

-> 120

Dengan melihat kemiripan cara kerja serta kode dari fungsi faktorial dan kali, kita dapat melihat bagaimana fungsi rekursif memiliki dua ciri khas:

1. Fungsi rekursif selalu memiliki kondisi yang menyatakan kapan fungsi tersebut berhenti. Kondisi ini harus dapat dibuktikan akan tercapai, karena jika tidak tercapai maka kita tidak dapat membuktikan bahwa fungsi akan berhenti, yang berarti algoritma kita tidak benar.

2. Fungsi rekursif selalu memanggil dirinya sendiri sambil mengurangi atau memecahkan data masukan setiap panggilannya. Hal ini penting diingat, karena tujuan utama dari rekursif ialah memecahkan masalah dengan mengurangi masalah tersebut menjadi masalah-masalah kecil.

Setiap fungsi rekursif yang ada harus memenuhi kedua persyaratan di atas untuk memastikan fungsi rekursif dapat berhenti dan memberikan hasil. Kebenaran dari nilai yang dihasilkan tentu saja memerlukan pembuktian dengan cara tersendiri. Tetapi sebelum masuk ke analisa dan pembuktian fungsi rekursif, mari kita lihat kegunaan dan contoh-contoh fungsi rekursif lainnya lagi.

Fungsi Rekursif dan Iterasi

Pembaca yang jeli akan menyadari bahwa kedua contoh fungsi rekursif yang diberikan

sebelumnya, faktorial dan kali, dapat diimplementasikan tanpa menggunakan fungsi rekursif. Berikut adalah contoh kode untuk perhitungan faktorial tanpa menggunakan rekursif:

def faktorial_iterasi(n): hasil = 1

for i in range(1, n + 1): hasil = hasil * i return hasil

Dalam menghitung nilai faktorial menggunakan iterasi, kita meningkatkan nilai hasil terus menerus, sampai mendapatkan jawaban yang tepat. Yang perlu kita pastikan benar pada fungsi ini adalah berapa kali kita harus meningkatkan nilai hasil. Jika jumlah peningkatan salah, maka hasil akhir yang didapatkan juga akan salah.

didefinisikan sebagai sebuah pohon dengan jumlah cabang yang selalu dua, secara alami adalah struktur data rekursif.

Binary Tree

Sebagai struktur rekursif, tentunya penelusuran binary tree akan lebih mudah dilakukan secara rekursif dibandingkan iterasi. Hal ini sangat kontras dengan, misalnya, pencarian karakter di dalam string. Sebagai data yang disimpan secara linear, pencarian karakter dalam string akan lebih mudah untuk dilakukan secara iteratif.

Untuk mempermudah ilustrasi, mari kita lakukan perbandingan antara implementasi rekursif dan iteratif untuk masalah yang lebih cocok diselesaikan dengan masing-masing pendekatan.

Misalnya, implementasi algoritma euclidean untuk menghitung faktor persekutuan terbesar (FPB) yang lebih cocok untuk diimplementasikan dengan metode rekursif seperti berikut: def gcd(x, y):

return x if y == 0 else gcd(y, x % y)

yang jika diimplementasikan dengan menggunakan iterasi adalah sebagai berikut: def gcd_iterasi(x, y):

while y != 0: temp = y y = x % temp x = temp return x

Jika dibandingkan dengan fungsi matematis dari algoritma euclidean:

tentunya implementasi secara rekursif lebih sederhana dan mudah dimengerti dibandingkan dengan secara iterasi.

Sekarang mari kita lihat contoh algoritima yang lebih cocok diimplementasikan secara iteratif, misalnya linear search. Implementasi standar linear search secara iteratif adalah sebagai berikut: def linear_search(lst, search):

for i in range(0, len(lst)): if lst[i] == search:

print("Nilai ditemukan pada posisi: " + str(i)) return 0

print("Nilai tidak ditemukan") return -1

yang jika diimplementasikan secara rekursif akan menjadi: def linear_search_rec(lst, search, pos):

Perhatikan bagaimana diperlukan lebih banyak pengecekan pada fungsi rekursif, serta tambahan parameter pos yang berguna untuk menyimpan posisi pengujian dan ditemukannya elemen yang dicari. Jika menggunakan iterasi variabel pos tidak dibutuhkan lagi karena posisi ini akan didapatkan secara otomatis ketika sedang menelusuri list. Dengan melihat jumlah argumen dan pengecekan yang harus dilakukan, dapat dilihat bahwa implementasi linear search menjadi lebih sederhana dan mudah dengan menggunakan metode iterasi.

Tail Call

Sesuai definisinya, dalam membuat fungsi rekursif pada satu titik kita akan harus memanggil fungsi itu sendiri. Pemanggilan diri sendiri di dalam fungsi tentunya memiliki konsekuensi tersendiri, yaitu pengunaan memori. Dengan memanggil dirinya sendiri, secara otomatis sebuah fungsi akan memerlukan memori tambahan, untuk menampung seluruh variabel baru serta proses yang harus dilakukan terhadap nilai-nilai baru tersebut. Penambahan memori ini seringkali menyebabkan stack overflow ketika terjadi pemanggilan rekursif yang terlalu banyak.

Tail call merupakan pemanggilan fungsi sebagai perintah terakhir di dalam fungsi lain. Sederhananya, ketika kita memanggil sebuah fungsi pada bagian akhir dari fungsi lain, kita melakukan tail call, seperti pada kode di bawah:

def fungsi(x): y = x + 10

return fungsi_lain(y)

Pada kode di atas, pemanggilan fungsi_lain sebagai kode terakhir yang dieksekusi oleh fungsi dapat dikatakan sebagai tail call. Ingat juga bahwa pemanggilan tidak harus berada di akhir fungsi secara fisik. Yang penting adalah bahwa kode terakhir yang dieksekusi adalah pemanggilan fungsi lain:

Pada contoh fungsi tail_call di atas, pemanggilan terhadap fungsi_1 maupun fungsi_2 adalah tail call, meskipun pemanggilan fungsi_1 tidak berada pada akhri fungsi secara fisik. Bandingkan dengan kode berikut:

def bukan_tail_call(n):

result = fungsi_lain(n % 5) return result * 10

yang bukan merupakan tail call, karena kode terakhir yang dieksekusi (result * 10e) adalah sebuah operasi, bukan pemanggilan fungsi. Cara kerja ini tentunya juga dibawa ke fungsi rekursif, di mana:

bukan merupakan tail call karena baik return 1 maupun n * faktorial(n - 1) bukanlah pemanggilan fungsi. Ingat bahwa n * faktorial(n - 1) merupakan operator perkalian, bukan pemanggilan fungsi karena faktorial(n - 1) akan harus mengembalikan hasil terlebih dahulu agar bisa dikalikan dengan n. Jika ingin membuat fungsi rekursif yang memanfaatkan tail call, kita harus memastikan kode terakhir yang dieksekusi adalah fungsi lain, tanpa operasi lanjutan. Misalnya, kita dapat menyimpan hasil kalkulasi sebagai parameter, seperti berikut: def faktorial_tc(n, r = 1):

if n <= 1: return r else:

untuk memastikan terdapat tail call di dalam fungsi.

Implementasi algoritma rekursif disarankan untuk mengadopsi tail call, karena natur dari fungsi rekursif yang memakan banyak memori. Tail call optimization, jika diimplementasikan oleh bahasa pemrograman, akan mendeteksi adanya tail call pada sebuah fungsi untuk kemudian dijalankan sebagai perulangan untuk menghindari penggunaan memori berlebihan.

Bahasa pemrograman yang mendukung tail call optimization biasanya adalah bahasa

pemrograman fungsional seperti Haskell, LISP, Scheme, dan Erlang. Python, sayangnya, tidak mendukung optimization.

Analisis Algoritma Rekursif

Melakukan analisis untuk algoritma rekursif pada dasarnya sama dengan melakukan analisis terhadap algoritma imparatif lain. Perbedaan utama pada algoritma rekursif ialah kita tidak dapat secara langsung melihat berapa kali bagian rekursif dari algoritma akan dijalankan. Pada

algoritma yang menggunakan perulangan for misalnya, kita dapat langsung menghitung jumlah perulangan untuk menghitung total langkah yang dibutuhkan. Dalam algoritma rekursif, jumlah perulangan tidak secara eksplisit bisa didapatkan karena informasi yang kita miliki adalah kapan algoritma berhenti, bukan berapa kali kode dieksekusi.

Misalnya, algoritma perhitungan faktorial yang telah dibahas sebelumnya: def faktorial(n):

return n if n == 1 else n * faktorial(n - 1)

Salah satu informasi yang didapatkan di sini adalah kapan algoritma berhenti melakukan rekursif, yaitu n == 1. Informasi lain yang kita miliki adalah berkurangnya jumlah data pada setiap pemanggilan faktorial. Bagaimana kita melakukan analisis algoritma ini? Cara termudahnya adalah dengan menggambarkan fungsi matematika dari faktorial terlebih dahulu: \[\begin{split}faktorial(n) = \begin{cases} 1 & \text{if } n = 1 \\ n * faktorial(n - 1) remainder(x, y)) & \text{if } n > 1 \end{cases}\end{split}\]

Melalui fungsi matematika ini, kita dapat mulai melakukan penurunan untuk fungsi perhitungan langkah fungsi \(faktorial\) untuk kasus \(n > 1\):

\[\begin{split}f(n) & = 1 + f(n - 1) \\ & = 1 + 1 + f(n - 2) \\ & = 1 + 1 + 1 + f(n - 3) \\ & ... \\ & = n + f(n - k)\end{split}\]

Dan tentunya kita dapat mengabaikan penambahan langkah \(n\) di awal, serta dengan syarat bahwa fungsi berhenti ketika \(n - k = 1\):

Maka dapat disimpulkan bahwa fungsi faktorial memiliki kompleksitas \(n - 1\), atau \(O(n)\). Ingat bahwa kunci dari perhitungan kompleksitas untuk algoritma rekursif terdapat pada fungsi matematis algoritma dan definisi kapan berhentinya fungsi rekursif tersebut.

Kesimpulan

Fungsi rekursif merupakan fungsi yang memanggil dirinya sendiri. Terdapat dua komponen penting dalam fungsi rekursif, yaitu kondisi kapan berhentinya fungsi dan pengurangan atau pembagian data ketika fungsi memanggil dirinya sendiri. Optimasi fungsi rekursif dapat dilakukan dengan menggunakan teknik tail call, meskipun teknik ini tidak selalu

diimplementasikan oleh semua bahasa pemrograman.

Selain sebagai fungsi, konsep rekursif juga terkadang digunakan untuk struktur data seperti binary tree atau list.

Divide and Conquer

Komputer pada awalnya diciptakan sebagai perangkat untuk melakukan kalkulasi secara otomatis dan akurat. Meskipun awalnya hanya berfokus pada kalkukasi numerik, komputer modern yang dijumpai sekarang telah melakukan kalkulasi pada banyak hal, seperti teks ataupun gambar. Berbagai kalkulasi dan analisa yang dilakukan komputer biasanya diimplementasikan melalui perangkat lunak. Dengan semakin besarnya ruang lingkup hal-hal yang dilakukan oleh komputer, perangkat lunak yang dikembangkan juga menjadi semakin kompleks. Algoritma, sebagai bagian dari perangkat lunak yang melakukan pemrosesan, juga memerlukan berbagai teknik baru. Misalkan, untuk menghitung total jumlah dari bilangan-bilangan yang ada di dalam sebuah list, kita dapat menggunakan perulangan sederhana:

nums = [1, 2, 3, 5, 6, 7, 19, 28, 58, 18, 28, 67, 13] total = 0

for i in range(0, len(nums)): total = total + nums[i]

print(total) # 255

Lalu apa yang dapat kita lakukan? Langkah pertama yang dapat kita lakukan adalah menerapkan teknik rekursif untuk membagi-bagikan masalah menjadi masalah yang lebih kecil. Jika awalnya kita harus menghitung total keseluruhan list satu per satu, sekarang kita dapat melakukan

perhitungan dengan memecah-mecah list terlebih dahulu: def sums(lst):

if len(lst) >= 1: return lst[0]

mid = len(lst) // 2 left = sums(lst[:mid]) right = sums(lst[mid:])

return left + right

print(sums(nums)) # 255

Apa yang kita lakukan pada kode di atas?

1. Baris if len(lst) >= 1 memberikan syarat pemberhentian fungsi rekursif, yang akan mengembalikan isi dari list ketika list berukuran 1 (hanya memiliki satu elemen).

2. Baris mid = len(lst) // 2 mengambil median dari list, sebagai referensi ketika kita membagi list menjadi dua bagian.

3. Baris left = sum(lst[:mid]) dan selanjutnya membagikan list menjadi dua bagian, dengan nilai mid sebagai tengah dari list.

Singkatnya, setelah membagikan list menjadi dua bagian terus menerus sampai bagian terkecilnya, kita menjumlahkan kedua nilai list tersebut, seperti pada gambar berikut:

Langkah Kerja Divide and Conquer

sistem operasi atau compiler kemudian akan membagi-bagikan tugas pembagian dan perhitungan lanjutan agar dapat dijalankan secara paralel, misalnya dengan membagikan tugas ke dalam beberapa core prosesor, atau bahkan ke dalam mesin lain (jika terdapat sistem dengan banyak mesin).

Dengan membagi-bagikan pekerjaan ke dalam banyak unit, tentunya pekerjaan akan lebih cepat selesai! Teknik memecah-mecah pekerjaan untuk kemudian dibagikan kepada banyak pekerja ini dikenal dengan nama divide and conquer.

Membangun Algoritma Divide and Conquer

Sebuah algoritma divide and conquer (selanjutnya disebut dengan D&C) memiliki tiga langkah, yaitu:

1. Divide (Memecah): pada langkah ini kita memecahkan masalah atau data ke dalam bentuk yang sama, tetapi dalam ukuran yang lebih kecil. Pemecahan langkah biasanya dilakukan dengan menggunakan algoritma rekursif, sampai ukuran data menjadi sangat kecil dan dapat diselesaikan dengan algoritma sederhana.

2. Conquer (Menaklukkan): dalam langkah ini kita mencoba menyelesaikan masalah atau data yang telah dipecahkan pada langkah pertama, dengan menggunakan algoritma sederhana.

3. Combine (Menggabungkan): setelah menjalankan langkah conquer, tentunya kita harus menggabungkan kembali hasil dari masing-masing pecahan yang ada, untuk

mendapatkan hasil akhir kalkulasi. Langkah combine mencoba mencapai hal tersebut. Algoritma D&C, jika diimplementasikan menggunakan library atau bahasa yang tepat akan meningkatkan efisiensi algoritma secara logaritmik. Mari kita lakukan analisis pada fungsi sum di atas, untuk melihat kompleksitas algoritmanya:

def sums(lst):

yang secara matematis dapat dituliskan seperti berikut:

\[\begin{split}f(n) & = 4 + f(\frac{n}{2}) + f(\frac{n}{2}) \\ & = 4 + 2f(\frac{n}{2})\ end{split}\]

\[\begin{split}f(n) & = 2f(\frac{n}{2}) \\ & = 2(2(\frac{n}{4})) \\ & = 2(2(2(\frac{n}{8}))) \\ & ... \\ & = 2^k(\frac{n}{2^k})\end{split}\]

dengan syarat berhenti adalah ketika \(k \geq 1\), sehingga:

\[\begin{split}\frac{n}{2^k} & = 1 \\ n & = 2^k \\ k & = \log_2 n\end{split}\]

Kompleksitas dari fungsi sums adalah \(O(\log n)\), meningkat dari \(O(n)\) pada algoritma awal! Secara umum, kompleksitas algoritma D&C adalah \(O(n \log n)\), jika ukuran data adalah \(n\), dan pada setiap langkahnya kita membagikan masalah ke dalam \(p\) sub-masalah.

Contoh D&C 1: Merge Sort

Merge sort, seperti namanya, merupakan algoritma yang dirancang untuk melakukan pengurutan terhadap sekumpulan bilangan. Ide utama dari merge sort sama dengan algoritma perhitungan total yang telah kita lakukan sebelumnya, yaitu membagi-bagikan keseluruhan list menjadi komponen kecil, dan kemudian mengurutkan komponen tersebut dan menggabungkannya kembali menjadi sebuah list besar.

Berikut adalah merge sort yang diimplementasikan dalam bahasa python: def merge_sort(lst):

if len(lst) <= 1: return lst

mid = len(lst) // 2

left = merge_sort(lst[:mid]) right = merge_sort(lst[mid:])

return merge(left, right)

dengan fungsi penjumlahan total yang kita bangun sebelumnya, dengan perbedaan pada bagian yang melakukan penggabungan list (return merge(left, right)).

Penggabungan list sendiri dilakukan dengan cukup sederhana dan gamblang, yaitu hanya membandingkan elemen-elemen dari dua buah list yang dikirimkan satu per satu, untuk kemudian disimpan ke dalam variabel result secara terurut. Untuk lebih jelasnya, mari kita coba bedah algoritma pada fungsi merge, langkah demi langkah.

Misalkan kita memanggil fungsi merge seperti berikut: left = [3, 5]

right = [1, 4] merge(left, right)

Note

Ingat bahwa list pada variabel left maupun right harus sudah terurut jika ukuran list lebih dari 1. Fungsi merge dengan argumen list berukuran \(>\) 1 hanya dipanggil dari hasil merge dua buah list berukuran satu dalam kasus merge_sort.

Jika kita mengikuti langkah demi langkah pada kode, maka pada setiap iterasi while kita akan mendapatkan nilai masing-masing variabel sebagai berikut:

# Awal fungsi

Untuk mempermudah pengertian, gambar di bawah menunjukkan proses pemecahan dan penggabungan kembali dari merge sort:

Proses divide terjadi ketika kotak dan panah berwarna merah, sementara conquer dan combine terjadi ketika kotak dan panah diberi warna biru. Proses conquer merupakan proses di mana kita mengurutkan elemen dalam list, dan combine adalah ketika kita menggabungkan hasil urutan dari list tersebut.

Contoh D&C 2: Binary Search

Binary search merupakan salah satu algoritma pencarian yang paling efisien, dengan kompleksitas \(O(\log n)\). Algoritma ini memanfaatkan teknik divide and conquer dengan memecah lingkup pencarian data menjadi setengahnya pada setiap kali divide. Kekurangan dari binary search yaitu bahwa algoritma ini hanya dapat digunakan pada sebuah data atau lsit yang telah terurut.

Langsung saja, implementasi binary search menggunakan python: def binary_search(data, search_val, min_idx, max_idx): if max_idx < min_idx:

print("%d not found in list"%search_val) return -1

mid_idx = (min_idx + max_idx) // 2 if data[mid_idx] > search_val:

return binary_search(data, search_val, min_idx, mid_idx - 1) elif data[mid_idx] < search_val:

return binary_search(data, search_val, mid_idx + 1, max_idx) else:

print("%d found in index %d"%(search_val, mid_idx)) return mid_idx

Mari kita lihat cara kerja binary search. Misalkan kita diberikan data berupa list bilangan seperti berikut:

[1, 2, 4, 6, 7, 8, 9, 10]

dan diminta untuk mencari letak angka 2 pada list tersebut. Sebelum mulai menjalankan algoritma, pastinya kita harus mengetahui nilai-nilai awal terelbih dahulu. Adapun nilai awal yang dibutuhkan untuk fungsi binary_search adalah sebagai berikut:

data = [1, 2, 4, 6, 7, 8, 9, 10] search_val = 2

min_idx = 0

max_idx = len(data) - 1 # 7

Setelah mendapatkan nilai tengah, kita lalu melakukan cek apakah nilai dari data pada indeks tersebut lebih besar atau lebih kecil dibandingkan nilai yang akan kita cari (2). Langkah pengecekan ini dilakukan pada perintah if berikut:

if data[mid_idx] > search_val: # nilai lebih besar daripada 2 elif data[mid_idx] < search_val: # nilai lebih kecil daripada 2 else:

# nilai adalah 2 (ditemukan)

Dalam kasus ini, nilai dari mid_idx adalah 3, dan karena data[3] berisi 6, maka kita akan melakukan pemotongan terhadap seluruh nilai pada data setelah 6, karena nilai tersebut sudah pasti tidak diperlukan lagi (ingat, data harus terurut pada binary search). Kita lalu memanggil fungsi binary_search lagi, kali ini dengan mencari hanya pada submasalah (list) berikut (perhatikan bagaimana pada pemanggilan binary_search yang kedua nilai max_idx kita ubah menjadi mid_idx - 1):

[1, 2, 4]

Dan dengan mengaplikasikan logika yang sama dengan tahap sebelumnya, kita akan langsung menemukan bilangan yang dicari.

Algoritma Greedy

Algoritma greedy merupakan jenis algoritma yang menggunakan pendekatan penyelesaian masalah dengan mencari nilai maksimum sementara pada setiap langkahnya. Nilai maksimum sementara ini dikenal dengan istilah local maximum. Pada kebanyakan kasus, algoritma greedy tidak akan menghasilkan solusi paling optimal, begitupun algoritma greedy biasanya

memberikan solusi yang mendekati nilai optimum dalam waktu yang cukup cepat.

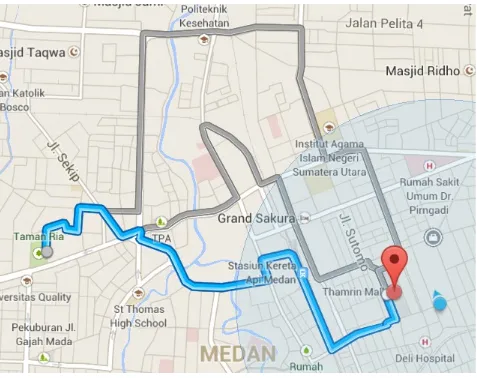
Jalur dari Titik A ke B

Graph Sederhana dari Titik A ke B

Dari gambar di atas, kita dapat melihat bagaimana sebuah peta jalur perjalanan dapat

Graph Berarah dari Titik A ke B

Untuk mencari jarak terpendek dari A ke B, sebuah algoritma greedy akan menjalankan langkah-langkah seperti berikut:

1. Kunjungi satu titik pada graph, dan ambil seluruh titik yang dapat dikunjungi dari titik sekarang.

2. Cari local maximum ke titik selanjutnya.

3. Tandai graph sekarang sebagai graph yang telah dikunjungi, dan pindah ke local maximum yang telah ditentukan.

4. Kembali ke langkah 1 sampai titik tujuan didapatkan.

Jika mengapliikasikan langkah-langkah di atas pada graph A ke B sebelumnya maka kita akan mendapatkan pergerakan seperti berikut:

Langkah Pertama Greedy

2. Local maximum adalah ke C, karena jarak ke C adalah yang paling dekat. 3. Tandai A sebagai titik yang telah dikunjungi, dan pindah ke C.

Langkah Kedua Greedy

5. Local maximum adaah ke D, dengan jarak 6.

Langkah Ketiga Greedy

7. (Langkah selanjutnya diserahkan kepada pembaca sebagai latihan).

Solusi Kurang Optimal dari Greedy

Tetapi ingat bahwa untuk kasus umum, kerap kali algoritma greedy memberikan hasil yang

cukup baik dengan kompleksitas waktu yang cepat. Hal ini mengakibatkan algoritma greedy sering digunakan untuk menyelesaikan permasalahan kompleks yang memerlukan kecepatan jawaban, bukan solusi optimal, misalnya pada game.

Implementasi Algoritma Greedy

Untuk memperdalam pengertian algoritma greedy, kita akan mengimplementasikan algoritma yang telah dijelaskan pada bagian sebelumnya ke dalam kode program. Seperti biasa, contoh kode program akan diberikan dalam bahasa pemrograman python. Sebagai langkah awal, tentunya kita terlebih dahulu harus merepresentasikan graph. Pada implementasi yang kita lakukan, graph direpresentasikan dengan menggunakan dictionary di dalam dictionary, seperti berikut:

DAG = {'A': {'C': 4, 'G': 9}, 'G': {'E': 6},

'D': {'E': 7},

Selanjutnya kita akan membuat fungsi yang mencari jarak terpendek dari graph yang dibangun, dengan menggunakan algoritma greedy. Definisi dari fungsi tersebut sangat sederhana, hanya sebuah fungsi yang mengambil graph, titik awal, dan titik akhir sebagai argumennya:

def shortest_path(graph, source, dest):

Jarak terpendek yang didapatkan akan dibangun langkah demi langkah, seperti pada algoritma greedy yang mengambil nilai local maximum pada setiap langkahnya. Untuk hal ini, tentunya kita akan perlu menyimpan jarak terpendek ke dalam sebuah variabel, dengan source sebagai isi awal variabel tersebut. Jarak terpendek kita simpan ke dalam sebuah list, untuk

menyederhanakan proses penambahan nilai. result = []

result.append(source)

Penelusuran graph sendiri akan kita lakukan melalui result, karena variabel ini

merepresentasikan seluruh node yang telah kita kunjungi dari keseluruhan graph. Variabel result

pada dasarnya merupakan hasil implementasi dari langkah 3 algoritma (“Tandai graph sekarang sebagai graph yang telah dikunjungi”). Titik awal dari rute tentunya secara otomatis ditandai sebagai node yang telah dikunjungi.

Selanjutnya, kita akan menelusuri graph sampai titik tujuan ditemukan, dengan menggunakan iterasi:

while dest not in result: current_node = result[-1]

dengan mengambil node yang sekarang sedang dicari local maximum-nya dari isi terakhir result. Pencarian local maximum sendiri lebih memerlukan pengetahuan python daripada algoritma:

# Cari local maximum

local_max = min(graph[current_node].values())

# Ambil node dari local maximum, # dan tambahkan ke result