BAB II
TINJAUAN PUSTAKA
2.1 Kriptografi
Kriptografi (Cryptography) berasal dari bahasa Yunani, terdiri dari dua suku kata
yaitu kripto dan graphia. Kripto artinya menyembunyikan, sedangkan graphia
artinya tulisan. Jadi, kriptografi adalah ilmu yang mempelajari teknik-teknik
matematika yang berhubungan dengan aspek keamanan informasi, seperti
kerahasiaan data, keabsahan data, integritas data, serta autentikasi data
(Buchmann, 2004). Tetapi tidak semua aspek keamanan informasi dapat
diselesaikan dengan kriptografi. Kriptorafi dapat pula diartikan sebagai ilmu atau
seni untuk menjaga keamanan pesan. Ketika suatu pesan dikirim dari suatu tempat
ke tempat lain, isi pesan tersebut. Untuk menjaga pesan, maka pesan tersebut
dapat diubah menjadi suatu kode yang tidak dapat dimengerti oleh pihak lain.
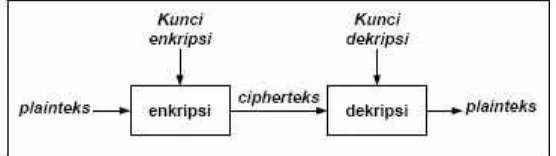
Enkripsi adalah sebuah proses penyandian yang melakukan perubahan
sebuah kode (pesan) dari yang bisa dimengerti (plaintext) menjadi sebuah kode
yang tidak bisa dimengerti (ciphertext). Sedangkan proses kebalikannya untuk
mengubah ciphertext menjadi plaintext disebut dekripsi. Proses enkripsi dan
dekripsi memerlukan suatu mekanisme dan kunci tertentu.
Kriptonalisis (cryptanalysis) adalah kebalikan dari kriptografi, yaitu suatu
ilmu untuk memecahkan mekanisme kriptografi dengan cara mendapatkan kunci
dari cipherteks yang digunakan untuk mendapatkan plainteks. Kriptologi
(cryptology) adalah ilmu yang mencakup kriptografi dan kriptonalisis.
Ada empat tujuan mendasar dari kriptografi yang juga merupakan aspek
keamanan informasi yaitu:
a. Privacy/Confidentiality: yaitu usaha menjaga informasi dari orang yang
tidak berhak mengakses (mengaransi bahwa data pribadi tetap pribadi).
b. Integrity: yaitu usaha untuk menjaga data atau sistem tidak diubah oleh
yang tidak berhak.
c. Authentication: yaitu usaha atau metoda untuk mengetahui keaslian dari
informasi, misalnya apakah informasi yang dikirim dibuka oleh orang
yang benar (asli) atau layanan dari server yang diberikan benar berasal
dari server yang dimaksud.
d. Availability: berhubungan dengan ketersediaan sistem dan data (informasi)
ketika dibutuhkan.
2.1.1 Terminologi Kriptografi
Di dalam kriptografi, akan sering ditemukan berbagai istilah (terminologi).
Adapun istilah-istilah yang kerap kali digunakan adalah sebagai berikut:
a. Pesan, Plaintext, dan Ciphertext
Pesan adalah data ataupun suatu informasi yang dapat dibaca dan
dimengerti maknanya. Dan nama lain untuk pesan ialah plaintext, atau teks
jelas. Ciphertext adalah suatu bentuk pesan yang bersandi. Disandikannya
suatu pesan adalah agar pesan tersebut tidak dapat oleh pihak lain.
b. Pengiriman dan Penerimaan
mengirim pesan kepada entitas lainnya. Sedangkan penerima adalah
entitas yang menerima pesan. Suatu pengiriman pesan, pengirim tentu
menginginkan pesan dapat dikirim secara aman. Untuk mengamankannya,
pengirim biasanya akan menyandikan pesan yang dikirimkan tersebut
c. Enkripsi dan Dekripsi
Suatu proses untuk menyandikan plaintext menjadi ciphertext disebut
enkripsi (encryption). Sedangkan proses pengembalian dari ciphertext
manjadi plaintext dinamakan dekripsi (decription). Enkripsi dan dekripsi
merupakan suatu pesan yang memetakan elemen-elemen antara kedua
himpunan tersebut. Misalkan P adalah himpunan plaintext, dan C adalah
himpunan ciphertext, maka fungsi enkripsi E memetakan P ke C, ditulis
E(P) = C. Dan fungsi dekripsi D memetakan C ke P, ditulis D(C) = P
d. Cipher dan Kunci
Algoritma kriptografi disebut juga cipher yaitu aturan atau fungsi
matematika yang digunakan untuk enkripsi dan dekripsi. Beberapa cipher
memerlukan algoritma yang berbeda untuk enkripsi dan dekripsi (Stalling,
2005). Untuk menjaga kerahasiaan pengiriman pesan dalam kriptografi
modern dibutuhkan kunci. Kunci (key) adalah parameter yang digunakan
untuk mentransformasi proses pengenkripsian dan pendekripsian pesan.
Biasanya, kunci berupa deretan bilangan maupun string. Dengan
menggunakan kunci K maka proses enkripsi dan dekripsi dapat ditulis
sebagai EK(P) = C dan DK(C) =P, dan kedua fungsi tersebut memenuhi
DK(EK(P)) = P
e. Kriptografi Kunci Simetris dan Asimetris
Sistem kriptografi merupakan kumpulan yang terdiri dari plaintext,
ciphertext, kunci, enkripsi serta dekripsi. Berdasarkan kunci yang
digunakan dalam proses enkripsi dan dekripsi, kriptografi dapat dibedakan
Kriptografi kunci simetri, sering disingkat menjadi kriptografi simetri,
kunci yang digunakan pada proses enkripsi dan dekripsi adalah sama. Oleh
karena itu, sebelum saling berkomunikasi kedua belah pihak harus
melakukan kesepakatan dalam menentukan kunci yang akan digunakan.
Keamanan menggunakan sistem ini terletak pada kerahasiaan kunci yang
akan digunakan. Sedangkan dalam sistem kriptografi kunci publik, kunci
yang digunakan dalam proses enkripsi dan dekripsi berbeda. Sistem ini
terdapat dua buah kunci, yaitu kunci publik dan kunci privat. Kunci
publik digunakan untuk proses enkripsi, dan kunci privat digunakan untuk
mendekripsikan pesan. Kunci publik bersifat tak rahasia, sedangkan kunci
privat hanya boleh diketahui oleh penerima pesan.
2.1.2 Penggunaan Kriptografi
Terdapat beberapa media yang menggunakan teknik kriptografi melalui jalur
internet (Schmeh, 2003) diantaranya adalah:
1. E-mail
E-mail merupakan surat elektronik yang telah disandikan menjadi daya
tarik utama dalam dunia internet.
2. World Wide Web (WWW)
World Wide Web (WWW) telah banyak digunakan sebagai alat untuk
mengakses basis data, administrasi sistem komputer dan pusat
perbelanjaan. Pada masing-masing keadaan tersebut, teknik enkripsi
sangat dibutuhkan.
3. Koneksi client-server
Koneksi client-server merupakan perkembangan sistem komputer
4. Jaringan rahasia virtual
Perusahaan dengan beberapa cabang sering mengelompokan jaringan lokal
dengan koneksi seperti ISDN. Semua data akan dienkripsi apabila berada
diluar jaringan perusahaan dan kemudian akan didekripsi apabila telah
berada di wilayah perusahaan.
5. Sistem pembayaran
Kriptografi menjaga keamanan dalam melakukan transaksi berupa transfer
uang melalui internet.
6. Remote access
Beberapa layanan seperti Telnet atau SSH berfungsi untuk mengakses
komputer dari jarak jauh menggunakan internet. Kriptografi berperan
dalam mengenkripsi data selama proses berlangsung.
2.1.3 Kriptografi Kunci Publik
Suatu sistem kriptografi terdiri atas kumpulan transformasi enkripsi dan dekripsi
disebut dengan sistem kriptografi kunci publik atau suatu sistem kriptografi
asimetris jika sepasang kunci yaitu kunci untuk proses enkripsi dinamakan kunci
publik, disebarkan kepada publik, dan kunci untuk proses dekripsi dinamakan
kunci privat, dijaga kerahasiaannya (Schmeh, 2003). Beberapa aspek penting pada
sistem kriptografi kunci publik dapat dijelaskan sebagai berikut:
1. Keamanan
Dengan adanya sistem kriptografi kunci publik, hanya kunci privat yang
harus dijaga kerahasiaannya sedangkan kunci publik disebarkan dengan
bebas.
2. Usia pemakaian
Sistem kriptografi kunci publik memiliki pasangan kunci yang dapat
digunakan tanpa perlu adanya perubahan dalam waktu yang lama.
Pada jaringan multiuser, lebih sedikit kunci privat yang dibutuhkan.
4. Pertukaran kunci
5. Pada Sistem kriptografi kunci publik, tidak dibutuhkan adanya pertukaran
kunci privat antar entitas.
2.1.3.1 Teori Bilangan
Teori bilangan menjadi dasar dalam kriptografi, khususnya sistem kriptografi
kunci publik. Bilangan yang dimaksudkan dalam hal ini adalah bilangan bulat
(integer) (Mollin, 2007). Beberapa teori bilangan yang digunakan dalam
menganalisis algoritma yang digunakan adalah aritmatika modular dan Greatest
Common Divisor (GCD).
2.1.3.1.1 Aritmatika Modular
Aritmetika modular digunakan dalam proses enkripsi dan dekripsi pada algoritma
RSA dan algoritma Rabin. Enkripsi dapat dilakukan menghitung nilai pesan
dipangkatkan dengan nilai kunci enkripsi yang didapat kemudian dengan
melakukan modulo pada nilai bilangan prima yang ditentukan sebelumnya.
Aritmatika modular sering dicontohkan sebagai pemahaman aritmatika jam.
(Kaisar, 2004). Misalkan dalam operasi a mod m berarti menghasilkan sisa jika a
dibagi dengan m. Bilangan m disebut modulus atau modulo, dan hasil arimatika
modulo m terletak di dalam himpunan {0, 1, 2, …, n-1} sehingga dapat
dinotasikan � �� �������= ��sedemikian sehingga:
m = n*q + r, 0 ≤ r < n (2.1)
Pembagi bersama terbesar atau disingkat PBB (Greatest Common Divisor atau
GCD) digunakan dalam rancangan algoritma RSA pada saat penentuan kunci
enkripsi. Kunci enkripsi harus merupakan anggota dari bilangan ganjil yang mana
GCD antara bilangan ganjil tersebut dengan nilai yang didapat harus bernilai 1.
Dalam notasi dapat dituliskan ����∈������, Ke∈����������,�� =1.
Greatest Common Divisor atau GCD dari bilangan suatu a dan b adalah
bilangan bulat terbesar d sedemikian sehingga d | a dan d | b. Dalam hal ini kita
nyatakan bahwa GCD (a,b) = d.Misalkan dalam menentukan GCD (5,2) = 1.
Didapati bahwa nilai a adalah 5 dan nilai b adalah 2.Untuk mempermudah dapat
dilihat pada algoritma berikut ini:
2.1.3.2 Pembangkitan Bilangan Prima
Pembangkitan bilangan prima (Prime Number Generate) merupakan cara dalam
penentuan bilangan prima yang sudah diformula dan akan digunakan dalam
pembangkitan kunci bilangan prima. Terdapat beberapa teori tentang pengujian
bilangan prima seperti algoritma Primality Proving, Pengujian Bilangan Prima
Lucas-Lehmer dalam Bilangan Mersenne, Teorema Pocklington, Teorema Proth,
Sophie Germain’s Prime Density Conjecture dan beberapa pengujian bilangan
prima lainnya.
2.1.3.3 Teorema Fermat
Pierre de Fermat (dibaca Fair-ma) merupakan seorang matematikawan
berkebangsaan Perancis (1607-1665).Fermat megikuti pendidikan di Universitas
Toulouse dan kemudian mempelajari ilmu hukum di Universitas Orleans. Setelah
mendapatkan gelar sarjana hokum, Fermat menjadi pengajar di kantor
pemerintahan di Toulose. Namun sepanjang hidupnya dia memiliki ketertarikan
yang dalam terhadap teori angka dan matematika. (Mollin, Richard A. 2007).
Pada teori Fermat dinyatakan suatu bilangan prima p dapat dipastikan
keprimaannya. Jika bilangan p adalah sebuah bilangan prima dan a bukan
merupakan kelipatan dari p, dan 1 ≤ �� < ��. Maka dapat dinotasikan dalam t
dengan rumus: �� ��
−1 ≡ 1
� ������� ; 1 ≤ ��< ��, atau dapat dituliskan juga sebagai:
��
��
−1
Penggunaan terorema Fermat pada rancangan algoritma Rabin sangat
penting karena pembangkitan bilangan prima merupakan awal proses algoritma.
Dengan rumus tersebut dapat dinyatakan suatu bilangan prima atau tidak prima.
Misalkan sebuah bilangan bernilai 5, dapat dibuktikan keprimaannya dengan nilai
p= 3. Berdasarkan syarat bahwa 1 ≤ ��< 3, didapat nilai a yang mungkin adalah 1
dan 2. Kedua bilangan akan diuji dengan teorema Fermat yaitu:
• Untuk nilai a = 1, maka dapat dilakukan pengujian �� ��
−1
� �������≡ 1,
= 13-1mod 3 ≡ 12mod 3 ≡ 1 (memenuhi teorema Fermat)
• Untuk nilai a = 2 , maka dapat dilakukan pengujian ��
��
−1
� �������≡ 1,
= 23-1mod 3 ≡ 22mod 3 ≡ 1
(memenuhi teorema Fermat)
Dari pengujian setiap batas nilai adidapati bahwa nilai 3 merupakan
bilangan prima karena memenuhi syarat yang ada pada teorema Fermat. Dan
konsep Fermat dapat digunakan untuk pengujian bilangan prima lainnya.
2.1.4 Algoritma RSA
Algoritma RSA dijabarkan pada tahun 1977 oleh tiga orang yaitu Ron Rivest, Adi
Shamir danLen Adleman yang berasal dari Massachusetts Institute of Technology.
Algoritma ini dipatenkan oleh Massachusetts Institute of Technology pada tahun
1983 di Amerika Serikat (Stallings, 2005).
Algoritma RSA adalah sebuah algoritma pada enkripsi kunci publik. RSA
merupakan algoritma pertama yang cocok digunakan untuk digital signature
karena kehandalannya dalam proses enkripsi. Hal ini menjadikan algoritma yang
lebih banyak dikembangkan dalam bidang kriptografi public key.
2.1.4.1 Proses Algoritma RSA
Proses atau cara kerja dari algoritma RSA dapat dilihat sebagai berikut:
1. Menentukan dua bilangan prima p ≠ q secara acak dan terpisah untuk
tiap-tiap p dan q.
2. Melakukan perhitungan n= p*q. (n merupakan hasil perkalian dari p
dikalikan dengan q)
3. Melakukan perhitungan nilai totient φ(n) = (p-1)(q-1).
4. Menentukan nilai kunci enkripsi e dengan syarat bahwa nilangan tersebut
merupakan bilangan bulat (integer) 1 < e < φ(n) dimana nilai GCD (φ(n),
e) = 1.
5. Menghitung kunci enkripsi yang dilakukan dengan perhitungan kunci
dekripsi dengan rumus d ≡ e -1mod φ(n).
6. Setelah mendapatkan kunci-kunci tersebut maka dapat dilakukan proses
enkripsi maupun proses dekripsi.
7. Rumus untuk melakukan proses enkripsi adalah c = m emod n
8. Rumus untuk melakukan proses dekripsi adalah m = c d mod n
2.1.4.2 Contoh Kasus Algoritma RSA
Algoritma RSA disimulasikan dalam sebuah simulasi pengiriman pesan yang
dilakukan antara Alice dan Bob. Alice mengizinkan Bob untuk mengirimkan
sebuah pesan pribadi (private message). Dalam algoritma RSA multiple-key,
1. Alice (penerima) dan Bob (pengirim) menyepakati dua buah bilangan
prima sebagai kunci privat dari pesan yang akan dikirimkan. Misalkan
kunci tersebut adalah bernilai p=631 dan q=311.
2. Setelah disepakati kedua bilangan prima tersebut kemudian digunakan
untuk menghitung nilai totient dengan rumus n = p*q, sehingga didapat
nilai: n = (631)*(311) = 196241
3. Langkah selanjutnya adalah menghitung nilai totient dengan rumus
ϕ(n) =(p–1)(q-1),
sehingga didapat nilai: ϕ(n) = (631-1)*(311-1))= 195300.
Nilai n dan nilai totientakan digunakan dalam perhitungan nilai kunci
enkripsi.
4. Dari nilai totient yang didapat, maka Bob dapat menghitung nilai kunci
enkripsi e yang digunakan dalam program dengan syarat bahwa nilai
1<e<ϕ(n) dan juga nilai e relatif prima dengan ϕ(n). Hal ini dapat dihitung
dengan menghitung GCD (ϕ(n),e)=1. Dalam perhitungan didapati:
GCD (195300, e) = 1, 1<e<195300
e = 78899
Didapat nilai e yang memungkinkan dan disepakati oleh keduanya adalah
e=78899. Dengan nilai kunci enkripsi ini makan selanjutnya dapat
dilakukan proses enkripsi.
5. Kunci dekripsi juga langsung ditetapkan oleh kedua belah pihak dengan
syarat rumusan d = e-1 mod ϕ (n). Dari nilai e yang didapat sebelumnya
maka dapat dihitung nilai d dengan langkah sebagai berikut :
d = e-1 mod ϕ (n)
d = 78899-1 mod 195300
d = 17399
Kunci dekripsi digunakan untuk mengembalikan nilai ciphertext ke dalam
6. Proses enkripsi merupakan proses dimana pesan yang sebelumnya berupa
plaintext yang dikodekan menjadi ciphertext. Terlebih dahulu Bob akan
membuat pesan rahasia berupa teks. Dalam kasus ini pesan yang akan
digunakan adalah kode100. Dari rumus perhitungan enkripsi c = me mod n, makadapat dihitung kode ciphertext dari setiap pesan tersebut sebagai
berikut:
Pesan yang akan dikirim m = 100
Nilai dari setiap plaintextP1= 100, maka nilai ciphertext dari setiap pesan
dengan perhitungan :
c = m e mod n
c = 10078899 mod 196241
c = 31538
7. Setelah mendapatkan semua kode ciphertext maka dapat dirangkai seluruh
kode yang menghasilkan ciphertext sebesar 31538. Pesan inilah yang
akan dikirimkan kepada Alice, sehingga pihak lain tidak akan mengetahui
makna pesan sebenarnya.
8. Alice dapat mendapatkan pesan sebenarnya dengan melakukan proses
dekripsi. Dari rumus perhitungan dekripsi P = Cd mod n, makadapat
dihitung kode plaintext dari setiap chipertexttersebut sebagai berikut:
c = 31538
Nilai dari setiap plaintext:
m = cdmod n p1= c1dmod n
p1= 3153817399 mod196241
p1=100
Setelah mendapatkan semua plaintext terhitung maka dapat dirangkai
Dari contoh didapat bahwa Alice dapat membuka kembali pesan yang
sudah dienkripsi dengan melakukan proses dekripsi.
2.1.5 Algoritma Rabin
Algoritma Rabin pertama sekali diperkenalkan pada tahun 1979 oleh Michael O.
Rabin. Algoritma Rabin merupakan salah satu sistem kriptografi asimetris yang
kemampuan keamanan datanya dibuktikan secara matematika karena
menggunakan metode pemfaktoran bilangan secara cepat.
2.1.5.1 Pembangkitan Kunci
Sama seperti sistem kriptografi asimetri lainnya, algoritma Rabin juga
menggunakan sistem kunci publik dan kunci pribadi. Kunci publik nantinya akan
digunakan pada proses enkripsi dan dapat diketahui oleh semua pihak (tidak
rahasia), sementara kunci pribadi digunakan oleh penerima pesan untuk proses
dekripsi dan bersifat rahasia.
Algoritma pembangkitan kuncinya adalah sebagai berikut:
1. Pilih dua buah bilangan prima besar sebarang yang saling berbeda (p dan
q).
2. Hitung n = p.q
n adalah kunci publik. Bilangan prima p dan q adalah kunci pribadi.
Untuk mengenkripsi pesan hanya dibutuhkan kunci publik n, sedangkan
untuk dekripsi, dibutuhkan bilangan p dan q sebagai kunci pribadi.
2.1.5.2 Proses Enkripsi
Teknik Rabin merupakan algoritma kriptografi kunci publik, maka semua orang
dekripsi hanya dapat dilakukan dengan menggunakan kunci privat oleh orang
yang bersangkutan.
Proses enkripsi pada teknik Rabin sangat sederhana. Proses enkripsi
tersebut dapat dituliskan dengan rumus berikut:
n m c= 2mod
Proses enkripsi yang sederhana ini menyebabkan proses enkripsi teknik Rabin ini
dapat dilakukan dengan waktu yang singkat karena tidak memiliki proses yang
rumit. Kesederhanaan ini merupakan keuntungan yang dimiliki oleh teknik Rabin
untuk menghadapi keterbatasan sumber dayayang ada pada media kriptografi.
2.1.5.3 Proses Dekripsi
Proses dekripsi pada teknik Rabin dilakukan dengan menggunakan sebuah rumus
sederhana, namun membutuhkan teorema Chinese remainder. Teorema ini
digunakan untuk mendapatkan plainteks yang benar. Namun yang menjadi poin
penting dari teknik ini adalah teknik Rabin tidak menghasilkan jawaban plainteks
tunggal. Jawaban yang dihasilkan pada teknik Rabin ini terdiri dari 4
kemungkinan jawaban, tidak menghasilkan satu jawaban yang pasti. Rumus yang
digunakan untuk mendapatkan kemungkinan jawaban yang benar (pesan asli)
adalah sebagai berikut:
m1 = c (p+1)/4 mod p
m2 = (p – c (p+1)/4) mod p
m3 = c (q+1)/4 mod q
m4 = (q – c (q+1)/4) mod q
Teknik Rabin selalu menghasilkan empat kemungkinan hasil, yang
diberikan semuanya kepada orang yang melakukan dekripsi terhadap pesan
pesan berbeda pada akhirnya, namun penerima pesan dapat memilih pesan yang
benar dengan tidak terlalu sulit, karena pesan yang benar seharusnya akan terlihat
jelas dibandingkan dengan ketiga hasil dekripsi yang lain.
2.1.6 Tujuan Kriptografi
Tujuan dari kriptografi adalah sebagai berikut :
a. Kerahasiaan (confidentiality), merupakan suatu layanan yang digunakan
untuk menjaga isi dari informasi dari pihak-pihak yang tak berhak untuk
mendapatkannya.
b. Integritas Data (data integrity), merupakan suatu layanan dimana
menjamin bahwa pesan masih asli, dan belum dimanipulasi oleh pihak -
pihak yang tidak berhak. Realisasi layanan ini di dalam kriptografi, adalah
dengan menggunakan tanda tangan digital.
c. Otentifikasi (authentication), merupakan suatu layanan yang berhubungan
dengan identifikasi. Misalnya, mengidentifikasi suatu kebenaran
pihak-pihak yang berkomunikasi (entitas) maupun mengidentifikasi kebenaran
sumber pesan. Sama seperti poin (b), di dalam kriptografi, layanan ini
diwujudkan dengan menggunakan tanda tangan.
d. Nir-penyangkalan (non-repudiation), merupakan suatu layanan untuk
mencegah entitas yang saling berkomunikasi melakukan penyangkalan.
Misalkan salah satu dari entitas menyangkal telah mengirim maupun
menerima pesan.
2.2 Steganografi
Steganografi adalah sebuah seni dan ilmu untuk menyembunyikan sebuah pesan
dengan cara yang sedemikian rupa sehingga tidak ada orang lain, selain dari
penerima yang dituju yang mengetahui mengenai pesan tersebut (Wayner, 2009).
Keunggulan steganografi dari kriptografi adalah kemampuannya untuk membuat
suatu pesan rahasia menjadi tidak terlihat, atau tidak mengundang orang lain yang
tidak mengetahui untuk peduli atau penasaran, lain halnya dengan kriptografi
membuat orang lain menjadi penasaran dan ingin mengetahui arti dari pesan acak
tersebut, hingga akhirnya melakukan percobaan untuk menerjemahkan pesan
tersebut.
Steganografi biasanya terdiri dari dua sistem, yaitu sistem untuk
menyembunyikan pesan dan sistem untuk mengambil pesan. Dalam sistem-sistem
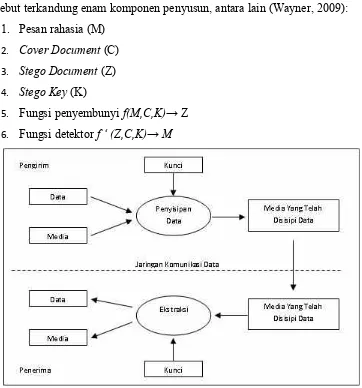
tersebut terkandung enam komponen penyusun, antara lain (Wayner, 2009):
1. Pesan rahasia (M)
2. Cover Document (C)
3. Stego Document (Z)
4. Stego Key (K)
5. Fungsi penyembunyi f(M,C,K)→ Z
6. Fungsi detektor f ‘ (Z,C,K)→ M
Gambar 2.2 Proses Penyisipan dan Ekstraksi pada Steganografi
2.2.1 Metode Least Significant Bit (LSB)
Steganografi mempunyai 2 metode, yaitu MSB (Most Significant Bit) dan LSB
data yang akan disembunyikan. Sedangkan LSB adalah kebalikan dari MSB, yaitu
sebuah metode menyembunyikan data pada bit bawah (LSB) pada data pixel yang
menyusun file tersebut (Wayner, 2009).
Metode LSB hanya mampu menyimpan informasi dengan ukuran terbatas.
Seperti untuk file atau citra bitmap 24 bit maka setiap pixel (titik) pada gambar
tersebut terdiri dari susunan tiga warna merah, hijau dan biru (RGB) yang
masing-masing disusun oleh bilangan 8 bit (byte) dari 0 sampai 255 atau dengan format
biner 00000000 sampai 11111111. Dengan demikian pada setiap pixel file bitmap
24 bit dapat menyisipkan 3 bit data.
2.2.2 Chaotic Least Significant Bit (CLSB)
Salah satu metode yang paling sederhana dalam steganografi adalah
penyembunyian pesan pada Least Significant Bit dari setiap pixel pada
cover-image nya, karena pada gambar digital perubahan satu-dua bit pada setiap pixel
tidak akan terlihat oleh mata telanjang. Sebelum proses penyembunyian pesan
dilakukan, terlebih dahulu ditentukan lokasi penyembunyiannya.
Penentuan dari lokasi penyembunyian pada gambar digital ditentukan
dengan cara sebagai berikut (Susany, 2005):
1. Untuk cover-image RGB c (x , y) = [Rc , Gc , Bc] berukuran MxN,
tentukan sebuah random seed dan bangkitkan pseudorandom number
kemudian susun menjadi sebuah pseudo-image RGB p (x , y) = [Rp , Gp ,
Bp] berukuran MxN.
2. Hitung jarak antara c (x , y) dan p (x , y) dengan menggunakan rumus jarak
dua vector
2 2
) (
) (
) (
) ,
(x y Rc Rp Gc Gp Bc Bp
d = − + − + −
3. Penyembunyian dimulai dari lokasi dengan jarak terkecil hingga jarak
Setelah penentuan lokasi selesai, maka proses selanjutnya adalah
melakukan penyembunyian pesan. Penyembunyian pesan pada gambar digital
dengan format RGB (masing-masing 8 bit) dilakukan dengan proses sebagai
berikut:
1. Tentukan random seed dan bangkitkan pseudorandom number
i
3. Bit-bit informasi ai akan disembunyikan pada pixel c(x,y) dengan
ketentuan:
a. Sembunyikan 3 bit ai di LSB Red, Green, Blue jika p(x,y)= 0
b. Sembunyikan 1 bit ai di LSB Red jika p(x,y)= 1
c. Sembunyikan 1 bit ai di LSB Green jika p(x,y)= 2
d. Sembunyikan 1 bit ai di LSB Blue jika p(x,y)=3
4. Tentukan random seed kedua dengan cara ROL (random seed) kemudian
bangkitkan pseudorandom number xi yang baru sebanyak bit data ai.xi
akan menentukan apakah ai akan disembunyikan di LSB pertama atau
LSB kedua sebuah komponen c(x,y) dengan ketentuan sebagai berikut:
Proses deteksi informasi tersembunyi secara umum sama dengan proses
penyembunyian informasi. Perbedaannya hanya pada saat pengambilan informasi
dari LSB sebuah komponen c(x,y) (langkah keempat pada proses penyembunyian)
menggunakan (Susany, 2005):
buat. Beberapa penelitian yang berkaitan yang telah dilakukan oleh peneliti lain
ditunjukkan pada tabel 2.1
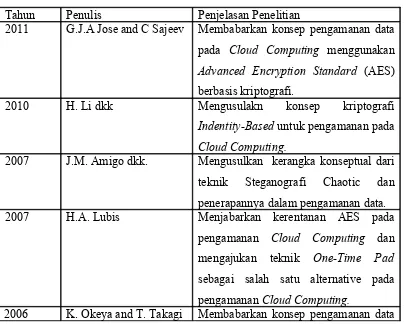
Tabel 2.1. Penelitian Terkait
Tahun Penulis Penjelasan Penelitian
2011 G.J.A Jose and C Sajeev Membabarkan konsep pengamanan data
pada Cloud Computing menggunakan
Advanced Encryption Standard (AES)
berbasis kriptografi.
2010 H. Li dkk Mengusulakn konsep kriptografi
Indentity-Based untuk pengamanan pada
Cloud Computing.
2007 J.M. Amigo dkk. Mengusulkan kerangka konseptual dari
teknik Steganografi Chaotic dan
dengan mengkombinasikan algoritma
RSA dengan CRT (Chinese Remainder
Theorem) dan perbandingannya dengan
algoritma Rabin.
2005 S. Soplanit dkk Menjelaskan konsep pengamanan data
dengan metode Chaotic Least
Significant Bit Encoding (CLSBE) yang
diimplementasikan pada telepon
genggam.
2.4 Perbedaan dengan Penelitian Terkait
Dalam beberapa penelitian yang telah ditampilakan pada tabel 2.1 terdapat
beberapa perbedaan dengan penelitian yang dilakukan oleh penulis kali ini. Pada
penelitian yang ditampilkan pada tabel 2.1, konsep pengamanan data dilakukan
dengan suatu algoritma kriptografi tertentu ataupun menggunakan teknik
steganografi tertentu. Sedangkan penelitian yang dilakukan penulis kali ini
menitikberatkan pada pengkombinasian antara kriptografi dan steganografi pada
proses pengamanan data.
2.5 Kontribusi Penelitian
Penelitian ini memberikan kontribusi tentang pemahaman tentang aspek
keamanan data pada sistem komunikasi jaringan terutama pada Cloud Computing,
apalagi data yang dikirimkan bersifat rahasia. Pada Cloud Computing, penyedia
layanan biasanya telah menggunakan konsep keamanan data tertentu untuk
pengamanan data pengguna layanannya, dengan tujuan agar pengguna merasa
aman terhadap data yang dikirimkan atau disimpan pada layanan Cloud
Computing.
Melalui penelitian kali ini, penulis mengajukan konsep pengamanan
kombinasi kriptografi Rabin dan steganografi Chaotic LSB untuk sistem