Pengendalian Posisi Sistem Magnetic Levitation Ball Menggunakan MRAC-PID

Pengendalian Posisi Sistem Magnetic Levitation Ball

Menggunakan MRAC-PID

Dian Mursyitah1, Ahmad Faizal2, Rechy Vernandhez3 , Parmo4 Program Studi Teknik Elektro, Fakultas Sains dan Teknologi, UIN SUSKA RIAU1,2,3 Program Studi Teknik Sipil, Fakultas Sains dan Teknologi, UIN Sunan Ampel Surabaya4

Jl. HR. Soebrantas Km. 155 Pekanbaru - Riau e-mail: dmursyitah@uin-suska.ac.id1

Abstrak

Magnetic Levitation Ball memiliki prinsip kerja melayangkan bola baja dengan memanfaatkan medan elektromagnetik. Magnetic Levitation Ball merupakan sistem non linear yang sulit dikendalikan terutama saat diberi gangguan. Metode kendali Model Reference Adaptive Controller (MRAC) dipilih sebagai solusi karena kemampuannya yang baik dalam mengatasi gangguan. Prinsip kerjanya adalah mampu membuat respon keluaran sistem, mengikuti respon keluaran model referensi yang telah dirancang sebaik mungkin. Namun terdapat kelemahanpadaresponwaktudantidakmampumeredamosilasi, sehinggaditambahkanpengendali PID untukmengatasikelemahan MRAC tersebut. Hasil respon MRAC-PID tanpagangguanmemberikanrespon yang bagus dengan, rise time pada 0.0196 detik, error = 0.0155, overshoot = 0.09 %. MRAC-PID juga memperlihatkan respon yang bagus saat diberi gangguan sinyal kendali dan sinyal masukan, dengan overshoot = 0.5 % dan error IAE = 0.01555

Kata Kunci: Magnetic Levitation Ball, MRAC, MIT Rule PID. Abstract

Magnetic Levitation Ball has the working principle of casting steel balls using electromagnetic fields.Magnetic Levitation Ball is a non linear system that is difficult to control, especially when given disturbance.The working principle is to be able to make the system output response, following the reference model output response that has been designed as well as possible. However, there is a weakness in the response time and is unable to reduce oscillations, so that a PID controller is added to overcome the weaknesses of the MRAC. MRAC-PID response results without interruption provide a good response with, rise time at 0.0196 seconds, error = 0.0155, overshoot = 0.09%. MRAC-PID also shows a good response when given interference control signals and input signals, with overshoot = 0.5% and IAE error = 0.01555

Keyword :Magnetic Levitation Ball, MRAC, MIT Rule PID.

1. Pendahuluan

Magnetic Levitation Ball merupakan proses pelayangan sebuah benda dengan memanfaatkan medan magnet. Gaya elektromagnetik digunakan untuk melawan efek dari gaya gravitasi. Magnetic Levitation Ball dapat didefinisikan sebagai proses melayangkan benda di ruang bebas dengan menangkal gaya gravitasi yang bekerja padanya. Obyek yang akan dilayangkan ditempatkan di bawah sebuah elektromagnet. Dengan kekuatan medan magnet yang dihasilkan oleh elektromagnet yang dikendalikan dengan tepat akan melawan gaya gravitasi pada objek yang dilayangkan [1]. Masalah utamanya adalah Magnetic Levitation Ball adalah sistem yang non linear, sehingga menimbulkan fenomena respon yang tidak stabil. Posisi objek yang dilayangkan juga rentan terhadap gangguan, sehingga dibutuhkan pengendalian agar posisi objek tetap stabil dan mampu beradaptasi dari gangguan.

Beberapa penelitian telah dilakukan untuk mengendalikan posisi objek pada Magnetic Levitation Ball ini antara lain ;penelitian yang berjudul “ Pemodelan dan Simulasi Sistem Control Magnetic Levitation Ball “. Pada penelitian ini dilakukan pengendalian posisi bola baja dari solenoid menggunakan pengendali Proportional Integral Derivative ( PID ) pada posisi bola 0.0032 m. Hasil penelitian menunjukkan kestabilan respon sistem pada pemberian Kp sebesar 1.5 x 1010, Kd sebesar 495, dan Ki sebesar 9 x 107. Kestabilan sistem dicapai pada waktu 3.5 detik. Namun adanya gangguan pada sistem menyebabkan respon kembali tidak stabil sehingga PID harus di tuning ulang [2].

adalah 4 detik dari 10 detik waktu simulasi. Penyebabnya adalah perubahan pada posisi pelayangan mempengaruhi nilai Kp, Ki dan Kd dari PID yang sudah dijadwalkan menggunakan gain scheduling, sehingga perlu di tuning ulang [3][4]

Beberapa penelitian menunjukkan respon yang kurang baik dengan error yang relative besar terutama saat diberi gangguan. Pengendali yang dibutuhkan adalah pengendali yang mampu beradaptasi terhadap gangguan. Penulis memilih Model Reference Adaptive Control (MRAC), karena prinsip kerjanya yang mampu membuat performansi keluaran sistem mengikuti performansi keluaran model referensi yang sudah ditetapkan. Pada MRAC, respon sistem dapat dibuat sebagus mungkin untuk dijadikan model referensi yang nantinya akan di ikuti oleh plant, MRAC juga dapat beradaptasi terhadap perubahan parameter yang dapat mengganggu keluaran, sehingga cukup baik untuk mengatasi gangguan. Untuk merancang pengendali MRAC, ada dua metode yang digunakan yaitu metode MIT Rule dan metode kestabilan lyapunov. Metode MIT Rule dipilih karena memiliki turunan matematis yang lebih sederhana dibandingkan metode kestabilan lyapunov.[7][8][9][10].

Setelah pengujian secara simulasi, pengendali MRAC ternyata memiliki kelemahan pada respon yang lambat, error yang besar, dan berosilasi. Hal ini besar kemungkinan disebabkan oleh sifat non linieritas sistem maglev ball. Untuk itu, pengendali MRAC akan dikombinasikan dengan PID. Diharapkan dengan adanya Proportional (P) respon sistem menjadi cepat, Integral (I) mengurangi error, dan Derivative (D) mengurangi overshoot dari respon keluaran plant, agar dapat mencapai respon kestabilan yang diinginkan.

2. Metode Penelitian

Metode Penelitian dimulai dengan studi literatur, validasi model matematis sistem maglev ball, kemudian dilanjutkan dengan perancangan pengendali MRAC, perancangan pengendali PID dan kombinasi kedua pengendali. Langkah selanjutnya adalah mensimulasikan model matematis sistem bersama hasil rancangan pengendali dan diberi gangguan, dan langkah terakhir adalah hasil pembahasan dan penarikan kesimpulan.Pengujian model matematis sistem maglev ball[1][2][5] Gambar 1 memperlihatkan model dan struktur pelayangan magnet pada bola baja (magnetic levitation ball). Adapun komponen dan struktur Magnetic Levitation Ball ini terdiri dari:

1. Digital to Analog Converter (DAC) yang berfungsi sebagai pengubah sinyal digital menjadi sinyal analog.

2. Power amplifier berfungsi sebagai sumber arus yang konstan.

3. Solenoida berfungsi sebagai magnet untuk melawan gaya gravitasi. Dan bola baja yang berfungsi sebagai benda yang akan dilayangkan.

4. Sensor Posisi berfungsi untuk menentukan jarak benda dengan elektromagnet.

5. Analog to Digital Converter (ADC) berfungsi untuk mengubah sinyal analog menjadi sinyal digital

Gambar 1. Sistem maglev ball[1][2][5]

dinyatakan model matematis telah valid, sehingga dapat dilanjutkan pada perancangan pengendali dengan metode yang berbeda. Berdasarkan hasil penurunan model matematis diperoleh bentuk state space equation sebagai berikut[1][2][5]:









model state spacemenjadi :









Tabel1 Nilai-nilai parameter darimagnetic ball levitation [1][2][5]

Parameter Symbol Nilai

Ball diameter Dk 12.7e-3m

Ball mass M 0.0084kg

Jarak dari dasar Td 0.0019 m

Batas jarak = 0.0019 -Dk L 0.0063 m

Viscose friction Kfv 0.02 N.s/m

Gravity Acceleration constant G 9.81m/s2

Aggregated coil constant kF 0.606x10-6N/V

Converter gain KDA 10

Coil bias xL0 8.26x10-3m

Position sensor constant Kx 797.4603

Analog to digital converter gain KAD 0.2 Maximum DA converter output voltage UDam 5 V

Coil resistance Rc 3.5 Ω

Coil inductance Lc 30x10-3H

Current sensor gain Ks 13.33

Power amplifier gain Kam 100

Setelah mensubtitusikan nilai-nilai parameter dari magnetic ball levitation dariTabel1, state space (2) menjadi :

783 . 12766 381

. 2

313 . 16606

2

 



s s

TF

(4)

Perancangan Pengendali MRAC[7][8][9]

Perancangan MRAC dimulai dengan mendapatkan turunan sensitivitas , untuk mendapatkan turunan tersebut dapat dilakuakn penurunan matematis berdasarakan formulasi MIT Rule seperti yang ditunjukkan pada persamaan (5).

    

      

 J e e

dt d

(5)

Kemudian di asumsikan bahwa pengendali memiliki umpan balik adaptif ( ) dan umpan balik adaptif ( ). Selanjutnya adalah menurunkan umpan balik adaptif ( ) dan umpan balik adaptif ( ) untuk mendapatkan sistem ( . Namun, input dapat ditulis ulang menggunakan kedua umpan balik, umpan balik ini bisa digunakan untuk mendapatkan persamaan [7][8][9].

plant

c y

u

u  1  2

(6)

(7)

( ) (8)

(9)

Selanjutnya adalah mencari nilai error dengan mengambil turunan parsial error dengan nilai ( ) dan ( ). Nilai tidak termasuk parameter, oleh karena itu tidak penting saat mengevaluasi turunannya.

( ) (10)

(11)

(12)

(13)

Turunan sensitivitas yang diperoleh mengandung parameter dari plant. Jika modelnya mendekati plant aktual, karakteristik model dapat disesuaikan dengan karakteristik plant, sehingga memberikan turunan sensitivitas sebagai berikut:

Mengambil turunan dari umpan balik MRAC, maka didapatkan :

(15)

Selanjutnya adalah menerapkan MIT Rule,aturan update parameter untuk masing-masing yang diturunkan.Sehingga untuk membentuk filter, nilai error dan menjadi :

(

) (16)

(

) (17)

Persamaan yang telah diturunkan kemudian dibuat dalam bentuk skema standar dari pengendali MRAC yang ditunjukkan pada Gambar 2.

Gambar 2.Skema MRAC dengan Metode MIT Rule[7][8][9]

Model referensi diperoleh dengan mengikuti persamaan karakteristik orde dua karena sistem termasuk sistem berorde dua :

(18)

Perancangan model referensi adalah dengan ζ = 1, dan , didapatkan = 200 yang didasarkan pada kriteria 2% untuk nilai settling time, maka fungsi alih model referensinya menjadi :

(19)

Dengan nilai fungsi alih model referensi berdasarkan skema MRAC pada Gbr.7 adalah / , setelah di substitusikan ke persamaan (25) maka nilai akan sama

dengan nilai . Selanjutnya adalah nilai filter dan dibuat menyerupai fungsi alih model referensi, karena filter harus menyaring keluaran agar mengikuti keluaran model referensi, sehingga nilai filter yang diberikan menjadi :

(20)

Perancangan Pengendali MRAC-PID

0 0.5 1 1.5 2 2.5 3 0

0.2 0.4 0.6 0.8 1 1.2 1.4

Waktu (s)

P

o

si

si

(

m

)

Respon Sistem

∫ (21)

Dengan persamaan PID di atas, maka disubstitusikan ke dalam Simulink dengan mengambil umpan balik keluaran plant MRAC, sehingga blok Simulink menjadi :

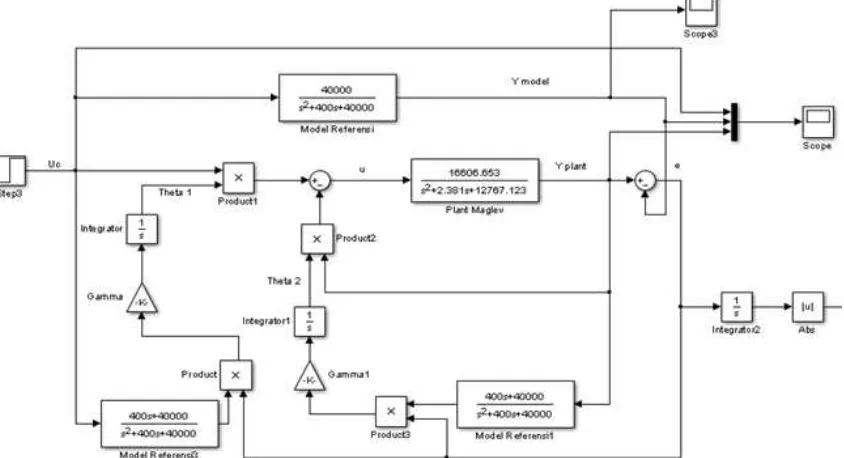
Gambar 3. Blok Simulink Pengendali MRAC-PID pada Magnetic Levitation Ball

3. Hasil dan Pembahasan

3.1. Hasil Simulasi Sistem Maglev Ball Secara Open Loop

Hasil simulasi sistem maglev ball secara open loop sesuai dengan model matematis sistem yang ditunjukkan pada persamaan (4), hasil respon sistem ditunjukkan pada Gambar 4).

Gambar 4. Hasil Respon Sistem Maglev Ball Secara Open Loop

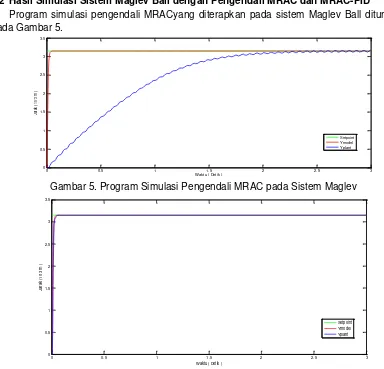
3.2 Hasil Simulasi Sistem Maglev Ball dengan Pengendali MRAC dan MRAC-PID

Program simulasi pengendali MRACyang diterapkan pada sistem Maglev Ball ditunjukkan pada Gambar 5.

Gambar 5. Program Simulasi Pengendali MRAC pada Sistem Maglev

Gambar 6. Hasil Respon Sistem Maglev Ball Menggunakan Pengendali MRAC-PID

3.3. Hasil analisa respon ditunjukkan pada Tabel 2.

Tabel 2. Analisa Respon Sistem Maglev Ball Menggunakan Pengendali MRAC

Parameter MRAC MRAC-PID

Time Constant(τ) 0.7943 Detik 0.0150 Detik Rise time (5%-95%) 1.6635 Detik 0.0196 Detik Settling Time (+3%) 2.6382 Detik 0.0849 Detik Delay Time (+3%) 0.5969 Detik 0.0150 Detik

IAE 2.153 0.0155

Maximum Overshoot Osilasi 0.09 %

Peak Time Osilasi 0.065 Detik

Berdasarkan perbandingan MRAC dan MRAC-PID pada Tabel.2, Nilai PID diperoleh dengan menggunakan metode heuristic dengan melihat error minimum dan hasil respon yang paling baik. Metode heuristic yang dilakukan mendapatkan Kp = 2, Ki = 11, dan Kd = 0.0125. Tabel 2 menunjukkan bahwa keluaran pengendali MRAC-PID memiliki perfomansi yang baikdibandingkan dengan pengendali MRAC. Penambahan pengendali PID mampu membuat Rise Time lebih cepat, error dan overshoot menjadi lebih kecil.

0 0.5 1 1.5 2 2.5 3

0 0.5 1 1.5 2 2.5 3 3.5

Waktu ( Detik )

Ja

ra

k

(

10

-3 m

)

Setpoint Ymodel Yplant

0 0.5 1 1.5 2 2.5 3

0 0.5 1 1.5 2 2.5 3 3.5

Waktu ( Detik )

J

a

ra

k

(

1

0

-3 m

)

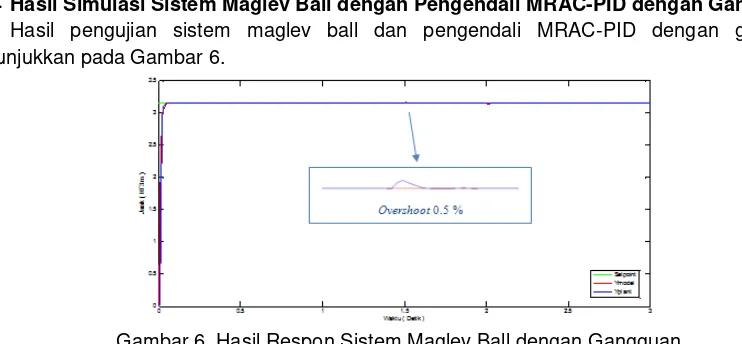
3.4 Hasil Simulasi Sistem Maglev Ball dengan Pengendali MRAC-PID dengan Gangguan Hasil pengujian sistem maglev ball dan pengendali MRAC-PID dengan gangguan ditunjukkan pada Gambar 6.

Gambar 6. Hasil Respon Sistem Maglev Ball dengan Gangguan

Berdasarkan pengujian dan analisa dari grafik respon yang dihasilkan, didapatkan overshoot sebesar 0.5% saat diberikan gangguan di detik 1.5 hingga detik ke 2 sebesar 10% dari set point. Walaupun masih terdapat error sebesar 0.01555, namun angka tersebut masih dapat diterima.

4 Kesimpulan

Efek penambahan PID pada MRAC adalah meredam osilasi, memperbaiki rise time yang menjadi lebih cepat, dan meminimalisir error. MRAC-PID juga berhasil mempertahankan respon saat diberi gangguan sinyal kendali dan sinyal masukan, dimana keluaran plant mampu mengikuti model referensinya walaupun ada overshoot sebesar 0.5 % dan error IAE sebesar 0.01555 saat diberi gangguan 10 % dari setpoint.

5 Ucapan Terimakasih

Penulis mengucapkan terimaskasih kepada mahasiswa : Rechy Vernandhez yang telah membantu melaksanakan penelitian ini

Daftar Pustaka

[1] Williams, Lance. “Electromagnetic Levitation Thesis”. 2005.

[2] Wibowo, DwiBasuki. “ Pemodelandan Simulasi Sistem Control Magnetic Lavitation Ball”. Universitas Diponegoro, 2012.

[3] Kurniawan, RahmatAndi. “Pengendalian Posisi Sistem Magnetic Lavitation Ball Menggunakan PID Gain

Schedulling”. JurusanTeknikElektro, Universitas Islam Negeri Sultan Syarif Kasim Riau, 2016.

[4] Fadlun, Wira. “Penerapan Metode Kendali Nonlinear Berbasis Sistem Servo pada Sistem Magnetic Levitation

Ball”. UniversitasTeknologi Yogyakarta. 2017.

[5] Khaled, A. M. Ali. “Modeling and Parameters Identification of A Magnetic Levitation Model”. The Islamic University

of Gaza, 2009.

[6] M.S.Abu. Nasr. “Fuzzy Gain Scheduling Control For Non-Linear Systems”.The Islamic University of

Gaza, 2013.

[7] K. J. Astrom and B. Wittenmark. “Adaptive control”. 2nd ed.. Dover Publications. New York. 2001.

[8] Garikayi, T. “ Model Reference Adaptive Control System for Moistre Regulation in Cotton Ginning ”

.Harare Institue of Technologi. Zimbabwe. 2013.

[9] Sevcik, Keith. “Model Reference Adaptive Control“. Drexel University. Philadelphia. 2014.