METODE BEDA HINGGA UNTUK SOLUSI NUMERIK
DARI PERSAMAAN BLACK-SCHOLES
HARGA OPSI PUT AMERIKA
SURITNO
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2008
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis Metode Beda Hingga untuk Solusi Numerik dari Persamaan Black-Scholes Harga Opsi Put Amerika adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Juni 2008
Suritno
ABSTRACT
SURITNO.
Finite Difference Method for the Numerical Solution of the Black-Scholes Equation for the Price of American Put Option. Under supervision ofENDAR H. NUGRAHANI and DONNY CITRA LESMANA
For the evaluation of American options, a general closed-form analytical solution does not exist yet. The basic reason is that the corresponding partial differential equation, known as Black-Scholes equation, needs to be solved with a free boundary value. A common way to deal with this problem is to apply numerical methods. The objectives of this paper are: to explore the determination of American put option price through analytical approximation and to compare the methods of determining American put option price with explicit, implicit and Crank-Nicholson finite difference methods. The results show that analytical approximation of American put option price can be formulated. Compared to other methods, the explicit finite difference method by transformation of variable is the best method according to its computing time.
Keywords: Black-Scholes, American put option, analytical approximation, finite
RINGKASAN
SURITNO. Metode Beda Hingga untuk Solusi Numerik dari Persamaan Black-Scholes Harga Opsi Put Amerika. Dibimbing oleh ENDAR H. NUGRAHANI dan DONNY CITRA LESMANA .
Kontrak opsi (selanjutnya disebut opsi) adalah suatu jenis kontrak antara dua pihak, satu pihak memberi hak kepada pihak lain untuk menjual atau membeli aset tertentu pada harga dan periode waktu tertentu. Aset tertentu dalam penelitian ini adalah saham. Terdapat dua jenis kontrak opsi yang paling mendasar, yaitu opsi call dan opsi put. Suatu opsi call memberikan hak kepada pembeli untuk membeli suatu aset tertentu dengan jumlah tertentu pada harga yang telah ditentukan selama periode waktu tertentu pula. Sedangkan opsi put memberikan hak kepada pembeli untuk menjual suatu aset tertentu dengan jumlah tertentu pada harga yang telah ditentukan selama periode waktu tertentu pula. Penggunaan hak untuk menjual atau membeli aset dalam kontrak opsi dikatakan sebagai tindakan eksekusi. Berdasarkan waktu eksekusi terdapat dua tipe opsi, yaitu opsi Eropa dan opsi Amerika. Opsi Eropa hanya dapat dieksekusi pada waktu jatuh tempo, sedangkan opsi Amerika dapat dieksekusi pada sebarang waktu sampai dengan jatuh tempo. Harga opsi Eropa dapat ditentukan dengan menggunakan formula Black-Scholes yang merupakan solusi analitik dari persamaan Black-Scholes, namun untuk opsi Amerika belum terdapat solusi analitik, sehingga penelitian-penelitian yang selama ini dilakukan untuk menentukan harga opsi Amerika adalah menggunakan pendekatan analitik, stokastik dan numerik. Pendekatan numerik yang sering dilakukan untuk menentukan nilai suatu opsi adalah dengan menggunakan metode beda hingga dan metode lattice (binomial dan trinomial).
Berdasarkan hal tersebut, maka penelitian ini bertujuan mengeksplorasi penentuan harga opsi put Amerika dengan pendekatan analitik dan membandingkan metode penentuan harga opsi put Amerika secara numerik dengan metode beda hingga eksplisit, implisit dan Crank-Nicholson.
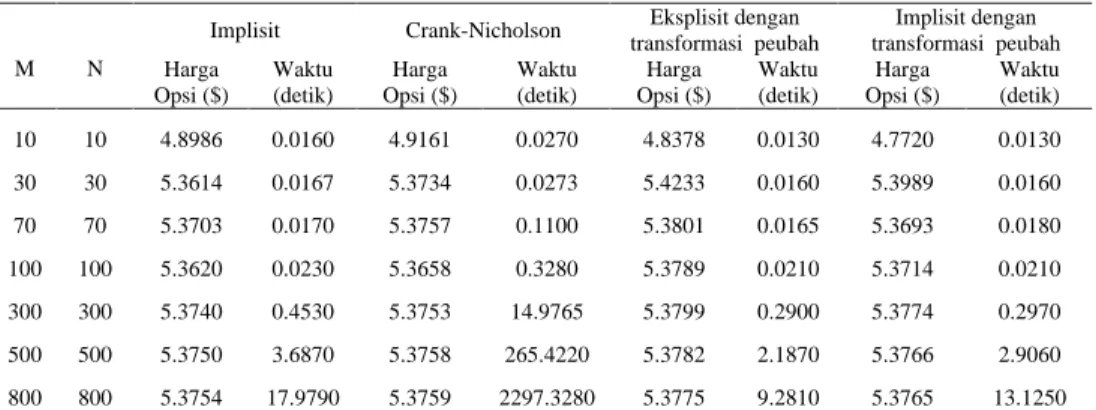
Metode penelitian yang digunakan adalah studi pustaka, dengan langkah pertama menurunkan persamaan Black-Scholes. Selanjutnya dengan persamaan ter-sebut dicari formula untuk harga opsi put Amerika dengan menggunakan pendekatan analitik. Langkah berikutnya menentukan solusi numerik persamaan Black-Scholes yang merupakan harga opsi put Amerika dengan menggunakan metode beda hingga. Metode beda hingga yang digunakan untuk menentukan harga opsi put Amerika adalah metode implisit, Crank-Nicholson dan eksplisit serta implisit dengan transformasi peubah. Untuk memperoleh output berupa harga opsi put Amerika, metode beda hingga tersebut diimplementasikan pada software Matlab. Untuk mengimplementasikan pada Matlab terlebih dahulu disusun kode programnya dengan menggunakan parameter-parameter input, yaitu: S (harga saham awal), K (harga eksekusi), r (suku bunga), (volatilitas), T (waktu jatuh tempo), M (banyaknya partisi untuk harga saham) dan N (banyaknya partisi untuk waktu). Dari hasil simulasi pada komputer dapat dilihat perbandingan harga opsi put Amerika dan waktu komputasi yang digunakan serta hubungan antara harga opsi put Amerika dengan parameter-parameter S, r dan T .
Dari hasil penelitian ini dapat disimpulkan bahwa: 1) harga opsi put Amerika dengan pendekatan analitik dapat dinyatakan dalam suatu formula yang memuat
parameter
S
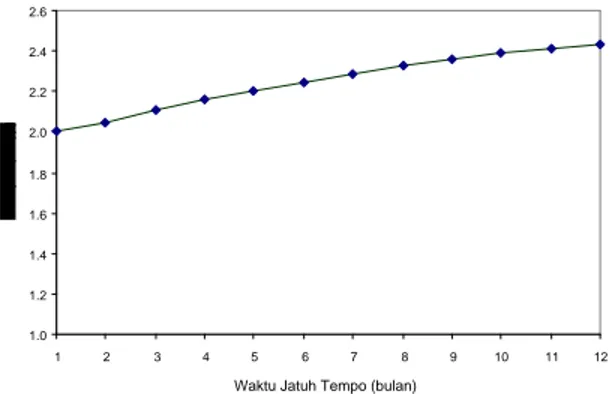
yang menyatakan harga kritis saham, 2) penentuan harga opsi put Amerika dengan menggunakan metode beda hingga, menunjukkan bahwa metode beda hingga eksplisit dengan transformasi peubah merupakan metode yang lebih baik dibandingkan dengan ketiga metode lainnya berdasarkan waktu komputasinya, dan 3) berdasarkan hasil simulasi diperoleh informasi: semakin tinggi harga saham pada saat kontrak opsi dibuat maka harga opsi semakin rendah, semakin tinggi suku bunga pada saat kontrak opsi dibuat maka harga opsi semakin rendah dan semakin lama waktu jatuh tempo maka harga opsi semakin tinggi.Kata kunci: persamaan Black-Scoles, opsi put Amerika, pendekatan analitik, metode beda hingga
© Hak cipta milik Institut Pertanian Bogor, tahun 2008
Hak cipta dilindungi Undang-undang
1.
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa
mencantumkan atau menyebutkan sumber
a. Pengutipan hanya untuk kepentingan pendidikan, penelitian,
penulisan karya ilmiah, penyusunan laporan, penulisan kritik
atau tinjauan suatu masalah.
b. Pengutipan tidak merugikan kepentingan yang wajar
Institut Pertanian Bogor.
2.
Dilarang mengumumkan dan memperbanyak sebagian atau
seluruh karya tulis dalam bentuk apapun tanpa izin Institut
Pertanian Bogor.
METODE BEDA HINGGA UNTUK SOLUSI NUMERIK
DARI PERSAMAAN BLACK-SCHOLES
HARGA OPSI PUT AMERIKA
SURITNO
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2008
Judul Tesis : Metode Beda Hingga untuk Solusi Numerik dari Persamaan Black-Scholes Harga Opsi Put Amerika
Nama : Suritno
NRP : G551060281
Disetujui
Komisi Pembimbing
Dr. Ir. Endar H. Nugrahani, MS
Donny Citra Lesmana, M.Fin.Math
Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana
Matematika Terapan
Dr. Ir. Endar H. Nugrahani, MS Prof. Dr. Ir. Khairil A. Notodiputro, MS
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Nopember 2007 ini ialah masalah opsi Amerika, dengan judul Metode Beda Hingga untuk Solusi Numerik dari Persamaan Black-Scholes Harga Opsi Put Amerika.
Terima kasih penulis ucapkan kepada Ibu Dr. Ir. Endar H. Nugrahani, MS dan Bapak Donny Citra Lesmana, M.Fin.Math selaku pembimbing, serta kepada Bapak Drs. Effendi Syahril, Grad. Dipl. selaku penguji luar komisi. Tak lupa ucapan terima kasih penulis sampaikan kepada Departemen Agama Republik Indonesia yang telah memberikan beasiswa. Ungkapan terima kasih juga disampaikan kepada istri dan anak serta seluruh keluarga, atas segala doa dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat
Bogor, Juli 2008
Suritno
RIWAYAT HIDUP
Penulis dilahirkan di Sleman pada tanggal 24 Oktober 1967 dari ayah Pawirowiryo dan ibu Wagirah. Penulis merupakan putra ketujuh dari tujuh bersaudara.
Tahun 1986 penulis lulus dari MAN Yogyakarta II jurusan IPA. Pada tahun 1987 melanjutkan pendidikan di IKIP PGRI Yogyakarta. Penulis memilih Jurusan Pendidikan Matematika pada Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam dan selesai pada tahun 1991.
Tahun 1991 sampai dengan tahun 1995 penulis bekerja di IKIP PGRI Yogyakarta. Pada tahun 1995 masuk PNS dan mengajar di MTs Negeri Tempel Sleman. Pada tahun 2001 pindah tugas mengajar di MTs Negeri Godean Sleman. Pada tahun 2006 penulis lulus seleksi masuk Program Magister Program Studi Matematika Terapan di Institut Pertanian Bogor lewat jalur Beasiswa Utusan Daerah Departemen Agama Republik Indonesia.
DAFTAR ISI
Halaman DAFTAR TABEL... DAFTAR GAMBAR... DAFTAR LAMPIRAN... xii xiii xiv I II III IV V VI PENDAHULUAN……….. 1.1 Latar Belakang………... 1.2 Tujuan Penelitian... LANDASAN TEORI... 2.1 Aset yang Mendasari Opsi... 2.2 Nilai Opsi... 2.3 Tipe Opsi... 2.4 Keuntungan Opsi... 2.5 Faktor-faktor yang Mempengaruhi Harga Opsi... 2.6 Persamaan Black-Scholes... 2.7 Formulasi Harga Black-Scholes... 2.8 Solusi Persamaan Black-Scholes... 2.9 Ketaksamaan Black-Scholes untuk Opsi Amerika... 2.10 Masalah Nilai Batas Opsi Put Amerika... PENDEKATAN ANALITIK UNTUK HARGA OPSI AMERIKA... 3.1 Penentuan Harga Opsi Call Amerika... 3.2 Penentuan Harga Opsi Put Amerika... METODE BEDA HINGGA... 4.1 Diskretisasi dari suatu Persamaan... 4.2 Aproksimasi Turunan Parsial... 4.3 Syarat Batas dan Syarat Akhir... 4.4 Transformasi Peubah... 4.5 Metode Beda Hingga Eksplisit... 4.6 Metode Beda Hingga Implisit... 4.7 Metode Beda Hingga Crank-Nicholson... 4.8 Metode Beda Hingga Eksplisit dengan Transformasi Peubah... 4.9 Metode Beda Hingga Implisit dengan Transformasi Peubah... 4.10 Analisis Kestabilan... HASIL SIMULASI... 5.1 Implementasi pada Matlab... 5.2 Hasil Simulasi dengan Matlab... SIMPULAN... 1 1 34 4 4 5 6 7 8 11 16 18 19
21 21 25
28 28 29 31 31 33 34 36 37 38 39
46 46 47
52
x
DAFTAR PUSTAKA... LAMPIRAN... 53 54
xi
DAFTAR TABEL
Halaman 1 2 3 4Perbandingan harga opsi dan waktu komputasi... Harga opsi put Amerika dengan harga saham awal yang bervariasi... Harga opsi put Amerika dengan suku bunga bervariasi... Harga opsi put Amerika dengan waktu jatuh tempo yang bervariasi...
47 49 50
50
DAFTAR GAMBAR
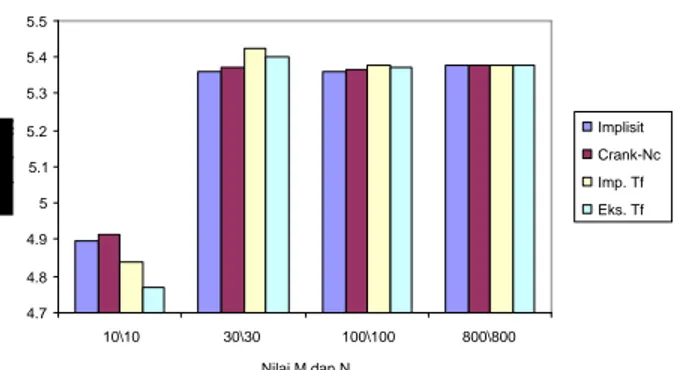
Halaman 1 2 3 4 5 6 7 8 9Grid untuk aproksimasi beda hingga... Skema beda hingga eksplisit... Skema beda hingga implisit... Perbandingan harga opsi...
Perbandingan waktu komputasi... Waktu komputasi metode Crank-Nicholson...
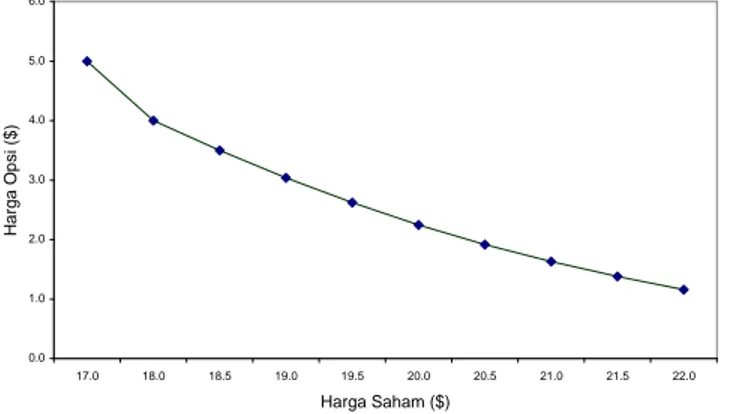
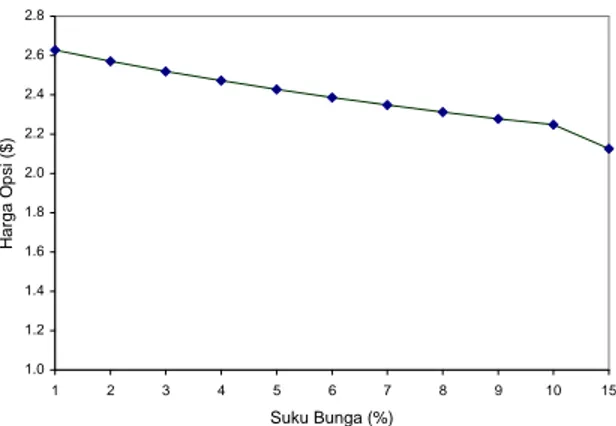
Hubungan harga opsi degan harga saham awal... Hubungan harga opsi dengan suku bunga... Hubungan harga opsi degan waktu jatuh tempo...
29 33 34 48 48 48 49 50 51
xiii
DAFTAR LAMPIRAN
Halaman 1 2 3 4 5 6 7 8 9 10 Penurunan Persamaan (2.8)………. Penentuan rataan dan standar deviasi peubah Q... Penurunan Persamaan (2.25)... Penurunan Persamaan (4.16)... Penurunan Persamaan (4.20)... Penyederhanaan (4.41)... Program metode beda hingga implisit... Program metode beda hingga Crank-Nicholson... Program metode beda hingga eksplisit dengan transformasi peubah... Program metode beda hingga implisit dengan transformasi peubah...55 55 56 57 58 59 59 61 63 65
xiv
BAB I PENDAHULUAN 1.1 Latar Belakang
Dalam dunia keuangan, dikenal adanya pasar keuangan (financial market) yang terdiri atas pasar uang (money market) dan pasar modal (capital market). Pada pasar uang terjadi jual beli aset keuangan dalam jangka pendek, sedangkan untuk pasar modal terjadi jual beli aset keuangan untuk jangka panjang. Pasar modal terdiri atas pasar obligasi, pasar saham dan pasar untuk derivatif (Bodie et al. 2006).
Hull (2003) menyatakan bahwa derivatif adalah instrumen keuangan yang nilainya didasarkan atau diturunkan dari aset yang mendasarinya. Beberapa produk derivatif antara lain: kontrak berjangka (future contract), kontrak forward dan kontrak opsi. Kontrak berjangka merupakan suatu kewajiban untuk membeli atau menjual suatu aset pada harga yang telah ditentukan pada saat jatuh tempo. Kontrak forward merupakan perjanjian untuk melakukan penyerahan aset di masa mendatang pada harga yang disepakati.
Kontrak opsi (selanjutnya disebut opsi) adalah suatu jenis kontrak antara dua pihak, satu pihak memberi hak kepada pihak lain untuk menjual atau membeli aset tertentu pada harga dan periode waktu tertentu (Niwiga 2005). Terdapat dua jenis kontrak opsi yang paling mendasar, yaitu opsi call dan opsi put. Suatu opsi call memberikan hak kepada pembeli untuk membeli suatu aset tertentu dengan jumlah tertentu pada harga yang telah ditentukan selama periode waktu tertentu pula. Sedangkan opsi put memberikan hak kepada pembeli untuk menjual suatu aset tertentu dengan jumlah tertentu pada harga yang telah ditentukan selama periode waktu tertentu pula. Penggunaan hak untuk menjual atau membeli aset dalam kontrak opsi dikatakan sebagai tindakan eksekusi. Berdasarkan waktu eksekusi terdapat dua tipe opsi, yaitu opsi Eropa dan opsi Amerika. Opsi Eropa hanya dapat dieksekusi pada waktu jatuh tempo, sedangkan opsi Amerika dapat dieksekusi pada sebarang waktu sampai dengan waktu jatuh tempo (Hull 2003).
Pada tahun 1973, Fisher Black, Myron Scholes (Hull 2003) berhasil menentukan solusi analitik dari suatu persamaan Black-Scholes-Merton. Solusi analitik tersebut dikenal sebagai formula Black-Scholes. Formula Black-Scholes
2
itu menyatakan harga dari opsi call Eropa. Harga opsi put Eropa dapat ditentukan melalui kesetaraan antara put dan call.
Pada opsi Amerika terdapat kebebasan waktu eksekusi, maka hingga saat ini belum terdapat solusi analitik. Penelitian-penelitian yang selama ini dilakukan untuk menentukan harga opsi Amerika adalah menggunakan pendekatan analitik, stokastik dan numerik (Pauly 2004).
Penelitian penentuan harga opsi Amerika dengan pendekatan analitik telah dilakukan oleh MacMillan, kemudian dikembangkan oleh Barone-Adesi dan Whaley (Hull 2003). Eksplorasi penentuan harga opsi Amerika dengan pende-katan analitik hingga saat ini masih terus dikembangkan. Hull dan White (1990) menyatakan bahwa dua pendekatan numerik yang sering dilakukan untuk menentukan nilai suatu derivatif adalah dengan menggunakan metode beda hingga dan metode lattice (binomial dan trinomial).
Beberapa penelitian yang menggunakan pendekatan numerik untuk menentukan harga opsi Amerika antara lain dilakukan oleh Kerman (2002) dengan menggunakan metode beda hingga dengan cara mengubah Persamaan Black-Scholes menjadi persamaan difusi. Niwiga (2005) juga menggunakan me-tode numerik, yaitu dengan cara menerapkan meme-tode beda hingga pada Persamaan Black-scholes-Merton, yang hasil simulasinya memperlihatkan perbandingan antara harga opsi put Amerika menggunakan metode beda hingga implisit dan Crank-Nicholson. Brenan dan Schwartz, Geski dan Shastri dalam Hull dan White (1990) menyatakan bahwa akan lebih efisien menggunakan transformasi logaritma terhadap harga saham ketika menggunakan metode beda hingga, sehingga dalam penelitian ini juga akan digunakan transformasi logaritma untuk harga saham.
Berdasarkan uraian di atas, harga opsi Eropa dapat ditentukan dengan menggunakan formula Black-Scholes yang merupakan solusi analitik dari persamaan Black-Scholes-Merton, namun untuk opsi Amerika belum terdapat solusi analitik, sehingga dalam penelitian ini akan diekplorasi penentuan harga opsi Amerika dengan pendekatan analitik, serta penggunaan pendekatan numerik beda hingga untuk menentukan harga opsi Amerika.
3
1.2 Tujuan Penelitian
Tujuan penelitian ini adalah:
1 mengeksplorasi penentuan harga opsi put Amerika dengan pendekatan analitik,
2 membandingkan metode penentuan harga opsi put Amerika secara numerik
4
BAB II
LANDASAN TEORI
Salah satu instrumen derivatif yang mempunyai potensi untuk dikem-bangkan adalah opsi. Opsi adalah suatu kontrak antara dua pihak, salah satu pihak (sebagai pembeli) mempunyai hak untuk membeli atau menjual suatu aset tertentu dengan harga yang telah ditentukan pula, pada atau sebelum waktu yang ditentukan. Pemegang opsi tidak diwajibkan untuk menggunakan haknya atau akan menggunakan haknya jika perubahan dari harga aset yang mendasarinya akan menghasilkan keuntungan baik dengan menjual atau membeli aset yang mendasari tersebut.
2.1 Aset yang Mendasari Opsi
Dalam perdagangan opsi terdapat beberapa aset yang mendasari, antara lain opsi indeks (index option), opsi valuta asing (foreign currency option) opsi berjangka (future option) dan opsi saham (stock option). Opsi indeks adalah suatu opsi dengan aset yang mendasarinya adalah indeks pasar saham. Opsi valuta asing adalah suatu opsi dengan aset yang mendasarinya adalah mata uang asing dengan kurs tertentu, sedangkan opsi berjangka adalah suatu opsi dengan aset yang mendasarinya adalah kontrak berjangka.
Opsi saham adalah suatu opsi dengan aset yang mendasarinya adalah saham. Bursa Amerika yang memperdagangkan opsi saham antara lain The Chicago Board Option Exchange (CBOE), The Philadephia Stock Exchange (PHLX), The American Stock Exchange (AMEX), The Pacific Stock Exchange (PSE), dan New York Stock Exchange (NYSE). Bursa Indonesia yang memperdagangkan opsi saham adalah Bursa Efek Jakarta (BEJ). Dalam penelitian ini yang digunakan adalah opsi saham.
2.2 Nilai Opsi
2.2.1 Nilai intrinsik
Nilai intrinsik opsi adalah nilai ekonomis, menggambarkan keuntungan investor jika opsi dieksekusi dengan segera. Jika nilai ekonomis dari eksekusi opsi dengan segera tidak positif, maka nilai intrinsik adalah nol. Untuk opsi call, nilai
5
intrinsik akan positif jika harga saham yang terjadi St lebih besar dari pada harga eksekusi (harga yang ditetapkan pada saat jatuh tempo). Sedangkan untuk
opsi put nilai intrinsik akan positif jika harga saham berlaku St kurang dari harga eksekusi K .
2.2.2 Nilai waktu
Nilai waktu adalah selisih antara nilai intrinsik dengan harga opsi. Harga atau premi suatu opsi adalah nilai yang wajar dari suatu opsi yang ditentukan oleh pasar kompetitif yang dibayarkan oleh pembeli opsi pada saat kontrak dibuat.
2.3 Tipe Opsi
Terdapat dua tipe kontrak opsi yang paling mendasar, yaitu opsi call dan opsi put. Suatu opsi call memberikan hak kepada pembeli untuk membeli suatu aset tertentu dengan jumlah tertentu pada harga eksekusi (strike price, exercise price) sampai waktu jatuh tempo. Sedangkan opsi put memberikan hak kepada pembeli untuk menjual suatu aset tertentu dengan jumlah tertentu pada harga eksekusi sampai waktu jatuh tempo. Dalam kontrak opsi call tersebut ada empat hal utama, yaitu:
? harga aset yang mendasari yang akan dibeli ? jumlah aset yang mendasari yang dapat dibeli ? harga eksekusi aset yang mendasari
? tanggal berakhirnya hak membeli, atau disebut dengan expiration date.
Pada kontrak opsi put empat hal tersebut identik dengan yang tertuang dalam opsi call.
Transaksi opsi akan terkait dengan pelaksanaan hak. Berdasarkan waktu pelaksanaannya opsi dibagi menjadi dua, yaitu opsi Eropa dan opsi Amerika. Misalkan harga saham awal (pada saat disetujui kontrak) adalah S, waktu jatuh
tempo T dan harga eksekusi adalah K, serta c c S t, menyatakan harga opsi call Eropa pada saat t, dan p p S t, menyatakan harga opsi put Eropa pada saat t. Nilai intrinsik dari opsi call Eropa pada saat jatuh tempo dapat dituliskan sebagai suatu payoff atau penerimaan bagi pemegang kontrak opsi yaitu
6
max T , 0
c S K .
Jika ST K, opsi dikatakan dalam keadaan in the money. Pemegang opsi akan mengeksekusi opsi call, yaitu dengan menjual saham dengan harga S T yang lebih besar dari K, dan akan mendapatkan hasil sejumlah ST K. Jika ST K opsi call dikatakan dalam keadaan at the money. Sedangkan apabila ST K opsi call dikatakan dalam keadaan out of the money. Kondisi payoff dari opsi put Eropa adalah
max T, 0 p K S .
Jika ST K , opsi tidak bernilai sehingga pemegang opsi tidak menggunakan haknya. Hubungan antara harga opsi call Eropa dengan put Eropa yang dikenal dengan put-call-parity, dapat dinyataan sebagai berikut:
,
rT
c Ke p S
dengan r menyatakan suku bunga bebas risiko.
Apabila C C S t, menyatakan harga opsi call Amerika dan ,
P P S t menyatakan harga opsi put Amerika, maka payoff pada waktu maturity untuk call adalah:
max , 0
C S T K . Sedangkan untuk opsi put
max , 0 P K S T .
2.4 Keuntungan Opsi
Dengan melaksanakan perdagangan opsi, akan dapat diperoleh beberapa manfaat seperti berikut ini.
? Manajemen risiko: penerbit opsi put atas suatu aset yang mendasari dapat melakukan hedging, yaitu berinvestasi pada suatu aset untuk mengurangi risiko portofolio keseluruhan. Hal ini dilakukan bila harga aset yang mendasarinya turun dratis secara tiba-tiba, sehingga dapat menghindari risiko kerugian.
7
? Memberikan waktu yang fleksibel: untuk opsi tipe Amerika, maka pemegang opsi call maupun opsi put dapat menentukan apakah akan melaksanakan haknya atau tidak hingga masa jatuh tempo berakhir.
? Menyediakan sarana spekulasi: para investor dapat memperoleh keuntungan jika dapat menentukan dengan tepat kapan membeli opsi put atau call. Apabila diperkirakan harga naik maka akan membeli opsi call, dan sebaliknya bila harga cenderung turun maka akan membeli opsi put.
? Penambahan pendapatan: perusahaan yang menerbitkan saham akan memperoleh tambahan pemasukan apabila menerbitkan opsi warrant, yaitu berupa premi dari opsi tersebut.
2.5 Faktor-Faktor yang Mempengaruhi Harga Opsi
2.5.1 Harga aset yang mendasari dan harga eksekusi
Jika suatu opsi call dieksekusi pada suatu waktu di masa yang akan datang, pembayarannya sebesar selisih antara harga aset yang mendasari dan harga eksekusi. Suatu opsi call akan menjadi lebih bernilai jika harga aset yang mendasari meningkat dan kurang bernilai jika harga eksekusi meningkat.
Sementara pada opsi put, pembayaran atas eksekusi hak adalah sebesar selisih antara harga eksekusi dan harga aset yang mendasarinya.
2.5.2 Tanggal jatuh tempo
Untuk tipe Amerika, dari kedua macam opsi baik opsi call maupun opsi put menjadi lebih berharga jika waktu jatuh temponya semakin meningkat. Sementara untuk tipe Eropa nilai terhadap opsi baik call mupun put tidak terpengaruh dengan jatuh tempo, hal ini berkenaan dengan waktu eksekusi hak.
2.5.3 Volatilitas
Volatilitas atas aset yang mendasari adalah sebuah ukuran tingkat ketidakpastian mengenai pergerakan aset yang mendasari tersebut di masa datang. Jika volatilitas semakin meningkat maka akan semakin meningkat pula peluang aset yang mendasari untuk mengalami peningkatan atau penurunan terhadap suatu opsi.
8
2.5.4 Suku Bunga Bebas Risiko (Risk free interest rate)
Suku bunga bebas risiko mempengaruhi harga suatu opsi. Jika tingkat suku bunga dalam perekonomian mengalami kenaikan akan mempengaruhi harapan kenaikan harga aset yang mendasari (dalam hal ini saham). Dengan mengasum-sikan bahwa semua peubah tetap, maka harga opsi put akan menurun jika suku bunga bebas risiko mengalami peningkatan. Begitu pula sebaliknya, harga opsi call akan selalu meningkat seiring dengan peningkatan suku bunga bebas risiko.
2.6 Persamaan Black-Scholes
Fischer Black dan Myron Scholes pada tahun 1973 dalam merumuskan nilai opsi call Eropa mendasarkan pada beberapa asumsi berikut ini:
Harga dari aset yang mendasari mengikuti proses Wiener dengan dan
konstan.
Tidak ada biaya transaksi dan pajak. Tidak ada pembayaran dividen pada opsi.
Tidak terdapat peluang arbitrase, yaitu suatu peluang untuk memperoleh keuntungan tanpa risiko.
Short selling diijinkan.
Suku bunga bebas risiko r adalah konstan dan sama untuk semua waktu jatuh tempo.
Untuk memodelkan Persamaan Black-Scholes didefinisikan atau ditentukan beberapa istilah berikut:
Definisi 1 (Proses Stokastik)
Proses stokastik X X t t, H adalah suatu koleksi (himpunan) dari peubah acak. Untuk setiap t pada himpunan indeks H, X t adalah suatu peubah acak
dan t sering diinterpretasikan sebagai waktu (Ross 1996).
Definisi 2 (Gerak Brown)
Proses stokastik X X t t, H disebut proses gerak Brown jika (Ross 1996): 1 X 0 0.
9
2 Untuk 0 t1 t2 t peubah acak n X ti X ti1 ,i 1, 2, 3,...,n saling bebas.
3 Untuk setiap t 0, X t berdistribusi normal dengan rataan 0 dan varian 2t .
Definisi 3 (Gerak Brown Geometris)
Jika X t t, 0 adalah gerak Brown, maka proses stokastik Z t t, 0 yang
didefinisikan Z t eX t disebut gerak Brown geometris (Ross 1996).
Definisi 4 (Proses Wiener )
Proses Wiener adalah Gerak Brown dengan rataan 0 dan variansi 1 (Niwiga 2005).
Definisi 5 (Proses Wiener Umum)
Proses Wiener Umum untuk suatu peubah acak X dapat dinyatakan sebagai berikut (Hull 2003):
( )
dX t adt bdW t (2.1)
adt disebut sebagi komponen deterministik dan bdW t( ) menyatakan komponen stokastik, serta W t( ) adalah proses Wiener, sedangkan a dan b masing-masing menyatakan rataan dan standar deviasi dari X.
Definisi 6 (Proses Ito’)
Proses Ito’ adalah proses Wiener umum dengan a dan b menyatakan suatu fungsi dari peubah acak X dan waktu t. Secara aljabar proses Ito’ dapat dinyatakan sebagai berikut (Hull,2003):
, ,
dX t a X t t dt b X t t dW t (2.2)
Definisi 7 (Lemma Ito’)
Misalkan proses X t memenuhi (2.2) dan fungsi Y t f X t t, adalah kontinu serta turunan-turunan ft X t t, , fX X t t, , fXX X t t, kontinu, maka Y t f X t t memenuhi persamaan berikut (Gihman 1972): ,
10
2 1 , , , , 2 t X XX dY t f X t t dt f X t t dX t f X t t dX t (2.3) dengan 2 2 , , t X XX f f f f f f t X X dan 2 2 0, . dt dW t dt dtdW t dW t dt
Definisi 8 (Model Harga Saham)
Jika S harga saham pada waktu t, µ adalah parameter konstan yang menyatakan tingkat rata-rata pertumbuhan harga saham dan volatilitas harga saham, maka model dari perubahan harga saham, yaitu (Hull 2003):
. dS t S t dt S t dW t
(2.4) Berdasarkan ketentuan-ketentuan di atas akan diturunkan persamaan Black-Scholes. Misalkan X(t) mengikuti proses Wiener umum, yaitu persamaan (2.1). Persamaan ini dapat dikembangkan menjadi (2.2). Selanjutnya akan ditentukan model dari proses harga saham S. Diasumsikan bahwa tidak terjadi pembayaran dividen pada saham. Misalkan S(t) adalah harga saham pada waktu t. Mengingat proses Ito’, perubahan S(t) akan memiliki nilai harapan drift rate S . Parameter menyatakan tingkat rata-rata pertumbuhan harga saham dan
S t dt disebut komponen deterministik. Karena harga saham juga dipengaruhi oleh faktor ketidakpastian maka komponen stokastiknya adalah S t dW t , dengan menyatakan volatilitas harga saham. Volatilitas harga saham mengindikasikan tingkat risiko dari harga saham. Dengan demikian model dari
harga saham adalah berbentuk (2.4), yaitu: dS t S t dt S t dW t . Dengan (2.4) ini, dapat diterapkan lemma Ito’ untuk suatu fungsi V(S,t), yaitu nilai opsi dengan harga saham S pada waktu t, sehingga diperoleh:
2 2 2 2 1 . 2 V V V V dV S S dt S dW t S t S S
(2.5)
11
Untuk menghilangkan proses Wiener dipilih sebuah portofolio yang diinves-tasikan pada saham dan derivatif. Strategi yang dipilih adalah membeli satu opsi
dan menjual S V
saham. Misalkan adalah nilai portofolio yang dimaksud,
maka . S S V V
(2.6)
Perubahan portofolio pada selang waktu dt didefinisikan sebagai
d dV V dS. S
(2.7)
Dengan menyubstitusikan (2.3) dan (2.5) ke dalam (2.7) diperoleh
2 2 2 2 1 . 2 V V d S dt t S
(2.8)
(Bukti dapat dilihat pada lampiran 1)
Return dari investasi sebesar pada saham takberisiko akan memiliki pertumbuhan sebesar r dt dalam selang waktu dt, dengan r adalah suku bu-ngan bebas resiko. Agar tidak terdapat peluang arbitrase, nilai pertumbuhan ini harus sama dengan ruas kanan dari (2.8), yaitu:
2 2 2 2 2 1 . 2 V V r dt S dt t S
(2.9)
Substitusi (2.6) ke dalam (2.9), menghasilkan
2 2 2 2 2 1 2 V V V rV rS dt S dt t t S 0 2 1 2 2 2 2 rV t V S V rS S V S . (2.10) Persamaan (2.10) ini dikenal sebagai persamaan Black-Scholes.
2.7 Formulasi Harga Black-Scholes
Hull (2003) menunjukkan bahwa salah satu cara untuk menentukan solusi analitik persamaan Black-Scholes, yang merupakan harga opsi dan disebut formula Black-scholes, adalah dengan menggunakan pendekatan penilaian risiko
12
netral. Untuk sebuah opsi call Eropa, nilai harapan payoff dari opsi call pada saat jatuh tempo adalah
. 0 , max ˆ S K E T
(2.11)
Didefinisikan g(ST) adalah fungsi kepekatan peluang dari S , maka T
. 0 , max ˆ T T K T T K S K g S dS S E
(2.12)
Misalkan G lnS, maka 1, 2 12 dan 0
2 t G S S G S S G . Berdasarkan lemma Ito’ diperoleh 2 2 2 1 1 1 1 0 2 dG S S dt S dW t S S S
1 2 2 dt dW t .
Karena dan konstan maka G lnS mengikuti gerak Brown dengan rataan
2 2 1 dan variansi 2. Berdasarkan (2.3), S dS
merupakan tingkat pengembalian dari harga saham.
Bentuk pengembalian dari harga saham yang dapat diprediksi dan bersifat deterministik adalah dt. Sebagai contoh dari pengembalian yang bersifat
deterministik adalah pengembalian dari sejumlah dana yang diinvestasikan di bank yang bersifat bebas risiko. Karena bersifat bebas risiko maka ekspektasi dari harga saham dapat dikatakan sebagai tingkat suku bunga r, sehingga konstanta dapat diganti dengan r. Karena G lnS berubah dari 0 sampai dengan T dan
S
G ln mengikuti gerak Brown, maka ln S berdistribusi normal dengan rataan T
r 2
2 1
dan variansi 2T.
Misalkan pada waktu t = 0 nilai G ln S0 dan pada waktu T nilai G lnST, maka pada selang waktu t 0 sampai dengan T, lnST lnS0 adalah berdis-tribusi normal dengan rataan dan variansi seperti di atas, sehingga diperoleh:
13
\ lnST lnS0 ~N r T, T 2
1 2
atau dapat dituliskan lnS berdistribusi normal dengan T
T S ln ~N S r T, T 2 1 ln 0 2 .
Dengan demikian lnST berdistribusi normal dengan rataan T r S m 0 2 2 1 ln
dan standar deviasi
T
s . (2.13) Selanjutnya didefinisikan pula sebuah peubah Q dengan
Q = ln . T m ST
(2.14)
Substitusi m dari (2.13) ke dalam (2.14) diperoleh
T r T S S T Q T 2 1 ln ln 1 2 0 ,
maka peubah Q juga berdistribusi normal dengan rataan 0 dan standar deviasi 1, dan fungsi kepekatan peluang dari Q dinyatakan dengan h(Q), yaitu
. 2 1 Q2/2 e Q h
(2.15)
(Bukti dapat dilihat pada lampiran 2) Persamaan (2.14) diubah menjadi
.
Q T m TS
e
(2.16)
maka, perubahan batas integral pada sisi kanan dari (2.12), dari integral menurut
T
S menjadi integral menurut Q adalah sebagai berikut: Jika ST , maka Q = .
Jika ST K maka K =
e
Q T m sehingga Q = Tm K ln
.
Dengan menggunakan (2.15), (2.16) dan perubahan batas integral serta
14
dQ Q h K e K S E s m K m Qs T / ln 0 , max ˆ = s m K m Qs dQ Q h e / ) (ln ) ( – s m K dQ Q h K / ) (ln ) ( = s m K Q m Qs dQ e e / ) (ln 2 / 2 2 1 – s m K dQ Q h K / ) (ln ) ( = s m K m Qs Q dQ e / ) (ln 2 / ) 2 2 ( 2 2 1 – s m K dQ Q h K / ) (ln ) ( = s m K m s s Q dQ e / ) (ln 2 / ) 2 ) ( ( 2 2 2 1 – s m K dQ Q h K / ) (ln ) ( = s m K s Q s m dQ e e / ) (ln 2 / ) ) ( ( 2 / 2 2 2 1 – s m K dQ Q h K / ) (ln ) ( = s m K s m dQ s Q h e / ) (ln 2 / ) ( 2 – ( ) , / ) (lnK m s dQ Q h K sehingga (2.12) dapat dinyatakan dengan
0 , max ˆ S K E T = s m K s m dQ s Q h e / ) (ln 2 / ) ( 2 – ( ) . / ) (lnK m s dQ Q h K (2.17) Jika N(x) didefinisikan sebagai suatu fungsi berdistribusi normal kumulatif, maka s m K s m dQ s Q h e / ) (ln 2 / ) ( 2 = em 2T/2[1 N[(lnK m)/s s]]
= em 2T/ 2[ [( lnN K m) /s s]].
Peubah m pada ruas kanan yang terdapat dalam tanda kurung siku persamaan di
atas disubstitusi dengan (2.13) dan s = T maka diperoleh ,
s m K T m s m h Q s dQ e N K S r T T T e / ) (ln 2 0 2 / 2 / / 2 ln ln ) ( 2 2
2 2 / 2 2 0 ln / / 2 m T e N S K r T T T
15
2 2 / 2 0 ln / / 2 m T e N S K r T T
em 2T/2N d1 , dengan / . 2 / ln 2 0 1 S K r T T d
Dengan alasan yang seperti di atas, maka
(ln ) / ln ( ) 1 K m s K m K h Q dQ K N S
KN ln K m S . (2.18)
Dengan menyubstitusikan m dan s pada (2.13) ke dalam (2.18) diperoleh
2 0 (ln ) / ( ) ln ln / 2 K m s K h Q dQ KN K S r T T
2 0 ln / / 2 KN S K r T T
= KN d2 , dengan 2 2 ln 0/ / , 2 d S K r T T
sehingga (2.12) menjadi Eˆ[max(ST – K, 0)] 1 2 2 / 2 d KN d N em T
elnS0 r 2/2T 2T/2N d1 KN d2
=S0erTN d1 KN d2 . (2.19) Berdasarkan argumentasi penilaian risiko netral, harga opsi call Eropa yang dilambangkan dengan c adalah nilai harapan yang didiskon pada suku bunga bebas risiko yang dapat dinyatakan sebagai
0 , max ˆ S K E e c rT T . (2.20) Dengan substitusi (2.19) ke dalam (2.20) diperoleh formula Black-Scholes untuk opsi call Eropa tanpa membayarkan dividen pada saat kontrak opsi dibuat, yaitu
16
0 1 2 rT c S N d Ke N d
(2.21)
dan dengan put-call-parity diperoleh harga opsi put Eropa
2 0 1 rT p Ke N d S N d dengan 2 1 ln 0/ / 2 d S K r T T dan 2 2 ln 0/ / 1 2 d S K r T T d T .
2.8 Solusi Persamaan Black-Scholes
Berikut ini akan ditunjukkan bahwa cS, t pada (2.21) merupakan solusi dari (2.10), maka kita tentukan turunan-turunan (2.21) terhadap t dan S serta peubah T diganti dengan T t.
Turunan d1 terhadap S adalah
2 1 ( / ) 1 t T t T K K S S d
t T S 1 . (2.22)
Dari persamaan d2 d1 T t, turunan terhadap t dan S berturut-turut adalah t T t d t d 2 2 1
dan 2 1 d d T t S S S
sehingga 2 1 d d S S . (2.23)
17
Turunan parsial (2.21) terhadap t adalah'
( ) ( ) 1 2 1 2 2 ' d r T t r T t ' d c SN d rK N d K N d t t t
= 1 ( ) 2 1 2 1 ' d r T t '( ) d SN d rK N d SN d t t = 1 2 ( ) 1 2 ' d d r T t SN d rK N d t t . (2.24)
Substitusi (2.23) ke dalam (2.24) diperoleh
( ) 1 2 ' 2 r T t c SN d rK N d t T t
(2.25) dengan ( ) 1 2 ' ' r T t SN d N d Ke . (2.26) (Bukti dapat dilihat pada lampiran 3)
Turunan parsial (2.21) terhadap S adalah
( ) 1 2 1 1 2 ( ) ' d r T t ' d c N d SN d K N d S S S (2.27)
Substitusi (2.23) dan (2.26) ke dalam (2.27) diperoleh
1 2 1 1 1 ( ) ' d ' d c N d SN d SN d S S S
1 1 1 1 1 ( ) ' d ' d c N d SN d SN d S S S
= N d1
(2.28) 2 1 1 2 ' d c N d S S (2.29) Substitusi (2.22) ke dalam (2.29) diperoleh
2 1 2 1 ' c N d S S T t
(2.30)
Peubah V pada (2.10) diubah dengan c maka menjadi
0 2 1 2 2 2 2 2 rc S c S S c rS t c (2.31)
18
2 2 2 ( ) 1 2 2 1 ' 2 2 r T t c c c rS S rc SN d rK N d t S S T t
2 2 1 1 1 1 ' 2 rSN d S N d S T t
( ) 1 2 r T t r SN d K N d
= rSN d1 rSN d1 + 2 2 1 1 1 1 ' ' 2 2 SN d S N d T t S T t + rK r T t( )N d2 rK r T t( )N d2 = 0
2. 9 Ketaksamaan Black-Scholes untuk Opsi Amerika
Persamaan (2.4) menyatakan bahwa model perubahan harga saham adalah
. dS t S t dt S t dW t
Seperti halnya pada penurunan Persamaan Black-Scholes, dibentuk suatu porto-folio dengan membeli sebuah opsi put Amerika dan menjual sejumlah saham,
maka diperoleh:
V S . Dengan memilih V
S
dan analogi (2.8), maka nilai portofolio berubah
menjadi dt S V S t V d 2 2 2 2 2 2 1 .
Pada Persamaan Black-Scholes untuk opsi Eropa argumentasinya adalah dibentuk suatu persamaan dengan return takberisiko, agar tidak terjadi peluang arbitrase. Namun ketika opsi pada portofolio itu opsi Amerika, diperoleh pendapatan tidak lebih banyak dari suku bunga bebas risiko portofolio itu, sehingga dt S V S V r dt r d .
19
Alasannya adalah pemegang opsi Amerika mengontrol kapan dia akan meng-eksekusi. Jika eksekusinya tidak optimal, maka nilai perubahan portofolio akan kurang dari return tanpa risiko, sehingga didapat pertidaksamaan:
dt S V S V r dt S V S t V 2 2 2 2 2 2 1 atau 0 2 1 2 2 2 2 2 rV S V S S V rS t V . (2.32)
Pertidaksamaan (2.32) adalah merupakan ketaksamaan Black-Scholes opsi Ame-rika. Pertidaksamaan (2.32) dapat dinyatakan sebagai berikut:
0 2 1 2 2 2 2 2 rV S V S S V rS t V (2.33) 0 2 1 2 2 2 2 2 rV S V S S V rS t V . (2.34)
Dengan adanya ketaksamaan tersebut, maka perlu adanya nilai batas untuk menentukan nilai opsi put Amerika
2.10 Masalah Nilai Batas Bebas Opsi Put Amerika
Pauly (2004) menyatakan, kondisi batas bawah untuk opsi put Amerika adalah
, , ,
V S t K S S t . (2.35)
Hal ini dengan alasan sebagai berikut: jika 0 = V = K – S seseorang dapat membeli opsi put V, dan segera mengeksekusinya, yaitu dengan membeli S dan menjualnya sebesar K. Dengan demikian ia memperoleh pendapatan tidak berisiko sebesar
0
K S V . Karena Black-Scholes dengan asumsi tidak terjadi kesempatan arbitrase, maka (2.35) adalah kendala yang benar untuk opsi put Amerika.
Misalkan S(t) menyatakan harga kritis saham sedemikian sehingga opsi akan
optimal apabila dieksekusi lebih awal dan 0 S t K, jika S S t maka opsi akan dieksekusi, namun jika S t S opsi tidak dieksekusi. Dengan demikian (2.35) dapat dinyatakan dengan:
20
, ( ) ( , ) ( ) , ( ) . K S S S t V S t K S S t S
(2.36)
Karena S(t) tidak diketahui posisinya, penyelesaian terhadap V(S,t) ini disebut masalah nilai batas bebas (free boundary-value problem), sehingga ketika
( )
S S t K nilai V S t, K S , serta V harus memenuhi (2.33), sehingga nilai opsi put Amerika memenuhi:
0 2 1 2 2 2 2 2 rV S V S S V rS t V ( , ) V S t K S. (2.37)
Pada saat S t S , nilai V(S,t) (K S) , serta V harus memenuhi (2.34), sehingga nilai opsi put Amerika memenuhi:
0 2 1 2 2 2 2 2 rV S V S S V rS t V ) ( ) , (S t K S V (2.38)
Dengan demikian masalah nilai batas bebas dari opsi put Amerika adalah sebagai berikut: untuk S < S(t) 0 2 1 2 2 2 2 2 rV S V S S V rS t V V S t( , ) K S untuk S(t )< S 0 2 1 2 2 2 2 2 rV S V S S V rS t V V(S,t) (K S) . Syarat batas 0 lim ( , ) 0 lim ( , ) S S V S t V S t K dan syarat akhir V S t t( ( ), ) K S t( ) . (2.39)
21
BAB III
PENDEKATAN ANALITIK UNTUK HARGA OPSI AMERIKA
Penelitian dengan pendekatan analitik untuk menentukan harga opsi Amerika telah dilakukan oleh beberapa peneliti. Salah satu peneliti adalah MacMillan, yang selanjutnya dikembangkan oleh Barone-Adesi dan Whaley (Hull 2003). Mereka memisahkan harga opsi menjadi dua komponen, yaitu: harga opsi Eropa dan premi eksekusi awal. Kemudian diperoleh persamaan diferensial parsial untuk premi eksekusi awal. Dari persamaan diferensial tersebut, akan diberikan beberapa asumsi penyederhanaan untuk mendapatkan persamaan kuadratik untuk mengaproksimasi solusi.
3.1 Penentuan Harga Opsi Call Amerika
Mengacu pada Hull (2003), untuk menentukan harga opsi Amerika dengan pendekatan analitik digunakan beberapa pemisalan, yaitu: misalkan v adalah harga
opsi, dengan 2 2 , S v v S v vS SS dan t v
vt serta K menyatakan harga eksekusi. Kemudian misalkan V S, t dan vS, T masing-masing menyatakan harga opsi Amerika dan Eropa. Harga opsi call dinyatakan oleh C S,t untuk opsi Amerika dan c S,T untuk opsi Eropa.
Misalkan opsi tidak memberikan dividen, sehingga persamaan diferensial parsial yang menyatakan harga opsi call Amerika berdasarkan (2.10) diberikan oleh
2 2
1
0
2 S CSS rSCS Ct rC . (3.1) Selanjutnya premi eksekusi awal didefinisikan oleh
T S c T S C T S, ( , ) , . (3.2) dengan S menyatakan harga saham, dan T waktu jatuh tempo serta (3.2) harus memenuhi 2 2 1 0 2 S SS rS S t r . (3.3) Misalkan
22
2 2 , 1 , h e r t T r , dan S, h( )g S,h . (3.4) Dari (3.4) diperoleh SS SS S S hg , hg dan t t t hg hg . h tg h gSSt ghht
h 1 g h0 ghh 1 h g hh gh. (3.5) Selanjutnya kedua ruas (3.3) dikalikan dengan 22 sehingga didapat persamaan
2 2 2 2 2 2 2 0 SS S t r r S S . (3.6) Substitusi (3.4) ke dalam (3.6) diperoleh
2
0
SS S t
S S hg
r , (3.7) dan substitusi (3.5) ke dalam (3.7) diperoleh
2 0 SS S h S hg Shg h g hh g hg r 2 0 SS S h g S g Sg h h g g r h
2 0 r SS S h g S g Sg re g g r h 2 1 0 SS S h g S g Sg h g g h 2 1 0 SS S h g S g Sg h g h . (3.8) Pendekatan analitik diperoleh dengan mengasumsikan suku terakhir pada (3.8) dapat diabaikan karena nilainya relatif kecil. Asumsi tersebut didasarkan pada hal-hal berikut.
Untuk , maka lim1 h = lim1 1 e r = lime r = 0, sedangkan untuk 0 , maka lim 0
23
Dengan demikian maka diperoleh
2 0
SS S
g S g Sg
h . ( 3.9) Persamaan (3.9) adalah persamaan diferensial biasa orde dua yang
mempunyai dua solusi yang berbentuk aS . Misalkan g aS dan disubstitusikan ke dalam (3.9) diperoleh
2 1 2 1 0 S aS S aS aS h 2 1 0 aS h . (3.10) Akar polinomial karakteristik dari (3.10) adalah
2 1 1 4 1 1 2 h 2 2 1 4 1 1 2 h . (3.11) Karena 4 /h 0, maka 1 0 dan 2 0 sehingga solusi umum (3.9) adalah
2 1 2 1 ) (S aS a S g . (3.12) Nilai 1 dan 2 berdasarkan (3.11) dapat ditentukan, selanjutnya akan
ditentukan koefisien a 1 dan a2. Karena 1 0 dan misalkan a1 0 maka
1 2
1 2
0 0
lim ( ) lim
S g S S a S a S . Hal ini kontradiksi dengan kenyataan bahwa
ketika S 0, mendekati nol. Misalkan a1 0 maka diperoleh persamaan
2 2 , , c S ha S S C . (3.13) Persamaan (3.13) merupakan pendekatan untuk harga opsi call Amerika. Untuk menentukan a diperhatikan beberapa kondisi berikut: 2
1 untuk S 0, berakibat max S K 0 sehingga ketika S meningkat maka ,
C S T akan mendekati S K,
2 jika S menyatakan harga kritis saham sedemikian sehingga opsi akan optimal
24
opsi call Amerika diberikan oleh (3.13), dan untuk S S harga opsi call Amerika adalah S K.
Dengan memperhatikan kondisi di atas maka
2 2 , ha S S c K S . (3.14) Untuk menentukan nilai S , diferensialkan (3.14) terhadap S maka berdasarkan , (2.28) diperoleh 2 1 1 2 2 1 N d S h a S
(3.15) dengan 2 1 ln / 2 S K r d S .
Dengan menggunakan (3.15) dapat ditentukan nilai dari a2, yaitu
2 1 2 1 2 1 N d S a h S . (3.16) Substitusi (3.16) ke dalam (3.14), maka diperoleh
2 2 1 1 2 1 , N d S S K c S h S h S 1 2 1 , N d S c S S
1 2 , 1 S c S N d S . (3.17) Setelah a 2 dapat ditentukan, maka harga opsi call Amerika adalah sebagai berikut:
untuk S S , maka substitusi (3.16) ke dalam (3.13) diperoleh
2 2 1 1 2 1 , , N d S C S c S h S h S 2 2 1 2 1 , N d S S c S S S 2 1 2 , 1 S S c S N d S S ,
25
sedangkan untuk S S harga opsi call Amerika adalah S K. Dengan demikian harga opsi call Amerika adalah
S S K S S S S S A S c S C jika , jika , / , , 2 2 (3.18) untuk nilai 2 1 2 1 S A N d S .
3.2 Penentuan Harga Opsi Put Amerika
Misalkan P S T, menyatakan harga opsi put Amerika dan p S, T untuk opsi Eropa. Persamaan diferensial parsial yang menyatakan harga opsi put Amerika diberikan oleh
1 2 2 0
2 S PSS rSPS Pt rP . Misalkan premi eksekusi awal untuk opsi put Amerika didefinisikan oleh
, ( , ) , S T P S T p S T
(3.19)
dengan S, h( )g S h . ,
Pada opsi put Amerika nilai a2 0, karena 2 0 dan premi eksekusi awal untuk opsi put Amerika harus mendekati nol ketika S mendekati tak hingga. Sehingga harga pendekatan untuk opsi put Amerika dinyatakan oleh
1 1 , , p S haS S P . (3.20) Untuk menentukan nilai dari a , diperhatikan kondisi berikut: 1
jika S menyatakan harga kritis saham sedemikian sehingga opsi akan optimal
apabila dieksekusi lebih awal, maka berdasarkan (2.36), untuk S S harga opsi put Amerika diberikan oleh (3.20), dan untuk S S harga opsi put Amerika adalah K S .
Dengan memperhatikan kondisi di atas maka
1
1
,
K S p S ha S . (3.21) Untuk menentukan nilai S , didiferensialkan (3.21) terhadap S maka diperoleh
1 1
1 1 1
1 N d S h a S
26
dengan 2 1 ln / 2 S K r d S .
Dengan menggunakan (3.22) dapat ditentukan nilai dari a1, yaitu
1 1 1 1 1 1 N d S a h S . (3.23) Substitusi (3.23) ke dalam (3.21) diperoleh
1 1 1 1 1 1 , N d S S K S p S h h S
1 1 1 , N d S S p S 1 1 , 1 S p S N d S . (3.24) Setelah a1dapat ditentukan, maka harga opsi put Amerika adalah sebagai berikut. Untuk S S , maka substitusi (3.23) ke dalam (3.20) diperoleh
1 1 1 1 1 1 , , N d S S P S p S h h S
1 1 1 1 1 , N d S S S p S S 1 1 1 , 1 S S p S N d S S ,
sedangkan untuk S S harga opsi put Amerika adalah K S. Dengan demikian harga opsi put Amerika adalah
S S S K S S S S A S p S P jika , jika , / , , 1 1 (3.25) dengan A1 1 N d S1 S / 1 .
27
Untuk menentukan nilai opsi put dengan menggunakan formula (3.25), maka
terlebih dahulu ditentukan nilai S dengan metode numerik, misalnya dengan metode Newton yang tidak akan dibahas lebih lanjut.
28
BAB IV
METODE BEDA HINGGA
Salah satu metode numerik untuk menyelesaikan persamaan diferensial parsial adalah metode beda hingga. Metode beda hingga adalah suatu metode numerik untuk menyelesaikan suatu persamaan diferensial dengan mengaprok-simasi turunan-turunan persamaan tersebut menjadi sistem persamaan linear. Metode beda hingga dalam penelitian ini adalah metode eksplisit, implisit, Crank-Nicholson dan eksplisit serta implisit dengan transformasi peubah.
Untuk menerapkan metode beda hingga pada suatu permasalah persamaan diferensial parsial beberapa hal perlu diperhatikan, yaitu: diskretisasi dari suatu persamaan, bentuk aproksimasi beda hingga, kondisi syarat akhir dan syarat batas serta kestabilan dari skema beda hinga.
4.1 Diskretisasi dari suatu Persamaan
Misalkan V(S,t) menyatakan nilai opsi maka Persamaan Black-Scholes dapat dinyatakan . 0 ) , ( ) , ( ) , ( 2 1 ) , ( 2 2 2 2 rV S t S t S V rS S t S V S t t S V (4.1)
Peubah yang menentukan terhadap nilai V adalah S dan t. S menyatakan harga saham dan t menyatakan waktu berlakunya opsi, tmax T , sehingga diskretisasi (4.1) adalah terhadap S dan t. Bidang (S,t) dipartisi menjadi grid, dan aproksimasi untuk interval di antara grid adalah S
dan t . Kemudian pada t didefinisikan
terdapat N+1 titik, yaitu t0, ,t t1 2, ..., t . Titik-titik tersebut untuk mendiskretkan N turunan terhadap waktu, serta t tn 1 tn dan t T/N. Misalkan pada S terdapat M+1 titik, yaitu S0, S S1, 2, ..., SMax. Titik-titik tersebut untuk mendiskretkan turunan terhadap harga saham S, dengan S Sm 1 Sm dan
max/ .
S S M Dengan demikian pada bidang (S,t) terdapat M 1 N 1 grid, seperti terlihat pada Gambar 1. Titik j i, pada tiap-tiap grid berhubungan de-ngan harga saham ke j S dan waktu ke i t. Selanjutnya nilai dari opsi pada wak-tu ti ketika harga saham Sj dinyatakan oleh:
29
( , ) ( , ) ( , ) i j j i v v j S i t v S t V S t
(4.2) dengan j 0, 1, 2, ,M dan i 0, 1, 2, , N. Smax 2 S
So o o o o 0 o o o o o t 2 t 3 t
T
Gambar 1 Grid untuk aproksimasi beda hingga
4.2. Aproksimasi Turunan Parsial
Aprosimasi untuk turunan parsial t v , S v dan 2 2 t v
diperoleh dari ekspansi
deret Taylor. Aproksimasi untuk turunan pertama dan turunan kedua seperti berikut ini.
4.2.1 Aproksimasi untuk turunan pertama
Misalkan V , t S dinyatakan oleh vij, ekspansi deret Taylor untuk v , t S S dan v ,t S S adalah sebagai berikut:
3 2 2 2 2 1 , , S S S v S S v S t v S S t v
(4.3) 3 2 2 2 2 1 , , S S S v S S v S t v S S t v . (4.4)
30
S S S t v S S t v S v , , S v v S v ij i j 1 . (4.5)
Menggunakan Persamaan (4.4) diperoleh persamaan beda mundur, yaitu:
S S S S t v S t v S v , , S v v S v ij i j 1 . (4.6)
Hasil pengurangan (4.4) dari (4.3) diperoleh persamaan beda pusat, yaitu
2 , , 2 v t S S v t S S v S S S
S v v S v ij i j 2 1 1 (4.7)
Ekspansi deret Taylor untuk v(t t,S) dan v(t t,S) adalah sebagai berikut:
3 2 2 2 2 1 , , t t t v t t v S t v S t t v (4.8) 3 2 2 2 2 1 , , t t t v t t v S t v S t t v (4.9) Menggunakan (4.8) dan (4.9), aproksimasi terhadap
t v
adalah sebagai berikut
Aproksimasi beda maju:
t v v t v ij i j 1 (4.10)
Aproksimasi beda mundur:
t v v t v ij i j 1 (4.11)
4.2.2 Aproksimasi untuk turunan kedua
Aproksimasi 2
2
S v
diperoleh dengan cara menjumlahkan (4.3) dan (4.4) sehingga
diperoleh: 2 2 2 2 , 2 , , v t S S v t S v t S S v S S S
31
2 1 1 2 2 2 i i i j j j v v v v S S . (4.12) Persamaan (4.11) disebut aproksimasi beda pusat simetris.
4.3 Syarat Batas (boundary condition) dan Syarat Akhir (terminal condition)
Untuk menentukan harga opsi put Amerika dengan menggunakan metode beda hingga, diperlukan kondisi syarat batas dan syarat akhir. Nilai opsi put pada saat T adalah max(K – ST, 0), dengan ST menyatakan harga saham pada saat T,
sehingga
max( , 0), 0,1, 2,..., .
N j
v K j S j M (4.13) Persamaan (4.13) menyatakan syarat akhir, sehingga penentuan nilai pada v tidak di awal periode tetapi di akhir periode. Hal ini dilakukan dengan bergerak mundur dari waktu maturity sampai waktu nol. Nilai opsi put pada saat harga saham sama dengan nol adalah K, sehingga
0 , 0,1, 2,..., . i
v K i N
(4.14)
Apabila harga saham meningkat, maka nilai opsi put akan mendekati nol pada saat S = Smax, sehingga
0, 0,1, 2,..., .
i M
v i N (4.15) Persamaan (4.14) dan (4.15) adalah merupakan syarat batas.
Pada pendahuluan telah disebutkan bahwa penelitian ini akan menggunakan transformasi peubah, yaitu harga saham S diubah (ditransformasi) menjadi ln S , sehingga pembahasan berikut mengenai transformasi peubah.
4.4 Transformasi Peubah
Brennan dan Schwartz dalam Hull dan White menyatakan bahwa ketika S adalah harga saham, persamaan Black-Scholes lebih efisien menggunakan ln S daripada S apabila metode beda hingga diterapkan, karena jika konstan maka standar deviasi dari ln S juga konstan. Transformasi standar deviasi ln S pada interval t tidak bergantung pada S dan t (Hull & White 1990).
Didefinisikan y lnS dan V S t, W y t, adalah harga opsi pada waktu t. Turunan parsial (bukti lihat lampiran 4) terhadap S, t dan y adalah: