Bab 4
V V e e k k t t o o r r d d i i B B i i d d a a n n g g d d a a n n d d i i R R ua u an n g g
Vektor merupakan besaran yang mempunyai arah. Pada bab ini akan dijelaskan tentang vektor di bidang dan di ruang, yang disertai operasi dot product, cross product, dan penerapannya pada proyeksi vektor dan perhitungan luas suatu segitiga di ruang 3-dimensi. Setiap vektor tersebut dapat dinyatakan secara geometris sebagai segmen garis berarah pada bidang atau ruang, dengan notasi garis berpanah. Ekor panah garis tersebut merupakan titik awal vektor, sedangkan ujung panah sebagai titik akhir (ujung) vektor tersebut.
4.1 OPERASI VEKTOR
Seperti halnya matriks, setiap vektor dapat di dikenakan operasi aljabar, seperti penjumlahan dan perkalian. Notasi vektor dapat dituliskan dengan menggunakan huruf kecil dicetak tebal atau huruf kecil dengan garis diatasnya. Sedangkan unsur vektor tersebut ditulis berurutan atau seperti matriks satu kolom atau memakai notasi vektor satuan i ˆ , , dan . jˆ kˆ
Contoh 4.1 :
Berikut adalah beberapa contoh notasi vektor :
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
=
3 2 1
c c c c a = (a
a.
1, a , a
2 3) kˆ c.
b. b = b
1i ˆ +b
2jˆ +b
348 Bab 4 ● Vektor di Bidang dan di Ruang Penjumlahan Vektor
u v
Misalkan dan adalah vektor – vektor yang berada di ruang yang sama, maka vektor u + didefinisikan sebagai v sebuah vektor yang titik awalnya sama dengan titik awal u dan titik akhirnya merupakan titik ujung dari vektor v (setelah digeser sehingga titik awal vektor v diletakan pada ujung vektor
u . Agar lebih jelas, perhatikan ilustrasi berkut ini :
u
v
v yang digeser
v u +
Gambar 4.1 Ilustrasi penjumlahan dua buah vektor pada bidang
Perkalian Vektor
a. Perkalian vektor dengan skalar
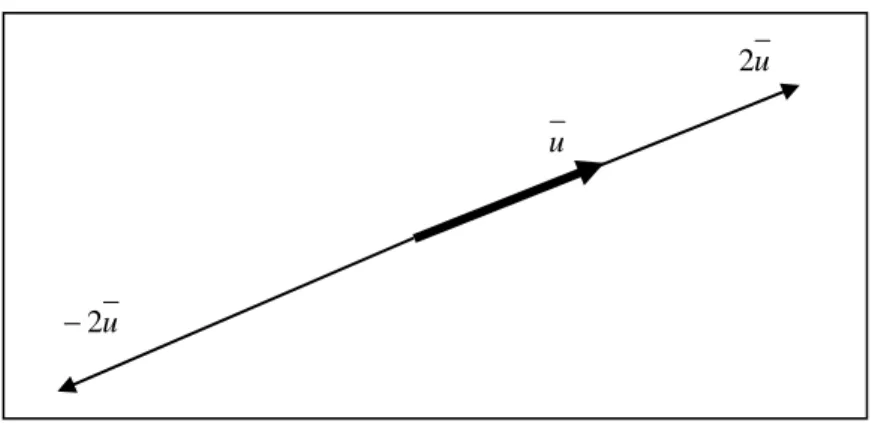
Vektor nol didefinisikan sebagai vektor yang memiliki panjang nol. Misalkan u vektor tak nol dan k adalah skalar, k ∈ ℜ . Perkalian vektor u dengan skalar k, k didefinisikan sebagai u vektor yang panjangnya k kali panjang vektor u dengan arah memiliki ketentuan sebagai berikut :
• Jika k > 0 Æ searah dengan u
• Jika k < 0 Æ berlawanan arah dengan u
Aljabar Linear Elementer – Adiwijaya 49
u
u 2
u
− 2
Gambar 4.2 Ilustrasi perkalian vektor dengan skalar Secara analitis, kedua operasi pada vektor diatas dapat dijelaskan sebagai berikut :
b
a dan merupakan vektor-vektor di ruang (R
Diketahui
3)
yang komponen–komponennya adalah a = ( a
11a
2, a
3) dan
( b
1, b
2, b
3b = ) maka :
( a
1b
1, a
2b
2, a
3b
3)
b
a + = + + +
•
( a
1b
1, a
2b
2, a
3b
3)
b
a − = − − −
•
( ka
1, ka
2, ka
3)
a
k =
•
b. Perkalian anatara dua buah vektor.
Perkalian antara dua buah vektor hanya dapat dilkakukan jika kedua vektor tersebut berada pada ruang yang sama.
Perkalian antara dua buah vektor tersebut meliputi : o Hasil kali titik (dot product)
o Hasil kali silang (cross product)
Berikut ini akan dijelaskan secara lebih detil tentang dua jenis
perkalian antara dua buah vektor.
50 Bab 4 ● Vektor di Bidang dan di Ruang 4.2 HASIL KALI TITIK
Hasil kali titik merupakan operasi antara dua buah vektor yang akan menghasilkan skalar. Misal a dan adalah b vektor pada ruang yang sama maka hasil kali titik antara a dan
b didefinisikan oleh
α cos b a b
a • = , (4.1)
a dan b masing-masing merupakan panjang vektor a dimana
dan b serta α merupakan sudut yang dibentuk antara vektor a dan vektor b . Ingat kembali definisi panjang (norm) suatu vektor semasa si sekolah menengah, yaitu : jika a r = ( a 1 , a 2 ) maka
2 2 1 2 a a
a r = + . Contoh 4.2 :
Tentukan hasil kali titik dari dua vektor berikut : b
a = 2i dan = 2i + 2j Jawab :
b
a
Karena tan α = 1 , artinya α = 45
0Sehingga
Aljabar Linear Elementer – Adiwijaya 51
2
a b 8 1
a b cos α
. = = 2
= 2 2
2 1
2 = 4
Bagaimana cara menghitung hasil kali titik di R
Ndan dua buah vektor tanpa diketahui sudut antar kedua vektor tersebut? Untuk hal tersebut, ingat kembali tentang aturan cosinus :
β
c a
α b δ
2 2
Gambar 4.3 Ilustrasi aturan cosinus
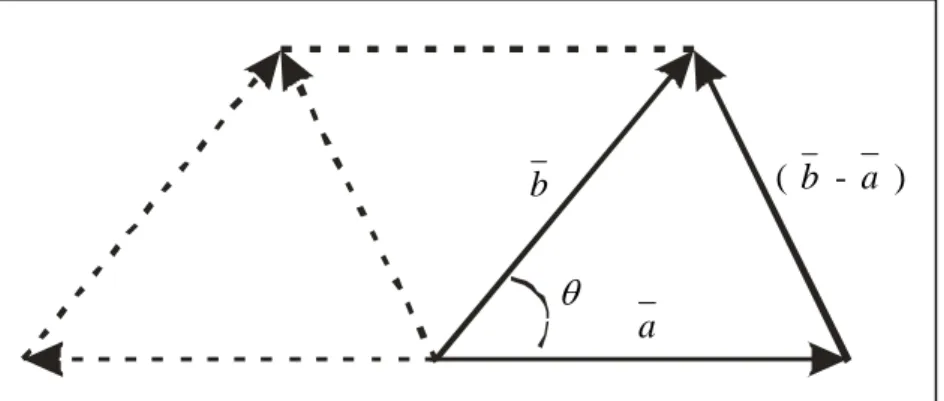
Selanjutnya, akan dijelaskan hubungan dua vektor posisi dengan aturan cosinus. Perhatikan ilustrasi dua vektor di ruang R
2berikut ini :
Gambar 4.4 Ilustrasi aturan cosinus dua vektor dan selisihnya a = b + c
2– 2 bc cos α
b - a ) b (
θ
a
52 Bab 4 ● Vektor di Bidang dan di Ruang
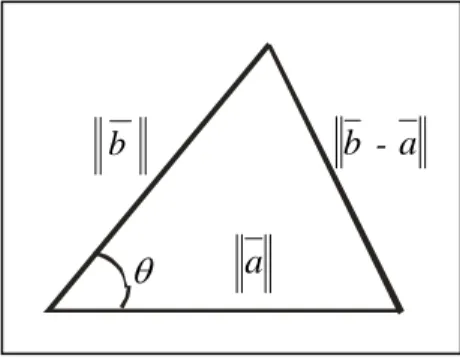
Notasi vektor pada Gambar 4.4, akan dirubah dalam notasi panjang (norm) vektor, yaitu :
a
b - a b
θ
Gambar 4.5 Aturan Cosinus Norm Dua Vektor dan Selisihnya Menurut aturan cosinus pada ilustrasi diatas, maka :
α cos
2
2
2 2
b a b
a a
b − = + −
Selanjutnya :
⎥⎦ ⎤
⎢⎣ ⎡
2+
2− −
22
1
a b b a
θ = cos b a
Seperti telah kita ketahui bahwa : b
a cos θ a b
(1) = .
2
a = a + a
(2)
1 2 2 2+ a
3 2+ …. + a
n2 2b = b + b + b
(3)
1 2 2 2 3 2+ …. + b
n2(
1 1)
2(
2 2)
2(
22
... b
na
na
b a
b a
b − = − + − + + − )
(4)
=
n n n
n
n n
a b a
b a b
a a
a b b
b
2 ...
2 2
...
...
1 1
2 2
2 2 1 2 2
2 2 1
−
−
−
−
+ + + + + + + maka akhirnya diperoleh :
n n
b a b
a b a
a • b =
1 1+
2 2+ ... +
Aljabar Linear Elementer – Adiwijaya 53
Contoh 4.3 :
Tentukan kembali hasil kali titik dari dua vektor berikut berikut dengan rumus di atas
a = 2i dan = 2i + 2j b Jawab :
2 2 1
1
b a b
a b
a • = +
= 2 (2) + 0 (2) = 4
Berikut ini adalah sifat – sifat hasil kali titik : a
b b a • = • (i)
( b c ) ( ) ( ) a b a c
a • + = • + • (ii)
( ) a b k a b a k b k R
k • = • = • , dimana ∈
(iii)
Proyeksi Ortogonal Suatu Vektor
Secara geometri, proyeksi ortogonal suatu vektor terhadap vektor lain dapat diilustrasikan sebagai berikut :
w a
b b a
oy r r Pr
a b
Gambar 4.6 Proyeksi Ortogonal Vektor Terhadap Vektor
54 Bab 4 ● Vektor di Bidang dan di Ruang a
proy
c = b c =k untuk suatu kelipatan k b ∈ ℜ
Misalkan maka .
Sementara itu, w merupakan suatu komponen dari vektor a yang tengah lurus terhadap b .
Perhatikan bahwa c w a = + Sehingga :
( w + c ) • b b
a •
=
b c b w • + •
=
= c • b
2b k
b b k
=
•
=
Dengan demikian
b
2b a • k = .
Oleh karena itu, kita peroleh bahwa :
b
2b a •
a
proy b = . b
Berikut adalah contoh perhitungan untuk memperoleh vektor hasil proyeksi ortogonal suatu vektor terhadap vektor yang lain.
Contoh 4.4 :
Tentukan proyeksi ortogonal vektor w = terhadap
vektor
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
−
−
3 4 2
v =
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
− 4
3
1
Aljabar Linear Elementer – Adiwijaya 55 Jawab :
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
−
−
=
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
−
= −
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
−
− +
− +
= −
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
− − + +
⎟ ⎟
⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
−
⎟ •
⎟ ⎟
⎠
⎞
⎜ ⎜
⎜
⎝
⎛
−
−
=
= •
4 3 1
4 3 1 26
26
4 3 1 26
) 12 ( ) 12 ( 2
4 3 1 ) 4 ( 3 1
4 3 1 3
4 2 Pr
2 2
2 2
v v
v w w
oy
v4.3 HASIL KALI SILANG (CROSS PRODUCT)
Hasil kali silang merupakan perkalian antara dua vektor yang akan menghasilkan suatu vektor baru
Definisi :
v
Misal dan adalah vektor di ruang (R u
3) maka vektor yang tegak lurus terhadap keduanya ( u dan ) adalah sehingga v w
w = u × v . Ini membuktikan bahwa w ⊥ u dan w ⊥ v .
u v w u × v
Secara geometri, misal =(0,0,1) dan =(0,1,0), jika =
maka w yang tegak lurus terhadap dan yang searah sumbu u v
x negatif. Arah vektor w di tentukan dengan menggunakan
56 Bab 4 ● Vektor di Bidang dan di Ruang aturan tangan kanan, dimana arah empat jari dari vektor u menuju vektor v sehingga ibu jari searah dengan arah vektor . w
u
w
v
y Z
x
Gambar 4.7 Ilustrasi Hasilkali Silang antara Dua Vektor Cara menentukan vektor yang mempunyai hasil kali silang w antara dua vektor yaitu u dan adalah sebagai berikut : v
w = u × v
3 2 1
2 1
ˆ ˆ ˆ
v v v
u u u
k j i =
2 1
2
ˆ
1v v
u k u
3 2
3
ˆ
2v v
u i u
3 1
3
ˆ
1v v
u j u
= − +
= (u
2v
3-u
3v
2) i ˆ +(u
3v
1-u
1v
3) +(u jˆ
1 2v -u v
2 1) k ˆ Contoh 4.5 :
( 1 , 2 , − 2 )
= v u
u
w = × v = ( 3 , 0 , 1 )
Tentukan , dengan dan .
Aljabar Linear Elementer – Adiwijaya 57
Jawab :
v u w = ×
3 2 1
3 2 1
ˆ ˆ ˆ
v v v
u u u
k j i =
3 1
3
ˆ 1
v v
u j u
−
2 1
2
ˆ
1v v
u k u
3 2
3
ˆ 2
v v
u i u
= +
= (u
2v
3-u
3v
2) i ˆ +(u
3v
1-u
1v
3) +(u jˆ
1v
2-u
2v )
1kˆ = ( 2 . 1 − 0 ( − 2 ) ) iˆ + ( 3 ( − 2 ) − 1 . 1 ) jˆ + ( 1 . 0 − 3 . 2 ) kˆ = 2 i ˆ − 7 ˆ j − 6 k ˆ
Beberapa sifat hasil kali silang yang perlu diketahui adalah:
Misal dan di ruang (R u v
3) maka:
( ) = 0
• u x v a. u
( ) = 0
• u x v
b. v
( )
22 2
2
u v u v
v
u × = − •
c.
Dari sifat ketiga dapat kita simpulkan bahwa:
( u v )
v
u ⋅ − •
=
2 2v
2u ×
( )
22
2
⋅ − ⋅ ⋅ cos α
= u v u v
(
2 2 2α )
2
2
⋅ − ⋅ ⋅ cos
= u v u v
(
2α )
2
2
⋅ 1 − cos
= u v
α
2 2
2
⋅ ⋅ sin
= u v
Sehingga kita memperoleh hubungan : sin α
⋅
⋅
= u v v
x
u
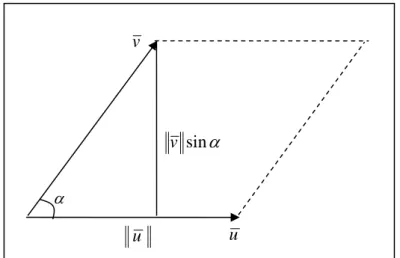
58 Bab 4 ● Vektor di Bidang dan di Ruang Untuk memudahkan pemahaman rumusan diatas, perhatikan ilustrasi berikut :
u v
α
α sin v
u
Gambar 4.8 Hasilkali Silang Dua Vektor dengan Daerah yang Dibentuknya
Dengan mengacu pada gambar 4.8, beberapa hal yang diperoleh antara lain :
u v
• Luas jajaran-genjang yang dibentuk oleh vektor &
adalah u × v
u v , , dan ( u v
• Luas segitiga yang dibentuk oleh – ) adalah u × v
2 1
Agar dapat memperoleh pemahaman lebih dalam berikut adalah contoh aplikasi hasilkali silang dalam menghitung luas segitiga.
Contoh 4.6 :
Diketahui titik-titik diruang (R³ ) adalah :
A = (1, –1, –2), B = (4, 1, 0), dan C = (2, 3, 3)
Dengan menggunakan hasilkali silang, tentukan luas
segitiga ABC !
Aljabar Linear Elementer – Adiwijaya 59
Jawab:
AB AC
a. Misalkan, dan adalah vektor yang berimpit pada titik A.
AB = B – A= (4, 1, 0) – (1, –1, –2) Tulis
= (3, 2, 2)
AC = C – A= (2, 3, 3) – (1, –1, –2) = (1, 4, 5)
Dengan menggunakan kedua vektor tersebut diperoleh :
5 4
1
2 2
3
ˆ ˆ
ˆ j k
i
× AC AB =
= 2 i ˆ − 13 ˆ j + 10 k ˆ
Sehingga luas segitiga ABC yang berimpit di A adalah :
= AB 2
1 × AC
= 4 169 100 2
1 + +
= 273 2 1
BA dan BC
b. Misalkan, adalah vektor yang berimpit pada titik B.
BA = a − b = (1,-1,-2) – (4,1,0)
= (-3,-2,-2)
BC = c − b = (2,3,3) – (4,1,0)
= (-2,2,3)
60 Bab 4 ● Vektor di Bidang dan di Ruang
3 2 2
2 2 3
ˆ ˆ ˆ
−
−
−
−
k j