TEORI DAN APLIKASI MATRIKS P. SEMBIRING

TEORI DAN APLIKASI

MATRIKS

P

P

P

P.... SEMBIRING

SEMBIRING

SEMBIRING

SEMBIRING

2018

Jl. Universitas No. 9 Medan 20155, Indonesia Telp. 061-8213737; Fax 061-8213737 www.usupress.usu.ac.id

© USU Press 2018

Hak cipta dilindungi oleh undang-undang; dilarang memperbanyak menyalin, merekam sebagian atau seluruh bagian buku ini dalam bahasa atau bentuk apapun tanpa izin tertulis dari penerbit. ISBN 978-602-465-030-8

Perpustakaan Nasional: Katalog Dalam Terbitan (KDT)

Teori dan Aplikasi Matriks / P. Sembiring -- Medan: USU Press 2018. iii, 126 p.; ilus.: 29 cm

Bibliografi

Dengan mengucapkan syukur kepada Tuhan Yang Maha Esa, yang telah melimpahkan rahmat serta petunjuk-Nya kepada penulis, sehingga penulis dapat menyelesaikan buku ini dengan segala keterbatasan.

Matrik merupakan salah satu ilmu dasar yang sangat banyak digunakan dalam berbagai disiplin ilmu seperti Teknik, Kimia, Fisika, Pertanian, dll.

Dalam buku ini diuraikan secara mendasar tentang teori dan aplikasi matrik itu sendiri. Dalam penelitian, terdapat banyak metode yang akan digunakan termasuk penggunaan matrik.

Mengingat pentingnya kegiatan penelitian, maka penulis berkeinginan untuk menyusun buku ini untuk dijadikan salah satu bahan referensi bagi penelitian yang menggunakan matrik.

Penulis menyadari bahwa dalam menyusun buku ini masih terdapat kekurangan. Segala kritik dan saran yang membangun akan sangat berharga bagi penyempurnaan lebih lanjut.

Akhir kata, penulis menyampaikan ucapan terima kasih yang sebesar-besarnya kepada semua pihak telah memberikan semangat dan bantuan kepada penulis.

Medan, Maret 2018

KATA PENGANTAR ... i

DAFTAR ISI ... ii

BAB I MATRIK ... 1

1. Defenisi ... 1

2. Matrik Bujur Sangkar (Square Matrices) ... 1

3. Matrik yang Sama (Equal Matrices) ... 2

4. Matrik Nol (Zero Matrices)... 2

5. Beberapa Operasi Matrik ... 2

a. Penjumlahan Matrik ... 2

b. Perkalian Matrik (Multiplication Matrices) ... 3

c. Perkalian Partisi Matrik (Product by Partitioning) ... 5

6. Beberapa Model-Model Matrik (Some Types of Matrices) ... 7

a. Matrik Satuan (The Identity Matrices) ... 7

b. Matrik-Matrik Bujur Sangkar Istimewa (Special Square Matrices) ... 9

c. Matrik Invers untuk Pergandaan... 9

d. Matrik Transpose (The Transpose of a Matrices) ... 9

e. Matrik-Matrik Simetris (The Symetric Matrices) ... 11

f. Matrik Anti Simetris (Skew Symetric Matrices) ... 11

g. Matrik Adjoint (Classical Adjoint Matrices) ... 11

h. Matrik Bersekawan (The Conjugate of Matrices) ... 13

i. Matrik Hermitian (Hermitian Matrices) ... 15

7. Rank Matrik (The Rank of a Matrices) ... 15

a. Minor Matrik ... 15

b. Defenisi ... 15

8. Transportasi Elementer pada Baris dan Kolom Suatu Matrik ... 16

9. Matrik Ekuivalen ... 16

10. Matrik Elementer ... 17

11. Sistem Persamaan Linier Diselesaikan dengan Matrik ... 18

a. Sistem Persamaan Linier Non Homogen ... 18

b. Sistem Persamaan Linier Homogen ... 20

12. Transformasi Linier ... 21

a. Defenisi ... 21

b. Teorema Dasar (Basic Theorem) ... 21

13. Persamaan Karakteristik dari Sebuah Matrik ... 25

14. Matrik Modul ... 27

BAB II DETERMINAN ... 31

1. Permutasi ... 31

5. Determinan Derajat Tiga ... 32

6. Komplemen Minor dan Komplemen Aljabar ... 37

7. Menghitung Harga Determinan ... 38

a. Ekspansi Laplace (The Laplace Expansion) ... 38

b. Metode Chio ... 39

8. Sistem Persamaan Linier Diselesaikan dengan Determinan ... 41

a. Sistem Persamaan Linier dengan n Persamaan dan n Anu .... 41

b. Sistem Persamaan Linier Non Homogen dengan m Persamaan dan n Anu ... 47

BAB III INVERS MATRIK... 49

BAB IV MENGGUNAKAN MATLAB UNTUK MENCARI INVERS MATRIK ... 57

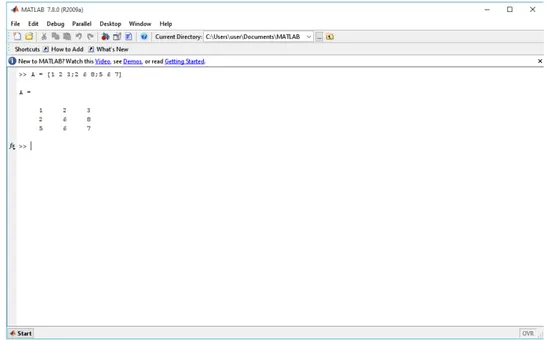
1. MATLAB (Matrix Laboratory) ... 57

2. Menggunakan Aplikasi MATLAB ... 57

3. Mencari Invers Matrik dengan MATLAB ... 59

4. Contoh Mencari Invers Matrik dengan MATLAB ... 61

BAB V ANALISIS FAKTOR PENGARUH MAHASISWA TERLAM- BAT MENYELESAIKAN STUDI DI FMIPA USU ... 71

I. Pendahuluan ... 71

II. Tinjauan Pustaka ... 71

III. Tujuan dan Manfaat Penelitian ... 71

IV. Metode Penelitian ... 75

V. Analisa Pembahasan ... 75

VI. Kesimpulan dan saran ... 89

BAB VI ANALISIS PENGARUS LAJU INFLASI DI INDONESIA ... 91

I. Analisis Situasi ... 91

II. Tinjauan Pustaka ... 92

III. Perumusan Masalah ... 92

IV. Tujuan dan Manfaat Kegiatan ... 93

V. Pelaksanaan Kegiatan ... 94

VI. Modul Penuntun Seminar ... 95

VII. Kesimpulan dan Saran ... 125

BAB I

MATRIK

1. Defenisi

Matrik ialah suatu kumpulan elemen-elemen dimana subscript (indeks) pertama = 1, 2, 3, … , , menyatakan baris, dalam subscript indeks kedua = 1, 2, 3, … , , menyatakan kolom yang disusun menurut baris dan kolom sehingga berbentuk empat persegi panjang atau bujur sangkar, yang dibatasi oleh kurung siku-siku , kurung kecil atau garis rangkap tegak lurus ‖ ‖. (Pasukat Sembiring).

Notasi matrik ditulis dengan huruf balok, misalnya : , , , … dst. Bentuk umum dari suatu matrik adalah:

a a a … a a a a … a . . . . . . . . . . . . a a a … a !"

" " " # (1) dimana: a$% = elemen-elemen matrik

Subscript (Indek I), = 1, 2, 3, … , , menyatakan baris Subscript (Indek II), = 1, 2, 3, … , , menyatakan kolom.

Biasa juga matrik (1) disebut matrik: A _× = (a_$%) dimana m × n adalah ukuran matrik A atau A _× = (a_$%) untuk i = 1, 2, 3, … , m, dan j = 1, 2, 3, … , n

Contoh: × .= / 1 4 2 2 −1 0 0 2 1 −5 1 24

Matrik yang hanya terdiri dari satu baris disebut vektor baris dan yang terdiri dari hanya dari satu kolom disebut vektor kolom.

2. Matrik Bujur Sangkar (Square Matrices)

Matrik bujur sangkar yang berderajat adalah suatu matrik dimana banyaknya baris sama dengan banyaknya kolom, jadi = .

Bentuk umum matrik bujur sangkar berdrajat adalah:

5 6 5 = 5 = 7 a a … a a a … a … … … … a a … a 8

dimana: a , a , a , … , a = elemen-elemen diagonal a + a + a + ⋯ + a = trace dari A. Contoh: 6 = = / 1 3 1 2 1 4 4 7 64 3. Matrik Yang Sama (Equal Matrces)

Dua matrik A = (a_$%) dan B = (b_$%) dikatakan sama jika dan hanya jika derajat dan elemen-elemen yang bersesuaian sama yaitu ? = @ untuk = 1, 2, 3, … , dan = 1, 2, 3, … , .

4. Matrik Nol (Zero Matrices)

Matrix nol adalah suatu matrik dimana tiap-tiap elemennya adalah nol dan diberi simbol 0.

Bilamana A = matrik nol maka matrik ditulis A = 0. Contoh:

A = /0 0 00 0 0

0 0 04 atau = 0 5. Beberapa Operasi Matrik

a. Penjumlahan Matrik

Jika A = [aij] dan B = [bij] adalah matrik-matrik m x n, maka A ± B didefinisikan sebagai matrix Cm x n = Cij, dimana tiap elemen dari C adalah sama dengan penjumlahan elemen-elemen yang bersesuaian (seletak) dari A dan B. Jadi A ± B = [aij± bij].

± =

a a … a %… a a a … a %… a … … … … a$ a$ … a$%… a$

… … … … a a … a %… a !"

" " " # ± b b … b %… b b b … b %… b … … … … b$ b$ … b$%… b$ … … … … b b … b %… b !" " " " # = c c … c %… c c c … c %… c … … … … c$ c$ … c$%… c$ … … … … c c … c %… c !" " " " # Maka A ± B = C

Dua matrik dengan derajat yang sama dikatakan conformable untuk penjumlahan atau pengurangan dan dua matrik dengan derajat yang berbeda tidak dapat dijumlahkan atau dikurangkan disebut non-conformable untuk penjumlahan dan pengurangan.

Penjumlahan dari k matrik-matrik A adalah suatu matrik dari derajat yang sama seperti A dan tiap-tiap dari elemen matrik adalah k kali elemen-elemen yang bersesuaian dengan elemen-elemen dari A didefinisikan : Jika k suatu skalar maka didapat kA = Ak adalah bentuk matrik yang ditentukan dengan mengalikan tiap elemen-elemen dari A dengan k.

Dalam hal yang istimewa, - A disebut negatip dari matrik A adalah bentuk matrix yang ditentukan dengan mengalikan tiap-tiap elemen A dengan – 1 atau kebalikan semua tanda elemen-elemen matrik yang bersangkutan.

Untuk tiap-tiap A didapat A + (- A) = 0, dimana 0 menunjukkan matrik nol dari derajat yang sama seperti derajat matrik A.

Jika matrix-matrix A, B, C adalah conformable untuk penjumlahan, maka berlaku :

i. A + B = B + A ; (hukum komutatif) ii. A + (B + C) = (A + B) + C ; (hukum asosiatif) iii. k (A + B) = kA + kB

= (A + B) k ; k adalah scalar b. Perkalian Matrik (Multiplication Matrices)

Pandang matrik A yang terdiri dari satu baris dan matrik B terdiri dari satu kolom, misalnya :

Vektor baris A1 x m = [a11 a12 a13 … a1m]

dan vektor kolom Bm x 1 = b b b … b !" " " # Maka C1 x 1 = A1 x m . Bm x 1

= [a11 a12 a13 … a1m] b b b … b !" " " #

= [a11b11 + a12b21 + … + a1m bm1] = /C a D . bD

DE

Jadi operasi perkalian baris dan kolom yaitu tiap elemen dari kolom matriks pertama dikalikan dengan elemen yang bersesuaian dengan elemen dari baris matriks ke dua dan hasil perkalian dijumlahkan.

Contoh :

Ditentukan : A = [a11 a12 a13] , B = / a a a 4 Penyelesaian : AB = a a a /aa a 4 = a a + a a + a a

Dari perkalian AB dalam suatu derajat dimana matrik Am x p = [aij] dan matrik Bp x n = [bij] adalah suatu bentuk matrik Cm x n [Cij].

dimana Cij = aij bij + ai2 b2j + … + aip bpj = C a_$Db_D% , i = 1, 2, … , m ; j = 1, 2, … , n

G

DE

Matrik A terdiri dari m baris dan B terdiri dari n kolom.

Dalam bentuk C = A . B, dimana tiap baris dari A sekali dan hanya sekali dikalikan dengan tiap kolom dari B. Elemen Cij dari C adalah perkalian dari kolom ke i dari A dan baris ke j dari B.

Perkalian AB dapat diselesaikan (didefinisikan) jika A conformable B untuk perkalian dimana banyaknya kolom dari A = banyaknya baris dari B.

Jika A conformable B untuk perkalian dimana AB dapat diselesaikan; maka B tidak perlu dengan conformable A untuk perkalian. (BA mungkin atau tidak mungkin diselesaikan). Contoh : 1. Ditentukan : A H = / a a a a a a 4 , Ib bb b J = /

a b + a b a b + a b a b + a b a b + a b a b + a b a b + a b 4

Operasi matrik-matrik A, B, C adalah conformable untuk menyatakan penjumlahan dan perkalian, maka didapat :

i. A (B + C) = AB + AC , (hukum distributif I) ii. (A + B) C = AC + BC , (hukum distributif II) iii. A (BC) = (AB) C, (hukum asosiatif)

Tetapi : iv. AB ≠BA, secara umum

v. AB = 0, berarti tidak perlu dengan A = 0 atau B = 0 vi. AB = AC, berarti tidak perlu dengan B = C

Contoh : 1. Ditentukan : = /−3 2 −11 −1 1 −2 1 0 4 , B = / 1 3 2 2 6 4 1 3 24 Penyelesaian : A . B = / 1 −1 1 −3 2 −1 −2 1 0 4 / 1 3 2 2 6 4 1 3 24 = / 1 − 2 + 1 3 − 6 + 3 2 − 4 + 2 −3 + 4 − 1 −9 − 12 − 3 −6 + 8 − 2 −2 + 2 + 0 −6 + 6 + 0 −4 + 4 + 04 = / 0 0 0 0 0 0 0 0 04 Maka A . B = 0 , meskipun A ≠ 0 , B ≠ 0.

c. Perkalian Partisi Matrik (Products by Partitioning)

Diambil A = aij dengan derajat a x α dan B = bij dengan derajat d x b. Dalam bentuk perkalian AB, matrix A adalah bagian partisi terdiri dari a matrix untuk derajat 1 x d dan B terdiri dari derajat d x 1.

Contoh :

Ditentukan : Matrik-matrik partisi A dan B dengan derajat seperti dalam garis-garis yang tergambar.

A = / a xd a xd a xd − − − − − − − − − − − a xd a xd a xd 4 B = d xb d xb − − − − − − − d xb d xb − − − − − − − d xb d xb !" " " #

Penyelesaian : Dengan partisi matrik didapat: A = / A A A − − − − − − − A A A 4 B = B B − − − − − B B − − − − − B B !" " " # A . B = / A A A − − − − − − − A A A 4 . B B − − − − − B B − − − − − B B !" " " #

= IA B + A B + A B A B + A B + A B_{A B + A B + A B A B + A B + A B J}

= IC C_{C C J} Maka A . B = C Contoh : Ditentukan : A = /1 0 10 1 1 0 0 14 , B = / 1 0 0 0 1 0 1 1 04

Penyelesaian : Dengan partisi matrix, didapat :

A = / 1 0 1 0 1 1 0 0 14 = IA A A A J B = / 1 0 0 0 1 0 1 1 04 = IB B B B J A . B = IA A A A J . IBB BB J

= PQ1 00 1R Q 1 0 0 1R x Q11R 1 1 Q1 00 1R Q00R x Q11R 0 0 0 Q1 0_{0 1R x 1 1 1 0 0 Q}0_{0R x 1 0} S = /Q 1 0 0 1R T Q1 11 2R Q00R T Q00R 0 0 T 1 1 0 T 0 4 = /Q 2 1 1 2R Q00R 1 1 0 4 Maka A . B = / 2 1 0 1 2 0 1 1 04 Secara umum :

Diambil A, B, C, … dengan b matrik-matrik bujur sangkar. A dipartisi kedalam matrik-matrik bagian dengan derajat tertentu.

7 d xd d xd ⋯ d xd d xd d xd ⋯ d xd ⋮ ⋮ ⋮ ⋮ d xd d xd ⋯ d xd 8 = 7 A A … A A A … A ⋯ ⋯ ⋯ ⋯ A A … A 8

dan B, C, … dipartisi dengan perhitungan yang sama.

Jadi penjumlahan – penjumlahan, pengurangan-pengurangan dan perkalian-perkalian mungkin dibentuk dengan menggunakan matrik-matrik A11, A12, … ; B11, B12, … ; C11, C12, ….

6. Beberapa Model-model Matrik (Some Types of Matrices) a. Matrik satuan (The Identity Matrices)

i. Matrik segitiga atas (Upper Triangular Matrices)

Matrix bujur sangkar A mempunyai elemen-elemen aij = 0 untuk i > j disebut matrik segitiga atas.

Bentuk umum matrik segitiga atas :

a a a … a 0 a a … a 0 0 a … a ⋯ ⋯ ⋯ ⋯ ⋯ 0 0 0 … a !" " " #

ii. Matrik segitiga bawah (a lower triangular matrices)

Matrik bujur sangkar A mempunyai elemen-elemen aij = 0 untuk i > j disebut matrik segitiga bawah.

Bentuk umum matrik segitiga bawah : 7

a 0 0 … 0 a a 0 … 0 ⋯ ⋯ ⋯ ⋯ ⋯ a a a … a

8

iii. Matrik diagonal (a diagonal matrices) Matrik D = 7 a 0 0 … 0 0 a 0 … 0 ⋯ ⋯ ⋯ ⋯ ⋯ 0 0 0 … a 8 dimana

Diagonalnya adalah diagnonal dari kedua matrik segitiga atau dari bawah disebut matrik diagonal atau ditulis sebagai berikut : D = diag . (a11, a22, …, ann)

iv. Matrik skalar (a skalar matrices)

Jika dalam matrik diagonal D, a11 = a22= … = ann= k, maka D disebut matrik skalar.

Bentuk umum matrik skalar : D = 7

k 0 … 0 0 k … 0 … … … … 0 0 … k 8

v. Matrik satuan (the identity matrices)

Jika k = 1, maka matrik D disebut matrik satuan derajat n dan ditulis In. Bentuk umum matrix satuan :

I = 7 1 0 … 0 0 1 … 0 … … … … 0 0 … 1 8

Sifat-sifat Matrik Satuan

Jika ditentukan matrik Am x n, Am x n = In = matrik bujur sangkar dan In x n = In matrik satuan, maka didapat :

i. Am x n . In = An x m dan =In . An =An ii. In . An x m = An x m dan In . An = An

b. Matrik-matrik bujur sangkar istimewa (special square matrices)

i. Jika dari matrik-matrik bujur sangkar A dan B berlaku AB = BA maka A dan B disebut kommutatif (commate). Matrik bujur sangkar An komutatif dengan dirinya sendiri, jadi An . An = An . An.

ii. Jika dari matrik-matrik bujur sangkar AB = BA, maka A dan b disebut anti komutatif (anti commute).

iii. Jika matrik Ak+1 _{= A, maka :}

1. Matrik A disebut periodic untuk k = bilangan bulat positif.

2. Matrik A terdiri dari periode k untuk k = bilangan bulat positif terkecil. 3. Matrik A disebut idempotent untuk k = 1, jadi A2 = A.

iv. Jika matrik Al = 0, maka

1. Matrik A disebut nikpotent untuk p = bilangan bulat positif.

2. Matrik A disebut nilpotent dengan indek p untuk p = bilangan bulat positip terkecil.

c. Matrik invers untuk pergandaan

i. Jika AB = BA = I dimana A dan B adalah matrik-matrik bujur sangkar, maka dikatakan B invers dari A dan ditulis B = A-1.

Sebaliknya berlaku juga A invers dari B ditulis A = B-1.

ii. Jika A dan B adalah matrix-matrix bujur sangkar dari derajat yang sama dengan invers-invers masing-masing A-1 dan B-1 maka (AB)-1 = B-1 . A-1 atau dapat dikatakan invers dari perkalian dan matrik menghasilkan matrik invers yaitu perkalian matrik untuk derajat sebaliknya.

iii. Jika matrik A2 = I, maka I disebut involutory matrik yaitu sebuah matrik yang inversnya adalah dirinya sendiri, contohnya matrik satuan.

d. Matrik Transpose (The Transpose of a Matrices)

Transpose dari matrik Am x n dimana i = 1, 2, …, m dan j = 1, 2, …, n adalah matrik An x m yang ditukar penulisan semua baris ke i menjadi kolom ke j.

Transpose dari matrik A ditulis : At atau A1.

Andaikan matrik Am x n = (a_$%)→∑] _H (a_%$), maka diperoleh : Sifat-sifat matrik transpose, yaitu :

i. (A + B)t =At +Bt Bukti : Andaikan A = (a_$%) B = (b_$%) (A + B)t = ^(a_$%) x (b_$%)_] = (C_$%)] = (C_%$) (3)

At + Bt = (a_$%)] x (b_$%)] = (a_%$) x (b_%$)

= (C_%$) (4) Dari persamaan (3) dan (4), maka terbukti (A + B)t = At + Bt

ii. (At)t = A Bukti : Andaikan A = (a_$%) At = (a_%$) Maka (At)t = (a_%$)] = (a_$%) Jadi (At₎t _{= A} iii. k (At) = (kA)t Bukti : Andaikan A = (a_$%) At = (a_%$) k . At = k (a_%$) = (k a_%$) (5) (k A)t = ^k (a_$%)_] = (k a_$%) = (k a_%$) (6) Dari persamaan (5) dan (6) didapat :

k A] _{= kA} ] iv. (AB)t = Bt . At

Bukti : Andaikan A = (a_$%) B = (b_%D)

Maka elemen pada baris ke i dan kolom ke j dari A.B = ai1 . bij + ai2 . b2j + … + ain . bnj

= elemen pada baris ke i dan kolom ke i dari (AB)t. Di lain pihak baris ke j dari Bt adalah kolom ke j dari B = [b1j, b2j, …, bnj]

dan kolom ke i dari At _{= baris ke i dari A} = 7 a$ a$ … a_$ 8

Jadi elemen pada baris ke j dan kolom ke i dari B] _{. A}] _{= (b} %, b %, … , b %) 7 a$ a$ … a$ 8

= b1j . ai1 + b2j ai2 + … + bnj ain = ai1 b2j + ai2 . b2j + … + ain bnj

Jadi dapat disimpulkan untuk semua i dan j maka (AB)t= Bt . At. e. Matrik-matrik Simetris (Symetric Matrices)

Matrik A bujur sangkar sedemikian hingga At = A adalah disebut simetris. Jadi matrix bujur sangkar A = [aij] adalah simetris maka [aij] = [aji] untuk semua nilai i dan j.

f. Matrik anti simetris (Skew symetric matrices)

Matrik A bujur sangkar sedemikian hingga At _{= -A adalah disebut skew} simetris. Jadi matrix bujur sangkar A adalah skew simetris maka [aij] = - [aji] untuk semua i dan j.

Jelas bahwa dalam hal ini elemen-elemen diagonal utamanya harus semuanya = 0, karena untuk i = j terdapat [aii] = - [aii]

2 [aii] = 0 [aii] = 0 g. Matrik adjoint (Classical adjoint matrices)

Andaikan matrik A = [aij], kofaktor dari elemen aij = Aij, maka transpose dari matrik [Aij] disebut matrix adjoint dari A.

Bentuk umum matrix adjoint. Adj. A = 7 A A … A A A … A … … … … A A … A 8 | adj. A . | = |A| |adj . A | = |A|

|adj . A | = |A| a _{dimana |A| ≠ 0} Contoh :

Ditentukan : A = /

2 3 −4 0 −4 2

Penyelesaian : A11 = c−4 2 −1 5c = (-4) . 5 – 2 . (-1) = - 18 A12 = - c0 2 1 5c = - (0 . 5 – 2 . 1) = 2 A13 = c0 −4 1 −1c = 0 . (-1) – (-4) . 1 = 4 A21 = -c3 −4 1 5 c = - 2 . 5 – −4 . −1 = - 11 A22 = c2 −4 1 5 c = 2 . 5 – (-4) . 1 = 14 A23 = - c2 3 1 −1c = - (2 . (-1) – 3 . 1) = 5 A31 = c 3 −4 −4 2 c = 3 . 2 –(-4 . (-4) = - 10

A32 = - c2 −4 0 2 c = - (2 . 2 – (-4) . 0) = - 4 A33 = c2 3 0 −4c = 2 . (-4) - 3 . 0 = - 8 Maka adjoint A = / A A A A A A A A A 4 = / −18 −11 −10 2 14 −4 4 5 −84 |adj . A| = |A| a = e 2 3 −4 0 −4 2 1 −1 5 e dimana |A| ≠ 0 n = 3 = [2.(-4) . 5 + 3.2.1 + (-4).0 . (-1)-(-4).1 – 2.2.(-1 - 3.05]2 = [-46]2 Maka |adj. A| = 2116

h. Matrik bersekawan (The Conjugate of Matrices)

Jika a, b = bilangan real dan i = √−1 maka z = a + bi disebut bilangan kompleks (a complex number).

Jika z = a + bi maka conjugatenya adalah zh = a + bıhhhhhhhhh = a = bi.

Jika z1 = a + bi dan z2 = zh1 = a – bi, maka zj2 - zh1 = a – bıhhhhhhh = a + bi dimana zh2 adalah conjugate dari conjugate bilangan kompleks z itu sendiri.

Jika z1= a + bi dan z2 = c + di, maka :

1. Conjugate dari penjumlahan dua bilangan kompleks sama dengan jumlah dari masing-masing conjugate-conjugatenya.

Jadi : z1 + z2 = (a + bi) + )c + di) = (a + c) + (b + d) i z + z

hhhhhhhhhh = (a + c) – (b + d) i = (a + bi) + )c – di) = zh2 + zh1

2. Conjugate dari perkalian dua bilangan kompleks sama dengan perkalian dari masing-masing conjugatenya.

Jadi : z1 . z2 = (a + bi) . (c + di) = (ae – bd) + (ad + bc) i z . z

hhhhhhh = (ac – bd) – (ad + bc) i = (a – bi) (c – di)+\ = zj . zj

Jika elemen-elemen dalam sebuah matrik A yang elemen-elemennya terdiri dari bilangan-bilangan kompleks, diganti dengan masing-masing conjugatenya maka diperoleh conjugate dari matrix A, ditulis Aj dibaca A conjugate.

Contoh : Ditentukan,

A = Q2 − 7i_{5 1 + 3iR}3i Penyelesaian : Conjugate dari matrik A adalah :

A = Q2 + 7i_{5 1 − 3iR}−3i Jika : Aj = conjugate dari matrik A

Bj = conjugate dari matrik B k = skalar,

maka 1. Aj = A

2. ^kAhhhh_ = kh . Aj

Berdasarkan ketentuan g.(1) dan g.(2), maka didapat :

1. Conjugate dari penjumlahan dua matrix sama dengan jumlah dari masing-masing conjugate-conjugatenya. Jadi A + Bhhhhhhh = Aj + Bj.

2. Conjugate dari perkalian dua matrix sama dengan perkalian dari conjugate-conjugatenya dengan derajat yang sama.

Jadi, A + Bhhhhhhh = Aj + Bj.

3. Transpose dari Aj disebut Aj] atau A* (A conjugate transpose).

Jadi transpose dari conjugate A sama dengan conjugate dari transpose A atau (Aj)t _{= (}Aj]₎ Contoh : Ditentukan : A = Q2 − 7i 3i 5 1 + 3iR Aj = Q2 + 7i_{5 1 − 3iR}−3i Penyelesaian :

Dari Aj, didapat: (Aj)t = Q2 + 7i −3i −3i 1 − 3iR Dan dari A, didapat : A = Q2 − 7i 5

−3i 1 + 3iR Aj = Q2 + 7i] 5

−3i 1 − 3iR Maka Aj = (Aj)] t → terbukti.

i. Matrik Hermitian (Hermitian Matrices)

Sebuah matrik bujur sangkar A = [aij] sedemikian hingga Aj = A dimana aij ] = aji untuk semua nilai i dan j, maka A disebut matrix hermitian.

Matrik skew-hermitian adalah matrik yang elemen-elemen diagonal utamanya terdiri dari elemen nol atau imaginar murni (fine imaginaries).

Jika A adalah sebuah matrik bujur sangkar, maka : 1. A + Ahhh = matrik hermitian

^A + Ahhh_ = B = matrik hermitian. 2. A - Ahhh = matrik skew-hermitian

^A − Ahhh_ = C = matrix skew-hermitian. 7. Rank Matrik (The Rank of a Matrices) a. Minor matrik

Pandanglah suatu matrik A dengan m baris dan n kolon.

Jika diambil s baris dan t kolom dari matrik A dimana s ≤ m dan t ≤ n, maka elemen-elemen dari s baris dan t kolom ini merupakan suatu matrik yang disebut minor matrik dari matrik A.

Contoh :

Dari matrik A =

a a a … a a a a … a a a a … a … … … … … a a a … a !"

" " #

Jika s = t= 3 maka minor matrik dari matrik A adalah : /aa aa aa

a a a 4

Jika s = m dan t = n, maka minor matrik dari matrik A adalah matrik A sendiri. Jika s = t, maka didapat suatu minor matrik kwadrat (square minor matrices). b. Definisi

Sebuah matrik A yang ≠ O, mempunyai rank sebesar r, jika dengan r baris det.A ≠ 0 dan minor matrik dari matrix A = 0 dengan (r + 1) baris.

Rank dari matrik A ditulis : rank (A) = r (A) = r. i. Jika matrik A = 0, maka r (A) = r = 0.

ii. Jika rank (A) = r (A) dan |A|≠ 0, maka matrik bujur sangkar dengan n baris dan n kolom dikatakan non singular.

iii. Jika r < n dan |A| = 0, maka matrik A disebut singular.

Persamaan dari rank matrik ini sangat penting dalam menyelesaikan persamaan-persamaan linier karena dengan mengetahui besarnya rank dari Sistem matrik A sebagai matrik koefisien dengan persamaan AX = B maka dapat ditentukan apakah persamaan ini mempunyai penyelesaian atau tidak.

8. Transformasi Elementer Pada Baris Dan Kolom Suatu Matrik

Yang dimaksud dengan transformasi elementer pada baris dan kolom suatu matrix adalah sebagai berikut :

a. i. Penukaran tempat baris ke i dan ke j.

(Baris ke i dijadikan baris ke j dan baris ke j dijadikan baris ke i). Ditulis : Hij (A).

ii. Penukaran tempat kolom ke i dan kolom ke j.

(kolom ke i dijadikan kolom ke j dan kolom ke j dijadikan kolom ke i). Ditulis : Kij (A)

b. i. Memperkalikan baris ke i dengan skalar k. ditulis : Hi(k) (A)

ii. Memperkalikan kolom ke i dengan skalar k. ditulis : Ki(k) (A)

c. i. Menjumlahkan baris ke i dengan k kali baris ke j. ditulis : Hij(k) (A).

ii. Menjumlahkan kolom ke i dengan k kali kolom ke j. ditulis : Kij(k) (A)

d. i. Menjumlahkan k1 kali baris ke i dengan k2 kali baris ke j. ditulis : Hi(k1) j(k2) (A).

ii. Menjumlahkan k1 kali kolom ke i dengan k2 kali kolom ke j. ditulis : Ki(k1) j(k2) (A).

e. Invers dari transformasi elementer.

Invers suatu transformasi elementer juga suatu transformasi elementer, yaitu sebagai berikut :

i. Hij-1 _{(A) = Hij (B)} Kij-1 _{(A) = Kij (B)} ii. Hi-1 (k) (A) = Hik

Dl (B). Ki-1 (k) (A) = Kik

Dl (B). iii. Hij-1 _{(k) (A) = Hij (-k) (B).}

Kij-1 (k) (A) = Kij (-k) (B). 9. Matrik Ekuivalen

Dua matrik disebut ekuivalen apabila salah satu matriknya diperoleh dari yang lain dengan transformasi elementer terhadap baris dan atau kolom.

Kalau transformasi elementernya hanya pada baris saja dikatakan ekuivalen baris, kolom pada kolom saja dikatakan ekuivalen kolom.

Contoh : 1. Ditentukan : A = Q2 3 1 4 1 0R , B = Q4 1 02 3 1R Penyelesaian : A = Q2 3 1 4 1 0R H2 (A) Q4 1 0 2 3 1R = B Maka : A ∼ B 2. Ditentukan : A = Q3 0 2 1 4 1 3 2R , B = Q5 1 3 13 0 2 1R Penyelesaian : A = Q3 0 2 1 4 1 3 2R K12(1) Q5 1 3 1 3 0 2 1R K12(-1) Q3 0 2 1 5 1 3 1R H12 Q5 1 3 1 3 0 2 1R = B Maka A ∼ B 10. Matrik Elementer

Jika dikerjakan sebuah transformasi elementer terhadap suatu matrik satuan I maka matrik hasil transformasi elementer itu disebut matrik elementer. Contoh :

Dari matrik satuan :

I = /1 0 00 1 0 0 0 14 Diperoleh : a. H12 (I) = / 0 1 0 1 0 0 0 0 14 b. H31(k) _{(I) =} / 10 01 00 0 + k. 1 0 + k. 1 1 + k. 14 = / 1 0 0 0 1 0 k 0 14

∼

∼

∼

∼

c. K12 (I) = / 0 1 0 1 0 0 0 0 14 d. K31(k) (I) = / 1 0 0 + m. 1 0 1 0 + m. 0 0 0 0 + m. 04 = /1 0 m0 1 0 0 0 14

11. Sistem Persamaan Linier Diselesaikan Dengan Matrik a. Sistem persamaan linier non homogen

i. Penyelesaian Sistem persamaan linier non homogen dengan m persamaan dan

n anu

Bentuk umum :

C a$% . x%= c$ %E

Dimana : i = 1, 2, …, m

aij = koefisien dari persamaan ci = c1, c2, …, cm≠ 0

atau a11 x1+ a12 x2 + … + a1n xn = c1

a21 x1 + a22 x2 + … + a2n xn = c2 (7)

… … … … am1 x1+ am2 x2 + … + amn xn = cn

Sistem persamaan (7) mempunyai penyelesaian dikatakan consistent dan jika tidak mempunyai penyelesaian dikatakan inconsistent.

Persamaan (7) dapat ditulis : 7 a a ⋯ a a a ⋯ a ⋯ ⋯ ⋯ ⋯ a a ⋯ a 8 7 x x ⋯ x 8 = 7 c c ⋯ c 8 A . X = C

Dimana A = (aij) = matrik koefisien i.j = 1, 2, …, n.

X = [x1, x2, …, xn] C = [c1, c2, …, cm]

Jika matrik koefisien A, himpunan kolom-kolomnya ditambah dengan vektor-vektor kolom C yang ditulis.

7 a a ⋯ a a a ⋯ a ⋯ ⋯ ⋯ ⋯ a a ⋯ a 8 = AC

Disebut matrik lengkap (augmented matrix)

1. Jika rank matrik koefisien = rank matrik [AC] = (matrik lengkap) maka Sistem persamaan linier

C a$% . a$% . x% = c$ , i = 1, 2 , . . , m %E

dapat diselesaikan dan dikatakan consistent.

2. Jika dalam sebuah Sistem yang consistent r < n, n – r amn dapat dipilih karena itu matrix koefisien dari sisa r amn adalah dari rank r.

Bilamana (n-r) amn ditunjukkan beberapa nilai adalah ditentukan dengan tunggal (unique).

ii. Sistem persamaan linier non homogen dengan n persamaan dan n amn. Bentuk umum : C a_$% . x_%= c_$ %E Dimana i = 1, 2, …, n. ci ≠ 0 AX = C atau a11 x1 + a12 x2+…+ a1n xn = c1

a21 x1 + a22 x2 + … +a2n xn = c2 (8)

… … … … an1 x1 + an2 x2 + … + ann xn = cn

Jadi Sistem persamaan linier on homogen dengan n persamaan dan n amn mempunyai penyelesaian tunal jika rank dari matrik koefisien A adalah = n dengan |A|≠ 0. Sistem persamaan linier (8) diselesaikan dengan menggunakan A-1, yaitu sebagai berikut :

Jika |A|≠ 0,maka A-1 ada dan penyelesaian dari Sistem persamaan linier AX = C adalah :

A-1 A.X = A-1 C I.X = A-1 C Jadi X = A-1 _C

b. Sistem Persamaan Linier Homogen

i. Penyelesaian Sistem persamaan linier homogen dengan n persamaan dan n amn.

Bentuk umum :

C a$% . k% = 0, i = 1,2, … , m %E

atau a11 x1 + a12 x2+…+ a1n xn = c1 a21 x1 + a22 x2 + … +a2n xn = c2 … … … … an1 x1 + an2 x2 + … + ann xn = cn

7 a a ⋯ a a a ⋯ a ⋯ ⋯ ⋯ ⋯ a a ⋯ a 8 7 x x ⋯ x 8 = 7 0 0 ⋯ 0 8 (9)

Jadi jika r(A) = n maka A adalah matrix bujur sangkar dan supaya ada penyelesaian non trivial maka [A] = 0 jika vektor baris dan vektor kolom linier dependen. Jika r(A) < n maka ada penyelesaian trivial yang lain, jadi Sistem persamaan linier (9) mempunyai penyelesaian linier independent (n-r) yaitu tiap penyelesaian adalah kombinasi dari (n-(n-r) dan setiap kombinasi linier adalah suatu penyelesaian.

Jika Sistem persamaan linier non homogen AX = C adalah consistent, maka penyelesaian umum (n complek solution) atau penyelesaian lengkap dari Sistem ini diberikan oleh penyelesaian umum dari X = 0 ditambah tiap penyelesaian partikulir dari AX = C. Jadi sebagai kesimpulan dapat dibuat skhema dari Sistem persamaan linier, yaitu sebagai berikut :

Sistem Persamaan Linier

Non Homogen Homogen

mempunyai jawab tak punya jawab Selalu ada jawab (consistent) (inconsistent)

12. Transformasi Linier a. Definisi

Pandanglah X = [x11, x12, …, xn] dan Y = [y1, y2, …, yn] sebagai dua vektor dalam ruang Rn (F) dengan keadaan koordina relatif untuk baris dari space yang mana.

Andaikan koordinat dari X dan Y dihubungkan oleh : y1 = a11 x1 + a12 x2 + … + a1n xn

y2 = a21 x1 + a22 x2 + … + a2n xn (10)

… … … y2 = a21 x1 + a22 x2 + … + a2n xn

atau Y = AX dimana A = [aij] dalam F

Jadi persamaan (10) adalah sebuah transformasi T yang mana transformasi ini mentransformasikan setiap vektor X dari Rn _{(F) ke vektor Y yang lain dari} space yang sama, maka transformasi disebut bayangan (image).

Jika dalam persamaan (10), X, ditransformasikan ke Y1 (X1→ Yo 1) dan X2 ditransformasikan ke Y2 (X2→ Yo 2) dan berlaku :

1. k X1→ k Yo 1 untuk setiap skalar k.

2. k1 X1 + k2 X2→ ko 1 Y1 + k2 Y2 untuk tiap pasangan skalar k1 dan k2. Maka transformasi ini disebut transformasi linier.

b. Teorema Dasar (Basic Theorema) Jika dalam transformasi linier (10)

X = [1, 0, …, 0] = V1maka Y = [a11, a21, …, an1]1 atau secara umum :

Jika X = Vj→ Y = [a1j, a2j, …, anj] Jadi :

i. Transformasi linier (10) adalah ditentukan dengan tunggal (unique) dimana bayangan Y1, … Yn dari vektor baris yan diketahui, masing-masing kolom dari A mempunyai koordinat dari bayangan vektor-vektor ini.

ii. Transformasi linier (10) disebut non singularjika bayanan dari vektor-vektor Xi tertentu yang menentukan vektor-vektor-vektor-vektor Yi. Dengan kata lain transformasi ini disebut singular.

iii. Transformasi linier (10) adalah non singular jika dan hanya jika A merupakan matrix dari transformasi non singular.

iv. Transformasi linier yang non singular mentransformasikan vektor-vektor linier independent (dependent) ke vektor-vektor linier independent (dependent).

v. Bayangan transformasi (10) non singular dari vektor space (Rkn (F) adalah vektor space Rkn (F) dengan dimensi vektor space yang tertutup.

Dalam partikulir, transformasi ini adalah sebuah mapping onto dari Rn (F) itu sendiri.

Invers dari Y = AX adalah

X = A-1 Y , A-1 = non singular

mentransformasikan himpunan dari vektor-vektor Y1, Y2, …, Yn yang merupakan komponen-komponen kolom dari A kedalam vektor baris dari space itu.

Hal ini juga disebut transformasi linier.

vi. Vektor dasar Vi dari Rn _{(F) mungkin ditransformasikan kedalam setiap} himpunan dari n vektor-vektor untuk n linier independen dengan transformasi linier yang non singular.

vii. Jika Y = AX mentransformasikan sebuah vektor X ke sebuah vektor Y, Z = BY mentransformasikan Y ke Z dan jika W = CZ mentransformasikan Z ke W, jadi Z = BY = (BA) X menstransformasikan X ke Z dan W = (CBA) X menstransformasikan X ke W.

viii. Bilamana setiap dua himpunan dari n vektor-vektor untuk n linier independent ditentukan, keadaan ini merupakan transformasi linier yang non singular yang mana menstransformasikan vektor-vektor dari satu himpunan ke vektor-vektor dari himpunan yang lain.

Contoh :

Dari suatu transformasi linier Y = AX diketahui A = /

1 3 2 2 1 1

4 2 34 dalam ruang dimensi 3. didapat :

a. Bayangan dari X = [4, 0, 5] adalah :

Y = / 1 3 2 2 1 1 4 2 34 / 4 0 34 = / 1.4 + 3.0 + 2.5 2.4 + 1.0 + 1.5 4.4 + 2.0 + 3.54

= / 14 13 314 = [14, 13, 31]

b. Vektor X yang mempunyai bayangan Y + [4. 0. 5] dapat dicari sebagai berikut : Y = AX AX = Y /1 3 22 1 1 4 2 34 / x x x 4 = / 4 0 54 /TT T 4 = / 1 3 2 2 1 1 4 2 34 a /40 54 Andaikan A = /1 3 22 1 1 4 2 34 A-1 = qr%.s_|s| adj.A = / A A A A A A A A A 4

Dari A didapat : A11 = c1 1 2 3c = 1.3 – 1.2 = 1 A12 = - c2 1 4 3c = - (2.3 – 1.4) = -2

A13 = c2 1 4 2c = (2.2 – 1.4) = 0 A21 = - c3 2 2 3c = - (2.3 – 2.2) = - 5 A22 = c1 2 4 3c = 1.3 – 2.4 = - 5 A23 = - c1 3 4 2c = - (1.2 – 3.4) = 10 A31 = c3 2 1 1c = 3.1 – 2.1) = 1 A32 = - c1 2 2 1c = - (1.1 – 2.2) = 3 A33 = c1 3 2 1c = 1.1 – 3.2) = - 5

Maka adj. A = / 1 −5 1 −2 −5 3 0 10 −54 |A| = e 1 3 2 2 1 1 4 2 3e = 1.1.3 + 3.1.4 + 2.2.2 – 2.1.4 – 1.1.2 – 3.2.3 = -5 Jadi A-1 = /a atat u u at4 at = 7 −_t 1 −_t t 1 −t 0 −2 1 8 /TT T 4 = 7 −_t 1 −_t t 1 −t 0 −2 1 8 /40 54 = 7 −_t . 4 + 1 . 0 + −_t . 5 t . 4 + 1 . 0 + − t . 5 0 . 4 + −2 . 0 + 1 . 5 8 /TT T 4 = 7 −1._t −1_t 5 8 Maka X = Q−1. t , −1t, 5R = 7 −1._t −1_t 5 8

13. Persamaan Karakteristik dari Sebuah Matrik

Bentuk Y = AX dimana vektor Y = [y1, y2, …, yn] ditransformasi linierkan menjadi bentuk :

Dimana : A = [aij] denan i, j = 1, 2, …, n α = skalar

X = [x1, x2, …, xn]

= vektor karakteristik dari A

AX = invarian vektor sesudah transformasi Jadi : α X – AX = 0

(α I – A) X = 0

atau (α - a11) x1 + -a12 x2 + … + -a1n xn= 0 -a21 x1 + (α - a22) x2 + … + -a2n xn = 0

… … … … (11) … … … … -anix1 + -an2 x2 + … + (α - ann) xn = 0 7 ∝ −a − a ⋯ − a −a ∝ −a ⋯ − a ⋯ ⋯ ⋯ ⋯ −a a ⋯ ∝ −a

8

Sistem persamaan linier homoen (11) mempunyai penyelesaian non trivial jika dan hanya jika :

|∝ I − A| = 0 atau |∝ I − A| = 7 ∝ −a11 − a12 ⋯ − a1n −a21 ∝ −a22 ⋯ − a2n ⋯ ⋯ ⋯ ⋯ −an1 an2 ⋯ ∝ −ann

8 = 0

Jika |∝ I − A| diexpansikan (dijabarkan) maka didapat polynomial p (α) dengan

derajat n dalam α yang disebut polynomial (persamaan) karakteristik dari matrix A.

Jadi p (α) = αn _{+ a1α}n-1 _{+ … + an-1+ an-1α + an = 0 (12)}

= |∝ I − A| (13)

Karena berderajat n, maka mempunyai n akar-akar yang disebut akar-akar karakteristik yang juga sering disebut akar-akar laten (latent rosts) dan eigen value. Dan untuk setiap αi dengan i = 1, 2, …, n terdapat penyelesaian untuk xi yang

disebut vektor-vektor karakteristik atau vektor laten (latent vektor) dan eigen vektor.

Misalkan akar-akarnya αi, αi2, …, αn maka p (α) = (α - α2) … (α - αn) (14) Untuk α = 0, maka persamaan (12) menjadi p (0) = an (15) dan persamaan (13) menjadi p (0) = |0 I − A|

= |−A|

= (-1)n|A| (16)

Dari persamaan (15) dan (16) didapat : an = (-1)n|A| = p (0)

dan untuk α = 0, maka persamaan (14) menjadi : p (0) = (0 - α1) (0 - α2) … (0 - αn)

= (-α1) (-α2) … (-αn)

= (-1)n . α1 . α2 … αn (17)

Dari persamaan (16) dan (17) didapat : (-1)n|A| = (-1)n . α1 ,α2, …, αn

|A| = α1 ,α2, …, αn

Jadi jika α1 dengan i = 1, 2, …, n adalah akar-akar karakteristik dari matrix A maka |A| = α1, α2, …, αn. Dan jika αi = α maka persamaan |αi – I – A| = 0 mempunyai penyelesaian non trivial.

14. Matrik Modul

Untuk setiap αi (i = 1, 2, …, n) dari α I-A X = 0 memberikan vektor kolom: X$ = 7 x x … x 8

Maka matrik M = [X1, X2, …, Xn] yang disebut modul. Contoh :

Ditentukan : Matrik bujur sangkar : A = /

1 1 −2 −1 2 1

0 1 −14 Penyelesaian : Dari matrik A didapat :

a11 = 1 , a12 = 1 , a13 = -2 a21 = -1 , a22 = 2 , a23 = 1 a31 = 0 , a32 = 1 , a33 = -1 Jadi :

p ∝ = /∝ −11 ∝ −2−1 −12

(α-1).(α-2).(α-1)+(-1).(-1).0+2.1.(-1).(α-2).0–(α-1).(-1).(-1)–(-1).1.(α+1) = 0 (α-1).(α+1).(α-2) – 2 – (α-1) + (α-1) = 0 (α-1) (α+1) (α-2) = 0 Jadi α-1 = 0 →α1 = 1 α+1 = 0 →α2 = -1 α-2 = 0 →α3 = 2

Maka eigen value adalah α1 = 1 α2 = -1 α3 = 2 Selanjutnya dicari eigen vektornya. Untuk α1 = 1, didapat : P (α1 = 1) = /1 − 11 1 − 2−1 −12 0 −1 1 + 14 / x x x 4 = 0 /0 −1 21 −1 −1 0 −1 2 4 / x x x 4 = / 0 0 04 P1. x + −1 . x + −1 x0. x + −1 . x + 2x 0. x + −1 . x + 2. x S = / 0 0 04 Maka – x2 + 2x3 = 0 (18) x2 – x2 – x3 = 0 (19) – x2 + 2x3 = 0

Dari persamaan (18) dan (19), didapat x1 – 3x3 = 0 x1 = 3x3 x1 = 3x3→ persamaan (19) 3x3 – x2 – x3 = 0 x2 = 2x3 Diambil (dipilih)_ x3 = 1 → x1 = 3.x3 = 3 x2 = 2.x3 = 2

Jadi eigen vektornya adalah : x1 = [x1, x2, x3]1 = [3, 2, 1] = /32 14 Untuk α2 = -1, didapat : P (α2 = -1) = /−1 − 11 −1 − 2−1 −12 0 −1 −1 + 14 / x x x 4 = 0 /−2 −1 21 −3 −1 0 1 0 4 / x x x 4 = / 0 0 04 P1. x + −3 . x + −1 x−2 . x + −1 . x + 2x 0. x + 1 . x + 0. x S = / 0 0 04 Maka -2x2– x3+ 2x3= 0 x1 – 3x2 – 1x3 = 0 (20) x2= 0 x2 = 0 → persamaan (20) -2x1 – 0 + 2.x3 = 0 2x1 = 2x3 x1 = x3 Diambil (dipilih), x3 = 1 → x1 = 1 Jadi eigen vektornya adalah :

X2 = [x1, x2, x3]1 = [1, 0, 1]1

= / 1 0 14 Untuk x3 = 2, didapat : P (α1 = 1) = /2 − 11 2 − 2−1 −12 0 −1 2 + 14 / T T T 4 = 0 /1 −1 21 0 −1 0 −1 3 4 / T T T 4 = / 0 0 04 P1. T + −1 . T + 2T1. T + 0. T + −1 T 0. T + −1 . T + 3. T S = / 0 0 04 Maka x1 – x2 + 2x3 = 0 x1 – x3 = 0 (21) – x2 + 3x3 = 0 Dari persamaan (21) didapat x1 = x3 Diambil (dipilih) x3 = 1 → x1 = x3

= 1 Dan -x2 + 3x3 = 0

x2 = 3

Jadi eigen vektornya adalah : X3 = [x1, x2, x3]1 = [1, 3, 1]1

= / 1 3 14 Maka matrik modul dari A adalah :

M = [X1, X2, X3]1

= /3 1 12 0 3 1 1 14

BAB II

DETERMINAN

1. Permutasi

Kalau ada sejumlah unsur yang berbeda-beda, maka setiap susunan yang mungkin dibentuk dengan unsur-unsur itu disebut permutasi.

a. Banyaknya permutasi pada n unsur ialah n! = n (n-1) (n-2) … 2.1

= 1.2. … (nn-2).(n-1).(n)

b. Dari n unsur ada x unsur yang sama maka banyaknya permutasi ialah : p = n!_x!

c. Dari n unsur, ada sekelompok x unsur yang sama dan sekelompok y unsur lain yang juga sama, maka banyaknya permutasi ialah :

p = _{n! y!}n! Contoh :

Dari bilangan integer a.b.c, maka banyaknya permutasi ialah a.b.c, acb, bpc, bca, cab, cba = 3! = 6 permutasi.

Dan dari bilangan integer 1.2.3.4 maka banyak permutasi ialah 4! = 24 permutasi yaitu :

1 2 3 4 , 2 1 3 4 , 3 1 2 4 , 4 1 2 3 1 3 2 4 , 2 3 1 4 , 3 2 1 4 , 4 2 1 3 2. Inversi Dalam Suatu Permutasi

Dalam satu permutasi jika bilangan integer (index) terbesar mendahului bilangan integer (index) terkecil dikatakan bilangan-bilangan itu membentuk suatu inversi.

Jika inversi tersusun menurut urutan naik, maka dikatakan tidak ada inversi dan permutasinya dikatakan permutasi pokok.

Jika inversi sama, maka permutasi dikatakan sama.

Jumlah inversi dari suatu permutasi ialah bilangan yang menunjukkan berapa kali suatu anka diikuti oleh angka yang lebih rendah nilainya dalam suatu urutan yang normal yaitu urutan dari bilangan yang paling kecil (satu) sampai dengan bilangan yang paling besar (n).

3. Determinan Derajat n

Determinan derajat n ialah n2 bilangan-bilangan yang disusun dalam suatu bujur sangkar yang harga determinannya dapat ditentukan dimana

bilangan-bilangan itu disebut elemen-elemen dari determinan, subscript (index) pertama dari tiap-tiap elemen menunjukkan nomor baris dan subscript kedua dari tiap-tiap elemen menunjukkan nomor kolom serta banyaknya baris dan kolom harus sama yang menunjukkan derajat determinan tersebut. ( Pasukat Sembiring ).

Bentuk umum dari determinan derajat n ialah : |A| = 7

a a a ⋯ a a a a ⋯ a ⋯ ⋯ ⋯ ⋯ ⋯ a a a ⋯ a

8

= za_$%z

dimana aij = elemen-elemen dari determinan

subscript I = i = menyatakan baris = 1, 2, …, n

subscript I = j = menyatakan kolom = 1, 2, …, n.

|A| = C δ% % ⋯% a % a % a % ⋯ a % |

dimana : δ_{% % …%} = ± 1

a % , a % , a % … a % = perkalian elemen-elemen dari dekominan ρ = n! permutasi j1 j2 … jn dari bilangan integer 1, 2, … n. 4. Determinan Derajat Dua

Bentuk umum determinan derajat dua ialah : Qa_a a_{a R , n = 2}

i, j = 1, 2 Penyelesaian :

-Qa_a a_{a R = δ}12 a11 a22 + δ21 a12 a21 = a11 a22 – a12 a21

Penyelesaian ini disebut aturan Cramer. 5. Determinan Derajat Tiga

Bentuk umum determinan derajatnya ialah : /aa aa aa

a a a 4 , n = 3

Penyelesaian : a. / a a a a a a a a a 4 = δ a a a + δ a a a + δ a a a + δ a a a + δ a a a + δ a a a = a a a – a a a – a a a + a a a + a a a – a a a = a a a − a a – a a a − a a + a a a − a a = a Qa_a a_{a R − a Q}a_a a_{a R + a Q}a_a a_{a R}

Berdasarkan penyelesaian (a) dapatlah dianggap penyelesaian determinan derajat tiga terjadi sebagai berikut :

= a a a + a a a + a a a – a a a – a a a a11 – a a a Dimana elemen-elemen yang terletak pada satu garis (gambar panah) di perkalikan dan didepannya diberi tanda seperti pada pangkal tanda panah.

Penyelesaian ini disebut aturan SARRUS. Minor dan Kofaktor

Jika minor dari suatu |A| = za$%z derajat n, elemen-elemen dari salah satu barus dan salah satu kolom dikeluarkan, misalnya baris ke i dan kolom ke j maka sisanya ialah determinan derajat (n-1) yang disebut minor dari aij disingkat denan Mij, sedang xij = (-1)i+j Mij disebut kofaktor dari aij.

Contoh : Diketahui : |A| = /aa aa aa a a a 4 Penyelesaian : 1. Minor : M11 = Qa_a a_{a R}

M12 = Qa_a a_{a R} M13 = Qa_a a_{a R} 2. Kofaktor : ∝ = 1 } |M | = + |M | ∝ = −1 } _{|M |} = -|M | ∝ = −1 } _{|M |} = |M |

Maka |A| = a |M | − a |M | + a |M | = a11α11 + a12α12 + a13α13

Sifat-sifat Determinan

Jika tiap-tiap elemen dari suatu baris (kolom) suatu determinan |A| adalah nol, maka harga |A| = 0.

Bukti :

Setiap hasil kali dari rumus :

|A| = C δ% % ⋯% a % a % a % ⋯ a % |

Akan mengandung elemen nol, jadi masing-masing hasil kali mempunyai nilai nol, sehingga jumlahnya = 0.

Jadi |A| = 0 → terbukti.

Jika tiap-tiap elemen dari satu baris (kolom) dari suatu determinan derajat n = |A| dikalikan dengan bilangan skalar k maka harga determinan setelah tiap-tiap elemen dari satu baris (kolom) dikalikan dengan k sama dengan k kali determinan semula (= |A| = |B|.

Jadi

|B| = k Czδ% % ⋯% a % a % ⋯ a % z |

Contoh :

Baris (kolom) pertama dikalikan k

~

ka ka ka … ka a a a … a

… … … … … a a a … a

~ = k ~

a a a … a a a a … a

⋯ ⋯ ⋯ ⋯ ⋯ a a a … a

~ = ~ ka a a … a ka a a … a ⋯ ⋯ ⋯ ⋯ ⋯ ka a a … a ~

a. i. Jika baris kolom) yang berdekatan dari satu determinan derajat n dipertukarkan maka harga determinan setelah dipertukarkan

≡ |B| = − |A|

ii. Jika baris kolom ke I ditukar dengan baris kolom ke I + p dari satu determinan derajat n = |A| maka harga determinan yang baru = -1 p |A|.

b. Jika dua baris (kolom) yang bersesuaian dari |A| adalah sama, maka |A| = 0. Bukti : Andaikan |A| = k

|B| = k, dimana |B| didapat dari |A| dengan jalan pertukaran dua baris (kolom)

Karena baris (kolom) yang ditukar itu, maka jelas |B| = |A| sehingga k1 = k. Tetapi seharusnya k1 = -k menurut sifat c yang merupakan akibat dari pertukaran dua baris (kolom) dalam

k = - k k + k = 0 2k = 0

k = 0 → |A| = 0 jadi terbukti.

c. Jika elemen-elemen dari dua baris kolom) yang bersesuaian adalah sebanding maka harga determinan = 0.

d. Jika tiap elemen dari baris kolom) pertama dari |A| dinyatakan dalam bentuk binomial aij = bij + cij (j = 1, 2, …, n)

Jadi |A| = C δ% % ⋯% b % + c$% . a % a % ⋯ a % | = C δ% % ⋯% b % . a % a % ⋯ a % | + + C δ% % ⋯% c % . a % a % ⋯ a % |

= ~

b b b … b a a a … a … … … … … a a a … a

~ + ~

c c c … c a a a … a … … … … … a a a … a

~

e. Jika tiap-tiap elemen dari baris (kolom) ke i dari |A| adalah jumlah dari p baris (kolom), jadi |A| dapat dikatakan sebagai jumlah dari p determinan. Elemen-elemen dalam baris (kolom) ke i dari p determinan ini masing-masing ke 1, 2, …, p baris (kolom) dari jumlah baris-baris (kolom-kolom) lain dari |A| ini.

f. Hara dari suatu determinan tidak berubah jika elemen-elemen dari suatu baris (kolom) ke i ditambahkan dengan k kali elemen-elemen yang bersesuaian dari baris kolom) yang lain.

~ ~ a a a ⋯ a a a a ⋯ a ⋯ ⋯ ⋯ ap ap ap ⋯ ap ⋯ ⋯ ⋯ ah ah ah ⋯ ah ⋯ ⋯ ⋯ an an an ⋯ an ~ ~ = ~ ~ a a ⋯ a a a ⋯ a ⋯ ⋯ ⋯ ap ap ⋯ ap ⋯ ⋯ ⋯

a‰ + kaG a‰ + kaG ⋯ a‰ + kaG

⋯ ⋯ ⋯

a a ⋯ a ~ ~

g. Jumlah hasil perkalian dari elemen-elemen suatu baris (kolom) dengan kofaktor-kofaktor dari elemen-elemen yang bersesuaian dari baris (kolom) lainnya dari suatu |A| adalah 0.

a11α11 + a12α12 + a13α13 + … + a1nα1n = |A| = 0

h. Jika ai = 0 untuk I < j dan aij ≠ 0 untuk i ≥ j maka |A| = diagonal pokok. i. Harga dari |A|, dimana jumlah dari perkalian tiap=tiap elemen dari sebuah

baris (kolom) dari |A| dengan kofaktornya adalah sebagai berikut : |A| = ai1 αi1 + ai2 αi2 + … + ain αin

= C a$D ∝$D DE

= aij α1j + a2j α2j + … + anj αnj = C a_D% ∝_D% , i, j = 1, 2, … n

6. Komplemen minor dan komplemen aljabar (Minora and Algebraic complements)

Ditentukan : cA%_$Š, _Š,$‹%‹, _{, …, $}…, %_ŒŒ _{c = ~} a$ ,% a$ ,% … a$ ,% a$ ,% a$ ,% … a$ ,% … … … … a$ ,% a$ ,% … a$ ,% ~

dimana index i1, i2, …, im = menyatakan baris 1, 2, …, n. index j1, j2, …, jm = menyatakan kolom 1, 2, …, n. dan cA%_$Œ•Š, _{Œ•Š, $}%_Œ•‹Œ•‹, _{, …, $}…, %Ž_{Ž c = ~} a$ } ,% } a$ } ,% } … a$ } ,% a$ } ,% } a$ } ,% } … a$ } ,% … … … … a_{$ } ,% }} a_{$ } ,% }} … a_{$ } ,%} ~

dimana index im+1 , im+2 , …, in = menyatakan baris m+1, m+2, … n. indexm+1 , jm+2 , …, jn = menyatakan kolom m+1, m+2, … n.

1 ≤ m < n Maka : cA_$ Š, $‹, …, $Œ %Š, %‹, …, %Œ _{c dan cA} $Œ•Š, $Œ•‹, …, $Ž %Œ•Š, %Œ•‹, …, %Ž _c

disebut komplemen minor dari A.

−1 p cA%_$Š, _{Š, $}%_‹‹, _{, …, $}…, %Œ_{Œ c untuk p= i1 + i2 + … +im + j1 + j2+ … + jm}

Disebut komplemen aljabar dari : cA%_$Œ•Š, _{Œ•Š, $}%_Œ•‹Œ•‹, _{, …, $}…, %Ž_{Ž c}

Dan −1 q cA_$

Œ•Š, $Œ•‹, …, $Ž

%Œ•Š, %Œ•‹, …, %Ž _{c untuk q = im+1+ im+2 + … + in +}

Jm+1 + jm+2 + … + jn Disebut komplemen aljabar dari cA_$

Š, $‹, …, $Œ

%Š, %‹, …, %Œ _c Contoh :

Ditentukan : |A| = |aij|. Penyelesaian: a. Komplemen minor : zA ,_,tz = ca_a a t at c Dan zA ,.,t_{, ,t}z = e a a . a t a a a t a. a. a.t e

b. −1 }t} } zA ,_,tz = − zA ,_,tz

adalah komplemen aljabar dari zA ,.,t_{, ,t}z dan −1 } }.} }.,t z _{, ,.},.,tz = − z _{, ,.},.,tz adalah komplemen aljabar dari z _,t, z

7. Menghitung Harga Determinan

a. Ekspansi Laplace (The Laplace Expansion)

Ekspansi dari suatu determinan |A| dengan derjaat n secara baris (kolom) adalah kejadian khusus dari expansi Laplace. Dengan menggunakan komplemen minor dan komplemen aljabar didapat ekspansi Laplace yaitu sebagai berikut :

|A| = C −1 • | cA%_$Š, _{Š, $}%‹, _{‹, …, $}…, %Œ_{Œ c . cA} $Œ•Š, $Œ•‹, …, $Ž %Œ•Š, %Œ•‹, …, %Ž _c dimana : s = i1+ i2 + … + im + j1 + j2 + … + jm ρ = a … a } _{H $ ’“} minor − minor cA_$%Š, _{Š, $}%_‹‹, _{, …, $}…, %Œ_{Œ c} Contoh : Ditentukan : |A| = ~

a a a a . a a a a . a a a a . a. a. a. a.. ~

Penyelesaian :

Ekspansi menurut minor dari dua baris yang pertama. zA ,_, z komplemennya : zA ,._,.z zA ,_, z komplemennya : zA ,._,.z zA ,._, z komplemennya : zA ,_,.z zA ,_, z komplemennya : zA ,._,.z zA ,._, z komplemennya : zA ,_,.z zA ,._, z komplemennya : zA ,_,.z

Maka : |A| = −1 } } } _zA , , _{z . zA} ,. ,._z + −1 } } } zA ,_, z . zA ,._,.z + −1 } } }.zA ,._, z . zA ,_,.z + −1 } } } zA ,_, z . zA ,._,.z + −1 } } }.zA ,._, z . zA ,_,.z + −1 } } }.zA ,._, z . zA ,_,.z

= zA ,_, z . zA ,._,.z − zA ,_, z . zA ,._,.z + zA ,._, z . zA ,_,.z + zA ,_, z . zA ,._,.z − zA ,._, z . zA ,_,.z + zA ,._, z . zA ,_,.z = ca_a a_a . .c . c a a a_. a_. c + caa a c . ca aa. aa...c + ca_a a_a . .c . c a a a. a. c + c a a a a c . caa. aa...c − c_aa a_a ._.c . ca_a. a_a. c + ca_a a_a ._.c . ca_a. a_a. c = (a11 . a22 – a12 . a21) . (a33 . a44 – a34 . a43) –

(a11 . a23 – a13 . a21) . (a32 . a44 – a34 . a42) + (a11 . a24 – a14 . a21) . (a32 . a43 – a33 . a42) + (a12 . a23 – a13 . a22) . (a31 . a44 – a34 . a41) – (a12 . a24 – a14 . a22) . (a31 . a43 – a33 . a41) + (a13 . a14 – a14 . a23) . (a31 . a42 – a32 . a41). b. Metode Chio

Metode Chio ini sebagai dasar bagi komputer untuk menghitung determinan.

Pandanglah determinan derajat n :

|A| =

a a a ⋯ a a a a ⋯ a a a a ⋯ a ⋯ ⋯ ⋯ ⋯ ⋯ a a a ⋯ a !" " " #

Untuk menghitung harga determinan ini pertama kali dikeluarkan factor a11 dari baris pertama, jadi :

|A| = a qŠŠ qŠŠ qŠ‹ qŠŠ qŠ” qŠŠ ⋯ qŠŽ qŠŠ a a a ⋯ a a a a ⋯ a ⋯ ⋯ ⋯ ⋯ ⋯ a a a ⋯ a ! " " " # = a 1 b b ⋯ b a a a ⋯ a a a a ⋯ a ⋯ ⋯ ⋯ ⋯ ⋯ a a a ⋯ a !" " " # dimana b = qŠ‹ qŠŠ , b = qŠ” qŠŠ , … , b = qŠŽ qŠŠ

selanjutnya elemen-elemen dari baris kedua dari determinan dikurangkan dengan perkalian elemen-elemen baris pertama dan elemen-elemen baris kedua.

|A| = a ~ ~

1 b b ⋯ b a − 1. a a − b . a a − b . a ⋯ a − b . a a − 1. a a − b . a a − b . a ⋯ a − b . a

⋯

a − 1. a a − b . a a − b . a ⋯ a − b . a ~ ~ = a ~ ~ 1 b b ⋯ b 0 a a ⋯ b 0 a a ⋯ b ⋯ 0 a a ⋯ b ~ ~ = a _~~ a a ⋯ a a a ⋯ a ⋯ a a ⋯ a ~ ~

Operasi ini diimbangi lagi dengan cara seperti di atas sehingga terdapat :

|A| = a . a _~~ 1 b ⋯ b 0 a ⋯ a ⋯ ⋯ 0 a ⋯ a ~ ~

= a . a _~~ a ⋯ a ⋯ ⋯ ⋯ a ⋯ a ~ ~ |A| = a a a _~~ 1 ⋯ b 0 ⋯_⋯ ⋯ 0 ⋯ a ~~ = a . a a … a Hasil yang dikerjakan diatas ialah : = a11 kali determinan berderajat (n – 1) = a11 . a kali determinan berderajat (n – 2) = a11 . a22 . a kali determinan berderajat (n – 3) ⋮

= a11 . a . a … a kali determinan berderajat satu.

8. Sistem Persamaan Linier Diselesaikan Dengan Determinan a. Sistem Persamaan Linier Dengan n Persamaan dan n Anu

Sistem persamaan-persamaan linier dalam mana banyaknya m persamaan tidak selalu sama dengan banyaknya n anu.

Jadi mungkin m = n dan m > n, m< n atau m ≠ n. Bentuk umum :

C a$% . a% = c$ $,%E

(1) Dimana aij , ci = constant.

xj = anu (variable)

Himpunan harga-harga (x1, x2, ..., xn)1 atau vektor-vektor penyelesaian disebut penyelesaian dari Sistem persamaan linier (1) jika himpunan ini memenuhi semua Sistem persamaan linier (1).

Kalau mempunyai penyelesaian maka penyelesaian Sistem persamaan linier non homogen dikatakan consistant dan jika tidak mempunyai penyelesaian maka dikatakan inconsistant.

D =

a a a ⋯ a a a a ⋯ a a a a ⋯ a ⋯ ⋯ ⋯ ⋯ ⋯ a a a ⋯ a !" " " #

Jadi : x = •Š • = 7 –ŠŠ qŠ‹ qŠ” ⋯ qŠŽ –‹Š q‹‹ q‹” ⋯ q‹Ž –”Š q”‹ q”” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ –ŽŠ qŽ‹ qŽ” ⋯ qŽŽ 8 7 qŠŠ qŠ‹ qŠ” ⋯ qŠŽ q‹Š q‹‹ q‹” ⋯ q‹Ž q”Š q”‹ q”” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ qŽŠ qŽ‹ qŽ” ⋯ qŽŽ 8 x = •‹ • = 7 qŠŠ –Š qŠ” ⋯ qŠŽ q‹Š –‹ q‹” ⋯ q‹Ž q”Š –” q”” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ –ŽŠ –Ž qŽ” ⋯ qŽŽ 8 7 qŠŠ qŠ‹ qŠ” ⋯ qŠŽ q‹Š q‹‹ q‹” ⋯ q‹Ž q”Š q”‹ q”” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ qŽŠ qŽ‹ qŽ” ⋯ qŽŽ 8 x = •” • = 7 qŠŠ qŠ‹ –Š ⋯ qŠŽ q‹Š q‹‹ –‹ ⋯ q‹Ž q”Š q”‹ –” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ –ŽŠ –Ž –Ž ⋯ qŽŽ 8 7 qŠŠ qŠ‹ qŠ” ⋯ qŠŽ q‹Š q‹‹ q‹” ⋯ q‹Ž q”Š q”‹ q”” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ qŽŠ qŽ‹ qŽ” ⋯ qŽŽ 8

Dan sebenarnya dicari sampai dengan xn. Xn = •_•Ž = 7 qŠŠ qŠ‹ qŠ” ⋯ –Š q‹Š q‹‹ q‹” ⋯ –‹ q_{⋯ ⋯ ⋯ ⋯ ⋯}”Š q”‹ q”” ⋯ –” –ŽŠ –Ž‹ qŽ” ⋯ qŽŽ 8 7 qŠŠ qŠ‹ qŠ” ⋯ qŠŽ q‹Š q‹‹ q‹” ⋯ q‹Ž q”Š q”‹ q”” ⋯ q”Ž ⋯ ⋯ ⋯ ⋯ ⋯ qŽŠ qŽ‹ qŽ” ⋯ qŽŽ 8

Contoh :

Ditentukan : Sistem persamaan linier : 2x + 2x – x – x_. = 1 2x – 4x + 3x + 2x_. = 8 3x + 2x – 2x – 3x_. = 7 x + x – x + x. = 0 Penyelesaian : D = ~ 2 2 − 1 − 1 2 − 4 3 2 3 2 − 2 − 3 1 1 − 1 1 ~ = e−4 32 −2 −32 1 −1 1 e − 2 e 2 3 2 3 −2 −3 1 −1 1 e + −1 e 2 −4 2 3 2 −3 1 1 1 e — 1 e 2 −4 3 3 2 −2 1 1 −1e e−4 32 −2 −32 1 −1 1 e = (-4).(-2).1+3.(-3).1+2.3.(-1)-2.(-2).1-2.(-3).(-1)-3.3.1 = 5 e2 33 −2 −32 1 −1 1 e = 2.(-2).1+3.(-3).1+2.3.(-1)-2.(-2).1-2.(-3).(-1)-3.3.1 = 30 e2 −4 23 2 −3 1 1 −1e = 2.2.1+(-4).(-3).1+2.3.1-2.2.1-2.(-3).1-(-4).3.1 = 36 e2 −4 33 2 −2 1 1 −1e = 2.2.(-1)+(-4).(-2).1+3.3.1-3.2.1-2.(-2).1-(-4).3.(-1) = -1 D = 3.5 – 2.(-30) + (-1) . 36 –(-1) (-1) = 33 D1 = ˜ 1 2 − 1 − 1 8 − 4 3 2 7 2 − 2 − 3 0 1 − 1 1 ˜

D1 = 1 . e−4 32 −2 −32 1 −1 1 e − 2 e 8 3 2 7 −2 −3 0 −1 1 e + −1 e 8 −4 2 7 2 −3 0 1 1 e — 1 e 8 −4 3 7 2 −2 0 1 −1e e−4 32 −2 −32 1 −1 1 e = −4 . −2 . 1 + 3 −3 . 1 + 2.2. −1 − 2. −2 . 1— 4. −3 . −1 − 3.2.1 = 5 e8 37 −2 −32 0 −1 1e = 8. −2 . 1 + 3. −3 . 0 + 2.7 −1 − 2. −2 . 0 − 8. −3 . −1 − 3.7.1 = -75 e8 −4 27 2 −3 0 1 1 e = 8.2.1 + 3. −4 . −3 . 0 + 2.7.1 − 2.2.0 − 8. −3 . 1 − −4 .7.1 = 82 e8 3 27 2 −2 0 1 −1e = 8.2. −1 + −4 . −2 . 0 + 3.7.1 − 3.2.0 − 8. −2 . 1 − −4 . 7. −1 = - 7 D1 = 1 . 5 – 2 . (-75) + (-1) . 82 – (-1) . (-7) = - 66 x = •Š • x = ™™ Maka x = 2 D2 = ~ 2 1 − 1 − 1 2 8 3 2 3 7 − 2 − 3 1 0 − 1 1 ~ = 2 e8 37 −2 −32 0 −1 1 e − 1 e 2 3 2 3 −2 −3 0 −1 1 e + −1 e 2 8 2 3 7 −3 1 0 1 e — 1 e 2 8 3 3 7 −2 1 0 −1e e8 37 −2 −32 0 −1 1e = 8. −2 . 1 + 3. −3 . 0 + 2.7 −1 − 2. −2 . 0 − 8. −3 . −1 − 3.7.1 = -75 e2 33 −2 −32 0 −1 1e = 2. −2 . 1 + 3 −3 . 1 + 2.3 −1 − 2. −2 . 1 − 2. −3 . −1 − 3.3.1 = - 30 e2 8 23 7 −3 1 0 1 e = 2.7.1 + 8. −3 . 1 + 2.3.0 − 2.7.1 − 2. −3 . 0 = 8.3.1 = - 48

e2 8 33 7 −2 1 0 −1e = 2.7. −1 + 8. −2 . 1 + 3.3.0 − 3.7.1 − 2. −2 . 0 − 8.3. −1 = - 27 D2 = 2.(-75) – 1.(-30) + (-1).(-48) – (-1).(-27) = - 99 x = •‹ • x = ašš Maka x = -3 D3 = ~ 2 2 1 − 1 2 − 4 8 2 3 2 7 − 3 1 1 0 1 ~ = 2 e−4 8 22 7 −3 1 0 1 e − 2 e 2 8 2 3 7 −3 1 0 1 e + 1 e 2 −4 2 3 2 −3 1 1 1 e — −1 e 2 −4 8 3 2 7 1 1 0e e−4 8 22 7 −3 1 0 1e = −4 . 7.1 + 8. −3 . 1 + 2.2.0 − 2.7.1 − −4 . −3 . 0 − 8.2.1 = - 82 e2 8 23 7 −3 1 0 1 e = 2.7.1 + 8. −3 . 1 + 2.3.0 − 2.7.1 − 2. −3 . 0 − 8.3.1 = - 48 e2 −4 23 2 −3 1 1 1e = 2.2.1 + −4 . −3 . 1 + 2.3.1 − 2.2.1 − 2 −3 . 1 − −4 . 3.1 = - 36 e2 −4 83 2 7 1 1 0e = 2.2.0 + −4 . 7.1 + 8.3.1 − 8.2.1 − 2.7.1 − −4 . 3.0 = - 34 D3 = 2.(-82) – 2.(-48) + 1.36 – (-1) . (-34) = - 66 x = •” • x = a™™ Maka x = -2 D4 = ~ 2 2 − 1 1 2 − 4 3 8 3 2 − 2 7 1 1 − 1 0 ~

= 2 e−4 3 82 −2 7 1 −1 0e − 2 e 2 3 8 3 −2 7 1 −1 0e + 1 e 2 −4 8 3 2 7 1 1 0e — 1 e 2 −4 3 3 2 −2 1 1 1 e e−4 3 82 −2 7 1 −1 0e = −4 . −2 . 0 + 3.7.1 + 8.2. −1 − 8. −2 . 1 − −4 . 7. −1 − 3.2.0 = - 7 e2 3 83 −2 7 1 −1 0e = 2. −2 . 0 + 3.7.1 + 8.3. −1 − 8. −2 . 1 − 2.7. −1 − 3.3.0 = 27 e2 −4 83 2 7 1 1 0e = 2.2.0 + 9 − 4 .7.1 + 8.3.1 − 8.2.1 − 2.7.1 − −4 . 3.0 = - 34 e2 −4 33 2 −2 1 1 1 e = 2.2. −1 + −4 . −2 . 1 + 3.3.1 − 3.2.1 − 2. −2 . 1 − −4 . 3. −1 = - 1 D4 = 2.(-7) – 2.27 + (-1) . (-34) – 1.(-1) = - 33 x. = •› • x. = a Maka x_. = -1

ii. Jika ai = 0, maka Sistem persamaan linier adalah Sistem persamaan linier homogen dengan n persamaan dan n anu.

Bentuk umum : C a$% . x%= 0 $,%E atau a x + a x + … + a x = 0 a x + a x + … + a x = 0 … … … … a x + a x + … + a x = 0

Jika determinan dari D = aij ≠ 0, maka penyelesaiannya dikatakan penyelesaian trivial (trivial solution) dan jika D = aij = 0, maka penyelesaiannya dikatakan penyelesaian non trivial.

b. Sistem Persamaan Linier Non Homogen Dengan m Persamaan dan n Anu Bentuk Umum : C a$% . x$ = c$ , $E , , … $,%E atau a x + a x + … + a x = c a x + a x + … + a x = c … … … … a x + a x + … + a x = c jadi a x + a x + … + a x − c = 0 a x + a x + … + a x − c = 0 … … … … a x + a x + … + a x − c = 0 atau a x + a x + … + a x + d x } = 0 a x + a x + … + a x + d x } = 0 … … … … a x + a x + … + a x + d x } = 0 dimana : m = n + 1 d1, d2, …, dm = c – c , …, - cm x _} = xm = 1

Jadi x = x = … = xn = xm = 0 dan D = 0, maka penyelesaiannya adalah konsisten yang merupakan penyelesaian tunggal (miqua solution).

Jika m > n, maka dapat diambil (m – n) anu harga-harga yang sembarang, sehingga m anu, yang harus dihitung dari m persamaan. Dengan diambilnya

m − n buah bilangan sembarang maka banyaknya vektor penyelesaiannya adalah tak terhingga (non tham one solution).

Contoh :

Ditentukan : Sistem persamaan linier non homogen dengan 3 persamaan dan 2 anu.

2x + 3x = 1 3x – 2x = d 5x + 6x = 4

Penyelesaian : Sistem persamaan linier yang ditentukan dirobah bentuknya menjadi: 2x + 3x – 1 = 0 3x – 2x – d = 0 5x + 6x – 4 = 0 atau 2x + 3x – 1x = 0 3x – 2x – dx = 0 5x + 6x – 4x = 0 , jika x = 1 maka x = x = 0 dan D = 0. Jadi e 2 3 1 3 −2 −d 5 6 4 e = 0 2.(-2).(-4)+3.(-d).5+(-1).3.6-(-1).(-2).5-2.(-d).6-3.3.(-4) = 0 12 d = 96 d = 8 Maka nilai d = 8.

BAB III

INVERS MATRIK

Beberapa cara untuk mencari invers matrik bujur sangkar.

a. Jika An = matrik bujur sangkar berderajat n dan An-1 _{= invers matrik bujur} sangkar berderajat n,

Maka An . An-1 =In dimana In = matrik satuan berderajat n = matrik invers. Selanjutnya dihitung elemen-elemen dari An-1.

Maka matrik invers An-1 dapat ditentukan. Contoh : Ditentukan : A = Q2 1 4 3R Penyelesaian : Andaikan A-1 = Q_aa a_a .R Maka AA-1 = Q2 1 4 3R Qaa aa.R

= I2a + 1a 2a + 1a. 4a + 3a 4a + 3a.J = I

Maka I2a + 1a_{4a + 3a} 2a + 1a_{4a + 3a}.

.J = Q1 00 1R Jadi : 2a1 + 1a3 = 1

a1 = cu c c. c 4a1 + 3a3 = 0 = Maka a1 = 1 a3 = c. uc c. c = a. } Maka a2 = -2