BahanKuliahMekanikaBahanKuliah1

Mekanika Bahan

PENDAHULUAN

Mekanika adalah suatu ilmu yang mempelajari hubungan antara gaya

yang bekerja pada benda kaku. Dalam mekanika bahan ditekankan pada

kekuatan bahan yang berlawanan dengan mekanika. Kekuatan bahan

berkaitan dengan hubungan antara gaya luar yang bekerja dan pengaruhnya

terhadap gaya dalam benda. Dalam hal ini benda tidak lagi dikatakan kaku

ideal, deformasi meskipun kecil tetap diperhitungkan. Sifat bahan suatu

struktur atau mesin mempengaruhi pemilihan dan ukuran yang memenuhi

kekuatan dan kekakuan.

Perbedaan

antara

mekanika

dengan

kekuatan dapat diperlihatkan pada gambar di

atas. Jumlah momen terhadap titik penumpu

dapat menetapkan harga P untuk dapat

mengungkit

beban

W

tadi.

Disini

kita

menganggap batang cukup rigid dan kuat.

Dalam kekuatan bahan, kita harus menyelidiki

dulu apakah batang tersebut tidak akan patah

atau cukup ulet sehingga batang tersebut tidak

melengkung tanpa beban.

MATERI PERKULIAHAN

A. Tegangan dan Perubahan Panjang Akibat Gaya Normal

Mempelajari Pelbagai sifat bahan, analisa gaya dalam, tegangan normal

dan geser, regangan dan tegangan izin, lingkaran mohr.

B. Tegangan dan Lendutan Akibat Momen Lentur

Mempelajari penurunan rumus lentur, tegangan akibat momen lentur,

lendutan, menentukan lendutan dengan diagram bidang momen.

C. Tegangan dan Lendutan Akibat Gaya Lintang

Mempelajari penurunan rumus geser, tegangan geser maksimum,

lendutan akibat gaya lintang

D. Tegangan Puntir/Torsi

Penurunan rumus puntir, teganngan geser puntir, pelbagai cara

pemecahan.

E. Tekuk

Mempelajari beban kritis, batasan rumus Euler dan rumus Tetmayer,

tekuk pada kolom pendek, langsing, dan kolom beban eksentris.

F. Dasar-dasar Statis Tak Tentu

Mempelajari dasar-dasar statis tak tentu, balok tiga tumpuan, Struktur

balok menerus, pelbagai cara pemecahan.

B. Tegangan dan Lendutan Akibat Momen Lentur

Bila suatu beban vertikal bekerja pada balok yang terletak di atas dua

tumpuan atau pada balok kantilevel, maka balok tersebut akan mengalami lentur,

yang mengakibatkan terjadinya perubahan bentuk pada batang berupa lendutan.

Pada umumnya balok merupakan bagian konstruksi bangunan yang

digunakan untuk mengalihkan beban-beban vertikal menjalar ke arah horisontal

yang menimbulkan lentur, dan mengakibatkan balok mengalami lendutan, yang

akhirnya akan menyebabkan timbulnya tegangan lentur pada penampang balok.

Perhatikan

Gambar 1

. Selembar kertas yang diletakan di atas dua

perletakan, tidak mampu di bebani, akan tetapi bila kertas tersebut dilipat-lipat,

maka kertas tersebut akan menjadi lebih kaku dan mampu dibebani, Mangapa ?

Gambar 1.

Perhatikan

Gambar 2

. Bila sebatang balok kantilever dibebani dengan

beban vertikal P pada ujungnya, maka akan menimbulkan lentur pada balok

tersebut, lentur ini menyebabkan terjadinya perubahan bentuk berupa lendutan,

yang kemudian mengakibatkan timbulnya tegangan pada penampang balok

tersebut, dimana lapisan bagian atas dari penampang balok akan mengalami

tegangan tarik, sedangkan pada bagian bawah balok akan mengalami tegangan

tegangan tekan.

Terdapat beberapa kondisi yang dapat menerangkan lebih jelas tentang

lendutan yang terjadi pada balok kantilevel, mulai dari perubahan lendutan yang

diakibatkan oleh perubahan besarnya beban P, sampai dengan perubahan

panjang, bentuk penampang , jenis bahan, dan cara perletakan penampang

pada balok yang digunakan.

Kondisi tersebut dapat dilukiskan sebagai berikut :

a. Bila beban P diperbesar

b. Bila Panjang balok l diperbesar

c. Bila jenis bahan balok berbeda

d. Bila balok diletakan rebah atau tegak

Gambar 2.

P d2 2P 2l P d d1 l l P d l E1 P d l E2 P d l d l d4

Dari kondisi di atas dapat disimpulkan bahwa lendutan akibat beban terpusat

pada konstruksi batang mempunyai hubungan sebagai berikut:

I

E

n

l

P

k

d

Dimana K merupakan faktor yang tergantung pada bentuk konstruksi, dan I

merupakan faktor penampang balok, n menunjukan bahwa rumus tersebut

bukan fungsi linear.

Selanjutnya pada balok di atas dua perletakan yang dimuati beban P akan

melengkung atau melentur. Lentur ini akan menimbulkan lendutan dan tegangan

pada balok tersebut seperti

Gambar 3

. Perubahan bentuk ini akan menyebabkan

lapisan atas balok mangalami tegangan tekan, sedangkan lapisan bawahnya

akan mengalami tegangan tarik. Sifat ini pula yang ditemui pada balok kantilevel,

batang tepi atas mengalami tegangan tarik dan tepi bawah mengalami tegangan

tekan. Lebih lanjut hal ini menerangkan keadaan sebagai berikut:

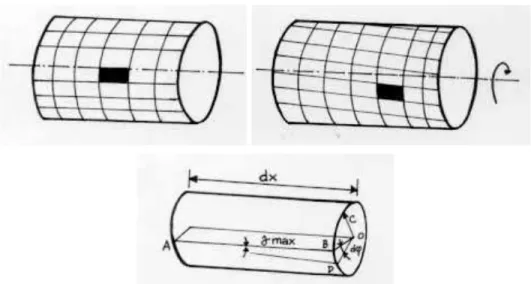
Jika sebatang balok dibebani oleh sebuah gaya lintang, maka balok

tersebut akan melendut dan bila diambil sebagian elemen balok tersebut,

berdasarkan

Hipotesa Bernoulli

dan perilaku elastis bahan sesuai dengan

hukum Hooke

akan memberikan diagram sebagai berikut:

Dari

sini

kita

dapat

menentukan

pembagian tegangan pada penampang

balok, kita dapatkan tegangan tekan pada

serat atas dan tegangan tarik pada serat

bawah.

Tegangan lentur yang bekerja pada

penampang melintang adalah seharga

dengan gaya kopel D dan T yang bekerja

dengan panjang lengan Z.

Kopel ini membentuk momen yang

dibutuhkan

untuk

keseimbangan.

Sedangkan gaya-gaya D san T diibentuk

oleh tegangan total

σ yang bekerja pada

penampang melintang D sama dengan

volume tegangan tekan dan T sama

dengan volume tegangan tarik.

h

Z

h

b

T

h

b

D

3

2

2

2

1

2

2

1

dimana Z adalah jarak antara titik berat volume tegangan tekan dan volume

tegangan tarik terhadap garis normal.

Momen dalam M menjadi :

M

D

Z

T

Z

dimana : D = gaya tekan ; T =

gaya tarik

Untuk penampang segi empat :

6

3

2

2

2

1

bh

2

h

b

h

M

; jika

2

6

1

bh

W

_X

;

W

x

tergantung dari bentuk penampang melintang dan disebut Momen Tahanan,

Pembahasan secara umum teori lenturan dan penurunan rumus tegangan lentur :

Sebatang balok yang melentur dengan penampang melintang sembarang,

bila diamati deformasi pada elemen nya. Menurut Hipotesa Bernolli bahwa jika

titik berat penampang tidak ditengah-tengah tinggi balok, deformasi pada serat

atas dan serat bawah akan berbeda, sedangkan menurut Hukum Hooke

tegangan pada serat atas akan berbeda dengan tegangan pada serat bawah.

Dengan mengambil sebuah elemen dengan panjang l

o

pada batang yang

mengalami lentur, dapat diperoleh gambaran deformasi dan penyebaran

tegangan seperti

Gambar 4.

Gambar 4.

Pada elemen kecil tak terhingga

∆A bekerja sebuah tegangan σ, dan gaya

∆K = σ. ∆A akan menyebabkan bekerjanya momen pada garis netralnya sebesar

∆M = ∆K . y.

Tegangan σ dapat dinyatakan sebagai :

y

y

_b B

;

sehingga

y

A

y

A

K

B B

Dan

y

A

y

y

K

M

B B 2

; oleh karena

tiap-tiap elemen menghasilkan sebuah ∆M , sehingga jika dijumlahkan akan

diperoleh

y

A

y

M

B B 2

; dan karena

B B

y

konstan, maka persamaan

momen dapat ditulis :

y

A

y

M

B

B 2

; jika

I

_X

y

2

A

jakni momen inersia

penampang terhadap sumbu X melalui titik berat penampang, maka tegangan

akibat lentur dapat dihitung dengan menggunakan rumus

y

I

M

X

; dan jika

kita bandingkan dengan rumus umum

y

I

M

σ

X

dengan rumus

M

W

X

,

maka kita dapat memperoleh bentuk hubungan :

y

I

W

X X

yakni antara Momen

Ketahanan dengan Momen Inersia.

Hal yang sama dapat dibuktikan dengan menghitung regangan pada

elemen balok yang mengalami lentur

Gambar 5

:

Gambar 5

Momen M pada

gambar 5a

menimbulkan momen lentur murni pada batang

sederhana AB. Jika batang tidak kaku sempurna serta gaya dalam masih dalam

batas elastik maka sumbu batang akan melendut. Menurut

Hipotesa Bernoulli

bila batas elastis belum dilampaui, maka setiap bagian batang akan tetap datar

seperti sebelumnya. Hal ini berarti bahwa perubahan panjang tiap-tiap lapisan

sejajar dengan sumbu batang berbanding lurus dengan jarak terhadap sumbu

dapat diperoleh perbandingan :

R

y

EF

EF

GH

; sedangkan menurut

Hukum

Hooke

pada lapisan tersebut terjadi regangan :

E

y

; sehingga diperoleh

tegangan pada lapisan tersebut adalah :

y

r

E

y

; hal ini menunjukan bahwa

tegangan pada tiap-tiap lapisan berbanding lurus dengan jarak dari sumbu netral.

Dimana tegangan pada bagian atas sumbu netral bersifat tekan dan tegangan

pada bagian bawah sumbu netral bersifat tarik.

Bila gaya yang bekerja pada penampang dA adalah :

dT

_y

dA

atau

dA

y

r

E

dT

dari persamaan ini dapat dihitung gaya tarik pada bagian tarik

sebesar :

y

dA

r

E

T

h1 0

;

Dengan cara yang sama didapat pula gaya tekan sebesar :

y

dA

r

E

K

h₂

0

Perlu diketahui pada konstruksi yang hanya menderita momen lentur murni

sumbu netralnya terletak pada lapisan yang mengalami tegangan sama dengan

nol, dengan kata lain :

0

0

dA

y

r

E

A

; berarti

0

1 0

dA

y

h

yang berarti sumbu netral didapat bila y = 0,

atau sumbu netral berimpit dengan sumbu batang. Selanjutnya gaya tarik

maupun gaya tekan akan menimbulkan momen terhadap sumbu netral sebesar :

dA

y

r

E

y

dT

dM

2

; dengan demikian jumlah momen untuk seluruh

penampang :

y

dA

r

E

M

A 0 2

; berdasarkan keseimbangan maka momen pada

persamaan diatas akan melawan momen lentur Mx, sehingga dapat diperoleh

tegangan lentur pada lapisan sejauh y dari sumbu netral adalah :

dA

y

y

M

Y X 2

;

I

y

M

Y X

)

(

5

,

18

0

2

75

,

0

20

0

20

kn

V

V

V

x

q

B B B

0

B

M

0

V

m

kn

M

M

M

x

x

q

x

r r r

.

5

,

38

0

2

2

2

75

,

0

2

20

0

2

20

2

Contoh Soal :

1. Diketahui sebuah balok kantilevel seperti gambar dibawa, mempunyai

penampang balok segi empat.

Penampang balok pada pot C - C

Tentukan tegangan lentur maksimum yang terjadi pada sebuah irisan 2 m dari

Ujung bebas

Penyelesaian :

Persyaratan keseimbangan :

maka :

maka :

B Mr L m VB 40 cm 30 cm 2 m C Q = 75kg/m’ C A 20 kn

2. Seperti soal nomor 1, andaikata penampang potongan c-c seperti gambar

berikut :

satuan: mm

Ditentukan titik berat penampang

Dicari momen inersia luasan penampang terhadap sumbu z-z. Maka :

Besarnya tegangan lentur maksimum pada potongan c-c 2m dari ujung bebas

Penampang balok AB

ukuran : mm

Tentukan tegangan lentur maksimum !

Solusi :

Mencari titik berat dan letak garis sumbu netral

Mencari gaya reaksi tumpuan

Agar momen maksimum maka :

Jadi nilai momen maksimum

Tegangan lentur maksimum untuk serat atas

Lendutan Dan Putaran Sudut

Dalam merencanakan sebatang balok akan melibatkan tegangan dan lendutan, hal ini dapat dilihat dari sebatang balok yang ditumpu di atas dua perletakan menahan momen M di kedua ujungnya. Seperti gambar 6, maka balok tersebut akan melendut sekaligus menimbulkan tegangan. ( a ) ( b ) Gambar 6.

Lendutan tersebut dapat dinyatakan dengan suatu persamaan diferensial dalam salib sumbu ortogonal X-Y, dan dianggap bahwa bentuk lengkungan dari lendutan ini pada setiap titik hanya tergantung kepada besarnya momen lentur pada titik tersebut. Dari persamaan :

diperoleh hubungan antara lengkungan, momen dan kekakuan batang dengan persamaan :

untuk menggambarkan lengkungan tersebut dapat dicari persamaan garis lengkung di titik tertentu yakni X, bila garis singgung di titik X membentuk sudut putar θ, maka

atau ds M M

dA

y

r

E

M

A 0 2

EI

M

r

1

dx

dy

tg

dx

dy

arctg

dθ r dx x

dan selanjutnya bila jari-jari lengkungan r dan panjang busur diferensial lengkungan ds akan didapat hubungan persamaan

tanda negatif didapatkan dari kesepakatan bahwa momen lentur positif bila sumbu batang melengkung ke bawah, dengan kata lain titik pusat lengkungan berada di sebelah atas sumbu batang. Dari uraian tersebut dapat dikatakan bahwa sudut θ menjadi semakin kecil bila titik X semakin jauh dari titik A. Dengan kata lain kelengkungan lendutannya sangat rata dengan kelengkungan yang sangat kecil, sudut θ menjadi sangat kecil, sehingga

Karena, bila θ kecil, maka , sehingga

bila persamaan di atas di selesaikan dengan subsitusi, maka akan diperoleh :

dari Gambar 7b, karena maka di dapat:

, dengan mendiferensialkan diperoleh

dengan mengsubsitusi persamaan ini kedalam persamaan :

ds

d

r

1

cos

dx

ds

1

cos

dx

d

ds

d

r

1

dx

ds

ds

dx

dx

dx

dy

darctg

ds

d

r

1

Gambar 7. 2 2 2

dy

dx

ds

2 / 1 2 2 2 / 1 2

1

1

dx

y

d

dx

dy

dx

ds

2 2 2

1

dx

dy

dx

y

d

dx

dy

arctg

dx

d

dx

ds

sehingga pada akhirnya didapatkan :

persamaan ini adalah persamaan garis elastis pada balok yang

sangat lentur, sedangkan seperti kita ketahui bahwa setiap balok konstruksi umumnya mempunyai kekakuan tertentu, sehingga sudut θ menjadi sangat kecil, dan dapat dikatakan juga bernilai sangat kecil, dan nilai sudah dapat diabaikan tanpa mengurangi ketelitian.

Dengan demikian persamaan garis elastis menjadi :

; 2 2

dx

y

d

EI

M

Z X 2 / 3 2 2 2

1

1

dx

dy

dx

y

d

ds

dx

dx

dx

dy

darctg

ds

d

r

2 / 3 2 2 2

1

dx

dy

dx

y

d

EI

M

Z X

dx

dy

tg

2

dx

dy

1

2 2

pers

M

dx

y

d

EI

_X

Contoh Soal :

1. Carilah persamaan garis elastis dari kantilevel yang dimuati beban titik P seperti Gambar dibawah ini.

Momen lentur di titik C adalah :

Dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa :

Untuk x = l , maka θ = 0 dan y = 0, maka akan diperoleh

Sehingga persamaan garis elastis menjadi :

Lendutan terbesar terletak pada titik B, bila x = 0, yaitu :

Dan putaran sudut di titik B menjadi : l C x P B A

x

P

M

_x 2 1 3 1 2 2 2 2 2

6

1

2

1

C

x

C

x

P

y

EI

C

x

P

dx

dy

EI

x

P

dx

y

d

EI

M

dx

y

d

EI

_X 3 2 2 1

3

1

2

1

Pl

C

Pl

C

2 2 3 2 3

2

1

2

1

3

1

2

1

6

1

Pl

Px

EI

Pl

x

Pl

Px

y

EI

3

3

1

Pl

y

EI

maks 2

2

1

Pl

EI

_maks

2. Carilah persamaan garis elastis dari kantilevel yang dimuati beban penuh terbagi rata q seperti Gambar dibawah ini.

Momen lentur di titik C adalah :

Dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa :

Untuk x = l , maka θ = 0 dan y = 0, maka akan diperoleh

Sehingga persamaan garis elastis menjadi :

Lendutan terbesar terletak pada titik B, bila x = 0, yaitu :

Dan putaran sudut di titik B menjadi : 2

2

1

x

q

M

_x 2 1 4 1 3 2 2 2 2 2

24

1

6

1

2

1

C

x

C

x

q

y

EI

C

x

q

dx

dy

EI

x

q

dx

y

d

EI

M

dx

y

d

EI

_X 4 2 3 1

8

1

6

1

l

q

C

l

q

C

)

(

6

1

)

3

4

(

24

1

3 3 4 3 4

l

x

q

EI

l

x

l

x

q

y

EI

4

8

1

ql

y

EI

maks 3

6

1

ql

EI

_maks l C x q B A

3. Carilah persamaan garis elastis dari kantilevel yang dimuati momen M seperti Gambar dibawah ini.

Momen lentur di titik C adalah :

dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa :

Untuk x = l , maka θ = 0 dan y = 0, maka akan diperoleh

Sehingga persamaan garis elastis menjadi :

Lendutan terbesar terletak pada titik B, bila x = 0, yaitu :

Dan putaran sudut di titik B menjadi : l C x B A

M

M

_x 2 1 2 1 2 2 2 2

2

1

C

x

C

x

M

y

EI

C

x

M

dx

dy

EI

M

dx

y

d

EI

M

dx

y

d

EI

2 2 1

2

1

l

M

C

l

M

C

l

M

x

M

EI

l

M

x

l

M

x

M

q

y

EI

2 2 2

)

2

1

(

2

1

2

2

1

l

M

y

EI

_maks

l

M

EI

_maks M

4. Cari persamaan garis elastis dari sebuah balok sederhana yang menumpu di atas dua tumpuan sendi dan rol, dan dimuati beban titik P seperti gambar di bawah ini.

Tentukan persamaan momen setiap bagian dengan batas : Untuk batas :

Untuk batas :

dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa :

Untuk batas :

Untuk batas :

Untuk x = a ,maka nilai lendutan pada titik C sama, baik untuk batas maupun untuk batas , sehingga didapat hasil

P D C A B x b a l

0

x

a

M

X

P

b

x



a

x



M

_X

P

b

x

P

x

a



2 1 3 1 2 2 2 2 2

6

2

C

x

C

x

b

P

y

EI

C

x

b

P

dx

dy

EI

x

b

P

dx

y

d

EI

M

dx

y

d

EI







4 2 3 1

C

C

C

C

0

x

a

a

x



4 3 3 3 3 2 2 2 2 2 2

6

6

2

2

C

x

C

a

x

P

x

b

P

y

EI

C

a

x

P

x

b

P

dx

dy

EI

a

x

P

x

b

P

dx

y

d

EI

M

dx

y

d

EI







0

x

a

a

x



Selanjutnya bila x = 0, di dapat lendutan y = 0 yakni pada tumpuan A, menurut persamaan pada batas , maka diperoleh :

Kemudian bila x = l, di dapat lendutan y = 0 yakni pada tumpuan B, menurut persamaan pada batas , maka diperoleh :

0

x

a

0

0

0

0

0

6

2

4 2 2 2 2 1 3 1 2 2 2 2 2

C

C

C

C

C

x

C

x

b

P

y

EI

C

x

b

P

dx

dy

EI

x

b

P

dx

y

d

EI

M

dx

y

d

EI







a

x





























6

6

0

6

6

0

6

6

2

2

2

2

2 2 1 3 2 2 3 3 3 3 4 3 3 3 3 2 2 3 2 2 2 2 2 2

b

b

P

C

C

b

b

P

C

C

a

P

b

P

C

x

C

a

x

P

x

b

P

y

EI

C

a

x

P

b

P

dx

dy

EI

C

a

x

P

x

b

P

dx

dy

EI

a

x

P

x

b

P

dx

y

d

EI

M

dx

y

d

EI

Dari hasil persamaan – persamaan di atas maka diperoleh persamaan garis elastis dan persamaan putaran sudut sebagai berikut :

Untuk batas : - Persamaan garis elastis

- Persamaan putaran sudut

Untuk batas :

- Persamaan garis elastis

- Persamaan putaran sudut

0

x

a

a

x



2 2 2 2 2 3 2 1 3

6

0

6

6

6

x

b

x

b

P

y

EI

x

b

b

P

x

b

P

y

EI

C

x

C

x

b

P

y

EI













2 2 2 2 2 2 1 2

3

6

6

2

2

x

b

b

P

dx

dy

EI

b

b

P

x

b

P

dx

dy

EI

C

x

b

P

dx

dy

EI













6

6

0

6

6

6

6

6

3 2 2 2 2 2 3 3 4 3 3 3

a

x

P

x

b

x

b

P

y

EI

x

b

b

P

a

x

P

x

b

P

y

EI

C

x

C

a

x

P

x

b

P

y

EI













2

3

6

6

2

2

2

2

2

2

2 2 2 2 2 2 2 2 3 2 2 3 2 2

a

x

P

x

b

b

P

dx

dy

EI

l

b

b

P

a

x

P

x

b

P

dx

dy

EI

C

a

x

P

x

b

P

dx

dy

EI

C

a

x

P

x

b

P

dx

dy

EI













5. Cari persamaan garis elastis dari sebuah balok sederhana yang menumpu di atas dua tumpuan sendi dan rol, dan dimuati beban terbagi rata seperti gambar di bawah ini.

Momen lentur di titik C adalah :

Dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa :

Untuk x = 0, maka y = 0, maka akan diperoleh

Berhubung beban adalah beban terbagi rata penuh, menghasilkan persamaan momen berbentuk parabola dan puncaknya terletak pada tengah bentang , dimana garis singgung puncak parabola sejajar dengan sumbu batang, sehingga putaran sudut

substitusikan ke persamaan di atas sehingga diperoleh nilai q C A B x l 2

2

1

2

1

x

q

x

q

M

_x



2 1 4 3 1 3 2 2 2 2 2 2 2 2 2

24

12

1

6

4

2

2

2

1

2

1

C

x

C

x

q

x

q

y

EI

C

x

q

x

q

dx

dy

EI

x

q

x

q

dx

y

d

EI

x

q

x

q

dx

y

d

EI

M

dx

y

d

EI

_X









0

2

C

0

dx

dy



2

1

x

24

3 1



q

C

Persamaan garis elastis dan persamaan putaran sudut menjadi :

Lendutan terbesar terletak pada tengah bentang, bila , yaitu :

Dan putaran sudut di tumpuan A dan B menjadi :

)

4

6

(

24

1

)

2

(

24

1

3 2 3 4 3 3

x

x

q

EI

x

x

x

q

y

EI









4

384

5

l

q

y

EI

maks 3

24

1

l

q

EI

_maks



2

1

x

6. Carilah persamaan garis elastis dari balok di atas dua tumpuan yang dimuati momen M seperti Gambar dibawah ini.

Momen lentur di titik C adalah :

dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa :

Untuk x = 0 dan y = 0, di titik A maka diperoleh

Untuk x = l , dan y= 0, di titik B maka diperoleh

Sehingga persamaan garis elastis dan persamaan putaran sudut menjadi :

x

R

M

x A 2 1 3 1 2 2 2 2 2

6

2

C

x

C

x

M

y

EI

C

x

M

dx

dy

EI

x

M

dx

y

d

EI

M

dx

y

d

EI

_X







0

2

C

6

2

6

6

2 3









M

x

M

EI

x

M

x

M

y

EI

x C A B b a l M

6

6

0

6

1 1 3 2 1 3











M

C

C

M

C

x

C

x

M

y

EI

Lendutan maksimum, bila , yaitu :

Dan putaran sudut di titik A dan B menjadi :

7. Carilah persamaan garis elastis dan persamaan putaran sudut dari balok di atas dua tumpuan yang dimuati momen M = 24 tm seperti Gambar dibawah ini, diminta menggambarkan diagram lendutan dan putaran sudutnya.

Momen lentur di titik C adalah :

dengan menggunakan persamaan garis elastis, maka lendutan diperoleh dengan cara seperti dibawa : x C A B b a L = 12 m M = 24 tm













577

,

0

3

3

1

6

2

0

6

2

2 2

x

M

x

M

M

x

M

dx

dy

EI

EI

M

EI

M

B A

3

6





0

dx

dy

x

R

M

x A 2 1 3 1 2 2 2 2 2

6

2

C

x

C

x

M

y

EI

C

x

M

dx

dy

EI

x

M

dx

y

d

EI

M

dx

y

d

EI

X







Untuk x = 0 dan y = 0, di titik A maka diperoleh

Untuk x = l , dan y= 0, di titik B maka diperoleh

Sehingga persamaan garis elastis dan persamaan putaran sudut menjadi :

Diagram lendutan dan putaran sudut didapat dengan memasukan nilai mulai dari 1,00 meter sampai dengan 12 meter kedalam variabel x dari persamaan di atas, dan diperoleh tabel sebagai berikut : Titik x 0 1 2 3 4 5 6 7 8 9 10 11 12 Putaran Sudut 48 . 10 7 47 . 10 7 44 . 10 7 39 . 10 7 32 . 10 7 13 , . 10 7 12 . 10 7 1 . 10 7 16 . 10 7 33 . 10 7 52 . 10 7 73 . 10 7 96 . 10 7 Lendutan 0 47 ,6 . 10 6 93 ,4 .1 0 9 13 5. 10 9 17 0,7 .1 0 9 19 8,4 .1 0 9 21 6. 10 9 22 1,7 .1 0 9 21 3,4 .1 0 9 18 9. 10 9 14 6,7 .1 0 9 74 ,4 .1 0 9 0

Lendutan terbesar didapat, bila atau

0

2

C

7 2 2 7 3 3

10

48

000

.

1

6

2

10

48

3

000

.

1

6

6

x

M

x

M

EI

x

x

x

M

x

M

y

EI









6

6

0

6

1 1 3 2 1 3











M

C

C

M

C

x

C

x

M

y

EI

0

dx

dy

7 7 2 7 2 2

10

25

,

22170

928

.

6

10

48

000

.

1

0

10

48

000

.

1

6

2

y

EI

lendutan

dengan

A

titik

dari

meter

x

x

x

M

x

M

EI





Lendutan dengan integrasi persamaan gaya lintang dan persamaan beban

Persamaan diferensial dasar untuk kurve lendutan suatu balok adalah :

Persamaan ini dapat diintegrasikan untuk setiap kasus untuk mendapatkan lendutan. Persamaan lain dapat diperoleh dengan menggantikan momen lentur dengan gaya lintang V dengan intensitas beban q dari beban terdistribusi.

Diketahui hubungan antara M, V dan q, yakni:

bila melakukan diferensiasi pada persamaan dasar kurve lendutan akan diperoleh:

Sehingga diperoleh persamaan diferensial untuk balok prismatis (EI konstan) menjadi:

1

2 2

Pers

M

dx

y

d

EI

_X

V

dx

dM

q

dx

dV

V

dx

dM

dx

y

d

EI

dx

d

2 2

q

dx

dV

dx

y

d

EI

dx

d

2 2 2 2

3

4 4

Pers

q

dx

y

d

EI

2

3 3

Pers

V

dx

y

d

EI

Contoh soal :

1. Tentukan persamaan kurve lendutan pada balok kantilever AB dengan distribusi pembebanan segi tiga, dengan intensitas maksimum q0, dan tentukan lendutan dan putaran sudut di titik B.

Penyelesaian :

Intensitas beban distribusi dinyatakan dengan persamaan :

Dengan menggunakan persamaan ke 3 :

Integrasi pertama persamaan 3

Untuk x = l maka gaya lintang V = 0, sehingga

Subsitusikan nilai C1 ke persamaan di atas : l x q0 B A









x

q

q

x

q

q

x x 0 0

:

:

1 2 0 0 3 3 0 0 0 0 0 4 4 4 4

2

C

x

q

x

q

dx

y

d

EI

x

q

q

x

q

q

x

q

dx

y

d

EI

q

dx

y

d

EI























0 1 1 2 0 0 1 2 0 0 3 3

2

1

2

0

2

q

C

C

q

q

C

x

q

x

q

dx

y

d

EI

2 2 0 3 3 2 2 0 0 2 0 0 3 3

2

2

2

2

2

1

2

x

x

q

dx

y

d

EI

x

x

q

q

x

q

x

q

dx

y

d

EI

















Maka gaya lintang di balok adalah

Dengan mengintegrasikan untuk ke dua kalinya kita mendapat persamaan :

Persamaan ini sama dengan persamaan momen lentur M (pers 1), karena momen lentur adalah nol pada ujuang bebas balok, jakni pada saat x = l, maka diperoleh nilai C2 = 0

Integrasi ketiga menghasilkan

Untuk x = 0 Putaran sudut pada jepitan = 0 atau , diperoleh

Substitusi nilai C3, diperoleh persamaan putarna sudut :

Integrasi ke empat menghasilkan

Untuk x = 0 lendutan pada jepitan = 0 atau y = 0, maka diperoleh

Substitusikan nilai C4, diperoleh persamaan lendutan :

Putaran sudut di ujung jepitan atau pada titik B diperoleh dengan memasukan nilai X = l

adalah sebesar : 2 0

2

x

q

V





2 0 3 3

2

x

q

dx

y

d

EI





2 3 0 2 2

6

x

C

q

dx

y

d

EI





3 4 0 3 0 3 0 2 2

24

6

6

C

x

q

dx

dy

EI

x

q

M

x

q

dx

y

d

EI













0

dx

dy

24

3 0 3



q

C

4 3 0 4 0 3 0 4 0

24

120

24

24

C

x

q

x

q

y

EI

q

x

q

dx

dy

EI













120

4 0 4



q

C

120

24

120

24

24

4 0 3 0 4 0 3 0 4 0















q

x

q

x

q

y

EI

q

x

q

dx

dy

EI

EI

q

B

24

3 0



EI

q

B

30

4 0



2. Tentukan persamaan kurve lendutan untuk balok di atas dua tumpuan dengan beban overstek sebesar P seperti gambar, dan tentukan besar lendutan dan putaran sudut di titik C.

Penyelesaian :

Karena gaya reaksi bekerja diperletakan A dan B, maka terdapat dua persamaan diferensial yang berbeda, yakni masing-masing untuk bagian AB dan Bagian BC.

Reaksi pada perletakan A adalah sebesar P/2 dengan arah kebawa, sedangkan pada perletakan B adalah sebesar 3P/2 dengan arah keatas. Dengan melihat gambar di atas ternyata gaya lintang pada bagian AB dan bagian BC masing-masing adalah :

Dengan menggunakan persamaan 2 untuk bagian balok AB,

Integrasi pertama di peroleh

Momen lentur di titik A = 0, pada saat x = 0, maka C1 = 0, sehingga persamaan menjadi 3P/2 P/2 P l/2 C A _B l



x

P

V

AB

;

0

2

2

3

;



x



P

V

_BC 1 2 2 3 3 3 3

2

2

C

x

P

dx

y

d

EI

P

dx

y

d

EI

V

dx

y

d

EI

AB



x

x

P

M

x

P

dx

y

d

EI

0

2

2

2 2

Demikian pula pada bagian BC

Integrasi pertama di peroleh

Momen lentur di titik C = 0 pada saat x = 3l/2, sehingga diperoleh

Sehingga persamaan menjadi

Integrasi selanjutnya akan menghasilkan persamaan putaran sudut : Untuk bagian AB :

dan untuk bagiab BC :

karena putaran sudut di titik B harus sama, pada saat x = l maka :

lanjutkan integrasi perikutnya akan menghasilkan persamaan lendutan : untuk bagian AB : 2 2 2 3 3 3 3

C

x

P

dx

y

d

EI

P

dx

y

d

EI

V

dx

y

d

EI

BC

2

3

2



P

C

2

3

0

2

3

2

3

2 2









P

x

P

M

P

x

P

dx

y

d

EI

3 2 2 2

4

2

C

x

P

dx

dy

EI

x

P

dx

y

d

EI

4 2 2 2

2

3

2

2

3

C

x

P

x

P

dx

dy

EI

P

x

P

dx

y

d

EI





4

3

2

3

2

4

2

3

2

4

4 3 4 2 2 3 2 4 2 3 2











P

C

C

C

P

P

C

P

C

x

P

x

P

C

x

P

5 3 3 3 2

12

4

C

x

C

x

P

y

EI

C

x

P

dx

dy

EI

lendutan pada titik A = 0 pada saat x = 0, sehingga C5 = 0 persamaan menjadi

lendutan pada titik B = 0 pada saat x = l, diperoleh :

substitusi nilai C3 kepersamaan diatas akan diperoleh persamaan lendutan pada bagian AB

dan nilai C4

dan untuk bagian BC :

lendutan di titik B = 0 pada saat x = l,

substitusi nilai C4, maka diperoleh persamaan lendutan pada bagian BC

lendutan di ujuang overstek titik C : x = 3l/2

6 2 2 3 2 2

6

5

4

3

6

6

5

2

3

2

C

x

P

x

P

x

P

y

EI

P

x

P

x

P

dx

dy

EI









x

C

x

P

y

EI

3 3

12

4

6

5

4

3

6

3 6 6 2 2 3







P

C

C

x

P

x

P

x

P

y

EI

12

2 3



P

C

6

5

4

3

12

4

3

2 4 4 2 4 3









P

C

P

C

P

P

C

C

x

P

x

P

y

EI

12

12

2 3



4

6

5

4

3

6

3 2 2 3





P



x

P

x

P

x

P

y

EI

EI

P

C

8

3



Lendutan dan Putaran sudut dengan Metode Superposisi

Metode Superposisi merupakan konsep yang menyatakan bahwa lendutan suatu balok yang dihasilkan oleh beberapa beban yang bekerja secara simultan dapat diperoleh dengan mengsuperposisikan lendutan yang diakibatkan oleh beban yang sama yang bekerja secara terpisah. Hal ini dapat dilihat dari sifat persamaan diferensial kurve lendutan ( Persamaan 1,2, dan 3) yang merupakan persamaan diferensial linear, sehingga penyelesaian persamaan tersebut untuk beberapa kondisi pembebanan dapat ditambahkan secara aljabar atau disebut Superposisi.

Sebagai ilustrasi dari metode superposisi dapat dilihat pada balok sederhana ACB yang terletak pada tumpuan A dan B, dibebani dengan beban terpusat dan beban terbagi rata seperti tergambar.

dengan menggunakan metode superposisi didapatkan efek dari masing-masing beban yang bekerja secara terpisah kemudian digabungkan hasilnya. Untuk beban terbagi rata saja lendutan ditengah bentang dan putaran sudut sebesar :

dan untuk beban terpusta P nilai yang didapatkan sebesar : l/2 P C A B l/2 l/2 C A B l/2 A C B

EI

q

B A

24

3 0 1 1



EI

P

C

48

3 2



EI

P

B A

16

2 2 2



EI

q

C

384

5

4 1



dengan menggabung kedua hasil , maka diperoleh lendutan dan putran sudut akibat beban terpusat dan beban terbagi rata sebesar :

Lendutan dan Putaran Sudut dengan Metode Momen Area

Asumsi yang digunakan dalam menurunkan metode momen area sama dengan yang digunakan dalam menurunkan persamaan diferensial kurve lendutan, dengan menggunakan hubungan antara lengkungan, momen dan kekakuan batang dengan persamaan :

dan selanjutnya bila jari-jari lengkungan r dan panjang busur diferensial lengkungan ds akan didapat hubungan persamaan

sehingga dengan mengsubstitusi kedua persamaan akan diperoleh :

EI

P

EI

q

A A B A

16

24

2 0 2 1





EI

P

EI

q

C C C

48

384

5

4 3 2 1





EI

M

r

1

ds

d

r

1

ds

EI

M

d

r

untuk balok dengan putaran sudut kecil, maka kita dapat mengganti ds dengan dx

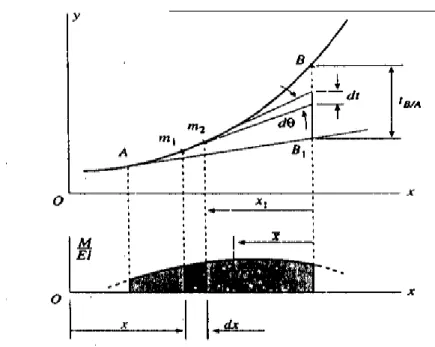
besaran mempunyai interpretasi geomatrik sederhana, tepat dibawah balok pada gambar di atas digambarkan sebuah diagram M/EI. Ternyata diagram M/EI mempunyai bentuk yang sama dengan bidang momen asalkan angka kekakuan EI konstan.

Besaran adalah luas strip yang lebarnya dx didalam diagram M/EI, Dengan mengintegrasikan dθ antara titik A dan B dari kurve lendutan :

Apabila persamaan ini diselesaikan, maka integral di sebelah kiri menjadi θB – θA, yang sama dengan sudut θB/A antara garis singgung di B dan A, sedangkan integral di sebelah kanan sama dengan luas diagram M/EI antara titik A dan B.

= - [ Luas Daigram M/EI antara titik A dan B ]

Tinjau kembali kurve lendutan antara titik A dan B , gambar garis singgung pada titik A berpotongan dengan garis vertikal yang melalui titik B di B1, bila jarak vertikal antara titik B dan B1 diberi notasi tB/A , sebagai deviasi tangensial B terhadap A.

EI dx M

dx

EI

M

d

EI dx M B A B A

EI

dx

M

d

B A A B

EI

dx

M

/

Untuk menentukan deviasi tangesial, diambil dua titik m1 dan m2 pada kurva lendutan, bila sudut antara dua garis singgung dikedua titik adalah dθ dan segmen pada garis BB1 antara kedua garis singgung adalah dt, karena sudut antara garis singgung dengan sumbu x sangat kecil, maka jarak vertikal dt sama dengan x1dθ, dimana x1 adalah jarak horisontal dari titik B ke elemen kecil m1m2, dan karena dθ = Mdx/EI, maka :

Untuk memudahkan hitungan dengan Momen Area methode yang menggunakan diagram Momen sebagai beban, maka perlu diketahu luas dan titik berat bidang-bidang momen yang umum ditemui seperti gambar dibawah ini.

Gambar (a) Gambar (b)

t

t 3 1 b a 3 1

a

b

t

b

Luas

2

1

t

Parabola

t

b

Luas

3

1

b 4 1

b

EI

M

diagram

luas

dari

pertama

Momen

t

EI

dx

M

x

t

EI

dx

M

x

dt

EI

dx

M

x

d

x

dt

A B b a A B B A B A / 1 / 1 1 1

Gambar (c) Gambar (d) Contoh Soal :

1. Hitung Putaran Sudut dan Lendutan di titik B dan sembarang titik dari kantilevel yang dimuati beban titik P seperti Gambar dibawah ini.

Penyelesaian :

Gambar bidang momen akibat beban terpusat P Jadikan bidang momen sebagai beban

Pindahan jepitan ke titik B dan Hitung reaksi di titik B akibat beban bidang momen Besar putaran sudut di titik B = reaksi tumpuan dititik B dibagi angka kekakuan EI

EI

P

EI

P

EI

Momen

Bidang

Luas

B

2

2

1

2







Lendutan dititik B = besarnya momen di titik B akibat beban bidang momen P.x Diagram Bid M P_l

t

Hiperbola

t

b

Luas

4

1

b 5 1

b

t

b

b 8 3

t

b

Luas

3

2

l C x P B A  3 1 2

2

1

2

1







P

Luas

P

Luas

EI

P

EI

P

EI

B

ttk

terhadap

M

Bid

Momen

B 3 2

3

3

2

2

1







utaran sudut pada sembarang titik x :

sedang besarnya lendutan di sembarang titik x :

2. Sebuah kantilever dimuati dengan beban terbagi rata q, hitung putaran sudut dan lendutan di titik B, serta pada sembarang titik x.

Penyelesaian :

Gambar bidang momen akibat beban terbagi rata q Jadikan bidang momen sebagai beban

Pindahan jepitan ke titik B dan Hitung reaksi di titik B akibat beban bidang momen Besar putaran sudut di titik B = reaksi tumpuan dititik B dibagi dengan angka kekakuan EI.

EI

q

EI

q

EI

Momen

Bidang

Luas

B

6

2

1

3

1

3 2







Lendutan dititik B = besarnya momen di titik B akibat beban bidang momen 2 2

2

1

2

1

2

1

x

P

x

P

x

x

P

EI

x









EI

x

P

x

2

2 2



x

x

P

x

x

x

P

EI

_x











3

2

2

1

3

1

2

1





x

P

P

x

P

EI

x

3

1

2

1

6

1

3 2 l C x q B A  4 1  q 2 1

EI

q

EI

q

EI

B

ttk

terhadap

M

Bid

Momen

B

8

4

3

6

1

4 3







putaran sudut pada sembarang titik x :

sedang besarnya lendutan di sembarang titik x :

3. Balok sederhana di atas dua tumpuan, dimuati dengan beban terpusat P, hitung besarnya putaran sudut di kedua tumpuan dan putaran sudut dan lendutan pada sembarang titik X

Penyelesaian :

Gambar bidang momen akibat beban terpusat P dititik C Jadikan bidang momen sebagai beban

Hitung reaksi di titik A dan B akibat beban bidang momen x K 3 3 2 3

6

1

2

1

3

1

6

1

x

q

x

x

q

q

EI

x





EI

x

q

x

6

3 3



4 3 4 3

24

1

6

1

8

1

4

1

6

1

4

3

6

1

x

q

x

q

q

EI

x

x

q

x

q

EI

x x









Rb Ra P D C A B x b a l  b a P  b 3 1

Besar putaran sudut di titik A = reaksi tumpuan di titik A dibagi dengan angka kekakuan EI demikian pula dititik B

Bila nilai Ra dan Rb dibagi dengan angka kekakuan EI, maka akan diperoleh θa dan θb

Lendutan dititik B = besarnya momen di titik B akibat beban bidang momen

EI

q

EI

q

EI

B

ttk

terhadap

M

Bid

Momen

B

8

4

3

6

1

4 3







Besar pitaran sudut pada sembarang titik x adalah = besar gaya lintang akibat beban Bid.M dititik x dibagi dengan angka kekakuan EI

Besar lendutan pada sembarang titik x adalah = besar momen akibat beban Bid M dititik x dibagi angka kekakuan EI :

EI

x

b

x

b

P

x

x

b

P

b

x

b

a

P

EI

x

K

x

R

EI

x x a x

6

3

3

1

2

6

3

1

2 2 2 2

























6

2

1

3

6

2

1

3

a

b

a

P

b

a

P

a

R

b

b

a

P

b

a

P

b

R

b a









EI

a

b

a

P

EI

b

b

a

P

B A

6

6





EI

x

b

b

P

K

R

EI

x a x

6

3

2 2 2

Tekuk

Struktur

pemikul/kolom

beban dapat runtuh oleh berbagai faktor, tergantung dari jenis struktur; kondisi tumpuan; jenis beban; dan bahan yang digunakan, hal ini dapat dicegah dengan merencanakan struktur sedemikian rupa sehingga tegangan maksimum dan peralihan maksimum masih berada dalam batas-batas yang diijinkan, jadi kekuatan dan kekakuan merupakan faktor-faktor yang sangat menentukan dalan suatu perencanaan pemikul/kolom. Sedangkan faktor lain adalah tekuk

Hal-hal yang perlu diperhatikan dalam mempelajari Tekuk pada kolom, yakni :

1. Kemampuan sebuah kolom dalam memikul beban tergantung pada perbandingan panjang dengan ukuran penampangnnya.

2. Beban ultimate/Beban kritis (Pcr) dari sebuah kolom pendek tergantung hanya pada kekuatan bahan yang digunakan dan pada penampang melintangnya.

3. Sebuah kolom panjang/langsing dapat runtuh akibat beban yang jauh lebih kecil dari pada beban ultimate kolom pendek.

4. Tekuk adalah Kondisi dimana pemberian beban pada sebuah kolom panjang mengakibatkan kolom tersebut tiba-tiba mengalami ketidakstabilan dan melengkung ke arah lateral.

5. Jika sebuah kolom mengalami tekuk, maka kolom tersebut tidak dapat lagi memikul beban tambahan. Jika sebuah beban P > Pcr kolom akan mengalami deformasi terus-menerus sampai runtuh.

6. Gaya sentris adalah gaya yang resultantenya jatuh pada sumbu kolom, sedangkan gaya eksentris adalah kombinasi dari gaya aksial dan momen lentur, dimana resultante gaya jatuh diluar sumbu kolom sehingga selain menimbulkan beban sentris pada sumbu kolom juga menimbulkan momen eksentrisiteit, yang dapat menimbulkan bahaya tekuk.

A. Kolom Pendek

Sebuah kolom pendek yang menerima tekanan eksentris seperti Gambar 1. maka beban demikian dapat diuraikan sebagai gaya tekan P yang titik tangkapnya pada sumbu kolom ditambah dengan momen M = P . e terhadap sumbu kolom.

Gambar 1

Dengan uraian demikian maka pada setiap penampang akan mengalami tegangan normal

A

P

1 ; dan tegangan lentur

X

I

Y

M

2 , sehingga tegangan total yang diterima kolom

tersebut adalah : X

I

Y

M

A

P

, rumus tersebut merupakan persamaan linear.

Sedangkan nilai Y dapat bertanda positif maupun negatif, sehingga nilai tegangannya mungkin tarik atau tekan. Untuk Y = C1 (jarak terjauh serat kanan dari titik berat) , maka

persamaan diatas akan menjadi

X Maks

I

C

M

A

P

1 _{, tegangan pada daerah ini menjadi}

tekan maksimum, sedangkan bila Y = - C2 (jarak terjauh serat kiri dari titik berat), maka

persamaan akan menjadi

X Min

I

C

M

A

P

2

Dari persamaan terakhir dapat ditarik kesimpulan bahwa tegangan pada lapisan ini mungkin positif atau negatif. Karena pada umumnya kolom diharapkan selalu mendapatkan tegangan tekan, maka sangat perlu diketahui daerah dimana beban eksentris masih memberikan nilai tegangan tekan pada kolom, biasa daerah tersebut dinamakan Kern atau inti.

Untuk memperoleh batas kern atau inti dapat dilakukan dengan cara sebagai berikut :

c

1

c

2

C1 C2