Buku Ajar Metode Elemen Hingga (1)

(1)

(2)

MODUL AJAR METODE ELEMEN HINGGA

i

PENGANTAR

Segala puji bagi Allah SWT yang telah melimpahkan rahmat serta hidayah-Nya dalam penyelesaian modul ajar Metode Elemen Hingga ini. Mata kuliah Metode Elemen Hingga memiliki 2 mata kuliah prasyarat yaitu Matematika Teknik I dan Mekanika Kekuatan bahan II. Tujuan dari perkuliahan ini adalah agar mahasiswa mampu menjelaskan konsep dasar metode elemen hingga dan memformulasikan problem teknik dalam model serta dapat menyelesaikan pemodelan problem tersebut dalam struktur, frame, shell/plat pada matra garis, 2D, 3D. Materi dalam modul ini disampaikan dengan ringkas, sehingga pembaca tetap diharapkan mempelajari buku-buku yang telah dijadikan sumber pustaka dari modul ini.

Penghargaan dan ucapan terima kasih yang sebesar-besarnya kami sampaikan kepada semua pihak yang telah membantu dalam suksesnya penulisan modul ini. Semoga amal baik semua pihak yang terlibat dalam kegiatan ini diterima oleh Allah SWT, dan semoga modul ini bisa memberikan kontribusi dalam pendidikan nasional.

Malang, Desember 2014 Dr.Eng. Moch. Agus Choiron Dr.Eng. Anindito Purnowidodo Khairul Anam, MSc.

(3)

MODUL AJAR METODE ELEMEN HINGGA ii

DAFTAR ISI

PENGANTAR i DAFTAR ISI ii BAB I. PENDAHULUAN 1

BAB II. METODE KEKAKUAN/PERPINDAHAN 11

BAB III. PERSAMAAN DAN MATRIK KEKAKUAN UNTUK

STRUKTUR 31

BAB IV. KEMIRINGAN DAN LENDUTAN PADA BATANG 63 BAB V. DEFLEKSI/LENDUTAN (SPECIAL CASES) 74

BAB VI. STRUKTUR 89

DAFTAR PUSTAKA RPKPS

(4)

Dr.Eng. Moch. Agus Choiron, Dr.Eng. Anindito P dan Khairul Anam, MSc. Teknik Mesin UB

1

BAB I

PENDAHULUAN

1.1 Sejarah Pekembangan Metode Elemen Hingga

Metode Elemen Hingga, selanjutnya disebut sebagai MEH, adalah metode numerik yang digunakan untuk memecahkan permasalahan dalam bidang rekayasa atau pun bidang fisik lainnya. Permasalahan-permasalahan dalam bidang rekayasa yang dapat dipecahkan dengan metodei ini adalah meliputi analisa struktur, analisa tegangan, perpindahan panas dan masa, dan medan elektromagnetik.

Permasalahan-permsalahan yang melibatkan bentuk geometri, kondisi pembebanan dan sifat mekanik material yang komplek tidak mungkin untuk dipecahkan dengan menggunakan persamaan atau rumus matematis yang biasanya disebut dengan penyelesaian analitis. Penyelesaian analitis ini umumnya memerlukan penyelesaian persamaan deferensial parsial. Oleh karena itu, metode numerik seperti MEH adalah metode yang banyak digunakan untuk memecahkan permasalahan-permasalahan yang komplek tersebut. Hasil yang diperoleh dengan menggunakan metode MEH ini adalah berupa harga pendekatan dari sejumlah titik atau node pada kontinum bodi. Maka dalam pemodelan di dalam MEH, suatu bodi dibagi menjadi beberapa bodi atau unit yang lebih kecil yang disebut dengan elemen, yang mana elemen-element tersebut saling berhubungan dengan elemen lain pada titik-titik simpul elemen atau dikenal dengan node. Proses pembagian ini disebut dengan diskritisasi.

Perkembangan penggunaan MEH dimulai pada masa-masa perang dunia II, sekitar tahun 1940 an. Pada tahun 1941, Hrennikoff dan McHenry (1943) menggunakan elemen satu dimensi berupa elemen garis, yang sekarang dikenal sebagai elemen batang, untuk menganalisa tegangan pada suatu struktur. Selanjutnya, Courant mengenalkan interpolasi atau fungsi, dan metode kekakuan atau metode perpindahan baru dikembangkan pada tahun 1947 oleh Levy. Metode ini sangat menjanjikan dan berguna untuk analisa statika pada struktur pesawat. Pada masa-masa tersebut dilakukan secara manual atau tanpa menggunakan alat

(5)

2 bantu seperti pada masa saat ini. MEH menjadi semakin populer untuk digunakan setelah dikembangkannya prosesor kecepatan tinggi pada komputer.

Analisa dua dimensi menggunakan MEH pertama kali dikenalkan oleh Tuner dan kawan pada tahun 1956. Mereka berhasil menurunkan matrik untuk element truss, element batang, dan elemen-elemen untuk analisa kasus-kasus dua dimensi seperti element segitiga dan segi empat pada kondisi tegangan bisang. Disamping itu, Tuner dan kawan-kawan mengenalkan prosedur yang dikenal sebagai metode kekakuan langsung ( direct stiffness method ) dan matrik kekakuan struktrur. Bersama dengan perkembangan teknologi komputer, hasil kerja dari Tuner dkk menjadi perintis perkembangan persamaan kekakuan elemen hingga yang diekspresikan dalam notasi matrik. Istilah metode elemen hingga pertama kali dikenalkan oleh Clough pada tahun 1960 ketika elemen-elemen segitiga dan segi empat digunakan untuk analisa tegangan bidang (plane stress). Selanjutnya semenjak itu dikembangkan elemen-elemen yang berbentuk tiga dimensi seperti tetrahedral. Umumnya sebagian besar perkembangan elemen hingga pada tahun 1960 an sesuai untuk regangan dan perpindahan kecil pada perilaku material elastis dengan beban statis. Meskipun demikian untuk kasus defleksi yang besar dan analisa termal dikembangkan oleh Turner. Sedangkan untuk kasus-kasus non linier dipelopori oleh Gallagher. Disamping itu, Gallagher dan Padlog juga berhasil mengembangkan MEH untuk memecahkan kasus-kasu bukling pada tahun 1963. Sedangkan untuk kasus viskoelastisitas dikembangkan oleh Zienkiewicz pada tahun 1968.

Pada era 1970-an, dipelopori oleh Belytschko, MEH mampu menyelesaikan kasus-kasus pada struktur yang mengalami deformasi besar dan non linier. Hal ini meningkatkan kemampuan MEH untuk menyelesaikan problem-problem pada struktur. Semenjak awal perkembangan MEH sampai saat ini banyak mengalami kemajuan yang pesat, dan hampir semua analisa tegangan, defleksi dan deformasi di dalam perancangan struktur menggunakan metode MEH terutama untuk geometri dan kondisi beban yang komplek. Bahkan MEH sudah merupakan mata kuliah wajib yang harus ditempuh oleh mahasiswa yang belajar bidang rekayasa. Saat ini penggunaan dan penelitian MEH yang masih relatif baru adalah dalam bidang bioengineering. Dalam bidang ini penggunaan MEH masih

(6)

3 menemukan banyak kesulitan seperti permodelan untuk material dan geometri yang non linier serta tingkat kompleksitas yang relatif lebih tinggi dibanding pada bidang rekayasa. Meskipun demikian saat ini banyak usaha dilakukan untuk meningkatkan kemampuannya dalam menyelesaikan masalah dalam berbagai bidang rekayasa.

1.2 Matrik

Penguasaan metode perhitungan dengan menggunakan matrik adalah sangat perlu di dalam memformulasikan rumus kekakuan elemen dengan sederhana, menyelesaikan dengan cara manual (long hand solution) dari berbagai permasalahan, dan yang penting adalah metode perhitungan dengan menggunakan matrik sangat penting digunakan di dalam pemrograman komputer untuk menyelesaikan perhitungan numeris. Pada sub bab ini diingatkan kembali secara singkat tentang matrik dan notasinya yang umumnya digunakan dalam MEH. Disarankan bagi pembaca yang tidak mengenal metode matrik untuk mempelajari terlebih dahulu.

Matriks adalah suatu kumpulan bilangan yang diatur di dalam kolom dan baris sehingga membentuk segi empat siku-siku. Bilangan bilangan di dalam segi empat tersebut sering disebut disebut dengan elemen atau unsur. Dimensi matrik dinyatakan dengan ordo yang menyatakan banyaknya baris ( arah horizontal) dan banyaknya kolom (arah vertikal) dalam suatu matrik. Jadi suatu matrik yang mempunyai baris berjumlah m dan kolom berjumlah n maka matrik tersebut berordo m x n. Sebagai contoh adalah matrik gaya F, yang akan juga digunakan untuk mendiskripsikan suatu komponen gaya dalam elemen, terdiri dari gaya-gaya pada masing-masing node atau simpul (F1x, F1y, F1z, F2x, F2y, F2z,…….., Fnx, Fny, Fnz). Komponen-komponen gaya tersebut beraksi pada node (1,2,3,….., n ) yang juga mengakibatkan perpindahan (displacement) pada masing-masing node (d1x, d1y, d1z, d2x, d2y, d2z,…….., dnx, dny, dnz). Ke dua matrik tersebut dapat dinyatakan sebagai berikut.

(7)

Dr.Eng. Moch. Agus Choiron, Dr.Eng. Anindito P dan Khairul Anam, MSc. Teknik Mesin UB 4                                     nz ny nx z y x z y x F F F F F F F F F F F . . ] [ ₂ 2 2 1 1 1                                     nz ny nx z y x z y x d d d d d d d d d d d . . ] [ 2 2 2 1 1 1 (1-1)

Tanda subskrip disebelah kanan F dan d mengidentifikasikan nomer node dan arah dari gaya dan perpindahan. Misalnya, F1x adalah menunjukkan komponen gaya pada node 1 dan mempunyai arah yang sama dengan sumbu X. Matrik pada persamaan 1-1 disebut dengan matrik kolom yang mempunyai ordo m x 1. Tanda kurung [ ] digunakan dalam buku ini untuk menandakan matrik kolom. Sehingga

seluruh komponen gaya dan perpindahan di dalam kolom matrik dapat disimbulkan, masing-masing, sebagai [F] dan [d], sedangkan simbol F dan d dengan garis diatasnya menyatakan matrik secara umum artinya dapat berupa matrik kolom atau matrik segi empat.

Penggunaan matrik segi empat siku-siku secara umum dalam buku ini dinyatakan dengan simbol { }. Sebagai contoh matrik untuk menyatakan koefisien kekakuan elemen dan global, masing-masing disimbolkan sebagai {k} dan {K} dan dinyatakan seabagai berikut.

 

                    mn m m n n k k k k k k k k k k k . . . . . . . . . . . . . . . . . . 2 1 2 22 21 1 12 11 (1-2)

 

                    mn m m n n K k K K K K K K K K K . . . . . . . . . . . . . . . . . . 2 1 2 22 21 1 12 11

(8)

5 Pada buku ini akan dipelajari bahwa besar gaya global pada node F dan perpindahan global pada node d tergantung dari harga matrik kekakuan global K, dan dinyatakan sebagai berikut .

d

K

F



(1-3)

Persamaan 1-3 disebut persamaan kekakuan global . Dengan mensubtitusi persamaan 1-2 ke dalam persamaan 1-3 menjadi.

 

                                         nz y x mn m m n n d d d K k K K K K K K K F . . . . . . . . . . . . . . . . . . . . . 1 1 2 1 2 22 21 1 12 11 (1-4)

Pembahasan matrik kekakuan pada berbagai jenis elemen akan dilakukan pada bab selanjutnya. Disamping itu juga akan ditunjukkan suatu prosedur atau urutan bagaimana menyusun matrik kekakuan global K pada berbagai jenis struktur dan bagaimana cara mengetahui suatu perpindahan d pada tiap node. Untuk mengetahui itu maka penyelesaiannya dialkuakn dengan menggunakan metode martik. Jika jumlah nodenya sedikit, maka ordo matriknya juga akan kecil, sehingga dapat diselesaikan dengan cara manual (long hand solution). Akan tetapi jika jumlah nodenya banyak dan perpindahannya lebih dari satu arah, ke arah x, y dan z , maka konsekuensinya ukuran matriknya akan besar, sebagai contoh jika ada 100 node dan arah gaya ke semua arah (x,y,z) kita pertimbangkan, maka matrik kolom gaya F akan mempunyai berjumlah 300 baris, dan untuk matrik perpindahan d mempunyai dimensi yang sama dengan matrik gaya. Selanjutnya matrik kekakuan global mempunyai dimensi 300 X 300. Jika ini terjadi maka penyelesain secara manual sangat tidak efektif dan efisien. Oleh karena itu, untuk menyelesaikannya, dapat menggunakan bantuan komputer.

1.3 Peranan Komputer

Telah disebutkan bahwa komputer sangat berperan besar dalam operasi penyelesaian persamaan dalam MEH. Sebelum pengunaan komputer, meskipun sudah diketahui sebelumnya bahwa metode matrik dan MEH dapat digunakan

(9)

6 untuk menyelesaikan persoalan-persoalan komplek, tetapi penggunaannya tidak praktis dan memerlukan waktu yang sangat lama. Kondisi ini berubah semenjak tahun 1950-an, yang mana pada waktu itu mulai dikembangkan komersial komputer generasi pertama oleh IBM. Bahkan pada saat ini dengan bantuan personal komputer sudah dapat menyelesaikan ribuan persamaan dengan waktu yang sangat singkat dalam hitungan menit. Di samping itu sekarang sudah banyak dikembangkan program-program komputer berbasis elemen hingga. Diantara program – program tersebut bahkan dapat dieksekusi melalui personal komputer (PC) dengan satu processor saja, misalnya prgram ANSYS, Algor, Abaqus, MARC , SAP2000 dan lain-lain. Dengan bantuan kapasitas dan kecepatan memori, kemampuan PC dapat ditingkatkan kemampuannya dalam menyelesaikan persoalan dangan jumlah ribuan varibale tidak diketahui.

1.4 Prosedur Umum MEH

Ada dua pendekatan langsung yang digunakan di dalam MEH untuk menyelesaikan persoalan-persoalan pada mekanika struktur. Pendekatan pertama adalah yang disebut dengan metode gaya atau fleksibelitas. Pada metode ini menggunakan gaya internal sebagai harga yang tidak diketahui dan selanjutnya dipecahkan. Metode yang kedua disebut sebagai metode perpindahan atau kekakuan yang mengasumsikan perpindahan pada node sebagai harga yang tidak diketahui dan selanjutnya dipecahkan. Dari kedua metode ini, metode kekakuan atau perpindahan banyak digunakan, karena formulasinya lebih sederhana untuk analisa struktur. Oleh karena itu di dalam buku ini hanya menerangkan metode kekauan atau perpindahan saja.

Perlu diingat bahwa ada 8 langkah utama di dalam melakukan analisa dengan menggunakan MEH. Langkah-langkah tersebut meliputi :

Langkah ke 1. Memilih jenis elemen dan diskritisasi

Di dalam langkah ini bodi kontinum dibagi menjadi elemen-elemen yang terdiri dari beberapa node. Proses ini disebut diskritisasi. Sebelumnya, kita harus bisa menentukan jenis elemen yang sesuai untuk memodelkan kondisi fisik sebenarnya. Di dalam pendiskritan ini, memungkinkan ukuran elemen berbeda sesuai dengan kondisi geometri dari suatu struktur. Gambar 1.1

(10)

7 menunjukkan contoh dari diskritisasi dari suatu bodi dengan elemen. Gbr. 1.1a menunjukkan suatu bodi poros yang belum dibagi menjadi elemen-elemen, dan Gbr 1.1b menunjukkan diskritisasi dari bodi poros dengan elemen.

a). Bodi poros

b). Diskritisasi bodi poros

Gambar 1-1. Contoh diskritisasi

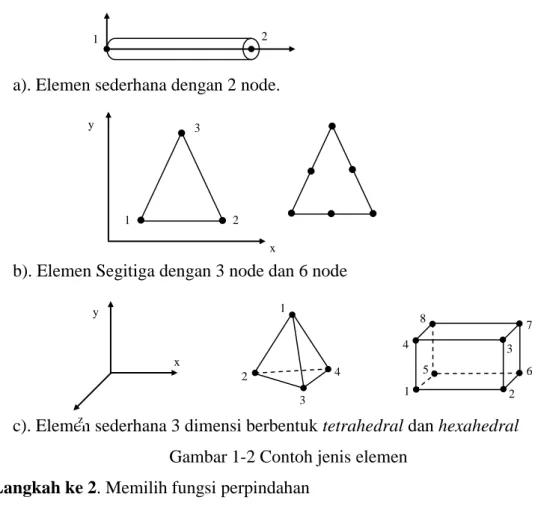
Pemilihan jenis suatu elemen dan dimensi (satu, dua atu tiga dimensi) pada saat melakukan analisa dengan menggunakan MEH tergantung dari beberapa faktor misalnya, kondisi pembebanan. Pemilihan ini harus dilakukan dengan tepat oleh seorang analisis atau disainer. Di samping itu, sering dijumpai untuk suatu kasus tertentu ada jenis elemen yang paling sesuai untuk menyelesaikan suatu kasus tersebut. Yang dimaksud sesuai disini adalah keakurasian hasil, efisiensi dan efektifitas yang berkenaan dengan pemrograman pada komputer. Untuk hal ini,maka pengalangaman dari seorang analisis atau disainer sangat menentukan hasil dari analisa. Gambar 1-2 berikut menunjukkan contoh dari beberapa jenis elemen. Gbr 1-2a adalah jenis elemen yang digunakan untuk merepresntasikan beam atau batang. Untuk Gbr 1-2b adalah contoh elemen dua dimensi yang mana node terletak pada masing-masing sudutnya atau dapat juga terdapat node tambahan diantara sudut-sudutnya. Elemen jenis ini biasa digunakan untuk menganalisa tegangan atau regangan bidang. Gbr 1-2c menunjukkan contoh elemen 3 dimensi sederhana berbentuk tetrhedral dan hexahedral.

(11)

8 a). Elemen sederhana dengan 2 node.

b). Elemen Segitiga dengan 3 node dan 6 node

c). Elemen sederhana 3 dimensi berbentuk tetrahedral dan hexahedral Gambar 1-2 Contoh jenis elemen

Langkah ke 2. Memilih fungsi perpindahan

Pada langkah ini kita menentukan fungsi perpindahan di dalam elemen. Fungsi mendifinisikan harga perpindahan dari tiap-tiap node dan jenis fungsi tersebut tergantung dari jumlah node yang digunakan di dalam elemen. Jenis fungsi yang sering digunakan adalah fungsi linier, kwadratik dan kubik polynomial. Jenis fungsi tersebut sering digunakan karena tidak rumit atau sederhana untuk memformulasikan elemen. Fungsi polinomial bisa didapat dengan menggunakan segitiga Pascal yang ditunjukkan pada Gambar 1-3.

Gambar 1-3 Segitiga Pascal untuk Polinimial

1 2 1 2 3 x y 1 ₂ 3 4 5 6 7 8 x y z 1 2 3 4 linier kwadratik kubik

(12)

9 Langkah ke 3. Mendefinisikan hubungan antara regangan/perpindahan dan tegangan/regangan

Hubungan regangan/ perpindahan dan tegangan/regangan adalah sangat penting untuk menurunkan tiap-tiap rumus elemen hingga. Untuk kasus deformasi elastis (kecil) pada satu dimensi, misalnya, pada arah x dengan perpindahan u, dinyatakan dengan strain, x, sebagai berikut.

dx du

x 

 (1-5)

Selanjutnya hubungan tegangan dan regangan dapat dinyatakan sesuai dengan hukum Hook, yang ditunjukkan pada rumus 1-6, yang mana x menyatakan

tegangan ke arah sumbu x dan E adalah modulus elastisitas.

x

x E

  (1-6)

Langkah ke 4 Menurunkan rumus dan matrik kekakuan elemen

Ada beberapa metode untuk menurunkan rumus dan kekakuan suatu elemen, yaitu yang pertama adalah metode kesetimbangan langsung (Direct

Equilibrium Method). Menurut metode ini, kekakuan matrik dan rumus elemen

yang berhubungan dengan gaya dan perpindahan pada node diperoleh dengan menggunakan kondisi kesetimbangan gaya. Karena rumus ini sederhana dan mudah, maka digunakan untuk menurunkan matrik kekakuan dan rumus elemen untuk elemen-elemen garis atau satu dimensi, misalanya untuk elemen pegas atau batang. Metode selanjutnya adalah metode untuk menurunkan rumus elemen dan matrik kekakuan untuk elemen-elemen dua dimensi dan tiga dimensi. Metode yang digunakan dikenal sebagai metode energi [35]. Penggunaan dari metode-metode tersebut akan ditunjukkan pada bab-bal selanjutnya.

Langkah ke 5. Menggabungkan rumus elemen untuk mendapat rumus global dan menentukan kondisi batas.

Pada langkah ini, rumus untuk satu elemen yang diturunkan pada langkah 4, digbung menjadi rumus global. Rumus global ini mencakup seluruh node yang ada pada suatu bodi.

(13)

10 Langkah ke 6. Menyelesaikan atau memecahkan derajat kebebasan yang tidak

diketahui.

Rumus 1-7 menunjukkan rumus kekakuan global dengan jumlah derajat kebebasan sebanyak n. Di sini kita mencari harga-harga d yang tidak diketahui, dan menentukan harga d sebagai kondisi batas. Contoh kondisi batas, misalnya pada suatu node memodelkan suatu jenis tumpuan jepit, maka perpindahan pada node tersebut ke arah sumbu x, y, z mempunyai harga nol. Sehingga kita bisa menentukan harga d pada node tersebut. Untuk mencari harga d yang tidak diketahui kita bisa menggunakan beberapa metode eleiminasi seperti metode

Gauss, atau iterasi Gauss-Seidel. Untuk menyelsaikan jumlah node yang

banyak atau dimensi matrik yang besar maka penyelesain menggunakan program computer adalah efektif.

 

                                         n nn n n n n d d d K k K K K K K K K F . . . . . . . . . . . . . . . . . . . . . 2 1 2 1 2 22 21 1 12 11 (1-7)

Langkah ke 7. Menghitung harga tegangan dan regangan pada elemen

Setelah dapat mengetahui harga-harga perpindahan pada masing masing node pada langkah ke 6, maka selanjutnya harga regangan dan tegangan dapat diketahui.

Langkah ke 8. Menginterprestasikan hasil

Pada langkah ini kita bisa melakukan analisa hasil pada model untuk

menentukan dimana terjadi tegangan atau regangan yang terbesar pada model. Dari sini kita bisa mengambil keputusan misalnya, bahwa suatu struktur mempunyai kekuatan atau tidak karena kondisi suatu pembebanan tertentu.

(14)

11

BAB II

METODE KEKAKUAN/PERPINDAHAN

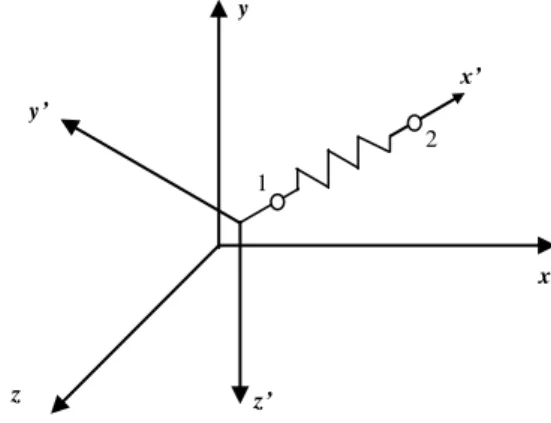
2.1 Difinisi Matrik Kekakuan

Untuk memahami metode kekakuan, maka familiar dengan matrik kekakuan adalah hal yang sangat penting. Matrik kekakuan k’ atau {k} didefinisikan sebagai suatu matrik sedemikian rupa sehingga f’= k’d’ untuk suatu elemen, yang mana k’ menunjukkan matrik kekakuan untuk koordinat lokal (x’, y’, z’) yang berhubungan dengan node d’ atau [d] untuk gaya-gaya f’ atau [f] yang bekerja pada satu elemen. Gambar 2.1 menunjukkan suatu elemen pegas satu dimensi dengan 2 node yang ditinjau dari koordinat lokal (x’, y’, z’) atau koordinat global (x, y, z)perbedaan koordinat lokal dan global pada suatu elemen.

Gambar 2.1 Koordinat lokal dan global

2.2 Penurunan Matrik Kekakuan untuk Elemen Pegas

Dengan menggunakan pendekatan kesetimbangan langsung, di sini diterangkan bagaimana menurunkan matrik kekakuan untuk elemen pegas satu dimensi dengan asumsi pegas tersebut mengikuti hukum Hook dan gaya yang bekerja hanya pada satu arah saja. Langkah-langkah yang digunakan untuk menurunkan matrik kekakuan adalah sesuai dengan langkah-langkah yang diterangkan di Bab I.

Langkah ke 1. Memilih Jenis Elemen

Sesui dengan yang kita ketahui pada langkah ini, jenis elemen pegas kita pilih. Gambar 2.2 menunjukkan jenis elemen pegas yang mempunyai dua node dengan panjang awal atau jarak awal antar node sebesar L. Sedangkan k adalah

1 2 x’ y’ z’ x y z

(15)

12 konstanta material pegas. Jika elemen pegas tersebut dikenakan beban sebesar T, maka masing masing node akan mengalami perpindahan sebesar d’1x dan

d’2x.

Gambar 2.2. Elemen pegas yang diberi beban T Langkah ke 2. Memilih fungsi perpindahan

Di sini kita menentukan fungsi matematis untuk merepresentasikan bentuk elemen yang terdeformasi. Karena sangat sulit untuk mendapat solusi eksak, maka dapat didekati dengan fungsi yang sering digunakan, yaitu polinomial. Karena elemen pegas menahan gaya aksial saja ke arah atau paralel dengan sumbu x’, maka derajat kebebasanya atau perpindahan pada koordinat lokal adalah d’1x dan d’2x. Di sini perpindahannya sesuai dengan fungsi u’ pada

masing-masing node. Selanjutnya kita tentukan fungsi perpindahan u’ ke arah aksial sepanjang elemen pegas. Karena perpindahannnya diasumsikan linier maka ;

' ' a₁ a₂x

u   (1-8)

Perlu diingat bahwa biasanya jumlah koefisien a adalah sama dengan jumlah derajat kebebabasan elemen. Untuk kasus elemen pegas ini, jumlahnya adalah dua, yaitu ke arah aksial atau paralel sumbu x’ saja pada masing-masing node. Jika persamaan (1-8) dinyatakan dalam bentuk matrik maka :

     2 1 } ' 1 { ' a a x u (1-9)

Selanjutnya kita dapat mengekspresikan u’ sebagai fungsi perpindahan d’1x dan

d’2x dengan cara mengevaluasi u’ pada tiap node. Pertama kita tentukan kondisi

batasnya misalkan pada node 1 adalah x’= 0 dan selanjutnya x’=L pada node 2, harga L adalah jarak antara node (Gbr.2.2). Sehingga kita dapat menentukan harga masing-masing koefisien sebagai berikut;

k 1 2 L 2 1 x’ x’ T T d’2x d’1x

(16)

Dr.Eng. Moch. Agus Choiron, Dr.Eng. Anindito P dan Khairul Anam, MSc. Teknik Mesin UB 13 1 1 ' 1 2 1 ' ) 0 ( ' a a x d a u    _x  (1-10a) L a d L a a d L u x x 2 ' 1 2 1 ' 2 ) ( '      (1-10b)

Sehingga harga a2 adalah,

L d d a x x ' 1 ' 2 2   (1-11)

Dengan mensubtitusi masing-masing koefisien ke persamaan (1-8) maka u’ dapat dinyatakan sebagai berikut

' ' ' 1 ' 2 ' 1 x L d d d u x x x          (1-12)

Jika persamaan (1-12) dinyatakan dalam bentuk matrik menjadi sebagai berikut

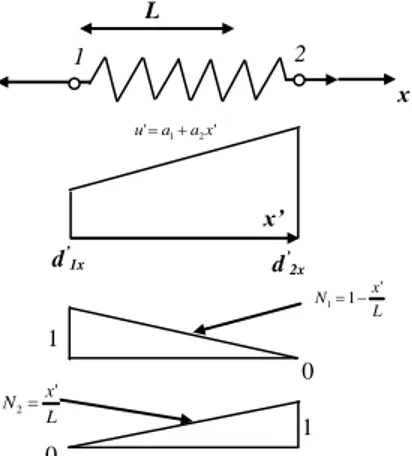
        _' 2 ' 1 } ' ' 1 { ' x x d d L x L x u atau _       _' 2 ' 1 2 1 } { ' x x d d N N u (1-13) Di sini L x N1 1 ' dan L x N2  ' (1-14)

Persamaan (1-14) ini disebut dengan fungsi bentuk, karena N mengekspresikan bentuk fungsi perpindahan yang telah diasumsikan di koordinat x’pada elemen. Jika diasumsikan linier, Gbr. 2.3 menunjukkan fungsi bentuk untuk masing-masing node. Gambar tersebut menunjukkan bahwa pada saat N1= 1 pada node

1 maka pada node 2, N2= 0 dan jika N2= 1 pada node 2 maka N1= 0 pada node

1. Untuk sembarang posisi pada koordinat belaku hubungan N1+ N2 = 1. N

juga disebut fungsi interpolasi, karena dengan cara mengintepolasikan, maka kita dapat memperoleh harga diantara harga node sesuai dengan fungsinya.

Gambar 2.3. Fungsi bentuk masing-masing node

L 2 1 x’ ' ' a1 a2x u  x’ d’1x d’2x L x N11 ' L x N2 ' 1 0 0

(17)

14 Langkah ke 3. Menentukan hubungan tegangan dan regangan

Gambar 2.4 menunjukkan elemen pegas yang mengalami perpanjangan (elongasi) atau terdeformasi disebabkan oleh gaya T. Besar elongasi sebesar d’1x kearah kiri (negatif) dan d’2x kearah kanan (positif) sepanjang sumbu x’.

Gambar 2.4. Perpanjangan pada elemen pegas Besar dari elongasi adalah ;

' 1 ' 2 ) 0 ( ' ) ( ' L u d x d x u      (1-15)

Untuk elemen pegas hubungan gaya dan perpindahan (elongasi) dapat langsung dinyatakan sebagai berikut.

 k

T  (1-16)

dengan mensubtitusi persamaan (1-15) ke persamaan (1-16), maka kita dapat hubungan sebagai berikut.



'



1 ' 2x d x d k T   (1-17)

Langkah ke 4. Menurunkan matrik kekakuan elemen

Selanjutnya kita turunkan matrik kekakuan elemen pegas. Dengan merujuk pada Gbr.2.4, sesuai dengan arah beban dan prinsip keseimbangan, maka dapat didapat ;

T

f₁'_x_'  f₂'_x_' T (1-18)

Dengan mesubtitusikan persamaan (1-18) didapat :



'



' 1 ' ' 2 ' ' 1x k d x d x f T   



'



' 1 ' ' 2 ' ' 2x k d x d x f T    (1-19)

atau dapat ditulis kembali sebagai berikut ;



'



' 2 ' ' 1 ' ' 1x k d x d x f  



'



' 1 ' ' 2 ' ' 2x k d x d x f   (1-20) k 1 2 L 2 1 x’ x’ T T d’2x d’1x

(18)

15 Jika persamaan (1-20) dinyatakan dalam bentuk matrik, menjadi seperti bentuk dibawah ini.                      ' ' 2 ' ' 1 ' ' 2 ' ' 1 x x x x d d k k k k f f _(1-21)

Dari persamaan (1-21) didapat matrik k’ yang merupakan matrik kekakuan lokal. Jika kita perhatikan matrik tersebut adalah simetris yang mana jumlah kolom dan baris sama ( m = n ).

       k k k k k' (1-22)

Langkah ke 5. Menggabungkan rumus elemen lokal menjadi rumus global

Prinsip pada langkah ini adalah menjumlahkan masing-masing kekakuan tiap elemen dan gaya tiap elemen sedemikian rupa atau dinyatakan sebagai berikut’.

 

_

  N e e k K 1 ) ( ' dan

 



  N e e f F 1 ) ( ' (1-23)

Langkah ke 5 ini dijelaskan lebih detail pada sub-bab selanjutnya Langkah ke 6. Menghitung perpindahan node

Pada langkah ini harga perpindahan dapat diketahui setelah diberikan kondisi batas, seperti tumpuan, pada persamaan-persamaan yang telah disusun pada langkah sebelumnya, sehinnga kita dapat menyelesaikan persamaan [F]={K}[D] secara simultan.

Langkah ke 7. Menghitung gaya-gaya pada elemen

Setelah perpindahan dapat diketahui haragnya,maka dengan cara subtitusi kembali pada persamaan (1-20), maka gaya pada masing masing elemen dapat diketahui.

2.3. Penggabungan Elemen Pegas

Struktur-struktur seperti truss, frame dan kontruksi jembatan, terdiri dari komponen-komponen struktur yang saling berhubungan satu dengan yang lainnya. Untuk menganalisanya maka, kekakuan seluruh struktur yang terdiri dari elemen-elemen harus ditentukan terlebih dahulu. Oleh karena itu di sini ditunjukkan bagaimana menyusun matrik kekakuan global (seluruh struktur) yang terdiri dari kekakuan lokal. Gbr. 2.5 menunjukkan dua elemen pegas yang saling berhubungan, dan sesuai dengan langkah 5, matrik kekakuan global akan disusun.

(19)

16 Gambar 2.5. Gabungan dua elemen pegas

Dengan menggunakan persamaan (1-21), maka dapat disusun untuk tiap elemen sebagai berikut; Elemen 1                      ) 1 ( ' 3 ) 1 ( ' 1 ' ' 3 ' ' 1 x x x x d d k k k k f f (1-24)

dan untuk elemen 2 adalah;

                     ) 2 ( ' 2 ) 2 ( ' 3 ' ' 2 ' ' 3 x x x x d d k k k k f f _(1-25)

Selanjutnya, karena ke dua elemen tersebut terhubung pada node 3, maka berlaku hubungan sebagai berikut ;

x x

x d d

d₃(1)_'  ₃(2)_'  ₃ (1-26)

Hubungan pada persamaan (1-26) disebut kontinyuitas atau syarat kompatibelitas . Kembali ke Gbr.2.5, terlihat bahwa karena node 3 adalah menghubungkan eleven 1 dan 2, maka gaya yang bekerja pada node 3 berlaku hubungan seperti berikut ini

) 2 ( ' 3 ) 1 ( ' 3 3x f x f x F   (1-27)

Selanjutnya pada node 1 dan 2 adalah ; ) 2 ( ' 2 2x f x F  dan F₁_x  f₁(_x1_') (1-28)

Dengan mensubtitusikan persamaan (1-24)-(1-26) ke dalam (1-27) dan (1-28), maka didapatkan persamaan berikut ini.



 

(2)



' 2 2 ) 2 ( ' 3 2 ) 1 ( ' 3 1 ) 1 ( ' 1 1 ) 2 ( ' 3 ) 1 ( ' 3 3x f x f x kd x k d x k d x k d x F        ) 2 ( ' 2 2 ) 2 ( ' 3 2 ) 2 ( ' 2 2x f x k d x k d x F    (1-29) ) 1 ( ' 3 1 ) 1 ( ' 1 1 ) 1 ( ' 1 1x f x kd x kd x F    1 f2x 2 k1 k2 1 2 3 f3x

(20)

17 Jika dalam bentuk matrik,

                               ) 1 ( ' 1 ) 2 ( ' 2 ' 3 1 1 2 2 1 2 2 1 1 2 3 0 x x x x x x d d d k k k k k k k k F F F (1-30)

Persamaan (1-30) dapat diatur sedemikian rupa sehingga bisa berurutan dari node 1 sampai ke node 3.                                 ' 3 ' 2 ' 1 2 1 2 1 2 2 1 1 3 2 1 0 0 x x x x x x d d d k k k k k k k k F F F (1-31)

Persamaan (1-31) dapat disederhanakan sebagai berikut ;

 

F 

 

K

 

d (1-32)

yang mana [F] disebut matrik gaya global pada masing-masing node, [d] disebut sebagai matrik perpindahan global dan {K} disebut matrik kekakuan global.

2.4. Penggabungan Matrik Kekakuan dengan Superposisi (Metode Kekakuan Langsung)

Metode Kekakuan Langsung sering digunakan karena lebih mudah untuk menyusun matrik kekakuan global. Metode ini berdasarkan superposisi pada tiap elemen pada suatu struktur . Merujuk pada persamaan (1-24) dan (1-25) yang mana masing-masing elemen kekakuannya adalah sebagai berikut ;

(1-33)

Pada rumus (1-33) simbol perpindahan d diletakkan pada masing-masing baris dan kolom pada matrik k, untuk menunjukkan masing-masing derajat kebebasan pada tiap-tiap node sesuai dengan harga k-nya.

Karena sistem pegas pada Gbr. 2.5 mempunyai 3 derajat kebebasan atau 1 derajat kebebasan pada masing-masing node, maka matrik kekakuan untuk

' 3 ' 1x d x d   ' 3 ' 1 1 1 1 1 1 x x d d k k k k k          ' 2 ' 3x d x d   ' 2 ' 3 2 2 2 2 2 x x d d k k k k k         

(21)

18 masing-masing elemen dapat dinyatakan dalam matrik yang berdimensi 3 x 3, maka persamaan (1-33) menjadi sebagi berikut ini;

Untuk Elemen 1 ;

(1-34)

Untuk Elemen 2 ;

(1-35)

Sesuai dengan kaidah kesetimbangan gaya maka gaya-gaya yang bekerja di tiap-tiap node pada persamaan (1-34) dan (1-35), menghasilkan resultan gaya ( gaya global), seperti berikut ini.

                            x x x x x x x F F F f f f f 3 2 1 ) 2 ( ' 3 ) 2 ( ' 2 ) 1 ( ' 3 ) 1 ( ' 1 0 0 (1-36)

Selanjutnya dengan mensubtitusikan persamaan (1-34) dan (1-35), maka didapatkan persamaan di bawah ini.

                                                        x x x x x x x x x F F F d d d k d d d k 3 2 1 ) 2 ( ' 3 ) 2 ( ' 2 ) 2 ( ' 1 2 ) 1 ( ' 3 ) 1 ( ' 2 ) 1 ( ' 1 1 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 1 0 1 (1-37)

Atau dapat dinyatakan sebagai persamaan di bawah ini

                                    x x x x x x F F F d d d k k k k k k k k 3 2 1 3 2 1 2 1 2 1 2 2 1 1 0 0 (1-38)

Dari persaman (1-38) dapat membuktikan bahwa dengan 3 derajat kebebasan maka akan terdapat matrik kekakuan global, K, yang berdimensi 3 x 3, dan mempunyai matrik kolom perpindahan dan gaya global yang masing-masing jumlah barisnya sama dengan jumlah derajat kebebasan sistem (struktur) dalam hal ini dua pegas yang ditunjukkan di dalam Gbr. 2.5. Perlu dicatat bahwa kunci

' 3 ' 2 ' 1x d x d x d                                ) 1 ( ' 3 ) 1 ( ' 2 ) 1 ( ' 1 ) 1 ( ' 3 ) 1 ( ' 2 ) 1 ( ' 1 1 1 0 1 0 0 0 1 0 1 x x x x x x f f f d d d k ' 3 ' 2 ' 1x d x d x d                                (2) ' 3 ) 2 ( ' 2 ) 2 ( ' 1 ) 2 ( ' 3 ) 2 ( ' 2 ) 2 ( ' 1 2 1 1 0 1 1 0 0 0 0 x x x x x x f f f d d d k

(22)

19 dari penyusunan persamaan kekakuan (1-38) adalah menggabungkan kekakuan tiap-tiap elemen, k, menjadi kekakuan global, K. Untuk menyusun matrik K secara efisien dan efektif dapat dilakukan secara langsung menjumlahkan nilai k pada masing node (Metode Kekakuan Langsung). Untuk itu kita tulis kembali matrik k pada masing-masing elemen dari persamaan (1-33). Seperti dinyatakan sebelumnya karena jumlah derajat kebebasannya adalah 3, maka matrik K pasti berdimensi 3 x 3, oleh karena itu kita langsung bisa membuat matrik dengan dimensi tersebut. Selanjut perhatikan masing-masing sel ( ditunjukkan dengan anak panah ) pada masing masing matrik k untuk masing masing elemen yang disusun kembali pada matrik K sesuai dengan sel nya, seperti dicontohkan pada Gbr. 2.6 berikut ini.

Gambar 2.6, Cara mengisi sel pada matrik K dari matrik k

2.5. Kondisi Batas

Agar supaya persamaan kekakuan global (1-4) dapat diselesaikan maka suatu struktur, misalnya pegas pada Gbr.2.5, harus mempunyai kondisi batas. Kondisi batas, dalam kasus ini adalah tumpuan. Jika struktur tersebut tidak mempunyai kondisi batas maka harga diterminan dari K menjadi singular, yaitu harga diterminannya adalah nol, dan tidak mempunyai matrik invers. Ini berarti struktur tersebut tidak stabil. Ada dua jenis kondisi batas , yaitu, kondisi batas homogen dan non homogen. Kondisi batas homogen terjadi pada tumpuan yang harga perpindahannya nol. Sedangkan untuk non homogen jika perpindahannya mempunyai harga tertentu atau tidak nol.

Untuk mengilustrasikan kondisi batas homogen, kita merujuk pada Gbr. 2.5 dan persamaan kekakuan global, (1-38), yang telah kita turunkan sebelumnya.

' 3 ' 1x d x d   ' 3 ' 1 1 1 1 1 1 x x d d k k k k k          ' 2 ' 3x d x d   ' 2 ' 3 2 2 2 2 2 x x d d k k k k k          x x x d d d₁ ₂ ₃ x x x

d

3 2 1























2 1 2 1 2 2 1 1

0

0 k

k

K

(23)

20 Dari Gbr. 2.5, dapat kita ketahui bahwa kondisi batas pada node 1 atau pada tumpuan, mempunyai harga perpindahan nol, sehingga persamaan (1-38), menjadi sebagai berikut.                                 x x x x x F F F d d k k k k k k k k 3 2 1 3 2 2 1 2 1 2 2 1 1 0 0 0 (1-39)

Jika dijabarkan maka persamaan (1-39) menjadi,

   

d x kd x Fx k₁ 0  0 ₂  ₁ ₃  ₁

 

0 k2d2x k2d3x F2x 0    (1-40)

 

k d x



k k



d x Fx k₁ 0  ₂ ₂  ₁ ₂ ₃  ₃ 

sesuai dengan Gbr. 2.5 harga F1x tidak diketahui, sedangkan harga F2x dan F3x

diketahui.

Jika rumus ke dua dan ke tiga pada persamaan (1-40) dirubah ke bentuk matrik maka,                       _xx F_xx F d d k k k k k 3 2 3 2 2 1 2 2 2 _(1-41)

Dari persamaan (1-39) dan (1-41) diketahui bahwa pada baris dan kolom ke satu pada matrik K pada persamaan (1-39) adalah berharga nol, hal ini terjadi karena pada baris ke satu matrik d merupakan kondisi batas (pada tumpuan, perpindahan berharga nol). Sehingga selanjutnya kita dapat menentukan harga perpindahan pada node 2 dan 3, sebagai berikut.

                  _                         x x x x x x F F k k k k k F F k k k k k d d 3 2 1 1 1 1 2 3 2 1 2 1 2 2 2 3 2 1 1 1 1 1 (1-42)

Jika harga perpindahan d2x dan d3x dapat ditentukan dari persamaan (1-42), maka

besar gaya pada node 1, yaitu F1x dapat dihitung dengan mensubtitusikan

perpindahan tersebut pada persamaan pertama pada (1-40).

   

d x kd x Fx

k₁ 0  0 ₂  ₁ ₃  ₁ atau k₁d₃_x F₁_x (1-43) Dari uraian ini dapat disimpulkan bahwa untuk kondisi batas homogen, baris dan kolom pada matrik K yang mempunyai harga perpindahannya nol dapat dihilangkan .

(24)

21 Selanjutnya dimisalkan pada node 1 ( tumpuan ) pada Gbr.2.7 mempunyai harga perpindahan tertentu, maka kondisi batas struktur tersebut dikatakan tidak homogen. Misalkan pada node 1, mempunyai harga perpindahan, d1x = L.

Gbr.2.7. Kondisi batas non homogen

Karena kondisi batasnya tidak berharga nol, maka persamaan kekakuan dalam bentuk matrik (1-38) dapat ditulis kembali dan menjadi persamaan berikut ini.

                                x x x x x F F F d d L k k k k k k k k 3 2 1 3 2 2 1 2 1 2 2 1 1 0 0 (1-44)

Selanjutnya persamaan dibawah ini hasil penjabaran dari persamaan (1-44).

   

L d x kd x Fx k₁   0 ₂  ₁ ₃  ₁

 

L k2d2x k2d3x F2x 0    (1-45)

 

L k d x



k k



d x Fx k1   2 2  1 2 3  3 

Besar harga gaya pada node 1, F1x, adalah besar gaya pada saat node 1 telah

berpindah sebesar L. Karena besar gaya pada masing-masing node 2 dan 3 diketahui sebesar F2x dan F3x, maka rumus ke dua dan ke tiga pada persamaan

dapat diselesaikan untuk mendapatkan harga d2x dan d3x. Selanjutnya dari

persamaan (1-45) menjadi sebagai berikut.

 

L k2d2x k2d3x F2x

0    (1-46)

 

L k d x



k k



d x Fx

k1   2 2  1 2 3  3



dan selanjutnya untuk menyederhanakan, yang mengandung variabel L dipindah pada sisi kanan persamaan.

x x x k d F d k2 2  2 3  2 (1-47) 1 f2x 2 k1 k2 1 2 3 f3x L

(25)

Dr.Eng. Moch. Agus Choiron, Dr.Eng. Anindito P dan Khairul Anam, MSc. Teknik Mesin UB 22



k k



d F k

 

L d k _x  _x  _x   ₂ ₂ ₁ ₂ ₃ ₃ ₁

Jika dinyatakan dalam bentuk matrik, menjadi ;

 

                        F k L F d d k k k k k x x x x 1 3 2 3 2 2 1 2 2 2 _(1-48)

Dari sini harga d2x dan d3x dapat ditentukan , sehingga dengan menggunkan rumus

pertama persamaan (1-43) harga F1x, dapat diketahui. Dari uraian penyelesaian

pada kondisi batas non homogen, dapat disimpulkan bahwa kolom dan baris pertama matrik K dan baris pertama pada matrik d yang berhubungan dengan kondisi batas tidak dapat dihapus karena merupakan perkalian dengan harga lebih besar dari nol dan hasilnya harus dipindah ke ruas kanan sebelum kita menyelesaikan perpindahan yang tidak diketahui (d2x dan d3x).

Contoh 2.1

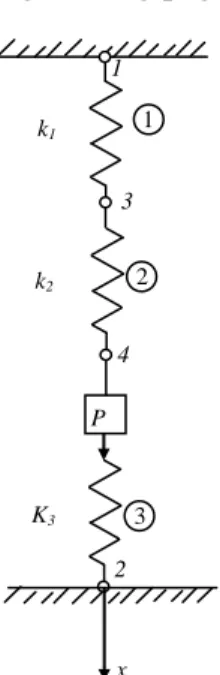
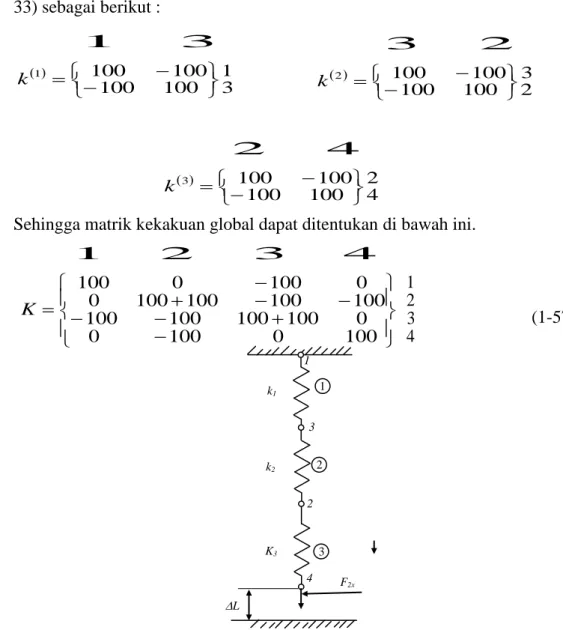
Suatu rangkaian pegas seperti ditunjukkan pada Gbr 2.8, mempunyai harga konstanta pegas k1= 2000 N/m, k2 = 4000 N/m dan k3 = 6000 N/m dan diberi beban P = 10 000 N pada node 4, tentukan ;

a. Matrik kekakuan global,

b. Besar perpindahan pada node 3 dan 4, c. Gaya reaksi pada node 1 dan 2

d. Gaya-gaya yang bekerja pada masing-masing pegas

Gambar 2.8. Rangakian pegas dengan beban P

1 2 k1 k2 1 4 3 P 3 2 K3 x

(26)

23 a). Untuk menyusun matrik kekakuan global, terlebih dahulu kita susun matrik kekakuan tiap tiap elemen pegas dengan merujuk pada persamaan (1-33) sebagai berikut :

Dengan menggunakan model superposisi dan Gbr. 2.6 kita mendapatkan matrik kekakuan global seperti di bawah ini.

                 6000 4000 4000 6000 0 4000 4000 2000 0 2000 6000 0 6000 0 0 2000 0 2000 K 4 3 2 1 (1-49)

b).Karena gaya global berhubungan dengan kekakuan dan perpindahan global, maka sesuai persamaan (1-38), didapatkan hubungan sebagai berikut ;

                                         x x x x x x x x d d d d F F F F 4 3 2 1 4 3 2 1 6000 4000 4000 6000 0 4000 4000 2000 0 2000 6000 0 6000 0 0 2000 0 2000 (1-50)

Dengan menggunakan prinsip penyelesaian kondisi batas homogen, yang mana harga perpindahan pada node 1, d1x = 0 dan pada node 2, d2x = 0, baris pertama

dan kedua, kolom pertama dan kedua dapat dihilangkan sehingga persamaan kekakuan diatas dapat disederhanakan sebagi berikut;

                   x x d d 4 3 6000 4000 4000 4000 4000 2000 10000 0 _(1-51)

Dari sini kita bisa mendaptakan harga d3x = 10/11 m dan d4x = 15/11 m ;

c).Untuk mendapatkan gaya global yang bekerja pada tiap node, maka persamaan (1-50) dapat digunakan kembali dan mensubtitusikan harga d3x dan d4x yang

telah diketahui harganya. 3 1   3 1 2000 2000 2000 2000 1          k 4 3   4 3 4000 4000 4000 4000 2          k 2 4   2 4 6000 6000 6000 6000 3          k 4 3 2 1

(27)

Dr.Eng. Moch. Agus Choiron, Dr.Eng. Anindito P dan Khairul Anam, MSc. Teknik Mesin UB 24                                            11 15 11 10 0 0 6000 4000 4000 6000 0 4000 4000 2000 0 2000 6000 0 6000 0 0 2000 0 2000 4 3 2 1 x x x x F F F F (1-52)

Dengan operasi perkalian matrik pada persamaan (1-52) maka harga gaya global pada masing-masing node adalah ;

(1-53) Elemen 1                    11 10 0 2000 2000 2000 2000 3 1 x x f f (1-54)

Atau jika disederhanakan.

N f _x 11 20000 1   f _x N 11 20000 3  Elemen 2                      11 15 11 10 4000 4000 4000 4000 4 3 x x f f (1-55) N f _x 11 20000 3   f _x N 11 20000 4  Elemen 3                    0 11 15 6000 6000 6000 6000 2 4 x x f f (1-56) N f _x 11 90000 4  f x N 11 90000 2   Contoh 2.2

Gambar 2-9 menunjukkan rangkaian elemen pegas, tentukan (a) Matrik kekakuan global, (b) Perpindahan pada node 3 dan 4, (c) Gaya-gaya global, (d) Gaya local pada masing-masing elemen. Node 1 adalah tetap sedangkan node 4 mempunyai

N F _x 11 90000 2   N F_x 11 110000 4  N F_x 11 20000 1   N F₃_x 0

(28)

25 perpindahan sebesar L = 0,2 m. Konstanta pada semua elemen pegas adalah sama, k = 100 kN/m.

a).Pertama terlebih dahulu kita susun matrik kekakuan tiap-tiap elemen pegas (1-33) sebagai berikut :

Sehingga matrik kekakuan global dapat ditentukan di bawah ini.

(1-57)

Gambar 2.8. Rangakian pegas dengan perpindahan L

b).Dengan menggunakan persamaan (1-38), gaya global dapat ditentukan sebagai berikut ;                                      2 . 0 0 100 0 100 0 0 100 100 100 100 100 100 100 100 0 0 100 0 100 0 0 3 2 4 1 x x x x d d F F (1-58)

Selanjutnya persamaan (1-58) dijabarkan dan jika diubah kedalam bentuk matrik menjadi seperti persamaan (1-59)

1 2 k1 k2 1 2 3 F2x 3 4 K3 L 3 1   3 1 100 100 100 100 1          k 2 3   2 3 100 100 100 100 2          k 4 2   4 2 100 100 100 100 3          k 4 3 2 1                  100 0 100 0 0 100 100 100 100 100 100 100 100 0 0 100 0 100 K 4 3 2 1

(29)

Dr.Eng. Moch. Agus Choiron, Dr.Eng. Anindito P dan Khairul Anam, MSc. Teknik Mesin UB 26                  x x d d 3 2 200 100 100 200 0 20 (1-59)

Sehingga harga perpindahan pada node 2, 3 dan 1 dapat ditentukan

m d _x 15 2 2  d x m 15 1 3 

c). Selanjutnya dengan mensubtitusi harga-harga perpindahan yang sudah diketahui ke persamaan (1-58) untuk menentukan gaya-gaya global.

                                           2 . 0 15 1 15 2 0 100 0 100 0 0 100 100 100 100 100 100 100 100 0 0 100 0 100 4 3 2 1 x x x x F F F F (1-60) 15 100 1   x F F₂_x 0 F₃_x 0 15 100 4x  F

d) Gaya local pada masing-masing elemen

Elemen 1                    15 1 0 100 100 100 100 3 1 x x f f (1-61) N f x 15 100 1   f x N 15 100 3  Elemen 2                      15 2 15 1 100 100 100 100 2 3 x x f f (1-62) N f _x 15 100 3   f _x N 15 100 2  Elemen 3                    2 . 015 2 100 100 100 100 4 2 x x f f (1-63) N f _x 15 100 2   f _x N 15 100 4 

(30)

27 2.6. Pendekatan Energi Potensial

Salah satu metode alternatif untuk menurunkan rumus elemen dan matrik kekakuan elemen adalah berdasarkan prinsip energi potensial minimum. Prinsip ini lebih sesuai untuk menurunkan rumus elemen yang lebih komplek yang mempunyai lebih banyak derajat kebebasan, seperti untuk elemen plain stress atau strain, tegangan aksis simetri, elemen plat bending dan elemen untuk kondisi tiga dimensi. Energi potensial minimum hanya sesuai untuk menurunkan rumus untuk kasus material elastis dan buku ini hanya membahas untuk kasus-kasus pada permodelan material elastis.

Energi potensial, Pe, dari struktur merupakan fungsi dari perpindahan. Pada elemen hingga perpindahan ini terjadi pada node dari suatu elemen dan dinyatakan sedemikian rupa sehingga Pe Pe



d1,d2,...,dn



. Jika Pe

diminimalkan terhadap perpindahan maka akan menghasilkan kondisi setimbang. Untuk elemen pegas, maka akan dihasilkan persamaan f' k'd' seperti yang diturunkan pada sub-bab sebelumnya.

Total energi potensial didefinisikan sebagai jumlah energi regangan dalam, U, dan enegi potensial yang disebabkan oleh gaya luar ;

  U

Pe (1-64)

Energi regangan dalam, U, adalah kapasitas gaya internal atau tegangan untuk melakukan kerja yang mengakibatkan terjadinya regangan di dalal struktur. Sedangkan energi potensial yang disebabkan oleh gaya luar, , adalah body force, gaya traksi permukaan dan gaya yang bekerja pada node untuk melakukan kerja sehingga terjadi deformasi pada struktur.

Kembali pada hubungan linier antara gaya dan perpindahan pada pegas, yaitu F = k.x , yang mana k adalah konstanta pegas dan x adalah perpindahan. Perubahan (diferensial) usaha/kerja dalam atau energi regangan, dU, untuk perpindahan yang sangat kecil pada pegas adalah gaya dikali dengan perubahan perpindahan dimana gaya bekerja, dan dinyatakan sebagai berikut;

Fdx

(31)

28 dari persamaan pegas kita tahu bahwa gaya dinyatakan sebagai F = k.x dan jira hubungan ini disubtitusikan ke persamaan (1-65), maka menghasilkan hubungan di bawah ini.

xdx k

dU . (1-66)

Maka total energi regangannya adalah :

xdx k U x . 0



 atau U k x

 

k x x Fx 2 1 . 2 1 . 2 1 2    (1-67)

Persamaan ini menunjukkan bahwa besar total energi remangan adalah luas area dibawah kurve gaya-perpindahan, seperti ditunjukkan pada Gbr. 2.9.

Gambar 2.9. Hubungan perpindahan dan gaya pada pegas

Jika energi potensial yang disebabkan oleh gaya luar adalah  = - F.x dan dengan mensubtitusikan persamaan (1-67) maka persamaan (1-64) menjadi;

x F x k Pe . . 2 1 2  (1-68)

Selanjutnya kita perhatikan contoh 3 berikut ini untuk memahami konsep dari prinsip energi minimum dengan menganalisa pegas dengan satu derajat kebebasan. Dari contoh ini ditunjukkan bahwa kondisi setimbang dari pegas adalah pada saat energinya minimum.

Contoh 2.3

Dimisalkan ada pegas dengan konfigurasi seperti ditunjukkan pada Gbr.2.10

Gambar 2.10. Pegas yang diberi beban F

k F x F x k F= 2000 N k= 500 N/m 2 1 x

(32)

29 Untuk mengevaluasi energi potencial pada pegas tersebut maka kita dapat menggunakan persamaan (1-68). x F x k P_e . . 2 1 2 

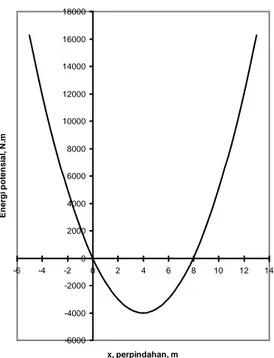
Untuk memudahkan maka selanjutnya kita subtitusikan harga perpindahan, x, misalnya antara – 5 sampai dengan 13, dan selanjutnya dapat kita plot dalam kurve hubungan Pe dan x, seperti dalam Gbr.2.11. Dari gambar tersebut dapat

diketahui harga minimum dari petensial energi, yang mengindikasikan juga bahwa pada kondisi tersebut terjadi kesetimbangan. Dari sini dapat diketahui bahwa kondisi potensial enegi minimum terjadi pada perpindahan, ketika x = 4 m

-6000 -4000 -2000 0 2000 4000 6000 8000 10000 12000 14000 16000 18000 -6 -4 -2 0 2 4 6 8 10 12 14 x, perpindahan, m E n e rg i p o te n s ia l, N .m

Gambar 2.11. Hubungan antara energi potensial, Pe , dan perpindahan, x .

Untuk mengetahui harga energi potensial minimum dapat dilakukan dengan cara menurunkan persamaan energi potensial sebagai berikut;

0    x Pe (1-69) 0 2000 500 . . . 2 1 ₂             _     x F x k x x F x k x Pe (1-70)

Sehingga x = 4 m, dan selanjutnya harga ini disubtitusikan kembali ke persamaan (1-68) untuk mendapatkan harga Energi potensial Pe = -4000 N.m.

(33)

30 Dengan menggunakan prinsip energi potensial minimum maka kita dapat menurunkan rumus matrik kekakuan dari elemen pegas. Dari Gbr. 2.10 yang mana suatu elemen pegas yang dikenai beban F, maka harga energi potensialnya dapat dinyatakan sebagai berikut ini;





' 2 ' 2 ' 1 ' 1 2 ' 1 ' 2 2 1 x x x x x x e k d d f d f d P     (1-71)

Yang mana d₂'_xd₁'_xadalah deformasi dari elemen pegas, dan jika persamaan (1-71) dijabarkan maka menjadi;





' 2 ' 2 ' 1 ' 1 2 ' 1 ' 1 ' 2 2 ' 2 2 2 1 x x x x x x x x e k d d d d f d f d P      (1-72)

Dengan menggunakan prinsip energi potensial minimum, maka persamaan (1-72) diturnkan secara parsial sesuai dengan masing-masing node nya, menjadi sebagai berikut ini;



2 2



0 2 1 1 ' 1 ' 1 ' 2        x x x e f d d k x P (1-73)



2 2



0 2 1 2 ' 2 ' 1 ' 2       x x x e f d d k x P

Jika disederhanakan menjadi



 



' 1 ' 2 ' 1 ' 1 ' 2x d x k d x d x f x d k      (1-74)



 



' 2 ' 2 ' 1 ' 1 ' 2x d x k d x d x f x d k     

Atau jika dinyatakan dalam bentuk matrik, sebagai berikut ;

                   ' 2 ' 1 ' 2 ' 1 x x x x f f d d k k k k _(1-75)

Dari persamaan diketahui bahwa matrik kekakuan yang diturunkan dengan menggunakan prinsip energi potensial minimum mempunyai hasil yang sama dengan hasil yang didapat dengan menggunakan metode langsung.

(34)

31 BAB III

PERSAMAAN DAN MATRIK KEKAKUAN UNTUK STRUKTUR

Pada Bab II dijelaskan bagaimana menurunkan rumus elemen dan matrik kekakuan pada elemen pegas dengan satu derajat kebebasan. Pada Bab III ini akan dijelaskan bagaimana menurunkan rumus dan matrik kekakuan elemen lebih dari satu derajat kebebasan pada koordinat lokal atau global di suatu struktur berdasarkan metode kekakuan langsung. Pertama akan dijelaskan penurunan rumus dan matrik kekakuan batang atau truss elastis dengan menggunakan tahapan yang telah dijelaskan pada Bab II. Karena elemen pada struktur arahnya tidak selalu paralel dengan suatu arah tertentu yang telah kita tentukan, maka perlu suatu cara untuk mentransformasikan vektor dari koordinat lokal ke koordinat global dengan menggunakan konsep matrik transformasi. Dengan matrik transformasi, kita dapat mengekspresikan matrik kekakuan ke sembarang arah pada koordinat global. Selanjutnya dijelaskan juga bagaimana menyusun matrik kekakuan untuk truss pada ruang atau tiga dimensi.

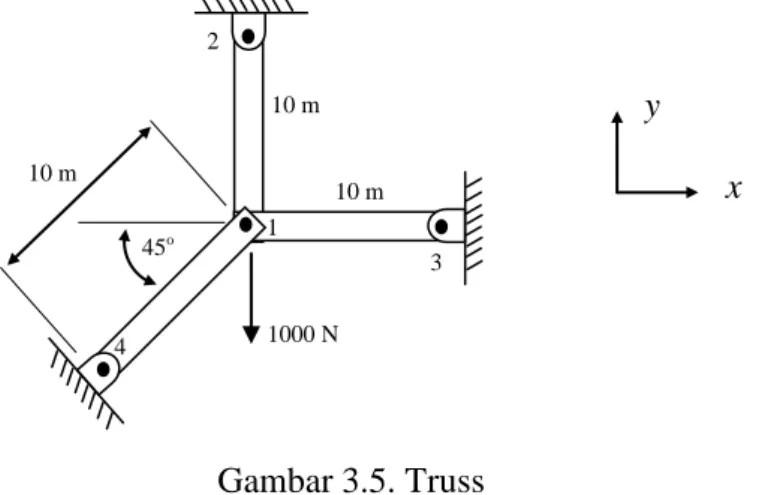
3.1. Matrik Kekakuan Elemen Batang Pada Koordinat Lokal

Gambar 3.1 menunjukkan suatu struktur truss 2 dimensi, yang mana jika salah satu batang truss yang ditunjukkan dengan anak panah, dapat ditinjau dengan dua sistem koordinat, yaitu koordinat global (sumbu X-Y) dan koordinat lokal (x’-y’). Diasumsikan batang truss tersebut mempunyai arah dengan sudut α terhadap koordinat global dan mempunyai panjang L dengan luas penampang A konstan. Karena gaya yang bekerja pada tiap batang truss, T, adalah selalu paralel dengan arah batang, maka arah T berhimpit dengan arah sumbu x’(koordinat lokal).

Dalam menganalisa beban pada struktur, dalam hal ini adalah truss, dengan menggunakan Metode Elemen Hingga, setiap batang pada truss dianggap sebagai satu elemen yang mempunyai arah orientasi yang berbeda-beda . Oleh karena itu pertama kita menurunkan rumus elemen dan matrik kekakuan pada salah satu batang atau elemen seperti ditunjukkan pada Gbr. 3.1. Tahapan yang kita gunakan adalah tahapan-tahapan yang telah diterangkan pada Bab II.