i | P a g e
KEOPTIMALAN NAÏVE BAYES DALAM KLASIFIKASI
SEMINAR
Diajukan sebagai syarat akhir mata kuliah seminar Di Program Studi Ilmu Komputer
diajukan oleh:
MUHAMMAD AMMAR SHADIQ 056946/PS/IK/05
Kepada
TIM SEMINAR PROGRAM STUDI ILMU KOMPUTER PROGRAM STUDI ILMU KOMPUTER
FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS PENDIDIKAN INDONESIA JUNI, 2009
ii | P a g e
KEOPTIMALAN NAÏVE BAYES DALAM KLASIFIKASI SEMINAR
yang telah dipersiapkan dan disusun oleh diajukan oleh:
MUHAMMAD AMMAR SHADIQ 056946/PS/IK/05
telah siap dipertahankan di depan Dewan Penguji pada tanggal 26 Juni 2009
telah disetujui oleh:
Pembimbing Utama
Eddy Prasetyo Nugroho
Mengetahui,
Ketua Jurusan/Program Studi Ketua Tim Seminar
Ilmu Komputer Jurusan/Program Studi
FPMIPA UPI FPMIPA UPI Ilmu Komputer
Heri Sutarno M.T Dr. Wawan Setiawan M.Kom
iii | P a g e
KATA PENGANTAR
Klasifikasi adalah salah satu tugas yang penting dalam data mining, dalam klasifikasi sebuah pengklasifikasi dibuat dari sekumpulan data latih dengan kelas yang telah di tentukan sebelumnya Naive Bayes adalah salah satu Algoritma Klasifikasi yang populer, Performa naïve bayes yang kompetitif dalam proses klasifikasi walaupun menggunakan asumsi keidependenan atribut (tidak ada kaitan antar atribut). Asumsi keidependenan atribut ini pada data sebenarnya jarang terjadi, namun walaupun asumsi keidependenan atirbut tersebut dilanggar performa pengklasifikasian naïve bayes cukup tinggi, hal ini dibuktikan pada berbagai penelitian empiris.
Pada karya tulis ini penulis mencoba mengesplorasi alasan mengapa performa Algoritma Klasifikasi Naïve Bayes memiliki performa yang bersaing dibandingkan dengan Algoritma-algoritma klasifikasi lainnya dengan cara melakukan penelitian teoritis terhadap algoritma Naïve Bayes dalam tugas klasifikasi.
iv | P a g e
DAFTAR ISI
KATA PENGANTAR ... iii
DAFTAR ISI ... iv ABSTRAKSI ... 1 BAB I PENDAHULUAN ... 2 1.1 Latar Belakang ... 2 1.2 Rumusan Masalah ... 5 1.3 Batasan Masalah... 5
1.4 Tujuan dan Manfaat Penelitian ... 5
BAB II TELAAH PUSTAKA ... 6
2.1 Pengklasifikasian dalam Data Mining & Machine Learning ... 6
2.1.1 Pendefinisian istilah dalam klasifikasi ... 6
2.1.2 Proses pembentukan model ... 7
2.2 Peluang Bersyarat dalam Statistika ... 8
2.3 Teorema Bayes dalam statistika ... 10
2.4 Teorema Bayes dalam Klasifikasi pada Data Mining & Machine Learning .... 13
2.4.1 Perkalian Kartesius(cartesian product) ... 14
2.4.2 Contoh Teorema Bayes dalam Klasifikasi ... 15
2.4.3 Kekurangan Teorema Bayes dalam Klasifikasi ... 16
2.5 Algoritma Naïve Bayes dalam Data Mining & Machine Learning ... 16
2.5.1 Contoh Teorema Bayes dalam Klasifikasi ... 17
2.5.2 Perbandingan Teorema Bayes dan Naïve Bayes dalam Nilai Probabilitas dan Nilai Klasifikasi ... 17
BAB III METODOLOGI PENULISAN ... 18
BAB IV ANALISIS INTESIS ... 19
4.1 Bukti Naïve Bayes tidak saja optimal pada asumsi idependen ... 19
4.2 Keoptimalan Lokal ... 21
4.3 Keoptimalan global ... 25
BAB V KESIMPULAN ... 26
1 | P a g e
ABSTRAKSI
Naïve Bayes adalah salah satu algoritma pembelajaran induktif yang paling efektif dan efisien untuk machine learning dan data mining. Performa naïve bayes yang kompetitif dalam proses klasifikasi walaupun menggunakan asumsi keidependenan atribut (tidak ada kaitan antar atribut). Asumsi keidependenan atribut ini pada data sebenarnya jarang terjadi, namun walaupun asumsi keidependenan atirbut tersebut dilanggar performa pengklasifikasian naïve bayes cukup tinggi, hal ini dibuktikan pada berbagai penelitian empiris.
Pada paper ini, penulis akan memaparkan penggunaan naïve bayes dalam tugas klasifikasi data, membuktikan potensi naïve bayes untuk digunakan dalam data yang memiliki korelasi antara atribut dan mengajukan penjelasan mengenai keoptimalan naïve bayes dalam kondisi tertentu.
Kata Kunci : Bayesian Theorem, Naïve Bayes, Data Mining, Classification, Optimal Classification.
2 | P a g e
BAB I PENDAHULUAN
1.1 Latar Belakang
Klasifikasi adalah salah satu tugas yang penting dalam data mining, dalam klasifikasi sebuah pengklasifikasi dibuat dari sekumpulan data latih dengan kelas yang telah di tentukan sebelumnya. Performa pengklasifikasi biasanya diukur dengan ketepatan (atau tingkat galat) [6].
Teorema Bayes adalah teorema yang digunakan dalam statistika untuk menghitung peluang untuk suatu hipotesis, Bayes Optimal Classifier [2] menghitung peluang dari suatu kelas dari masing-masing kelompok atribut yang ada, dan menentukan kelas mana yang paling optimal.
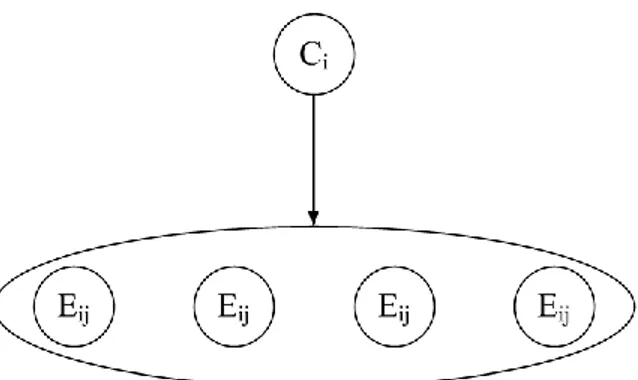
Umumnya kelompok atribut E direpresentasikan dengan sekumpulan nilai atribut (x1,x2,x3,….,xn) dimana xi adalah nilai atribut Xi. C adalah variable klasifikasi dan c
adalah nilai dari C.
Pengklasifikasian adalah sebuah fungsi yang menugaskan data tertentu kedalam sebuah kelas. Dari sudut pandang peluang [7], berdasarkan aturan Bayes kedalam kelas c adalah :
Untuk menentukan pilihan kelas, digunakan peluang maksimal dari seluruh c dalam C, dengan fungsi :
Karena nilai konstan untuk semua kelas, maka dapat diabaikan. sehingga menghasilkan fungsi :
3 | P a g e
Gambar 1 : Ilustrasi Teorema Bayes.
Pengklasifikasian menggunakan Teorema Bayes ini membutuhkan biaya komputasi yang mahal (waktu prosessor dan ukuran memory yang besar) karena kebutuhan untuk menghitung nilai probabilitas untuk tiap nilai dari perkalian kartesius untuk tiap nilai atribut dan tiap nilai kelas.
Data latih untuk Teorema Bayes membutuhkan paling tidak perkalian kartesius dari seluruh kelompok atribut yang mungkin, jika misalkan ada 16 atribut yang masing-masingnya berjenis Boolean tanpa missing value, maka data latih minimal yang dibutuhkan oleh Teorema Bayes untuk digunakan dalam klasifikasi adalah 216 = 65.536 data, sehingga ada 3 masalah yang dihadapi untuk menggunakan teorema Bayes dalam pengklasifikasian, yaitu :
(1) kebanyakan data latih tidak memiliki varian klasifikasi sebanyak itu (oleh karenanya sering diambil sample)
(2) jumlah atribut dalam data sample dapat berjumlah lebih banyak (lebih dari 16) (3) jenis nilai atribut dapat berjumlah lebih banyak [lebih dari 2 – Boolean]
terlebih lagi untuk jenis nilai atribut yang bersifat tidak terbatas 1 - ∞ seperti numeric dan kontiniu.
(4) jika suatu data X tidak ada dalam data latih, maka data X tidak dapat di klasifikasikan, karena peluang untuk data X di klasifikasikan kedalam suatu kelas adalah sama untuk tiap kelas yang ada.
4 | P a g e Untuk mengatasi berbagai permasalahan diatas, berbagai varian dari
pengklasifikasian yang menggunakan Teorema Bayes diajukan, salah satunya adalah Naïve Bayes, yaitu penggunaan Teorema Bayes dengan asumsi keidependenan atribut. Asumsi keidependenan atribut akan menghilangkan kebutuhan banyaknya jumlah data latih dari perkalian kartesius seluruh atribut yang dibutuhkan untuk mengklasifikasikan suatu data [4].
(2)
Gambar 2 : Ilustrasi Naïve Bayes.
Dampak negative dari asumsi Naïve tersebut adalah keterkaitan yang ada antara nilai-nilai atribut diabaikan sepenuhnya. Dampak ini secara intuitif akan berpengaruh dalam pengklasifikasian, namun percobaan empiris mengatakan sebaliknya. Hal ini tentu saja cukup mengejutkan, karena dalam pengaplikasian dunia nyata, asumsi diabaikannya keterkaitan antara atribut selalu dilanggar [1].
Pertanyaan yang muncul adalah apakah yang menyebabkan baiknya performa yang didapatkan dari pengaplikasian asumsi Naïve ini? Karena secara intuitif, asumsi keidependenan atribut dalam dunia nyata hampir tidak pernah terjadi. Seharusnya dengan asumsi tersebut performa yang dihasilkan akan buruk.
Domingos dan Pazzani (1997) pada papernya untuk menjelaskan performa Naïve Bayes dalam fungsi zero-one loss. Fungsi zero-one loss ini mendefinisikan error hanya sebagai pengklasifikasian yang salah. Tidak seperti fungsi error yang lain
5 | P a g e seperti squared error, fungsi zero-one loss tidak memberi nilai suatu kesalahan perhitungan peluang selama peluang maksimum ditugaskan kedalam kelas yang benar. Ini berarti bahwa Naïve Bayes dapat mengubah peluang posterior dari tiap kelas, tetapi kelas dengan nilai peluang posterior maksimum jarang diubah. Sebagai
contoh, diasumsikan peluang sebenarnya dari dan ,
sedangkan peluang yang dihasilkan oleh Naïve Bayes adalah dan . nilai peluang tersebut tentu saja berbeda jauh, namun pilihan kelas tetap tidak terpengaruh.
1.2 Rumusan Masalah
Menentukan metode yang sesuai dalam mengklasifikasikan nasabah yang good credit risk.
1.3 Batasan Masalah
Batasan masalah dari penelitian ini adalah bahwa penelitian ini sebatas analisis area keoptimalan algoritma pengklasifikasi Naïve Bayes tidak terbatas kepada jenis data yang akan di klasifikasikan.
1.4 Tujuan dan Manfaat Penelitian
Tujuan dari penelitian ini adalah untuk mengesplorasi batasan-batasan keoptimalan algoritma klasifikasi Naïve Bayes dan mencoba menjelaskan mengenai alasan mengapa algoritma klasifikasi Naïve Bayes berfungsi dengan baik pada berbagai jenis data.
Manfaat dari penelitian ini adalah: Menjelaskan keoptimalan algoritma klasifikasi Naïve Bayes.
6 | P a g e
BAB II TELAAH PUSTAKA
Untuk memulai penelitian ini, kajian pustaka dilakukan terhadap seluruh aspek yang berhubungan dengan penelitian yang dilakukan, aspek-aspek tersebut adalah :
1. Pengklasifikasian dalam Data Mining & Machine Learning 2. Peluang Bersyarat dalam Statistika
3. Teorema Bayes dalam Statistika
4. Teorema Bayes dalam Klasifikasi pada Data Mining & Machine Learning 5. Algoritma Naïve Bayes dalam Data Mining & Machine Learning
Asdf
2.1 Pengklasifikasian dalam Data Mining & Machine Learning
Klasifikasi adalah salah satu tugas yang penting dalam data mining, dalam klasifikasi, sebuah pengklasifikasi dibuat dari sekumpulan data latih dengan kelas yang telah ditentukan sebelumnya.
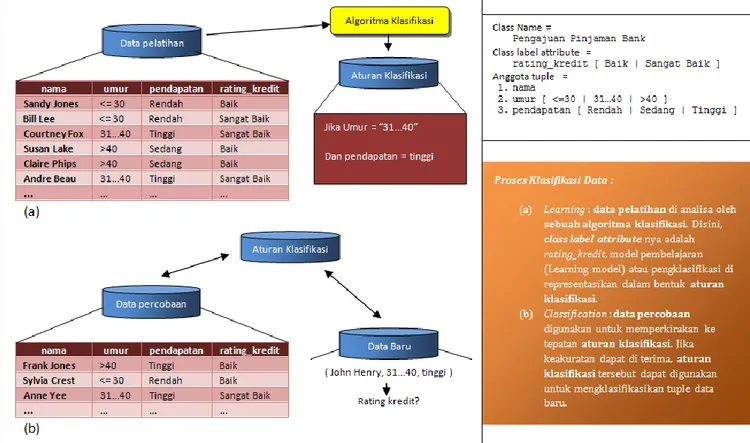
Klasifikasi data adalah proses dua langkah. Pada langkah pertama, sebuah model dibangun menggambarkan sebuah kumpulan kelas data atau konsep dari populasi data yang telah ditentukan sebelumnya (misalkan data pengajuan pinjaman bank). Model tersebut dibangun dengan menganalisa data latih yang digambarkan oleh atribut-atribut. Tiap tuple di asumsikan untuk dimiliki oleh kelas yang telah di tentukan, seperti di tentukan oleh salah satu atribut, yang dinamakan class label attribute. Langkah kedua adalah menguji model yang telah dibangun kepada data uji untuk mengukur ketepatan atau performa model dalam mengklasifikasi data uji. Setelah pengukuran performa selesai dilakukan, pengambil keputusan dapat memutuskan untuk menggunakan model tersebut atau mengulang pembuatan model dengan data latih atau metode yang berbeda untuk menghasilkan model klasifikasi yang lebih baik.
2.1.1 Pendefinisian istilah dalam klasifikasi
Pada gambar 1, contoh yang digunakan adalah data pengajuan pinjaman bank, dengan atribut-atribut nama, umur, pendapatan dan rating kredit dengan nama, umur, pendapatan sebagai data tuple dan seterusnya akan disebut sebagai atribut saja, sedangkan atribut rating kredit sebagai class label atribute dimana seterusnya akan disebut sebagai kelas. Nilai-nilai yang
7 | P a g e terdapat dalam data (seperti nama = Frank Jones, umur = >40, pendapatan = Tinggi, dan rating_kredit = baik) disebut sebagai kumpulan nilai atribut, dimana seterusnya akan disebut sebagai kumpulan atribut saja. Aturan Klasifikasi yang dibuat dari kumpulan-kumpulan atribut pada data pelatihan dan Algoritma Klasifikasi disebut sebagai model klasifikasi.
2.1.2 Proses pembentukan model
Motode-metode klasifikasi dan prediksi dapat di bandingkan dan dievaluasi berdasarkan kriteria-kriteria berikut :
Predictive accuracy : adalah kemampuan model untuk secara benar memprediksikan label kelas dari data baru atau yang belum pernah di temui sebellumnya.
Speed : adalah biaya komputasi yang dilibatkan dalam menggenerate dan menggunakan model.
Robustness : adalah kemampuan model untuk membuat prediksi yang tepat terhadap data yang cacat atau data dengan nilai yang hilang.
Scalability : adalah kemampuan untuk membuat model secara efisien terhadap data yang berjumlah banyak.
8 | P a g e Interpretability : adalah tingkat kejelasan dan kemengertian yang di berikan oleh model.
Hal-hal tersebut diatas akan didiskusikan dalam bab ini. Kontribusi komunitas peneliti database kepada klasifikasi dan prediksi untuk data mining menegaskan pada aspek skalabilitas, khususnya pada induksi pohon keputusan.
2.2 Peluang Bersyarat dalam Statistika
Dua peristiwa dikatakan mempunyai hubungan bersyarat jika peristiwa yang satu menjadi syarat peristiwa yang lain. Contohnya adalah peluang suatu kejadian c bila diketahui bahwa kejadian E telah terjadi, dinyatakan dengan P(c|E), atau dengan kata lain peluang bersyarat untuk terjadinya peristiwa c dengan syarat E. Lambang P(c|E) biasanya dibaca „peluang c terjadi bila diketahui E terjadi‟ atau lebih sederhana lagi „peluang c, bila E diketahui‟.
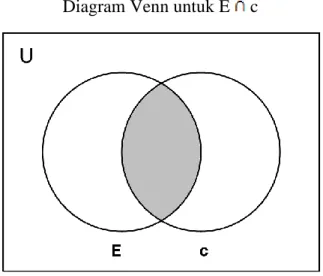
Dari penjelasan singkat diatas mungkin anda telah mengetahui bahwa penghitungan dilakukan dengan operasi Irisan Himpunan (intersection) dengan lambang , atau dengan operator logika konjungsi (dan) dengan lambang Λ, irisan dan konjungsi dilakukan terhadap nilai himpunan c dan E.
Diagram Venn untuk E c
Gambar 3: Diagram Venn untuk E c
Table 1: Tabel kebenaran untuk E Λ c.
E c E Λ c
1 1 1
1 0 0
0 1 0
9 | P a g e Namun jika hanya dengan operator-operator tersebut, penghitungan peluang yang terjadi
bukanlah penghitungan peluang bersyarat, untuk penghitungan peluang bersyarat kita membutuhkan peluang nisbi dari E, yaitu peluang E dan c muncul ditambah peluang E dan c‟muncul, ditambah E dan c” muncul, dst. Atau dengan kata lain peluang E muncul pada masing-masing kasus c. Rumusnya dapat di tuliskan sebagai berikut :
(P(E c)+P(E c‟)+P(E c”)+…..+P(E cn)).
Nilai peluang bersyarat P(c|E) di dapatkan dari nilai irisan atau konjungsi dari E dan c dibagi dengan Peluang nisbi dari E. didapatkanlah rumus :
Catatan : Karena pada kasus data mining kebanyakan data yang dikomputasi berbentuk himpunan, maka disini dan seterusnya akan digunakan operator irisan himpunan untuk mendefinisikan rumus peluang bersyarat.
Contoh Peluang Bersyarat
Untuk mempermudah pemahaman perhatikan contoh soal jika data-datanya sebagai berikut,
Carilah peluang seorang pelanggan membeli komputer dengan syarat Pendapatan pelanggan tersebut Sedang.
Jawaban :
c : Beli Komputer = Ya. c‟ : Beli Komputer = Tidak. E : Pendapatan = sedang.
P(c|E) = P(membeli komputer = ya | pendapatan = sedang). ID Pendapatan Beli Komputer
1 Tinggi Tidak 2 Tinggi Tidak 3 Tinggi Ya 4 Sedang Ya 5 Rendah Ya 6 Rendah Tidak 7 Rendah Ya 8 Sedang Tidak 9 Rendah Ya 10 Sedang Ya 11 Sedang Ya 12 Sedang Ya 13 Tinggi Ya 14 Sedang Tidak
10 | P a g e P(E) adalah peluang nisbi pelanggan berpendapatan sedang, yaitu peluang pelanggan
berpendapatan sedang yang membeli komputer ditambah pelanggan berpendapatan sedang yang tidak membeli komputer. P(E c)+P(E c‟) = (4/14)+(2/14) = 6/14. P(E c) adalah pelanggan yang berpendapatan sedang membeli komputer = 4/14.
Yaitu pelanggan yang berpendapatan sedang 2/3-nya akan membeli komputer, yaitu 66.6…% kemungkinan bahwa pelanggan berpendapatan sedang membeli komputer.
Untuk peluang pelanggan berpendapatan sedang Tidak membeli komputer, peluangnya dihitung dengan :
Sedangkan untuk peluang pelanggan yang berpendapatan tinggi dan rendah membeli komputer, nilainya secara berurut adalah 2/4 dan 3/4.
2.3 Teorema Bayes dalam statistika
Teorema bayes dinamakan berdasarkan Thomas Bayes yang pertama kali mengemukakan teorema ini.
Misalkan E adalah kumpulan atribut. Dalam sudut pandang Bayesian, E diartikan sebagai “Bukti”. Seperti biasa E di deskripsikan oleh pengukuran yang dibuat dari sebuah kumpulan atribut berjumlah n.
Misalkan C adalah beberapa kelas. Untuk masalah klasifikasi, kita ingin menentukan P(c|E), yaitu probabilitas bahwa hipotesis kelas c adalah benar untuk “bukti” atau data observasi kumpulan atribut data E. dengan kata lain, kita mencari probabilitas bahwa kumpulan atribut E termasuk kepada kelas C, dengan kita mengetahui gambaran atribut dari E.
P(c|E) adalah Probabilitas Posterior*, atau sebuah Probabilitas Posteriori, dari c yang diujikan pada E. sebagai contoh, misalkan dunia tuple data kita dibatasi oleh data pelanggan dengan atribut umur dan pendapatan, dan E adalah pelanggan dengan umur 35 tahun dengan pendapatan Rp 4.000.000. Misalkan c adalah Hypotesis bahwa pelanggan akan membeli sebuah komputer.
11 | P a g e Maka P(c|E) merefleksikan probabilitas bahwa pelanggan E (dengan atribut umur=35 thn, pendapatan Rp 4.000.000) akan membeli sebuah komputer dengan informasi yang didapatkan berupa umur dan pendapatan pelanggan.
Secara kontras, P(c) adalah Probabilitas Prior***, atau Probabilitas Priori, dari c. sebagai contoh, ini adalah probabilitas bahwa pelanggan manapun akan membeli sebuah komputer atau tidak, tidak memandang dari umur, pendapatan ataupun informasi lainnya :
Jumlah data = 14
c1 = Membeli Komputer = “ya” c2 = Membeli Komputer = “tidak”
Dari 14 data, yang membeli_komputer=”ya”= 9 orang, dan yang tidak membeli_komputer = “tidak” = 5 orang. Maka P(C) adalah : P(c1) = P(Membeli_Komputer = “ya) = 9 /14 = 0.643
P(c2) = P(Membeli_Komputer = “tidak) = 5/14 = 0.357
Sama halnya, P(E|c) adalah Probabilitas Posteriori dari E yang diujicobakan dengan Kelas c. yaitu probabilitas bahwa sebuah pelanggan, E, berumur 35 thn(31…40) dengan pendapatan $40K (sedang) :
Jumlah data = 14
c1 = Membeli Komputer = “ya” c2 = Membeli Komputer = “tidak”
Dari 14 data, yang membeli_komputer=”ya”= 9 orang, dan yang tidak membeli_komputer = “tidak” = 5 orang E1 = Pelanggan berumur 31…40 thn yang Membeli_komputer = ”ya” berjumlah 4 orang.
E2 = Pelanggan berumur 31…40 thn yang Membeli_komputer = ”tidak” berjumlah 0 orang. E3 = Pelanggan dengan pendapatan sedang yang membeli_komputer = “ya” berjumlah 4 orang. E4 = Pelanggan dengan pendapatan sedang yang membeli_komputer = “tidak” berjumlah 2 orang. Maka P(E|C) adalah :
P(E1|c1) = P( umur = 31…40 | beli_komputer = “ya”) = 4/9 = 0.444 P(E2|c2) = P( umur = 31…40 | beli_komputer = “tidak”) = 0/5 = 0 P(E3|c1) = P( pendapatan = sedang | beli_komputer = “ya”) = 4/9 = 0.444 P(E4|c2) = P( pendapatan = sedang | beli_komputer = “tidak”) = 2/5 = 0.4
P(X) adalah Probabilitas Prior dari X. menggunakan contoh diatas, adalah probabilitas bahwa seseorang dari kumpulan pelanggan adalah berumur 35 thn dan berpenghasilan $40K :
Jumlah Data = 14
Dari 14 data, pelanggan dengan umur 31…40 = 4 orang, <30 = 5 orang dan >40 = 5 orang. Pelanggan dengan pendapatan sedang = 6 orang, rendah = 4 orang dan tinggi = 4 orang.
P(X11) = P( umur = 31…40 ) = 4/14 = 0.285 P(X21) = P( Pendapatan = sedang) = 6/14 = 0.428
Untuk nilai atribut lain (selain diatas), dihitung dengan cara yang sama: P(X12) = P( umur = <30 ) = 5/14 = 0.357
P(X13) = P( umur = >40 ) = 5/14 = 0.537 P(X22) = P( pendapatan = rendah ) = 4/14 = 0.285 P(X23) = P( pendapatan = tinggi ) = 4/14 = 0.285
12 | P a g e “Bagaimanakan probabilitas-probabilitas tersebut di estimasi?” P(H), P(X|H) dan P(X) dapat di estimasi dari data yang diberikan, seperti akan kita lihat di bawah. Teorema Bayes berguna dalam menyediakan sebuah cara untuk mengkalkulasi Probabilitas Posterior P(H|X) dari P(H), P(X) dan P(H|X). Teorema bayes adalah :
Untuk lebih memahami pengertian-pengertian yang sulit diatas, mari kita amati sebuah contoh kasus.
Contoh Pengklasifikasian 2 kelas:
Pada suatu universitas, mahasiswanya terdiri dari 60% Laki-laki dan 40% Perempuan.
Mahasiswa perempuan menggunakan rok atau celana panjang dengan perbandingan yang sama. Sedangkan seluruh mahasiswa Laki-laki menggunakan celana panjang. Seorang pengamat melihat seorang mahasiswa (acak) dari kejauhan. Yang dapat di lihat pengamat tersebut adalah bahwa mahasiswa tersebut menggunakan celana panjang. Berapakah probabilitas mahasiswa yang dilihat oleh pengamat tersebut adalah mahasiswa perempuan?
Jawaban :
Jelas bahwa probabilitasnya kurang dari 40%, tetapi berapakah tepatnya? Apakah setengahnya, karena hanya setengah mahasiswa Perempuan yang menggunakan celana panjang? Jawaban yang benar dapat dihitung dengan teorema bayes.
Hipotesis H adalah mahasiswa yang diamati adalah Perempuan, dan bukti X adalah mahasiswa yang diamati menggunakan celana panjang. Untuk menghitung P(H|X), pertama-tama kita harus mengetahui:
P(H), atau probabilitas bahwa mahasiswa tersebut adalah perempuan, tanpa memandang informasi lainnya. Karena pengamat mengamati seorang mahasiswa secara acak, artinya seluruh mahasiswa memiliki probabilitas yang sama untuk diamati, dan banyaknya mahasiswa perempuan adalah 40%, maka probabilitasnya adalah 0.4.
P(H‟), atau probabilitas bahwa mahasiswa tersebut adalah Laki-laki, tanpa memandang informasi lainnya (H‟ adalah komplemen dari H). Banyaknya mahasiswa laki-laki adalah 60%, maka probabilitasnya adalah 0.6.
13 | P a g e P(X|H), atau probabilitas bahwa mahasiswa yang diamati menggunakan celana panjang
adalah perempuan. Karena mahasiswa perempuan menggunakan Rok dan celana panjang dengan perbandingan yang sama(50%), maka probabilitasnya adalah 0.5.
P(X|H‟), atau probabilitas bahwa mahasiswa yang diamati menggunakan celana panjang adalah laki-laki. Karena seluruh laki-laki di universitas tersebut menggunakan celana panjang(100%), maka probabilitasnya adalah 1.
P(X), atau probabilitas dari seorang mahasiwa (yang dipilih secara acak) menggunakan celana panjang, tanpa memandang informasi lainnya. Karena P(X) =
P(X|H)P(H)+P(X|H‟)P(H‟), maka nilainya adalah (0.5 × 0.4) + (1 × 0.6) = 0.8.
Seperti yang telah di ramalkan sebelumnya, probabilitasnya kurang dari 40%. Tepatnya 25%. Cara lainnya untuk mendapatkan hasil yang sama sebagai berikut.
Dimisalkan pada universitas tersebut ada 100 orang mahasiswa, 60 mahasiswa laki-laki dan 40 mahasiswa perempuan. Diantara seluruh mahasiswa ini, 60 mahasiswa laki-laki dan 20
mahasiswa perempuan menggunakan celana panjang, berarti yang menggunakan celana panjang berjumlah 80 orang, dengan 20 diantaranya perempuan. Oleh karenanya kemungkinan
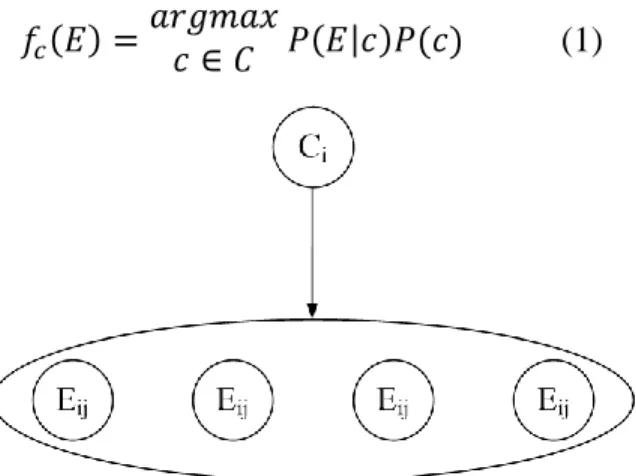
mahasiswa yang menggunakan celana panjang adalah perempuan sama dengan 20/80 = 0.25 2.4 Teorema Bayes dalam Klasifikasi pada Data Mining & Machine Learning Pengklasifikasian adalah sebuah fungsi yang menugaskan data atau kelompok atribut tertentu kedalam sebuah kelas. Dari sudut pandang peluang [7], berdasarkan aturan Bayes kedalam kelas c adalah :
Untuk menentukan pilihan kelas, digunakan peluang maksimal dari seluruh c dalam C, dengan fungsi :
Karena nilai konstan untuk semua kelas, maka dapat diabaikan. sehingga menghasilkan fungsi :
14 | P a g e (1)
Gambar 4 : Ilustrasi Teorema Bayes.
Pengklasifikasian menggunakan Teorema Bayes ini membutuhkan biaya komputasi yang mahal (waktu prosessor dan ukuran memory yang besar) karena kebutuhan untuk menghitung nilai probabilitas untuk tiap nilai dari perkalian kartesius untuk tiap nilai atribut dan tiap nilai kelas. 2.4.1 Perkalian Kartesius(cartesian product)
Perkalian Kartresian digunakan karena merupakan salah satu operasi dasar dalam Himpunan.
Himpunan digunakan untuk mengelompokkan objek secara bersama-sama. [Matematika Diskrit, Rinaldi Munir 2005]
Operasi dari Perkalian Kartesius adalah operasi menghubungkan tiap elemen dari suatu himpunan atribut dengan tiap elemen dari himpunan atribut lainnya.
Contoh :
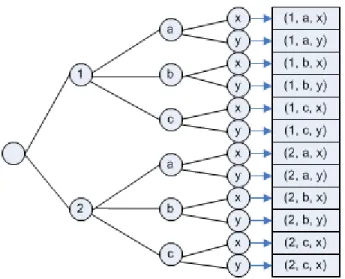
Himpunan atribut A memiliki anggota : {1,2} Himpunan atribut B memiliki anggota : {a, b, c} Himpunan atribut C memiliki anggota : {x, y}
Kardinalitas A x B x C, yaitu |A x B x C| = |A|.|B|.|C| = 2.3.2 = 12.
15 | P a g e Jadi, A x B x C = {(1, a, x), (1, a, y), (1, b, x), (1, b, y), (1, c, x), (1, c, y), (2, a, x), (2, a,
y), (2, b, x), (2, b, y), (2, c, x) , (2, c, y)}
2.4.2 Contoh Teorema Bayes dalam Klasifikasi
Pelamar IPK Psikologi Wawancara Diterima
P1 Bagus Tinggi Baik Ya
P2 Bagus Tinggi Baik Ya
P3 Bagus Tinggi Baik Tidak
P4 Bagus Sedang Baik Ya
P5 Bagus Sedang Buruk Ya
P6 Bagus Rendah Buruk Tidak
P7 Cukup Tinggi Baik Ya
P8 Cukup Sedang Baik Ya
P9 Cukup Sedang Buruk Ya
P10 Cukup Rendah Buruk Tidak
P11 Kurang Tinggi Baik Ya
P12 Kurang Sedang Buruk Tidak
P13 Kurang Rendah Baik Ya
Table 2 : Data Latih Wawancara
Kelompok Atribut E adalah IPK = Bagus, Psikologi = Tinggi, Wawancara = Baik, Kelas-kelas C adalah c1 = diterima, c2 = ditolak. maka kelas kelompok atribut E adalah :
Class Name =
Penerimaan Pegawai Class label attribute =
Diterima [ Ya | Tidak ] Identifier =
Pelamar
Atribut dan Anggota atribut =
1. IPK [ Bagus | Cukup | Kurang ]
2. Psikologi [ Rendah | Sedang | Tinggi ] 3. Wawancara [ Baik | Buruk ]
16 | P a g e Karena yang dipilih adalah nilai yang terbesar, maka kelompok atribut E ditugaskan pada kelas c1.
2.4.3 Kekurangan Teorema Bayes dalam Klasifikasi
Data latih untuk Teorema Bayes membutuhkan paling tidak perkalian kartesius dari seluruh kelompok atribut yang mungkin, jika misalkan ada 16 atribut yang masing-masingnya berjenis Boolean [0,1] tanpa missing value, maka data latih minimal yang dibutuhkan oleh Teorema Bayes untuk digunakan dalam klasifikasi adalah 216 = 65.536 data, sehingga ada 3 masalah yang dihadapi untuk menggunakan teorema Bayes dalam pengklasifikasian, yaitu :
(1) kebanyakan data latih tidak memiliki varian klasifikasi sebanyak itu (oleh karenanya sering diambil sample)
(2) jumlah atribut dalam data sample dapat berjumlah lebih banyak (lebih dari 16) (3) jenis nilai atribut dapat berjumlah lebih banyak [lebih dari 2 – Boolean] terlebih lagi
untuk jenis nilai atribut yang bersifat tidak terbatas 1 - ∞ seperti numeric dan kontiniu. jika suatu data X tidak ada dalam data latih, maka data X tidak dapat di klasifikasikan, karena peluang untuk data X di klasifikasikan kedalam suatu kelas adalah sama untuk tiap kelas yang ada.
2.5 Algoritma Naïve Bayes dalam Data Mining & Machine Learning
Untuk mengatasi berbagai permasalahan diatas, berbagai varian dari pengklasifikasian yang menggunakan Teorema Bayes diajukan, salah satunya adalah Naïve Bayes, yaitu
penggunaan Teorema Bayes dengan asumsi keidependenan atribut. Asumsi keidependenan atribut akan menghilangkan kebutuhan banyaknya jumlah data latih dari perkalian kartesius seluruh atribut yang dibutuhkan untuk mengklasifikasikan suatu data [4].
17 | P a g e
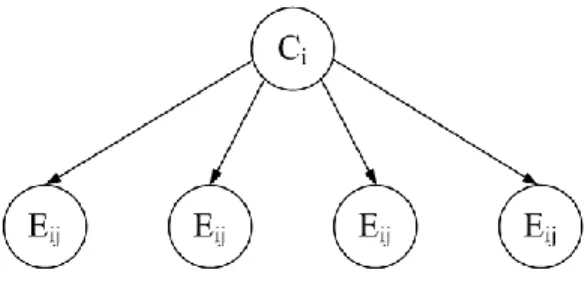
Gambar 5 : Ilustrasi Naïve Bayes.
2.5.1 Contoh Teorema Bayes dalam Klasifikasi
Pada table 2, Kelompok Atribut E adalah e1 IPK = Bagus, e2 Psikologi = Tinggi, e3 Wawancara = Baik, Kelas-kelas C adalah c1 = diterima, c2 = ditolak. maka kelas kelompok atribut E adalah :
Karena yang dipilih adalah nilai yang terbesar, maka kelompok atribut E ditugaskan pada c1. 2.5.2 Perbandingan Teorema Bayes dan Naïve Bayes dalam Nilai Probabilitas dan
Nilai Klasifikasi
Nilai Peluang atau probabilitas biasanya digunakan sebagai nilai acuan didalam pengambilan keputusan, namun berbeda halnya dengan klasifikasi. Pada klasifikasi nilai probabilitas kelas yang terbesar yang dipilih untuk mengklasifikasikan suatu kelompok atribut terhadap kelas-kelas lainnya.
Kelas c1 = Diterima Kelas c2 = Ditolak
Teorema Bayes = 72/468 = (72/468)/(72/468+36/468) = 2/3 = 66.666…% = 36/468 = (36/468)/(72/468+36/468) = 1/3 = 33.333…% Naïve Bayes 2160/28561 =(2160/28561)/( 2160/28561+960/28561) = 2160/3120 = 9/13 = 69.230…% 960/28561 =(960/28561)/( 2160/28561+960/28561) =960/3120 = 4/13 = 30.769…%
Tabel 3 menunjukkan perbandingan nilai probabilitas pada data latih di table 2 untuk Kelompok Atribut E untuk e1 IPK = Bagus, e2 Psikologi = Tinggi, e3 Wawancara = Baik, Kelas-kelas C adalah c1 = diterima, c2 = ditolak. Walaupun nilai peluang yang diperhitungkan bernilai salah, namun pemilihan kelas tetap sama, yaitu ditunjukkan untuk nilai probabilitas yang terbesar pada kelas c1.
18 | P a g e
BAB III METODOLOGI PENULISAN
Metode peneleitian dilakukan dengan cara studi pustaka secara menyeluruh dan komprehensif. Dalam menganalisis nilai keoptimalan, dilakukan pembandingan studi empiris dengan
membandingkan 28 test set yang diambil dari repository data latih UCI (Hans 2000) untuk pembuktian perbandingan nilai keoptimalan algoritma Naïve Bayes dibandingkan dengan Algoritma Klasifikasi Data Mining yang lain.
Untuk niali keoptimalan sendiri, telah dinyatakan bahwa Naïve Bayes Bersifat optimal dalam kondisi atribut bersifat Independen penuh [2,4,5], untuk itu dilakuakan perbandingan dengan cara mengemulasi kondisi Keindependenan Atribut penuh dengan kondisi Atribut yang tidak Independen, hasil dari pembandingan ini membuktikan bahwa Kondisi keoptimalan Naïve Bayes lebih luas daripada yang dikira sebelumnya.
19 | P a g e
BAB IV ANALISIS INTESIS
4.1 Bukti Naïve Bayes tidak saja optimal pada asumsi idependen
Seperti yang telah di ketahui bahwa naïve Bayes bernilai optimal ketika seluruh atribut bernilai independen terhadap atribut lainnya. Pada bagian ini akan dibandingkan antara nilai naïve bayes yang seluruh atribut independen terhadap atribut lainnya dan nilai naïve bayes yang tidak seluruh atributnya independen.
Misalkan sebuah data latih, dengan atribut A, B dan C yang bersifat Boolean, dan kelas dan , dengan peluang yang sebanding untuk tiap kelas . A dan B berkorelasi penuh (A = B), sehingga B dapat diabaikan.
Prosedur klasifikasi optimal untuk sebuah data tuple adalah untuk menugaskan data tuple tersebut kedalam kelas jika :
Kelas positif :
Dan sebaliknya, menugaskan kelompok atribut kepada kelas jika : Kelas negatif :
Kelas acak :
Sedangkan prosedur klasifikasi Naïve Bayes yang tidak optimal memperhitungkan juga nilai B seperti halnya nilai B sama sekali tidak berkorelasi dengan nilai A. hal ini sama dengan menghitung nilai A dua kali. Untuk naïve bayes rumusnya adalah :
Kelas positif :
Kelas negatif :
Kelas Acak :
Dengan mengaplikasikan naïve bayes untuk pengklasifikasian yang optimal, maka dapat di representasikan sebagai
20 | P a g e Karena , maka nilai dan tidak perlu dihitung dan dapat diabaikan dalam perhitungan, nilai P(A) dan P(C) juga mengeliminasi satu sama lainnya dalam operasi pengurangan, sehingga nilai P(A) dan nilai P(C) tidak perlu di hitung, sehingga setelah pengeliminasian perhitungan yang tidak di perlukan dan didapatkan :
Untuk perhitungan korelasi optimal.
Sedangkan untuk perhitungan korelasi dengan Naïve Bayes :
Karena dalam peluang nilai peluang maksimal adalah 1, maka dapat dituliskan P( |A) + P( |C) = 1
P( |A) =1 - P( |C) Misalkan P( |A) = p dan P( |C) = q
Sehingga rumusnya menjadi
untuk nilai peluang optimal dengan asumsi keidependenan atribut.
untuk nilai peluang naïve bayes tanpa keidependenan atribut.
21 | P a g e
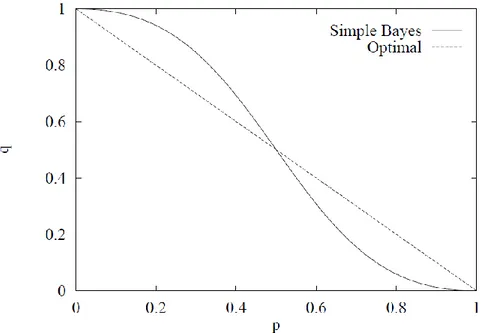
Gambar : Kurva Perbandingan Naive Bayes
Kurva diatas memperlihatkan bahwa walaupun asumsi keidependenan atribut dilanggar, karena B=A, pengklasifikasian naïve bayes dengan asumsi atribut yang tidak independen tidak sama dengan pengklasifikasian naive bayes optimal dengan keidependenan atribut hanya di dua bagian sempit, satu diatas kurva dan satu lagi dibawah, di tempat lain, naïve bayes menghasilkan klasifikasi yang benar, yaitu pada (0,1) ( , ,) (1,0) ini menunjukkan bahwa penggunaan klasifikasi naïve bayes bisa lebih luas daripada yang dikira sebelumnya.
4.2 Keoptimalan Lokal
Keoptimalan lokal adalah nilai keoptimalan yang didapatkan untuk sebuah kumpulan atribut saja, sedangkan keoptimalan global adalah untuk seluruh kumpulan atribut. Sebelumnya didefinisikan beberapa hal :
Definisi 1
Misalkan C(E) adalah kelas sebenarnya dari contoh E, dan Cx(E) adalah kelas
yang di tugaskan oleh pengklasifikasi X, maka zero-one loss dari X pada E , didefinisakan sebagai :
22 | P a g e (3)
Zero-one loss adalah ukuran yang tepat jika tugas yang harus dilakukan adalah klasifikasi. Dimana zero-one loss memberikan ukuran nilai 1 kepada kesalahan pengklasifikasian. Pada situasi tertentu, kesalahan pengklasifikasian memiliki ukuran prioritas yang berbeda, sebagai contohnya, pada diagnosa medis, ukuran kesalahan mengklasifikasikan seorang pasien yang sakit sebagai sehat berbeda dengan mengklasifikasikan pasian sehat sebagai sakit.
Umumnya, seringkali muncul data latih dengan nilai kelompok atribut yang sama tetapi memiliki kelas yang berbeda. Ini merefleksikan fakta bahwa atribut-atribut tersebut tidak mengandung seluruh informasi untuk menentukan kelas. Maka, secara umum, sebuah data latih E tidak akan dihubungkan dengan suatu kelas saja, tetapi dengan peluang kelas P(Ci|E) yang berbentuk vektor, dimana komponen ke I merepresentasikan
perbandingan nilai munculnya E pada kelas Ci. Ukuran Kesalahan zero-one loss dari X
pada E adalah :
Dimana adalah kelas yang ditugaskan X kepada E dan adalah
keakuratan dari X pada E. definisi ini disederhanakan menjadi persamaan 3 saat sebuah kelas memiliki probabilitas 1 diberikan E.
Definisi 2 :
Ukuran bayes untuk sebuah data latih adalah nilai galat zero-one loss yang terendah yang didapatkan dari pengklasifikasian manapun pada data latih tersebut [1].
Definisi 3:
sebuah pengklasifikai adalah optimal secara lokal untuk sample jika dan hanya jika nilai zero-one loss pada sample tersebut adalah sama dengan ukuran bayes. Definisi 4:
Sebuah pengklasifikasi adalah optimal secara global untuk sample jika dan hanya jika pengklasifikasian tersebut bernilai optimal untuk tiap sample pada kumpulan sample tersebut. Sebuah pengklasifikasi adalah optimal secara global untuk sebuah
23 | P a g e
masalah jika dan hanya jika pengklasifikasi tersebut optimal secara lokal untuk tiap sample yang mungkin dari masalah tersebut.
Zero –one loss harus dibedakan dengan squared error loss untuk perhitungan galat peluang, perbedaan ini didifenisikan sebagai :
Dimana X adalah prosedur hampiran dan C adalah variable kelas dimana peluangnya ingin dicari. Jika ada ketidakpastian yang berhubungan dengan P(C|E), square error loss didefinisikan sebagai nilai yang diharapkan dari expresi diatas. Fikiran utama dari paper ini, di deskripsikan pada bagian ini, yang dapat dijelaskan sebagai berikut. Saat asumsi independen dilanggar, persamaan 2 akan menjadi suboptimal sebagai
probabilitas.
Sebagai contoh, misalkan ada dua kelas, yaitu kelas dan , dan dan sebagai nilai peluang kedua kelas yang sebenarnya. Klasifikasi optimal adalah menugaskan E kepada kelas . Misalkan naïve bayes mendapatkan
dan . asumsi independen dilanggar dengan sangat jauh, dan square error loss sangat besar, tetapi naïve bayes masih mendapatkan keputusan klasifikasi yang benar, dan meminimalisir zero-one loss.
Misalkan ada dua kelas secara umum, yaitu kelas dan seperti sebelumnya,
Sekarang kita akan menciptakan kondisi yang dibutuhkan untuk keoptimalan local dari naïve bayes dan memperlihatkan bahwa volume dari daerah keoptimalan naïve bayes adalah setengah dari volume .
Teorema 1
Naïve bayes optimal secara local dibawah zero-one loss untuk data E jika dan
hanya jika untuk E.
Bukti : Pengklasifikasian naïve bayes optimal saat zero-one loss memiliki nilai yang paling minimum. Saat minimum loss adalah didapatkan dari
24 | P a g e menugaskan ke kelas . Pengklasifikasi naïve bayes menugaskan ke kelas saat
berdasarkan persamaan 2, yaitu saat . Oleh karenanya jika , maka naïve bayes adalah optimal. Sebaliknya, saat , zero-one loss minimum didapatkan dengan menugaskan E ke kelas , dimana pengklasifikasian naïve bayes lakukan saat . Olehkarenanya pengklasifikasian naïve bayes optimal saat . Saat keputusan manapun akan optimal, sehingga pertidaksamaan dapat di representasikan sebagai berikut:
Pengklasifikasian naïve bayes optimal di bawah zero-one loss pada setengah dari volume dari seluruh ruang nilai yang mungkin dari
Bukti : Karena adalah sebuah peluang, dan dan adalah produk dari peluang, hanya menempati nilai dalam kubus [0,1]3. Daerah dari kubus tersebut yang memuaskan kondisi pada teorema 1 ditunjukkan oleh daerah abu-abu pada gambar 4. Dapat di perhatikan bahwa daerah abu-abu menempati setengah dari volume total kubus. Tetapi tidak seluruh pasangan dan mewakili kobinasi peluang yang benar. Karena tidak dibatasi, maka projeksi dari ruang semesta dari kombinasi peluang yang valid pada seluruh bidang adalah sama. Dengan teorema 1, daerah keoptimalan dari bidang dan sebaliknya. Oleh karenanya, jika adalah area dari projeksi dan adalah daerah optimal dari , daerah optimal untuk adalah , dan volume total dari keoptimalan adalah .
25 | P a g e Secara kontras dibawah squared error loss, persamaan 2 optimal sebagai kumpulan estimasi peluang P(Ci|E) hanya pada saat asumsi independen bertahan, yaitu pada bidang dan bertemu. Oleh karenanya daerah dari keoptimalan persamaan 2 dibawah squared error loss adalah sangat kecil dibandingkan dengan zero-one loss. Pengklasifikasian naïve bayes efektif sebagai pemprediksi optimal untuk kelas yang paling sering muncul pada sebuah kondisi yang lebih besar dimana asumsi independen dilanggar. Notasi sebelumnya dari keterbatasan pengklasifikasi naïve bayes sekarang dapat dilihat sebagai kesalahan pengaplikasian intuisi
berdasarkan keterbatasan squared error loss pada performa pengklasifikasi naïve bayes pada zero-one loss.
4.3 Keoptimalan global
Ekstensi dari teorema 1 pada keoptimalan global adalah langsung. Misalkan p,r dan s pada data E di indexkan sebagai .
Teorema 2
Pengklasifikasian naïve bayes optimal secara global pada zero-one loss untuk sebuah sample (data set) ∑ jika dan hanya jika
Bukti : dengan definisi 4 dan teorema 1
Membuktikan kondisi ini secara langsung pada test sample secara umum tidak dapat dilakukan, karena pembuktian membutuhkan penemuan peluang kelas yang sebenarnya dari setiap kelompok atribut tersebut pada sample. Lebih jauh, membuktikannya pada sebuah permasalahan membutuhkan komputasi yang seukuran dengan banyaknya kumpulan atribut yang dimungkinkan.
26 | P a g e
BAB V KESIMPULAN
Pada paper ini telah ditunjukkan bahwa pengklasifikasian Naïve Bayes dibawahpengukuran galat zero-one loss memiliki potensi pengaplikasian yang lebih luas dari yang dikira sebelumnya dan menunjukkan perbedaan pengaplikasian zero-one loss dan squared error loss dalam pengklasifikasian data, walaupun pembuktian secara mendalam belum dapat dilakukan karena sifat abstraksi data yang sangat tinggi, asumsi-asumsi keoptimalan yang telah dijabarkan diatas paling tidak dapat memberikan acuan untuk pengaplikasian pada data untuk klasifikasi pada sebuah permasalahan tertentu.
27 | P a g e
DAFTAR PUSTAKA
[1] Domingos, P., and Pazzani, M. (1997). On the optimality of the Simple Bayesian Classifier under Zero-One Loss.
[2] Tom M. Mitchell (1997). Machine Learning. New York, NY: McGraw-Hill. [3] Duda, R.O., and Hart, P.E. (1973). Pattern classification and scene analysis. New
York, NY: Wiley.
[4] Berson, A., and Smith S. J. (2001). Data Warehousing, Data Mining, & OLAP. New York, NY : McGraw-Hill.
[5] Han, J., and Kamber M. (2000). Data Mining, Concept and Techniques. New York, NY : Morgan Kaufmann.
[6] Walpole, E. R., Myers, R. H. (1995). Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuan, Edisi ke-4. Bandung, ITB.
[7] Prof. DR. Sudjana., M.A., M.Sc (1996). Metoda Statistika, Edisi ke-6. Bandung, Tarsito.