Welcome to ePrints Sriwijaya University - UNSRI Online Institutional Repository
Teks penuh
Gambar
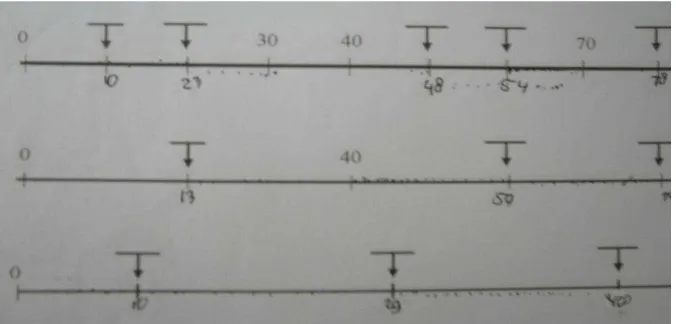
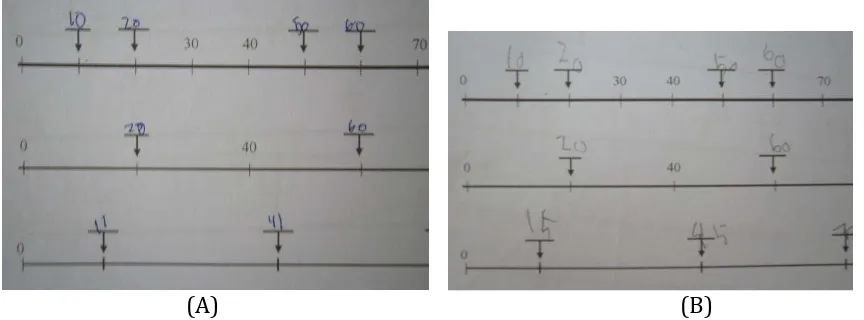
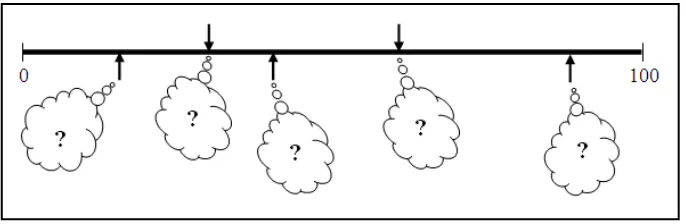

Dokumen terkait
Tutor menjelaskan garis besar seluruh materi yang dibahas dalam satu matakuliah dari pertemuan 2-7. Tutor memberi solusi mengenai konsep yang kurang
Jumlah penduduk Kota Payakumbuh pada tahun 2015 adalah 127.826 jiwa, dengan. pertumbuhan penduduk pada tahun 2015
Menyelesaikan masalah tentang momentum, impuls dan hubungan antara impuls dan momentum serta tentang hukum kekekalan momentum Tes Tertulis tentang impuls, momentum dan hukum
Hasil penelitian ini diharapkan dapat memberikan informasi yang bermanfaat mengenai relevansi dari pengungkapan Good Corporate Governance (GCG) dalam laporan
[r]
Deasy Natacha 2012-012-403 Samuel Reven Lorenzo 2012-012-405. PROGRAM
Demikian biodata ini saya buat dengan sebenarnya untuk memenuhi salah satu persyaratan dalam pengajuan Hibah Program Kreativitas Mahasiswa bidang Karsa Cipta.. Penghargaan
Retinopati merupakan penyebab morbiditas utama pada pasien diabetes dengan akibat akhir yang paling ditakuti adalah kebutaan. Kegagalan terapi laser untuk