A graph, G, consists of two sets V and E. V is a finite non-empty set of vertices. E is a set of pairs of vertices, these pairs are called edges.
Ellis Horowitz, Sartaj Sahni, “Fundamentals of Data
Structures”
A graph consists of a set of nodes (or vertices) and a set of arcs ( or edges).
Each arc in a graph is specified by a pair of nodes. Aarn M. Tenebaum , “Data Structures Using C and C++”
Graph, termasuk struktur non linear, yang oleh beberapa buku literatur didefinisikan
sebagai berikut :
Dari definisi diatas dapat disimpulkan, bahwa graph adalah kumpulan dari
simpul dan busur yang secara matematis dapat dinyatakan sebagai berikut :
G = (V, E)
Dimana :G = Graph,
V = Simpul atau Vertex, atau Node, atau Titik. E = Busur atau Edge, atau arc.
Contoh sebuah graph Simpul = Titik, Node atau Vertex.
Disini diambil istilah Vertex (dilambangkan dengan V). Dalam gambar diilustrasikan dengan lingkaran V = { v1, v2, ………….., v5}
Baca : V terdiri dari v1, v2, ……… v5.
Matematik : V adalah himpunan dengan anggota v1, v2, v3, ….v5
Busur = Arc, Edge
Disini diambil istilah Edge (dilambangkan dengan E) E = { e1, e2, …………., e7 A B C E D v1 Gambar 12.1 a Contoh sebuah Graph
e1 e2 e3 e4 e5 e6 e7 v4 v5 v3 v2
Catatan : Busur sebenarnya hanyalah sebuah kejadian (incidence) dimana dua dua buah simpul mempunyai hubungan satu sama lain. Sehingga dapat dikatakan, busur adalah dua buah simpul yang berpasangan. Untuk menyatakan dua buah simpul berpasangan, maka dalam gambar diilustrasikan dengan sebuah garis yang mengubungkan kedua buah simpul tersebut. Jadi sebenarnya secara fisik garis itu tidak ada. Untuk menyatakan sebuah busur yang merupakan pasangan simpul v1 dan v2 biasanya ditulis sebagai berikut :
e
v1,v2 ataue
1,2 atau (1,2)Bab
12.1. Graph Tak Berarah dan Graph Berarah.
Dilihat dari ‘bentuk’ busur (baca: ‘ urutan penyebutan pasangan dua buah simpul), graph dapat dibedakan menjadi 2 macam :
1. Graph Tak Berarah (undirected graph atau non-directed graph), dan 2. Graph berarah (directed graph atau sering ditulis digraph)
Contoh graph tak berarah (Gambar-12.2) dan graph berarah (Gambar-12.3)
.
A B C E D v1 Gambar 12.2
Contoh sebuah Graph Tak Berarah e1 e2 e3 e4 e5 e6 e7 v4 v5 v3 v2 A B C E D v1 Gambar 12.3
Contoh sebuah Graph Berarah e1 e2 e3 e4 e5 e6 e7 v4 v5 v3 v2 e8 e9 e10
Graph tak berarah (undirected graph atau non-directed graph).
Pada graph tak berarah, urutan simpul dalam sebuah busur, tidak dipentingkan. Sehingga pada busur e1, dapat disebut busur A,B atau B,A. Hal ini dapat diidentikkan dengan sebuah jalan yang yang menghubungkan dua buah titik, yang dapat dilalui dari dua arah. Pada Gambar 12.2 terlihat bahwa dari A dapat ke B, dan dari B dapat ke A melalui jalan yang sama.
Graph berarah (directed graph).
Pada graph berarah, urutan simpul mempunyai arti. Pada Gambar 10.3, telihat busur
A,B adalah busur e1. Sedangkan busur B,A adalah busur e8. Hal ini dapat
Gambar 12.1 b Gambar 12.1 c Gambar 12.1 d Gambar 12.1e
Full connected Graph Sebuah graph mungkin hanya terdiri dari satu simpul (Gambar-12.1 b)
Sebuah graph belum tentu semua simpulnya terhubung dengan busur (Gambar-12.1
c)
Dalam sebuah graph mungkin saja ada simpul yang tak terhubung dengan simpul lainnya oleh busur (Gambar-12.d)
Dalam sebuah graph kemungkinan semua simpul saling berhunbungan (Gambar-12.1
12.2. Graph Berbobot (Weighted Graph).
Apabila setiap busur mempunyai sebuah nilai yang menyatakan hubungan antara dua buah simpul, maka busur tersebut dikatakan mempunyai bobot, dan graph disebut graph berbobot atau weighted graph. Bobot sebuah busur dapat menyatakan panjang sebuah jalan antara dua buah titik, atau jumlah rata-rata kendaraan per hari yang melalui sebuah jalan atau mungkin saja selisih nilai antara dua buah simpul dan sebagainya. Contoh graph berbobot diperlihatkan pada Gamabr-12.4 dan Gambar-12.5
Gambar 12.4
Contoh sebuah Graph berbobot Tak Berarah A B C E D 5 4 3 12 3 6 8 A B C E D Gambar 12.5
Contoh sebuah Graph berbobot Berarah 5 3 4 3 6 8 12 4 7 10
Catatan : Dalam penggambaran sebuah graph berbobot, panjang busur (baca : bobot hubungan antara dua buah simpul) mungkin tidak digambarkan secara panjang yang proporsional dengan bobotnya. Misal, ada kemungkinan 5 digambarkan lebih panjang dari 7. Hal ini biasa dalam teknis penggambaran.
12.3. Graph Sederhana (Simple Graph), dan Graph Tak Sederhana (complex graph).
Graph sederhana adalah graph yang mempunyai busur (baca : hubungan antara dua buah simpul) paling banyak hanya satu ‘macam’. Graph pada Gambar-12.2, Gambar-12.3, Gambar-12.4, Gambar-12.5 adalah contoh graph sederhana, baik berarah atau tak berarah, berbobot atau tak berbobot. Apabila dalam suatu graph ada paling sedikit dua buah simpul yang mempunyai hunbungan lebih dari satu macam, atau ada busur yang membentuk loop (busur yang ‘keluar dari’ dan ‘masuk ke’ simpul yang sama), atau yang menyatakan hubungan didalam simpul itu sendiri, maka graph tersebut dikatakan graph tidak sederhana (complex graph), atau sering juga disebut multi graph, seperti yang dicontohkan pada Gambar-12.6.
a b c d
Gambar-12.6 Graph Tidak Sederhana
12.4. Sub Graph .
Sub graph adalah bagian dari graph. Bahkan graph itu sendiri merupakan sub graph dari dirinya sendiri. Berikut ini dicontohkan hanya untuk graph sederhana tak berbobot dan tak berarah seperti pada Gamabr-12.7.
Gambar-12.7 A B C E D a. Graph G. b. Graph G1 A B C E D A B C E D c. Graph G2 d. Graph G3 A B C E A B C E D A B C E e. Graph G4 f.Graph G5 Keterangan Gambar-12.7. :
G1 merupakan sub graph dari graph G.
G2 merupakan sub graph dari G1 sehingga G2 juga merupakan sub graph dari graph G
G2 dan G3 merupakan subgraph yang membentuk struktur pohon sehingga disebut
Spanning Tree.
Spanning Tree adalah sub graph yang membentuk pohon dengan jumlah simpul sama
dengan yang dimiliki oleh graph aslinya.
Tree adalah graph tanpa cycle. (pengertian cycle, lihat keterangan berikutnya) G4, G5 juga merupakan sub graph dengan jumlah simpul yang lebih sedikit dari dari jumlah
simpul graph aslinya.
Dari ilustrasi diatas, terlihat bahwa :
1. Jumlah simpul suatu subgraph mungkin sama atau mungkin juga lebih sedikit dari
jumlah simpul graph aslinya. Secara matematik dinyatakan : V’
⊆
V12.5. Full Connected Graph .
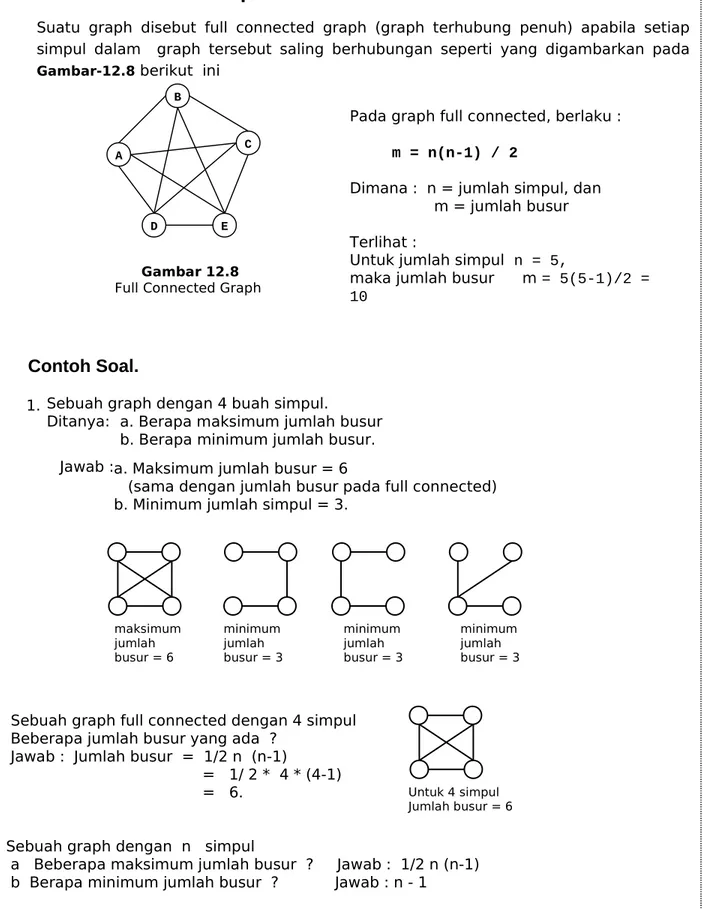
Suatu graph disebut full connected graph (graph terhubung penuh) apabila setiap simpul dalam graph tersebut saling berhubungan seperti yang digambarkan pada Gambar-12.8 berikut ini
Gambar 12.8 Full Connected Graph
B
D
A C
E
Pada graph full connected, berlaku : m = n(n-1) / 2
Dimana : n = jumlah simpul, dan m = jumlah busur Terlihat :
Untuk jumlah simpul n = 5,
maka jumlah busur m = 5(5-1)/2 = 10
1. Sebuah graph dengan 4 buah simpul.
Ditanya: a. Berapa maksimum jumlah busur b. Berapa minimum jumlah busur. Jawab :a. Maksimum jumlah busur = 6
(sama dengan jumlah busur pada full connected) b. Minimum jumlah simpul = 3.
maksimum jumlah busur = 6 minimum jumlah busur = 3 minimum jumlah busur = 3 minimum jumlah busur = 3
Contoh Soal.
2. Sebuah graph full connected dengan 4 simpul Beberapa jumlah busur yang ada ?
Jawab : Jumlah busur = 1/2 n (n-1)
= 1/ 2 * 4 * (4-1) = 6.
3. Sebuah graph dengan n simpul
a Beberapa maksimum jumlah busur ? Jawab : 1/2 n (n-1) b Berapa minimum jumlah busur ? Jawab : n - 1
Untuk 4 simpul Jumlah busur = 6
4. Sebuah graph full connected dengan n simpul.
Berapa jumlah busur ? Jawab : 1/2 n ( n - 1 ) 5. Sebuah Graph terdiri dari 75 busur .
Berapa minimum jumlah simpul ?
Jawab : Jumlah busur maksimum = ½ n ( n -1 ) Jadi : 75 < ½ n (n-1) 150 < n (n-1)
6. Sebuah graph terdiri dari 75 busur Berapa maksimum jumlah simpul ?
Jawab : Jumlah simpul maksimum = 75 + 1
= 76 tidak mungkin lebih dari 76 Perhitungan : 75 = n - 1 n = 76 Secara matematis mencari nilai n disini agak sulit sbb: dengan trial and error didapat n = 13 karena 13*12=156 dan benar 150 < 156 Jadi n = 13 Jumlah simpul (n)
Menggunakan tabel mungkin lebih praktis sbb: Maximum jumlahbusur (=full connected) ( n(n-1)/2 1 2 3 4 5 6 7 8 9 10 11 12 13 14 0 1 3 6 10 15 21 28 36 45 55 66 78 91 75 berada disini diantara 66 dan 78
Jadi jumlah simpul tak mungkin 12, karena kalau n =12 maka jumlah busur paling banyak 66.
Untuk jumlah busur = 75,
maka n bisa 13, 14, 15, ……….., 76 Yang mimimum adalah 13
Jadi jumlah simpul minimum = 13 atau minimum n = 13 1 2 1 2 3 75 75 76 Jumlah busur = 75 Jumlah simpul
12.6. Beberapa Istilah pada Graph.
Beberapa istilah atau pengertian yang digunakan pada graph. 1. Incident.
Apabila e merupakan busur dengan simpul-simpulnya adalah v dan w yang ditulis e=(v,w), maka v dan w disebut ‘terletak’ pada e, dan e disebut incident dengan v dan w
2. Degree (derajat) , indegree dan outdegree.
Degree sebuah simpul adalah jumlah busur yang incident dengan simpul tersebut. Pada Gambar 12-2, degree simpul A atau v1 = 2. Dan degree simpul B atau v2 = 3. Sedangkan pada Gambar-12.3 degree simpul B atau v2 = 5.
Indegree sebuah simpul pada graph berarah, adalah jumlah busur yang kepalanya (head) incident pada
simpul tersebut, atau dapat dikatakan jumlah busur yang ‘masuk’ atau menuju simpul tersebut.
Outdegree sebuah simpul pada graph berarah, adalah
jumlah busur yang buntutnya (tail) incident pada simpul tersebut, atau dapat dikatakan jumlah busur yang ‘keluar’ atau berasal dari simpul tersebut.
Pada
Gambar-12.3 indegree simpul B adalah 2 danoutdegree = 3
3. Adjacent.
Pada graph tak berarah, dua buah simpul disebut adjacent bila ada busur yang ‘menghubungkan’ kedua simpul tesebut Pada Gambar-12.10a simpul v dan simpul w disebut adjacent.
Pada graph berarah, sebuah simpul v disebut adjacent dengan simpul w, ( v is adjacent to w) apabila ada busur dari w ke v. Pada Gambar-12.10b simpul v adjacent dengan simpul w.
e
v
w
Gambar-12.9e
v
w
Gambar-12.10ae
v
w
Gambar-12.10b 4. Successor dan Predecessor.Pada graph berarah, bila simpul v adjacent dengan simpul w, lihat Gambar-12.10b, maka disebut simpul v adalah successor (pengganti atau pelanjut) simpul w, dan simpul w adalah predecessor (pendahulu) dari simpul v
A B C E D v1 Gambar 12.2 Graph Tak Berarah e1 e2 e3 e4 e5 e6 e7 v4 v5 v3 A B C E D v1 Gambar 12.3 Graph Berarah e1 e2 e3 e4 e5 e6 e7 v4 v5 v3 v2 e8 e9 e10
5. Path.
Sebuah path adalah serangkaian ( a sequence) simpul-simpul yang berbeda, yang adjacent secara berturut turut dari simpul satu ke simpul berikutnya. Gambar-12.11 a
,
menggambarkan path dari simpul 1 ke simpul 4 pada graph tak berarah, sedangkan Gambar–12.11 b,
menggambarkan path pada graph berarah.Gambar-12..11 a b 1 2 4 3 1 2 4 3 c d Directed Cycle 1 2 4 3 1 2 4 3 6. Cycle.
Cycle adalah path yang terdiri dari sekurang-kurangnya 3 simpul sedemikian rupa simpul yang terakhir adjacent dengan simpul pertama. Gambar-12.11 c
,
menggambarkan cycle 4 buah simpul pada graph tak berarah, sedangkan Gambar-12.11 d,
menggambarkan cycle pada graph berarah. Cycle sering juga diterjemahkan menjadi path yang melingkar, atau path yang membuat suatu lingkaran.12.7. Representasi Graph.
Dalam pemrograman, agar data data yang ada dalam graph dapat diolah, maka graph harus dinyatakan dalam suatu struktur data yang dapat mewakili graph tersebut. Dalam hal ini graph perlu direpresentasikan kedalam bentuk array dua dimensi yang sering juga disebut matrix, atau direpresentasikan dalam bentuk
linked-list. Bentuk mana yang dipilih, biasanya tergantung kepada efisiensi dan
kemudahan dalam membuat program. Berikut ini beberapa bentuk representasi graph :
I. Representasi graph dalam bentuk matrix : 1. Adjacency Matrix
2. Inverse Adjacency Matrix (hanya unuk Graph Berarah) 3. Insidence Matrix
4. Vector Matrix
II. Representasi graph dalam bentuk Linked List : 1. Adjanency List
2. Matrix yang terbentuk adalah matrix symetris dengan sumbu symetris adalah diagonal dari titik kiri atas ke titik kanan bawah. Lihat Gambar-12.13
Terlihat bagian matrix sebelah ‘atas’ sumbu symetris sama dengan bagian matrix sebelah ‘bawah’ sumbu symetris.
0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 A B C D E A B C D E Gambar 12.13 Adjacency Matrix sumbu symetris
3. Data yang terdapat baik dalam row maupun column, dapat menyatakan degree sebuah simpul.
Contoh : baik row D (row 3) maupun column D (column 3) jumlah angka 1 sama dengan 3 buah. Ini menyatakan bahwa degree simpul D adalah = 3.
Lihat Gambar-12.14 adanGambar-12 b
0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 A 0 B 1 C 2 D 3 E,4 A 0 B1 C2 D3 E4 Gambar 12.14 a Adjacency Matrix A B C E D Gambar 12.14 b Graph 12.7.1.1. Adjacency Matrix Graph Tak Berarah (Undirected Graph)
A B C E D Gambar 10.12 a Graph 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 A 0 B 1 C 2 D 3 E 4 A 0 B1 C2 D3 E4 Gambar 10.12 b Adjacency Matrix
Matrix yang digambarkan pada Gambar-10.12 b merupakan representasi dalam bentuk Adjacency Matrix dari graph yang digambarkan pada Gambar-10.12 a. Beberapa hal yang dapat dilihat atau dapat diterangkan pada Adjacency Matrix tersebut adalah sebagai berikut :
1. Matrix yang terbentuk adalah matrix bujur sangkar n * n
,
dimana n = jumlah simpul yang ada dalam graph tersebut. Matrix ini menyatakan hubungan antara simpul satu dengan simpul lainnya (simpul-simpul yang adjacent ).Setiap elemen matrix diisi dengan angka 0 atau angka 1.
Angka 1, menyatakan ada hubungan (ada busur) atau adjacent antara dua buah Simpul.
Contoh : angka 1 pada elemen (1,4) menyatakan ada hubungan antara Simpul B dan Simpul E
Representasi Adjacency Matrix dalam Bahasa C / C++.
A B C E D Gambar 12.15a Graph 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 A 0 B 1 C 2 D 3 E 4 0 1 2 3 4 Gambar 10.15 b Adjacency Matrix A B C D EUntuk menyatakan simpul-simpul dibuatkan sebuah array yang berisi nama atau identitas simpul :
Char NmS [5] = “ABCDE”;
Untuk Matrix dapat dibuat dengan : char A[5][5] = { “01010”, “10101”, “01011”, “10101”, “01110” }; char A[5][5] = { “01010”, “10101”, “01011”, “10101”, “01110” };
Untuk merepresentasikan graph 10.15a menjadi Adjacency Matrix dapat dibuat dengan instruksi sebagai berikut :
int A[5][5] = { 0,1,0,1,0, 1,0,1,0,1, 0,1,0,1,1, 1,0,1,0,1, 0,1,1,1,0 }; Atau dengan : int A[5][5] = { 0,1,0,1,0, 1,0,1,0,1, 0,1,0,1,1, 1,0,1,0,1, 0,1,1,1,0 };
Bila ingin menggunakan tipe karakter (char), dapat ditulis sebagai berikut : Perhatikan Gambar-10.15 a.
A, B, C, D dan E adalah Nama Simpul, atau Nomor Simpul atau Identitas
Simpul yang dapat disimpan dalam array satu dimensi tipe karakter sebagai berikut :
char NmS [5] = “ABCDE”;
0 1 2 3 4
NmS
Bila dibuat dengan tipe char maka untuk menyatakan nilai harus menggunakan tanda kutip. Sebagai contoh :
if( A[i][j] ==
‘1’ )
2. Matrix yang terbentuk mungkin symetris mungkin juga tidak symetris. Menjadi symetris bila hubungan antara dua buah simpul (v1 dan v2) terdapat busur dari v1 ke v2 dan juga terdapat busur dari v2 ke v1.
3. Hal pokok yang ingin dinyatakan oleh matrix ini adalah : Busur yang ‘keluar’ dari suatu simpul. Dengan demikian, data yang terdapat dalam suatu row, dapat menyatakan outdegree simpul yang bersangkutan.
Contoh : Jumlah elemen yang nilainya = 1 pada row B (row 1) ada 3 elemen, ini menyatakan outdegree simpul B = 3.
Lihat Gambar-10.17c
12.7.1.2. Adjacency Matrix Graph Berarah (Directed Graph)
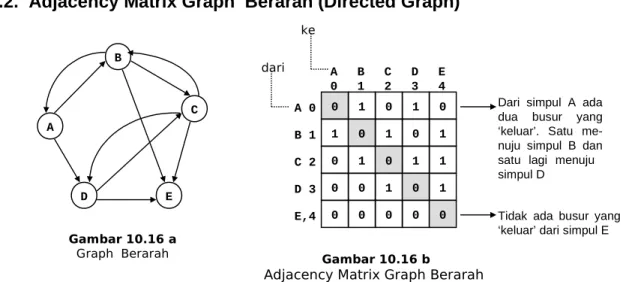
Matrix yang digambarkan pada Gambar-10.16 b merupakan adjacency matrix dari graph berarah yang digambarkan pada Gambar-10.16 a. Beberapa hal yang dapat dilihat atau dapat diterangkan pada adjacency matrix tersebut adalah sebagai berikut :
1. Matrix yang terbentuk adalah matrix bujur sangkar n * n, dimana n = jumlah simpul yang ada dalam graph tersebut. Matrix ini menyatakan hubungan satu arah antara simpul satu dengan simpul lainnya.
A B C E D Gambar 10.16 a Graph Berarah B Gambar 10.17 b outdegree simpul B = 3 A B C E D Gambar 10.17 a 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 A 0 B 1 C 2 D 3 E,4 A 0 B1 C2 D3 E4 Gambar 10.16 b
Adjacency Matrix Graph Berarah dari
ke
Dari simpul A ada dua busur yang ‘keluar’. Satu me-nuju simpul B dan satu lagi menuju simpul D
Tidak ada busur yang ‘keluar’ dari simpul E
Gambar 10.17 c Outdegree simpul B = 3
Yang ‘keluar’ dari simpul B ada 3 busur yaitu ‘menuju’ simpul A, simpul C dan simpul E. (lihat elemen yang berisi nilai 1)
dari 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 A 0 B 1 C 2 D 3 E,4 A 0 B1 C2 D3 E4 ke
4. Data yang terdapat dalam suatu column, dapat menyatakan indegree simpul yang bersangkutan.
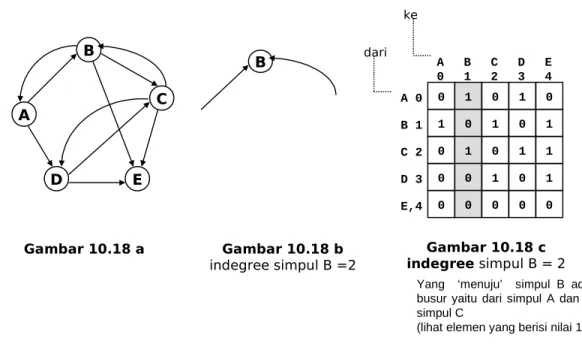
Contoh : Jumlah elemen yang nilainya = 1 pada column B (column 1) ada 2 elemen, ini menyatakan indegree simpul B = 2.
Lihat Gambar-12.18c Gambar 10.18 c indegree simpul B = 2 Gambar 10.18 b indegree simpul B =2 Gambar 10.18 a A B C E D B
Yang ‘menuju’ simpul B ada 2 busur yaitu dari simpul A dan dari simpul C
(lihat elemen yang berisi nilai 1) dari 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 A 0 B 1 C 2 D 3 E,4 A 0 B1 C2 D3 E4 ke
12.7.1.3. Inverse Adjacency Matrix Graph Berarah (Directed Graph)
Matrix yang digambarkan pada Gambar-10.19 b merupakan Inverse adjacency matrix dari
graph berarah yang digambarkan pada Gambar-12.19 a
.
Hal pokok yang ingin dinyatakan oleh matrix ini adalah : busur yang menuju ke suatu simpul.Perbedaan pokok dengan adjacency matrix adalah :
1. Data yang ada dalam suatu row, menyatakan indegree, dan 2. Data yang ada dalam column, menyatakan outdegree.
Gambar 12.19 a Graph Berarah A B C E D 0 1 0 0 0 1 0 1 0 0 0 1 0 1 0 1 0 1 0 0 0 1 1 1 0 A 0 B 1 C 2 D 3 E,4 A 0 B 1 C 2 D 3 E 4 Gambar 12.19 b
Adjacency Matrix Graph Berarah Menuju
ke dari
Hanya ada satu busur yang menuju simpul A yaitu yang dari simpul B.
Ada tiga busur yang menuju sim-pul E yaitu dari simpul B, C dan D
12.7.1.4. Adjacency Matrix Graph Berbobot Tak Berarah (Weighted Undirected Graph)
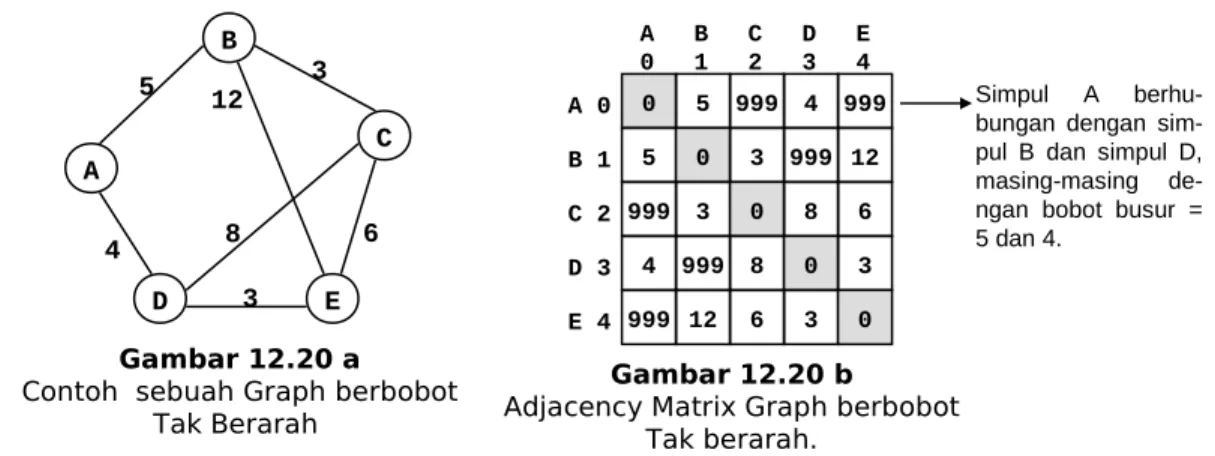
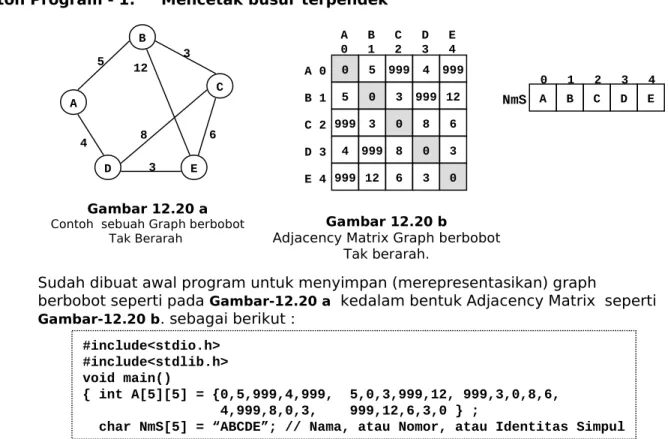
Nilai yang ada dalam tiap elemen matrix, menyatakan bobot busur yang menghubungkan dua buah simpul yang bersangkutan. Untuk dua buah simpul yang tidak berhubungan langsung atau tidak dihubungkan langsung oleh sebuah busur, maka dianggap dihubungkan oleh sebuah busur yang nilai bobotnya tidak terhingga. Dalam pemrograman, karena keperluan algoritma, maka untuk menyatakan nilai tak terhingga, dapat digunakan sebuah nilai yang dipastikan lebih besar dari total bobot seluruh busur yang ada atau yang mungkin ada. Contoh lihat Gambar-10.20. Simpul A dan simpul C tidak berhubungan langsung melalui sebuah busur, maka untuk elemen matrix yang bersangkutan diisi dengan nilai 999, karena nilai 999 dalam kasus ini dianggap cukup mewakili nilai tak terhingga.
0 5 999 4 999 5 0 3 999 12 999 3 0 8 6 4 999 8 0 3 999 12 6 3 0 A 0 B 1 C 2 D 3 E 4 A 0 B1 C2 D3 E4 Gambar 12.20 b
Adjacency Matrix Graph berbobot Tak berarah.
Simpul A berhu-bungan dengan sim-pul B dan simsim-pul D, masing-masing de-ngan bobot busur = 5 dan 4.
Gambar 12.20 a Contoh sebuah Graph berbobot
Tak Berarah A B C E D 5 4 3 12 3 6 8
12.7.1.5. Incidence Matrix Graph Tak Berarah.
Incidence matrix ini dengan ukuran n * m ( n = jumlah simpul, dan m = jumlah busur) merepresentasikan hubungan antara simpul dengan busur
A B C E D v1 Gambar 12.21 a Graph Tak Berarah
e1 e2 e3 e4 e5 e6 e7 v4 v5 v3 v2 1 1 0 0 0 1 0 1 1 0 0 0 1 0 1 0 1 0 0 1 0 0 0 1 0 A 0 B 1 C 2 D 3 E,4 e1 0 e21 e32 e43 e54 Gambar 12.21 b Incidence Matrix 0 0 0 0 0 1 1 0 1 1 e6 5 e76 Matrix n * m
n = jumlah simpul, dan m = jumlah busur 1 1 0 0 0 1 0 1 1 0 0 0 1 0 1 0 1 0 0 1 0 0 0 1 0 A 0 B 1 C 2 D 3 E,4 e1 0 e21 e32 e43 e54 Gambar 12.21 c Incidence Matrix 0 0 0 0 0 1 1 0 1 1 e6 5 e76
Busur yang ada hubungan dengan simpul B adalah busur : e1, e3, dan e4.
Terlihat dalam row (baris) B terdapat 3 buah angka ‘1’
artinya : Dari Simpul B ‘keluar’ 3 buah busur, yaitu e1, e3, dan e4
Simpul yang dihubungkan oleh busur e2 adalah simpul A dan D. Terlihat : Kolom suatu Incidence Matrix memperlihatkan hubungan antara dua buah simpul. (hanya dua buah simpul)
0 5 999 4 999 5 0 3 999 12 999 3 0 8 6 4 999 8 0 3 999 12 6 3 0 A 0 B 1 C 2 D 3 E 4 A 0 B1 C2 D3 E4 Gambar 12.20 b
Adjacency Matrix Graph berbobot Tak berarah.
Gambar 12.20 a Contoh sebuah Graph berbobot
Tak Berarah A B C E D 5 4 3 12 3 6 8
Sudah dibuat awal program untuk menyimpan (merepresentasikan) graph
berbobot seperti pada Gambar-12.20 a kedalam bentuk Adjacency Matrix seperti Gambar-12.20 b. sebagai berikut :
#include<stdio.h> #include<stdlib.h> void main()
{ int A[5][5] = {0,5,999,4,999, 5,0,3,999,12, 999,3,0,8,6, 4,999,8,0,3, 999,12,6,3,0 } ;
char NmS[5] = “ABCDE”; // Nama, atau Nomor, atau Identitas Simpul
A B C D E 0 1 2 3 4
NmS
Soal-1 : Lengkapi program diatas untuk mencetak busur yang paling pendek, serta berapa
panjang busurnya. Bila busurnya lebih dari satu buah, maka sebutkan nama busurnya satu per satu. Untuk menyebutkan nama busur maka yang disebut adalah nama Simpul-Asal dan Simpul-Tujuan. Bila program Anda benar, maka harus tercetak : 3
B C D E
3 adalah panjang busur yang terpendek, B C dan D E adalah nama busurnya
Jawab :
int I, J, Brs, Kol, Min;
Min = 100; // anggapan tidak ada busur // yang panjangnya >= 100 for(I=0; I<=4; I++)
{ for(J=0; J<=4; J++)
{ if(A[I][J] != 0 && A[I][J] != 999) { if(X < Min) { Min = X; Brs = I; Kol = J; } } } }
printf(“\n %i”, Min);
printf(“\n %c %c”, NmS[Brs], NmS[Kol]);
Program ini masih kurang lengkap karena hanya mencetak nama busur terpendek yang pertama kali ditemui yaitu B C.
Sedangkan busur berikutnya D Minyimpan index Baris di Brs dan index Kolom di Kol
Mencetak semua busur yang terpendek : int I, J, Min;
Min = 100; // anggapan tidak ada busur // yang panjangnya >= 100 for(I=0; I<=4; I++)
{ for(J=0; J<=4; J++)
{ if( A[I][J] != 0 && A[I][J] != 999) { if( A[I][J] < Min)
{ Min = A[I][J]; }
} } }
printf(“\n %i”, Min); for(I=0; I<=4; I++) { for(J=0; J<=4; J++) { if (A[I][J] == Min) { printf(“\n %c %c”, NmS[I], NmS[J] ); } } }
Mencetak busur seba-nyak nilai terkecil yang ada dalam matrix
Mencetak nilai terkecil
Soal-2 : Lengkapi program diatas untuk mencetak hubungan antar simpul.
Bila program Anda benar, maka harus tercetak :
Jawab : A : B D B : A C E C : B D E D : A C E E : B C D Gambar 12.20 a Contoh sebuah Graph berbobot
Tak Berarah A B C E D 5 4 3 12 3 6 8
Mencetak Hubungan Antar Simpul : int I, J;
for(I=0; I<=4; I++)
{ printf(“\n %c : “, NmS[I] ); for(J=0; J<=4; J++)
{ if( A[I][J] != 0 && A[I][J] != 999) { printf(“%c “, NmS[J] );
} } } }
A : B D , menyatakan bahwa Simpul-A ada hubungan
12.7.1.6. Vector Matrix Graph Tak Berarah.
A B C E D v1 Gambar 12.22 a Graph Tak Berarahe1 e2 e3 e4 e5 e6 e7 v4 v5 v3 v2 1 2 0 0 0 3 4 0 3 4 7 0 2 5 6 0 4 6 7 0 A 0 B 1 C 2 D 3 E,4 e 0 e 1 e 2 e 3 Gambar 12.22 b Vector Matrix Simpul C berhubungan dengan busur : e3, e4, dan e7
Vector Matrix ini merepresentasikan hubungan simpul dan busur dengan cara lain, yang berbeda dengan Incidence Matrix.
Ukuran matrixnya : n * (n-1) Dengan n = jumlah simpul, dan
(n-1) = jumlah maksimum busur yang mungkin incedence dengan sebuah simpul
12.7.1.7. Soal-soal Latihan Mandiri.
1. Gambarkan adjacency matrix graph berikut ini :
2. Gambarkan graph yang adjacency matrixnya diberikan sebagai berikut :
A B C E D a b 0 1 1 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 1 0 1 0 A 0 B 1 C 2 D 3 E 4 A 0 B1 C2 D3 E4 0 1 1 0 0 0 0 1 0 1 1 1 0 1 0 1 0 1 0 1 0 0 0 1 0 A 0 B 1 C 2 D 3 E 4 A 0 B1 C2 D3 E4 A B C E D
12.7.2.1. Adjacency List Graph Tak Berarah.
12.7.2. Representasi Graph Dalam Bentuk Linked-List. .
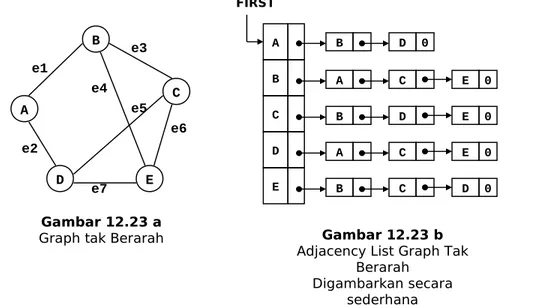
Gambar 12.23 b Adjacency List Graph Tak
Berarah Digambarkan secara
sederhana
Graph pada Gambar-12.23a
,
bila ingin direpresentasikan dalam bentuk Linked-List, dapat diilustrasikan secara sederhana seperti pada Gambar-12.23 b.
Dari ilustrasi sederhana tersebut terlihat ada 5 buah simpul A, B, C, D, dan E yang dibariskan dari atas ke bawah seperti Gambar 12.24 a. Kemudian dari masing-masing simpul ‘keluar’ pointer ke arahkanan yang menunjuk simpul-simpul lain. Salah satu contoh, yang digambar ulang pada
Gambar 10.24 b, dimana terlihat simpul A menunjuk simpul B dan simpul D. A B C D E FIRST B D 0 A C E 0 B D E 0 A C E 0 B C D 0 A B C E D Gambar 12.23 a Graph tak Berarah e1 e2 e3 e4 e5 e6 e7 Gambar 10.24 b A B C D E PSimpul B D 0 Gambar 10.24 a A B C D E PSimpul Perhatikan Gambar-12.24 a.
Ada 5 buah simpul A, sampai E, yang dalam Adjacency List digambar urut abjad. Perhatikan Gambar-12.24 b.
Simpul A berhubungan dengan simpul B dan simpul D. Dalam Adjacency List, simpul B ditulis lebih dulu dari simpul D, sesuai dengan urutan abjad.
Kedua hal diatas merupakan kesepakatan dalam menggambar simpul-simpul dalam Adjacency List. Sama halnya dengan aplikasi pada Adjacency Matrix.
Gambar Adjacency List yang digambarkan pada Gambar-12.23 b
.
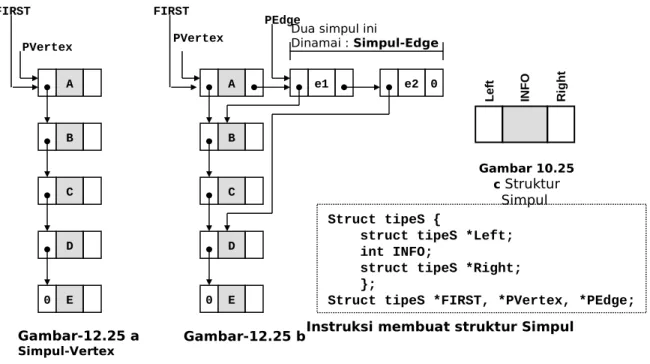
hanyalah sebagai ilustrasi hubungan simpul-simpul secara konsep. Hubungan sebenarnya yang dinyatakan dalam sebuah program dapat dilihat pada Gambar 12.25 berikut ini :PVertex A B C D 0 E Gambar-12.25 a Simpul-Vertex Gambar-12.25 b L ef t IN F O R ig h t Gambar 10.25 c Struktur Simpul
Pada Adjacency List , kita perlu membedakan antara Vertex dan
Simpul-Edge. Simpul-Vertex untuk menyatakan simpul atau Vertex, dan Simpul-Edge untuk
menyatakan hubungan antar simpul yang biasa disebut busur. Struktur keduanya bisa sama, bisa juga tidak sama, tergantung kebutuhan. Untuk memudahkan pembuatan program, struktur kedua macam simpul dibuat sama seperti yang digambarkan pada Gambar-10.25 c. Yang membedakan antara Simpul-Vertex dan Simpul-Edge, adalah anggapan terhadap simpul tersebut. Dalam contoh ini, terlihat struktur simpul dibuat terdiri dari 3 elemen. Satu elemen untuk INFO, dan dua elemen untuk pointer. Pointer disebelah kiri disebut Pointer Left, dan pointer disebelah kanan disebut Pointer Right.
Bila simpul dianggap sebagai Simpul-Vertex, maka :
Pointer Left digunakan untuk menunjuk simpul berikutnya dalam untaian simpul-simpul yang ada, atau diisi NULL bila sudah tidak ada simpul yang perlu ditunjuk. Sedangkan Pointer Right digunakan untuk menunjuk Simpul-Edge yang pertama.
Bila simpul dianggap sebagai Simpul-Edge, maka :
Pointer Left digunakan untuk menunjuk Simpul-Vertex ‘tujuan’ yang berhubungan dengan Simpul-Vertex ‘asal’, dan Pointer Right digunakan untuk menunjuk Simpul-Edge berikutnya bila masih ada, atau niisi NULL bila tak ada lagi Simpul-Busur yang ditunjuk..
FIRST PVertex PEdge A e1 e2 0 B C D 0 E FIRST Struct tipeS {
struct tipeS *Left; int INFO;
struct tipeS *Right; };
Struct tipeS *FIRST, *PVertex, *PEdge; Instruksi membuat struktur Simpul
Dua simpul ini
Perhatikan bagian representasi graph yang diambil dari representasi graph Gambar-12.25 bsebelumnya, sebagai berikut :
Pointer ini diperlukan hanya untuk menujuk simpul berikutnya, dalam suatu untaian simpul secara kese-luruhan Bukan me-nyatakan hubungan busur antar simpul
Pointer ini menunjuk simpul pertama yang berhubungan dengan simpul A, dalam hal ini adalah Simpul-B
Dua buah Simpul-Edge ini menunjukkan bahwa ada dua busur yang ‘keluar’ dari Simpul A.
Pointer ini menunjuk simpul ke-dua yang berhubungan dengan simpul A, dalam hal ini adalah Simpul-D
Pointer ini berisi NULL yang menyatakan tidak ada lagi busur dari A. Gambar 10.25 e Hubungan Simpul Dan Busur A PVertex e1 e2 0 PEdge Gambar 12.25 d Graph tak Berarah A B C E D e1 e2 Contoh Soal :
Susun penggalan program untuk mencetak nama nama simpul yang berhubungan dengan simpul C A B C E D Gambar 12.25 ea Graph tak Berarah
e3
e5 e6
PVertex = FIRST;
while(PVertex->INFO != ‘C’ && PVertex->Left != NULL ) {PVertex = PVertex->Left;
}
if(PVertex->INFO == ‘C’ ) { if(PVertex->Right == NULL)
{ printf(“Simpul C tidak berhubungan dengan “); printf(“simpul lain “);
} else
{ PEdge = PVertex;
while (PEdge->Right != NULL ) { PEdge = PEdge->Right; printf(“%c “, PEdge->Left->INFO) ; } } } else
printf(“Simpul C Tidak Ada “);
Akan tercetak : B D E A B C D 0 E FIRST PEdge e3 e5 e6 0 PVertex Gambar 12.25 f Bagian dari Adjacency List
Graph tak Berarah
Instruksi :
printf(“%c “, Pedge->Left->INFO); yang akan mencetak : B atau D atau E
A B C E D Gambar 12.26 a Graph tak Berarah e1
e2
Kembali kita perhatikan gambar graph dan Adjacency List yang digambar ulang sebagai berikut :
Kita tinjau hubungan Simpul A dengan Simpul B dan Simpul-D, seperti terlihat pada graph Gambar-12.26 a
.
Bagaimana hubungan ini dinyatakan dalam bentuk Adjacency List.Pada Gambar-12.26 b terlihat pointer Right Simpul A, yaitu PVertex->Right menunjuk sebuah Linked List yang terdiri dari dua buah simpul. Pointer Left dari simpul pertama menunjuk Simpul B, dan Pointer Left simpul ke-dua menunjuk Simpul D. Ini menyatakan Simpul A berhubungan dengan Simpul B dan Simpul D.
A B C E D Gambar 12.27 a Graph tak Berarah e1 e3 e4 PVertex PEdge A e1 e3 B C D 0 E FIRST e4 0 Untuk Simpul-B yang berhubungan dengan Simpul-A, C dan E, Adjacency List, dapat digambarkan seperti pada Gambar-12.27 b
PVertex PEdge A e1 e2 0 B C D 0 E Gambar-12.26 b FIRST
Terlihat dalam Adjacency List ini Simpul A ada hubungan dengan Simpul B dan Simpul D. Hubungan dinyatakan dengan melalui dua buah Simpul-Busur.
Q R
Bila pointer Q dan pointer R menunjuk simpul seperti pada Gambar 12.27b, maka Q->Left menunjuk simpul C dan R->Left menunjuk E
A B C E D Gambar 12.28 a Graph tak Berarah e1 e2 e3 e4 e5 e6 e7 Gambar 12.29 a Linked-List Graph Tak
berarah Tak berbobot A B C D 0 E PVertex e1 e2 0 e1 e3 PEdge e3 e2 e5 e4 e4 0 e5 e6 0 e7 0 e6 e7 0 Gambar 12.28 b Linked-List Graph Berbobot Tak berarah
digambarkan secara lengkap A e1 e2 0 B e1 e3 e4 0 C e3 e5 e6 0 D e2 e5 e7 0 0 E e4 e6 e7 0 B D A C E B D E A C E B C D FIRST Gambar 12.29 b Adjacency List Graph Tak
Berarah Digambarkan secara sederhana A B C D E FIRST B D 0 A C E 0 B D E 0 A C E 0 B C D 0
Selengkapnya dapat digambarkan sebagai berikut :
Selanjutnya gambarnya dapat disederhanakan seperti Gambar 10.29 a
atau bahkan cukup dengan Gambar-10.29 b
A B C E D 5 2 7 8 2 12 3 A B C D E FIRST
12.7.2.2. Adjacency List Graph Berbobot Tak Berarah
Ajacency List Graph Tak Berarah, sama dengan adjacency List Graph Berarah dimana arah busurnya selalu pberpasangan. Bila ada busur dari A ke B, harus ada juga busur dari B ke A. Adjacency List Graph Tak Berarah diperlihatkan pada Gambar 10-27 b berikut ini :
Gambar 12.27
Graph Berbobot Tak Berarah Gambar 12.28
Adjacency-List Graph Berbobot Tak berarah
digambarkan secara sederhana
A B C D 0 E PVertex 5 2 0 5 3 PEdge 3 2 8 12 12 0 8 2 0 7 0 2 7 0 Gambar 12.29 Adjacency-List Graph Berbobot Tak berarah digambarkan secara B 5 D 2 0 A 5 C 3 E 12 0 B 3 D 8 E 2 0 A 2 C 8 E 7 0 B 12 C 2 D 7 0
12.7.2.3. Adjacency List Graph Berarah dan Berbobot Gambar 12.30 b Adjacency-List Graph Berarah Dan Berbobot Digambarkan secara sederhana
Graph pada Gambar-12.30 a
,
bila ingin direpresentasikan dalam bentuk Adjacency List, dapat diilustrasikan secara sederhana seperti pada Gambar-10.30 b. Ilustrasi sebenarnya dalam pemrograman dapat digambarkan seperti pada Gambar-12.30 c.Pointer yang menunjuk ke simpul yang ditunjuk olehbusur berikutnya. Info berisi data Bila simpul ini digunakan untuk Vertex, maka berisi data untyuk Vertex. Bila simpul ini digunakan untuk Edge, maka berisi bobot Edge tersebut.
Pointer yang menunjuk simpul berikutnya dalam suatu graph. Sama dengan Adjacency List graph tidak berarah dan tidak berbobot sebelumnya, untuk graph berbobot Simpul-Vertex dan Simpul-Edge dibuat seragam yaitu terdiri dari 3 elemen. Untuk graph berbobot, INFO Simpul-Edge berisi bobot busur tersebut. Gambar 12.30 a Graph Berarah Dan berbobot A B C E D 5 2 7 12 9 14 3 6 Gambar 12.30 c Linked-List Graph Tak
berarah Tak berbobot A B C D 0 E PVertex 5 2 0 6 3 0 PEdge 9 12 7 0 14 0 Gambar 1230 d Struktur sebuah Simpul
digunakan baik untuk Vertex
maupun untuk Edge
A B C D E FIRST B 5 D 2 0 A 6 C 3 0 E 9 0 C 12 E 7 0 B 14 0
12.7.2.4. Inverse Adjacency List Graph Berarah dan Berbobot
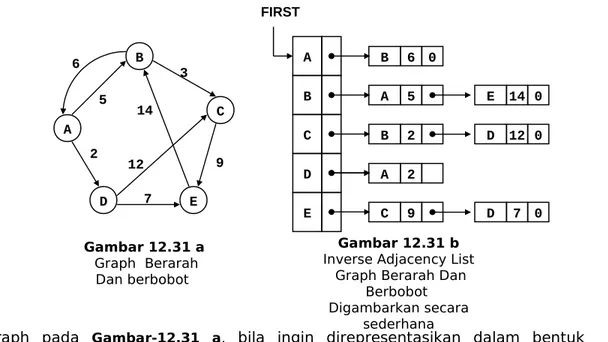
Gambar 12.31 b Inverse Adjacency List
Graph Berarah Dan Berbobot Digambarkan secara
sederhana
Graph pada Gambar-12.31 a, bila ingin direpresentasikan dalam bentuk Inverse Adjacency-List, dapat diilustrasikan secara sederhana seperti pada Gambar-12.31 b. Ilustrasi sebenarnya dalam pemrograman dapat mencontoh Adjacency List yang digambarkan pada Gambar-12.30 c halaman sebelumnya.
Dalam Inverse Adjacency List graph berarah, ditunjukkan simpul apa saja yang menunjuk simpul tertentu. Pada Gambar-12.31 b terlihat pointer yang menuju atau menunjuk Simpul-B adalah berasal dari Simpul A dengan bobot 5 dan dari Simpul-E dengan bobot 14. Gambar 12.31 a Graph Berarah Dan berbobot A B C D E FIRST B 6 0 D 12 0 A 5 E 14 0 B 2 A 2 D 7 0 C 9 A B C E D 5 2 7 12 9 14 3 6
Catatan:Contoh diatas adalah untuk graph berarah dan berbobot. Bila graphnya tidak berbobot strukstur simpulnya tetap 3 elemen, tapi elemen INFO pada Simpul-Edge, tidak perlu diisi, atau diabaikan.
Gambar 12.31 b Inverse Adjacency List
Graph Berarah Dan A B C D E FIRST A 5 E 14 0 Q Q
Walaupun arah panahnya dari B ke A, tapi maksudnya untuk menyatakan bahwa :
Dari simpul mana saja, terdapat busur yang menunjuk B.
Dari contoh ini, terlihat ada busur dari simpul A dengan bobot = 5, dan ada busur dari E dengan bobot = 14 yang menunjuk simpul B Kalau Q dan R menunjuk simpul seperti
pada gambar, maka Q->Left menujnjuk A, dan R->Left menunjuk simpul E.
Gambar 12.32 a Graph Berarah dan berbobot A B C E D 5 2 7 12 9 14 3 6 Gambar 12.32 c Adjacency-List Graph Gambar-12.32 a A B C D 0 E PVertex 5 2 0 6 3 0 PEdge 9 12 7 0 14 0 0 5 999 2 999 6 0 3 999 999 999 999 0 999 9 999 999 12 0 7 999 14 999 999 0 A 0 B 1 C 2 D 3 E 4 A 0 B 1 C 2 D 3 E 4 Gambar 12.32 b Adjacency Matrix Graph Gambar-10.32 a Contoh Program –1 :
Perhatikan graph yang digambarkan pada Gambar-10.32a, dan Adjacency Matrix graph tersebut yang digambarkan pada Gambar-10.32 b.
#include<stdio.h> typedef struct tipeS { struct tipeS *Left; char INFO;
struct tipeS *Right; };
typedef Struct tipeS Simpul;
Simpul *P,*FIRST,*LAST, *PVertex, *PEdge, *Q, *R, *S; Simpul *PointS[5];
void main()
{ int A[5][5] = {0,5,999,2,999, 6,0,3,999,999, 999,999,0,999,9, 999,999,12,0,7, 999,14,999,999,0 } ;
char NmS[5] = “ABCDE”; // Nama, atau Nomor, atau Identitas Simpul int I,J;
Sudah ditulis program sebagai berikut :
Soal : Tambahkan (lengkapi) program diatas untuk membuat Adjacency List graph
Gambar-10.32 a, yang diilustrasikan pada Gambar-10.32 c.
Jawab:
// Membuat Simpul Awal Linked-List “ABCDE”. I=0; J=0;
P=(Simpul*)malloc(sizeof(Simpul));
P->INFO = NmS[0]; //ingat INFO tipenya : char, FIRST = P; LAST=P;
P->Left=NULL; P->Right=NULL;
PointS[0] = P; // menyimpan alamat Simpul pertama
Langkah-1:
Langkah-1 ini menghasilkan sebuah simpul sebagai berikut :
A LAST FIRST P Gambar 12.32 cd Simpul awal Adjacencyd-List Graph Gambar-12..32 a
Gambar 12.33 b Adjacencyd-List A B C D 0 E PVertex 5 2 0 6 3 0 PEdge 9 12 7 0 14 0
for(I=1; I<=4; I++)
{ P=(Simpul*)malloc(sizeof(Simpul));
P->INFO = NmS[I]; //ingat INFO tipenya : char,
LAST_>Left = P; LAST=LAST->Left; P->Left=NULL; P->Right=NULL;
PointS[I] = P; // menyimpan alamat semua
Simpul }
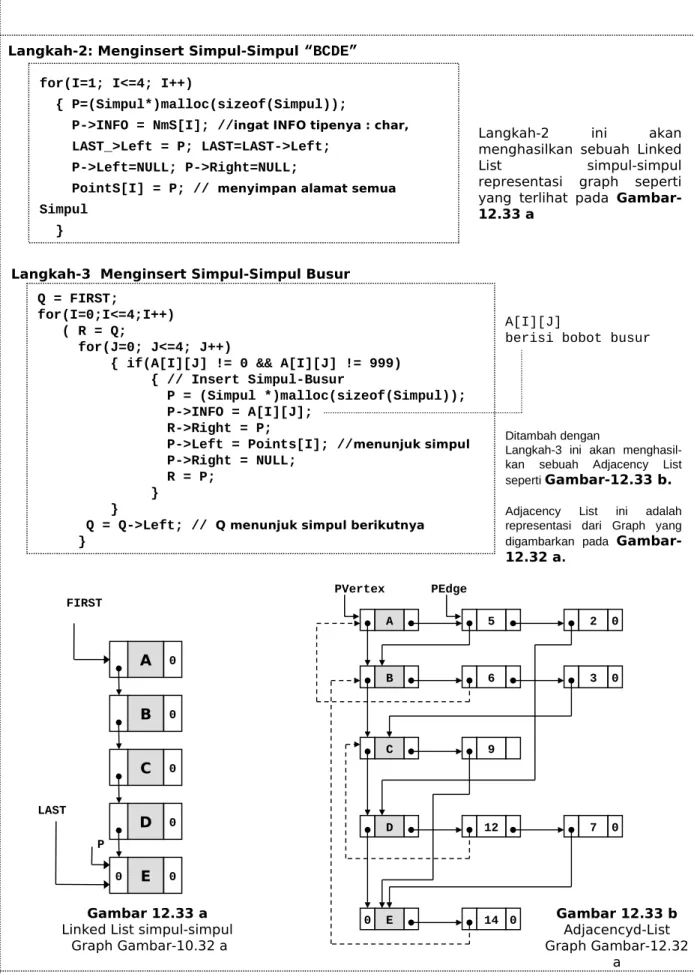
Langkah-2: Menginsert Simpul-Simpul “BCDE”
Langkah-2 ini akan menghasilkan sebuah Linked List simpul-simpul representasi graph seperti yang terlihat pada Gambar-12.33 a
Q = FIRST;
for(I=0;I<=4;I++) ( R = Q;
for(J=0; J<=4; J++)
{ if(A[I][J] != 0 && A[I][J] != 999) { // Insert Simpul-Busur
P = (Simpul *)malloc(sizeof(Simpul)); P->INFO = A[I][J];
R->Right = P;
P->Left = Points[I]; //menunjuk simpul
P->Right = NULL; R = P;
} }
Q = Q->Left; // Q menunjuk simpul berikutnya
}
Langkah-3 Menginsert Simpul-Simpul Busur
FIRST A 0 LAST P B 0 C 0 D 0 0 E 0 Gambar 12.33 a Linked List simpul-simpul
Ditambah dengan
Langkah-3 ini akan menghasil-kan sebuah Adjacency List seperti Gambar-12.33 b. Adjacency List ini adalah representasi dari Graph yang digambarkan pada Gambar-12.32 a.
A[I][J]
Gambar 12.33 c Adjacencyd-List sebuah graph A B C D 0 E FIRST 5 2 0 6 3 0 9 12 7 0 14 0 Contoh Program –2 :
Sudah ada Adjacency List sebuah Graph berbobot dan berarah seperti yang diperlihatkan pada Gambar-1233 c.
Juga sudah tersedia pointer Pvertex, Pedge, P, Q, R, S yang dapat menunjuk sebuah simpul.
Soal.
Susun program (penggalan program) untuk mencetak hubungan antar simpul garaph tersebut.
Bila program Anda benar, maka akan tercetak : A : B D B : A C C : E D : C E E : B A : B D
maksudnya dari simpul A ada busur yang menuju B dan D
Q = FIRST; While(Q != NULL)
( printf(“\n %c : “, Q->INFO); // Q->INFO bertipe int dicetak dengan format %c R = Q->Right; while( R != NULL) { printf(“%c “, RLeftINFO); R = R->Right; }
Q = Q->Left; // Q menunjuk simpul berikutnya
} Jawab :
Kalau ingin disertakan bobot masing-masing busur sehingga tercetak misalnya :
Maka instruksi printf(“%c “, R->Left->INFO); perlu diganti menjadi :
printf(“%c %i “, R->Left->INFO, R->Right->INFO);
12.7.3. Soal-soal Latihan Mandiri.
1. Gambarkan Adjacency List untuk graph Gambar-12.34 a.
2. Gambarkan Adjacency List sebuah graph bila Ajacency Matrix graph tersebut diilustrasikan pada Gambar-12.34 b.
3. Gambarkan Adjacency List sebuah graph berarah bila Inverse Adjacency Matrix graph tersebut digambarkan pada Gambar-12.34 c.
4. Gambarkan sebuah graph tak berarah bila Adjacency List graph tersebut digambarkan pada Gambar-12.34 d.
5. Gambarkan sebuah graph berarah bila Inverse Adjacency List graph tersebut digambarkan pada Gambar12.34 e.
6. Tulis penggalan program untuk mencetak hubungan antar simpul sebuah graph bila Adjacency Matrix Graph tersebut diperlihatkan oleh Gambar-12.34 b
7. Tulis penggalan program untuk mencetak hubungan antar simpul sebuah graph bila Inverse Adjacency List Graph tersebut diperlihatkan pada Gambar-12..34 e
0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 0 0 1 0 1 0 0 0 0 0 A 0 B 1 C 2 D 3 E,4 A 0 B 1 C 2 D 3 E 4 Gambar 12.34 a Graph 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 1 1 0 A 0 B 1 C 2 D 3 E 4 A 0 B 1 C 2 D 3 E 4 Gambar 12.34 b Adjacency Matrix B A D E C Gambar 12.34 c Inverse Adjacency Matrix
Gambar 12.34 d Adjacency List Graph Tak
A B C D E FIRST B D 0 A C E 0 B D E 0 A C E 0 B C D 0 Gambar 12.34 e Inverse Adjacency List
A B C D E FIRST B 6 D 12 0 A 5 E 14 0 B 2 A 2 D 7 0 C 9 C 14 0