DEKOMPOSISI –
– ANTIAJAIB PADA
GRAF OLEANDER
SKRIPSI
Windi Mutia Jamilus (11150940000002)
PROGRAM STUDI MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI SYARIF HIDAYATULLAH JAKARTA 2020 M / 1441 H
i
DEKOMPOSISI –
– ANTIAJAIB PADA
GRAF OLEANDER
SKRIPSI Diajukan kepada
Universitas Islam Negeri Syarif Hidayatullah Jakarta Fakultas Sains dan Teknologi
Untuk Memenuhi Salah Satu Persyaratan dalam Memperoleh Gelar Sarjana Matematika (S.Mat)
Oleh:
Windi Mutia Jamilus 11150940000002
PROGRAM STUDI MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UIN SYARIF HIDAYATULLAH JAKARTA
iv
PERSEMBAHAN
Skripsi ini saya persembahkan untuk orang yang saya cintai dan saya
sayangi , terlebih untuk Bapak Yong Liza dan Ibu Setiyowati beserta
kedua adikku Diana Febria Liza dan El – Zahra Firda Yoti
MOTTO
“Jangan menunggu. Takkan pernah ada waktu yang tepat”
(Napoleon Hill)
v
KATA PENGANTAR
Assalamu’alaikum Wr. Wb.
Alhamdulillah, puji syukur kehadirat Tuhan Yang Maha Kuasa atas segala limpahan rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan penyusunan skripsi dengan judul “Dekomposisi – – Antiajaib Pada Graf Oleander” dapat terselesaikan dengan baik. Tidak lupa sholawat dan salam
semoga senantiasa tercurah limpahkan kepada pemimpin kita semua yakni Nabi Muhammad SAW.
Penyusunan skripsi ini disusun untuk memenuhi salah satu tugas wajib bagi penulis sebagai persyaratan untuk memperoleh gelar sarjanan matematika (S. Mat). Harapan penulis semoga skripsi ini menambah banyak wawasan bagi penulis maupun para pembaca.
Penulis menyadari bahwa laporan ini dapat diselesaikan karena dukungan dan bantuan dari beberapa pihak. Untuk itu, pada kesempatan ini penulis ingin menyampaikan terima kasih kepada :
1. Ibu Prof. Dr. Lily Surraya Eka Putri, M.Env.Stud., selaku Dekan Fakultas Sains dan Teknologi Universitas Islam Negeri Syarif Hidayatullah Jakarta. 2. Ibu Dr. Suma’inna, M.Si., selaku Ketua Program Studi Matematika Fakultas
Sains dan Teknologi UIN Syarif Hidayatullah Jakarta
3. Ibu Irma Fauziah, M.Sc., selaku Sekretaris Program Studi Matematika Fakultas Sains dan Teknologi UIN Syarif Hidayatullah Jakarta.
4. Ibu Nur Inayah, M.Si., selaku Dosen Pembimbing I yang telah membimbing dan mengarahkan penulis selama melakukan penyusunan skripsi ini, serta memberikan banyak pengajaran yang bisa didapat penulis.
5. Bapak Yudi Mahatma, M.Si., selaku Dosen Pembimbing II yang telah membimbing dan mengarahkan penulis selama melakukan penyusunan skripsi ini, serta memberikan banyak pengajaran yang bisa didapat penulis.
vi 6. Ibu dan Bapak Dosen Program Studi Matematika yang telah memberikan
ilmu- ilmunya dan pengalaman yang bermanfaat.
7. Kedua orang tua, bapak Yong Liza dan Ibu Setiyowati yang selalu memberikan dukungan dan do’a untuk penulis semangat dalam menyelesaikan penulisan skripsi tersebut.
8. Kedua adik tersayang, Diana Febria Liza dan El- Zahra Firda Yoti yang menyemangati penulis untuk menyelesaikan skripsi.
9. Suci Martina, Mustika Rahayu, Maria Ulfah Latifah, Marisa Dwi Sari, Sri Putri, Intan S, Dini yang selalu menyemangati penulis untuk menyelesaikan skripsi.
10. Soffi Nur Marsitoh, Via Aulianita Anwar, Esa Maharani, Muhammad Fahmi, Veren Mego Lintang, Sylvi yang selalu menyemangati dan menemani penulis menyelesaikan skripsi.
11. Kepada teman–teman seperjuangan Matematika 2015, terimakasih untuk dukungan, semangat, bantuan, dan solidaritas selama ini.
12. Pihak lain yang telah membantu baik itu do’a atau bantuan lainnya dari awal penyusunan skripsi sampai saat ini.
Penulis sadar bahwa skripsi ini masih banyak kekurangan. Besar harapan penulis untuk menerima kritik dan saran yang bersifat membangun di kemudian hari untuk memperbaiki kekurangan yang ada. Sekali lagi semoga laporan ini dapat bermanfaat bagi pembaca.
Wassalamu’alaikum Wr. Wb.
Ciputat, Januari 2020
viii
ABSTRAK
Windi Mutia Jamilus, Dekomposisi – – Antiajaib pada Graf Oleander,
dibawah bimbingan Dr. Nur Inayah, M.Si dan Yudi Mahatma, M.Si.
Misalkan graf ( ) dengan ) sebagai himpunan titik dari graf dan adalah himpunan sisi dari graf . Suatu pelabelan dekomposisi – –antiajaib pada graf adalah suatu fungsi bijektif { | | | |} yang memetakan sisi dan titik pada graf G. Sedemikian sehingga { ( – ) } Untuk suatu subgraf dari dengan dan merupakan dua bilangan positif serta merupakan banyaknya subgraf di . Tujuan peneliti adalah menentukan dekomposisi – – antiajaib pada graf oleander untuk dengan nilai .
ix
ABSTRACT
Windi Mutia Jamilus, Dekomposisi – –Antimagic Decomposition On Oleander Graph, unter the guidance Dr. Nur Inayah, M.Si and Yudi Mahatma,
M.Si.
Graph with as the point set of graph , and as the side set of graph . labeling of decomposition - - anti magic on graph is an bijective function { | | | |} which maps sides and points on the Graph . So that { }. For some subgraph from with and are two positive numbers and n is the numbers of subgraphs in . The objective of the researcher is to determine the decomposition - - antimagic on the oleander graph for with values . Keywords: Antimagic, Decomposition, Oleander Graph
x
DAFTAR ISI
HALAMAN JUDUL ... i PERNYATAAN ... ii PENGESAHAN ... iii PERSEMBAHAN ... iv KATA PENGANTAR ... vPERNYATAAN PERSETUJUAN ... vii
ABSTRAK...viii
ABSTRACT ... ix
DAFTAR ISI ... x
DAFTAR GAMBAR ... xii
BAB I ... 1 PENDAHULUAN ... 1 1.1 Latar Belakang ... 1 1.2 Perumusan Masalah ... 3 1.3 Pembatasan Masalah ... 3 1.4 Tujuan Penulis ... 3 1.5 Manfaat Penulis ... 3 BAB II ... 4
TINJAUAN PUSTAKA DAN LANDASAN TEORI ... 4
2.1 Terminologi Graf ... 4
2.2 Jenis – Jenis Graf ... 5
2.3 Jalan, Lintasan, Lintasan Tertutup ... 6
2.4 Subgraf ... 6
2.5 Graf Isomorfik ... 7
2.6 Fungsi ... 7
2.7 Pelabelan Total H Antiajaib ... 8
2.8 Dekomposisi Graf ... 8
xi
DEKOMPOSISI – – ANTIAJAIB PADA ... 9
GRAF OLEANDER ... 9
3.1.1 Definisi Graf Oleander ... 9
3.1.2 Dekomposisi – – Antiajaib pada Graf Oleander ... 10
BAB IV ... 37
KESIMPULAN DAN SARAN ... 37
4.1 Kesimpulan ... 37
4.2 Saran ... 37
REFERENSI ... 38
xii
DAFTAR GAMBAR
Gambar 1.1 Ilustrasi hubungan persaudaraan sesama umat manusia dalam teori
graf. ... 2
Gambar 2.1 Graf G ... ... 4
Gambar 2.2 Graf Lingkaran ... 5
Gambar 2.3 Graf Matahari ... 6
Gambar 2.4 Graf dan Subgraf Dari ... 7
Gambar 2.5 Graf isomorfik terhadap ... 7
Gambar 3.1 Graf Oleander ... 10
Gambar 3.2 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan Dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan ... 15
Gambar 3.3 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan ... 20
Gambar 3.4 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan ... 25
Gambar 3.5 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan ... 30
Gambar 3.6 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan ... 35
1
BAB I
PENDAHULUAN
1.1 Latar Belakang
Bagi dunia, keilmuan matematika berperan penting sebagai bahasa simbolik yang memungkinkan terwujudnya komunikasi yang cermat dan tepat. Matematika dapat menyampaikan informasi secara jelas namun singkat. Jika suatu rumus dituliskan secara verbal maka memerlukan kalimat panjang, dimana makin banyak kata – kata maka makin besar pula peluang kesalahan informasi dan salah interpretasi. Maka dalam bahasa matematika cukup ditulis dengan model sederhana ( Suriasumatri, 2001; 203).
Teori graf pertama kali diperkenalkan pada tahun 1736 oleh Euler. Suatu graf terdiri atas pasangan berurut dari titik yang merupakan himpunan tak kosong dari graf dan merupakan himpunan sisi dari graf . Graf digunakan untuk menghubungkan suatu objek - objek tertentu. Dimana suatu titik menjadi objek dan sisi menjadi lintasan atau hubungan antar objek tersebut.
Dalam Al-Qur’an terdapat ayat yang mengandung teori graf jika dipahami mendalam, salah satunya dalam surat Al-Hujurat ayat 3:
Artinya : “Hai manusia, sesungguhnya kami menciptakan kamu dari seorang laki–laki dan seorang perempuan dan menjadikan kamu berbangsa-bangsa dan bersuku–suku supaya kamu saling kenal mengenal. Sesungguhnya orang yang paling mulia kamu disisi Allah ialah orang yang paling takwa diantara kamu. Sesungguhnya Allah Maha Mengetahui lagi Maha Mengenal”. [Q.S. Al-Hujurat:13].
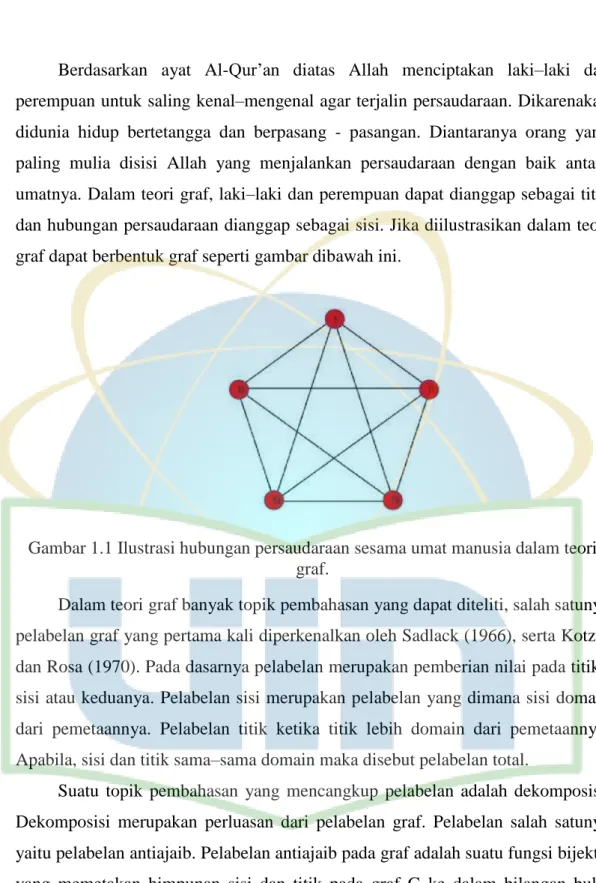
2 Berdasarkan ayat Al-Qur’an diatas Allah menciptakan laki–laki dan perempuan untuk saling kenal–mengenal agar terjalin persaudaraan. Dikarenakan didunia hidup bertetangga dan berpasang - pasangan. Diantaranya orang yang paling mulia disisi Allah yang menjalankan persaudaraan dengan baik antara umatnya. Dalam teori graf, laki–laki dan perempuan dapat dianggap sebagai titik dan hubungan persaudaraan dianggap sebagai sisi. Jika diilustrasikan dalam teori graf dapat berbentuk graf seperti gambar dibawah ini.
Gambar 1.1 Ilustrasi hubungan persaudaraan sesama umat manusia dalam teori graf.
Dalam teori graf banyak topik pembahasan yang dapat diteliti, salah satunya pelabelan graf yang pertama kali diperkenalkan oleh Sadlack (1966), serta Kotzig dan Rosa (1970). Pada dasarnya pelabelan merupakan pemberian nilai pada titik , sisi atau keduanya. Pelabelan sisi merupakan pelabelan yang dimana sisi domain dari pemetaannya. Pelabelan titik ketika titik lebih domain dari pemetaannya. Apabila, sisi dan titik sama–sama domain maka disebut pelabelan total.
Suatu topik pembahasan yang mencangkup pelabelan adalah dekomposisi. Dekomposisi merupakan perluasan dari pelabelan graf. Pelabelan salah satunya yaitu pelabelan antiajaib. Pelabelan antiajaib pada graf adalah suatu fungsi bijektif yang memetakan himpunan sisi dan titik pada graf G ke dalam bilangan bulat positif { | | | |} yang memenuhi { – } untuk bilangan bulat positif dan tertentu serta banyaknya subgraf dan .
3 Penulisan mengenai dekomposisi khususnya antiajaib sejauh ini masih belum begitu banyak dikenal orang dan masih banyak graf khusus lainnya yang belum ditemukan dekomposisinya, salah satunya graf oleander. Graf Oleander adalah penggabungan dari graf matahari dengan menambahkan sisi – sisi.
Akibatnya penulis tertarik untuk meneliti graf Oleander. Oleh karena itu, peneliti ini akan membahas mengenai “ Dekomposisi – – Antiajaib pada Graf Oleander”.
1.2 Perumusan Masalah
Berdasarkan latar belakang yang telah diuraikan, maka perumusan masalah dalam penulisan ini bagaimana membangun dekomposisi – – antiajaib pada graf Oleander.
1.3 Pembatasan Masalah
Pembatasan masalah dalam penulisan adalah mengkontruksi dekomposisi – – antiajaib untuk graf Oleander dengan dan terdekomposisi atas graf .
1.4 Tujuan Penulis
Tujuan yang ingin dicapai dalam penulisan ini adalah untuk membangun dekomposisi – – antiajaib pada graf Oleander serta mengembangkan graf Oleander.
1.5 Manfaat Penulis
Manfaat yang didapat penulis dalam melakukan penulisan skripsi tersebut adalah menambah wawasan penulis maupun pembaca mengenai teori graf, khususnya mengenai dekomposisi – – antiajaib pada graf Oleander. Selain itu dapat meningkatkan keterampilan berfikir mengenai teori graf dekomposisi. Hasil penulisan ini diharapkan dapat membantu mengembangkan ilmu teori graf dalam masalah pelabelan khususnya dekomposisi – antiajaib pada suatu graf khusus.
4
BAB II
TINJAUAN PUSTAKA DAN LANDASAN TEORI
2.1 Terminologi Graf
Suatu graf merupakan pasangan terurut dari dan . Dimana merupakan himpunan tak kosong dari titik pada graf dan merupakan himpunan dari sisi graf yang menghubungan sepasang titik. Berdasarkan definisi tersebut, dapat disimpulkan bahwa graf memiliki titik minimal satu dan kemungkinan tidak memiliki himpunan sisi. Graf yang hanya mempunyai himpunan titik dan tidak memiliki anggota himpunan sisi disebut dengan graf kosong (empty graph).
Gambar 2.1 Graf G.
Pada Gambar 2.1 dapat dilihat bahwa graf memiliki himpunan titik { } dan himpunan sisi { }. Saling terhubung langsung ketika dua buah titik bertetanggaan dengan sisi yang menghubungkan buah titik tersebut. Dapat di lihat dari gambar 2.1 sisi yang berarti sisi menghubungkan titik dan titik , dan begitu juga untuk sisi yang lainnya. Selain itu, terdapat istilah order dan size, order merupakan banyaknya unsur pada himpunan titik dinotasikan | | sedangkan size merupakan banyaknya unsur pada sisi dinotasikan | |.
5 2.2 Jenis – Jenis Graf
Dalam teori graf, setiap graf diklasifikasikan menjadi beberapa jenis yang diklasifikasikan berdasarkan ada atau tidak adanya sisi ganda, loop (gelang) dan orientasi arah.
Berdasarkan ada atau tidak adanya gelang ataupun sisi ganda, graf diklasifikasi menjadi dua jenis yaitu graf sederhana dan graf tak sederhana. Graf sederhana adalah graf yang tidak memiliki sisi ganda maupun gelang, sedangkan graf tak sederhana adalah graf yang memiliki sisi ganda ataupun gelang.
Suatu orientasi arah pada sisi graf dapat diklasifikasikan menjadi dua jenis yaitu graf berarah dan graf tak berarah. Graf berarah adalah graf yang memiliki orientasi arah pada sisinya, sedangkan graf tak berarah adalah graf yang tidak memiliki orientasi arah pada sisinya.
Selain jenis – jenis klasifikasi yang telah dijelaskan. Ada beberapa graf yang telah diberikan penamaan serta pendefinisian sendiri dengan mengklasifikasikan menjadi graf khusus sederhana, seperti :
1. Graf lingkaran
Graf lingkaran dinotasikan dengan adalah suatu graf sederhana yang setiap titiknya berderjat dua dengan n titik. Jika pada adalah
maka sisi–sisinya
6 2. Graf matahari
Graf matahari dinotasikan dengan ( ) adalah graf yang diperoleh dari graf lingkaran setiap simpul pada graf lingkaran diberi tambahan satu simpul berderajat satu. Graf matahari mempunyai himpunan titik { } dan himpunan sisi { – } { }.
Gambar 2.3 Graf Matahari . 2.3 Jalan, Lintasan, Lintasan Tertutup
Jalan merupakan suatu graf yang urutan titik dan sisi terhingga dan bergantian antara titik–titik dan sisi–sisi dalam suatu graf dengan ketentuan untuk setiap yang menghubungkan pada dan dimana dan bukan suatu gelang. Jalan dapat dinotasikan dengan . Suatu jalan pada graf dibentuk dengan titik dan sisi yang dapat diulang boleh lebih satu kali. Sedangkan lintasan adalah jalan yang tidak boleh dilewati lebih dari satu kali. Lintasan tertutup adalah lintasan yang memiliki titik awal dan titik akhir yang sama.
2.4 Subgraf
Graf dikatakan subgraf dari graf jika ditulis dengan , jika dan sehingga mengandung yang merupakan subgraf . Spanning subgraf dari apabila .
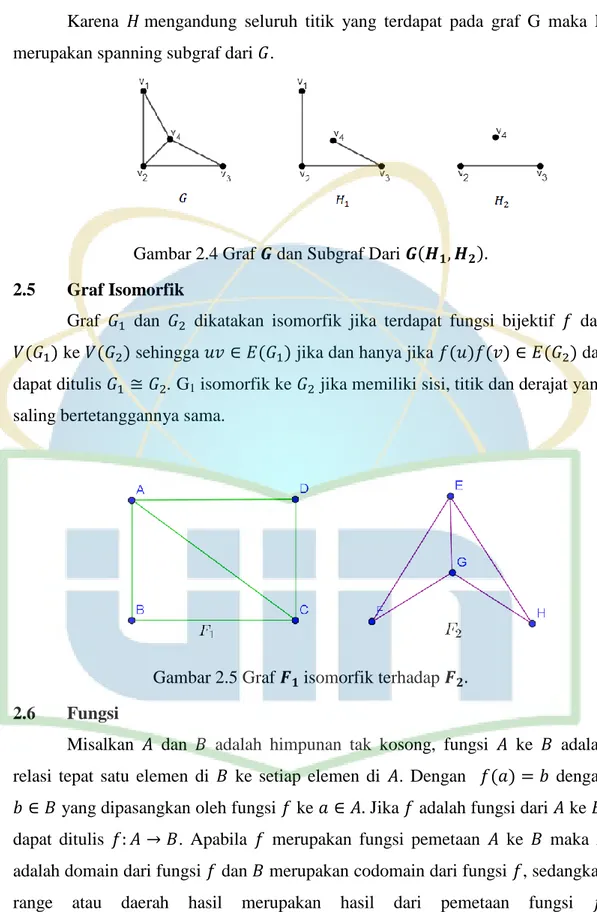
7 Karena mengandung seluruh titik yang terdapat pada graf G maka H merupakan spanning subgraf dari .
Gambar 2.4 Graf dan Subgraf Dari 2.5 Graf Isomorfik
Graf dan dikatakan isomorfik jika terdapat fungsi bijektif dari ke sehingga jika dan hanya jika dan dapat ditulis . G1 isomorfik ke jika memiliki sisi, titik dan derajat yang saling bertetanggannya sama.
Gambar 2.5 Graf isomorfik terhadap 2.6 Fungsi
Misalkan dan adalah himpunan tak kosong, fungsi ke adalah relasi tepat satu elemen di ke setiap elemen di . Dengan dengan yang dipasangkan oleh fungsi ke Jika adalah fungsi dari ke , dapat ditulis . Apabila merupakan fungsi pemetaan ke maka adalah domain dari fungsi dan merupakan codomain dari fungsi , sedangkan range atau daerah hasil merupakan hasil dari pemetaan fungsi .
8 Berdasarkan uraian diatas, fungsi dibedakan menjadi tiga jenis yaitu, fungsi injektif( satu – satu), fungsi surjektif(pada), dan fungsi bijektif (satu – satu pada). Fungsi injektif (satu – satu) dikatakan jika dan hanya jika yang berakibat untuk setiap . Fungsi surjektif (pada) jika dan hanya jika setiap terdapat sehingga . Fungsi bijektif (satu – satu pada) jika dan hanya jika fungsi tersebut memuat satu – satu dan pada.
2.7 Pelabelan Total H Antiajaib
Misalkan graf dan merupakan graf berhingga. Fungsi bijektif { | | | |} pada pelabelan total – – antiajaib dimana untuk yang isomorfik dengan , maka bobot dari setiap subgrafnya berbentuk lintasan barisan aritmatika { – } dengan bilangan bulat positif merupakan banyaknya subgraf dan bilangan bulat positif merupakan jarak.
∑ ∑
2.8 Dekomposisi Graf
Suatu keluarga { } dari subgraf dikatakan suatu dekomposisi- dari , jika isomorfik dengan , untuk , maka , untuk untuk Graf adalah suatu fungsi bijektif dari { | | | |} sehingga { – } untuk dan merupakan bilangan bulat positif serta adalah banyaknya anggota dari .
9
BAB III
DEKOMPOSISI –
– ANTIAJAIB PADA
GRAF OLEANDER
Pada penelitian ini menghasilkan lima teorema dekomposisi – – antiajaib pada graf Oleander dengan langkah awal menentukan graf yang dapat di dekomposisi dan menentukan dekomposisi dari graf tersebut. Graf Oleander terdekomposisi atas untuk setiap { }. Setelah itu melakukan pelabelan dengan memetakan setiap titik dan sisi pada graf Oleander ke dalam himpunan bilangan bulat positif dengan suatu fungsi bijektif yang disesuaikan dengan nilai . Terdapat 5 pelabelan yang berbeda dengan nilai untuk Pelabelan graf Oleander dimulai dari titik maupun dari sisi. Jika titik dan sisi pada graf Oleander sudah dilabelin untuk setiap . Kemudian menghitung pola bobot masing – masing subgraf dari graf tersebut terdekomposisi atas . Setelah itu buat pola bobot subgraf untuk . Setelah mendapatkan pola bobot pelabelannya, langkah terakhir membuktikan fungsi tersebut dapat berlaku untuk setiap bilangan bulat positif.
Berikut adalah tahap – tahap mencari dekomposisi – – antiajaib pada graf Oleander.
3.1.1 Definisi Graf Oleander
Menurut Ariesta, graf Oleander dinotasikan dengan adalah graf yang diperoleh dari graf matahari dengan menambahkan sisi–sisi. Himpunan sisi dari graf tersebut dipartisi menjadi empat bagian, yaitu
(i) Sisi lingkar dengan { } untuk (ii) Sisi tegak dengan { } untuk
(iii) Sisi longkap satu dengan { }untuk , (iv) Sisi miring dengan { }untuk .
10 Oleh karena itu, graf Oleander dapat didefinisikan dengan . Gambar graf Oleander dapat dilihat pada Gambar 3.1.
Gambar 3.1 Graf Oleander .
3.1.2 Dekomposisi – – Antiajaib pada Graf Oleander
Dalam penulisan ini, terdapat lima pelabelan yang berbeda berdasarkan nilai untuk untuk . Dari lima pelabelan tersebut maka didapat lima teorema serta pembuktian bahwa sisi dan titik dari lima teorema tersebut memiliki fungsi bijektif { | | | |}.
TEOREMA 3.1. Graf Oleander memiliki dekomposisi - – antiajaib untuk dan .
Bukti. Misalkan adalah fungsi bijektif yang memetakan sisi dan titik ke dalam bilangan bulat positif seperti berikut :
– { } { } { }
11 { } { { } { } { }
Berdasarkan pelabelan titik dan sisi untuk setiap subgrafnya maka akan di buktikan bahwa titik dan sisi pada graf memiliki sifat bijektif.
a.
Ambil sebarang dan Berakibat ( ) Maka satu – satu. { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada pada
b.
Ambil sebarang dan Berakibat Maka satu - satu. { } { }
12 Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
c.
Ambil sebarang dan Berakibat Maka satu satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
pada
d. ( )
Ambil sebarang dan ( )= Berakibat ( ) Maka satu – satu { } { } Kardinal himpunan { Kardinal himpunan { }
13 Karena satu satu maka pada
pada
e. ( ) {
Ambil sebarang dan
( ) ) Jika { } maka Jika { } { , n} maka
Tidak mungkin karena dibatasi oleh
Tidak mungkin karena dibatasi oleh Maka satu satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
14 f. ( )
Ambil sebarang dan
( )= Berakibat ( ) Maka satu - satu { } { } Kardinal himpunan { } Kardinal himpunan { } Karena satu satu maka pada
pada
Telah di buktikan bahwa sisi dan titik memiliki sifat bijektif. Lalu,
menghitung bobot tiap subgraf yang terdekomposisi tersebut dengan . maka menghasilkan pola ( ) pada graf oleander seperti berikut:
( ) { ( ) ( ) ( ) ( ) ( ) ( ) { } ( ) ( ) ( ) ( )
Berdasarkan pola bobot ( ) di atas, di dapatkan hasil masing – masing subgraf terdekomposisi sebagai berikut :
15 Penjelasan dari uraian di atas terdapat di lampiran 1. Dengan mensubtitusikan semua nilai , maka dari pelabelan tersebut menghasilkan bobot yang berbentuk suatu barisan aritmatika dengan dan .
Ilustrasi dari teorema 3.1 dapat dilihat pada Gambar 3.2 (1) dan (2).
Gambar 3.2 (1) Dekomposisi – – Antiajaib pada Graf Oleander
dengan . Dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan .
Setiap unsur di berikan label yang sesuai sehingga diperoleh bobot ( ) untuk setiap yang berbentuk sebuah deret aritmatika yaitu {65, 66,67} dengan n = 3. Hal ini berlaku juga untuk n = 4 dimana diperoleh bobot ( ) untuk yang dapat membentuk sebuah deret matematika yaitu {85,86,87,88}.
TEOREMA 3.2. Graf Oleander memiliki dekomposisi - – antiajaib untuk dan .
Bukti. Misalkan f adalah fungsi bijektif yang memetakan sisi dan titik ke dalam bilangan bulat positif seperti berikut :
f( ) { }
f( ) { { }
f( ) – { }
16 – { } { { }
Berdasarkan pelabelan titik dan sisi untuk setiap subgrafnya maka akan di buktikan bahwa titik dan sisi memiliki sifat bijektif
a.
Ambil sebarang dan Berakibat ( ) Maka satu - satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada pada
b. {
Ambil sebarang dan Jika { } Maka Jika { } Maka
Tidak mungkin terjadi karena telah dibatasi satu - satu
17
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
c.
Ambil sebarang dan Berakibat Maka satu - satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
pada
d. ( ) {
Ambil sebarang dan ( )= Jika { } maka Jika { } { , n} maka
18
Tidak mungkin karena dibatasi oleh
Tidak mungkin karena dibatasi oleh satu satu.
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
e. ( )
Ambil sebarang dan
( ) = Berakibat ( ) Maka satu - satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
19 f. ( ) {
Ambil sebarang dan
( )= Berakibat Jika { } Maka ( ) Jika { } maka
Tidak mungkin karena dibatasi oleh satu satu.
{ } { } Kardinal himpunan { }
Kardinal himpunan { } Karena satu satu maka pada
pada
Telah di buktikan bahwa sisi dan titik memiliki sifat bijektif. Lalu,
menghitung bobot tiap subgraf yang terdekomposisi tersebut dengan . maka menghasilkan pola ( ) pada graf Oleander seperti berikut:
20 ( ) { ( ) ( ) ( ) ( ) ( ) ( ) { } ( ) ( ) ( ) ( )
Berdasarkan pola bobot ( ) diatas, didapatkan hasil masing – masing subgraf terdekomposisi sebagai berikut :
{ }
Penjelasan dari uraian di atas terdapat di lampiran 1. Dengan mensubtitusikan semua nilai , maka dari pelabelan tersebut menghasilkan bobot yang berbentuk suatu barisan aritmatika dengan dan .
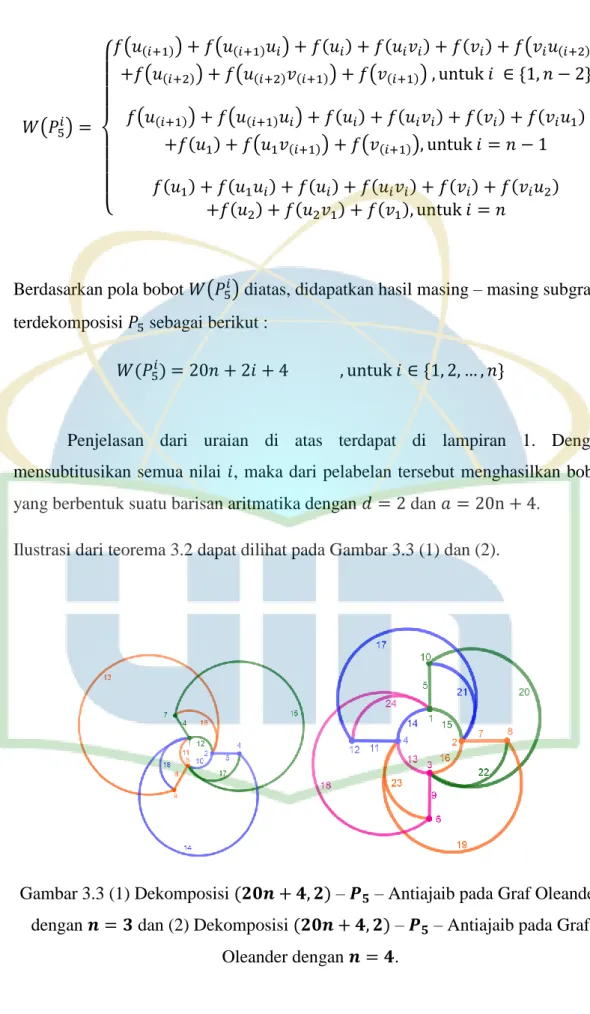
Ilustrasi dari teorema 3.2 dapat dilihat pada Gambar 3.3 (1) dan (2).
Gambar 3.3 (1) Dekomposisi – – Antiajaib pada Graf Oleander
dengan dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan .
21
Setiap unsur di berikan label yang sesuai sehingga diperoleh bobot ( ) untuk setiap . Yang berbentuk sebuah deret aritmatika yaitu {66, 68, 70} dengan n = 4. Hal ini berlaku juga untuk n = 4 dimana diperoleh bobot ( ) untuk yang dapat membentuk sebuah deret aritmatika yaitu {86, 88, 90, 92}.
TEOREMA 3.3. Graf Oleander memiliki dekomposisi ( - - antiajaib untuk dan d=3.
Bukti. Misalkan f adalah fungsi bijektif yang memetakan sisi dan titik ke dalam bilangan bulat positif seperti berikut :
{ } { { } { } { } f( ) = { { } = { { }
Berdasarkan pelabelan titik dan sisi untuk setiap subgrafnya maka akan di buktikan bahwa titik dan sisi memiliki sifat bijektif.
a.
Ambil sebarang dan Berakibat ( ) Maka pada { } { } Kardinal himpunan {
22 Kardinal himpunan { }
Karena satu satu maka pada pada
b. {
Ambil sebarang dan Jika { } Maka Jika { } Maka
Tidak mungkin terjadi karena telah dibatasi oleh satu - satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
c.
Ambil sebarang dan Berakibat
Maka
23 satu - satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
d. ( )
Ambil sebarang dan ( )= Berakibat ( ) Maka satu - satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
pada
e. ( ) {
Ambil sebarang dan ( ) ) Jika Jika { } maka
24
Tidak mungkin karena dibatasi oleh satu - satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
f. ( ) { Ambil sebarang dan
( )= Jika maka Jika { } maka Tidak mungkin karena dibatasi oleh satu satu
{ } { } Kardinal himpunan { }
Kardinal himpunan { } Karena satu satu maka pada
25 Telah di buktikan bahwa sisi dan titik memiliki sifat bijektif. Lalu,
menghitung bobot tiap subgraf yang terdekomposisi tersebut dengan . maka menghasilkan pola ( ) pada graf Oleander seperti berikut:
( ) { ( ) ( ) ( ) ( ) ( ) ( ) { } ( ) ( ) ( ) ( )
Berdasarkan pola bobot ( ) diatas, didapatkan hasil masing – masing subgraf terdekomposisi sebagai berikut :
{ }
Penjelasan dari uraian diatas terdapat dilampiran 1. Dengan mensubtitusikan semua nilai , maka dari pelabelan tersebut menghasilkan bobot yang berbentuk suatu barisan aritmatika dengan dan
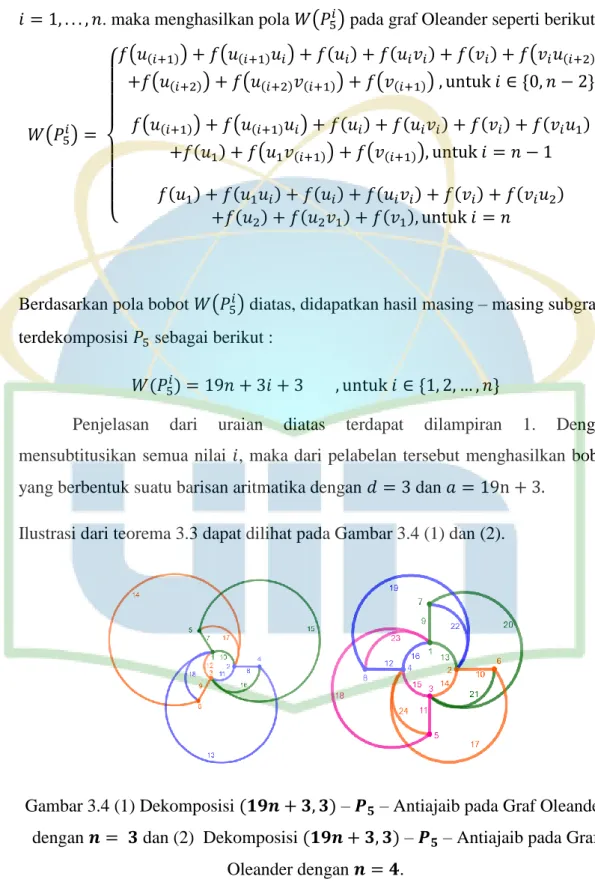
Ilustrasi dari teorema 3.3 dapat dilihat pada Gambar 3.4 (1) dan (2).
Gambar 3.4 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan dan (2) Dekomposisi – – Antiajaib pada Graf
26 Setiap unsur di berikan label yang sesuai sehingga diperoleh bobot ( ) untuk setiap . Yang berbentuk sebuah deret aritmatika yaitu {63, 66, 69}dengan n = 3. Hal ini berlaku juga untuk n = 4 dimana diperoleh bobot ( ) untuk yang dapat membentuk sebuah deret aritmatika yaitu {82, 85, 88, 91}.
TEOREMA 3.4. Graf Oleander memiliki dekomposisi (19n + 3,4) – – antiajaib untuk dan .
Bukti. Misalkan f adalah fungsi bijektif yang memetakan sisi dan titik ke dalam bilangan bulat positif seperti berikut :
{ } = { { } { } = { { } { } = { { } { }
Berdasarkan pelabelan titik dan sisi untuk setiap subgrafnya maka akan di buktikan bahwa titik dan sisi memiliki sifat bijektif
a.
Ambil sebarang dan Berakibat
( ) Maka
27
{ } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada pada
b. {
Ambil sebarang dan Jika { } Maka Jika { } Maka
Tidak mungkin terjadi karena telah dibatasi satu - satu
c.
Ambil sebarang dan Berakibat Maka satu – satu
28
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
d. ( ) {
Ambil sebarang dan ( )= Berakibat Jika { } Maka Jika { } Maka
Tidak mungkin terjadi karena telah dibatasi satu - satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
e. ( )
Ambil sebarang dan
( ) Berakibat
29 ( ) Maka satu - satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
pada
f. ( ) {
Ambil sebarang dan
( ) = Berakibat Jika maka Jika maka
Tidak mungkin karena satu satu
{ } { } Kardinal himpunan { }
Kardinal himpunan { } Karena satu satu maka pada
30 Telah di buktikan bahwa sisi dan titik memiliki sifat bijektif. Lalu,
menghitung bobot tiap subgraf yang terdekomposisi tersebut dengan . maka menghasilkan pola ( ) pada graf Oleander seperti berikut:
( ) { ( ) ( ) ( ) ( ) ( ) ( ) { } ( ) ( ) ( ) ( )
Berdasarkan pola bobot ( ) diatas, didapatkan hasil masing – masing subgraf terdekomposisi sebagai berikut :
{ }
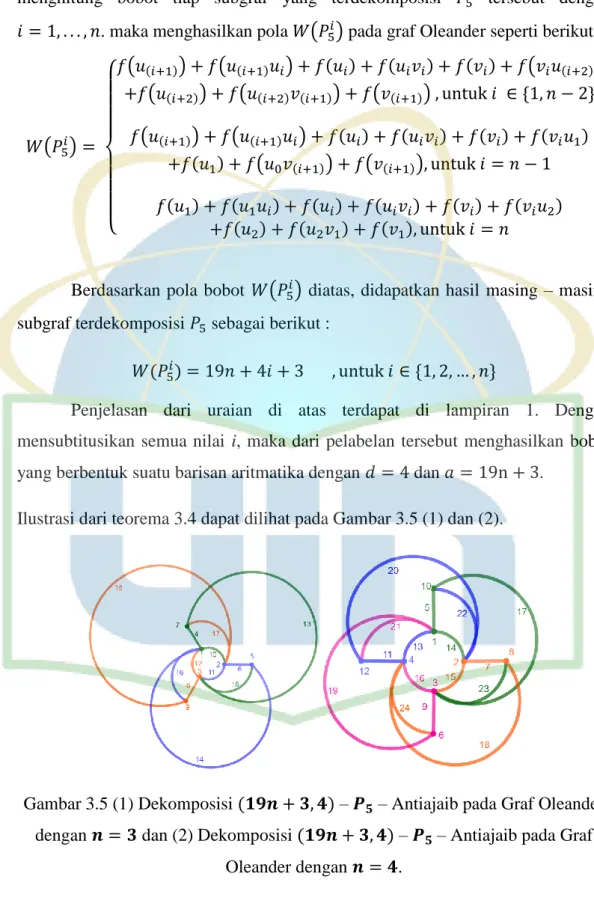
Penjelasan dari uraian di atas terdapat di lampiran 1. Dengan mensubtitusikan semua nilai i, maka dari pelabelan tersebut menghasilkan bobot yang berbentuk suatu barisan aritmatika dengan dan .
Ilustrasi dari teorema 3.4 dapat dilihat pada Gambar 3.5 (1) dan (2).
Gambar 3.5 (1) Dekomposisi – – Antiajaib pada Graf Oleander
dengan dan (2) Dekomposisi – – Antiajaib pada Graf Oleander dengan .
31 Setiap unsur di berikan label yang sesuai sehingga diperoleh bobot ( ) untuk setiap . Yang berbentuk sebuah deret aritmatika yaitu {64,68,72} dengan n = 3. Hal ini berlaku juga untuk n = 5 dimana diperoleh bobot ( ) untuk yang dapat membentuk sebuah deret aritmatika yaitu {83, 87, 91, 95}.
TEOREMA 3.5. Graf Oleander memiliki dekomposisi (18n + 2,5) - – antiajaib untuk dan .
Bukti. Misalkan adalah fungsi bijektif yang memetakan sisi dan titik ke dalam bilangan bulat positif seperti berikut :
{ } = { { } = { } { } { } { }
Berdasarkan pelabelan titik dan sisi untuk setiap subgrafnya maka akan di buktikan bahwa titik dan sisi setiap subgraf memiliki sifat bijektif.
a.
Ambil sebarang dan Berakibat ( ) Maka satu – satu { } { } Kardinal himpunan { Kardinal himpunan { }
32 Karena satu satu maka pada
pada
b. {
Ambil sebarang dan Jika { } Maka Jika { } Maka
Tidak mungkin terjadi karena telah dibatasi satu - satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
c.
Ambil sebarang dan Berakibat Maka satu - satu
33 d. { } { }
Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
pada
e. ( )
Ambil sebarang dan ( )= Berakibat ( ) Maka satu - satu { } { } Kardinal himpunan { Kardinal himpunan { } Karena satu satu maka pada
pada
f. ( )
Ambil sebarang dan
( ) Berakibat ( ) Maka
34 satu - satu
{ } { } Kardinal himpunan {
Kardinal himpunan { } Karena satu satu maka pada
pada
g. ( )
Ambil sebarang dan
( )= Berakibat ( ) Maka satu - satu { } { } Kardinal himpunan { } Kardinal himpunan { } Karena satu satu maka pada
pada
Telah di buktikan bahwa sisi dan titik memiliki sifat bijektif. Lalu,
menghitung bobot tiap subgraf yang terdekomposisi tersebut dengan . maka menghasilkan pola ( ) pada graf oleander seperti berikut:
35 ( ) { ( ) ( ) ( ) ( ) ( ) ( ) { } ( ) ( ) ( ) ( )
Berdasarkan pola bobot ( ) diatas, didapatkan hasil masing – masing subgraf terdekomposisi sebagai berikut :
= { }
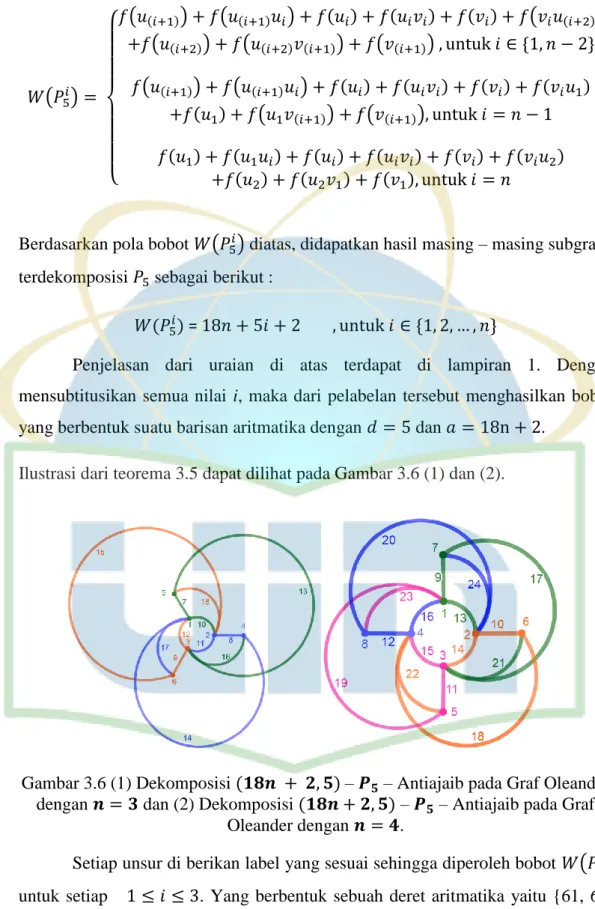
Penjelasan dari uraian di atas terdapat di lampiran 1. Dengan mensubtitusikan semua nilai i, maka dari pelabelan tersebut menghasilkan bobot yang berbentuk suatu barisan aritmatika dengan dan .
Ilustrasi dari teorema 3.5 dapat dilihat pada Gambar 3.6 (1) dan (2).
Gambar 3.6 (1) Dekomposisi – – Antiajaib pada Graf Oleander dengan dan (2) Dekomposisi – – Antiajaib pada Graf
Oleander dengan .
Setiap unsur di berikan label yang sesuai sehingga diperoleh bobot ( ) untuk setiap . Yang berbentuk sebuah deret aritmatika yaitu {61, 66, 72} dengan n = 3. Hal ini berlaku juga untuk n = 4 dimana diperoleh bobot
36 ( ) untuk yang dapat membentuk sebuah deret aritmatika yaitu {79, 84, 89, 94}.
Berdasarkan hasil yang diperoleh, terdapat pola label yang berbeda untuk setiap nilai dan setiap n. Hasil dari pemaparan teorema tersebut juga mendapatkan lima macam nilai yang sesuai dengan nilai yang diperoleh. Pada dan mendapatkan nilai yang sama, sedangkan pada dan memiliki nilai yang sama, tetapi untuk memiliki nilai yang berbeda dengan yang lainnya. Berikut akan disajikan nilai yang di dapatkan dari lima teorema tersebut ke dalam bentuk tabel.
Orn d 1 2 3 4 5 Or3 65 66 63 64 61 Or4 85 86 82 83 79 Or5 105 106 101 102 97 Or6 125 126 120 121 115 Or7 145 146 139 140 133 . . . . . . . . . . . . . . . . . .
37
BAB IV
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan hasil dan pembahasan yang telah dilakukan sebelumnya, maka dapat disimpulkan bahwa graf Oleander dengan , dengan { } memiliki dekomposisi – – antiajaib dengan nilai dan berbeda. Nilai untuk dan memiliki nilai yang sama sedangkan nilai untuk dan memiliki nilai yang sama tetapi untuk memiliki nilai yang berbeda dengan yang lainnya seperti pada tabel 4.1. pada penelitian ini penulis dapat menghasilkan lima teorema yang sesuai dengan nilai dan yang didapatkan. Berikut telah disajikan dalam bentuk tabel Dekomposisi – – Antiajaib Pada Graf Oleander.
1,2 3,4 5
4.2 Saran
Berikut adalah beberapa saran dari peneliti yang terkait dengan penelitian ini agar dapat lebih berkembang mengenai dekomposisi – – antiajaib pada graf Oleander, yaitu :
1. Membuat suatu aplikasi untuk mengetahui graf tersebut dapat dilabelkan secara dekomposisi untuk beberapa graf.
2. Mengembangkan dekomposisi – – Antiajaib pada graf khusus lainnya.
38
REFERENSI
[1] N. Inayah, A. Liando dan J.Moragas, “Magic and Antimagic H-
Decompositions,” Discrete Mathematics, vol. 312, pp. 1367-1371, 2012.
[2] Ariestha Widyastuty, “ Bilangan Terhubung Pelangin Untuk Graf
Oleander, ” vol. 2 .no. 1. 2017.
[3] P. R. Musthofa dan Y. Kuswardi, “DEKOMPOSISI GRAF MATAHARI
(Cn (K1)), ” Journal of Mathematics and Mathematics Education, vol. 8, hal. 20 – 30, 2018.
[4] Romain Boulet, “Spectral characterizations of sun graphs and broken
sungraph, ” DMTCS, vol. 11:2, hal. 149 – 160, 2009.
[5] Bondy, J. A dan U. S. R Murty, 1976. Graph Theory with Application.
Macmillan, London.
[6] Syafrizal S, Medika GH, Yulianti L. 2013. The Rainbow Connection of
Fan and Sun. Applied Mathematical Sciece;7:3155-3160.
[7] M. Irvan Septiar Musti, N. Inayah, I. Fauziah, “Dekomposisi (a,d) – P4 – Antiajaib Super Pada Graf Generalized Petersen, “ LOG!K@, vol.6,
pp. 84- 95, 2016.
[8] N. Hartsfield dan G. Ringel, “Supermagic and Antimagic Graphs, ” J.Rec.Math, vol.21, pp. 107-115, 1989.
[9] N. Inayah, R. Simanjuntak, A. N. M. Salman and K. I. A. Syuhada, "Super
(a,d)-H-antimagic total labelings for shackles of a connected graph," The Australasian Journal of Combinatorics, 2013.
[10] N. Inayah, A. N. M. Salman and R. Simanjuntak, "On (a,d)-H-antimagic coverings of graphs," The Journal of Combinatorial Mathematics and
39
LAMPIRAN
Lampiran 1. Dekomposisi – – Antiajaib Pada Graf Oleander Berdasarkan pelabelan setiap titik dan sisi pada subgraf , misalkan dengan . Diperoleh bobot untuk masing – masing subgraf ( ) pada graf oleander sebagai berikut:
Jika { – } maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( ) ( ) ( )
= – –
Nilai dapat diperoleh dari selisih antara ( ) dengan ( ) untuk { – }
( ) ( )
–
Jika – maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( )
( – ) ( – – ) ( – ) –
40
Nilai d dapat diperoleh dari selisih antara dengan untuk
=
– – –
Jika , maka bobot ( ) yang diperoleh adalah
( ) =
( – ) ( – ) – –
Nilai dapat diperoleh dari selisih antara dengan untuk =
–
41
Lampiran 2. Dekomposisi – – Antiajaib Pada Graf Oleander Berdasarkan pelabelan setiap titik dan sisi pada subgraf , misalkan dengan . Diperoleh bobot untuk masing – masing subgraf ( ) pada graf oleander sebagai berikut:
Jika { – }, maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( ) ( ) ( )
= ( – ) ( – ) – –
Nilai dapat diperoleh dari selisih antara ( ) dengan ( ) untuk { – }
= ( ) ( )
–
Jika – maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( )
( – ) ( – ) ( – )
42 Nilai dapat diperoleh dari selisih antara dengan untuk –
=
– – –
Jika maka bobot ( ) yang diperoleh adalah
( ) =
–
Nilai dapat diperoleh dari selisih antara dengan untuk
=
–
43
Lampiran 3. Dekomposisi – – Antiajaib Pada Graf Oleander Berdasarkan pelabelan setiap titik dan sisi pada subgraf , misalkan dengan . Diperoleh bobot untuk masing – masing subgraf ( ) pada graf oleander sebagai berikut:
Jika { – }, maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( ) ( ) ( )
( – ) –
Nilai dapat diperoleh dari selisih antara ( ) dengan ( ) untuk { – }
= ( ) ( )
–
Jika – , maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( )
( – ) –
44 Nilai dapat diperoleh dari selisih antara dengan untuk –
=
– – –
Jika , maka bobot ( ) yang diperoleh adalah
( ) =
Nilai dapat diperoleh dari selisih antara dengan untuk =
–
45
Lampiran 4. Dekomposisi – – Antiajaib Pada Graf Oleander Berdasarkan pelabelan setiap titik dan sisi pada subgraf , misalkan
dengan . Diperoleh bobot untuk masing – masing subgraf ( ) pada graf oleander sebagai berikut:
Jika { – }, maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( ) ( ) ( )
( – ) –
Nilai dapat diperoleh dari selisih antara ( ) dengan ( ) untuk { – }
= ( ) ( )
–
Jika – maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( )
( – ) ( – )
46 Nilai dapat diperoleh dari selisih antara dengan untuk –
=
– – –
Jika , maka bobot ( ) yang diperoleh adalah
( ) =
Nilai dapat diperoleh dari selisih antara dengan untuk =
–
47
Lampiran 5. Dekomposisi – – Antiajaib Pada Graf Oleander Berdasarkan pelabelan setiap titik dan sisi pada subgraf , misalkan dengan . Diperoleh bobot untuk masing – masing subgraf ( ) pada graf oleander sebagai berikut:
Jika { – } maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( ) ( ) ( )
( – ) –
Nilai dapat diperoleh dari selisih antara ( ) dengan ( ) untuk { – }
= ( ) ( )
–
Jika – , maka bobot ( ) yang diperoleh adalah
( ) = ( ) ( ) ( ) ( )
( – )
48 Nilai dapat diperoleh dari selisih antara dengan untuk –
=
– – ( – )
Jika maka bobot ( ) yang diperoleh adalah
( ) =
Nilai dapat diperoleh dari selisih antara dengan untuk =
–