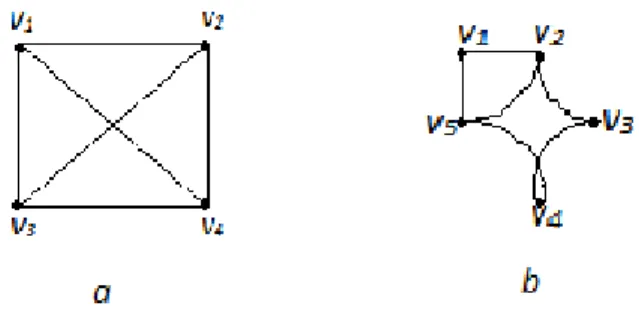PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Oleh

MARULI HUTAPEA 117021037/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2013

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Diajukan Sebagai Salah Satu Syarat

Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

MARULI HUTAPEA 117021037/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2013

Judul Tesis : PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

Nama Mahasiswa : Maruli Hutapea Nomor Pokok : 117021037

Program Studi : Magister Matematika

Menyetujui, Komisi Pembimbing

(Prof. Dr. Saib Suwilo, M.Sc) (Prof. Dr. Opim Salim S, MSc)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)

Tanggal lulus: 04 Juni 2013

Telah diuji pada Tanggal 04 Juni 2013

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Saib Suwilo, M.Sc Anggota : 1. Prof. Dr. Opim Salim S, M.Sc

2. Prof. Dr. Herman Mawengkang 3. Prof. Dr. Tulus, M.Si

PERNYATAAN

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sumbernya

Medan, Juni 2013 Penulis,

Maruli Hutapea

i

ABSTRAK

Dalam menyelesaikan persoalan degree constrained minimum spanning tree pada graph G(V, E) berbobot terhubung tak berarah merupakan permasalahan un- tuk menemukan spanning tree T di G dengan total panjang edge yang minimum dan degree dari setiap verteks vi di T dibatasi oleh bi dimana d^T(vi) ≤ bi. Un- tuk menyelesaikan permasalahan degree constrained minimum spanning tree di- lakukan dengan memodifikasi algoritma kruskal, dimana sebuah edge diterima di T, jika edge tidak membentuk cycle pada edge terdahulu yang berada di T dan verteks-verteks ujungnya memenuhi batas maksimum degree yang diberikan, yaitu d^T(vj) ≤ bj dan d^T(vk) ≤ bk.

Kata Kunci : Graph, Degree constrained, Spanning tree

ii

ABSTRACT

The degree constrained minimum spanning tree (DCMST) on undirected weighted connected graph G(V,E) is a problem to fins a spanning tree T in G with whose total edge length is minimal and the degree of each vertex vi in T at most a given value bi where d^T(vi) ≤ bi. For solving this problem, we modified kruskal algorithm, an edge received in T, if an edge did not produce any cycle with preceding edge in T and a both endpoints should not exceed some given maximum degrees that d^T(vj) ≤ bj and d^T(vk) ≤ bk.

Keywords: Graph, Degree constrained, Spanning tree

iii

KATA PENGANTAR

Dengan segala kerendahan hati dan penuh sukacita, penulis mengucap- kan puji syukur ke hadirat Tuhan Yang Maha Kuasa atas segala anugrah dan berkat-Nya yang telah diberikan, sehingga penulis dapat menyelesaikan tesis de- ngan judul: PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE. Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Studi Magister Matematika SPs Universitas Sumatera Utara.

Penulis menyadari bahwa terselesaikannya Tesis ini tidak lepas dari bantuan dan dukungan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis menyampaikan terimakasih sebesar-besarnya kepada :

Prof. Dr. dr. Syahril Pasaribu, DTMH, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara

Dr. Sutarman, M.Sc selaku Dekan FMIPA Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Magister Matematika di FMIPA Universitas Sumatera Utara Medan.

Prof. Dr. Herman Mawengkang selaku Ketua Program Studi Magister Mate- matika FMIPA Universitas Sumatera Utara dan selaku Pembanding Utama yang telah banyak memberikan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

Prof. Dr. Saib Suwilo, M.Sc selaku Sekretaris Program Studi Magister Mate- matika FMIPA Universitas Sumatera Utara dan selaku Pembimbing Utama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

Prof. Dr. Opim Salim S, M.Sc selaku Pembimbing Kedua yang juga telah banyak memberikan bimbingan kepada penulis dalam penulisan tesis ini.

Prof. Dr. Tulus, M.Si selaku Pembanding Kedua yang telah banyak mem- berikan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

iv

Seluruh Staf Pengajar pada Program Studi Magister Matematika FMIPA Uni- versitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan.

Saudari Misiani, S.Si selaku Staf Administrasi Program Studi Magister Ma- tematika FMIPA Universitas Sumatera Utara yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.

Tak lupa penulis mengucapkan terimakasih sebesar-besarnya dan penghar- gaan setinggi-tingginya kepada orangtua tercinta, Ayahanda Alm. Paimin Hu- tapea dan Ibunda Sumiantauli br Simanjuntak yang telah mencurahkan kasih sayang dan dukungan kepada penulis, kepada adik-adik Mawarni Hutapea, Megawati Hutapea serta Istri Netty Saulina br Lumbangaol S.Pd dan anak-anak Olivia Hutapea dan David Hutapea yang telah memberikan se- mangat dan dorongan kepada penulis dalam penulisan tesis ini.

Kepada Pemerintah Provinsi Sumatera Utara (Pemprovsu) atas bantuan da- lam peningkatan pendidikan kualitas guru untuk Daerah Sumatera Utara dalam memberikan Beasiswa Pemprovsu. Dr. Hamonangan Nainggolan, M.Sc dan seluruh rekan-rekan mahasiswa angkatan 2011/2012 pada Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan bantuan moril dan dorongan kepada penulis dalam penulisan tesis, penulis berterima kasih atas semua bantuan yang diberikan. Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempur- naan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya baik perkembangan ilmu pengetahuan.

Medan, Penulis,

Maruli Hutapea

v

RIWAYAT HIDUP

Maruli Hutapea dilahirkan di Lawe Perbunga (Aceh Tenggara) pada tanggal 22 desember 1974 dari pasangan Bapak Alm. Paimin Hutapea & Ibu Sumiantauli br Simanjuntak dan merupakan anak pertama dari tiga bersaudara. Penulis mena- matkan pendidikan Sekolah Dasar (SD) tahun 1989 di SD negeri dikabupaten langkat, Sekolah Lanjutan Tingkat Pertama (SLTP) Negeri 3 binjai pada tahun 1992, Sekolah Menengah Atas (SMA) Sw eka prasetya, kota Medan pada tahun 1995. Menamatkan kuliah S-1 dari UNIMED dikota medan tahun 2000. Dan mendapat gelar sarjana pendikan (S.Pd). Menikah dengan Netty Saulina br Lumbangaol S.Pd, bulan juli tahun 2001 dan dikarunia dua anak yaitu Olivia Hutapea dan David Hutapea.

Pengalaman mengajar pertama sekali di sekolah yayasan perguruan eka prasetya pada tahun 1999 bulan juli pada unit sekolah SMP, pada tahun 2003 mengajar di SMK-BM (SMEA) dan menjadi guru bantu yang dibiayai dari dana APBN, disekolah SMK-BM (SMEA) Eka Prasetya yang terletak di wilayah Deli Serdang. Pada tahun 2006 menjadi PNS di SMA Negeri 1 sunggal sampai sekarang.

Pada tahun 2011 penulis mengikuti program magister matematika di sekolah pasca sarjana universitas sumtra utara, penulis sungguh banyak mendapat pengalaman belajar yang sangat berharga.

vi

DAFTAR ISI

Halaman

PERNYATAAN i

ABSTRAK ii

ABSTRACT iii

KATA PENGANTAR iv

RIWAYAT HIDUP vi

DAFTAR ISI vii

DAFTAR GAMBAR ix

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 2

1.3 Tujuan Penelitian 2

1.4 Manfaat Penelitian 2

BAB 2 KAJIAN PUSTAKA 3

2.1 Graph 3

2.1.1 Definisi graph 3

2.1.2 Konsep dasar graph 3

2.1.3 Incident dan degree 5

2.1.4 Graph bipartie 6

2.1.5 Walk, path, dan cycle 6

2.1.6 Subgraph 8

2.1.7 Graph terhubung, graph tidak terhubung dan komponen 8

2.1.8 Jembatan 10

vii

2.2 Degree 11

2.3 Tree 11

2.3.1 Verteks ujung dalam tree 14

2.3.2 Sisi Pemotong 14

2.4 Spanning Tree 15

2.4.1 Jarak spanning tree (distance of spanning tree) 16

BAB 3 HASIL DAN PEMBAHASAN 18

3.1 Degree Constrained Minimum Spanning Tree 18 3.2 Modifikasi DCMST dengan Metode Algoritma Kruskal 20

BAB 4 KESIMPULAN DAN SARAN 28

4.1 Kesimpulan 28

4.2 Saran 28

DAFTAR PUSTAKA 29

viii

DAFTAR GAMBAR

Nomor Judul Halaman

2.1 Graph 4

2.2 Graph berbobot 4

2.3 (a) Graph lengkap dan (b) Graph sederhana 5

2.4 Verteks ujung dan verteks terisolasi 5

2.5 Graph 7

2.6 (G) graph dan (T) subgraph 8

2.7 (a) Graph terhubung dan (b) Graph tak terhubung 9

2.8 Bridge 10

2.9 Tree 12

2.10 Spanning tree dari G 15

3.1 Degree constrained minimum spanning tree dari G 19

3.2 Graf berbobot 24

3.3 Edge dari bobot terkecil 25

ix

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Diajukan Sebagai Salah Satu Syarat

Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

MARULI HUTAPEA 117021037/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2013

Judul Tesis : PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

Nama Mahasiswa : Maruli Hutapea Nomor Pokok : 117021037

Program Studi : Magister Matematika

Menyetujui, Komisi Pembimbing

(Prof. Dr. Saib Suwilo, M.Sc) (Prof. Dr. Opim Salim S, MSc)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)

Tanggal lulus: 04 Juni 2013

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Oleh

MARULI HUTAPEA 117021037/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2013

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Diajukan Sebagai Salah Satu Syarat

Untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Universitas Sumatera Utara

Oleh

MARULI HUTAPEA 117021037/MT

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN 2013

Judul Tesis : PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

Nama Mahasiswa : Maruli Hutapea Nomor Pokok : 117021037

Program Studi : Magister Matematika

Menyetujui, Komisi Pembimbing

(Prof. Dr. Saib Suwilo, M.Sc) (Prof. Dr. Opim Salim S, MSc)

Ketua Anggota

Ketua Program Studi Dekan

(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)

Tanggal lulus: 04 Juni 2013

Telah diuji pada Tanggal 04 Juni 2013

PANITIA PENGUJI TESIS

Ketua : Prof. Dr. Saib Suwilo, M.Sc Anggota : 1. Prof. Dr. Opim Salim S, M.Sc

2. Prof. Dr. Herman Mawengkang 3. Prof. Dr. Tulus, M.Si

PERNYATAAN

PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE

TESIS

Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing dituliskan sumbernya

Medan, Juni 2013 Penulis,

Maruli Hutapea

i

ABSTRAK

Dalam menyelesaikan persoalan degree constrained minimum spanning tree pada graph G(V, E) berbobot terhubung tak berarah merupakan permasalahan un- tuk menemukan spanning tree T di G dengan total panjang edge yang minimum dan degree dari setiap verteks vi di T dibatasi oleh bi dimana d^T(vi) ≤ bi. Un- tuk menyelesaikan permasalahan degree constrained minimum spanning tree di- lakukan dengan memodifikasi algoritma kruskal, dimana sebuah edge diterima di T, jika edge tidak membentuk cycle pada edge terdahulu yang berada di T dan verteks-verteks ujungnya memenuhi batas maksimum degree yang diberikan, yaitu d^T(vj) ≤ bj dan d^T(vk) ≤ bk.

Kata Kunci : Graph, Degree constrained, Spanning tree

ii

ABSTRACT

The degree constrained minimum spanning tree (DCMST) on undirected weighted connected graph G(V,E) is a problem to fins a spanning tree T in G with whose total edge length is minimal and the degree of each vertex vi in T at most a given value bi where d^T(vi) ≤ bi. For solving this problem, we modified kruskal algorithm, an edge received in T, if an edge did not produce any cycle with preceding edge in T and a both endpoints should not exceed some given maximum degrees that d^T(vj) ≤ bj and d^T(vk) ≤ bk.

Keywords: Graph, Degree constrained, Spanning tree

iii

KATA PENGANTAR

Dengan segala kerendahan hati dan penuh sukacita, penulis mengucap- kan puji syukur ke hadirat Tuhan Yang Maha Kuasa atas segala anugrah dan berkat-Nya yang telah diberikan, sehingga penulis dapat menyelesaikan tesis de- ngan judul: PERSOALAN DEGREE CONSTRAINED MINIMUM SPANNING TREE. Tesis ini merupakan salah satu syarat untuk menyelesaikan studi pada Program Studi Magister Matematika SPs Universitas Sumatera Utara.

Penulis menyadari bahwa terselesaikannya Tesis ini tidak lepas dari bantuan dan dukungan dari berbagai pihak. Oleh karena itu, dengan segala kerendahan hati penulis menyampaikan terimakasih sebesar-besarnya kepada :

Prof. Dr. dr. Syahril Pasaribu, DTMH, M.Sc(CTM), Sp.A(K) selaku Rektor Universitas Sumatera Utara

Dr. Sutarman, M.Sc selaku Dekan FMIPA Universitas Sumatera Utara yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Magister Matematika di FMIPA Universitas Sumatera Utara Medan.

Prof. Dr. Herman Mawengkang selaku Ketua Program Studi Magister Mate- matika FMIPA Universitas Sumatera Utara dan selaku Pembanding Utama yang telah banyak memberikan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

Prof. Dr. Saib Suwilo, M.Sc selaku Sekretaris Program Studi Magister Mate- matika FMIPA Universitas Sumatera Utara dan selaku Pembimbing Utama yang telah banyak memberikan bimbingan dan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

Prof. Dr. Opim Salim S, M.Sc selaku Pembimbing Kedua yang juga telah banyak memberikan bimbingan kepada penulis dalam penulisan tesis ini.

Prof. Dr. Tulus, M.Si selaku Pembanding Kedua yang telah banyak mem- berikan arahan serta motivasi kepada penulis dalam penulisan tesis ini.

iv

Seluruh Staf Pengajar pada Program Studi Magister Matematika FMIPA Uni- versitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perkuliahan.

Saudari Misiani, S.Si selaku Staf Administrasi Program Studi Magister Ma- tematika FMIPA Universitas Sumatera Utara yang telah banyak memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.

Tak lupa penulis mengucapkan terimakasih sebesar-besarnya dan penghar- gaan setinggi-tingginya kepada orangtua tercinta, Ayahanda Alm. Paimin Hu- tapea dan Ibunda Sumiantauli br Simanjuntak yang telah mencurahkan kasih sayang dan dukungan kepada penulis, kepada adik-adik Mawarni Hutapea, Megawati Hutapea serta Istri Netty Saulina br Lumbangaol S.Pd dan anak-anak Olivia Hutapea dan David Hutapea yang telah memberikan se- mangat dan dorongan kepada penulis dalam penulisan tesis ini.

Kepada Pemerintah Provinsi Sumatera Utara (Pemprovsu) atas bantuan da- lam peningkatan pendidikan kualitas guru untuk Daerah Sumatera Utara dalam memberikan Beasiswa Pemprovsu. Dr. Hamonangan Nainggolan, M.Sc dan seluruh rekan-rekan mahasiswa angkatan 2011/2012 pada Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan bantuan moril dan dorongan kepada penulis dalam penulisan tesis, penulis berterima kasih atas semua bantuan yang diberikan. Penulis menyadari bahwa tesis ini masih jauh dari sempurna, untuk itu penulis mengharapkan kritik saran untuk penyempur- naan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihak-pihak lain yang memerlukannya baik perkembangan ilmu pengetahuan.

Medan, Penulis,

Maruli Hutapea

v

RIWAYAT HIDUP

Maruli Hutapea dilahirkan di Lawe Perbunga (Aceh Tenggara) pada tanggal 22 desember 1974 dari pasangan Bapak Alm. Paimin Hutapea & Ibu Sumiantauli br Simanjuntak dan merupakan anak pertama dari tiga bersaudara. Penulis mena- matkan pendidikan Sekolah Dasar (SD) tahun 1989 di SD negeri dikabupaten langkat, Sekolah Lanjutan Tingkat Pertama (SLTP) Negeri 3 binjai pada tahun 1992, Sekolah Menengah Atas (SMA) Sw eka prasetya, kota Medan pada tahun 1995. Menamatkan kuliah S-1 dari UNIMED dikota medan tahun 2000. Dan mendapat gelar sarjana pendikan (S.Pd). Menikah dengan Netty Saulina br Lumbangaol S.Pd, bulan juli tahun 2001 dan dikarunia dua anak yaitu Olivia Hutapea dan David Hutapea.

Pengalaman mengajar pertama sekali di sekolah yayasan perguruan eka prasetya pada tahun 1999 bulan juli pada unit sekolah SMP, pada tahun 2003 mengajar di SMK-BM (SMEA) dan menjadi guru bantu yang dibiayai dari dana APBN, disekolah SMK-BM (SMEA) Eka Prasetya yang terletak di wilayah Deli Serdang. Pada tahun 2006 menjadi PNS di SMA Negeri 1 sunggal sampai sekarang.

Pada tahun 2011 penulis mengikuti program magister matematika di sekolah pasca sarjana universitas sumtra utara, penulis sungguh banyak mendapat pengalaman belajar yang sangat berharga.

vi

DAFTAR ISI

Halaman

PERNYATAAN i

ABSTRAK ii

ABSTRACT iii

KATA PENGANTAR iv

RIWAYAT HIDUP vi

DAFTAR ISI vii

DAFTAR GAMBAR ix

BAB 1 PENDAHULUAN 1

1.1 Latar Belakang 1

1.2 Perumusan Masalah 2

1.3 Tujuan Penelitian 2

1.4 Manfaat Penelitian 2

BAB 2 KAJIAN PUSTAKA 3

2.1 Graph 3

2.1.1 Definisi graph 3

2.1.2 Konsep dasar graph 3

2.1.3 Incident dan degree 5

2.1.4 Graph bipartie 6

2.1.5 Walk, path, dan cycle 6

2.1.6 Subgraph 8

2.1.7 Graph terhubung, graph tidak terhubung dan komponen 8

2.1.8 Jembatan 10

vii

2.2 Degree 11

2.3 Tree 11

2.3.1 Verteks ujung dalam tree 14

2.3.2 Sisi Pemotong 14

2.4 Spanning Tree 15

2.4.1 Jarak spanning tree (distance of spanning tree) 16

BAB 3 HASIL DAN PEMBAHASAN 18

3.1 Degree Constrained Minimum Spanning Tree 18 3.2 Modifikasi DCMST dengan Metode Algoritma Kruskal 20

BAB 4 KESIMPULAN DAN SARAN 28

4.1 Kesimpulan 28

4.2 Saran 28

DAFTAR PUSTAKA 29

viii

DAFTAR GAMBAR

Nomor Judul Halaman

2.1 Graph 4

2.2 Graph berbobot 4

2.3 (a) Graph lengkap dan (b) Graph sederhana 5

2.4 Verteks ujung dan verteks terisolasi 5

2.5 Graph 7

2.6 (G) graph dan (T) subgraph 8

2.7 (a) Graph terhubung dan (b) Graph tak terhubung 9

2.8 Bridge 10

2.9 Tree 12

2.10 Spanning tree dari G 15

3.1 Degree constrained minimum spanning tree dari G 19

3.2 Graf berbobot 24

3.3 Edge dari bobot terkecil 25

ix

BAB 1 PENDAHULUAN

1.1 Latar Belakang

Minimum spanning tree merupakan sebuah permasalahan dalam suatu graph yang aplikasinya baik secara langsung maupun tidak langsung yang telah dipela- jari. Salah satu contoh dalam kehidupan sehari-hari, banyak diantaranya dapat dipresentasikan secara grafik terdiri atas titik-titik dan garis-garis yang menghu- bungkan titik-titik tersebut. Misalnya, titik-titik tersebut mewakili kota, dengan garis-garis mewakili jalan yang menghubungkan kota tersebut dengan kota lainnya atau bisa juga titik-titik itu mewakili manusia dengan garis mewakili hubungan manusia tersebut dengan manusia yang lainnya. Pada matematika, hubungan titik dan garis yang demikian diamati oleh suatu objek disebut dengan graph.

Teori graph pertama kali diperkenalkan oleh Leonhard Euler pada tahun 1736 ketika mencoba membuktikan kemungkinan untuk melewati empat daerah yang terhubung dengan tujuh jembatan di atas sungai Pregel di Konigsberg, Ru- sia dalam sekali waktu. Pembuktian Euler tersebut ditulis dalam karya tulisnya yang berjudul Solution Problematis ad geometriam situs pertinensi. Masalah jem- batan Konigsberg tersebut dapat dinyatakan dalam istilah graph dengan menen- tukan keempat daerah itu sebagai titik (vertex) dan ketujuh jembatan sebagai sisi (edge) yang menghubungkan pasangan titik yang sesuai (Dossey 1992). Se- jak itu, penelitian terhadap graph terus mengalami perkembangan seiring dengan semakin bervariasinya masalah yang dihadapi. Salah satu diantaranya adalah permasalahan degree constrained minimum spanning tree (DCMST).

Permasalahan DCMST pada graph merupakan permasalahan untuk mene- mukan spanning tree dengan total bobot minimum dan memenuhi batasan de- gree yang diinginkan. Garey dan Jhonson (1979) menyatakan bahwa DCMST merupakan NP-hard, karenanya total bobot yang optimal menjadi masalah pro- gram linear maka diperlukan suatu metode pendekatan untuk menyelesaikan- nya. Ribiero dan Souza (2001) menggunakan Variable Neighborhood Search.

Khrisnamoorthy, et al., (2001) mempresentasikan dan membandingkan bebera- 1

2

pa heuristik, pendekatan simulasi annealing, relaksasi lagrang dan metode branch and bound. Binh dan Nguyen (2008) menggunakan algoritma partikel Swarm, algoritma ini menggunakan beberapa metode baru untuk memilih vektor dari partikelnya. Ning et al., (2008) menggunakan teknik reduksi terlebih dahulu un- tuk mengurangi ukuran graph, kemudian menyelesaikan DCMST dengan meng- gunakan algoritma Kruskal. Tanpa menggunakan teknik reduksi terlebih dahulu, penelitian ini akan memodifikasi algoritma Kruskal untuk menyelesaikan DCMST.

Algoritma metaheuristik Variable Neighborhood Descent (VND) adalah algoritma untuk memecahkan masalah dengan menggunakan set neighborhood dalam pen- carian dan penemuan local search sehingga akan mencapai global optimum yang dikembangkan oleh Hansen dan Mladenoviv (1999). Dalam proses pencarian glob- al optimum, VND melakukan pergantian set neighborhood secara deterministik.

Apnena (2011) menyelesaikan masalah TALBP dengan algoritma VND dengan kriteria minimisasi jumlah stasiun kerja.

1.2 Perumusan Masalah

Perumusan masalah dalam penelitian ini adalah menemukan bobot mini- mum dari persoalan degree constrained minimum spanning tree dengan memodi- fikasi algoritma kruskal.

1.3 Tujuan Penelitian

Adapun yang menjadi tujuan dari penelitian ini adalah menganalisis ser- ta mengoptimalkan persoalan degree constrained minimum spanning tree dengan menemukan bobot minimum yang memenuhi batasan-batasan degree yang di- inginkan.

1.4 Manfaat Penelitian

Hasil dari penelitian ini diharapkan agar dapat menambah pemahaman dan pengetahuan mengenai penerapan bobot minimum yang memenuhi batasan de- gree dalam menyelesaikan degree constrained minimum spanning tree, juga di- harapkan dapat menambah referensi bagi pembaca dan dapat digunakan sebagai alat pertimbangan bagi pengambil keputusan dari berbagai alternatife pilihan.

BAB 2

KAJIAN PUSTAKA

2.1 Graph

2.1.1 Definisi graph

Teori graph merupakan pokok bahasan yang sudah tua usianya namun memiliki banyak terapan sampai saat ini. Graph digunakan untuk mempresen- tasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Represen- tasi visual dari graph adalah dengan menyatakan objek sebagai noktah, bulatan atau titik, sedangkan hubungan antara objek dinyatakan dengan garis.

Secara matematis, graph didefinisikan sebagai berikut :

Definisi 1 Graph G didefinisikan sebagai pasangan himpunan (V, E) yang dalam hal ini :

V : Himpunan tidak kosong dari simpul-simpul (vertices atau node) atau

{v1, v2, . . . , vn} dan E : Himpunan sisi (edges atau arc) yang menghubungkan sepasang simpul atau {e1, e2, . . . , en}, dimana V tidak boleh kosong dari dua titik (vi, vj), dimana i dan j boleh sama.

2.1.2 Konsep dasar graph

Suatu graph G =(V,E) merupakan himpunan objek V = {v1, v2, v3, . . .}

disebut verteks (disebut juga point atau node) dan himpunan E = {e1, e2, . . .}

yang elemennya disebut edge (disebut juga line atau arc), sehingga untuk setiap edge em dikenal sebagai penghubung pasangan verteks (vi, vj). Verteks vi, vj yang dihubungkan oleh edge em disebut verteks ujung dari em. Suatu graph dapat di- representasikan secara grafis dengan cara setiap verteks direpresentasikan sebagai titik dan setiap edge vi, vj sebagai garis dari titik vi ke titik vj.

3

4

Contoh 2.1 : Berikut diberikan representasi dari graph.

Gambar 2.1 Graph

Dari gambar 2.1 dapat diketahui bahwa V (G) = {v1, v2, v3, v4} dan E(G) = {v1v1, v1v2, v1v3, v1v4, v2v3, v2v4, v3v3, v3v4}

Berdasarkan definisinya, edge merupakan penghubung pasangan verteks vj, vk

dan untuk suatu edge yang memiliki kedua verteks ujung yang sama disebut loop, jika setiap egde pada graph diberi suatu nilai atau bobot disebut graph berbobot.

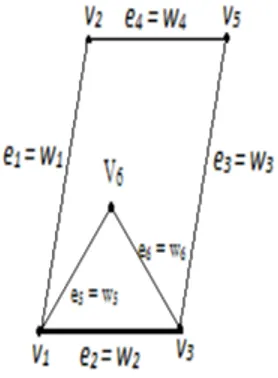
Contoh 2.2 : Berikut diberikan representasi dari graph berbobot.

Gambar 2.2 Graph berbobot

Graph yang tidak memiliki loop ataupun edge ganda disebut graph sederhana.

Graph setiap verteks dihubungkan tepat satu edge ke verteks lainnya disebut graph lengkap.

Contoh 2.3 : Berikut diberikan representasi dari graph sederhana dan graph lengkap.

5

Gambar 2.3 (a) Graph lengkap dan (b) Graph sederhana

2.1.3 Incident dan degree

Ketika verteks v1 merupakan verteks ujung dari beberapa edge ej, vi, dan ej

dikatakan incident satu sama lain. Dua edge nonparalel dikatakan adjacent jika mereka incident pada verteks yang sama. Dengan cara yang sama, dua verteks dikatakan adjacent jika mereka merupakan verteks ujung dari edge yang sama.

Jumlah edge incident dari suatu verteks vi, dengan edge yang merupakan loop dihitung 2 disebut degree dari verteks tersebut. Degree dari suatu verteks dino- tasikan dengan degG(vi) atau deg vi atau d(v). Verteks yang tidak memiliki egde incident disebut verteks terisolasi. Sedangkan verteks yang berdegree satu disebut verteks pendent atau verteks ujung.

Contoh 2.4 : Berikut diberikan representasi dari verteks ujung dan verteks ter- isolasi.

Gambar 2.4 Verteks ujung dan verteks terisolasi

Teorema 2.1 Untuk sembarang graph jumlah degree dari seluruh verteks G sama dengan dua kali jumlah edge di G .

6

Bukti. Diberikan graph G dengan n verteks v1, v2, . . . , vn dan e edge. Karena setiap edge memiliki tepat dua verteks vi, dan vj (untuk loop, i=j), maka edge memberikan kontribusi 2 degree, yakni 1 degree untuk verteks vi dan 1 degree un- tuk verteks vj. Hal ini mengakibatkan penjumlahan degree dari seluruh variabel verteks di G adalah dua kali dari edge di G, yaitu :

Σⁿ_i=1d(vi) = 2e

Teorema 2.2 Dari Teorema 2.1 diketahui bahwa

Σⁿ_i=1d(vi) = 2e

Jika verteks yang berdegree ganjil dan berdegree genap dipisahkan, maka per- samaan diatas dapat dibentuk menjadi :

Σⁿ_i=1d(vi) = Σevend(vj) + Σoddd(vk)

Karena Σⁿ_i=1d(vi) adalah genap, dan Σevend(vj) juga genap, maka Σoddd(vk) ju- ga suata bilangan genap. Karena d(vk) adalah ganjil, maka syarat agar jumlah seluruh d(vk) genap, banyaknya vk haruslah genap. Hal ini membuktikan bahwa banyak verteks berdegree ganjil pada suatu graph selalu genap.

2.1.4 Graph bipartie

Suatu graph G disebut graph bipartie apabila V(G) merupakan gabungan dari 2 himpunan tak kosong V1 dan V2 dan setiap garis dalam G menghubungkan suatu titik dalam V1 dengan titik dalam V2. Apabila dalam graph bipartie, setiap titik dalam V1 berhubungan dengan setiap titik dalam V2, maka graphnya disebut graph bipartie lengkap. Jika V1 terdiri dari m titik dan V2 terdiri dari n titik, maka graph bipartie lengkapnya sering diberi simbol Km,n

2.1.5 Walk, path, dan cycle

Diberikan graph G dengan verteks v dan w. Sebuah walk dengan panjang m dari v ke w didefinisikan sebagai barisan edge dan dituliskan sebagai berikut :

(v0, v1), (v1v2), . . . , (vm−1vm)

7

untuk m > 0, v0 = v dan vm = w. Sebuah walk biasa dinotasikan dengan v→^ww dan panjangnya dinotasikan dengan l(w).

Sebuah trail dari v ke w adalah walk dari v ke w tanpa perulangan edge.

Sebuah path didefinisikan sebagai sebuah trail tanpa perulangan verteks. Path tertutup adalah path yang dimulai dan diakhiri dengan verteks yang sama. Se- buah cycle merupakan sebuah path tertutup, dan sebuah loop merupakan sebuah cycle dengan panjang 1.

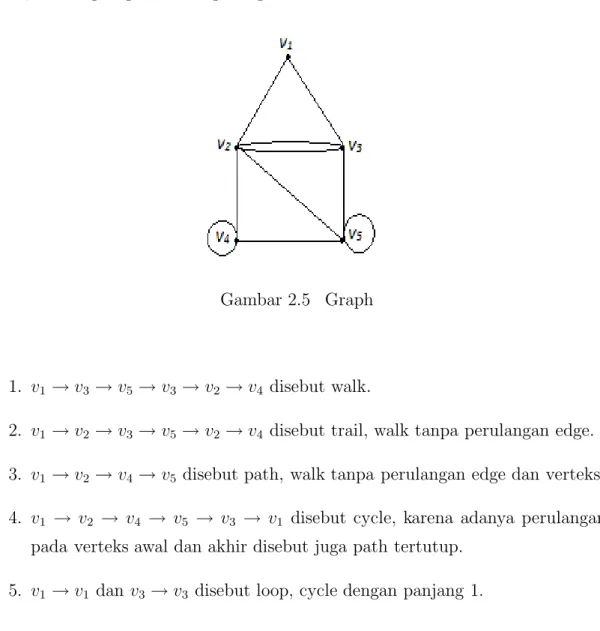
Contoh 2.5 : Sebagai contoh masing - masing untuk walk, trail, path, cycle, dan loop dapat dilihat pada gambar berikut :

Gambar 2.5 Graph

1. v1 → v3 → v5→ v3 → v2 → v4 disebut walk.

2. v1 → v2 → v3→ v5 → v2 → v4 disebut trail, walk tanpa perulangan edge.

3. v1 → v2 → v4→ v5 disebut path, walk tanpa perulangan edge dan verteks.

4. v1 → v2 → v4 → v5 → v3 → v1 disebut cycle, karena adanya perulangan pada verteks awal dan akhir disebut juga path tertutup.

5. v1 → v1 dan v3 → v3 disebut loop, cycle dengan panjang 1.

8

2.1.6 Subgraph

Suatu subgraph dari G adalah graph yang memiliki verteks dan edge yang ada di G. Jika G dan T merupakan dua graph dengan himpunan verteks V(T), V(G) dan himpunan E(T) dan E(G) sehingga V (T ) ⊆ V (G) dan E(T ) ⊆ E(G), maka T disebut subgraph G atau G disebut supergraph T.

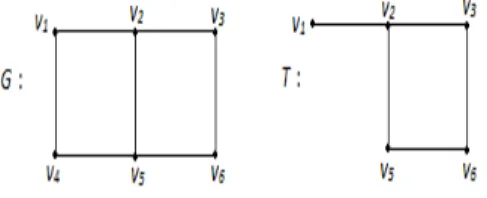
Contoh 2.6 : Berikut diberikan representasi dari subgraph G.

Gambar 2.6 (G) graph dan (T) subgraph

Berdasarakan definisinya, maka dapat dikatakan bahwa :

1. Setiap graph merupakan subgraph itu sendiri.

2. Sebuah subgraph dari subgraph G merupakan subgraph G.

3. Sebuah verteks tunggal di G merupakan subgraph G.

4. Sebuah edge tunggal di G, bersama dengan verteks ujungnya, juga meru- pakan subgraph G.

2.1.7 Graph terhubung, graph tidak terhubung dan komponen

Diberikan graph G dengan v dan w merupakan dua verteks di G. Graph G dikatakan terhubung jika dan hanya jika diberikan sebarang dua verteks v dan w di G sedemikian hingga paling sedikit satu path dari v ke w. Selebihnya, G dikatakaan tidak terhubung.

Pada gambar 2.7 menunjukkan bahwa (a) adalah graph terhubung karena terdapat path dari satu verteks ke verteks yang lainnya, dan (b) adalah graph tak terhubung karena tidak terdapat path dari v1ke v3. Dari gambar 2.3 dapat dilihat bahwa graph tersebut terdiri dari dua bagian. bagian pertama adalah verteks v1,

9

v2dengan edge v1v2, sedangkan bagian kedua adalah verteks v3, v4dan v5, dengan edge v3v4, v3v5, dan v4v5. Masing - masing bagian ini disebut komponen.

Contoh 2.7 : Berikut diberikan representasi dari 2 buah graph terhubung dan tidak terhubung.

Gambar 2.7 (a) Graph terhubung dan (b) Graph tak terhubung

Teorema 2.3 Suatu graph G dikatakan tidak terhubung jika dan hanya jika verteks himpunan V dapat dibagi ke dalam dua komponen tak kosong, himpunan bagian V1 dan V2 terpisah, sehingga tidak ada edge di G yang memiliki satu verteks ujung didalam himpunan bagian V1 begitu juga di himpunan bagian V2.

Bukti : Andaikan komponen ada. Anggap dua sembarang verteks a dan b di G, sehingga a ∈ V1 dan b ∈ V2. Tidak ada path yang bisa diantara verteks a dan b:

sebaliknya terdapat paling sedikit satu edge yang dimiliki verteks ujung V1 dan lainnya di V2. Akibatnya jika komponen ada, G tidak terhubung.

Dan sebaliknya, andaikan G menjadi graph tidak terhubung. Anggap sebuah verteks a di G. Andaikan V1 menjadi himpunan seluruh verteks yang dihubungkan oleh path ke a. Karena G tidak terhubung, maka V1 tidak memasukkan semua verteks G. Selebihnya verteks akan berbentuk (tak kosong) himpunan V2. Tidak ada verteks di V1 yang dihubungkan ke sebarang V2 dengan sebuah edge. Hal ini berakibat adanya komponen.

Teorema 2.4 Jika suatu graph memiliki tepat dua vertek berdegree ganjil, pasti terdapat path yang menyertai dua vertek tersebut.

Bukti : Andaikan G sebuah graph dengan seluruh verteknya berdegree genap kecuali verteks v1 dan v2, yang berdegree ganjil. Berdasarkan teorema 2.2, hal

10

ini berlaku untuk seluruh graph, oleh karenanya untuk setiap komponen graph tak terhubung, tak ada graph yang bisa memiliki jumlah ganjil dari verteks ganjil.

Karenanya, di graph G v1 dan v2harus bisa pada komponen yang sama, akibatnya pasti ada path diantaranya.

2.1.8 Jembatan

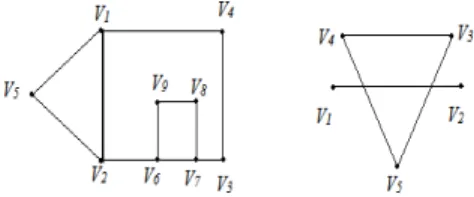
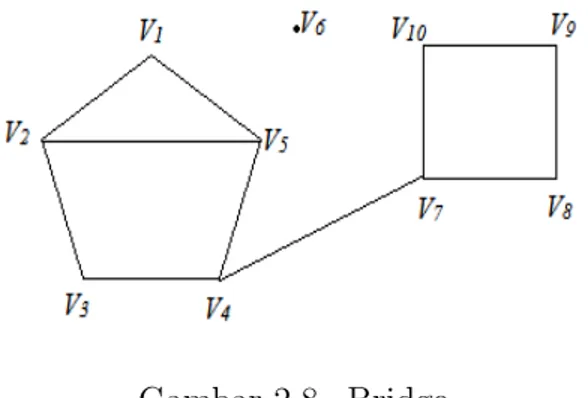
Teori graph ditulis pertama kali tahun 1736 oleh seorang matematikawan Swiss yang bernama Leonard Euler. Yang digunakan untuk menyelesaikan masalah jembatan Konigsberg. Jika suatu graf adalah G = (V, E) maka V merupakan himpunan tak kosong dari simpul-simpul (vertices), misalkan V = {v1, v2, ..., vn} Suatu edge vivj pada graph G terhubung dikatakan bridge jika penghapusan edge vivj mengakibatkan G menjadi tidak terhubung.

Contoh 2.8 : Berikut diberikan representasi dari bridge.

Gambar 2.8 Bridge

v4v7 merupakan bridge karena penghapusan edge v4v7 akan menyebabkan graph menjadi tidak terhubung.

Algoritma untuk Jembatan :

1. Tentukan banyak komponen k(G)

2. Tentukan banyak komponen dari k(G − e) if k(G)<k(G − e)

e adalah jembatan else

11

e bukan jembatan end

2.2 Degree

Derajat titik v (simbol d(v)) adalah jumlah garis yang berhubungan dengan titik v dan garis suatu loop dihitung dua kali. Derajat total G adalah jumlah derajat semua titik dalam G.

Teorema 2.5 Derajat total suatu graph selalu genap.

Bukti : Jika G tidak memiliki garis sama sekali berarti derajat totalnya = 0 yang merupakan bilangan genap, sehingga teorema terbukti.

Teorema 2.6 Derajat sembarang graph, jumlah titik yang berderajat ganjil adalah genap.

Bukti : Jika G tidak mempunyai garis sama sekali berarti banyaknya titik yang berderajat ganjil = 0 yang merupakan bilangan genap sehingga teorema terbukti dengan sendirinya.

2.3 Tree

Suatu tree merupakan graph terhubung tanpa adanya cycle. Untuk graph tak terhubung dan tanpa cycle disebut forest. Suatu verteks tunggal juga terma- suk tree yang disebut trivial tree.

12

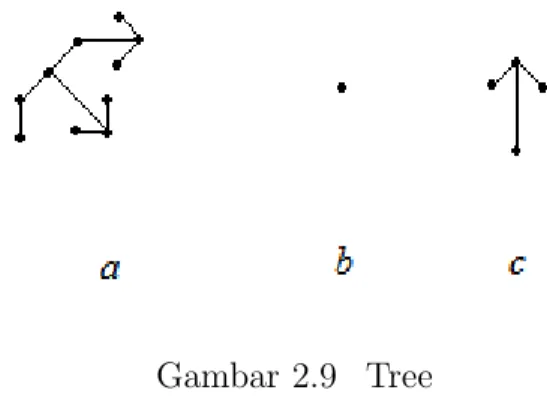
Contoh 2.9 : Berikut diberikan representasi dari tree.

Gambar 2.9 Tree

Teorema 2.7 Hanya ada satu path antara setiap pasangan verteks di tree T.

Bukti : Karena T terhubung, maka terdapat paling sedikit satu path diantara semua pasangan verteks di T. Sekarang anggap bahwa diantara dua verteks a dan b di T terdapat path yang berbeda. Penggabungan dari dua path yang berbeda akan menghasilkan cycle, karenanya T bukanlah tree, begitu juga sebaliknya.

Teorema 2.8 Jika pada graph G hanya ada satu path diantara setiap pasangan verteks, maka G merupakan tree.

Bukti : Adanya path diantara setiap pasangan verteks menjamin bahwa G ter- hubung. Suatu cycle di G (dengan dua atau lebih verteks) secara tidak langsung menyatakan bahwa terdapat paling sedikit satu pasangan verteks a,b sehingga terdapat dua path yang berbeda antara a dan b. Karena G hanya memiliki satu path diantara setiap pasangan verteks, maka G tidak bisa memiliki cycle. Oleh karena itu, G merupakan tree.

Teorema 2.9 Suatu tree dengan n verteks memiliki n-1 edge.

Bukti : Hasilnya akan diperlihatkan dengan induksi. Andaikan ek menjadi edge di T dengan verteks ujung vi dan vj, berdasarkan teorema 2.3 tidak ada path lain diantara vi dan vj, kecuali ek. Oleh karenanya jika ek dihapus, maka T menjadi

13

graph tak terhubung. Selanjutnya, T −ek akan membentuk dua komponen, karena tidak ada cycle di T, maka masing-masing memiliki lebih sedikit dari n verteks, dengan induksi, masing-masing memiliki edge lebih sedikit dari jumlah verteks didalamnya. Dengan demikian T − ek mengandung n − 2 edge. Hal ini berakibat T memiliki tepat n − 1 edge.

Teorema 2.10 Untuk sebarang graph terhubung dengan n verteks dan n-1 edge merupakan tree.

Bukti : Berdasarkan definisi graph terhubung, terdapat paling sedikit satu path di G, berdasarkan teorema 2.3 tidak ada path lain diantara vi dan vj, kecuali ek, berdasarkan definisi suatu tree merupakan graph terhubung tanpa adanya cycle, karenanya berdasarkan teorema 2.7, suatu tree dengan n verteks memiliki n-1 edge. Hal ini berakibat graph terhubung dengan n verteks n-1 edge merupakan tree.

Teorema 2.11 Suatu graph merupakan tree jika dan hanya jika graph tersebut terhubung.

Bukti : Andaikan graph G merupakan tree, berdasarkan definisi suatu tree meru- pakan graph terhubung tanpa adanya cycle. Andaikan G tidak terhubung, maka berdasarkan teorema 2.1 graph bukanlah tree. Hal ini berakibat bahwa untuk graph yang merupakan tree, haruslah graph terhubung.

Teorema 2.12 Suatu graph G dengan n vertkes, n-1 edge, dan tanpa cycle adalah terhubung.

Bukti : Andaikan bahwa ada sedikit cycle graph G dengan n verteks dan n-1 edge yang tak terhubung. Pada kasus ini, G akan mengandung dua atau lebih sedikit komponen cycle. Tanpa kehilangan sifat umumnya, andaikan G memiliki komponen g1 dan g2. Lalu tambahkan sebuah edge e diantara suatu verteks v1

di g1, dan v2 di g2. Karena tidak ada path, diantara v1 dan v2 di G, tambahkan

14

e tanpa membentuk cycle. Dengan demikian G ∪ e memiliki cycle sedikit, graph terhubung dari n verteks dan n edge, dan tanpa cycle adalah terhubung.

Berdasarkan teorema-teorema tersebut, dapat disimpulkan bahwa suatu graph G dengan n verteks disebut tree, jika :

1. G terhubung dan tanpa cycle, atau

2. G terhubung dan memiliki n - 1 edge, atau 3. G tanpa cycle dan memiliki n - 1 edge, atau

4. Tepat terdapat satu path diantara setiap pasangan verteks di G, atau 5. G paling tidak merupakan graph terhubung.

2.3.1 Verteks ujung dalam tree

Verteks ujung merupakan verteks dengan jumlah degree adalah 1.

Teorema 2.13 Pada sebarang tree (dengan dua atau lebih verteks), terdapat pal- ing sedikit dua verteks ujung.

Bukti : Karena tree yang memiliki n verteks dan n - 1 edge, maka 2(n-1) degree terbagi diantara n verteks. Karenanya tidak akan bisa ada verteks yang tidak memiliki degree, paling sedikit harus memiliki dua verteks yang berdegree 1 dalam degree. Tentu saja ini hanya berlaku jika n ≥ 2.

2.3.2 Sisi Pemotong

Sebuah sisi e pada graph G adalah sebuah sisi e, demikian sehingga ω(G − e) ≥ ω(G), dengan ω(G) sebagai banyaknya komponen dari G.

Teorema 2.14 Sebuah sisi e pada graph G merupakan sisi pemotong jika dan hanya jika e termuat dalam nonsiklus dari G.

Teorema 2.15 Sebuah graph G adalah sebuah pohon jika dan hanya jika setiap sisinya merupakan sisi pemotong.

15

Teorema 2.16 Setiap graph terhubung memuat sebuah pohong rentang.

Sebuah simpul v pada graph disebut simpul pemotong jika E(G) dapat dipar- tisikan ke dalam dua himpunan bagian E1 dan E2 demikian sehingga G[E1] dan G[E2] hanya mempunyai irisan pada simpul v. Jika G merupakan graph non triv- ial dan tidak mengandung loop, maka v merupakan simpul pemotong dari G jika dan hanya jika ω(G − v) ≥ ω(G).

Teorema 2.17 Sebuah simpul v pada pohon G merupakan simpul pemotong dari G jika dan hanya jika deg(v) > 1.

Teorema 2.18 Setiap graph terhubung non trivial yang tanpa loop mempunyai paling sedikit dua simpul yang tidak merupakan simpul pemotong.

2.4 Spanning Tree

Suatu tree T dikatakan spanning tree dari graph G terhubung, jika T adalah suatu subgraph G dan T mengandung seluruh verteks G. Dengan kata lain, T dikatakan spanning tree jika T terhubung, mengandung n verteks G dan n-1 edge.

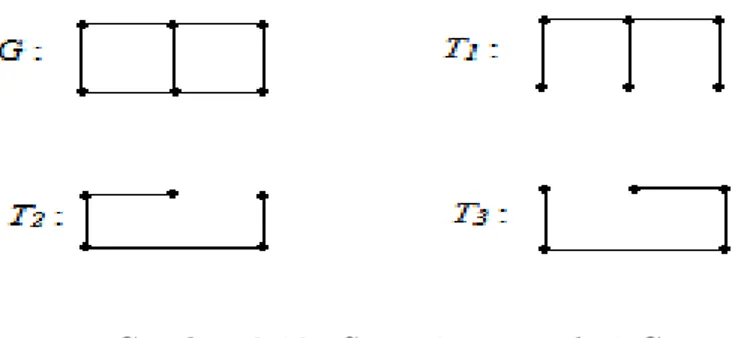
Contoh 2.2.2 : Berikut diberikan representasi dari spannning tree.

Gambar 2.10 Spanning tree dari G

Dari gambar 2.10, untuk T1 graph menghasilkan spanning tree dengan 6 verteks dan 5 edge. Untuk menemukan spanning tree dari graph G terhubung dapat dilakukan dengan cara yang sederhana. Jika G tidak memiliki cycle, maka

16

G merupakan spanning tree itu sendiri. Jika G memiliki cycle maka hapus semua edge yang membentuk cycle, dengan G masih terhubung.

Proposisi 2.12

Setiap graph terhubung memiliki paling sedikit satu spanning tree.

Bukti : Andaikan G adalah suatu graph terhubung. Jika G bebas cycle, maka G itu sendiri merupakan spanning tree. Jika tidak, G memiliki paling sedikit satu cycle C1. dengan teorema, yakni subgraph G tetap terhubung meski satu edge C1

dihapus. Jika subgraph bebas cycle, maka subgraph tersebut merupakan spanning tree. Jika tidak, maka paling sedikit ada satu cycle di C2, dan seperti sebelumnya, hapus edge di C2 untuk memperoleh spanning tree. Jika tidak, lakukan seperti sebelumnya hingga diperoleh subgraph T dari G yang terhubung dan bebas cycle.

T juga mengandung seluruh verteks G karena tidak ada verteks di G yang dihapus.

Oleh karenanya T merupakan spanning tree untuk G.

2.4.1 Jarak spanning tree (distance of spanning tree)

Misalkan G = (V, E), bersama dengan fungsi jarak d : E → N . Untuk selanjutnya G terhubung, dan T merupakan spanning tree dari G, maka nilainya:

d(T ) =X

e∈T

de

merupakan penjumlahan seluruh jarak pada semua edge di T , disebut dengan jarak spanning tree.

Untuk setiap spanning tree T dari G akan mempunyai total jarak d(T ). Dari semua spanning tree T dari G, terdapat spanning tree yang mempuyai jarak d(T ) minimum.

Minimum spanning tree merupakan suatu permasalahan dalam suatu graph yang aplikasinya banyak, baik secara langsung maupun tidak langsung. Salah satu contoh aplikasi secara langsung adalah permasalahan pemasangan jaringan dengan meminimasi jumlah penggunaan kabel atau pipa untuk menghubungkan bangunan secara bersamaan (connected). Untuk aplikasi secara tidak langsung termasuk seperti mereduksi data storage dan cluster analisys. Beberapa per-

17

masalahan jaringan juga bisa direduksi ke dalam permasalahan minimum span- ning tree kemudian diselesaikan dengan cara tersebut. Permasalahan minimum spanning tree juga dapat digunakan untuk menyelesaikan permasalahan graph yang lain, seperti travelling salesman problem (TSP).

Hasil literatur memberikan informasi bahwa penelitian tentang penggunaan suatu algoritma untuk menentukan minimum spanning tree dan implementasinya pada suatu graph berbobot pernah dilakukan oleh sejumlah peneliti, yaitu Gloor et al., (1993) memperkenalkan pembuktian kebenaran suatu algoritma dengan melakukan visualisasi. Greenberg (1998) membandingkan algoritma Prim dan algoritma Kruskal dalam mencari minimum spanning tree dengan menggunakan graph yang terhubung dengan bobot tidak negative pada sisi-sisinya. Pop dan Zelina (2004) melakukan penelitian dengan menyajikan algoritma waktu ekspo- nensial untuk graph tidak berarah yang memiliki simpul-simpul n yaitu algorit- ma heuristik berbasis kruskal, algoritma heuristic berbasis prim, dan algoritma heuristic berbasis pendekatan global-lokal.

BAB 3

HASIL DAN PEMBAHASAN

3.1 Degree Constrained Minimum Spanning Tree

Teorema 3.1 Setiap graf terhubung mempunyai sekurang-kurangnya satu span- ning tree.

Bukti :

Jika G suatu graf terhubung dan G tidak mempunyai sirkuit maka spanning treenya adalah G sendiri, jika G mempunyai sebuah sirkuit maka spanning treenya dapat diperoleh dengan menghilangkan sisi pembentuk sirkuit tersebut. Selanjut- nya jika G mempunyai banyak sirkuit (lebih dari satu sirkuit) maka cara diatas dapat diulangi sampai sisi terakhir pembentuk sirkuit dihilangkan.

Teorema 3.2 Jika G adalah graf berbobot, maka bobot perentang T dari G di- definisikan dengan jumlah bobot semua sisi di T. pohon perentang yang berbeda mempunyai bobot yang berbeda pula. Di antara semua pohon perentang di G, pohon perentang yang berbobot minimum dinamakan pohon merentang minimum (minimum spanning tree).

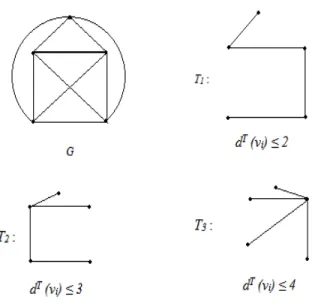
Andaikan G merupakan graph terhubung, T merupakan subgraph dari G, d^T(vi) merupakan degree dari verteks viyang ada di T, dan bi merupakan batasan degree di T. Degree constrained minimum spanning tree T adalah menemukan spanning tree di G, sehingga d^T(vi) ≤ bi, untuk setiap verteks vi di T.

Teorema 3.3 Diberikan graph G dimana T merupakan degree constrained mini- mum spanning tree dari G.

18

19

Gambar 3.1 Degree constrained minimum spanning tree dari G

Andaikan G = (V,E) adalah suatu graph berbobot terhubung tak berarah dengan V = {v1, v2, . . . , vn} adalah himpunan verteks dan E = {e1, e2, . . . , em} mewakili bobot dari setiap edge, mempunyai bobot merupakan bilangan real non negatif. Subgraph dari G bisa dideskripsikan menggunakan vektor X = {x1, x2, . . . , xm} disetiap elemen xi, didefinisikan oleh:

xi =n 1

0 jika edge terpilih jika tidak terpilih

Andaikan T menjadi subgraph G, T dikatakan spanning tree dari G jika T terhubung, mengandung seluruh verteks G, dan tidak cycle. Kemudian anggap d(vi) degree dari verteks vi di G dan K(vi) himpunan degree pada G serta bi

merupakan batasan degree d^T(vi) di T, persoalan degree constrained minimum spanning tree dapat diformulasikan ke dalam program integer sebagai berikut :

Fungsi Tujuan :

M inz(x) = Σ^m_i=1wixi

20

Kendala :

1. Σ^m_i=1xi = |V | − 1

2. Σ^m_i=1xi ≤ |N | − 1, ∀N ⊂ V, |N | ≥ 3

3. Σx_i∈K(v_i)xi ≤ bi, 1 ≤ bi ≤ |V | − 1, i = 1, 2, . . . , n 4. xi ∈ {0, 1}, xi ∈ E

Dari formulasi tersebut, kendala pertama menyatakan bahwa hanya ada n − 1 edge yang terpilih, karenanya kendala kedua menjamin bahwa edge yang diperoleh akan menghubungkan seluruh verteks tanpa terjadi cycle, sedangkan kendala ketiga merupakan batas degree yang dikehendaki.

3.2 Modifikasi DCMST dengan Metode Algoritma Kruskal

Pada dasarnya persoalan degree constrained minimum spanning tree meru- pakan perkembangan dari permasalahan minimum spanning tree dengan syarat memenuhi batasan degree yang diberikan. Karenanya algoritma yang biasa digu- nakan untuk menyelesaikan minimum spanning tree dapat pula digunakan untuk menyelesaikan permasalahan degree constrained minimum spanning tree. Salah satunya adalah algoritma kruskal.

Ning et al., (2008) menggunakan algoritma kruskal untuk menyelesaikan permasalahan degree constrainde minimum spanning tree dengan terlebih dahu- lu menggunakan teknik reduksi untuk mengurangi ukuran graph dengan cara menghilangkan edge yang dianggap tidak perlu.

Algoritma kruskal pertama kali diperkenalkan pada tahun 1956 oleh Joseph Kruskal untuk menyelesaikan minimum spanning tree. Algoritma kruskal ditulis kembali pada tahun 1957 oleh Loberman dan Weinberger, namun pencantuman nama mereka ditolak (Erickson, 2011). Dalam menyusun algoritma kruskal, sisi- sisi graf diurutkan terlebih dahulu berdasarkan bobotnya dari kecil ke besar. Sisi yang dimasukkan kedalam himpunan T adalah susu graf G sedemikian sehingga T adalah pohon. Pada keadaan awal, sisi-sisi sudah diurut berdasarkan bobot yang

21

membentuk pohon, masing-masing pohon di hutan hanya berupa satu buah sim- pul. Hutan tersebut dinamakan hutan merentang. Sisi dari graf G ditambahkan ke T jika tidak membentuk siklus di T.

Langkah-langkah pada algoritma kruskal adalah sebagai berikut:

Langkah 0 : Sisi-sisi dari graf sudah diurut menarik berdasarkan bobotnya dari bobot kecil ke bobot besar.

Langkah 1 : T masih kosong.

Langkah 2 : Pilih sisi (u,v) dengan bobot minimum yang tidak membentuk sirkuit di T. Tambahkan (u,v) ke dalam T.

Langkah 3 : Ulangi langkah 2 sebanyak n-1 kali.

Berikut diberikan algoritma Kruskal KRUSKAL (V,E): Mulai :

1. Urutkan ei∈ E for i : 1

2. T ← (V, E − {ei})

Untuk setiap verteks (vj, vk) ∈ V Masukkan himpunan V ke T 3. Untuk i ← 1 ke |E|

a. (vj, vk) ← tandai edge ke i di E b. Jika (vj) 6= (vk)

Gabungkan (vj, vk) Tambahkan (vj, vk) ke T c. Jika |(vj, vk)| < |V | − 1

Hasil T.

Akhir

22

Keterangan :

1. Seluruh edge ei yang ada di E diurutkan berdasarkan nilai bobot, dimana w(ei) ≤ w(e2) ≤ . . . ≤ w(em).

2. Seluruh verteks vi di V dimasukkan ke T.

3. Untuk edge awal di T merupakan edge dengan nilai bobot paling minimum.

a. Untuk edge vj, vk selanjutnya akan dimasukkan ke T, periksa vjvk ter- lebih dahulu, jika verteks vj tidak berada dalam tree yang sama dengan verteks vk (edge vjvk tidak membentuk cycle), maka gabungkan edge vjvk, lalu tambahkan vjvk ke T.

b. Jika jumlah edge yang ada di T = |V | − 1, maka hentikan pencarian edge vj, vk karena sudah menghasilkan minimum spanning tree T.

Sebuah simpul v pada graph disebut simpul pemotong jika E(G) dapat dipartisikan ke dalam dua himpunan bagian E4 dan E2 demikian sehingga G[E1] dan G[E2] hanya mempunyai irisan pada simpul v. Jika G merupakan graph non trivial dan tidak mengandung loop, maka v merupakan simpul pemotong dari G jika dan hanya jika ω(G − v) ≥ ω(G).

Algoritma Bridge

1. Set T = ∅ 2. for i : 1 to m 3. Select on edge ei

4. if E 6= E − {ei}

5. Then T ← E = Ei−1S {ei} 6. else let T = (Ei), stop 7. return T

23

Bukti :

1. Set T sebagai himpunan tree dengan Vi ∈ V di G adalah tree yang terpisah 2. Set himpunan E yang memuat seluruh edge di graf G

3. Ambil ei ∈ E dengan bobot paling minimum, yaitu ei = min(V, E − {ei}) untuk i = 1, ..., m. Lakukan pengulangan untuk i = 1, 2, ...m

4. Pastikan bahwa tidak terdapat edge yang membentuk cycle, dengan E 6=

{ei}

5. Jika edge yang diperoleh tidak membentuk cycle, maka gabungkan edge ke T. Minimum Spanning Tree T.

6. Jika edge membentuk cycle, maka T = (ei). Selesai 7. Kembali ke T

Asumsikan terdapat suatu graf G = (V,E) dengan T adalah minimum span- ning tree di G. Maka prosedur modifikasi kruskal dalam menentukan jembatan di graf G adalah :

1. T = ∅

2. for i : 1 to m 3. while |T | < n − 1 4. do pilih ei

5. then T ← E = Ei−1

S{ei}

6. if TS

{ei} tidak memuat cycle 7. Then T : TS

{ei}

24

Pemodifikasian algoritma Kruskal perlu dilakukan sehingga dapat diterap- kan untuk menyelesaikan Degree constrained minimum spanning tree. Adapun permasalahan degree constrained minimum spanning tree secara sederhana dapat dijelaskan sebagai berikut, diberikan graph G berbobot terhubung tak berarah, kemudian ditemukan spanning tree T dengan total edge minimal dan d(vi) ≤ bi, untuk setiap verteks vi di T.

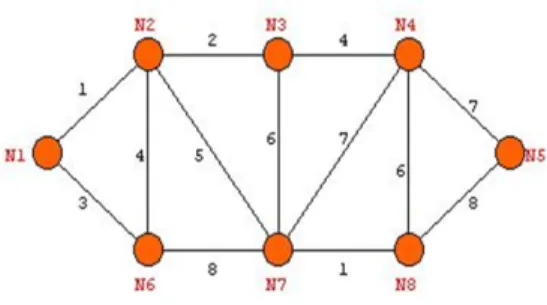
Contoh :

1. Graf berbobot

Gambar 3.2 Graf berbobot

25

2. Pilih edge dimulai dari bobot terkecil.

Gambar 3.3 Edge dari bobot terkecil

3. Jika v2 dan v7 atau langkah keenam dihapus, berarti itu bukan merupakan bridge.

Permasalahan degree constrained minimum spanning tree pada graph G terhubung tak berarah merupakan permasalahan menemukan spanning tree T di G dengan total panjang edge yang minimum dan degree setiap verteks vi di T memenuhi bi yang diberikan (d^T(vi) ≤ bi). Karena adanya pembatas degree dari setiap verteks vi di T, untuk memodifikasi algoritma kruskal ada beberapa hal yang perlu diperhatikan, yaitu :

1. Batasan degree vi di T, untuk kasus tertentu pada graph G yang memiliki beberapa bridge, menyebabkan T tidak dapat ditemukan. Untuk itu, semua edge vj, vk yang merupakan bridge harus dimasukkan ke dalam T.

2. Suatu edge vj, vk diterima pada T jika vj, vk tidak membentuk cycle dengan edge terdahulu yang ada di T dan (d^T(vj) ≤ bj) dan (d^T(vk) ≤ bk).

26

Untuk hasil modifikasi algoritma Kruskal tersebut dinamakan algoritma Kruskal DCMST. Berikut diberikan algoritma Kruskal DCMST :

Kruskal DCMST (V,E),d^T(vi) ≤ bi : Mulai :

1. T ← (V, φ).

untuk setiap verteks vi ∈ V . Masukkan Himpunan (vi) V (G⁰) = V (G)

E(G⁰) = E(G)

2. ∀(vj, vk) ∈ E yang merupakan bridge.

Tambahkan (vj, vk) ke T

3. Urutkan ei∈ E yang bukan bridge berdasarkan bobot.

4. a. (vj, vk) ← tandai edge ke i di E.

b. Jika (vj) 6= (vk) dan (d^T(vj) ≤ bj, d^T(vk) ≤ bk).

Gabungkan (vj, vk) Tambahkan (vj, vk) ke T.

c. Jika |(vj, vk)| = |V | − 1.

Hasil T.

Akhir.

Keterangan :

1. Seluruh verteks vi di V dimasukkan ke T.

2. Jika G memuat sirkuit, bentuklah G’ dengan V(G’) = V(G) dan E(G’) = E(G)-{satu garis yang membentuk sirkuit}. Dengan cara pembuatan itu, G’ tetap merupakan graf yang terhubung karena garis yang dihapus adalah garis yang membentuk sirkuit. Jika G’ sudah tidak memuat sirkuit, berarti G’ merupakan pohon rentang.

3. Masukkan semua edge vj, vk ∈ E yang merupakan bridge (cut edge) di G.

27

4. Urutkan edge ei ∈ E yang bukan bridge berdasarkan nilai bobot, dimana w(e1) ≤ w(e2) ≤ . . . ≤ w(em).

5. Pilih edge vj, vk dengan nilai bobot paling minimum.

a. untuk edge vj, vk selanjutnya yang akan dimasukkan ke T, periksa vj, vk

terlebih dahulu, jika verteks vj tidak sama dengan verteks vk (edge vj, vk tidak membentuk cycle) dan degree verteks vj di T memenuhi bj(d^T(vj) ≤ bj) serta degree verteks vk di T memenuhi bk(d^T(vk) ≤ bk) maka gabungkan edge vj, vk lalu tambahkan vj, vk ke T.

b. Jika jumlah edge yang ada di T = |V | − 1, maka hentikan pencarian edge vj, vk karena sudah menghasilkan degree constrained minimum spanning tree T.

Waktu minimal yang diperlukan oleh algoritma Kruskal untuk melakukan proses dari tahap awal hingga menghasilkan degree constrained minimum spanning tree adalah O(E log V).

Karena pemilihan edge berdasarkan nilai dari bobot setiap edge (vj, vk) yang telah terurut dilakukan hal berikut, jika verteks vj dan vk merupakan dua tree yang berbeda, maka tambahkan (vj, vk) ke forest, kombinasikan dua tree ke dalam tree tunggal. Proses dihentikan jika edge (vj, vk) tepat berjumlah |V | − 1. Pada batasan degree vi di T pada graph G yang memiliki beberapa bridge, menye- babkan T tidak dapat ditemukan. Untuk itu, semua edge vj, vk yang merupakan bridge harus dimasukkan kedalam T. Selanjutnya untuk edge vj, vk yang akan dimasukkan ke T, harus diperiksa vj, vk terlebih dahulu. Jika verteks vj tidak be- rada pada tree yang sama dengan verteks vk (edge vj, vk tidak membentuk cycle) dan degree verteks vj di T memenuhi bj(d^T(vj) ≤ bj) serta degree verteks vk di T memenuhi bk(d^T(vK) ≤ bk), maka gabungkan edge vj, vk, lalu tambahkan vj, vk

ke T.

BAB 4

KESIMPULAN DAN SARAN

4.1 Kesimpulan

Persoalan degree constrained minimum spanning tree merupakan permasala- han menemukan spanning tree T di G dengan total panjang edge minimum dan degree dari setiap verteks vi di T memenuhi bi yang diberikan (d^T(vi) ≤ bi).

Karena adanya batasan degree dari setiap verteks vi di T.

4.2 Saran

Persoalan degree constrained minimum spanning tree dapat diselesaikan de- ngan menggunakan algoritma kruskal yang telah dimodifikasi. Namun, untuk lebih mempermudah menyelesaikan degree constrained minimum spanning tree dengan metode lain yang mungkin lebih efisien dan efektif agar dapat lebih mu- dah dipahami.

28

DAFTAR PUSTAKA

Binh H.T.T dan Nguyen T.B. (2008). New particle swarm optimization algorithm for solving degree constrained minimum spanning tree. LNAI, 5351 (2008), 1077-1085.

Dossey, J. (1992). The Nature of Mathematics : Its Role and Its Influence. In D.

Grouws, ed., Handbook of Research on Math Teaching and Learning. New York : Macmillan Publishing.

Erickson J. (2011). Algorithms. Departement of Computer Science University of Illinois, Urbana-Champaign.

Garey, M.R., D.S. Johnson. (1979). Computers and Intractability, A Guide to the Theory of NP-Completensess. Freemann, San Francisco.

Krishnamoorthy, M., A.T. Ernst, Y.M. Sharaiha. (2001). Comparison of Algoritms for the Degree Constrained Minimum Spanning Tree. Journal Heuristics, vol.

7.no. 6,pp. 587-611.

Kruskal, J.B. (1956). On the Shortest Tree og a Graph and the Traveling Salesman Problem. Proc. Amer, Math. Soc, vol. 7. pp 48-50.

Ning A, Ma L, dan Xiong X. (2008). A new algorithm for degree constrained minimum spanning tree based on the reduction technique. Progress in Natural Science, 18 (2008), 495-499.

Ribiero C.C dan Souza M.A. (2002). Variable neighbourhood search for the degree constrained minimum spanning tree problem. Descrete applied mathematics, 118; 43-54.

Sri Kusuma Dewi dan Hari Purnomo. (2005). Penyelesaian Masalah Optimasi de- ngan Teknik-teknik Heuristik,Yogyakarta,

Vasudev C. (2006). Graph Theory with Applications. New Delhi: New age inter- national publisher.

29