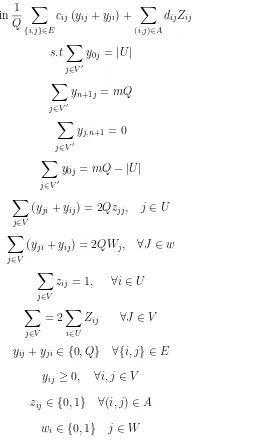rapannya di banyak bidang ilmu adalah Teori Graph. Salah satunya adalah bidang jaringan telekomunikasi. Digunakan graph gabungan, dimana titik transisi dan pusat depot diasosiasikan dengan node, sementara sambungan antara node adalah edge atau arc berbobot.
Berikut akan dijelaskan mengenai teori dasar graph yang akan digunakan untuk mendesain m-ring star.
2.1 Graph
Suatu graph terdiri dari dua bilangan yaitu titik dan garis. Titik pada suatu graph disebut verteks dan garis yang menghubungkan dua titik disebut edge atau arc (untuk garis berarah). Secara formal suatu graph G didefinisikan sebagai berikut:
Sebuah graf terdiri dari dua bagian, yaitu sebagai berikut.
1. Sebuah himpunan V = V(G) memiliki elemen-elemen yang dinamakan verteks, titik, atau simpul.
2. Sebuah kumpulan E = E(G) merupakan pasangan terurut dari verteks-verteks yang berbeda dinamakan sisi atau edge.
2.1.1 Graph sederhana
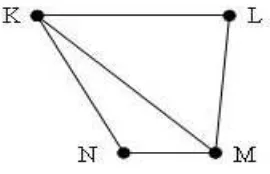
Gambar 2.1 Simple graph
2.1.2 Graph tak sederhana
Graph yang mempunyai edge ganda dan atau loop dinamakan graph tak sederhana atau unsimple graph.
Gambar 2.2 Graph tidak sederhana
2.1.3 Graph berbobot
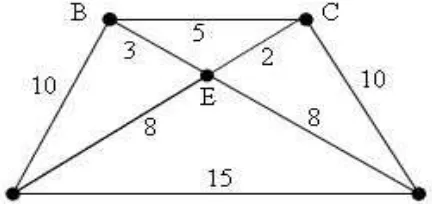
Graph berbobot atau graph berlabel adalah graph yang setiap edgenya diberi sebuah nilai (bobot). Bobot pada tiap edge dapat menyatakan biaya transportasi dari suatu kota ke kota lainnya atau jarak antara dua tempat atau waktu tempuh antara dua tempat dan lain-lainnya. Berikut ini adalah contoh graph berbobot
Gambar 2.4 Sebuah multigraf dengan tiga simpul dan lima edge
Pada Gambar 2.4 , G adalah graf dengan:
V ={P, Q, R}
E ={(P, Q),(P, Q),(P, R),(R, R),(Q, R)}
= {e1, e2, e3, e4, e5}
G mengandung edge ganda, e1 dan e2, yang menghubungkan dua verteks yang sama, yaitu P dan Q. G juga mengandung sebuah loop e4, yang titik-titik ujungnya sama, yaitu verteks R. Karena itu, graf di atas merupakan multigraf.
Berdasarkan pada orientasi arah padaedge, maka secara umum graf dapat dibedakan atas 2 jenis sebagai berikut.
1. Graf tak berarah (undirected graph)
Graf yang sisinya tidak mempunyai orientasi arah. Gambar 2.4 merupakan gam-bar graf tak berarah.
2. Graf berarah (directed graphatau digraph)
Gambar 2.5 Graf berarah
M-ring star mendesain:
1. Susunan titik yang tidak teratur sebanyak m melewati pusat depot dan beberapa node lainnya.
2. Sekumpulan koneksi langsung dari pelanggan yang belum dikunjungi ke sebuah node dengan sebuah ring. Jumlah pelanggan yang dihubungkan ke ring akan dibatasi oleh Q (kapasitas dari ring). Tujuannya adalah meminimalkan biaya ring dan biaya koneksi pelanggan (min : cost ring + cost customer ).
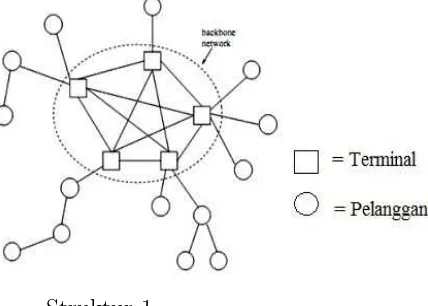
Berikut adalah beberapa contoh struktur m-ring star :
Struktur 2
Lebih jelasnya mRSK adalah sebagai berikut : misalkan gabungan graph G = (V, E ∪A) dimana V = 0, n+ 1∪V′ adalah sekumpulan node, E = {(i, j) : i, j ∈
V, i 6= j} adalah sekumpulan edge dan A adalah sekumpulan arc. Kumpulan node V′ terbagi atas dua subset : U berisi node untuk setiap pelanggan dan W berisi node untuk titik transit (disebut juga Steiner node). Node 0 mewakili depot dan node n+ 1 merupakan terminal. Untuk setiap pelanggan i ∈U misal Ci ⊂ V
′
adalah himpunan bagian dari node, dimana pelanggan i bisa terhubung. Diasumsikan bahwa i ∈ Ci
untuk semua pelanggan i ∈ U dan pelanggan itu akan terhubung dengan sendirinya jika ia berada didalam ring. Susunan A mewakili koneksi yang mungkin antara satu node dengan pelanggan yakni A={(i, j) : i∈ U, j ∈ Ci}. Susunan E adalah susunan yang mungkin dari edge ring. Setiap edge e = {i, j} ∈ E dihubungkan dengan biaya rute yang tidak negatif ce =cij, dimana (i, j) ∈ A dihubungkan dengan biaya koneksi
yang tidak negatif (dengan dii = 0 untuk semua i ∈U ). Diberikan sebuah himpunan
bagian E′ ⊂E, V(E′
) ditandai sebagai susunan titik untuk paling tidak satuedgepada
E′. Dapat dikatakan bahwa pelanggan i ditempatkan untuk sebuah ring R apabila dihubungkan oleh rute simple (yakni i ∈ V(E′)) atau dihubungkan dengan sebuah node dari ring (yakni ada sebuah edge j sehingga (i, j)∈A′).
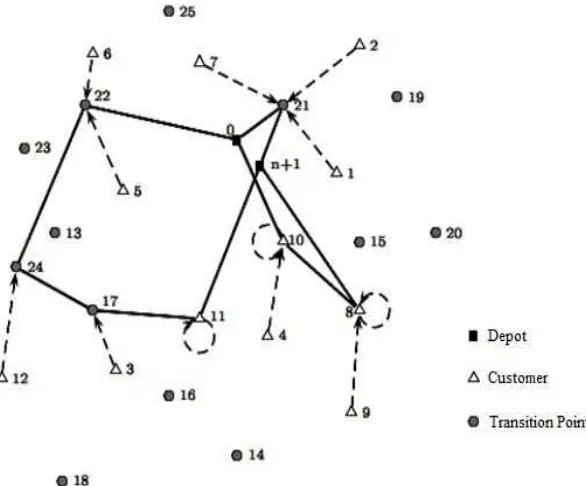
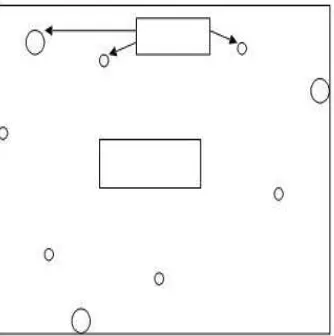
Gambar 2.6 menunjukkan solusi dari mRSK yang sesuai dimana n = 25 dan m = 3.|U|= 12,|W|= 13 danQ= 6. Dari gambar tersebut titik transisi dilambangkan dengan lingkaran dan pelanggan dengan segitiga, pusat depot dilambangkan dengan dua persegi hitam, garis yang tidak putus dilambangkan untuk garis rute dan garis putus-putus sebagai koneksi.
Gambar 2.6 m-Ring star berkapasitas
2.2 Formulasi Matematika
Formulasi matematika untukm-RSK dalam tesis ini digunakan formulasi dua arus komoditas. Formulasi dua arus komoditas m-RSK menggunakan model graph yang mengasosiasikan setiap edge {i, j} ∈ E dengan dua arc yang berlawanan dan dengan dua variabel arus yang bersesuaian yij danyji. Kedua Arc mempunyai biaya yang sama
cij ditetapkan bahwa dalam penyelesaianm-RSK layak total arus pada setiapedgedari
ring tepat sama dengan Q. Variabel y mengidenti?kasi setiap ring melalui dua path arus. Pada path pertama yang bergerak dari node 0 ke noden+ 1, arusyij menyatakan
jumlah pemakai yang dilayani oleh ring setelah mengunjungi node i. Pada path yang berlawanan yang bergerak dari node n+ 1 ke node 0, variable yij menyatakan jumlah
Formulasi dua arus komoditas m-RSK adalah sebagai berikut :
Persamaan (2.3) menetapkan bahwa arus keluar node 0 sama dengan jumlah pelanggan, sementara persamaan (2.4) menetapkan bahwa arus keluar pada node n+ 1 sama dengan total kapasitas dari ke m ring. Persamaan (2.5) mengindikasikan bahwa tidak ada arus masuk node n+ 1 sementara persamaan (2.6) menetapkan bahwa arus yang masuk node 0 sama dengan kapasitas residual ring. Diharuskan bahwa Q unit arus melalui setiap edge pada ring, maka untuk setiap node ring total arus yang masuk dan keluar dari node haruslah sama dengan 2Q. Ini ditetapkan oleh persamaan (2.7) dan (2.8). Persamaan (2.9) menjamin bahwa setiap pelanggan dialokasikan kepada satu node.Persamaan (2.10) adalah batasan konservasi arus yang memperhitungkan bahwa setiap pelanggan menerima satu unit arus dari node 0 dan satu unit arus dari node n+ 1. Batasan (2.11) menetapkan persyaratan biner bahwa edgee={i, j} ∈E harus-lah dikunjungi atau tidak oleh ring, yang dengan demikian menjelaskan fungsi tujuan (2.2).
2.3 Vehicle Routing Problem
Vehicle Routing Problem (VRP)merupakan persoalan mRSK karena melibatkan banyaknya pelanggan dengan permintaan tertentu yang dilayani oleh satu atau bebe-rapa pusat jaringan. VRP pertama kali dipaparkan oleh Dantzig dan Ramser (1954). VRP adalah permasalahan kompleks dari optimisasi kombinatorial, yang merupakan gabungan dari dua permasalahan, yaitu Travelling Salesman Problem (TSP) dan Bin Packing Problem (BPP). VRP merupakan NP-Hard, sehingga permasalahan ini sulit dipecahkan.
an dituangkan dalam sebuah graf, baik graf berarah G = (V, A), graf tidak berarah G = (V, E), maupun graf campuran G = (V, A∪ E). Penggunaan bentuk graf ini disesuaikan dengan daerah yang akan dikunjungi kendaraan pengangkut. Graf tak ber-arah digunakan jaringan jalan skala besar, meliputi negara dan negara bagian atau propinsi. Sedangkan graf berarah digunakan untuk jaringan jalan skala kecil, misal untuk menggambarkan jalan-jalan dalam satu kota.
Verteks menggambarkan depot, pelanggan ataupun persimpangan jalan. Him-punan verteks dilambangkan dengan V = (v0, . . . , vn). Verteks v0 mewakili pusat, di mana terdapat kendaraan pengangkut identik sejumlahk dengan kapasitas Q. Sedang-kan verteks lainnya melambangSedang-kan kota atau pelanggan, yang memiliki permintaan di. Arc atau edge menggambarkan jalan-jalan yang ada. Edge dapat bersifat berarah
(i, j) ∈ A, di mana A = {(v1, vj) : i 6= j, v1, vj ∈ V} dan tidak berarah, ℓ ∈ E.
Bi-aya dan jarak perjalanan dilambangkan olehcij, yang didefinisikan pada A, sedangkan
waktu non-negatif dilambangkan oleh tij, yang juga didefinisikan pada A.
Setiap verteks vi dalam V diasosiasikan dengan sejumlah barang qi yang akan
diantarkan oleh satu kendaraan. V RP bertujuan untuk menentukan sejumlah k rute kendaraan dengan total biaya yang minimum, bermula dan berakhir di sebuah depot. Adapun setiap verteks dalam V dikunjungi tepat sekali oleh satu kendaraan. Jadi, biaya dari solusi masalah ini adalah FV RP(S) =
Pk
Gambar 2.7 Contoh Visualisasi Input dari Vehicle Routing Problem (sumber: Massimo Paolucci, 2001, p5)
Gambar 2.8 Salah satu output dari persoalan VRP dari input gambar 2.7 (sumber: Massimo Paolucci, 2001, p5)