Perencanaan Struktur Rangka Baja Beraturan Tahan Gempa Berdasarkan SNI 03-1726-2002 dan FEMA 450.

(1)

PERENCANAAN STRUKTUR RANGKA BAJA

BERATURAN TAHAN GEMPA BERDASARKAN

SNI 03-1726-2002 DAN FEMA 450

Calvein Haryanto

NRP : 0621054

Pembimbing : Yosafat Aji Pranata, S.T.,M.T.

JURUSAN TEKNIK SIPIL

FAKULTAS TEKNIK

UNIVERSITAS KRISTEN MARANATHA

BANDUNG

ABSTRAK

Wilayah Indonesia mencakup daerah-daerah yang mempunyai tingkat resiko gempa yang tinggi diantara beberapa daerah gempa diseluruh dunia. Hampir setiap tahun terjadi bencana akibat gempa bumi di berbagai tempat di Indonesia. Gempa yang terjadi dapat mengakibatkan kerusakan yang menimbulkan korban jiwa serta dampaknya besar terhadap ekonomi dan pembangunan daerah di wilayah tersebut.

Tujuan penulisan Tugas Akhir ini adalah melakukan perencanaan struktur gedung baja tahan gempa berdasarkan peraturan SNI 03-1726-2002 dan FEMA 450, dan pembahasan meliputi penentuan ukuran profil baja yang digunakan sebagai elemen struktur balok dan kolom, gaya geser dasar, peralihan, desain sambungan, dan perhitungan pondasi.

(2)

DAFTAR ISI

SURAT KETERANGAN TUGAS AKHIR ...i

SURAT KETERANGAN SELESAI TUGAS AKHIR ...ii

ABSTRAK ...iii

KATA PENGANTAR...iv

DAFTAR ISI...vi

DAFTAR NOTASI DAN SINGKATAN...ix

DAFTAR GAMBAR...xii

DAFTAR TABEL ...xiv

DAFTAR LAMPIRAN ...xvi

BAB 1 PENDAHULUAN ... 1

1.1 Latar Belakang ... 1

1.2 Tujuan Penulisan... 2

1.3 Ruang Lingkup Penulisan ... 2

1.4 Sistematika Penulisan ... 3

BAB 2 TINJAUAN LITERATUR ... 4

2.1 Baja ... 4

2.1.1 Perilaku Tegangan-Regangan ... 6

2.1.2 Sifat Mekanis Baja ... 7

2.1.3 Jenis Profil Baja Struktur ... 8

2.1.4 Struktur Balok Baja WF... 9

2.1.5 Lendutan (Deflection) ... 17

2.1.6 Sambungan... 18

2.2 Beban... ... 20

2.2.1 Beban Gravitasi... 20

2.2.2 Beban Gempa ... ... 22

2.3 Peraturan Gempa SNI 1726 - 2002 ... 22

2.3.1 Gempa Rencana dan Kategori Gedung ... 22

(3)

2.3.3 Wilayah Gempa... 26

2.3.4 Pembatasan waktu getar alami fundamental ... 28

2.3.5 Beban Gempa Nominal Statik Ekuivalen ... 28

2.3.6 Waktu Getar Alami Fundamental ... 30

2.3.7 Analisis Statik Ekuivalen ... 30

2.3.8 Kinerja Struktur Gedung ... 30

2.4 Peraturan Gempa FEMA 450... 32

2.5 Perangkat Lunak ETABS... 33

2.6 Pondasi ... 33

2.6.1 Klasifikasi Pondasi Tiang ... 34

2.6.2 Perencanaan Pondasi... 35

BAB 3 STUDI KASUS DAN PEMBAHASAN... 39

3.1 Data Struktur dan Diagram Bagan Alir Studi ... 39

3.1.1 Data Gedung... 40

3.1.2 Data Material... 40

3.1.3 Data Tanah ... 40

3.1.4 Diagram Bagan Alir Studi... 40

3.2 Analisis Struktur Terhadap Beban Gempa... 42

3.2.1 Analisis Struktur Terhadap Beban Gempa Berdasarkan SNI 03-1726-2002... 43

3.2.2 Analisis Struktur Terhadap Beban Gempa Berdasarkan FEMA 450... 49

3.3 Hasil Analisis Struktur dan Desain ... 53

3.3.1 Hasil Analisis Struktur Gedung ... 53

3.3.2. Desain Sambungan... 54

3.4 Perencanaan Pondasi... 59

3.4.1 Perencanaan Pondasi yang didesain berdasarkan SNI 03-1726-2002... 59

(4)

3.5 Pembahasan... 64

BAB 4 KESIMPULAN DAN SARAN ... 67

4.1 Kesimpulan ... 67

4.2 Saran... 68

DAFTAR PUSTAKA ... 69

(5)

DAFTAR NOTASI DAN SINGKATAN

A Luas penampang profil melintang, mm2

g

A Luas penampang bruto, mm2

n

A Luas penampang netto, mm2

p

A Luas penampang ujung tiang, m2

s

A Luas selimut tiang, m2

f

b Lebar pelat sayap, mm

b

C Faktor untuk menghitung gradien momen kekuatan balok

b

d Diameter baut nominal pada daerah tak berulir, mm E Modulus elastisitas baja, MPa

s

f Tegangan sisa; 70 MPa untuk penampang giling, 114 MPa untuk penampang las

f_u Tegangan putus minimum, MPa

f_y Tegangan leleh minimum, MPa

cr

f Tegangan tekan kritis, MPa

s

f Gesekan selimut satuan, ton/m2

b u

f Tegangan tarik putus baut, MPa

G Modulus geser baja

I_x Momen inersia sumbu-x, mm4

I_y Momen inersia sumbu-y, mm4 J Konstanta puntir, mm4

c

k Faktor panjang tekuk

L Panjang bentang, mm

L_b Jarak antara penopang lateral, mm

p

(6)

1

M Momen ujung terkecil, N-mm

2

M Momen ujung terbesar, N-mm

nx

M Momen lentur nominal penampang komponen struktur terhadap sumbu x

ny

M Momen lentur nominal penampang komponen struktur terhadap sumbu y m Jumlah bidang geser

p

M Momen lentur yang menyebabkan seluruh penampang mengalami tegangan leleh, N-mm

n Jumlah baut

p Keliling tiang, m

u

P Beban aksial terfaktor, N

c

q Tahanan ujung konus

s

Q Daya dukung selimut tiang

p

Q Daya dukung ujung tiang

d

R Kuat rencana, N R_n Kuat nominal, N

R_u Beban terfaktor atau kuat perlu, N

y

r Jari-jari girasi terhadap sumbu lemah, mm

x

r Jari-jari girasi terhadap sumbu kuat, mm

x

S Modulus elastis penampang pada sumbu-x, mm3

y

S Modulus elastis penampang pada sumbu-y, mm3

d

T Kuat tarik rencana, N

f

t Tebal sayap, mm

p

t Tebal pelat, mm

w

t Tebal badan dari profil, mm

d

(7)

V_n Kuat geser nominal baut, N Z Modulus plastis

μ Rasio poisson

c

 Parameter kelangsingan

p

 Batas perbandingan lebar terhadap tebal untuk penampang kompak

r

 Batas maksimum untuk penampang tak kompak

 Faktor reduksi

b

 Faktor reduksi kuat lentur

n R

 Kuat rencana

L

(8)

DAFTAR GAMBAR

Gambar 2.1 Diagram Tegangan-Regangan Baja ... 6

Gambar 2.2 Profil-Profil Standar ... 8

Gambar 2.3 Elemen Tarik dan Tekan Kondisi Elatis ... 9

Gambar 2.4 Diagram Distribusi Tegangan Lentur... 10

Gambar 2.5 Penampang Balok Profil IWF ... 11

Gambar 2.6 Balok yang Ditumpu Lateral ... 13

Gambar 2.7 Perilaku Balok ... 14

Gambar 2.8 Tata Letak Baut ... 20

Gambar 2.9 Respons Spektrum Gempa Rencana ... 27

Gambar 2.10 Perkiraan Jenis Tanah dari CPT ... 35

Gambar 2.11 Perhitungan Daya Dukung Ujung ... 36

Gambar 3.1 Model 3D... 39

Gambar 3.2 Diagram Bagan Alir ... 41

Gambar 3.3 Nilai periode Getar ... 42

Gambar 3.4 Massa Bangunan ... 43

Gambar 3.5 Respons Spektrum Wilayah 3 ... 44

Gambar 3.6 Input Beban (Fy) pada Statik ekuivalen... 46

Gambar 3.7 Input Beban (Fx) pada Statik ekuivalen... 46

Gambar 3.8 Input Beban (Fy) pada Statik ekuivalen... 51

Gambar 3.9 Input Beban (Fx) pada Statik ekuivalen... 51

(9)

Gambar 3.11 Lendutan Balok yang Didesain Berdasarkan FEMA 450 ... 53

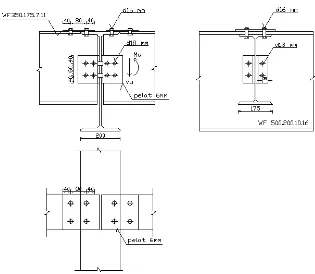
Gambar 3.12 Detail Sambungan Balok-Kolom ... 54

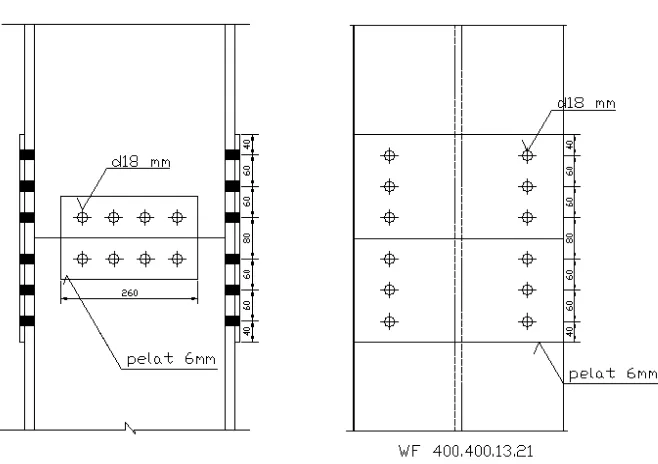
Gambar 3.13 Detail Sambungan Kolom-Kolom... 55

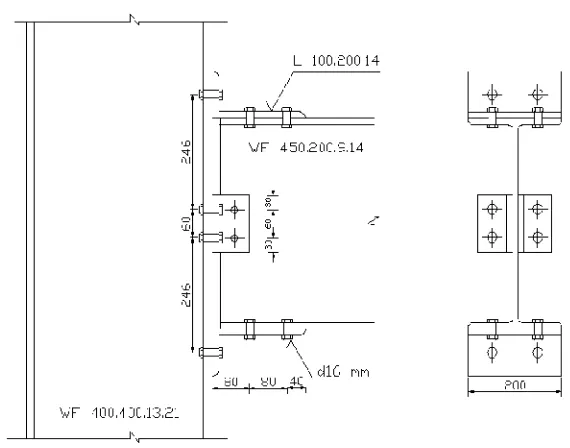
Gambar 3.14 Detail Sambungan Balok Induk-Balok Anak... 55

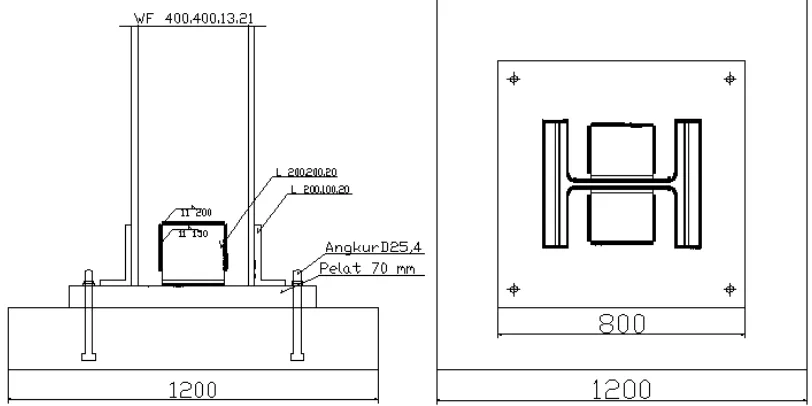
Gambar 3.15 Detail Sambungan Kolom-Perletakan... 56

Gambar 3.16 Detail Sambungan Balok-Kolom ... 57

Gambar 3.17 Detail Sambungan Kolom-Kolom... 57

Gambar 3.18 Detail Sambungan Balok Induk-Balok Anak... 58

Gambar 3.19 Detail Sambungan Kolom-Perletakan... 58

Gambar 3.20 Detail Pondasi yang Didesain Berdasarkan SNI 03-1726-2002 ... 61

(10)

DAFTAR TABEL

Tabel 2.1 Sifat Mekanis Baja ... 8

Tabel 2.2 Batas Lendutan Maksimum ... 18

Tabel 2.3 Berat Sendiri Bahan Bangunan dan Komponen Gedung... 21

Tabel 2.4 Faktor Keutamaan I Untuk Berbagai Kategori Gedung dan Bangunan... 23

Tabel 2.5 Faktor Daktilitas Maksimum, Faktor Reduksi Gempa Maksimum, Faktor Tahanan Lebih Struktur dan Faktor Tahanan Lebih Total Beberapa Jenis Sistem dan Subsistem Struktur Gedung... 24

Tabel 2.6 Koefisien  yang membatasi waktu getar alami fundamental struktur gedung……… 28

Tabel 3.1 Nilai Ty(Ray) pada SNI 03-1726-2002 ... 47

Tabel 3.2 Nilai Tx(Ray) pada SNI 03-1726-2002 ... 47

Tabel 3.3 Nilai Fy Berdasarkan FEMA 450 ... 50

Tabel 3.4 Nilai Fx Berdasarkan FEMA 450 ... 50

Tabel 3.5 Nilai Ty(Ray) pada FEMA 450 ... 52

Tabel 3.6 Nilai Tx(Ray) pada FEMA 450 ... 52

Tabel 3.7 Perbandingan Nilai Fx... 64

Tabel 3.8 Perbandingan Nilai Fy... 64

Tabel 3.9 Gaya-gaya Dalam dan Lendutan... 65

Tabel 3.10 Gaya Dalam Pada Kolom... 65

Tabel 3.11 Reaksi Tumpuan ... 65

(11)

Tabel 3.13 Perbedaan Desain Sambungan Kolom-Kolom ... 66

Tabel 3.14 Perbedaan Desain Sambungan Balok Induk-Balok Anak... 66

Tabel 3.15 Perbedaan Desain sambungan Kolom-Perletakan ... 67

(12)

DAFTAR LAMPIRAN

Lampiran 1 Pemodelan Gedung... 71

Lampiran 2 Nilai Periode Getar ... 83

Lampiran 3 Pembahasan Rasio P/M ... 85

Lampiran 4 Desain Sambungan ... 132

Lampiran 5 Data Sondir ... 157

Lampiran 6 Output Program LPILE Plus 4.0 ... 161

Lampiran 7 Output Program Concrete Pile Cap Design... 168

Lampiran 8 Batas Layan dan Batas Ultimate... 174

Lampiran 9Preliminary Desain Balok, Kolom, Pelat ... 179

Lampiran 10 Denah Struktur... ... 185

(13)

LAMPIRAN I

(14)

A. Pemodelan Gedung

Langkah-langkah dalam pemodelan gedung dengan menggunakan software ETABS

yaitu:

1. Membuka program dengan mengklik ikon atau diambil dari start program.

Gambar L.1.1 Tampilan Awal Program

2. Setelah membuka program, langkah awal yaitu merubah satuan di pojok kanan

bawah.

3. Kemudian membuat grid dan jarak grid sesuai dengan model yang akan dibuat

dengan cara mengklik File–New Model– No (new model initialization) – Ok

(15)

Gambar L.1.2 Tampilan Untuk Membuat Jumlah Grid, Lantai serta Tinggi Bangunan

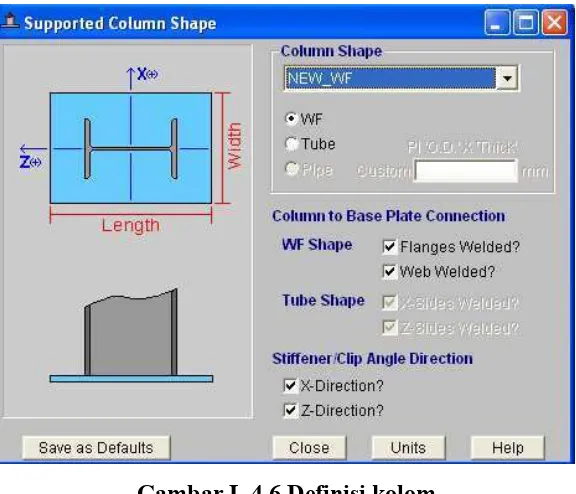
4. Mendefinisikan material dari struktur yang digunakan

Define – Material properties – conc/steel – Modify/show material - Klik OK

(16)

5. Lalu klik pada tulisan Steel (Tulisan akan berwarna biru bila di klik) – Modify

Show, diubah nama material pada kotak material name, input data material yang

diketahui seperti fy, fu, serta modulus elastisitas.

Gambar L.1.4 Input Data Material

6. Mendefinisikan penampang balok dan kolom bangunan yaitu:

Define – Frame section – Add/ Wide Flange –input data penampang – klik OK

(17)

Sebelumnya telah dilakukan preliminary desain, dimana hasilnya selengkapnya pada

Lampiran 9.

Gambar L.1.6 Input Data Balok, kolom

7. Definisikan pelat dengan cara klik define – Wall/Slab/Deck section maka akan

telihat tampilan sebagai berikut:

(18)

8. Pilih Slab kemudian klik Modify/Show Section, input data pelat kemudian klik OK

Gambar L.1.8 Input Data Pelat

9. Membuat beban yang terjadi dengan cara Define – Static Load cases – input jenis

(19)

Gambar L.1.9 Membuat Beban

Dalam Tugas Akhir ini, perencanaan beban gempa dihitung menggunakan dua

cara yaitu SNI 03-1726-2002 dengan FEMA 450. Oleh karena itu, secara umum

gedung akan dianalisis dua kali.

Model pertama adalah beban gempa berdasarkan SNI 03-1726-2002, maka

seperti terlihat pada Gambar L.1.9 beban gempa seperti quake, dihitung sesuai

dengan rumus-rumus peraturan SNI 03-1726-2002.

Model kedua adalah beban gempa berdasarkan FEMA 450, maka seperti

terlihat pada Gambar L.1.9 beban gempa seperti quake, dihitung sesuai dengan

(20)

10. Definisikan kombinasi beban yang ada dengan cara Define – Load combinations

– input kombinasi – Klik Ok

Gambar L.1.10 Kombinasi Beban

Dalam Tugas Akhir ini, kombinasi yang digunakan ada 18, yang terdiri dari:

a. Comb 1 (1,4.(SDL+DL)

b. Comb 2 (1,2.(SDL+DL) + 1,6.(LL))

c. Comb 3 (1,2.(SDL+DL)+0,5(LL)EQx0,3.EQy

d. Comb 4 (1,2(SDL+DL)+0,5(LL)0,3.EQxEQy

e. Comb 5 (0,9(SDL+DL)EQx0,3.EQy

(21)

11. Penggambaran balok IWF ke grid dengan cara Draw – Draw Lines objects –

Draw Line – gambar balok dari joint ke joint.

Gambar L.1.11 Menggambar Balok

12. Gambar kolom dengan cara Draw – Draw Lines objects – create columns –

gambar kolom pada tiap joint – klik OK.

Gambar L.1.12 Menggambar Kolom

13. Penggambaran pelat dengan cara Draw – Draw Area Objects – Draw Areas –

Input properties object sesuai dengan properties pelat – Klik joint terluar.

Gambar L.1.13 Menggambar Pelat

14. Tentukan restraint pada tumpuan : Select plan level base – select semua joint –

(22)

Gambar L.1.14Restraint _Tumpuan

B. Pemodelan Beban Gravitasi

Beban gravitasi yang diperhitungkan adalah :

 Beban Mati (DL) dihitung sendiri oleh program ETABS

 Beban Mati Tambahan (SDL) = 112 kg/m2

 Bebah Hidup = 300 kg/m2

Adapun langkah- langkah memasukkan data beban ke dalam ETABS yaitu :

1. Beban pada pelat dengan cara : Select pelat – Assign – Shell/ Area Load – Uniform

–pilih jenis beban yang akan digunakan.

(23)

2. Beban pada balok dengan cara: Select balok yang menerima beban dinding –

Assign – Frame/ line load – Distributed – Pilih jenis beban yang akan digunakan –

Klik OK.

(24)

C. Pusat Massa

Dalam Tugas Akhir ini, lantai dimodelkan sebagai lantai diagfragma rigid.

Artinya massa dipusatkan pada satu titik.

(25)

LAMPIRAN II

(26)

Nilai Periode Getar

Mode Period UX UY UZ SumUX SumUY SumUZ RX RY RZ SumRX SumRY SumRZ

1 1.071123 0.0003 81.7143 0 0.0003 81.7143 0 99.5709 0.0004 0.0638 99.5709 0.0004 0.0638

2 0.981274 79.6819 0.0003 0 79.6822 81.7146 0 0.0003 99.6976 0.0005 99.5712 99.698 0.0643

3 0.834068 0.0005 0.0677 0 79.6826 81.7823 0 0.0798 0.0006 80.2177 99.6511 99.6986 80.282

4 0.34946 0.0001 10.9812 0 79.6827 92.7635 0 0.1053 0 0.0075 99.7563 99.6986 80.2895

5 0.329379 12.6302 0 0 92.3129 92.7636 0 0 0.0005 0 99.7563 99.699 80.2896

6 0.271697 0 0.0063 0 92.3129 92.7699 0 0.0001 0 11.8792 99.7564 99.699 92.1687

7 0.191944 0 4.3038 0 92.313 97.0737 0 0.2219 0 0.0024 99.9783 99.699 92.1712

8 0.18584 4.9335 0 0 97.2465 97.0737 0 0 0.2878 0 99.9783 99.9868 92.1712

9 0.148318 0 0.002 0 97.2465 97.0757 0 0.0001 0 4.6868 99.9784 99.9868 96.858

10 0.126056 0 1.7857 0 97.2465 98.8614 0 0.0007 0 0.0002 99.9791 99.9868 96.8581

11 0.123557 1.7736 0 0 99.0201 98.8614 0 0 0.0001 0 99.9791 99.9869 96.8581

(27)

LAMPIRAN III

(28)

Pembahasan Rasio P-M

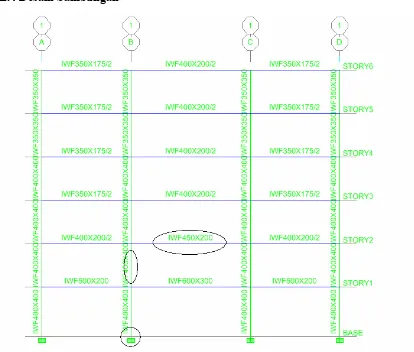
Gambar L.3.1 Balok dan Kolom yang Ditinjau

A. Pembahasan Rasio P-M Gedung yang Didesain Berdasarkan SNI 1726-2002

Desain Balok

Elevation-B (B17) Story 2

Karakteristik Profil :

WF = 300.150.6,5.9 (BJ37)

d = 300 mm bf = 150 mm

tw = 6,5 mm tf = 9 mm

L = 6000 mm Ag = _{4, 678.10 mm}3 2

Ix = 7,21.10 7 4

10 mm Iy = _{5,08.10 mm}6 4

x

(29)

5 3 x

S =4,81.10 mm S =6,77.10 mm_y 4 3

c

r =13mm

f c

h'=d-2.t -2.r h'=256mm





w f w

A = d-2.t .t A =1833mm_w 2

 





2

x f f w f

1

Z =b.t . d-t + t . d-2.t 4

5 3

x

Z =5,22.10 mm

2 2

y f f w

1 1

Z = .t .b + .(d-2.t ).t 2 4

5 3

y

Z =1,04.10 mm

Data Material:

Modulus Elastisitas:

s

E =200000MPa

Tegangan Leleh sayap dan Badan:

y

f =240MPa

Tegangan Sisa:

r

f =70MPa (rolled beam)

Faktor reduksi

0,9

  _c 0,85 _b 0,9 Faktor modifikasi Tegangan Leleh:

y

R =1,5jika f_y 250MPa

y

Maka R =1,5_y

Besaran penampang yang perlu dihitung:

L y r

f =f -f f =70MPa_r G=0,8.10 MPa5

L

f =170MPa



3







3

f f f w

1

(30)

 

2

w f

1

I = . d-t

2

    

_{ } 

 

2 w

I =21170,25mm

Momen Leleh: M =S .f_y _x _y M =115,44.10 Nmm_y 6

Momen Plastis: M =Z .f_p _x _y M =125,3x10 Nmm_p 6

Momen Batas Tekuk: M =(f -f ).S_r _y _r _x M =81,77.10 Nmm_r 6 (karena

tegangan leleh flens dan badan sama)

Gaya aksial Leleh: P =A .f_y _g _y P =1,123.10 N_y 6

Periksa Kekompakan Penampang:

Harus memenuhi syarat kekompakan penampang pada Tabel 15.7-1 (SNI

03-1729-2002)

Pada Pelat sayap:

f f

f

b

λ =

2.t f=8,333

p y

170

λ =

f λ =10,97ps

Kesimpulan: Penampang kompak

Pada Pelat badan:

w w

h'

λ =

t λ =39,38w

p y

1680

λ =

f λ =108,54p

Kesimpulan: Penampang kompak (λ <λ_w _p)

1. Menghitung Kapasitas Momen Balok B-13

1.a Kondisi batas tekuk lokal

(31)

Pada pelat sayap:

pf y

170

λ =

F λ =10,97pf

rf

y r

370

λ =

f -f λ =28,38rf

f=8,333



Momen Nominal Tekuk Lokal pada pelat sayap: (M_nFLB)

nFLB p f pf

M =M jikaλ λ







f pf



nFLB p p r pf f

rf pf

λ -λ

M =M - .(M -M )jikaλ <λ <λ

λ -λ rf

6 nFLB p

M =M =125,3x10 Nmm

nFLB

M =112752000Nmm



Pada pelat badan:

pw y 1680 λ = f         108, 44 pw   rw y 2550 λ = f         164, 61 rw   w λ =39,38

Momen Nominal Tekuk Lokal pada pelat badan:

nWLB p w

M =M jikaλ _pw







w pw



nWLB p p r pw

rw pw

λ -λ

M =M - .(M -M )jikaλ

λ -λ  w rw

2 rf

nFLB r f

f λ

M = .M jikaλ

λ rf

  _

 

(32)

2 rw

nWLB r w

w λ

M = .M jikaλ

λ rw

  _

 

 

6 nWLB p

M =M =125,3x10 Nmm

nWLB

M =112752000Nmm



1.b Kondisi batas tekuk lateral

Panjang tak bertumpu:

b

L =6000mm

Batas-batas jarak pengekang lateral:

 

2 2 6 11

w y

1 1

I = .h .I = . 300 .5,08.10 =1,143.10

4 4

p y

y

E 200000

L =1,76.r . =1,76.32,9. =1671,54mm

F 240

3

1 5

π E.G.J.A π 200000.80000.98714,75.4,678.10

X = . =12553,68MPa

S 2 4,81.10 2

2

2 5 11

-4 4 2 w

2 6

Y

I

S 4,81.10 1,143.10

X =4. . =4. . =3,34.10 mm /N G.J I 80000.98714,75 5,08.10

          _ _ 2 1

r y 2 L

L

X

L =r . . 1+ 1+X .F F       -4 2 r 12553,68

L =32,9. . 1+ 1+3,34.10 .170 =7929,5mm 170       Maka, b

L =6000mm L =1671,54mm_p L =7929,5mm_r

Keterangan: “Bentang pendek” jika L_b L_p

“ Bentang menengah jika L <L <L_p _b _r

“ Bentang panjang jika L_b L_r

(33)

Momen Nominal Tekuk Lateral (M_nLTB)

Momen Plastis

6 p

M =125,3x10 Nmm

Momen Batas Tekuk

r y r

M =S.(f -f )=81770000Nmm

Menghitung nilai C :_b

Gambar L.3.2 Momen Maksimum

Data Momen yang didapat dari ETABS untuk menghitung nilai Cb:

Momen di ¼ bentang (Ma) = 3140308,957 Nmm

Momen di ½ bentang (Mb) = 654605,411 Nmm

Momen di ¾ bentang (Mc) = 2817192,817 Nmm

Momen maksimum = 7243461,697 Nmm

maks b

maks A B c

12,5.M

C = 2,3

2,5.M +3.M +4.M +3.M 

b

12,5.7243461,697

C = 2,3

2,5.7243461,697+3.3140308,957+4.654605,411+3.2817192,817

b

C =2,242,3

Menghitung Momen kritis:

 

2

y f

w

I . d-t C =

4

 

  -7 6

w

C =1,075x10 m

21 1 s y

A =E .I .G.J=8,02x10

2

28 s

2 y w

π.E

A = .I .C =3,04x10 L

 

 

 

cr b 1 2

π

M =C . . A +A L

11 cr

(34)

Momen Nominal Tekuk Lateral pada sumbu-x: (M_nLTBx)

nLTBx

M = M_pjika L_b L_p

nLTBx

M =





r

b r p1 r

r p L -L C . M + M -M

L -L

  

 _ _

 _ _

 

jika L <L <L_p _b _r

nLTBx cr p1

M =minM ,M jika L_b L_r

Jadi M_nLTBx= 114672264,4 Nmm

nLTBx

M =

 104247513,15 Nmm

Momen nominal Tekuk Lateral pada sumbu-y:( M_nLTBy)

Momen plastis pada sumbu –y:

py y y y y

M = min (Z .F ,1,5S .F )

py

M =24372000 Nmm

nLTBy

M =21934800Nmm 

1.c Menghitung Momen Nominal (M )_n

Momen nominal pada sumbu-x: (M )_nx

nx nFLB nWLB nLTBx p

M = min (M ,M ,M ,M )

nx

M = 114672264,4 Nmm

Momen Nominal pada sumbu-y: (M )_ny

ny nLTBy

M =M

ny

M =24372000 Nmm

Maka besarnya kapasitas momen adalah sebagai berikut:

Kapasitas momen pada sumbu-x: (M )_nx

nx M =

(35)

Kapasitas momen pada sumbu-y: (M )_ny

ny

M = 21934800 Nmm 

2. Menghitung kapasitas Tarik Balok B-17

Kuat tarik nominal: (P )_nt

nt g y

P =A .f P =1122720N_nt

Maka besarnya kapasitas tarik adalah sebagai berikut: (P_nt)

nt

P =1010448N



3. Menghitung Kapasitas Tekan Balok B-17

3.a Hitung tegangan kritis: F_crl

c

k =1 ( beban aksial tidak ada)

k c

L =k .L L = 6000mm_k

x y

r = min (r ,r ) r = 32,9mm

y k c s f L λ = .

π.r E λ =2,01c



c



2

cr1 y c

F =_ 0,658.λ .F jikaλ 1,5_ 

c

cr1 2 y c

0,877

F = .F jikaλ 1,5

λ     _ _  _ _    cr1 F =52,10MPa

3.b Hitung Tegangan kritis dengan memperhitungkan tekuk puntir lentur:

2

y f

w

(36)

Tegangan Tekuk elastik puntir lentur:(Fe)





2 s w e 2 x y k

π .E .C 1

F = +G.J

I +I K.L

 

 

  e

F =178,69MPa y e e f λ =

F λ =1,159e

Maka besarnya Tegangan kritis dengan memperhitungkan tekuk puntir lentur:

 

2

e

λ

cr2 y c

f = 0,658 .f jikaλ 1,5

 

  cr1 _e2 y c

0,877

f = .f jikaλ 1,5

λ     _ _  _ _    cr1 F =156,69MPa

Besarnya Kuat tekan nominal adalah:

cr

F =156,69MPa

nc g cr

P =A .F P =732995,82N_nc

Sehingga besarnya kapasitas tekan balok adalah:

nc

P =659696,238N



4. Menghitung Kapasitas Gaya Geser Balok B-13

4.a Gaya Geser Nominal pada sumbu-x:

w1 w

A = d.t A = 1950 mm_w1 2

a = 6000 mm

n 2 5 k =5+ a h'       _{ }   _{ }    n

k = 5,009

Maka besarnya gaya geser nominal pada sumbu-x:

w w

h'

λ =

(37)

n s

nx y w1 w

y k .E V =(0,6.F .A )jikaλ 1,10.

F

 

 _ _

 

n s n s n s

nx y w1 w

y w y y

k .E 1 k .E k .E

V =0,6.F .A .1,10. . jika 1,10. λ <1,37.

F λ F F

 



 

 

 

w1 n s n s

nx 2 w

y w

0,9.A .k .E k .E V = jikaλ 1,37.

F

λ 

nx

V =280800N

4.b Gaya geser Nominal pada sumbu-y:

w2 f f

5 A = .b .t

3       2 w2 A =2250mm

Maka besarnya gaya geser nominal pada sumbu-y:

ny y w2

V =0,6.F .A V = 324000 N_ny

Maka besarnya kapasitas gaya geser adalah sebagai berikut:

Kapasitas gaya geser pada sumbu-x:

nx

V =252720N



Kapasitas gaya geser pada sumbu-y:

ny

V =291600N 

Selanjutnya, akan dihitung rasio tegangan akibat gaya geser yang bekerja:

Rasio tegangan pada sumbu-x:

ux nx

V = V

 0,000 Hasil Output ETABS: Rasio= 0,000

Rasio tegangan pada sumbu-y:

uy ny

V = V

5. Menghitung Faktor Modifikasi Momen (Cm)

m

(38)

6.Menghitung Faktor Amplikasi Momen (_b)

Data yang diperlukan:

g y

cr 2

c A .F P =

λ P = 277894,1115 Ncr

Maka faktor Amplikasi momen adalah sebagai berikut:

1 1 m b u cr C P P        

1 1, 02 b

 

Dari hasil kombinasi pembebanan dan kapasitas balok yang didapat diatas,

maka dapat dihitung persamaan interaksi akibat gaya aksial dan momen sebagai

berikut:

Rasio = u ux uy u

nt b nx b ny nt

M

P 8 M P

+ . + jika 0, 2

P 9 .M .M P

         _ _      uy

u ux u

nt b nx b ny nt

M

P M P

+ + jika <0,2

2. P  .M  .M P

  

 _ _

 _ _

 

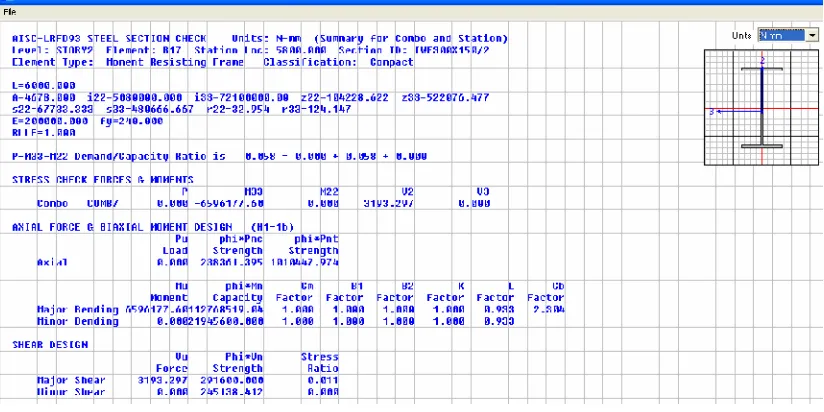
[image:38.612.115.527.463.669.2]

Maka rasio = 0,062 Hasil Output ETABS: Rasio= 0,058

(39)

Desain Kolom

Karakteristik Profil:

WF = 400.400.13.21 (BJ37)

d = 400 mm b = 400 mm_f

w

t =13 mm t = 21 mm_f

L = 3500 mm Ag = 21870 mm2

8 4

x

I = 6,66.10 mm I = 2,24.10 mm_y 8 4

x

r =175 mm r = 101 mm_y

5 3

x

S =33,3.10 mm S =11,2.10 mm_y 5 3

c

r = 22 mm

f c

h'=d-2.t -2.r h'= 314 mm





w f w

A = d-2.t .t A = 4654 mm_w 2

 





2

x f f w f

1

Z =b.t . d-t + t . d-2.t 4

6 3

x

Z =3,66.10 mm

2 2

y f f w

1 1

Z = .t .b + .(d-2.t ).t 2 4

6 3

y

Z =1,69.10 mm

Data Material:

s

E =200000MPa

Tegangan Leleh Flens dan Badan:

y

f =240MPa

Tegangan Sisa:

r

Faktor reduksi

0,9

(40)

Faktor modifikasi Tegangan Leleh:

y

Maka R =1,5_y

L y r

f =f -f f =70MPa_r _{G=0,8.10 MPa}5

L

f =170MPa



3







3

f f f w

1

J= . 2.b .t + d-2.t .t 3

    

    

 

4

J= 3256126 mm

 

2

w f

1

I = . d-t

2      _{ }    2 w

I = 35910,25 mm

Momen Plastis: M =Z .f_p _x _y M =878,4.10 Nmm_p 6

Momen Batas Tekuk: M =(f -f ).S_r _y _r _x M = 566,1.10 Nmm_r 6 (karena

Gaya aksial Leleh: P =A .f_y _g _y P = 5,25.10 N_y 6

03-1729-2002)

Pada Pelat sayap:

f f

f

b

λ =

2.t λ = 9,5f

p y

170

λ =

f λ =10,97ps

f ps

(41)

Pada Pelat badan:

w w

h'

λ =

t λ =24,9w

p y

1680

λ =

f λ =108,54p

Kesimpulan: Penampang kompak (λ <λ_w _p)

1. Menghitung Kapasitas Momen Kolom C-7 (Lantai 2)

Momen Nominal Tekuk lokal (berdasarkan Tabel 7.5-1)

Pada pelat sayap:

pf y

170

λ =

F λ =10,97pf

rf

y r

370

λ =

F -F λ =28,38rf

f

λ =9,5

nFLB p f pf

M =M jika λ λ







f pf



nFLB p p r pf f rf

rf pf

λ -λ

2 rf

nFLB r f

f λ

M = .M jikaλ

λ rf

  _

 

 

6 nFLB p

M =M =878,4.10 Nmm

nFLB

M =790560000Nmm



Pada pelat badan:

u u

pw

y y

2, 75.N N

1680

λ = 1 jika 0,125

.N .N

fy b b

 _ _

    

 _ _

(42)

u u

y y

N N

500 665

max . 2,33 , jika 0,125

.N f .N

pw b b y y F    _ _ _{ }  _ _   _ _     pw

λ = 42,93

u rw b y y N 2550

λ = . 1 0,74

.N F       _ _  _ _   rw

λ =87,26 λ =24,9w

nWLB p w

M =M jika λ _pw







w pw



nWLB p p r pw w rw

rw pw

λ -λ

M =M - .(M -M ) jika λ <λ <λ

λ -λ

2 rw

nWLB r w

w λ

M = .M jika λ

λ rw

  _

 

 

6 nWLB p

M =M =878,4.10 Nmm

nWLB

M =790560000Nmm



b

L =3500mm

 

2 2 8 12

w y

1 1

I = .h .I = . 400 .2,24.10 =8,96.10

4 4

p y

y

E 200000

L =1,76.r . =1,76.101. =5131,49 mm 240

f

1 5

π E.G.J.A π 200000.80000.3256126.21870

X = = . = 22517,78 MPa

S 2 33,3.10 2

2

2 ₅ ₁₂

-5 4 2 w

2 8

Y

I

S 33,3.10 8,96.10

X =4. . =4. . = 2,61.10 mm /N G.J I 80000.3256126 2,24.10

 

 

(43)

2 1

r y 2 L

L

X

L =r . . 1+ 1+X .F F

 

 

 

-5 2 r

22517, 78

L =101. . 1+ 1+2,61.10 .170 =18930,14 mm 170

 

 

 

Maka,

b

L =3500mm L = 5131,49 mm_p L = 18930,14 mm_r

Keterangan: “ Bentang pendek” jika L_b L_p

“ Bentang menengah jika L <L <L_p _b _r

“ Bentang panjang jika L_b L_r

Kesimpulan: bentang pendek

Momen Plastis

6 p

M =878,4.10 Nmm

Momen Batas Tekuk

6

r y r

M =S.(f -f )= 566,1.10 Nmm

(44)

Data Momen yang didapat dari ETABS untuk menghitung nilai cb:

Momen di ¾ bentang (Mc) = 8773199 Nmm

maks b

maks A B c

12,5.M

C = 2,3

2,5.M +3.M +4.M +3.M 

b

12,5.20154851, 7

C 2,3

2,5.20154851, 7 3.10512168,1 4.869484, 48 3.8773199

 

  

b

C =2,252,3

 

2

y f

w

I . d-t C = 4     12 w

C = 8,04.10

25 1 s y

A =E .I .G.J=1,17.10

2

25 s

2 y w

π.E

A = .I .C =5,8.10 L

 

 

 

cr b 1 2

π

M =C . . A +A L

10 cr

M =1,69x10 Nmm

nLTBx

M =





r

b r p1 r

r p L -L C . M + M -M

L -L

  

 _ _

 _ _

 jika Lp  Lb Lr

nLTBx cr p1

M =minM ,M jika L_b L_r

Jadi M_nLTBx=M_p=878,4x10 Nmm6

nLTBx

M =

(45)

py y y y y

M =min(Z .F ,1,5S .F )

py

M =403200000 Nmm

nLTBy

M =362880000 Nmm 

M =min(M ,M ,M ,M )

nx

M =878,4x10 Nmm6

ny nLTBy

M =M

ny

M = 403200000 Nmm

nx M =

 790560000 Nmm

ny

M =362880000 Nmm 

2. Menghitung kapasitas Tarik Kolom C-7 (Lantai 2)

nt g y

P =A .f

6 nt

P =5,25x10 N

nt

P = 4723920 N

(46)

3. Menghitung Kapasitas Tekan Kolom C-7 (Lantai 2)

Faktor panjang efektif kc, ditentukan dengan menggunakan faktor G:

A

G = 1,0 (jepit)

A B

B

66600 66600

I ₊

Σ( ) ₃₅₀ ₃₅₀

L

G = = =15,8

I 7210 7210

Σ( ) +

L 600 600

                        c k = 2

k c

L =k .L L =7000 mm_k

x y

r=min(r ,r ) r= 101mm

y k c s f L λ = .

π.r E λ =0,76c

 

2

c

λ

cr1 y c

F =_ 0,658 .f _jikaλ 1,5

 

c

cr1 2 y c

0,877

F = .f jikaλ 1,5

λ     _ _  _ _    cr1

F = 195,71 MPa

 

2

y f

w

I . d-t C =

4

 

  12

w

C =8,04x10





2 s w e 2 x y z k

π .E .C 1

F = +G.J

I +I K .L         e

(47)

y e

e f

λ =

F λ =0,37e

 

2

e

λ

cr2 y c

F = 0,658 .f jikaλ 1,5

 

 

e

cr2 2 y c

0,877

F = .f jikaλ 1,5

λ     _ _  _ _    cr2

F =226,63 MPa

cr cr1 cr2 F =min(F ,F )

cr

F =195,71 MPa

nc g cr

P =A .F P =4280114,486 N_nc

Sehingga besarnya kapasitas tekan kolom adalah:

nc

P =3852103,04 N



1

M = 12905778 Nmm (momen ujung terkecil)

2

M = 20154851,7 Nmm (momen ujung terbesar)

Kurvatur = 2 (double curvature)

1 2 m

1 2

min(M ,M )

β =

max(M ,M ) jika kurvatur > 2

1 2 m

1 2 min(M ,M )

β =

-max(M ,M )

 

 

  jika kurvatur < 1

m m

C =0,6-0,4.β

(48)

u

N = 2445642,9N

y k cx x s F L λ = .

π.r E λ =0,44cx

y k cy y s F L λ = .

π.r E λ =0,76cy

g y crx 2

cx A .F

N =

λ Ncrx= 108446281 N

g y cry 2

cy

A .F N =

λ Ncry=36349030,47 N

Maka faktor Amplikasi momen adalah sebagai berikut:

1 1 m b x u crx C N N         1 0,35 b x  

1 max( 1 ,1)

b x b x

   b x1 1, 00

1 1 m b y u cry C N N     _ _   1 0,36 b y  

1 max( 1 ,1)

b y b y

   b y1 1, 00

6. Menghitung Kapasitas Gaya Geser Kolom C-7 (Lantai 2)

w1 w

A =d.t A =5200mm_w1 2

(49)

n 2 5 k =5+ a h'       _{ }   _{ }    n k = 5,04

w w

h'

λ =

t λ =24,15w

n s

nx y w1 w

y k .E V =(0,6.f .A )jikaλ 1,10.

f

 

 _ _

 

n s n s n s

nx y w1 w

y w y y

k .E 1 k .E k .E

V =0,6.F .A .1,10. . jika 1,10. λ <1,37.

F λ F F

 



 

 

 

w1 n s n s

nx 2 w

y w

0,9.A .k .E k .E V = jikaλ 1,37.

F

λ 

nx

V = 748800 N

w2 f f

5 A = .b .t

3       2 w2 A =1400mm

ny y w2

V =0,6.f .A V =2016000 N_ny

nx

V =673920 N



ny

V = 1814400N 

ux

(50)

ux nx

V 640,96

= =0,001 V 673920

 Hasil Output ETABS: Rasio= 0,001

uy

V didapat dari nilai maksimum kombinasi = 11020,21 N

uy ny

V _11020,21

= =0,006 V 1814400

 Hasil Output ETABS: Rasio= 0,006

Dari hasil kombinasi pembebanan dan kapasitas kolom yang didapat diatas,

berikut:

Rasio = u ux uy u

nt b nx b ny nt

M

N 8 M N

+ . + jika >0,2

N 9 .M .M N

   

  

 _ _

 _ _

 

uy

u ux u

nt b nx b ny nt

M

N M N

+ + jika <0,2

2. N  .M  .M N

  

 _ _

 _ _

 

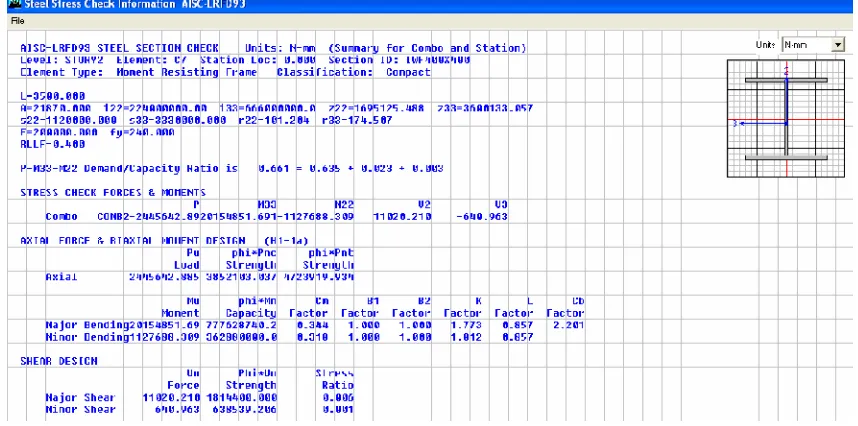
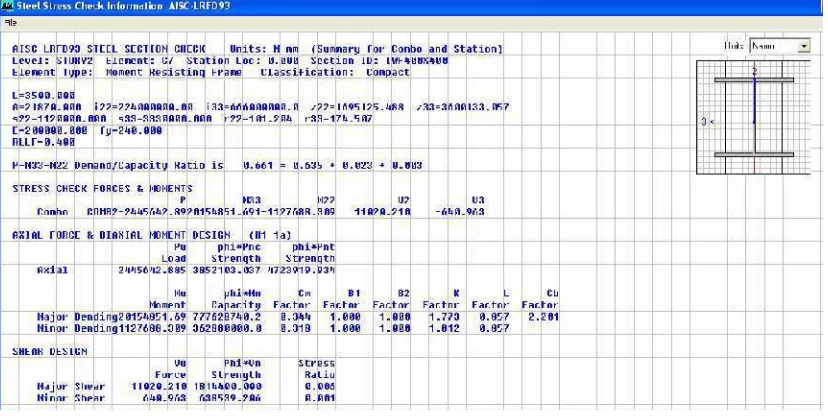
[image:50.612.110.539.442.655.2]

Maka rasio = 0,660 Hasil Output ETABS: Rasio= 0,661

(51)

B. Pembahasan Rasio P-M Gedung yang Didesain Berdasarkan FEMA 450 Desain Balok

Elevation-B (B17) Story 2

Karakteristik Profil :

WF = 300.150.6,5.9 (BJ37)

d = 300 mm bf = 150 mm

tw = 6,5 mm tf = 9 mm

L = 6000 mm Ag = 4, 678.10 mm3 2

Ix = 7,21.1010 mm7 4 Iy = _{5,08.10 mm}6 4

x

r =124 mm r =32,9 mm_y

5 3

x

S =4,81.10 mm S =6,77.10 mm_y 4 3

c

r =13mm

f c

h'=d-2.t -2.r h' = 256mm





w f w

A = d-2.t .t A =1833mm_w 2

 





2

x f f w f

1

Z =b.t . d-t + t . d-2.t 4

5 3

x

Z =5,22.10 mm

2 2

y f f w

1 1

Z = .t .b + .(d-2.t ).t 2 4

5 3

y

Z =1,04.10 mm

Data Material:

Modulus Elastisitas :

s

E =200000MPa

y

f =240MPa

Tegangan Sisa:

r

Faktor reduksi

0,9

(52)

Faktor modifikasi Tegangan Leleh:

y

Maka R =1,5_y

L y r

f =f -f f =70MPa_r _{G=0,8.10 MPa}5

L

f =170MPa



3







3

f f f w

1

J= . 2.b .t + d-2.t .t 3             4 J=98714,75mm

 

2

w f

1

I = . d-t

2      _{ }    2 w I =21170,25mm

Momen Plastis: M =Z .f_p _x _y M =125,3x10 Nmm_p 6

Momen Batas Tekuk: M =(f -f ).S_r _y _r _x M =81,77.10 Nmm_r 6 (karena

Gaya aksial Leleh: P =A .f_y _g _y P =1,123.10 N_y 6

03-1729-2002)

Pada Pelat sayap:

f f

f

b

λ =

2.t f=8,333

p y

170

λ =

f λ =10,97ps

(53)

Pada Pelat badan:

w w

h'

λ =

t λ =39,38w

p y

1680

λ =

f λ =108,54p

Kesimpulan: Penampang kompak ( _w  _p)

1. Menghitung Kapasitas Momen Balok B-13

Pada pelat sayap:

pf y

170

λ =

F λ =10,97pf

rf

y r

370

λ =

f -f λ =28,38rf

f=8,333



nFLB p f pf

M =M jikaλ λ







f pf



nFLB p p r pf f

rf pf

λ -λ

λ -λ rf

2 rf

nFLB r f

f λ

M = .M jikaλ

λ rf

  _

 

 

6 nFLB p

M =M =125,3x10 Nmm

nFLB

M =112752000Nmm

(54)

Pada pelat badan: pw y 1680 λ = f         108, 44 pw   rw y 2550 λ = f         164, 61 rw   w λ =39,38

nWLB p w







w pw



nWLB p p r pw

rw pw

λ -λ

M =M - .(M -M )jikaλ

λ -λ  w rw

2 rw

nWLB r w

w λ

M = .M jikaλ

λ rw

  _

 

 

6 nWLB p

M =M =125,3x10 Nmm

nWLB

M =112752000Nmm



b

L =6000mm

 

2 2 6 11

w y

1 1

I = .h .I = . 300 .5,08.10 =1,143.10

4 4

p y

y

E 200000

L =1,76.r . =1,76.32,9. =1671,54mm

F 240

3

1 5

π E.G.J.A π 200000.80000.98714,75.4,678.10

X = . =12553,68MPa

S 2 4,81.10 2

2

2 ₅ ₁₁

-4 4 2 w

2 6

Y

I

S 4,81.10 1,143.10

X =4. . =4. . =3,34.10 mm /N G.J I 80000.98714,75 5,08.10

 

 

(55)

2 1

r y 2 L

L

X

L =r . . 1+ 1+X .F F

 

 

 

-4 2 r

12553,68

L =32,9. . 1+ 1+3,34.10 .170 =7929,5mm 170

 

 

 

Maka,

b

L =6000mm L =1671,54mm_p L =7929,5mm_r

Keterangan: “Bentang pendek” jika L_b L_p

“ Bentang menengah jika L_p  L_b L_r

Kesimpulan: bentang menengah

Momen Plastis

6 p

M =125,3x10 Nmm

Momen Batas Tekuk

M =S.(f -f )=81770000Nmm_r _y _r

Menghitung nilai c :_b

Gambar L.3.6 Momen Maksimum

Data Momen yang didapat dari ETABS untuk menghitung nilai cb:

Momen di ¾ bentang (Mc) = 2821972,465 Nmm

(56)

maks b

maks A B c

12,5.M

C = 2,3

2,5.M +3.M +4.M +3.M 

b

12,5.7253024,32

C = 2,3

2,5.7253024,32 +3.3145095,258+4.654608,737+3.2821972,465

b

C =2,242,3

 

2

y f

w

I . d-t C =

4

 

  -7 6

w

C =1,075x10 m

21 1 s y

A =E .I .G.J=8,02x10

2

28 s

2 y w

π.E

A = .I .C =3,04x10 L

 

 

 

cr b 1 2

π

M =C . . A +A L

11 cr

M =2,045x10 Nmm

nLTBx

M = M_pjika L_b L_p

nLTBx

M =





r

b r p1 r

r p L -L C . M + M -M

L -L

  

 _ _

 _ _

nLTBx cr p1

Jadi M_nLTBx= 114672264,4 Nmm

nLTBx

M =

 104247513,15 Nmm

py y y y y

M = min (Z .F ,1,5S .F )

py

M =24372000 Nmm

nLTBy

(57)

M = min (M ,M ,M ,M )

nx

M = 114672264,4 Nmm

ny nLTBy

M =M

ny

M =24372000 Nmm

nx M =

 104247513,15 Nmm

ny

M = 21934800 Nmm 

2. Menghitung kapasitas Tarik Balok B-17

nt g y

P =A .F P =1122720N_nt

nt

P =1010448N



3. Menghitung Kapasitas Tekan Balok B-17

c

k =1 ( beban aksial tidak ada)

k c

L =k .L L = 6000mm_k

x y

(58)

y k c s f L λ = .

π.r E λ =2,01c



c



2

cr1 y c

F =_ 0,658.λ .F jikaλ 1,5_ 

c

cr1 2 y c

0,877

F = .F jikaλ 1,5

λ     _ _  _ _    cr1 F =52,10MPa

2

y f

w

I .(d-2.t ) C = 4     11 w C =1,075x10





2 s w e 2 x y k

π .E .C 1

F = +G.J

I +I K.L

 

 

  e

F =178,69MPa y e e f λ =

F λ =1,159e

 

2

e

λ

cr2 y c

f = 0,658 .f jikaλ 1,5

 

  cr1 _e2 y c

0,877

f = .f jikaλ 1,5

λ     _ _  _ _    cr1 F =156,69MPa

cr

F =156,69MPa

nc g cr

P =A .F P =732995,82N_nc

Sehingga besarnya kapasitas tekan balok adalah:

nc

P =659696,238N

(59)

4. Menghitung Kapasitas Gaya Geser Balok B-13

w1 w

A = d.t A = 1950 mm_w1 2

a = 6000 mm

n 2 5 k =5+ a h'       _{ }   _{ }    n

k = 5,009

w w

h'

λ =

t w 39,385

n s

nx y w1 w

y k .E V =(0,6.F .A )jikaλ 1,10.

F

 

 _ _

 

n s n s n s

nx y w1 w

y w y y

k .E 1 k .E k .E

V =0,6.F .A .1,10. . jika 1,10. λ <1,37.

F λ F F

 



 

 

 

w1 n s n s

nx 2 w

y w

0,9.A .k .E k .E V = jikaλ 1,37.

F

λ 

nx

V =280800N

w2 f f

5 A = .b .t

3       2 w2 A =2250mm

ny y w2

V =0,6.F .A V = 324000 N_ny

nx

V =252720N

(60)

ny

V =291600N 

ux nx

V = V

uy ny

V = V

m

C =1 ujung-ujung batang yang bisa bertranslasi

g y

cr 2

c A .F P =

λ P = 277894,1115 Ncr

Maka faktor Amplikasi momen adalah sebgai berikut:

1 1 m b u cr C P P        

1 1, 02 b

 

Dari hasil kombinasi pembebanan dan kapasitas balok yang didapat diatas,

berikut:

Rasio = u ux uy u

nt b nx b ny nt

M

P 8 M P

+ . + jika 0, 2

P 9 .M .M P

         _ _  _ _   uy

u ux u

nt b nx b ny nt

M

P M P

+ + jika <0,2

2. P  .M  .M P

  

 _ _

  

 

(61)

[image:61.612.115.529.90.297.2]

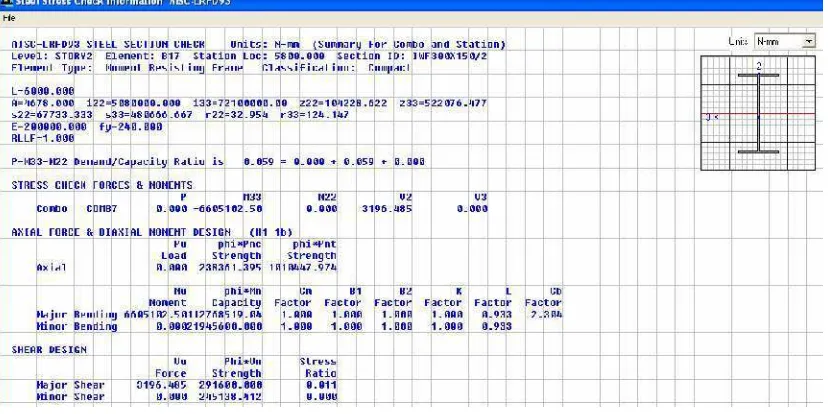
Gambar L.3.7 Nilai Output Balok yang Didesain Berdasarkan FEMA 450

Desain Kolom

Karakteristik Profil:

WF = 400.400.13.21 (BJ37)

d = 400 mm b = 400 mm_f

w

t =13 mm t = 21 mm_f

L = 3500 mm Ag = 21870 mm2

8 4

x

I = 6,66.10 mm I = 2,24.10 mm_y 8 4

x

r =175 mm r = 101 mm_y

5 3

x

S =33,3.10 mm S =11,2.10 mm_y 5 3

c

r = 22 mm

f c

h'=d-2.t -2.r h'= 314 mm





w f w

A = d-2.t .t A = 4654 mm_w 2

 





2

x f f w f

1

Z =b.t . d-t + t . d-2.t 4

6 3

x

Z =3,66.10 mm

2 2

y f f w

1 1

Z = .t .b + .(d-2.t ).t 2 4

6 3

y

(62)

Data Material:

s

E =200000MPa

y

f =240MPa

Tegangan Sisa:

r

f =70MPa (rolled beam)

Faktor reduksi

0,9

  _c 0,85 _b 0,9 Faktor modifikasi Tegangan Leleh:

1,5

y

R  jika F_y 250MPa

1,3

y

R  jika F_y 290MPa

Maka R =1,5_y

L y r

f =f -f f =70MPa_r _{G=0,8.10 MPa}5

L

f =170MPa



3







3

f f f w

1

J= . 2.b .t + d-2.t .t 3

    

    

 

4

J= 3256126 mm

 

2

w f

1

I = . d-t

2      _{ }    2 w

I = 35910,25 mm

Momen Plastis: M =Z .f_p _x _y M =878,4.10 Nmm_p 6

Momen Batas Tekuk: M =(f -f ).S_r _y _r _x M = 566,1.10 Nmm_r 6 (karena

tegangan leleh sayap dan badan sama)

(63)

03-1729-2002)

Pada Pelat sayap:

f f

f

b

λ =

2.t λ = 9,5f

p y

170

λ =

f λ =10,97ps

f ps

 

Kesimpulan: penampang kompak

Pada Pelat badan:

w w

h'

λ =

t λ =24,9w

p y

1680

λ =

f λ =108,54p

Kesimpulan: Penampang kompak ( _w  _p)

1. Menghitung Kapasitas Momen Kolom C-7 (Lantai 2)

Pada pelat sayap:

pf y

170

λ =

F λ =10,97pf

rf

y r

370

λ =

F -F λ =28,38rf

f

λ =9,5

nFLB p f pf

(64)







f pf



nFLB p p r pf f rf

rf pf

λ -λ

2 rf

nFLB r f

f λ

M = .M jikaλ

λ rf

  _

 

 

6 nFLB p

M =M =878,4.10 Nmm

nFLB

M =790560000Nmm



Pada pelat badan:

u pw

y y

2, 75. N

1680

λ = 1 jika 0,125

. .N

f

u

b y b

N N    _ _       _ _   u y y N 500 665

max . 2,33 , jika 0,125

. .N

f

u pw

b y y b

N N F    _ _ _{ }  _ _   _ _     pw

λ = 42,93

u rw b y y N 2550

λ = . 1 0,74

.N F       _ _  _ _   rw λ =87,26 w λ =24,9

nWLB p w







w pw



nWLB p p r pw w rw

rw pw

λ -λ

2 rw

nWLB r w

w λ

M = .M jikaλ

λ rw

  _

 

 

6 nWLB p

M =M =878,4.10 Nmm

nWLB

M =790560000Nmm

(65)

b

L =3500mm

 

2 2 8 12

w y

1 1

I = .h .I = . 400 .2,24.10 =8,96.10

4 4

p y

y

E 200000

L =1,76.r . =1,76.101. =5131,49 mm 240

f

1 5

π E.G.J.A π 200000.80000.3256126.21870

X = = . = 22517,78 MPa

S 2 33,3.10 2

2

2 ₅ ₁₂

-5 4 2 w

2 8

Y

I

S 33,3.10 8,96.10

X =4. . =4. . = 2,61.10 mm /N G.J I 80000.3256126 2,24.10

            2 1

r y 2 L

L

X

L =r . . 1+ 1+X .F F       -5 2 r 22517, 78

L =101. . 1+ 1+2,61.10 .170 =18930,14 mm 170       Maka, b

L =3500mm L = 5131,49 mm_p L = 18930,14 mm_r

Keterangan: “ Bentang pendek” jika L_b L_p

“ Bentang menengah jika L_p  L_b L_r

Kesimpulan: bentang pendek

Momen Plastis

6 p

M =878,4.10 Nmm

Momen Batas Tekuk

6

r y r

(66)

Gambar L.3.8 Momen pada Kolom

Data Momen yang didapat dari ETABS untuk menghitung nilai Cb:

Momen di ¾ bentang (Mc) = 8773199 Nmm

maks b

maks A B c

12,5.M

C = 2,3

2,5.M +3.M +4.M +3.M 

b

12,5.20154851, 7

C 2,3

2,5.20154851, 7 3.10512168,1 4.869484, 48 3.8773199

 

  

b

C =2,252,3

 

2

y f

w

I . d-t C =

4

 

 

12 w

C = 8,04.10

25 1 s y

A =E .I .G.J=1,17.10

2

25 s

2 y w

π.E

A = .I .C =5,8.10 L

 

 

(67)

cr b 1 2 π

M =C . . A +A L

10 cr

M =1,69x10 Nmm

nLTBx

M =





r

b r p1 r

r p L -L C . M + M -M

L -L

  

 _ _

 _ _

nLTBx cr p1

Jadi M_nLTBx=M_p=878,4x10 Nmm6

nLTBx

M =

 790560000 Nmm

py y y y y

M =min(Z .F ,1,5S .F )

py

M =403200000 Nmm

nLTBy

M =362880000 Nmm 

1.c Menghitung Momen Nominal (M_n)

Momen nominal pada sumbu-x: (M_nx)

M =min(M ,M ,M ,M )

nx

M =_{878,4x10 Nmm}6

ny nLTBy

M =M

ny

(68)

nx M =

 790560000 Nmm

ny

M =362880000 Nmm 

2. Menghitung kapasitas Tarik Kolom C-7 (Lantai 2)

nt g y

P =A .f

6 nt

P =5,25x10 N

nt

P =4723920 N



3. Menghitung Kapasitas Tekan Kolom C-7 (Lantai 2)

Faktor panjang efektif kc, ditentukan dengan menggunakan faktor G:

A

G = 1,0 (jepit)

A B

B

66600 66600

I ₊

Σ( ) ₃₅₀ ₃₅₀

L

G = = =15,8

I 7210 7210

Σ( ) +

L 600 600

                        c k = 2

k c

L =k .L L =7000 mm_k

x y

r=min(r ,r ) r= 101mm

y k c s f L λ = .

(69)

 

2 c

λ

cr1 y c

F = 0,658 .f jikaλ 1,5

 

 

c

cr1 2 y c

0,877

F = .f jikaλ 1,5

λ     _ _  _ _    cr1

F = 195,71 MPa

 

2

y f

w

I . d-t C =

4

 

  12

w

C =8,04x10





2 s w e 2 x y z k

π .E .C 1

F = +G.J

I +I K .L         e

F = 1748,34 MPa

y e

e f

λ =

F λ =0,37e

Maka besarnya tegangan kritis dengan memperhitungkan tekuk puntir lentur:

 

2

e

λ

cr2 y c

F = 0,658 .f jikaλ 1,5

 

 

e

cr2 2 y c

0,877

F = .f jikaλ 1,5

λ     _ _  _ _    cr2

F =226,63 MPa

Besarnya kuat tekan nominal adalah:

cr cr1 cr2 F =min(F ,F )

cr

F =195,71 MPa

nc g cr

P =A .F P =4280114,486 N_nc

Sehingga besarnya kapasitas tekan kolom adalah:

nc

P =3852103,04 N

(70)

1

M = 12905778 Nmm (momen ujung terkecil)

2

M = 20154851,7 Nmm (momen ujung terbesar)

Kurvatur = 2 (double curvature)

1 2 m

1 2

min(M ,M )

β =

max(M ,M ) jika kurvatur > 2

1 2 m

1 2 min(M ,M )

β =

-max(M ,M )

 

 

  jika kurvatur < 1

m m

C =0,6-0,4.β

m C =0,34

u

N = 2445642,9N

y k cx x s F L λ = .

π.r E λ =0,44cx

y k cy y s F L λ = .

π.r E λ =0,76cy

g y crx 2

cx A .F

N =

λ Ncrx= 108446281 N

g y cry 2

cy

A .F N =

λ Ncry=36349030,47 N

Maka faktor Amplikasi momen adalah sebgai berikut:

m 1 u crx C N 1-N b x         1 0,35 b x  

1 max( 1 ,1)

b x b x

(71)

m 1 u cry C N 1 N b y     _ _   1 0,36 b y  

1 max( 1 ,1)

b y b y

   b y1 1, 00

6. Menghitung Kapasitas Gaya Geser Kolom C-7 (Lantai 2)

w1 w

A =d.t A =5200mm_w1 2

a = 3500 mm

n 2 5 k =5+ a h'       _{ }   _{ }    n k = 5,04

w w

h'

λ =

t λ =24,15w

n s

nx y w1 w

y k .E V =(0,6.f .A )jikaλ 1,10.

f

 

 _ _

 

n s n s n s

nx y w1 w

y w y y

k .E 1 k .E k .E

V =0,6.F .A .1,10. . jika 1,10. λ <1,37.

F λ F F

 



 