Analisis kesalahan siswa dalam menyelesaiakan soal limit fungsi aljabar dan upaya remidiasinya di kelas XI IPS SMA Seminari Mertoyudan tahun ajaran 2016 2017

(1)

i

ANALISIS KESALAHAN SISWA DALAM MENYELESAIAKAN SOAL LIMIT FUNGSI ALJABAR DAN UPAYA REMIDIASINYA DI KELAS XI

IPS SMA SEMINARI MERTOYUDAN TAHUN AJARAN 2016/2017

SKRIPSI

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika

Disusun Oleh:

Agustina Dhevin Merinda Damayanti NIM. 131414003

PROGRAM STUDI PENDIDIKAN MATEMATIKA

JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM

FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS SANATA DHARMA

(2)

(3)

(4)

iv

HALAMAN PERSEMBAHAN

Dengan penuh syukur, aku persembahkan skripsi ini untuk: Tuhan Yesus Kristus dan Bunda Maria yang senantiasa menyertaiku,

memberiku berkat, dan kasih untukku

Orang tuaku Ibu Scholastika Sutarsih yang selalu memberiku dukungan, doa, semangat dan kasih sayang yang tiada henti-hentinya, serta (Alm) Bapak Anancletus Eko Sudiyarto yang sudah mendoakanku

dari jauh

Mbakku yang jauh disana, Maria Edha Ika Damayanti yang selalu memberikanku semangat, doa, cinta, serta dukungan untukku Kedua ponakanku yang Y.M.V Nugraha Yoga Pratama dan Lidya Kharisma Yoga Papuane yang selalu memberi cinta dan semangat Sahabat-sahabatku yang selalu memberikan dukungan dan semangat

Simon, mb Yanu, L. Dina, R. Dina, Dora, Cahyo, Tri, Ipo, Emi, Gerard

(5)

v

HALAMAN MOTTO

Tuhan tahu segala kelemahanmu

Dia mengerti segala kelemahanmu

Oleh karena itu, jangan berhenti berjuang bersama-Nya

Karena dia tidak pernah membiarkan engkau sendiri

(6)

(7)

(8)

viii ABSTRAK

Agustina Dhevin Merinda Damayanti, 2017. Analisis Kesalahan Siswa dalam Menyelesaiakan Soal Limit Fungsi Aljabar dan Upaya Remidiasinya Di Kelas XI IPS SMA Seminari Mertoyudan Tahun Ajaran 2016/2017. Skripsi. Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan Ilmu Pengetahuan Alam, Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta.

Penelitian ini bertujuan untuk mengetahui jenis-jenis kesalahan yang dilakukan siswa dan faktor-faktor penyebab siswa kelas XI IPS SMA Seminari Mertoyudan dalam menyelesaikan soal pada materi Limit Fungsi Aljabar. Disamping itu penelitian ini juga bertujuan untuk mengetahui pengaruh pembelajaran remedial dalam mengatasi kesalahan dalam menyelesaikan soal pada materi Limit Fungsi Aljabar.

Subyek penelitian ini adalah siswa kelas XI IPS SMA Seminari Mertoyudan tahun ajaran 2016/2017 yang berjumlah 31 siswa. Metode penelitian yang digunakan adalah deskriptif kualitatif. Data yang dikumpulkan melalui observasi, tes diagnostik, wawancara, dan tes remedial.

Hasil penelitian menunjukkan bahwa (1) kesalahan-kesalahan yang dilakukan siswa antara lain: kesalahan data dalam mengabaikan data penting yang sudah ada dan menggantinya dengan data yang tidak relevan, menggunakan syarat yang tidak sesuai dengan informasi yang diberikan; kesalahan menginterpretasikan data; kesalahan memahami definisi; kesalahan teknis antara lain kesalahan-kesalahan dalam perhitungan, menghilangkan notasi limit, menambahkan notasi limit; kesalahan dalam pembagian bilangan nol; kesalahan dalam penggunaan tanda kurung; kesalahan dalam mendistribusikan; kesalahan dalam mengerjakan soal dengan menghilangkan/ menghapuskan variabel, koefisien, atau konstanta; kesalahan menggunakan logika dalam penarikan kesimpulan; kesalahan konsep. (2) faktor-faktor penyebab siswa melakukan kesalahan antara lain: belum menguasai materi prasyarat; kurang teliti; kurang memahami definisi; belum memahami konsep dasar; takut dan ragu dalam menyelesaikan soal; bingung dengan cara yang akan digunakan untuk meyelesaikan soal; memiliki sugesti negative terhadap pelajaran matematika; dan waktu yang diberikan kurang. (3) kesalahan siswa dalam menyelesaikan soal limit fungsi aljabar berkurang setelah diadakan remedial dan ada peningkatan hasil belajar siswa.

(9)

ix ABSTRACT

Agustina Devin Merinda Damayanti, 2017. The Students’ Mistakes Analysis of Working on Questions about Limit of Algebraic Function and The Remedial Efforts In Grade XI Social Science Seminari Mertoyudan Senior High School in The Academic Year 2016/2017.Thesis, Mathematics Education Study Program, Department of Mathematics and Science, Faculty of Teachers Training and Education, Sanata Dharma University, Yogyakarta.

This research aimed to find out types of mistakes that were done by the students and cause factors of the students grade XI social science in Seminari Mertoyudan in working on questions about Limit of Algebraic Function. Besides, this research also aimed to find out the influences of a remedial learning in solving the mistakes while working on questions about Algebra of Limits Functions.

The research subjects are the students grade XI social science in Seminari Mertoyudan Senior High School, in the academic year 2016/2017 which consist 31 students. The research method applied was qualitative descriptive research. The data were collected through interview diagnostic observation test and remedial test.

The research results showed that (1) the mistakes were done by the students, i.e. the data mistakes in ignoring the important data and changing with the data that were not relevant, applying the requirements which were not suitable to the information given; the mistakes in interpreting the data; the mistakes in comprehending the definition; the technical mistakes, i.e. the mistakes in counting, eliminating the limit notation, adding the limit notation, the mistakes in zero number of division; the mistakes in applying the brackets; the mistakes in distributing; the mistakes in working on the questions because eliminating/deleting variables, coefficients, or constants; the mistakes in applying the logic in making the conclusion; the mistakes in concept. (2) the cause factors of the students making the mistakes, i.e. they hadn’t comprehended pre-requirement materials; were less of concern; did not comprehend the definition; hadn’t comprehended the basic concept; were afraid of working on the questions; were confused with the procedures which would be applied to work on the quetions; had negative feeling in mathematics lesson; and were less of the time. (3) the students’ mistakes in working on the questions about algebra of the limits functions were reduced after the remedial implementation and there were improvement in students learning results.

(10)

x

KATA PENGANTAR

Puji dan syukur kehadirat Tuhan Yesus Kristus atas berkat dan kasih-Nya dalam penyusunan skripsi yang berjudul “Analisis Kesalahan Siswa dalam Menyelesaiakan Soal Limit Fungsi Aljabar dan Upaya Remidiasinya Di KelasXI IPS SMA Seminari Mertoyudan Tahun Ajaran 2016/2017”sehingga penulis dapat menyelesaikannya dengan baik dan tepat waktu.

Penulisan skripsi ini merupakan tugas akhir untuk memenuhi syarat kelulusan guna memperoleh gelar Sarjana Pendidikan Universitas Sanata Dharma. Penulisan skripsi ini dapat diselesaikan dengan baik yang tidak terlepas dari banyak pihak yang turut mendukung, memberikan doa, materi, serta bantuan dan semangat yang sangat bemanfaat bagi penulis. Oleh karena itu, melalui kesempatan ini penulis mengucapkan terimakasih kepada:

1. Bapak Rohandi, Ph.D., selaku Dekan Fakultas Keguruan dan Ilmu Pendidikan, Universitas Sanata Dharma Yogyakarta;

2. Bapak Dr. Hongki Julie, M.Si., selaku Ketua Program Studi Pendidikan Matematika, Jurusan Pendidikan Matematika dan IPA;

3. Bapak Beni Utomo, M.Sc., selaku dosen pembimbing akademik yang telah memberikan dukungan dan semangat;

(11)

xi

5. Bapak Febi Sanjaya, M.Sc , selaku dosen yang meluangkan waktunya untuk memvalidasi perangkat penelitian;

6. Segenap dosen dan seluruh staff sekretariat JPMIPA yang sudah membantu dalam proses administrasi;

7. Romo Y. Alis Windu Prasetya, SJ, selaku kepala SMA Seminari Mertoyudan yang telah mengijinkan peneliti untuk melaksanakan penelitian;

8. Ibu Agnes Wardani, S.Pd., selaku Guru Matematika kelas XI SMA Seminari Mertoyudan yang telah membantu dalam pelaksanaan penelitian;

9. Siswa (para seminaris) kelas XI IPA dan XI IPS yang sudah membantu peneliti sebagai subyek penelitian;

10. Ibu Scholastika Sutarsih, mbakku Maria Edha Ika Damayanti, ponakkanku Y.M.V Nugraha Yoga Pratama dan Lidya Kharisma Yoga Papuane, serta keluargaku yang tidak bisa kusebutkan satu per satu atas doa, cinta, kasih sayang, perhatian, semangat, masukan, motivasi, dan selalu membantu dalam penyusunan skripsi;

11. Universitas Sanata Dharma yang telah membiayai kuliah selama 4 tahun penuh melalui program beasiswa Driyarkara;

(12)

xii

13. Simon Tuhu Setiawan yang sudah memberi dukungan, motivasi, dan semangat;

14. Teman-teman Pendidikan Matematika 2013 yang telah memberikan dukungan dan semangat;

15. OMK Santo Kristoforus Banyutemumpang yang selalu memberikan semangat dan dukungan;

16. Semua pihak yang tidak dapat disebutkan satu per satu yang telah membantu pelaksanaan penelitian dan penyusunan skripsi.

Penulis menyadari bahwa masih banyak kekurangan dan kelemahan dalam penyusunan skripsi ini, maka dari itu penulis mengharapkan kritik dan saran dari berbagai pihak. Semoga skripsi ini dapat bermanfaat bagi semua pihak dan dapat dikembangkan menjadi penelitian yang lebih baik.

(13)

xiii DAFTAR ISI

HALAMAN JUDUL ...i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN ... iii

HALAMAN PERSEMBAHAN ...iv

HALAMAN MOTTO ...v

PERNYATAAN KEASLIAN KARYA ...vi

LEMBAR PERNYATAAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIK... vii

ABSTRAK ... viii

ABSTRACT...ix

KATA PENGANTAR ...x

DAFTAR ISI... xiii

DAFTAR TABEL...xvi

DAFTAR GAMBAR ... xvii

DAFTAR LAMPIRAN...xx

BAB I PENDAHULUAN...1

A.Latar Belakang Masalah ...1

B.Identifikasi Masalah...4

C.Rumusan Masalah...4

D.Tujuan Penelitian ...5

(14)

xiv

F.Batasan Istilah ...6

G.Manfaat Penelitian ...8

BAB II LANDASAN TEORI ...9

A.Analisis Kesalahan ...9

B.Kategori Jenis Kesalahan...10

C.Faktor Penyebab Kesalahan ...25

D.Limit Fungsi Aljabar ...27

E.Pembelajaran Remidial ...36

F.Metode Pembelajaran Remidial ...39

G.Kerangka Berfikir ...41

BAB III METODE PENELITIAN ...43

A.Jenis Penelitian ...43

B.Tempat dan Waktu Penelitian...43

C.Subjek dan Objek Penelitian...44

D.Variabel Penelitian...44

E.Metode Pengumpulan Data ...45

F.Instrumen Pengumpulan Data ...46

G.Teknik Analisis Data ...49

H.Validitas dan Reliabilitas ...51

BAB IV ANALISIS HASIL PENELITIAN DAN PEMBAHASAN...56

A.Deskripsi Pelaksanaan Penelitian ...56

B.Observasi ...57

(15)

xv

D.Upaya Remidiasi...104

BAB V PENUTUP ...118

A.Kesimpulan ...118

B.Kelemahan Penelitian ...121

C.Saran ...122

DAFTAR PUSTAKA ...124

(16)

xvi

DAFTAR TABEL

Tabel 2.1 Contoh kategori jenis kesalahan dalam mengerjakan soal-soal Limit

Fungsi Aljabar ...21

Tabel 2.2 Tabel Nilai ...28

Tabel 3.1 indikator pencapaian hasil belajar...47

Tabel 3.2 Pedoman Wawancara...48

Tabel 3.3 Validitas Soal Uji Coba ...53

Tabel 3.4 Tabel Koefisien Reliabilitas...55

Tabel 4.1 Kegiatan Pelaksanaan Penelitian ...57

Tabel 4.2 Nilai Tes Diagnostik ...60

Tabel 4.3 Analisis Kesalahan Siswa dalam Menyelesaikan Soal Nomor 1...62

Tabel 4.10 Presentase Kesalahan yang Dilakukan Siswa Kelas XI IPS ...101

Tabel 4.11 Daftar Nilai Tes Diagnostik dan Tes Remidiasi Siswa Kelas XI IPS106 Tabel 4.12 Pengaruh Remidiasi Ditinjau dari Kesalahan ...115

(17)

xvii

DAFTAR GAMBAR

Gambar 2.1 Diagram Sistematis ...29

Gambar 2.2 Grafik

 

1 1 3     x x x f y ...29

Gambar 2.3 Grafik f

 

x Lε...30

Ganbar 2.4 Grafik 0xcδ ...31

Gambar 4.1 Jawaban S4 pada soal nomor 1 ...77

(18)

xviii

Gambar 4.30 Jawaban S4 pada soal remidi nomor 3...106

(19)

xix

(20)

xx

DAFTAR LAMPIRAN

Lampiran A.1 Surat Ijin Penelitian ...126

Lampiran A.2 Surat Keterangan Telah Melakukan Penelitian ...128

Lampiran B.1 Validasi Instrumen Soal Uji Coba dan Lembar Observasi oleh Dosen ...129

Lampiran B.2 Validasi Instrumen Soal Uji Coba dan Lembar Observasi oleh Guru Mata Pelajaran ...133

Lampiran C Hasil Observasi di Kelas...137

Lampiran D.1 Lembar Soal Tes Uji Coba dan Diagnostik ...138

Lampiran D.2 Kunci Jawaban dan Pedoman Penskoran ...139

Lampiran E.1 Hasil Uji Validitas...142

Lampiran E.2 Hasil Uji Reliabilitas...143

Lampiran F Hasil Pekerjaan Siswa pada Tes Diagnostik ...144

Lampiran G Transkrip Wawancara...162

Lampiran H Hasil Pekerjaan Ulang Siswa dalam Pembelajaran Remidial ...185

Lampiran I Lembar Soal Tes Remidial...191

Lampiran J Kunci Jawaban dan Pedoman Penskoran...192

(21)

1 BAB I PENDAHULUAN

A. Latar Belakang Masalah

Matematika merupakan ilmu pasti dan matematika berkembang sejalan dengan peradaban manusia. Oleh sebab itu, matematika sangatlah penting untuk dipahami dan dipelajari. Akan tetapi banyak orang beranggapan bahwa untuk mempelajari matematika diperlukan bakat istimewa yang tidak dimiliki setiap orang. Kebanyakan orang berpandangan bahwa untuk dapat mempelajari matematika perlu kecerdasan yang tinggi, akibatnya banyak orang tidak termotivasi untuk belajar matamatika dan menganggap bahwa dirinya tidak mampu permasalahan matematika. Padahal tanpa mereka sadari banyak hal yang berkaitan dengan matematika yang dapat mereka temui di kehidupan sehari-hari.

Penguasaan matematika siswa di Indonesia bisa dikatakan masih kurang. Berdasarkan survey anak di usia 15 tahun dan 16 tahun dibidang matematika yang dilakukan sebuah organisasi dalam naungan Organization Economic Cooperation and Development (OECD) yang bernama Program for International Student Assessment (PISA) Indonesia selalu berada pada urutan bawah dibandingkan Negara lainnya. Pada tahun 2012 Indonesia menempati urutan ke 64 dari 65 negara di dunia (OECD, 2012).

(22)

PISA tahun 2009 menunjukkan bahwa siswa yang mampu menjawab soal dengan benar pada geometri sebesar 47,5%, statistik sebesar 61,9%, aljabar sebesar 41,4%, dan bilangan sebesar 53,7%. Dari hasil studi PISA tahun 2009 menunjukkan bahwa tingkat kesulitan paling besar yang dihadapi oleh siswa yaitu pada soal aljabar. Hal ini ditunjukkan dari hasil secara keseluruhan yaitu hanya 41,4% siswa yang dapat menjawab dengan benar. Sangat kecil dibandingkan dengan soal pada materi yang lain (Aini, 2014).

Keterampilan berhitung dirasa belum cukup dalam menyelesaiakan soal matematika, tetapi juga membutuhkan kemampuan pemahaman konseptual dan prosedural serta kreativitas dalam menyelesaikannya. Dalam pelaksanaan pembelajaran matematika, guru sering mengeluh tentang sulitnya siswa dalam menyelesaikan soal matematika, yang seharusnya diselesaikan dengan cara yang mudah malah dipersulit oleh siswanya sendiri. Jika kesalahan siswa dalam menyelesaikan soal matematika tidak diperbaiki maka siswa akan menghadapi masalah dalam belajar matematika. Kesalahan yang dilakukan oleh siswa perlu diidentifikasi serta perlu diperbaiki untuk mengetahui kesalahan-kesalahan apa saja yang sering dilakukan oleh siswa dalam pengerjaan soal matematika. Setelah mengetahui kesalahan apa saja yang sering dilakukan siswa, guru dapat memberikan pengajaran remedial agar siswa juga tahu dimanakah letak kesalahan yang dilakukan oleh siswa guna meningkatkan mutu pembelajaran Matematika.

(23)

hanya ada sedikit kesalahan yang terjadi ketika siswa menyelesaikan soal tersebut, akan tetapi hasilnya siswa melakukan banyak kesalahan. Adapun alasan-alasan siswa melakukan kesalahan antara lain adalah kurangnya memahami metode-metode penyelesaian yang dipakai. Metode yang masih kurang dipahami adalah metode mengalikan dengan akar sekawan, pada metode ini siswa masih sering salah. Metode pemfaktoran pun terkadang siswa masih salah dalam memfaktorkannya. Disamping kurangnya pemahaman mengenai metode-metode penyelesaian limit fungsi yang menjadi kendala lain adalah kurangnya ketelitian siswa, siswa masih kurang teliti dalam pengerjaan soal.

Berdasarkan hasil wawancara dengan guru matematika di SMA Seminari Mertoyudan, diketahui bahwa masih banyak siswa yang tidak memahami materi Limit Fungsi Aljabar yang dapat dilihat dari hasil belajar siswa yang belum mencapai nilai KKM dan banyaknya siswa mengeluh karena materi yang dipelajari sangatlah rumit. Hal ini dikarenakan banyaknya teorema-teorema yang digunakan dalam menyelesaikan soal limit serta banyaknya rumus yang digunakan sehingga membuat siswa bingung dalam menyelesaiakan persoalan yang diberikan.

(24)

B. Identifikasi Masalah

Berdasarkan latar belakang yang ditemukan oleh peneliti, maka diperoleh identifikasi masalah sebagai berikut:

1. Kurangnya pemahaman siswa terhadap konsep matematika sehingga masih banyak siswa melakukan kesalahan dalam menyelesaikan soal matematika. 2. Konsep matematika dinilai sangat abstrak dan membutuhkan kecerdasan

yang tinggi.

3. Siswa SMA Seminari Mertoyudan menganggap materi Limit Fungsi Aljabar sangatlah sulit dipelajari.

C. Rumusan Masalah

Berdasarkan identifikasi masalah yang telah dipaparkan di atas, peneliti membuat rumusan masalah yang selanjutnya akan dikaji dalam penelitian yaitu sebagai berikut:

1. Apa saja jenis kesalahan siswa kelas XI IPS SMA Seminari Mertoyudan dalam menyelesaikan soal pada materi Limit Fungsi Aljabar?

2. Faktor-faktor apa saja yang menyebabkan siswa XI IPS SMA Seminari Mertoyudan melakukan kesalahan dalam menyelesaikan soal pada materi Limit Fungsi Aljabar?

(25)

D. Tujuan Penelitian

Berdasarkan rumusan masalah yang telah dibuat maka tujuan dari penelitian ini adalah

1. Mengetahui jenis-jenis kesalahan yang dilakukan siswa kelas XI IPS SMA Seminari Mertoyudan dalam menyelesaikan soal pada materi Limit Fungsi Aljabar.

2. Mengetahui faktor-faktor yang menyebabkan siswa XI IPS SMA Seminari Mertoyudan melakukan kesalahan dalam menyelesaikan soal pada materi Limit Fungsi Aljabar.

3. Mengetahui pengaruh pembelajaran remedial dalam mengatasi kesalahan siswa kelas XI IPS SMA Seminari dalam menyelesaikan soal pada materi Limit Fungsi Aljabar.

E. Batasan Masalah

(26)

mengambil beberapa siswa yang dikenai pembelajaran remedial karena keterbatasan waktu dan banyaknya kegiatan siswa yang dilakukan di asrama.

F. Batasan Istilah

Berikut ini adalah istilah-istilah yang digunakan dalam penelitian. Untuk mencegah terjadinya kesalahpahaman akibat perbedaan pandangan dan pemikiran, maka perlu adanya penegasan dengan istilah-istilah tersebut.

1. Analisis

Analisis adalah proses pencarian jalan keluar (pemecahan masalah) yang berangkat dari dugaan akan kebenarannya; penyelidikan terhadap suatu peristiwa untuk mengetahui keadaan yang sebenarnya; penguraian suatu pokok atas berbagai bagian dan penelaahan bagian itu sendiri serta hubungan antar bagian untuk mendapatkan pengertian yang tepat dan pemahaman makna keseluruhan. Analisis yang dimaksud dalam penelitian ini adalah mengklasifikasikan jenis kesalahan yang dilakukan siswa dalam menyelesaikan soal pada materi Limit Fungsi Aljabar yang terdapat dalam tes diagnostik serta faktor penyebab kesalahan yang dapat diketahui melalui wawancara.

2. Kesalahan

(27)

3. Analisis kesalahan

Analisis kesalahan adalah penyelidikan terhadap kekeliruan siswa dalam menyelesaikan soal Limit Fungsi Aljabar berdasarkan hasil pekerjaan siswa serta wawancara.

4. Limit Fungsi Aljabar

Limit Fungsi Aljabar adalah salah stau pokok bahasan yang diajarkan di kelas XI IPS semester 2.

5. Upaya Remidiasi

Upaya remidiasi dalam penelitian ini merupakan usaha yang dilakukan untuk membantu siswa yang mengalami kesulitan menguasai kompetensi yang telah ditentukan agar mencapai hasil belajar yang lebih baik. Upaya remidiasi dilakukan untuk membantu siswa yang belum tuntas menguasai kompetensi yang ditetapkan melalui kegiatan pembelajaran tambahan. Melalui kegiatan remidiasi siswa dibantu untuk membantu siswa menyadari dan membetulkan kesalahan-kesalahan yang dilakukan dalam mengerjakan soal limit fungsi aljabar. Siswa yang mengikuti remidiasi adalah siswa yang banyak mengalami kesalahan dan kurang dari KKM yang ditentukan dalam mengerjakan soal-soal limit fungsi aljabar.

G. Manfaat Penelitian 1. Bagi Siwa

(28)

mengetahui faktor penyebab siswa melakukan kesalahan dalam menyelesaikan soal Limit Fungsi Aljabar. Diharapkan dari penelitian ini bisa menjadi pembelajaran bagi siswa agar tidak mengulangi kesalahan tersebut.

2. Bagi Guru

Dari hasil penelitian ini diharapkan dapat memberikan gambaran kepada guru terhadap jenis-jenisa kesalahan yang dilakukan siswa dalam menyelesaikan soal Limit Fungsi Aljabar. Guru mendapat referensi dalam memilih konsep, metode, serta strategi kegiatan pembelajaran, sehingga dapat meminimalisir kesalahan-kesalahan yang dilakukan oleh siswa dan dapat meningkatkan hasil belajar siswa.

3. Bagi peneliti

(29)

9 BAB II

LANDASAN TEORI

A. Analisis Kesalahan

Analisis adalah suatu upaya penyelidikan untuk melihat, mengamati, mengetahui, menemukan, memahami, menelaah, mengklasifikasikan, dan mendalami serta menginterpretasikan fenomena yang ada (menurut Wijaya dan Marsiyah dalam Pratama 2016:8). Analisis adalah proses pencarian jalan keluar (pemecahan masalah) yang berangkat dari dugaan akan kebenarannya; penyelidikan terhadap suatu peristiwa untuk mengetahui keadaan yang sebenarnya; penguraian suatu pokok atas berbagai bagian dan penelaahan bagian itu sendiri serta hubungan antar bagian untuk mendapatkan pengertian yang tepat dan pemahaman makna keseluruhan (dalam Tim Reality, 2008:47).

Menurut Kamus Besar Bahasa Indonesia (Tim Penyusun, 1988), kesalahan secara umum dapat dipandang sebagai hasil tindakan yang tidak tepat, yang menyimpang dari aturan, norma atau suatu sistem yang sudah ditentukan. Tindakan yang tidak tepat itu dapat mengakibatkan tujuan tidak tercapai secara maksimal atau bahkan gagal.

(30)

yang tidak dapat dibaca sehingga siswa melakukan kekeliruan karena tidak mampu lagi membaca tulisannya sendiri.

Menurut peneliti, kesalahan dalam matematika dapat diartikan sebagai suatu pemahaman yang kurang tepat dalam mempelajari matematika sehingga siswa keliru dalam menyelesaikan masalah matematika dan mengalami beberapa kesulitan. Kesalahan dalam matematika dapat diperlihatkan dari hasil perhitungan yang kurang tepat dalam mengolah angka-angka yang tersedia dan dapat juga diperlihatkan dari kesalahan menggunakan teorema-teorema dalam matematika.

B. Kategori Jenis Kesalahan 1. Jenis kesalahan menurut Hadar

Menurut Hadar dkk (1987) dalam tulisannya yang berjudul An Empirical Classification Model For Error in High School Mathematics, jenis-jenis kesalahan yang sering dilakukan oleh siswa dibedakan menjadi 6 jenis yaitu:

a. Kesalahan data

Kategori ini meliputi kesalahan-kesalahan yang dapat dihubungkan dengan ketidaksesuian antara data yang diberikan dalam soal dengan data yang dikutip oleh siswa yang meliputi kesalahan-kesalahan sebagai berikut:

(31)

2) Mengabaikan data penting yang sudah ada dan menggantinya dengan data yang tidak relevan.

3) Menguraikan syarat-syarat (dalam pembuktian, perhitungan, penemuan) yang sebenarnya tidak dikehendaki soal.

4) Mengartikan sebagian informasi tidak sesuai dengan teks yang sebenarnya.

5) Menggunakan syarat yang tidak sesuai dengan informasi yang diberikan.

6) Menggunakan angka pengganti suatu variabel untuk variabel yang lain.

7) Kesalahan menyalin soal dari lembar soal ke lembar jawab. b. Kesalahan menginterpretasikan data

Kategori ini meliputi kesalahan matematika yang berkaitan dengan ketidaksesuaian dalam menerjemahkan suatu pernyataan matematika yang dideskripsikan dalam suatu bahasa ke bahasa yang lain yang meliputi kesalahan-kesalahan sebagai berikut:

1) Menerjemahkan pernyataan dalam bahasa sehari-hari ke dalam bahasa atau persamaan matematika dengan arti yang berbeda.

2) Menuliskan simbol dari suatu konsep dengan simbol lain yang artinya berbeda.

(32)

c. Kesalahan menggunakan logika dalam penarikan kesimpulan

Pada umumnya yang termasuk dalam kategori ini adalah kesalahan-kesalahan dalam menartik kesimpulan dari suatu informasi yang diberikan atau dari kesimpulan sebelumnya, yaitu:

1) Dari pernyataan bentuk implikasi pq, siswa menarik kesimpulan sebagai berikut:

- Bila qdiketahui, maka ppasti terjadi

- Bila diketahui psalah, maka qpasti juga salah

2) Kesimpulan dari pernyataan pqdengan kebalikan baik bentuk positif q patau dengan bentuk negatif ~ p~ q

3) Menyimpulkan bahwa pq ketika qbukan merupakan akibat dari

p

d. Kesalahan menggunakan definisi atau teorema

Kesalahan ini merupakan suatu penyimpangan dari prinsip, aturan, teorema atau definisi yang pokok dan khas. Kesalahan-kesalahan ini antara lain:

1) Kesalahan memahami definisi

Misal : variabel dari bentuk 6x2yz3 adalah x2yz3 2) Kesalahan memahami teorema

(33)

e. Penyelesaian yang tidak diperiksa kembali

Kesalahan ini terjadi jika setiap langkah yang ditempuh oleh peserta tes benar, akan tetapi hasil akhir yang diberikan bukan penyelesaian dari soal tersebut.

f. Kesalahan teknis

Kategori kesalahan teknis meliputi kesalahan-kesalahan berikut: 1) Kesalahan-kesalahan perhitungan.

2) Kesalahan dalam mengutip data dari tabel.

3) Kesalahan dalam memanipulasi simbol-simbol aljabar dasar. 4) Menghilangkan limit

5) Menambah limit

2. Menurut Dawnkins (2006), mengemukakan beberapa kesalahan yang sering dilakukan siswa dalam mengerjakan soal aljabar sebagai berikut:

a. Kesalahan dalam pembagian dengan bilangan nol

Kesalahan yang sering dilakukan siswa dalam pembagian nol yaitu

menghitunng 0 0 2

 atau 2

0 2

 . Pembagian bilangan nol yang benar

yaitu bahwa 0 2

tidak terdefinisi.

b. Kesalahan dalam penggunaan tanda kurung

(34)

Contoh:

1) Menentukan kuadrat dari 3x

2 2 2 2 9 ) ( ) 3 (

3x  x  x benar

2 2

3 ) 3

( x  x tidak benar

Dalam kasus ini tanda kurung digunakan untuk meyakinkan bahwa yang dikuadratkan adalah 3 bukan hanyax x saja.

2) Menentukan kuadrat dari 2 4 ) 2 )( 2 ( ) 2

( 2     benar

4 2 2 ) 2

( 2    tidak benar

Banyak siswa sebenarnya tahu bahwa secara teknik mereka diharuskan mengkuadratkan 2, tetapi mereka malas dan tidak menuliskan tanda kurung dalam menyelesaikan soal tersebut, dengan alasan mereka akan mengingat tanda kurung saat memeriksa kembali hasil pekerjaan mereka. Namun banyak siswa akhirnya lupa tanda kurung dan menuliskan 4 pada akhir pekerjaan.

3) Mengurangkan 4a5 dari a2 3a5 5 4 5 3 ) 5 4 ( 5 3 2

2 _ _ _ _ _ _ _ _ _

a a a a a a benar a a   2 10 ) 5 4 ( 5 3 2

2 _ _ _ _ _ _ _

a a a

a

a tidak benar

c. Kesalahan dalam mendistribusikan Contoh:

(35)

40 8 ) 10 2 (

4 x2   x2  benar 10 8 ) 10 2 (

4 x2   x2  tidak benar 2) Mengalikan 3(2x5)2

) 25 20 4 ( 3 ) 5 2 (

3 x 2  x2  x benar

75 60 12 2  

 x x

2 2 ) 15 6 ( ) 5 2 (

3 x  x tidak benar

225 180

36 2  

 x x

d. Kesalahan dalam mengasumsikan penjumlahan

Kesalahan ini terjadi saat siswa mengasumsikan bahwa sifat pada

y x y

x ) 2 2

(

2    akan berlaku untuk semua bentuk aljabar yang mirip dengan bentuk tersebut. berikut ini bentuk aljabar yang dianggap memiliki sifat yang sama dengan 2(x y)2x2y oleh siswa:

2 2 2

)

(x y x  y .

e. Kesalahan dalam mengerjakan soal dengan menghilangkan/ menghapuskan variabel, koefisien, atau konstanta

Contoh: ) 6 ( ) 1 ( ) 9 2 ( ) 6 )( 7 3 ( ) 1 ( ) 9 2 )( 7 3 ( 2 2 2 2            x x x x x x x x

Kesalahan dalam menggunakan notasi “/” untuk menunjukkan

(36)

yaitu x

3 2

atau

x

3 2

. Dalam hal ini siswa belum tentu mengerti pecahan

mana yang dimaksud.

3. Kesalahan Konsep atau Prinsip Dasar

Berdasarkan teori Marpaung (dalam Haryani, 2008; 75), kesalahan konsep atau prinsip dasar disebabkan karena subyek kurang menguasai kemampuan melakukan abstraksi sehingga subyek tidak melihat kesamaan pokok dan mengabaikan perbedaan-perbedaan atau sifat-sifat yang mendasar. Subyek gagal mengalami pendewasaan mental sehingga banyak mengalami masalah dalam pemahaman konsep-konsep matematika secara umum.

4. Menurut Hadar, dkk, Dawkins dan Marpaung

Melihat klasifikasi kesalahan yang dikemukakan oleh Hadar, dkk, Dawkins, dan Marpaung peneliti memilih untuk menggabungkan klasifikasi kesalahan tersebut dalam melakukan analisis data penelitian. Adapun klasifikasi kesalahan yang digunakan dalam penelitian adalah sebagai berikut:

a. Kesalahan Data (Ka)

(37)

1) Menambahkan data yang tidak ada hubungannya dengan soal. (Ka.1) 2) Mengabaikan data penting yang sudah ada dan menggantinya dengan

data yang tidak relevan. (Ka.2)

3) Mengartikan sebagian informasi tidak sesuai dengan teks yang sebenarnya. (Ka.3)

4) Menggunakan syarat yang tidak sesuai dengan informasi yang diberikan. (Ka.4)

5) Menggunakan angka pengganti suatu variabel untuk variabel yang lain. (Ka.5)

6) Kesalahan menyalin soal dari lembar soal ke lembar jawab. (Ka.6) b. Kesalahan menginterpretasikan data (Kb)

Kategori ini meliputi kesalahan matematika yang berkaitan dengan ketidaksesuaian dalam menerjemahkan suatu pernyataan matematika yang dideskripsikan dalam suatu bahasa ke bahasa yang lain.

c. Kesalahan menggunakan definisi atau teorema (Kc)

Kesalahan ini merupakansuatu penyimpangan dari prinsip, aturan, teorema atau definisi yang pokok dan khas. Kesalahan-kesalahan ini antara lain:

1) Kesalahan memahami definisi (Kc.1)

Misal : variabel dari bentuk 6x2yz3 adalah x2yz3 2) Kesalahan memahami teorema (Kc.2)

(38)

d. Penyelesaian yang tidak diperiksa kembali (Kd)

Kesalahan ini terjadi jika setiap langkah yang ditempuh oleh peserta tes benar, akan tetapi hasil akhir yang diberikan bukan penyelesaian dari soal tersebut.

e. Kesalahan teknis (Ke)

Kategori kesalahan teknis meliputi kesalahan-kesalahan berikut: 1) Kesalahan-kesalahan perhitungan. (Ke.1)

2) Kesalahan dalam memanipulasi simbol-simbol aljabar dasar (Ke.2) 3) Menghilangkan limit (Ke.3)

4) Menambah limit (Ke.4)

f. Kesalahan dalam pembagian dengan bilangan nol (Kf)

Kesalahan yang sering dilakukan siswa dalam pembagian nol yaitu menghitunng 0

0 2

 atau 2

0 2

 . Pembagian bilangan nol yang benar

yaitu bahwa 0 2

tidak terdefinisi.

g. Kesalahan dalam penggunaan tanda kurung (Kg)

Kesalahan ini disebabkan karena siswa tidak paham pentingnya penggunaan tanda kurung atau siswa menganggap tanda kurung tidak diperlukan dalam langkah-langkah tertentu.

Contoh:

1) Menentukan kuadrat dari 4x

2 2 2 2 9 ) ( ) 3 (

3x  x  x benar

2 2

3 ) 3

(39)

Dalam kasus ini tanda kurung digunakan untuk meyakinkan bahwa yang dikuadratkan adalah 3 bukan hanyax x saja.

2) Menentukan kuadrat dari 2 4 ) 2 )( 2 ( ) 2

( 2     benar

4 2 2 ) 2

( 2    tidak benar

Banyak siswa sebenarnya tahu bahwa secara teknik mereka diharuskan mengkuadratkan 2, tetapi mereka malas dan tidak menuliskan tanda kurung dalam menyelesaikan soal tersebut, dengan alasan mereka akan mengingat tanda kurung saat memeriksa kembali hasil pekerjaan mereka. Namun banyak siswa akhirnya lupa tanda kurung dan menuliskan 4 pada akhir pekerjaan.

3) Mengurangkan 4a5 dari a2 3a5 5 4 5 3 ) 5 4 ( 5 3 2

2 _ _ _ _ _ _ _ _ _

a a a a a a benar a a   2 10 ) 5 4 ( 5 3 2

2 _ _ _ _ _ _ _

a a a

a

a tidak benar

h. Kesalahan dalam mendistribusikan (Kh) Contoh:

1) Mengalikan 4(2x2 10) 40 8 ) 10 2 (

4 x2   x2  benar 10 8 ) 10 2 (

4 x2   x2  tidak benar 2) Mengalikan 3(2x5)2

) 25 20 4 ( 3 ) 5 2 (

(40)

75 60 12 2  

 x x

2 2 ) 15 6 ( ) 5 2 (

3 x  x tidak benar

225 180

36 2 _ _

 x x

i. Kesalahan dalam mengerjakan soal dengan menghilangkan/ menghapuskan variabel, koefisien, atau konstanta (Ki)

Contoh: ) 6 ( ) 1 ( ) 9 2 ( ) 6 )( 7 3 ( ) 1 ( ) 9 2 )( 7 3 ( 2 2 2 2            x x x x x x x x

j. Kesalahan menggunakan logika dalam penarikan kesimpulan (Kj)

Pada umumnya yang termasuk dalam kategori ini adalah kesalahan-kesalahan dalam menartik kesimpulan dari suatu informasi yang diberikan atau dari kesimpulan sebelumnya

k. Kesalahan Konsep (Kk)

(41)

[image:41.595.137.504.229.740.2]

Berikut ini adalah contoh kategori kesalahan dalam mengerjakan soal Limit Fungsi Aljabar.

Tabel 2.1

Contoh kategori jenis kesalahan dalam mengerjakan soal-soal Limit Fungsi Aljabar

No

.

Jenis Kesalahan Contoh Kesalahan

1. Penyalahgunaan Data

a. Menambahkan data yang tidak

ada hubungannya dengan soal.

b. Mengabaikan data penting

yang sudah ada dan

menggantinya dengan data

yang tidak relevan.

c. Menguraikan syarat-syarat

(dalam pembuktian,

perhitungan, penemuan) yang

sebenarnya tidak dikehendaki

soal.

d. Mengartikan sebagian

informasi tidak sesuai dengan

teks yang sebenarnya.

e. Menggunakan syarat yang

tidak sesuai dengan informasi

Soal: tentukan nilai limit berikut.

x

x 2 lim

2



Akan tetapi siswa menuliskan soal

seperti berikut: x x 2 lim 2  Kategori kesalahan:

Mengartikan sebagian informasi

tidak sesuai dengan teks yang

(42)

yang diberikan.

f. Menggunakan angka pengganti

suatu variabel untuk variabel

yang lain.

g. Kesalahan menyalin soal dari

lembar soal ke lembar jawab.

2. Kesalahan menginterpretasikan

data

a. Menerjemahkan pernyataan

dalam bahasa sehari-hari ke

dalam bahasa atau persamaan

matematika dengan arti yang

berbeda.

b. Menuliskan simbol dari suatu

konsep dengan simbol lain

yang artinya berbeda.

c. Kesalahan mengartikan grafik.

2 4 5 4

lim   



 x x

x

Akan tetapi siswa menuliskan soal

seperti berikut:

2 4 5 4

lim   



 x x

x        _     _x x x x x 2 4 5 4 lim Kategori kesalahan:

Menuliskan simbol dari suatu konsep

dengan simbol lain yang artinya

berbeda

3. Kesalahan menggunakan logika

dalam menarik kesimpulan.

a. Mengambil kesimpulan tidak

benar, misalnya memberikan q

sebagai akibat dari p tanpa

dapat menjelaskan urutan

pembuktian yang betul.

2 2 lim

2  

 _x

x

Kategori kesalahan:

Siswa mengambil kesimpulan yang

tidak benar dan tidak dapat

(43)

betul.

4. Kesalahan menggunakan definisi

atau teorema

a. Menerapkan suatu teorema

pada kondisi yang tidak

sesuai.

b. Menerapkan sifat distributif

untuk fungsi atau operasi yang

bukan distributif.

c. Tidak teliti atau tidak tepat

dalam mengutip definisi,

rumus, atau teorema.

Soal: tentukan nilai imit berikut ini

2 2 2 2

2( 2) lim 2

lim   



 x x x

x

Kategori:

Menerapkan sifat distributif untuk

fungsi atau operasi yang bukan

distributif.

5. Penyelesaian tidak diperiksa

kembali

3 . 2 lim ) 3 2 ( lim 1 2

1      

 x x x x x

x 0 3 1 . 2

1  



6. Kesalahan yang dilakukan siswa

dalam penggunaan tanda kurung

Soal: tentukan nilai limit berikut

5 2 2 3

2(2 ) lim2

lim x x

x

x  

Siswa salah mengubah (2x3)2

menjadi 2x5

7. Kesalahan dalam menggunakan

sifat komutatif.

4 1 lim 4 lim 0 2

0    

 x x x

x

Siswa salah dalam mengubah

4

2 _

(44)

8. Kesalahan dengan menghilangkan

/ menghapus variabel

) 6 )( 7 3 ( ) 1 ( ) 9 2 )( 7 3 ( lim 2 2

1  

   

 _x _x

x x x x ) 6 ( ) 1 )( 9 2 ( lim 2 2 1      _x x x x

Siswa salah dalam menghapus

) 7 3 ( x

9. Kesalahan dalam menghapuskan

variabel dan koefisien saat

menyederhanakan pecahan bentuk

aljabar.

Contoh kesalahan sama dengan

contoh nomor 8

10. Kesalahan dalam pembagian

dengan bilangan nol

2 0 2 2 lim

0  

 _x

x

11. Kesalahan dalam penggunaan

tanda kurung

contoh nomor 6

12. Kesalahan dalam

mendistribusikan

9 ) 3 )( 3 ( ) 3 (

lim 2 2

3      

  x

x

13. Kesalahan dalam mengerjakan

soal dengan menghilangkan/

menghapus variabel, koefisien,

atau konstanta

(45)

C. Faktor Penyebab Kesalahan

Faktor penyebab kesalahan secara umum dapat diklasifikasikan menjadi dua bagian, yaitu faktor kognitif dan non kognitif.

1. Faktor Kognitif

Faktor kognitif adalah segala sesuatu yang berhubungan dengan kemampuan intelektual siswa dalam memproses atau mencerna matematika ke dalam pikiran, Suwarsono (1982).

2. Faktor Non Kognitif

Menurut Burton (dalam M. Entang, 1984:13-14), kesulitan belajar yang membuatnya melakukan kesalahan di kelompokkan menjadi dua kategori yaitu faktor yang terdapat dalam diri siswa dan faktor yang terdapat di luar siswa.

a. Faktor yang terdapat dalam diri siswa

1) Kelemahan secara fisik (suatu pusat susunan syaraf tidak berkembang secara sempurna luka atau cacat, atau sakit) sehingga sering membawa gangguan emosional yang menghambat usaha-usaha belajar secara optimal.

(46)

terarah, kurang semangat (kurang gizi, kelelahan/ overwork), kurang menguasai keterampilan dan kebiasaan fundamental dalam belajar. 3) Kelemahan-kelemahan emosional, misalnya memiliki rasa tidak aman

(insecurity), penyesuaian yang salah (adjustment) terhadap orang-orang, situasi, dan tuntutan-tuntutan tugas dan lingkungan, tercekam rasa pobia, dan tidak matangan (immaturity).

4) Kelemahan yang disebabkan oleh karena kebiasaan dan sikap-sikap yang salah, antara lain: banyak melakukan aktivitas yang bertentangan dan tidak menunjang pekerjaan sekolah (menolak/ malas belajar, sering bolos atau tidak mengikuti pelajaran); gagal untuk berusaha memusatkan perhatian; kurang kooperatif dan menghindari tanggung jawab; dan gugup.

5) Tidak memiliki keterampilan-keterampilan dan pengetahuan dasar yang diperlukan seperti ketidak mampuan membaca, berhitung, kurang menguasai pengetahuan dasar untuk susuatu bidang studi yang sedang diikiutinya secara sekuensial (meningkat dan beruntun), kurang menguasai bahasa asing, serta memiliki kebiasaan belajar dan cara bekerja yang salah.

b. Faktor yang terletak di luar diri siswa

(47)

pengelolaan kegiatan dan pengalaman belajar mengajar, dan sebagainya); terlalu berat beban belajar (siswa) dan atau mengajar (guru), terlampau besar populasi siswa dalam kelas, terlalu banyak menuntut siswa dalam kegiatan di luar; terlalu sering pindah sekolah, atau program, tinggal kelas; kelemahan dari system belajar mengajar pada tingkat-tingkat pendidikan (dasar asal) sebelumnya; kelemahan yang terdapat dalam kondisi rumah tangga (pendidikan, status sosial ekonomi, keutuhan keluarga, ketentraman dan kemanan sosial psikologis; terlalu banyak kegiatan di luar jam sekolah atau terlalu banyak terlibat kegiatan extra-curricular; dan kekurangan gizi.

D. Limit Fungsi Aljabar

Istilah limit dalam matematika hampir sama artinya dengan istilah mendekati. Akibatnya, nilai limit sering dikatakan sebagai nilai pendekatan. Berikut ini adalah penjelasan limit fungsi berdasarkan Purcell (1987):

1. Definisi Limit a. Secara Intuisi

Pandang fungsi yang ditentukan oleh rumus

1 1 )

(

3

  

x x x f

Fungsi f tidak terdefinisikan di x1 karena di x1, f(x)

berbentuk 0 0

. Tetapi masih dapat diselidiki apa yang terjadi dengan

) (x

(48)

Untuk x1









1 1 1 1 1 ) ( 2 3         x x x x x x x f 1

2 _ _

x x

Untuk xmendekati 1, maka nilai f(x) mendekati 3, ditulis









1 1 1 lim 1 1 lim 2 1 3 1          _x x x x x x x x 3 1 lim 2 1    

 x x

x

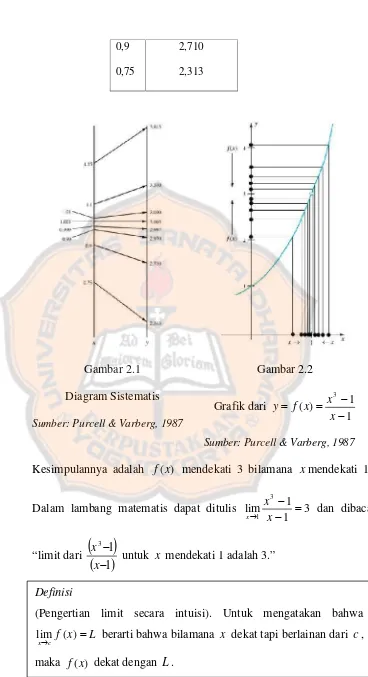
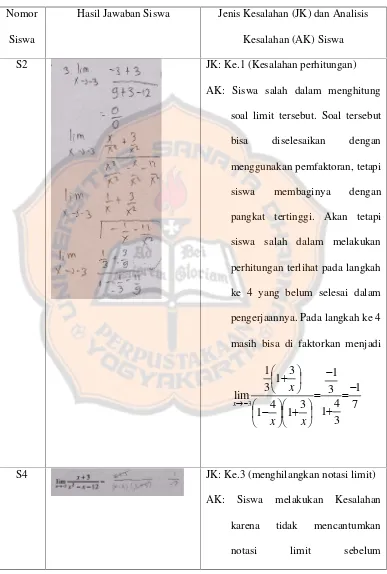
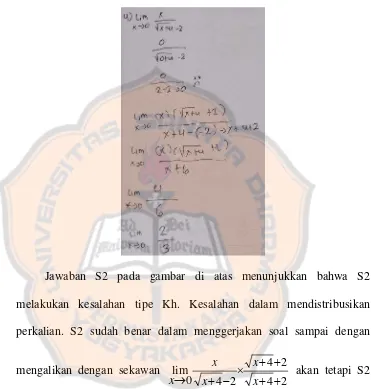
[image:48.595.140.509.248.740.2]

Dapat dilihat dengan menunjukkan nilai-nilai ini dalam sebuah skematis dan mensketsakan grafik y f(x)

(49)

[image:49.595.138.506.74.751.2]

0,9 0,75 2,710 2,313 Gambar 2.1 Diagram Sistematis

Sumber: Purcell & Varberg, 1987

Gambar 2.2 Grafik dari 1 1 ) ( 3     x x x f y

Kesimpulannya adalah f(x) mendekati 3 bilamana xmendekati 1.

Dalam lambang matematis dapat ditulis 3 1

1 lim

3

1  



 _x

x

x dan dibaca

“limit dari

 

1 1 3   x x

untuk x mendekati 1 adalah 3.”

Definisi

(Pengertian limit secara intuisi). Untuk mengatakan bahwa

L x f

c

x ( )

(50)

b. Membuat Definisi Persis (Matematis)

Kita ganti bilangan-bilangan kecil positif dengan memakai huruf Yunani yaitu ε (epsilon) dan δ(delta).

Mengatakan bahwa f(x) berbeda dari L lebih kecil dari ε sama saja dengan mengatakan

ε

 L x f( )

ε ε   

 f x L

L ( )

[image:50.595.139.511.252.557.2]

Yang berarti f(x) terletak dalam selang terbuka (Lε,Lε) seperti gambar di bawah ini

Untuk x cukup tetapi berlainan dengan c sama saja dengan mengatakan bahwa untuk suatu δ, x terletak dalam selang terbuka

) ,

(cδ cδ dengan c tidak diikutkan. δ

 

 x c

0

Perhatikan bahwa xc δ akan memberikan selang cδ xcδ , sedangkan 0 xc mensyaratkan bahwa xcdikecualikan. Selang dengan pengecualian yang diuraikan tersebut dapat dilihat pada gambar di bawah ini

Gambar 2.3

 

x Lε f

(51)

2. Limit-limit Sepihak

Bilamana suatu fungsi memiliki lompatan, maka limit tidak ada pada setiap titik lompatan. Untuk fungsi-fungsi yang demikian, adalah wajar untuk memperkenalkan limit-limit sepihak. Andaikan lambang xc

berarti bahwa x mendekati c dari kanan, dan andaikan xc berarti bahwa x mendekati c dari kiri.

Gambar 2.4 δ

 

x c

0

Definisi

(Pengertian persis tentang limit). Mengatakan bahwa

L x f

c

x ( )

lim berarti bahwa untuk setiap ε 0 yang diberikan (betapapun kecilnya), terdapat δ 0yang berpadanan sedemikian sehingga f(x)L ε asalkan bahwa 0 xc δ ; yakni

ε

δ  

 

x c f(x) L

0

Definisi

(Limit kiri dan limit kanan). Untuk mengatakan bahwa f x L

c

x ( ) lim

berarti bahwa bilamana x dekat tetapi pada sebelah kanan c, maka )

(x

f adalah dekat ke L. Serupa, untuk mengatakan bahwa

L x f

c

x ( )

(52)

Akibat dariteorema A a. Jika lim f(x)

c

x  tidak ada atau xlimc f(x)tidak ada, maka limxc f(x) tidak ada.

b. Jika lim f(x) c

x  ada atau xlimc f(x)ada, tetapi xlimc f(x)xlimc f(x), maka )

( lim f x

c

x tidak ada.

Kita ganti bilangan-bilangan kecil positif dengan memakai huruf Yunani yaitu ε (epsilon) dan δ (delta).

3. Teorema Limit Teorema A

L x f

c

x ( )

lim jika dan hanya jika f x L

c x





 ( )

lim dan f x L

c x    ( ) lim Definisi

Mengatakan f x L

c

x ( )

lim berarti bahwa untuk tiap ε 0, terdapat 0



δ yang berpadanan sedemikian sehingga ε

δ   

 

 x c f(x) L

0

Teorema A

(Teorema limit utama). Andaikan n bilangan bulat positif, k konstanta,

f dan g adalah fungsi-fungsi yang memiliki limit di c, maka

a. k k

c x 

lim

b. limf(x) f(c) c

x 

c. limk.f(x) klim f(x) c x c

x  

d.



f x g x



f x g

 

x

c x c

x c

x ( ) ( ) lim ( )lim

(53)

4. Limit Fungsi Aljabar

Cara penyelesaian Limit Fungsi Aljabar a. Metode substitusi

Jika fungsi f(x) mempunyai nilai tertentu untuk xc, maka

) ( ) (

lim f x f c

c

x  , asalkan ₀

0 ) (c  . Teorema B

(Teorema Substitusi). Jika f suatu fungsi polinom atau rasional, maka )

( ) (

lim f x f c

c

x 

Asalkan dalam kasus fungsi rasional nilai penyebut di c tidak nol.

Teorema C

(Teorema Apit). Andaikan f,g dan h adalah fungsi-fungsi yang

memenuhi f(x)g(x)h(x) untuk semua x dekat c, kecuali mungkin

di c. Jika f x h x g x L

c x c

x c

x ( )lim ( )lim ( )

lim

e.



f x g x



f x g

 

x

c x c

x c

x ( ) ( ) lim ( )lim lim

f.



f x g x



f x g

 

x

c x c

x c

x ( ) ( ) lim ( )lim lim g. ) ( lim ) ( lim ) ( ) ( lim x g x f x g x f c x c x c x  

  , dengan syarat limxcg(x)0 h.



 





 



n

c x n c

x f x  lim f x lim i. n c x n c

x f(x) lim f(x) lim



(54)

b. Metode Pemfaktoran Jika ) ( ) ( ) ( x h x g x

f  dan dengan substitusi langsung xc diperoleh

0 0 ) ( ) ( ) (   x h x g c

f , bentuk g(x) dan h(x) difaktorkan lebih dahulu

sehingga memiliki faktor yang sama yang dapat disederhanakan

sedemikian sehingga

0 0 ) (c 

f . Selanjutnya perhitungan limit dapat

dilakukan dengan cara substitusi.

Secara umum, cara menyelesaikan limit fungsi f(x) bentuk tak tentu dengan memfaktorkan adalah sebagai berikut

) ( ) ( lim ) ( ) ( ) ( ) ( lim ) ( ) ( lim ) ( lim 2 2 2

2 _S _x

x H x S c x x H c x x h x g x f x x x

x     

 



c. Metode Mengalikan dengan Akar Sekawan

Beberapa Fungsi yang akan ditentukan Limitnya merupakan sebuah Fungsi irasional sehingga sulit untuk difaktorkan. Untuk bentuk seperti ini, kita harus menghilangkan tanda akar dengan cara mengalikannya dengan akar sekawan. Setelah itu baru difaktorkan. Cara merasionalkan penyebut suatu pecahan telah kita pelajari di kelas 1, antara lain:

1) Pecahan berbentuk

(55)

2) Pecahan berbentuk

b a

c

 dikalikan dengan a b b a   sehingga diperoleh b a b a c b a b a b a c b a c          ) (

Materi Limit Fungsi Aljabar di SMA a. Limit Fungsi f(x) untuk xc

Langkah-langkah menentukan f x c R

a

x ( ), 

lim sebagai berikut

1) Tentukan nilai lim f(x) dengan mensubstitusikan nilai xc pada fungsi f(x). Dengan demikian kita memperoleh lim f(x) f(c).

c

x 

Jika 0 0 

c , maka nilai lim f(x) c

x telah diperoleh. Jika

0 0 ) (c 

f (bentuk tak tentu), maka teruskan ke langkah 2.

2) Tentukan lim ( )

2 f x

x dengan cara memfaktorkan.

b. Limit fungsi f(x) untuk x

1) Bentuk ) ( ) ( lim x h x g x

Jika kita lakukan substitusi langsung pada limit tersebut maka akan diperoleh bentuk

 

. Penyelesaian di atas dilakukan dengan cara

(56)

2) Bentuk lim



f(x) g(x)



x 

Bentuk limit tersebut dapat diselesaikan dengan cara mengalikan

dengan bentuk sekawannya, yaitu

) ( ) ( ) ( ) ( x g x f x g x f  

, kemudian

membaginya dengan x pangkat tertinggi dari pembilang dan penyebutnya

E. Pembelajaran Remidial

Menurut M. Entang (1984:11) pengajaran remedial merupakan upaya pendidik dalam membantu siswa yang mendapatkan kesulitan dalam belajar dengan jalan mengulang atau mencari alternatif kegiatan lain sehingga siswa yang bersangkutan dapat mengembangkan dirinya seoptimal mungkin dan dapat memenuhi kriteria tingkat keberhasilan minimal yang diharapkan.

Setianingrum (2010; 20-22) menjelaskan bahwa dalam melaksanakan kegiatan pengajaran remedial, seorang guru dituntut untuk:

1. Menelaah kembali siswa yang akan diberi bantuan

(57)

2. Alternatif tindakan

Jika telah mendapatakan gambaran yang lengkap tentang siswa yang memerlukan bantuan, barulah direncanakan alternatif tindakan sesuai dengan karakteristik kesulitan yang dihadapinya. Alternatif tindakan ini bisa berupa:

a. Mengulangi bahan yang telah diberikan (mengerjakan ulang).

b. Mencoba alternatif kegiatan lain yang setara dengan kegiatan belajar-mengajar yang sudah ditempuhnya dan memiliki tujuan yang sama baik yang sifatnya instruksional maupun efek pengiring misalnya dengan metode tutor sebaya.

(58)

d. Evaluasi pengajaran remedial

Pada akhir kegiatan pengajaran remedial hendaknya dilakukan evaluasi kembali (reevaluasi) sampai sejauh mana pengajaran remedial tersebut dapat meningkatkan prestasi mereka yaitu dengan melakukan tes remedial.

(59)

F. Metode Pembelajaran Remidial

Metode-metode dalam pengajaran remedial menurut Thulus Hidayat (dalam Setianingrum, 2014; 22-25) adalah sebagai berikut:

1. Metode pemberian tugas

Siswa yang mengalami kesulitan belajar dibantu dengan memberikan tugas tertentu untuk dilaksanakan. Jenis dan sifat tugas sesuai dengan latar belakang kesulitan belajarnya. Pemberian tugas ini dapat secara individual maupun kelompok, sesuai dengan kesulitannya. Dengan metode ini siswa diharapkan:

a. Mampu memahami diri

b. Lebih memperluas bahan yang dipelajari c. Dapat memperbaiki cara belajar yang lama 2. Metode diskusi

Digunakan untuk menciptakan interaksi individu dengan kelompok untuk memperbaiki kesulitan. Dengan diskusi diharapkan:

a. Siswa dapat mengenal diri dan kesulitannya serta menemukan pemecahannya

b. Menumbuhkan kepercayaan diri

c. Mengembangkan kerjasama antar pribadi d. Menumbuhkan rasa tanggung jawab 3. Metode tanya jawab

(60)

a. Memahami dirinya sendiri b. Menumbuhkan rasa harga diri c. Meningkatkan motivasi belajar

d. Menciptakan hubungan yang erat antara guru dan siswa-siswa 4. Metode kerja kelompok

Anggota kelompok beriknteraksi satu dengan yang lain dengan maksud terjadinya perbaikan pada siswa-siswa yang mengalami kesulitan belajar. Hal ini disebabkan karena:

a. Adanya pengaruh anggota kelompok yang pandai dan berpengalaman b. Kehidupan kelompok dapat meningkatkan minat belajar

c. Memupuk rasa tanggung jawab 5. Metode tutor

Tutor adalah teman sebaya yang ditunjuk untuk membantu teman-temannya yang mengalami kesulitan belajar dengan memberi petunjuk oleh guru pembimbingnya. Tutor ini ditunjuk atas dasar prestasi mereka dan hubungan sosial serta mendapat sambutan yang sesuai dengan teman-temannya. Kebaikan metode tutor:

a. Terciptanya hubunngan yang lebih akrab antara tutor dengan yang diberi pelajaran

b. Bagi tutor tugas tutorisasinya berarti menambah kekayaan dan menambah motivasi belajar

(61)

6. Pengajaran individual

Metode ini menunjukkan adanya interaksi antara guru dengan siswa secara individual dalam proses belajar mengajar. Dalam metode pembelajaran individual pendekatannya bersifat individual sesuai dengan kesulitan yang dihadapi siswa. Adapun materi yang diberikan mungkin mengulangi bahan lama, mungkin materi baru, dan mungkin pula bahan pengayaan yang telah dimiliki siswa. Hal ini tergantung kepada kesulitan yang dialami. Kesulitan yang dialami individu ini bersifat terpantik yaitu bersifat menyembuhkan atau memperbaiki cara belajar siswa. Untuk melakukan pengajaran individual guru dituntut memiliki kemampuan membimbing dan bersikap sabar, ulet, bertanggung jawab, menerima, dan memahami. Guru harus menciptakan suasana yang kondusif dengan siswa agar proses pembelajaran berlangsung dengan baik.

G. Kerangka Berfikir

(62)

Langkah-langkah yang dilakukan dalam penelitian ini diawali dengan observasi kegiatan belajar mengajar dalam materi Limit Fungsi Aljabar. Kegiatan observasi ini dilakukan agar mengetahui kondisi belajar siswa sebagai gambaran awal penelitian dan sebagai salah satu sumber penyebab siswa melakukan kesalahan. Setelah semua materi disampaikan oleh guru, barulah peneliti memberikan tes diagnostik kepada siswa. Tes diagnostik diberikan untuk memperoleh data kesalahan-kesalahan apa saja yang dilakukan siswa dalam menyeleseaikan soal Limit Fungsi Aljabar kemudian dikelompokkan menurut jenis kesalahannya.

(63)

43 BAB III

METODE PENELITIAN

A. Jenis Penelitian

Jenis penelitian yang diambil oleh peneliti adalah penelitian deskriptif kualitatif. Penelitian kualitatif adalah penelitian yang bermaksud untuk memahami fenomena tentang apa yang dialami oleh subyek penelitian misalnya perilaku, persepsi, motivasi, tindakan, dll, serta holistik, dan dengan cara deskripsi dalam bentuk kata-kata dan bahasa, pada suatu konteks khusus yang alamiah dan dengan memanfaatkan berbagai metode ilmiah (Moleong, 2008: 6).

Penelitian kualitatif bertujuan untuk mendapatkan pemahaman yang sifatnya umum terhadap kenyataan sosial dari perspektif partisipan. Pemahaman tersebut tidak ditentukan terlebih dahulu, tetapi didapat setelah melakukan analisis terhadap kenyataan sosial yang menjadi fokus penelitian.

B. Tempat dan Waktu Penelitian 1. Tempat pengambilan data

Pengambilan data dilakukan di SMA Seminari Mertoyudan yang terletak di Jl. Mayjend Bambang Soegeng No. 15 Mertoyudan, Magelang. 2. Waktu penelitian

(64)

C. Subyek dan Objek Penelitian

Subyek dalam penelitian ini adalah siswa kelas XI IPS SMA Seminari Mertoyudan pada semester genap tahun ajaran 2016/2017 yang berjumlah 31 siswa. Dari 31 siswa tersebut akan dipilih beberapa siswa yang memerlukan bantuan karena mengalami kesulitan belajar yang ditandai dengan melakukan kesalahan dalam menyelesaiakan Limit Fungsi Aljabar dan hasil belajar siswa yang tidak mencapai KKM untuk diberikan upaya remidiasi. Objek yang diteliti adalah kesalahan-kesalahan yang dilakukan siswa dalam menyelesaikan soal-soal pada materi Limit Fungsi Aljabar.

Dalam penelitian kualitatif, suatu subyek penelitian dipilih karena secara tipikal dapat mewakili fenomena yang diteliti. Maka dari itu, teknik pemilihan subyek yang digunakan oleh peneliti adalah purpose sampling. Purpose samplingadalah teknik pengambilan sampel sumber data dengan pertimbangan tertentu (Sugiyono, 2008). Pertimbangan dalam pemilihan subyek yang dimaksud adalah subyek yang dipilih dapat memberikan informasi dengan baik berkaitan dengan kesalahan yang dilakukan saat menyelesaikan Limit Fungsi Aljabar serta subyek bersedia untuk diwawancarai.

D. Variabel Penelitian

Variabel-variabel dalam penelitian ini, yaitu:

(65)

2. Faktor-faktor yang mempengaruhi siswa dalam melakukan kesalahan dalam menyelesaikan soal Limit Fungsi Aljabar.

3. Kesalahan yang dilakukan siswa dalam remedial.

E. Metode Pengumpulan Data

Dalam penelitian ini, peneliti menggunakan tiga metode pengumpulan data, yaitu:

1. Observasi

Observasi merupakan metode atau cara-cara menganalisis dan mengadakan pencatatan secara sistematis mengenai tingkah laku dengan melihat atau mengamati individu atau kelompok secara langsung (Ngalim Purwanto dalam Basrowi dan Suwandi, 2008: 93-94). Metode ini digunakan untuk melihat dan mengamati secara langsung keadaan di kelas agar peneliti memperoleh gambaran yang lebih luas tentang permasalahan yang diteliti yaitu kesalahan dalam menyelesaikan soal Limit Fungsi Aljabar.

2. Tes tertulis

Tes tertulis terdiri dari 2 tes, yaitu tes diagnostik dan tes remedial. a. Tes Diagnostik

(66)

b. Tes Remidial

Tes remedial adalah tes yang digunakan untuk mengevaluasi hasil pembelajaran remedial. Tes remedial diberikan setelah siswa menerima pembelajaran remedial. Tes remedial bertujuan untuk membantu siswa memperbaiki kesalahannya. Tes remedial diberikan pada siswa yang banyak melakukan kesalahan dan nilainya belum mencapai KKM. Tes remedial akan dilakukan di luar jam pelajaran.

3. Wawancara

Wawancara adalah percakapan dengan maksud tertentu oleh dua pihak, yaitu pewawancara (interviewer) sebagai pengaju/ pemberi pertanyaan dan yang diwawancarai (interviewee) sebagai pemberi jawaban atas pertanyaan itu. Wawancara ini digunakan untuk mengetahui jenis kesalahan yang dilakukan siswa saat menyelesaikan soal yang diberikan yaitu tentang Limit Fungsi Aljabar serta faktor penyebab kesalahan siswa dalam menyelesaiakan soal Limit Fungsi Aljabar.

F. Instrumen Pengumpulan Data 1. Tes Diagnostik

(67)

Aljabar. Setelah tes diagnostik diberikan, peneliti mengelompokkan kesalahan-kesalahan siswa dalam mengerjakan soal Limit Fungsi Aljabar berdasarkan kategori yang telah disusun oleh peneliti.

Tabel 3.1

Indikator pencapaian hasil belajar

Kompetensi Dasar Indikator Soal Soal

3.1 Menghitung limit fungsi

aljabar sederhana di

suatu titik

3.2 Menggunakan sifat limit

fungsi untuk

menghitung bentuk tak

tentu fungsi aljabar

Menghitung Limit Fungsi

Aljabar di suatu titik

1, 2, 3

Menghitung Limit Fungsi

Aljabar dengan

menggunakan sifat-sifat

limit

4, 5, 6, 7

2. Wawancara

(68)

Tabel 3.2 Pedoman Wawancara

No. Pertanyaan Jawaban

1 Bagaimana proses yang kamu lakukan dalam

menyelesaikan soal ini?

2 Mengapa kamu menjawab demikian?

3 Apa penyebab kesulitan dalam mengerjakan

soal tes?

4 Dimanakah letak kesulitan soal tersebut?

3. Tes remedial

(69)

G. Teknik Analisis Data

Menurut Miles dan Huberman (1992) membagi analisis data dalam penelitian kualitatif ke dalam tiga tahap, yaitu:

1. Reduksi data

Reduksi data merujuk pada proses pemilihan, pemfokusan, abstraksi, penyederhanaan, dan pentransformasian “data mentah” yang terjadi dalam

catatan-catatan lapangan tertulis.mereduksi data berarti merangkum, memilih hal-hal yang relevan, memfokuskan pada hal-hal yang penting. Reduksi data merupakan suatu bentuk analisis yang mengelompokkan dan membuang data yang tidak perlu, dan mengorganisasikan data yang sejenis. Kegiatan ini mengarah pada menyeleksi, memfokuskan, menyederhanakan, dan mengabstraksikan serta mentransformasikan data mentah yang didapat di lapangan dengan alat bantu rekam. Tahap reduksi data dalam penelitian ini meliputi:

a. Mengoreksi hasil pekerjaan siswa, kemudian dilakukan dengan dugaan awal kesalahan yang dilakuka