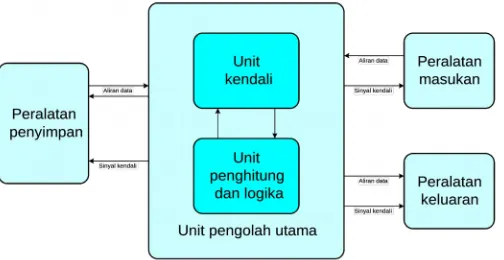
Gambar 18.1 Unsur-unsur dasar komputer digital
Komponen
Sistem Digital
18
Untuk mengolah informasi diskrit dapat digunakan komponen-komponen elektronik yang dapat menanggapi sinyal biner. Dalam bab-bab sebelum ini telah diuraikan bagaimana diode dan transistor dapat digunakan sebagai saklar dalam gerbang logika. Komputer digital terdiri atas gerbang-gerbang logika dan unsur-unsur penyimpan yang diatur sedemikian rupa sehingga mampu mengolah data dengan kecepatan tinggi.
Komputer digital memegang peran penting dalam masyarakat modern. Sangat besar sumbangan yang diberikan oleh komputer digital itu dalam pengembang ilmu, bisnis, dan industri. Ilmuwan dan insinyur menggunakan matematika sebagai bahasa untuk pemodelan hukum-hukum dan sifat-sifat fisika. Algoritma penyelesaian masalah sering sudah lama diketahui, tetapi waktu yang diperlukan untuk menyelesaikan masalah itu secara manual umumnya sangat sulit dilakukan dan memakan waktu yang sangat lama. Komputer digital dapat menyelesaikan persoalan itu dalam waktu yang sangat singkat dan secara lebih akurat. Saat ini komputer telah merambah ke mana-mana dalam kehidupan manusia modern, mulai dari bisnis besar dan kecil sampai ke dunia pendidikan dan hiburan di rumah. Robot yang dikendalikan komputer bukan hal yang baru di dunia industri, mesin ketik telah digantikan oleh pengolah kata (word processor) dengan komputer. Anak-anak di bawah umur lima tahun sudah mampu menggunakan komputer untuk bermain (game).
Komputer digital merupakan salah satu contoh yang jelas untuk sistem digital. Contoh lainnya meliputi kalkulator, alat ukur digital, kamera digital, sentral telepon otomatis, dan lain-lain. Karakteristik sistem digital adalah manipulasi unsur-unsur informasi diskrit.
and logic unit) dan unit kendali, merupakan otak komputer itu. Bagian tersebut menyelia aliran informasi dan urutan tata kerja serta melakukan perhitungan dan operasi logika. Unit penyimpan (memory unit) digunakan untuk menyimpan kode program dan data. Unit penyimpan menyimpan data untuk sementara setelah menerima dari masukan sebelum diproses dan sebelum diberikan ke peralatan keluaran.
Dalam bab sebelum ini dan dua bagian pertama dalam bab ini semua rangkaian yang telah dibahas sepenuhnya adalah rangkaian logika kombinasi, karena keluarannya sepenuhnya tergantung kepada masukan pada saat keluaran itu diamati. Dalam praktik kadang-kadang diinginkan suatu keluaran rangkaian yang tergantung juga kepada nilai-nilai masukan sebelumnya di samping nilai-nilai yang ada pada saat itu; rangkaian logika yang memenuhi persyaratan itu disebut
rangkaian logika urutan (sequential logic circuit).
Keluaran gerbang logika dasar ditentukan oleh masukan saat itu, dan sebagai tanggapan terhadap berbagai macam masukan itu rangkaian logika kombinasi tersebut ‘mengambil keputusan’. Untuk penggunaan sederhana hal itu sudah mencukupi, tetapi banyak penggunaan yang memperhitungkan keadaan sebelumnya dalam proses pengambilan keputusan. Dengan alasan itu komponen pengambil keputusan tersebut memerlukan komponen penyimpan untuk menyimpan perintah dan hasilnya. Keluaran rangkaian logika urutan semacam itu dipengaruhi oleh masukan sebelumnya di samping masukan saat itu.
Rangkaian penyimpan harus mempunyai dua keadaan yang berbeda dan harus tetap pada keadaan itu sampai mendapat perintah untuk berubah. Rangkaian itu harus mampu berubah dengan cepat dari satu keadaan ke keadaan yang lain. Dalam sistem digital dan komputer, rangkaian urutan lebih banyak dipakai ketimbang rangkaian kombinasi. Hal itu adalah karena data yang diterima oleh sistem itu datangnya berurutan dari suatu bagian ke bagian yang lain; di samping itu juga rangkaian kombinasi memerlukan perangkat keras lebih banyak sehingga lebih mahal harganya. Rangkaian urutan lebih sederhana, oleh karena itu lebih murah harganya. Tetapi rangkaian urutan itu lebih sukar untuk dirancang dibandingkan dengan rancangan untuk rangkaian kombinasi.
Dengan selesainya bab ini pembaca diharapkan dapat:
mengenal cara merancang rangkaian kombinasi khususnya rangkaian penjumlah dan pembanding;
mengenal beberapa komponen komputer digital;
mengenal berbagai macam rangkaian flip-flop;
penerapan flip-flop dalam rangkaian penghitung dan register.
18.1 Komponen Kombinasi
Dengan menguasai latar belakang yang telah diberikan di bab sebelum ini, perencanaan suatu rangkaian logika kombinasi akan dengan mudah dapat dilakukan. Langkah-langkah perancangan itu adalah sebagai berikut:
1 Tentukan banyaknya keluaran dan masukan dari suatu rangkaian yang diinginkan dan tetapkan lambang-lambang ke masing-masing rangkaian itu.
masukan dan keluarannya.
3 Turunkan pernyataan Boole yang paling sederhana untuk masing-masing fungsi keluaran.
4 Gambar rangkaian logikanya.
Prosedur itu akan diterapkan di sini dengan merancang beberapa rangkaian kombinasi yang umum dijumpai dalam sistem digital.
Sebagai contoh, rangkaian logika yang disebut penjumlah (adder) digunakan dalam sistem komputer digital untuk mendapatkan jumlah bilangan biner. Aturan aritmatika untuk penjumlahan bilangan biner bulat positif dapat dituliskan sebagai berikut:
0 ditambah 0 sama dengan 0 0 ditambah 1 sama dengan 1 1 ditambah 0 sama dengan 1
1 ditambah 1 sama dengan 0 dengan bawaan 1
Tiga operasi yang pertama menghasilkan jumlah yang besarnya satu angka, tetapi bila bit (binary digit – angka biner) penambah dan yang ditambahkan sama dengan 1, jumlah biner itu terdiri dari dua angka. Bit dengan derajat yang lebih tinggi pada hasil penjumlahan itu disebut bawaan. Bila bilangan penjumlah dan yang dijumlahkan terdiri dari beberapa angka, bawaan yang diperoleh dari hasil penjumlah suatu pasangan angka ditambahkan ke pasangan angka berikutnya dengan orde yang lebih tinggi.
Rangkaian logika kombinasi yang melakukan operasi penjumlahan dua bit disebut
setengah-penjumlah (half-adder). Rangkaian yang melakukan penjumlahan tiga bit (dua bit dan bawaan sebelumnya) adalah penjumlah-penuh (full adder). Nama penjumlah itu berdasarkan kenyataan bahwa dua buah setengah-penjumlah dapat digunakan untuk mengimplementasikan setengah-penjumlah-penuh
Operasi rangkaian logika setengah-penjumlah dapat diuraikan menurut definisi berikut:
Jika penambah dan yang ditambah keduanya sama dengan nol, jumlahnya adalah sama dengan nol. Jika penambah sama dengan nol dan yang ditambah sama dengan satu atau jika yang ditambah sama dengan nol dan penambahnya sama dengan satu, maka jumlahnya sama dengan satu. Jika penambah dan yang ditambah keduanya sama dengan satu jumlahnya sama dengan nol dan bawaannya sama dengan satu.
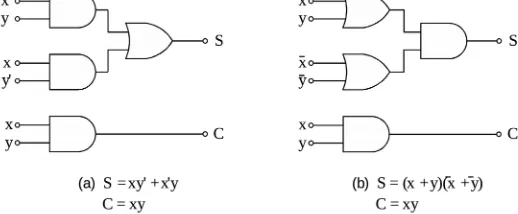
Untuk memperjelas definisi di atas diberikan lambang-lambang x dan y untuk penambah dan yang ditambahkan, S (sum – jumlah) untuk jumlah serta C (carry – bawaan) untuk bawaannya. Rangkaian itu memerlukan dua masukan, x dan y, dan dua keluaran, S dan C. Setelah banyaknya dan nama variabel masukan dan keluarannya itu ditetapkan, disiapkan daftar kebenaran yang memberikan fungsi setengah-penjumlah itu secara pasti. Daftar kebenaran itu diberikan pada Daftar 18.1.
Daftar 18.1 Daftar kebenaran setengah-penjumlah
x y S C
Gambar 18.2 Implementasi rangkaian setengah-penjumlah
0 1 1 0
1 0 1 0
1 1 0 1
Keluaran S mewakili bit yang paling kurang berarti (least significant bit – LSB) pada hasil penjumlahan itu. Keluaran bawaan itu adalah 0 kecuali jika kedua masukannya sama dengan 1.
Fungsi Boole sederhana untuk kedua keluaran itu dapat langsung diperoleh dari daftar kebenaran tersebut. Pernyataan-pernyataan Boole itu adalah
S = x'y + xy' (18.1)
C = xy (18.2)
Diagram logika untuk implementasi setengah-penjumlah itu ditunjukkan pada Gambar 18.2(a), yang merupakan jumlah hasil kali. Gambar 18.2(b) menunjukkan implementasi dalam bentuk hasil kali jumlah
) )( (x y x y
S (18.3)
C = xy (18.4)
Setengah-penjumlah tersebut terbatas kemampuannya, yaitu hanya dapat menjumlahkan dua bit tunggal. Meskipun dapat menghasilkan bawaan untuk pasangan penjumlahan berikutnya, rangkaian tersebut tidak dapat menerima bawaan dari pasangan bit dengan kedudukan yang lebih rendah.
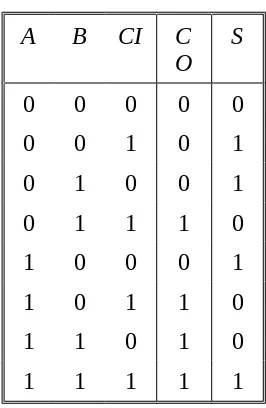
Penjumlah-penuh adalah rangkaian kombinasi yang membentuk jumlah tiga bit masukan. Rangkaian itu terdiri dari tiga masukan dengan dua keluaran. Dua variabel masukan, yang dinamakan A dan B, mewakili dua bit yang dijumlahkan dan masukan ketiga, CI, mewakili bawaan dari kedudukan dengan orde di bawahnya. Diperlukan dua keluaran karena jumlah hitung tiga bit mempunyai setara desimal yang berkisar dari nol sampai dengan tiga, dan dua atau tiga dalam bilangan biner memerlukan dua angka. Kedua keluaran itu adalah S untuk jumlahnya dan CO untuk bawaannya, seperti halnya dengan pada
setengah-penjumlah. Daftar kebenaran untuk rangkaian penjumlah-penuh itu diberikan pada Daftar 18.2.
Gambar 18.3 Rangkaian penjumlah-penuh
A B CI C
O S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Delapan baris di bawah variabel-variabel masukan itu menunjukkan semua kemungkinan kombinasi 1 dan 0 yang dapat dimiliki oleh ketiga variabel masukan tersebut. Bit 1 dan 0 untuk variabel keluaran tersebut ditentukan dari jumlah hitung bit-bit masukannya. Keluaran S sama dengan 1 bila hanya satu masukan sama dengan 1 atau bila ketiga masukannya sama dengan 1. Keluaran CO
mempunyai bawaan 1 jika dua atau tiga masukannya sama dengan 1.
Hubungan logika antara masukan dan keluaran pada rangkaian penjumlah-penuh itu dapat dinyatakan dalam dua fungsi Boole; satu untuk setiap variabel keluarannya dan didapatkan pernyataan Boole berikut:
S = A'B'CI + A'BCI' + AB'CI' + ABCI (18.5)
CO = AB + ACI + BCI (18.6)
Pernyataan di atas dapat direalisasikan dengan menggunakan bermacam gerbang logika. Tetapi realisasi yang paling sederhana untuk keluaran S adalah dengan gerbang XOR. Rangkaian untuk penjumlah penuh itu diberikan pada Gambar 18.3. Pada gambar tersebut masing-masing variabelnya diberi tikalas (subscript) guna menunjukkan bahwa rangkaian tersebut dapat disusun sambung-menyambung membentuk penjumlah penuh dalam berapa bit pun.
Guna membentuk penjumlah dua bilangan biner dengan n-bit, n buah penjumlah penuh itu disusun sambung-menyambung dengan masukan CIi dihubungkan
Gambar 18.4 Penjumlah biner 4-bit
Gambar 18.5 Rangkaian pembanding dua bit
mendapatkan penjumlahan dua bilangan biner n-bit, A dan B, dapat disusun beberapa rangkaian penjumlah penuh dengan keluaran bawaan CIi masing-masing
penjumlah penuh itu dihubungkan ke keluaran bawaan COi-1 dari penjumlah
sebelumnya. Gambar 18.4 menunjukkan hubungan empat penjumlah penuh yang bekerja sebagai rangkaian yang menjumlahkan dua bilangan biner empat bit. Kemasan rangkaian terpadu MSI (medium-scale integrated circuit) tersedia untuk
penjumlah biner empat bit dan salah satu contohnya adalah 74LS283.
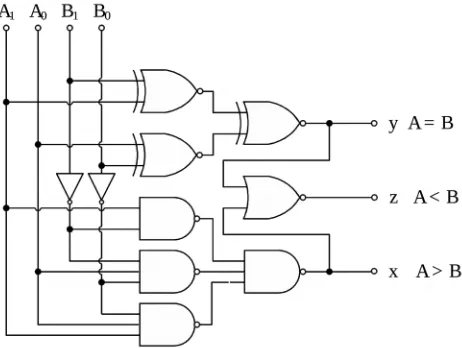
Pembanding (comparator) adalah rangkaian kombinasi yang dapat membandingkan dua bilangan A dan B, dan menentukan besar relatifnya. Hasil pembandingan itu diperagakan di sini dengan tiga keluaran yang menunjukkan apakah A > B, A = B atau A < B. Macam-macam data digital yang dapat dibandingkan antara lain adalah bilangan biner, bilangan desimal yang diwakili oleh sandi biner atau setiap himpunan informasi diskrit berurut lainnya. Dengan mengikuti prosedur yang telah diuraikan pada awal bagian ini, dapat dilakukan perencanaan suatu rangkaian yang membandingkan besar relatif dua bilangan biner yang masing-masing panjangnya dua bit. Rangkaian hasilnya diberikan pada Gambar 18.5.
Suatu rangkaian yang membandingkan dua bilangan biner A dan B, dengan masing-masing bilangan itu panjangnya dua bit, harus mempunyai dua masukan untuk setiap bilangan itu. Empat variabel masukan itu diberi nama A1, A0, B1 dan
mempunyai tiga keluaran, satu untuk setiap kemungkinan A > B, A = B atau A < B, yang berturut-turut diberi lambang x, y dan z. Daftar kebenaran untuk hubungan masukan dan keluaran rangkaian tersebut diberikan pada Daftar 18.3. Tampak dalam daftar itu hanya satu keluaran sama dengan 1 untuk setiap kombinasi masukannya. Ada empat kombinasi masukan yang membuat keluaran ‘sama dengan’, y, sama dengan 1, yaitu untuk A1A0 = B1B0. Enam kombinasi
masukan memberikan keluaran ‘lebih besar dari’, x, sama dengan 1 jika A1A0 > B1B0. Sisanya adalah keluaran ‘kurang dari’, z, untuk A1A0 < B1B0. Setelah
disederhanakan ternyata y dapat diimplementasikan dengan menggunakan dengan 3 gerbang XNOR dua masukan. Di samping itu hanya dua masukan yang diimplementasikan langsung, yaitu x dan y, sedangkan keluaran z dapat dengan diimplementasikan menggunakan kenyataan bahwa y = 0 dan x = 0, maka z = 1. Oleh karena itu z dapat dinyatakan sebagai z = x'y' dan diimplementasikan dengan mudah dan murah menggunakan satu gerbang NOR. Penyederhanaan fungsi-fungsi Boole tidak diberikan dalam buku ini. (Penyederhanaan itu dapat dipelajari dalam buku Dasar-Dasar Rangkaian Logika Digital oleh penulis buku ini.)
Daftar 18.3 Daftar kebenaran untuk rangkaian pembanding
Masukan Keluaran
A > B A = B A < B
A1 A0 B1 B0 x y z
0 0 0 0 0 1 0
0 0 0 1 0 0 1
0 0 1 0 0 0 1
0 0 1 1 0 0 1
0 1 0 0 1 0 0
0 1 0 1 0 1 0
0 1 1 0 0 0 1
0 1 1 1 0 0 1
1 0 0 0 1 0 0
1 0 0 1 1 0 0
1 0 1 0 0 1 0
1 0 1 1 0 0 1
1 1 0 0 1 0 0
1 1 0 1 1 0 0
1 1 1 0 1 0 0
1 1 1 1 0 1 0
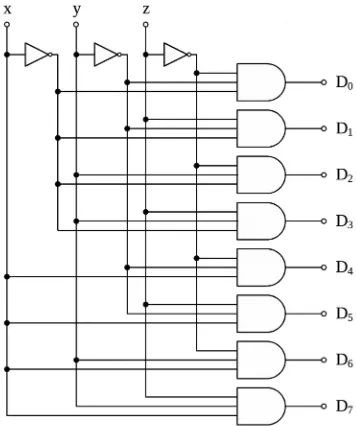
Gambar 18.6 Rangkaian dekoder 3-ke-8
sambung-menyambung sehingga dapat membandingkan bilangan 4n-bit dengan n = 1, 2, 3, dan seterusnya.
Unsur-unsur diskrit dalam suatu informasi diwakili oleh bilangan biner atau sandi biner pada suatu sistem digital. Misalnya suatu sandi biner atau bilangan biner dengan n bit mampu mewakili 2n unsur informasi diskrit. Suatu dekoder
(decoder) adalah suatu rangkaian kombinasi yang mengubah suatu sandi biner dengan n variabel masukan menjadi m saluran keluaran, satu untuk setiap unsur informasi diskrit. Suatu enkoder (encoder) adalah suatu rangkaian kombinasi yang menerima m saluran masukan, satu untuk setiap informasi diskrit, dan menghasilkan suatu sandi biner dengan n saluran keluaran. Suatu dekoder seperti yang ditunjukkan pada Gambar 18.6 suatu susunan gerbang-gerbang AND dengan n masukan dan 2n (atau kurang) keluaran. Enkoder dengan implementasi seperti
pada Gambar 18.7 mempunyai gerbang-gerbang OR dengan 2n (atau kurang)
masukan dengan n keluaran.
Tinjau suatu rangkaian dekoder biner ke oktal (tentang bilangan biner dan oktal, periksa Lampiran G) seperti yang ditunjukkan pada Gambar 18.6. Tiga masukan (x, y dan z) mewakili suatu bilangan biner dengan tiga bit. Delapan keluarannya (D0 sampai D7) mewakili angka-angka oktal dari 0 sampai dengan 7. Dekoder itu
terdiri dari sekelompok gerbang-gerbang AND yang menyandikan bilangan-bilangan biner masukannya. Rangkaian itu mencatu keluaran sebanyak kombinasi bilangan biner yang mungkin terjadi.
Gambar 18.7 Rangkaian enkoder 8-ke-3
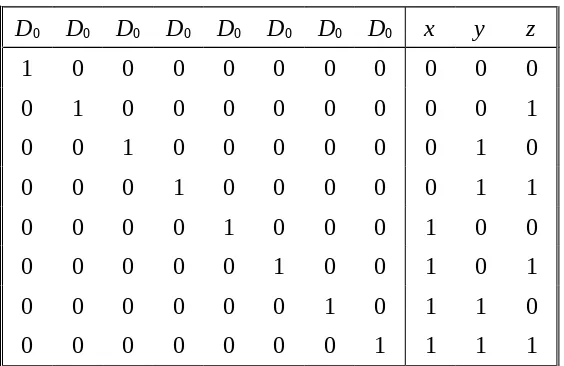
Daftar 18.4 Daftar kebenaran untuk dekoder biner ke oktal
Masukan Keluaran
x y z D0 D1 D2 D3 D4 D5 D6 D7
0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 1 0 0 0 0 0 0
0 1 0 0 0 1 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0
1 0 1 0 0 0 0 0 1 0 0
1 1 0 0 0 0 0 0 0 1 0
1 1 1 0 0 0 0 0 0 0 1
Contoh suatu enkoder ditunjukkan pada Gambar 18.7. Enkoder oktal ke biner itu terdiri dari delapan masukan, satu untuk masing-masing dari delapan angka itu, dan tiga keluaran yang menghasilkan bilangan binernya yang sesuai. Rangkaian itu terdiri dari gerbang-gerbang OR. Daftar kebenaran untuk rangkaian tersebut diberikan pada Daftar 18.5. Diandaikan hanya ada satu saluran masukan dengan logika-1 untuk setiap kalinya, selain dari itu masukan tersebut tidak mempunyai arti. Tampak bahwa rangkaian itu mempunyai delapan masukan; yang dapat memberikan 28 kemungkinan kombinasi, tetapi hanya delapan kombinasi yang
mempunyai arti. Kombinasi masukan yang lain sebanyak (28 – 8) adalah keadaan tak-acuh (don’t care condition), suatu keadaan yang tidak pernah terjadi karena dalam hal ini memang tidak diperlukan. Meskipun tidak pernah ada, keadaan tak-acuh itu sangat bermanfaat dalam penyederhanaan rangkaiannya.
Daftar 18.5 Daftar kebenaran untuk enkoder oktal ke biner
Gambar 18.8 Dekoder BCD ke tujuh-segmen
D0 D0 D0 D0 D0 D0 D0 D0 x y z
1 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 1 1
0 0 0 0 1 0 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0 1
0 0 0 0 0 0 1 0 1 1 0
0 0 0 0 0 0 0 1 1 1 1
Dekoder dan enkoder itu banyak sekali dipakai dalam sistem digital karena manusia umumnya lebih menyukai sistem desimal sedangkan peralatan digital menggunakan sistem biner dalam operasinya. Dekoder tersebut berguna untuk memperagakan unsur-unsur informasi diskrit biner yang tersimpan dalam register. Misalnya suatu angka desimal yang disandikan dalam BCD (binary coded decimal) empat bit dapat diperagakan dengan pertolongan rangkaian dekoder BCD ke desimal sehingga dapat memberikan tampilan angka desimal. TTL 7447, suatu dekoder BCD ke tujuh-segmen, beserta tampilannya ditunjukkan pada Gambar 18.8.
Rangkaian enkoder berguna untuk membentuk sandi-sandi biner bila tersedia
masing-masing informasi diskrit pada sebuah saluran. Contoh rangkaian enkoder ini dijumpai dalam komputer yaitu bila rangkaian tersebut menerima masukan dari masing-masing tombol ketik (key) pada papan-ketik (keyboard) komputer maka rangkaian enkoder itu akan menghasilkan kode delapan bit yang sesuai untuk huruf pada tombol yang bersesuaian itu diketik.
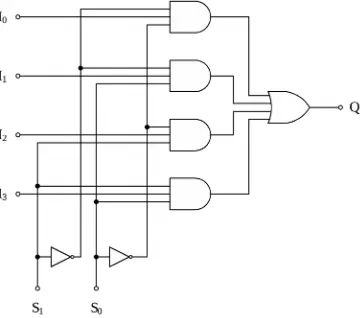
Gambar 18.9 Multiplekser 4-ke-1
seperti saklar pemilih. Demultiplekser adalah kebalikannya, rangkaian ini menerima informasi dari beberapa saluran dan membagikannya ke tujuan yang
jumlahnya lebih banyak.
Suatu multiplekser digital adalah suatu rangkaian kombinasi yang memilih data dari 2n masukan dan mengarahkannya menuju ke sebuah keluaran tunggal.
Pemilihan jalur pemindahan masukan ke keluaran itu diatur oleh suatu himpunan pemilih masukan. Biasanya suatu multiplekser dengan n variabel pemilih dapat memilih salah satu dari 2n sinyal masukan.
Daftar 18.6 Daftar kebenaran multiplekser 4-ke-1 Saluran
pemilih Keluaran
S1 S0 Q
0 0 I0
0 1 I1
1 0 I2
1 1 I3
Secara umum suatu multiplekser k-bit dengan m masukan memerlukan n saluran pemilih (dengan m = 2n) fungsi membuka sandi data masukannya. Terdapat k
keluaran, satu dengan sebuah gerbang OR, dan mk masukan, satu dengan sebuah gerbang AND. Rancangan pembuka sandi itu diulangi sebanyak k kali.
Gambar 18.9 menunjukkan suatu multiplekser 4-ke-1 dan daftar kebenarannya ditunjukkan oleh Daftar 18.6. Masing-masing masukan I0 sampai dengan I3 dipilih
oleh S0 dan S1 dan diarahkan ke keluaran Q. Cara kerja rangkaian itu adalah
sebagai berikut. Andaikan diinginkan untuk mengarahkan saluran masukan I2 ke
keluaran Q, maka nilai S (S1S0) adalah 10 dalam biner atau 2 dalam desimal. Hal
Gambar 18.10 Demultiplekser 1-ke-4
Multiplekser dengan masukan 2, 4, 8, dan 16 tersedia di pasaran dalam kemasan MSI. Sebagai contoh 74LS151 adalah multiplekser 8-ke-1 dan 74LS352 adalah
multiplekser 4-ke-1 kembar.
Suatu demultiplekser ditunjukkan pada Gambar 18.10. Sebuah saluran masukan diberikan ke salah satu dari keempat keluaran identik di bawah pengawasan dua saluran pemilih. Rangkaian itu terdiri dari empat gerbang AND dengan tiga masukan, masing-masing menerima masukan data bersama-sama dengan salah satu dari empat kemungkinan kombinasi variabel pemilih. Variabel masukan tunggal itu mempunyai jalur ke keempat keluaran itu tetapi informasinya diarahkan ke salah satu keluaran yang ditentukan oleh dua saluran pemilih tersebut. Jadi keluaran Q merupakan fungsi pemilih S dengan alamat yang ditentukan oleh S1S0. Suatu demultiplekser dapat berfungsi sebagai rangkaian
dekoder jika saluran masukan tunggal itu dihubungkan secara permanen dengan suatu sinyal yang bersesuaian dengan logika-1. Peralatan multiplekser dan demultiplekser bila digunakan bersama-sama berguna dalam suatu sistem di mana diinginkan untuk melipat-gandakan banyaknya saluran data, mengirimkannya melalui satu saluran dan mengubahnya kembali menjadi bentuk data aslinya pada ujung penerima untuk diproses. Jadi pada dasarnya demultiplekser adalah suatu distributor data dan multiplekser adalah suatu pemilih data.
18.2 Rangkaian Logika Urutan
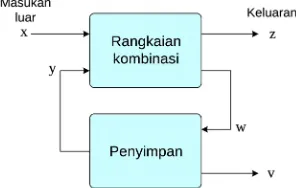
Gambar 18.11 Diagram blok logika urutan
Jalur-jalur sinyal yang ditunjukkan pada Gambar 18.11 itu berupa saluran tunggal yang mewakili saluran-saluran paralel majemuk; sinyal yang bertanda y dapat berupa n saluran y1, y2, ... , yn. Masukan sistem itu adalah x (yang berupa x1, x2, ...,
xm) dan keluarannya adalah z (yang dapat berupa z1, z2, ..., zk), dan seterusnya.
Masukan tambahan ke rangkaian kombinasi itu adalah keluaran dari penyimpan. Sinyal-sinyal itu disebut variabel keadaan (state variable) dan diberikan berupa y. Sinyal-sinyal itu mewakili pengaruh masa lampau rangkaian urutan tersebut pada keluarannya sekarang.
Keadaan (state) suatu unsur penyimpan atau sel biner adalah salah satu dari dua keadaan stabil yang dimiliki oleh sel biner tersebut. Informasi yang disimpan dalam sel itu dapat bernilai 1 bila berada dalam salah satu keadaan dan 0 bila dalam keadaan yang lain.
Rangkaian kombinasi itu sendiri melakukan operasi pengolahan informasi tertentu yang salah satu himpunan keluarannya, w, disebut variabel perangsang
(excitation variable), merupakan masukan ke penyimpan untuk menentukan nilai-nilai biner yang harus disimpan dalam unsur-unsur penyimpan itu untuk keadaan berikutnya. Proses itu jelas menunjukkan bahwa keluaran sistem, z, bukan hanya merupakan fungsi masukan luarnya saja, x, tetapi juga fungsi keadaan sekarang dalam penyimpannya. Keadaan berikutnya pada penyimpan tersebut adalah fungsi masukan luar dan keadaan sekarang. Jadi suatu rangkaian urutan ditentukan oleh urutan waktu masukan, keluaran dan keadaan-dalamnya.
Ada dua jenis utama pada rangkaian urutan tersebut. Penggolongan itu tergantung kepada pengaturan sinyalnya menurut waktu.
Sistem logika urutan praktis menggunakan amplitudo tetap, seperti tingkat
Gambar 18.12 Rangkaian flip-flop elektronik
kestabilan dan pembagian waktunya dapat dengan mudah diatur dengan langkah-langkah diskrit yang tersendiri.
18.3 Flip-Flop
Unsur penyimpan yang digunakan dalam rangkaian urutan menurut waktu adalah
flip-flop. Rangkaian tersebut merupakan sel biner yang dapat menyimpan satu bit informasi. Suatu rangkaian flip-flop mempunyai dua keluaran, satu dengan nilai normal dan yang lain adalah nilai komplemen bit yang tersimpan di dalamnya. Informasi biner dapat masuk ke suatu flip-flop dengan berbagai cara sehingga mengakibatkan tersedianya berbagai ragam jenis flip-flop. Masing-masing jenis flip-flop itu mempunyai karakteristik tersendiri yang diperlukan untuk pemakaian tertentu. Dalam bagian ini akan dibahas berbagai macam flip-flop dengan mendefinisikan sifat-sifat logikanya.
Rangkaian flip-flop atau bistable multivibrator (multivibrator dua keadaan stabil)
dapat mempertahankan suatu keadaan biner dalam waktu yang tak terbatas sampai suatu sinyal masukan baru datang untuk mengubah keadaan itu. Perbedaan utama di antara berbagai jenis flip-flop itu adalah banyaknya masukan yang dimiliki dan perilaku bagaimana masukan itu mempengaruhi keadaan biner dalam flip-flop tersebut. Flip-flop merupakan peralatan yang murah dan andal dan digunakan dalam semua jenis sistem pengolahan data digital. Rangkaian flip-flop ini ditemukan pada tahun 1919 oleh fisikawan Inggris, William Eccles dan F.W. Jordan, dan awalnya dikenal sebagai rangkaian pemicu Eccles-Jordan (Eccles-Jordan trigger circuit).
Cara kerja suatu flip-flop elektronik didasarkan atas perilaku transistor sebagai saklar. Tanpa adanya masukan ke saklar transistor pada Gambar 18.12, pembagi tegangan RA1-RB2 atau RA2-RB1 memberikan prategangan mundur ke sambungan
basis-emiter dan salah satu transistor itu dalam keadaan mati, atau saklar dalam keadaan BUKA. Dalam hal itu arus yang melalui RC (RC1 atau RC2) adalah nol
sehingga terdapat tegangan positif pada kutub keluarannya. Jika suatu masukan positif diberikan ke salah satu kutub B (B1 atau B2), VB meningkat, sambungan
basis-emiter mendapat prategangan maju, saklar TUTUP sehingga keluarannya menjadi nol.
Sinyal masukan yang diberikan ke kutub P akan menyebabkan kutub + pada RA
Gambar 18.13 Rangkaian flip-flop RS dasar
keluarannya. Saklar itu merupakan suatu gerbang NOR dan flip-flop pada gambar tersebut dibentuk dengan dua gerbang semacam itu.
Untuk mengikuti kerja flip-flop itu andaikan T1 dalam keadaan menghantar
(TUTUP) dan T2 mati (BUKA). Jika T1 menghantar, tegangan di titik P1 adalah
nol dan, dengan adanya tegangan negatif pada RB2, menjamin bahwa T2 mati.
Dengan T2 mati, tegangan P2 besar dan positif dan memberikan arus prategangan
melalui RA1 untuk menjamin T1 menghantar dan VP1 rendah. Dalam istilah logika,
Q = 0 dan itu merupakan suatu keadaan stabil yang dikatakan sebagai keadaan 0 dalam unsur penyimpan tersebut.
Suatu pulsa positif yang dikenakan ke kutub RESET (R) yang meningkatkan VB1
tidak akan memberikan pengaruh apa-apa karena T1 telah menghantar. Tetapi
suatu pulsa positif yang diberikan ke kutub SET (S) akan mengakibatkan T2 mulai
menghantar, tegangan P2 turun, prategangan maju pada T1 berkurang, tegangan P1
meningkat, prategangan T2 meningkat, tegangan P2 lebih turun lagi, T2 menjadi
jenuh, dan T1 mati. Tegangan keluarannya tinggi dan Q = 1. Hal itu menunjukkan
keadaan stabil yang satu lagi yang dikatakan sebagai keadaan 1 dalam unsur penyimpan tersebut. Jika suatu flip-flop dalam keadaan 1 menerima pulsa positif pada kutub Rnya, terjadi perubahan yang sebaliknya (karena unsur tersebut simetri bentuknya) dan unsur itu RESET ke keadaan 0. Umumnya perubahan keadaan itu dapat terjadi dalam beberapa nanodetik dan peralatan semacam itu
memenuhi syarat sebagai unsur penyimpan biner.
Flip-Flop RS Dasar. Suatu rangkaian flip-flop dapat disusun dengan dua gerbang NOR, seperti yang telah diuraikan di atas, atau dua gerbang NAND. Susunan itu ditunjukkan pada Gambar 18.13. Masing-masing rangkaian itu membentuk suatu flip-flop dasar yang merupakan dasar pengembangan bagi jenis-jenis flip-flop yang lain. Hubungan silang dari keluaran salah satu gerbang ke masukan gerbang yang lain merupakan suatu jalur umpan-balik. Dengan alasan itu rangkaian tersebut dapat digolongkan kepada rangkaian urutan tak-serempak. Masing-masing flip-flop itu mempunyai dua keluaran, Q dan Q, dan dua masukan, S (SET) dan R (RESET). Masukan SET membuat flip-flop menjadi dalam keadaan set atau bernilai logika-1 pada keluaran normalnya (Q), dan masukan RESET membuat flip-flop menjadi dalam keadaan bebas (CLR - clear) atau mempunyai nilai logika-0 pada keluaran normalnya. Jenis flip-flop ini sering dikenal sebagai
flip-flop RS gandengan langsung (direct coupled RS flip-flop); R dan S merupakan huruf-huruf pertama nama masukannya.
Daftar 18.7 Daftar kebenaran flip-flop dasar dengan gerbang NOR
1 0 1 0 bahwa keluaran suatu gerbang NOR adalah 0 jika salah satu masukannya sama dengan 1 dan keluaran gerbang NOR adalah 1 hanya jika semua masukannya sama dengan 0. Sebagai titik awal, diandaikan masukan set adalah 1 dan masukan reset sama dengan 0. Karena gerbang B mempunyai sebuah masukan 1, keluaran Q harus sama dengan 0 yang mengakibatkan kedua masukan ke gerbang A itu sama dengan 0 dan keluarannya, Q, sama dengan 1. Bila masukan set dikembalikan ke 0, keluarannya tetap sama. Hal itu adalah karena keluaran Q tetap 1 sehingga masih ada sebuah masukan 1 pada gerbang B, yang selanjutnya membuat keluaran Q tetap 0. Akibatnya kedua masukan ke gerbang A sama dengan 0 dan keluaran Q tetap sama dengan 1. Dengan cara yang sama dapat dibuktikan bahwa suatu 1 pada masukan reset akan mengubah keluaran Q menjadi 0 dan Q menjadi 1. Bila masukan reset itu dikembalikan ke 0 keluarannya tidak berubah.
Bila sebuah 1 diberikan bersama-sama ke masukan set dan reset, kedua keluarannya, Q dan Q, menjadi 0. Dalam praktik keadaan semacam itu harus dihindari.
Suatu flip-flop mempunyai dua keadaan stabil. Bila Q = 1 dan Q = 0 dikatakan flip-flop itu dalam keadaan set (atau keadaan 1). Dan Q = 0 dan Q = 1 merupakan keadaan bebas (atau keadaan 0). Keluaran Q dan Q merupakan komplemen antara yang satu dengan yang lain dan dikatakan sebagai keluaran normal dan komplemen flip-flop tersebut. Keadaan biner suatu flip-flop diambil dari nilai keluaran normalnya.
Dalam operasi normal, kedua masukan suatu flip-flop akan tetap 0 kecuali bila keadaan flip-flop itu akan diubah. Pengenaan 1 sesaat ke masukan set menyebabkan flip-flop itu menjadi dalam keadaan set. Masukan set itu harus kembali ke 0 sebelum suatu 1 diberikan ke masukan resetnya. Pengenaan 1 sesaat ke masukan reset menyebabkan flip-flop tersebut menjadi dalam keadaan bebas kembali. Bila kedua masukannya itu mula-mula sama dengan 0, dan bila suatu 1 dikenakan ke masukan set sedangkan flip-flop itu dalam keadaan set atau bila sebuah 1 yang diberikan ke masukan reset sedangkan flip-flop itu dalam keadaan bebas, maka keadaan keluarannya tidak akan berubah. Bila sebuah 1 dikenakan sekali gus ke masukan set dan reset, kedua keluarannya akan sama dengan 0. Keadaan itu tidak terdefinisi dan biasanya dihindari. Jika kedua masukan itu menjadi 0 kembali, keadaan flip-flop menjadi tak-tentu dan tergantung kepada masukan mana yang menerima 1 lebih lama sebelum kembali ke 0.
Daftar 18.8 Daftar kebenaran flip-flop dasar dengan gerbang NAND
Gambar 18.14 Flip-flop RS menurut waktu
1 0 0 1
1 1 0 1 (Setelah S = 1, R = 0)
0 1 1 0
1 1 1 0 (Setelah S = 0, R = 1)
0 0 1 1
Rangkaian flip-flop dasar NAND pada Gambar 18.13 yang di tengah bekerja dengan kedua masukannya dalam keadaan normal sama dengan 1 kecuali bila keadaan flip-flop itu akan diubah. Pengenaan 0 sesaat ke masukan set menyebabkan keluaran Q menjadi 1 dan Q' menjadi 0, membuat flip-flop menjadi dalam keadaan set. Setelah masukan set itu kembali ke 1, 0 sesaat pada masukan reset akan menyebabkan keadaan flip-flop menjadi bebas. Bila kedua masukan itu menjadi 0 bersama-sama, kedua keluaran pada flip-flop itu sama dengan 1; suatu keadaan yang harus dihindari dalam praktik.
Flip-Flop RS menurut waktu. Suatu flip-flop dasar pada dasarnya adalah suatu rangkaian urutan tak-serempak. Dengan menambah suatu gerbang ke setiap masukan rangkaian dasar itu, flip-flop tersebut dapat diubah untuk menanggapi masukan selama adanya suatu pulsa waktu. Flip-flop RS menurut waktu yang
ditunjukkan pada Gambar 18.14 sebelah kiri itu terdiri dari flip-flop NOR dasar dengan dua gerbang AND. Keluaran kedua gerbang AND tersebut tetap 0 selama pulsa waktu (yang diberi lambang CP – clock pulse) sama dengan 0, tanpa memandang nilai masukan S dan Rnya. Bila pulsa waktu itu menjadi 1, informasi dari masukan S dan R diijinkan untuk masuk ke flip-flop dasar tersebut. Keadaan set tercapai dengan S = 1, R = 0 dan CP = 1. Untuk mengubahnya menjadi keadaan bebas, masukan S harus 0, R = 1 dan CP = 1. Dengan masukan R dan S yang keduanya sama dengan 1, adanya pulsa waktu akan menyebabkan kedua keluaran flip-flop itu sesaat sama dengan 0. Bila pulsa waktu itu hilang, keadaannya menjadi tak-tentu; dapat dalam keadaan set atau bebas, tergantung apakah masukan set atau reset yang lebih lama sama dengan 1 sebelum berubah menjadi 0 pada akhir pulsa waktu tersebut.
Tanggapan flip-flop menurut waktu merupakan praktik yang umum dijumpai dalam sistem digital karena perubahan dalam sistem itu umumnya diinginkan terjadi serentak menurut kendali sumber waktu. Oleh sebab itu, flip-flop menurut waktu disebut sebagai suatu rangkaian urutan serempak.
sebelah kanan. Gerbang AND dengan masukan pulsa waktu dapat dilukis di luar lambang tersebut, atau suatu lambang dengan tanda CP digunakan untuk menunjukkan bahwa keluaran flip-flop tersebut tidak akan terpengaruh kecuali bila ada pulsa waktu pada masukan yang bertanda CP itu.
Dalam praktik flip-flop menurut waktu itu sering kali diinginkan untuk membuat flip-flop tersebut dalam keadaan set atau bebas tanpa harus menunggu datangnya pulsa waktu. Untuk itu umumnya flip-flop menurut waktu selalu dilengkapi dengan masukan set atau reset langsung. Masukan langsung itu sering diberi label SET atau CLR (clear – bebas) untuk membedakannya dengan masukan S (set) dan R (reset) yang bekerja menurut waktu seperti yang ditunjukkan pada Gambar 18.14 sebelah kanan itu.
Pada awal penggunaan suatu flip-flop sering tidak dapat diramal perilakunya, dalam hal semacam itu masukan SET dan CLR berguna untuk mengawali operasi suatu sistem dengan keadaan flip-flop yang terdefinisi.
Daftar 18.9 Daftar karakteristik flip-flop RS menurut waktu
Q S R Q(t + 1)
Daftar karakteristik flip-flop tersebut ditunjukkan pada Daftar 18.9. Daftar itu merupakan ringkasan operasi flip-flop dalam bentuk daftar. Q adalah keadaan biner flip-flop pada suatu waktu yang diketahui (yang dikatakan sebagai keadaan sekarang), kolom-kolom R dan S memberikan nilai-nilai yang dapat terjadi untuk masukannya dan Q(t + 1) adalah keadaan flip-flop setelah timbulnya suatu pulsa waktu (dikatakan sebagai keadaan berikutnya).
Gambar 18.15 Flip-flop D
(kecuali bila flip-flop itu telah berada dalam keadaan set sebelumnya). Jika masukan D itu sama dengan 0, keluaran gerbang 4 menjadi 0 yang mengubah flip-flop tersebut menjadi dalam keadaan bebas.
Daftar 18.10 Daftar karakteristik flip-flop D
Q D Q(t+1) ‘data’ ke dalam flip-flop. Rangkaian flip-flop itu pada dasarnya adalah rangkaian flip-flop RS dengan sebuah pembalik di masukan Rnya. Adanya penambahan pembalik itu mengurangi banyaknya masukan dari dua menjadi satu. Di samping itu karena keluaran Q tidak akan menerima masukan D sampai datangnya suatu pulsa waktu, bentuk itu sering juga disebut sebagai flip-flop tertunda (delay flip-flop).
Lambang untuk flip-flop D menurut waktu itu diberikan pada Gambar 18.15 sebelah kanan. Seperti halnya dengan setiap flip-flop menurut waktu, flip-flop D juga dilengkapi dengan masukan SET dan CLR. Daftar karakteristik flip-flop D itu diberikan oleh Daftar 18.10. Persamaan karakteristik itu membuktikan bahwa keadaan berikutnya pada flip-flop tersebut sama seperti masukan D dan tidak tergantung kepada nilai keadaan sekarangnya.
Flip-Flop JK merupakan perbaikan dari flip-flop RS sehingga keadaan tak-tentu pada jenis RS menjadi terdefinisi untuk jenis JK tersebut. Masukan J dan K berlaku seperti masukan R dan S (perhatikan bahwa untuk suatu flip-flop JK, huruf J adalah untuk set dan huruf K untuk bebas). Bila masukan J dan K diberikan secara serentak, nilai flip-flop itu berubah menjadi komplemennya; yaitu jika mula-mula Q = 1, akan berubah menjadi Q = 0 dan sebaliknya.
Gambar 18.16 Flip-flop JK
Gambar 18.17 Flip-flop T
Daftar 18.11 Daftar karakteristik flip-flop JK
Q J K Q(t + 1)
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0
Flip-Flop T adalah flip-flop JK dengan masukan tunggal. Seperti yang tampak pada Gambar 18.16, flip-flop T itu didapatkan dari jenis JK jika kedua masukannya dijadikan satu. Nama ‘T’ (toggle – artinya saklar pengalih dua keadaan) itu diperoleh karena kemampuan flip-flop itu untuk mengubah keadaannya. Apapun keadaan sekarang flip-flop T itu akan berubah menjadi komplemennya setiap kali pulsa waktu diberikan pada saat masukan T itu bernilai 1.
Lambang dan persamaan karakteristik flip-flop T itu ditunjukkan pada Gambar 18.17. Daftar karakteristiknya diberikan oleh Daftar 18.6.
Keempat jenis flip-flop yang diperkenalkan di atas dapat tersedia dalam keadaan
tanpa pengaturan waktu. Flip-flop tanpa masukan waktu tersebut berguna untuk operasi tak-serempak. Keempat jenis itu merupakan jenis yang umum dijumpai dalam rangkaian digital dan tersedia di pasaran.
Daftar 18.12 Daftar karakteristik flip-flop T
0 0 0
0 1 1
1 0 1
1 1 0
18.4 Register
Register adalah sekumpulan flip-flop yang digunakan untuk menyimpan data. Masing-masing flip-flop dalam register tersebut menyimpan satu bit. Jadi suatu register dengan n flip-flop mampu menyimpan informasi sebesar n bit. Ada dua jenis utama register tersebut: register penyimpan (storage register), yang digunakan hanya untuk menyimpan data, dan register geser (shift register), suatu rangkaian untuk menyimpan dan menggeser (atau memanipulasikan) data. Dalam bagian ini akan diuraikan operasi suatu register geser. Register ini mempunyai banyak pemakaian dalam perencanaan sistem digital dan tersedia dalam bentuk IC sebagai fungsi MSI, salah satu contohnya adalah 74LS178 yang merupakan register geser universal empat bit.
Diagram logika suatu register geser universal empat bit ditunjukkan pada Gambar 18.18. Register itu terdiri dari empat flip-flop menurut waktu dengan masukan D. Register tersebut digunakan untuk penyimpan sementara suatu data sebesar empat bit. Data itu dapat dipindahkan ke dalam atau ke luar register dengan tiga cara yang berlainan yang diatur oleh sinyal pengendali P, SR dan SL.
Ketiga cara itu berturut-turut adalah pemindahan paralel, pemindahan geser kanan secara seri dan pemindahan geser kiri secara seri. Operasi ketiga bentuk pemindahan itu akan diuraikan berikut ini.
Pemindahan paralel. Dengan P = 1, SR = 0, SL = 0, data yang tersedia pada
masukan x0 sampai x3 dipindahkan menjadi A0 sampai A3 pemindahan paralel
karena semua flip-flop menerima data baru sekali gus dalam satu pulsa waktu. Data yang tersimpan dalam register itu dipindahkan ke luar secara paralel dengan mencacah keluaran keempat flip-flopnya.
Geser kanan. Dengan SR = 1, P = 0, SL = 0, data dalam register itu digeser ke
kanan dengan datangnya setiap pulsa waktu. Masing-masing flip-flopnya menerima data baru dari tetangganya di sebelah kiri dan flip-flop A3 menerima
data dari masukan luar IR. Data dipindahkan ke luar dengan mencacah keluaran
flip-flop A0. Pemindahan itu dinamakan pemindahan seri karena satu bit
Gambar 18.18 Register geser universal 4-bit
Geser kiri. Dengan SL = 1, P = 0 dan SR = 0, data dalam register itu digeser ke
kiri. Masing-masing flip-flopnya menerima data baru dari tetangganya di sebelah kanan dan A0 menerima data dari masukan luar IL. Data itu dipindahkan ke luar
dengan mencacah keluaran A3. Proses itu juga merupakan pemindahan seri tetapi
arahnya ke kiri.
Masukan D pada masing-masing flip-flop itu menerima data dari tiga sumber yang berbeda. Suku pertama, kedua dan ketiga pada setiap fungsi itu memberikan persyaratan berturut-turut untuk geser kiri, paralel dan geser kanan. Hanya satu dari ketiga sinyal pengatur itu yang sama dengan 1 untuk setiap waktu. Jika dua atau tiga sinyal pengatur itu bernilai logika-1 pada saat yang sama, masukan D ke suatu flip-flop akan menanggapi secara OR untuk bit-bit data masukannya.
Ada empat flip-flop dan sembilan masukan (plus masukan CP) dalam diagram logika pada Gambar 18.18 itu, sehingga daftar atau diagram masukannya akan terdiri dari 16 keadaan dan 29 kombinasi masukan. Hanya beberapa dari kombinasi masukan itu dapat terjadi selama operasi normal. CP itu dapat diartikan sebagai pulsa waktu (clock pulse) atau pulsa hitung (count pulse) yang akan dibahas dalam bagian berikut.
Gambar 18.19 Diagram keadaan penghitung riak biner 4-bit
18.5 Penghitung
Suatu rangkaian urutan yang bekerja menurut urutan keadaan yang telah ditentukan dengan pemberian pulsa-pulsa masukan disebut penghitung (counter). Fungsi dasar suatu penghitung adalah ‘mengingat’ berapa pulsa masukan yang telah diberikan ke masukannya; jadi dalam istilah dasarnya, penghitung itu merupakan suatu sistem penyimpan (memory system). Pulsa masukan, yang disebut pulsa hitung, dapat berupa pulsa waktu atau pulsa yang berasal dari sumber luar dan dapat terjadi pada setiap selang waktu tertentu atau secara sebarang. Urutan keadaan dalam suatu penghitung dapat mengikuti suatu hitungan biner atau urutan keadaan yang lain. Penghitung tersebut dapat ditemui di hampir setiap peralatan yang menggunakan logika digital. Penghitung ini digunakan untuk menghitung banyaknya kejadian yang timbul dan berguna untuk menghasilkan urutan waktu guna mengatur operasi dalam suatu sistem digital. Sebenarnya penghitung adalah register yang bekerja menurut urutan keadaan yang telah ditentukan bila menerima masukan. Jam, penghitung frekuensi (frequency counter), komputer, dan berbagai macam peralatan digital mengandung penghitung tersebut.
Penghitung riak biner (binary ripple counter) merupakan rangkaian penghitung digital paling dasar yang melakukan fungsi biner yang paling dasar pula. Rangkaian tersebut terdiri dari suatu hubungan seri antara beberapa flip-flop T tanpa gerbang logika. Setiap flip-flop dipicu oleh keluaran flip-flop sebelumnya. Untuk memahami operasi penghitung itu perlu ditinjau diagram keadaan pada Gambar 18.19 dan diselidiki urutan bilangan-bilangan dalam lingkaran-lingkaran tersebut. Dengan memperhatikan ke-16 bilangan berurut tersebut tampak bahwa setiap kali terjadi perubahan keadaan bit dengan kedudukan terendah dikomplemenkan. Bit kedua dari belakang dikomplemenkan setiap terjadi perubahan bit terendah dari 1 ke 0. Demikian pula selanjutnya setiap bit dalam urutan bilangan biner itu dikomplemenkan setiap kali terjadi perubahan bit dari 1
Gambar 18.20 Penghitung biner 4-bit tak serempak
Gambar 18.21 Diagram waktu penghitung pada Gambar 18.20
Diagram logika penghitung riak biner empat bit ditunjukkan pada Gambar 18.20 dan diagram waktunya diberikan oleh Gambar 18.21. Diagram logika itu terdiri dari empat flop T dengan keluaran flop yang satu menjadi masukan flip-flop yang berikutnya di sebelah kirinya. Flip-flip-flop pertama dikomplemenkan untuk setiap pulsa hitung. Flip-flop yang lain dikomplemenkan bila keluaran normal flip-flop sebelumnya berubah dari 1 ke 0. Setiap flip-flop itu bertugas sebagai sumber untuk memicu flip-flop berikutnya dan sinyal itu menjalar melalui penghitung tersebut seperti gerakan ‘riak gelombang’, flip-flop itu berubah satu-per-satu dengan urutan yang cepat. Hal itu berlawanan dengan penghitung
serempak dengan semua flip-flopnya berubah secara serentak dengan datangnya pulsa hitung.
Seperti yang ditunjukkan pada Gambar 18.19, setelah pula kelima belas (1111), penghitung kembali ke keadaan 0 (0000). Dalam hal ini penghitung dengan 4 bit semacam itu dikatakan sebagai modulo-16; jadi penghitung riak itu disebut juga sebagai penghitung mod-16. Tampak pada Gambar 18.20 bahwa 4 flip-flop T diperlukan untuk menghasilkan hitungan dari 0 sampai dengan 24 – 1 atau 15, dan
kembali ke 0. Arti kata modulo adalah sisa dari suatu operasi pembagian, dalam hal ini menunjukkan bahwa penghitung itu tidak memberikan sisa bila dibagi dengan bilangan yang mengikuti kata modulo itu. Jadi suatu penghitung mod-n
akan memberikan urutan hitung dari 0 sampai dengan n – 1 dan kembali ke 0 lagi. Penghitung mod-n akan memerlukan flip-flop T sebanyak m sedemikian hingga (2m – 1) lebih besar atau sama dengan nilai hitung n yang terbesar dalam penghitung modulo-n , atau
sehingga
m ≥ log2 n (18.8)
Contoh 18.1
Berapa flip-flop T yang diperlukan untuk membuat penghitung modulo-50?
Jawab
Untuk suatu penghitung modulo-50, n adalah 50, jadi
log2 50 = 0,3010 5,6439
Sesuai dengan Persamaan (18.8), bilangan bulat lebih besar yang terdekat dengan 5,6439 adalah 6. Jadi diperlukan 6 flip-flop T untuk membuat penghitung modulo-50
Perubahan keadaan yang terjadi dalam penghitung itu terjadi selama perubahan sinyal dari 1 ke 0. Oleh karena itu maka keluaran normal salah satu flip-flop dihubungkan ke masukan CP pada flip-flop berikutnya. Masukan T secara permanen dihubungkan ke sinyal logika-1 sehingga perubahan keadaan itu sepenuhnya diatur oleh masukan CP. Diagram waktu untuk setiap flip-flop pada gambar itu ditunjukkan pada Gambar 18.21. Tampak di situ bahwa pemicuan perubahan dilakukan pada saat pulsa pemicunya mulai menurun.
Pemicuan semacam itu disebut sebagai pemicuan tepi akhir. Pemicuan tepi awal, perubahan keadaan terjadi pada saat pulsa pemicu mulai menanjak, juga dimungkinkan. Kecuali untuk flip-flop Q0, tampak bahwa perubahan keadaan itu
tidak disebabkan oleh masukan pulsa melainkan oleh perubahan sinyal dari 1 ke 0 pada flip-flop sebelumnya.
Penghitung riak itu tersedia dalam kemasan MSI. Sebagai contoh 74LS93 adalah penghitung riak 4-bit.
Gambar 18.22 Penghitung biner serempak 4-bit
Keunggulan penghitung serempak ini dibandingkan dengan penghitung riak adalah karena operasinya berlangsung dengan kecepatan yang tinggi. Bila suatu pulsa hitung masukan datang, semua flip-flop itu dipicu dan keadaannya dapat berubah secara serentak. Kelambatan waktu pada saat masukan dikenakan sampai semua flip-flop mencapai keadaan berikutnya sama dengan waktu peralihan sinyal sebuah flip-flop. Sinyal itu menjalar melalui gerbang AND selama selang waktu antara pulsa sehingga sinyal dalam masukan T pada flip-flop itu telah mencapai nilai keadaan mantap (steady state) untuk menunggu pulsa hitung berikutnya. Dalam suatu penghitung riak biner sinyal itu menjalar, atau beriak, melalui semua flip-flopnya dan sampai semua flip-flop itu telah berubah keadaannya – misalnya dari 1111 ke 0000; kelambatan totalnya sama dengan waktu peralihan keempat
flip-flopnya itu. Penghitung riak tersebut mempunyai logika yang sederhana sehingga harganya murah. Penghitung jenis riak itu dipakai jika kecepatan bukan merupakan faktor yang menentukan.
Berbagai penghitung serempak n-bit tersedia dalam kemasan MSI, di antaranya adalah 74′163 adalah penghitung serempak 4-bit universal.
18.6 Jam Digital
Salah satu rangkaian digital yang sering dijumpai adalah jam digital. Gambar 18.23 menunjukkan diagram blok suatu jam digital dengan peraga tujuh-segmen yang bekerja berdasarkan frekuensi listrik PLN 50 Hz. PLN memberikan bentuk gelombang sinusoida 50 Hz sebagai bagian dari bakuan listrik PLN. Sinusoida itu adalah masukan ke ADC 1 bit yang menghasilkan 1 bila sinusoida itu positif dan 0 bila sinusoida itu negatif. ADC tersebut menghasilkan sinyal pewaktu yang tepat dengan periode
50 1
Pulsa-pulsa menit itu diberikan ke masukan modulo-10. Modulo-10 ini terdiri atas empat flip-flop T. Nilai-nilai masing-masing flip-flop T itu menghasilkan nilai-nilai biner yang bersesuaian dengan angka 0 sampai dengan 9. Suatu dekoder BCD ke tujuh-segmen mengubah nilai-nilai BCD menit itu menjadi format peragaan tujuh-segmen yang bersesuaian. Jadi, angka menit yang terkanan pada jam digital itu dapat diperagakan.
Setiap sepuluh menit penghitung menit modulo-10 itu menghasilkan suatu pulsa yang diberikan ke penghitung modulo-6. Penghitung ini memberikan pulsa setiap sepuluh menit yang menghasilkan angka puluhan menit bagi jam itu.
Setiap jam penghitung modulo-6 (dengan hitungan puluhan menit) menghasilkan satu pulsa yang selanjutnya diberikan ke penghitung modulo-12. Penghitung modulo-12 ini menggunakan empat flip-flop T yang menghasilkan nilai-nilai biner yang bersesuaian dengan angka 0 sampai 11. Logika kombinasi mengubah pola biner itu menjadi sandi-sandi yang diperlukan untuk menggerakkan dua peraga tujuh-segmen yang memperagakan angka-angka jam yang bersesuaian. Arloji digital dan jam yang bekerja dengan baterai menggunakan pewaktu kristal kuarsa yang berdetak dengan frekuensi 32 kHz.
Soal-Soal
18.1 Rancangkan suatu rangkaian kombinasi yang menerima suatu bilangan dua bit dan menghasilkan keluaran yang berupa bilangan biner yang besarnya pangkat dua bilangan masukannya.
18.2 Rancangkan suatu rangkaian kombinasi yang mengubah angka biner dari 0 sampai dengan 9 ke BCD.
18.3 Suatu dekoder BCD ke tujuh-segmen seperti pada Gambar 18.8 adalah suatu rangkaian kombinasi yang menerima sebuah angka desimal dalam BCD dan menghasilkan keluaran sesuai untuk bagian-bagian tertentu pada sebuah penunjuk peraga (LCD atau LED) yang dipergunakan untuk
memperagakan angka desimal. Tujuh keluaran dekoder itu (a, b, c, d, e, f, dan g) memilih bagian yang sesuai dan membentuk angka desimal sesuai dengan sandi masukannya. Susunlah daftar kebenarannya.
18.4 Berilah contoh penggunaan multiplekser dan demultiplekser.
18.5 Apa yang membedakan antara rangkaian logika kombinasi dan rangkaian logika urutan?
18.6 Jelaskan cara kerja rangkaian flip-flop elektronik. 18.7 Sebutkan macam-macam flip-flop yang Anda ketahui.
18.8 Apa yang terjadi bila masukan S = R = 0 untuk suatu flip-flop RS dengan gerbang NOR?
18.9 Apa yang terjadi pada flip-flop RS menurut waktu dengan gerbang NAND bila masukan S = R = 1?
18.10 Apa yang menyebabkan flip-flop D dikatakan sebagai flip-flop tertunda? 18.11 Apa beda antara flip-flop D dan flip-flop T?
18.12 Jelaskan cara kerja macam-macam register yang Anda ketahui. 18.13 Jelaskan cara kerja macam-macam penghitung yang Anda ketahui.
18.14 Berapa banyak flip-flop yang diperlukan untuk menyusun suatu penghitung modulo-60, modulo-10, modulo-6, dan modulo-12?
BCD, 512 berkala, 516
bistable multivibrator, 517 bit, 505