BAB 10
Segmentasi
Citra
Setelah bab ini berakhir, diharapkan pembaca dapat memahami berbagai istilah berikut dan juga dapat mempraktikkan beberapa penerapannya.
Segmentasi citra Deteksi garis
Deteksi tepi
Peng-ambangan dwi-aras
Peng-ambangan global Vs. lokal Peng-ambangan aras-jamak
Peng-ambangan dengan metode Otsu Peng-ambangan adaptif
Peng-ambangan berdasarkan entropi Segmentasi warna
10.1 Pengantar Segmentasi Citra
Segmentasi citra merupakan proses yang ditujukan untuk mendapatkan objek-objek yang terkandung di dalam citra atau membagi citra ke dalam beberapa daerah dengan setiap objek atau daerah memiliki kemiripan atribut. Pada citra yang mengandung hanya satu objek, objek dibedakan dari latarbelakangnya. Contoh ditunjukkan pada Gambar 10.1. Pada citra yang mengandung sejumlah objek, proses untuk memilah semua objek tentu saja lebih kompleks. Contoh penerapan segmentasi yaitu untuk membuat “Magic Wand”, yang biasa terdapat pada perangkat pengedit foto. Contoh pada Gambar 10.2 menunjukkan penggunaan “Magic Wand” pada Adobe Photoshop. Contoh tersebut memperlihatkan pemilihan area yang ditandai dengan warna khusus.
(b) Citra daun (a) Hasil segmentasi dalam bentuk biner
Area ini diperoleh melalui “Magic Wand”
Gambar 10.2 Pemilihan citra berdasarkan warna, yang intinya diperoleh melalui segmentasi. Bagian terpilih ditandai dengan garis terputus-putus
Gambaran berbagai aplikasi segmentasi serta acuan yang digunakan dapat dilihat pada Tabel 10.1. Secara prinsip, segmentasi dilakukan untuk mendapatkan objek yang menjadi perhatian.
Tabel 10.1 Aplikasi segmentasi pada citra
Objek Citra Kegunaan
Segmentasi
Acuan yang Digunakan
Mobil Mobil, jalan, dan latarbelakang
Pelacakan mobil Gerakan dan warna Struktur
permukaan bumi
Foto satelit Pengklasifikasian area
Tekstur dan warna Wajah orang Kerumunan orang
di pasar
Pengenalan wajah Warna, bentuk, dan tekstur Apel Kumpulan apel
pada ban berjalan
Pemilahan buah apel berdasarkan ukuran
Bentuk, warna, ukuran
Segmentasi juga biasa dilakukan sebagai langkah awal untuk melaksanakan klasifikasi objek. Gambar 10.3 menperlihatkkan hal ini. Setelah segmentasi citra dilaksanakan, fitur yang terdapat pada objek diambil. Sebagai
contoh, fitur objek dapat berupa perbandingan lebar dan panjang objek, warna rata-rata objek, atau bahkan tekstur pada objek. Selanjutnya, melalui pengklasifikasi, jenis objek dapat ditentukan. Sebagai contoh, pengklasifikasi menyatakan bahwa daun termasuk golongan Aglaonema.
Teknik segmentasi citra didasarkan pada dua properti dasar nilai aras keabuan: ketidaksinambungan dan kesamaan antarpiksel. Pada bentuk yang pertama, pemisahan citra didasarkan pada perubahan mendadak pada aras keabuan. Contoh yang menggunakan pendekatan seperti itu adalah detektor garis dan detektor tepi pada citra. Cara kedua didasarkan pada kesamaan antarpiksel dalam suatu area (Acharya dan Ray, 2005). Termasuk dalam cara kedua ini yaitu:
peng-ambangan berdasarkan histogram; pertumbuhan area;
pemisahan dan penggabungan area; pengelompokan atau pengklasifikasian; pendekatan teori graf;
pendekatan yang dipandu pengetahuan atau berbasis aturan.
Berdasarkan teknik yang digunakan, segmentasi dapat dibagi menjadi empat kategori berikut(Rangayyan, 2005):
1) teknik peng-ambangan; 2) metode berbasis batas; 3) metode berbasis area;
Segmentasi Citra Ekstraksi Fitur Pengklasifikasi Citra masukan Objek daun Fitur-fitur pada daun Jenis tanaman
Gambar 10.3 Segmentasi sebagai langkah awal sistem klasifikasi
10.2 Deteksi Garis
Deteksi garis pada citra dapat diperoleh melalui penggunaan “cadar” (mask) dengan contoh tercantum pada Gambar 10.4 (Gonzalez & Woods, 2002). Cadar (a) berguna untuk memperoleh garis horizontal, cadar (b) untuk mendapatkan garis yang berorientasi 45o, cadar (c) untuk memperoleh garis tegak, dan cadar (d) untuk mendapatkan garis yang berorientasi -45o.
−1 −1 −1 2 2 2 −1 −1 −1 −1 −1 2 −1 2 −1 2 −1 −1 −1 2 −1 −1 2 −1 −1 2 −1 2 −1 −1 −1 2 −1 −1 −1 2 (a) (b) (c) (d)
Gambar 10.4 Empat pasang cadar untuk mendeteksi keberadaan garis
Fungsi deteksi berikut berguna untuk menguji cadar-cadar yang terdapat pada Gambar 10.4. Fungsi tersebut sekaligus dapat dipakai untuk menguji cadar-cadar yang lain.
Program : deteksi.m
function [G] = deteksi(F, H, potong, pembulatan)
% DETEKSI Melakukan operasi korelasi kernel H dengan citra F % H harus mempunyai tinggi dan lebar ganjil
% Argumen potong bersifat opsional. Apabila
% bernilai true, bagian citra yang tidak diproses % akan dipotong. Bawaan = false
% Argumen pembulatan bersifat opsional.
% Apabila bernilai true, pembulatan dengan uint8 % tidak dilakukan. Bawaan = true
% % Hasil: citra G if nargin < 3 potong = false; end if nargin < 4 pembulatan = true; end
[tinggi_f, lebar_f] = size(F); [tinggi_h, lebar_h] = size(H);
if rem(lebar_h,2) == 0 || rem(tinggi_h,2) == 0 disp('Lebar dan tinggi H harus ganjil'); return; end m2 = floor(tinggi_h/2); n2 = floor(lebar_h/2);
% Menentukan ukuran hasil beserta % penentu ofset koordinat if potong == true sisi_m2 = m2; sisi_n2 = n2; G = zeros(tinggi_f - 2 * m2, lebar_f - 2 * n2); else sisi_m2 = 0; sisi_n2 = 0; G = zeros(size(F)); end F2=double(F);
for y=m2+1 : tinggi_f-m2 for x=n2+1 : lebar_f-n2
% Pelaksanaan korelasi F(baris, kolom) jum = 0; for p=-m2 : m2 for q=-n2 : n2 jum = jum + H(p+m2+1,q+n2+1) * ... F2(y+p, x+q); end end
G(y - sisi_m2, x - sisi_n2) = jum; end end if pembulatan == true G = uint8(G); end Akhir Program
Dengan fungsi di atas, bagian pinggir citra yang tidak diproses akan dibuang sekiranya argumen ketiga tidak diberikan atau diberi nilai false. Dengan demikian, ukuran G akan dipengaruhi oleh ukuran H. Nilai true pada argumen ketiga akan membuat bagian tepi yang tidak diproses berwarna hitam, membentuk seperti bingkai. Argumen keempat digunakan untuk menentukan eksekusi uint8 atau tidak. Dalam banyak hal, argumen keempat tidak perlu disebutkan karena umumnya memang hasil deteksi tepi akan memotong nilai yang di bawah nol dan yang di atas 255. Namun, di belakang akan ada aplikasi yang memerlukan fungsi deteksi tetapi tanpa perlu melakukan pemotongan seperti itu.
Contoh berikut menunjukkan penggunaan deteksi untuk mendapatkan garis tegak:
>> H1 = [-1 -1 -1; 2 2 2; -1 -1 -1]; >> Img = imread('C:\Image\jaring.png'); >> G = deteksi(Img, H1); imshow(G,[0 1]) >>
Hasil deteksi garis dapat dilihat pada Gambar 10.5(b). Terlihat bahwa garis vertikal tidak tampak. Namun, garis miring dan mendatar tetap terdeteksi.
(a) Citra jaring.png (b) Hasil deteksi garis horizontal
Gambar 10.5 Contoh deteksi garis horizontal
Gambar 10.6 memperlihatkan perbedaan hasil yang menggunakan masing- masing satu dari keempat cadar yang tercantum di Gambar 10.4.
Segmentasi Citra 409
Gambar 10.6 Contoh hasil deteksi garis untuk empat arah yang berbeda terhadap gambar pada Gambar 10.5(a)
Deteksi garis juga dapat diperoleh melalui transformasi Hough. Transformasi tersebut dibahas, misalnya, oleh Davies (1990).
10.3 Deteksi Tepi
Deteksi tepi berfungsi untuk memperoleh tepi objek. Deteksi tepi memanfaatkan perubahan nilai intensitas yang drastis pada batas dua area. Definisi tepi di sini adalah “himpunan piksel yang terhubung yang terletak pada batas dua area” (Gonzalez & Woods, 2002). Perlu diketahui, tepi sesungguhnya mengandung informasi yang sangat penting. Informasi yang diperoleh dapat berupa bentuk maupun ukuran objek.
Umumnya, deteksi tepi menggunakan dua macam detektor, yaitu detektor baris (Hy) dan detektor kolom (Hx). Beberapa contoh yang tergolong jenis ini adalaah operator Roberts, Prewitt, Sobel, dan Frei-Chen.
Deteksi tepi dapat dibagi menjadi dua golongan. Golongan pertama disebut deteksi tepi orde pertama, yang bekerja dengan menggunakan turunan atau diferensial orde pertama. Termasuk kelompok ini adalah operator Roberts,
Prewitt, dan Sobel. Golongan kedua dinamakan deteksi tepi orde kedua, yang
menggunakan turunan orde kedua. Contoh yang termasuk kelompok ini adalah
Laplacian of Gaussian (LoG).
Tabel 10.2 memberikan definisi turunan orde pertama dan kedua baik pada bentuk yang kontinu maupun diskret. Bentuk diskret sangat berguna untuk melakukan deteksi tepi. Adapun Gambar 10.7 menunjukkan hubungan antara fungsi citra dan deteksi tepi orde pertama dan orde kedua. Perlu diketahui, terkait dengan turunan, tepi sesungguhnya terletak pada:
nilai absolut maksimum pada turunan pertama; persilangan nol (zero-crossing) pada turunan kedua.
Tabel 10.2 Turunan orde pertama dan kedua pada bentuk kontinu dan diskret
Turunan Bentuk kontinu Bentuk diskret
𝑑𝑓 𝑑𝑥 ∆𝑥→0lim 𝑓(𝑦, 𝑥 + ∆𝑥)𝑓(𝑦, 𝑥) ∆𝑥 f(y,x+1)f(y,x) 𝑑𝑓 𝑑𝑦 ∆𝑥→0lim 𝑓(𝑦 + ∆𝑦, 𝑥)𝑓(𝑦, 𝑥) ∆𝑦 f(y+1,x)f(y,x) ∇𝑓(𝑦, 𝑥) [𝑑𝑓 𝑑𝑦, 𝑑𝑓 𝑑𝑥] [f(y, x+1)f(y,x), f(y+1,x)f(y,x)]
Turunan Bentuk kontinu Bentuk diskret 𝑑2𝑓 𝑑𝑥2 lim ∆𝑥→0 (𝑑𝑓𝑑𝑥)(𝑦, 𝑥 + ∆𝑥) (𝑑𝑓𝑑𝑥) 𝑓(𝑦, 𝑥) ∆𝑥 f(y,x+1)- 2f(y,x)+f(y,x-1) 𝑑2𝑓 𝑑𝑦2 lim ∆𝑥→0 (𝑑𝑓𝑑𝑦) (𝑦 + ∆𝑦, 𝑥) (𝑑𝑓𝑑𝑦) 𝑓(𝑦, 𝑥) ∆𝑦 f(y+1,x) -2f(y,x)+f(y-1,x) ∇2𝑓(𝑦, 𝑥) 𝑑2𝑓 𝑑𝑥2+ 𝑑2𝑓 𝑑𝑦2 f(y,x+1)+f(y,x1) -4f(y,x)+f(y+1,x)+f(y-1,x) 𝑑 𝑑𝑥𝑓(𝑥) 𝑓(𝑥) 𝑑2 𝑑𝑥2𝑓(𝑥)
(a) Fungsi citra
(b) Deteksi tepi
derivatif orde pertama
(c) Deteksi tepi derivatif orde kedua Persilangan nol
(zero-crossing) Nilai maksimum
Batas
a b
Apabila profil citra mempunyai tepi dengan bentuk tanjakan (ramp), fungsi dan turunannya ditunjukkan berikut ini.
Profil aras keabuan Turunan pertama Turunan kedua
Profil citra dapat berupa tepi dengan bentuk atap, garis, undakan, atau tanjakan. Tepi tanjakan Tepi garis Tepi undakan Tepi atap
Contoh pada Gambar 10.7(a) menunjukkan keadaan fungsi intensitas citra f(y,x) pada arah x dengan bentuk tepi tanjakan yang landai. Gambar 10.7(b) menunjukkan keadaan turunan pertama pada arah x. Puncak pada Gambar 10.7(b) menyatakan letak tepi pada turunan pertama, sedangkan persilangan nol pada Gambar 10.7(c) menyatakan letak tepi pada turunan kedua. Apabila nilai batas dikenakan pada turunan pertama, puncak tidak lagi menjadi tepi. Akibatnya, terdapat dua nilai yang memenuhi (yaitu a dan b). Kedua nilai tersebut akan menjadi piksel-piksel tepi. Berbeda halnya pada turunan kedua, tepi akan selalu berupa satu piksel. Hal itu terlihat pada perpotongan fungsi turunan kedua dengan sumbu x. Akibatnya, ketebalan tepi akan selalu berupa satu piksel.
Untuk memahami profil citra yang berhubungan dengan tepi, perhatikan matriks yang berukuran 4 x 6 berikut.
[ 168 168 168 168 168 168 0 0 0 0 0 0 168 168 168 168 168 168 0 0 0 0 0 0 ]
Pada contoh tersebut perubahan nilai dari sisi kiri (168) ke sisi kanan (0) sangat drastis, tidak bertahap. Profil citra tersebut berupa tepi undakan. Adapun matriks berikut mengandung tepi tanjakan:
168 168 168 138 87 30 0 0 0 168 168 168 138 87 30 0 0 0 168 168 168 138 87 30 0 0 0
Perhatikan, terjadi perubahan nilai secara bertahap dari transisi 168 ke 0.
Contoh dalam bentuk citra:
tepi undakan tepi tanjakan
Deteksi tepi dengan turunan orde pertama dilakukan dengan menggunakan operator gradien. Operator gradien didefinisikan sebagai vektor
𝒗𝒇 = [ 𝐺𝑥 𝐺𝑦] = [ 𝑑𝑓 𝑑𝑥 𝑑𝑓 𝑑𝑦 ] (10.1)
Besaran vektor dihitung menggunakan rumus ∇𝑓 = 𝑚𝑎𝑔(∇f) = [𝐺𝑥2+ 𝐺𝑦2] 1/2 = [(𝑑𝑓 𝑑𝑥) 2+ (𝑑𝑓 𝑑𝑦) 2]1/2 (10.2)
Namun, untuk alasan penyederhanaan komputasi, operasi akar ditiadakan sehingga besaran vektor tersebut dihampiri melalui
∇𝑓 ≈ 𝐺𝑥2+ 𝐺
𝑦2 (10.3)
Perlu diketahui, besaran gradien sering disebut sebagai “gradien” saja.
Adapun turunan orde kedua yang biasa digunakan dalam pengolahan citra dihitung dengan menggunakan Laplacian. Perhitungannya seperti berikut:
∇2𝑓(𝑦, 𝑥) = 𝑑2𝑓(𝑦,𝑥) 𝑑𝑥2 +
𝑑2𝑓(𝑦,𝑥)
𝑑𝑦2 (10.4)
Cadar yang digunakan pada deteksi tepi dalam buku ini telah disesuaikan agar proses terhadap citra dapat dilakukan secara korelasi (bukan konvolusi). Itulah sebabnya, ada kemungkinan cadar yang digunakan pada buku ini berbeda dengan cadar di literatur lain.
Berbagai teknik deteksi tepi bekerja dengan cara yang berbeda. Masing-masing memiliki kekuatan (Crane, 1997). Itulah sebabnya, eksperimen pada suatu aplikasi dengan menggunakan berbagai teknik deteksi tepi perlu dilakukan untuk mendapatkan hasil yang terbaik.
10.3.1 Operator Roberts
Operator Roberts, yang pertama kali dipublikasikan pada tahun 1965, terdiri atas dua filter berukuran 2x2. Ukuran filter yang kecil membuat komputasi sangat cepat. Namun, kelebihan ini sekaligus menimbulkan kelemahan, yakni sangat terpengaruh oleh derau. Selain itu, operator Roberts memberikan tanggapan yang lemah terhadap tepi, kecuali kalau tepi sangat tajam (Fisher, dkk., 2003).
(b) Gx (a) Posisi pada citra f
z1 z2 z3 z4 x x+1 y y+1 1 0 0 -1 0 -1 1 0 (c) Gy
Gambar 10.8 Operator Roberts (b) dan (c) serta posisi pada citra f
Bentuk operator Roberts ditunjukkan pada Gambar 10.8. Misalkan, f adalah citra yang akan dikenai operator Roberts. Maka, nilai operator Roberts pada (y, x) didefinisikan sebagai
𝑟(𝑦, 𝑥) = √(𝑧1− 𝑧4)2+ (𝑧
3− 𝑧2)2 (10.5)
Dalam hal ini, z1 = f(y, x), z2 = f(y, x+1), z3 = f(y+1, x), dan z4 = f(y+1, x+1). Fungsi roberts berikut berguna untuk memperoleh tepi pada citra berskala keabuan.
Program : roberts.m
function [G] = roberts(F)
% ROBERTS Pemerolehan tepi objek pada citra F % melalui operator Roberts
% Hasil: citra G
[m, n] = size(F); F=double(F); for y=1 : m-1 for x=1 : n-1 G(y, x) = sqrt((F(y,x)-F(y+1,x+1))^2 + ... (F(y+1,x)-F(y,x+1))^2) ; end end G = uint8(G); Akhir Program
Contoh penggunaan fungsi roberts:
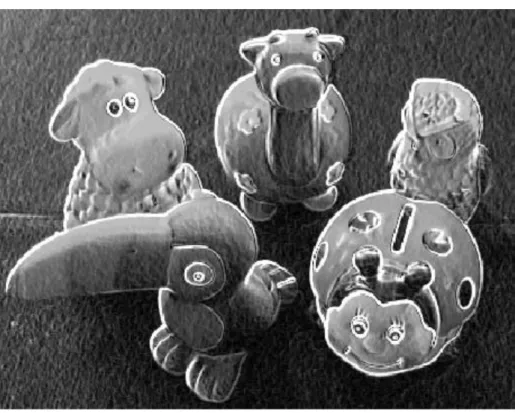
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> G = roberts(Img);
>> imshow(G) >>
(a) Citra mainan.png
(b) Hasil deteksi tepi dengan operator Roberts
Gambar 10.9 Pengenaan operator Roberts pada citra mainan.png
10.3.2 Operator Prewitt
Operator Prewitt dikemukakan oleh Prewitt pada tahun 1966. Bentuknya terlihat pada Gambar 10.10. Untuk mempercepat komputasi, bagian yang bernilai nol tidak perlu diproses. Oleh karena itu, perhitungan dengan operator Prewitt ditulis menjadi
𝑟(𝑦, 𝑥) = sqrt((f(y-1,x-1)+f(y,x-1)+f(y+1,x-1) -
f(y-1,x+1)-f(y,x+1)-f(y+1,x+1))^2 + (10.6) (f(y+1,x-1)+ f(y+1,x) + f(y+1,x+1) -
f(y-1,x-1) - f(y-1,x) - f(y-1,x+1))^2))
(b) Gx
(a) Posisi pada citra f (c) Gy
1 0 1 0 -1 -1 1 0 -1 -1 -1 0 0 -1 0 1 1 1 x x+1 y y+1 x-1 y-1 z1 z2 z4 z5 z3 z6 z7 z8 z9
Gambar 10.10 Operator Prewitt (b) dan (c) serta posisi pada citra f
Fungsi prewitt berikut berguna untuk melakukan pengujian operator
Prewitt terhadap citra berskala keabuan.
Program : prewitt.m
function [G] = prewitt(F)
% PREWITT Pemerolehan tepi objek pada citra F % melalui operator Prewitt
% Hasil: citra G [m, n] = size(F); F=double(F); G=zeros(m,n); for y=2 : m-1 for x=2 : n-1
G(y, x) = sqrt((F(y-1,x-1) + F(y,x-1) + F(y+1,x-1) - ... F(y,x) - F(y,x+1) - F(y+1,x+1))^2 + ...
(F(y+1,x-1)+ F(y+1,x) + F(y+1,x+1) - ... F(y-1,x-1) - F(y-1,x) - F(y-1,x+1))^2) ; end end G = uint8(G); Akhir Program
Contoh penggunaan fungsi prewitt:
>> G = prewitt(Img); >> imshow(G)
>>
Hasil deteksi tepi pada citra mainan.png dapat dilihat pada Gambar 10.11.
Gambar 10.11 Hasil deteksi tepi dengan operator Prewitt. Hasil tepi lebih tegas daripada hasil dengan operator Roberts
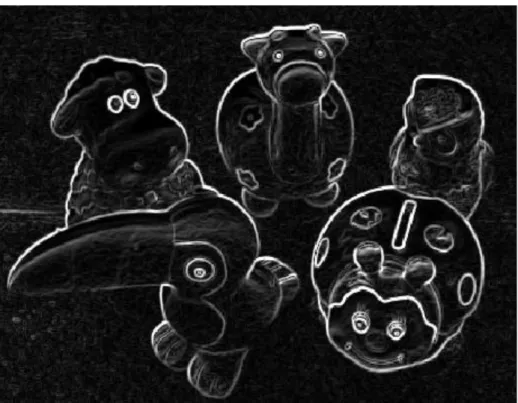
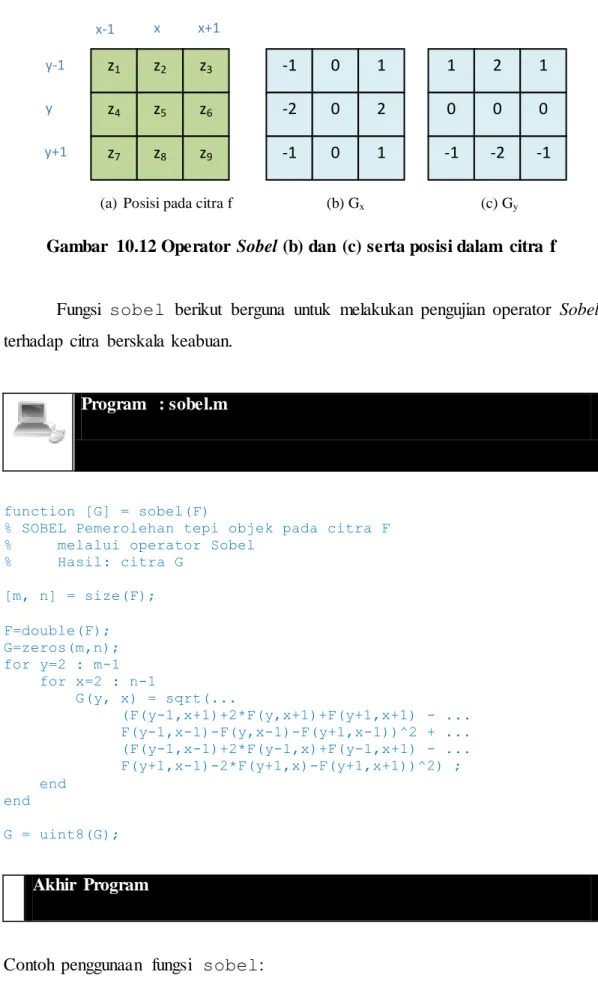
10.3.3 Operator Sobel
Operator Sobel dapat dilihat pada Gambar 10.12. Operator Sobel lebih sensitif terhadap tepi diagonal daripada tepi vertikal dan horizontal Hal ini berbeda dengan operator Prewitt, yang lebih sensitif terhadap tepi vertikal dan horizontal (Crane, 1997).
Fungsi deteksi dapat digunakan untuk mengamati efek cadar Gx dan Gy pada operator Prewitt secara individual. Contoh penggunaannya seperti berikut:
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> Gx = [ 1 0 -1; 1 0 -1; 1 0 -1];
>> G = deteksi(Img, Gx); imshow(G) >>
(b) Gx (a) Posisi pada citra f
-1 0 -2 0 (c) Gy 1 2 -1 0 1 1 2 0 0 1 0 -1 -2 -1 x x+1 y y+1 x-1 y-1 z1 z2 z4 z5 z3 z6 z7 z8 z9
Gambar 10.12 Operator Sobel (b) dan (c) serta posisi dalam citra f
Fungsi sobel berikut berguna untuk melakukan pengujian operator Sobel terhadap citra berskala keabuan.
Program : sobel.m
function [G] = sobel(F)
% SOBEL Pemerolehan tepi objek pada citra F % melalui operator Sobel
% Hasil: citra G [m, n] = size(F); F=double(F); G=zeros(m,n); for y=2 : m-1 for x=2 : n-1 G(y, x) = sqrt(... (F(y-1,x+1)+2*F(y,x+1)+F(y+1,x+1) - ... F(y-1,x-1)-F(y,x-1)-F(y+1,x-1))^2 + ... (F(y-1,x-1)+2*F(y-1,x)+F(y-1,x+1) - ... F(y+1,x-1)-2*F(y+1,x)-F(y+1,x+1))^2) ; end end G = uint8(G); Akhir Program
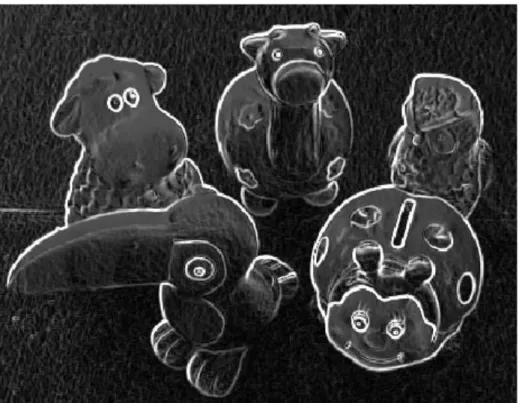
Contoh penggunaan fungsi sobel:
>> G = sobel(Img); >> imshow(G)
>>
Hasil deteksi tepi pada citra mainan.png dapat dilihat pada Gambar 10.13.
Gambar 10.13 Hasil deteksi tepi dengan operator Sobel
10.3.4 Operator Frei-Chen
Operator Frei-Chen (kadang disebut operator isotropik) ditunjukkan pada Gambar 10.14. Operator ini mirip dengan operator Sobel, dengan setiap angka 2 diganti menjadi √2.
(b) Gx (a) Posisi pada citra f
-1 0 -√2 0 (c) Gy 1 √2 -1 0 1 1 √2 0 0 1 0 -1 -√2 -1 x x+1 y y+1 x-1 y-1 z1 z2 z4 z5 z3 z6 z7 z8 z9
Fungsi freichen berikut berguna untuk melakukan pengujian operator
Frei-Chen terhadap citra berskala keabuan.
Program : freichen.m
function [G] = freichen(F)
% FREICHEN Pemerolehan tepi objek pada citra F % melalui operator Frei-Chen
% Hasil: citra G [m, n] = size(F); akar2 = sqrt(2); F=double(F); G=zeros(m,n); for y=2 : m-1 for x=2 : n-1 G(y, x) = sqrt(... (F(y-1,x+1)+akar2*F(y,x+1)+F(y+1,x+1) - ... F(y-1,x-1)-F(y,x-1)-F(y+1,x-1))^2 + ... (F(y-1,x-1)+akar2*F(y-1,x)+F(y-1,x+1) - ... F(y+1,x-1)-akar2*F(y+1,x)-F(y+1,x+1))^2) ; end end G = uint8(G); Akhir Program
Contoh penggunaan fungsi freichen:
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> G = freichen(Img);
>> imshow(G) >>
Gambar 10.15 Hasil deteksi tepi dengan operator Frei-Chen
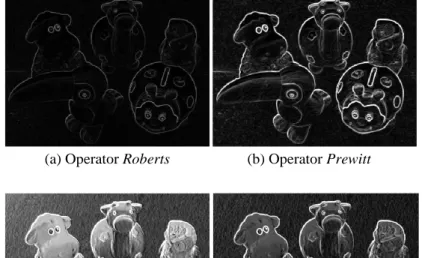
Gambar 10.16 memperlihatkan perbedaan secara visual hasil deteksi tepi dengan menggunakan operator Roberts, Prewitt, Sobel, dan Frei-Chen. Perlu diketahui, hasil pada gambar tersebut masih berskala keabuan. Untuk menjadi citra biner, perlu dilakukan peng-ambangan yang mulai dibahas pada Subbab 10.4. Contoh hasil peng-ambangan dapat dilihat pada Gambar 10.17.
(a) Operator Roberts (b) Operator Prewitt
(c) Operator Sobel (d) Operator Frei-Chen
Gambar 10.16 Perbedaan hasil deteksi tepi dengan menggunakan keempat macam operator
(a) Hasil deteksi tepi dengan
operator Roberts (a) Hasil deteksi tepi dengan
operator Roberts
(b) Hasil setelah peng-ambangan dengan nilai ambang 20
Gambar 10.17 Contoh hasil deteksi tepi dan peng-ambangan
10.3.5 Operator Laplacian
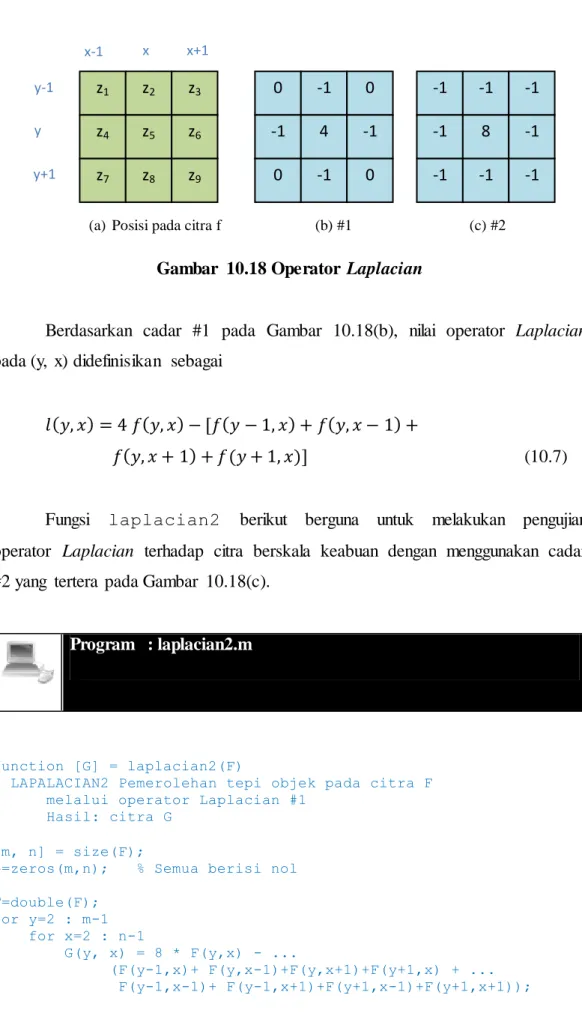
Operator Laplacian merupakan contoh operator yang berdasarkan pada turunan kedua. Operator ini bersifat omnidirectional, yakni menebalkan bagian tepi ke segala arah. Namun, operator Laplacian memiliki kelemahan, yakni peka terhadap derau, memberikan ketebalan ganda, dan tidak mampu mendeteksi arah tepi (Gonzalez & Woods, 2002). Contoh cadar ditunjukkan pada Gambar 10.18.
(b) #1 (a) Posisi pada citra f
0 -1 -1 4 (c) #2 0 -1 0 -1 0 -1 -1 -1 8 -1 -1 -1 -1 -1 x x+1 y y+1 x-1 y-1 z1 z2 z4 z5 z3 z6 z7 z8 z9
Gambar 10.18 Operator Laplacian
Berdasarkan cadar #1 pada Gambar 10.18(b), nilai operator Laplacian pada (y, x) didefinisikan sebagai
𝑙(𝑦, 𝑥) = 4 𝑓(𝑦, 𝑥) − [𝑓(𝑦 − 1, 𝑥) + 𝑓(𝑦, 𝑥 − 1) +
𝑓(𝑦, 𝑥 + 1) + 𝑓(𝑦 + 1, 𝑥)] (10.7)
Fungsi laplacian2 berikut berguna untuk melakukan pengujian operator Laplacian terhadap citra berskala keabuan dengan menggunakan cadar #2 yang tertera pada Gambar 10.18(c).
Program : laplacian2.m
function [G] = laplacian2(F)
% LAPALACIAN2 Pemerolehan tepi objek pada citra F % melalui operator Laplacian #1
% Hasil: citra G
[m, n] = size(F);
G=zeros(m,n); % Semua berisi nol F=double(F); for y=2 : m-1 for x=2 : n-1 G(y, x) = 8 * F(y,x) - ... (F(y-1,x)+ F(y,x-1)+F(y,x+1)+F(y+1,x) + ... F(y-1,x-1)+ F(y-1,x+1)+F(y+1,x-1)+F(y+1,x+1));
end end
G = uint8(G);
Akhir Program
Contoh penggunaan fungsi laplacian2:
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> G = laplacian2(Img);
>> imshow(G) >>
Hasil deteksi tepi pada citra mainan.png dapat dilihat pada Gambar 10.19.
Gambar 10.19 Hasil deteksi tepi menggunakan operator Laplacian #2
10.3.6 Operator Laplacian of Gaussian
Deteksi tepi orde kedua yang makin kurang sensitif terhadap derau adalah
yang memuluskan citra dan berdampak pada pengurangan derau pada citra. Akibatnya, operator mereduksi jumlah tepi yang salah terdeteksi (Crane, 1997).
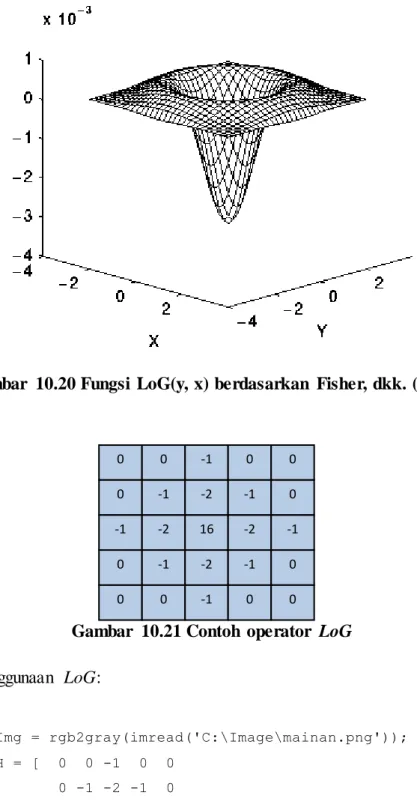
Menurut Fisher, dkk. (2003), operator LoG diperoleh melalui konvolusi dengan 𝐿𝑜𝐺(𝑦, 𝑥) = − 1 𝜋𝜎4[1 − 𝑥2+𝑦2 2𝜎2 ] 𝑒 −(𝑥2+𝑦2 ) 2𝜎2 (10.8)
Fungsi di atas disebut sebagai filter topi Meksiko (the Mexican hat filter) karena bentuknya seperti topi yang biasa dikenakan orang Meksiko (lihat Gambar 10.20). Dalam hal ini, semakin besar nilai , semakin besar pula cadar yang diperlukan. Contoh cadar berukuran 5 x 5 yang mewakili operator LoG ditunjukkan pada Gambar 10.21 (Gonzalez & Woods, 2002).
Dalam praktik, terdapat berbagai variasi rumus yang digunakan dalam LoG. Gonzalez dan Woods (2002) menggunakan rumus seperti berikut: 𝐿𝑜𝐺(𝑦, 𝑥) = − [𝑥 2+ 𝑦2− 𝜎2 𝜎4 ] 𝑒 −(𝑥2+𝑦2) 2𝜎2
Nixon dan Aguido (2002) menggunakan rumus:
𝐿𝑜𝐺(𝑦, 𝑥) = 1 𝜎2[ 𝑥2+ 𝑦2 𝜎2 − 2] 𝑒 −(𝑥2+𝑦2) 2𝜎2
Adapun Crane (1997) menggunakan rumus:
𝐿𝑜𝐺(𝑦, 𝑥) = 1 𝜋𝜎4[1 − 𝑥2+ 𝑦2 2𝜎2 ] 𝑒 −(𝑥2+𝑦2) 2𝜎2
Gambar 10.20 Fungsi LoG(y, x) berdasarkan Fisher, dkk. (2003)
Gambar 10.21 Contoh operator LoG
Contoh penggunaan LoG:
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> H = [ 0 0 -1 0 0 0 -1 -2 -1 0 -1 -2 16 -2 -1 0 -1 -2 -1 0 0 0 -1 0 0]; >> G = deteksi(Img, H); imshow(G) >>
Hasil deteksi tepi pada citra mainan.png dapat dilihat pada Gambar 10.22.
0 0 -1 0 0
0 -1 -2 -1 0
-1 -2 16 -2 -1
0 -1 -2 -1 0
Gambar 10.22 Contoh hasil deteksi tepi dengan LoG
Nixon & Aguado (2002) memberikan cara yang dapat digunakan untuk memperoleh cadar LoG berdasarkan nilai dan ukuran. Cara tersebut tertuang dalam algoritma berikut.
ALGORITMA 10.1 – Memperoleh cadar LoG
Masukan:
Ukuran : ukuran cadar
: Deviasi standar Keluaran: h (M, N): Cadar LoG cadarLoG(ukuran, ): 1. cx floor((ukuran-1) / 2) 2. cy cx 3. jum 0 4. FOR y 0 TO ukuran -1 FOR x 0 TO ukuran -1 nx x – cx ny y – cy
nilai 1 𝜎2[ 𝑛𝑥2+ 𝑛𝑦2 𝜎2 − 2] 𝑒 −(𝑛𝑥2+ 𝑛𝑦2 ) 2𝜎2 h(y+1, x+1) nilai
jum jum + nilai END-FOR
END-FOR
5. // Lakukan normalisasi FOR y 1 TO ukuran FOR y 1 TO ukuran h(y, x) h(y, x) / jum
END-FOR END-FOR 6. RETURN h
Pada algoritma di atas, normalisasi dilakukan agar jumlah koefisien pada cadar bernilai 1. Implementasi perolehan cadar LoG dapat dilihat pada cadarLoG.m.
Program : cadarLoG.m
function [H] = cadarLoG(ukuran, sigma)
% CADARLOG Menghasilkan cadar LoG berdasarkan % Nixon dan Aguido (2002)
% Masukan:
% ukuran : ukuran cadar % sigma : Deviasi standar % Keluaran : H = cadar LoG cx = floor((ukuran-1) / 2); cy = cx; jum = 0; H = zeros(ukuran, ukuran); for y=0 : ukuran-1
for x=0 : ukuran -1 nx = x - cx; ny = y - cy; nilai = 1 / (sigma ^ 2) * ... ((nx^2 + ny^2)/(sigma^2)-2) * ...
exp((-nx^2 - ny^2) / (2 * sigma^2)); H(y+1, x+1) = nilai;
jum = jum + nilai; end
end
% Lakukan normalisasi for y=1 : ukuran
for x=1 : ukuran
H(y,x) = H(y,x) / jum; end
end
Akhir Program
Contoh penggunaan cadarLoG untuk memperoleh cadar LoG berukuran 7 x 7 dengan = 0,6 : >> cadarLoG(7, 0.6) ans = -0.0000 -0.0000 -0.0002 -0.0008 -0.0002 -0.0000 -0.0000 -0.0000 -0.0029 -0.1085 -0.3335 -0.1085 -0.0029 -0.0000 -0.0002 -0.1085 -2.0930 -1.8361 -2.0930 -0.1085 -0.0002 -0.0008 -0.3335 -1.8361 18.9348 -1.8361 -0.3335 -0.0008 -0.0002 -0.1085 -2.0930 -1.8361 -2.0930 -0.1085 -0.0002 -0.0000 -0.0029 -0.1085 -0.3335 -0.1085 -0.0029 -0.0000 -0.0000 -0.0000 -0.0002 -0.0008 -0.0002 -0.0000 -0.0000 >>
Adapun contoh berikut untuk memperoleh cadar LoG berukuran 7 x 7 dengan = 1 : >> cadarLoG(7, 1) ans = -0.0385 -0.3221 -1.0499 -1.5146 -1.0499 -0.3221 -0.0385 -0.3221 -2.1404 -4.7962 -5.2717 -4.7962 -2.1404 -0.3221 -1.0499 -4.7962 0 11.8132 0 -4.7962 -1.0499 -1.5146 -5.2717 11.8132 38.9532 11.8132 -5.2717 -1.5146
-1.0499 -4.7962 0 11.8132 0 -4.7962 -1.0499 -0.3221 -2.1404 -4.7962 -5.2717 -4.7962 -2.1404 -0.3221 -0.0385 -0.3221 -1.0499 -1.5146 -1.0499 -0.3221 -0.0385
>>
Cadar LoG akan bermanfaat untuk kepentingan pemrosesan dengan operator Marr-Hildreth, yang dibahas pada Bagian 10.4.10.
10.3.7 Operator Difference of Gaussian
Mengingat LoG memerlukan komputasi yang besar, Difference of Gaussian (DoG) biasa digunakan sebagai hampiran terhadap LoG. Fungsi DoG berupa
𝐷𝑜𝐺(𝑦. 𝑥) =𝑒 −(𝑥2+𝑦2) 2𝜎1 2 2𝜎12 − 𝑒 −(𝑥2+𝑦2) 2𝜎22 2𝜎22 (10.9)
Terlihat bahwa DoG dilaksanakan dengan melakukan konvolusi citra dengan sebuah cadar yang merupakan hasil pengurangan dua buah cadar Gaussian dengan nilai yang berbeda. Gambar 10.23 menunjukkan dua cadar yang dapat digunakan untuk melaksanakan DoG (Crane, 1997).
(a) Cadar berukuran 7 x 7 0 0 0 -1 -1 -1 0 0 0 0 -2 -3 -3 -3 -3 -3 -2 0 0 -3 -2 -1 -1 -1 -2 -3 0 -1 -3 -1 9 9 9 -1 -3 -1 -1 -3 -1 9 9 9 -1 -3 -1 -1 -3 -1 9 9 9 -1 -3 -1 0 -3 -2 -1 -1 -1 -2 -3 0 0 -2 -3 -3 -3 -3 -3 -2 0 0 0 0 -1 -1 -1 0 0 0 (b) Cadar berukuran 9 x 9 0 0 -1 -1 -1 0 0 0 -2 -3 -3 -3 -2 0 -1 -3 5 5 5 -3 -1 -1 -3 5 16 5 -3 -1 -1 -3 5 5 5 -3 -1 0 -2 -3 -3 -3 -2 0 0 0 -1 -1 -1 0 0
Gambar 10.23 Contoh cadar DoG
Contoh penggunaan DoG:
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> H = [ 0 0 -1 -1 -1 0 0 0 -2 -3 -3 -3 -2 0 -1 -3 5 5 5 -3 -1 -1 -3 5 16 5 -3 -1 -1 -3 5 5 5 -3 -1 0 -2 -3 -3 -3 -2 0 0 0 -1 -1 -1 0 0 ]; >> G = deteksi(Img, H); imshow(G) >>
Gambar 10.24 Hasil deteksi tepi menggunakan DoG
10.3.9 Operator Canny
Operator Canny, yang dikemukakan oleh John Canny pada tahun 1986, terkenal sebagai operator deteksi tepi yang optimal. Algoritma ini memberikan tingkat kesalahan yang rendah, melokalisasi titik-titik tepi (jarak piksel-piksel tepi yang ditemukan deteksi dan tepi yang sesungguhnya sangat pendek), dan hanya memberikan satu tanggapan untuk satu tepi.
Terdapat enam langkah yang dilakukan untuk mengimplementasikan deteksi tepi Canny (Green, 2002). Keenam langkah tersebut dijabarkan berikut ini.
Langkah 1:
Pertama-tama dilakukan penapisan terhadap citra dengan tujuan untuk menghilangkan derau. Hal ini dapat dilakukan dengan menggunakan filter
Gaussian dengan cadar sederhana. Cadar yang digunakan berukuran jauh lebih
Gambar 10.25 Contoh cadar Gaussian dengan theta = 1,4
Langkah 2:
Setelah penghalusan gambar terhadap derau dilakukan, dilakukan proses untuk mendapatkan kekuatan tepi (edge strength). Hal ini dilakukan dengan menggunakan operator Gaussian.
Selanjutnya, gradien citra dapat dihitung melalui rumus:
y
x
G
G
G
(10.10)Langkah 3:
Langkah ketiga berupa penghitungan arah tepi. Rumus yang digunakan untuk keperluan ini:
theta = tan-1(G
y, Gx) (10.11)
Langkah 4:
Setelah arah tepi diperoleh, perlu menghubungkan antara arah tepi dengan sebuah arah yang dapat dilacak dari citra. Sebagai contoh, terdapat susunan piksel berukuran 5 x 5 seperti terlihat pada Gambar 10.26. Dengan melihat piksel “a” tampak bahwa a hanya memiliki 4 arah berupa 0o, 45o, 90o, dan 135o.
2 4 5 4 2 4 9 12 9 4 5 12 15 12 5 4 9 12 9 4 2 4 5 4 2 1 / 115
Segmentasi Citra 437
X X X X X
X X X X X
X X a X X
X X X X X
X X X X X
Gambar 10.26 Matriks piksel berukuran 5x5
Selanjutnya, arah tepi yang diperoleh akan dimasukkan ke dalam salah satu kategori dari keempat arah tadi berdasarkan area yang tertera pada Gambar 10.27. Berikut adalah aturan konversi yang berlaku:
135
90
45
0
arah
j H j TH ij T i j j HI ij H H iy
w
f
y
x
w
f
y
) ( ) ( ) ( ) ( ) ( ) ( (10.12)45
o
135
o
90
o
Gambar 10.27 Area untuk mengonversi arah tepi ke dalam kategori salah satu dari arah 0o, 45o, 90o, dan 135o
Semua arah tepi yang berkisar antara 0 dan 22,5 serta 157,5 dan 180 derajat (warna biru) diubah menjadi 0 derajat. Semua arah tepi yang berkisar antara 22,5 dan 67,5 derajat (warna kuning) diubah menjadi 45 derajat. Semua arah tepi yang
berkisar antara 67,5 dan 112,5 derajat (warna merah) diubah menjadi 90 derajat. Semua arah tepi yang berkisar antara 112,5 dan 157,5 derajat (warna hijau) diubah menjadi 135 derajat.
Langkah 5
Setelah arah tepi diperoleh, penghilangan non-maksimum dilaksanakan. Penghilangan non-maksimum dilakukan di sepanjang tepi pada arah tepi dan menghilangkan piksel-piksel (piksel diatur menjadi 0) yang tidak dianggap sebagai tepi. Dengan cara seperti itu, diperoleh tepi yang tipis.
Langkah 6:
Langkah keenam berupa proses yang disebut hysteresis. Proses ini menghilangkan garis-garis yang seperti terputus-putus pada tepi objek. Caranya adalah dengan menggunakan dua ambang T1 dan T2. Lalu, semua piksel citra yang bernilai lebih besar daripada T1 dianggap sebagai piksel tepi. Selanjutnya, semua piksel yang terhubung dengan piksel tersebut dan memiliki nilai lebih besar dari T2 juga dianggap sebagai piksel tepi.
Bagian penting yang perlu dijelaskan adalah penghilangan non-maksimum dan peng-ambangan histeresis. Penghilangan non-maksimum dilakukan dengan mula-mula menyalin isi larik Grad (yang berisi besaran gradien) ke Non_max. Selanjutnya, penghilangan non-maksimum dilaksanakan dengan memperhatikan dua titik tetangga yang terletak pada arah tepi (yang tersimpan dalam Theta). Misalnya, arah tepi adalah 0. Apabila titik yang menjadi perhatian mempunyai koordinat (r, c), dua titik tetangga berupa (r, c-1) dan (r, c+1). Apabila gradien titik perhatian lebih besar daripada gradien kedua tetangga, nilainya akan dipertahankan. Sebaliknya, jika nilai titik perhatian lebih kecil daripada nilai salah satu atau kedua gradien tetangga, nilainya akan diabaikan (diubah menjadi nol). Seluruh kemungkinan proses seperti itu dijabarkan dalam Gambar 10.28.
Arah tepi 135o: if (Grad(i,j) <= Grad(i+1,j+1)) || ... (Grad(i,j) <= Grad(i-1,j-1)) Non_max(i,j) = 0; end Arah tepi 45o: if (Grad(i,j) <= Grad(i-1,j+1)) || ... (Grad(i,j) <= Grad(i+1,j-1)) Non_max(i,j) = 0; end i+1, j-1 i, j i-1, j+1 i, j i-1, j-1 i, j+1 Arah tepi 90o: if (Grad(i,j) <= Grad(i+1,j) ) || ... (Grad(i,j) <= Grad(i-1,j)) Non_max(i,j) = 0; end i, j i-1, j i, j+1 Arah tepi 0o: if (Grad(i,j) <= Grad(i,j+1)) || ... (Grad(i,j)<= Grad(i,j-1)) Non_max(i,j) = 0; end i, j-1 i, j i, j+1
Gambar 10.28 Penghilangan non-maksimum
Peng-ambangan histeresis dilakukan dengan melibatkan dua ambang T1 (ambang bawah) dan ambang T2 (ambang atas). Nilai yang kurang dari T1 akan diubah menjadi hitam (nilai 0) dan nilai yang lebih dari T2 diubah menjadi putih (nilai 255). Lalu, bagaimana nilai yang lebih dari atau sama dengan T1 tetapi kurang dari T2? Oleh karena itu, untuk sementara nilai pada posisi seperti itu diberi nilai 128, yang menyatakan nilai abu-abu atau belum jelas, akan dijadikan 0 atau 255.
Selanjutnya, dilakukan pengujian untuk mendapatkan kondisi seperti tercantum pada Gambar 10.29. Apabila kondisi seperti itu terpenuhi, angka 128 diubah menjadi 255. Proses pengujian seperti itu dilakukan sampai tidak ada lagi perubahan dari nilai 128 menjadi 255. Tahap selanjutnya, semua piksel yang bernilai 128 yang tersisa diubah menjadi nol.
255 255 255 128 255 255 255 255 255 255 255 255 255 255 255 255 255 255 j-1 j j+1 i-1 i i+1
Gambar 10.29 Pengujian untuk mengubah nilai 128 menjadi 255
Implementasi operator Canny dapat dilihat pada canny.m. Sejumlah keterangan diberikan pada skrip, untuk menjelaskan kode.
Program : canny.m
function [K] = canny(F, ambang_bawah, ambang_atas) % CANNY Pemerolehan tepi objek pada citra F
% melalui operator Canny % Masukan:
% ambang_bawah = batas bawah untuk ambang histeresis % Nilai bawaan 011
% ambang_atas = batas atas untuk ambang histeresis % Nilai bawaan 0,3
% Hasil: citra G
% Menentukan nilai ambang bawaan if nargin < 2 ambang_bawah = 0.1; end if nargin < 2 ambang_atas = 0.3; end % Kernel Gaussians HG = [ 2 4 5 4 2 4 9 12 9 12 5 12 15 12 5 4 9 12 9 12 2 4 5 4 2 ] / 115.0; [hHG, wHG] = size(HG); h2 = floor(hHG / 2); w2 = floor(wHG / 2);
% Kenakan operasi Gaussian
G = double(deteksi(F, HG, true));
% Pastikan hasilnya berada antara 0 sampai dengan 255 [m, n] = size(G);
for i = 1 : m for j = 1 : n G(i, j) = round(G(i, j)); if G(i, j) > 255 G(i, j) = 255; else if G(i, j) < 0 G(i, j) = 0; end end end end
% Kenakan perhitungan gradien dan arah tepi Theta = zeros(m, n); Grad = zeros(m, n); for i = 1 : m-1 for j = 1 : n-1 gx = (G(i,j+1)-G(i,j) + ... G(i+1,j+1)-G(i+1,j)) / 2; gy = (G(i,j)-G(i+1,j) + ... G(i,j+1)-G(i+1,j+1)) / 2; Grad(i, j) = sqrt(gx.^2 + gy.^2); Theta(i,j) = atan2(gy, gx); end end
% Konversi arah tepi menjadi 0, 45, 90, atau 135 derajat [r c] = size (Theta);
if Theta < 0
Theta = Theta + pi; % Jangkauan menjadi 0 s/d pi end
for i = 1 : r for j = 1 : c
if (Theta(i,j) < pi/8 || Theta(i,j) >= 7/8*pi) Theta(i,j) = 0;
elseif (Theta(i,j)>=pi/8 && Theta(i,j) < 3*pi/8 ) Theta(i,j) = 45;
elseif (Theta(i,j) >=3*pi/8 && Theta(i,j) < 5*pi/8 ) Theta(i,j) = 90; else Theta(i,j) = 135; end end end % penghilangan non-maksimum Non_max = Grad; for i = 1+h2 : r-h2 for j = 1+w2 : c-h2 if Theta(i,j) == 0 if (Grad(i,j) <= Grad(i,j+1)) || ... (Grad(i,j)<= Grad(i,j-1)) Non_max(i,j) = 0; end
elseif Theta(i,j) == 45 if (Grad(i,j) <= Grad(i-1,j+1)) || ... (Grad(i,j) <= Grad(i+1,j-1)) Non_max(i,j) = 0; end elseif Theta(i,j) == 90 if (Grad(i,j) <= Grad(i+1,j) ) || ... (Grad(i,j) <= Grad(i-1,j)) Non_max(i,j) = 0; end else if (Grad(i,j) <= Grad(i+1,j+1)) || ... (Grad(i,j) <= Grad(i-1,j-1)) Non_max(i,j) = 0; end end end end % Pengambangan histeresis
ambang_bawah = ambang_bawah * max(max(Non_max)); ambang_atas = ambang_atas * max(max(Non_max));
Histeresis = Non_max;
% --- Penentuan awal untuk memberikan nilai % --- 0, 128, dan 255 for i = 1+h2 : r-h2 for j = 1+w2 : c-w2 if (Histeresis(i,j) >= ambang_atas) Histeresis(i,j) = 255; end
if (Histeresis(i,j) < ambang_atas) && ... (Histeresis(i,j) >= ambang_bawah) Histeresis(i,j)= 128; end if (Histeresis(i,j) < ambang_bawah) Histeresis(i,j) = 0; end end end
% --- Penggantian angka 128 menjadi 255
% --- Berakhir kalau tidak ada lagi yang berubah ulang = true; while ulang ulang = false; for i = 1+h2 : r-h2 for j = 1+w2 : c-w2 if (Histeresis(i,j) == 128) if (Histeresis(i-1, j-1) == 255) && ... (Histeresis(i-1, j) == 255) && ... (Histeresis(i, j+1) == 255) && ... (Histeresis(i, j-1) == 255) && ... (Histeresis(i, j+1) == 255) && ... (Histeresis(i+1, j-1) == 255) && ... (Histeresis(i+1, j) == 255) && ...
(Histeresis(i+1, j+1) == 255) Histeresis(i,j) = 255;
ulang = true; % Ulang pengujian end end end end end
% --- Penggantian angka 128 menjadi 0 % --- untuk yang tersisa
for i = 1+h2 : r-h2 for j = 1+w2 : c-w2 if (Histeresis(i,j) == 128) Histeresis(i,j) = 0; end end end % Buang tepi for i = 1+h2 : r-h2 for j = 1+w2 : c-w2 K(i-1,j-1) = Histeresis(i,j); end end Akhir Program
Contoh penggunaan fungsi canny:
>> Img = imread('C:\Image\lena256.png'); >> G = canny(Img, 0.05, 0.15); imshow(G) >>
Contoh di atas menggunakan peng-ambangan berupa 0,05 untuk batas bawah dan 0,15 untuk batas atas. Hasilnya dapat dilihat pada Gambar 10.30.
(b) Efek Gaussian (a) Citra lena256.tif
(d) Penghilangan non-maksimum
(c) Besaran gradien
(e) Hasil operator Canny
Gambar 10.30 Contoh hasil antara hingga hasil akhir pada pengenaan operator Canny
10.3.10 Operator Zero-Crossing
Operator zero-crossing atau dikenal dengan nama lain yaitu operator
Marr-Hildreth sebenarnya adalah operator LoG yang dilengkapi dengan upaya untuk
menemukan zero crossing. Zero-crossing menyatakan tanda perubahan pada tepi-tepi dalam citra. Sebagaimana telah dibahas di depan, zero-crossing merupakan perpotongan dengan sumbu X pada turunan kedua (Gambar 10.7). Operasi inilah yang membuat operator Marr-Hildreth mampu menghasilkan kurva yang tertutup, yang tidak dapat dipenuhi oleh operator Canny.
Ada beberapa teknik yang dapat digunakan untuk melakukan pemrosesan
zero-crossing, misalnya seperti yang dibahas pada Crane (1997) atau pada Nixon
dan Aguido (2002). Algoritma yang didasarkan pada Nixon dan Aguido dapat dilihat berikut ini.
ALGORITMA 10.2 – Memproses zero crossing
Masukan:
g: Citra hasil pemrosesan LoG, berukuran MxN
ukuran : Ukuran cadar
: Deviasi standar Keluaran:
k: citra hasil pemrosesan operator Marr-Hildreth zerocross(g, ukuran, ) :
1. // Bentuk larik k yang seluruhnya bernilai 0 FOR y 1 TO M FOR y 1 TO M k(y, x) 0 END END 2. FOR y 2 TO M-1 FOR kolom 2 TO N-1
bag1 rerata(g(x-1, y-1), g(x, y), g(x-1, y-1), g(x, y)) bag2 rerata(g(x, y-1), g(x+1, y), g(x, y-1), g(x+1, y)) bag3 rerata(g(x, y-1), g(x+1, y), g(x+1, y-1), g(x+1, y)) bag4 rerata(g(x, y), g(x+1, y+1), g(x, y), g(x+1, y+1)) terbesar max(bag)
terkecil min(bag)
IF (terbesar > 0) AND (terkecil < 0) k(y,x) 255
END-IF END-FOR END-FOR 3. RETURN k
Implementasi operator zero-crossing dapat dilihat pada zerocross.m.
Proses zero-crossing yang digunakan pada algoritma di depan dilaksanakan dengan memanfaatkan jendela berukuran 3 x 3. Setiap piksel yang diperoleh melalui operasi Laplacian dikenai jendela tersebut. Adapun perhitungan yang dilakukan adalah dengan mula-mula menghitung nilai rerata dari empat bagian (masing-masing berukuran 2 x 2) seperti yang diperlihatkan pada Gambar 10.31. Berdasarkan keempat bagian tersebut, nilai terbesar dan nilai terkecil
diperoleh. Piksel yang nilai terbesarnya melebihi nol dan nilai terkecilnya kurang dari nol akan dijadikan sebagai tepi (diberi nilai 255).
Bagian 2 Bagian 4
Bagian 3 Bagian 1
Piksel pusat dalam jendela 3 x 3 Gambar 10.31 Area untuk deteksi zero-crossing
pada jendela berukuran 3 x 3
Implementasi operator Marr-Hilbreth ditunjukkan di bawah ini.
Program : zerocross.m
function [K] = zerocross(F, ukuran, sigma) % ZEROCROSS Pemerolehan tepi objek pada citra F % melalui operator Marr-Hildreth
% Hasil: citra K
H = cadarLoG(ukuran, sigma); pembulatan = false;
potong = true;
G = deteksi(F, H, potong, pembulatan);
% Proses zero crossing K = zeros(size(G)); [m, n] = size(K); for y=2 : m-1 for x=2: n-1 jum = 0;
for p = x-1 : x for q = y-1 : y jum = jum + G(q,p); end end rerata0 = jum / 4; jum = 0; for p = x-1 : x for q = y : y+1 jum = jum + G(q,p); end end rerata1 = jum / 4; jum = 0; for p = x : x+1 for q = y-1 : y jum = jum + G(q,p); end end rerata2 = jum / 4; jum = 0; for p = x : x+1 for q = y : y+1 jum = jum + G(q,p); end end rerata3 = jum / 4;
terbesar = max([rerata0 rerata1 rerata2 rerata3]); terkecil = min([rerata0 rerata1 rerata2 rerata3]); if (terbesar > 0) && (terkecil < 0)
K(y,x) = 255; end end end return Akhir Program
Contoh penggunaan fungsi zerocross:
>> Img = imread('C:\Image\lena256.png'); >> G = zerocross(Img, 7,1); imshow(G) >>
Lima contoh hasil pemrosesan dengan operator Harr-Hildreth dengan nilai berbeda dapat dilihat pada Gambar 10.32.
(b) Zero crossing 7 x 7, =1 (a) Citra lena256.tif
(d) Zero crossing 9 x 9, =1
(c) Zero crossing 7 x 7, =0.6
(e) Zero crossing 9 x 9, =0.6 (e) Zero crossing 9 x 9, =0.5 Gambar 10.32 Hasil penerapan operator Marr-Hilldreth pada lena256.png
Contoh berikut menunjukkan penggunaan fungsi zerocross pada citra bangunan2.png:
>> Img = imread('C:\Image\bangunan2.png'); >> G = zerocross(Img,7,1); imshow(G)
>>
(a) Citra bangunan2.png
(b) Hasil operator Marr-Hilldreth
Gambar 10.33 Operator Marr-Hilldreth pada bangunan2.png
Apabila dikehendaki untuk menggunakan yang besar, ukuran cadar juga perlu diperbesar. Sebagai pedoman kasar, ukuran cadar yang diperlukan sebesar round(6 ) + 1 .
10.3.11 Operator Gradien Kompas
Operator gradien kompas adalah jenis operator yang mencari tepi dengan menggunakan delapan arah mata angin. Prosesnya adalah melakukan konvolusi terhadap citra dengan menggunakan 8 cadar. Hasil operasinya berupa nilai maksimum dari kedelapan konvolusi. Empat contoh operator beserta delapan cadar masing- masing dapat dilihat pada Gambar 10.34 (Crane, 1997).
Prewitt Kirsch Robinson 3-level Robinson 5-level Timur H1 1 1 −1 1 −2 −1 1 1 −1 5 −3 −3 5 0 −3 5 −3 −3 1 0 −1 1 0 −1 1 0 −1 1 0 −1 2 0 −2 1 0 −1 Timur Laut H2 1 −1 −1 1 −2 −1 1 1 −1 −3 −3 −3 5 0 −3 5 5 −3 0 −1 −1 1 0 −1 1 1 0 0 −1 −2 1 0 −1 2 1 0 Utara H3 −1 −1 −1 1 −2 1 1 1 1 −3 −3 −3 −3 0 −3 5 5 5 −1 −1 −1 0 0 0 1 1 0 −1 −2 −1 0 0 0 1 2 −1 Barat Laut H4 −1 −1 1 −1 −2 1 1 1 1 −3 −3 −3 −3 0 5 −3 5 5 1 1 −1 1 −2 −1 1 1 −1 −2 −1 0 −1 0 1 0 1 2 Barat H5 −1 1 1 −1 −2 1 −1 1 1 −3 −3 5 −3 0 5 −3 −3 −3 −1 0 1 −1 0 1 −1 0 1 −1 0 1 −2 0 2 −1 0 1 Barat Daya H6 1 1 1 −1 −2 1 −1 −1 1 −3 5 5 −3 0 5 −3 −3 −3 0 1 1 −1 0 1 −1 −1 0 0 1 2 −1 0 1 −2 −1 0 Selatan H7 1 1 1 1 −2 1 −1 −1 −1 5 5 5 −3 0 −3 −3 −3 −3 1 1 1 0 0 0 −1 −1 −1 1 2 1 0 0 0 −1 −2 −1 Tenggara H8 1 1 1 −1 −2 1 −1 −1 1 5 5 −3 5 0 −3 −3 −3 −3 1 1 0 1 0 −1 0 −1 −1 2 1 0 1 0 −1 0 −1 −2
Gambar 10.34 Operator gradien kompas
Fungsi kompas berikut berguna untuk melakukan pengujian operator gradien kompas terhadap citra berskala keabuan dengan menggunakan cadar yang tertera pada Gambar 10.35.
Program : kompas.m
function [G] = kompas(F, jenis)
% KOMPAS Melakukan operasi dengan operator kompas % Argumen F berupa citra berskala keabuan dan % jenis berupa tipe operator
% 1 = Prewitt % 2 = Kirsch % 3 = Robinson 3-level % 4 = Robinson 4-level % % Hasil: citra G if nargin < 2 jenis = 1; end % Operator kompas Prewitt1 = [1 1 -1;1 -2 -1;1 1 -1]; Prewitt2 = [1 -1 -1;1 -2 -1;1 1 -1]; Prewitt3 = [-1 -1 -1;1 -2 1;1 1 1]; Prewitt4 = [-1 -1 1;-1 -2 1;1 1 1]; Prewitt5 = [-1 1 1;-1 -2 1;-1 1 1]; Prewitt6 = [1 1 1;-1 -2 1;-1 -1 1]; Prewitt7 = [1 1 1;1 -2 1;-1 -1 -1]; Prewitt8 = [1 1 1;-1 -2 1;-1 -1 1]; Kirsch1 = [5 -3 -3;5 0 -3;5 -3 -3]; Kirsch2 = [-3 -3 -3;5 0 -3; 5 5 -3]; Kirsch3 = [-3 -3 -3;-3 0 -3;5 5 5]; Kirsch4 = [-3 -3 -3;-3 0 5;-3 5 5]; Kirsch5 = [-3 -3 5;-3 0 5;-3 -3 -3]; Kirsch6 = [-3 5 5;-3 0 5;-3 -3 -3]; Kirsch7 = [5 5 5;-3 0 -3;-3 -3 -3]; Kirsch8 = [5 5 -3;5 0 -3;-3 -3 -3]; Robinson3_1 = [1 0 -1;1 0 -1;1 0 -1]; Robinson3_2 = [0 -1 -1;1 0 -1;1 1 0]; Robinson3_3 = [-1 -1 -1;0 0 0;1 1 0]; Robinson3_4 = [1 1 -1;1 -2 -1;1 1 -1]; Robinson3_5 = [-1 0 1;-1 0 1;-1 0 1]; Robinson3_6 = [0 1 1;-1 0 1;-1 -1 0]; Robinson3_7 = [1 1 1;0 0 0;-1 -1 -1]; Robinson3_8 = [1 1 0;1 0 -1;0 -1 -1]; Robinson5_1 = [1 0 -1;2 0 -2;1 0 -1]; Robinson5_2 = [0 -1 -2;1 0 -1;2 1 0]; Robinson5_3 = [-1 -2 -1;0 0 0;1 2 -1]; Robinson5_4 = [-2 -1 0;-1 0 1;0 1 2]; Robinson5_5 = [-1 0 1;-2 0 2;-1 0 1]; Robinson5_6 = [0 1 2;-1 0 1;-2 -1 0]; Robinson5_7 = [1 2 1;0 0 0;-1 -2 -1]; Robinson5_8 = [2 1 0;1 0 -1;0 -1 -2];
Prewitt(:,:,1) = Prewitt1; Prewitt(:,:,2) = Prewitt2; Prewitt(:,:,3) = Prewitt3; Prewitt(:,:,4) = Prewitt4; Prewitt(:,:,5) = Prewitt5; Prewitt(:,:,6) = Prewitt6; Prewitt(:,:,7) = Prewitt7; Prewitt(:,:,8) = Prewitt8; Kirsch(:,:,1) = Kirsch1; Kirsch(:,:,2) = Kirsch2; Kirsch(:,:,3) = Kirsch3; Kirsch(:,:,4) = Kirsch4; Kirsch(:,:,5) = Kirsch5; Kirsch(:,:,6) = Kirsch6; Kirsch(:,:,7) = Kirsch7; Kirsch(:,:,8) = Kirsch8; Robinson3(:,:,1) = Robinson3_1; Robinson3(:,:,2) = Robinson3_2; Robinson3(:,:,3) = Robinson3_3; Robinson3(:,:,4) = Robinson3_4; Robinson3(:,:,5) = Robinson3_5; Robinson3(:,:,6) = Robinson3_6; Robinson3(:,:,7) = Robinson3_7; Robinson3(:,:,8) = Robinson3_8; Robinson5(:,:,1) = Robinson5_1; Robinson5(:,:,2) = Robinson5_2; Robinson5(:,:,3) = Robinson5_3; Robinson5(:,:,4) = Robinson5_4; Robinson5(:,:,5) = Robinson5_5; Robinson5(:,:,6) = Robinson5_6; Robinson5(:,:,7) = Robinson5_7; Robinson5(:,:,8) = Robinson5_8;
% Tentukan operator yang dipakai if jenis == 1 Opr = Prewitt; elseif jenis == 2 Opr = Kirsch; elseif jenis == 3 Opr = Robinson3; elseif jenis == 4 Opr = Robinson5; else error('Operator kedua: 1 s/d 4'); end
% Lakukan proses konvolusi F = double(F); [m, n] = size(F); for y=2 : m-1 for x=2 : n-1 % Pelaksanaan konvolusi for i=1 : 8
Grad(i) = Opr(1,1,i) * F(y+1, x+1) + ... Opr(1,2,i) * F(y+1, x) + ... Opr(1,3,i) * F(y+1, x-1) + ...
Opr(2,1,i) * F(y, x+1) + ... Opr(2,2,i) * F(y, x) + ... Opr(2,3,i) * F(y, x-1) + ... Opr(3,1,i) * F(y-1, x+1) + ... Opr(3,2,i) * F(y-1, x) + ... Opr(3,3,i) * F(y-1, x-1); end maks = max(Grad); G(y-1, x-1) = maks; end end G = uint8(G); Akhir Program
Contoh penggunaan fungsi kompas:
>> Img = rgb2gray(imread('C:\Image\mainan.png')); >> G = kompas(Img, 1);
>> imshow(G) >>
Angka 1 pada pemanggilan fungsi kompas menyatakan bahwa operator yang dipakai adalah Prewitt. Angka yang dapat digunakan pada argumen kedua berupa 1, 2 ,3, atau 4, dengan ketentuan sebagai berikut:
1 = Prewitt 2 = Kirsch
3 = Robinson 3-level 4 = Robinson 4-level
Gambar 10.35 memperlihatkan contoh hasil deteksi tepi dengan keempat operator tersebut.
(a) Prewitt (b) Kirsch
(c) Robinson 3-level (c) Robinson 5-level
Gambar 10.35 Hasil deteksi tepi dengan operator gradien kompas
10.4 Peng-ambangan Dwi-Aras
Segmentasi yang paling sederhana dilaksanakan dengan menggunakan ambang intensitas. Nilai yang lebih kecil daripada nilai ambang diperlakukan sebagai area pertama dan yang lebih besar daripada atau sama dengan nilai ambang dikelompokkan sebagai area yang kedua. Dalam hal ini, salah satu area tersebut berkedudukan sebagai latarbelakang. Cara seperti itulah yang disebut ambangan dwi-aras (bi-level thresholding) atau terkadang dinamakan peng-ambangan intensitas. Secara matematis, hal itu dinyatakan dengan
𝑏(𝑦, 𝑥) = 𝑓(𝑥) = {1, 𝑢𝑛𝑡𝑢𝑘 (𝑦, 𝑥) ≥ 𝑇
0, 𝑢𝑛𝑡𝑢𝑘 (𝑦, 𝑥) < 𝑇 (10.13)
Pada rumus di atas, T menyatakan ambang intensitas. Dalam praktik, nilai 1 atau 0 pada Persamaan 10.13 dapat dipertukarkan.
Peng-ambangan intensitas biasa digunakan untuk memisahkan tulisan hitam yang berada di atas secarik kertas putih. Namun, perlu diketahui, peng-ambangan ini mempunyai kelemahan, yaitu:
1) tidak memperlihatkan hubungan spasial antarpiksel; 2) sensitif terhadap pencahayaan yang tidak seragam;
3) hanya berlaku untuk keadaan yang ideal (misalnya, latarbelakang hitam dan objek berwarna putih).
(a) ipomoea.png (b) Histogram citra
Gambar 10.36 Citra daun dan histogramnya
Salah satu cara untuk menentukan nilai ambang adalah dengan memperhatikan histogram citra. Sebagai contoh, perhatikan Gambar 10.36. Berdasarkan histogram, pemisahan dapat dilakukan dengan memilih nilai ambang pada bagian lembah. Sebagai contoh, nilai di sekitar 100 dapat digunakan sebagai nilai ambang. Untuk mengujinya, mula-mula siapkan skrip berikut.
Program : ambang.m
function [G] = ambang(F, t)
% AMBANG Menentukan nilai ambang yang digunakan % untuk melakukan pengambangan
% F = Citra berskala keabuan % t = nilai ambang
%
% Keluaran: G = Citra biner
[m, n] = size(F); for i=1 : m
if F(i,j) <= t G(i,j) = 0; else G(i,j) = 1; end end end Akhir Program
Contoh peng-ambangan dengan nilai ambang sebesar 100:
>> Img = imread('C:\Image\ipomoea.png'); >> G = ambang(Img, 100);
>> imshow(1-G) >>
Penggunaan 1-G dalam imshow ditujukan untuk membalik nilai 1 dan 0. Dengan ungkapan tersebut, bagian daun akan diberi nilai 1 (putih). Contoh hasilnya dapat dilihat pada Gambar 10.37.
(a) ipomoea.tif (b) Hasil pengambangan
Gambar 10.37 Hasil pembalikan latarbelakang dan objek
Persoalan utama dalam peng-ambangan intensitas terletak pada penentuan nilai ambang (T) secara otomatis. Salah satu cara yang dilakukan adalah dengan menentukan nilai ambang iteratif secara interaktif (Gonzalez & Woods, 2002;
Acharya & Ray, 2005). Algoritma untuk menentukan T secara iteratif adalah seperti berikut.
ALGORITMA 10.3 – Memperoleh nilai ambang secara iteratif
Masukan:
f (M,N): Citra berskala keabuan berukuran M baris dan N kolom
Keluaran:
nilai ambang T ambang_adaptif(f):
1. Pilihlah satu nilai untuk menentukan nilai ambang (T To). 2. Bagilah citra menjadi dua bagian dengan menggunakan T
sebagai nilai ambang.
3. Hitunglah nilai rata-rata pada kedua area (1 dan 2). 4. Hitunglah nilai ambang: T 𝜇1+𝜇2
2
5. Ulangi langkah 2 sampai dengan 4 sampai tidak ada perubahan nilai T.
6. RETURN T
Peng-ambangan iteratif dikenal juga dengan sebutan peng-ambangan optimal.
Algoritma peng-ambangan iteratif dituangkan dalam bentuk program seperti berikut.
Program : titeratif.m
function [t1] = titeratif(F)
% TITERATIF Menentukan nilai ambang yang digunakan % untuk melakukan pengambangan
% F = Citra berskala keabuan %
% Keluaran: G = Citra biner [m, n] = size(F); F = double(F); t0 = 127; while true rata_kiri = 0; rata_kanan = 0; jum_kiri = 0; jum_kanan = 0; for i=1 : m for j=1 : n if F(i, j) <= 127
rata_kiri = rata_kiri + F(i,j); jum_kiri = jum_kiri + 1;
else
rata_kanan = rata_kanan + F(i,j);
jum_kanan = jum_kanan + 1; end
end end
rata_kiri = rata_kiri / jum_kiri; rata_kanan = rata_kanan / jum_kanan;
t1 = (rata_kiri + rata_kanan) / 2.0; if (t0 - t1) < 1
break; % Keluar dari while end t0 = t1; end t1 = floor(t1); Akhir Program
Pengujian fungsi titeratif dapat dilihat di bawah ini.
>> Img = imread('C:\Image\ipomoea.png'); >> t = titeratif(Img) t = 130 >> G = ambang(Img, t); >> imshow(1-G) >>
Hasil di atas menyatakan bahwa nilai ambang yang dihasilkan oleh fungsi titeratif adalah 130. Penggunaan 1-G dalam imshow adalah untuk membalik nilai 1 dan 0. Nilai 1 menjadi 0 dan nilai 0 menjadi 1. Dengan ungkapan tersebut, bagian daun akan diberi nilai 1 (putih). Contoh hasilnya dapat dilihat pada Gambar 10.38.
(a) ipomoea.tif (b) Hasil peng-ambangan
Gambar 10.38 Contoh hasil peng-ambangan secara iteratif
10.5 Peng-ambangan Global Vs. Lokal
Terkait dengan nilai ambang yang digunakan pada segmentasi citra, terdapat istilah peng-ambangan global dan peng-ambangan lokal. Pengertiannya sebagai berikut.
Apabila nilai ambang t bergantung hanya pada satu nilai aras keabuan f(y, x), peng-ambangan disebut sebagai global. Dalam hal ini, semua piksel dalam citra akan ditentukan oleh satu nilai ambang t.
Peng-ambangan disebut lokal kalau nilai ambang t bergantung pada f(y, x) dan g(y, x) dengan g(y,x) menyatakan properti citra lokal pada titik (y, x). Dalam hal ini, properti citra lokal dapat diperoleh melalui statisti (misalnya rerata tetangga di sekitar titik (y, x) ). Dengan kata lain, nilai ambang untuk setiap piksel ditentukan oleh nilai piksel tetangga. Dengan demikian, nilai ambang untuk piksel masing-masing belum tentu sama.
10.6 Peng-ambangan Aras-jamak
Pada peng-ambangan beraras-jamak (multilevel thresholding), citra dibagi menjadi beberapa bagian dengan menggunakan beberapa nilai ambang, Cara seperti itu dilakukan kalau pada histogram terdapat puncak-puncak yang membedakan antara satu objek terhadap yang lain. Sebagai contoh, perhatikan Gambar 10.39(a) dan kemudian lihatlah pada histogram yang terdapat pada Gambar 10.39(b).
(a) benda.png (b) Histogram
T1 T2
Objek lingkaran
Objek kotak
Gambar 10.39 Contoh citra dengan beberapa puncak dan lembah yang terpisah
Contoh berikut menunjukkan algoritma yang digunakan pada peng-ambangan aras-jamak yang menggunakan dua buah nilai ambang.
ALGORITMA 10.3 – Segmentasi dengan peng-ambangan aras-jamak
Masukan:
f (MxN): Citra berskala keabuan (berukuran MxN) Keluaran: g (M, N): Citra biner ambang_aras_jamak(ukuran, ): FOR y 1 TO ukuran -1 FOR x 1 TO ukuran -1 nx x – cx ny y – cy
nilai 1 𝜎2[ 𝑛𝑥2+ 𝑛𝑦2 𝜎2 − 2] 𝑒 −(𝑛𝑥2+ 𝑛𝑦2 ) 2𝜎2 h(y+1, x+1) nilai
jum jum + nilai END-FOR
END-FOR 7. RETURN g
Implementasi berdasarkan algoritma di atas dapat dilihat di bawah ini.
Program : arasjamak.m
function [G] = arasjamak(F, t1, t2) % Pengambanan dengan dua nilai ambang % F = Citra berskala keabuan % t1 = nilai ambang bawah % t2 = nilai ambang atas %
% Keluaran: G = Citra biner [m, n] = size(F); for i=1 : m for j=1:n if F(i,j) <= t1 || F(i,j) >= t2 G(i,j) = 0; else G(i,j) = 1; end end end Akhir Program
Contoh penggunaan fungsi arasjamak:
>> Img = imread('C:\Image\benda.png'); >> G = arasjamak(Img, 50, 100); imshow(G); >>
Hasilnya dapat dilihat pada Gambar 10.40(b). beberapa contoh penggunaan nilai ambang yang lain dapat dilihat pada Gambar 10.40(c) hingga 10.40(f).
(a) benda.png (b) Nilai ambang t1=50 dan t2=100
(c) Nilai ambang t1=175 dan t2=200 (d) Nilai ambang t1=220 dan t2=230
(e) Nilai ambang t1=235 dan t2=250 (f) Nilai ambang t1=220 dan t2=250
Gambar 10.40 Hasil penerapan nilai ambang jamak
Contoh lain dapat dilihat di bawah ini:
>> Img = imread('C:\Image\ipomoea.png'); >> G = arasjamak(Img, 50, 100); imshow(G); >>
Hasilnya dapat dilihat pada Gambar 10.41(b). Terlihat bahwa dengan cara seperti itu, bayangan daun dapat dihilangkan.
(a) ipomoea.png (b) Pengambangan t1=50, t2=100
Gambar 10.41 Contoh peng-ambangan aras jamak pada ipomoea.png
10.7 Peng-ambangan dengan Metode Otsu
Metode Otsu dipublikasikan oleh Nobuyuki Otsu pada tahun 1979. Metode ini menentukan nilai ambang dengan cara membedakan dua kelompok, yaitu objek dan latarbelakang, yang memiliki bagian yang saling bertumpukan, berdasarkan histogram (lihat Gambar 10.42).
Nilai ambang (t)
Kelas 1 Kelas 2
Gambar 10.42 Penentuan nilai ambang untuk memperoleh hasil yang optimal
Prinsip metode Otsu dijelaskan berikut ini. Pertama-tama, probabilitas nilai intensitas i dalam histogram dihitung melalui
𝑝(𝑖) =𝑛𝑖
𝑁 , 𝑝(𝑖) ≥ 0, ∑ 𝑝(𝑖) = 1 256
1 (10.14)
dengan ni menyatakan jumlah piksel berintensitas i dan N menyatakan jumlah
semua piksel dalam citra. Jika histogram dibagi menjadi dua kelas (objek dan latarbelakang), pembobotan pada kedua kelas dinyatakan sebagai berikut:
𝑤1(𝑡) = ∑𝑡𝑖 =1𝑝(𝑖) (10.15)
𝑤2(𝑡) = ∑𝐿 𝑝(𝑖)
𝑖=𝑡+1 = 1 − 𝑤1(𝑡) (10.16)
Dalam hal ini, L menyatakan jumlah aras keabuan. Rerata kedua kelas dihitung melalui:
𝑚1(𝑡) = ∑𝑡𝑖=1𝑖. 𝑝(𝑖)/𝑊1(𝑡) (10.17) 𝑚2(𝑡) = ∑𝑡 𝑖. 𝑝(𝑖)
𝑖 =1 /𝑊2(𝑡) (10.18)
Varians kedua kelas dinyatakan dengan rumus:
𝜎12(𝑡) = ∑ (1 − 𝑚1)2. 𝑝 (𝑖) 𝑊1(𝑡) 𝑡 𝑖=1 (10.19) 𝜎22(𝑡) = ∑ (1 − 𝑚2)2. 𝑝(𝑖) 𝑊2(𝑡) 𝐿 𝑖 =𝑡+1 (10.20)
Varians total dapat dinyatakan dengan 𝜎2(𝑡) = 𝜎
𝑊2(𝑡) + 𝜎𝐵2(𝑡) (10.21)
Dalam hal ini, 𝜎𝑊2 dinamakan sebagai within-class variance (WCV) dan 𝜎 𝐵2 disebut sebagai between-class variance (BCV). WCV dapat dinyatakan dengan
𝜎𝑊2(𝑡) = 𝑊
1(𝑡). 𝜎1(𝑡)2+ 𝑊2(𝑡). 𝜎2(𝑡)2 (10.22) Rumus di atas menunjukkan bahwa WCV adalah jumlah varians kelas secara individual yang telah diboboti dengan probabilitas kelas masing-masing. Adapun BCV dinyatakan dengan
𝜎𝐵2(𝑡) = 𝑊1. [𝑚1(𝑡) − 𝑚𝑇]2+ 𝑊
2. [𝑚2(𝑡) − 𝑚𝑇]2 (10.23) Dalam hal ini, mT adalah rerata total (𝑚𝑇 = ∑𝑁𝑖 =1𝑖. 𝑝(𝑖)).
Nilai ambang optimum dapat diperoleh dengan dua cara. Cara pertama dilaksanakan dengan meminimumkan WCV. Cara kedua dilaksanakan dengan memaksimumkan BCV. Namun, berdasarkan kedua cara tersebut, cara yang kedua lebih menghemat komputasi.
Implementasi berikut didasarkan pada Persamaan 10.23. Skrip ditulis tanpa memperhatikan optimasi komputasi. Pendekatan lain, yang memperhatikan kecepatan komputasi, dapat dilihat pada Demirkaya, dkk. (2009).
Program : otsu.m
function [ambang] = otsu(F)
% OTSU Memperoleh nilai ambang menggunakan metode Otsu % F = Citra berskala keabuan
[m, n] = size(F); jum_piksel = m * n; % Kosongkan histogram for i=1 : 256 h(i) = 0; end % Hitung histogram for i=1 : m for j=1 : n intensitas = F(i,j); h(intensitas+1) = h(intensitas+1) + 1; end end % Hitung p(i) for i=1 : 256
p(i) = h(i) / jum_piksel; end
% Hitung rerata total mT = 0;
for i=1 : 256
mT = mT + i * p(i); end