LANDASAN TEORI
2.1.Suara Pernapasan
Menurut Sovijärvi et al. (2000), suara pernapasan adalah semua suara yang berhubungan dengan pernapasan termasuk suara napas, suara adventif, suara batuk, suara dengkur, suara bersin, dan suara dari otot pernapasan. Sebagai catatan bahwa suara yang timbul saat bernafas tidak termasuk dalam suara pernapasan.
Menurut Baydar (2003), suara pernapasan dapat diklasifikasi menjadi dua kelompok seperti suara napas dan suara adventif (abnormal). Suara napas yang terdengar dari dada subyek yang sehat disebut suara napas normal. Suara napas normal keduanya yaitu inspirasi dan ekspirasi. Keduanya terjadi ketika udara bergerak masuk dan keluar selama siklus pernapasan reguler. Suara adventif merupakan suara pernapasan tambahan dalam suara napas. Suara ini terjadi tanpa terduga selama siklus pernapasan reguler. Variabilitas yang cukup besar dalam karakteristik struktur suara pernapasan di antara individu, terkadang membuat sulit untuk memastikan keabnormalan suatu suara.
Gavriely & Cugell (1995) membagi suara adventif menjadi dua jenis utama. Yang pertama yaitu suara adventif kontinu, yang dinamakan, wheeze, rhonchi, dan stridor. Yang kedua yaitu suara adventif diskontinu, yang dinamakan, crackle dan
squawk. Kehadiran suara adventif diskontinu biasanya mengindikasi penyakit paru.
Menurut Matondang et al. (2003) suara napas dasar terdiri dari beberapa bagian yaitu:
a. Suara napas vesikular
suara ekspirasi dan terdengar seperti membunyikan „fff‟ dan „www‟. Suara
napas abnormal akan melemah karena terjadi penyempitan bronkus (bronkostenois) dan setiap keadaan yang menyebabkan ventilasi berkurang atau bertambahnya hambatan konduksi suara, atau keduanya. Keadaan tersebut terdapat pada pasien yang menderita pneunomia, edema paru, pneumotoraks atau emfisema.
b. Suara napas bronkial
Pada suara ini terdengar inspirasi keras yang disusul oleh ekspirasi yang lebih keras, dapat disamakan seperti bunyi „khkhkh‟. Dalam keadaan normal, suara napas bronkial hanya terdengar pada bronkus bear kanan dan kiri, di daerah parasternal atas di dada depan dan di daerah interskapular di belakang. Bila suara napas bronkial terdengar di tempat lain, berarti terdapat konsolidasi yang luas misalnya pada pneumonia lobaris.
c. Suara napas amforik
Suara napas ini menyerupai bunyi tiupan di atas mulut botol kosong, dapat didengar pada kaverne.
d. Cog-wheel breath sound
Menyatakan terdapatnya suara napas terputus-putus, tidak kontinu, baik pada fase inspirasi maupun fase ekspirasi.
e. Metamorphosing breath sound
Suara napas ini dimulai dengan suara yang halus kemudian mengeras, atau dimulai dengan vesikular kemudian berubah menjadi bronkial.
Sedangkan suara napas tambahan pada auskultasi terdiri dari: a. Ronki basah dan ronki kering
ekstraluminar. Ronki kering lebih jelas terdengar pada fase ekspirasi daripada fase inspirasi.
b. Krepitasi
Adalah suara alveoli. Krepitasi normal dapat terdengar di belakang bawah dan samping pada waktu inspirasi sesudah istirahat dalam keadaan telentang dalam beberapa waktu.
c. Bunyi gesekan pleura (pleural fiction rub)
Terdapat pada pleuritis fibrinosa suara yang terdengar adalah suara gesekan kasar seolah-olah dekat dengan telinga, baik pada fase inspirasi maupun ekspirasi.
d. Sukusio Hippocrates
Terdapat pada seropneumotoraks, yakni kalau dada digerak-gerakkan akan terdengar suara kocokan, suara ini jarang terdengar pada anak-anak. Pada keadaan ini biasanya dinding perut bagian atas tampak amat cekung.
2.2.Suara Napas Abnormal
Menurut Schriber (2011), ada beberapa jenis suara napas abnormal. Empat jenis yang paling umum adalah:
1. Rales (Crackles)
Merupakan suara yang mengklik kecil, menggelegak, atau gemeretak suara di paru-paru. Diyakini terjadi ketika udara membuka ruang udara tertutup. Rales dapat dibagi lagi lebih lanjut sebagai moist, dry, fine, dan coarse.
2. Ronki
Merupakan suara yang menyerupai mendengkur. Terjadi ketika udara diblokir atau menjadi kasar melalui saluran udara besar.
3. Wheezing
Wheezing dan suara abnormal lainnya terkadang dapat terdengar tanpa
stetoskop. 4. Stridor
Merupakan suara seperti Wheezing yang didengar ketika seseorang bernafas. Biasanya terjadi adalah karena penyumbatan aliran udara dalam pipa udara (trakea) atau di bagian belakang tenggorokan.
2.3.Karakteristik Suara Paru-paru dan Noise
Menurut Sukresno et al. (2009), puncak suara paru-paru normal biasanya terdapat pada frekuensi di bawah 100 Hz. Energi suara paru-paru menurun dengan tajam antara 100 - 200 Hz, tetapi masih dapat dideteksi pada atau di atas 800 Hz dengan alat sensitif.
Menurut Earis & Cheetham (2000), noise atau gangguan sinyal seperti suara otot pernapasan, suara gerak dada, suara jantung, dan suara frekuensi rendah lain, terdapat diantara frekuensi 50 sampai dengan 150 Hz.
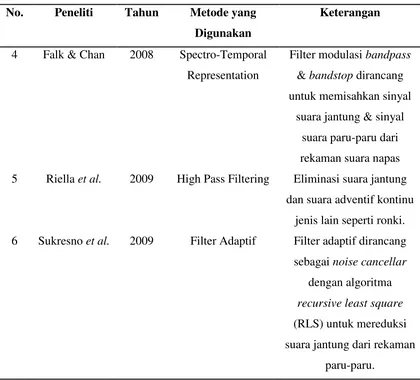
2.4.WAVE
Gambar 2.1 Format file WAVE
Penjelasan mengenai gambar 2.1 dapat dilihat pada tabel 2.1.
Tabel 2.1 Deskripsi format berkas WAVE
Offset Ukuran Nama Deskripsi
0 4 ChunkID “RIFF” dalam bentuk ASCII
(0x52494646 big endian form) 4 4 ChunkSize (36 + Subchunk2Size) atau (4 + (8 +
Tabel 2.1 Deskripsi format berkas WAVE (lanjutan)
Offset Ukuran Nama Deskripsi
20 2 AudioFormat PCM = 1
Nilai lebih dari 1 mengindikasi beberapa bentuk kompresi
22 2 NumChannels Mono = 1, Stereo = 2, dll 24 4 SampleRate 8000, 44100, dll
28 4 ByteRate SampleRate * NumChannels * BitsPerSample/8
32 2 BlockAlign NumChannels * BitsPerSample/8 34 2 BitsPerSample 8 bits = 8, 16 bits = 16, dll
36 4 Subchunk2ID “data” (0x64617461 big-endian form) 40 4 Subchunk2Size NumSamples * NumChannels *
BitsPerSample/8
44 * Data Data aktual suara
2.5.Wavelet Transform
Walker & Foo (2003) menyatakan bahwa metode fourier hanya merinci konten spektral sebuah sinyal dalam domain frekuensi. Informasi domain waktu untuk kejadian tertentu menghilang selama transformasi fourier karena preservasi dari kejadian waktu tidak dianggap. Kondisi ini dapat diabaikan jika sinyal stasioner. Namun, untuk sinyal stasioner seperti ucapan, waktu dan informasi domain frekuensi penting untuk menghindari hilangnya informasi yang signifikan dalam sinyal. Walker & Foo (2003) mengajukan analisis wavelet sebagai metode alternatif untuk mengatasi masalah pada Fourier. Wavelet menggunakan konsep analisis multiresolusi (contohnya representasi waktu dan skala frekuensi) untuk memproduksi dekomposisi yang presisi dari sinyal sehingga didapatkan representasi sinyal yang akurat. Detil karakteristik seperti diskontinuitas kecil, kesamaan, dan bahkan derivasi orde tinggi yang dapat disembunyikan oleh analisis fourier konvensional dapat terungkap.
Wavelet merupakan keluarga dari fungsi ψa,b(t) diturunkan dari sebuah base
wavelet ψ(t), disebut dengan “mother wavelet”, oleh dilatasi dan translasi (Cohen &
( ) √ ( ) (2.1)
Dimana a adalah parameter dilatasi (skala) dan b adalah parameter translasi. Continuous wavelet transform dari satu dimensi (1-D) fungsi f(t) L2( ), dimana
L2( ) menunjuk vector space yang dapat diukur, square-integrable 1-D fungsi f(t), didefinisikan dalam Hilbert space, sebagai proyeksi fungsi di atas wavelet set ψa,b(t),
sebagai contoh pada persamaan (2.2).
( ) 〈 〉 √ ∫ ( ) ( ) (2.2)
Dimana * merepresentasikan konjugasi kompleks. Oleh karena set ψa,b(t)
merentang space berisikan f(t), rekonstruksi f(t) dapat dicapai melalui inverse wavelet transform (IWT), didefinisikan pada persamaan (2.3).
( ) ∫ ∫ ( )
( )
(2.3)
Dimana didefinisikan pada persamaan (2.4) dan ̂( ) adalah fourier
transform (FT) dari ψ(t).
∫ | ̂( )|| | (2.4)
2.6.Analisis Multiresolusi
g[n] ↓↓22
Gambar 2.2 Penerapan dekomposisi pada Discrete Wavelet Transform; dimana g[n] adalah high pass filter; h[n] adalah low pass filter
Analisis wavelet pada dasarnya merupakan pergeseran dan penskalaan suatu bentuk energi terbatas yang disebut mother wavelet ψ(t) terhadap sinyal yang diinginkan. Sehingga transformasi wavelet diskrit dapat dituliskan pada persamaan (2.5).
( ) ⁄ ( ) (2.5)
Dimana j adalah parameter perluasan (penskalaan) dan k adalah parameter pergeseran. Dalam praktisnya, transformasi wavelet yang diwujudkan dalam dekomposisi sinyal masukan, terbagi menjadi dua bentuk gelombang berdasarkan jenis filter yang digunakan. Low pass filter menghasilkan suatu bentuk gelombang yang disebut aproksimasi dan high pass filter menghasilkan bentuk gelombang acak yang disebut detail. Pembentukan kedua gelombang tersebut menggunakan pendekatan analisis resolusi jamak terhadap frekuensi yang berbeda. Yang dimaksud dengan resolusi adalah pemisahan dari setiap sinyal yang berubah-ubah menjadi bobot (skala) deret cuplikan yang digeser. Jadi, analisis resolusi jamak berhubungan dengan penskalaan wavelet. Gelombang yang dihasilkan dari pemfilteran low pass yaitu aproksimasi, akan diperluas oleh satu fungsi translasi yang disebut father wavelet atau fungsi penskalaan yang dapat ditulis pada persamaan (2.6).
Adapun gelombang yang dihasilkan dari filtrasi high pass yaitu detail akan diperluas oleh suatu fungsi translasi dengan parameter penskalaan tertentu yang disebut mother wavelet atau fungsi wavelet yang dapat dituliskan pada persamaan (2.7).
( ) ⁄ ( ) (2.7)
Sehingga hubungan fungsi wavelet dan fungsi penskalaan untuk sinyal masukan s dapat dituliskan pada persamaan (2.8).
( ) ∑ ( ) ∑ ∑ (2.8)
Dalam perluasan ini, koefisien-koefisien Ck ditunjukkan sebagai
koefisien-koefisien aproksimasi pada skala J0. Adapun koefisien-koefisien dj,k
merepresentasikan detail sinyal pada skala yang berbeda. Hubungan koefisien-koefisien wavelet terhadap sinyal masukan dapat ditulis dalam persamaan (2.9) dan persamaan (2.10).
( ) ( ) (2.9)
( ) ( ) (2.10)
2.7. Denoising
Prinsip kerja proses menghilangkan gangguan sinyal atau noise menggunakan transformasi wavelet diskrit pada dasarnya dibagi menjadi tiga proses (Fahruzi, 2012), yaitu:
1. Proses dekomposisi sinyal suara menjadi band-band frekuensi. Dekomposisi yang dilakukan pada sinyal suara sampai level 8 dengan menggunakan Daubechies (db4) sebagai mother wavelet-nya.
2. Detail koefisien pada proses dekomposisi digunakan untuk menemukan nilai standar untuk proses denoising sinyal suara.
direkonstruksi secara up sampling untuk menghasilkan sebuah sinyal suara yang bersih dari noise.
2.8.Threshold
Ada dua jenis teknik dalam melakukan threshold, yaitu soft thresholding dan hard thresholding (Mertins, 1999). Soft thresholding ditunjukkan dalam persamaan
non-linier (2.11). Hard thresholding ditunjukkan dalam persamaan non-non-linier (2.12).
̂( ) { ( ) ( )
Signal-to-noise ratio secara umum dapat didefinisikan sebagai rasio berdimensi power
sinyal dengan power noise yang terkandung dalam sebuah rekaman (Johnson, 2006).
(
) (2.13)
dimana:
Psignal = power rata-rata sinyal
Pnoise = power rata-rata noise
Asignal = root mean square (RMS) amplitudo sinyal
Anoise = root mean square (RMS) amplitudo noise
Jika terdapat sebuah set n {x1, x2, ..., xn}, maka RMS dapat didefinisikan seperti pada persamaan (2.14).
SNR dapat disajikan dalam desibel seperti pada persamaan (2.15).
[( ) ] ( ) (2.15)
Semakin besar nilai SNR, menunjukkan perbaikan terhadap sinyal. Sebaliknya semakin kecil nilai SNR, menunjukkan bahwa sinyal mengalami penurunan kualitas atau mengalami kerusakan (Sukresno et al. 2009).
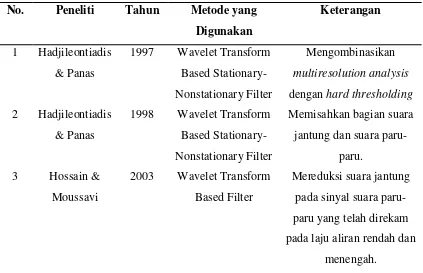
2.10.Penelitian Terdahulu
Di bagian ini akan dijabarkan beberapa penelitian terdahulu. Pada tabel 2.2 akan dijelaskan beberapa penelitian terdahulu yang berkaitan dengan topik ini.
Tabel 2.2 Penelitian Terdahulu No. Peneliti Tahun Metode yang pada laju aliran rendah dan
Tabel 2.2 Penelitian Terdahulu (lanjutan) No. Peneliti Tahun Metode yang
Digunakan
Keterangan
4 Falk & Chan 2008 Spectro-Temporal Representation
Filter modulasi bandpass & bandstop dirancang untuk memisahkan sinyal
suara jantung & sinyal suara paru-paru dari rekaman suara napas 5 Riella et al. 2009 High Pass Filtering Eliminasi suara jantung
dan suara adventif kontinu jenis lain seperti ronki. 6 Sukresno et al. 2009 Filter Adaptif Filter adaptif dirancang
sebagai noise cancellar dengan algoritma recursive least square
(RLS) untuk mereduksi suara jantung dari rekaman

![Gambar 2.2 Penerapan dekomposisi pada Discrete Wavelet Transform; dimana g[n]](https://thumb-ap.123doks.com/thumbv2/123dok/3802640.1830380/8.595.105.523.84.222/gambar-penerapan-dekomposisi-pada-discrete-wavelet-transform-dimana.webp)