BAB IV HASIL DAN PEMBAHASAN

(1)

BAB IV

HASIL DAN PEMBAHASAN

4.1 Solusi Numerik Model H-R dengan RKF45

Model H-R yang terbentuk dari tiga persamaan differensial orde satu yang saling berhubungan atau terkopel. Persamaan tersebut bersifat autonomous yang berarti berdiri sendiri secara eksplisit dari variabel penyusunnya tanpa variabel waktu yang mempengaruhinya, meskipun diturunkan dari fungsi waktu. H-R mengembangkan persamaan analitiknya dari tahun 1982 s.d. 1984 untuk meniru dinamika sistem yang terjadi dalam penjalaran impuls pada sel saraf. Model ini merupakan model penyederhanaan (simplify model) yang mengacu pada fenomena eksperimen yang telah dilakukan oleh Hodgkin-Huxley atau yang lebih dikenal dengan model H-H.2,3,4,5 _Penjaralan impuls saraf pada satu sel saraf memperlihatkan dinamika yang kompleks dan khas. Fenomena tersebut diantaranya adalah adanya potensial istirahat, potensial ambang (threshold), hingga timbulnya potensial aksi atau spike.1 _{Namun hal tersebut hanya} merupakan sebagian kecil dari fenomena-fenomena lain yang lebih kompleks dan menarik untuk dipelajari.

Pada mulanya H-R menemukan persamaan penjalaran impuls saraf dengan dua buah variabel peubah dari persamaan differensial biasa orde satu yang autonomous, persamaan ini merupakan model H-R yang lebih dikenal dengan slow fast system.5_Sistem persamaan ini dianggap berhasil untuk meniru fenomena spike penjalaran impuls pada sel saraf dan menutupi kelemahan dari model penyederhanaan yang ditemukan oleh FitzHug-Nagumo (FH-N). Namun model ini masih memiliki kekurangan untuk menjelaskan

fenomena firing-adapting. Sehingga pada tahun 1984 H-R memformulasikan persamaannya menjadi tiga persamaan differensial orde satu yang saling terkopel. Penambahan satu peubah disamping dua peubah sebelumnya dimaksudkan untuk memperlihatkan tingkah laku penjalaran yang lebih nyata seperti (bursting dan adaptation).3

Persamaan analitik yang dibangun oleh H-R merupakan persamaan non-linier yang tidak mudah dipecahkah untuk mencari solusi fisisnya, sehingga didalam ilmu sains penyelesaian solusi tersebut dapat dilakukan secara numerik.9_{Banyak metode numerik yang} sudah dikenal dapat memecahkan solusi dari persamaan differensial biasa, diantaranya metode Euler, Hund, dan Runge-Kutta. Dalam kasus ini penyelesaian numerik dari model H-R dilakukan dengan metode RKF45 (lihat 2.6 Runge-Kutta-Fehlberg 45). Metode ini adalah penyempurnaan dari metode Runge-Kutta orde 4 dan teruji lebih baik dengan menghasilkan nilai kesalahan (error value) yang paling kecil dari metode sebelumnya.

Implementasinya adalah memasukkan persamaan H-R ke dalam metode RKF45. Metode RKF45 mencacah sejumlah titik sehingga menghasilkan trayektori dalam ruang fasa tertentu berdasarkan persamaan berupa fungsi yang dibentuk dari model H-R. Terdapat tiga fungsi dari persamaan H-R yang bisa dibentuk dari persamaannya (persamaan 5 hal. 7):

I z x ax y f_x   2 3  (14a)

y

dx

f

y





2

1

(14b)

)

(

b

x

z

f

_z







_e



(14c) Ketiga fungsi yang telah dibentuk tersebut disubstitusikan ke metode RKF45 sebagai berikut (lihat persamaan 11 dan 13 pada hal. 9):

(2)



k k k



x

y

z

hf

kx

₁



,

, (15a)



_k _k _k



y x y z hf ky₁ , , , (15b)



k k k



z

x

y

z

hf

kz

₁



,

,       _ _ _  ₁ ₁ ₁ 2 ₄ 1 , 4 1 , 4 1 kz z ky y kx x hf kx _x _k _k _k , (15c)       _ _ _  ₁ ₁ ₁ 2 4 1 , 4 1 , 4 1 kz z ky y kx x hf ky _y _k _k _k , (15d) , 4 1 , 4 1 , 4 1 1 1 1 2       _ _ _ hf x kx y ky z kz kz _z _k _k _k (15e) , 32 9 32 3 , 32 9 32 3 , 32 9 32 3 2 1 2 1 2 1 3                    kz kz z ky ky y kx kx x hf kx k k k x (15f) , 32 9 32 3 , 32 9 32 3 , 32 9 32 3 2 1 2 1 2 1 3                    kz kz z ky ky y kx kx x hf ky k k k y (15g) , 32 9 32 3 , 32 9 32 3 , 32 9 32 3 2 1 2 1 2 1 3                    kz kz z ky ky y kx kx x hf kz k k k z (15h) , 2197 7296 2197 7200 2197 1932 , 2197 7296 2197 7200 2197 1932 , 2197 7296 2197 7200 2197 1932 3 2 1 3 2 1 3 2 1 4                             kz kz kz z ky ky ky y kx kx kx x hf kx k k k x (15i) , 2197 7296 2197 7200 2197 1932 , 2197 7296 2197 7200 2197 1932 , 2197 7296 2197 7200 2197 1932 3 2 1 3 2 1 3 2 1 4                             kz kz kz z ky ky ky y kx kx kx x hf ky k k k y (15j)

(3)

, 2197 7296 2197 7200 2197 1932 , 2197 7296 2197 7200 2197 1932 , 2197 7296 2197 7200 2197 1932 3 2 1 3 2 1 3 2 1 4                             kz kz kz z ky ky ky y kx kx kx x hf ky k k k Z (15k) , 4104 845 513 3680 8 216 439 , 4104 845 513 3680 8 216 439 , 4104 845 513 3680 8 216 439 4 3 2 1 4 3 2 1 4 3 2 1 5                                kz kz kz kz z ky ky ky ky y kx kx kx kx x hf kx k k k x (15l) , 4104 845 513 3680 8 216 439 , 4104 845 513 3680 8 216 439 , 4104 845 513 3680 8 216 439 4 3 2 1 4 3 2 1 4 3 2 1 5                                kz kz kz kz z ky ky ky ky y kx kx kx kx x hf ky k k k y (15m) , 4104 845 513 3680 8 216 439 , 4104 845 513 3680 8 216 439 , 4104 845 513 3680 8 216 439 4 3 2 1 4 3 2 1 4 3 2 1 5                                kz kz kz kz z ky ky ky ky y kx kx kx kx x hf kz k k k z (15n) , 40 11 4104 1859 2565 3544 2 27 8 , 40 11 4104 1859 2565 3544 2 27 8 , 40 11 4104 1859 2565 3544 2 27 8 5 4 3 2 1 5 4 3 2 1 5 4 3 2 1 6                                   kz kz kz kz kz z ky ky ky ky ky y kx kx kx kx kx x hf kx k k k x (15o) , 40 11 4104 1859 2565 3544 2 27 8 , 40 11 4104 1859 2565 3544 2 27 8 , 40 11 4104 1859 2565 3544 2 27 8 5 4 3 2 1 5 4 3 2 1 5 4 3 2 1 6                                   kz kz kz kz kz z ky ky ky ky ky y kx kx kx kx kx x hf ky k k k y (15p)

(4)

, 40 11 4104 1859 2565 3544 2 27 8 , 40 11 4104 1859 2565 3544 2 27 8 , 40 11 4104 1859 2565 3544 2 27 8 5 4 3 2 1 5 4 3 2 1 5 4 3 2 1 6                                   kz kz kz kz kz z ky ky ky ky ky y kx kx kx kx kx x hf kz k k k z (15q)

Konstanta-konstanta tersebut dibangun berdasarkan metode RKF45 yang akan membentuk perubahan titik-titik untuk trayektori dengan menggunakan persamaan orde 5 (lihat 2.7 Metode Runge-Kutta-Fehlberg 45) disajikan sebagai berikut:                              6 5 4 3 1 1 55 2 50 9 56430 28561 12825 6656 135 16 kx kx kx kx kx x x k k (16a)                              6 5 4 3 1 1 55 2 50 9 56430 28561 12825 6656 135 16 ky ky ky ky ky y y k k (16b)                              6 5 4 3 1 1 55 2 50 9 56430 28561 12825 6656 135 16 kz kz kz kz kz z z k k (16c)

Untuk

k



1

dimana

t

₁

,

x

₁

,

y

₁

,

z

₁ nilai yang disesuaikan sebagai inisial dan n (jumlah iterasi) merupakan batas iterasi

k

(

k



1

s.d. n ).

t

_k1



t

_k



h

merupakan perubahan waktu dengan

n t

h ,



t

adalah selang waktu diinginkan untuk meninjau trayektori dari persamaan H-R. Perlu diketahui dalam metode RKF45 syarat untuk meninjau iterasi titik data dengan akurasi tinggi diperlukan nilai nyang jauh lebih besar dari



t

.

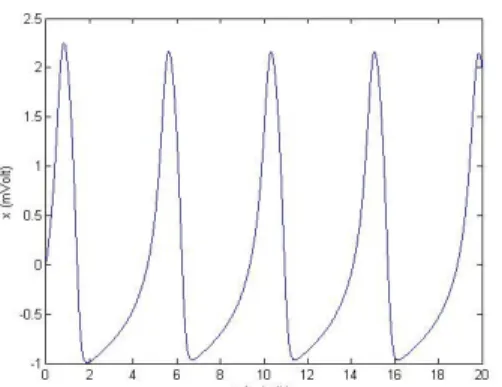
Penjelasan diatas merupakan tahapan untuk menemukan sebuah solusi numerik berupa grafik trayektori untuk membuat simulasi sistem dinamika penjalaran impuls di dalam sel saraf dengan menggunakan perangkat lunak MATLAB yang dapat dilihat pada Gambar 5. Grafik tersebut merupakan simulasi yang memperlihatkan fenomena terbentuknya potensial aksi dengan nilai



3

satuan potensial sehingga dapat disesuaikan dengan nilai yang sebenarnya dari nilai potensial aksi berdasarkan eksperimen H-H. Konstanta-konstanta yang terdapat dalam persamaan H-R dapat dijelaskan sebagai berikut (lihat 2.5 Model Matematika Hindmarsh-Rose) :

a dan

b

yang menjelaskan tentang pengaruh dari potensial membran saat (slow dynamics). Slow dynamics adalah keadaan saat terbukannya saluran Na+ yakni saat potensial didalam membran sel saraf mulai meningkat menuju potensial aksi. Perubahan variabel ini akan merubah nilai potensial aksi dan lamanya proses perubahan potensial menuju potensial aksi. Dalam kasus ini perubahan nilai akan membuat perbandingan baru untuk menerka kuantitas dari proses pembentukan potensial aksi, bahkan dengan perubah sampai tertentu harga tertentu dapat membuat trayektori simulasi potensial

(5)

aksi yang tidak sesuai dengan fenomena yang ada. Aplikasinya ada pada keadaan sel saraf mahluk hidup yang memiliki fenomena berbeda untuk menyatakan kuantitas proses terbentuknya potensial aksi. Perubahan varibel a dan

b

dibandingkan antara Gambar 5, Gambar 6, dan Gambar 7. Perubahan variabel tersebut berkaitan dengan karakteristik dari bukaan pintu Na+ _{setiap sel saraf} dan bergantung juga pada kondisi fisik dari sel saraf. Semakin lama bukaan dari pintu Na+ _{maka akan mengakibatkan} pembentukan potensial aksi yang semakin terlambat pada Gambar 7. Variabel

d

adalah konstanta yang ditentukan dari percobaan sehingga tidak ada penjelasan khusus dari perubahan variabel ini pada terbentuknya potensial aksi, namun apabila variabel ini diubah maka trayektori yang terbentuk akan menunjukkan fenomena lain diluar fenomena yang dicari dari simulasi ini.

I adalah arus masukan, dalam hal ini bukan merupakan besarnya arus yang persis diberikan pada suatu sel saraf hidup, namun merupakan arus dugaan dari kuantitas fenomena potensial aksi yang telah didapatkan sebelumnya. Variabel



adalah recovery variable dan

x

_e adalah titik keseimbangan dari dua dimensi sistem H-R yang akan bernilai dirinya sendiri apabila tidak ada inputan didalam sistem (dapat dilihat dengan menggunakan GUI pada sub-bab

4.3).5 Gambar 6. Simulasi potensial aksi

dengan perangkat lunak MATLAB dari persamaan H-R.

I



1 .

78 

A

,

a



5

, , 14  b

d



5

,



0.001, dan



5 1



2 1 _   e x .

Perubahan potensial aksi saat slow dynamics akibat perubahan nilai a dan

b

.

Gambar 5. Simulasi potensial aksi

I



1 .

78 

A

,

a



3

, , 4  b

d



5

,



0.001, dan



5 1



2 1 _   e x .

Potensial aksi merambat melalui membran sel saraf dan membentuk potensial aksi.

(6)

Dinamika spiking merupakan pola potensial aksi yang menjalar sepanjang akson sel saraf tanpa mengalami bursting yang artinya tidak ada pengulangan secara serempak pada suatu kumpulan perambatan potensial aksi. Perilaku bursting dianggap pola penjalaran yang khas, karena menumpuknya potensial aksi dalam satu waktu penjalaran yang singkat, dimisalkan seperti laju tranfer sinyal neurotransmiter persatuan panjang akson. Adapun perilaku fast spiking merupakan perilaku umum pada sel saraf yang menunjukkan pengulangan spiking secara normal dalam periode yang lebih cepat. Fast Spiking terjadi pada sel saraf dengan hantaran impuls searah. Dengan memvariasikan I maka didapatkan sejumlah data yang tersaji pada Tabel 3 berikut :

Gambar 7. Simulasi potensial aksi

I



1 .

78 

A

,

a



2

, , 9  b

d



5

,



0.001, dan



5 1



2 1 _   e x .

Pada variasi nilai tertentu perubahan nilai a dan

b

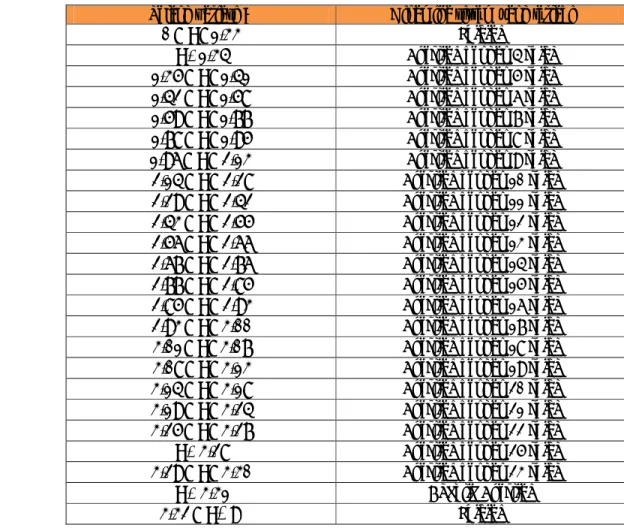
membuat simulasi diluar fenomena pada I yang sama.

Tabel 3. Dinamika sistem penjalaran impuls pada sel saraf dengan variasi I input

Selang variasi I Dinamika sistem yang terjadi

33 .

1

0  I



Spiking

34 .

1 

I

Bursting dengan 4 spike

41 .

1

35 .

1  I



58 .

1

42 .

1  I



77 .

1

59 .

1  I



95 .

1

78 .

1  I



13 .

2

96 .

1  I



28 .

2

14 .

2  I



42 .

2

29 .

2  I



55 .

2

43 .

2  I



66 .

2

56 .

2  I



76 .

2

67 .

2  I



85 .

2

77 .

2  I



93 .

2

85 .

2  I



00 .

3

93 .

2  I



07 .

3

01 .

3  I



13 .

3

08 .

3  I



18 .

3

14 .

3  I



24 .

3

19 .

3  I



27 .

3

25 .

3  I



28 .

3 

I

30 .

3

29 .

3  I



31 .

3 

I

Chaotic Bursting





 I

32 .

3

Spiking

(7)

(a)

(b)

(c)

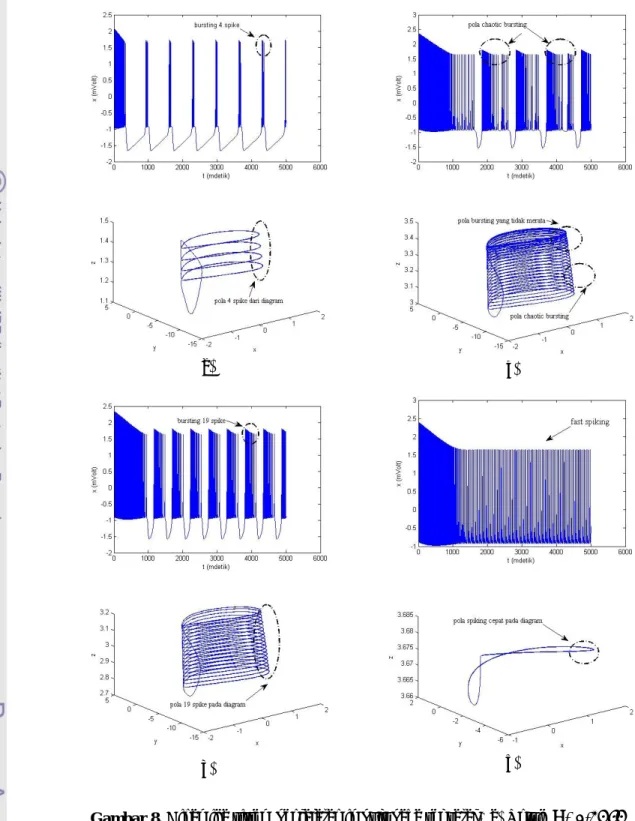
(d)

Gambar 8. Dinamika sistem penjalaran impuls pada sel saraf. (a) Untuk

I



1 .

34 

A

Busting dengan 4 spike. (b) Untuk

I



3 .

08 

A

Busting dengan 19 spike. (c) Untuk

A

(8)

Tabel diatas merupakan sebuah hasil simulasi yang memperlihatkan fenomena-fenomena terbentuknya potensial aksi didalam penjalaran impuls pada sel saraf. Terlihat dari tabel semakin besarnya inputan arus searah

I

mengakibatkan semakin terbentuknya fenomena bursting yang dimulai dari fenomena dasar yakni spiking. Terlihat pada kenaikan selang



0 .

05 

A

terbentuklah sebuah spike tambahan hingga pada

I



3 .

27 

A

tepat berakhirnya penjumlahan spike pada bursting secara linear. Perlu diketahui fenomena bursting merupakan sebuah fenomena terbentuknya penumpukan jumlah potensial aksi atau spike pada waktu tertentu dan membentuk pola yang teratur sepanjang penjalaran impuls didalam sel saraf. Fenomena ini sangat umum terjadi dan menjadi hal yang penting untuk memperlihatkan kondisi normal dan tidaknya suatu sel saraf dari karakteristiknya menyampaikan sinyal neutransmiter 5_. Jumlah spike yang terbentuk bergantung dari besarnya arus yang di berikan pada setiap jenis dari sel saraf.

Analisa penambahan linier pada arus dan pembentukan spike pada bursting terhenti saat arus berada pada

A

I



3 .

27 

karena pada saat

A

I



3 .

28 

potensial aksi menjalar dengan pola spike bursting yang meningkat menjadi 25 spike dan kembali menurun menjadi 23 spike fenomena selanjutnya merupakan fenomena chaotic bursting yang berarti terjadi fenomena kacau pada bursting. Terjadinya hal tersebut merupakan temuan yang terkait dengan keterbatasan persamaan H-R dalam menjelaskan fenomena penambahan jumlah spike yang linier untuk setiap penambahan jumlah arus. Namun hal tersebut tidak sepenuhnya menjadi kelemahan dari model ini, pada kenyataannya model ini juga menjelaskan tentang kekacauan pulsa dari potensial aksi yang menjalar dalam sebuah sel saraf akibat berlebihnya impuls yang diberikan 1_,

sehingga mengakibatkan sel saraf mengalami chaos 9_{Sementara itu untuk}

A

I



3 .

32 

simulasi persamaan memperlihatkan fenomena spiking secara periodik yang akan semakin cepat dengan penambahan arus.

4.2 Analisa Bifurkasi dan Dinamika Sistem

Tingkah laku potensial aksi (singgle spiking) yang telah dibahas sebelumnya merupakan sebagian kecil dari fenomena penjalaran impuls pada sel saraf. Masih banyak fenomena lainnya yang terjadi dan merupakan fenomena yang wajib untuk diketahui dan dipelajari, diantaranya adalah tingkah laku bursting, chaotic bursting, bursting adapting, dan lain-lain. Tingkah laku tersebut dapat dilihat dari grafik simulasi dengan variasi inputan

I arus pada persamaan atau impuls (rangsangan) dan keadaan dari sel saraf (konstanta dalam persamaan) sendiri. Dalam kasus ini analisis bifurkasi dan dinamika sistem merupakan analisis yang yang digunakan untuk menganalisa persamaan sehingga dapat membentuk beberapa fenomena diatas.

Seperti yang telah disebutkan sebelumnya pengertian bifurkasi adalah perubahan trayektori dalam ruang fasa (dalam hal ini potensial aksi) yang terjadi disekitar titik kestabilan. Titik kestabilan merupakan titik yang ditentukan dengan membuat semua fungsi dari persamaan differensial terkopel sama dengan nol. Kasus ini menggunakan tiga persamaan differensial H-R 11_:









                z x x b f y dx f I z x ax y f e z y x



2 3 2 1 (17a)               0 0 0 x y x f f f (17b)

(9)









                 0 0 1 0 2 3 2 z x x b y dx I z x ax y e



(17c) Kemudian didapatkan persamaan polinomial sebagai berikut :









_            0 1 2 3 I bx bx x a d x e (18) untuk

I



1 .

78

,

a



3

, b4,

d



5

, 001 . 0 



, dan



5 1



2 1 _   e x ,

Akar-akar dari persamaan tersebut adalah titik kestabilan

x

₀dalam ruang fasa yang bergantung pada variasi I . Dengan mengetahui titik kestabilan untuk x maka didapatkan titik kestabilan untuk ydan

z

yakni :

                     1.6223 6.3504 -1.2125 -0 0 0 z y x

Tingkah laku penjalaran impuls pada sel saraf untuk setiap besar inputan (variasi

I ) akan menunjukan nilai titik kestabilan yang selalu berubah, hal tersebut berakibat pada timbulnya pola-pola penajalaran impuls yang bervariasi dalam selang waktu tertentu dan memastikan adanya fenomena-fenomena yang telah disebutkan sebelumnya (bursting, chaotic bursting, bursting adapting, dan lain-lain) pada suatu harga

I dalam selang tertentu pula. Sehingga dapat dianalisa dan diprediksi bagaimana dinamika sistem penjalaran impuls yang akan terjadi di dalam sel saraf. Namun sebelum menganalisa dinamika sistem lebih lanjut perlu dilakukan pengkarakterisasian dari harga-harga keseimbangan untuk mengetahui jenis bifurkasi dari pembentuk dinamika sistemnya.

Harga eigen merupakan harga yang didapatkan dari titik kritis pada suatu sistem dengan melakukan substitusi nilai

salah satu nilai atau seluruhnya dari

0 0 0

,

y

,

z

x

kedalam suatu matriks untuk melakukan pengkarakterisasian. Karakterisasi disini adalah untuk mengetahui jenis bifurkasi apa yang telah dialami suatu sistem dari persamaan eksak pembentuknya. Harga eigen karakteristik didapatkan dengan melakukan linearisasi persamaan H-R untuk membentuk Jacobian Matrix (lihat persamaan 8 hal. 8) 11_:

                



0 0 1 2 1 1 2 3 2 b dx ax x J , (19a)

persamaan matriks harga eigen karakteristik adalah sebagai berikut :

X

J





(19b)

dimana

J

merupakan matrik persegi

N



dan



merupakan harga eigen karakteristik yang dapat ditentukan dengan menyelesaikan persamaan karakteristik berikut (lihat persamaan 10 hal. 8) 11,12





0 det

J

 I





, dimana I adalah matriks identitas 0 0 0 1 2 1 1 2 3 det 0 0 0 0 0 0 0 0 0 1 2 1 1 2 3 det 2 2                                      









b dx ax x b dx ax x (20) sesuai dengan aturan Cramer maka didapatkan persamaan polinomial untuk

(10)

0 ) 2 )( 1 )( ( ) )( 1 )( 1 ( ) ( ) 1 ( ) 2 3 ( 2                                                   dx b ax x











(21) untuk

I



1 .

78

,

a



3

, b4,

d



5

, 001 . 0 



, dan



5 1



2 1 _   e x ,

Maka didapatkan akar-akar dari harga eigen karakteristik sebagai berikut:

-12.7193

1





,

0.0018i

+

0.0166

2





,

0.0018i.

-0.0166

3





Harga-harga eigen karakteristik diatas menentukan jenis-jenis bifurkasi pada dinamika sistem penjalaran impuls pada sel saraf. Dengan menggunakan Tabel 2 (hal. 8) harga eigen yang dimiliki sistem saat I 1.78 adalah terdiri dari bilangan rill dan kompleks sehingga titik fokus terbentuk pada ruang fasa. Pada perubahan input berupa

I

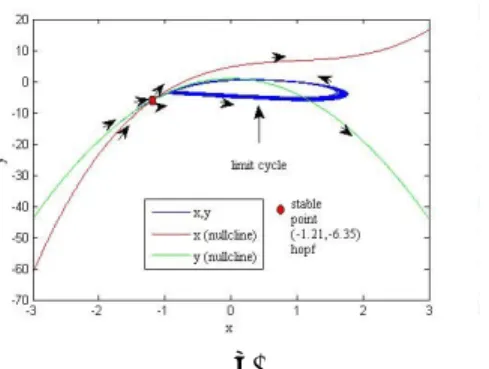
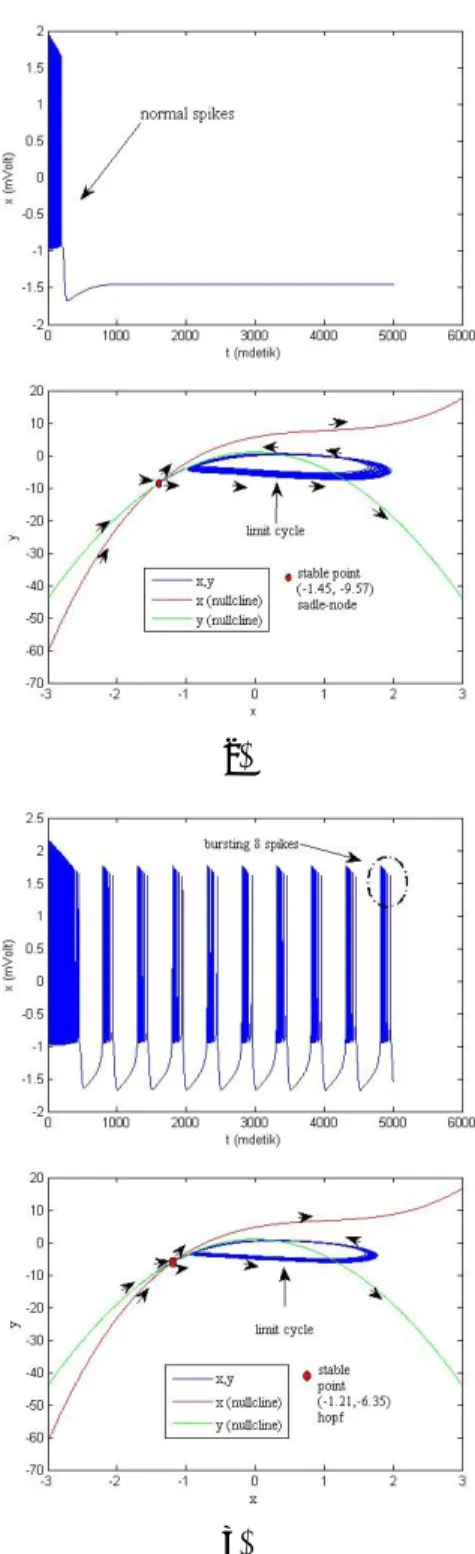
akan merubah pola trayektori yang terjadi pada sistem pola tersebut dijelaskan pada Gambar 9a dan Gambar 9b.

(a)

(b)

Gambar 9. Analisa bifurkasi pada

persamaan H-R

Pada Gambar 9a merupakan pola potensial aku si yang bentuk dari pola bifurkasi pada trayektori Gambar 9b dimana pada Gambar 9 pola trayektori membentuk suatu kecenderungan bifurkasi yang terjadi dari sistem dan membentuk bifurkasi Hopf dan bifurkasi Sadle-Node. Bifurkasi Hopf pada dasarnya melibatkan trayektori yang bersifat periodik dimana terjadi perubahan jenis titik kritis dari titik fokus dengan atraktor positif menjadi atraktor negatif disertai dengan kemunculan limit cycle. Limit cycle merupakan sebuah trayektori berbentuk lingkaran yang bersifat periodik yang muncul akibat perubahan kestabilan fokus. Sedangkan bifurkasi Sadle-Node yang mungkin terjadi akibat munculnya dua atau lebih dari titik kritis. Dalam kasus ini jumlah Limit cycle akan menentukan pola spiking yang terjadi didalam sistem persamaan H-R.

Tabel 4 menunjukkan beberapa titik yang mengidentifikasi bifurkasi yang terjadi pada dinamika sistem penjalaran impuls di dalam sel saraf berdasarkan model H-R. Titik-titik tersebut dihasilkan dari perubahan input berupa

I arus searah yang diubah untuk menemukan beberapa titik kritis pada sistem dan menemukan karakteristik dari trayektori sistem. Pola bifurkasi berperan penting dalam menemukan sejumlah fenomena dalam penjalaran impuls saraf atau pembentukan pola potensial aksi selama menjalar sepanjang sel saraf.

(11)

Tabel 4. Bifurkasi yang terjadi pada

dinamika sistem dengan variasi I input

I           0 0 0 z y x           3 2 1



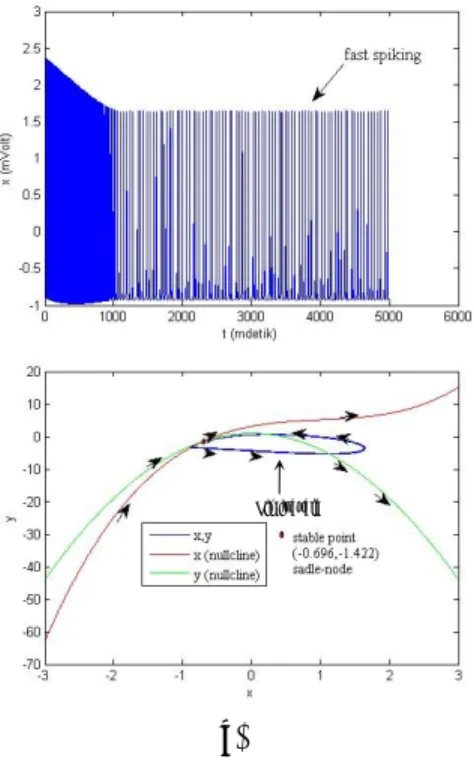
Jenis bifurkasi 0.81             ) 66 . 0 57 . 9 45 . 1             01 . 0 02 . 0 03 . 16 Sadle-Node 1.78             62 . 1 35 . 6 21 . 1              i i 002 . 0 02 . 0 002 . 0 02 . 0 72 . 12 Hopf 3.32             68 . 3 42 . 1 69 . 0           002 . 0 19 . 0 82 . 6 Sadle-Node

Pada titik tertentu dalam trayektori membentuk suatu pola bifurkasi seperti tertera pada Gambar 10a dan Gambar 10c adalah bifurkasi Sadle-Node terbentuk dengan melihat harga eigen karakteristik bernilai rill dan lebih dari satu. Sementara itu bifurkasi Hopf Gambat 10b terbentuk dari adanya nilai eigen karakteristik yang bernilai imajiner. Letak titik kesetimbangan pada sistem selalu berubah dengan perubahan nilai input I berupa arus searah yang akan menjadikan sistem membentuk suatu pola potensial aksi yang menjalar sepanjang sel saraf.

(a)

(b)

(12)

(c)

Gambar 10. Analisis bifurkasi dengan

variasi I input. (a) Bifurkasi Sadel-Node

I



0 .

81

_{. (b) Bifurkasi Hopf}

78 .

1 

I

_{. (c) Bifurkasi Sadel-Node}

32 .

5 

I

Analisa dinamika sistem pada penjalaranan impuls di dalam sel saraf akan melihat lebih luas dari yang sebenarnya terjadi pada persamaan. Dengan adanya titik-titik kesimbangan dan jenis bifurkasi yang menyertainya sistem tersebut berubah terhadap variasi

I inputan, kemudian perubahan trayektori yang menunjukkan bagaimana persamaan membangun suatu dinamika sistem pada sel saraf.

4.3 GUI untuk Dinamika Sistem H-R dengan MATLAB

Graphical User Interface atau yang disingkat GUI merupakan suatu sarana singkat dan populer untuk menampilkan aplikasi perangkat lunak sehingga lebih mudah digunakan. Didalam pembuatan GUI para programmer (pembuat perangkat lunak) haruslah

memperhitungkan segi kenyamanan pengguna untuk mengakses perangkat lunak tersebut. Sehingga apa yang dimaksud dari aplikasi yang dibuat akan mudah dimengerti oleh pengguna. Dinamika sistem penjalaran impuls pada sel saraf dengan menggunakan model H-R memiliki banyak aspek dan variabel yang ditinjau. Pada sub-bab sebelumnya telah dibahas mengenai solusi numerik yang menampilkan bentuk fisis dari persamaan H-R dan kemudian telah dibahas mengenai dinamika sistem serta bifurkasinya. Namun kesemua hal tersebut hanya dapat diakses dan dipahami oleh pihak-pihak tertentu. GUI kali ini akan menampilkan suatu aplikasi tentang simulasi penjalaran impuls pada sel saraf dengan menggunakan model H-R.

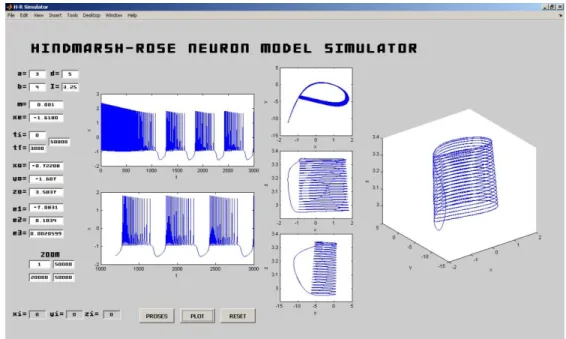
Pada Gambar 11 diperlihatkan fisik dari aplikasi yang dimaksud. Pada aplikasi tersebut terdapat variabel, konstanta, dan inputan yang menyusun persamaan H-R, serta terdapat pula keluaran apabila program dijalankan dengan menekan tombol ‘PROSES’ dan hasil akan ditampilkan pada axis pertama (lihat Gambar 11). Tombol tersbut merupakan pemicu program yang akan menjalankan serangkaian proses simulasi dengan metode RKF45 yang telah disebutkan sebelumnya dari model H-R. Bila telah menampakkan hasil pada grafik keluaran yang pertama maka dapat menganalisa tindajaun berikutnya dengan menekan tombol ‘PLOT’. Penggunaan tombol ‘PLOT’ adalah untuk mengakses kotak edit dibawah label ‘ZOOM’ sehingga semua axis akan terisi dengan keluaran yang diinginkan serta dapat dianalisis dengan melihat label dari setiap axis (lihat Gambar 12). Sedangkan tomnol ‘RESET’ adalah tombol untuk mengembalikan semua kondisi aplikasi setelah melakukan perubahan terhadapat variabel, konstanta, dan inputan dari persamaan H-R.

(13)

Gambar 11. GUI simulasi H-R model. Sejumlah kontanta dan input dapat diubah untuk

melakukan analisis dari penjalaran impuls pada sel saraf. Keluaran pertama setelah menekan tombol ‘PROSES’.

Gambar 12. ‘Penggunaan tombol ‘PLOT’. Untuk mendapatkan grafik yang lebih dekat

(14)

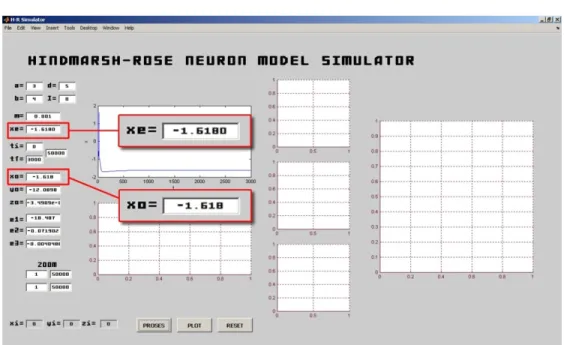
Pada sub bab sebelumnya dibahas mengenai konstanta x_eyang merupakan titik keseimbangan saat sistem jika tidak diberi arus atau impuls. Gambar 8 pada GUI disajikan saat

I



0

maka akan terbentuk titik keseimbangan pada

e

x

x₀  hal tersebut berarti pada

kondisi tidak diberi arus sistem akan berada dalam keseimbangan titik-titik tersebut dan inilah merupakan fisis dari sifat sel saraf yang selalu menuju pada keadaan seimbang sesaat setelah diberi rangsangan berupa arus atau impuls.

Gambar 13. ‘Sifat dari konstanta x_esebagai titik kesembangan bagi x₀ pada saat

I



0

pada sistem’. Nilai tersebut menjelaskan sifat sel saraf yang selalu menuju ke keadaan semula sesaat setelah diberi rangsangan.

BAB V

KESIMPULAN DAN SARAN

5. 1 Kesimpulan

Simulasi dinamika sel saraf menggunakan model Hindmarsh-Rose merupakan suatu simulasi yang dapat dilakukan untuk menjelaskan tentang dinamika penjalaran yang terjadi didalam sel saraf. Model ini dapat menunjukkan fenomena-fenomena seperti spiking-bursting dan chaotic bursting dengan mengubah input berupa arus searah yang merupakan fenomena pengembangan dari model penjalaran impuls didalam sel saraf. Perubahan

input berupa arus searah akan mengakibatkan transisi fenomena dari spike menjadi bursting dan memunculkan fenomena chotic bursting sepanjang penjalaran impuls didalam sel saraf. Fenomena chotic bursting memungkinkan terbentuknya fase peningkatan jumlah spike untuk kenaikan



0 .

05 

A

dari input kedalam sistem. Peningkatan tersebut terjadi secara linier pada range input

A

I



3 .

27 

dan menampakkan fenomena menyimpang pada range diatas input tersebut oleh keterbatasan dari persamaan dan perilaku dari sel saraf yang sebenarnya.

Metode RKF 45 merupakan metode numerik untuk memecahkan persamaan