LAPORAN AKHIR No. 03/HB-PENELITIAN/LPPM-UKP/VII/2016

LAPORAN AKHIR

No. 03/HB-PENELITIAN/LPPM-UKP/VII/2016

Pengembangan Lebih Lanjut

Metode Elemen Hingga Berbasis Kriging

untuk Analisis Pelat Reissner-Mindlin dan 3D

Solids

Oleh:

Wong Foek Tjong, 00-034 Januar Budiman, 09-011

LEMBAGA PENELITIAN DAN PENGABDIAN KEPADA MASYARAKAT UNIVERSITAS KRISTEN PETRA

TAHUN 2016

Dibiayai oleh LPPM Universitas Kristen Petra, sesuai dengan Surat Perjanjian Penugasan Pelaksanaan Hibah Penelitian Nomor: 03/HB-PENELITIAN/LPPM-UKP/XII/2015, tanggal 11 Desember 2015

Metode elemen hinga (MEH) merupakan metode numerik yang paling luas digunakan dalam desain-desain produk rekayasa, mulai dari alat-alat sederhana sampai pesawat ruang angkasa. Dalam penerapan metode ini, elemen-elemen yang mudah dipakai adalah elemen-elemen sederhana seperti elemen segitiga tiga node untuk model matematis 2D dan elemen tetrahedron empat node untuk model 3D. Namun sayangnya elemen-elemen sederhana ini tidak dapat menghasilkan solusi yang akurat dan terlebih gradien dari field variable diskontinu di batas-batas elemen.

MEH berbasis Kriging (MEH-K) telah diusulkan sebagai alternatif dari MEH konvensional. Prinsip dari metode ini adalah mengganti fungsi pendekatan solusi dalam MEH konvensional dengan fungsi interpolasi Kriging. Interpolasi Kriging ini melibatkan nodes yang bukan hanya berasal dari elemen itu sendiri tetapi juga melibatkan nodes dari beberapa lapis elemen di sekitarnya. Dengan MEH-K, solusi yang dihasilkan lebih akurat dan gradien field variable yang diperoleh ’halus’ walaupun tetap menggunakan elemen-elemen hingga sederhana.

Dalam penelitian terdahulu MEH-K telah dikembangkan untuk menganalisis pelat Reissner-Mindlin (dinamakan Pelat-K). Namun elemen yang telah dikembangkan masih memiliki kelemahan shear locking, yaitu menjadi terlalu kaku (mengunci) ketika tebal pelat mengecil. Dalam penelitian ini elemen Pelat-K dikembangkan lagi dengan mengadopsi teknik discrete shear gap (DSG) sebagai upaya untuk mengatasi shear locking. Cara-cara penerapan teknik DSG yang diujicoba ada tiga jenis, yaitu: (1) mengadopsi langsung rumus untuk matriks kekakuan geser elemen pelat segitiga linier, (2) menggunakan shear gap dari interpolasi Kriging pada titik-titik sudut segitiga, (3) menggunakan shear gap dari interpolasi Kriging pada titik-titik sudut segitiga dan dua titik tengah sisi segitiga. Hasil pengujian memperlihatkan bahwa teknik DSG dengan cara (1) dan (2) dapat memperlemah efek shear locking namun masih belum dapat mengeliminasi shear locking secara menyeluruh.

Dalam penelitian terdahulu MEH-K juga telah dikembangkan untuk menganalisis benda elastis tiga dimensi (dinamakan K-Solid). Dalam penelitian ini dikukan penyelidikan range parameter Kriging yang sesuai dan jumlah titik sampel kuadratur yang cukup akurat untuk analisis 3D. Dari penyelidikan parameter Kriging dihasilkan rumus empiris untuk penetapan nilai parameter korelasi sebagai fungsi dari jumlah nodes dalam suatu domain of influencing nodes. Dari penyelidikan jumlah titik kuadratur didapati bahwa 11 titik untuk integrasi volume dan 7 titik untuk integrasi permukaan dapat memberikan hasil yang cukup akurat. Elemen K-Solid yang dikembangkan diujikan pada sejumlah benchmark problems. Pengujian numerik ini memperlihatkan bahwa elemen K-Solid dapat memberikan hasil yang sangat akurat baik untuk perpindahan maupun tegangan. Akan tetapi untuk benda 3D yang tipis hasil-hasil dari MEH-K ternyata konvergen ke arah yang berbeda dari solusi referensi.

PRAKATA

Syukur kepada Tuhan Yang Mahaesa bahwa kami dapat menyelesaikan penelitian pengembangan lanjutan metode elemen hingga berbasis Kriging.

Penulis mengucapkan terima kasih kepada Lembaga Penelitian dan Pengabdian kepada Masyarakat, Universitas Kristen Petra, atas dana penelitian yang diberikan. Penulis berterima kasih kepada mahasiswa Program Magister Teknik Sipil, yaitu Welly P. (NIM. 01514020) dan Danny W. (NIM. 01514014), yang telah melaksanakan perumusan, pemrograman dan pengujian numerik dalam rangka penyelesaian tesis program magister mereka.

Masih terdapat kelemahan-kelemahan dari prosedur yang dikembangkan yang akan diperbaiki lagi dalam penelitian yang akan datang. Penulis berharap penelitian ini dapat dipublikasikan pada suatu jurnal internasional bereputasi dan dengan demikian memberikan kontribusi bagi pengembangan teknik komputasi.

DAFTAR ISI HALAMAN SAMPUL ... 1 HALAMAN PENGESAHAN ... 2 RINGKASAN ... 3 PRAKATA ... 4 DAFTAR ISI ... 5 BAB 1. PENDAHULUAN ... 7 1.1. Latar Belakang ... 7 1.2. Tujuan... 9 1.3. Ruang Lingkup ... 9 1.4. Manfaat Penelitian... 9

BAB 2. STUDI PUSTAKA ... 10

2.1. Metode Kekakuan Langsung ... 10

2.2. Interpolasi Kriging dalam Metode Elemen Hingga ... 10

2.3. Pelat Lentur ... 12

2.4. Formulasi Metode Discrete Shear Gap ... 15

2.4.1. Cara 1: shape function linier ………. 15

2.4.2. Cara 2: shape function Kriging titik segitiga linear ……….. 16

2.4.3. Cara 3: shape function Kriging lima titik segitiga ……….... 16

2.5. Teori Elastisitas 3D Solids ... 19

BAB 3. METODE PENELITIAN ... 21

3.1. Diagram Alir Metodologi Penelitian ... 21

3.2. Proses Perhitungan ... 22

BAB 4. HASIL DAN PEMBAHASAN ... 23

4.1. Elemen Pelat Reissner-Mindlin Berbasis Kriging ... 23

4.1.1. Pengujian Shear Locking pada Pelat Bujursangkar dengan Perletakan Jepit 23 4.1.2. Pengujian Keakuratan Elemen pada Pelat Bujursangkar dengan Perletakan Sendi ………... 26

4.2.1. Penyelidikan Jumlah Sampling Point yang Efisien untuk Menghitung Integral

Volume ……….. 32

4.2.2. Penyelidikan Jumlah Sampling Point yang Efisien untuk Menghitung Integral Permukaan ……….. 36

4.2.3. Penyelidikan Range yang Cocok untuk Parameter Korelasi pada Covariance Function ……….. 37

BAB 5. KESIMPULAN DAN SARAN ... 40

5.1. Elemen Pelat Reissner-Mindlin Berbasis Kriging ... 40

5.2. Elemen 3D Solids Berbasis Kriging ... 41

BAB 6. RENCANA TAHAPAN BERIKUTNYA ... 42

6.1. Elemen Pelat Reissner-Mindlin Berbasis Kriging ... 42

6.2. Elemen 3D Solids Berbasis Kriging ... 42

DAFTAR PUSTAKA ………. 43

LAMPIRAN: Instrumen Penelitian ... 45

Susunan Organisasi Tim Peneliti dan Pembagian Tugas ... 45

Biodata Ketua Peneliti ……… 46

Biodata Anggota Peneliti ……… 49

BAB 1. PENDAHULUAN

1.1. Latar Belakang

Saat ini metode elemen hingga (MEH) secara luas digunakan sebagai metode numerik untuk menyelesaikan berbagai masalah dalam bidang rekayasa dan ilmu pengetahuan (Bathe, 1996; Cook, Malkus, Plesha, & Witt, 2002; Zienkiewicz & Taylor, 2000a). Kemampuan dan keserbagunaan dari MEH telah teruji selama beberapa dekade dalam praktek nyata bidang rekayasa. Salah satu isu dalam MEH adalah pembentukan mesh. Pengguna MEH dalam praktek cenderung lebih menyukai menggunakan elemen yang sederhana, seperti elemen segitiga tiga node untuk masalah dua dimensi (2D) dan elemen tetrahedron empat node untuk masalah tiga dimensi (3D), karena mesh dari elemen-elemen itu lebih mudah dibuat otomatis dan lebih dapat diterapkan untuk prosedur mesh adaptif. Akan tetapi, elemen-elemen tersebut sering memberikan solusi dengan akurasi buruk, terutama untuk gradient dari field variables seperti tegangan atau resultan tegangan pada mekanika solid dan struktur.

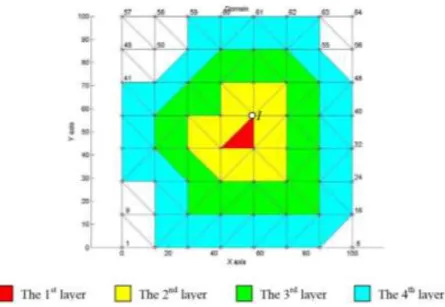
Suatu varian MEH yang memungkinkan mendapatkan solusi akurat meskipun dengan memakai mesh elemen-elemen sederhana diusulkan oleh Plengkhom & Kanok-Nukulchai, (2005). Dalam metode yang diusulkan ini, Kriging shape function digunakan sebagai pengganti shape function polinom dalam MEH konvensional. Kriging shape function ini dibangun dari nilai-nilai variabel pada node yang bukan hanya milik elemen itu sendiri tetapi juga dari node di sekeliling elemen seperti diilustrasikan pada Gambar 1. Jumlah elemen yang dilibatkan dalam pembentukan Kriging shape function dapat dua lapis elemen sekitar atau lebih. Elemen-elemen inti dan sekitarnya ini membentuk daerah dari node yang berpengaruh terhadap interpolasi Kriging dalam elemen inti dan dinamakan domain of influencing nodes (DOI, lihat Gambar 1). Metode yang disusulkan ini selanjutnya disebut sebagai Kriging-based FEM (K-FEM) atau metode elemen hingga berbasis Kriging (MEH-K).

Dengan MEH-K, field variable yang akurasinya tinggi dan gradiennya dapat diperoleh hanya dengan menggunakan bentuk elemen yang paling sederhana. Perbaikan solusi MEH dapat diperoleh tanpa adanya penambahan node pada elemen atau perubahan struktur mesh. Formulasi dan pemrograman MEH-K sangat serupa dengan MEH konvensional sehingga program MEH umum yang sudah ada dapat dengan mudah dimodifikasi untuk mengikutkan MEH-K. Suatu kelemahan dari metode ini adalah fungsi interpolasinya diskontinu pada batas antarelemen (nonconforming). Masalah diskontinuitas

ini dan pengaruhnya pada konvergensi hasil MEH-K telah diselidiki oleh Wong & Kanok-Nukulchai (2009) dan didapati bahwa meskipun MEH-K nonconforming, dengan pemilihan Kriging parameter yang sesuai MEH-K dapat lolos weak patch tests hasil-hasil MEH-K selalu konvergen.

Gambar 1. Elemen dua dimensi dengan DOI satu sampai empat lapis (Sumber: Wong, 2009)

Dalam penelitian Plengkhom dan Kanok-Nukulchai (2005), MEH-K diterapkan untuk menyelesaikan masalah 1D bar dan 2D solid. Dalam penelitian selanjutnya, metode ini diperbaiki dengan penggunaan parameter korelasi adaptif dan dengan mengenalkan fungsi korelasi quartic spline dan dikembangkan untuk analisis pelat Reissner-Mindlin (Wong & Kanok-Nukulchai, 2006a, 2006b). Selanjutnya MEH-K dikembangkan dan diterapkan untuk analisis struktur shell (Wong & Kanok-Nukulchai, 2008; Wong, 2009), analisis 2D solid dengan material discontinuity, 3D solids, dan multiscale simulation (Wichain Sommanawat, 2010; Wichian Sommanawat & Kanok-Nukulchai, 2009).

Dalam pengembangan MEH-K untuk analisis balok, pelat dan shell yang shear-deformable, seperti juga dalam MEH konvensional, kesulitan utamanya adalah fenomena shear locking. Dalam konteks balok Timoshenko, masalah shear locking dapat diatasi dengan metode selective-reduced integration (Wong & Syamsoeyadi, 2011) atau dengan mengadopsi metode discrete shear gap (Bletzinger, Bischoff, & Ramm, 2000; Wong & Sulistio, n.d.). Namun dalam masalah pelat Reissner-Mindlin dan shear-deformable shells sampai saat ini belum ada perumusan MEH-K yang dapat mengeliminasi shear lcoking.

masalah shear locking untuk analisis pelat Reissner-Mindlin. Metode yang digunakan adalah dengan mengadopsi teknik discrete shear gap dalam perumusan MEH-K.

Seperti dijelaskan sebelumnya, MEH-K telah dikembangkan untuk analisis 3D solids (Sommanawat, 2010). Meskipun demikian, dalam penelitian ini range parameter Kriging yang cocok untuk analisis 3D tidak diberikan secara spefik dan belum terdapat penyelidikan lebih lanjut mengenai jumlah titik integrasi yang optimal. Selain itu contoh-contoh numerik yang diberikan masih terbatas untuk menilai konvergensi dari MEH-K untuk 3D solids. Karena itu tujuan lain dari penelitian ini adalah pengembangan dan penyelidikan lebih lanjut MEH-K untuk 3D solids.

1.2. Tujuan

Tujuan penelitian ini adalah:

 Mengembangkan MEH-K yang disertai dengan penggunaan teknik discrete shear gap untuk mengeliminasi kelemahan shear locking.

 Mengembangkan dan menyelidiki lebih jauh MEH-K untuk analisis 3D solids.

1.3. Ruang Lingkup

Ruang lingkup dari penelitian ini adalah sebagai berikut:

 Model struktur yang ditinjau adalah pelat Reissner-Mindlin dan 3D solids.

 Analisis struktur dibatasi untuk analisis statik linier.

 Mesh terbuat dari elemen segitiga 3 node untuk analisis pelat Reissner-Mindlin dan elemen tetrahedron 4 node untuk analisis 3D solids.

 Upaya eliminasi shear locking dalam pelat Reissner-Mindlin dilakukan dengan mengadopsi teknik discrete shear gap (Bletzinger et al., 2000).

 Pemrograman menggunakan program MATLAB

 Pre dan post-processing untuk 3D solids menggunakan software GID.

1.4. Manfaat Penelitian

Penelitian ini akan memberikan kontribusi berupa metode perhitungan alternatif untuk analisis struktur pelat Reissner-Mindlin dan 3D solids. Keunggulan metode altenatif ini adalah perhitungan dapat dilakukan dengan mesh yang sederhana namun keakuratan hasil perhitungan cukup baik.

Luaran dari penelitian ini adalah program analisis struktur dengan MEH-K untuk masalah pelat Reissner-Mindlin dan program untuk masalah 3D solids. Luaran lainnya adalah publikasi pada seminar nasional Konferensi Pascasarjana di Institut Teknologi Bandung tahun 2016 dan pada International Journal for Numerical Methods in Engineering, suatu jurnal internasional bereputasi dalam bidang metode numerik.

BAB 2. STUDI PUSTAKA

2.1. Metode Kekakuan Langsung

Metode kekakuan langsung merupakan implementasi dari MEH yang paling luas digunakan (Cook et al., 2002; Felippa, 2013; Hutton, 2004; Logan, 2007). Dalam metode ini, persamaan keseimbangan struktur dalam bentuk matriks

𝐊𝐃 = 𝐅 (1)

di mana K adalah matriks kekakuan struktur, D adalah vektor (matriks kolom) perpindahan titik-titik nodal, dan F adalah vektor gaya pada titik-titik nodal, dirakit (assembled) dari persamaan-persamaan keseimbangan seluruh elemen yang membentuk struktur itu. Persamaan keseimbangan suatu elemen adalah

𝐤𝐝 = 𝐟 (2)

di mana k adalah matriks kekakuan elemen, d adalah vektor perpindahan titik-titik nodal elemen, dan f adalah vektor gaya pada titik-titik nodal elemen.

Tidak seperti dalam MEH konvensional, dalam MEH-K orde matriks k, d dan f dapat berbeda-beda untuk setiap elemen bergantung kepada jumlah nodes dalam DOI. Semakin banyak lapis elemen yang digunakan dalam pembentukan interpolasi Kriging, semakin besar pula orde matriks-matriks elemen dan biaya komputasi semakin mahal. Proses perakitan dari persamaan elemen (2) menjadi persamaan struktur (1) melibatkan semua degress of freedom dalam semua node dalam DOI.

2.2. Interpolasi Kriging dalam Metode Elemen Hingga

Interpolasi Kriging adalah teknik geostatistik untuk interpolasi ruang yang banyak digunakan dalam ilmu geologi dan pertambangan. Nama Kriging diambil dari nama seorang insinyur pertambangan Afrika Selatan bernama Danie G. Krige (Olea, 1999; Tongsuk & Kanok-Nukulchai, 2004). Dengan menggunakan interpolasi ini, maka suatu titik yang tidak

diketahui nilai variabelnya dapat diinterpolasi dari nilai-nilai variabel yang telah diketahui di sekitar titik tersebut.

Tinjau suatu fungsi (field variable) u(x) yang didefinikan pada sebuah domain Ω yang terdiri dari sekumpulan node yang tersebar xi, i = 1,2, ..., N, di mana N adalah jumlah node pada seluruh domain Ω. Untuk suatu titik x0 yang sedang diamati, definisikan suatu domain berpusat pada titik x0 dan mencakup sejumlah titik-titik berdekatan (domain ini adalah domain of influencing node, DOI). Diasumsikan setiap nodal field variable dalam DOI, u(x1), ..., u(xn) berpengaruh pada nilai field variable titik x0,. Untuk memperkirakan nilai dari u(x0) tersebut, diperlukan sebuah asumsi untuk nilai perkiraan uh yang merupakan kombinsai linier dari u(x1), ..., u(xn), yang dapat dirumuskan sebagai berikut:

𝑢h_(𝐱

0) = ∑𝑛𝑖=1λ𝑖𝑢(𝐱𝑖) (3)

di mana λi adalah Kriging weights dan n adalah jumlah node yang berada di dalam DOI dari titik x0. Dikarenakan nilai dari u(x1), ..., u(xn) dipandang sebagai realisasi dari sebuah variabel acak, maka persamaan (3) dapat ditulis:

𝑈h_(𝐱

0) = ∑𝑛𝑖=1λ𝑖𝑈(𝐱𝑖) (4)

Untuk menentukan Kriging weights, estimator 𝑈h(𝐱0) ini disyaratkan unbiased, yaitu

E[𝑈h_(𝐱

0) − 𝑈(𝐱0)] = 0 (5)

Syarat lainnya adalah variansi dari kesalahan estimator, yaitu var[𝑈h_(𝐱

0) − 𝑈(𝐱0)]

dibuat minimum. Dengan memakai metode Lagrange untuk masalah constrained optimization ini dihasilkan sistem persamaan Kriging sebagai berikut:

𝐑𝛌 + 𝐏𝛍 = 𝐫(𝐱_𝟎) (6) 𝐏T_{𝛌 = 𝐩(𝐱} 𝟎) (7) di mana, 𝐑 = [𝐶(𝐡11) … 𝐶(𝐡1𝑛 ) … … … 𝐶(𝐡_𝑛1) … 𝐶(𝐡_𝑛𝑛)] , 𝐏 = [ 𝑝1(𝐱1) … 𝑝𝑚(𝐱1) … … … 𝑝₁(𝐱_𝑛) … 𝑝_𝑚(𝐱_𝑛)] (8) 𝛌 = [𝜆1 … 𝜆𝑛]𝑇, 𝛍 = [𝜇1 … 𝜇𝑚]𝑇 (9) 𝐫(x₀) = [𝐶(𝐡10) … 𝐶(𝐡𝑛0)]𝑇, 𝐩(𝐱0) = [𝑝1(𝐱0) … 𝑝𝑚(𝐱0)]𝑇 (10)

di mana R adalah matriks kovarians berukuran n × n dari variabel acak antara dau nilai nodal yang ditinjau pada titik xi dan xj, 𝐶(𝐡𝑖𝑗); P adalah matriks basis polinomial berukuran n × m, λ adalah vektor Kriging weights berukuran n × 1, μ adalah vektor pengali Lagrange

berukuran m × 1, r(x0) adalah vektor kovarians antara dua node. n × 1, p(x0) adalah vektor

basis polinomial berukuran m ×1.

Menyelesaikan sistem persamaan Kriging (6)-(7) menghasilkan Kriging weights. Lalu disubstitusi ke nilai perkiraan uh. Sehingga persamaan (3) dapat ditulis kembali seperti berikut:

𝑢h_(𝐱

0) = 𝛌T𝐝 (11)

di mana d=[u(x1) ... u(xn)]Tadalah matriks vektor nilai nodal n × 1. Agar dapat mengikuti pola pada MEH, maka simbol x0 dapat diganti menjadi simbol x. Dengan demikian

persamaan di atas dapat ditulis seperti berikut:

𝑢ℎ_{(𝐱) = 𝐍(𝐱)𝐝 = ∑ 𝑁} 𝑖 𝑛

𝑖=1 (𝐱)𝑢𝑖 (12)

Dalam MEH, matriks shape function pada interpolasi Kriging adalah 𝐍(𝐱) = 𝛌𝑇(𝐱). Sebuah matriks shape function harus memiliki beberapa properti sehingga cocok digunakan dalam MEH. Shape function interpolasi Kriging memenuhi dua properti yaitu Kronecker delta property dan consistency property. Dengan Kronecker delta property, shape function interpolasi Kriging dapat melalui semua nilai nodal dan dapat memiliki prosedur yang sederhana dalam menentukan essential boundary conditions. Ada juga consistency property, supaya MEH-K dapat lolos standar patch test dan shape function interpolasi Kriging tidak mengubah polinomialnya.

Basis polinom yang berperan dalam pembentukan shape function Kriging merupakan fungsi-fungsi basis pembentuk polinomial. Semakin tinggi derajat polinomial m yang digunakan maka semakin banyak juga DOI yang diperlukan, karena jumlah titik nodal dalam DOI, n, harus lebih besar atau sama dengan derajat polinomial yang digunakan, m, agar interpolasi Kriging dapat terbentuk.

2.3. Pelat Lentur

Yang dimaksud dengan pelat adalah sebuah bentuk datar dengan ketebalan yang sangat kecil dibandingkan dengan dimensi lainnya (Cook et al., 2002; Felippa, 2013; Hutton, 2004; Logan, 2007). Sebuah pelat datar, seperti balok lurus, menerima beban lateral dengan lentur. Secara umum, sebuah pelat memiliki bending moments pada dua arah dan sebuah twisting moment.

Terdapat dua teori pelat, yang pertama melarang adanya deformasi geser transversal, sedangkan yang kedua memperhitungkannya. Pada keduanya, tegangan normal pada arah ketebalannya dianggap nol. Teori pertama dinamakan thin-plate theory atau Kirchoff theory.

Teori kedua dinamakan Mindlin theory atau juga sering digunakan istilah Reissner-Mindlin theory.

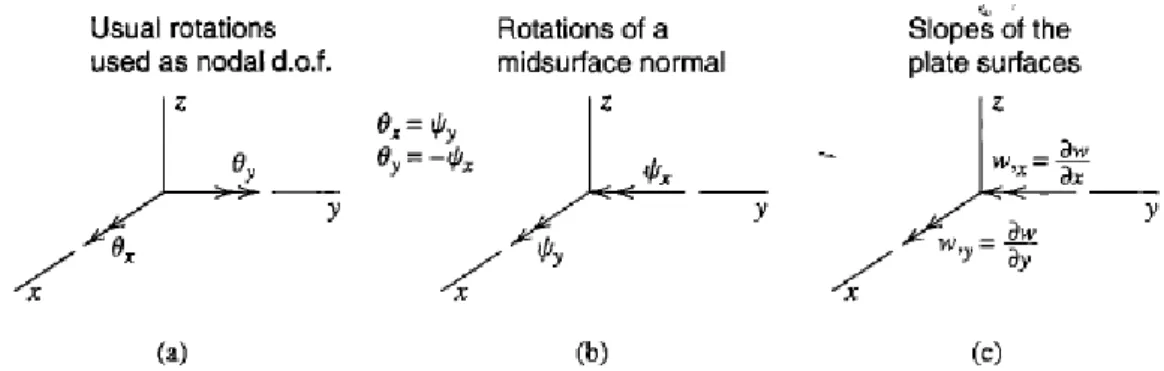
Notasi yang digunakan pada plate bending, dapat dilihat pada Gambar 2. Pelat diletakkan pada bidang xy. Arah panah yang digunakan untuk menggambarkan rotasi adalah menggunakan aturan tangan kanan.

Gambar 2. Notasi untuk komponen rotasi dari mid-surface dan kemiringan permukaan pelat (Sumber: Cook et al., 2002)

Sebuah pelat dengan ketebalan t memiliki mid-surface pada jarak t/2 dari tiap permukaan lateral. Untuk analisa, digunakan bidang xy pada mid-surface pelat sehingga z = 0 menggambarkan mid-surface.

Perilaku pelat diidealisasikan dengan mengatakan bahwa sebuah garis yang lurus dan tegak terhadap mid-surface sebelum dibebani akan tetap lurus tetapi tidak harus tegak terhadap deformed mid-surface. Rotasi dari garis lurus ini memiliki komponen ψx dan ψy. Sehingga sebuah titik yang tidak berada pada mid-surface memiliki perpindahan arah x sebesar u, seperti pada Gambar 3. Begitu juga untuk arah y dengan perpindahannya sebesar v. Sehingga, untuk perpindahan dan rotasi kecil, regangannya dapat diperoleh dari persamaan berikut:

(13) di mana koma menandakan penurunan terhadap variabel selanjutnya dan w adalah defleksi lateral (arah z) dari mid-surface. Regangan untuk arah ketebalan εz tidak diperlukan. Persamaan di atas adalah basis dari teori pelat Mindlin, yang memperbolehkan deformasi geser transversal yang artinya γyz dan γzx tidak harus nol.

Gambar 3. (a) Sebuah elemen pelat (b) Penampang pelat yang mengalami deformasi, dilihat dari arah sumbu y+ (Sumber: Cook et al., 2002)

Tegangan pada penampang pelat dapat dilihat pada Gambar 4. Tegangan tersebut berhubungan dengan momen dan gaya per unit panjang pada bidang xy. Sehingga persamaannya adalah sebagai berikut:

(14) di mana momen Mx dan My adalah bending moments, sementara Mxy adalah twisting moment. Deformasi di mana garis yang tegak terhadap mid-surface diasumsikan tetap lurus, menghasilkan tegangan σx, σy, dan τxy yang berubah secara linear terhadap z.

Gambar 4. (a) Tegangan dan gaya lateral merata q pada elemen pelat

(b) Momen & gaya geser transversal yang berhubungan dengan tegangan pada (a) (Sumber: Cook et al., 2002)

Matriks kekakuan elemen pelat lentur dapat ditunjukkan sebagai penjumlahan dari kekakuan bending [kb] dan kekakuan geser transversal [ks], sebagai berikut:

[𝑘] = ∫ [𝐵_𝐴 𝑏]T[𝐷𝑏][𝐵𝑏] 𝑑𝐴+ ∫ [𝐵_𝐴 𝑠]T[𝐷𝑠][𝐵𝑠] 𝑑𝐴 (15a)

[𝑘𝑏]: = ∫ [𝐵_𝐴 𝑏]T[𝐷𝑏][𝐵𝑏] 𝑑𝐴 (15b)

[𝑘𝑠]: = ∫ [𝐵_𝐴 𝑠]T[𝐷𝑠][𝐵𝑠] 𝑑𝐴 (15c)

Dalam persamaan ini [Bb] adalah matriks penghubung vektor kurvatur dan vektor perpindahan titik nodal, [Bs] adalah matriks penghubung vektor regangan geser dan vektor perpindahan titik nodal, [Db] adalah matriks elastisitas lentur, dan [Ds] adalah matriks elastisitas geser. Rincian lengkap matriks-matriks ini dapat dilihat pada buku-buku teks elemen hingga seperti Bathe, 1996; Cook et al., 2002; Zienkiewicz & Taylor, 2000b.

2.4. Formulasi Metode Discrete Shear Gap

Metode discrete shear gap (DSG) yang digunakan untuk mengeliminasi shear locking diterapkan dalam perumusan elemen pelat berbasis Kriging dengan berbagai cara. Cara pertama dilakukan dengan mengadopsi secara langsung dari formulasi Bletzinger et al. (2000), yaitu menggunakan shape function linear. Cara kedua dan ketiga dikembangkan lebih lanjut dengan menggunakan shape function Kriging untuk menentukan discrete shear gap pada sejumlah titik dalam segitiga. Cara kedua menggunakan integrasi garis pada titik elemen segitiga linear sejumlah 3 node. Cara ketiga menggunakan integrasi garis pada titik elemen segitiga kuadratik sejumlah 5 node.

2.4.1. Cara 1: shape function linier

Dengan mengadopsi secara langsung formulasi DSG dari Bletzinger et al. (2000), didapatkan metode pertama berikut.

𝑎 = 𝑥₂− 𝑥₁ 𝜉₁= 0 𝜂₁= 0

𝑏 = 𝑦₂− 𝑦₁ 𝜉₂= 1 𝜂₂= 0

𝑐 = 𝑦₃− 𝑦₁ 𝜉₃= 0 𝜂₃= 1

𝑑 = 𝑥₃− 𝑥₁

Gambar 5. Elemen tiga node Sumber: Bletzinger et al., 2000

Regangan geser dapat ditemukan melalui perhitungan berikut Bletzinger et al. (2000): {𝛾_𝛾𝜉 𝜂} = 𝐁s𝐝 (16) 𝐁s= _2𝐴1 [ 𝑏 − 𝑐 −𝐴 0 𝑐 −𝑎𝑐₂ −𝑏𝑐₂ −𝑏 𝑏𝑑₂ 𝑏𝑐₂ 𝑑 − 𝑎 0 −𝐴 −𝑑 𝑎𝑑₂ 𝑏𝑑₂ 𝑎 −𝑎𝑑₂ −𝑎𝑐₂] (17)

2.4.2. Cara 2: shape function Kriging titik segitiga linear

Dengan menggunakan shape function Kriging pada perhitungan shear gap diperoleh rumusan untuk regangan geser sbb.:

{𝛾_𝛾𝜉

𝜂} = 𝐉 −1_𝐁

DSG 1𝐁DSG 2𝐝 (18)

di mana 𝐉−1_{adalah invers dari matriks Jacobian yang diberikan oleh}

𝐉−𝟏 ₌ 1 2A[ 𝑐

−𝑏

−𝑑 𝑎 ] (19)

Matriks 𝐁_{DSG 1} adalah matriks interpolasi regangan geser dari discrete shear gap pada titik-titik nodal, diberikan oleh

𝐁_{𝐃𝐒𝐆 𝟏} = [−1 0 1 0 0 0

0 −1 0 0 0 1] (20)

Matriks 𝐁_{DSG 2} adalah matriks yang menghasilkan discrete shear gap dari perpindahan titik nodal, yaitu 𝐁_{𝐃𝐒𝐆 𝟐} = [ 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 … 0 −1 −𝑎 ∫ 𝑁₀1 1𝑑𝜉 −𝑏 ∫ 𝑁₀1 1𝑑𝜉 1 −𝑎 ∫ 𝑁₀1 2𝑑𝜉 −𝑏 ∫ 𝑁₀1 2𝑑𝜉 0 … −𝑏 ∫ 𝑁₀1 𝑛𝑑𝜉 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 … 0 −1 −𝑑 ∫ 𝑁₀1 1𝑑𝜂 −𝑐 ∫ 𝑁₀1 1𝑑𝜂 0 −𝑑 ∫ 𝑁₀1 2𝑑𝜂 −𝑐 ∫ 𝑁₀1 2𝑑𝜂 1 … −𝑐 ∫ 𝑁₀1 𝑛𝑑𝜂] (21) d adalah vektor perpindahan titik nodal.

2.4.3. Cara 3: shape function Kriging lima titik segitiga

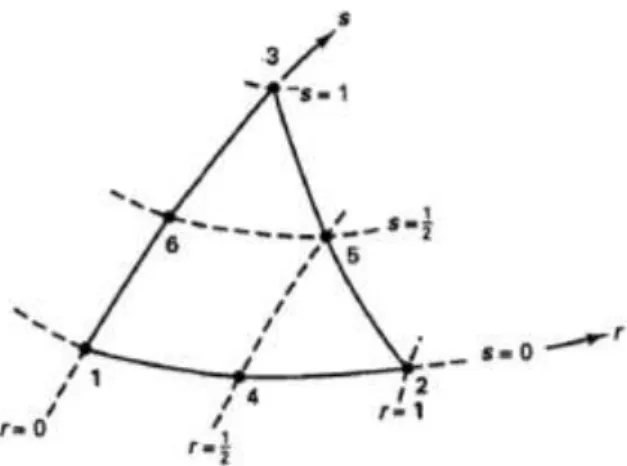
Dikarenakan adanya tambahan node pada titik tengah elemen segitiga kuadratik seperti ditunjukkan pada Gambar 6, terdapat tambahan shear gap yang harus ditinjau pada titik tambahan tersebut. Untuk metode ini, titik tambahan untuk mendefinisikan shear gap yang digunakan hanyalah titik 4 dan titik 6 dalam Gambar 6.

Gambar 6. Elemen segitiga kuadratik Sumber: Bathe (1996)

Matriks 𝐁_{DSG 1} untuk kasus ini diberikan oleh

𝐁𝐃𝐒𝐆 𝟏= [

𝑁_{𝑞 1,𝜉} 0 𝑁_{𝑞 2,𝜉} 0 𝑁_{𝑞 3,𝜉} 0 𝑁_{𝑞 4,𝜉} 0 𝑁_{𝑞 6,𝜉} 0

0 𝑁_{𝑞 1,𝜂} 0 𝑁_{𝑞 2,𝜂} 0 𝑁_{𝑞 3,𝜂} 0 𝑁_{𝑞 4,𝜂} 0 𝑁_{𝑞 6,𝜂}]

(22a) di mana tanda koma menyatakan turunan parsial terhadap ξ atau η dan Nqi, i=1,…,6, 𝑖 ≠ 5, adalah sbb.: 𝑁_{𝑞 1}= 1 − 3𝜉 − 3𝜂 + 2𝜉2_{+ 4𝜉𝜂 + 2𝜂}2 _(22b) 𝑁_{𝑞 2} = −𝜉 + 2𝜉2_{+ 2𝜉𝜂 (22c)} 𝑁_{𝑞 3} = −𝜂 + 2𝜉𝜂 + 2𝜂2 _(22d) 𝑁_{𝑞 4} = 4𝜉 − 4𝜉2 _{− 4𝜉𝜂 (22e)} 𝑁_{𝑞 6} = 4𝜂 − 4𝜂2_{− 4𝜉𝜂 (22f)}

𝐁_{𝐃𝐒𝐆 𝟐} = [ 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 … 0 −1 −𝑎 ∫ 𝑁₀1 1𝑑𝜉 −𝑏 ∫ 𝑁₀1 1𝑑𝜉 1 −𝑎 ∫ 𝑁₀1 2𝑑𝜉 −𝑏 ∫ 𝑁₀1 2𝑑𝜉 0 … −𝑏 ∫ 𝑁₀1 𝑛𝑑𝜉 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 … 0 −1 −𝑑 ∫ 𝑁₀1 1𝑑𝜂 −𝑐 ∫ 𝑁₀1 1𝑑𝜂 0 −𝑑 ∫ 𝑁₀1 2𝑑𝜂 −𝑐 ∫ 𝑁₀1 2𝑑𝜂 1 … −𝑐 ∫ 𝑁₀1 𝑛𝑑𝜂 −1 + 𝑁1(1₂, 0) −𝑎 ∫₀1/2𝑁1𝑑𝜉 −𝑏 ∫₀1/2𝑁1𝑑𝜉 𝑁2(1₂, 0) −𝑎 ∫₀1/2𝑁2𝑑𝜉 −𝑏 ∫₀1/2𝑁2𝑑𝜉 𝑁3(1₂, 0) … −𝑏 ∫₀1/2𝑁𝑛𝑑𝜉 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 … 0 −1 + 𝑁₁(0,1₂) −𝑑 ∫₀1/2𝑁₁𝑑𝜂 −𝑐 ∫₀1/2𝑁₁𝑑𝜂 𝑁₂(0,1₂) −𝑑 ∫₀1/2𝑁₂𝑑𝜂 −𝑐 ∫₀1/2𝑁₂𝑑𝜂 𝑁₃(0,1₂) … −𝑐 ∫₀1/2𝑁_𝑛𝑑𝜂_] (23)

2.5. Teori Elastisitas 3D Solids

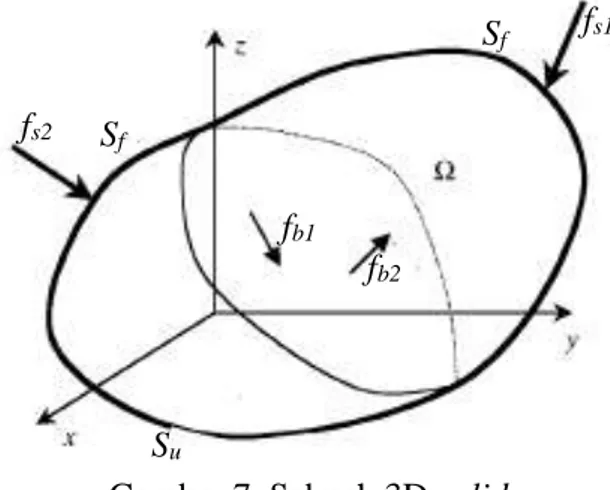
Tinjau 3D solids yang memiliki daerah volume Ωdan dibatasi oleh sebuah permukaan S. Permukaan S dibagi menjadi dua yaitu permukaan di mana terjadinya prescribed displacement disebut Su sedangkan permukaan di mana terjadinya beban luar disebut Sf, seperti didilustrasikan pada Gambar 7. Persamaan kesetimbangan 3D solids dapat ditulis dengan notasi indeks sebagai berikut:

σij.j + fbi = 0 pada seluruh daerah Ω (24) dengan essential boundary conditions:

ui = 𝑢_𝑖𝑆𝑢 pada permukaan Su (25)

dan dengan natural boundary conditions:

σij . nj = fsi pada permukaan Sf yang mengalami beban (26) Suatu 3D solids dapat dibebani body force yang terdistribusikan dalam volume Ω ataupun surface traction yang terdistribusi pada permukaan Sf.

Gambar 7. Sebuah 3D solids

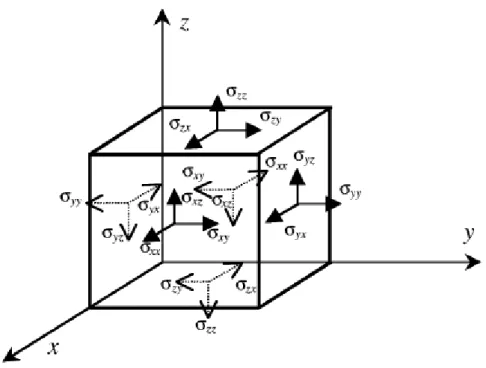
Terdapat sembilan komponen tegangan dalam ruang tiga dimensi pada suatu elemen diferensial dengan panjang dx, dy dan dz seperti pada Gambar 8. Adanya kesetimbangan momen pada pusat elemen ruang tiga dimensi, sehingga mudah disadari bahwa σxy = σyx; σxz = σzx; σzy = σyz. fs1 Sf fb2 fb1 Su fs2 _Sf

Gambar 8. Komponen tengangan dalam suatu elemen yang sangat kecil

Oleh karena itu terdapat enam nilai tegangan yang independen yang dapat dituliskan dalam bentuk matriks sebagai berikut,

σT _{= { σxx σyy σzz σxy σyz σxz} (27)}

Dengan begitu juga terdapat enam komponen regangan yang berhubungan tengangan, dapat ditulis dalam bentuk matriks sebagai berikut,

εT _{= { εxx εyy εzz εxy εyz εxz} (28)}

Komponen regangan dapat dibentuk dari turunan dari perpindahan sbb.

{ε} = { ε𝑥𝑥 ε_𝑦𝑦 ε_𝑧𝑧 ε_𝑥𝑦 ε_𝑦𝑧 ε_𝑥𝑧} = { 𝜕𝑢 𝜕𝑥 𝜕𝑣 𝜕𝑦 𝜕𝑤 𝜕𝑧 𝜕𝑢 𝜕𝑦+ 𝜕𝑣 𝜕𝑥 𝜕𝑣 𝜕𝑧+ 𝜕𝑤 𝜕𝑦 𝜕𝑤 𝜕𝑥 + 𝜕𝑢 𝜕𝑧} (29)

Dalam persamaan ini u, v, w adalah komponen perpindahan dengan arah x, y, z. Dapat disimpulkan bahwa regangan εxx, εyy, dan εzz adalah perubahan dalam panjang per satuan panjang dari elemen yang sangat kecil yang awalnya sejajar dengan sumbu x, y dan z ketika

elemen mengalami deformasi, regangan ini disebut regangan normal. Regangan εxy, εyz, dan εxz adalah perubahan pada sudut awal yang terbentuk antara dx, dy, dan dz ketika elemen mengalami deformasi, regangan ini disebut dengan regangan geser. Hubungan perpindahan dengan regangan dapat ditulis dalam bentuk matriks berikut ini:

{𝜀} = [𝐿]{𝑢} (30)

di mana [L]merupakan matriks operator diferensial, matriks yang menghubungkan regangan dengan perpindahan {𝑢} = {𝑢1 𝑢2 𝑢3}.

Persamaan konstitutif yang memberikan hubungan tegangan dan regangan dalam sebuah material kadang disebut dengan Hooke’s law. Hooke’s law untuk material anisotropik dapat ditulis dalam bentuk matriks sebagai berikut:

{𝜎} = [𝐷]{𝜀} (31)

di mana matriks [D] adalah matriks material, yang didapat melalui eksperimen. Persamaan konstitutif dapat ditulis secara eksplisit sebagai berikut:

{ 𝜎𝑥𝑥 𝜎_𝑦𝑦 𝜎_𝑧𝑧 𝜎_𝑥𝑦 𝜎𝑦𝑧 𝜎𝑥𝑧} = [ 𝐷₁₁ 𝐷11 𝐷11 𝐷₁₁ 𝐷11 𝐷₁₁ 𝐷12 𝐷₂₂ 𝐷11 𝐷₁₁ 𝑠𝑦𝑚 𝐷11 𝐷13 𝐷23 𝐷33 𝐷11 𝐷₁₁ 𝐷₁₁ 𝐷₁₄ 𝐷24 𝐷34 𝐷₄₄ 𝐷11 𝐷₁₁ 𝐷15 𝐷₂₅ 𝐷35 𝐷₄₅ 𝐷₅₅ 𝐷11 𝐷16 𝐷₂₆ 𝐷36 𝐷₄₆ 𝐷₅₆ 𝐷₆₆] = { σ𝑥𝑥 σ_𝑦𝑦 σ_𝑧𝑧 σ_𝑥𝑦 σ𝑦𝑧 σ𝑥𝑧} (32)

Dengan melakukan substitusi pada persamaan (31) dengan persamaan (30) didapatkan persamaan berikut:

{𝜎} = [𝐷][𝐿]{𝑢} (33)

BAB 3. METODE PENELITIAN

3.1. Diagram Alir Metodologi Penelitian

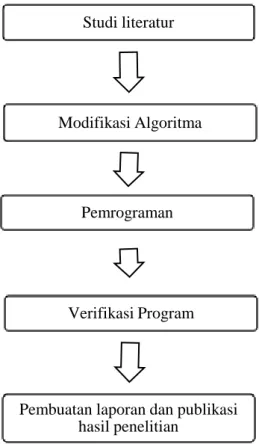
Langkah-langkah yang akan dilakukan dalam penelitian ini diperlihatkan pada bagan alir penelitian pada Gambar 9. Langkah pertama adalah studi literatur mengenai pemrograman metode elemen hingga berbasis Kriging.

Langkah kedua adalah modifikasi metode elemen hingga berbasis Kriging (MEH-K) yang sudah ada dengan penggunaan metode discrete shear gap (DSG) untuk analisis pelat Reissner-Mindlin dan modifikasi untuk analisis masalah 3D solids.

Langkah ketiga adalah penulisan / pembuatan program komputer berdasarkan algoritma yang telah dimodifikasi untuk penelitian ini. Pemrograman dilakukan dengan menggunakan program MATLAB untuk perhitungan numerik dan penampilan grafik.

Langkah keempat adalah melakukan verifikasi hasil program dengan menggunakan sejumlah benchmark problems untuk analisis pelat Reissner-Mindlin dan 3D solids. Dari hasil tersebut, dapat diambil kesimpulan mengenai penelitian dan pengembangan MEH-K ini Langkah terakhir adalah melakukan dokumentasi hasil penelitian serta publikasi pada seminar internasional dan jurnal internasional bereputasi.

Gambar 9. Diagram alir penelitian

3.2. Proses Perhitungan

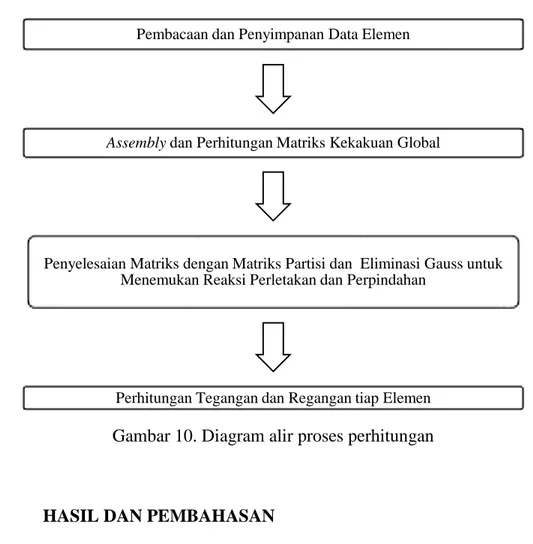
Proses perhitungan yang dilakukan dalam program ini meliputi penerapan boundary conditions dan perhitungan matriks untuk menghasilkan tegangan dan regangan pada tiap elemen. Proses perhitungan dapat dilihat pada Gambar 10.

Studi literatur

Modifikasi Algoritma

Pemrograman

Verifikasi Program

Pembuatan laporan dan publikasi hasil penelitian

Gambar 10. Diagram alir proses perhitungan

BAB 4. HASIL DAN PEMBAHASAN

4.1. Elemen Pelat Reissner-Mindlin Berbasis Kriging

Hasil dan pembahasan di sini dibatasi untuk mengevaluasi efektivitas berbagai strategi penerapan teknik DSG seperti yang diuraikan pada subbab 2.4 dalam mengatasi kesulitan shear locking, dan keakuratan berbagai alternatif penerapan teknik DSG tersebut dibandingkan dengan perumusan elemen pelat berbasis Kriging murni berdasarkan asumsi perpindahan (Wong, 2009). Penamaan berbagai alternatif metode tersebut adalah sbb.:

1. MEH-K biasa, dengan menggunakan koordinat global

2. MEH-K dengan DSG, langsung diadopsi dari Bletzinger (DSG 1)

3. MEH-K dengan DSG, menggunakan shape function Kriging pada 3 node (DSG 2) 4. MEH-K dengan DSG, menggunakan shape function Kriging pada 5 node (DSG 3)

4.1.1. Pengujian Shear Locking pada Pelat Bujursangkar dengan Perletakan Jepit

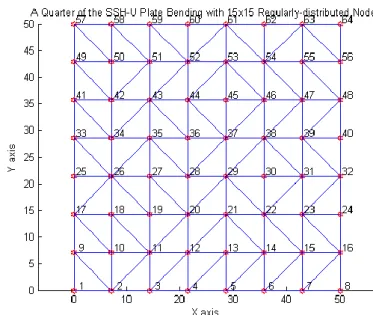
Sebuah pelat segiempat berukuran 100×100 dengan pembagian mesh seperempat bagian atas kanan pelat tersebut seperti yang diperlihatkan pada Gambar 11 digunakan untuk pengujian. Digunakan perletakan jepit untuk tumpuan di keempat sisi pelat segiempat. Properti material yang digunakan adalah E = 2,0 × 106 dan v = 0,3. Dikarenakan bentuknya

Pembacaan dan Penyimpanan Data Elemen

Assemblydan Perhitungan Matriks Kekakuan Global

Penyelesaian Matriks dengan Matriks Partisi dan Eliminasi Gauss untuk Menemukan Reaksi Perletakan dan Perpindahan

yang simetris, dapat dilakukan pengujian pada salah satu kuadrannya saja. Dilakukan pengujian pada beberapa variasi ketebalan pelat yaitu L/h = 5, 10, 100, 1000, 10000 dan 100000. Untuk pengujiannya, dicari nilai defleksi yang terjadi di titik pusat pelat.

Gambar 11. Mesh seperempat bagian kanan-atas pelat bujursangkar Sumber: Wong (2009)

Hasil normalisasi nilai yang didapat terhadap solusi eksak berdasarkan teori pelat tipis untuk masing-masing rasio L/h kemudian dibandingkan. Hasil konvergensi masing-masing metode terlihat pada Gambar 12. Terlihat bahwa dengan aplikasi DSG cara ke-1, kinerja elemen-elemen P1-1-QS, P2-2-QS, dan P3-3-QS relatif sama. Aplikasi DSG dengan cara ke-2 dapat meredakan efek shear locking, namum masih tetap belum menghilangkan shear locking. Aplikasi DSG dengan cara ke-3 tidak berhasil, hasilnya malah lebih buruk daripada perumusan MEH-K semula. Dapat disimpulkan bahwa aplikasi DSG dengan cara ke-2 merupakan cara yang paling baik dan secara perumusan konsisten dengan rumus interpolasi yang Kriging yang dipakai untuk mengaproksimasi defleksi dan rotasi.

(a)

(b)

(c)

Gambar 12. Pengujian shear locking elemen pelat berbasis Kriging: (a) linier, (b) kuadratik, dan (c) kubik, dengan berbagai cara aplikasi teknik DSG pada pelat segiempat dengan

4.1.2. Pengujian Keakuratan Elemen pada Pelat Bujursangkar dengan Perletakan Sendi Pelat bujursangkar berukuran 100 × 100 yang sama seperti pada penyelidikan shear locking digunakan untuk pengujian keakuratan berbagai alternatif aplikasi metode DSG. Properti material yang digunakan pun juga sama, namun di sini digunakan perletakan sendi sebagai tumpuan di sisi pelat. Rasio panjang terhadap ketebalan di ambil L/h=100, yang merupakan ketebalan di mana teori pelat berlaku dengan baik. Untuk menunjukkan keakuratan dari berbagai metode MEH-K-DSG ini akan digambarkan profil displacement, momen dan gaya geser dibandingkan dengan profil solusi eksak referensinya.

Hasil plot profil-profil defleksi, rotasi terhadap sumbu y, momen arah x, momen arah y dan gaya geser arah x sepanjang sumbu x (lihat Gambar 11) dapat dilihat pada Gambar 13 sampai dengan Gambar 17. Untuk plot gaya geser arah x hanya ditampilkan hasil plot nilai dari metode DSG 1 dan DSG 2 saja karena gaya geser hasil dari metode lainnya menghasilkan nilai yang terlalu berfluktuasi dari solusi eksak. Dari gambar-gambar tersebut terlihat bahwa elemen dengan DSG 1 dan DSG 2 dapat memberikan hasil-hasil yang keakuratannya untuk defleksi dan rotasi hampir sama dengan perumusan MEH-K tanpa DSG, namun sayangnya keakuratan momen lentur dari MEH-K “terganggu” dengan perumusan DSG tersebut sehingga pada beberapa titik menjadi kurang akurat dibandingkan yang dari perumusan MEH-K semula. Untuk gaya geser, ternyata maish terjadi fluktuasi meskipun sudah lebih baik daripada perumusan MEH-K semula. Terlihat secara konsisten bahwa hasil-hasil dengan DSG 2 lebih baik daripada dengan DSG 1.

(a)

(b)

(c)

Gambar 13. Plot defleksi pelat bujursangkar dengan perletakan sendi hasil analisis dengan: (a) elemen Kriging linier, (b) elemen Kriging kuadratik, (c) elemen Kriging kubik

(a)

(b)

(c)

Gambar 14. Plot rotasi y pelat bujursangkar dengan perletakan sendi hasil analisis dengan: (a) elemen Kriging linier, (b) elemen Kriging kuadratik, (c) elemen Kriging kubik

(a)

(b)

(c)

Gambar 15. Plot Mx pelat bujursangkar dengan perletakan sendi hasil analisis dengan: (a) elemen Kriging linier, (b) elemen Kriging kuadratik, (c) elemen Kriging kubik

(a)

(b)

(c)

Gambar 16. Plot My pelat bujursangkar dengan perletakan sendi hasil analisis dengan: (a) elemen Kriging linier, (b) elemen Kriging kuadratik, (c) elemen Kriging kubik

(a)

(b)

(c)

Gambar 17. Plot Qx pelat bujursangkar dengan perletakan sendi hasil analisis dengan: (a) elemen Kriging linier, (b) elemen Kriging kuadratik, (c) elemen Kriging kubik

4.2. Elemen 3D Solids Berbasis Kriging

Seperti telah diungkapkan dalam Bab 1 bahwa salah satu tujuan penelitian ini adalah mencari range paramenter korelasi yang sesuai untuk analisis benda 3D dengan MEH-K dan jumlah sampling point yang efisien untuk menghitung integral volume maupun integral permukaan yang muncul dalam persamaan diskrit MEH-K. Oleh karena itu pembahasan di sini difokuskan pada kedua hal tersebut.

4.2.1. Penyelidikan Jumlah Sampling Point yang Efisien untuk Menghitung Integral Volume Cantilever beam problem dengan beban geser parabolik di ujung (Gambar 18.(a)) digunakan untuk mempelajari perbedaan hasil dengan berbagai jumlah sampling point 1, 4, 5, 11, 15, dan 16. Balok ini dibebani gaya geser berdistribusi parabolik dengan besar total 10 satuan searah sumbu z di sisi kanan dan dijepit pada sisi kiri. Material yang digunakan adalah material isotropik dengan properti yaitu modulusYoung, E, sebesar 1000 dan Poisson`s ratio, v, sebesar 0,25. Mesh dibuat dengan bantuan software GiD, diperlihatkan pada Gambar 18 (b).

(a) (b)

Gambar 18. (a) Model cantilever beamproblem, (b) Cantilever beam dengan mesh GiD ukuran 0,5

Keakuratan hasil analisis dinilai dengan melihat relative error perpindahan arah z pada permukaan yang dibebani, Ruz, yang didefinisikan sbb.

𝑅𝑢𝑧 =𝑢𝑧

𝑎𝑝𝑝_−𝑢 𝑧𝑒𝑥𝑎𝑐𝑡

di mana 𝑢_𝑧𝑎𝑝𝑝dan 𝑢𝑧𝑒𝑥𝑎𝑐𝑡 masing-masing adalah hasil perhitungan MEH-K dan exact solution

dari perpindahan arah z pada permukaan yang dikenai beban parabola. Selain itu keakuratan hasil analisis juga dinilai dengan relative error strain energy, RU, yang didefinisikan sbb.

𝑅𝑈 =𝑅𝑈𝑎𝑝𝑝_𝑅𝑈−𝑅𝑈𝑒𝑥𝑎𝑐𝑡𝑒𝑥𝑎𝑐𝑡× 100% (35)

di mana RUapp _{dan RU}exact _{masing-masing adalah hasil perhitungan MEH-K dan exact} solution dari strain energy.

Hasil analisis dengan berbagai sampling point dalam MEH-K dengan berbagai lapisan lapisan domain of influence (DOI) dan basis polinom dengan fungsi korelasi Gauss dan quartic spline masing-masing dapat dilihat pada Tabel 1 dan 2. Dari tabel-tabel ini terlihat relativestrain energy dan perpindahan dengan menggunakan jumlah sampling point 4, 5, 11, 15 dan 16 memiliki nilai yang mirip. Agar perhitungan efisien namun keakuratannya cukup, dalam perhitungan-perhitungan selanjutnya dipilih jumlah sampling point 𝑛 = 11 untuk basis polinom kuadratik dan kubik dan n=1 untuk basis polinom linier.

Tabel 1. Hasil analisis cantilever beam dengan K-FEM berfungsi korelasi Gauss Basis Polinom Lapisan DOI Jumlah Sampling Point θ Relative Error Strain Energy

Rata - Rata Relative ErrorPerpindahan Arah z 1 4,4910 3,9567 4 4,4910 3,9567 5 4,4910 3,9567 11 4,4910 3,9567 15 4,4910 3,9567 16 4,4910 3,9567 1 3,9081 4,1766 4 1,3838 1,6061 5 1,3821 1,6037 11 1,3685 1,5896 15 1,3685 1,5896 16 1,3685 1,5896 1 6,3440 7,0826 4 1,9185 2,4560 5 1,9123 2,4465 11 1,8688 2,3951 15 1,8699 2,3971 16 1,8690 2,3955 1 4,0775 4,3938 4 1,4244 1,6534 5 1,4200 1,6473 11 1,4190 1,6482 15 1,4195 1,6486 16 1,4192 1,6483 1 6,0311 6,6305 4 1,9582 2,4183 5 1,9607 2,4169 11 1,8706 2,3194 15 1,8722 2,3216 16 1,8709 2,3199 1 7,8178 8,4426 4 2,4870 2,8888 5 2,5569 2,9516 11 2,3581 2,7460 15 2,3623 2,7509 16 2,3591 2,7472 2,2 2,2 2 3 3 3 1 3 2,2 2 2 0,7 1 1 0,2 0,7 2 1

Tabel 2. Hasil analisis pada cantilever beam dengan MEH-K berfungsi korelasi quartic spline Basis Polinom Lapisan DOI Jumlah Sampling Point θ Relative Error Strain Energy

Rata - Rata Relative ErrorPerpindahan Arah z 1 4,4910 3,9567 4 4,4910 3,9567 5 4,4910 3,9567 11 4,4910 3,9567 15 4,4910 3,9567 16 4,4910 3,9567 1 2,2078 2,5803 4 0,3983 0,0950 5 0,4609 0,1112 11 0,3250 0,0913 15 0,3157 0,0932 16 0,3227 0,0918 1 2,8653 3,4198 4 0,2297 0,6968 5 0,1698 0,6357 11 0,2865 0,7524 15 0,2982 0,7646 16 0,2893 0,7553 1 3,2520 3,6618 4 0,6664 1,0653 5 0,6042 1,0020 11 0,7301 1,1287 15 0,7396 1,1376 16 0,7324 1,1309 1 3,5867 4,0927 4 0,5655 0,9844 5 0,5154 0,9323 11 0,6376 1,0557 15 0,6478 1,0664 16 0,6401 1,0583 1 4,1183 4,5756 4 0,9752 1,3363 5 0,9285 1,2841 11 1,0416 1,3978 15 1,0523 1,4096 16 1,0442 1,4006 0,7 3 3 2 2 0,4 2 3 0,7 1 2 0,4 1 3 0,7 0,1 1 1

4.2.2. Penyelidikan Jumlah Sampling Point yang Efisien untuk Menghitung Integral Permukaan

Dalam implementasi MEH-K untuk 3D solids, selain diperlukan perhitungan integrasi volume, terutama untuk perhitungan matriks kekakuan, juga diperlukan integrasi permukaan untuk menghitung vektor gaya nodal ekuivalen akibat suatu surface traction. Untuk menyelidiki jumlah sampling point yang efisien dalam menghitung equvalent nodal load, tinjau problem yang sama seperti pada penyelidikan sebelum ini, yakni cantilever beam dengan ukuran panjang, L = 5 satuan, tinggi, D = 3 satuan dan tebal, W = 1 satuan. Tetapi dalam penyelidikan ini dilakukan mesh ulang cantilever beam dengan memberi tambahan garis lurus pada jarak 𝑥 = 2,5 yang membagi permukaan cantilever beam menjadi dua bagian. Tujuan membagi cantilever beam menjadi dua agar dapat mengambil nodal value pada jarak 𝑥 = 2,5. Gambar 19 menunjukkan hasil mesh cantilever beam oleh GiD dengan ukuran 0,553.

Gambar 19. Hasil generate mesh cantilever beam oleh GiD ukuran 0,553

Balok kantilever tersebut dianalisis dengan menggunakan berbagai jumlah sampling point. Patokan yang dipakai untuk menilai relative error dari equvalent nodal load adalah hasil analisis dengan 12 sampling point. Tabel 3 memperlihatkan besar nilai relative error dari equvalent nodal load pada MEH-K dengan parameter korelasi Gauss dan quartic spline pada berbagai basis polinom. Hasil analisis ini menujukkan bahwa 6 dan 7 sampling point sudah cukup untuk menghasilkan equvalent nodal load yang konsisten pada MEH-K. Pada basis polinom linier cukup hanya dengan 3 sampling point sudah menghasilkan nilai yang konsisten. Untuk penelitian selanjutnya dipakai 7 sampling point pada integrasi luas agar menghasilkan equvalent nodal load yang konsisten pada MEH-K.

Tabel 3 Nilai relative error dari equvalent nodal load pada MEH-K dengan parameter korelasi Gaussdan quartic spline

4.2.3. Penyelidikan Range yang Cocok untuk Parameter Korelasi pada Covariance Function Range parameter korelasi dari fungsi korelasi Gaussian dan quartic spline didapatkan dengan cara mencari batas atas dan batas bawah yang memenuhi rule of thumb yang diusulkan oleh Plengkhom & Kanok-Nukulchai, 2005. Problem yang digunakan untuk mencari range tersebut adalah 3D patch test problem yang diambil dari referensi Macneal & Harder, 1985 dan cantilever beam seperti pada penyelidikan sebelum ini (subbab 4.2.1). Patch test problem adalah berupa kubus sebesar 1 unit, menggunakan material isoptropik dengan properti 𝐸 = 1 × 106 dan 𝑣 = 0,25 (Macneal & Harder, 1985). Pembuatan mesh dilakukan dengan program GiD dan hasilnya diperlihatkan pada Gambar 20.

Maximum (%) Rata-Rata (%) 3 0,242 0,088 4 0,000 0,000 6 0,000 0,000 3 4,559 1,789 4 5,801 2,298 6 0,092 0,040 7 0,055 0,025 12 0,000 0,000 3 7,370 2,412 4 8,357 2,939 6 0,163 0,060 7 0,057 0,030 12 0,000 0,000 3 3,862 1,472 4 4,803 1,790 6 0,161 0,051 7 0,148 0,038 12 0,000 0,000 3 4,957 1,600 4 5,640 1,976 6 0,043 0,021 7 0,097 0,026 12 0,000 0,000

Relative Error Equvalent

Nodal Load pada Permukaan

yang Terkena Traction

Fungsi Korelasi Basis Polinom Lapisan DOI θ Jumlah Sampling Point untuk Integrasi Luas Gaussian dan Quartic

Spline Gaussian Quartic Spline 1 1 T he ta A da pt if s es ua i J um la h N ode da la m D O I de nga n F akt or S ka la r 0,5 2 2 3 3 2 2 3 3

Gambar 20. 3D patch test problem dengan mesh hasil GiD (ukuran 0,2)

Hasil penyelidikan batas-batas parameter korelasi θ pada kedua problem tersebut untuk MEH-K dengan fungsi korelasi Gauss dan quartic spline masing-masing diperlihatkan pada Gambar 21 dan 22. Berdasarkan grafik-grafik ini, degnan bantuan software Microsoft Excel diperoleh persamaan regresi untuk batas-batas atas dan bawah sbb:

Gambar 21. Batas atas dan batas bawah parameter korelasi θ untuk MEH-K dengan fungsi korelasi Gauss

Gambar 22. Batas atas dan batas bawah parameter korelasi θ untuk MEH-K dengan fungsi korelasi Gauss

Untuk fungsi korelasi Gaussian

𝜃 batas atas = { 0,24𝑛 − 0,76 −0,0005𝑛2 _{+ 0,1309𝑛 + 0,5999} 0,0125𝑛 + 7,775 untuk 4 ≤ 𝑛 < 14 untuk 14 ≤ 𝑛 ≤ 130 untuk 𝑛 > 130 (36)

𝜃 batas bawah = {_{0,0071𝑛 − 0,0632 untuk 𝑛 < 4}0 untuk 4 (37)

Untuk fungsi korelasi quartic spline

𝜃 batas atas = { 0,11𝑛 − 0,34 −0.0002𝑛2_{+ 0,0589𝑛 + 0,3172} 0,0125𝑛 + 2,675 untuk 4 ≤ 𝑛 < 14 untuk 14 ≤ 𝑛 ≤ 130 untuk 𝑛 > 130 (38) 𝜃 batas bawah = 0,1 (39)

Parameter korelasi dapat diaplikasikan dalam MEH-K secara adaptif sesuai jumlah node dalam DOI dengan persamaan sbb.

𝜃 = (1 − 𝑓) × 𝜃 batas atas + 𝑓 × 𝜃 batas bawah (40) di mana f adalah faktor skala dengan batas 0 ≤ 𝑓 < 1.

BAB 5. KESIMPULAN DAN SARAN

Dalam penelitian ini telah dikembangkan MEH-K untuk analisis pelat lentur (dengan teknik DSG) dan 3D solids. Kesimpulan dan saran untuk kedua bagian penelitian ini adalah sbb.

5.1. Elemen Pelat Reissner-Mindlin Berbasis Kriging

MEH-K dengan beberapa metode aplikasi DSG untuk analisis pelat Reissner-Mindlin sudah dirumuskan, diprogram dan diuji kinerjanya. Metode aplikasi ini mencakup:

1. MEH-K dengan DSG, langsung diadopsi dari Bletzinger (DSG 1)

2. MEH-K dengan DSG, menggunakan shape function Kriging pada 3 node (DSG 2) 3. MEH-K dengan DSG, menggunakan shape function Kriging pada 5 node (DSG 3) Dari hasil pengujian kinerja ini dapat disimpulkan bahwa:

1. Secara umum, fenomena shear locking belum benar-benar bisa dieliminasi dengan menerapkan ketiga metode aplikasi DSG ini. Metode DSG 2 menunjukkan hasil terbaik pada pengujian shear locking. Bahkan metode DSG 2 dapat menghasilkan nilai yang benar-benar akurat pada masalah pelat lingkaran dengan perletakan jepit, di mana metode lainnya menunjukkan fenomena shear locking.

2. Ketiga metode aplikasi DSG mampu menghasilkan plot grafik defleksi dan rotasi yang cukup baik. Sedangkan pada plot momen, terdapat beberapa fluktuasi dari nilai eksak yang sama pada tiap metode DSG. Perbedaan yang terlihat terjadi pada plot gaya geser, di mana metode DSG 3 berfluktuasi cukup jauh dibandingkan lainnya.

Metode aplikasi DSG 2 sementara dapat digunakan untuk mengurangi pengaruh fenomena shear locking, namun belum sampai tahap mengeliminasi secara keseluruhan. Penulis menyarankan agar metode DSG ini dapat dimodifikasi lebih lanjut untuk usaha mengeliminasi shear locking pada analisis pelat Reissner-Mindlin. Salah satunya dengan menggunakan interpolasi Kriging pada perumusan matriks BDSG 1, di mana sebelumnya hanya digunakan shape function linear atau kuadratik saja. Selain itu, sebagai alternatif dapat ditinjau pula metode eliminasi shear locking dengan perumusan mixed variational method (Hale & Baiz, 2012).

5.2. Elemen 3D Solids Berbasis Kriging

MEH-K dengan beberapa metode aplikasi DSG untuk analisis pelat Reissner-Mindlin sudah dirumuskan, diprogram dan diuji kinerjanya. Metode aplikasi ini mencakup:

1. Dari penyelidikan jumlah sampling point yang efisien pada MEH-K 3D solids didapati bahwa 11 sampling point untuk integrasi volume dan 7 sampling point untuk integrasi surface traction merupakan jumlah sampling point yang sudah cukup akurat.

2. Dari penyelidikan parameter korelasi, θ, diperoleh range parameter yang cocok untuk analisis 3D solids. Berdasarkan range ini diusulkan rumus-rumus parameter korelasi sebagai fungsi dari jumlah nodes dalam suatu domain of influencing nodes, baik untuk fungsi korelasi Gauss maupun quartic spline.

3. Pada hasil-hasil analisis terlihat fungsi korelasi quartic spline menghasilkan nilai yang lebih stabil dan baik daripada fungsi korelasi Gaussian.

4. Hasil-hasil pengujian memperlihatkan bahwa MEH-K 3D solids dapat memberikan solusi yang sangat akurat dan distribusi tegangan yang cukup halus. MEH-K 3D solids dengan basis polinom kuadratik sudah dapat menyelesaikan masalah dengan cukup akurat.

BAB 6. RENCANA TAHAPAN BERIKUTNYA

Rencana tahapan penelitian selanjutnya untuk pengembangan MEH-K adalah sbb.

6.1. Elemen Pelat Reissner-Mindlin Berbasis Kriging

MEH-K dengan teknik DSG untuk analisis pelat Reissner-Mindlin ternyata tidak dapat sepenuhnya menghilangkan shear locking dan menyebabkan hasil-hasil momen lentur dan momen puntir sedikit berfluktuasi. Akhir-akhir ini Hale & Baiz (2012) menyajikan perumusan berdasarkan suatu mixed variational form untuk menghasilkan meshfree method yang bebas locking untuk pelat Reissner-Mindlin berdasarkan fungsi basis maximum-entropy. Teknik ini akan dicoba dalam konteks MEH-K untuk menghilangkan shear locking.

Dengan demikian rencana penelitian selanjutnya adalah pengembangan elemen pelat Reissner-Mindlin berbasis Kriging dengan mixed variational method.

6.2. Elemen 3D Solids Berbasis Kriging

Serangkaian pengujian numerik memperlihatkan bahwa elemen K-Solids dengan Kriging berbasis kuadratik dan dua lapis elemen merupakan elemen yang paling efisien. Elemen ini akan dikembangkan lagi untuk analisis dinamik getaran bebas.

DAFTAR PUSTAKA

Bathe, K. J. (1996). Finite Element Procedures. New Jersey: Prentice-Hall. Retrieved from http://www.amazon.com/Finite-Element-Procedures-K-J-Bathe/dp/097900490X Bletzinger, K.-U., Bischoff, M., & Ramm, E. (2000). A unified approach for

shear-locking-free triangular and rectangular shell finite elements. Computers & Structures, 75(3), 321–334. doi:10.1016/S0045-7949(99)00140-6

Cook, R. D., Malkus, D. S., Plesha, M. E., & Witt, R. J. (2002). Concepts and Applications of Finite Element Analysis (4th ed.). John Wiley & Sons, Ltd.

Felippa, C. A. (2013). Introduction To Finite Element Methods (ASEN 5007) Course Material. Retrieved October 1, 2013, from

http://www.colorado.edu/engineering/cas/courses.d/IFEM.d/

Hale, J. S., & Baiz, P. M. (2012). A locking-free meshfree method for the simulation of shear-deformable plates based on a mixed variational formulation. Computer Methods in Applied Mechanics and Engineering, 241-244, 311–322. doi:10.1016/j.cma.2012.06.010 Hutton, D. V. (2004). Fundamentals of Finite Element Analysis. McGraw-Hill Higher

Education. Retrieved from

http://books.google.com/books/about/Fundamentals_of_Finite_Element_Analysis.html?i d=QEDDjwEACAAJ&pgis=1

Logan, D. L. (2007). A First Course in the Finite Element Method (4th ed.). Toronto: Nelson. Macneal, R. H., & Harder, R. L. (1985). A Proposed Standard Set of Problems to Test Finite

Element Accuracy. Finite Elements in Analysis and Design, 1(1), 3–20. doi:http://dx.doi.org/10.1016/0168-874X(85)90003-4

Olea, R. A. (1999). Geostatistics for Engineers and Earth Scientistics. Boston: Kluwer Academic Publishers. Retrieved from

http://books.google.co.id/books/about/Geostatistics_for_Engineers_and_Earth_Sc.html?i d=bKoD2mM0RHUC&redir_esc=y

Plengkhom, K., & Kanok-Nukulchai, W. (2005). An Enhancement of Finite Element Method with Moving Kriging Shape Functions. International Journal of Computational

Methods, 02(04), 451–475. doi:10.1142/S0219876205000594

Sommanawat, W. (2010). Kriging-based Finite Element Method for Material Discontinuities and Multiscale Simulation. Asian Institute of Technology.

Sommanawat, W., & Kanok-Nukulchai, W. (2009). Multiscale simulation based on kriging based finite element method. Interaction and Multiscale Mechanics, 2(4), 387–408. Retrieved from

http://technopress.kaist.ac.kr/?page=container&journal=imm&volume=2&num=4# Tongsuk, P., & Kanok-Nukulchai, W. (2004). Further Investigation of Element-free Galerkin

Method using Moving Kriging Interpolation. International Journal of Computational Methods, 01(02), 345–365. doi:10.1142/S0219876204000162

Wong, F. T. (2009). Kriging-based Finite Element Method for Analyses of Plates and Shells. Asian Institute of Technology, Pathumthani.

Analyses of Reissner-Mindlin plates. In Proceedings of the Tenth East-Asia Pacific Conference on Structural Engineering and Construction, Emerging Trends: Keynote Lectures and Symposia, (pp. 509–514). Bangkok: Asian Institute of Technology. Wong, F. T., & Kanok-Nukulchai, W. (2006b). On Alleviation of Shear Locking in the

Kriging-Based Finite Element Method. In Proceedings of International Civil

Engineering Conference “Towards Sustainable Engineering Practice” (pp. 39–47). Surabaya: Petra Christian University.

Wong, F. T., & Kanok-Nukulchai, W. (2008). A Kriging-based Finite Element Method for Analyses of Shell Structures. In Proceedings of the Eighth World Congress on

Computational Mechanics and the Fifth European Congress on Computational Methods in Applied Sciences and Engineering (p. a1247). Venice: IACM and ECCOMAS. Wong, F. T., & Kanok-Nukulchai, W. (2009). On the Convergence of the Kriging-based

Finite Element Method. International Journal of Computational Methods, 06(01), 93– 118. doi:10.1142/S0219876209001784

Wong, F. T., & Sulistio, A. (n.d.). Kriging-based Timoshenko Beam Element with the Discrete Shear Gap Technique to Eliminate the Shear Locking.

Wong, F. T., & Syamsoeyadi, H. (2011). Kriging-based Timoshenko Beam Element for Static and Free Vibration Analyses. Civil Engineering Dimension, 13(1), 42–49. Retrieved from http://puslit2.petra.ac.id/ejournal/index.php/civ/article/view/18107 Zienkiewicz, O. C., & Taylor, R. L. (2000a). The Finite Element Method, Volume 1: The

Basis (Fifth Edit.). Massachusetts: Butterworth-Heinemann.

Zienkiewicz, O. C., & Taylor, R. L. (2000b). The Finite Element Method, Volume 2: Solid Mechanics (Fifth edit.). Oxford: Butterworth-Heinemann.

LAMPIRAN:

Instrumen Penelitian

Luaran dan instrumen penelitian ini adalah:

1. Program komputer dalam Matlab (Matlab codes) untuk mengeksekusi analisis statik linier 3D solids dengan MEH-K.

2. Program komputer dalam Matlab untuk mengeksekusi analisis statik linier pelat Reissner-Mindlin dengan MEH-K yang dirumuskan dengan berbagai aplikasi teknik DSG.

Susunan Organisasi Tim Peneliti dan Pembagian Tugas

No Nama NIP/NIDN Bidang Ilmu

Alokasi Waktu (jam/minggu)

Uraian Tugas

1 Wong Foek Tjong 00034 / 0720036901 Mekanika Komputasi 2.5 Mengkoordinasi tim peneliti Studi literatur dan penyusunan algoritma program 2 Januar Budiman 09011 / 0701015503 Mekanika Komputasi, Fincancial Engieering 0.5 Memberikan masukan-masukan selama penelitian Proofreading publikasi penelitian

Biodata Ketua Peneliti A. Identitas Diri

1 Nama lengkap (dengan gelar) Wong Foek Tjong, Ph.D. 2 Jenis Kelamin Laki-laki

3 Jabatan Fungsional Lektor 4 NIP/NIK/Identitas Lainnya 00034

5 NIDN 0720036901

6 Tempat dan Tanggal Lahir Bandung, 20 Maret 1969

7 E-mail wftjong@petra.ac.id

8 Nomor Telepon/HP 031-8430578 / 081-322052946

9 Alamat Kantor Program Studi Teknik Sipil, Universitas Kristen Petra, Jl. Siwalankerto 121-131

10 Nomor Telepon/Faks 031-2983391 / 031-2983392 11 Matakuliah yang Diampu 1. Metode Elemen Hingga

2. Matematika I 3. Matematika II

B. Riwayat Pendidikan

S-1 S-2 S-3

Nama Perguruan Tinggi Universitas Katolik Parahyangan, Bandung

Institut Teknologi Bandung

Asian Institute of Technology, Thailand Bidang Ilmu Teknik Sipil Rekayasa Struktur Structural Engineering

Tahun Masuk - Lulus 1988-1994 1995-1998 2003-2009

Judul Skripsi/Tesis/Disertasi Analisis Dinamik Struktur Berderajat Kebebasan Banyak Terhadap Beban acak Ergodik

Kontrol Vibrasi Aktif Struktur Menggunakan Observer Jaringan Saraf Tiruan

Kriging-based Finite Element Method for Analyses of Plates and Shells

Nama Pembimbing/Promotor Paulus Kartawijaya Herlien Dwi Setio Worsak Kanok-Nukulchai

C. Pengalaman Penelitian dalam 5 Tahun Terakhir

(Bukan skripsi, Tesis, maupun Disertasi)

No. Tahun Judul Penelitian

Pendanaan

Sumber *) _{Jumlah (Juta Rp.)} 1 2009 Metode elemen hingga berbasis Kriging untuk

analisis statik dan getaran bebas balok Timoshenko

Sendiri 3,000,000 2 2009 Pengujian elemen-elemen cangkang dalam

commersial software SAP2000

Sendiri 3,000,000 3 2011 Pengujian elemen-elemen cangkang dalam

commersial software SAP2000 untuk analisis nonlinier geometri

Sendiri 3,000,000 4 2012 Pengembangan jaring elemen segitiga regangan

konstan yang adaptif

balok Timoshenko berbasis Kriging dan aplikasinya untuk analisis stabilitas struktur 6 2013 Pengujian elemen cangkang berbasis Kriging

untuk menganalisis cangkang yang tebalnya bervariasi

Sendiri 3,000,000 7 2013 Pengembangan website untuk pembelajaran

metode kekakuan langsung pada struktur rangka bidang dua dimensi

LPPM UK Petra

3,000,000 8 2014 Pengembangan website untuk pembelajaran

metode elemen hingga untuk analisis plane stress/ plane strain

LPPM UK Petra

3,000,000 9 2014 Pengujian elemen-elemen cangkang dalam

commersial software Abaqus untuk analisis linier dan nonlinier geometri

Sendiri 3,000,000 10 2014 Studi elemen membran dengan derajat

kebebasan rotasi

Sendiri 3,000,000 11 2015 Kajian Berbagai Metode Integrasi Langsung

untuk Analisis Dinamis

Sendiri 3,000,000 12 2015 Pengembangan Elemen Discrete

Kirchhoff-Mindlin Triangle untuk Analisis Getaran Bebas dan Tekuk Pelat

Sendiri 3,000,000 13 2015 Pengembangan Elemen Discrete

Kirchhoff-Mindlin Quadrilateral untuk Analisis Tekuk Pelat

Sendiri 3,000,000

D. Pengalaman Pengabdian kepada Masyarakat dalam 5 Tahun Terakhir

No. Tahun Judul Pengabdian kepada Masyarakat Pendanaan

Sumber *) _{Jumlah (Juta Rp.)} 1 2010 Usulan rehabilitasi gedung gereja GPIB genta

kasih

Universitas Kristen Petra

- 2 2011 Memberikan lokakarya pengajaran matematika

kepada guru-guru SMA Petra

Universitas Kristen Petra

2,000,000 3 2013 Memberikan lokakarya pengajaran matematika

kepada guru-guru SMA Petra

Universitas Kristen Petra

2,000,000 4 2014 Memberikan persiapan matematika teknik untuk

lulusan SMA

Universitas Kristen Petra

2,000,000 5 2015 Memberikan persiapan matematika teknik untuk

lulusan SMA

Universitas Kristen Petra

2,000,000 *) _{Tuliskan sumber pendanaan, baik dari skema pengabdian kepada masyarakat DIKTI maupun dari sumber} lainnya

E. Publikasi Artikel Ilmiah dalam Jurnal dalam 5 Tahun Terakhir

No Judul Artikel Ilmiah Nama Jurnal Volume/Nomor/Tahun 1 A Break-Through Enhancement of FEM using

Node-based Kriging Interpolation

IACM Expressions 23/ 2008 2 On the Convergence of the Kriging-based Finite

Element Method International Journal of Computational Methods 6 / 2009

3 Kriging-based Finite Element Method: Element-by-element Kriging Interpolation

Civil Engineering Dimension

11 / 2009 4 Kriging-based Timoshenko Beam Element for

Static and Free Vibration Analyses

Civil Engineering Dimension

F. Pemakalah Seminar Ilmiah (Oral Presentation) dalam 5 Tahun Terakhir

No Nama Pertemuan Ilmiah/Seminar

Judul Artikel Ilmiah Waktu dan Tempat

1 The Eighth World Congress on Computational Mechanics (WCCM8) and the Fifth European Congress on Computational Methods in Applied Sciences and Engineering

A Kriging-based Finite Element Method for Analyses of Shell Structures

30 June-4 July 2008, Venice, Italy

2 The First Indonesian Structural Engineering and Materials Symposium

A Breakthrough Enhancement of FEM using Kriging Interpolation

17-18 November 2011, Bandung

3 The Sixth Civil Engineering Conference in Asian Region and Annual HAKI Conference

Kriging-based Finite Element Methods for Analyses of Shear Deformable Beams and Plates

20-22 August 2013, Jakarta

4 The Fifth International Conference of Euro-Asia Civil Engineering Forum

Testing of Kriging-based Finite Element to Shell Structures with Varying Thickness

15-18 September 2015, Surabaya

G. Karya Buku dalam 5 Tahun Terakhir

No Judul Buku Tahun Jumlah

Halaman

Penerbit 1

2

H. Penghargaan dalam 10 Tahun Terakhir (Dari Pemerintah, Asosiasi atau Institusi Lainnya)

No Jenis Penghargaan Institusi Pemberi Penghargaan Tahun 1 The Best Student Paper Award International Association for

Computational Mechanics

2007

Surabaya, 21 Juli 2016 Ketua peneliti,